Spatial patterning of excitatory and inhibitory neuropil territories during spinal circuit development
Funding information: An NIH NINDS K01NS04820001 award, University of Miami Provost Award and start-up funds from the University of Miami to JED and a Travel Fellowship from the Company of Biologist to QY supported this research.
Abstract
To generate rhythmic motor behaviors, both single neurons and neural circuits require a balance between excitatory inputs that trigger action potentials and inhibitory inputs that promote a stable resting potential (E/I balance). Previous studies have focused on individual neurons and have shown that, over a short spatial scale, excitatory and inhibitory (E/I) synapses tend to form structured territories with inhibitory inputs enriched on cell bodies and proximal dendrites and excitatory inputs on distal dendrites. However, systems-level E/I patterns, at spatial scales larger than single neurons, are largely uncharted. We used immunostaining for PSD-95 and gephyrin postsynaptic scaffolding proteins as proxies for excitatory and inhibitory synapses, respectively, to quantify the numbers and map the distributions of E/I synapses in zebrafish spinal cord at both an embryonic stage and a larval stage. At the embryonic stage, we found that PSD-95 puncta outnumber gephyrin puncta, with the number of gephyrin puncta increasing to match that of PSD-95 puncta at the larval stage. At both stages, PSD-95 puncta are enriched in the most lateral neuropil corresponding to distal dendrites while gephyrin puncta are enriched on neuronal somata and in the medial neuropil. Significantly, similar to synaptic puncta, neuronal processes also exhibit medial-lateral territories at both developmental stages with enrichment of glutamatergic (excitatory) processes laterally and glycinergic (inhibitory) processes medially. This establishment of neuropil excitatory-inhibitory structure largely precedes dendritic arborization of primary motor neurons, suggesting that the structured neuropil could provide a framework for the development of E/I balance at the cellular level. J. Comp. Neurol. 525:1649–1667, 2017. © 2016 Wiley Periodicals, Inc.
1 INTRODUCTION
Rhythmic motor behaviors, such as breathing, walking, and swimming, require coordination between excitatory and inhibitory neurotransmission (Goulding, 2009). During the development of spinal circuits, a balance between excitation and inhibition (E/I balance) is achieved even as new neurons exit the cell cycle and integrate into these circuits (Brustein et al., 2003b). Disrupting this E/I balance can result in seizures that are a common symptom in human neurodevelopmental disorders, such as autism, startle disease, and glycine encephalopathy (Eichler & Meier, 2008; Ganser & Dallman, 2009; Harvey, Topf, Harvey, & Rees, 2008; Kozol et al., 2016; Ogino & Hirata, 2016). Previous studies have shown that excitatory and inhibitory synapses often form distinct territories on postsynaptic dendrites (Gulyás, Megías, Emri, & Freund, 1999; Megias, Emri, Freund, & Gulyas, 2001), and that E/I balance can be impacted by the relative distribution of excitatory and inhibitory synapses (Liu, 2004). These studies, however, have focused on dendritic branches of single neurons, while E/I balance is a phenomenon that is observed and maintained not only at the level of individual neurons but also globally at the level of neural circuits (Borodinsky et al., 2004; Knogler, Liao, & Drapeau, 2010). Therefore, to further understand E/I balance in the spinal locomotory circuits, we investigate the distributions of excitatory and inhibitory synapses and processes in the spinal neuropil at the systems level.
In the spinal cord, neuronal somata in the medial cord are flanked by lateral neuropils that are enriched in both excitatory and inhibitory synapses (Tripodi & Arber, 2012). While the types of neurons in spinal circuits are well characterized, the organization of the spinal neuropil has received much less attention. Despite lacking an obvious layering seen in other neuropils like that of the optic tectum (Baier, 2013), previous studies have shown swimming speed and birth order-related organization of interneuron processes along the medial-lateral (M-L) axis of the zebrafish spinal neuropil (McLean & Fetcho, 2009; McLean, Masino, Koh, Lindquist, & Fetcho, 2008; Kinkhabwala et al., 2011). Here, we set out to map excitatory and inhibitory synapses and processes along this spinal neuropil M-L axis to provide insights into how E/I balance is established and maintained in motor circuits.
The zebrafish (Danio rerio) spinal circuits have some unique characteristics that lend themselves to the study of neural circuit development. These circuits consist of a similar variety of neuron types as those of mammals but have fewer neurons per type (Goulding, 2009), simplifying analysis. These neurons are quite well studied at the level of both physiological connectivity and their role in locomotory behaviors providing critical context for this study (Liao & Fetcho, 2008; McLean & Fetcho, 2009; McLean et al., 2008; Satou et al., 2009, 2013). Furthermore, stereotyped rhythmic motor behaviors can be used as direct readouts for E/I balance (Abrams et al., 2015; Brustein et al., 2003b; Burgess & Granato, 2007; Ganser et al., 2013; Kozol et al., 2015). To test whether excitatory and inhibitory synapses and processes form different territories at the systems level, we quantified their distributions in the zebrafish spinal neuropil at two qualitatively distinct developmental stages: 48 hrs postfertilization (hpf), a late embryonic stage characterized by rapid neurogenesis, synaptogenesis, and simple behaviors, and 120 hpf, a larval stage when most neurons are integrated into motor circuits supporting a larger repertoire of rhythmic motor behaviors (Brustein, Marandi, Kovalchuk, Drapeau, & Konnerth, 2003a; Higashijima, Mandel, & Fetcho, 2004). To visualize excitatory and inhibitory synapses, we used antibodies against two postsynaptic scaffolding proteins that commonly serve as proxies for stabilized synapses: anti-post-synaptic density 95 (PSD-95) for excitatory synapses and anti-gephyrin for inhibitory synapses (Craig, Banker, Chang, McGrath, & Serpinskaya, 1996; Meyer & Smith, 2006; Niell, Meyer, & Smith, 2004). To quantify spatial distributions of excitatory and inhibitory synapses across the neuropil, we adopted a statistical program from plant ecology (Wiegand & Moloney, 2004, 2014). In addition, we also analyzed glutamatergic and glycinergic neuronal processes along the M-L axis of the spinal cord. To understand how this M-L pattern is associated with the growth of laterally extending postsynaptic neuronal dendrites in the neuropil, we tracked dendritic morphology of caudal primary motor neurons during development. Such an analytic strategy allowed us to show that motor neuron dendrites grow into a systems-level structure of laterally enriched PSD-95-positive puncta/glutamatergic processes and medially enriched gephyrin-positive puncta/glycinergic processes as the spinal cord circuits achieve E/I balance.
2 MATERIALS AND METHODS
2.1 Fish care and embryo rearing
Experiments were conducted on offspring from Danio rerio wild-type strains AB, Tubingen, and BWT (a fish store strain from Long Island) as well as transgenic lines Tg(vglut2a:dsred) and Tg(glyt2:gfp) (McLean, Fan, Higashijima, Hale, & Fetcho, 2007; Miyasaka et al., 2009; Satou et al., 2013). Zebrafish were maintained on a 14-hr light and 10-hr dark cycle at 28.5 °C and fed twice daily. Fertilized eggs were obtained by natural crossing after removing a divider at first light. Embryos were raised in glass petri dishes with system water at 28.5 °C in an incubator with the same light/dark cycle, and staged according to Kimmel, Ballard, Kimmel, Ullmann, and Schilling (1995). Zebrafish embryos and larvae were collected between 24 and 120 hpf. All animal protocols were approved by the Institutional Animal Care and Use Committee of University of Miami.
2.2 Antibody characterization
Antibodies used in this study are summarized in Table 1.
| Antibody | Immunogen | Manufacturer, Cat. #, RRID, host species | Concentration used |
|---|---|---|---|
| Primary | |||
| Anti-gephyrin | Purified rat gephyrin (Epitope: phosphorylation at Ser-270 and Thr-276) |
Synaptic Systems Cat.# 147011 RRID: AB_887717mouse IgG1 monoclonal |
1:500 |
| Anti-postsynaptic density 95 (PSD-95) | Recombinant rat PSD-95 |
EMD Millipore Corporation Cat.# MAB1596 RRID: AB_2092365mouse IgG2a monoclonal |
1:500 |
| Secondary | |||
| IRDye 800CW anti-mouse | Mouse IgG |
LI-COR Biosciences Cat.# 926-32210 RRID: AB_621842goat polyclonal |
1:12,000 |
| Alexa 488-conjugated anti-mouse IgG | Mouse IgG |
Molecular Probes Cat.# A-11029 RRID: AB_2534088goat polyclonal |
1:2,000 |
| Alexa 568-conjugated anti-mouse IgG2a | Mouse IgG2a |
Molecular Probes Cat.# A-21134 RRID:AB_2535773goat polyclonal |
1:2,000 |
| Alexa 488-conjugated anti-mouse IgG1 | Mouse IgG1 |
Molecular Probes Cat.# A-21121 RRID: AB_141514goat polyclonal |
1:2,000 |
A gephyrin antibody (Synaptic Systems, Göttingen, Germany, RRID: AB_887717) was used to label inhibitory postsynapses. The specificity of this gephyrin antibody in zebrafish was verified with Western blot (Figure 1a). Briefly, whole-cell extracts were prepared from 72 hpf zebrafish larvae. De-yolked larvae were homogenized in 2x SDS sample buffer (120 mM Tris base, 3.3% SDS, 5% β-mercaptoethanol; 2 µl for each larva) in EZ-Grind resin tubes with matching pestles (Geno Technology, Maryland Heights, MO). The tubes were then boiled for 10 min and centrifuged at 10,000 × g for 5 min before collecting the supernatant. Protein equivalent to 17 zebrafish larvae was loaded per lane and separated by 7.5% (w/v) SDS-PAGE and blotted onto nitrocellulose membrane (Bio-Rad, Hercules, CA). IRDye 800CW anti-mouse (1:12,000, LI-COR Biosciences, Lincoln, NE, RRID: AB_621842) was used as the secondary antibody. The blot was scanned with an Odyssey imager (LI-COR Biosciences) to detect fluorescent protein bands. This gephyrin antibody has also been used in a previous study for labeling inhibitory synapses in zebrafish and revealed a punctate pattern representing individual inhibitory postsynapses that were shown to colocalize with the glycine receptor (Ganser et al., 2013).
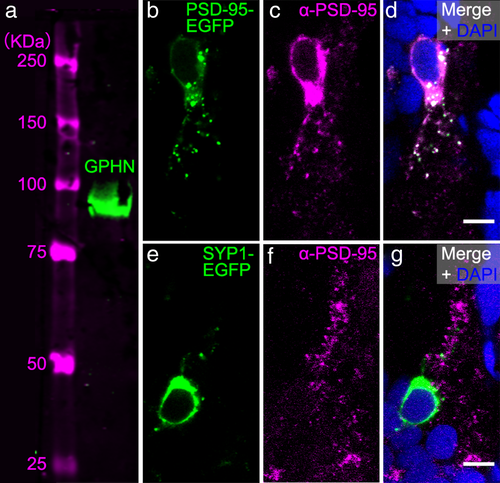
Commercially available antibodies for gephyrin (GPHN) and postsynaptic density 95 (PSD-95) recognize these proteins in zebrafish. (a) Western blot of a protein sample from 72 hpf larvae labeled with GPHN antibody reveals a single ∼93 kilodalton (kDa) green band. Magenta bands to the left show protein ladder with sizes indicated. (b–d) To test whether the PSD-95 antibody would recognize zebrafish PSD-95 protein, we overexpressed zebrafish PSD-95-EGFP fusion protein (green, b) and immunostained preps with PSD-95 antibody (α-PSD-95, magenta, c). PSD-95 antibody staining overlaps with PSD-95-EGFP as shown in the overlay with the DAPI-labelled nuclei (blue, d). (e-g) To further test the specificity of PSD-95 antibody, we overexpressed zebrafish synaptophysin 1 (SYP1)-EGFP fusion protein (green, e) and immunostained preps with PSD-95 antibody (magenta, f). PSD-95 antibody staining in the magenta channel fails to overlap with SYP1-EGFP as shown in the overlay with DAPI (g). Images in (b–g) are zoomed-in views of EGFP-expressing cell bodies from transverse-sections of 72 hpf zebrafish spinal cord. Scale bar, 5 µm
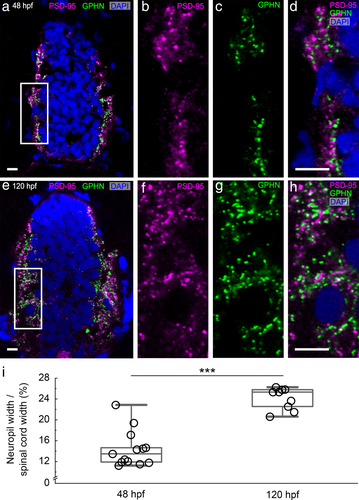
Antibody staining against postsynaptic density 95 (PSD-95) and gephyrin (GPHN) labels individual excitatory and inhibitory postsynapses. (a–h) Transverse sections through fast-frozen 48 hpf embryos (a–d) and 120 hpf larvae (e–h) were stained for excitatory PSD-95 (magenta) and inhibitory GPHN (green) postsynaptic scaffolding proteins. DAPI labels nuclei (blue). Representative images for each stage are displayed as groupings of four images. The leftmost image (a, e) gives a low magnification view of the full spinal cord with the regions boxed in white magnified in the subsequent three images (b–d, f–h). Scale bar, 5 µm. (i) A box plot shows that the percentage of the spinal cord width occupied by each lateral neuropil region increases from 48 to 120 hpf. The box plot shows the median (the line inside the boxes), the first and the third quartiles (the lower and upper boundaries of the boxes) and the range (the whiskers below and above the boxes) for samples at each stage. Each open circle represents data from one transverse section of a single zebrafish embryo or larva. Asterisks indicate statistical significance (Mann–Whitney U test, ***p ≤ .001)
A PSD-95 antibody (EMD Millipore Corporation, Billerica, MA, RRID: AB_2092365) was used to label excitatory postsynapses (Fong, Rao, Crump, & Craig, 2002). This antibody does not work in Western blot with zebrafish protein samples (our unpublished data). Therefore, to test the utility of this antibody for immunohistochemistry, we overexpressed either zebrafish PSD-95 protein fused with enhanced green fluorescent protein (PSD-95-EGFP) using acetylated tubulin promotor driving Gal4 (actub:Gal4) and UAS:PSD-95-EGFP plasmids (Niell et al., 2004), or a zebrafish presynaptic protein synaptophysin 1 fused with EGFP using actub:Gal4 and UAS:SYP1-EGFP plasmids (Meyer & Smith, 2006), respectively, in zebrafish embryos (Figure 1b–g). Plasmid DNAs were prepared using Qiagen Miniprep kits (Qiagen, Valencia, CA). The PSD-95 or SYP1 plasmid was co-injected with the Gal4 plasmid at a 1:1 ratio and total concentration of 30 ng/µl in 1x Hanks’ balanced salt solution (GIBCO, Thermo Fisher Scientific, Rockford, IL) into 1–4 cell stage wild-type zebrafish embryos. Injected embryos were raised in glass petri dishes with system water until 72 hpf and were sorted for GFP-expressing spinal neurons. Sorted larvae were then anesthetized, fixed, cryosectioned, immunostained and imaged as described in the next subsection.
2.3 Immunohistochemistry of postsynaptic scaffolding proteins
Cryosectioning and antibody staining of wild-type zebrafish embryos at 48 hpf and larvae at 120 hpf were performed as previously described (Ogino et al., 2011). Briefly, zebrafish embryos or larvae anesthetized in 0.02% 3-aminobenzoic acid ethyl ester (MS222, Sigma-Aldrich, St. Louis, MO) were embedded in O.C.T. compound (Tissue-Tek, Sakura, Torrance, CA) and gradually frozen in liquid nitrogen. Thirty micrometer-thick transverse sections from the middle of the fish trunk (within five segments of the anus) were then collected on a cryostat (CM-1850, Leica, Wetzlar, Germany) at −25 μm and mounted on poly L-lysine coated slides (Newcomer Supply, Middleton, WI) prior to a 10-min fixation in 4% formaldehyde (diluted from 16%, Pierce, Thermo Fisher Scientific). Sections were immunostained with anti-PSD-95 (mouse IgG2a, 1: 500) and anti-gephyrin (mouse IgG1, 1: 500; Table 1). Staining was carried out using the Sequenza slide staining system (Thermo Fisher Scientific). Alexa 568-conjugated anti-mouse IgG2a (1:2,000) and Alexa 488-conjugated anti-mouse IgG1 (1:2,000) were used as secondary antibodies (Table 1). Stained sections were mounted in Vectashield/DAPI (Vector Laboratories, Burlingame, CA). Images were captured on a confocal microscope (TCS SP5, Leica) using a 1.4 NA 63 × oil objective (Leica). Images were acquired at 0.08 × 0.08 × 0.4 µm voxel size.
2.4 Identification and counting of synapses
Confocal images were processed using Image J (NIH, RRID: nif-0000-30467). To avoid the impact of variation along the anterior-posterior axis, we analyzed PSD-95 and gephyrin puncta in three images (one each near the top, the middle, and the bottom of the stack) from a representative z-stack in each fish. A z-stack was considered representative when it fulfilled the following criteria: (1) the stack was taken within five segments from the anus along the anterior-posterior axis, (2) the tissue was intact, and (3) the section in the stack was well-oriented with respect to both anterior-posterior and dorsal-ventral axes. When multiple z-stacks met these criteria for a single fish, then the stack with the best signal-to-noise ratio was chosen for analysis. Measurements from these three images were averaged and these averaged values were then used to calculate the mean and the standard error of the mean for a given sample and to conduct statistical tests between samples. Image brightness and contrast were adjusted to maximize visibility of synaptic puncta and reduce background noise before using a customized Matlab (Math Works, Natick, MA, RRID: nlx_153890) program to identify, localize and count PSD-95 and gephyrin puncta as described in previous studies (Ganser et al., 2013; Morgan, Schubert, & Wong, 2008; Soto et al., 2011). Briefly, the Matlab program first thresholded the image iteratively by sampling every other gray value between 0 and 255, identifying local peaks in intensity. Each peak represented the center of a punctum. Only puncta with diameters ranging from 0.15 to 2 µm were counted. Adjacent puncta were separated according to the positions of their peaks. Then, all possible puncta were filtered according to their peak intensity, average intensity, size, and internal contrast (the difference between the highest and lowest intensities within a given punctum, which becomes more stringent as its filtering value increases). The filtering criteria were adjusted for each image by comparing the filtered puncta to the original image to optimally separate the actual puncta and false-positive selections (Figure 3). The final outputs of this Matlab program provided the numbers of PSD-95 and gephyrin puncta as well as the spatial coordinates of each punctum in each transverse-section of the spinal cord.
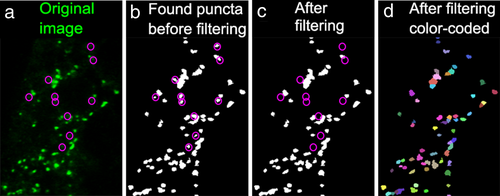
The puncta-finding Matlab program filters synaptic puncta from background. From left to right, the panels show (a) the original image in green, (b) all puncta found in this image based on local intensity peaks, (c) puncta that remain after filtering processes, and (d) all individual puncta randomly assigned different colors to illustrate the separation of adjacent puncta. The magenta circles in (a–c) mark the positions of false-positive puncta removed during the filtering processes
Because puncta are enriched in neuropils, to calculate puncta density, we measured the area of puncta type-specific background staining in Image J. This background staining was restricted to the neuropil and likely reflects nonsynaptic expression of PSD-95 and gephyrin. The puncta density was defined as the total puncta number divided by area of background staining (different for PSD-95 and gephyrin) in the neuropil.
2.5 Analysis of synapse distribution patterns in the spinal neuropil
To determine the distribution of PSD-95 and gephyrin puncta in the neuropil, we used Ripley's L-function statistics in Programita software (Wiegand & Moloney, 2004, 2014). These spatial statistics quantify the distribution of points in space, and classify the given distribution as either clumped/clustered, random or regular/dispersed. The Ripley's L-function results were represented in L-function curves (Figure 5a). Figure 6 provides examples for L-function curves of different dot distributions generated in Matlab.
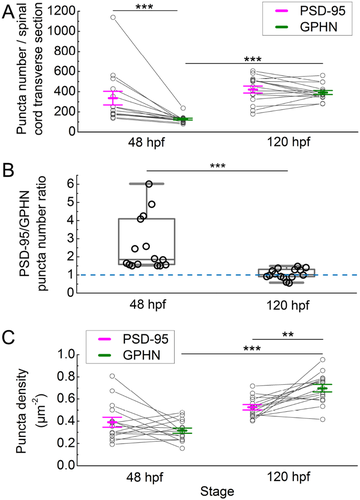
Postsynaptic density 95 (PSD-95) and gephyrin (GPHN) puncta exhibit distinct developmental patterns. (a) The number of PSD-95 and GPHN puncta per spinal cord section are plotted at 48 and 120 hpf. (b) The ratios of PSD-95/GPHN puncta numbers are plotted at 48 and 120 hpf. The dashed blue line indicates a ratio of 1. (c) The densities of PSD-95 and GPHN puncta in the spinal neuropil are plotted at 48 and 120 hpf. In (a) and (c), mean ± standard error of the mean overlay individual data points. Lines link the data points for PSD-95 and GPHN puncta from the same fish. In (b), box plots show the median (the line inside the boxes), the first and the third quartiles (the lower and upper boundaries of the boxes) and the range (the whiskers below and above the boxes) for samples at each stage. Each open circle represents the data from one transverse section of a single zebrafish embryo or larva. Statistical comparisons in (a) and (c) utilized two-way ANOVA (puncta type × stage) with post hoc Bonferroni. Statistical comparisons in (b) utilized the Mann–Whitney U test. Asterisks indicate statistical significance (**p ≤ .01, ***p ≤ .001)
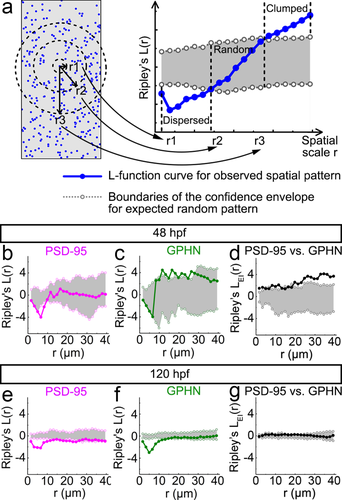
Point-pattern analysis of postsynaptic density 95 (PSD-95) and gephyrin (GPHN) puncta shows that GPHN puncta cluster more tightly than PSD-95 puncta. (a) Illustration for the numerical implementation of Ripley's L-function. The left diagram represents a puncta distribution (blue puncta), with r1, r2, and r3 representing different spatial scales (black). The number of puncta inside the circle with radius r is calculated and compared to the number calculated according to a null model of random distribution. Only the puncta within the defined study area (gray) are included in the analysis. The r1, r2, and r3 spatial scale values correspond to the r1, r2, and r3 values on the x-axis of the L-function plot on the right. The L-function curve for the given puncta spatial pattern is indicated in blue with the 95% confidence envelope for random distribution indicated in gray. The position of the L-function curve at a given spatial scale relative to the confidence envelope reveals the spatial pattern of the given puncta distribution: clumped/clustered (above the envelope), random (within the envelope), or dispersed/regular (below envelope). (b–g) Ripley's L-functions are calculated separately for PSD-95 (b, e) and GPHN puncta (c, f), and together for the relative localization of PSD-95 and GPHN puncta (d, g) at 48 (b–d) and 120 hpf (e–g). In each L-function plot, the L-function curve is indicated by solid line with darker color and filled circles, and boundaries of the confidence envelope are indicated by the light-colored dotted lines with open circles. The x-axis shows the scale radius (r), ranging from 0 to about half the height of spinal cord transverse sections, 40 µm. Each L-function graph is generated from images of 15 fish from 3 independent experiments
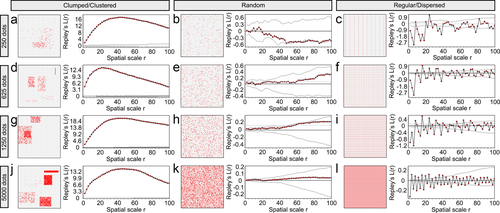
Ripley's L-function can detect three different point distribution patterns (clumped/clustered to the left-a, d, g, and j; random in the middle-b, e, h, and k; and regular/dispersed to the right-c, f, i, and l). Point patterns were generated with Matlab in a 100 × 100 square region. Each row shows the three distribution patterns generated with the same number of points: 250 in the top row, 625 in the second row, 1,250 in the third row, and 5,000 in the last row. In each subfigure, the left panel shows the actual point distribution and the right panel shows the corresponding L-function curve (the line with red data points) and the 95% confidence envelope for random distribution. The confidence envelopes in the clumped/clustered distributions with 1,250 and 5,000 points are very small thus they can hardly be seen on the L-function curve figures
In our L-function analysis, the location of each punctum was provided by the output of our puncta-finding Matlab program; a single image from the middle of each z-stack was used for the L-function analysis. To define the boundary of the spinal neuropil, we wrote a Matlab script to draw boundaries around the irregularly shaped neuropil regions. Since Programita could only analyze a single study area with a specified boundary each time, in each image, only one side (left or right) of the spinal neuropil was randomly picked for the analysis. Data of all the fish at the same stage were treated as repeated trials to generate separate PSD-95 and gephyrin L-function curves.
During the L-function analysis, the univariate spatial pattern (clumped/random/regular) of puncta was analyzed using Ripley's K(r) function. The K(r) function was defined as the expected number of puncta within distance r from a randomly chosen point. Under complete spatial randomness, K(r) = πr2, which is the area of a circle with radius r. L(r) was defined as √(K(r)/π) – r; the expected value of L(r) was zero under the null hypothesis of complete spatial randomness for the given distribution of puncta. To account for random variations, 95% confidence envelopes were generated for expected L(r) values under the null hypothesis. These confidence envelopes were obtained from 500 simulations using a random arrangement of puncta and random translation, that is, changing positions of puncta randomly in simulations. When the observed L(r) values were larger or smaller than the confidence envelopes of the expected L(r), the spatial patterns (clumped/clustered or regular/dispersed, respectively) of the puncta were statistically significant at distance r (Figure 5a). Since distance r represented the radius of the sampling circles in the analysis, we set our maximum scale as 40 µm, about half the height of spinal cord transverse sections.
To determine the distribution of PSD-95 and gephyrin puncta relative to one another, we also conducted bivariate L-function analysis. This bivariate pattern analysis quantified how each gephyrin punctum was distributed relative to each focal PSD-95punctum to examine whether the two puncta types occur on average more or less frequently as near neighbors than expected if they were randomly distributed. The bivariate K function KEI(r) is defined as the expected number of inhibitory puncta (gephyrin, referred as Pattern I) within a given distance r of an arbitrary excitatory punctum (PSD-95, referred as Pattern E), divided by λI, the density of Pattern I puncta: λIKEI(r) = E[#(points of Pattern I ≤ r from an arbitrary punctum of Pattern E)]; E[] is the expectation operator and # represents “the number of.” Under independence of the two puncta patterns, KEI(r) = πr2, regardless of the individual univariate patterns. The L-function for bivariate analysis was defined as LEI(r) = √(KEI(r)/π) − r. A 95% confidence envelopes of the LEI(r) functions were calculated from 500 simulations of the null model of complete spatial randomness, which assumed independence between puncta Patterns E and I. LEI(r) values larger than the confidence envelope indicated that there were on average significantly more Pattern I gephyrin puncta within distance r of Pattern E PSD-95 puncta than expected under independence (positive correlation). Similarly, LEI(r) values smaller than the confidence envelope indicated on average significantly less Pattern I gephyrin puncta than expected within distance r of Pattern E PSD-95 puncta (negative correlation).
2.6 Analysis of synapse distributions along the M-L axis
To quantify the M-L distribution of PSD-95 and gephyrin puncta, we wrote a Matlab program to identify the midpoints between the most lateral and the most medial puncta along the dorsal-ventral axis in each neuropil region. By connecting these midpoints together, we generated a midline to bisect each neuropil region. In this way, we could calculate the numbers of PSD-95 and gephyrin puncta located in each half to determine the proportion of PSD-95 and gephyrin puncta in the lateral half of the neuropil (Figure 7a).
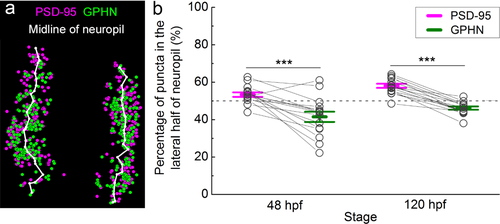
Relative spatial enrichment of gephyrin (GPHN) puncta medially and postsynaptic density 95 (PSD-95) puncta laterally in the spinal neuropil. (a) To test for distribution of puncta along the M-L axis of the neuropil, the midline of the neuropil was calculated in Matlab (white line; see Materials and Methods). (b) The percentage of PSD-95 and GPHN puncta located in the lateral half of neuropil is plotted at 48 and 120 hpf. Each pair of open circles connected by a line represents PSD-95 and GPHN puncta calculations from a single embryo/larva. Dashed grey line at 50% represents no M-L spatial bias. Asterisks indicate statistical significance (***p ≤ .001, two-way ANOVA, post hoc Bonferroni correction)
To capture M-L distribution patterns independent of an outlined neuropil, we wrote a Matlab script to divide the spinal cord into 100 bins along the horizontal axis, allowing us to calculate the M-L frequencies of PSD-95 and gephyrin puncta. For each image, the data from the left and right halves (50 bins/hemi-spinal cord) were pooled together for analyses of the frequency distributions of PSD-95 and gephyrin puncta from the most medial (0%) to the most lateral (50%) spinal cord (Figure 8a).
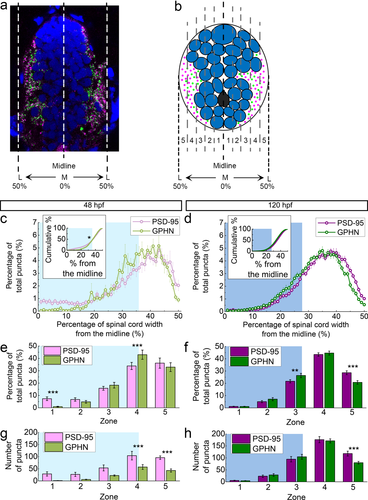
Postsynaptic density 95 (PSD-95) and gephyrin (GPHN) puncta show distinct M-L distributions. (a) A representative spinal cord section stained for PSD-95 (magenta), GPHN (green), and DAPI-labeled nuclei (blue). The spinal cord midline is defined as 0%, with spinal cord lateral edges defined as 50%. (b) A stylized section shows five M-L zones (Zone 1: 0–10%, Zone 2: 11–20%, Zone 3: 21–30%, Zone 4: 31–40%, Zone 5: 41–50%) used in (e–h). In (c–h), the cyan/blue regions in the background indicate Zones occupied by neuronal somata at 48 (cyan) and 120 hpf (blue). (c, d) M-L distributions of PSD-95 and GPHN puncta at 48 (c) and 120 hpf (d). Average percentages of PSD-95/total PSD-95 and GPHN/total GPHN distributed at 1% intervals along the M-L axis at each stage (48 hpf, n = 10; 120 hpf, n = 15) are graphed. Inserts show the cumulative probability curves. (e, f) Bar graphs compare the percentages of PSD-95 and GPHN puncta in each zone at 48 (e) and 120 hpf (f). (g, h) Bar graphs compare the numbers of PSD-95 or GPHN puncta in each zone at 48 (g) and 120 hpf (h). Statistical tests in the inserts in (c, d) are Kolmogorov–Smirnov test. Statistical tests in (e–h) are three-way ANOVA, followed by post hoc Bonferroni corrections. Asterisks indicate statistical significance (*p ≤ .05, **p ≤ .01, ***p ≤ .001)
2.7 Retrograde labeling of caudal primary motor neurons
To label caudal primary motor neurons, 24–96 hpf wild-type embryos and larvae were anesthetized in 0.02% MS222, transferred to a room-temperature slanted agarose plate (1.2% agarose [Promega, Madison, WI] in system water), and injected in ventral musculature in anal segments with a 25% solution of 10,000 molecular weight Texas Red dextran (Molecular Probes, Thermo Fisher Scientific) in 10% Hanks’ buffer as previously described (Hale, Ritter, & Fetcho, 2001). Injected zebrafish were then transferred to system water to recover for about 24 hrs and to allow retrograde transport of the dextran dye to fill the entire motor neuron before fixation, sectioning, and imaging.
2.8 Tracing caudal primary motor neuron dendritic arbors
Images of Texas Red dextran-labeled caudal primary motor neurons were processed using Image J. The brightness and contrast were adjusted to maximize visibility of dendritic branches and reduce background noise. Tracing and reconstruction of dendritic arbors were done in Neuromantic (version 1.7.5; http://www.rdg.ac.uk/neuromantic/, RRID: nif-0000-00197). Since labeled motor neuron dendrites are continuous three-dimensional structures, they could be easily distinguished from speckled background staining in z-stack images (Supporting Information movie 2). The lateral distance of caudal primary motor neuron dendrites was defined as the horizontal distance between the lateral boundary of the soma and the most lateral tip of the dendritic arbor in the traverse section. In sections with back-filled motor neurons, we also measured the average width of the corresponding neuropil region; to increase the sample size, we also measured the width of one of the two neuropil regions in sections without labeled neurons.
2.9 Cryosectioning and imaging of fish with labeled interneurons or motor neurons
Embryos and larvae from Tg(vglut2a:dsred)/Tg(glyt2:gfp) transgenic lines were collected at 48 and 120 hpf, respectively. Dextran-injected wild-type embryos and larvae were collected 24 hrs after the injection. Collected zebrafish embryos and larvae were anesthetized in 0.02% MS222 prior to fixation with 4% formaldehyde for 24 hrs at 4 °C, and followed by overnight incubation in 30% sucrose solution at 4 °C. Embryos and larvae were then embedded in tissue freezing medium (TFS, Durham, NC) and frozen at −20 °C in the cryostat. 30 µm-thick transverse sections from the middle of fish trunk (within five segments of the anus) were collected at −20 °C and mounted on poly L-lysine coated slides. Sections were then washed with 1 × phosphate buffered saline (1 × PBS, diluted from 10 × PBS, Cellgro, Corning, Manassas, VA) with 0.4% Triton-X (Avantor, Center Valley, PA) in the Sequenza slide staining system before mounting in Vectashield/DAPI. Images were acquired at 0.08 × 0.08 × 0.4 µm voxel size on the confocal microscope using the 1.4 NA 63 × oil objective.
2.10 Analysis for the M-L territories of neuronal processes in the neuropil
Images of Tg(vglut2a:dsred;glyt2:gfp) transverse spinal cord sections were processed in Image J. The brightness and contrast were adjusted to maximize visibility of neuronal processes and reduce background noise. For analysis, the section with the best signal-to-noise ratio for DsRed and green fluorescent protein (GFP) in the spinal neuropil was chosen from each z-stack. For each of these images, one side of the two spinal neuropil regions (left or right) was chosen randomly for the analysis. To avoid the interference of the fluorescence of neuronal somata, a rectangle that encompassed the widest region of each neuropil was analyzed. To ensure that we sampled the same region in the neuropil in different individual fish, we defined the dorsal-ventral position of the rectangle to span from the top of primary motor neuron somata (calculated based on the sections with backfilled primary motor neurons) to the bottom of the central canal (based on the gap in DAPI staining). The height of this rectangle was then scaled to the total height of the spinal cord in each section with labeled neuronal processes; and the width of the rectangle was set to encompass the neuropil region. The mean intensities of DsRed and GFP pixels at each M-L position were analyzed in Image J using the “Plot Profile” function. This output was then normalized to a 0–100 relative intensity scale, in which 0 corresponds to the background intensity and 100 corresponds to the maximal intensity. To compare the overall M-L distribution trends of glutamatergic (DsRed) and glycinergic (GFP) processes, we used Matlab to fit curves to the respective fluorescent intensity values of all fish at each stage. At 48 hpf, the DsRed curve adjusted R2 = .5651 (the sum of squares due to error (SSE) = 8.912 × 10−4), and the GFP curve adjusted R2 = .6621 (SSE = 7.712 × 10−4); at 120 hpf, the DsRed curve adjusted R2 = .5883 (SSE = 5.475 × 10−4), and the GFP curve adjusted R2 = .6985 (SSE = 8.610 × 10−4).
2.11 Statistics
Statistical tests were conducted in JMP 11 Pro (SAS Institute Inc., Cary, NC). When data satisfied the requirements for independence, normality, and homogeneity of variance, they were analyzed by ANOVA. Within the same developmental stage, PSD-95 and gephyrin data were extracted from the same fish. Therefore, to account for variability among different individuals, the unit “fish” was set as a random blocking variable. The p values for the first-order interaction in two-way ANOVA and the second-order interaction in three-way ANOVA are reported in results unless noted otherwise. When the p values for these interactions were not significant, the significant main effects in two-way ANOVA and the significant first-order effects in three-way ANOVA are also reported in results. Bonferroni correction was applied for post hoc Student's t-tests. For data that did not pass tests of normality, the Mann–Whitney U test was used to determine statistical significance. Kolmogorov–Smirnov tests were conducted to compare cumulative probability distributions.
3 RESULTS
3.1 PSD-95 and gephyrin-positive puncta exhibit distinct developmental patterns
To develop tools to quantify excitatory and inhibitory synapses, we vetted antibodies against PSD-95 (excitatory) and gephyrin (inhibitory) postsynaptic scaffolding proteins in zebrafish (Figure 1; described in detail in methods section). Using these antibodies, we mapped the location of individual PSD-95 and gephyrin-positive puncta in spinal cord transverse sections of 48 hpf embryos and 120 hpf larvae (Figure 2a–h). At both stages, PSD-95 and gephyrin-positive puncta are enriched laterally in the spinal neuropils that flank medially clustered neuronal somata. As development progresses and more puncta are formed, the neuropil region becomes significantly wider (48 hpf 14.31 ± 0.64% of the spinal cord width, n = 15 fish; 120 hpf 24.07 ± 0.70% of the spinal cord width, n = 9 fish; Mann–Whitney U test, p = .0002; Figure 2i).
Using a custom Matlab program to identify each synaptic punctum in transverse sections of spinal cord (Ganser et al., 2013; Morgan et al., 2008; Soto et al., 2011; Figure 3), we determined how puncta numbers change from the embryonic to the larval stage. Our analysis shows distinct developmental patterns for PSD-95 and gephyrin-positive puncta (two-way ANOVA, puncta type × stage F(1, 28) = 7.27, p = .0117; Figure 4). While the number of PSD-95 puncta varies between individual fish, the average number does not change significantly with development (48 hpf 336.00 ± 67.26, n = 15 fish; 120 hpf 420.98 ± 34.35, n = 15 fish; p > .75). By contrast, the number of gephyrin puncta varies less between individual fish and does increase significantly during development (48 hpf 128.47 ± 9.37, n = 15 fish; 120 hpf 391.73 ± 20.05, n = 15 fish; p < .001). With respect to the PSD-95/gephyrin puncta ratio, at 48 hpf, there are significantly more PSD-95 puncta than gephyrin puncta (p < .001), which is evident in every individual fish examined (Figure 4a). Therefore, at 48 hpf, the ratio of PSD-95 to gephyrin puncta is heavily skewed toward PSD-95, however, by 120 hpf, the PSD-95/gephyrin puncta ratio declines to nearly 1 (48 hpf 2.61 ± 0.38, n = 15 fish; 120 hpf 1.07 ± 0.07, n = 15 fish; Mann–Whitney U test, p < .0001; Figure 4b).
As with numbers of puncta, we also found that the densities of PSD-95 and gephyrin puncta change with development (two-way ANOVA, puncta type × stage F(1, 56) = 14.15, p = .0004). To calculate density, we divided the number of puncta by the area of background staining specifically associated with each antibody (see methods). Though there are more PSD-95 puncta than gephyrin puncta at 48 hpf (Figure 4a), their densities are similar (PSD-95 0.39 ± 0.04 µm-2, n = 15 fish; gephyrin 0.32 ± 0.02 µm−2, n = 15 fish). While the density of PSD-95 puncta stays constant during development, the density of gephyrin puncta increases significantly from 48 to 120 hpf (p < .001). At 120 hpf, with similar numbers (Figure 4a), gephyrin puncta exhibit a higher density than PSD-95 puncta (PSD-95 0.53 ± 0.02 µm-2, n = 15 fish; gephyrin 0.70 ± 0.04 µm-2, n = 15 fish; p < .01; Figure 4c).
3.2 PSD-95 and gephyrin puncta exhibit distinct spatial patterns during spinal circuit development
To determine the developmental changes of synapse distributions in the landscape of the neuropil, we analyzed postsynaptic puncta with an analytic method known as Ripley's L-function. This spatial statistic has been widely used in ecology to analyze the distribution of objects in a landscape (Wiegand & Moloney, 2004, 2014). Ripley's L-function compares the observed distribution of puncta to a null model of random distribution, and can detect distribution patterns at any spatial scale (r, Figure 5a), from the immediate neighborhood to the entire study area (Wiegand & Moloney, 2004, 2014). As a result, at any spatial scale, Ripley's L-function can assign puncta distributions to one of three patterns: clumped, random, or dispersed (see Materials and Methods; Figures 5a and 6). With this approach, we found that PSD-95 and gephyrin puncta exhibit distinct spatial patterns. At 48 hpf, PSD-95 puncta are randomly distributed in the spinal neuropil (Figure 5b) while gephyrin puncta are clumped (Figure 5c). With development, both PSD-95 and gephyrin puncta become more dispersed (Figure 5e,f). Interestingly, at both stages, the L-function curves for both puncta types show highly dispersed distributions within a 10-µm scale compared to more random or clumped distributions at larger scales. Such a drop in L-function curves at small scales is typical of point patterns that exhibit regular spacing (Figure 6, Regular/Dispersed). These L-function results at small spatial scales indicate that both PSD-95 and gephyrin puncta tend to maintain a certain distance from other puncta of the same type in the neuropil.
We also examined how excitatory and inhibitory synaptic puncta distribute with respect to puncta of the other type (Figure 5d,g). In striking contrast to the highly dispersed small-scale pattern seen within puncta type, we no longer see such a dispersed pattern between puncta types. This relative analysis shows that with respect to each other PSD-95 and gephyrin puncta are clumped at 48 hpf (Figure 5d) and randomly distributed at 120 hpf (Figure 5g).
3.3 PSD-95 and gephyrin puncta are enriched in distinct M-L regions in the spinal neuropil
Using a custom Matlab program to both define the cross-sectional area of each neuropil and divide neuropil regions into medial and lateral halves (see Materials and Methods; Figure 7a), we quantified the enrichment of excitatory and inhibitory puncta along the M-L axis. We found a greater portion of PSD-95 than gephyrin puncta in the lateral half of the neuropil at 48 hpf (PSD-95 53.42 ± 1.21 %, n = 15 fish; gephyrin 41.54 ± 2.75 %, n = 15 fish; p < .001; Figure 7b). This pattern of enrichment holds at 120 hpf (PSD-95 58.10 ± 1.08 %, n = 15 fish; gephyrin 46.23 ± 0.88 %, n = 15 fish; p < .001; two-way ANOVA, puncta type × stage F(1, 28) = 0.00, p = .9993; puncta type F(1, 28) = 68.89, p < .0001; Figure 7b). These data indicate that the distinct M-L enrichment of PSD-95 and gephyrin puncta is established by 48 hpf and sharpened by 120 hpf.
Given the observed M-L enrichment of PSD-95 and gephyrin puncta, we next examined the frequency distributions of PSD-95 and gephyrin puncta along the M-L axis of each spinal cord cross-section. These sections have a medial cell body region packed with DAPI-stained nuclei that is flanked by lateral neuropil regions enriched in synaptic puncta (Figure 8a,b). At 48 hpf, PSD-95 puncta both decorate the cell body region and are enriched in the lateral neuropil, while gephyrin puncta are enriched in the medial neuropil adjacent to the cell body region (Figure 8c). The cumulative probability curves show a statistically significant difference between the M-L distributions of PSD-95 and gephyrin puncta at this stage that is largely due to the exclusive presence of PSD-95 in the cell body region (Kolmogorov–Smirnov test, p = .0397; Figure 8c). At 120 hpf, both PSD-95 and gephyrin curves are largely excluded from the medial cell body region and enriched in the neuropil (Figure 8d).
This developmental difference in M-L distribution is more evident when each hemi-cord is divided into five M-L zones (Zone 1–5) with Zone 1 starting at the midline and Zone 5 ending at the lateral edge of the spinal cord (three-way ANOVA, zone × puncta type × stage F(4,114) = 10.29, p < .0001; Figure 8b). Both PSD-95 and gephyrin puncta are most abundant laterally, with gephyrin puncta significantly more enriched in Zone 4, the zone adjacent to the cell body region (p < .001; Table 2; Figure 8e). As the spinal cord develops, the neuropil region makes up a greater proportion of the spinal cord (Figure 2i; cyan/blue shading in Figures 8c–h and 9a–d). At 48 hpf, the neuropil occupies half of Zone 4 and all of Zone 5 and by 120 hpf it grows to occupy a quarter of Zone 3 and all of Zones 4 and 5 (Figure 2i; Figure 8e,f). At both 48 and 120 hpf then, gephyrin puncta are more enriched than PSD-95 in zones adjacent to the cell body region (Figure 8e,f). PSD-95 puncta, on the other hand, are more enriched in Zone 5 at 120 hpf, which corresponds to the most lateral part of the neuropil (p < .001; Table 2; Figure 8f).
| M-L zones | |||||||
|---|---|---|---|---|---|---|---|
| Data type | Stage | Puncta type | Zone 1 | Zone 2 | Zone 3 | Zone 4 | Zone 5 |
| Puncta number | 48 hpf | PSD-95 | 28.83 ± 8.79 | 27.01 ± 8.55 | 53.65 ± 12.28 | 104.22 ± 17.64 | 95.97 ± 7.21 |
| Gephyrin | 1.21 ± 0.46 | 5.95 ± 1.13 | 22.32 ± 2.69 | 57.40 ± 9.93 | 42.97 ± 6.64 | ||
| 120 hpf | PSD-95 | 5.51 ± 1.05 | 22.39 ± 4.83 | 94.51 ± 11.25 | 176.23 ± 12.90 | 118.02 ± 10.07 | |
| Gephyrin | 4.29 ± 0.71 | 28.59 ± 5.44 | 104.59 ± 10.26 | 171.24 ± 8.42 | 79.84 ± 5.54 | ||
| Frequency | 48 hpf | PSD-95 | 7.36 ± 1.49 % | 6.75 ± 1.37% | 15.82 ± 1.55% | 33.88 ± 2.88% | 36.19 ± 4.10% |
| Gephyrin | 0.93 ± 0.32 % | 4.83 ± 1.10% | 18.30 ± 2.30% | 42.99 ± 3.73% | 32.95 ± 3.56% | ||
| 120 hpf | PSD-95 | 1.18 ± 0.18% | 5.07 ± 0.88% | 21.68 ± 1.29% | 43.46 ± 1.37% | 28.61 ± 1.57% | |
| Gephyrin | 1.13 ± 0.19% | 7.11 ± 1.26% | 26.37 ± 1.74% | 44.64 ± 1.61% | 20.76 ± 1.45% | ||
This developmental change in M-L distributions is also clearly reflected in the absolute numbers of synaptic puncta per transverse spinal cord section (three-way ANOVA, stage × zone × puncta type F(4, 109) = 1.02, p = .4028; stage × zone F(4, 87) = 24.65, p < .0001; zone × puncta type F(4, 109) = 4.94, p = .0011; stage × puncta type F(1, 109) = 30.29, p < .0001; Figures 8g,h and 9c,d). At 48 hpf, there are significantly more PSD-95 than gephyrin puncta (Figure 4a). This trend is reflected in all zones, though the differences between PSD-95 and gephyrin puncta numbers are only statistically significant in the neuropil region (p < .001 for both Zones 4 and 5; Table 2; Figure 8g). At 120 hpf, when the numbers of PSD-95 and gephyrin puncta become more evenly matched (Figure 4a), there are still significantly more PSD-95 puncta than gephyrin puncta in Zone 5 (p < .001; Table 2; Figure 8h). Therefore, though the overall puncta ratio is about 1 at this stage, the PSD-95/gephyrin puncta ratio in Zone 5 is skewed towards PSD-95.
To assess developmental changes in PSD-95 and gephyrin puncta along the M-L axis, we compared each puncta type across 48 and 120 hpf (Figure 9). With respect to the percentage of total puncta (Figure 9a,b), PSD-95 puncta show the greatest developmental increase in Zone 4 (p < .01), while gephyrin puncta increase in Zone 3 (p < .05) but decrease in Zone 5 (p < .001). With respect to puncta numbers, both PSD-95 and gephyrin exhibit significant developmental increases in Zones 3 and 4 (PSD-95 Zone 3 p < .05; PSD-95 Zone 4 p < .001; gephyrin Zone 3 p < .001; gephyrin Zone 4 p < .001; Table 2; Figure 9c,d).
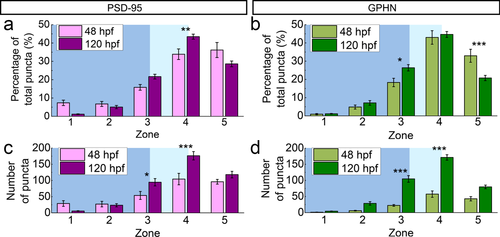
Developmental changes of postsynaptic density 95 (PSD-95) and gephyrin (GPHN) puncta in their M-L distributions. (a, b) Bar graphs compare puncta percentages at 48 and 120 hpf in the five M-L zones for PSD-95 (a) and GPHN puncta (b). (c, d) Bar graphs compare puncta numbers at 48 and 120 hpf in the five M-L zones for PSD-95 (c) and GPHN puncta (d). Statistical tests for both comparisons are three-way ANOVA, followed by post hoc Bonferroni corrections. Asterisks indicate statistical significance (*p ≤ .05, **p ≤ .01, ***p ≤ .001)
3.4 At embryonic stages, PSD-95 forms puncta in the medial spinal cord
At 48 hpf, ∼10% of PSD-95 puncta are found in the cell body region near the midline of the spinal cord, where gephyrin is largely absent (Zone 1, p < .001; Table 2). By the larval stage, PSD-95 puncta numbers have decreased medially in Zone 1 and both PSD-95 and gephyrin have increased laterally in Zones 3 and 4 (Table 2; Figure 9c,d).
3.5 Distributed enrichment of postsynaptic puncta is matched by M-L enrichment of glutamatergic and glycinergic neuronal processes
To test whether excitatory and inhibitory neuronal processes also show differential enrichment along the M-L axis, we quantified M-L neuropil territories occupied by glutamatergic and glycinergic processes. To do this, we used a zebrafish vglut2a:dsred;glyt2:gfp double transgenic line, in which all glutamatergic neurons express DsRed and all glycinergic neurons express GFP (McLean et al., 2007; Miyasaka et al., 2009; Satou et al., 2013). In the spinal cord, glutamate and glycine are the major excitatory and inhibitory neurotransmitters, respectively (Higashijima et al., 2004); thus, most excitatory and inhibitory neuronal processes are labeled, enabling the analysis of their respective neuropil territories.
We find that at both 48 and 120 hpf, glutamatergic and glycinergic neuronal processes exhibit even sharper M-L enrichment than excitatory and inhibitory postsynaptic puncta: the glycinergic processes are enriched in the medial neuropil and the glutamatergic processes are enriched in the lateral neuropil (Figure 10; Supporting Information movie 1). To quantify this spatial pattern, we analyzed the mean intensity of vglut2a:DsRed and glyt2:GFP in the neuropil. We restricted analysis to the neuropil region occupied by the primary motor neuron, from the base of the central canal to the height of the primary motor neuron somata (white rectangles in 10 C & F). The height of the primary motor neuron in Figure 10 is estimated as a proportion of the total spinal cord height based on stage-appropriate primary motor neuron backfill sections in Figure 11. At both 48 and 120 hpf, the peaks of GFP and DsRed intensities are located in the medial and lateral neuropil, respectively, exhibiting significantly different cumulative probability distributions (Kolmogorov–Smirnov test, 48 hpf: p = 1.11 × 10−5; Figure 10h; 120 hpf: p = 4.41 × 10−5; Figure 10j).
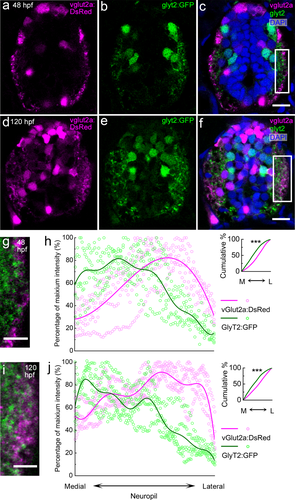
vglut2a:DsRed+ and glyt2:GFP+ neuronal processes occupy different M-L territories in the spinal neuropil. (a–f) Transverse-section view of the vglut2a:dsred;glyt2:gfp double transgenic line at 48 (a–c) and 120 hpf (d–f). vglut2a:DsRed (magenta) labels all glutamatergic interneurons and their processes. glyt2:GFP (green) labels all glycinergic interneurons and processes. DAPI (blue) labels nuclei. At both stages, both glutamatergic and glycinergic processes are enriched in the neuropil, lateral to all neuronal somata. Scale bar, 10 µm. (g, i) Magnified views of the regions boxed in white rectangles in (c) and (f), respectively. Scale bar, 5 µm. (h, j) The relative intensity of vglut2a:DsRed (magenta) and glyt2:GFP (green) in the neuropil along the M-L axis for multiple zebrafish (h, 48 hpf, n = 6; j, 120 hpf, n = 4). Distribution trend curves (solid lines) are fitted to DsRed and GFP intensities. Inserts show the cumulative probability curves, with asterisks indicating statistical significance (***p ≤ .0001, Kolmogorov–Smirnov test).
3.6 Primary motor neuron dendrites grow into the highly structured spinal neuropil
To understand how motor neurons fit into this excitatory-inhibitory neuropil structure, we tracked the growth of caudal primary motor neuron dendrites from 48 to 120 hpf. These primary motor neurons exit the cell cycle during gastrulation (Myers, Eisen, & Westerfield, 1986) and are some of the first neurons to become integrated into the motor circuit, receiving hundreds to thousands of synaptic inputs from excitatory and inhibitory interneurons once mature. To make these contacts during development, motor neurons extend their dendrites laterally into the spinal neuropil (Tripodi & Arber, 2012).
Axons of caudal primary motor neurons project to synapse on the ventral muscles by 21 hpf (Myers et al., 1986), therefore, to retrogradely label their dendrites, we injected Texas-Red dextran into ventral musculature (Hale et al., 2001; Supporting Information movie 2). At 48 hpf, dendrites of these neurons are still quite short and variable in number (Figure 11). Dendrites become less variable in number (Figure 11o), extend laterally from 72 to 96 hpf, and eventually form a complex, multi-branching dendritic arbor by 120 hpf (Figure 11b–m). This dendritic growth is strongly correlated with the widening of the spinal neuropil over the same time period (adjusted R2 = .9587, p = .0139; Figure 11n; Table 3).
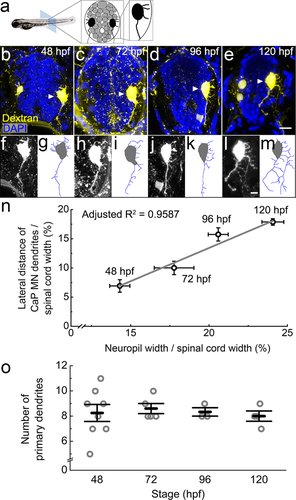
Primary motor neurons extend dendrites into the growing lateral neuropil from 48 to 120 hpf. (a) The diagram shows the organization of tightly packed cell bodies (gray) in a spinal cord transverse section. Black cells represent the primary motor neurons whose axons exit the spinal cord to innervate muscle. (b–e) Representative images show full spinal cord transverse sections with retrogradely labeled motor neurons injected with Texas Red dextran (yellow) at four developmental stages, 48 (b), 72 (c), 96 (d), and 120 hpf (e). DAPI labels nuclei (blue). To capture dendritic morphology, the motor neuron channel is a z-projection of confocal images from a 30-µm transverse section. In 48 and 120 hpf images, some ventral-projecting secondary motor neurons are also labeled. Caudal primary motor neurons are indicated by white arrowheads. Since other tissues also take up the dextran, which happens more often at earlier stages, speckled background staining and boundary of the spinal cord are also visible. Scale bar, 10 µm. (f–m) Zoomed-in images of the labeled caudal primary motor neurons (f, h, j, and l) as well as tracings of the dendritic arbor (g, i, k, and m) at 48 (f, g), 72 (h, i), 96 (j, k), and 120 hpf (l, m). Scale bar, 5 µm. (n) There is a strong correlation between the longest motor neuron dendrite and the width of the spinal cord during development. Data represent the means at four developmental stages, 48, 72, 96, and 120 hpf. Error bars represent the standard error of the mean (neuropil width: 48 hpf, n = 15 fish; 72 hpf, n = 19 fish; 96 hpf, n = 15 fish; 120 hpf, n = 9 fish; motor neuron dendrites: 48 hpf, n = 7 neurons; 72 hpf, n = 8 neurons; 96 hpf, n = 9 neurons; 120 hpf, n = 4 neurons). Adjusted R2 = 0.9759 (p ≤ .01). (o) Numbers of primary dendrites per caudal primary motor neuron during development. Each circle represents one individual caudal primary motor neuron. Error bars represent the standard error of the mean. No significant difference is found between different stages (one-way ANOVA, F(3, 16) = 0.14, p = .9335)
| 48 hpf | 72 hpf | 96 hpf | 120 hpf | |
|---|---|---|---|---|
| Neuropil width (µm) | 3.44 ± 0.55 | 8.83 ± 0.60 | 10.33 ± 0.42 | 11.17 ± 0.40 |
| Neuropil width / spinal cord width | 14.31 ± 0.64% | 17.77 ± 1.27% | 20.59 ± 0.64% | 24.07 ± 0.70% |
| Lateral distance of CaP MN dendrites (µm) | 3.00 ± 0.37 | 5.35 ± 0.66 | 8.11 ± 0.54 | 8.86 ± 0.13 |
| Lateral distance of CaP MN dendrites / spinal cord width | 6.92 ± 1.08% | 10.01 ± 1.14% | 15.74 ± 1.13% | 17.88 ± 0.56% |
Although both the neuropil width and the lateral extent of caudal primary dendrites increase about 50% from 48 to 120 hpf, the total number of primary dendrites per motor neuron stays relatively constant during this period (48 hpf 8.25 ± 0.67, n = 8 neurons; 72 hpf 8.60 ± 0.40, n = 5 neurons; 96 hpf 8.33 ± 0.33, n = 3 neurons; 120 hpf 8.00 ± 0.41, n = 4 neurons; one-way ANOVA, F(3, 16) = 0.14, p = .9335; Figure 11o). This indicates that most of the primary dendrites are formed around 48 hpf when the number of dendrites is highly variable and are thereafter stabilized to average 8–9 primary dendrites per cell. Therefore, motor neuron dendrites grow and branch laterally into a widening neuropil that is already structured with respect to excitatory and inhibitory enrichment along the M-L axis.
4 DISCUSSION
In this study, we quantified PSD-95 and gephyrin puncta as well as glutamatergic and glycinergic processes in the zebrafish spinal neuropil to directly compare their relative developmental and spatial patterns as they relate to E/I balance. In contrast to most other studies of structured excitatory and inhibitory (E/I) territories that have focused on individual neurons (Bleckert et al., 2013; Brown & Fyffe, 1981; Burke and Glenn, 1996; Druckmann et al., 2014; Fyffe, 1991; Grande, Armstrong, Neuber-Hess, & Rose, 2005; Grande, Bui, & Rose, 2010; Kim et al., 2012; Megias et al., 2001; Morgan, Soto, Wong, & Kerschensteiner, 2011; Rotterman, Nardelli, Cope, & Alvarez, 2014; Soto et al., 2011), our study examined E/I territories at the level of the neuropil and found PSD-95 puncta/glutamatergic processes enriched in the lateral neuropil and gephyrin puncta/glycinergic processes enriched in the medial neuropil. This structured neuropil is established early in development, before primary motor neurons elaborate their dendritic arbors, suggesting that it could provide a framework for individual spinal neuron E/I balance.
4.1 Differential regulation of excitatory and inhibitory synaptogenesis
To assess excitatory and inhibitory patterns of synaptogenesis, we used PSD-95 and gephyrin staining as proxies for excitatory and inhibitory synapses, respectively. PSD-95 anchors glutamate receptors at excitatory postsynapses (El-Husseini, Schnell, Chetkovich, Nicoll, & Bredt, 2000), and is often used as a marker for excitatory postsynaptic sites (Cho, Hunt, & Kennedy, 1992; Morgan et al., 2008; Niell et al., 2004; Soto et al., 2011). In zebrafish, PSD-95 has been observed at excitatory postsynaptic sites where it is associated with stabilized excitatory synapses (Meyer, Trimmer, Gilthorpe, & Smith, 2005; Niell et al., 2004). Playing the analogous role at inhibitory synapses, postsynaptic gephyrin scaffolds both GABA and glycine receptors (Tretter et al., 2012; Tyagarajan & Fritschy, 2014). Consistent with this, previous studies in zebrafish have demonstrated colocalization of gephyrin with glycine receptors (Ganser et al., 2013; Ogino et al., 2011).
One important caveat however is that both PSD-95 (Rao, Kim, Sheng, & Craig, 1998; Tao-Cheng, Azzam, Crocker, Winters, & Reese, 2015) and gephyrin (Dumoulin, Levi, Riveau, Gasnier, & Triller, 2000; Levi, Chesnoy-Marchais, Sieghart, & Triller, 1999) have the capacity to form nonsynaptic puncta. In the case of PSD-95, such nonsynaptic puncta are seen developmentally prior to becoming part of mature synapses (Rao et al., 1998). In the case of gephyrin, nonsynaptic puncta form in the absence of inhibitory inputs (Levi et al., 1999). Therefore, especially in the context of early development, it is important to be cautious about equating a punctum with a functional synapse. Indeed one pattern unique to the embryonic stage in our study was the presence of PSD-95 puncta on cell bodies tightly packed in the middle of the spinal cord, a region shown in previous studies to be populated by Glial-Fibrillary-Acidic-Protein-positive neural and oligodendrocyte precursors at 48 hpf (Kim et al., 2008). By the larval stage, both these precursors and the medial PSD-95 puncta disappear as neurons exit the cell cycle and differentiate (Park, Mehta, Richardson, & Appel, 2002). Based on previous studies, we suggest two possible roles for these embryonic, medial PSD-95 puncta: (1) mediating excitatory drive for spontaneous activity known to be required for aspects of neuronal differentiation (Spitzer, 2006; Warp et al., 2012) and/or (2) functioning as pre-patterned postsynapses that cluster neurotransmitter receptors prior to presynaptic innervation, similar to pre-patterning shown for acetylcholine receptors at mammalian and zebrafish neuromuscular junctions (Lefebvre, Jing, Becaficco, Franzini-Armstrong, & Granato, 2007; Yang et al., 2001). Our finding of these embryonic, medial PSD-95 puncta highlights the need for future studies to elucidate roles played by postsynaptic scaffolding protein puncta prior to synapse formation.
By quantifying synaptic puncta at embryonic and larval stages, we found that PSD-95 and gephyrin puncta already exhibit spatial structure in the embryonic neuropil that is maintained and sharpened at the larval stage. This early establishment suggests that such spatial structure is germane to the spinal neuropil, and is therefore likely to influence connectivity of spinal circuits.
Despite stable spatial patterning, PSD-95 and gephyrin puncta exhibit qualitatively distinct changes during development. From the embryonic to the larval stage, the number of gephyrin puncta significantly increases whereas the number of PSD-95 puncta remains fairly constant. Such differences occur even though both excitatory and inhibitory neurons are added during this time (Higashijima et al., 2004; McLean & Fetcho, 2009). This phenomenon could be explained by different pruning and/or stability dynamics operating on excitatory and inhibitory synapses (Kano & Hashimoto, 2009; Okabe, 2002; Rubinski & Ziv, 2015; Wyatt & Balice-Gordon, 2003). Future studies are needed to elucidate distinct rules of engagement for excitatory and inhibitory synapse formation and maintenance.
4.2 Ripley's L-function provides a method for analyzing synapse patterns at the systems level
To quantify synapse distributions during spinal circuit development, we applied Ripley's L-function (Wiegand & Moloney, 2004, 2014). Ripley's L-function is a spatial statistic, that like nearest neighbor analysis (Clark & Evans, 1954), compares the observed distribution of puncta to a null model of random distribution. Unlike the nearest neighbor analysis, which detects distribution patterns only in the immediate neighborhood and can be largely impacted by the area chosen, Ripley's L-function is a second-order statistic that detects patterns at all scales in the entire study area (Wiegand & Moloney, 2004, 2014). As such, it was of great utility for analyzing puncta distributions in a complex and relatively large (compared to synaptic puncta) study area like the spinal neuropil.
Our Ripley's L-function analyses revealed the following spatial patterns. First, for both individual and relative distributions, we found that puncta patterns become more dispersed with development. This trend toward dispersed distributions may result from synapse pruning (Flores & Mendez, 2014; Kano & Hashimoto, 2009) and/or more diverse neuron groups forming synapses in less occupied neuropil regions (Druckmann et al., 2014).
In analyses of either excitatory or inhibitory puncta, the Ripley's L-function shows hyper-dispersed patterns (Wiegand & Moloney, 2014) at spatial scales under 10 µm. Such regular spacing between synapses of like type has been observed previously among inhibitory synapses in the zebrafish spinal cord (Ganser et al., 2013), in individual mouse retinal ganglion neurons (Bleckert et al., 2013) and in hippocampal pyramidal neurons (Druckmann et al., 2014). Our results indicate that such regular spacing of adjacent synapses of the same type exists even at the neuropil level, between synapses in different neurons, suggesting that there may be intrinsic, systems-level mechanisms underlying this spacing between synapses of the same type.
4.3 Glutamatergic and glycinergic neuronal processes are segregated along the M-L axis suggesting population-specific regulation during development
Our findings suggest that the M-L structure of PSD-95 and gephyrin puncta can at least partly be explained by the M-L segregation of glutamatergic and glycinergic neuronal processes in the spinal neuropil (Kimura, Okamura, & Higashijima, 2006; Liao & Fetcho, 2008; Satou et al., 2013; Figure 9). Such a pattern cannot be secondary to M-L segregation of excitatory and inhibitory interneurons because these two types of neuronal somata occupy similar M-L domains in the zebrafish spinal cord (Higashijima et al., 2004; Figure 9a,d; Supporting Information movie 1). There is ample precedent for patterning of neural processes in various neuron types and organisms. For example, in the rat striatum, cholinergic fibers enrich in the lateral neuropil (Burke & Karanas, 1990) due to an M-L gradient of nerve growth factor (Altar, Dugich-Djordjevic, Armanini, & Bakhit, 1991). In the mouse spinal cord, Sonic hedgehog secreted from the floor plate forms an M-L gradient that restricts serotonergic axon growth to the lateral neuropil (Song et al., 2012). In the fly nerve cord, Slit and Netrin are secreted from the midline, signaling through Robo and Frazzled, respectively, to direct growth of motor neuron dendrites (Brierley, Blanc, Reddy, Vijayraghavan, & Williams, 2009; Furrer, Kim, Wolf, & Chiba, 2003; Mauss, Tripodi, Evers, & Landgraf, 2009) as well as the positioning along the M-L axis of longitudinal axons (Rajagopalan, Vivancos, Nicolas, & Dickson, 2000). In vertebrates, Slit/Robo signaling is not only crucial for the lateral positioning of longitudinal tracts from the brain to the spinal cord (Kastenhuber et al., 2009; Song et al., 2012), but also controls the M-L positioning of commissural axons after crossing the midline (Reeber et al., 2008). Our observations suggest the possibility that excitatory and inhibitory processes follow different guidance cues during circuit formation thereby resulting in the differential M-L enrichment of excitatory and inhibitory neuronal processes and synapses.
4.4 Linking patterns at the cellular level to patterns at the systems level
Though it remains unclear how neuropil E/I structure relates to neuronal E/I structure, many phenomena revealed by our systems-level analyses have been previously found at the level of single dendritic branches and/or neurons. These include spatial patterning such as a regular spacing between adjacent synapses of the same type (Druckmann et al., 2014) and clumping of inhibitory synapses (Kim et al., 2012; Megias et al., 2001) as well as the establishment of discrete E/I synapse territories. Distal-excitatory/proximal-inhibitory synaptic patterns have been observed in mammalian cortical and hippocampal pyramidal neurons (Gulyás et al., 1999; Kim et al., 2012; Megias et al., 2001; Spruston, 2008), in which inputs from distal excitatory synapses are amplified with a higher gain (Branco & Hausser, 2011) and proximal inhibitory synapses delay, block, and shape the dendritic spikes initiated from the distal dendrites (Andrasfalvy & Mody, 2006; Berger & Luscher, 2003; Kim, Beierlein, & Connors, 1995; Miles, Toth, Gulyas, Hajos, & Freund, 1996; Perez-Garci, Gassmann, Bettler, & Larkum, 2006; Pouille & Scanziani, 2001). These phenomena also include temporal patterns like the developmental decrease of the excitatory/inhibitory puncta ratio, which has also been observed in bistratified, direction-selective retina ganglion cells (Bleckert et al., 2013). Two possible explanations for similarities between cellular and systems-level patterns are: (1) that synapse distribution patterns are unique on individual neurons; and patterns from different neurons converge to form the pattern observed at the neuropil level, and (2) that synapse spatial patterns are globally regulated at the systems level, which thereby determines neuronal dendritic morphologies and the cellular-level patterns. Distinguishing these possibilities would provide important insights into the way neural circuits are organized: bottom-up or top-down.
We suggest that E/I neuropil structure may help to produce E/I balance at the cellular level because the establishment of E/I structure in the neuropil at or before 48 hpf largely precedes the growth and branching of motor neuron dendrites from 72 to 120 hpf (Figure 10; Jontes, Buchanan, & Smith, 2000; Kishore & Fetcho, 2013; McLean & Fetcho, 2009; Myers et al., 1986). While a comprehensive analysis of E/I synaptic localization on motor neuron dendrites is currently lacking, points of contact between different types excitatory and inhibitory interneurons onto motor neurons support the idea that motor neuron connectivity is influenced by the structured neuropil. For example, three types of inhibitory glycinergic interneurons contact the motor neuron in the medial neuropil (Liao & Fetcho, 2008; Satou et al., 2009). Conversely, glutamatergic Circumferential Descending interneurons contact motor neurons in the lateral neuropil on distal dendrites (Kimura et al., 2006) where they provide critical excitatory drive to initiate locomotory behaviors (Ausborn, Mahmood, & El Manira, 2012; Eklof-Ljunggren et al., 2012; Ljunggren, Haupt, Ausborn, Ampatzis, & El Manira, 2014; Satou et al., 2013). Interestingly, we found that even at 120 hpf when the overall PSD-95/gephyrin puncta ratio is close to 1, this ratio in the most lateral neuropil occupied by distal motor neuron dendrites is still skewed towards PSD-95. Taken together, the high PSD-95/gephyrin puncta ratio in the most lateral neuropil could play an important role in boosting excitatory inputs, while the inhibitory synapses enriched in the medial neuropil are probably vital for inhibiting motor neurons during alternating left-right bending.
To bridge this gap between cells and circuits, techniques are needed to label excitatory and inhibitory synapses on visualized single neurons in the circuits. Synapse-staining strategies are often incompatible with the labeling of neuronal morphology, due to their distinct fixation requirements (Ogino et al., 2011; Schneider Gasser et al., 2006). Thus, novel techniques that allow simultaneous labeling of excitatory and inhibitory synapses and individual neurons would facilitate observations of excitatory and inhibitory synapse patterns on diverse spinal neurons, without the physiological side effects of overexpressing postsynaptic scaffolding proteins (Prange, Wong, Gerrow, Wang, & El-Husseini, 2004; Yu & De Blas, 2008). Such novel techniques include mGRASP (Kim et al., 2012), intrabodies for PSD-95 and gephyrin (Gross et al., 2013) and ENABLED labeling strategies (Fortin et al., 2014), all of which have been established in mammals (Druckmann et al., 2014; Fortin et al., 2014; Gross et al., 2013; Kim et al., 2012). Future work applying these techniques in zebrafish will allow us to understand how synapse patterns at different levels impact each other, thus providing valuable insights into how neural circuits are organized and how their organization enables their function.
5 CONCLUSIONS
By quantifying E/I structure in the spinal neuropil, we found that excitatory and inhibitory synapses exhibit distinct temporal and spatial patterns in the zebrafish spinal cord. Excitatory synapses outpace inhibitory synapses during early synaptogenesis while inhibitory synapses are more clumped in distribution at both early and late stages. Furthermore, excitatory and inhibitory synapses exhibit distinct enrichment along the M-L axis that is probably caused at least in part by distinct M-L neuropil territories occupied by glutamatergic and glycinergic neuronal processes. Such M-L patterns for excitatory and inhibitory synapses and neuronal processes are established early in development before spinal neurons have elaborated their dendritic arbors. Our observations suggest this excitatory/inhibitory neuropil structure plays an important role in spinal circuit development by providing a framework for E/I balance at the cellular level.
ACKNOWLEDGMENTS
We would like to thank UM Biology Imaging Core manager Dr. James Baker for help with confocal imaging and Ricardo Cepeda for fish care. We would like to acknowledge Dr. Martin Meyer for providing PSD-95 and SYP1 fusion protein constructs, Dr. Hiromi Hirata for his assistance in generating fast-frozen tissue sections, Dr. Rachel O. Wong and members of her lab for hosting Qing Yan to learn to implement and modify their Matlab-assisted puncta-finding programs, and Dr. Jiang Jiang for teaching Qing Yan to program in Matlab. We would also like to thank Dr. Don De Angeles for lending his expertise with spatial modeling in ecosystems to our neuroscience research, and Dr. Kevin Collins, Dr. James Baker, Dr. Akira Chiba, Robert Kozol and David James for critical reading of the manuscript.
CONFLICT OF INTEREST STATEMENT
The authors declare that they have no competing interests.
ROLE OF AUTHORS
QY carried out experiments, performed M-L analyses, Matlab analyses, and was the lead writer of the manuscript. LZ designed statistical analyses for the data. BZ carried out the Ripley's L-function analyses. QY and JED designed and coordinated the work. QY and JED drafted the manuscript and all authors contributed to the preparation of the manuscript. All authors approved the final manuscript.