From uncertainty and entropy to coherence and consciousness
Abstract
Understanding the neural basis of consciousness remains a fundamental challenge in neuroscience. This study proposes a novel framework that conceptualizes consciousness through the lens of uncertainty reduction and negative entropy, emphasizing the role of coherence in its emergence. Sensory processing may operate as a Bayesian inference mechanism aimed at minimizing the brain's uncertainty regarding external stimuli, and conscious awareness emerges when uncertainty is reduced below a critical threshold. Computationally, this corresponds to minimizing informational uncertainty, while at a physical level it corresponds to reductions in thermodynamic entropy, thereby linking consciousness to negentropy. This study emphasizes the role of coherence in conscious perception and challenges existing models like Integrated Information Theory by exploring the potential contributions of quantum coherence and entanglement. Although direct empirical validation is currently lacking, we propose the hypothesis that consciousness acts as a cooling mechanism for the brain, as measured by the temperature of neuronal circuits. This perspective affords new insights into the physical and computational foundations of conscious experience and indicates a possible direction for future research in consciousness studies.
Key points
What is already known about this topic?
-
Sensory perception is inherently uncertain due to neural noise and incomplete information, requiring the brain to perform causal inference to construct a coherent experience. Although the Integrated Information Theory (IIT) defines consciousness as irreducible information from individual components, a consciousness model grounded in the definitions of information may offer greater advantages.
What does this study add?
-
This study proposes a new model of consciousness based on standard information theory, where perception emerges as uncertainty is minimized. It argues that conscious perception arises when the brain reduces uncertainty below a critical threshold, linking this process to the minimization of thermodynamic entropy and the potential role of quantum coherence and entanglement. This framework offers a precise and testable alternative to IIT, advancing our understanding of consciousness through measurable information-theoretic metrics.
1 INTRODUCTION
Sensory perception starts with an external stimulus (S) that evokes a neural response (R). The stimulus is not directly accessible to the brain, and making it a latent or hidden variable. Thus, the brain has access, not to the stimulus but to a representation of it (i.e., the neural response). For two reasons, R is not a perfect representation of S. First, the neural response is noisy, and second, the neural response contains insufficient information about the stimulus. The fact that the neural response is an imperfect representation of the stimulus means that, for the brain, the stimulus is under-determined by the response—the stimulus cannot be decoded unambiguously from the response. As a result, the brain is left with uncertainty about the stimulus.1
Given the incompleteness of sensory data, the brain performs causal inference to supplement the insufficient information and thus reduce its uncertainty about external stimuli.2 The idea that causal inference is at the core of sensory processing is widely accepted in contemporary neuroscience and serves as a central component of many leading theories of perception, including the free energy principle3 and Bayesian causal inference theory.4
This study presents a model of sensory processing and conscious perception that is based on the concepts of uncertainty and information, here used as in information theory, as established by Shannon.5 In this regard, the model of consciousness proposed in this paper contrasts with one of the most prominent theories of consciousness, Integrated Information Theory (IIT). Integrated information, as defined by the IIT, refers to information that is irreducible and generated by a system as a whole, transcending the sum of its parts, which it considers consciousness to be.6 In this theory, information and the concomitant uncertainty are utilized in a manner that diverges significantly from their use in classical information theory. Within the framework of IIT, information possesses the qualities of being causal and intrinsic, with its assessment stemming from the intrinsic vantage point of a system. In comparison, Shannon information, characterized by its observational and extrinsic nature, is evaluated from the external stance of an observer.7 A model of consciousness grounded in standard and widely accepted definitions of information and uncertainty may offer advantages over models that diverge from these standard definitions.
2 UNCERTAINTY AND ENTROPY
2.1 Background of uncertainty
Uncertainty is an intrinsic part of neural computation, whether pertaining to sensory processing, motor control, or cognitive reasoning.8 In sensory processing, uncertainty originates from two main sources: internal noise and insufficient information.
Internal noise (or neuronal noise) is the part of a neural response to a stimulus that cannot be accounted for by the stimulus. Internal noise is partly due to random effects (for example, stochastic neurotransmitter release or random opening and closing of ion channels), and partly due to uncontrolled but nonrandom effects.9 Internal noise leads to uncertainty via “neural response variability,” which refers to the fact that the same stimulus can lead to different neural responses in different trials. In other words, repeated presentation of the same stimulus to an observer will each time produce a different pattern of neural activity tuned to specific features of that stimulus.10
When the same sensory variable (such as the direction of motion of a visual stimulus) or motor command is presented, the spike count of cortical neurons varies greatly from trial to trial, typically conforming to Poisson-like statistics. It is essential to recognize that variability and uncertainty are intertwined: Had there been no neuronal variability, that is, if neurons fired in an identical manner every time the same object was seen, one would always be certain about the presented object.11 Although Ma et al.11 have correctly identified response variability as a source of uncertainty, it should be emphasized that response variability is not the only source of uncertainty in sensory processing. Another source of uncertainty stems from the fact that the neural response to a stimulus lacks sufficient information about the stimulus, partly due to the inability of sensory receptors to extract all relevant information from external stimuli, and partly from inherent limitations of cortical neurons to process the information coming from sensory receptors.
Pouget et al.12 notes the focus on the uncertainty stemming from internal noise. However, uncertainty is intrinsically embedded in the structure of most relevant computations, regardless of whether internal noise is present. In computer vision, uncertainty has long been studied in terms of “ill-posed problems.” Most questions about an image are ill-posed as images lack sufficient information for unambiguous answers. The aperture problem in motion processing is a well-known example: When a bar moves behind an aperture, there are infinitely many 2D motions consistent with the image, so the image alone fails to specify the motion of the object. Although this example may seem artificial, as most images are not of bars behind apertures, it presents a real problem for the nervous system: All visual cortical neurons view the world through their receptive fields (like apertures). Moreover, similar problems occur in computing the 3D structure of the world, localizing auditory sources, and other computations.
In fact, many (if not all) of the problems that sensory systems must solve are ill-posed. For example, vision is considered ill-posed since the retinal image might be an arbitrarily complex function of the visual scene, and thus the information in the image is inadequate to define the unique scene.13 No matter whether the origin of uncertainty is noise or insufficient information, once the brain receives a sensory input, it starts a process to minimize uncertainty about the cause of the input (i.e., the stimulus), which constitutes the essence of sensory perception.
In psychophysical experiments that involve sensory processing, uncertainty is often quantified using the information-theoretic measure of mutual information, which increases with reductions in the uncertainty (entropy) within neural circuits, given particular characteristics of sensory stimuli.14 In electrophysiological recordings during visual or auditory perception tasks, mutual information measures how much the observation of a spike train (or multiple spike trains from several neurons) reduces the uncertainty about the external stimulus.15
2.2 Uncertainty minimization
In information theory, uncertainty means lack of information, and minimizing uncertainty corresponds to obtaining information (or knowledge). In the context of sensory perception, uncertainty refers to the brain's lack of information about an external stimulus. In this context, uncertainty is a property of the brain's belief about the stimulus.1 Here, “belief” is a technical term for the brain's knowledge about the stimulus. Mathematically, belief can be viewed as a “probability distribution”16 whose width reflects the amount of uncertainty; the more spread out the probability distribution, the more uncertainty there is.1
Different lines of evidence support the idea that the brain actually represents uncertainty in the form of probability distributions. For example, functional magnetic resonance imaging (fMRI) studies demonstrate that in the human visual cortex, sensory uncertainty is represented by a probability distribution encoded in the activity of neuron populations as a whole.17 As another example, by employing multielectrode recording in the visual cortices of behaving monkeys, Walker et al.18 demonstrated that the same population of neurons that encodes a stimulus also encodes the uncertainty about that stimulus, represented as the width of the probability distribution.
To test whether sensory uncertainty is actually encoded as the width of a probability distribution in the activity of cortical neurons, van Bergen and Jehee19 conducted an fMRI study of the human visual cortex while participants were subjected to the well-known perceptual illusion of serial dependence. Their findings directly demonstrated that the width of the probability distributions resulting from population activities in visual areas V1, V2, and V3 can indeed serve as a metric of the amount of sensory uncertainty within these areas.
Therefore, at each stage of sensory processing, the same probability distribution that represents the knowledge (i.e., belief) also represents the lack of knowledge (i.e., uncertainty) of the brain about the stimulus. In order to minimize uncertainty (and hence obtain knowledge), the brain manipulates and integrates the probability distributions encoded by different populations of neurons across the cerebral cortex. Minimizing uncertainty through the manipulation and integration of probability distributions is in fact a kind of probabilistic inference. If this is performed according to Bayes' rule, it is called Bayesian inference. Psychophysical experiments have confirmed that the brain performs Bayesian inference in order to cope with uncertainty in both perception and action.20 This perspective leads to a Bayesian approach to sensory perception, where the brain is a Bayesian observer of the hidden stimulus (S) generating the neural response (R).21
2.3 Uncertainty minimization via Bayesian inference
P(S|R) is called the posterior probability distribution (or the posterior belief). It captures everything that the brain knows about the stimulus after considering the response. The posterior belief not only reflects the most probable value of the stimulus but also reflects (through the width of the distribution) the uncertainty of the brain about the stimulus.22
P(R|S), the response probability distribution, reflects the likelihood of all the different stimuli that could have given rise to the observed response.23 In the framework of hierarchical predictive coding, P(R|S) corresponds to bottom-up effects that depend upon prediction error from the level below.24
P(S) is called the prior belief. More precisely, it is the prior probability distribution over the stimulus. It captures (or contains) any information the brain has about the stimulus before considering the response. Prior beliefs originate from the statistical regularities of the environment.25 In the framework of hierarchical predictive coding, P(S) corresponds to top-down predictions.
P(R), the prior probability distribution over the response, is called the “marginal likelihood” or “model evidence.” P(R) is just a normalization factor that ensures that P(S|R) is a proper probability distribution over S.
In the context of the free-energy principle, the negative logarithm of the model evidence is called the surprise; thus, maximizing the model evidence corresponds to minimizing the surprise.26 From the perspective of stochastic thermodynamics, the time average of this surprise is called entropy or uncertainty.27 A Bayesian brain aiming to maximize its evidence is, in essence, attempting to minimize its entropy. This implies that it defies the Second Law of Thermodynamics, offering a principled account of self-organization despite the natural inclination toward disorder.28 Therefore, maximizing the model evidence corresponds to minimizing not only the variational free energy but also the thermodynamic entropy.29
The Bayes formula implies that in order to perform Bayesian inference, the brain needs two critical ingredients: first, a representation of the prior and likelihood functions, and second, a mechanism to multiply the distributions.12 The product of the likelihood function and the prior is a joint probability distribution, denoted P(R,S), called the generative model.30
This can be summarized in the following statement: Sensory perception is a process of uncertainty minimization by means of Bayesian inference. This statement is an explanation of perception at the computational and algorithmic levels, but it tells us nothing about perception at an implementational level. How do neurons implement Bayesian inference and uncertainty minimization?
2.4 The neural implementation of uncertainty minimization
In general, very little is known about how the brain implements uncertainty minimization and Bayesian inference. The mechanisms by which the brain represents probability distributions and then combines prior knowledge with likelihood functions are poorly understood. While experimental studies employing fMRI, EEG, magnetoencephalography and intracranial recordings have shed some light on the brain areas where Bayesian computations may take place, the implementation of these computations at the level of neuronal populations remains unclear. Studies using neural network models provide proof of concept that such implementation is possible in principle, but the mechanisms actually employed by the networks of brain neurons remain a topic of future research.4
Information is what reduces uncertainty, and uncertainty means lack of information. In order to explain (at an implementational level) the mechanism by which the brain minimizes uncertainty, we need to answer the following question: What is the most basic element that represents information in the brain? The most widely accepted answer to this question is that the nervous system relies on action potential as the core units of information and signaling.31 In the brain, information is encoded through action potentials (spikes).32 Since action potential is an all-or-nothing phenomenon, it can be viewed as a digital signal that carries information in brain computations.33
In spike-based computation, several possibilities exist for representing information: the spike rate of individual neurons, spike timing of individual neurons, spike correlations within single neurons, and spike correlations across a population of neurons (e.g., synchronous spikes).34 Experimental evidence shows that all these possibilities are actually realized in the brain, and different types of spike-based coding schemes are used by the brain in different contexts. For instance, the spike rate (spike count per unit time) often has a greater influence on behavioral decisions than the timing of spikes or spike count.35 In the retina, the occurrence of a visual stimulus can be represented with high precision by the spike timings of individual ganglion cell action potentials.36
Although spike-based computation is currently the standard view in neuroscience, it should not be forgotten that neurons can potentially perform far more computations than spikes would allow, as there is an enormous and largely hidden layer of computation at the molecular level within neurons.37 For example, neurons can represent and process sensory information using intracellular calcium ions rather than action potentials. Experimental evidence clearly indicates that in response to sound stimulus, cricket auditory neurons perform chemical computation through the temporal dynamics of intracellular calcium ion concentration.38 Another potential substrate for chemical computation in neurons is subcellular oscillators. Even a small network of coupled intracellular oscillators can potentially perform complex computations. For example, it has been demonstrated that just three interacting oscillators can recognize (or predict) the color of a randomly selected point with an accuracy of 95%.39
Chemical computation lies at the heart of biology, driving the remarkable processes of life from protein synthesis and bacterial life cycles to the intricate functions of the human brain.40 However, unlike spike-based computation, chemical computation in the brain has not yet been fully explored. We still do not understand the nature and the logic of the chemical computations performed within a single neuron.41
Whether the brain computes with electrical spikes or chemical substrates, it must minimize its information-theoretic uncertainty at the computational and algorithmic levels in order to obtain information about the environment. What is regarded as uncertainty in information theory is formally equivalent to entropy in thermodynamics.42, 43 Although information-theoretic uncertainty and thermodynamic entropy are measures of two different quantities, they are so fundamentally related to each other that the laws of thermodynamics are considered nothing but theorems in information theory.44 For this reason, it is plausible to argue that in the brain, minimizing uncertainty at computational and algorithmic levels corresponds to minimizing thermodynamic entropy at an implementational level. In other words, sensory perception involves the minimization of not only the brain's information-theoretic uncertainty but also its thermodynamic entropy—the entropy of the physical substrate that represents information in brain computations.
3 ENTROPY AND COHERENCE
In thermodynamics and statistical mechanics, entropy is a measure of disorder,45, 46 such that the lower the entropy of a system, the more ordered the system is. This applies to any physical system, regardless of whether the elements of the system are action potentials, calcium ions, or subcellular oscillators. All these elements can in principle encode information and represent probability distributions for brain computations. As argued by Timme and Lapish,47 systems with probability distributions skewed toward specific states exhibit lower entropy, reflecting reduced uncertainty. In contrast, systems with probabilities evenly distributed across multiple states have higher entropy, indicating greater uncertainty. When a variable is entirely confined to a single state (with a probability of 1), its entropy reaches 0, signifying no uncertainty.
Zero entropy is the minimum possible thermodynamic entropy that a system can achieve in classical physics. In the context of sensory information processing, zero thermodynamic entropy corresponds to the state in which the uncertainty of the brain about an external stimulus is 0, which means that the brain is completely certain about the stimulus. This is the ultimate limit of entropy (and uncertainty) minimization, or equivalently, the ultimate limit of certainty that the brain can achieve in sensory perception. However, this limit only holds so long as we assume that the brain computes only with classical information, because quantum information allows for a level of certainty that surpasses traditional certainty.48 This extraordinary effect is due to entangled states that contain quantum information. Entanglement is a quantum resource that allows entropy to become negative (i.e., less than zero) even though this is forbidden in classical physics.49 When the entropy of a system becomes negative, the system becomes far more ordered than is possible in the classical regime. This highly ordered state of a system is called a quantum coherent (or pure) state. Quantum coherence is deeply related to quantum entanglement, both of which arise from the superposition principle—the ability of quantum systems to exist in multiple states simultaneously.50, 51
4 COHERENCE AND ENTROPY
Experimental evidence indicates that quantum entanglement and coherence might be involved in several different biological phenomena, including photosynthesis in plants and bacteria.52 The discovery of long-lasting quantum coherence in the photosynthetic Fenna–Matthews–Olson complex suggests that quantum coherence may play a functional role in energy transport within biological molecules.50 In addition to energy transfer in biological systems, coherence and entanglement might also be involved in the functioning of the avian magnetic compass and the way some birds navigate.53 Consciousness is another biological phenomenon in which entanglement and coherence probably play an important role.54 Here, it should be emphasized that while the role of quantum coherence in photosynthesis is strongly supported by experimental evidence, its involvement in the avian compass has less empirical support, and its association with the emergence of consciousness remains largely speculative and lacks empirical grounding.
A recent theory of consciousness (the quantum mechanics, biology, information theory, and thermodynamics [QBIT] theory) suggests that in order for sensory processing to proceed to the point of conscious perception, quantum entanglement and coherence are indispensable.55-57 According to the QBIT theory, when the information-theoretic uncertainty of the brain about a stimulus decreases below a critical threshold, the brain becomes conscious of that stimulus.58-60 This critical threshold is proposed to be 0. Therefore, in order for the brain to become conscious of a stimulus, information-theoretic uncertainty (and hence thermodynamic entropy) must become <0 (i.e., negative).
5 CONCLUSION
Sensory perception is a computational process through which the brain attempts to minimize its uncertainty about an external stimulus by means of Bayesian inference. Depending on how much uncertainty is minimized during this process, the stimulus is perceived either consciously or unconsciously by the brain. Conscious perception occurs only if the information-theoretic uncertainty decreases below a critical threshold. This is an extreme threshold that lies beyond the limits achievable by classical resources such as energy. To generate consciousness, the brain needs quantum resources, including entanglement.
The emergence of consciousness is associated not only with a decrease in information-theoretical uncertainty at a computational level but also with a decrease in thermodynamic entropy at the implementational level of the physical substrate that carries (or encodes) information. This physical substrate is as yet unknown, although cellular spikes and subcellular oscillators are promising candidates. A reduction in entropy corresponds to an increase in order, and quantum coherence is the maximum possible order that a physical substrate can assume.57 It is proposed that when the brain becomes conscious of a stimulus, its uncertainty and the entropy of the computing substrate become negative. If the computing substrate is spiked, the emergence of consciousness is associated with the coherent firing of neurons across the brain. If the substrate is a chemical oscillator, the emergence of consciousness is associated with the coherent oscillations of subcellular entities across the brain. In any case, coherent brain activity is a signature of consciousness (Figure 1).
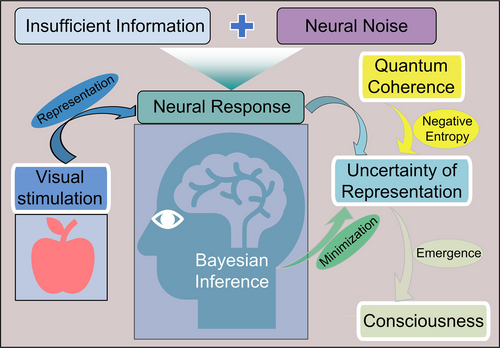
The model of consciousness based on information theory positing contra the Integrated Information Theory that perception arises from uncertainty minimization (negative entropy).
A challenge facing the QBIT theory is that it is currently supported by no direct empirical evidence; it is entirely speculative. A concept addressing this, outlined in a previous paper,56 concerns the relationship between entropy minimization and heat removal. Exporting entropy out of a system corresponds to removing heat from the system, lowering the temperature of the system, and hence making the system cooler. Therefore, the neuronal computations necessary for extreme uncertainty (entropy) minimization, which are essential for the emergence of consciousness, not only do not generate heat but in fact remove it, thereby cooling the underlying neuronal medium. This suggests that consciousness may act as a cooling mechanism for the brain, a hypothesis that could be confirmed or refuted with instruments specifically engineered to measure the temperature of neuronal circuits engaged in producing conscious experiences.
AUTHOR CONTRIBUTIONS
Majid Beshkar: Conceptualization; investigation; validation; supervision; writing—original draft; writing—review and editing.
ACKNOWLEDGMENTS
The author declares that no financial support was received for the research, authorship, and/or publication of this article.
CONFLICT OF INTEREST STATEMENT
The author declares no conflicts of interest.
ETHICS STATEMENT
Ethics approval was not needed in this study.
Open Research
DATA AVAILABILITY STATEMENT
Data sharing is not applicable to this article as no new data were created or analyzed in this study.




