Enhanced Electrical Conductivity of Polyoxometalates by Bridging with Mixed-Valent Multinuclear Platinum Complexes
Abstract
Polyoxometalates (POMs) are nanosized molecular metal oxide anion clusters with tuneable structures and functionalities, and they exhibit a redox chemistry and catalytic activity in multielectron redox processes. These are typically poor electrical conductors (<10−10 Scm−1), which is attributed to negligible electronic interactions among anions in the solid state. Since the reduced electrons on the d0 metals in POMs are delocalized, electrical conductivity was improved when judicious pathways for the electrons were created by bridging the POMs. Utilized with the electronic interactions between bridging oxygen atoms with the highest occupied molecular orbital in the POMs and the metal dz2 orbitals in the multinuclear platinum complexes, and three mixed-valent assemblies were synthesized and characterized. Simply mixing Keggin-type or Dawson-type POMs with tetranuclear or trinuclear platinum complexes in solution afforded three single crystals, and all three compounds were paramagnetic with mixed oxidation states and better conductivities at room temperature than the parent compounds.
Introduction
POMs are spherical polynuclear metal complexes with high-valent metals linked by oxygen atoms, and they exhibit modulatory properties depending on the encapsulated ions, metal species, and number of metals.1 Since many electrons are reduced to the degenerate metal dxy orbitals constituting the lowest unoccupied molecular orbital (LUMO) of POMs, which resemble fragments of metal oxide lattices, they have been used industrially as acid catalysts1c and promising candidates for catalysis of multielectron transfer reactions such as water oxidation. Since these multinuclear molecules have diverse fundamental properties, such as structure, geometry, and adjustable redox properties, and multiple uses electrocatalysis, electronic devices, and electrochemical energy storage and conversion,2 improving the electrical conductivities of POMs is important; however, they are insulators because the electrons are isolated within a single cluster due to the limited intercluster interactions.
POMs have clustered structures in which several d0 metals are bridged by oxygen (Oe) atoms.1a, 1b Each metal is coordinated equatorially by four Oe atoms and axially by one terminal oxygen (Ot) atom which reduces the contact with other molecules. The frontier molecular orbitals in POMs, which include the metal dxy LUMO and Oe 2p as the highest occupied molecular orbital (HOMO), are degenerate due to the symmetrical multinuclear structures.3 Due to this degeneracy, the addition of electrons to the formally d0 metal of POMs usually results in Class-II mixed-valence behaviour according to the Robin and Day classification,4 in which the valence is in the intermediate state between “bound” and “delocalized”. Therefore, if POMs are assembled such that the delocalized electrons move well through the path to the neighbouring POM, the electrical conductivity will increase; however, molecular POMs are closed systems exhibiting negative charge repulsion in the crystals.
To develop POMs with excellent molecular conductivities, we have tried to connect the POMs with judiciously chosen cationic molecules. Prior to our study, coordination bonds Ot and cationic metal ions or metal complexes were used to prepare several infinite POM-based assemblies that constitute a unique class of materials between metal–organic frameworks and zeolites.1h, 5 In contrast, we focused on the bridging Oe atoms because the degenerate Oe 2p orbitals are the HOMO,3 which is directly related to the valence band, since the degenerate metal dxy orbitals of the LUMO are spatially blocked by the protruding Ot atoms. To enable communication with the Oe 2p orbitals, we selected one-dimensional (1D) platinum-based multinuclear complexes as cationic links for the POMs, in which the platinum atoms axially contacted other atoms with dz2 orbitals.6 Here, we will show crystal structures and properties of three kinds of mixed-valent and paramagnetic 1D assemble comprised of POMs and platinum complexes showing enhanced electrical conductivities.
Results and Discussion
Syntheses of Assembles Containing POMs and Multinuclear Platinum Complexes
For POMs, Keggin-type [PMo12O40]3−(={PMo12}3−) and Dawson-type [P2Mo18O62]6−(={P2Mo18}6−) were selected; these have spherical structures constructed of twelve or eighteen molybdenum atoms containing PO43− anions inside the cages. As reported previously3, 7 and confirmed in Figures S1–S11, both {PMo12}3− and {P2Mo18}6− can be reduced by multiple electrons at the degenerate Mo dxy orbitals, facilitating easy oxidation of their counterparts. As platinum-based multinuclear complexes, [Pt2(piam)2(NH3)4]2n+ (={Pt4}n+, piam=pivalamidate, n=4–6)8 and [Pt2Pd(piam)4(NH3)4]n+ (={Pt2Pd}n+, n=2–4),9 which have 1D tetranuclear Pt−Pt−Pt−Pt and trinuclear Pt−Pd−Pt alignments, respectively, were selected. Both compounds can be oxidized and reduced by two electrons, {Pt4}4+↔{Pt4}5+↔{Pt4}6+ and {Pt2Pd}2+↔{Pt2Pd}3+↔{Pt2Pd}4+, at σ-type orbitals overlapping with each of the other metal dz2 filled frontier molecular orbitals.6, 9 Compounds {Pt4}5+ and {Pt2Pd}3+ have delocalized unpaired electrons over their 1D backbones;8a, 9 in particular, {Pt4}5+ is well known as “platinum blue”10 and is also categorized as a Class-II mixed-valent compound.4a Simply mixing {PMo12}3− or {P2Mo18}6− with {Pt4}4+ or {Pt2Pd}2+ in the appropriate solvents and slow evaporation afforded dark blue single crystals of [{PMo12O40}{Pt2(piam)2(NH3)4}2]n ⋅ 6nMe2CO (1), dark green single crystals of [{PMo12O40}{Pt2Pd(piam)4(NH3)4}]n ⋅ 5nMeCN (2), and green single crystals of (NH4)n[{P2Mo18O62}{Pt2(piam)2(NH3)4}2]n ⋅ nH2O ⋅ 4nMeCN (3).
Crystal Structures of Assembles 1–3
A single-crystal X-ray analysis revealed that compound 1 had a 1D structure (Figure 1a), where {PMo12} and {Pt4} were alternately aligned with close distances of 3.42 Å between the bridging oxygen and platinum atoms, supported by quadruple hydrogen bonds with donor ligands in {Pt4}. This close distance was shorter than the oxygen–platinum van der Waals radii, which are approximately 1.5 Å11 and 2.1 Å12 for Oe and Pt, respectively. As shown in Figures 1b and 1c, compounds 2 and 3 also formed 1D structures composed of alternate alignments of POM and multinuclear complexes. In 2, the distance between {PMo12} and {Pt2Pd} was 3.40 Å, similar to that in 1, whereas in 3, shorter 2.84 Å and 3.41 Å distances between bridging oxygen and platinum atoms were observed due to the presence of four crystallographically independent platinum atoms. In the crystals, each 1D chain was packed in a parallel fashion (Figures 1d–f), and solvent molecules were accommodated among the chains. In particular, in 3, channels with diameters of approximately 6 Å contained acetonitrile, water, and ammonium ions. The shortest intercluster Ot−Ot distances were estimated to be 6.1 Å (1), 3.1 Å (2), and 3.2 Å (3). In 1 and 2, the central P atom is surrounded by a cube of eight disordered oxygen atoms, and the Mo atoms are situated at the corners of a regular cuboctahedron due to the crystallographic symmetry.
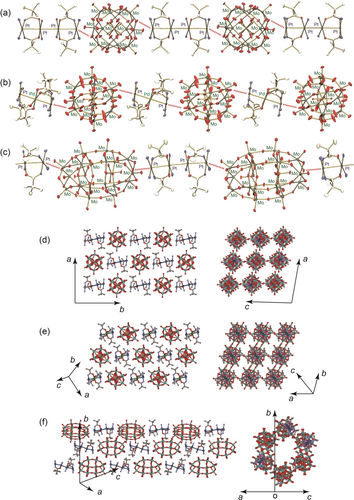
Crystal structures and packing views for (a and d) [{PMo12O40}{Pt2(piam)2(NH3)4}2]n ⋅ 6nMe2CO (1), (b and e) [{PMo12O40}{Pt2Pd(piam)4(NH3)4}]n ⋅ 5nMeCN (2), and (c and f) (NH4)n[{P2Mo18O62}{Pt2(piam)2(NH3)4}2]n ⋅ nH2O ⋅ 4nMeCN (3). Hydrogen atoms, NH4+, and solvent molecules are omitted for clarity.
Metal Oxidation States and Behaviours of Unpaired Electron in Assembles 1–3
Considering the chemical formulae, the overall charges were 0 for {PMo12}–{Pt4} in 1, 0 for {PMo12}–{Pt2Pd} in 2, and −1 for {P2Mo18}–{Pt4} in 3. The formal metal oxidation states in {Pt4} and {Pt2Pd} were assumed by comparing the metal–metal distances because the HOMOs in these complexes are dz2 orbitals that sensitively influence the metal–metal bonds.6 The intra- and inter-Pt−Pt distances were 1: 2.8153(6) Å and 2.9068(8) Å, and 3: 2.7446(4), 2.8188(4) Å and 2.8443(5) Å, which were similar to those of [Pt2(piam)2(NH3)4]25+ with a Pt(+2.25) average oxidation state.8a Additionally, in {Pt2Pd}, the oxidized form had shorter metal–metal distances, where the Pt−Pd distance (2.6535(3) Å) in 2 was closer to that of [Pt2Pd(piam)4(NH3)4]3+ (2.6601(9) Å) than that of [Pt2Pd(piam)4(NH3)4]2+ (2.8500(5) Å),9 resulting in {Pt2Pd(+2.33)}3+. Consequently, the charges of the POMs were {PMo12}5− in 1, {PMo12}3− in 2, and {P2Mo18}6− in 3, and the molybdenum average oxidation state in 1 was Mo(+5.83) due to two-electron reduction, although those in 2 and 3 were not changed to Mo(+6) from parent ones. The reduced {PMo12}5− in 1 was also confirmed by the alternating short and long bond lengths (ABLs),13 where the Oe atoms with off-centre displacements among two Mo atoms led to short and long distances in the Mo−Oe bonds. The differences in ABL distortions tend to decrease with the reduction in POMs. For example, when comparing the short and long Mo−Oe distances in {PMo12}3− and one-electron reduced {PMo12}4−, the differences of in {PMo12}4− is smaller than those in {PMo12}3−. As explained in Supporting Information with Tables S3–4 and Figure S15, the average distances for the short and long bonds were 1.868(3) Å and 1.939(3) Å for 1, 1.816(2) Å and 1.988(2) Å for 2, and 1.834(3) Å and 2.041(3) Å for 3; the average distances found in 1 strongly supported {PMo12}5−.13
Infrared (IR) spectroscopy and X-ray photoelectron spectroscopy (XPS) also supported these assignments. It is possible to estimate the metal oxidation states of POM by comparison with IR spectra.14 The Mo=Ot stretching vibration in the IR spectrum for 1 was observed at 952 cm−1 (Figure 2b), shifting lower from 962 cm−1 in Na3[PMo12O40] (Figure 2a), indicating the lower oxidation state in Mo atoms.14 Additionally, the Mo−Ob−Mo (890–850 cm−1) and Mo−Oc−Mo (800–760 cm−1) stretching vibrations, where Ob and Oc were the Oe atoms in the corner-sharing and edge-sharing octahedra, respectively, became broader than the original ones.
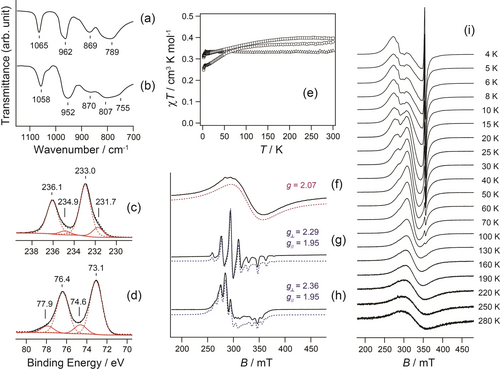
IR spectra (KBr pellet) of (a) Na3[PMo12O40] and (b) 1. (c) Mo 3d3/2 and 3d5/2 core levels of XPS for 1. Resolved red dotted and solid lines correspond to Mo(+6) and Mo(+5), respectively. (d) Pt 4f5/2 and 4f7/2 core levels of XPS for 1. Resolved red solid and dotted lines correspond to Pt(+3) and Pt(+2), respectively. (e) Temperature dependence of χT of 1 (circle), 2 (square), and 3 (triangle) per {POM}–{Pt complex} unit. Continuous wave EPR spectra measured at room temperature for powder samples of (f) 1, (g) 2, and (h) 3. Solid lines are the measured spectra, and dotted lines are the simulations. (i) Temperature dependence of EPR spectra for powder samples of 1 in the range 4–280 K.
The XPS spectra of 1 showed that the Mo 3d3/2 and 3d5/2 binding energies were 236.1 and 233.0 eV, respectively, which were characteristic of Mo(+6),15 accompanied by those for Mo(+5) at 234.9 and 231.7 eV (Figure 2c). Deconvolution of these four peaks resulted in a Mo(+6) to Mo(+5) area ratio of 1.00 : 0.20, leading to an average oxidation state of Mo(+5.83), which was similar to the value estimated by single-crystal X-ray analysis. However, in the Pt 4f5/2 and 4f7/2 regions for 1 (Figure 2d), the binding energies for Pt(+3) were 77.9 and 74.6 eV, and those for Pt(+2) were 76.4 and 73.1 eV,16 with an area ratio of 0.17 : 1.00 for Pt(+3) and Pt(+2), respectively, leading to the average oxidation state of Pt(+2.15). However, in regions 2 and 3, the peaks in the Mo region indicate a single component of Mo(+6) (Figure S18); however, a weak Mo(+5) peak was observed in region 2, and the peaks in the Pt region constitutes the two components for Pt(+3) and Pt(+2) (Figure S19). Based on the area ratio in 2 to 3, Pt(+3) : Pt(+2)=0.55 : 1.00 and 0.28 : 1.00, the average Pt oxidation states were calculated as Pt(+2.35) and Pt(+2.22), respectively. Furthermore, for 2, the Pd 3d3/2 and 3d5/2 binding energies were 344.4 and 338.3 eV for Pd(+3) and at 343.0 and 337.5 eV for Pd(+2), respectively, with an area ratio of Pd(+3) : Pt(+2)=0.51 : 1.00 (Figure S20), although the parent [Pt2Pd(piam)4(NH3)4](PF6)3 with {Pt2Pd(+2.33)} was difficult to be distinguish with XPS.9 Consequently, IR and XPS supported the formal oxidation states estimated with the single-crystal X-ray analyses, {PMo(+5.83)12}–{Pt(+2.25)4} in 1, {PMo(+6)12}–{Pt2Pd(+2.33)} in 2, and {P2Mo(+6)18}–{Pt(+2.25)4} in 3, whose mixed-valence resulted in unpaired electrons in the metals.
Figure 2e shows the magnetic susceptibility data for 1–3 over the temperature range 2–300 K. The χT values at 300 K were 0.38, 0.40, and 0.34 cm3 K mol−1 for 1, 2, and 3, respectively, similar to the spin-only value of 0.375 cm3 K mol−1, indicating that one unpaired electron was present in the {POM}–{Pt complex}. With decreasing temperature, the χT values gradually decreased to 0.25, 0.31, and 0.32 cm3 K mol−1 at 2 K; the data were fitted to the Curie–Weiss law χ=C/(T–θ), yielding 1: C=0.39 cm3 K mol−1 and θ=−9.9 K; 2: C=0.42 cm3 K mol−1 and θ=−12.2 K; and 3: C=0.33 cm3 K mol−1 and θ=−0.4 K (Figures S21–S23). The negative θ values indicated weak antiferromagnetic interactions. Figure 2f–h shows the electron paramagnetic resonance (EPR) spectra of powders 1–3 at room temperature. The spectrum for 1 contained an isotropic signal with g=2.07, whereas those for 2 and 3 contained axial-type signals with hyperfine splitting. Whether the axial-type or isotropic signals are observed in EPR in this case depends on the mobility of the unpaired electrons, as explained below. Five separate signals with g⊥=2.29, g//=1.95, A⊥=345×10−4 cm−1, and A//=325×10−4 cm−1 were found for 2, which is typical for dz2 spin delocalized on Pt−Pd−Pt,9 where two 195Pt nuclei (I=1/2 with an abundance of 33.7 %) exhibited splitting without the 105Pd nuclei (I=5/2 with an abundance of 22 %), supporting the oxidation state {Pt2Pd(+2.33)}. In contrast, in 3, nine separated signals with g⊥=2.36, g//=1.95, A⊥=220×10−4 cm−1, and A//=180×10−4 cm−1 were typical for dz2 spin delocalized on Pt−Pt−Pt−Pt,8a where four 195Pt nuclei affect the splitting, supporting the oxidation state {Pt4(+2.25)}.
Figure 2i shows the variable-temperature EPR spectra (T=4–280 K) for a powdered sample of 1. In addition to a broad isotropic signal without hyperfine structure, axial-type signals with g⊥=2.48 and g//=1.91 and sharp isotropic signals with g=1.95 appeared below 100 K (Figure S24). Considering these g values, the axial-type and sharp isotropic signals were attributed to dz2 spin delocalized on Pt−Pt−Pt−Pt8a and Mo dxy spin,4b, 17 respectively, and the intensities increased with decreasing temperature. These two signals indicated that 1 contained two unpaired electrons, a Pt dz2 spin with {PMo(+5.83)12}–{Pt(+2.25)4} and a Mo dxy spin with {PMo(+5.92)12}–{Pt(+2)4}, suggesting that the broad isotropic signal was a coreless signal. Consequently, bistable oxidation states, {PMo(+5.83)12}–{Pt(+2.25)4}↔{Pmo(+5.92)12}–{Pt(+2)4}, were observed for 1, and the unpaired electron hopped between {PMo12} and {Pt4}.
As shown in Figure 2i, the coreless isotropic signals became sharper as the temperature increased from 4 to 40 K, whereas above 40 K, the g values of the coreless signals are similar over the whole temperature range (Figure S25b), and both the Pt dz2 and Mo dxy signals completely disappeared above 100 K. The electron hopping frequency monotonically increased with increasing temperature, which was proportional to the peak-to-peak linewidth of the EPR signals.4b, 17d Assuming that the hopping frequency can be expressed by the Arrhenius equation, an activation energy of 0.02 eV was obtained (Figure S25c), which was approximately half that for hopping in {PMo12}4− (0.035 eV).4b, 17d In other words, the activation barrier of {PMo(+5.83)12}–{Pt(+2.25)4}↔{PMo(+5.92)12}–{Pt(+2)4} was 0.02 eV, which was lower than that for delocalization in {PMo12}4−, meaning that the unpaired electron in {PMo12} more easily hopped to {Pt4}. Additionally, for 2, below 100 K, Mo dxy signals appeared in addition to the signal for the dz2 spin (Figures S26 and S27), which was caused by partially reduced Mo(+5), as discussed later. However, for 3, only Pt dz2 signals were observed over the whole temperature range (Figure S29).
Absorption Spectra and DFT Calculations
Figure 3a shows diffuse reflectance spectra of 1–3 at room temperature. All three compounds exhibited intense and broad absorption peaks in the visible and near-infrared regions, with peak maxima at 705 (1), 1037 (2), and 725 (3) nm. It is well known that mixed-valent compounds exhibit intervalence charge-transfer (IVCT) bands at approximately 600–1200 nm with deep blue or green colours,4a which were also observed for both the POMs1a, 18 and platinum multinuclear complexes.6b To determine the reason for the absorption band observed in Figure 3a, the molecular orbitals of the {Pt complex}–{POM}–{Pt complex} were determined with density functional theory (DFT) and time-dependent (Td)-DFT calculations. Figure 3b shows the frontier orbitals of 1 calculated with the model [{Pt2(NHCOCH3)2(NH3)4}2{PMo12O40}{Pt2(NHCOCH3)2(NH3)4}2]5+ with S=1 (Figures S30–31). Both the α- and β-HOMOs were Mo dxy orbitals in {PMo12}, whereas both the α- and β-HOMO–1 and HOMO–2 orbitals were dz2 orbitals over Pt−Pt−Pt−Pt. The estimated Mulliken charges were {Pt4}4.86+–{PMo12}4.74−–{Pt4}4.88+ (Table S7), which were consistent with the experimental results. Td-DFT calculation revealed the transitions from these dz2 orbitals to vacant Mo dxy orbitals serving as α-LUMOs at 666.2 nm (f=0.1389) and to vacant Pt dz2 orbitals serving as β-LUMOs at 660.1 nm (f=1.2804), which coincided well with the observed values (Figure S30).
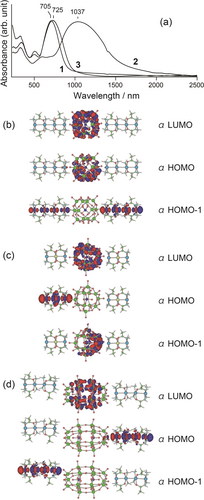
(a) Diffuse reflectance spectra of 1–3 with MgO at room temperature. The obtained reflectance spectra were converted to absorption spectra using the Kubelka–Munk function. Molecular orbitals estimated by the DFT calculation on the model of (b) [{Pt2(NHCOCH3)2(NH3)4}2{PMo12O40}{Pt2(NHCOCH3)2(NH3)4}2]5+ for 1, (c) [{Pt2Pd(NHCOCH3)4(NH3)4}{PMo12O40}{Pt2Pd(NHCOCH3)4(NH3)4}]+ for 2, and (d) [{Pt2(NHCOCH3)2(NH3)4}2{P2Mo18O62}{Pt2(NHCOCH3)2(NH3)4}2]4+ for 3.
For 2, the Td-DFT calculations based on [{Pt2Pd(NHCOCH3)4(NH3)4}{PMo12O40}{Pt2Pd(NHCOCH3)4(NH3)4}]3+ with S=1 showed an intense absorption at 503.8 nm (f=0.5148) attributed to the IVCT in {Pt2Pd}, which is quite far from the observed value (Figure S32). Therefore, similar calculations were conducted for one-electron reduced [{Pt2Pd(NHCOCH3)4(NH3)4}{PMo12O40}{Pt2Pd(NHCOCH3)4(NH3)4}]2+ with S=1/2 (Figures S34–35) or two-electron reduced [{Pt2Pd(NHCOCH3)4(NH3)4}{PMo12O40}{Pt2Pd(NHCOCH3)4(NH3)4}]+ with S=1 (Figures S36–37), and the results were relatively consistent with the observed results. As observed for the α- and β-HOMO in the one-electron reduced model and for the α-HOMO–1 in the two-electron reduced model, the added electrons were in the Mo dxy orbitals of {PMo12}, which led to destabilization of the filled orbitals with lower energy absorptions. For example, Td-DFT calculations for a one-electron reduced model show that the absorption at 1093.7 nm (f=0.0051) was attributable to α/β-HOMO→LUMO+15 (Figure S34), and the two-electron reduced model showed that the absorption at 1069.7 nm (f=0.0063) was attributable to α/β-HOMO→LUMO+11 (Figure S36), both of which corresponded to charge transfer from {Pt2Pd} to {PMo12}. Consequently, partial reduction at {PMo12} could occur, although crystal structure and IR results showed that the formal oxidation state of 2 was {PMo(+6)12}–{Pt2Pd(+2.33)}. In fact, the XPS data showed small peaks attributed to the reduced Mo(+5) (Figure S18d), and the EPR spectrum obtained at low temperature showed Mo dxy spins (Figure S26), supporting this assignment. However, for 3, DFT calculations were conducted with the [{Pt2(NHCOCH3)2(NH3)4}2{P2Mo18O62}{Pt2(NHCOCH3)2(NH3)4}2]4+ model and S=1, and absorptions at 626.7 nm (f=1.4065) and 620.3 nm (f=0.2570) were attributed to IVCT in {Pt4} (Figure S39). Since there was a slight difference between the calculated and observed values, calculation of two-electron injection model with S=1 were also conducted (Figure S41), revealing that the absorption at 708.3 nm (f=0.1942) was attributed to IVCT in {P2Mo18}; however, 3 was not involved in the reduction based on the EPR results.
Electrical Conductivity
Figure 4 shows the results of DC electrical conductivity measurements. The single crystal was too small to be terminalized properly, so the possibility of using pellets was investigated (Figures S45). The current–voltage (I–V) characteristics were linear, and the conductivities were evaluated from the slopes of the lines as 1.0×10−8 (1), 7.0×10−8 (2), and 3.0×10−7 (3) Scm−1. The conductivities at room temperature increased in the order 1<2<3. The conductivity of Dawson-type [Pr4N]6[S2MoV2MoVI16O60] ⋅ solv with mixed valence was 1.6×10−12 S cm−1,11 meaning that for 3 was approximately 106 times greater than that of the parent compound. As shown in Figure 4, the resistivities for 1–3 increased exponentially with decreasing temperature, indicating thermally activated semiconductor behaviour. The activation energies were estimated from the slopes of the Arrhenius plots as 1: 0.60 eV at 270–297 K, 2: 0.48 eV at 239–298 K, and 3: 1.70 eV at 273–300 K (Figures S46–S48). The temperature dependence of conductivity was also successfully measured using single crystal 3, and the activation energy was found to be 0.35 eV at 238–286 K (Figure S49). Since the maximum absorption energies found in the diffuse reflectance spectra were 1.76 (1), 1.20 (2), and 1.71 (3) eV, indicating approximately 1 eV optical band gaps for 1–3, the estimated activation energies were valid. The greater activation energy of 3 compared with those of 1 and 2 was attributed to the structural geometry of {P2Mo18}. Unlike the Keggin-type {PMo12}, where each metal occupies an equivalent site, the Dawson-type {P2Mo18} contained two types of Mo atoms, six Mo atoms at the polar edges and twelve Mo atoms at other edges.
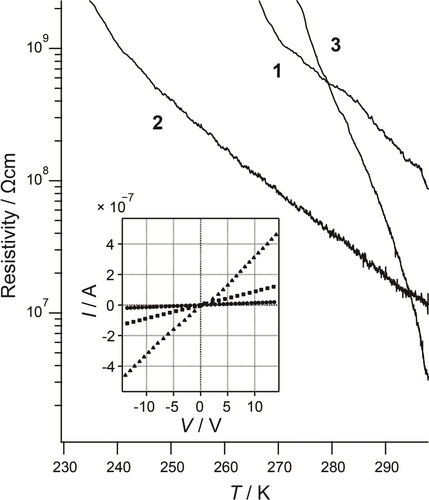
Temperature dependence of resistivity of 1–3. The electronic properties were measured with compressed pellet attached by two Au wires. Insert: Current–voltage relationship of 1 (circle), 2 (square), and 3 (triangle) at room temperature.
To date, two mechanism for POM conductivity have been reported: proton conductivity19 and framework conductivity.20 Both are realized in channel-surrounded POMs, where the latter conductivity is related to organic conductors such as tetrathiafulvalene (TTF) accommodated in the pores.20 Table 1 summarizes the conductivity and activation energies of related previous compounds, indicating that compound 1–3 conducts electricity relatively well compared to these compounds. To our knowledge, there is few examples of an intrinsically conducting framework, where (TTFPyH)2[PMoVMoVI11O40] with strong electron-donor TTF derivatives shows a conductivity of 6.3×10−7 Scm−1 at room temperature.21 The conductivities of mixed-valent assemblies 1–3 were similar to this pioneered compound, and the intrinsic conductivity of the POMs was enhanced by the electronic interaction between the Oe p orbital and Pt dz2 orbital.
Compounds |
Conductivity at r.t. (Scm−1) |
Activation energy (eV) |
Measured sample |
References |
|---|---|---|---|---|
(TTFPyH)2[PMoVMoVI11O40] |
6.3×10−7 |
0.42 |
single crystal |
[21] |
(Et4N)6[S2MoV2MoVI16O60] ⋅ solv |
1.17×10−8 |
0.27 |
single crystal |
[11] |
(Et4N)6[S2MoV2MoVI16O60] ⋅ solv |
2.15×10−10 |
0.44 |
pellet |
[11] |
(Pr4N)6[S2MoV2MoVI16O60] ⋅ solv |
4.78×10−12 |
0.39 |
single crystal |
[11] |
(Pr4N)6[S2MoV2MoVI16O60] ⋅ solv |
1.60×10−12 |
0.55 |
pellet |
[11] |
(Bu4N)6[S2MoV2MoVI16O60] ⋅ solv |
8.99×10−13 |
0.58 |
single crystal |
[11] |
K3.5Li1.5[Co(H2O)4]4[NaP5W30O110] ⋅ 0.5H2O |
9.2×10−5 |
– |
single crystal |
[2b] |
K3.5Li1.5[Co(H2O)4]4[NaP5W30O110] ⋅ 0.5H2O |
2.1×10−7 |
– |
single crystal |
[2b] |
1 |
1.0×10−8 |
0.60 |
pellet |
this work |
2 |
7.0×10−8 |
0.48 |
pellet |
this work |
3 |
3.0×10−7 |
1.70 |
pellet |
this work |
3 |
6.9×10−7 |
0.35 |
single crystal |
this work |
Conclusion
In this manuscript, spherical POMs and multinuclear platinum complexes were one-dimensionally assembled in the solid state, and their physical properties were thoroughly investigated. Three assembles 1–3 have mixed-valent metal oxidation states and unpaired electrons on metal d orbitals, showing semiconducting behaviours with a conductivity of 10−6 Scm−1, which was 105 times greater than that of the parent POMs. Since molecular conductors have the advantages of designability and precise control of the band structures, these mixed-valent assemblies are expected to be useful in modulating electrical transport properties via judicious combinations of POMs and multinuclear complexes.
Deposition Numbers 2301017 (for 1), 2301018 (for 2), 2301019 (for 3) contain the supplementary crystallographic data for this paper. These data are provided free of charge by the joint Cambridge Crystallographic Data Centre and Fachinformationszentrum Karlsruhe Access Structures service.
Acknowledgments
This work was supported by JSPS KAKENHI (Scientific Research (C) 21K05098), and CASIO Science Promotion Foundation, Shimadzu Science Foundation, TEPCO Memorial Foundation, Futaba Electronics Memorial Foundation, Kato Foundation for Promotion of Science, Research Foundation for the Electrotechnology of Chubu, Toyota Physical and Chemical Research Institute, Foundation of Public Interest of Tatematsu, Fujimori Science and Technology Foundation, the Koshiyama Research Grant, and Takahashi Industrial and Economic Research Foundation. Theoretical calculations were performed using the Research Center for Computational Science, Okazaki, Japan. A part of this work was conducted in Institute for Molecular Science, supported by Advanced Research Infrastructure for Materials and Nanotechnology in Japan (JPMXP1223MS1031) of the Ministry of Education, Culture, Sport, Science and Technology (MEXT), Japan.
Conflict of Interests
The authors declare no conflict of interest.
Open Research
Data Availability Statement
The data that support the findings of this study are available in the supplementary material of this article.




