Platform trials allow efficient evaluation of multiple interventions for a specific disease. The HEALEY ALS Platform Trial is testing multiple investigational products in parallel and sequentially in persons with amyotrophic lateral sclerosis (ALS) with the goal of rapidly identifying novel treatments to slow disease progression. Platform trials have considerable operational and statistical efficiencies compared with typical randomized controlled trials due to their use of shared infrastructure and shared control data. We describe the statistical approaches required to achieve the objectives of a platform trial in the context of ALS. This includes following regulatory guidance for the disease area of interest and accounting for potential differences in outcomes of participants within the shared control (potentially due to differences in time of randomization, mode of administration, and eligibility criteria). Within the HEALEY ALS Platform Trial, the complex statistical objectives are met using a Bayesian shared parameter analysis of function and survival. This analysis serves to provide a common integrated estimate of treatment benefit, overall slowing in disease progression, as measured by function and survival while accounting for potential differences in the shared control group using Bayesian hierarchical modeling. Clinical trial simulation is used to provide a better understanding of this novel analysis method and complex design. ANN NEUROL 2023;94:547–560

The HEALEY ALS Platform trial includes multiple innovative design features, including early stopping for success or futility, sharing of control participants, and a Bayesian shared parameter model that integrates evaluation of both function and survival when estimating treatment effectiveness. This manuscript describes these features and how we evaluate their performance.

Platform trials evaluate multiple interventions, usually within the same disease. They allow both operational and statistical efficiency compared with a traditional randomized clinical trial that evaluates a single therapy.^1-4 Platform trials have been successfully implemented in several medical fields, including oncology,^5-9 neurology,^10-13 and infectious disease.^14-17

The synergy and efficiency offered from a platform trial is especially important for a disease with a dramatic unmet medical need and a large investigational product pipeline, such as amyotrophic lateral sclerosis (ALS). The HEALEY ALS Platform Trial is a multicenter, randomized, placebo-controlled, adaptive, perpetual platform trial.¹² The primary aim of the trial is to estimate the safety and effectiveness of novel investigational products (IP) among persons with ALS. The platform trial is governed by a master protocol (MP) that specifies the global design of the trial (HEALEY ALS Platform Trial Research Partners [massgeneral.org]). Regimen-specific appendices specify the unique tailoring of the design for each regimen, and they are used to evaluate a particular IP. The regimen-specific appendices describes the preclinical and clinical background supporting the study of a given IP, any deviation from the schedule of activities specified in the MP, the physical and pharmacologic characteristics of the IP, its mode of administration and dosing, the placebo treatment used to mask treatment assignment within the regimen, any additional eligibility criteria beyond those specified in the MP, and any modifications to the primary and interim analyses specified in the MP.

Participants are screened and randomized in two stages (regimen and treatment group). Participants and investigators know the regimen to which a participant was assigned, but are blind to the regimen-specific treatment group to which they were randomized. The first stage consents participants to the platform trial, determines eligibility based on the common criteria specified in the MP, and openly assigns eligible participants at random and in equal ratio to one of the active regimens at the participant's site. The second stage consents participants to their assigned regimen, determines eligibility based on the applicable regimen-specific appendices, and blindly randomizes the participant to active treatment or the regimen-specific placebo at a ratio of 3:1. Primary analyses of each regimen use data from placebo participants shared from other regimens (Figure 1).

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

HEALEY ALS Platform Trial Schematic

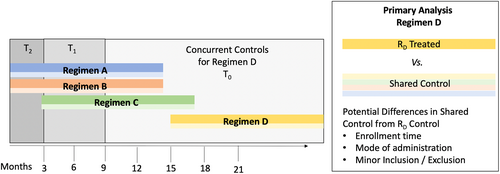
The HEALEY ALS Platform Trial has a control cohort that includes shared placebo-treated participants across regimens and across time (Figure 1).^{2, 4} The sharing of placebo participants from other regimens allows fewer total participants randomized, and greater allocation of participants to active treatment within each regimen without decreasing power relative to traditional designs with 1:1 randomization.

Although sharing of placebo data across regimens increases statistical efficiency and reduces overall allocation to placebo, analyses involving shared controls require careful consideration to avoid bias.^{2, 4} Regimens in the platform trial may differ with respect to enrollment time, mode of IP administration, and eligibility criteria related to safety (Figure 1). Throughout this manuscript, we refer to these potential differences across regimens due to differences in mode of administration and minor additional inclusion/exclusion as “regimen-specific effects,” and potential differences across regimens due to differences in enrollment time as “time-trend effects.” The platform trial attempts to minimize regimen-specific effects by enrolling under the common conditions set by the master protocol, at the same sites, with the same visit schedule, and outcome collection training.

In addition to the innovative platform trial design and sharing of control participant data across regimens, the HEALEY ALS Platform Trial design also includes an innovative Bayesian primary analysis model that considers specific regulatory guidance within the specific disease area of ALS. A Bayesian approach is used to create a shared parameter model of function and survival, and adjust for potential differences in the shared control across regimens.

Traditional approaches to primary analyses in drug development often use frequentist statistics. Frequentist statistics assume that quantities of interest, such as treatment effects, are fixed and use repeated sampling to evaluate the likelihood of the data under that assumption. For example, the regulatory guidance in ALS mentions a nonparametric frequentist joint rank test of function and survival.^{18, 19} This frequentist test results in a p-value that gives the likelihood that one would observe a test statistic as extreme or more extreme than what was observed in the trial if the null hypothesis were true and the treatment effect was null (ie, no benefit on the treatment). The frequentist approach makes no assumption about the magnitude of the true effect of treatment.

The Bayesian approach assigns probability distributions to quantities of interest (prior distributions); for example, a treatment effect, and combines these prior assumptions with the likelihood of the observed data to yield updated probabilities of quantities of interest (posterior distributions).^20-22 The updating is performed using Bayes' theorem. In general, prior distributions may be noninformative, weakly informative, or may be informed by previous experiences, and must be prespecified before an analysis. The probabilistic framework of Bayesian statistics may be more intuitive and is used increasingly in clinical trial design to: (1) inform future studies with historical results, (2) frequently update emerging evidence to make prespecified adaptations over the course of a trial, and (3) to combine multiple sources of information using meta-analytic approaches and hierarchical models.^23-26

Both frequentist and Bayesian approaches may use hierarchical models, where source-specific effects (eg, differences among regimens, differences among participants within regimen, differences among observations of the same participant) are modeled to account for different sources of variance while still allowing for inclusion of information from multiple sources.^27-29 The source-specific effects are assumed to come from a common probability distribution with unknown mean and variance parameters. In a Bayesian hierarchical analysis, a second level of prior distributions (called hyperpriors) are also placed on these overall underlying unknown parameters. This allows for sharing (ie, borrowing) of information across sources that is dynamic and dependent on the observed variability among these sources. Hierarchical models are typically structured to more heavily borrow information if the observed variability across sources is small, and to borrow little information if observed variability across sources is large. Examples of utilization of Bayesian hierarchical models within the clinical trial setting include: (1) borrowing information from adult clinical trials in pediatrics,³⁰ (2) supplementing randomized controls with historical controls,³¹ (3) borrowing information across multiple subtypes of a disease within a basket trial,^32-34 and (4) borrowing information across different groups of controls or across different periods of time within a platform trial.^{5, 6, 10, 12, 15, 17}

The Bayesian shared parameter primary analysis model within the HEALEY ALS Platform Trial provides an integrated estimate of treatment benefit between function and survival, and utilizes the Bayesian hierarchical model framework to allow dynamic sharing of information in controls across regimens (regimen-specific random effects) and account for differences in control effects over time (time–trend effects). This model construction accommodates both the statistical complexities of a platform trial and consideration of the regulatory guidance for ALS. In the following sections, we illustrate the use of clinical trial simulation to describe performance of the model to a diverse group of industry, regulatory, scientific, and patient stakeholders.

Statistical Modeling of an Adaptive Platform Trial in ALS

Regulatory Guidance and Traditional Statistical Approaches in ALS

When considering a complex/innovative trial design with potential regulatory oversight, early and frequent communication with regulatory agencies can help pave the way to acceptance.³⁵ The HEALEY ALS Platform trial was developed through early and frequent communication between trial investigators and the Food and Drug Administration to ensure the results from the platform trial would generate evidence supportive of regulatory review of novel agents if positive results are obtained.

Regulatory guidance in ALS states: “If patient function is intended to be assessed as the primary outcome, mortality should be integrated into the primary outcome by an analysis method that combines survival and function into a single overall measure, such as the joint rank test”.^{18, 19} Thus, primary analyses in trials of ALS should integrate function and survival.

One possible approach to integrating function and survival within a single primary analysis suggested by the Food and Drug Administration is a joint rank test of survival and function (Combined Assessment of Function and Survival [CAFS]) that scores each participant against all other participants based first on survival time, if relative survival time is observed, and on change from baseline in the Revised Amyotrophic Lateral Sclerosis Functional Rating Scale (ALSFRS-R) total score to the last common observation time if relative survival time is not observed (eg, if one participant discontinues follow-up prior to mortality of the other participant). The pairwise scores are summed and then ranked, and a nonparametric test is used to compare the ranks of participants in the treatment group with the ranks of participants in the control group. The benefit of this approach is that it relies on limited assumptions. The main assumption is that death at any date during follow-up is worse than any amount of ALSFRS-R decline before death. Limitations of this approach within a traditional clinical trial setting are that: (1) it does not provide a clinically meaningful treatment effect estimate, and (2) the nonparametric approach does not accommodate sources of variance other than person-level variance, and does not directly accommodate adjustments for baseline covariates. A solution to the latter has been to perform a linear regression of the ranks that adjusts for meaningful baseline covariates. However, the ranks (being correlated with one another) violate the assumption of independent observations within the linear regression framework and are uniformly distributed. Extension of the joint rank analysis to accommodate the regimen-specific and time–trend effect present in a platform trial has not previously been explored. Alternative parametric joint analysis methods of function and survival have been proposed within the frequentist settings.^{36, 37}

Primary Analysis in the HEALEY ALS Platform Trial: Bayesian Shared Parameter Model of Function and Survival

In the HEALEY ALS Platform Trial, the primary analysis population for a given regimen is guided by the intention-to-treat principle, and includes all participants randomized to the active treatment arm within the analysis regimen, all participants concurrently randomized to the control arm within the analysis regimen, and control participants from other regimens that form a shared control (Figure 1).

The primary analysis method is a Bayesian shared parameter model of function and survival that provides an integrated estimate of a clinically interpretable treatment effect on both outcomes, and allows for dynamic sharing of controls across regimens in the Bayesian hierarchical modeling framework by introducing regimen-specific effects and time-trend effects.^{31, 38, 39} Within the Bayesian framework, the information in the likelihoods from both the functional outcome and the survival outcome are used to update the prior belief of overall treatment benefit across the population. This results in a posterior estimate of a common integrated slowing in the rate of disease progression between the two outcomes, referred to as the disease rate ratio (DRR). This common slowing in disease progression over time is akin to the ratio of slopes in a slope analysis of function or a hazard ratio (HR) in proportional hazards survival analysis, and has the same meaningful clinical interpretation. Values of DRR <1 indicate treatment benefit, a slowing of functional progression, and slowing of time to death. For example, a DRR of 0.5 would equate to a 50% slowing in disease progression where a treated participant would be expected to progress to the same state as a control participant in double the amount of time.

The assumption of a common treatment effect in both function and survival is not required to provide meaningful inference. If the effects on the two components are different, the overall integrated measure provides an estimate of the treatment effect that is averaged across the two endpoints with a weight determined by the frequency of observed survival.

The primary efficacy hypothesis test to be evaluated for a given regimen is the following:

H_{0} : DRR \geq 1;

H_{A} : DRR < 1 .

The null hypothesis $(H_{o})$ will be rejected for a regimen at the final analysis if the Bayesian posterior probability that the treatment is superior to the control group ( $H_{A} : DRR < 1$ ) is ≥0.979. The threshold for the final analysis of 0.979 was chosen to control the simulated type I error at 2.5% across a wide range of null simulation scenarios (Table 2).

The functional component of the Bayesian shared parameter model is a repeated measures model of ALSFRS-R total score at baseline through 24 weeks for all participants who survived. Participants who have experienced mortality will not contribute to the functional component of the analysis; this ensures a higher priority to the survival component, as done with the CAFS analysis. The ALSFRS-R repeated measures model of survivors is based on a linear rate of progression in ALSFRS-R through 24 weeks for control participants and a proportional slowing in the rate of progression for treated participants at each time point. The model assumes observations of ALSFRS-R are normal random variables and incorporates the following parameters (described in Table 1): (1) fixed effects for the overall mean baseline value of ALSFRS-R (intercept) per regimen and treatment arm; (2) participant-level random effects in the baseline value of the ALSFRS-R (intercept); (3) participant-level random effects in the rate of progression (slope per month); (4) multiplicative/proportional effects to the slope for, treatment versus control: denoted as DRR, baseline standardized covariate effects for a set of prespecified covariates, regimen-specific effects, and time-trend effects; and (5) regimen and treatment arm-specific values for measurement error.

TABLE 1. Bayesian Shared Parameter Model Parameters + Prior Distributions

Parameter	Notation	Prior distribution	Prior justification
Common parameters
Treatment effect: DRR Therapeutic benefit of a regimen	$\exp (θ)$	$\exp (θ) ~ Unif (0, 2)$	NI with equal weight on DRR <1 and DRR $\geq$ 1.
Functional component $Y_{ij} = (α_{r_{i}, t_{i}} + γ_{i}) - β_{i} * \exp (η_{r_{i}} + ρ_{d_{i}} + δ_{C} * C_{i} + θ * t_{i}) * X_{i, j} + ϵ_{i, j};$ $ϵ_{i, j} ~ N {(0, σ_{r_{i}, t_{i}})}^{2}$ $Y_{ij}$ is the total ALSFRS-R score measured at time $X_{ij}$ during visit j for participant i, that has baseline covariates $C_{i}$ . $r_{i}$ : regimen of participant i; 1 for analysis regimen, 2, …, N_R for other regimens adding to shared control $t_{i}$ : treatment arm of participant i; 0 control, 1 for active treatment $d_{i}$ : time of randomization of participant i; 0 for current, 1, …, D number of additional 6-month intervals preceding current time period
Intercept Regimen (R) and treatment arm (T) specific intercept	$α_{R, T}$	$α_{R, T} ~ N (38, 10^{2})$	NI centered on value from historical trials
Participant (i) specific random effect on intercept	$γ_{i}$	$γ_{i} ~ N (0, σ_{γ}^{2});$ $σ_{γ} ~ Unif (0, 10)$	Hierarchical prior with common mean (0) and SD. NI hyperprior on SD (10 is over twice SD observed in historical trials).
Participant (i) specific random slope (per month)	$β_{i}$	$β_{i} ~ N (μ_{β}, σ_{β, t (i)}^{2});$ $μ_{β} ~ N (1, 1^{2});$ $σ_{β, T} ~ Unif (0, 2)$	Hierarchical prior with common mean and treatment-specific SD. Hyperprior on mean centered on historical value. NI hyperprior on SD (2 is over twice SD observed in historical trials).
Regimen (R) specific multiplicative random slope effects (log scale). Differences in slope of shared controls across the regimens.	$η_{R}$	$η_{R} ~ N (0, σ_{η}^{2});$ $1 / σ_{η}^{2} ~ Gamma (1, . 05^{2})$	Hierarchical prior centered on no effect. Hyperprior on precision is informed based on variability in rates of progression from historical trials.
Time (d) trend effects (log scale). Differences in slope due to time of randomization time. Current time-period (d = 0) is the referent group.	$ρ_{d}$	$ρ_{0} = 0; ρ_{d} ~ N (ρ_{d - 1}, σ_{ρ}^{2}); d = 1, \dots D; σ_{ρ} ~ Unif (0, 2) .$	Mean centered on previous time-period. NI hyperprior on SD across time-periods.
Baseline standardized covariate (C) effects (log scale) Differences in slope due to baseline standardized covariates	$δ_{C}$	$δ_{C} ~ N (0, 1^{2})$	NI prior centered on no effect.
Measurement error Regimen (R) and treatment arm (T) specific measurement error	$σ_{R, T}$	$σ_{R, T} ~ Unif (0, 4)$	NI prior (4 is over twice that observed in historical trials)
Survival component $λ_{i} = λ_{0} * \exp (θ * t_{i})$ $λ_{i}$ is the hazard rate of mortality in a proportional hazards model for participant i that experienced the event. $t_{i}$ : treatment arm of participant i; 0 control, 1 for active treatment
Baseline hazard rate	$λ_{0}$	$Gamma (.01,1)$	NI prior centered on value from historical trials

Abbreviations: ALSFRS-R = Revised Amyotrophic Lateral Sclerosis Functional Rating Scale; DRR = disease rate ratio; NI = non-informative; SD = standard deviation;

The survival component is an exponential proportional hazards model with a constant baseline hazard rate for all control participants, and a multiplicative proportional hazard ratio for treat versus control, the DRR. Given the low expected rate of mortality within this study (5% over 24 weeks) and to avoid overparameterization, we did not include covariate, regimen-specific, or time-trend effects in the survival component.

Within a Bayesian analysis, prior distributions must be specified for all model parameters. Table 1 lists all parameters together with their prior distributions. Most of the prior distributions in the primary analysis model are chosen to be weakly informative (ie, with a large amount of variability) to allow the posterior distributions to primarily reflect what is observed in the data. The Bayesian posterior distribution of all model parameters is calculated using Markov chain Monte Carlo.

Within any primary analysis, key assumptions of the analysis must be clearly defined, and sensitivity analyses performed to assess the sensitivity of the primary analysis result to each assumption. This is especially important with complex designs and analyses. The list of the major model assumptions for the primary analysis model in the HEALEY ALS Platform Trial and the analyses that are recommended to be conducted to test the sensitivity of the results to each assumption are as follows. First, linear progression of ALSFRS-R over 24 weeks. This assumption is justified based on investigation of historical trial data with similar inclusion/exclusion criteria over a 24-week duration. Sensitivity analysis: piecewise linear (4-week intervals) rates of progression within the functional component. Second, proportional treatment effect over time. Sensitivity analysis: different treatment effects across time (4-week intervals) within the functional component. Third, common treatment effect between function and survival. Sensitivity analysis: allow for different treatment effects between function and survival. Fourth, Similarity in shared controls. Sensitivity analyses: regimen-only controls analysis, concurrently randomized controls analysis, and analysis across a range of fixed borrowing of controls across regimens.

Additionally, given the nonparametric nature and limited assumptions required by the joint rank CAFS analysis, the CAFS analysis will be performed as a key supportive analysis.

Characterizing a Complex Design with Clinical Trial Simulations

In complex and innovative trial designs, such as the HEALEY ALS Platform Trial, there are no simple mathematical formulas to calculate operating characteristics of a trial design and primary analysis. Rather, virtual clinical trial simulations are used to characterize and understand these operating characteristics prior to trial execution.²⁷ Virtual patient outcomes under different assumptions for key design parameters are simulated, creating example trials that can be analyzed using the proposed primary analysis. Thousands of example trials may be simulated under each scenario, and overall operating characteristics may be summarized to quantify important characteristics of the proposed design (eg, type I error, power, treatment effect estimates, early stopping frequencies) and optimize the design under a range of plausible assumptions. An additional benefit of trial simulation is that single example trials may be presented to demonstrate and better understand complexities of the design performance and analysis methods.

Clinical trial simulations were used in the HEALEY ALS Platform Trial to optimize the design (inclusion/exclusion criteria, sample size and length of follow-up, adaptive rules for stopping early for futility or success, inclusion of important baseline covariates in the analysis). Additionally, simulations were used to demonstrate how the innovative primary analysis methods: (1) integrate function and survival, and (2) account for differences in shared controls across regimens. For demonstration of the use of clinical trial simulation in a complex trial design we focus on the innovative primary analysis method and save the discussion of the adaptive design for future publication. This demonstration was crucial for demonstration of a novel design and analysis to a diverse set of industry, regulatory, scientific, and patient partners on the innovative approach.

Clinical Trial Simulations in ALS

Clinical trial simulation requires assumptions to be made about the underlying data. Ideally, these assumptions are evidence based. Within ALS, assumptions are required for both ALSFRS-R and survival to simulate virtual patient outcomes. These outcomes are simulated under different assumptions for key design parameters. The Pooled Resource Open-Access ALS Clinical Trials Database (PRO-ACT) is a database of >10,000 de-identified clinical patient records from 23 different phase II/III clinical trials in ALS.⁴⁰ This database is a valuable resource to generate evidence-based participant-level simulations of ALSFRS-R and survival in ALS.

A simulation database is created from the PRO-ACT database using each participant who meets the HEALEY ALS platform trial major inclusion/exclusion criteria and has at least three ALSFRS-R measurements over the course of at least 24 weeks, including the baseline visit. For each of these participants, an intercept, slope, and residual standard-error is calculated from a participant-specific linear regression of the measured ALSFRS-R within the PRO-ACT database as a function of the month of each measured visit. Additionally, any covariates and survival information are recorded for each of these participants. Simulated clinical trial datasets of participant-level data are then created by sampling individual participants from the PRO-ACT simulation database, recording observed baseline covariates and simulating ALSFRS-R values at a fixed visit schedule based on the participant-specific intercept, slope, and residual standard error. The PRO-ACT simulation database is used for clinical trial simulation within the HEALEY ALS Platform Trial to better understand the trial design, and is not used to supplement the randomized trial data from the platform trial.

Example Overall Operating Characteristics of HEALEY ALS Platform Trial

In a multi-arm platform trial, there are many different combinations and patterns of regimen entry into the trial, meaning the number of active regimens may differ depending on the entry and exit times of regimens. In this example, our simulations predominantly focused on a base pattern of three regimens entering the trial simultaneously without a staggered entry. This pattern matches the planned start of the platform trial. Each of the regimens enrolls up to 160 participants, randomized 3:1 active versus control. Treatment effect assumptions will vary across the first regimen, and operating characteristics will be reported for this regimen. The other two regimens will be assumed to be null (ie, no benefit on ALSFRS-R or survival). Other combinations of staggered entry and therapeutic are possible, but outside the scope of this manuscript.

Trial simulations are performed across a range of simulation scenarios, where each scenario represents a distinct set of assumptions for key parameters. These include the following scenarios. First, base scenario: change in ALSFRS-R progression for regimen-specific controls is the same as the PRO-ACT database among those who meet the trial eligibility criteria, with a common 0% or 30% slowing for both function and survival for an effective treatment. This scenario assumes a mortality rate of 5% and a non-mortality dropout rate of 2% per month. Second, sensitivity scenarios: differential treatment benefit across function and survival, and increased mortality rates (10% and 20%, respectively). Third, sensitivity scenarios: ALSFRS-R systematic differences in control slopes across regimens: 10% slower than the analysis regimen and 10% faster than the analysis regimen.

For each scenario and treatment effect, we simulate 10,000 clinical trials and report average operating characteristics (ie, probability of success and mean treatment effect estimate).

Table 2 shows the overall operating characteristics for a single regimen for the Bayesian shared parameter analysis of function and survival for each of the aforementioned simulation scenarios. Under the base set of simulation assumptions (row 1 highlighted), there is an overall one-sided type I error rate of 2.4% for the regimen, and a power of 77% for a 30% slowing in disease progression common to function and survival. These operating characteristics demonstrate the design has adequate power and type I error control. The sensitivity simulation scenarios are discussed below.

TABLE 2. HEALEY ALS Platform Trial Operating Characteristics for Base and Sensitivity Scenarios

Scenario			Null DRR 1.0		Alternative DRR 0.70
ALSFRS-R progression analysis regimen	Mortality rate	Treatment effect survival	Type I error	Mean est. DRR	Power	Mean est. DRR
Same as PRO-ACT	5%	Common	0.024	1.00	0.77	0.69
	5%	DRR Mort = 1.0	0.024	1.00	0.72	0.71
	10%	Common	0.023	1.00	0.77	0.69
	10%	DRR Mort = 1.0	0.023	1.00	0.67	0.72
	20%	Common	0.024	1.00	0.77	0.69
	20%	DRR Mort = 1.0	0.024	1.00	0.56	0.75
10% slower	5%	Common	0.060	0.96	0.85	0.66
10% faster	5%	Common	0.010	1.05	0.67	0.72

Abbreviation: DRR = disease rate ratio, est, = estimated; Mort = mortality.

Characterization of Primary Analysis: Integration of Function and Survival

Within the Bayesian shared parameter model, the weight that each component has on the estimation of the overall treatment effect depends on the percentage of participants within each component. If there are more mortality events, then more weight will be given to the effect on survival. Table 2 provides type I error, power, and the shared treatment effect parameter (DRR) estimates for the base scenario (5% 6-month mortality), as well as scenarios when the mortality rate is increased (10–20% 6-month mortality). Power and average DRR estimates are provided for treatment effect scenarios where the true DRR for function and survival is the same and equal to 0.70, and when the true DRR for function and survival is different (null effect on survival).

Under a common treatment effect assumption between function and survival, the type I error, power, and the mean estimated DRR are not sensitive to the assumption of the percentage of 6-month mortality. Under scenarios when the treatment effect for survival is null (HR 1.0) and there is a 30% slowing in ALSFRS-R (DRR 0.70), the power and estimated DRR decrease as the rate of mortality increases. This is due to the overall treatment effect being more heavily weighted by the null survival effect. Under scenarios with 5%, 10% or 20% 6-month mortality rate, no treatment benefit on survival HR, and a true DRR equal to 0.70, we observe that the estimate of the common percent slowing (1-DRR) decreases by 2–6% (absolute) relative to scenarios with both true DRR and true HR 0.70.

Results from an example simulated trial for the Bayesian shared parameter analysis, as well as results from the sensitivity analysis allowing different effects between function and survival, are shown in Figure 2. The common treatment effect between function and survival is estimated to be a 24% slowing, and both the Bayesian shared parameter model (posterior probability DRR <1: 0.982) and the CAFS analysis (p-value 0.013) are deemed significant (treatment slows progression). The sensitivity analysis with the two components estimated separately have a 27% slowing in function and a 4% decrease in survival.

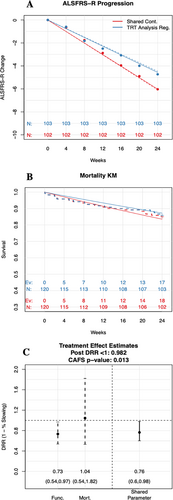
Additionally, results from two sets of simulated example trials with different mortality rates and different survival treatment effects are shown in Table 3. Figure 2 is one example trial within this set (bolded and italicized). Within each set of simulated trials, we fix the ALSFRS-R data for each participant, as well as the survival data of participants in the placebo arm. We then let the survival data on the active treatment arm vary to explore how the proposed Bayesian shared parameter primary analysis and the CAFS analysis respond to an increasing number of deaths on the active treatment arm. The point at which inference about benefit from treatment switches from significant to non-significant, the tipping point, reveals how sensitive a given analysis is to an excess of deaths in the active arm.

TABLE 3. Comparison of Bayesian Shared Parameter Analysis and CAFS in Simulated Example Trials

Deaths shared control	Deaths treated	Posterior mean estimate		CAFS p-value	Posterior probability of DRR <1
Deaths shared control	Deaths treated	Survival HR	Common DRR	CAFS p-value	Posterior probability of DRR <1
Example trials 10% control survival rate
11	6	0.66	0.71	0.001^a	0.998^a
11	7	0.77	0.73	0.003^a	0.993^a
11	8	0.87	0.74	0.004^a	0.992^a
11	9	0.96	0.75	0.006^a	0.988^a
11	10	1.06	0.75	0.009^a	0.982^a
11	11	1.13	0.78	0.013^a	0.979^a
11	12	1.21	0.78	0.014^a	0.976
11	13	1.27	0.78	0.017^a	0.975
11	14	1.33	0.80	0.028	0.961
11	16	1.45	0.80	0.036	0.959
11	17	1.49	0.82	0.058	0.939
11	19	1.57	0.85	0.085	0.917
Example trials 15% control mortality rate
18	11	0.68	0.73	0.002^a	0.994^a
18	13	0.81	0.73	0.003^a	0.991^a
18	14	0.87	0.74	0.005^a	0.988^a
18	17	*1.04*	*0.76*	*0.013*^a	*0.982*^a
18	18	1.10	0.77	0.015^a	0.975
18	19	1.15	0.78	0.022^a	0.973
18	21	1.27	0.79	0.028	0.972
18	23	1.36	0.80	0.035	0.956
18	24	1.41	0.81	0.056	0.950
18	26	1.48	0.82	0.091	0.948
18	27	1.52	0.84	0.135	0.908
18	29	1.58	0.88	0.233	0.853

Abbreviations: CAFS, combined assessment of function and survival; DRR, disease rate ratio, HR, hazard ratio.
^a Indicates significant result. Highlighted row corresponds to example trial from Figure 2.

Within these example trials, as more participants on the active treatment arm experience mortality, the common treatment effect estimate between function and survival (DRR), increases toward 1 (no effect of treatment), and the posterior probability that the treatment slows the rate of progression (DRR <1) decreases. This is like the change seen in the CAFS joint rank analysis: as mortality in the active treatment arm increases, its p-value becomes less significative. The two sets of example trials differ in the overall mortality rate (Example set 1 has a lower rate than Example set 2). Comparison of the two sets of example trials shows that the sensitivity of the results to the survival hazard ratio depends on the overall mortality rate (the survival HR is smaller at the tipping point for Example set 2 than for Example set 1). These examples demonstrate that the proposed Bayesian shared parameter model adequately integrates treatment effects on function and survival, gives results consistent with CAFS, and that the degree to which the common treatment effect is informed by the survival component depends on the mortality rate.

Characterization of Primary Analysis: Accounting for Potential Differences in Shared Controls Across Regimens

Under rare circumstances, it is conceivable that the ALSFRS-R progression rate in the regimen being analyzed could have systematic differences from all other regimens (Table 2; sensitivity scenarios for type I error, power, and DRR estimates). Under the extreme assumption that participants in the analysis regimen progress at a 10% slower rate of progression on ALSFRS-R than those in all other regimens, there is an increased type I error of 6% and a small positive bias in the treatment effect estimate of 0.96 (4% slowing in progression). Under the assumption that participants in the analysis regimen progress at a 10% faster rate of progression on ALSFRS-R than those in all other regimens, the type I error decreases to 1% with a small negative bias in the treatment effect estimate equal to 1.05 (5% increase in progression). The sensitivity of these results is due to the borrowing across regimens for the shared control.

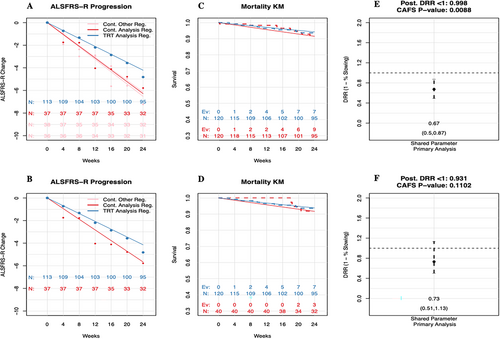
Sensitivity analyses with regimen-only controls can shed light on a potential type I error inflation due to differences across shared controls. Consistency in results between the primary analysis using all shared controls, as well as the sensitivity analysis using only regimen-specific controls, provides confidence that the positive primary analysis results are not biased by the shared controls (Figure 3).

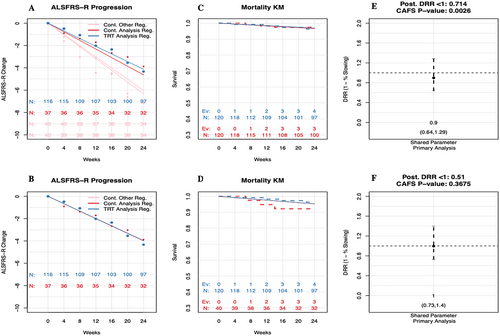
Additionally, the dynamic sharing of controls across regimens within the primary Bayesian analysis provides protection against a type I error (Figure 4). Within this example, the Bayesian shared parameter model analysis leads to a null result. However, because the traditional CAFS analysis uses all shared controls and the amount of sharing is not dynamic, the results of this analysis are more sensitive to the increased rate of progression in the two shared control groups; and the CAFS analysis leads to a statistically significant result. Both analyses are null under the sensitivity analysis using only regimen-specific controls.

Limitations

The HEALEY ALS Platform Trial targets a broad patient population that was chosen to provide a balance between statistical power and generalizability of results. As such, the sample size required for this trial may be larger than other recent ALS trials that enriched for participants with early disease, faster progression rates, or both. Additionally, to maintain the statistical efficiency of a shared control group that is balanced across all regimens, the HEALEY ALS Platform Trial requires that all regimens enroll a similar patient population. Enrollment of this common population across regimens limits the ability of each regimen to target distinct biological subgroups or genetic subtypes. As the field of ALS clinical research evolves, it will be important for the HEALEY ALS Platform Trial to adapt to advances in our understanding of disease mechanisms, prognosis of disease progression, biomarkers of neurodegeneration, and measures of disease severity or stage by allowing for prospective updates to the design of future regimens.

Additional limitations include the choice of the primary outcome and duration of treatment. Given that mortality rates are expected to be very low in this study over a 24-week period, the primary outcome measure is expected to be mostly driven by ALSFRS-R. From a practical standpoint, this implies the Bayesian primary analysis is likely to provide results similar to a mixed model for ALSFRS-R over 24 weeks. This approach limits the ability of the platform trial to evaluate sustained functional benefit and long-term survival. The platform was designed as an initial efficient evaluation of numerous novel therapies in ALS. As such, a treatment duration of 24 weeks was chosen for the randomized double-blind period with the expectation that if results from the platform were promising, a regimen would likely need a subsequent confirmatory trial. Finally, changes in the standard of care for treatment of ALS, including recent Food and Drug Administration approvals, can complicate interpretation of results when using nonconcurrently randomized controls in the primary analysis. Inclusion of a time trend and regimen-specific random effects, and evaluation of sensitivity analyses using analysis sets restricted to concurrently randomized controls or regimen-only controls are intended to mitigate this concern.

Conclusions and Future Directions

Platform trials allow operational and statistical efficiencies compared with traditional randomized controlled trials. Sharing of control participants across regimens are the backbone of the statistical efficiency gains, but the sharing creates the need for additional statistical complexity. Bayesian hierarchical modeling can be used to account for potential differences among the shared controls in ways that a joint rank model cannot.

Within ALS, regulatory guidance recommends a primary analysis that integrates function and survival. In the context of a platform trial with shared control participants across regimens, the statistical approaches mentioned as examples in the guidance do not accommodate the added complexities of the shared control, and do not provide a clinically interpretable and meaningful estimate of treatment effect. The HEALEY ALS Platform Trial uses an innovative Bayesian shared parameter primary analysis method to integrate function and survival, provide a clinically interpretable and meaningful treatment effect, and account for potential differences in shared controls. The acceptability of this innovative approach and demonstration that the method accommodates the required statistical needs was obtained through clinical trial simulation. The innovative approach provides similar integration of function and survival as the more traditional CAFS analysis, while mitigating the risk of erroneous conclusions if there are differences in the shared control across regimens by introducing a regimen-specific random effect and time–trend effect in the Bayesian hierarchical modeling framework.

With the innovative primary analysis approach, such as the one described herein, it is important to list the main assumptions of the analysis method, and provide prespecified sensitivity analyses to assess the sensitivity of primary results to each of these assumptions. Additionally, within the ALS platform trial setting, the more traditional and nonparametric joint rank CAFS analysis is performed as a key secondary analysis. It is important that results from the primary analysis are consistent with results from sensitivity analyses and key secondary CAFS analysis. Significant discrepancies may affect the interpretation of the study results. Simulations demonstrate the consistency of these analyses under expected scenarios, as well as scenarios in which they would be expected to differ.

There are additional operational complexities brought about by the shared controls within a platform setting that must be considered. Although controls are shared in the statistical analysis for each regimen, participant-level control data must be carefully protected, especially if participants have not completed their study participation within another regimen, to mitigate any potential risk of unblinding. Additionally, as shared control data will be used in future regimens, careful consideration needs to be made on the level of detail regarding what is published on the shared controls to mitigate the risk of bias for future regimens due to design considerations/changes being made based on data that will be included in the analysis. When, how, and with whom shared control data and summaries can be shared, while still meeting the goals of reporting and transparency, is an important topic that needs to be considered and properly documented in a data sharing and reporting plan. Consideration of these additional complexities is an area of future discussion.

Acknowledgements

We thank the ALS community, including people living with ALS, their families, and advocates, ALS clinicians and scientists, ALS foundations and non-profits, industry leaders, and regulators for engaging discussions, thoughtful feedback, and enthusiastic support during the planning and launch of the HEALEY ALS Platform Trial. We acknowledge the participating sites of the Northeast ALS Consortium (NEALS), all site teams, and the central Data and Safety Monitoring Board. We thank Dr M.A. Bind for her thoughtful comments and revisions to the manuscript. The HEALEY ALS Platform Trial is funded and made possible by the AMG Charitable Foundation, Tackle ALS, The ALS Association, ALS Finding A Cure, Muscular Dystrophy Association, ALS One, Arthur M. Blank Family Foundation, I AM ALS, Tambourine ALS Collaborative, and many other community fundraising initiatives and donors. For more information, please visit HEALEY ALS Platform Trial (massgeneral.org).

Author Contributions

M.Q., B.R.S., E.A.M., M.A.D., M.V., L.C., S.P., J.D.B., M.C., A.S., H.Y., K.D., J.A., J.S., and M.C. contributed to the conception and design of the study. M.Q. and B.R.S. contributed to drafting the text, and preparing the tables and figures. M.Q., B.R.S., E.A.M., M.A.D., M.V., L.C., S.P., J.D.B., M.C., A.S., H.Y., K.D., J.A., J.S., and M.C. contributed to manuscript revision. The members of the HEALEY ALS Platform Trial Study Group and their institutional affiliations are included in a supplementary table.

Potential Conflicts of Interest

Nothing to Report.

Open Research

Data Availability Statement

Data used in the preparation of this article were obtained from the Pooled Resource Open-Access ALS Clinical Trials (PRO-ACT) Database. As such, the following organizations and individuals within the PRO-ACT Consortium contributed to the design and implementation of the PRO-ACT Database and/or provided data, but did not participate in the analysis of the data or the writing of this report: (1) ALS Therapy Alliance, (2) Knopp Biosciences, (3) Neuraltus Pharmaceuticals, Inc., (4) Neurological Clinical Research Institute, MGH, (5) Northeast ALS Consortium, (6) Novartis, (7) Prize4Life Israel, (8) Regeneron Pharmaceuticals, Inc., (9) Sanofi, (10) Teva Pharmaceutical Industries, Ltd., and (11) The ALS Association.

Supporting Information

References

1Saville BR, Berry SM. Efficiencies of platform clinical trials: a vision of the future. Clin Trials 2016; 13: 358–366.
10.1177/1740774515626362
PubMed Web of Science® Google Scholar
2Woodcock J, LaVange LM. Master protocols to study multiple therapies, multiple diseases, or both. N Engl J Med 2017; 377: 62–70.
10.1056/NEJMra1510062
CAS PubMed Web of Science® Google Scholar
3Berry SM, Connor JT, Lewis RJ. The platform trial: an efficient strategy for evaluating multiple treatments. JAMA 2015; 313: 1619–1620.
10.1001/jama.2015.2316
PubMed Web of Science® Google Scholar
4 Food and Drug Administration Center for Drug Evaluation and Research, Center for Biologics Evaluation and Research, Research Oncology Center of Excellence. Master protocols: efficient clinical trial design strategies to expedite development of oncology. Drugs and Biologics 2018; FDA-2018-D-3292.
Google Scholar
5Alexander BM, Ba S, Berger MS, et al. Adaptive global innovative learning environment for glioblastoma: GBM AGILE. Clin Cancer Res 2018; 24: 737–743.
10.1158/1078-0432.CCR-17-0764
PubMed Web of Science® Google Scholar
6Barker AD, Sigman CC, Kelloff GJ, et al. I-SPY 2: an adaptive breast cancer trial design in the setting of neoadjuvant chemotherapy. Clin Pharmacol Ther 2009; 86: 97–100.
10.1038/clpt.2009.68
CAS PubMed Web of Science® Google Scholar
7Papadimitrakopoulou V, Lee JJ, Wistuba II, et al. The BATTLE-2 study: a biomarker-integrated targeted therapy study in previously treated patients with advanced non-small-cell lung cancer. J Clin Oncol 2016; 34: 3638–3647.
10.1200/JCO.2015.66.0084
CAS PubMed Web of Science® Google Scholar
8Parker CC, James ND, Brawley CD, et al. Radiotherapy to the primary tumour for newly diagnosed, metastatic prostate cancer (STAMPEDE): a randomised controlled phase 3 trial. Lancet 2018; 392: 2353–2366.
10.1016/S0140-6736(18)32486-3
PubMed Web of Science® Google Scholar
9Simon R. Critical review of umbrella, basket, and platform designs for oncology clinical trials. Clin Pharmacol Ther 2017; 102: 934–941.
10.1002/cpt.814
PubMed Web of Science® Google Scholar
10Bateman RJ, Benzinger TL, Berry S, et al. The DIAN-TU next generation Alzheimer's prevention trial: adaptive design and disease progression model. Alzheimers Dement 2017; 13: 8–19.
10.1016/j.jalz.2016.07.005
PubMed Web of Science® Google Scholar
11Mills SM, Mallmann J, Santacruz AM, et al. Preclinical trials in autosomal dominant AD: implementation of the DIAN-TU trial. Rev Neurol 2013; 169: 737–743.
10.1016/j.neurol.2013.07.017
CAS PubMed Web of Science® Google Scholar
12Paganoni S, Berry JD, Quintana M, et al. Adaptive platform trials to transform amyotrophic lateral sclerosis therapy development. Ann Neurol 2022; 91: 165–175. https://doi.org/10.1002/ana.26285.
10.1002/ana.26285
PubMed Web of Science® Google Scholar
13Connick P, De Angelis F, Parker RA, et al. Multiple sclerosis- secondary progressive multi-arm randomisation trial (MS-SMART): a multiarm phase IIb randomised, double-blind, placebo-controlled clinical trial comparing the efficacy of three neuroprotective drugs in secondary progressive multiple sclerosis. BMJ Open 2018; 8:e021944.
10.1136/bmjopen-2018-021944
PubMed Web of Science® Google Scholar
14Huang DT, McCreary EK, Bariola JR, et al. The UPMC OPTIMISE-C19 (OPtimizing treatment and impact of monoclonal antIbodieS through evaluation for COVID-19) trial: a structured summary of a study protocol for an open-label, pragmatic, comparative effectiveness platform trial with response-adaptive randomization. Trials 2021; 22: 363. https://doi.org/10.1186/s13063-021-05316-3.
10.1186/s13063-021-05316-3
CAS PubMed Web of Science® Google Scholar
15Angus DC, Berry S, Lewis RJ, et al. The REMAP-CAP (randomized embedded multifactorial adaptive platform for community-acquired pneumonia) study. Rationale and design. Ann Am Thorac Soc 2020; 17: 879–891.
10.1513/AnnalsATS.202003-192SD
PubMed Web of Science® Google Scholar
16Angus DC, Derde L, Al-Beidh F, et al. Effect of hydrocortisone on mortality and organ support in patients with severe COVID-19: the REMAP-CAP COVID-19 corticosteroid domain randomized clinical trial. JAMA 2020; 324: 1317–1329.
10.1001/jama.2020.17022
CAS PubMed Web of Science® Google Scholar
17Hayward G, Butler CC, Yu L, et al. Platform randomised trial of INterventions against COVID-19 In older peoPLE (PRINCIPLE): protocol for a randomised, controlled, open-label, adaptive platform, trial of community treatment of COVID-19 syndromic illness in people at higher risk. BMJ Open 2021; 11:e046799. https://doi.org/10.1136/bmjopen-2020-046799.
10.1136/bmjopen-2020-046799
PubMed Google Scholar
18 Food and Drug Administration Center for Drug Evaluation and Research. Amyotrophic Lateral Sclerosis: Developing Drugs for Treatment Guidance for Industry, 2019. FDA-2013-N0035.
Google Scholar
19Berry JD, Miller R, Moore DH, et al. The combined assessment of function and survival (CAFS): a new endpoint for ALS clinical trials. Amyotroph Lateral Scler Frontotemporal Degener 2013; 14: 162–168. https://doi.org/10.3109/21678421.2012.762930.
10.3109/21678421.2012.762930
CAS PubMed Web of Science® Google Scholar
20Gelman A, Shalizi CR. Philosophy and the practice of Bayesian statistics. Br J Math Stat Psychol 2013; 66: 8–38.
10.1111/j.2044-8317.2011.02037.x
CAS PubMed Web of Science® Google Scholar
21Spiegelhalter DJ, Abrams KR, Myles JP. Bayesian approaches to clinical trials and health-care evaluation. Chichester: Wiley, 2004.
10.1002/0470092602
Google Scholar
22 Food and Drug Administration Center for Devices and Radiological Health, Center for Biologics Evaluation and Research. Guidance for the Use of Bayesian Statistics in Medical Device Clinical Trials, February 2010.
Google Scholar
23Viele K, Berry S, Neuenschwander B, et al. Use of historical control data for assessing treatment effects in clinical trials. Pharm Stat 2014; 13: 41–54.
10.1002/pst.1589
PubMed Web of Science® Google Scholar
24 Food and Drug Administration Center for Drug Evaluation and Research. Center for Biologics Evaluation and Research Adaptive Designs for Clinical Trials of Drugs and Biologics, November 2019.
Google Scholar
25McGlothlin AE, Viele K. Bayesian hierarchical models. JAMA 2018; 320: 2365–2366.
10.1001/jama.2018.17977
PubMed Web of Science® Google Scholar
26Lim J, Walley R, Yuan J, et al. Minimizing patient burden through the use of historical subject-level data in innovative confirmatory clinical trials: review of methods and opportunities. Ther Innov Regul Sci 2018; 52: 546–559. https://doi.org/10.1177/2168479018778282.
10.1177/2168479018778282
PubMed Web of Science® Google Scholar
27Jansen JP, Crawford B, Bergman G, Stam W. Bayesian meta-analysis of multiple treatment comparisons: an introduction to mixed treatment comparisons. Value Health 2008; 11: 956–964.
10.1111/j.1524-4733.2008.00347.x
PubMed Web of Science® Google Scholar
28Sutton AJ, Abrams KR. Bayesian methods in meta-analysis and evidence synthesis. Stat Methods Med Res 2001; 10: 277–303.
10.1177/096228020101000404
CAS PubMed Web of Science® Google Scholar
29Smith TC, Spiegelhalter DJ, Thomas A. Bayesian approaches to random-effects meta-analysis: a comparative study. Stat Med 1995; 14: 2685–2699.
10.1002/sim.4780142408
CAS PubMed Web of Science® Google Scholar
30Gamalo-Siebers M, Savic J, Basu C, et al. Statistical modeling for Bayesian extrapolation of adult clinical trial information in pediatric drug evaluation. Pharm Stat 2017 Jul; 16: 232–249. https://doi.org/10.1002/pst.1807.
10.1002/pst.1807
PubMed Web of Science® Google Scholar
31Lake SL, Quintana MA, Broglio K, et al. Bayesian adaptive design for clinical trials in Duchenne muscular dystrophy. Stat Med 2021; 40: 4167–4184.
10.1002/sim.9021
PubMed Web of Science® Google Scholar
32Berry SM, Broglio KR, Groshen S, Berry DA. Bayesian hierarchical modeling of patient subpopulations: efficient designs of phase II oncology clinical trials. Clin Trials 2013; 10: 720–734.
10.1177/1740774513497539
PubMed Web of Science® Google Scholar
33Broglio KR, Zhang F, Binbing Y, et al. A comparison of different approaches to Bayesian hierarchical models in a basket trial to evaluate the benefits of increasing complexity. Statistics in Biopharmaceutical Research 2021; 14: 324–333. https://doi.org/10.1080/19466315.2021.2008484.
10.1080/19466315.2021.2008484
Web of Science® Google Scholar
34Subbiah V, Lassen PU, Elez E, et al. Dabrafenib plus trametinib in patients with BRAF^V600E-mutated biliary tract cancer (ROAR): a phase 2, open-label, single-arm, multicentre basket trial. Lancet Oncol 2020; 21: 1234–1243.
10.1016/S1470-2045(20)30321-1
CAS PubMed Web of Science® Google Scholar
35 Food and Drug Administration Center for Drug Evaluation and Research. Center for Biologics Evaluation and Research. Interacting with the FDA on Complex Innovative Trial Designs for Drugs and Biological Products, December 2020.
Google Scholar
36van Eijk RP, Eijkemans MJ, Rizopoulos D, et al. Comparing methods to combine functional loss and mortality in clinical trials for amyotrophic lateral sclerosis. Clin Epidemiol 2018; 10: 333–341.
10.2147/CLEP.S153196
PubMed Web of Science® Google Scholar
37Van Eijk RP, Roes KCB, Greef-van der Sandt I, et al. Functional loss and mortality in randomized clinical trials for amyotrophic lateral sclerosis: to combine, or not to combine—that is the Estimand. Clin Pharmacol Ther 2022; 111: 817–825. https://doi.org/10.1002/cpt.2533.
10.1002/cpt.2533
PubMed Web of Science® Google Scholar
38Wang G, Berry S, Xiong C, et al. A novel cognitive disease progression model for clinical trials in autosomal-dominant Alzheimer's disease. Stat Med 2018; 37: 3047–3055.
10.1002/sim.7811
PubMed Web of Science® Google Scholar
39Quintana M, Shrader J, Slota C, et al. Bayesian model of disease progression in GNE myopathy. Stat Med 2019; 38: 1459–1474.
10.1002/sim.8050
CAS PubMed Web of Science® Google Scholar
40Atassi N, Berry J, Shui A, et al. The PRO-ACT database: design, initial analyses, and predictive features. Neurology 2014; 83: 1719–1725.
10.1212/WNL.0000000000000951
CAS PubMed Web of Science® Google Scholar

Citing Literature

Volume94, Issue3

September 2023

Pages 547-560

Design and Statistical Innovations in a Platform Trial for Amyotrophic Lateral Sclerosis

Abstract

Statistical Modeling of an Adaptive Platform Trial in ALS

Regulatory Guidance and Traditional Statistical Approaches in ALS

Primary Analysis in the HEALEY ALS Platform Trial: Bayesian Shared Parameter Model of Function and Survival

Characterizing a Complex Design with Clinical Trial Simulations

Clinical Trial Simulations in ALS

Example Overall Operating Characteristics of HEALEY ALS Platform Trial

Characterization of Primary Analysis: Integration of Function and Survival

Characterization of Primary Analysis: Accounting for Potential Differences in Shared Controls Across Regimens

Limitations

Conclusions and Future Directions

Acknowledgements

Author Contributions

Potential Conflicts of Interest

Open Research

Data Availability Statement

Supporting Information

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Design and Statistical Innovations in a Platform Trial for Amyotrophic Lateral Sclerosis

Abstract

Statistical Modeling of an Adaptive Platform Trial in ALS

Regulatory Guidance and Traditional Statistical Approaches in ALS

Primary Analysis in the HEALEY ALS Platform Trial: Bayesian Shared Parameter Model of Function and Survival

Characterizing a Complex Design with Clinical Trial Simulations

Clinical Trial Simulations in ALS

Example Overall Operating Characteristics of HEALEY ALS Platform Trial

Characterization of Primary Analysis: Integration of Function and Survival

Characterization of Primary Analysis: Accounting for Potential Differences in Shared Controls Across Regimens

Limitations

Conclusions and Future Directions

Acknowledgements

Author Contributions

Potential Conflicts of Interest

Open Research

Data Availability Statement

Supporting Information

References

Citing Literature

Figures

References

Related

Information