Volume 39, Issue 3 pp. 744-761

RESEARCH ARTICLE

Open Access

When cointegration is interrupted: Price transmission analysis in the Italian dairy-feed industry

Luca Cattivelli,

Luca Cattivelli

Independent researcher, Fidenza, Parma, Italy

Search for more papers by this author

Federico Antonioli,

Corresponding Author

Federico Antonioli

[email protected]

Unit D.4 Economics of the Food System, Joint Research Centre, European Commission, Sevilla, Spain

Correspondence Federico Antonioli, Unit D.4 Economics of the Food System, Joint Research Centre, European Commission, Edificio Expo Calle Inca Garcilaso 3, Sevilla 41092, Spain.

Email: [email protected]

Search for more papers by this author

Luca Cattivelli,

Luca Cattivelli

Independent researcher, Fidenza, Parma, Italy

Search for more papers by this author

Federico Antonioli,

Corresponding Author

Federico Antonioli

[email protected]

Unit D.4 Economics of the Food System, Joint Research Centre, European Commission, Sevilla, Spain

Correspondence Federico Antonioli, Unit D.4 Economics of the Food System, Joint Research Centre, European Commission, Edificio Expo Calle Inca Garcilaso 3, Sevilla 41092, Spain.

Email: [email protected]

Search for more papers by this author

First published: 13 January 2023

https://doi.org/10.1002/agr.21797

Citations: 1

Luca Cattivelli and Federico Antonioli contributed equally to this manuscript.

Share a link

Email
Wechat
Bluesky

Abstract

We analyze price transmission dynamics in the under-investigated feed supply chain, applying a special case of the Threshold Vector Error Correction model where the cointegrating relationship is interrupted. Weekly Italian dairy feed and corn prices are used, finding evidence of asymmetric price transmission when the feed industry's margins are squeezed and highly volatile. The proposed Interrupted Threshold Cointegration model represents a valid complement to existing threshold and regime-switching techniques, allowing for the application of an agile nonstructural error correction model when standard cointegration tests fail to detect any long-run relationship between price series. [EconLit Citations: Q11, Q13, C24].

Abbreviations

ADF: Augmented Dickey-Fuller
ECT: error correction term
F-ADF: Fourier ADF
F-LM: Fourier LM
ITC: interrupted threshold cointegration
MEC: Markov error correction
OLS: ordinary least square
POs: Producers' Organizations
PP: Phillips–Perron
PT: price transmission
STC: smooth transition cointegration
TAR: threshold autoregressive
TVECM: Threshold Vector Error Correction Model
ZA: Zivot–Andrews

1 INTRODUCTION

The analysis of price transmission (PT) dynamics in the field of agricultural economics relies on a long and rich literature of empirical applications (Lloyd, 2017; von Cramon-Taubadel & Goodwin, 2021). Cointegration represent the mostly applied econometric strategy for detecting the existence of a long-run equilibrium between prices, often under the assumption of uninterrupted linkage over time. Nevertheless, such assumption may result hazardous: trade costs (Beghin & Schweizer, 2021; Lence et al., 2018), transaction, processing, and storage costs (Santeramo, 2022; von Cramon-Taubadel & Goodwin, 2021), and/or changes in policies and economic scenarios (for instance consumers preferences) may generate periods in which movements toward a long-run equilibrium do not occur (Psaradakis et al., 2004). For instance, depending on opening and closing borders policies, prices of the same agricultural commodity in different geographical areas may alternate periods of comovement with periods of isolation (Esposti & Listorti, 2018). Likewise, substitution effects may hinder the relationship between commodities of the same nature but with different quality cues (Antonioli et al., 2019). We present a more flexible technique, relaxing the rigid assumption of an uninterrupted long-term linkage between prices and building on the unrestricted two-regime threshold autoregressive (TAR) model with an autoregressive unit root developed by Caner and Hansen (2001). Relying on Kim's (2003) “segmented cointegration” and the subsequent “interrupted cointegration” approach of Martins and Gabriel (2014), a particular case of two-regimes Threshold Vector Error Correction Model (TVECM) where one of the two regimes is not cointegrated is described, allowing for several interruption in the long-run relationship. We refer to this specification as the interrupted threshold cointegration (ITC) model, in which cointegration may occur in just one of the two external regimes. To the best of the authors' knowledge, this is the first time that the Caner and Hansen (2001) cointegration test is applied in agricultural economics. The widely applied band-TVECM, developed by Balke and Fomby (1997) and Lo and Zivot (2001), determines three regimes—hence two thresholds—in which the between-regime, the “band,” is not cointegrated. However, this model is suitable only when the long-run equilibrium adjustments disappear near the equilibrium.1 The ITC considers a two-regime system in which the cointegration relationship is activated and deactivated according to a transition variable driving the system, hence only when the threshold is overcome cointegration exists. Therefore, the ITC does not restrict the cointegration relationship to be inactive within-the-band and near the long-run equilibrium. The regime-switching Markov error-correction (MEC) model is another widely used technique in PT analysis, defined as a two-regime Markov switching VECM in which one regime is not cointegrated (Martins & Gabriel, 2014; Psaradakis et al., 2004). Although similar, the ITC differs in terms of the transition variable: while the MEC is driven by a hidden, nonmeasurable, Markov chain, the ITC permits the researcher to freely choose the transition variable defining the regimes, embracing climate-, economic- or policy-related elements, alongside the most commonly used marketing margin.

We provide an empirical application of the ITC, investigating the interaction between Italian feed and corn prices. The feed industry represents a compelling case study, both for its strong dependence on raw agricultural commodities and its economic importance in agricultural production. The Italian milk-cow feed industry represents an important market, accruing for 8% of the overall agrifood industry's turnover, with feed costs accounting for more than 50% of the operational expenses for an average Italian milk producer (European Commission, 2018). Italian feed prices strongly depend on corn, which represents 60% of the overall raw inputs used in the feed formula (Assalzoo, 2021; FEFAC, 2021; ISTAT, 2021). Both the volatility and levels of the equilibrium error, the marketing margin—have been used as transition variables in the attempt to capture the market forces driving the vertical linkage between corn and feed producers. We describe how the application of standard cointegration tests would fail to reject the null of no cointegration, preventing the application of related error correction models. On the contrary, the ITC allows to detect for an (interrupted) cointegrating relationship between the two price series, where the equilibrium error is mean-reverting in one regime and contains a unit-root in the other. Results unveil the presence of asymmetric behavior, as only when margins are squeezed or highly volatile the feed industry responds to corn price dynamics. We contribute on both the modeling and economic side by applying a special case of TVECM that allows for interruptions in the long-run relationship and considering an under-investigated agrifood sector. Despite a fair number of applications cemented the close correlation between corn and feed prices—primarily because of the competition between ethanol and feed production (Hanif et al., 2021; Koirala et al., 2015; Tejeda & Goodwin, 2011)—, research efforts devoted to understand the functioning of the feed markets are scant. Exceptions are represented by the study of Schulte and Musshoff (2018) on the horizontal transmission of feed prices across North-Western Germany regions, and that of Ben-Kaabia et al. (2005), using feed prices to investigate the vertical price transmission for the Spanish poultry sector. The remainder of the paper is the following: Section 2 provides the reader with a general but updated background on PT analysis in agricultural markets; Section 3 describes the main features of the Italian feed supply chain and its agents, motivating the use of the ITC model; Section 4 presents the ITC modeling technique; Section 5 explains the data used and the first preliminary statistical results on the price series; Section 6 implements the ITC model to the price transmission process in the Italian feed industry, presenting its empirical results; finally, Section 7 concludes and draws final remarks.

2 PRICE TRANSMISSION ANALYSIS IN THE AGRICULTURAL SECTOR

The analysis of both horizontal (i.e., same commodities in different geographical areas) and vertical (i.e., between different agents of the same product's supply chain) PT process has a long history in the agricultural economic field—see the recent works of Kouyaté and von Cramon-Taubadel (2016), Lloyd (2017), and von Cramon-Taubadel and Goodwin (2021). The last 20 years marked a tumultuous run for the agrifood sector, with mergers and acquisitions and vertical integration dynamics raising worries about concentration levels (Hirsch et al., 2021; Sexton, 2013; Sexton & Xia, 2018), especially in light of the low bargaining power of primary producers (Bonanno et al., 2018). Moreover, crises and policy reforms narrowed the interest of researchers in understanding how such events influence the functioning of markets and their efficiency (Antonioli & Santeramo, 2021; Penone et al., 2022; Ramsey et al., 2021). Quoting Lloyd (2017), the analysis of price transmission dynamics “[…] gives us a yardstick with which to measure the functioning of markets” (p. 17), and “measuring the degree of vertical price transmission […] helps to identify potential market failures” (European Commission, 2009a, p. 5). Market efficiency presupposes that in a competitive market with perfect information, price differentials reflect the cost of marketing services, and shocks are instantaneously transmitted between agents, hence PT should be symmetric (Abdulai, 2002; Goodwin & Schroeder, 1991).2 Nevertheless, the literature concludes on the significant gap between empirical results and the theoretical economic background, suggesting asymmetries as the rule rather than the exception (Bakucs et al., 2014; Meyer & Cramon-Taubadel, 2004; Peltzman, 2000; Rezitis & Tsionas, 2019). The vertical dimension of price transmission often represents highly complex relationships with vertical integration processes not visible to the researcher (Adjemian et al., 2016; Lan et al., 2022; von Cramon-Taubadel & Goodwin, 2021). The increasing use of nonlinear models—particularly representing regime changes—provide for the effect of such nonobservable mechanisms, especially under the form of transaction and processing costs, with significant nonlinear price dynamics turning as an indicator for market inefficiencies (Cakir, 2021; Mai et al., 2018). Despite the traditional focus on market power (McCorriston et al., 2001; Yu & Gould, 2019), the PT literature endeavors to offer further economic insights explaining food chains' inefficiencies, like the presence of adjustment costs (Chavas & Mehta, 2004), policy interventions (Brummer et al., 2009; Santeramo & Cioffi, 2012), the degree of perishability and storability of the products concerned (Santeramo, 2015; Santeramo & von Cramon-Taubadel, 2016) or product differentiation (Antonioli et al., 2019; Livat et al., 2019), among others. Policy analysis is witnessing an increasing interest by nonlinear PT applications: Mofya-Mukuka and Abdulai (2013) employ a threshold cointegration to disentangle the impact of policy reforms on the PT between the world and domestic coffee market prices in Zambia and Tanzania; Wang and Wei (2021), study how China's soybean price policy shapes both domestic and global soybean prices, thus their effect on welfare; Götz et al. (2016) apply a smooth transition cointegration (STC) model to study the effects of export controls on the domestic Ukraine wheat price; and, in a similar fashion, Antonioli and Santeramo (2021) explain how the Common Agricultural Policy reform of 2003 shaped price transmission dynamics in the Italian dairy market.3 Climate-change-related research questions are also entering the PT literature: Hatzenbuehler et al. (2021) study how different growing conditions and planted areas influence the United States chickpea price changes, modeling regime shifts in the linear fashion of Gregory and Hansen (1996); Baffes et al. (2019) investigate the role of variables related to harvest cycles, weather anomalies, and trade policies on Tanzanian corn price using the standard ECM; Hatzenbuehler et al. (2020) how Nigerian grain prices transmit under different anomalous-weather periods; Zamani et al. (2021) disentangle the role of different temperatures on price transmission dynamics in the Iranian poultry value chain. Finally, other scholars attempt to disentangle the role of different variables on the behavior of PT, for which the application of the ITC model may be beneficial for allowing interruptions along the long-run relationship between prices and for spotting different regimes according to the trigger. Lundberg et al. (2021) investigate the relationship between oil and agricultural commodity prices accounting for heterogeneity across time horizons, while Chavas and Pan (2020) study dynamic linkages between farm and retail pork prices in China, disentangling how consumer income and feed costs shape the price relationship.

3 THE ITALIAN FEED INDUSTRY

The Italian feed industry represents a vital sector within the agrifood industry, with an estimated turnover, in 2020, of about 8 billion euros and a whole output of more than 15 million tonnes of compound feed, of which 2.5 Mio tonnes of feed destined to milk cows, relying upon 420 production units (Assalzoo, 2021). Compound feed is defined by the European Commission (2009b) as “a mixture of at least two feed materials in the form of complete or complementary feed,” representing the primary feedstuff used for feeding dairy cattle. The latter represents 40% of the sectorial turnover, and 23% of the overall Italian feed production (Assalzoo, 2021). Within the EU-27, Italy represents the fifth cow-feed and total feed producer with shares of 8% (3.4 Mio tonnes) and 10% (14.5 Mio tonnes), respectively (FEFAC, 2021).4 In Europe, livestock is the most important outlet for EU-cereals: 61% of total production goes to animal feeding, of which 28% to the feed industry, and 33% to on-farm feed use. In Italy, corn represents 43% of the whole cereal category, and 71% of total available corn on the Italian territory (i.e., domestic production and imports, excluding exports) is destined to compound feed production (Assalzoo, 2021; ISTAT, 2021). Considering also the corn directly used as a simple feedstuff, then 90% of harvested corn in Italy is destined for cattle feeding (USDA, 2012). The northern Italian regions of Emilia-Romagna, Lombardy, Veneto, and Piedmont accrue for 77% and 67% of both volume and feed production units, respectively (Assalzoo, 2021), gathering about 80% of corn producers and 82% of the entire Italian corn production (ISTAT, 2021). Feed costs are particularly relevant for farmers: the European Commission (2018) estimates that, for the average Italian milk-producing unit, 52% of total operational costs are represented by purchases of compound feed, while home-grown feed represents only 15% of total feeding costs. The Italian feed supply chain is composed of three main steps (Serra, 2009), as described in Figure 1. The first step is the agricultural production of corn, with 100,000 producers distributed on a surface of 590,000 hectares (ISTAT, 2021). According to ISMEA (2021), one-third of corn volume is used in farm, mainly for animal feeding. Over the total domestic production, around 30% is sold to operators, whom store the production and eventually resell it to feed producers (these operators also market half of the imported corn). Consortia, cooperatives, and producers' organizations (POs) collect the major share of corn production, 60%, for later deliver it to the feed industry. The feed industry buys 10% of corn volume directly from farmers and about half of the total imports.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The Italian corn-feed supply chain, 2018. *Source*: Authors' elaboration on data extracted from ISMEA (2021), Assalzoo (2021), and ISTAT (2021).

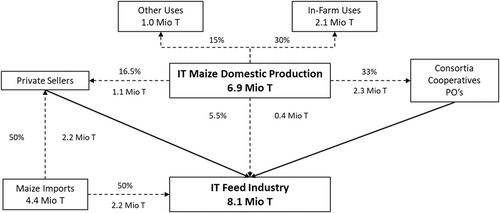
According to latest data available, the first six industrial feed producers gather 42% of both total volume and value (Mambriani, 2009). The first company, Veronesi, accrues nowadays a market share of 22% (Veronesi, 2020), being the eighth largest feed producer in Europe with a final output of more than 3 million tonnes in 2009 (Wesseler et al., 2015). Following the European trend, the Italian feed industry is witnessing a decrease in units of production, with −30% for the period 2010–2020 (Assalzoo, 2011, 2021; FEFAC, 2021) and a stable volume of production, pointing to an increasing concentration (see Figure 2).

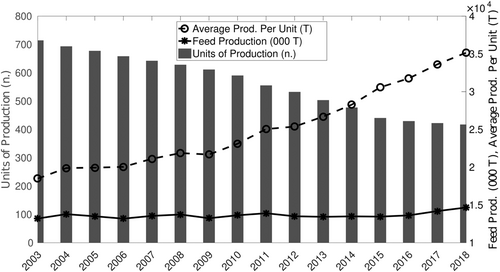
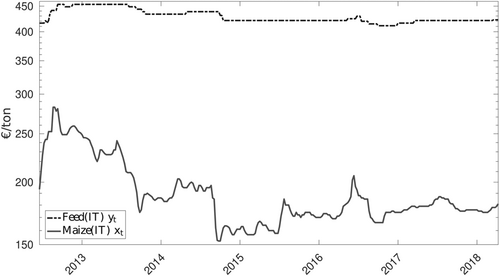
Figure 3 shows a quite flat price series for feedstuff, with some peaks occurring when the price of corn features significant upwards spikes.5 Under the methodological point of view, this may resemble a first challenging issue for standard cointegration models, as tests would fail to reject the null of no long-run relationship, hindering the possibility to use PT models; second, such a price system could be better described by an interrupted cointegration dynamic, where feed and corn price series comove during certain time windows, followed by periods in which they move independently the one to the other. As one of the characteristics of the ITC model is that of using a trigger variable to define the regimes, we rely on profit margins, both in levels and volatility measure. Indeed, as far as the magnitude of price transmission coefficients cannot be generally attached to the existence (or absence) of market power—and more generally other market inefficiencies—whether margins are significantly affected by supply or demand shifters is first evidence of inefficient market mechanisms (Kinnucan & Zhang, 2015; Lloyd et al., 2006; von Cramon-Taubadel & Goodwin, 2021; Weldegebriel, 2004).

4 INTERRUPTED THRESHOLD COINTEGRATION

According to the seminal paper of Engle and Granger (1987), a bivariate time series

{{\boldsymbol{p}}}_{t}=({x}_{t},{y}_{t})^{\prime}

is said to be cointegrated with cointegrating vector

{\boldsymbol{\beta }}=(1,-\beta )^{\prime}

, if

{{\boldsymbol{p}}}_{t}

is a vector of integrated time series where a linear combination

{\boldsymbol{\beta }}^{\prime} {{\boldsymbol{p}}}_{t}

is stationary, that is, the following relation holds:

{y}_{t}=\mu +{\beta x}_{t}+{z}_{t},

(1)

where the equilibrium error

{z}_{t}

, is assumed to be stationary, that is,

{{\boldsymbol{\beta }}}^{^{\prime} }{{\boldsymbol{p}}}_{t}=0

is the cointegration condition for which deviations from the long-run equilibrium are stationary, and

\mu

is a real parameter (Engle & Granger, 1987). Several works on PT hinge on nonlinear cointegration models and threshold modeling techniques, testing for asymmetric dynamics in the PT process (e.g., Ben-Kaabia & Gil, 2007; Hassouneh et al., 2010; Lence et al., 2018). Such asymmetric dynamics can be modeled through discontinuous adjustments in

{z}_{t}

through a TAR model of order (k) as follows:

{\unicode{x02206}z}_{t}=\left\{\begin{array}{c}{m}^{(u)}+{\rho }^{(u)}{z}_{t-1}+{\sum }_{i=1}^{k}{\gamma }_{i}^{(u)}\unicode{x02206}{z}_{t-i}+{\epsilon }_{t},\unicode{x02007}\mathrm{if}{\unicode{x02007}}{s}_{t-1}\ge c,\\ {m}^{(l)}+{\rho }^{(l)}{z}_{t-1}+{\sum }_{i=1}^{k}{\gamma }_{i}^{(l)}\unicode{x02206}{z}_{t-i}+{\epsilon }_{t},\unicode{x02007}\mathrm{if}{\unicode{x02007}}{s}_{t-1}\lt c,\end{array}\right.\,

(2)

where

c\in R

is a threshold parameter,

{s}_{t-1}

is the transition variable assumed to be strictly stationary and ergodic,

{m}^{(\bullet )}

and

{\gamma }_{i}^{(\bullet )}

are real parameters, and

{\epsilon }_{t}

a series of i.i.d. zero-mean random variables with finite variance; the apexes (u) and (l) refer to the upper and lower regime with respect to the threshold value, respectively. As in Equation (1), cointegration between

{x}_{t}

and

{y}_{t}

exists only if the equilibrium error

{z}_{t}

follows a stationary process. Nevertheless, the condition of strict stationarity for

{z}_{t}

can be satisfied even if one of the two regimes is nonstationary, as shown by Caner and Hansen (2001), who proposed a two-regime TAR model with an autoregressive unit root. In their model, the upper (lower) regime is stationary while the other contains a unit-root, without violating the global stationary property of the series

{z}_{t}

. Imposing the Caner and Hansen (2001) specification6 for

{z}_{t}

the cointegration model in Equations (1)–(2) can be considered a particular case of the larger family of two-regimes TVECM where one of the two regimes is not cointegrated, allowing for several interruption in the long-run relationship depending on the value of the transition variable

{s}_{t}

. We refer to this specification then as the ITC model, which, in other words, specifies a TVECM with two regimes, where the

{z}_{t}

—hereafter error correction term (ECT)—follows a particular TAR specification allowing to detect of long-run relationship between prices even when cointegration is not continuous. The ITC can be represented as the standard TVECM7:

{\unicode{x02206}{\boldsymbol{p}}}_{t}=\left\{\begin{array}{c}{{\boldsymbol{\omega }}}^{(u)}+{{\boldsymbol{\alpha }}}^{(u)}{z}_{t-1}+{\sum }_{i=1}^{k}{{\rm{\Gamma }}}_{i}^{(u)}{\unicode{x02206}{\boldsymbol{p}}}_{t-i}+{{\boldsymbol{\upsilon }}}_{t},\unicode{x02007}\mathrm{if}{\unicode{x02007}}{s}_{t-1}\ge c,\\ {{\boldsymbol{\omega }}}^{(l)}+{{\boldsymbol{\alpha }}}^{(l)}{z}_{t-1}+{\sum }_{i=1}^{k}{\Gamma }_{i}^{(l)}{\unicode{x02206}{\boldsymbol{p}}}_{t-i}+{{\boldsymbol{\upsilon }}}_{t},\unicode{x02007}\mathrm{if}{\unicode{x02007}s}_{t-1}\lt c,\end{array}\right.

(3)

where

{\omega }^{(\bullet )},{\alpha }^{(\bullet )}

are vectors of real parameters,

{\Gamma }_{i}^{(\bullet )},{i}=\mathrm{1,2},\text{\unicode{x02026}},k

are

(2\times 2)

matrices of (real) short-run parameters,

{{\boldsymbol{\upsilon }}}_{t}

are i.i.d. vectors of zero mean error terms with covariance matrix

{{\rm{\Sigma }}}_{1}

and

{z}_{t-1}={y}_{t-1}-\mu -{\beta x}_{t-1}

. The peculiarity of the ITC consists in the

{{\boldsymbol{\alpha }}}^{(\bullet )}

, as one of the twos is a vector of zeros, generating a noncointegrated regime. Concerning the model's parameters, they can be obtained with a simple three-stage procedure: (1) in the first step,

\beta

and

\mu

are obtained via OLS,8 estimating the cointegration regression

{y}_{t}=\mu -{\beta x}_{t}+{z}_{t}

and obtaining the residuals

{\hat{z}}_{t}

; (2) the parameters appearing in Equation (2) are estimated via concentrated OLS, as in Caner and Hansen (2001). For a grid of

c

values,

{{m}^{(\bullet )},\rho }^{(\bullet )},{\gamma }_{i}^{(\bullet )}

are estimated via OLS, then the concentrated OLS estimates with the minimum residual variance are selected; (3) in the last step,

{{\boldsymbol{\omega }}}^{(\bullet )},{{\boldsymbol{\alpha }}}^{(\bullet )},{{\rm{\Gamma }}}_{i}^{(\bullet )}

in (3) are estimated via OLS, taking

{z}_{t}

from step 1 and

c

from step 2.

4.1 Testing procedure

The standard approach for testing for threshold cointegration would consist in the following methodological steps: (i) preliminary testing for the presence of unit-root in both price series; (ii) when both price series contain a unit-root (series are nonstationary), test for (linear) cointegration (e.g., the Johansen test); (iii) if series are cointegrated, determine whether such a relationship is nonlinear and of threshold-type; (iv) if linearity is rejected, a bivariate TVECM can be specified and estimated. Nevertheless, when the dynamics of the ECT, ${z}_{t}$ , does not follow a simple autoregressive process, standard unit-root tests as the augmented Dickey-Fuller (ADF) test may fail to differentiate a pure unit-root process from a TAR process with one of the two regimes (potentially) nonstationary (Gonzalo & Gonzalez, 1997). Following Caner and Hansen (2001), we propose an alternative methodology not requiring a preliminary test of linear cointegration, and allowing to describe a case in which the equilibrium term ${z}_{t}$ is characterized by nonstationary behavior in one of the two outer regimes; accordingly, different unit-root tests are proposed to better define the nature of the ECT,9 and that do not suffer from reduced power nested in unit-root tests when nonlinearity is present in the data generating process—contrary to the test strategy followed by Balke and Fomby (1997) for threshold cointegration and Hansen and Seo (2002) for nonlinearity. The proposed different methodology hinges on the main following steps: (i) preliminary testing for the presence of unit-root in both price series; (ii) when both price series contain a unit-root (series are nonstationary), test for nonlinearity; (iii) if nonlinear price dynamics are found, testing whether prices are threshold cointegrated and whether such long-run relationship is interrupted.

4.1.1 Nonlinearity test

The first step consists on testing whether model (3) is actually nonlinear, thus testing the alternative (null) hypothesis that parameters in the upper and lower regime are different (equal). The multivariate extension of the linearity test developed in Caner and Hansen (2001), a sup-Wald (W) test, is then used to compare the estimated residual covariance matrices from the linear model (i.e.,

{\hat{{\rm{\Sigma }}}}_{0}

) and the nonlinear alternative (i.e.,

{\hat{{\rm{\Sigma }}}}_{1}

)10:

W=T(\mathrm{log}(\text{det}{\hat{{\rm{\Sigma }}}}_{0})-\mathrm{log}(\text{det}{\hat{{\rm{\Sigma }}}}_{1})).

(4)

Under the null hypothesis of no threshold effect, the parameter $c$ is not identified, resulting in a nonstandard testing problem. Caner and Hansen (2001) showed, via Monte Carlo simulations, that the best way to obtain the critical values of their test statistics is the residual bootstrap procedure, which outperforms first-order asymptotic techniques. For this reason, we adopt a bootstrap approximation to the asymptotic distribution of $W$ for the calculation of critical values and p values (see Appendix A for more details).

4.1.2 Cointegration test

The second main step consists in testing the null of non-cointegration in both regimes against the alternatives of a standard threshold cointegration or an interrupted threshold cointegration, that is, prices co-move only in one of the two regimes. As already mentioned, such cointegration tests are nonstandard as related to unit-root tests in the presence of nonlinearity (Caner & Hansen, 2001; Gonzalo & Gonzalez, 1997), besides suffering from unidentified parameters under the null. Following Caner and Hansen (2001), the null hypothesis

{H}_{0}

is no cointegration in both the upper (u) and lower (l) regime, whereas two alternative hypothesis can be specified; the first alternative

{H}_{1}

is the well-known case of threshold cointegration, where

{z}_{t}

is stationary and ergodic in both regimes:

{H}_{1}:{\rho }^{(u)}\lt 0,\unicode{x02007}{\rho }^{(l)}\lt 0.{\rm{;}}

the second alternative

{H}_{2}

considers the case in which one of the two regimes is nonstationary:

{H}_{2}:({\rho }^{(u)}\lt 0\phantom{\rule{}{0ex}}\unicode{x02007}\text{with}\,{\rho }^{(l)}=0)\unicode{x02007}\text{or\unicode{x02007}}({\rho }^{(l)}=0\phantom{\rule{}{0ex}}\unicode{x02007}\text{with}\,{\rho }^{(u)}\lt 0).

(5)

To distinguish between the null and the alternative hypothesis, the one-sided Wald test statistic is proposed11: $R={({t}^{(u)})}^{2}{{\mathbb{I}}}_{{\hat{\rho }}^{(u)}\lt 0}+{({t}^{(l)})}^{2}\,{{\mathbb{I}}}_{{\hat{\rho }}^{(u)}\lt 0}$ , where ${t}^{(u)}$ and ${t}^{(l)}$ are obtained from OLS regression of Equation (5) as $t$ statistics of ${\hat{\rho }}^{(u)}$ and ${\hat{\rho }}^{(l)}$ and ${\mathbb{I}}$ is the indicator function. In such a way, one can easily understand whether the data-generating process follows ${H}_{0}$ or not. When $R$ is significant, ${H}_{0}$ can be rejected, although ${H}_{1}$ and ${H}_{2}$ are not yet distinguishable. Caner and Hansen (2001) solve the problem by examining the individual t statistics $-{t}^{(u)}$ and $-{t}^{(l)}$ : when only one of the two statistics is significant there is discontinuity in the cointegration relation (i.e., ${H}_{2}$ ), while when both significant, the system follows the standard threshold cointegration process (i.e., ${H}_{1}$ ). Critical values for ${t}^{(u)},{t}^{(l)}$ , and $R$ can be calculated under the null of no cointegration in both regimes via a residual bootstrap procedure (see Appendix A for further details). The interesting advantage of this cointegration test strategy is that it can be performed independently from the result of standard linear-cointegration tests, in contrast with methodological steps presented in Balke and Fomby (1997), Hansen and Seo (2002), and Lo and Zivot (2001).

5 DATA AND PRELIMINARY RESULTS

The econometric analysis hinges on two series of Italian corn ( ${x}_{t}$ ) and feed price for milk-cows ( ${y}_{t}$ ) (Figure 3). We retrieved the price series from the Chamber of Commerce of Bologna and the Chamber of Commerce of Forlì-Cesena for corn and milk-cow feed prices, respectively. Both Chambers are located in the Emilia-Romagna region, representing one of the most representative territories regarding both feed and corn production, as described in Section 3. Our data set consists of nearly 6 years of weekly data (303 observations), from the 25th week of 2012 to the 15th week of 2018 for the Italian feed and corn prices.12

All series are expressed in logarithms to mitigate price fluctuations, to increase the likelihood of stationarity after first differencing, and to interpret results in percentage change terms (Ben-Kaabia & Gil, 2007). Three different (standard) unit-root tests are employed: the ADF, the PP test proposed by Phillips and Perron (1988) and the KPSS test proposed by Kwiatkowski et al. (1992), all clearly indicating that both price series are I(1) as shown in Table 1. To exclude the presence of structural breaks in the price series, we consider unit root test with structural breaks: the Zivot and Andrews (1992) test (ZA), the LM test of Lee and Strazicich (2013), and, finally the Fourier ADF (F-ADF) and Fourier LM (F-LM) test of Enders and Lee (2012). Excepted for the ZA test for the feed price series and the LM test for the corn price series, all tests indicate the absence of any structural break in both price series (Table 1).

Table 1. Unit-root tests on corn and feed price series, p values

Variable	ADF	PP	KPSS	ZA	LM	F-ADF	F-LM
Corn prices ${x}_{t}$	>0.10	>0.10	<0.01***	>0.05	<0.01***	>0.10	>0.10
Feed prices ${y}_{t}$	>0.10	>0.10	<0.01***	<0.01***	>0.10	>0.10	>0.10

Note: The stationary alternative hypothesis specifications include the intercept for all but KPSS test. Trends are not included as the price series have none (see Figure 3). Significance level: ***1%.
Source: Authors' elaboration.

Testing for Granger causality (Granger, 1969) leads to the conclusion that the corn price Granger-causes the feed price.13 We investigate the relationship between the two series by applying the more standard cointegration analysis, that is, we test for the presence of cointegration between the two series adopting both Engle–Granger and Johansen tests. The Engle and Granger test, with both the ADF and PP statistics, fails to reject the null of noncointegration at the 5% level, independently of the order of the price variables in the cointegration relationship.14 The Johansen test delivers similar results, with the noncointegration hypothesis failed to be rejected at the 5% level. In conclusion, the two series appear to be noncointegrated according to the most commonly used standard (linear) cointegration tests. Nevertheless, as both cointegration tests may be invalidated by the presence of structural breaks, additional and different approaches are applied. First, the Gregory and Hansen (1996) approach allows for the detection of a cointegrating relationship where the null hypothesis is non-cointegration against an alternative of cointegration with one structural break at an unknown point in time. This test considers three model's specifications: (i) model C that includes a level-shift in the relationship of cointegration; (ii) model C/T that is as model C plus a linear trend; (iii) finally, model C/S that adds to model C/T the possibility of a shift in the slope coefficient. The critical values of the ADF, Z_t, and Z_α test statistics are taken from Gregory and Hansen (1996) considering the case with 300 and a number of lags selected with a downward-t procedure15 (Table 2).

Table 2. Gregory and Hansen (1996) results

Gregory and Hansen (1996) test	ADF	${{\boldsymbol{Z}}}_{{\boldsymbol{t}}}$	${{\boldsymbol{Z}}}_{{\boldsymbol{a}}}$
C (level-shift in the relationship of cointegration)	−5.36*	−4.37	−27.98
Critical values 5%	−5.28	−5.28	−53.58
Critical values 1%	−5.77	−5.77	−63.64
C/T (model C plus a linear trend)	−5.87	−4.44	−27.86
Critical values 5%	−5.57	−5.57	−59.76
Critical values 1%	−6.05	−6.05	−70.27
C/S (model C/T plus a shift in the slope coefficient)	−5.49	−4.32	−27.37
Critical values 5%	−6.00	−6.00	−68.94
Critical values 1%	−6.51	−6.51	−80.15

Note: The null hypothesis consists of no-cointegration against the alternative of cointegration with one structural break at an unknown date. Significance level: *10%.
Source: Authors' elaboration.

The ADF test fails to reject the null for all but model C, for which the null is rejected at the 5% level. However, given that the ADF test suffers from size distortions that leads to over-rejection of the null, we conclude that there are no evidence of a regime shift in the cointegrating relationship. To test for the presence of more than one regime shift in the cointegrating relationship, the Gregory and Hansen (1996) approach is extended to allow for two breaks, which corresponds to the Hatemi-J (2008) test.16 Again, the test fails to reject the null of no cointegration for all three model specifications (Table 3). Therefore, recalling that the application of the standard TVECM requires the system to be cointegrated, the latter approach could not be estimated for the current price system.

Table 3. Results of the Hatemi-J (2008) test

Hatemi-J (2008) test statistics	ADF	${{\boldsymbol{Z}}}_{{\boldsymbol{t}}}$	${{\boldsymbol{Z}}}_{{\boldsymbol{a}}}$
C/S	−6.53	−5.53	−36.48
Critical values 5%	−7.35	−7.35	−104.86
Critical values 1%	−7.83	−7.83	−118.58

Note: The null hypothesis consists of no-cointegration against the alternative of cointegration with two structural breaks at an unknown date.
Source: Authors' elaboration.

6 THE ITC MODEL FOR THE FEED–CORN RELATIONSHIP

At this point, the researcher would conclude the two prices are not cointegrated, preventing the use of error correction model approaches and switching to different approaches such as vector autoregressive models. Nevertheless, the ITC approach, as detailed in Section 4, does not depend on the standard cointegration tests that would lead to the rejection of the hypothesis of a (continuous) long-run relationship between Italian feed and corn prices. We then follow the methodological steps outlined in Sections 4 and 4.1 and eventually estimate an ITC model as in (3). As detailed above, the researcher is free to choose any trigger variable she believes able to drive the price dynamics. Latter studies on PT analysis were sceptical regarding the magnitude of price transmission coefficients as a reliable indicator of the existence (or absence) of market inefficiencies, suggesting that the extent to which margins are affected by supply or demand shifters is a first signal of inefficiencies (Kinnucan & Zhang, 2015; von Cramon-Taubadel & Goodwin, 2021). Therefore, the ECT is used as the transition variable, both in its levels ( ${s}_{t}={\hat{z}}_{t}$ ) and volatility ( ${s}_{t}={\sigma }_{t}^{2}$ ). The latter has been estimated through a GARCH(1,1) process ${\sigma }_{t}^{2}=\omega +{\alpha r}_{t-1}^{2}+{\beta \sigma }_{t-1}^{2}$ , where ${r}_{t}=100({\hat{z}}_{t}-{\hat{z}}_{t-1}).$ Representing the marketing margin, using both levels and the volatility measure of ECT allows accounting for both endogenous and exogenous market factors and see how the agents of the supply chain react. The level of ECT, as usually done in the relevant literature (Ben-Kaabia & Gil, 2007; Lo & Zivot, 2001), describes different regimes depending on the size of the marketing margins of the feed industry, giving insights on the potential exertion of market power. The volatility of the ECT (Ganneval, 2016) helps in understanding the effect that margins' uncertainty and risk play in the PT dynamics, with price cycles influenced by exogenous shocks such as climate and environmental events, altering both supply and demand of corn and feed. For both transition variables the W test rejects the null of linearity, hence one can proceed to testing for cointegration in each regime (Table 4). Whenever the null of non-cointegration is rejected for one regime only, the system features an interrupted-cointegration: price series share a common stochastic trend only when the transition variable is above (the upper regime) or below (the lower regime) the estimated threshold value. Whenever the test rejects the null for both regimes, the system can be modeled via a standard threshold cointegration model. The usual battery of test on residuals is performed (Table 4), showing that no autocorrelation (Ljung–Box test) or heteroscedasticity (ARCH test) is present, while the null hypothesis of normal distribution is strongly rejected. Nevertheless, although the nonnormality of residuals may bring doubts about the efficiency of OLS estimators, it does not affect its consistency properties. All in all, the results on residuals are satisfactory.

Table 4. Summary results of the ITC model for the two transition variables

	ECT volatility	ECT levels
Number of lags (BIC)	1	5
Threshold: c	0.663	−0.017
% observations in the lower regime (l)	83.50	15.18
Linearity test: p-val of W	0.029**	0.048**
Cointegration test: p-val of R	0.001***	0.000***
Cointegration test: p-val of ${t}^{(l)}$	0.923	0.000***
${\alpha }^{(l)}$ for feed prices		−0.072***
${\alpha }^{(l)}$ for corn prices		−0.110
Cointegration test: p-val of ${t}^{(u)}$	0.001***	0.718
${\alpha }^{(u)}$ for feed prices	−0.194***
${\alpha }^{(u)}$ for corn prices	0.040
Tests on residuals
Ljung-Box (lag = 1) for feed prices	0.475	0.156
Ljung-Box (lag = 1) for corn prices	0.510	0.623
Ljung-Box (lag = 52) for feed prices	0.596	0.325
Ljung-Box (lag = 52) for corn prices	0.824	0.370
ARCH (lag = 1) for feed prices	0.638	0.235
ARCH (lag = 1) for corn prices	0.452	0.759
ARCH (lag = 52) for feed prices	0.376	1.000
ARCH (lag = 52) for corn prices	1.000	0.999
Jarque–Bera for feed prices	<0.01***	<0.01***
Jarque–Bera for corn prices	<0.01***	<0.01***

Note: The $\alpha$ coefficients are not displayed when the corresponding cointegration t-test fails the rejection of the null at the 5% level. For the definition of c, see (5); for $\alpha$ see (7); the Linearity test statistics is defined in (9); while the cointegration test statistics in (11). The Ljung-Box, ARCH, and Jarque-Bera tests are conducted on the residuals of Equation (3).
Significance level: ***1%, **5%, and *10%.
Source: Authors' elaboration.

6.1 ECT volatility

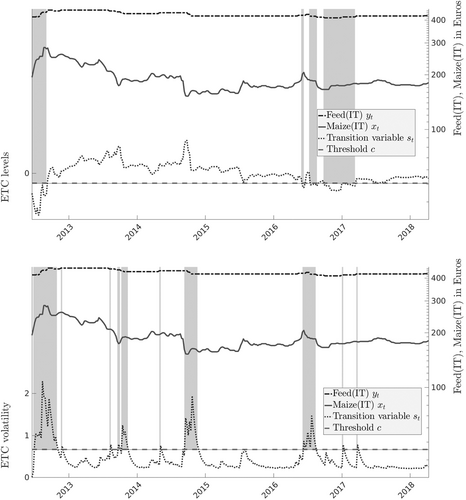
First, we investigate whether the margin's volatility bears any impact on the price transmission dynamics between corn and feed prices.17 The W test rejects the null of linearity at the 5% level, and the R test rejects the null of noncointegration hypothesis at the 1% level: the upper regime is cointegrated as per the significance of the coefficient α (i.e., the ECT term is stationary in the upper regime, while nonstationary in the lower regime). In other words, cow-feed, and corn prices share a long-run relationship with interruptions, comoving only when the volatility of the feed industry's margin is high—that is, above the threshold value c. The average value of the margin's volatility is 0.45, with a standard deviation of 0.35; being the threshold value 0.66, it reveals how prices comove when volatility is relatively high. Moreover, the ECT coefficient for the upper regime is significant only in the feed equation, signaling that the feed price is the one reverting the system towards the equilibrium. With a ${\alpha }^{(u)}$ coefficient of −0.19, roughly 20% of the shock is absorbed each period, with the system reaching the equilibrium again after 5 weeks approximately. Results describe how feed producers accommodate their selling price when the system is affected by high volatility. Therefore, when the market turns more uncertain and risky, feed operators prefer to attach their clearing market price to that of their main input, corn, probably fearing spikes in corn price. Indeed, Figure 4 clearly suggests how the system results cointegrated when cereal price spikes occur.

6.2 ECT levels

When considering the level of ECT—the marketing margin of feed producers—again both the W and the R tests reject the null of linearity and noncointegration, respectively, with the lower regime showing stationarity, hence cointegration (Table 4). The average value of the transition variable is close to zero and the threshold $c$ coincides with the (negative) standard deviation of the ECT, clearly defining how cointegration is activated only when deviations from the equilibrium margins are largely negative. The ICT delivers significant and negative estimates for the ECT in the feed equation, with a coefficient ${\alpha }^{(l)}$ of −0.07: only when margins are too low, the feed price tends to adjust back to the equilibrium at a rate of 7% per period, in line with results of Ben-Kaabia and Gil (2007) regarding poultry feed price in Spain. Such price behavior reflects the well-known “rocket and feather” dynamic described in Peltzman (2000): when margins are shrinking the system adjusts to the long-run equilibrium, lingering for about 14 weeks after the shock. This behavior can be explained by the increasing concentration in the Italian feed industry, with feed producers using their market power to maintain high margins for longer periods. Indeed, it is clear from the price patterns of Figure 3, how feed price increases are more pronounced than decreases, especially after a peak in the price of corn.

Overall, results point to the exogeneity of corn prices—they do not adjust to the steady-state when a shock occurs—while feed prices respond and bring back the system to its equilibrium when changes in the economic margins and their volatility occur.

7 CONCLUSIONS

We present the ITC model, a special case of TVECM with two regimes and where the cointegrating relationship is interrupted, hence active only in one of the two regimes. The Caner and Hansen (2001) approach is applied for the first time in agricultural economics, allowing to test for cointegration when the ECT follows a TAR process with an autoregressive unit root. Price transmission dynamics between corn and feed prices in the Italian market are investigated, proving the usefulness of the ITC technique. The scant literature on price transmission in the feed industry probably originates from the nature of price data: as often observed by researchers for consumer prices, feed prices smooth over large periods, adjusting to upper stages of the supply chain (corn producers) only when price changes are large. We proved how conventional cointegration tests—that is, Johansen, Engle–Granger, Gregory–Hansen, and Hatemi—would have failed in finding any long-run dynamics between price series, whereas the ITC model offers the opportunity to rigorously address the issue, allowing to detect a long-run relationship hence offering new evidence on asymmetries and market inefficiencies in the feed sector. First, a discontinuous long-run relationship between Italian corn and feed prices is found, with the feed price leading the relationship, hence bringing the system back to the equilibrium after a shock occurs. Second, the ITC spots asymmetries in the price dynamics that could be related to feed producers' market power: only when margins of the feed industry are squeezed and when highly volatile, the feed industry triggers a significant response, following the corn price dynamics. This behavior is consistent with the highly-fragmented Italian agricultural sector, opposite to a well-concentrated feed industry able to steer the market to their favor. However, as consistently argued by von Cramon-Taubadel and Goodwin (2021), latest empirical works on price transmission are highly context-specific, with vertical maneuvers (contracts, coordination) turning spot markets very thin and with researchers unable to observe such hidden information. This prevents any useful comparison with studies on similar but structurally different markets or sectors. Nevertheless, the exertion of market power seems having left a signature on price data, identifying in the Italian feed industry a case for which a closer scrutiny of the competent antitrust authority is deserved. All in all, the ITC approach allows for the application of an agile nonstructural error correction model for those economic systems that appear exempted of any long-run relationship according to linear cointegration tests, complementing existing threshold and regime-switching techniques. We offer an informative tool to study markets with incomplete price information, as often happens for price transmission analysis in developing and least developed countries, and for seasonal markets as fruits and vegetables (see among others, Hamulczuk et al., 2019; Reziti & Panagopoulos, 2008; Santeramo, 2015; Santeramo & von Cramon-Taubadel, 2016). In other words, the ITC disentangles how the cointegrating space behaves under different regimes triggered by transition variables the researcher chooses to use, serving also as a statistical tool to test for the significance of different triggers' role in the investigated economic system. However, this line of research is not exempt of limitations. First, the addition of one more regime would provide more insights into the impact of the triggers. Second, short-run dynamics, that is, impulse response functions, should be investigated to deepen the understanding on how the market behaves in the short-term according to the trigger variables. Finally, the development of the ITC using a different estimator, as the maximum-likelihood in the fashion of Johansen (1991), would undoubtedly offer a more powerful methodology for investigating PT dynamics.

ACKNOWLEDGMENT

The authors would like to thank Prof. José M. Gil and Prof. Marco Zuppiroli for constructive comments. All errors remain our own.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

DISCLAIMER

The authors are solely responsible for the content of the paper. The views expressed are purely those of the authors and may not in any circumstances be regarded as stating an official position of the European Commission.

Biographies

Luca Cattivelli graduated in Physics from the University of Parma and holds a Ph.D. in mathematical finance at Scuola Normale Superiore, Italy. His research interests are focused mainly on financial/agricultural econometrics and “random walks on graphs.” He works for international companies about data science projects.
Federico Antonioli is a Project Officer at the Joint Research Centre of Seville, Spain. He holds a doctorate in Agricultural Economics from the University of Ferrara. His research focuses mainly on food policy and their influence on the functioning of agrifood supply chains, particularly sustainable consumption patterns and trends, agricultural price transmission analysis, immigrant agricultural workforce and farms' performance, and farms' productivity.

Open Research

DATA AVAILABILITY STATEMENT

Due to the private nature of the data they cannot be shared publicly, so supporting data is not available.

Supporting Information

REFERENCES

Abdulai, A. (2002). Using threshold cointegration to estimate asymmetric price transmission in the Swiss pork market. Applied Economics, 34(6), 679–687.
10.1080/00036840110054035
Web of Science® Google Scholar
Adjemian, M. K., Saitone, T. L., & Sexton, R. J. (2016). A framework to analyze the performance of thinly traded agricultural commodity markets. American Journal of Agricultural Economics, 98(2), 581–596. https://doi.org/10.1093/ajae/aav074
10.1093/ajae/aav074
Web of Science® Google Scholar
Antonioli, F., Ben Kaabia, M., Arfini, F., & Gil, J. M. (2019). Price transmission dynamics for quality certified food products: A comparison between conventional and organic fluid milk in Italy. Agribusiness, 35(3), 374–393.
10.1002/agr.21568
Web of Science® Google Scholar
Antonioli, F., & Santeramo, F. G. (2021). On policy interventions and vertical price transmission: The Italian milk supply chain case. Journal of Agricultural and Resource Economics, 47, 342–354.
Web of Science® Google Scholar
Assalzoo. (2011). Annuario 2011. Technical report, Assalzoo. https://www.assalzoo.it/pubblicazioni/annuario/?pa=1
Google Scholar
Assalzoo. (2019). Annuario 2019. Technical report, Assalzoo. https://www.assalzoo.it/pubblicazioni/annuario/?pa=1
Google Scholar
Assalzoo. (2021). Annuario 2021. Technical report, Assalzoo. https://www.assalzoo.it/pubblicazioni/annuario/?pa=1
Google Scholar
Baffes, J., Kshirsagar, V., & Mitchell, D. (2019). What drives local food prices? Evidence from the Tanzanian maize market. The World Bank Economic Review, 33(1), 160–184.
10.1093/wber/lhx008
Web of Science® Google Scholar
Bakucs, Z., Fałkowski, J., & Fertő, I. (2014). Does market structure influence price transmission in the agro-food sector? A meta-analysis perspective. Journal of Agricultural Economics, 65(1), 1–25.
10.1111/1477-9552.12042
Web of Science® Google Scholar
Balke, N. S., & Fomby, T. B. (1997). Threshold cointegration. International Economic Review, 38(3), 627–645.
10.2307/2527284
Web of Science® Google Scholar
Beghin, J. C., & Schweizer, H. (2021). Agricultural trade costs. Applied Economic Perspectives and Policy, 43(2), 500–530. https://doi.org/10.1002/aepp.13124
10.1002/aepp.13124
Web of Science® Google Scholar
Ben-Kaabia, M., & Gil, J. M. (2007). Asymmetric price transmission in the Spanish lamb sector. European Review of Agricultural Economics, 34(1), 53–80.
10.1093/erae/jbm009
Web of Science® Google Scholar
Ben-Kaabia, M., Gil, M., & Ameur, M. (2005). Vertical integration and non-linear price adjustments: The Spanish poultry sector. Agribusiness, 21(2), 253–271. https://doi.org/10.1002/agr.20046
10.1002/agr.20046
Google Scholar
Bonanno, A., Russo, C., & Menapace, L. (2018). Market power and bargaining in agrifood markets: A review of emerging topics and tools. Agribusiness, 34(1), 6–23.
10.1002/agr.21542
Web of Science® Google Scholar
Brummer, B., Von Cramon-Taubadel, S., & Zorya, S. (2009). The impact of market and policy instability on price transmission between wheat and flour in Ukraine. European Review of Agricultural Economics, 36(2), 203–230.
10.1093/erae/jbp021
Web of Science® Google Scholar
Cakir, M. (2021). Retail pass-through of package downsizing. Agribusiness, 38, 259–278.
10.1002/agr.21724
Web of Science® Google Scholar
Caner, M., & Hansen, B. E. (2001). Threshold autoregression with a unit root. Econometrica, 69(6), 1555–1596.
10.1111/1468-0262.00257
Web of Science® Google Scholar
Chavas, J. P., & Pan, F. (2020). The dynamics and volatility of prices in a vertical sector. American Journal of Agricultural Economics, 102(1), 353–369.
10.1093/ajae/aaz038
Web of Science® Google Scholar
Chavas, J.-P., & Mehta, A. (2004). Price dynamics in a vertical sector: The case of butter. American Journal of Agricultural Economics, 86(4), 1078–1093.
10.1111/j.0002-9092.2004.00654.x
Web of Science® Google Scholar
von Cramon-Taubadel, S., & Goodwin, B. K. (2021). Price transmission in agricultural markets. Annual Review of Resource Economics, 13(1), 65–84. https://doi.org/10.1146/annurev-resource-100518-093938
10.1146/annurev-resource-100518-093938
Web of Science® Google Scholar
Enders, W., & Lee, J. (2012). A unit root test using a Fourier series to approximate smooth breaks*. Oxford Bulletin of Economics and Statistics, 74(4), 574–599. https://doi.org/10.1111/j.1468-0084.2011.00662.x
10.1111/j.1468-0084.2011.00662.x
Web of Science® Google Scholar
Engle, R. F., & Granger, C. W. J. (1987). Co-integration and error correction: representation, estimation, and testing. Econometrica, 55(2), 251–276.
10.2307/1913236
Web of Science® Google Scholar
Esposti, R., & Listorti, G. (2018). Price transmission in the Swiss wheat market: Does sophisticated border protection make the difference? The International Trade Journal, 32(2), 209–238.
10.1080/08853908.2017.1345668
Google Scholar
European Commission. (2009a). Analysis of price transmission along the food supply chain in the EU. European Commission. https://ec.europa.eu/economy_finance/publications/pages/publication16067_en.pdf
Google Scholar
European Commission. (2009b). European regulation (EC) No. 767/2009, Art. 3, letter h, 13 July 2009. Technical report, European Parliament. https://eur-lex.europa.eu/legal-content/en/ALL/?uri=CELEX%3A32009R0767
Google Scholar
European Commission. (2018). EU dairy farms report based on 2017 FADN data. Technical report, European Union.
Google Scholar
FEFAC. (2021). Feed & Food 2021. Technical report, FEFAC. https://fefac.eu/wp-content/uploads/2021/12/FF_2021_final.pdf
Google Scholar
Ganneval, S. (2016). Spatial price transmission on agricultural commodity markets under different volatility regimes. Economic Modelling, 52, 173–185.
10.1016/j.econmod.2014.11.027
Web of Science® Google Scholar
Goetz, L., & von Cramon_Taubadel, S. (2008). Considering threshold effects in the long-run equilibrium in a vector error correction model: An application to the German apple market. In 12th Congress of the European Association of Agricultural Economists.
Google Scholar
Gonzalo, J., & Gonzalez, M. (1997). Threshold unit root models. DES Working Papers. Statistics and Econometrics. WS 6214, Universidad Carlos III de Madrid.
Google Scholar
Goodwin, B. K., Grennes, T. J., & Wohlgenant, M. K. (1990). A revised test of the law of one price using rational price expectations. American Journal of Agricultural Economics, 72(3), 682–693.
10.2307/1243038
Web of Science® Google Scholar
Goodwin, B. K., & Schroeder, T. C. (1991). Cointegration tests and spatial price linkages in regional cattle markets. American Journal of Agricultural Economics, 73(2), 452–464.
10.2307/1242730
Web of Science® Google Scholar
Götz, L., Qiu, F., Gervais, J. P., & Glauben, T. (2016). Export restrictions and smooth transition cointegration: export quotas for wheat in Ukraine. Journal of Agricultural Economics, 67, 398–419. https://doi.org/10.1111/1477-9552.12149
10.1111/1477-9552.12149
Web of Science® Google Scholar
Granger, C. W. J. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica, 37(3), 424–438.
10.2307/1912791
Web of Science® Google Scholar
Greb, F., Cramon-Taubadel, S., Krivobokova, T., & Munk, A. (2013). The estimation of threshold models in price transmission analysis. American Journal of Agricultural Economics, 95(4), 900–916. https://doi.org/10.1093/ajae/aat006
10.1093/ajae/aat006
Web of Science® Google Scholar
Gregory, A. W., & Hansen, B. E. (1996). Residual-based tests for cointegration in models with regime shifts. Journal of Econometrics, 70(1), 99–126.
10.1016/0304-4076(69)41685-7
Web of Science® Google Scholar
Hamulczuk, M., Makarchuk, O., & Sica, E. (2019). Searching for market integration: Evidence from Ukrainian and European Union rapeseed markets. Land Use Policy, 87, 104078.
10.1016/j.landusepol.2019.104078
Web of Science® Google Scholar
Hanif, W., Areola Hernandez, J., Shahzad, S. J. H., & Yoon, S.-M. (2021). Tail dependence risk and spillovers between oil and food prices. The Quarterly Review of Economics and Finance, 80, 195–209. https://doi.org/10.1016/j.qref.2021.01.019
10.1016/j.qref.2021.01.019
Web of Science® Google Scholar
Hansen, B. E., & Seo, B. (2002). Testing for two-regime threshold cointegration in vector error correction models. Journal of Econometrics, 110(2), 293–318.
10.1016/S0304-4076(02)00097-0
Web of Science® Google Scholar
Hassouneh, I., Serra, T., & Gil, M. (2010). Price transmission in the Spanish bovine sector: the BSE effect. Agricultural Economics, 41(1), 33–42.
10.1111/j.1574-0862.2009.00423.x
Web of Science® Google Scholar
Hatemi-J, A. (2008). Tests for cointegration with two unknown regime shifts with an application to financial market integration. Empirical Economics, 35(3), 497–505.
10.1007/s00181-007-0175-9
Web of Science® Google Scholar
Hatzenbuehler, P. L., Abbott, P. C., & Abdoulaye, T. (2020). Growing condition variations and grain prices in Niger and Nigeria. European Review of Agricultural Economics, 47(1), 273–295.
10.1093/erae/jbz028
Web of Science® Google Scholar
Hatzenbuehler, P. L., Du, X., & Painter, K. (2021). Price transmission with sparse market information: The case of United States chickpeas. Agribusiness, 37(3), 665–682.
10.1002/agr.21672
Web of Science® Google Scholar
Hirsch, S., Lanter, D., & Finger, R. (2021). Profitability and profit persistence in EU food retailing: Differences between top competitors and fringe firms. Agribusiness, 37(2), 235–263.
10.1002/agr.21654
Web of Science® Google Scholar
ISMEA, (2021). Piano di settore cerealicolo. ISMEA. https://www.ismeamercati.it/flex/cm/pages/ServeBLOB.php/L/IT/IDPagina/3524#MenuV
Google Scholar
ISTAT (2021). Farm structure: Farms and agricultural area by crops. http://dati.istat.it/index.aspx?queryid=31592.
Google Scholar
Johansen, S. (1991). Estimation and hypothesis testing of cointegration vectors in Gaussian vector autoregressive models. Econometrica, 59, 1551–1580.
10.2307/2938278
Web of Science® Google Scholar
Kim, J.-Y. (2003). Inference on segmented cointegration. Econometric Theory, 19(4), 620–639.
10.1017/S0266466603194078
Web of Science® Google Scholar
Kinnucan, H. W., & Zhang, D. (2015). Notes on farm-retail price transmission and marketing margin behavior. Agricultural Economics, 46(6), 729–737.
10.1111/agec.12188
Web of Science® Google Scholar
Koirala, K. H., Mishra, A. K., D'Antoni, J. M., & Mehlhorn, J. E. (2015). Energy prices and agricultural commodity prices: Testing correlation using copulas method. Energy, 81, 430–436. https://doi.org/10.1016/j.energy.2014.12.055
10.1016/j.energy.2014.12.055
Web of Science® Google Scholar
Kouyaté, C., & von Cramon-Taubadel, S. (2016). Distance and border effects on price transmission: A meta-analysis. Journal of Agricultural Economics, 67(2), 255–271.
10.1111/1477-9552.12145
Web of Science® Google Scholar
Kwiatkowski, D., Phillips, P. C. B., Schmidt, P., & Shin, Y. (1992). Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics, 54(1-3), 159–178.
10.1016/0304-4076(92)90104-Y
Web of Science® Google Scholar
Lan, H., Lloyd, T. A., McCorriston, S., & Morgan, C. W. (2022). Retailer heterogeneity and price transmission. American Journal of Agricultural Economics, 104, 1679–1700. https://doi.org/10.1111/ajae.12286
10.1111/ajae.12286
Web of Science® Google Scholar
Lee, J., & Strazicich, M. C. (2013). Minimum LM unit root test with one structural break. Economics Bulletin, 33(4), 2483–2942.
Google Scholar
Lence, S. H., Moschini, G., & Santeramo, F. G. (2018). Threshold cointegration and spatial price transmission when expectations matter. Agricultural Economics, 49(1), 25–39. https://doi.org/10.1111/agec.12393
10.1111/agec.12393
Web of Science® Google Scholar
Livat, F., Alston, J. M., & Cardebat, J. M. (2019). Do denominations of origin provide useful quality signals? The case of Bordeaux wines. Economic Modelling, 81, 518–532.
10.1016/j.econmod.2018.06.003
Web of Science® Google Scholar
Lloyd, T. (2017). Forty years of price transmission research in the food industry: Insights, challenges and prospects. Journal of Agricultural Economics, 68(1), 3–21. https://doi.org/10.1111/1477-9552.12205
10.1111/1477-9552.12205
Web of Science® Google Scholar
Lloyd, T., McCorriston, S., Morgan, C. W., & Rayner, J. (2006). Food scares, market power and price transmission: The UK BSE crisis. European Review of Agricultural Economics, 33(2), 119–147.
10.1093/erae/jbl001
Web of Science® Google Scholar
Lo, M. C., & Zivot, E. (2001). Threshold cointegration and nonlinear adjustment to the law of one price. Macroeconomic Dynamics, 5(04), 533–576.
10.1017/S1365100501023057
Web of Science® Google Scholar
Lundberg, C., Skolrud, T., Adrangi, B., & Chatrath, A. (2021). Oil price pass through to agricultural commodities. American Journal of Agricultural Economics, 103(2), 721–742.
10.1002/ajae.12088
Web of Science® Google Scholar
Mai, T. C., Shakur, S., & Cassells, S. (2018). Testing vertical price transmission for Vietnam's Robusta coffee. Australian Journal of Agricultural and Resource Economics, 62(4), 563–575.
10.1111/1467-8489.12260
Web of Science® Google Scholar
Mambriani. (2009). I mangimi. Il Mercato del Latte. Rapporto 2009. Technical report, R. Pieri (Ed.), FrancoAngeli.
Google Scholar
Martins, L. F., & Gabriel, V. J. (2014). Modelling long run comovements in equity markets: a flexible approach. Journal of Banking & Finance, 47, 288–295.
10.1016/j.jbankfin.2014.05.029
Web of Science® Google Scholar
McCorriston, S., Morgan, C. W., & Rayner, A. J. (2001). Price transmission: The interaction between market power and returns to scale. European Review of Agricultural Economics, 28(2), 143-159.
10.1093/erae/28.2.143
Web of Science® Google Scholar
Meyer, J., & Cramon-Taubadel, S. (2004). Asymmetric price transmission: A survey. Journal of Agricultural Economics, 55, 581–611.
10.1111/j.1477-9552.2004.tb00116.x
Web of Science® Google Scholar
Mofya-Mukuka, R., & Abdulai, A. (2013). Policy reforms and asymmetric price transmission in the Zambian and Tanzanian coffee markets. Economic Modelling, 35, 786–795.
10.1016/j.econmod.2013.08.040
Web of Science® Google Scholar
Peltzman, S. (2000). Prices rise faster than they fall. Journal of Political Economy, 108(3), 466–502.
10.1086/262126
Web of Science® Google Scholar
Penone, C., Giampietri, E., & Trestini, S. (2022). Futures–Spot price transmission in EU corn markets. Agribusiness, 38(3), 679–709.
10.1002/agr.21735
Web of Science® Google Scholar
Phillips, P. C. B. (1987). Time series regression with a unit root. Econometrica, 55(2), 277–301.
10.2307/1913237
Web of Science® Google Scholar
Phillips, P. C. B., & Perron, P. (1988). Testing for a unit root in time series regression. Biometrika, 75(2), 335–346.
10.1093/biomet/75.2.335
Web of Science® Google Scholar
Psaradakis, Z., Sola, M., & Spagnolo, F. (2004). On Markov error-correction models, with an application to stock prices and dividends. Journal of Applied Econometrics, 19(1), 69–88.
10.1002/jae.729
Web of Science® Google Scholar
Ramsey, A. F., Goodwin, B. K., Hahn, W. F., & Holt, M. T. (2021). Impacts of COVID-19 and price transmission in U.S. meat markets. Agricultural Economics, 52(3), 441–458.
10.1111/agec.12628
PubMed Web of Science® Google Scholar
Reziti, I., & Panagopoulos, Y. (2008). Asymmetric price transmission in the Greek agri-food sector: some tests. Agribusiness, 24(1), 16–30. https://doi.org/10.1002/agr.20144
10.1002/agr.20144
Web of Science® Google Scholar
Rezitis, A. N., & Tsionas, M. (2019). Modeling asymmetric price transmission in the European food market. Economic Modelling, 76, 216–230.
10.1016/j.econmod.2018.08.004
Web of Science® Google Scholar
Santeramo, F. G. (2015). Price transmission in the European tomatoes and cauliflowers sectors. Agribusiness, 31(3), 399–413. https://doi.org/10.1002/agr.21421
10.1002/agr.21421
Web of Science® Google Scholar
Santeramo, F. G. (2022). Price dynamics, law of one price and quantile regressions. Journal of Agricultural and Resource Economics, 47(3), 513–528.
Web of Science® Google Scholar
Santeramo, F. G., & Cioffi, A. (2012). The entry price threshold in EU agriculture: Deterrent or barrier? Journal of Policy Modeling, 34(5), 691–704.
10.1016/j.jpolmod.2012.02.001
Web of Science® Google Scholar
Santeramo, F. G., & von Cramon-Taubadel, S. (2016). On perishability and vertical price transmission: Empirical evidences from Italy. Bio-Based and Applied Economics, 5(2), 199–214. https://doi.org/10.13128/BAE-18043
10.13128/BAE-18043
Web of Science® Google Scholar
Schulte, H., & Musshoff, O. (2018). Market structure of the feed industry in Germany: Causing asymmetric spatial price transmission? Journal of Agricultural & Food Industrial Organization, 17, 20180007. https://doi.org/10.1515/jafio-2018-0007
10.1515/jafio-2018-0007
Google Scholar
Serra, S. Z. M. (2009). Il commercio dei cereali. Conoscere il funzionamento per interpretare le dinamiche. Il Sole 24 Ore Edagricole, Rome.
Google Scholar
Sexton, R. J. (2013). Market power, misconceptions, and modern agricultural markets. American Journal of Agricultural Economics, 95(2), 209–219.
10.1093/ajae/aas102
Web of Science® Google Scholar
Sexton, R. J., & Xia, T. (2018). Increasing concentration in the agricultural supply chain: Implications for market power and sector performance. Annual Review of Resource Economics, 10(1), 229–251. https://doi.org/10.1146/annurev-resource-100517-023312
10.1146/annurev-resource-100517-023312
Web of Science® Google Scholar
Singerman, A., Lence, S. H., & Kimble-Evans, A. (2014). How related are the prices of organic and conventional corn and soybean? Agribusiness, 30(3), 309–330. https://doi.org/10.1002/agr.21364
10.1002/agr.21364
Web of Science® Google Scholar
Tejeda, H. A., and Goodwin, B. K. (2011). Dynamic price relationships in the grain and cattle markets, pre and post-ethanol mandate. In Selected Paper Prepared for Presentation at the Agricultural & Applied Economics Association 2011 AAEA &NAREA Joint Annual Meeting, Pittsburgh, Pennsylvania, July 24–26, 2011.
Google Scholar
Traorè, F., and Diop, I. (2021). Detecting threshold effects in price transmission (No. 0022; AGRODEP Technical Note).
Google Scholar
USDA (2012). Italian grain and feed report 2012. Technical report, USDA. https://www.thefarmsite.com/reports/contents/itgfmay12.pdf
Google Scholar
Veronesi (2020). Annual Report 2020. https://www.gruppoveronesi.it/en/annual-report-archive
Google Scholar
Wang, W., & Wei, L. (2021). Impacts of agricultural price support policy on price variability and welfare: Evidence from China's soybean market. Agricultural Economics, 52(1), 3–17.
10.1111/agec.12603
Web of Science® Google Scholar
Weldegebriel, H. T. (2004). Imperfect price transmission: Is market power really to blame ? Journal of Agricultural Economics, 55(1), 101–114.
10.1111/j.1477-9552.2004.tb00082.x
Web of Science® Google Scholar
Wesseler, J., Bonanno, A., Drabik, D., Materia, V., Malaguti, L., Meijer, M., & Venus, T. J. (2015). Overview of the agricultural inputs sector in the EU. European Union.
Google Scholar
Yu, C. J., & Gould, B. W. (2019). Market power and farm-retail price transmission: The case of US fluid milk markets. Agribusiness, 35(4), 537–555.
10.1002/agr.21606
Web of Science® Google Scholar
Zamani, O., Bittmann, T., & Loy, J. (2021). The role of temperature for seasonal market integration: A case study of poultry in Iran. Australian Journal of Agricultural and Resource Economics, 66, 187–215.
10.1111/1467-8489.12443
Web of Science® Google Scholar
Zivot, E., & Andrews, D. W. K. (1992). Further evidence on the great crash, the oil-price shock, and the unit-root hypothesis. Journal of Business and Economic Statistics, 10(3), 251–270. https://doi.org/10.1080/07350015.1992.10509904
10.1080/07350015.1992.10509904
Web of Science® Google Scholar

1 For an excellent critique on the band-TVECM, particularly concerning PT in trade analysis, see Lence et al. (2018).
2 This logic is also valid for horizontal PT analysis and the law of one price: price differentials between different geographical areas should reflect the transaction cost to move the product between these two locations (Goodwin et al., 1990).
3 See also Goetz and von Cramon_Taubadel (2008), Greb et al. (2013), and Traorè and Diop (2021) for recent reviews and nonlinear applications for horizontal price transmission analysis.
4 The first four feed producers are Spain (25.4 Mio tonnes), Germany (24 Mio tonnes), France (20.8 Mio tonnes), and the Netherlands (14.7 Mio tonnes) (FEFAC, 2021).
5 It is worth to note that Singerman et al. (2014) offer an interesting approach to cointegration in which a new specification for a jump process is applied. However, we believe that the ITC is more flexible and easy to interpret. Since comparison between the two approaches goes beyond the scope of this article, we left it to future research.
6 The mathematical definition of the Caner and Hansen (2001) specification will be given in Equation (5), which specifies the alternative hypothesis of cointegration test.
7 See Balke and Fomby (1997) for the relationship between TAR and TVECM parameters.
8 If the equilibrium error ${z}_{t}$ satisfies the “α mixing” conditions (assumption 2.1 in Phillips, 1987), then the least squares estimate of $\beta$ is super-consistent (Balke & Fomby, 1997). A sufficient condition for the TAR models with one nonstationary regime to be “α mixing” is the Markovianity of the transition variable ${s}_{t}$ (Gonzalo & Gonzalez, 1997).
9 Critical values for each statistics is retrieved via simulation using 20,000 replications.
10 The same test has been considered also in Lo and Zivot (2001).
11 The proposed Wald statistic is one-sided because it focuses only on the negative values of u and l.
12 Please, note that feed prices for milk-cow are no longer accessible.
13 Results available upon request.
14 Having considered a cointegration regression of the form ${y}_{t}=\mu +\beta {x}_{t}+{z}_{t}$ , the Engle–Granger test fails to reject the null hypothesis. Moreover, for robustness check, we also switched the position of the two variables in the cointegration regression ( ${x}_{t}={\mu }_{{1}}+{\beta }_{1}{y}_{t}+{v}_{t}$ ) performing a second Engle–Granger test failing to reject the null at the 10% level.
15 The maximum number of lags that we consider is 4, given that Table 1 of Gregory and Hansen (1996) gives the critical values only for 1,2,3, and 4 lags. The selected number of lags by the downward-t procedure is equal to 3.
16 The selected number of lags with the Hatemi procedure is equal to 3.
17 We estimate a GARCH as: ${\sigma }_{t}^{2}=0.017+{0.379r}_{t-1}^{2}+{0.621\sigma }_{t-1}^{2}$ , where the t-stats are, in order, 5.735, 14.642, and 6.869, respectively.

Citing Literature

Volume39, Issue3

Summer 2023

Pages 744-761

When cointegration is interrupted: Price transmission analysis in the Italian dairy-feed industry