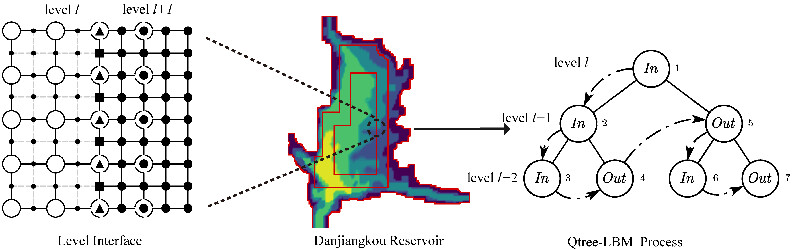
• A quadtree lattice Boltzmann model is developed to solve shallow water problems.
• The smoothed quadtree grid is introduced to capture the zigzag boundary.
• A general parallelized process for any number of hierarchical levels is proposed.

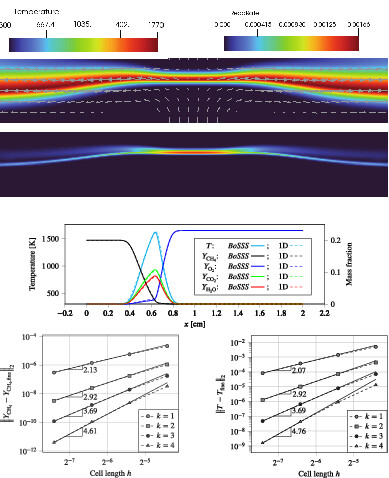
We present a fully coupled discontinuous Galerkin solver in a low-Mach framework using a one-step kinetic model with variable parameters. The solution of the discretized system is done with a globalized Newton method. The solution of the flame sheet problem allows us to obtain adequate initial conditions for the solution of the fully coupled problem. A counter diffusion flame is calculated, and our results are compared with the solution of the one-dimensional self-similar solution. A h-convergence study shows the expected high order convergence orders for nonreactive and reactive test cases.

The div-stable three-dimensional side centered unstructured finite volume formulation is proposed for the discretization of the three-dimensional immiscible incompressible multiphase fluid flows using arbitrary Lagrangian–Eulerian (ALE) formulation and a novel kinematic boundary condition that satisfies the local discrete geometric conservation law (DGCL) is implemented in order to ensure the mass conservation of each species at the machine precision. The unit normal vectors required for the surface tension forces are computed using several different approaches and the numerical results computed with the mean weighted by sine and edge length reciprocals (MWSELR) method show that the parasitic currents can be reduced to machine precision. The mass of the bubble is conserved irrespective of employed spatial and temporal resolutions and discontinuous pressure field is obtained in order to avoid errors due to the incompressibility restriction in the vicinity of liquid-liquid interfaces at large density and viscosity ratios.

In this paper, the method is extended to non-homogeneous boundary value problems, especially, the lubrication problem of coaxial bearings. In the case of different rotational angular velocities, the fluid field is still smooth, indicating that the lubrication performance is effective.