Financial Statements Insurance
Abstract
The fact that auditors are paid by the companies they audit creates an inherent conflict of interest. We analyze how the provision of financial statements insurance could eliminate this conflict of interest and properly align the incentives of auditors with those of shareholders. We first show that when the benefits to obtaining funding are sufficiently large, the existing legal and regulatory regime governing financial reporting (and auditing) results in low quality financial statements. Consequently, the financial statements of firms are misleading and firms that yield a low rate-of-return (low fundamental value) are over-funded relative to firms characterized by a high rate-of-return (high fundamental value). We present a mechanism whereby companies would purchase financial statements insurance that provides coverage to investors against losses suffered as a result of misrepresentation in financial reports. The insurance premia that companies pay for the coverage would be publicized. The insurers appoint and pay the auditors who attest to the accuracy of the financial statements of the prospective insurance clients. For a given level of coverage firms announcing lower premia would distinguish themselves in the eyes of the investors as companies with higher quality financial statements relative to those with higher premia. Every company would be eager to pay lower premia (for a given level of coverage) resulting in a flight to high audit quality. As a result, when financial statements insurance is available and the insurer hires the auditor, capital is provided to the most efficient firms.
The largest corporate bankruptcy filed in the United States, that of Enron in 2001, was preceded by a string of disclosures about audit failures, and errors in financial statements.1 The presence of such errors highlights the fact that market participants face two inter-related problems when pricing securities based on financial statements. First, they must assess the quality of the information contained in financial statements. Second, they must make projections about future cash flows and fold these projections back into an appropriate value for the security. Even if one assumes that accurate models are available for projecting cash flows and valuing securities, uncertainty about the quality of financial statements can lead to pricing distortions and inefficient market allocations of capital. The objective of this paper is to develop a market-based mechanism that can lead to a timely disclosure of financial statement quality and, thereby, a more efficient allocation of capital. We show that our proposed mechanism improves social welfare.2
The cascade of recent audit failures has given rise to a regulatory initiative, the Sarbanes-Oxley Act of 2002 (the Act), and to an ever growing commentary on ‘corporate governance’. A major theme of this literature is the role of ‘gatekeepers’ and, in particular, the failure of auditors to fulfill their role as independent gatekeepers.3 Indeed, the issue of auditor independence (or its absence) has occupied a major place in the debate over the failure of corporate governance and is the focus of much attention in the Sarbanes-Oxley Act.4 The Act seeks to address the problem by increased regulation and penalties, empowerment of audit committees, and reduction of the auditor's involvement with the client.5 But the Act does not untie the auditor/management knot: auditors continue to be hired and paid by the firms they audit.
Without joining the debate about the effectiveness of the Act,6 and as an alternative to, or supplement to, its mandates, this paper introduces a market-based financial statements insurance scheme (herafter, FSI)7 designed to eliminate conflicts of interest that inhere in the auditor–client relationship and, at the same time, to signal credibly the quality of financial statements. The model developed in this article shows that such a scheme would allow more accurate inferences regarding future cash flows to be drawn from financial statements, and thus permit more efficient resource allocations.
The social value of ex-ante self reporting has been recognized in the literature (Kaplow and Shavell, 1994). In essence, the FSI mechanism involves induced truthful ‘self reporting’ through the auditor's attestation of the quality of the financial statements even when such quality is poor and expected to trigger market sanctions when made public.8 In contrast, the current structure of incentives driving auditors' behaviour may not elicit unbiased reports. Auditors are paid by the companies they audit; this creates an inherent conflict of interest that is endemic to the relationship between the manager (the principal) and the auditor (the agent). We analyze, first, the financial statement quality equilibrium under the existing legal and regulatory regime governing auditing when managers obtain significant benefits both direct and indirect when they successfully raise capital. Defining quality as the inverse of the probability of overstatement in financial statements, we show that the natural equilibrium is one where lowest quality financial statements are chosen (resulting in a high probability of overstatement in the financial reports). Under these circumstances, firms that potentially yield a low rate-of-return (low fundamental value) cannot be identified easily and are overfunded relative to firms characterized by a high rate-of-return (high fundamental value). We show analytically that the introduction of FSI can lead to a better assessment of financial statement quality resulting in a much more accurate identification of low value firms.
The basic structure of FSI can be described as follows (details may be found in Appendix B, based on Ronen (2002)).9 Instead of appointing and paying auditors, companies purchase FSI that provides coverage to investors against losses suffered as a result of misrepresentation in financial reports. The premiums paid for that coverage are publicized. The insurance carriers appoint and pay the auditors, who attest to the accuracy of the financial statements of the prospective insurance clients. Those firms announcing lower premiums distinguish themselves in the eyes of the investors as companies with higher quality financial statements. In contrast, those with higher premiums reveal themselves as firms with lower quality financial statements. Every company will be eager to get higher coverage and pay lower premiums lest it be identified as the latter. A sort of Gresham's law would be set in operation, resulting in a flight to quality.
According to sound principles of corporate governance, auditors are supposed to be the agents of the shareholders. However, in practice, although shareholders (and audit committees) vote on management's recommendation of which auditor to hire, it is the management of the company that effectively engages the auditor and ultimately pays for the services. The fact that CEOs and CFOs control the fees paid for auditing and consulting services allows them to elicit actions, including opinions and assurances, that it desires from the auditor. The risk of losing fees from a long-term audit engagement—even in light of the limitations on non-audit services imposed by the Sarbanes-Oxley Act of 2002—may secure auditor compliance with management's objectives. We argue that the imperfect alignment of interests between managers and shareholders and the intractable conflict of interest imposed on auditors can be rectified through an agency relationship between the auditor and an appropriate principal, whose economic interests are aligned with the goal of promoting the quality of the financial statement.10 Within a free market mechanism, insurers can serve the role of such an intermediary.
The critical features of the FSI scheme underlying this study are: (a) the effect of publicizing the premium charged to different firms; and (b) the shift of control over the auditor's compensation and, hence, incentive structure from management to the insurer. We seek to formalize these two features and to demonstrate that FSI, when linked with appropriate disclosure provisions, leads firms to improve the quality of their disclosures voluntarily. A key economic feature underlying this result is the fact that the insurer's primary business is providing coverage and insurers are primarily asessed on whether their polices are generating profits. In contrast, an auditor's primary business is providing the audit service and the allocation of fees across services and coverage can be quite arbitrary. For this reason, the insurer sets the premium at a break-even level at least, whereas the auditor wishes to break even across the joint payments for audit services and indirect litigation coverage.
Model
We develop a model in which firms try to attract capital through their financial reports.11 The firm's management benefits from obtaining capital, but there is a social waste if firms with low rates-of-return are funded.12 We consider an economy with N firms, where each firm is of type i, i = 1, … , L where a type i firm will earn return ri with r1 < r2 < … < rL. The type of each firm f is drawn randomly by nature at the start of the period and is independent of other firms. The true type drawn by nature is unobservable at the start of the period but the managers of each firm f obtain a private signal, ωf, about their firm's type where ωf ∈ {ω1, ω2, … , ωL} represents the set of L possible signals observable by the firm. We denote by P(i|ωl) the probability that the end-of-period rate-of-return will be ri for a firm f that receives a private signal, ωl.
The strategic tool for obtaining capital is an audited financial report that is issued to investors. Although this report may not be directly falsified, it can be manipulated indirectly through a reduction in the quality of the statements.13 Based on his or her private signal, ωf, the firm's manager chooses accounting policies that determine the internal quality of the reporting system, denoted by q, where we assume  . The overall financial statement quality, x, is determined both by the firm's choice of internal quality, q, and the auditor's effort, e which lies in some real interval
. The overall financial statement quality, x, is determined both by the firm's choice of internal quality, q, and the auditor's effort, e which lies in some real interval 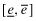 . The overall quality is determined as the function x = V(q, e) where V is strictly increasing in both q and e. We shall use x to denote the ordered pair {q, e} and x to denote the value V(q, e). When dealing with ordered pairs we use the natural coordinate order as follows:
. The overall quality is determined as the function x = V(q, e) where V is strictly increasing in both q and e. We shall use x to denote the ordered pair {q, e} and x to denote the value V(q, e). When dealing with ordered pairs we use the natural coordinate order as follows: 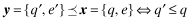 and e′ ≤ e. In contrast, the statement y ≤ x is an assertion that V(q′, e′) ≤ V(q, e) and does not indicate that each component is lower. Clearly,
and e′ ≤ e. In contrast, the statement y ≤ x is an assertion that V(q′, e′) ≤ V(q, e) and does not indicate that each component is lower. Clearly, 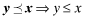 but the converse may not be true. For a given e, V (q, e) is a strictly increasing function of q and therefore, there is only one value of q such that the given value x is the same as V (q, e). For this reason, any function of q and e can also be treated as a function of x and e.
but the converse may not be true. For a given e, V (q, e) is a strictly increasing function of q and therefore, there is only one value of q such that the given value x is the same as V (q, e). For this reason, any function of q and e can also be treated as a function of x and e.
After firm f's type, i, and associated rate-of-return ri, is realized, a financial report θf ∈ {1, … , L} is disseminated to investors. Associated with each report θf = j is the rate-of-return rj, which we shall refer to as firm f's reported rate-of-return. rj may, of course, be different from the actual rate-of-return of firm f, ri. However, investors will not blindly accept rj; instead, they will use this implied (by the report) rate as well as their perceptions about audit quality to ‘infer’ an expected rate-of-return for firm f.
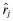 :
:
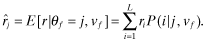 ()
()We assume that there is a minimum threshold rate, r*, such that funding firms with rates of return less than r* results in a social loss. r* is a random variable with a distribution G(r*) that represents the social cost of capital. r* is assumed to be independent of firms' rates of return and G is assumed to be convex.To exclude the trivial cases (a) where all firms should be funded (and there is no social loss resulting from misleading statements) and (b) where even the highest-type firm does not merit funding (and capital providers will not enter the market) we assume that r* is distributed over some interval 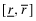 where
where 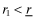 and
and  . The simplest example of a convex G satisfying these requirements is when r* is uniformly distributed over the interval
. The simplest example of a convex G satisfying these requirements is when r* is uniformly distributed over the interval 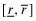 .
.
In the first-best scenario, in which the true rate-of-return is perfectly observed, only firms with rates of return higher than r* will obtain capital. In a second-best scenario, in which investors do not know each firm's type, they analyze the report, θf = j, and fund firm f if the inferred rate-of-return, 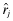 , is greater than the threshold rate r*. For simplicity, we assume that whenever
, is greater than the threshold rate r*. For simplicity, we assume that whenever 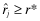 , investors contribute one unit of capital to the firm.14
, investors contribute one unit of capital to the firm.14
The managers of a firm typically benefit in both pecuniary and non-pecuniary ways from capital inflows.15 We represent the (portion) of the value of the firm appropriated by management by B (for benefits). In other words, by ensuring a capital inflow, the firm's management generates both a return which is passed back to shareholders and a benefit B for themselves. In this setting, low quality financial statements that misdirect capital lead to two basic types of losses (viewed from the perspective of investors).
First, when a firm of type i with (ri < r*) is funded (because the inferred rate-of-return 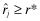 ), the investor suffers a a loss of 1 × (r* − ri) (recall that the investment involves one unit of capital). While such losses are straightforward, there is a second type of loss that also results from inferior accounting quality. Because investors are unable to distinguish the high type firms from low type firms, some high type firms may not be funded. So, if a firm k of high type, rk > r* is not funded, investors lose the amount 1 × (rk − r*). The total cost of misinvestment is the sum of these two losses (see example 3.2 for a complete loss calculation). That is, an inflated financial statement not only draws capital towards an inferior firm, it also indirectly starves superior firms (whose ‘honest’ reports are discounted in the same way as ‘dishonest’ reports) leading to both an actual loss and an opportunity loss.
), the investor suffers a a loss of 1 × (r* − ri) (recall that the investment involves one unit of capital). While such losses are straightforward, there is a second type of loss that also results from inferior accounting quality. Because investors are unable to distinguish the high type firms from low type firms, some high type firms may not be funded. So, if a firm k of high type, rk > r* is not funded, investors lose the amount 1 × (rk − r*). The total cost of misinvestment is the sum of these two losses (see example 3.2 for a complete loss calculation). That is, an inflated financial statement not only draws capital towards an inferior firm, it also indirectly starves superior firms (whose ‘honest’ reports are discounted in the same way as ‘dishonest’ reports) leading to both an actual loss and an opportunity loss.
Information Structure and Investor Beliefs
- the joint relationship of the true underlying type and the reported type for each level of overall quality x; and
- the (Bayesian) inference process of investors based on the relationship in 1 above and on their perceptions about the choice of x.
For each level of quality x, we have a joint distribution of reports and types denoted by P(j, i|x), i = 1, … , L; j = 1, … , L. We assume that x has no productive effects, that is, it does not affect the (unconditional) distribution of true types, P(i) or the joint probability P(i, ωf); so P(j, i|x) = P(j|i, x)P(i) and P(j, i|x, ωf) = P(j|i, x)P(i|ωf). We write this joint distribution as an L × L matrix
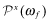 , or more simply, as
, or more simply, as
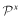 when ωf is pre-specified. In other words, given a firm f the private signal of which is ωf and quality choice is x, the ijth coeffecient of
when ωf is pre-specified. In other words, given a firm f the private signal of which is ωf and quality choice is x, the ijth coeffecient of
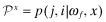 . Recall that for any two levels of overall quality x, y,
. Recall that for any two levels of overall quality x, y, 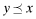 if, and only if, x entails both higher internal quality and higher audit effort than y. The next assumption develops a systematic ordering relationship between
if, and only if, x entails both higher internal quality and higher audit effort than y. The next assumption develops a systematic ordering relationship between
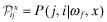 and
and
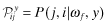 consistent with
consistent with 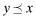 .
.
A lower x (in the natural co-ordinate partial order) ought to ‘increase’ the probability of overstatement; in addition, a higher x should make it easier to separate out true types. To capture these two features, we first assume that all errors in the financial report are overstatements; that is, a firm f of type i only receives reports θf = j ≥ i.16 Then we make the following assumption (further details are given in Appendix A):
Assumption 1. (A Formalization of Financial Statement Quality)
- (1)
For a given overall quality x, firms of higher type are more likely to issue high reports. That is, whenever i ≥ k, the relative likelihood of being reported as type j,
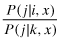 increases in j (i.e., for a fixed x, higher signals are ‘good news’ in the sense of Milgrom (1981).
increases in j (i.e., for a fixed x, higher signals are ‘good news’ in the sense of Milgrom (1981). - (2)
For a given type i, the reported type increases (in the sense of First Degree Stochastic Dominance) as overall quality is lowered, that is, for
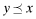 , P(·|i, y) FDSD's P(·|i, x).
, P(·|i, y) FDSD's P(·|i, x). - (3)
For any two quality levels
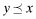 , there exists a column stochastic matrix Λyx with
, there exists a column stochastic matrix Λyx with
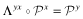 .17
.17
As noted in equation 1, the inferred return depends only on the beliefs νf regarding the overall quality chosen by firm f rather than on the firm's actual optimal choice 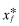 . The basic theme underlying our model is that firms can mislead investors by setting
. The basic theme underlying our model is that firms can mislead investors by setting 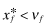 ; however, rational expectations requires that in equilibrium, the actual choice of x and market conjectures have to coincide. The equilibrium we derive takes both of these economic requirements into account. We return to this analysis after developing the liability structure that counteracts firms' desire to set low levels of overall quality.
; however, rational expectations requires that in equilibrium, the actual choice of x and market conjectures have to coincide. The equilibrium we derive takes both of these economic requirements into account. We return to this analysis after developing the liability structure that counteracts firms' desire to set low levels of overall quality.
Liability Structure
Both firms and auditors face penalties under provisions of the 1933 and 1934 Securities Acts and other statutory and case law when they issue financial reports that ex-post are found to be misleading. Additionally, financial statements with low overall quality may impose additional penalties on the auditor in the form of reputation loss. Our goal is to show that the allocative efficiency of capital increases with the provision of FSI. To make this point clearly, we fix the total recoveries obtainable through the legal system while varying the mechanism by which these recoveries are collected by investors. The firm's expected liability is denoted by 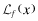 . We denote the auditor's expected liability by
. We denote the auditor's expected liability by 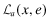 to emphasize the fact that the auditor is separately responsible for any deficiencies in the audit process caused by a low level of effort, e. The structure that we impose on the expected liability is:
to emphasize the fact that the auditor is separately responsible for any deficiencies in the audit process caused by a low level of effort, e. The structure that we impose on the expected liability is: 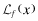 and
and 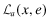 are both decreasing in x (under the usual partial order on x) and e. Notice that
are both decreasing in x (under the usual partial order on x) and e. Notice that 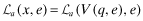 ; where it causes no confusion, we shall also write
; where it causes no confusion, we shall also write 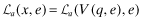 as
as 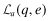 where
where 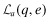 is decreasing in both q and e.18
is decreasing in both q and e.18
Funding and Managerial Benefits
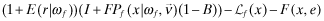 ()
()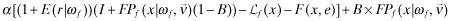 ()
()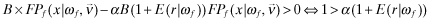 ()
()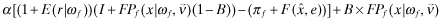 ()
()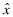 is the overall quality reported by the auditor to the insurer (see the next section). After receiving a private signal ωf, the managers choose x so as to maximize the payoff in equation (3) or (5) depending on whether insurance is available.
is the overall quality reported by the auditor to the insurer (see the next section). After receiving a private signal ωf, the managers choose x so as to maximize the payoff in equation (3) or (5) depending on whether insurance is available.The last part of our model development concerns the role of the auditor.
Auditor Incentives and Decisions
The auditor is the principal informational intermediary in the trading of securities. In our model, we take as a given that the auditor must supply information to investors but that the quality of this information depends on the incentives provided by the auditor's employer (either the firm or the insurer). Our goal is to study firm–investor interactions and not audit contracts or auditor behavior. To this end, we focus solely on whether the auditor's incentives lead to the true overall quality, x, being revealed to investors rather than on whether auditors will ‘shirk’.
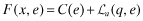 ()
()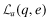 .22 For a given level of overall quality, x, q*(x) and e*(x) denote the choices of q and e that minimize the total cost of
.22 For a given level of overall quality, x, q*(x) and e*(x) denote the choices of q and e that minimize the total cost of 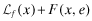 .
.Suppose FSI is available, a further consideration enters the picture—the report to the insurer about the choice of x. We denote this report by 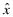 and write
and write 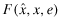 for the fees when the auditor is incentivized to report
for the fees when the auditor is incentivized to report 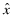 while the implemented overall quality of the firm is x. We distinguish between two cases: (a) auditor hired by the firm and (b) auditor hired by the insurer. We assume the auditor's report to the insurer is private and does not increase the auditor's exposure to litigation. We assume that the insurer can demand an ex-post adjustment if
while the implemented overall quality of the firm is x. We distinguish between two cases: (a) auditor hired by the firm and (b) auditor hired by the insurer. We assume the auditor's report to the insurer is private and does not increase the auditor's exposure to litigation. We assume that the insurer can demand an ex-post adjustment if 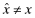 through increased future premia when the firm hires the auditor or through a transfer from the auditor when the insurer hires the auditor. We denote this adjustment by
through increased future premia when the firm hires the auditor or through a transfer from the auditor when the insurer hires the auditor. We denote this adjustment by 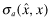 . The auditor is paid a fee commensurate with the
. The auditor is paid a fee commensurate with the  reported to the insurer. In addition, when the auditor is hired by the insurer, the auditor's initial fee will be paid by the insurer, but reimbursed by the firm and the fee will not be affected by the overall quality level x. Gathering all these points together, the audit fee paid by the firm,
reported to the insurer. In addition, when the auditor is hired by the insurer, the auditor's initial fee will be paid by the insurer, but reimbursed by the firm and the fee will not be affected by the overall quality level x. Gathering all these points together, the audit fee paid by the firm, 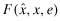 , has the following structure:
, has the following structure:
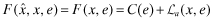
 ()
()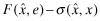 , is net of the ex-post adjustment and thus depends on all three variables,
, is net of the ex-post adjustment and thus depends on all three variables, 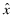 , x and e. To minimize
, x and e. To minimize 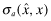 , the auditor is thus induced to report
, the auditor is thus induced to report 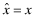 resulting in
resulting in 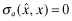 . In this way, the strategy whereby the auditor reveals x truthfully to the insurer in equilibrium is implemented. To sum up, when the firm hires the auditor, the auditor can be costlessly induced to report the overall quality level favoured by the firm (see also Proposition 1) whereas when the insurer hires the auditor, ex-post transfers induce the auditor to report quality truthfully to the insurer.23
. In this way, the strategy whereby the auditor reveals x truthfully to the insurer in equilibrium is implemented. To sum up, when the firm hires the auditor, the auditor can be costlessly induced to report the overall quality level favoured by the firm (see also Proposition 1) whereas when the insurer hires the auditor, ex-post transfers induce the auditor to report quality truthfully to the insurer.23Formalization
- (1) the effects of the public disclosure of FSI premia;
- (2) the economic rationale for allowing the insurer to control the auditor's contract.
- (I) The current regime where information about x is unavailable prior to the funding decision and investors base their decisions on (ex-ante) beliefs. The auditor is hired and paid by the client-firm and may not be truly independent.
- (II) Insurance is available; the auditor is hired by the client-firm and is truly independent. That is, the auditor cannot be induced to overstate x (although he or she can be induced to lower audit effort). Investors update their beliefs about x after observing the insurance premium.
- (III) Insurance is available and the auditor is hired by the client-firm and can be induced by the client-firm to overstate x. Investors update their beliefs about x after observing the insurance premium.
- (IV) FSI is available, premia are disclosed and the auditor is hired by the insurer. Investors update their beliefs about x after observing the premium.24
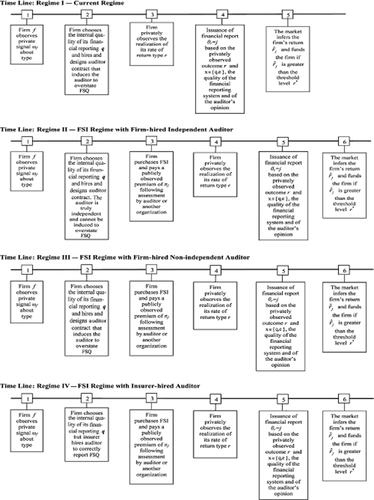
Time Lines for Programs I–IV
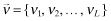 where νl denotes the beliefs regarding the (strategically optimal) level of x implemented by a firm f with private signal ωl.25 Thus, in Setting I, the inferred return for firm f upon observing a report θf = j under beliefs
where νl denotes the beliefs regarding the (strategically optimal) level of x implemented by a firm f with private signal ωl.25 Thus, in Setting I, the inferred return for firm f upon observing a report θf = j under beliefs 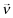 is given by (see Appendix A for the details):26
is given by (see Appendix A for the details):26
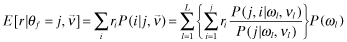 ()
()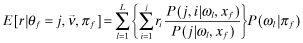 ()
()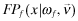 in Setting I and FPf (x|ωf, πf) in Settings II–IV. The decision problem for firm f's manager is the choice of quality xf = {qf, ef} that maximizes the benefits of funding net of the cost of implementing xf.
in Setting I and FPf (x|ωf, πf) in Settings II–IV. The decision problem for firm f's manager is the choice of quality xf = {qf, ef} that maximizes the benefits of funding net of the cost of implementing xf.The insurer is assumed to break even through a suitable choice of ex-ante premium, πf, and an ex-post adjustment. This assumption of ex-post break-even is common in the insurance literature and represents the ability to impose costs on the insured in the form of higher future premia. In our context, we assume that the insurer sets an initial premium 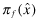 based on the auditor's report regarding the overall quality of the financial statements and imposes an ex-post adjustment
based on the auditor's report regarding the overall quality of the financial statements and imposes an ex-post adjustment 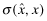 (on firm or auditor depending on the context) that allows the insurer to break even. However, the insurer does not wish to depend on this ex-post adjustment and tries to make it as small as possible. Lastly, we assume that the audit fee, F(x, e) in Programs I, II & III, and
(on firm or auditor depending on the context) that allows the insurer to break even. However, the insurer does not wish to depend on this ex-post adjustment and tries to make it as small as possible. Lastly, we assume that the audit fee, F(x, e) in Programs I, II & III, and 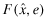 in Program IV, implements the audit effort e and report
in Program IV, implements the audit effort e and report  by the auditor.
by the auditor.
Program I: Current Regime
| maxq,e,F |
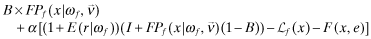
|
|
| subject to | ||
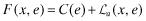
|
(AF) | |
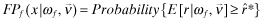
|
(FD) | |
| νf = x*(ωf) = (q*(ωf), e*(ωf)) | (RE) |
Program II: Premia Disclosed with independent auditor hired by the firm and reports 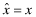
| maxq,e,F |
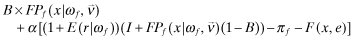
|
|
| subject to | ||
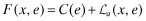
|
(AF) | |
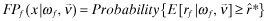
|
(FD) | |
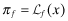
|
(BE) | |
| νf = x*(ωf) = (q*(ωf), e*(ωf)) | (RE) |
Program III: Premia Disclosed with a (non-independent) auditor hired by client-firm
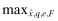
|
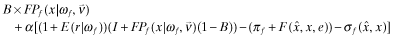
|
|
| subject to | ||
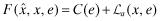
|
(AF) | |
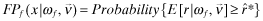
|
(FD) | |
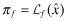
|
(IP) | |
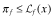
|
(CO) | |
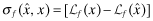
|
(BE) | |
| νf = x*(ωf) = (q*(ωf), e*(ωf)) | (RE) |
Program IV: FSI
| maxq,e,F |
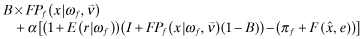
|
|
| subject to | ||
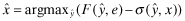
|
(AF) | |
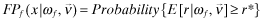
|
(FD) | |
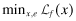
|
(IP) | |
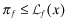
|
(CO) | |
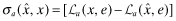
|
(BE) | |
| νf = x*(ωf) = (q*(ωf), e*(ωf)) | (RE) |
The objective function faced by managers in all four programs is to maximize benefits less expenses. Their goal is to maximize their own perquisites by boosting the firm's capital base through their reporting strategies less the expected cost of being over-aggressive. The main differences in this equation across the programs stems from disclosing the insurance premium (absent in Program I and present in all the others) and the nature of the ex-post transfer to the insurer (absent in Program II, made by the firm in Program III and by the auditor in Program IV). The insurance premium is revealed to the market in Programs II, III and IV and affects the probability of being funded. However, masking the overall quality of the financial statements (i.e., inducing 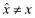 ) results in an ex-post transfer,
) results in an ex-post transfer, 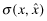 from the firm in Program III and from the auditor in Program IV.
from the firm in Program III and from the auditor in Program IV.
The (IP) equation represents the level of the premium set initially by the insurer based on the 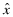 reported to them by the auditor. This premium is disclosed to investors as a signal on the overall quality. (Note that in Program II and IV,
reported to them by the auditor. This premium is disclosed to investors as a signal on the overall quality. (Note that in Program II and IV, 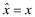 because the auditor either reports the the truth because he is independent or is induced to do so in equilibrium.) To keep the programs comparable, the cost of the audit is always borne by the firm. In other words, even when the insurer hires the auditor (under FSI), the costs of the audit are reimbursed by the client-firm.
because the auditor either reports the the truth because he is independent or is induced to do so in equilibrium.) To keep the programs comparable, the cost of the audit is always borne by the firm. In other words, even when the insurer hires the auditor (under FSI), the costs of the audit are reimbursed by the client-firm.
The (BE) equation represents the break-even condition for insurers. Both this equation and the (CO) condition are motivated by an assumption of perfect competition in the insurance industry. The (CO) condition is based on the logic that the firm can, if it chooses to do so, reveal its true overall quality to the insurer and obtain a fair premium. The insurer, in turn, is not worried about undercharging on the premium because the insurance contract allows for an ex-post adjustment if the initial assessment of x is erroneous.
In all four settings, the cost to investors of false reporting has a direct component that is remedied (at least partially) through the penalties imposed by the litigation system, and an indirect one measured as misapplied investment. As we are interested only in the relative levels of the indirect cost, we hold the direct costs, that is, the litigation penalties constant across regimes and ensure that these costs are borne by the client-firm in all settings. In Program I, this cost is paid directly by the client-firm. In Programs (II)–(IV), the expected costs are paid out by the firm as an insurance premium (note that with risk neutrality, the actual uncertain cost is the same, in utility terms, as the expected cost to both client-firm and insurer). In Program II, where the auditor is truly independent, x is assumed to be known by the insurer whereas in Programs III and IV the insurer has to rely either on the firm or the auditor to make an assessment of x.
The critical difference across Programs III and IV lies in the ex-post settlement associated with the (BE) constraint. In Program III, the insurer breaks even by settling up with the client-firm through a premium adjustment, 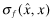 whereas in Program IV, the settling up takes place with the auditor. In fact, the structure ensures that
whereas in Program IV, the settling up takes place with the auditor. In fact, the structure ensures that 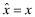 in Program IV and ex-post transfers do not take place in equilibrium.27 In Program III, the true overall quality of the financial statements is identified only ex-post through the litigation discovery process and if benefits to funding are large enough, the firm is willing to pay these ex-post transfers (after the true quality is revealed) in exchange for the ex-ante benefits of funding.
in Program IV and ex-post transfers do not take place in equilibrium.27 In Program III, the true overall quality of the financial statements is identified only ex-post through the litigation discovery process and if benefits to funding are large enough, the firm is willing to pay these ex-post transfers (after the true quality is revealed) in exchange for the ex-ante benefits of funding.
The (RE) equation expresses the rational expectations constraint that the beliefs about the x implemented by a firm with private signal ωf, νf coincides with the actual equilibrium choices, {q*, e*}. In contrast, the objective function of the manager is maximized holding beliefs constant. This structure is chosen to incorporate the following two economic features: (a) managers have the ability to set low x's without being detected ex-ante but (b) market beliefs will stabilize in equilibrium at x levels that will not be undercut by the manager.
We now turn to our main analysis concerning the equilibrium levels of x that are chosen by firms under each of the Programs (I)–(IV). In Programs (II)–(IV), the insurance premium is observable by investors. When the firm implements its optimal level of x, it has to take into account the reaction of investors to the financial report that will eventually be issued, and this reaction depends either on prior beliefs regarding x (Program I) or posterior beliefs formed after observing the insurance premium charged to the firm (Programs (II)–(IV)). x is assumed to be observable to the insurer in Program II but not observable in Programs (III)–(IV).
Results
To explain the dynamics of investor–firm interactions arising from the introduction of FSI, we analyze the equilibrium in all four programs. Our goal is to show that the implemented x is highest when insurance premia are revealed ex-ante to investors and the auditor is an agent of the insurer rather than the firm. We start with the simpler setting where the auditor is truly independent and reports the level of x implemented by the firm to the insurer. Note that this does not affect the audit effort or the probability of errors in the financial report. All it does is to ensure that the premium truly reflects the x implemented by the firm. We show that in this case (Program II), a simple disclosure of the FSI premium leads to a race to the ‘top’ and all firms implement high x. In contrast, if the firm can induce the auditor to misreport x to the insurer as in Program(III), all potential benefits of providing insurance are lost providing a rationale for the auditor to become an agent of the insurer as in Program (IV).
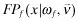 , given by:
, given by:
 ()
()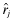 denote the inferred rate-of-return under beliefs
denote the inferred rate-of-return under beliefs 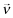 and observed report θf = j (we suppress the dependence on ωf and
and observed report θf = j (we suppress the dependence on ωf and 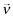 for notational clarity). In addition, in the special case when the beliefs are that the firm has chosen quality x (i.e., νf = x), we denote the vector of inferred returns by
for notational clarity). In addition, in the special case when the beliefs are that the firm has chosen quality x (i.e., νf = x), we denote the vector of inferred returns by 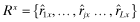 where
where 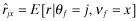 . With this notation, the next lemma lists a number of results that link inferred returns and funding probabilities using the information structure in Assumption 1.
. With this notation, the next lemma lists a number of results that link inferred returns and funding probabilities using the information structure in Assumption 1.
Lemma 1. (Reports, inferences and funding probabilities) Let νf denote the posterior beliefs about the implemented x and private signal type of firm f, and 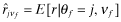 denote the inferred rate-of-return under belief νf.
denote the inferred rate-of-return under belief νf.
- (1)
A higher reported rate-of-return implies a (strictly) greater inferred rate-of-return that is,
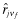 is increasing in j.
is increasing in j. - (2)
Let ωf denote the private signal observed by firm f. Then the firm's expected probability of funding by choosing quality x is given by:
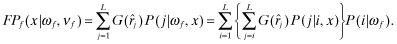 ()
() - (3)
Suppose that σf and νf are two different posterior beliefs about firm f with the following properties:
- a) Under νf, investors believe that xf = x and ωf = ωl with the prior probability P(ωl).
- b) Under σf, investors believe that xf = x and ωf = ω1 (with probability 1). (i.e., under belief νf, all types pool at x whereas under σf, only the ω1-type picks x).
- (4)
Let ωf denote the private signal observed by firm f and
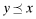 be two distinct levels of overall quality. Let Rx, Ry, denote the associated vectors of inferred returns (under beliefs νf = x and νf = y respectively) and Px, Py the probability vectors of observing a report j under quality x, y respectively. Then there is a column-stochastic matrix Γxy satisfying both the following (vector) equalities:
be two distinct levels of overall quality. Let Rx, Ry, denote the associated vectors of inferred returns (under beliefs νf = x and νf = y respectively) and Px, Py the probability vectors of observing a report j under quality x, y respectively. Then there is a column-stochastic matrix Γxy satisfying both the following (vector) equalities: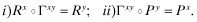
- (5)
Let r* be given and
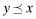 be two levels of quality. Let j, k denote the lowest reports such that
be two levels of quality. Let j, k denote the lowest reports such that 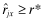 and
and 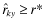 . Then
. Then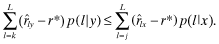
Proof See Appendix A. □
The next lemma shows how the probability of funding for firm f changes in the x choices.
Lemma 2. (Funding probability, welfare, and overall quality choice, x) Let ωf denote the private signal observed by firm f and x, y two quality levels with 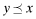 .
.
- (1)
For any investor beliefs
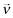 about the quality choice of firm f,
about the quality choice of firm f, 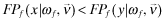 . Holding investor beliefs fixed, a reduction in quality (i.e., an inflation of the expected report) results in a larger probability of funding.
. Holding investor beliefs fixed, a reduction in quality (i.e., an inflation of the expected report) results in a larger probability of funding. - (2) Suppose that investor beliefs about quality accurately reflect the actual choices of the firm; then FPf (x|ωf, νf = x) > FPf (y|ωf, νf = y). Allowing investor beliefs to accurately reflect the actual quality chosen by the firm, a reduction in quality (i.e., an inflation of the expected report) results in a smaller probability of funding.
- (3) Suppose that investor beliefs about quality accurately reflect the actual choices of the firm; then welfare is increasing with overall quality.
- 1)
Fix any beliefs
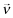 about the quality choices of firm f. From Lemma 1 (1),
about the quality choices of firm f. From Lemma 1 (1), 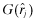 is increasing in j and by Assumption 1 (2), P(j|i, x) is strictly decreasing in x in the sense of FDSD; thus
is increasing in j and by Assumption 1 (2), P(j|i, x) is strictly decreasing in x in the sense of FDSD; thus 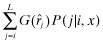 is strictly larger for lower x. Therefore, by Lemma 1 (2), the ex-ante funding probability,
is strictly larger for lower x. Therefore, by Lemma 1 (2), the ex-ante funding probability, 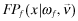 , is strictly decreasing in x.
, is strictly decreasing in x. - 2)
In this case, investor beliefs reflect the actual quality chosen by the firm, x. Denote by G(Rx), the vector
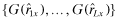 and analogously, define the vector
and analogously, define the vector 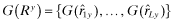 . It follows from Lemma 1 (2) that
. It follows from Lemma 1 (2) that 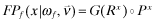 where Px the probability vector of reporting j under quality x, that is
where Px the probability vector of reporting j under quality x, that is 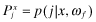 . Therefore, from Lemma 1, 4
. Therefore, from Lemma 1, 4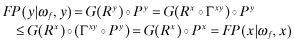
- 3)
Let
 . We will show that for each realized value of the cost of capital r*, the welfare loss is greater under y than under x. Let j, k be the lowest reports such
. We will show that for each realized value of the cost of capital r*, the welfare loss is greater under y than under x. Let j, k be the lowest reports such 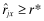 , respectively,
, respectively, 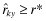 . By Lemma 1 (1) every report l ≥ j is funded under x while every l ≥ k is funded under y. The total social return from investment under quality x (respectively, y) is given by
. By Lemma 1 (1) every report l ≥ j is funded under x while every l ≥ k is funded under y. The total social return from investment under quality x (respectively, y) is given by 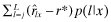 (respectively,
(respectively, 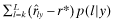 ). However, by Lemma 1 (5), the total return under x is greater than that under y, which is equivalent to increased social welfare within our context. □
). However, by Lemma 1 (5), the total return under x is greater than that under y, which is equivalent to increased social welfare within our context. □
The results in the two lemmas above help to derive the equilibria under the current regime when investors only discover x ex-post through litigation and in the setting where the disclosure of the insurance premium provides ex-ante information to the market.
Proposition 1. (Equilibrium in Program I (current regime)) If the benefits from funding, B, are such that for every y < x:
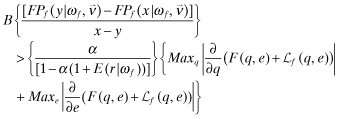 ()
()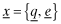 , that is, the lowest possible level of overall quality. Consequently, as benefits to the manager from funding increases, capital is allocated to low rate-of-return firms with greater probability.
, that is, the lowest possible level of overall quality. Consequently, as benefits to the manager from funding increases, capital is allocated to low rate-of-return firms with greater probability.
Proof Before proceeding to the proof, we note that Lemma 1 (1) implies that the term in parentheses on the left-hand-side is positive and that 4 implies that the right-hand-side is positive. The mean-value-theorem of calculus ensures that for any x = {q, e} and y = {q′, e′}:
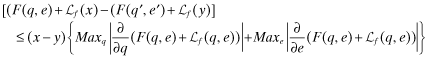 ()
()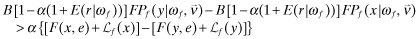 ()
()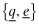 . Note also that B* is any value satisfying 12 with equality, then any B > B* also sets off a race to the bottom with regard to overall quality. □
. Note also that B* is any value satisfying 12 with equality, then any B > B* also sets off a race to the bottom with regard to overall quality. □
Proposition 1 shows that if the benefits to funding are large enough, it sets off a race to the bottom in terms of overall quality. We now proceed to analyze the effects of introducing FSI. Before presenting that argument, we note that if 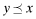 then the break-even premia associated with these quality levels, π(x) and π(y) satisfy π(x) < π(y). This is an immediate consequence of Assumption 1.
then the break-even premia associated with these quality levels, π(x) and π(y) satisfy π(x) < π(y). This is an immediate consequence of Assumption 1.
Assume that each firm purchases insurance and that the premiums charged to firms are observable. Suppose now that in equilibrium some firm f sets xf < xL, where xL is the quality choice of a firm receiving the highest possible private signal ωf. Then, the premium charged to firm f, πf, is strictly larger than πL—and investors will infer that firm f is of some type other than L. Thus, the inferred rate-of-return conditional on observing πf will be different from that based on the prior beliefs, 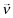 . We will show that the disclosure of πf and attendant changes in the inferred rate-of-return lead to an equilibrium where all firms pool at the highest level of internal quality.
. We will show that the disclosure of πf and attendant changes in the inferred rate-of-return lead to an equilibrium where all firms pool at the highest level of internal quality.
Proposition 2. (Equilibrium with revelation of premia (Program II)) If the benefits from funding, B, are such that for every y < x:
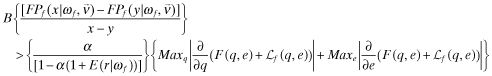
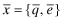 , that is, the highest possible level of overall quality. The association between management benefits (perquisites) and misallocation of capital is negated through the provision of insurance premia that are publicly disclosed (note, however, that in this program, we assume that the auditor will not misreport x to the insurer).
, that is, the highest possible level of overall quality. The association between management benefits (perquisites) and misallocation of capital is negated through the provision of insurance premia that are publicly disclosed (note, however, that in this program, we assume that the auditor will not misreport x to the insurer).
Proof Before proceeding to the proof, we note that x and y have been interchanged in the term in parentheses on the left-hand-side, and it is positive from Lemma 1 (2). Let 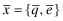 denote the highest quality choice of q and e. Denote the associated break-even premium by
denote the highest quality choice of q and e. Denote the associated break-even premium by 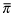 . A rational expectations equilibrium is given by the following beliefs:
. A rational expectations equilibrium is given by the following beliefs:
- (1)
whenever
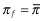 , then
, then 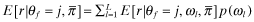 (conditional probability after observing
(conditional probability after observing 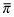 equals unconditional probability at the highest level of quality
equals unconditional probability at the highest level of quality 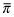 corresponding to beliefs that all firm-types choose the quality level
corresponding to beliefs that all firm-types choose the quality level 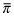 .);
.); - (2)
whenever
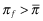 , then E[r|θf = j, πf] = E[r|θf = j, ω1, xf] where xf is the quality level corresponding to πf.
, then E[r|θf = j, πf] = E[r|θf = j, ω1, xf] where xf is the quality level corresponding to πf.
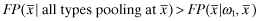 . Next for any
. Next for any 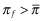 , the associated quality,
, the associated quality, 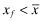 . Next, by Lemma 1 (2),
. Next, by Lemma 1 (2), 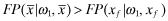 . Putting these two inequalities together,
. Putting these two inequalities together, 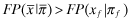 (under the belief structure outlined above). Therefore, the funding probability declines whenever
(under the belief structure outlined above). Therefore, the funding probability declines whenever 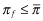 is observed, that is, whenever,
is observed, that is, whenever, 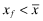 is implemented by firm f. As in Proposition 1, the condition on B ensures that the manager's utility is strictly greater with x rather than y. Therefore, every firm will implement
is implemented by firm f. As in Proposition 1, the condition on B ensures that the manager's utility is strictly greater with x rather than y. Therefore, every firm will implement 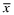 . □
. □
The fact that defections from high quality are detected and immediately penalized results in the ‘flight to quality’ documented in Proposition 1. Specifically, high-type firms gain from setting high x. If low-type firms can muddy investor perceptions through low x, high-type firms are also driven to exaggerate their own outcomes, leading to the result in Proposition 1. In contrast, in Proposition 1, by staying with high x, good firms force others to follow suit or be identified as low types. Thus, low-type firms either abandon their quest for capital or accept a much lower probability of being able to mislead investors in equilibrium.
We note that a key feature of the equilibrium derivation stems from the payoff structure of the insurer. Insurers do not benefit from firms obtaining funding. In contrast, the firm benefits directly from raising capital and high-type firms and low-type firms have different preferences over quality. If the firm controls the audit effort, alternative communication mechanisms for conveying quality (such as publicizing the audit fee) may fail (see Appendix C). The conflicting incentive structures (with regard to quality) across types makes it harder to make accurate inferences about quality based on the audit fee as compared with inferences based on the insurance premium.
The choice of audit effort (as opposed to the firm's type) constitutes an endogenous hidden action. Signaling about endogenous hidden action that is strategically chosen by some participants but unobservable to others is qualitatively different from signaling exogenous hidden information (DeGroote, 1990). Intuitively, if the hidden information is exogenous (such as the firm's type), then the sender chooses the best signal while holding type constant. However, if the hidden information is an action, the sender of the signal may change both the action and the signal. Under these circumstances, it is much harder to set up separating equilibria. For example, if a particular signal-action combination yields the highest payoff, all senders will choose that particular signal-action combination. In our context where there is both hidden exogenous and endogenous information, for any internal quality choice q of the firm, the insurer's payoff is always maximized at the cost minimizing level of audit effort; in contrast, even while holding internal quality fixed, the firm's payoffs are maximized either at high or low audit effort depending on the firm's type. For this reason, shifting the control of the audit effort to the insurer is critical in deriving the equilibrium in Program IV.
In general, one can obtain economically unintuitive sequential equilibria by specifying implausible off-equilibrium beliefs. The standard device to rule out ‘bad equilibria’ is to impose restrictions on such off-equilibrium beliefs. In the simple case of two rates of return discussed in the example (see below), a direct proof can be given that ‘pooling-at-the-top’ is the only equilibrium that meets the universal divinity test.
Lemma 3. (refinement test) The equilibrium where all firms pool at the highest level of overall quality x is the only one that satisfies the universal divinity refinement criterion.
Proof See Appendix A. □
Auditor as an Agent of the Insurer
In this section, we provide an economic rationale for shifting the responsibility for engaging an auditor from the firm to the insurer. We first discuss the situation where the firm purchases FSI but continues to hire the auditor (Program III).We emphasize that this is not an implementation of FSI—under FSI, the auditor is an agent of the insurer. Rather, we analyze this situation to highlight why FSI requires that the auditor stop being an agent of the firm. Let 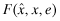 denote the cost to the firm of getting the auditor to exert effort e and report the quality as
denote the cost to the firm of getting the auditor to exert effort e and report the quality as 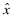 when the true quality is x. The auditor can be incentivized to report the true x but the firm may not desire the true x to be revealed.28
when the true quality is x. The auditor can be incentivized to report the true x but the firm may not desire the true x to be revealed.28
When the auditor continues as an agent of the firm truthful revelation of x may be impossible ex-ante. However, litigation will typically reveal the true x ex-post. The insurer will find it possible to make an adjustment 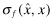 with the firm (because the insurer has a contractual relationship only with the firm). The key point is that this transfer is made ex-post and will not be known at the time of trading. Hence the firm does not internalize the cost of the low quality, ex-ante.
with the firm (because the insurer has a contractual relationship only with the firm). The key point is that this transfer is made ex-post and will not be known at the time of trading. Hence the firm does not internalize the cost of the low quality, ex-ante.
The initial premium observed by the market (Constraint (IP)) reflects the overall quality reported by the auditor to the insurance company rather than the true x. Under these circumstances, the firm will always have incentives to set low x to increase the probability of funding while incentivizing the auditor to over-report the x. Market participants will anticipate this and set funding strategies based on low x precipitating a race to the bottom as shown in the next proposition.
Proposition 3. (Equilibrium with the auditor as firm's agent) Assume that the benefits from funding, B, are such that for every y < x:
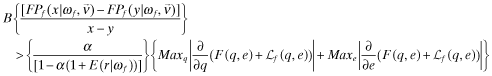
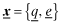 , that is, the lowest possible level of overall quality.
, that is, the lowest possible level of overall quality.
Proof We begin by noting that the insurer is indifferent across breaking even ex-ante or ex-post. From the insurer's perspective, the premium can be set based on the auditor's assessment of x, 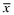 , and adjusted later through the transfer
, and adjusted later through the transfer 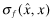 . As explained in the discussion preceding equation 7, the firm can (with no extra cost) incentivize the auditor to report
. As explained in the discussion preceding equation 7, the firm can (with no extra cost) incentivize the auditor to report 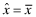 by setting fees as follows:
by setting fees as follows:
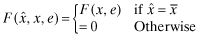
 (with off-equilibrium beliefs that any firm choosing
(with off-equilibrium beliefs that any firm choosing 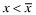 , as manifested in
, as manifested in 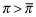 , received signal ω1). Therefore, all firms pay the premium corresponding to
, received signal ω1). Therefore, all firms pay the premium corresponding to 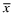 and, hence, investors learn nothing from observing the premium. For this reason, the ex-ante beliefs,
and, hence, investors learn nothing from observing the premium. For this reason, the ex-ante beliefs, 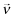 , are not updated after observing the client-firm's insurance premium and the equilibrium in Program III then becomes the same as in Program I, that is, one where all firms set the lowest possible level of x. Summarizing, the equilibrium is one where all firms choose the lowest level
, are not updated after observing the client-firm's insurance premium and the equilibrium in Program III then becomes the same as in Program I, that is, one where all firms set the lowest possible level of x. Summarizing, the equilibrium is one where all firms choose the lowest level 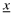 but pay premia corresponding to the highest level
but pay premia corresponding to the highest level 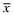 . The equilibrium beliefs of investors is that the overall quality is the lowest level resulting in the same equilibrium as in Program I. □
. The equilibrium beliefs of investors is that the overall quality is the lowest level resulting in the same equilibrium as in Program I. □
In contrast, Program IV leads to the same equilibrium as in Program II where all firms pool at the highest overall quality level. The key step again is the updating of beliefs by investors after observing the premium. We assume that the insurer offers a schedule 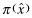 and sets the auditor's transfer function
and sets the auditor's transfer function 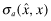 in such a way as to ensure that the auditor reveals x truthfully (see details in proposition 1). As a consequence, the equilibrium is the same as in Program II.
in such a way as to ensure that the auditor reveals x truthfully (see details in proposition 1). As a consequence, the equilibrium is the same as in Program II.
Proposition 4. (Equilibrium with the Auditor as the Insurer's Agent) Assume that the benefits from funding, B, are such that for every y < x:
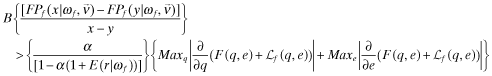
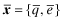 . In addition, if L = 2, this is the only equilibrium meeting the divinity criterion.
. In addition, if L = 2, this is the only equilibrium meeting the divinity criterion.
Proof Given that the auditor bears the cost of misreporting x, he or she would typically choose to underreport x. However, the competition (CO) constraint ensures that the firm can always get quoted a fair premium elsewhere and so the insurer does not wish x to be under-reported. Under these circumstances, the ex-ante premium πf correctly reflects the overall quality x chosen by the firm. The inferences drawn from πf are the same as in Program II resulting in the same equilibrium where all firms pool at the highest level of overall quality. □
An Example
We provide an example that demonstrates the effects of FSI in ensuring a flight to quality. In order to keep the example as simple as possible, we simplify the strategic role of the auditor and assume that the insurer can observe the x levels.
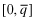 , where
, where 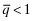 . Next, we assume that the private information is perfect, and that ωl = 1, 2 reveals the expected rate-of-return as rl. We set V(q, e) = q (that is, x = q) and P(i|i, q) = q for i = 1, 2. So with a quality level q, the probability that the firm's type is reported correctly is q, and, as there are only two types, the probability of the firm being misclassified is 1 − q. Let the beliefs of investors be represented by νi; the firm that receives a private signal that its rate-of-return is ri is expected to set its q at νi. Assuming that each firm-type is equally probable, the inferred rates-of return are as follows:
. Next, we assume that the private information is perfect, and that ωl = 1, 2 reveals the expected rate-of-return as rl. We set V(q, e) = q (that is, x = q) and P(i|i, q) = q for i = 1, 2. So with a quality level q, the probability that the firm's type is reported correctly is q, and, as there are only two types, the probability of the firm being misclassified is 1 − q. Let the beliefs of investors be represented by νi; the firm that receives a private signal that its rate-of-return is ri is expected to set its q at νi. Assuming that each firm-type is equally probable, the inferred rates-of return are as follows:
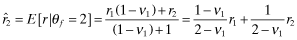 ()
()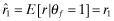 ()
()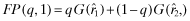 ()
()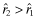 , it follows that the funding probability is strictly decreasing in q for every type 1 firm. In contrast, a firm with private signal ωl = 2 has a realized rate-of-return 2 and its funding probability is unaffected by the choice of q (because it's type cannot be overstated).
, it follows that the funding probability is strictly decreasing in q for every type 1 firm. In contrast, a firm with private signal ωl = 2 has a realized rate-of-return 2 and its funding probability is unaffected by the choice of q (because it's type cannot be overstated).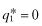 . The implied type of such a firm has l = 2 always. That is to say, such a firm is invariably misclassified. Thus the only report observable by investors is θf = 2 for every firm. It follows that when
. The implied type of such a firm has l = 2 always. That is to say, such a firm is invariably misclassified. Thus the only report observable by investors is θf = 2 for every firm. It follows that when 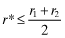 all firms are funded and when
all firms are funded and when 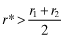 no firm is funded. As there are a total of N firms in the economy, N/2 of them (in expectation) are of high-type.
no firm is funded. As there are a total of N firms in the economy, N/2 of them (in expectation) are of high-type.
- (1)
Therefore, when all firms are funded, an expected amount of (N/2) units of capital are wrongly allocated and the associated loss is:
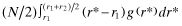 . 29
. 29 - (2)
When no firms are funded, a total of (N/2) firms may wrongly be denied capital with associated loss:
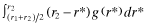 .
.
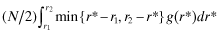 ()
()- both Firm types choose
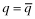 , i.e., the highest quality financial statement, and pay the associated (low) insurance premium
, i.e., the highest quality financial statement, and pay the associated (low) insurance premium 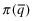 ;
; - any firm that is observed to have a premium
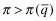 is classified as a type-1 firm.
is classified as a type-1 firm.
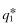 represent the equilibrium quality choice of Firm f that has received private signal ω1; either
represent the equilibrium quality choice of Firm f that has received private signal ω1; either 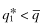 or
or 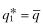 . If,
. If, 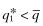 , the premium rate for firm f,
, the premium rate for firm f, 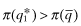 , and its inferred rate-of-return is r1 irrespective of the report. Therefore, it's probability of funding is G(r1). If, however, Firm f mimics the high private-signal firm and sets
, and its inferred rate-of-return is r1 irrespective of the report. Therefore, it's probability of funding is G(r1). If, however, Firm f mimics the high private-signal firm and sets 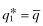 , the inferred rates of return are given by
, the inferred rates of return are given by
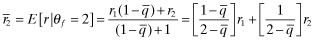
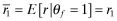
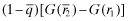 (i.e., by the higher probability of funding when the firm is reported as ‘type-2’). Note that the total social loss now becomes:
(i.e., by the higher probability of funding when the firm is reported as ‘type-2’). Note that the total social loss now becomes:
- (1)
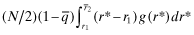 because low-type firms are funded; and
because low-type firms are funded; and - (2)
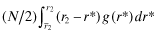 because high-type firms are not funded.
because high-type firms are not funded.
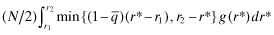 ()
()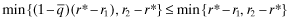 , 18 and 19 shows that the social loss is reduced through the provision of FSI.
, 18 and 19 shows that the social loss is reduced through the provision of FSI.Notice in this example that if a firm with private signal ωl = 1 sets 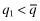 , then the best response for the firm with the high private signal is to set
, then the best response for the firm with the high private signal is to set 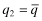 —this separating policy leads to funding with probability G(r2) at a minimum insurance cost. If, however, the firm with the high private signal sets
—this separating policy leads to funding with probability G(r2) at a minimum insurance cost. If, however, the firm with the high private signal sets 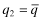 , the best strategy for a firm with low private signal is to ‘mimic’ and set
, the best strategy for a firm with low private signal is to ‘mimic’ and set 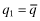 . Mimicry increases the funding probability (and leads to the equilibrium described above). In contrast, when the type-1 firm sets
. Mimicry increases the funding probability (and leads to the equilibrium described above). In contrast, when the type-1 firm sets 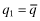 and the type-2 firm sets
and the type-2 firm sets 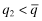 the situation is untenable in equilibrium because by increasing q slightly, the type-2 firm reduces insurance costs but still separates itself from the type-1 firm. Thus,
the situation is untenable in equilibrium because by increasing q slightly, the type-2 firm reduces insurance costs but still separates itself from the type-1 firm. Thus, 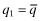 ,
, 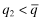 should never be an equilibrium. Hence, the only plausible equilibrium is for both firms to set
should never be an equilibrium. Hence, the only plausible equilibrium is for both firms to set 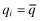 (see Lemma 1). □
(see Lemma 1). □
This example does not incorporate a role for the auditor, but a little reflection shows that the core intuition survives in a more complex setting where reports are influenced by an auditor acting under moral hazard. In particular, if the fee of the auditor is determined by the insurer, sufficient incentives may be provided to elicit truthful revelation regarding the auditor's assessment of the firm's x. Once x is known (perhaps imperfectly) to the insurer, premium levels reveal this information to investors. In particular, when firms defect from the anticipated level of x, that is, if a firm has been charged a higher than anticipated premium πf, investors find out about this before trading. This allows investors to alter their funding strategies and we are then essentially back in the situation discussed in the example.
The example has the characteristics of a signaling model where firms are separated out through the level of the insurance premium but the cost associated with signals has a special structure that should be clarified. In a standard signaling model, there is a difference in cost for a given signal across types (arising from an exogenous factor related to type). This difference deters the low type from choosing the same signal as the high type. In contrast, in the setting of the example, the cost of financial statement quality is the same for all firms. The differential cost arises because the choice of high quality reveals the firm's true type and is thus indirectly more costly for the low-type firm.
Let  represent the beliefs of investors. In this example, the expected return on the high report, θ = 2, is some weighted average of r2 and r1 with the weights depending on
represent the beliefs of investors. In this example, the expected return on the high report, θ = 2, is some weighted average of r2 and r1 with the weights depending on 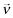 ; in addition, because firm 2 always issues report θ = 2, the weight on r2 is strictly positive. In contrast, the report θ = 1 necessarily implies that the rate-of-return is r1. Thus, rational investors would fund the report θ = 2 with a greater probability than the report θ = 1. In general, ensuring that higher reports are funded with greater probability requires some form of regularity assumption; in our formulation, this is the role of Assumption 1.
; in addition, because firm 2 always issues report θ = 2, the weight on r2 is strictly positive. In contrast, the report θ = 1 necessarily implies that the rate-of-return is r1. Thus, rational investors would fund the report θ = 2 with a greater probability than the report θ = 1. In general, ensuring that higher reports are funded with greater probability requires some form of regularity assumption; in our formulation, this is the role of Assumption 1.
The analysis in this example assumes that the insurance premium is based on the actual level of x chosen by firms. This was the setting analyzed in Proposition 1. More generally, the insurer relies on the auditor's assessment of x to set the premium. In such a setting, the auditor reports x strategically in order to maximize his or her own payoffs, and the revelation of the premium to investors does not break the race to the bottom with regard to overall quality so long as the auditor functions as an agent of management (Proposition 1). That is, firms would prefer to get the auditor to report a higher level of x to the insurance company and thereby to investors than the one that has been chosen. As rational insurers and investors will anticipate this ‘bias’, the equilibrium unravels to the lowest choice of x. In contrast, when the auditor functions as an agent of the insurer, the pooling at the highest quality again becomes the rational equilibrium (Proposition 1).
Conclusion
Several causes have been advanced in the media for the ‘accounting’ meltdown: irrational exuberance, infectious greed, moral turpitude of executives, unethical accountants, misleading financial statements and related ‘ills’. We have argued that the inherent conflict of interest in the auditor–client relationship and the unobservability of financial statement quality, coupled with incentives to ‘cook the books’ are among the potential culprits. FSI, as developed here, provides a market-based solution that acts as an effective check on the issuance of overly biased financial statements. First, the publicization of the insurance premium will credibly signal the quality of the insured's financial statements and direct investments toward better projects. Second, by transferring the auditor hiring decision to the insurer, FSI eliminates the auditor's inherent conflict of interest. At the same time, the ability to signal the quality of financial statements will provide companies with incentives to improve the quality of their financial statements. Hence, FSI will result in fewer misrepresentations and smaller shareholder losses.
Under the present regime, auditors' legal liability is not an effective tool for inducing truth telling in financial statements because the costs of such liability are essentially covered by the client-firms. As mentioned, the FSI scheme effectively eliminates the conflict of interest that came to light in the aftermath of accounting scandals. Yet FSI has other important benefits: the credible signalling of financial statement quality leads to an improvement of such quality, and consequently, decreases in shareholder losses, and the better channelling of savings to socially desirable projects.
Footnotes
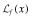 is imposed whereas the insurance premium πf is unavoidable as it is paid ex-ante. However, in the interest of keeping the comparison across the different settings as ‘clean’ as possible, we assume that the managers will have to face the reduction in share value associated with low quality choices either as higher premia or as a higher litigation payout.
is imposed whereas the insurance premium πf is unavoidable as it is paid ex-ante. However, in the interest of keeping the comparison across the different settings as ‘clean’ as possible, we assume that the managers will have to face the reduction in share value associated with low quality choices either as higher premia or as a higher litigation payout.Appendix A Details of the Information Structure
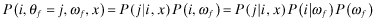 ()
()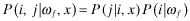 ()
()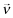 translate to a joint distribution of types and reports,
translate to a joint distribution of types and reports, 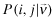 . This process involves the following steps.
. This process involves the following steps.
- (1) Firm f receives a private signal ωf with probability P(ωf). A firm receiving private signal ωf is conjectured to choose an overall quality of νf.
- (2) Under this belief, the joint distribution of reports and types for a firm receiving ωf is P(i, j|νf, ωf).
- (3)
Therefore, the joint distribution of
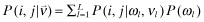
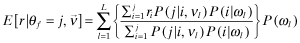 ()
()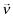 conditional on both report θf = j and premium πf by
conditional on both report θf = j and premium πf by 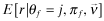 , we obtain:
, we obtain:
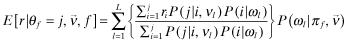 ()
()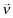 to estimate the private signal of firm f. To illustrate further, suppose that a firm with the lowest private signal type ω1 is assumed to choose a low x, ν1 with a resulting premium π1. Then, conditional on observing that firm f has been offered a low premium πf < π1, the probability weight
to estimate the private signal of firm f. To illustrate further, suppose that a firm with the lowest private signal type ω1 is assumed to choose a low x, ν1 with a resulting premium π1. Then, conditional on observing that firm f has been offered a low premium πf < π1, the probability weight 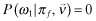 . In other words, firms will be able to reveal their private signals through the premiums they pay and thereby affect the inferred report-contingent rate-of-return.
. In other words, firms will be able to reveal their private signals through the premiums they pay and thereby affect the inferred report-contingent rate-of-return.The inferred rate-of-return for firm f depends on beliefs 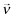 and can differ from the actual distribution, P(i|j, x). However, we impose the condition that in-equilibrium, νf = x(ωf) where x(ωf) denotes the x implemented by a firm f with private information ωf. This is an important point that needs to be emphasized. Firms have the ability to distort the perceived level of x but this is not a stable ‘equilibrium’ situation. For an equilibrium to be sustainable, it must be optimal for firms and auditors to set x levels that are consistent with investor beliefs.
and can differ from the actual distribution, P(i|j, x). However, we impose the condition that in-equilibrium, νf = x(ωf) where x(ωf) denotes the x implemented by a firm f with private information ωf. This is an important point that needs to be emphasized. Firms have the ability to distort the perceived level of x but this is not a stable ‘equilibrium’ situation. For an equilibrium to be sustainable, it must be optimal for firms and auditors to set x levels that are consistent with investor beliefs.
A Proof of Lemma 1 1) Suppose that k > j. We have to show that a firm s with report θs = k has a higher inferred rate-of-return than another, t, with report θt = j.
From 22:
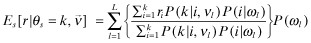
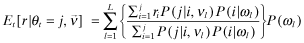 ()
()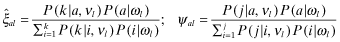
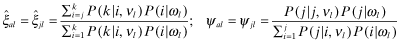
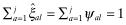 , that is,
, that is, 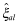 and ψal are probability distributions. Now let
and ψal are probability distributions. Now let 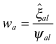 . Then:
. Then:
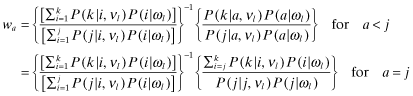
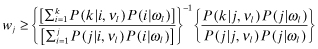
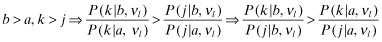
It follows that: 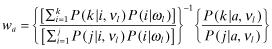 is increasing in a. Consequently,
is increasing in a. Consequently,
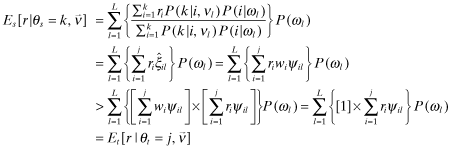 ()
()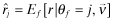 is increasing in j proving Lemma 1 (1).
is increasing in j proving Lemma 1 (1).2) Taking expectations over all reports j yields Lemma 1 (2).
3) As in Equation (23), if all firms pool at the quality level x,
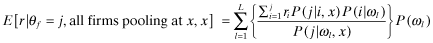

4) The proof is by construction: Γxy and Λyx are related as follows:
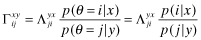
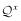 by
by

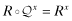 and
and 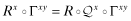 . Next, from the definition of Γxy it follows that:
. Next, from the definition of Γxy it follows that:
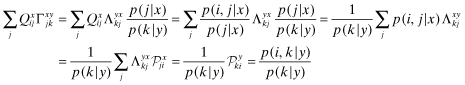 ()
()In other words, 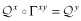 . So
. So
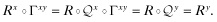
The final step is to show that Γxy ◦ Py = Px. Writing Py = [p(θ = 1|y), … , p(θ = L|y)],
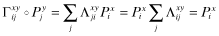
(5) Let Pxj, Pyk denote the vectors Px, Py with the first j (respectively, k) components set to 0. Let R* denote the constant vector whose L-components are all r*. Then
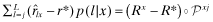 and
and
 . Because the columns of
. Because the columns of 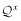 and
and 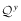 add to one, it follows that
add to one, it follows that 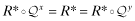 . Therefore:
. Therefore:
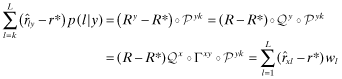 ()
()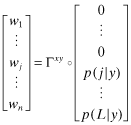 . Since all the
. Since all the 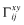 and
and 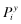 are positive, it follows that every component of
are positive, it follows that every component of 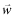 is less than the corresponding component of Γxy ◦ Py = Px. It follows that:
is less than the corresponding component of Γxy ◦ Py = Px. It follows that:
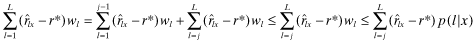
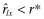 for l < j (j is the lowest signal for which
for l < j (j is the lowest signal for which 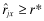 ) and wl ≥ 0 for every l while the second inequality follows from the fact that
) and wl ≥ 0 for every l while the second inequality follows from the fact that 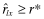 for l ≥ j and p(l|x) ≥ wl for every l. □
for l ≥ j and p(l|x) ≥ wl for every l. □ B Proof of Lemma 1 Suppose one of the two firms deviates to some off-equilibrium choice x resulting in some premium 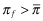 and the off-equilibrium beliefs of investors after observing πf are such that the firm receiving the signal ω2 is indifferent between choosing
and the off-equilibrium beliefs of investors after observing πf are such that the firm receiving the signal ω2 is indifferent between choosing 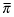 or πf. We will show that the firm with the signal ω1 would then strictly prefer to choose πf.
or πf. We will show that the firm with the signal ω1 would then strictly prefer to choose πf.
Denote the quality x corresponding to the premium πf by xf. Then the indifference assumption on ω2 is:
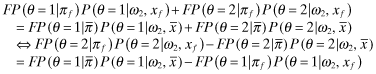 ()
()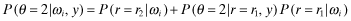
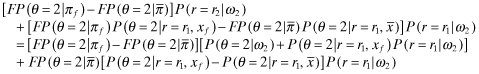 ()
()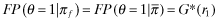 (because θ = 1 ⇒ r = r1) and (ii) P(θ = 2|ωj, y) = 1 − P(θ = 1|ωj, y) for every y, the right-hand-side of 28 becomes:
(because θ = 1 ⇒ r = r1) and (ii) P(θ = 2|ωj, y) = 1 − P(θ = 1|ωj, y) for every y, the right-hand-side of 28 becomes:
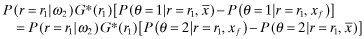 ()
() ()
()Rearranging equation 31, we obtain:
 ()
()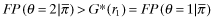 and the right-hand-side of 32 is negative (and hence, so is the left-hand-side). Now by the fact that signal ω2 is good news relative to ω1, it follows that:
and the right-hand-side of 32 is negative (and hence, so is the left-hand-side). Now by the fact that signal ω2 is good news relative to ω1, it follows that:
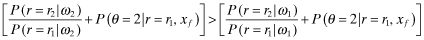 ()
()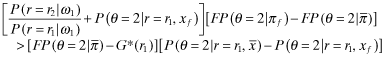
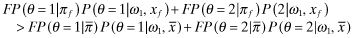 ()
()When L ≥ 3, the uniqueness of the equilibrium in meeting the divinity test can be established if the equilibrium funding probabilities have the following characteristic:
Assumption 2. (Inferences and Quality) Let 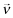 ,
, 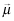 denote investor beliefs where νl > μl for every l. That is, under
denote investor beliefs where νl > μl for every l. That is, under 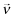 , investors believe that every firm chooses a higher quality than under
, investors believe that every firm chooses a higher quality than under 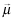 . Then investors are more discriminating under
. Then investors are more discriminating under 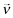 than under
than under 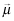 in the following sense: for any two reports j ≥ k the inferred returns satisfy:
in the following sense: for any two reports j ≥ k the inferred returns satisfy:
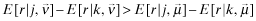 ()
()Appendix B Description of the FSI Process
The FSI process begins with companies that choose to purchase FSI that provide coverage against losses suffered as a result of omissions and misrepresentation (O&M—the inverse of x in our model) in the financial reports. Companies desiring such insurance will solicit from insurance carriers in the year prior (year t-1) insurance coverage for their shareholders against losses caused by O&M in financial statements that occur during the covered year (year t). The carriers would engage an underwriting reviewer (that could be either an independent organization or the external auditor) who would assess the risk of O&M by examining the soliciting companies' internal controls, management incentive structures, the competitive environment, the history of past O&M, past earnings surprises and the market's responses to such surprises, etc. Detailed underwriting review reports would be the basis for the carriers' decisions on whether to offer coverage, the maximum amount of such coverage, and the associated required premium, or they may offer a schedule of coverage amounts and premia.
Based on the insurance offers received, managers would put up in their proxies for shareholders' voting their own recommendation for buying FSI coverage at a given amount and premium (including zero coverage—no insurance). After the vote, the shareholders' approved coverage and premium (including the case of zero coverage) would be publicized, becoming common knowledge. Companies that opt for zero coverage and companies that chose not to solicit FSI coverage would revert to the existing regime under which they would hire an external auditor who opines on their statements. Companies whose shareholders approved insurance coverage would then select an external auditor from a list of audit firms approved by their chosen insurance carrier. The selected external auditor would be hired and paid by the carrier. Audit firms would also be rated by an independent organization (likely the same as the one that conducted the underwriting review). The selected external auditor would coordinate the audit plan with the underwriting reviewer to adopt it to the findings of the review. Eventually, the insurance coverage would become effective only if the auditor issues an unqualified opinion on year t financial statements (sometime in year t + 1). If the opinion is not unqualified there would be no coverage, or else, the policy terms would be renegotiated. In either case (no coverage or renegotiated coverage and premium) the renegotiated terms would be publicized. For companies with effective coverage, shareholders' claims for recovery, within the limits of the policies, for losses caused by omissions and misrepresentations that occurred during the covered year would be settled through an expedited judiciary process. A judiciary body, agreed upon in advance by both the insured and the insurer, would submit the claims upon the detection of O&M, hire the necessary experts to estimate the damages, and agree on a settlement within the policy limits with the carrier; the latter may hire its own experts to analyze the damages.30 The process is depicted in Figure A1.
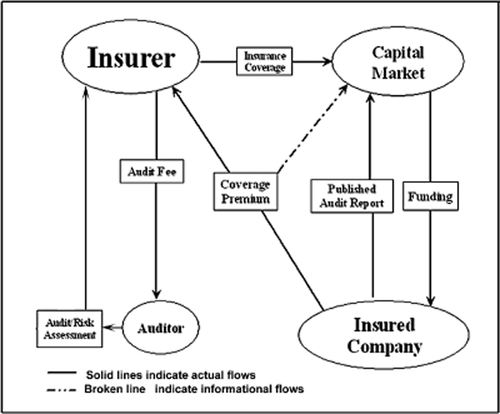
The FSI Process
Appendix C Alternative Signaling Mechanisms
 cannot be sustained; thus, disclosing the audit fee is not equivalent to providing FSI (Setting (IV)). In order to make the point as simply as possible, we shall suppress the subgame over audit incentives and assume that the ex-post transfers in place
cannot be sustained; thus, disclosing the audit fee is not equivalent to providing FSI (Setting (IV)). In order to make the point as simply as possible, we shall suppress the subgame over audit incentives and assume that the ex-post transfers in place 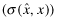 are sufficient to induce the auditor to report the true choice of x to the insurer, or equivalently, as audit effort is observable by the insurer, the true value of internal quality q. We define all the parameters for the problem.
are sufficient to induce the auditor to report the true choice of x to the insurer, or equivalently, as audit effort is observable by the insurer, the true value of internal quality q. We define all the parameters for the problem.
- x(q, e) = qe, q, e ∈ [0, 1]
-
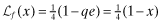
-
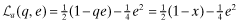
-
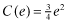
- (1)
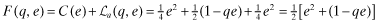
- (2)
at e = 0,
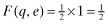 for every q and at e = 1,
for every q and at e = 1, 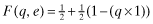 ; thus {q, e} = {0, 0} and {q, e} = {1, 1} result in the same audit fee
; thus {q, e} = {0, 0} and {q, e} = {1, 1} result in the same audit fee 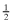 .
.
 is associated with both the highest and the lowest level of audit quality. Hence, it is not rational for investors to believe that the highest quality has been chosen. In fact, with an observed fee of
is associated with both the highest and the lowest level of audit quality. Hence, it is not rational for investors to believe that the highest quality has been chosen. In fact, with an observed fee of 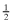 , for reasons similar to Proposition 1, the only possible rational belief about quality is that the lowest quality has been chosen and thus, the equilibrium with the highest quality choice is not sustainable in rational expectations.
, for reasons similar to Proposition 1, the only possible rational belief about quality is that the lowest quality has been chosen and thus, the equilibrium with the highest quality choice is not sustainable in rational expectations.
References
List of Symbols
- (1)
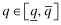 denotes internal quality
denotes internal quality - (2)
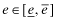 denotes audit effort
denotes audit effort - (3) x = V (q, e) denotes overall quality
- (4)
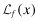 denotes the firm's expected liability if quality x is set
denotes the firm's expected liability if quality x is set - (5)
 denotes the auditor's expected liability when internal quality is q and audit effort is e
denotes the auditor's expected liability when internal quality is q and audit effort is e - (6) C(e) denotes the cost of audit effort e
- (7)
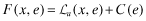 denotes the total audit fee needed to break even under overall quality x and audit effort e
denotes the total audit fee needed to break even under overall quality x and audit effort e - (8) ω1, … , ωL denotes the private signals of the firm
- (9) P(ωl) denotes the probability of a firm receiving private signal ωl
- (10)
 denotes beliefs about quality where xi denotes the overall quality chosen by a firm with private signal ωi
denotes beliefs about quality where xi denotes the overall quality chosen by a firm with private signal ωi - (11) r1 < … < rL denote the possible rates of return for a given firm.
- (12) P(i|ωl) denotes the probability that a firm of private signal ωl has realized return ri
- (13) θ = {1, … , L} are the possible financial reports that a firm might issue
- (14) P(i|j, ωl) denotes the probability that the rate-of-return of the firm is ri given that the financial report was j and the private signal was ωl
- (15) r* denotes the random cost of capital; G(r*) denotes the C.D.F of r*
- (16)
 is the probability that the firm will be funded on receiving, private signal ωl, choosing overall quality x when investors beliefs are represented by
is the probability that the firm will be funded on receiving, private signal ωl, choosing overall quality x when investors beliefs are represented by 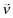
- (17) B is the private benefit reaped by the manager whenever the firm is funded




