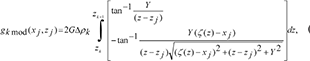Gravity anomalies of strike limited listric fault sources with analytically defined fault planes and arbitrary density contrast variations with depth
ABSTRACT
A method to compute the theoretical gravity anomalies of strike limited listric fault sources is presented along with a relevant computer code, GRLSTRCFLT. The fault plane of a listric fault structure is described with a polynomial function of arbitrary degree. Further, the density contrast within the structure is presumed to be varying randomly with depth comprehending the geological settings where the detached downthrown block of a fault structure is assumed consisting of both high and low density formations. The expression for the gravity anomaly to realize forward modelling is derived in the space domain using both analytical and numerical approaches. The validity and efficacy of the method is demonstrated with a set of synthetic fault models. The gravity anomaly computed at two selected offsets across the fault structure in either case reveals the fact that the magnitude of the anomaly is dependent on the offset of the profile.
INTRODUCTION
The calculation of theoretical gravity anomalies is indeed an important exercise in the modelling and inversion of gravity anomalies. In this direction, forward modelling is tantamount to describing the source body with an appropriate mathematical geometry with a known density and computing its gravity response. In the absence of an additional source of information, the solutions obtained either from modelling or inversion of gravity anomalies are always prone to be nonunique because of the fact that the gravity anomalies on the plane of observation can be explained by a variety of density distributions. On the other hand, for a known/assumed subsurface density distribution, forward modelling always yields a unique gravity signature. In this context, the step model becomes a popular geophysical geometry to which many gravity anomalies are attributed in regional and hydrocarbon explorations to analyse the gravity anomalies of fault structures. Although fault structures on continental regions often possess finite strike lengths (Peirce and Lipkov 1988), many techniques are available in literature to analyse the gravity anomalies treating such structures as simple 2D step models with uniform density (Paul et al. 1966; Geldart et al. 1966; Murthy and Rao 1980; Sundararajan et al. 1983; Murthy 1998; Abdelrahman et al. 2003). Realizing the fact that the density of sedimentary rocks increases with depth, Rao (1985) made use of a quadratic density function, Sundararajan and Brahmam (1998) adopted a linear density function whereas Chakravarthi and Sundararajan (2004) used a parabolic density function to analyse the gravity anomalies of 2D fault structures.
The variable density-depth models that are in vogue such as the exponential (Cordell 1973; Chai and Hinze 1988; Chappel and Kusznir 2008), hyperbolic (Litinsky 1989; Rao et al. 1994; Sari and Salk 2002), quadratic (Rao 1985; Gallardo-Delgado et al. 2003), cubic (García-Abdeslem 2005) and parabolic (Chakravarthi and Sundarajan 2004; Chakravarthi and Sundarajan 2007; Chakravarthi 2009) are strictly valid to describe the density variation of sedimentary rocks only when simple differential compaction is assumed to be the most important diagenetic process in the evolution of sedimentary basins. Nevertheless, the presence of either high density (such as compact basalts) or low density (such as volcanic tuff) formations or a combination of both either on the top, bottom or within the sedimentary column severely distort the subsurface density distribution and in such a case the measured density-depth data do not lend themselves to be modelled accurately by any of the enlisted density functions.
Furthermore, Jackson (1987) demonstrated that large normal faults associated with thick sedimentary sequences, such as the Gulf of Mexico and Niger Delta, are strongly curved in cross-section and become almost flat at depths within the upper crust whereas Torizin et al. (2009) demonstrated with a field example from northern Tien Shan in Central Asia that the subsurface fault geometries play an important role in seismic risk studies and the information on fault dips could improve the accuracy of the seismic source characterization. Goussev et al. (2006) also showed that the extensional tectonics often results in a down slope sliding of rock masses along fault planes that are usually listric in nature and in such cases the detached downthrown rock masses create lateral contrasts in the subsurface distribution of rock densities with reference to the basement and, accordingly, generate detectable step like gravity anomalies. The above interpretational strategies, which assume planar surfaces for the fault planes, find limited application in modelling of gravity anomalies due to strike limited listric fault sources. Although a few interpretational methods exist that can accommodate the geometry of listric fault structures to realize forward gravity modelling (Martín-Atienza and García-Abdeslem 1999; García-Abdeslem 2000, 2003; Zhang et al. 2001; Zhou 2008, 2009), these methods are efficient only with 2D sources. Therefore, there is a need to develop a new method to realize forward gravity modelling of strike limited listric fault sources, wherein the detached downthrown block of a fault structure is assumed consisting of both high and low density formations.
In this paper, I develop a forward modelling technique in the space domain coupled with a relevant code, GRLSTRCFLT, to calculate the theoretical gravity anomalies of fault structures treating them to be of strike limited sources (2.5D) with fault planes described by non-planar surfaces and the density contrast is assumed to be varying arbitrarily with depth. The validity of this technique is illustrated with a set of synthetic field examples.
FORWARD MODELLING – THEORETICAL CONSIDERATIONS
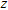 -axis is positive vertically downwards with the
-axis is positive vertically downwards with the 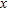 -axis transverse to the strike of a listric fault source (Fig. 1). The model is limited in the vertical direction between the limits,
-axis transverse to the strike of a listric fault source (Fig. 1). The model is limited in the vertical direction between the limits, 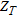 and
and 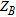 and along the strike direction between –
and along the strike direction between – 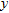 and
and 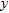 Furthermore, the anomalous source is bounded laterally by a polynomial function,
Furthermore, the anomalous source is bounded laterally by a polynomial function, 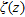 , on the left and towards the right it is extending to infinity. The fault structure consists of
, on the left and towards the right it is extending to infinity. The fault structure consists of 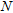 number of horizontal geological formations above the basement with each of these formations having a different density
number of horizontal geological formations above the basement with each of these formations having a different density 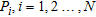 . Also, the profile, CD, passes along the
. Also, the profile, CD, passes along the 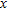 -axis and bisects the strike length,
-axis and bisects the strike length, 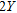 , of the fault structure. The gravity anomaly,
, of the fault structure. The gravity anomaly,  , at any point,
, at any point, 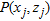 outside the source region can be expressed as:
outside the source region can be expressed as:
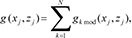 (1)
(1)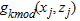 is the gravity effect of the
is the gravity effect of the 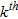 formation given by:
formation given by:
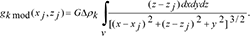 (2)
(2)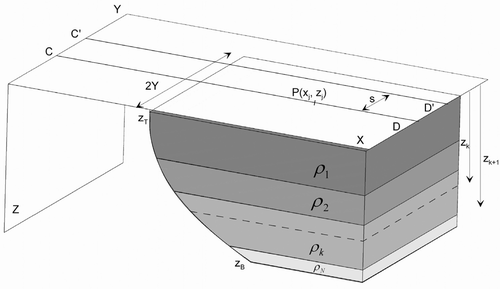
Schematic representation of a strike limited listric fault source. The detached downthrown block (hanging wall) is composed of  horizontal formations each having a contrasting density.
horizontal formations each having a contrasting density.
Here, 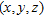 are the coordinates of an element volume within the
are the coordinates of an element volume within the 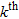 formation and
formation and 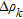 is the density contrast of the layer.
is the density contrast of the layer.
where 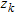 and
and 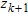 represent the depths to the top and bottom of the
represent the depths to the top and bottom of the 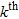 formation. It is to be realized that equation (3) is difficult to solve analytically because the polynomial,
formation. It is to be realized that equation (3) is difficult to solve analytically because the polynomial, 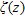 , may take any degree. In the present case, I make use of Simpson’s rule to numerically solve equation (3). Such an approach has a twofold advantage namely, i) it avoids the derivation of a lengthy analytical expression for the gravity anomaly of the structure and ii) it overcomes possible singularities during the computations. Furthermore, it is to be noted that equation (3) is strictly valid for the profile, CD, (Fig. 1) which runs across and bisects the strike length,
, may take any degree. In the present case, I make use of Simpson’s rule to numerically solve equation (3). Such an approach has a twofold advantage namely, i) it avoids the derivation of a lengthy analytical expression for the gravity anomaly of the structure and ii) it overcomes possible singularities during the computations. Furthermore, it is to be noted that equation (3) is strictly valid for the profile, CD, (Fig. 1) which runs across and bisects the strike length, 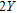 , of the structure. In case the gravity anomalies have to be computed on a profile C′D′, which runs at an offset,
, of the structure. In case the gravity anomalies have to be computed on a profile C′D′, which runs at an offset, 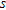 , (Fig. 1) across the structure, then equation (3) has to be solved twice by substituting
, (Fig. 1) across the structure, then equation (3) has to be solved twice by substituting 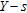 and
and 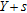 for
for 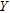 and taking the average of the two gravity values.
and taking the average of the two gravity values.
COMPUTER CODE
A computer program, GRLSTRCFLT, coded in Fortran 77 is presented in Appendix APPENDIX A to calculate theoretical gravity anomalies of strike limited listric fault sources among which the density contrast varies arbitrarily with depth. The main program reads input data and computes gravity effects of a few depth slices along each formation of the fault structure. The subroutine SIMPSN numerically integrates the gravity effects of the depth slices and returns the value to the main program. The input to the code consists in the number of observations (NOBS), degree of the polynomial (NDGRE) to describe the fault plane, half-strike length of the structure (STRIKE), offset of the profile (OFFSET), distance (X) and elevation (ELE) of each observation expressed in km, coefficients of the polynomial (CFTNT), number of subsurface formations (NFM), maximum depth of the fault (AMAXZ) expressed in km, basement density (BASEDEN) and density of each formation (DEN) expressed in g/cm3 and depth to each density interface (ZR) expressed in km. The parameters NOBS, NDGRE, NFM are integer numbers whereas the remaining input parameters are real numbers. The output file consists in the distance values and corresponding theoretical gravity anomalies.
EXAMPLES
The efficacy of the method is demonstrated with two synthetic listric fault models. In either case the observer is on top of the topography, at 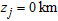 .
.
Theoretical example 1
Figure 2(a) shows the theoretical gravity anomalies due to a synthetic listric fault structure whose geometry is shown in Fig. 2(b). The geology of the structure resembles the geology of the Columbia River basalt plateau where the top 1.5 km thick basalt is followed successively by a 0.5 km thick section composed of volcanic tuff with alternate bands of shale and basalt, a 1.0 km thick section dominated with a series of 7 basalt flows with intermittent sand pulses and a 2.0 km thick section composed of sand, coal seams and shale with one intermittent basalt flow (Prieto et al. 1985). The measured density-depth data (shown as a continuous line in blue in Fig. 2c) from an available borehole (Shell Yakima minerals 1–33) within the Columbia River basalt plateau (Prieto et al. 1985) were used in the present case to realize the forward gravity modelling of the assumed fault structure. Further, one can notice from Fig. 2(c) that the density of subsurface formations vary significantly with depth making it difficult to simulate it with any of the existing density functions. Prieto et al. (1985) assigned an average value of 2.7 g/cm3 for the density of the basalt up to a depth of 1.5 km and 2.3 g/cm3 and 2.5 g/cm3 for the rest of the section (shown as a continuous line in red in Fig. 2c). For the present case, a 10th degree polynomial with a set of 11 coefficients (Table 1) was used to describe the fault plane (Fig. 2b). The theoretical gravity anomalies computed on a profile that runs at an offset, 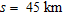 , across the strike of the fault model at 50 equispaced observations in the interval,
, across the strike of the fault model at 50 equispaced observations in the interval, 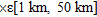 , using the parameters
, using the parameters 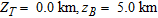 and
and 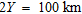 are shown in Fig. 2(a) as a continuous line in blue. The gravity response of the structure calculated at an offset,
are shown in Fig. 2(a) as a continuous line in blue. The gravity response of the structure calculated at an offset, 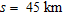 , using the density-depth model of Prieto et al. (1985) is also shown in Fig. 2(a) (continuous line in red) for comparison.
, using the density-depth model of Prieto et al. (1985) is also shown in Fig. 2(a) (continuous line in red) for comparison.
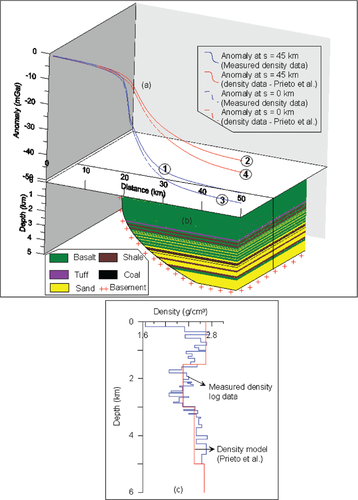
Model-I: gravity response (a) over a multi layered synthetic fault structure (b). Measured density – depth data from Shell Yakima Minerals 1-33 well, Columbia River basalt plateau is shown as a continuous line in blue and the assumed density-depth data by Prieto et al. (1985) are shown by a continuous line in red (c). The continuous lines in blue and red in the top panel show the gravity effects at an offset,  , using the measured and assumed density data whereas the dotted lines in corresponding colour codes represent the gravity effects at an offset,
, using the measured and assumed density data whereas the dotted lines in corresponding colour codes represent the gravity effects at an offset,  .
.
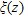 in case of examples
in case of examples| Coefficient | Assumed value |
|---|---|
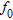 |
20.0140004378471 |
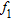 |
0.897689171219346 |
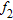 |
−3.0823817524197 |
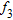 |
4.63487468044622 |
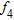 |
−2.51166389503386 |
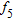 |
0.199792856967483 |
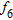 |
0.464645504896704 |
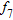 |
−0.254791694605796 |
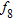 |
0.0611855138317142 |
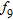 |
−0.00725303637304409 |
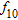 |
0.000345054117684027 |
Furthermore, to study the effect of the offset on the magnitude of the anomaly, forward modelling has been carried out along a profile that bisects the strike length of the fault structure by setting the offset, 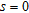 . The theoretical anomaly of the structure in each case is shown in Fig. 2(a) with dotted lines in corresponding colour codes. One can notice from Fig. 2(a) that the maximum magnitude of the gravity anomaly computed using the measured density log data at
. The theoretical anomaly of the structure in each case is shown in Fig. 2(a) with dotted lines in corresponding colour codes. One can notice from Fig. 2(a) that the maximum magnitude of the gravity anomaly computed using the measured density log data at 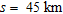 offset was –41.21 mGal whereas the one estimated at
offset was –41.21 mGal whereas the one estimated at 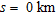 was –45.2 mGal (Fig. 2a). In case of the density model of Prieto et al. (1985), the maximum gravity anomaly observed at
was –45.2 mGal (Fig. 2a). In case of the density model of Prieto et al. (1985), the maximum gravity anomaly observed at 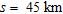 and
and 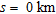 are –28.31 mGal and –33.1 mGal respectively. Therefore, the magnitude of the gravity anomaly increases with the increase in offset of the profile.
are –28.31 mGal and –33.1 mGal respectively. Therefore, the magnitude of the gravity anomaly increases with the increase in offset of the profile.
Theoretical example 2
Model 2 in Fig. 3(b) describes a typical geological setting, such as the one in the Saurashtra region (Dixit et al. 2000), where two sedimentary sequences with an average thickness of 1.0 km and 0.4 km each are sandwiched between two high density intermittent basalt flows each of which has an average thickness of 1.5 km (Fig. 3b). In this case, I assign 2.83 g/cm3 for the density of each basalt flow and 2.35 g/cm3 and 2.4 g/cm3 for the top and bottommost sedimentary sequences respectively (Fig. 3c). A 10th degree polynomial with a set of 11 coefficients, as in the case of model 1, was used to simulate the fault plane (Fig. 3b). The gravity effect of each subsurface formation computed on a profile that runs at a 45 km offset (Fig. 3a), across the strike of the fault model at 50 equispaced observations using the parameters 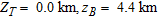 , and
, and 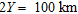 is shown in Fig. 3(a) along with the cumulative gravity of the structure (continuous line in blue). One can notice from Fig. 3(a) that the gradient of the gravity anomaly of each subsurface formation reduces with the increase in depth of the corresponding formation. Also, the high density basalt pulses, at depths within the sedimentary column (Fig. 3b), significantly distort the cumulative gravity signature (Fig. 3a) of the structure with the magnitude of the anomaly hardly exceeding 4 mGal. Furthermore, a maximum gravity anomaly was observed over the hanging wall of the structure and a low over the footwall (Fig. 3a), whereas in case of example 1 a gravity low was observed over the hanging wall and a high over the footwall, respectively (Fig. 2a).
is shown in Fig. 3(a) along with the cumulative gravity of the structure (continuous line in blue). One can notice from Fig. 3(a) that the gradient of the gravity anomaly of each subsurface formation reduces with the increase in depth of the corresponding formation. Also, the high density basalt pulses, at depths within the sedimentary column (Fig. 3b), significantly distort the cumulative gravity signature (Fig. 3a) of the structure with the magnitude of the anomaly hardly exceeding 4 mGal. Furthermore, a maximum gravity anomaly was observed over the hanging wall of the structure and a low over the footwall (Fig. 3a), whereas in case of example 1 a gravity low was observed over the hanging wall and a high over the footwall, respectively (Fig. 2a).
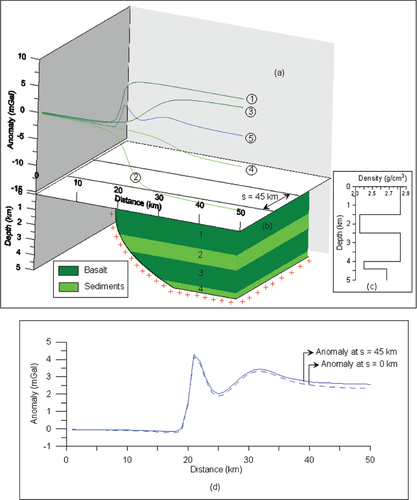
Model-II: gravity response (a) over a four-layered synthetic fault structure (b). Density depth data are shown by a continuous line (c). Gravity effect of each subsurface geological formation is shown in the top panel by a continuous line with a colour code used to represent the corresponding formation. Gravity responses of the structure along two selected profiles, one bisecting the strike length (dotted line in blue) and the other running at an offset of 45 km (continuous line in blue) are also shown (d).
The gravity anomalies of the structure computed at two off-sets 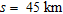 and
and 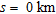 are shown in Fig. 3(d). In this case, the gravity anomaly estimated at an offset also portrays a higher magnitude than the corresponding one at zero offset.
are shown in Fig. 3(d). In this case, the gravity anomaly estimated at an offset also portrays a higher magnitude than the corresponding one at zero offset.
A sample input and output data files of the code are given in Appendix APPENDIX B and Appendix APPENDIX C , respectively.
CONCLUSIONS
A forward modelling technique coupled with a relevant code, LSTRKFALTG, is developed to calculate the theoretical gravity anomalies of strike limited listric fault sources. The density contrast within the fault structure is assumed to be varying randomly with depth. The fault plane of a listric fault is described with a polynomial function of arbitrary degree. Forward gravity modelling over a set of synthetic fault models reveals the fact that the magnitude of the gravity anomaly is dependent on the offset of the profile. It is to be noted that the method discussed in the text has certain limitations. In the derivation of the analytical gravity expression, it is assumed that the detached hanging wall of the fault structure consists of a series of geological formations having horizontal interfaces, which in reality may not be the case. The forward modelling scheme yields realistic results when implemented in situations where the assumptions are relatively valid.
ACKNOWLEDGEMENTS
I profusely thank the Associate Editor and anonymous reviewers for their excellent reviews on the manuscript. For encouragement and permission to publish this work, the author sincerely thanks the Director of the National Geophysical Research Institute, India. The Council of Scientific & Industrial Research, Government of India is acknowledged for its financial assistance under the YS-project.
APPENDIX A: GRLSTRCFLT – code for calculating theoretical gravity anomalies of strike limited listric fault sources with arbitrary density contrast variations with depth
Input:
NOBS: Number of observations
NDGRE: Degree of the polynomial
STRIKE: Half-strike length of the structure (km)
OFFSET: Offset of the profile
X: Distance to each observation (km)
ELE: Elevation of each observation (km)
CFTNT: Coefficients of the polynomial
NFM: Number of subsurface formations
AMAXZ: Maximum depth of the fault (km)
BASEDEN: Basement density (g/cm3)
DEN: Density of each formation (g/cm3)
ZR: Depth to each density interface (km)
Output:
ANO: Theoretical gravity anomaly (mGal)
-
DIMENSION X(100),GS(1000),Z(1000),YY(2),GG(2),CFTN T(15),
-
*GMOD(100),ELE(100),DEN(50),ZR(50),GDMOD(5000),WG C(500,400),
-
*ANO(500)
-
READ(5,*) NOBS,NDGRE,STRIKE,OFFSET
-
DO 10 I=1,NOBS
-
READ(5,*) X(I),ELE(I)
-
10 CONTINUE
-
READ(5,*) (CFTNT(J), J=1,NDGRE+1)
-
READ(5,*)NFM,AMAXZ,BASEDEN
-
READ(5,*)(DEN(J),J=1,NFM–1)
-
READ(5,*)(ZR(I),I=1,NFM)
-
EFFD=0
-
JJK=0
-
DO 100 KK=1,NFM
-
ZT=ZR(KK)
-
ZB=ZR(KK+1)
-
EFFD=EFFD+1
-
YY(1)=STRIKE+OFFSET
-
YY(2)=STRIKE–OFFSET
-
DX=(X(2)–X(1))/10
-
ZDIF=ZB–ZT
-
NDIV=IFIX(ZDIF/DX)+1
-
NA1=NDIV/2
-
IF(NDIV-2*NA1)20,25,20
-
20 NDIV=NDIV+1
-
25 DZ=ZDIF/NDIV
-
N2=NDIV+1
-
DO 30 JZ=1,N2
-
30 Z(JZ)=ZT +DZ*(JZ–1)
-
DC=DEN(EFFD)–BASEDEN
-
DO 80 K=1,NOBS
-
XX=X(K)
-
DO 60 JZ=1,N2
-
SUM=0.0
-
DO 40 JJ=1,NDGRE+1
-
40 SUM=SUM+CFTNT(JJ)*Z(JZ)**(JJ–1)
-
DO 50 KL=1,2
-
EFFY=YY(KL)
-
TR1=ATAN(EFFY/(Z(JZ)–ELE(K)))
-
TTP=(–XX+SUM)**2+EFFY**2+(Z(JZ)–ELE(K))**2
-
TR2=ATAN((EFFY*(–XX+SUM))/((Z(JZ)–
-
ELE(K))*SQRT(TTP)))
-
50 GG(KL)=13.3333*DC*(TR1–TR2)
-
60 GS(JZ)=((GG(2)+GG(1))/2)
-
CALL SIMPSN(GS,Z,N2,GC)
-
GMOD(K)=GC
-
JJK=JJK+1
-
GDMOD(JJK)=GMOD(K)
-
80 CONTINUE
-
IF(ZB–AMAXZ)100,110,110
-
100 CONTINUE
-
110 DO 130 L =1,NOBS
-
KLKL=LK
-
DO 120 JH=1,NFM–1
-
WGC(LK,JH GDMOD(KLKL)
-
KLKL=KLKL+NOBS
-
120 CONTINUE
-
130 CONTINUE
-
DO 150 IL=1,NOBS
-
SUM=0.0
-
DO 140 IH=1,NFM–1
-
140 SUM=SUM+WGC(IL,IH)
-
150 ANO(IL)=SUM
-
WRITE(6,800)
-
WRITE(6,900)
-
DO 160 JJ=1,NOBS
-
160 WRITE(6,1000)X(JJ),ANO(JJ)
-
WRITE(6,1100)
-
800 FORMAT(/3X,’THE FOLLOWING TABLE PROVIDES THE DISTANCE’/,
-
*3X,’AND THEORETICAL GRAVITY ANOMALIES OF A’/,
-
*3X,’STRIKE LIMITED LISTRIC FAULT SOURCE’/)
-
900 FORMAT(3X,23(‘-’),/6X,’DIS-
-
‘,6X,’THEORETICAL’/5X,’TANCE’,
-
*6X,’ANOMALY’/6X,’(KM)’,6X,’(MGAL)’/3X,23(‘-’))
-
1000 FORMAT(2(F10.4,3X))
-
1100 FORMAT(3X,23(‘-’))
-
STOP
-
END
-
SUBROUTINE SIMPSN(GS,Z,N,GC)
-
DIMENSION GS(9000),Z(9000)
-
DZ=Z(2)-Z(1)
-
SUM1=0.0
-
SUM2=0.0
-
NA1=N/2
-
N4=NA1-1
-
DO 70 I=1,NA1
-
N2=2*I
-
70 SUM1=SUM1+GS(N2)
-
DO 80 I=1,N4
-
N3=2*I+1
-
80 SUM2=SUM2+GS(N3)
-
GC=GS(1)+4*SUM1+2*SUM2+GS(N)
-
GC=GC*DZ/3.0
-
RETURN
-
END
APPENDIX B: Sample input data
| 50 | 10 | 50.0 | 45.0 |
| 1.0 | 0.0 | ||
| 2.0 | 0.0 | ||
| 3.0 | 0.0 | ||
| 4.0 | 0.0 | ||
| 5.0 | 0.0 | ||
| 6.0 | 0.0 | ||
| 7.0 | 0.0 | ||
| 8.0 | 0.0 | ||
| 9.0 | 0.0 | ||
| 10.0 | 0.0 | ||
| 11.0 | 0.0 | ||
| 12.0 | 0.0 | ||
| 13.0 | 0.0 | ||
| 14.0 | 0.0 | ||
| 15.0 | 0.0 | ||
| 16.0 | 0.0 | ||
| 17.0 | 0.0 | ||
| 18.0 | 0.0 | ||
| 19.0 | 0.0 | ||
| 20.0 | 0.0 | ||
| 21.0 | 0.0 | ||
| 22.0 | 0.0 | ||
| 23.0 | 0.0 | ||
| 24.0 | 0.0 | ||
| 25.0 | 0.0 | ||
| 26.0 | 0.0 | ||
| 27.0 | 0.0 | ||
| 28.0 | 0.0 | ||
| 29.0 | 0.0 | ||
| 30.0 | 0.0 | ||
| 31.0 | 0.0 | ||
| 32.0 | 0.0 | ||
| 33.0 | 0.0 | ||
| 34.0 | 0.0 | ||
| 35.0 | 0.0 | ||
| 36.0 | 0.0 | ||
| 37.0 | 0.0 | ||
| 38.0 | 0.0 | ||
| 39.0 | 0.0 | ||
| 40.0 | 0.0 | ||
| 41.0 | 0.0 | ||
| 42.0 | 0.0 | ||
| 43.0 | 0.0 | ||
| 44.0 | 0.0 | ||
| 45.0 | 0.0 | ||
| 46.0 | 0.0 | ||
| 47.0 | 0.0 | ||
| 48.0 | 0.0 | ||
| 49.0 | 0.0 | ||
| 50.0 | 0.0 | ||
| 20.0140004378471 | |||
| 0.897689171219346 | |||
| −3.0823817524197 | |||
| 4.63487468044622 | |||
| −2.51166389503386 | |||
| 0.199792856967483 | |||
| 0.464645504896704 | |||
| −0.254791694605796 | |||
| 0.0611855138317142 | |||
| −0.00725303637304409 | |||
| 0.000345054117684027 | |||
| 5.0 | 4.4 | 2.67 | |
| 2.83 | 2.35 | 2.83 | 2.4 |
| 0.0 | 1.5 | 2.5 | 4.0 |
APPENDIX C: Sample output
The following table provides the distance and theoretical gravity anomalies of a strike limited listric fault source
| Distance (km) | Theoretical anomaly (mGal) |
|---|---|
| 1.0000 | −0.0310 |
| 2.0000 | −0.0330 |
| 3.0000 | −0.0353 |
| 4.0000 | −0.0378 |
| 5.0000 | −0.0408 |
| 6.0000 | −0.0441 |
| 7.0000 | −0.0479 |
| 8.0000 | −0.0524 |
| 9.0000 | −0.0577 |
| 10.0000 | −0.0639 |
| 11.0000 | −0.0714 |
| 12.0000 | −0.0804 |
| 13.0000 | −0.0912 |
| 14.0000 | −0.1043 |
| 15.0000 | −0.1198 |
| 16.0000 | −0.1363 |
| 17.0000 | −0.1482 |
| 18.0000 | −0.1304 |
| 19.0000 | 0.0423 |
| 20.0000 | 1.5315 |
| 21.0000 | 4.2864 |
| 22.0000 | 3.8527 |
| 23.0000 | 2.8951 |
| 24.0000 | 2.2332 |
| 25.0000 | 2.0267 |
| 26.0000 | 2.1451 |
| 27.0000 | 2.4228 |
| 28.0000 | 2.7459 |
| 29.0000 | 3.0441 |
| 30.0000 | 3.2722 |
| 31.0000 | 3.4022 |
| 32.0000 | 3.4268 |
| 33.0000 | 3.3633 |
| 34.0000 | 3.2474 |
| 35.0000 | 3.1166 |
| 36.0000 | 2.9964 |
| 37.0000 | 2.8976 |
| 38.0000 | 2.8209 |
| 39.0000 | 2.7627 |
| 40.0000 | 2.7187 |
| 41.0000 | 2.6851 |
| 42.0000 | 2.6592 |
| 43.0000 | 2.6388 |
| 44.0000 | 2.6226 |
| 45.0000 | 2.6095 |
| 46.0000 | 2.5988 |
| 47.0000 | 2.5899 |
| 48.0000 | 2.5824 |
| 49.0000 | 2.5761 |
| 50.0000 | 2.5706 |



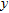 and
and 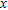 , equation (
, equation (