Optimal taxation with multiple incomes and types
Abstract
We analyze the optimal nonlinear income tax schedule for taxpayers with multiple incomes and multiple unobserved characteristics. We identify smoothness assumptions and extensions of the single crossing conditions that enable the characterization of the optimum through variational calculus. Both the tax perturbation and mechanism design approaches yield identical results when the number of incomes equals the number of unobserved characteristics. Notably, the mechanism design approach requires slightly less stringent assumptions than the tax perturbation approach. Additionally, we introduce a numerical method to determine the optimal tax schedule. Applied to couples, the optimal isotax curves are nearly linear and parallel. Additional contributions include a Pareto efficiency test and a condition on primitives ensuring the sufficiency of the government's necessary conditions, thereby guaranteeing the uniqueness of the solution.
1 Introduction
Studying optimal tax problems involving multiple income sources and dimensions of unobserved heterogeneity presents a significant challenge in the field of public finance. It is crucial to consider this dual-layered multidimensionality when exploring topics such as the optimal taxation of a couple's incomes, the optimal taxation of income from labor and capital, and the optimal means testing of benefits. However, the investigation of such issues introduces considerable theoretical challenges, complicating the formulation of policy recommendations.
Mirrlees (1976) pioneered a Mechanism Design (MD) approach to characterize the optimal incentive-compatible allocation of multiple taxable incomes. This approach results in a partial differential equation that proves challenging to interpret. Golosov, Tsyvinski, and Werquin (2014) develop a Tax Perturbation (TP) approach to characterize the optimal tax schedule. They, too, derive a partial differential equation describing the optimal tax function. Their formulation, however, offers the benefit of being expressed in terms of observable sufficient statistics.
The extent to which the MD approach by Mirrlees (1976) and the TP approach by Golosov, Tsyvinski, and Werquin (2014) are equivalent has not been examined yet. At first glance, it might appear that both approaches must be equivalent, since the taxation principle (Hammond (1979)) proves that selecting a tax function is equivalent to choosing an incentive-compatible allocation. However, this principle holds true only when there are no additional constraints on the tax schedule or the allocation of taxable incomes. Both Mirrlees' MD approach and Golosov, Tsyvinski, and Werquin's TP approach introduce additional smoothness assumptions—the former on the allocation and the latter on the tax schedule—to facilitate the application of variational calculus. These smoothness assumptions address the possibility that distinct types may be allocated the same income bundles, a situation referred to as “bunching,” or instances where the mapping between types and income is discontinuous, a situation referred to as “jumping.” In this paper, we derive optimal-tax formulas using both approaches. We study a model where taxpayers differ in multiple unobservable characteristics and in multiple incomes, and assume that individuals respond along the intensive margins. We assume that multidimensional versions of the single crossing conditions hold and make standard assumptions on the smoothness of the optimal-tax function and the optimal allocation. We show that under these assumptions the optimal-tax formulas derived through both approaches are equivalent when the number of unobservable characteristics equals the number of taxable incomes. The assumptions required to apply the TP approach are slightly more demanding than those required to apply the MD approach. With the TP approach, we need to assume the tax-function is thrice differentiable, whereas the MD approach only requires twice-differentiability of the tax function.
We also investigate the cases where the numbers of taxable incomes and characteristics are not equal. The TP approach solves the optimal-tax problem in the income space, whereas the MD approach solves the same problem in the type space. Therefore, if the number of characteristics exceeds the number of incomes, solving the optimal-tax problem with the TP approach reduces the dimensionality of the problem, and thus its complexity. Conversely, the MD approach reduces the dimensionality when the number of incomes exceeds the number of characteristics.
Determining the optimal tax schedule involves solving a partial differential equation, a task that is significantly more complex than solving the ordinary differential equation implied by the optimal tax formula for a single tax base. To illustrate the complexity, consider that in a one-dimensional scenario, one can examine the effects of perturbing the marginal tax rate at one income level. The optimal marginal tax rate at that income level is then determined by the ratio of mechanical and income effects at all incomes above, to compensated effects at the income level under consideration. However, in a multidimensional scenario, it is not possible to examine the effects of a change in the tax gradient at one combination of incomes without inducing additional changes in the tax gradients at other combinations of incomes.
We develop a numerical algorithm that tackles this geometric complexity and can solve the optimal multidimensional tax problem in its general form. We apply our algorithm to the taxation of couples. In our application, we adopt simplifying assumptions akin to those made by Kleven, Kreiner, and Saez (2007). We presume quasilinear and additively separable household preferences. Furthermore, consistent with the empirical literature, we assume that the labor supply of wives is more elastic (0.43) than that of husbands (0.11) (Bargain and Peichl (2016)). Lastly, we calibrate the joint distribution of skills nonparametrically, starting from the joint distribution of incomes in the Current Population Survey (CPS) of the US census.
To facilitate our exposition, we introduce the notion of an “isotax curve,” which refers to a set of income bundles that incur the same tax liability. Our findings indicate that the optimal isotax curves are nearly linear and parallel, with both spouses subjected to positive marginal tax rates. A joint income tax that discounts female income by approximately 53% closely approximates the fully optimized schedule in terms of social welfare. Additionally, we explore the concept of negative jointness, which stipulates that the optimal marginal tax rates of males should decrease with an increase in female income (and vice versa). Kleven, Kreiner, and Saez (2007) analytically demonstrate that negative jointness is desirable when the productivities of both spouses are assumed to be uncorrelated. However, our numerical findings suggest that this result does not hold up under a more realistic joint distribution of productivities.
In addition to our comparison between the MD approach and the TP approach, and our numerical algorithm, we make several theoretical contributions. First, we formulate a test to verify the Pareto efficiency of a given tax schedule. If the welfare weights revealed by the optimal tax formula are negative for certain income bundles, then reducing tax liabilities at these income bundles results in a self-financed Pareto improvement. This extends the revealed social preference approach of Werning (2007), Bourguignon and Spadaro (2012), Bargain, Dolls, Neumann, Peichl, and Siegloch (2014), Jacobs, Jongen, and Zoutman (2017), Scheuer and Werning (2017), Hendren (2020), and Bierbrauer, Boyer, and Hansen (2023) to a multidimensional context.
Second, we employ the MD approach to establish conditions under which the first-order conditions are sufficient to characterize the optimal allocation. This holds true when the government's Lagrangian is concave both with respect to the taxpayers' utilities, and with respect to the gradient of the mapping between the taxpayers' types and utilities. We analytically confirm that the specification used in our numerical exercise complies with these sufficiency conditions. Therefore, once we have obtained a numerical solution that satisfies the government's first-order conditions, we know that it is the unique solution. Consequently, there is no need to perform sensitivity analyses concerning the initial conditions of our algorithm.
Third, we address a concern in the TP approach, where it is assumed by both Saez (2001) and Golosov, Tsyvinski, and Werquin (2014) that incomes respond smoothly to tax perturbations. We contribute by explicitly outlining the assumptions about the tax schedule that ensure smooth responses of taxpayers to tax perturbations. Our assumptions rule out kinks in the tax schedule and the presence of multiple global optima, thereby ensuring that incremental tax perturbations do not lead to jumps in taxpayers' behavior.
Fourth, we introduce a new method to derive the optimal mechanism. When Mirrlees (1976) and Kleven, Kreiner, and Saez (2007) derive necessary conditions for the optimal incentive-compatible allocation, they use taxpayers' utilities and taxable incomes as controls. The challenge here is that there are numerous income allocations that satisfy their necessary conditions for the optimum. We show how for each such income allocation, the first-order incentive constraints imply the partial derivatives of the attained utilities with respect to the types. At this point, nothing guarantees that the obtained partial derivatives of the achieved utilities are mutually consistent, meaning they imply symmetric second-order partial derivatives. Mirrlees (1976, p. 343) and Kleven, Kreiner, and Saez (2007, p. 18) recognize this issue by stating that among the different solutions of the partial differential equation, only the one implying symmetric second-order cross- derivatives should be considered. We circumvent these challenges by dividing the government's problem into two stages. In the first stage, the government chooses the optimal type-to-utility mapping from the set of possible mappings. In the second stage, the taxable incomes are determined as functions of the utility profile and its partial derivatives.
Finally, we investigate the cases where the number of characteristics p differs from the number of incomes n. If the number of characteristics exceeds the number of incomes, opting for the TP method and using average sufficient statistics among taxpayers with identical income bundles reduces the complexity of the problem. This extends the findings of Saez (2001), Scheuer and Werning (2016) and Jacquet and Lehmann (2021) to situations where taxpayers have multiple income sources. Conversely, applying the MD approach in this setting is only feasible under strong restrictions on preferences (see, e.g., Choné and Laroque (2010), Rothschild and Scheuer (2013, 2014, 2016), Scheuer (2014), and Jacquet and Lehmann (2023) for the case).
When the number of incomes n exceeds the number of unobservable characteristics p, it generally makes more sense to use the MD approach. Indeed, by working within the type space rather than the income space, one reduces the problem's dimensionality. In this case, the government's problem involves the two-step process described above. The second step then is a subprogram that determines the most efficient distribution of income choices to produce the type-to-utility mapping that was selected in the first step. The solution to this subprogram is independent of government preferences and solely depends on the resource costs of providing these utility levels. Our findings shed light on similar subprograms implicitly present in the works of, among others, Atkinson and Stiglitz (1976), Golosov, Kocherlakota, and Tsyvinski (2003), Gerritsen, Jacobs, Rusu, and Spiritus (2025), and Ferey, Lockwood, and Taubinsky (2022).
Related literature
Our derivations crucially rely on assumptions on the smoothness of the allocations and of the tax schedule. Such assumptions are also found in the MD approaches proposed by Mirrlees (1976) and further developed by Kleven, Kreiner, and Saez (2007), and the TP approach of Golosov, Tsyvinski, and Werquin (2014). When comparing the two approaches, we rule out the possibilities of jumping and bunching.
While bunching can occur in one-dimensional models, it is more likely when taxpayers have multiple income sources and multidimensional unobserved characteristics. To see this, note that our paper is related to the multidimensional screening problem, which has been studied in the context of monopoly pricing by Armstrong (1996), Rochet and Choné (1998), and Basov (2005). Rochet and Choné (1998) demonstrate that bunching is a significant concern due to the interplay between the participation constraint and the second-order incentive constraints. However, our model does not include participation constraints, making the argument of Rochet and Choné (1998) not directly applicable to our model.
Still, Dodds (2023) shows that bunching is optimal in the optimal tax problem if social preferences are sufficiently close to maximin. The intuition is that, following Boadway and Jacquet (2008), the dual of the optimal tax problem with maximin social preferences consists in maximizing tax revenue subject to incentive constraints and a lower bound at the lowest utility level. The latter constraint is mathematically equivalent to the participation constraint in the monopoly model of Rochet and Choné (1998). Conversely, Kleven, Kreiner, and Saez (2007) argue that a range of moderate inequality aversions exists where bunching does not occur in the optimum. Therefore, the approach we adopt in this paper is valid when social preferences remain sufficiently far from maximin.
Most closely related to our work is a concurrent working paper by Golosov and Krasikov (2023). They study the optimal taxation of couples with a general tax function that depends on both spouses' incomes and allows for different earnings abilities for both spouses. Using a mechanism-design approach, they derive the optimum and focus on obtaining new theoretical results by applying the Coarea formula to the optimal tax expression. This method enables them to find closed-form solutions for various conditional moments of the optimal tax formula, such as linking optimal tax rates to the correlation in spousal earnings. Our study, on the other hand, combines the mechanism-design and tax-perturbation approaches. We demonstrate when these two methods yield the same optimal tax formula and discuss the pros and cons of each approach.
Another important paper on taxation with multiple dimensions of labor through MD tools is Boerma, Tsyvinski, and Zimin (2022). Their paper differs from ours in multiple aspects. First, they solve the government's problem using Legendre transformations. With this method, individual utility functions must be additively separable with isoelastic cost of effort. Conversely, neither our numerical algorithm nor our analytical results rely on such restrictions on individual preferences. Second, Boerma, Tsyvinski, and Zimin (2022) assume that production requires sorting between manual and cognitive labor. In this case, bunching is a robust property throughout the income distribution, for reasons similar to those set forth by Rochet and Choné (1998).
Our paper also relates to the literature, which studies multidimensional heterogeneity in the context where the government can only observe and tax a single income (e.g., Choné and Laroque (2010), Rothschild and Scheuer (2013, 2014, 2016), Lockwood and Weinzierl (2015), Jacquet and Lehmann (2021), Bergstrom and Dodds (2021)). We rely on the insights in this literature to formulate our expressions in terms of sufficient statistics. Specifically, in the context of multidimensional heterogeneity, sufficient statistics can be strongly endogenous to the tax schedule. We use the approach of Jacquet and Lehmann (2021) to overcome this issue by expressing our optimal tax formulas in terms of total elasticities that incorporate this endogeneity. We expand on this literature by allowing for multidimensional incomes in addition to multidimensional heterogeneity in unobserved characteristics.
Scheuer (2014) and Gomes, Lozachmeur, and Pavan (2018) study a setting with multidimensional heterogeneity in which agents choose to earn income in one of two different sectors, and the government can tax the income of each sector according to a separate tax schedule. The main difference with our approach is that in our model agents can earn multiple incomes at the same time.
Like in our application, Frankel (2014) studies the optimal taxation of couples in a setting with multidimensional heterogeneity and taxation of both male and female income. The main contrast between the approaches is that we allow for a continuous type distribution, whereas Frankel (2014) studies a discrete distribution of married couples. Cremer, Pestieau, and Rochet (2001, 2003) also consider multidimensional settings. However, they only allow labor income to be taxed nonlinearly, whereas taxes on commodity/capital are constrained to be linear.
The paper is organized as follows. We describe the problem of multidimensional optimal taxation in Section 2. Section 3 is devoted to the TP approach, and Section 4 is devoted to the MD approach. We compare both approaches in Section 5. We present our numerical algorithm and results in Section 6.
2 The model
2.1 Taxpayers
The economy consists of a unit mass of taxpayers who differ in a p-dimensional vector of characteristics denoted , that we call type. The type space is denoted and is assumed to be closed and convex. Types are distributed according to a twice continuously differentiable density denoted by , which is positive over .
Taxpayers make n choices. The n observable tax bases are denoted . We call these tax bases incomes for brevity.1 Taxpayers pay a tax that can depend on all incomes in a nonlinear way. Taxpayers who earn incomes x consume after-tax income .
The preferences of taxpayers of type w over consumption c and income choices x are described by a thrice continuously differentiable utility function defined over . Taxpayers enjoy utility from consumption but endure disutility to obtain income, so and . Let be the inverse of . That is, a taxpayer of type w earning incomes x should consume to enjoy utility level u. It follows that and . We assume the utility function is weakly concave in and indifference sets defined by are strictly convex in x.
2.2 Government
We compare two strategies to solve the government's problem.
- In the tax perturbation (TP) approach, we consider the effects of marginal reforms of the tax schedule , taking into account taxpayer's behavioral responses to tax reforms. The tax schedule is optimal only if any tax reforms induce no first-order effect on the government's objective.
- In the mechanism design (MD) approach, we acknowledge the taxation principle according to which selecting a tax schedule taking into account taxpayer's behavioral responses is equivalent to choosing an incentive-compatible allocation . At the second-best optimum, no incentive-compatible perturbation of the allocation should induce a first-order effect on the government's objective.
For tractability reasons, most authors make smoothness assumptions to pursue either of these two approaches. In the following sections, we clarify the relations between the assumptions. We proceed by first introducing the TP approach and the MD approach separately, in Sections 3 and 4, and comparing both approaches in Section 5.
3 The tax perturbation approach
In this section, we derive the optimal tax formula using the TP approach, which was previously derived by Golosov, Tsyvinski, and Werquin (2014). A necessary condition for a tax schedule to be optimal is that small perturbations of the schedule do not change social welfare. Golosov, Tsyvinski, and Werquin (2014) assume that individuals respond smoothly to such perturbations. We contribute by revealing underlying assumptions that ensure that the responses of the taxpayers to tax reforms are smooth. We also identify additional assumptions that allow the characterization of the optimum in a partial differential equation. Identifying these assumptions allows us to compare the TP approach to the MD approach.
Assumption 1.The tax schedule verifies the following assumptions:
Assumption 1(i) rules out kinks like those in piecewise linear tax schedules. Moreover, it ensures that the first-order conditions (8) are twice continuously differentiable in t, w, and x, provided that the direction is thrice continuously differentiable. We require thrice differentiability to derive Proposition 1 and 3, as we explain in more detail below. Assumption 1(ii) ensures that the first-order conditions (8) are associated with a local maximum of the taxpayers' program (7). Parts (i) and (ii) of Assumption 1 together enable one to apply the implicit function theorem to determine how a local maximum of (7) is affected by a small tax perturbation or a small change in types. Assumption 1(iii) rules out the existence of multiple global maxima. This prevents an incremental tax perturbation from causing a “jump” in the taxpayers' choices from one maximum to another. At such jumps, the derivative of with respect to the size t of the perturbation tends to infinity.3 If Assumption 1 is satisfied, then the function that solves (7) is continuously differentiable for t close to 0, that is, the behavioral responses to tax reforms are smooth.
Geometrically, Assumption 1 implies that for each type w, the indifference set defined by admits a single tangency point with the budget set defined by and lies strictly above the budget set elsewhere. Given that we assume that the indifference sets defined by are strictly convex, Assumption 1 is automatically verified if the tax schedule is linear (see Appendix A.1).
We characterize the optimal tax schedule under the presumption that Assumption 1 holds, which then needs to be verified ex post in applications. This approach is analogous with the standard first-order MD approach, which presumes that the second-order incentive constraints do not bind in the optimum, and verifies ex post that this is indeed the case (Mirrlees (1971, p. 188)).
At the optimum, there should not exist an infinitesimal perturbation of the tax schedule that would induce a first-order effect on the government's objective. Therefore, the right-hand side of (11) should be equal to zero for any direction . We derive an optimal tax formula from this requirement in Appendix A.4. To do so, we first rewrite (11) in the income space. For this purpose, let denote the range of the type set under the allocation . Let denote the joint density of incomes x, which is defined over . Furthermore, for each combination of incomes , let , , and , respectively, denote the means of , and among taxpayers that earn the combination of incomes . Second, we use the divergence theorem to rewrite the second line of (11). For this purpose, we need income densities and compensated responses to be continuously differentiable. Furthermore, we can only apply the divergence theorem on the income space if it is of dimension n. We thus make the following assumption.
Assumption 2.The number of characteristics is greater than or equal to the number of incomes (), the income space is of dimension n, and the sufficient statistics , , , and are continuously differentiable functions of x.
Proposition 1.If the optimal tax schedule satisfies Assumptions 1 and 2, the optimum verifies the Euler–Lagrange equation:
Proposition 1 provides necessary conditions for the government's optimum in the income space. It is consistent with Proposition 3 in Golosov, Tsyvinski, and Werquin (2014). The Euler–Lagrange equation (12a) provides a divergence equation that should hold for any income . Note that we use thrice differentiability of the tax schedule (Assumption 1(i) to derive the proposition. Equation (26b) in Appendix A.2 shows that the sufficient statistics depend on the second-order partial derivatives of the tax schedule. Since the right-hand side of (12a) once again contains partial derivatives of these sufficient statistics, we require the tax system to be at least thrice differentiable. Equations (12b) are boundary conditions that should hold at any income in the boundary of . Finally, Equation (12c) states that, starting from the optimum, a lump sum perturbation implies no first-order effect on the Lagrangian. Using (6), the latter condition determines the Lagrange multiplier λ. To provide more intuition, the working paper version of this article contains a heuristic proof of Proposition 1 based on a reform that uniformly changes tax liability within a closed convex subset of and changes marginal tax rates around that subset (Section III.3 of Spiritus et al. (2022)).
Proposition 2.Under Assumptions 1 and 2:
- (i) An incremental tax perturbation that decreases tax liabilities where , and that does not change tax liabilities elsewhere, is Pareto improving.
- (ii) A Pareto efficient tax schedule must lead to for all .
We have shown that the optimality conditions in Proposition 1 and the condition for a Pareto improvement in Proposition 2 are valid if Assumptions 1 and 2 hold. As Assumption 2 may appear overly demanding, we now discuss a microfoundation to demonstrate its plausibility.
Assumption 2′.The utility function satisfies:
- (i) The number of incomes is equal to the number of unobserved characteristics .
- (ii) The matrix is invertible.
- (iii) The mapping defined on is injective.
Together, Assumptions 1 and 2′ guarantee that the tax schedule effectively separates taxpayers by type, so no two types choose the same bundle of incomes. We thus obtain the following lemma, which we prove in Appendix A.6.
Lemma 1.Under Assumptions 1 and 2′, the mapping is a continuously differentiable bijection from into , and Assumption 2 holds.
Lemma 1 allows us to rewrite the necessary conditions for the optimal tax schedule in the type space. This is important because the type space is exogenous to the tax schedule whereas the income space is not. In the numerical computations, this enables us to solve the Euler–Lagrange partial differential equation over a fixed space. Additionally, it is useful because we will also be able to retrieve this optimal tax formula in the type space using the MD approach, proving the consistency of the two approaches. We derive the following proposition in Appendix A.7.9
Proposition 3.Under Assumption 2′, if the optimal tax schedule satisfies Assumption 1, the optimum verifies the Euler–Lagrange equation in the type space:
4 The mechanism design approach
In this section, we rederive the optimal tax system using the mechanism-design approach instead of the tax-perturbation approach. This exercise serves two purposes. First, it allows us to verify under what conditions the two approaches result in the same optimal-tax function. Second, we use the mechanism-design approach to verify under what conditions the solution to the government's first-order conditions uniquely describes the social maximum.
We restrict our attention to allocations that are continuously differentiable and satisfy the incentive constraint (16). This is formalized in Assumption 3.
Assumption 3.The allocation is continuously differentiable and incentive-compatible, that is, it verifies (16).
Our approach differs from the traditional approach in Mirrlees (1976), Kleven, Kreiner, and Saez (2007), and Renes and Zoutman (2017), who directly maximize Lagrangian (18) subject to the incentive constraint (17) with respect to both the utility profile and the allocation. As noted by Mirrlees (1976, p. 343) and Kleven, Kreiner, and Saez (2007, p. 18), the traditional approach hides a conceptual problem in the multidimensional context. To see this, consider an example in which utility is additively separable as in (14). In that case, for any given candidate allocation , the first-order incentive constraints (17) form a system of partial differential equations in . If there is only one type, , the system simplifies to an ordinary differential equation, which can be integrated to provide the corresponding mapping , up to a constant. Conversely, when , the system of partial differential equations (17) for a given candidate mapping yields a candidate for the gradient of with components for all . However, not every combination of mappings can be the gradient of a mapping . The utility profile must exhibit symmetric second-order cross-derivatives, that is, for all j, k, and all w. Hence, only candidate mappings that imply a utility profile that verifies for all j, k, and for all w, are implementable. These additional implementability constraints are irrelevant in one-dimensional optimal tax problems but cannot be ignored in the multidimensional case. Our approach overcomes this challenge by explicitly choosing the utility profile in the first stage, and choosing and from the incentive-compatible allocations that implement that utility profile in the second stage. Therefore, the solution automatically satisfies the implementability condition .
To apply methods from variational calculus to the government's problem (19)–(21), we make regularity assumptions about subprogram (21) in Assumption 4. First, we rule out the possibility that two allocations that yield the same utility profile also extract an identical amount of resources. Second, we make differentiability assumptions about the unique solution to subprogram (21). Together, these assumptions ensure the differentiability of the function L, defined in Equation (20), with respect to all of its arguments. We will provide a plausible microfoundation in Assumption 4′.
Assumption 4.Subprogram (21) admits a single solution for each . We denote this solution by and assume that it is twice continuously differentiable in .
Note that subprogram (21) selects n incomes subject to p constraints. Assumption 4 thus implies that the MD approach is generally restricted to cases with at least as many incomes as types, , although some exceptions exist, as we discuss in Section 5. Assumptions 3 and 4 allow us to derive necessary conditions for the FOMD problem (19) by considering continuously differentiable perturbations in the utility profile , and deducing the resulting perturbed allocations from subprogram (21). Assumption 4 ensures a unique perturbed allocation exists for every perturbed . Mirrlees (1976, p. 342) implicitly makes a similar assumption to ensure his system of equations (63) admits a single solution. This leads to the following proposition, which we prove in Appendix B.1.
Proposition 4.Under Assumption 4, if among the allocations that verify the first-order incentive constraints (17), the optimal one verifies Assumption 3, then the optimal utility profile must verify for all w in :
In a setting where the number of incomes equals the number of characteristics, , there is usually only one incentive-compatible allocation that can implement the same utility profile, because the number of free variables in the system of equations (17) is equal to the number of equations. In a setting with more incomes than types, , the same utility profile can typically be offered through multiple incentive compatible allocations. In that case, through subprogram (21), the n first-order conditions (22a) can be decomposed into p conditions characterizing the optimal profile and supplementary conditions describing how to decentralize the mapping at the lowest cost.
Several results in the literature that are derived in settings where correspond to these supplementary conditions. A famous example is the Atkinson and Stiglitz (1976) theorem, which states for that when preferences are weakly separable between leisure and consumption, commodity taxes should be uniform. This result remains valid regardless of social preferences for redistribution and can be seen as a way to realize a desired distribution of utilities with the least distortions (see also Jacobs and Boadway (2014)). In the same vein, Boadway and Keen (1993), Gauthier and Laroque (2009), and Jacobs and de Mooij (2015) retrieve first-best principles such as the Samuelson rule for the provision of public good or the Pigouvian tax rule in case of externalities in models with weakly separable preferences and one-dimensional unobserved heterogeneity. Another strand of literature considers capital income taxation in settings with endogenous labor supply and savings and one dimension of unobserved heterogeneity. Assuming that preferences, inherited wealth or returns to capital vary along the ability distribution, the Atkinson and Stiglitz (1976)'s theorem no longer applies and the optimal capital tax is nonzero.10 These authors show how to split the deadweight losses of redistribution between labor and capital income taxation, relying only on efficiency considerations without reference to social preferences for redistribution. Finally, the “new dynamic public finance” literature (Golosov, Kocherlakota, and Tsyvinski (2003)) considers models, where at each period, there is a new productivity drawn (a new dimension of unobserved heterogeneity) and agents make a labor supply and a saving decision at each period, such that where p is equal to the number of periods. The inverse Euler equation then describes how the planner should allocate consumption between the present period and each state of nature of the following period at the lowest cost. The finding that such supplementary efficiency conditions arise when is summarized in Corollary 1.
Corollary 1.When , subprogram (21) implies supplementary efficiency conditions describing how to decentralize a given mapping at the lowest cost.
An additional advantage of our approach is that it becomes straightforward to provide conditions under which the government's necessary conditions 22 are also unique and sufficient. We do so in the following proposition.
Proposition 5.Under Assumption 4, if for each type and each the mapping is concave and if an allocation verifies Assumption 3 and Equations 22, then it is the unique solution to the government's problem.
This result is especially important for our numerical simulations. We will demonstrate the use of Proposition 5 in Section 6, where we prove that in our simulations the mapping is concave. As we find in the simulations an allocation that verifies the necessary conditions, Proposition 5 then ensures that this allocation is the unique solution to the government's problem.
We now provide a microfoundation to show the plausibility of Assumption 4. This additional assumption allows us to retrieve the optimal tax formula in the type space provided by Proposition 3 using the FOMD approach, instead of the TP approach.
Assumption 4′.The number of incomes equals the number of unobserved characteristics, that is, , and the mapping
When the utility function is of the additively separable form described in (14), Assumption 4′ is equivalent to . Hence, Assumption 4′ is a way to extend the single crossing condition to a multidimensional context. Recall that in subprogram (21), for given type w, utility level u and utility gradient z, the government chooses the incentive compatible allocation x that maximizes the government's revenues. Because of the incentive constraints of subprogram (21), Assumption 4′ implies that for each type w, the value of uniquely determines the allocation x. The subprogram thus admits a single solution and Assumption 4 is verified. When the number of incomes is equal to the number of unobserved characteristics (), the incentive constraints of subprogram (21) imply that Assumption 4 also leads to Assumption 4′, so both assumptions are equivalent.
The fact that Assumptions 4 and 4′ are equivalent when enables us to show that the formulation of the optimality conditions in Proposition 3 can also be derived using the MD approach. We prove the following proposition in Appendix B.2.
Proposition 6.Under Assumption 4′, if among the allocations that verify the first-order incentive constraints (17), the optimal one verifies Assumption 3, then the optimum verifies the Euler–Lagrange equation (15a) in the type space with Boundary conditions (15b), and the Lagrange multiplier λ is determined by (15d).
We have thus shown that with the right assumptions, the same optimal-tax equations can be derived in the type space using either the FOMD approach or the TP approach. We elaborate further on the correspondence between the two approaches in the next section.
5 Comparing the TP and MD approaches
We now compare TP and MD approaches. In Section 5.1, we focus on the case when the numbers of incomes and characteristics are equal (), before turning our attention to the settings where incomes outnumber characteristics (, Section 5.2) and where characteristics outnumber incomes (, Section 5.3).
5.1 Equal numbers of incomes and characteristics ()
When the number of incomes n is equal to the number of characteristics p, we show in Propositions 3 and 6 that the same optimal tax formulas (15a)–(15c) can be obtained using either the TP or the MD approach. We thus show the consistency of both approaches for , as Saez (2001) does for . This result may not seem surprising in light of the taxation principle (Hammond (1979)), which states that choosing an incentive-compatible allocation is equivalent to choosing a tax function. However, neither the TP nor the MD approaches in the literature solve the fully general case, as they both adopt smoothness assumptions.
For tractability reasons, we conduct both approaches under extensions of the single crossing condition to the multidimensional case, namely Assumption 2′ in the TP approach, versus Assumption 4′ in the MD approach. Assumption 2′ states that for each , the mapping is globally invertible, that is, each bundle of marginal rates of substitution corresponds to at most one type. Assumption 4′ states that for each , the mapping is globally invertible, that is, each gradient of the utility profile corresponds to at most one vector of incomes. Note that local invertibility of both mappings are equivalent since the marginal utility of consumption times the Jacobian of is equal to minus the transpose of the Jacobian of . Furthermore, if preferences are additively separable as in Equation (14), Assumptions 2′ and 4′ are equivalent to the single crossing assumptions for . Otherwise, when preferences are not additively separable, the two assumptions differ only by assuming global invertibility of different mappings. From here on, we compare the TP and MD approaches when assuming preferences satisfy both Assumptions 2′ and 4′.
When the tax schedule is smooth in the sense of Assumption 1, we show in Appendix A.2 that the allocation is smooth in the sense of Assumption 3. Conversely, combining Assumption 3 with the left-hand side of individual first-order condition (3) implies that the marginal tax rates are only once-differentiable functions of type w, while Assumption 1 requires they are twice-differentiable in incomes x. Therefore, provided that the FOMD approach is valid, the TP approach is slightly more demanding than the MD approach as it requires stronger differentiability assumptions on the tax function.
A fundamental difference between the TP and MD approaches is the way they deal with bunching and jumping. Bunching and jumping are sometimes confused in the literature, but are actually polar issues. For instance, consider the case with a single crossing condition in place. It follows that is nondecreasing.11 In that case, bunching arises when the optimal mapping becomes constant. Conversely, jumping arises when is upward discontinuous. From a tax function perspective, bunching implies the presence of a kink, and hence a nondifferentiability in the tax function. Jumping can arise even if the tax function is smooth, for instance, if the tax function is so concave in some region that taxpayers' second-order conditions cannot be met and they prefer to locate elsewhere. It is difficult to address jumping in an MD approach, since this requires optimization over non-continuous allocations.12 Conversely, it is feasible to address bunching in the MD approach by adopting a second-order MD approach (see, e.g., Lollivier and Rochet (1983), Ebert (1992); and Boerma, Tsyvinski, and Zimin (2022)). On the other hand, the TP approach is better equipped to handle jumping, since jumping does not require a nondifferentiability in the tax function (see, e.g., Bergstrom and Dodds (2021)). Equivalence between the two approaches only arises when (i) one makes no smoothness assumptions whatsoever as in the taxation principle, or (ii) one makes sufficient assumptions to rule out both bunching and jumping as we do here.
A famous result in the multidimensional screening literature states that bunching is generic in the multidimensional nonlinear monopoly model of Armstrong (1996) and Rochet and Choné (1998). The latter state that bunching occurs “because of a strong conflict between participation constraints and second- order incentive compatible conditions.” However, as there are no participation constraints in our optimal tax problem, the argument of Rochet and Choné (1998) for bunching does not apply to our model.
The absence of a participation constraint does not necessarily imply the absence of bunching. Boadway and Jacquet (2008) show that when the government's objective is maximin, the dual of the optimal tax problem consists in maximizing tax revenue subject to incentive constraints and a lower bound at the lowest utility level. The latter constraint is mathematically equivalent to the participation constraint in the monopoly model of Rochet and Choné (1998). In addition, Proposition 4 in Dodds (2023) shows that bunching is optimal in the optimal tax problem if preferences are sufficiently close to maximin, using a continuity argument. Conversely, under an additive social welfare function and quasilinear preferences in consumption, no bunching occurs. It follows, as argued by continuity by Kleven, Kreiner, and Saez (2007), that a range of moderate inequality aversions exists for which no bunching occurs. In our simulations, we address this by considering relatively light preferences for redistribution.
5.2 Incomes outnumber characteristics ()
We now consider cases where incomes outnumber unobserved characteristics. The MD approach extends to the case where . The n first-order conditions (22a) given in Proposition 4 can be decomposed into p conditions characterizing the optimal profile and supplementary efficiency conditions describing how to decentralize the mapping at the lowest cost. These supplementary conditions can be reinterpreted in a TP approach as describing how to minimize tax distortions while keeping the utility profile unchanged.
It is much more difficult to apply the TP approach in this setting. This is because the range of the type set under the allocation has a lower dimension than its containing space. Our definitions of the boundary and of the unit vector normal to it in Proposition 1 are no longer meaningful and Proposition 1 loses its validity. More specifically, the divergence theorem used in the proof to Proposition 1 no longer applies.
Even if the TP approach as introduced by Golosov, Tsyvinski, and Werquin (2014), that we investigate in this paper, can no longer directly be applied in the context where , imposing additional assumptions may still enable the use of some version of the TP approach. Doing so generally requires assumptions that project the n-dimensional income space on the p-dimensional range of the type set under the allocation. For instance, in the context , Gerritsen et al. (2025) assume that all incomes are increasing in ability, allowing them to project n-dimensional income to one-dimensional type. Ferey, Lockwood, and Taubinsky (2022) make a similar assumption in their Theorem 1 (see their Condition 2-UD) when they assume . Under their assumptions, one can retrieve the supplementary efficiency conditions by considering tax reforms that increase marginal tax rates on labor income and decrease marginal tax rates on capital income (or vice versa) for some taxpayers without changing tax liabilities for the others. Finding restrictions that allow for the projection of the n-dimensional income space to the p-dimensional type space is significantly more complicated when . Contrarily, the MD-approach naturally applies in the p-dimensional type space and, therefore, does not require such a projection when .
5.3 Characteristics outnumber incomes ()
When the number of characteristics is larger than the number of incomes, , the TP approach continues to apply if one averages sufficient statistics among the different types assigned to the same income bundles. This averaging procedure enables projecting the p-dimensional type space into the n-dimensional income space. Assumption 2 ensures this projection can be done is a smooth way. Hence, we here generalize findings of Saez (2001), Scheuer and Werning (2016), and Jacquet and Lehmann (2021) to the case with multiple incomes .
Conversely, the MD approach does not immediately apply since subprogram (21) admits more constraints than free variables. This implies that starting from a utility profile , which satisfies the incentive constraints, there exist perturbations to that cannot be made incentive compatible by changing the allocation . This imposes additional constraints on the first stage (19) of the optimization problem (18). In the case where , there are different approaches to making these constraints tractable. First, Choné and Laroque (2010), Rothschild and Scheuer (2013, 2014, 2016) assume that labor supply decisions depend only on a one-dimensional function of type. Second, Jacquet and Lehmann (2023) assume preferences are additively separable between consumption and pre-tax income. Moreover, they assume that types matter only for the utility cost of earning pre-tax income. In all of these papers, restrictions on preferences imply that the type space can be projected onto a single dimension, thereby making the MD approach tractable. To the best of our knowledge, the literature has not yet been able to derive optimal tax formulas using the MD approach without such further assumptions on preferences when . Moreover, this hurdle is even more difficult to overcome in the case where the types are multidimensional. While we do not exclude that ways can be found to apply the MD approach more generally to the cases where , the TP approach deals with this case most naturally and Proposition 1 can be readily applied.
6 Numerical simulations
If both the type space and the income space are multidimensional, the optimal-tax formulas do not take the form of ordinary differential equations as in Mirrlees (1971), Diamond (1998), and Saez (2001), but they take the form of a second-order partial differential equation, as in Mirrlees (1976) and Golosov, Tsyvinski, and Werquin (2014). This significantly complicates the process of solving the optimal tax equations. To understand this, it helps to consider the effects of a tax perturbation from a geometric perspective. In the one-dimensional case, the change in the marginal tax rate at a given income level is directly connected to changes in tax liabilities at all higher incomes. In the multidimensional case, the relation is more complicated. To change the gradient of the tax function at a given point, one must change the tax liabilities near that point, causing changes in the tax gradient elsewhere; see, for instance, the graphical proof in the working paper version of this article, Section III.3 of Spiritus et al. (2022). To deal with this complexity, we rely on numerical simulations.
We calibrate the skill density using the Current Population Survey (CPS) of the US census of March 2016. We focus on married, mixed-gender couples that live together. We only consider income from labor. We drop couples in which either partner earns less than $1000 per year or in which either of the partners' incomes is top-coded. We drop same-sex couples because in our simulations we attach labor elasticities based on gender in each couple. From each observed couple, we recover their type from their labor earnings by inverting the first-order conditions (3). For this purpose, we use a rough approximation of the current tax schedule in the US by assuming a constant marginal tax rate of 37%, a figure which is consistent with Barro and Redlick (2011, Table 1). Next, we estimate the type density through a bi-dimensional kernel. We specify the social welfare function to be CARA with , where stands for the degree of inequality aversion. For our baseline simulation, we select β such that the assumed 37% tax rate coincides with the optimal linear tax rate. This leads to . Throughout the simulations, we assume that the government's revenue requirement equals 15% of GDP, which is close to the observed share of public spending in GDP for the US.
We first give an overview of the simulation algorithm, in Section 6.1. Next, in Section 6.2, we report the results of the simulations for the baseline calibration.
6.1 Simulation algorithm
The idea of our numerical algorithm is to first solve an optimal tax formula for given values of sufficient statistics, then to update the sufficient statistics using the tax schedule derived from the optimal tax formula, and to repeat this procedure until it converges to the optimal tax schedule. To do so, we can a priori use three optimal tax formulas, namely 12, 22, and 15. Let us explain why we choose 15. The optimal formula in 22 takes the form of a second-order nonlinear partial differential equation in the type space, which is numerically much more challenging than solving a linear second-order partial differential equation. Conversely, the optimal formula in Equations 12 is a linear second-order partial differential equation. However, it is defined in the income set . Hence, if one solves the optimal tax formula (12a) using the same income set from one iteration to the next, which is required given the boundary conditions (12b), then the corresponding typeset is changing from one iteration to the next. This is problematic when, for instance, comparing the values obtained for the tax revenue or for the social objective from one iteration to the next. Finally, the partial differential equation described in 15 is linear, provided that the sufficient statistics and are taken as given. In addition, it is defined over the fixed type set .
Here again, there is a difficulty. Equations (15a)–(15b) are defined in the type space, while stands for the gradient of tax liability with respect to incomes. However, one can rewrite (15a)–(15b) in terms of the gradient of tax liability in the skill space by scaling matrix by the matrix . We then iterate by (i) finding the mapping that solves Equations (15a)–(15b) for given matrix , Jacobian and type density and getting a tax schedule from this solution, and (ii) updating the matrix and the Jacobian given the new tax schedule. This hybrid approach thus combines the strength of the MD approach (a fixed typeset over which to integrate), with the strength of the TP approach (a linear PDE). We describe the algorithm in more detail in the Supplementary Materials (available at http://econtheory.org/supp/5479/supplement.pdf).
6.2 Results
Figure 1 displays the solution to the optimal tax problem using our baseline calibration. The optimal tax schedule is represented by the isotax curves, which are the loci of incomes for which the tax liability is constant at a given value. Male income is shown on the horizontal axis, while female income is shown on the vertical axis. The left panel displays the whole domain of the simulations running up to , while the right panel zooms in at incomes below , where we find most taxpayers, roughly 97% of males and 99% of females.
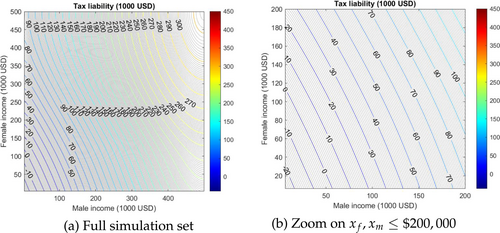
Isotax curves in the baseline case.
Strikingly, isotax curves are almost linear and parallel, except close to the boundaries. There, isotax curves are curved to satisfy boundary constraints (12b). This curvature pattern is most notable at high income levels where there are very few taxpayers. For lower incomes, the curvature only affects isotax curves very close to the lower bound.
Compared with the current economy, which is approximated by a linear tax rate of 37%, the optimal tax schedule leads to an improvement of the social objective equivalent to 0.82% of GDP in monetary terms. To understand which forces drive this gain, we decompose the welfare gain in different steps. Going from our approximation of the current economy (where we assume linear tax rates) to the optimal joint tax captures the welfare gain of allowing the joint income tax schedule to be nonlinear. We find this welfare gain to be only 0.03%. If we now maintain the requirement that the isotax curves are linear and parallel but remove the requirement that both marginal tax rates are equal, so where α is optimized, we obtain a welfare gain from the current economy equal to 0.81%. The optimal value of α is 2.13, which implies that female income is discounted by 53%. Hence, while the gain of optimizing the slope of the isotax curves (optimizing α) is economically significant, the welfare gain of relaxing the constraint that isotax curves must be linear and parallel appears to be small.
Kleven, Kreiner, and Saez (2007) show that under our individual and social preferences, when the abilities of both spouses are not correlated, the optimal marginal tax rates of each partner decrease in the income of the other partner. This is the so-called negative jointness of the optimal tax system. In a separate simulation with a population that replicates the moments of male and female incomes, but removes any correlation between the two, we confirm the optimality of the negative jointness of the tax system. In reality, however, the assumption that the skills of both partners are not correlated does not hold. We show in Figure 2 that the optimality of negative jointness is not robust to using more realistic type densities with positive assortative matching. Figure 2a (resp., Figure 2b) displays the marginal tax rate for females (males) as a function of their own income. Each curve graphs this marginal income while fixing male (female) income at the , , and percentile of the male (female) income distribution. In case of negative jointness, the curve corresponding to male (female) income at the percentile should be everywhere above the curve corresponding to male (female) income at and percentiles of the distribution. Figures 2a and 2b contradict this prediction, thereby rejecting the idea that negative jointness holds at the optimum. We rather find that, except at the very bottom of the income distribution, marginal tax rates exhibit minimal jointness, since in Figures 2a and 2b the three lines are close.13
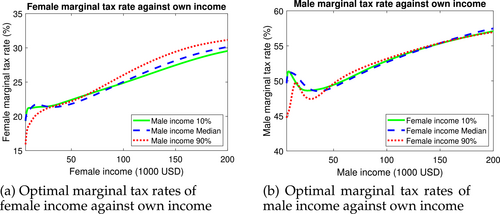
Optimal jointness.
7 Conclusion
We study the optimal tax problem with multiple incomes and multiple dimensions of unobserved heterogeneity. We identify assumptions on the smoothness of the allocation and of the tax schedule, and multidimensional extensions of the single crossing assumptions, that enable the use of variational calculus to characterize the optimum. When comparing the MD approach to the TP approach, we demonstrate that when the numbers of types and of incomes are equal, the latter implies slightly more demanding restrictions on the smoothness of the tax schedule. When there are more unobserved characteristics than incomes, the TP approach is more suitable than the MD approach. Conversely, when there are more incomes than unobserved characteristics, the TP approach as we apply it cannot be used to solve the problem. We show that in terms of rigor, the TP method is on par with the MD method.
We propose a numerical algorithm that addresses the difficulties inherent to the multidimensional tax problem. We apply this algorithm to the optimal taxation of couples. Our findings indicate that the optimal isotax curves are nearly linear and parallel. We show that the optimal negative jointness of the tax schedules when skills are uncorrelated does not hold up when a more realistic distribution is introduced.
In addition to our primary findings, we obtain several theoretical results. First, we identify a necessary condition for the tax schedule to be Pareto efficient. If this condition is not met, we describe a Pareto-improving tax reform. Second, we identify conditions that ensure the necessary conditions of the optimal tax problem are unique and sufficient. Third, we contribute to the TP approach by proposing conditions under which income bundles respond smoothly to small tax reforms. Fourth, we introduce a MD approach that encapsulates not only incentive constraints, but also the implementability constraints embedded in the multidimensional optimal tax problem. Lastly, we examine the cases where the number of incomes differs from the number of characteristics.
Appendix A: TP approach
A.1 Convexity of the indifference sets
A.2 Behavioral responses
A.3 The derivative of the perturbed Lagrangian
A.4 Proof of Proposition 1
A.5 Proof of Proposition 2
Note that the right-hand side of (13), and thus also , is continuous with respect to x. Consider a tax perturbation where is twice continuously differentiable, positive where and nil otherwise. Implementing such a perturbation with a small positive t increases taxpayers' welfare for those earning income bundles such that , and leave the other welfare unchanged, according to (28). Moreover, such perturbation is self-financed according to (31). It is therefore Pareto improving.
A.6 Proof of Lemma 1
Given that is defined as the range of the typeset under the allocation , it is sufficient to show that the mapping is injective to establish that it is a bijection. Assume there exists and such that . From Assumption 1, the first-order conditions (3) must be verified both at and at , so we get for all . According to part (iii) of Assumption 2′, these n equalities imply that . Differentiability of is ensured under Assumption 1 by the implicit function theorem applied to (3). Part (ii) of Assumption 2′ then ensures the Jacobian of is invertible (see (26e) in Appendix A.2).
A.7 Proof of Proposition 3
Appendix B: FOMD approach
B.1 Proof of Proposition 4
B.2 Derivation of the optimal tax formula in the type space
B.3 Proof of Proposition 5
If is concave, then for any perturbation p, the function defined in (33) is concave. Let be another utility profile that verifies (22a) and take the perturbation . As the utility profile verifies 22, we get that function admits a zero derivative at and is concave. So, and provides a strictly higher welfare than .
If two distinct allocations and verify 22, then following the reasoning above, strictly dominates and strictly dominates , a contradiction. So, at most one allocation can verify 22.




