Mechanism Design With Limited Commitment
Abstract
We develop a tool akin to the revelation principle for dynamic mechanism-selection games in which the designer can only commit to short-term mechanisms. We identify a canonical class of mechanisms rich enough to replicate the outcomes of any equilibrium in a mechanism-selection game between an uninformed designer and a privately informed agent. A cornerstone of our methodology is the idea that a mechanism should encode not only the rules that determine the allocation, but also the information the designer obtains from the interaction with the agent. Therefore, how much the designer learns, which is the key tension in design with limited commitment, becomes an explicit part of the design. Our result simplifies the search for the designer-optimal outcome by reducing the agent's behavior to a series of participation, truth telling, and Bayes' plausibility constraints the mechanisms must satisfy.
1 Introduction
The standard assumption in dynamic mechanism design is that the designer can commit to long-term contracts. This assumption is useful: it allows us to characterize the best possible payoff for the designer in the presence of adverse selection and/or moral hazard, and it is applicable in many settings. Often, however, this assumption is made for technical convenience. Indeed, when the designer can commit to long-term contracts, the mechanism-selection problem can be reduced to a constrained optimization problem thanks to the revelation principle.1 However, as the literature starting with Freixas, Guesnerie, and Tirole (1985) and Laffont and Tirole (1988) shows, when the designer can commit only to short-term contracts, the tractability afforded by the revelation principle is lost. Indeed, mechanism design problems with limited commitment are difficult to analyze without imposing auxiliary assumptions either on the class of contracts available to the designer, as in Acharya and Ortner (2017) and Gerardi and Maestri (2020), or on the length of the horizon, as in Skreta (2006, 2015).
This paper provides a “revelation principle” for dynamic mechanism-selection games in which the designer can only commit to short-term mechanisms. We study a class of mechanism-selection games between an uninformed designer and an informed agent with persistent private information. Although the designer can commit within each period to the terms of the interaction—the current mechanism—he cannot commit to the terms the agent faces later on, namely, the mechanisms that are chosen in the continuation game. First, we identify a set of mechanisms, and hence a mechanism-selection game, that is sufficient to replicate any equilibrium outcome of any mechanism-selection game. Second, we identify a set of strategies for the designer and the agent that is sufficient to replicate any equilibrium outcome of the identified mechanism-selection game. We illustrate how our result can be used to characterize the designer's optimal outcome as the solution to a constrained optimization problem that only involves the designer. In this problem, the designer chooses among mechanisms that satisfy the usual truth telling and participation constraints, and a third constraint, which captures the designer's sequential rationality.
The starting point of our analysis is the class of mechanisms we allow the designer to choose from. Following Myerson (1982) and Bester and Strausz (2007), we consider mechanisms as illustrated in Figure 1(a).
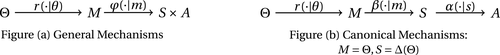
Mechanisms.
Having observed her private information (her type, 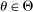 ), the agent privately reports an input message,
), the agent privately reports an input message, 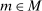 , to the mechanism, which then determines the distribution,
, to the mechanism, which then determines the distribution, 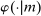 , from which an output message,
, from which an output message, 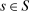 , and an allocation,
, and an allocation, 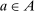 , are drawn. The output message and the allocation are publicly observable: they constitute the contractible parts of the mechanism.
, are drawn. The output message and the allocation are publicly observable: they constitute the contractible parts of the mechanism.
When the designer has commitment, the standard revelation principle implies that, without loss of generality, we can restrict attention to mechanisms satisfying three properties: (i)  , (ii)
, (ii) 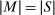 , and (iii) φ is such that by observing the output message, the designer learns the input message, in this case, the agent's type report. Moreover, the revelation principle implies we can restrict attention to equilibria in which the agent truthfully reports her type, which means the designer not only learns the agent's type report upon observing the output message but also learns the agent's true type.
, and (iii) φ is such that by observing the output message, the designer learns the input message, in this case, the agent's type report. Moreover, the revelation principle implies we can restrict attention to equilibria in which the agent truthfully reports her type, which means the designer not only learns the agent's type report upon observing the output message but also learns the agent's true type.
Why restricting attention to mechanisms that satisfy properties (i)–(iii) and to truth-telling equilibria is with loss of generality under limited commitment is therefore clear: upon observing the output message, the designer learns the agent's type report, and hence her type. Then the agent may have an incentive to misreport if the designer cannot commit to not react to this information. This intuition is behind the main result in Bester and Strausz (2001), which is the first paper to provide a general analysis of optimal mechanism design with limited commitment. The authors restrict attention to mechanisms such that the cardinality of the set of input and output messages is the same, and φ is such that, by observing the output message, the designer learns the input message.2 They show that to sustain payoffs in the Pareto frontier, mechanisms in which input messages are type reports are without loss of generality. However, focusing on truth-telling equilibria is with loss of generality. In a follow-up paper, Bester and Strausz (2007) lift the restrictions on the class of mechanisms (i.e., (ii) and (iii) above) and show in a one-period model that focusing on mechanisms in which input messages are type reports and on truth-telling equilibria is without loss of generality. The authors, however, do not characterize the set of output messages. Whether taking the set of input messages to be the set of type reports is without loss when the designer and the agent interact repeatedly is also unclear (see the discussion after Theorem 1).
The main contribution of this paper is to show that, under limited commitment, it is without loss of generality to take the set of output messages to be the set of the designer's posterior beliefs about the agent's type; that is, 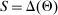 . Theorem 1 identifies a set of mechanisms, and hence a mechanism-selection game, that is enough to replicate any equilibrium outcome of any mechanism-selection game in which the designer chooses mechanisms as in Figure 1(a). In this game, which we denote the canonical game, the designer can only offer mechanisms in which input messages are type reports and output messages are beliefs. Moreover, Theorem 1 shows that any equilibrium of the canonical game can be replicated by a canonical equilibrium in which the agent always participates in the mechanisms offered in equilibrium by the designer, and input and output messages have a literal meaning: the agent truthfully reports her type, and if the mechanism outputs a given posterior, this posterior coincides with the designer's equilibrium belief about the agent's type. Furthermore, in a canonical equilibrium, the designer only offers the agent canonical mechanisms, in which conditional on the output message, the allocation is drawn independently of the agent's type report (see Figure 1(b)). Thus, like the standard revelation principle, Theorem 1 implies that to characterize the distributions over types and allocations that can be achieved in some equilibrium in some mechanism-selection game, it is without loss of generality to restrict attention to the analysis of the canonical equilibria of the canonical game.
. Theorem 1 identifies a set of mechanisms, and hence a mechanism-selection game, that is enough to replicate any equilibrium outcome of any mechanism-selection game in which the designer chooses mechanisms as in Figure 1(a). In this game, which we denote the canonical game, the designer can only offer mechanisms in which input messages are type reports and output messages are beliefs. Moreover, Theorem 1 shows that any equilibrium of the canonical game can be replicated by a canonical equilibrium in which the agent always participates in the mechanisms offered in equilibrium by the designer, and input and output messages have a literal meaning: the agent truthfully reports her type, and if the mechanism outputs a given posterior, this posterior coincides with the designer's equilibrium belief about the agent's type. Furthermore, in a canonical equilibrium, the designer only offers the agent canonical mechanisms, in which conditional on the output message, the allocation is drawn independently of the agent's type report (see Figure 1(b)). Thus, like the standard revelation principle, Theorem 1 implies that to characterize the distributions over types and allocations that can be achieved in some equilibrium in some mechanism-selection game, it is without loss of generality to restrict attention to the analysis of the canonical equilibria of the canonical game.
Theorem 1 provides researchers with a tractable way to analyze problems of mechanism design with limited commitment by making how much the designer learns about the agent an explicit part of the design. A major challenge in the received literature on limited commitment is how to keep track of how the agent's best response to the mechanism affects the information that the designer obtains from the interaction, which in turn affects the designer's incentives to offer the mechanism in the first place. Instead, our framework allows us to reduce the agent's best response to the designer's mechanism and its informational feedback to a familiar set of constraints that the mechanism must satisfy: the participation and incentive compatibility constraints for the agent, and the Bayes' plausibility constraint. This avoids having to consider complicated mixed strategies on the part of the agent (see Laffont and Tirole (1988), Bester and Strausz (2001)) and transforms it instead into a program that combines elements of mechanism design and information design. Indeed, we exploit the information design elements to derive properties of the mechanisms (see Proposition 1 and our companion work, Doval and Skreta (2020, 2021)).
We prove Theorem 1 under the assumption that the set of types is at most countable and extend Theorem 1 to the case in which the agent's type is drawn from a continuum (a leading case in mechanism design) in Theorem 2. As we explain in Section 4.1, the results in Aumann (1961, 1964) imply that with a continuum type space we cannot rely on the usual formulation of an extensive-form game. This is the reason that we first conduct our analysis under the assumption that the set of types is at most countable, deriving Theorem 1 in the standard game-theoretic framework. Section 4.2 then develops a new framework that circumvents the issues raised by Aumann, while allowing us to extend Theorem 1 to continuum type spaces. The framework is based on the idea that any fixed sequence of mechanisms determines a well-defined extensive-form game for the agent. Like in the mechanism-selection game, Theorem 2 shows it is without loss of generality to assume the designer offers the agent sequences of canonical mechanisms and to restrict attention to canonical equilibria within the extensive-form game defined by the mechanisms.
We apply our results to a seemingly well-understood problem and show that our tools can shed new light on it.3 As in Skreta (2006), Example 1 considers a seller, who owns one unit of a durable good, and interacts over two periods with a buyer with persistent and private information. In Example 1, the seller offers canonical mechanisms, whereas in Skreta (2006) the seller offers mechanisms in the class considered by Laffont and Tirole (1988) and Bester and Strausz (2001). In Section 3.1, we show how Theorem 1 can be used to reduce the characterization of the seller's maximum revenue to the characterization of the solution to a constrained optimization problem (see (OPT)). Furthermore, in Section 4.3, we argue that the solution to the program (OPT) also describes the seller's maximum revenue when the buyer's type is drawn from a continuum. We then show how to obtain the envelope representation of the agent's payoffs, and hence, the dynamic virtual surplus representation of the seller's payoff. As we explain in Section 4.3, characterizing the solution to (OPT) is outside the scope of this paper. Instead, we use the virtual surplus representation of the seller's payoff to show that, in contrast to the main result in Skreta (2006), the seller can do strictly better than in the optimal posted-price mechanism.4 Starting from the optimal posted-price mechanism, we show that the seller has a deviation to an alternative mechanism that combines posted prices with a form of rationing. This allows us to connect the mechanism design literature on the sale of a durable good with the work in theoretical industrial organization on alternative strategies for a durable goods monopolist, such as rationing (Denicolo and Garella (1999)).
By highlighting the canonical role of beliefs as the signals employed by the mechanism, Theorem 1 underscores the importance of jointly determining the mechanism together with how information is used in the mechanism and transmitted across periods. In doing so, it marries information design, which studies the design of information structures in a given institution, with mechanism design, which generally studies institutional design within a given information structure.
Related Literature
The paper contributes to the literature on mechanism design with limited commitment with an informed agent with persistent private information, referenced throughout the Introduction.5 Following the seminal contribution of Bester and Strausz (2001), a body of work studies optimal mechanisms under limited commitment in finite-horizon settings with finitely many types (e.g., Bisin and Rampini (2006), Hiriart, Martimort, and Pouyet (2011), Fiocco and Strausz (2015), Beccuti and Möller (2018)). However, the results in Bester and Strausz (2001) do not extend to settings with a continuum of types and/or infinite horizon. On the one hand, the proof strategy in Bester and Strausz (2001) relies on the assumption of finitely many types. On the other hand, their result only applies if the designer is earning his highest payoff consistent with the agent's payoff (see Lemma 1 in Bester and Strausz (2001)). Thus, implicit in their multistage extension is a restriction to equilibria of the mechanism-selection game that possess a Markov structure, which as shown by Ausubel and Deneckere (1989), may not be enough to characterize the designer's best equilibrium payoff in infinite-horizon settings. As a consequence, there is a small body of work that studies mechanism-selection games with a continuum of types and finite horizon (Skreta (2006, 2015), Deb and Said (2015)), or in infinite-horizon settings, imposing restrictions on the class of contracts that can be offered (e.g., Acharya and Ortner (2017), Gerardi and Maestri (2020)), or on the solution concept (e.g., Acharya and Ortner (2017)).
Due to the difficulties with the revelation principle, a large body of work in public finance, political economy, and taxation considers optimal time-consistent policies in settings where private information is fully nonpersistent (see Sleet and Yeltekin (2008), Farhi, Sleet, Werning, and Yeltekin (2012), Golosov and Iovino (2021)). Moreover, a large literature studies the effect of limited commitment within a specific class of mechanisms: price dynamics in the durable goods literature (Bulow (1982), Gul, Sonnenschein, and Wilson (1986), Stokey (1981)) and reserve price dynamics in auction settings (McAfee and Vincent (1997), Liu, Mierendorff, Shi, and Zhong (2019)).
By highlighting the role that the designer's beliefs about the agent play in mechanism design with limited commitment, our paper also relates to Lipnowski and Ravid (2020) and Best and Quigley (2017), who study models of direct communication between an informed sender and an uninformed receiver.
Organization
The rest of the paper is organized as follows. Section 2 describes the model and notation and Section 3 introduces the main theorem for at most countable type spaces. Section 4 extends our analysis to continuum type spaces. Throughout the paper, we use a two-period version of the model in Skreta (2006) to illustrate our results. Section 5 concludes and discusses further directions. Omitted statements and all proofs are in the Appendix (Appendices A–C) and in the Appendix in the Online Supplementary Material (Doval and Skreta (2022)) (Appendices D–E).
2 Model
Primitives
Two players, a principal (he) and an agent (she), interact over 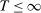 periods.6 Before the game starts, the agent observes her type,
periods.6 Before the game starts, the agent observes her type,  , which is distributed according to a full-support distribution
, which is distributed according to a full-support distribution 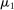 . We initially assume Θ is at most countable and consider continuum type spaces in Section 4. Each period, as a result of the interaction between the principal and the agent, an allocation
. We initially assume Θ is at most countable and consider continuum type spaces in Section 4. Each period, as a result of the interaction between the principal and the agent, an allocation 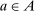 is determined. Let
is determined. Let 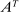 denote the set
denote the set  . When the agent's type is θ and the allocation is
. When the agent's type is θ and the allocation is 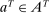 , the principal and the agent's payoffs are given by
, the principal and the agent's payoffs are given by 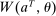 and
and 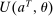 , respectively.
, respectively.
We allow for the possibility that past allocations influence what the principal can offer the agent in the future. Thus, for each 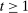 , a correspondence
, a correspondence 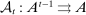 exists such that for every sequence of allocations up to period t,
exists such that for every sequence of allocations up to period t, 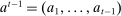 ,
, 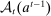 describes the set of allocations the principal can offer in period t (with the convention that when
describes the set of allocations the principal can offer in period t (with the convention that when 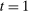 ,
, 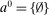 ). Furthermore, we assume an allocation
). Furthermore, we assume an allocation 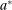 exists such that
exists such that 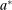 is always available. Below, allocation
is always available. Below, allocation 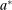 plays the role of the agent's outside option. Given the general structure of payoffs, it is without loss of generality to assume that
plays the role of the agent's outside option. Given the general structure of payoffs, it is without loss of generality to assume that 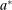 is time-independent.
is time-independent.
We impose some technical restrictions on our model.7 The sets Θ and A are Polish, that is, completely metrizable, separable, topological spaces. They are endowed with their Borel σ-algebra. We also assume Θ is compact. Endowing product sets with their product σ-algebra, we assume the principal and the agent's utility functions, W and U, are bounded measurable functions. Similarly, for each 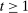 and for each
and for each 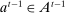 , the set
, the set 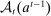 is a measurable set.
is a measurable set.
Mechanisms
In each period, the allocation is determined by a mechanism 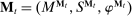 , where
, where 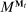 and
and 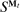 are the mechanism's input and output messages and
are the mechanism's input and output messages and 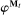 assigns to each
assigns to each 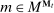 a distribution over
a distribution over 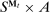 . We endow the principal with a collection
. We endow the principal with a collection 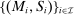 of input and output message sets, such that (i)
of input and output message sets, such that (i) 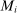 ,
, 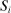 are Polish spaces, (ii)
are Polish spaces, (ii) 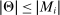 ,
, 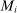 is at most countable, and (iii)
is at most countable, and (iii) 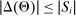 . Moreover, we assume
. Moreover, we assume 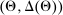 is an element in that collection. Let
is an element in that collection. Let 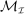 denote the set of all mechanisms with message sets
denote the set of all mechanisms with message sets 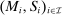 , that is,
, that is, 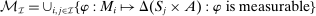 .
.
Three remarks are in order. First, we restrict the principal to choosing mechanisms in 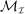 . This restriction allows us to have a well-defined strategy space for the principal, thereby avoiding set-theoretic issues related to self-referential sets.8 The analysis that follows shows the choice of the collection plays no further role in the analysis. Second, because each
. This restriction allows us to have a well-defined strategy space for the principal, thereby avoiding set-theoretic issues related to self-referential sets.8 The analysis that follows shows the choice of the collection plays no further role in the analysis. Second, because each 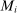 is at most countable, the set of mechanisms
is at most countable, the set of mechanisms 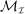 is a Polish space. As we discuss in Section 4, this property is key to being able to define a mechanism-selection game for a given collection
is a Polish space. As we discuss in Section 4, this property is key to being able to define a mechanism-selection game for a given collection 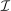 (see also footnote 9). Third, we note all aspects of the environment, except the agent's type
(see also footnote 9). Third, we note all aspects of the environment, except the agent's type 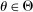 , are common knowledge between the principal and the agent.
, are common knowledge between the principal and the agent.
Mechanism-selection game(s)
Each collection 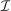 induces a mechanism-selection game, which we denote by
induces a mechanism-selection game, which we denote by 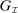 , and is defined as follows. At the beginning of each period, both players observe the realization of a public randomization device,
, and is defined as follows. At the beginning of each period, both players observe the realization of a public randomization device, 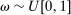 . The principal then offers the agent a mechanism,
. The principal then offers the agent a mechanism, 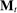 , with the property that for all
, with the property that for all 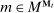 ,
, 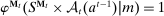 , where recall that
, where recall that 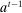 describes the allocations implemented through period
describes the allocations implemented through period  . Observing the mechanism, the agent decides whether to participate in the mechanism (
. Observing the mechanism, the agent decides whether to participate in the mechanism ( ) or not (
) or not (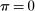 ). If she does not participate in the mechanism,
). If she does not participate in the mechanism, 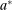 is implemented and the game proceeds to period
is implemented and the game proceeds to period 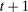 . Instead, if she chooses to participate, she sends a message
. Instead, if she chooses to participate, she sends a message 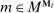 , which is unobserved by the principal. An output message and an allocation
, which is unobserved by the principal. An output message and an allocation 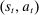 are drawn according to
are drawn according to 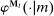 . The output message and the allocation are observed by both the principal and the agent, and the game proceeds to period
. The output message and the allocation are observed by both the principal and the agent, and the game proceeds to period 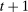 .
.
Histories
The game 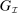 has two types of histories: public and private. Public histories capture what the principal knows through period t: the past realizations of the public randomization device, his past choices of mechanisms, the agent's participation decisions, and the realized output messages and allocations. We let
has two types of histories: public and private. Public histories capture what the principal knows through period t: the past realizations of the public randomization device, his past choices of mechanisms, the agent's participation decisions, and the realized output messages and allocations. We let  denote a public history through period t and let
denote a public history through period t and let 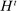 denote the set of all such histories. Instead, private histories capture what the agent knows through period t. First, the agent knows the public history of the game and her input messages into the mechanism (henceforth, the agent history). Second, the agent also knows her private information. We let
denote the set of all such histories. Instead, private histories capture what the agent knows through period t. First, the agent knows the public history of the game and her input messages into the mechanism (henceforth, the agent history). Second, the agent also knows her private information. We let 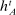 denote an agent's history through period t and let
denote an agent's history through period t and let 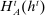 denote the set of agent histories consistent with public history
denote the set of agent histories consistent with public history 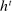 . Thus,
. Thus, 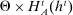 denotes the set of private histories consistent with public history
denotes the set of private histories consistent with public history 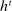 .
.
Belief System and Strategies
Private histories capture what the principal does not know about the agent in period t: he is uncertain about both the agent's payoff-relevant type, θ, and the agent history, 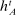 . Thus, a belief for the principal in period t at public history
. Thus, a belief for the principal in period t at public history 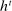 is a distribution
is a distribution 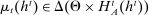 . The collection
. The collection 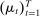 denotes the belief system.
denotes the belief system.
A behavioral strategy for the principal is a collection of measurable mappings 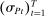 , where for each period t and each public history
, where for each period t and each public history 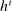 ,
, 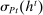 describes the principal's (possibly random) choice of mechanism at
describes the principal's (possibly random) choice of mechanism at 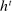 .9 Similarly, a behavioral strategy for the agent is a collection of measurable mappings
.9 Similarly, a behavioral strategy for the agent is a collection of measurable mappings 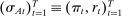 , where for each period t, each private history
, where for each period t, each private history 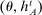 , and each mechanism,
, and each mechanism, 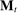 ,
, 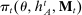 describes the agent's participation decision, whereas
describes the agent's participation decision, whereas 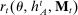 describes the agent's choice of input messages in the mechanism, conditional on participation.
describes the agent's choice of input messages in the mechanism, conditional on participation.
The tuple 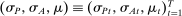 defines an assessment.
defines an assessment.
Equilibrium
For each collection 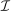 , we study the equilibria of the mechanism-selection game
, we study the equilibria of the mechanism-selection game 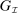 . By equilibrium, we mean Perfect Bayesian equilibrium (henceforth, PBE), informally defined as follows. An assessment
. By equilibrium, we mean Perfect Bayesian equilibrium (henceforth, PBE), informally defined as follows. An assessment 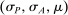 is a PBE if it is sequentially rational and the belief system satisfies Bayes' rule where possible. The formal statement is in Appendix A. For now, we note that if the principal's strategy space is finite, Θ is finite, and the mechanisms used by the principal have finite support, our definition of PBE coincides with that in Fudenberg and Tirole (1991).10
is a PBE if it is sequentially rational and the belief system satisfies Bayes' rule where possible. The formal statement is in Appendix A. For now, we note that if the principal's strategy space is finite, Θ is finite, and the mechanisms used by the principal have finite support, our definition of PBE coincides with that in Fudenberg and Tirole (1991).10
Equilibrium Outcomes
The prior 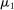 together with a strategy profile
together with a strategy profile 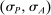 determine a distribution over the terminal nodes
determine a distribution over the terminal nodes 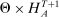 . We are interested instead in the distribution they induce over the payoff-relevant outcomes,
. We are interested instead in the distribution they induce over the payoff-relevant outcomes, 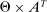 . We say
. We say 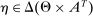 is a PBE outcome if a PBE of the mechanism-selection game exists that induces η. We denote by
is a PBE outcome if a PBE of the mechanism-selection game exists that induces η. We denote by 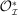 the set of PBE outcomes of
the set of PBE outcomes of 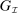 .
.
Throughout, we use the following example to illustrate the concepts in the paper.
Example 1.A seller (the principal) and a buyer (the agent) interact over two periods; that is,  . The seller owns one unit of a durable good and assigns value 0 to it. The buyer's value for the good, denoted by
. The seller owns one unit of a durable good and assigns value 0 to it. The buyer's value for the good, denoted by 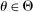 , is her private information. We denote by
, is her private information. We denote by 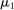 the seller's prior belief over Θ and by
the seller's prior belief over Θ and by 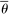 the maximum element of Θ. An allocation is a pair
the maximum element of Θ. An allocation is a pair 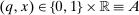 , where q indicates whether the good is sold (
, where q indicates whether the good is sold (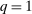 ) or not (
) or not (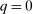 ), and x is a payment from the buyer to the seller. If the good is sold in period 1, the game ends; that is,
), and x is a payment from the buyer to the seller. If the good is sold in period 1, the game ends; that is, 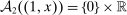 and
and 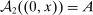 . Moreover, if the buyer rejects the mechanism, the good is not sold and no payments are made; that is,
. Moreover, if the buyer rejects the mechanism, the good is not sold and no payments are made; that is, 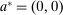 . Payoffs are as follows. If the final allocation is
. Payoffs are as follows. If the final allocation is 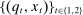 , the buyer and the seller's payoffs are
, the buyer and the seller's payoffs are 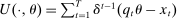 and
and 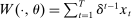 , respectively, where
, respectively, where 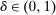 is a common discount factor.
is a common discount factor.
2.1 Canonical Mechanisms and Assessments
Theorem 1 singles out one mechanism-selection game and a class of assessments that allows us to replicate any equilibrium outcome of 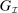 , for any collection
, for any collection 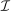 of input and output messages. We dub this extensive form the canonical game and the class of assessments, canonical assessments, which we formally define next.
of input and output messages. We dub this extensive form the canonical game and the class of assessments, canonical assessments, which we formally define next.
Canonical Game
The canonical game is the mechanism-selection game in which 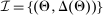 . We denote the set of equilibrium outcomes of the canonical game by
. We denote the set of equilibrium outcomes of the canonical game by 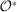 .
.
Definition 1. (Canonical mechanisms)A mechanism 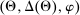 is canonical if the mapping
is canonical if the mapping 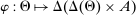 can be obtained as the composition of two mappings,
can be obtained as the composition of two mappings, 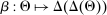 and
and 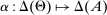 . Formally, for each θ and each pair of measurable subsets,
. Formally, for each θ and each pair of measurable subsets, 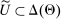 and
and 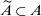 ,
, 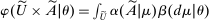 .
.
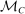 denote the set of canonical mechanisms.
denote the set of canonical mechanisms.
Remark 1. (Comparison with direct revelation mechanisms)A direct revelation mechanism is a special case of a canonical mechanism. To see this, recall that a direct revelation mechanism is a map 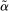 assigning to each type θ a distribution over allocations; that is,
assigning to each type θ a distribution over allocations; that is, 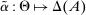 . A direct revelation mechanism then corresponds to a canonical mechanism
. A direct revelation mechanism then corresponds to a canonical mechanism 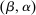 , where β assigns θ with probability 1 to the Dirac measure on θ,
, where β assigns θ with probability 1 to the Dirac measure on θ, 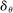 , and then sets
, and then sets 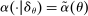 .
.
Canonical Assessments
A canonical assessment specifies behavior for the principal and the agent that is, in a sense, simple. First, the principal always chooses canonical mechanisms. Second, the agent best responds to the principal's equilibrium choice of mechanisms by participating. Third, input and output messages have literal meaning: Conditional on participating, the agent truthfully reports her type, and if the mechanism outputs 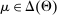 , μ coincides with the principal's updated beliefs about the agent's type. Formally, we have the following.
, μ coincides with the principal's updated beliefs about the agent's type. Formally, we have the following.
Definition 2. (Canonical assessments)An assessment 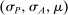 of mechanism-selection game
of mechanism-selection game 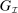 is canonical if the following holds for all
is canonical if the following holds for all 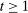 and all public histories
and all public histories 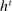 :
:
- 1. The principal offers canonical mechanisms, that is,
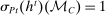 .
. - 2.
For all mechanisms
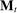 in the support of the principal's strategy at
in the support of the principal's strategy at 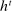 ,
,- (a) For all types θ in the support of the principal's beliefs in period t,
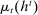 ,
, 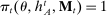 ,
, - (b) For all types θ in Θ,
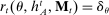 , and
, and - (c) The mechanism's output belief μ coincides with the principal's updated belief about the agent's type. Formally, for
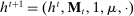 , the marginal of
, the marginal of 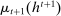 on Θ,
on Θ, 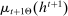 , coincides with μ.11
, coincides with μ.11
- (a) For all types θ in the support of the principal's beliefs in period t,
- 3. The agent's strategy depends only on her private type and the public history.12
We let 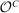 denote the set of equilibrium outcomes of the canonical game that are induced by canonical PBE assessments (henceforth, canonical PBE).
denote the set of equilibrium outcomes of the canonical game that are induced by canonical PBE assessments (henceforth, canonical PBE).
2.2 Discussion
We now discuss three aspects of the model that are important for what follows: the principal may offer randomized allocations, the principal and the agent have access to public randomization, and output messages are public.
Randomized Allocations
Randomized allocations are necessary to conclude that without loss of generality output messages coincide with the principal's posterior beliefs about the agent's type. Indeed, the principal could use 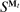 to encode randomizations on the allocation; for example, two tuples,
to encode randomizations on the allocation; for example, two tuples, 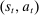 and
and  , may be associated with the same posterior belief. Because a canonical mechanism allows the principal to randomize on the allocation conditional on the posterior belief, we can collapse
, may be associated with the same posterior belief. Because a canonical mechanism allows the principal to randomize on the allocation conditional on the posterior belief, we can collapse 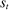 and
and 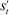 to one output message (the posterior belief).
to one output message (the posterior belief).
Public Randomization
Public randomization allows us to subsume two ways in which the principal may use the mechanism to coordinate continuation play in a PBE of the mechanism-selection game that would otherwise not be possible in a canonical PBE.
First, in the mechanism-selection game, the principal could use 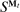 to coordinate continuation play; for example, two tuples
to coordinate continuation play; for example, two tuples 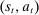 ,
, 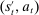 may be associated with two different continuation equilibria, but with the same posterior belief. This is one place, where the requirement that in a canonical PBE, output messages must coincide with the principal's updated beliefs may be more restrictive than allowing for arbitrary PBE assessments: beliefs are not a rich enough language to encode both the principal's updated beliefs and the suggested continuation play.13 As we explain after the statement of Theorem 1, the public randomization device in the canonical game allows us to subsume this coordination role of the output messages, which, in turn, allows us to conclude that without loss of generality, output messages coincide with the principal's posterior beliefs about the agent's type.14
may be associated with two different continuation equilibria, but with the same posterior belief. This is one place, where the requirement that in a canonical PBE, output messages must coincide with the principal's updated beliefs may be more restrictive than allowing for arbitrary PBE assessments: beliefs are not a rich enough language to encode both the principal's updated beliefs and the suggested continuation play.13 As we explain after the statement of Theorem 1, the public randomization device in the canonical game allows us to subsume this coordination role of the output messages, which, in turn, allows us to conclude that without loss of generality, output messages coincide with the principal's posterior beliefs about the agent's type.14
Second, in the mechanism-selection game, the principal could use the “name” of the mechanism to coordinate continuation play. To be concrete, consider Figure 2(a): In 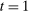 , the principal randomizes between two mechanisms, M and
, the principal randomizes between two mechanisms, M and  , each of which is followed by different continuation play, denoted by continuation(M) and continuation(
, each of which is followed by different continuation play, denoted by continuation(M) and continuation(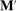 ), respectively. To replicate this in a canonical PBE, we need to determine for each mechanism the distribution over
), respectively. To replicate this in a canonical PBE, we need to determine for each mechanism the distribution over 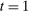 -allocations induced by the mechanism together with the agent's strategy. Suppose when coupled with the agent's strategy both M and
-allocations induced by the mechanism together with the agent's strategy. Suppose when coupled with the agent's strategy both M and 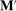 lead to the same canonical mechanism,
lead to the same canonical mechanism, 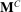 . This is another way in which the language of canonical mechanisms is coarser than that of the mechanisms in
. This is another way in which the language of canonical mechanisms is coarser than that of the mechanisms in 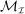 . In the mechanism-selection game, different indirect mechanisms can lead to different continuation equilibria, but to the same canonical mechanism. It is natural to conclude that, similar to the use of the public randomization device in the previous paragraph, we could replicate play in the mechanism-selection game via a canonical PBE in the canonical game as illustrated in Figure 2(b). In the canonical game, the principal offers mechanism
. In the mechanism-selection game, different indirect mechanisms can lead to different continuation equilibria, but to the same canonical mechanism. It is natural to conclude that, similar to the use of the public randomization device in the previous paragraph, we could replicate play in the mechanism-selection game via a canonical PBE in the canonical game as illustrated in Figure 2(b). In the canonical game, the principal offers mechanism 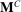 in
in 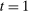 , and then we use the public randomization device in
, and then we use the public randomization device in 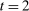 to replicate the continuation play associated with M and
to replicate the continuation play associated with M and 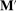 in the original assessment.
in the original assessment.
Different mechanisms lead to the same canonical mechanism.
However, the construction in Figure 2(b) may not be enough to replicate the original outcome distribution. To see this, suppose in the mechanism-selection game, both M and  are accepted with probability 1, so the principal's beliefs after nonparticipation are not pinned down by Bayes' rule. Furthermore, assume different off-path beliefs and different continuation equilibria are associated with the rejection of M and
are accepted with probability 1, so the principal's beliefs after nonparticipation are not pinned down by Bayes' rule. Furthermore, assume different off-path beliefs and different continuation equilibria are associated with the rejection of M and  . However, we can only assign one belief and one continuation equilibrium to the event in which the agent rejects
. However, we can only assign one belief and one continuation equilibrium to the event in which the agent rejects 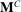 in Figure 2(b). It may not be possible to find one off-path belief and one continuation equilibrium that simultaneously make it optimal for the agent to participate in
in Figure 2(b). It may not be possible to find one off-path belief and one continuation equilibrium that simultaneously make it optimal for the agent to participate in 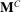 and sequentially rational for the principal to follow the prescribed continuation play.
and sequentially rational for the principal to follow the prescribed continuation play.
Instead, we can replicate the original outcome distribution using the construction in Figure 2(c): We use the public randomization device in 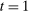 to encode the indirect mechanism that led to
to encode the indirect mechanism that led to 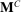 in the mechanism-selection game. It follows that in order to replicate the outcome distributions via canonical PBE public randomization may be needed even before play begins.
in the mechanism-selection game. It follows that in order to replicate the outcome distributions via canonical PBE public randomization may be needed even before play begins.
While the proof of Theorem 1 deals explicitly with the coordination role of the output message, it does not deal explicitly with the the issue illustrated in Figure 2, which can only arise if the principal is using mixed strategies. Instead, we first show in Lemma D.1 that it is without loss of generality to assume that the principal plays a pure strategy in the mechanism-selection game. Similar to the construction in Figure 2(c), we use the public randomization device in the mechanism-selection game to encode the mechanisms over which the principal is randomizing, effectively purifying the principal's strategy.
Public Output Messages
Because in the mechanism-selection game the output message is public, the agent is the only player with private information, which is the leading informational setting in the literature on mechanism design with limited commitment and short-term contracts referenced in the Introduction. Indeed, our only point of departure from this literature is the class of mechanisms we endow the principal with.
If, instead, output messages were observed only by the principal, he would become endogenously privately informed. Having an informed principal adds a new friction even in a one-shot interaction: the mere choice of a mechanism serves as a signal of the principal's private information. Little is known about dynamic and exogenously informed principal problems under commitment, let alone under limited commitment. For these reasons, the comparison of the equilibrium outcomes of the mechanism-selection game with public and private output messages is an open question.
3 Revelation Principle
Section 3 presents the main result of the paper: To characterize the set of equilibrium outcomes that can arise in some mechanism-selection game, it is enough to characterize the canonical PBE outcomes of the canonical game. Formally,
Theorem 1. (Revelation principle)For any PBE outcome of any mechanism-selection game 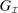 , an outcome-equivalent canonical PBE of the canonical game exists. That is,
, an outcome-equivalent canonical PBE of the canonical game exists. That is,
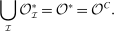
Theorem 1 plays the same role in mechanism design with limited commitment as the revelation principle does in the commitment case. First, it identifies a well-defined set of mechanisms, 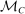 , that without loss of generality, the principal uses to implement any equilibrium outcome. Second, it simplifies the analysis of the behavior of the agent in the game induced by the mechanisms chosen by the principal: we can always restrict attention to assessments in which the agent participates and truthfully reports her type. As we illustrate through the application in Example 1, this restriction allows us to reduce the agent's behavior to a set of constraints that the mechanism must satisfy, as in the case of commitment.
, that without loss of generality, the principal uses to implement any equilibrium outcome. Second, it simplifies the analysis of the behavior of the agent in the game induced by the mechanisms chosen by the principal: we can always restrict attention to assessments in which the agent participates and truthfully reports her type. As we illustrate through the application in Example 1, this restriction allows us to reduce the agent's behavior to a set of constraints that the mechanism must satisfy, as in the case of commitment.
The proof of Theorem 1 follows from two observations. The first one is easy: because the canonical game is a mechanism-selection game, any PBE outcome of the canonical game is a PBE outcome of some mechanism-selection game; that is,  . The second one constitutes the bulk of the proof, which we overview below: we show that for any collection
. The second one constitutes the bulk of the proof, which we overview below: we show that for any collection  and for any PBE assessment of the mechanism-selection game
and for any PBE assessment of the mechanism-selection game 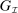 , an outcome-equivalent canonical PBE assessment of
, an outcome-equivalent canonical PBE assessment of 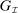 exists. Because in the canonical game the principal has fewer deviations than in
exists. Because in the canonical game the principal has fewer deviations than in 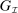 and in a canonical PBE assessment the principal plays a strategy that is available in the canonical game, it follows that for any PBE assessment of the mechanism-selection game, an outcome-equivalent canonical PBE assessment of the canonical game exists; that is,
and in a canonical PBE assessment the principal plays a strategy that is available in the canonical game, it follows that for any PBE assessment of the mechanism-selection game, an outcome-equivalent canonical PBE assessment of the canonical game exists; that is, 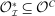 . Because
. Because 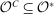 , this concludes the proof.
, this concludes the proof.
We now review the steps involved in the proof that any PBE outcome of the mechanism-selection game 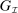 can be achieved in a canonical PBE of the canonical game.15 To simplify the presentation, we rely on the following construction.16 Given a mechanism M and the agent's participation and reporting strategies
can be achieved in a canonical PBE of the canonical game.15 To simplify the presentation, we rely on the following construction.16 Given a mechanism M and the agent's participation and reporting strategies 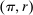 , we can extend the principal's mechanism and the agent's reporting strategy as follows. Extend the set of input messages so as to include a nonparticipation message,
, we can extend the principal's mechanism and the agent's reporting strategy as follows. Extend the set of input messages so as to include a nonparticipation message, 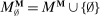 . Similarly, extend the set of output messages,
. Similarly, extend the set of output messages, 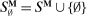 and define
and define  as follows:
as follows: 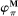 coincides with
coincides with 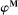 on
on 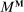 and assigns probability 1 to
and assigns probability 1 to 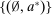 for
for 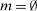 . Finally, define
. Finally, define 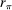 as follows:
as follows: 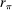 sends message ∅ with probability 1-π, and sends message
sends message ∅ with probability 1-π, and sends message 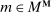 with probability
with probability 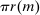 .
.
Input Messages as Type Reports
To fix ideas, consider the proof for the standard revelation principle in static settings. The extended mechanism, 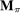 , together with the agent's extended reporting strategy, induce a mapping from Θ to distributions over
, together with the agent's extended reporting strategy, induce a mapping from Θ to distributions over 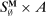 . This allows us to conclude we can replace the set of input messages with the set of type reports, as illustrated in Figure 3(a).
. This allows us to conclude we can replace the set of input messages with the set of type reports, as illustrated in Figure 3(a).
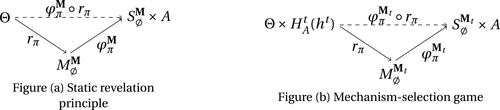
Type reports as input messages.
In the dynamic setting, however, this argument would only allow us to conclude we can rewrite the mechanism as a mapping from 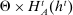 to distributions over
to distributions over  , as illustrated in Figure 3(b). Indeed, to replicate the agent's reporting strategy, the mechanism needs to obtain all the information on which the agent conditions her strategy, which potentially is
, as illustrated in Figure 3(b). Indeed, to replicate the agent's reporting strategy, the mechanism needs to obtain all the information on which the agent conditions her strategy, which potentially is  .
.
However, we show that given a PBE in which the agent conditions her strategy on the payoff-irrelevant part of her private history at some public history 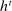 , another outcome-equivalent PBE exists in which she does not (see Proposition B.1).17 Thus, conditional on the public history
, another outcome-equivalent PBE exists in which she does not (see Proposition B.1).17 Thus, conditional on the public history 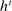 , the mechanism, together with the agent's reporting strategy, induces a mapping from Θ to distributions over
, the mechanism, together with the agent's reporting strategy, induces a mapping from Θ to distributions over 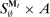 , so we can always take the set of input messages to be the set of type reports. This result relies on two observations. First, because input messages are payoff irrelevant and unobserved by the principal, if the agent chooses different strategies at
, so we can always take the set of input messages to be the set of type reports. This result relies on two observations. First, because input messages are payoff irrelevant and unobserved by the principal, if the agent chooses different strategies at 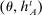 and
and 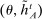 with
with 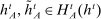 , she is indifferent between these two strategies. However, the principal may not be indifferent between these two strategies. Second, we build an alternative strategy for the agent that conditions only on
, she is indifferent between these two strategies. However, the principal may not be indifferent between these two strategies. Second, we build an alternative strategy for the agent that conditions only on 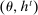 and yields the same outcome distribution, and hence the same payoff for the principal.
and yields the same outcome distribution, and hence the same payoff for the principal.
Two implications follow from this step. First, given a public history 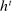 and the principal's choice of mechanism at
and the principal's choice of mechanism at 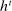 ,
, 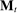 , the auxiliary mapping,
, the auxiliary mapping, 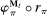 , only takes Θ as an input. The mapping
, only takes Θ as an input. The mapping 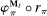 is a direct mechanism, where the set of input messages are type reports, and for which the agent finds it optimal to truthfully report her type. Second, the relevant part of the principal's beliefs in the game are about the agent's type, θ, and not the agent's private history,
is a direct mechanism, where the set of input messages are type reports, and for which the agent finds it optimal to truthfully report her type. Second, the relevant part of the principal's beliefs in the game are about the agent's type, θ, and not the agent's private history, 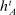 . This finding is important because although the auxiliary mapping allows us to replicate the distribution over period-t outcomes induced by the agent's strategy and the mechanism
. This finding is important because although the auxiliary mapping allows us to replicate the distribution over period-t outcomes induced by the agent's strategy and the mechanism  , in a dynamic game, we also need to replicate the distribution over continuation play, and the principal's beliefs are an important component of continuation play.
, in a dynamic game, we also need to replicate the distribution over continuation play, and the principal's beliefs are an important component of continuation play.
Output Messages as Beliefs and Canonical Mechanisms
As discussed in Section 2.2, the principal may have other uses for the output messages beyond encoding information about the agent: Conditional on the same posterior belief, (i) he may encode randomizations over the allocation, and (ii) he may use the output message to coordinate continuation play. As the proof of Theorem 1 shows, randomized allocations and public randomization allow us to subsume these two roles of the output messages.
Now, the potential challenge in using the public randomization device to subsume the second role of the output message is that, by definition, the use of the public randomization device in the canonical game can only depend on publicly available information. Instead, because in the auxiliary mapping the agent is reporting truthfully, the output message in the mechanism-selection game is drawn as a function of the agent's type, which allows the principal to coordinate future play above and beyond what he would be able to do by solely relying on the public randomization device in the canonical game.
To overcome this challenge, we leverage here that canonical mechanisms use beliefs as output messages. Note that beliefs are a sufficient statistic for the information about the agent's type that is encoded in the output messages of the mechanism-selection game. Thus, conditional on the induced belief and the allocation, the selection of continuation play contains no further information about the agent's type, which allows us to decompose the mechanism in the mechanism-selection game into a canonical mechanism in the canonical game that uses beliefs as output messages and a public randomization device.
The above argument also explains why, in a canonical mechanism, conditional on the output message, the allocation can be drawn independently of the agent's type (report). Ultimately, conditional on the induced belief, the allocation contains no further information about the agent's type.
Briefly, the proof of this result proceeds as follows (see Proposition B.2). Suppose that the principal offers 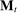 in period t. The principal's belief about the agent's type,
in period t. The principal's belief about the agent's type, 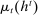 , together with the auxiliary mapping,
, together with the auxiliary mapping, 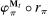 , induces a joint distribution over
, induces a joint distribution over 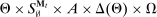 , where
, where 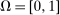 denotes the public randomization device in the mechanism-selection game. Because conditional on the induced posterior,
denotes the public randomization device in the mechanism-selection game. Because conditional on the induced posterior, 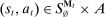 carries no further information about the agent's type, this allows us to “split” the mechanism into a transition probability β from Θ to
carries no further information about the agent's type, this allows us to “split” the mechanism into a transition probability β from Θ to 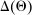 , a transition probability α from
, a transition probability α from 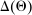 to A, and a transition probability ω from
to A, and a transition probability ω from 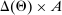 to
to 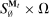 . The transition probability α plays the first role of the output message and highlights the importance of allowing the principal to offer randomized allocations. The transition probability ω corresponds to the public randomization device: by Kuratowski's theorem, we can always embed
. The transition probability α plays the first role of the output message and highlights the importance of allowing the principal to offer randomized allocations. The transition probability ω corresponds to the public randomization device: by Kuratowski's theorem, we can always embed 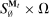 into
into 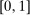 (see Srivastava (2008)).
(see Srivastava (2008)).
Three conceptual insights arise from this result. First, when the mechanism is canonical, the principal can separate the design of the information that the mechanism encodes about the agent's type from the design of the allocation. Second, the allocation has to be measurable with respect to the information generated by the mechanism: The more the principal desires to tailor the allocation to the agent's type, the more he has to learn about the agent's type through the mechanism.18 Third, it highlights the coordination role of the mechanism, which is subsumed by the public randomization device: beyond determining today's allocation and the information that is carried forward in the interaction, the mechanism allows the principal to coordinate future play.
Bayes' Rule, Truth Telling, and Participation
Underlying the previous step is the assumption that the beliefs associated with the output messages are determined via Bayes' rule. In particular, the principal is never surprised by any output message he observes. To ensure that beliefs are pinned down by Bayes' rule, Proposition B.2 shows we can “eliminate” from the mechanism all input messages that are used only by types to whom the principal assigns 0 probability. Eliminating these input messages, however, may change the participation decision for types not in the support of the principal's beliefs, which is why a canonical PBE assessment does not require that these types participate in the mechanism.19
Instead, it should be intuitive that the agent participates in the mechanism whenever her type is in the support of the principal's beliefs: By relying on the map between output messages and posterior beliefs and the public randomization device, we guarantee that, conditional on participation, the agent faces the same period-t allocation and distribution over continuations as when she did not participate. The map between output messages and beliefs allows us to identify which output message one should associate with the types that chose not to participate: the one that corresponds to the principal's updated belief conditional on nonparticipation.20 The map between output messages and the public randomization device allows us to replicate the distribution over continuations the agent faces in the PBE of the mechanism-selection game for those types that found it optimal to randomize between participating and not participating.
That beliefs in the support of the mechanism are determined via Bayes' rule has one practical implication that we exploit throughout our analysis of Example 1 and in our concurrent work (Doval and Skreta (2020, 2021)): the mechanism's disclosure rule together with the principal's belief about the agent's type induce a Bayes' plausible distribution over posteriors. As a consequence, we can apply tools from information design to derive qualitative properties of the principal's problem (see Proposition 1). This is where modeling participation as a decision that happens outside the mechanism as opposed to as an input message that locks the outside option as in Figure 3(b) is important: because nonparticipation is a zero-probability event, the principal's beliefs after nonparticipation are not pinned down via Bayes' rule, and hence cannot be necessarily obtained from a Bayes' plausible distribution over posteriors. At the same time, these beliefs cannot be ignored in the analysis, because they determine the continuations after nonparticipation, and hence, the agent's incentives to participate in the first place. By modeling participation as a decision that happens outside of the mechanism, we can rely on the tools of information design to design the mechanism's disclosure rule, while as we illustrate using the application in Example 1, the participation decision is summarized by a participation constraint (see (OPT)).
3.1 The Revelation Principle at Work
We now illustrate the simplifications afforded by Theorem 1 within the context of the application in Example 1. In particular, we show that in order to characterize the seller's revenue maximizing PBE outcome it is enough to characterize the solution to a constrained optimization problem, denoted (OPT), that only involves the seller. This is already in stark contrast to the existing work in mechanism design with limited commitment, which needs to keep track of how the buyer's best response to the seller's mechanism determines the information that the seller obtains from the interaction, which, in turn, affects the seller's incentives to offer the mechanism in the first place.
To arrive at the program that characterizes the seller's maximum revenue, we appeal to Theorem 1. First, in what follows, we restrict attention to the canonical game and to assessments in which the seller offers canonical mechanisms. Second, without loss of generality, we can consider assessments where the buyer's strategy does not depend on the payoff-irrelevant part of the private history. In particular, in 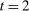 , the seller's optimal mechanism only needs to elicit the buyer's payoff relevant type, θ. Let
, the seller's optimal mechanism only needs to elicit the buyer's payoff relevant type, θ. Let 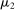 denote the seller's posterior belief in
denote the seller's posterior belief in 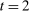 . The optimal mechanism in
. The optimal mechanism in 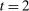 is a posted price regardless of the properties of
is a posted price regardless of the properties of 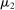 (see Proposition 2 in Skreta (2006)). For each belief, the seller may have in
(see Proposition 2 in Skreta (2006)). For each belief, the seller may have in 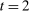 ,
, 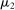 , we let
, we let 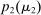 denote a selection from the set of optimal prices in
denote a selection from the set of optimal prices in 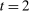 when his belief is
when his belief is 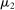 .21
.21
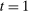 is to participate and truthfully report her type with probability 1, and (ii) when the output message is
is to participate and truthfully report her type with probability 1, and (ii) when the output message is 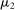 , the seller updates his belief to
, the seller updates his belief to 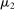 . Moreover, the assumption of quasilinearity implies that, without loss of generality, the seller does not randomize on the transfers: below
. Moreover, the assumption of quasilinearity implies that, without loss of generality, the seller does not randomize on the transfers: below 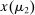 denotes the expected payment conditional on
denotes the expected payment conditional on 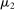 , and
, and 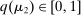 denotes the probability with which the good is sold. Thus, we can write the seller's problem as follows:
denotes the probability with which the good is sold. Thus, we can write the seller's problem as follows:
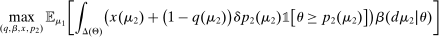 (OPT)
(OPT)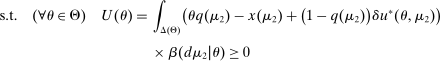 (PC)
(PC)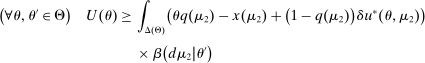 (IC)
(IC)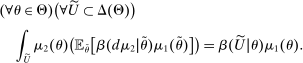 (BP)
(BP)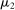 when the output message is
when the output message is  appears twice in the above expression: First, in Equation (BP), which is the Bayes' plausibility constraint and, second, in the objective function, where the seller's payoff in
appears twice in the above expression: First, in Equation (BP), which is the Bayes' plausibility constraint and, second, in the objective function, where the seller's payoff in  when the agent's type is θ and his belief is
when the agent's type is θ and his belief is  corresponds to whether θ buys the good at a price of
corresponds to whether θ buys the good at a price of 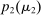 . The latter affords an important simplification: instead of writing the seller's program as one in which the seller chooses a mechanism for period 1 and one for period 2 subject to the constraint that the period 2 mechanism is optimal given the seller's belief in
. The latter affords an important simplification: instead of writing the seller's program as one in which the seller chooses a mechanism for period 1 and one for period 2 subject to the constraint that the period 2 mechanism is optimal given the seller's belief in 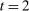 , the program (OPT) has the seller maximize over one-period mechanisms by replacing the seller's best response in
, the program (OPT) has the seller maximize over one-period mechanisms by replacing the seller's best response in 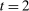 in the seller's objective function.
in the seller's objective function.The two remaining constraints in (OPT) are the buyer's participation and incentive compatibility constraints (equations (PC) and (IC)). The buyer's payoff in the mechanism, 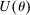 , is determined as follows. For each
, is determined as follows. For each 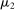 in the support of
in the support of 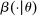 , she receives the good with probability
, she receives the good with probability 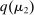 and makes a payment of
and makes a payment of 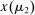 ; with the remaining probability, no trade occurs, and she obtains a continuation payoff,
; with the remaining probability, no trade occurs, and she obtains a continuation payoff, 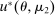 , which describes her optimal decision of whether to buy the good at
, which describes her optimal decision of whether to buy the good at 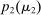 . The participation constraint states that the buyer has to earn a payoff of at least 0 by participating. Indeed, because nonparticipation is a 0 probability event, we can specify that upon rejection of the mechanism, the seller believes the buyer's valuation is
. The participation constraint states that the buyer has to earn a payoff of at least 0 by participating. Indeed, because nonparticipation is a 0 probability event, we can specify that upon rejection of the mechanism, the seller believes the buyer's valuation is 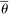 , so that in
, so that in 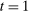 , the seller chooses a price of
, the seller chooses a price of 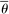 when the buyer chooses not to participate. The incentive compatibility constraint states that when her type is θ, the buyer cannot obtain a higher payoff by reporting that her type is
when the buyer chooses not to participate. The incentive compatibility constraint states that when her type is θ, the buyer cannot obtain a higher payoff by reporting that her type is 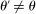 . When the buyer reports
. When the buyer reports 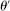 , she obtains a different distribution over output messages
, she obtains a different distribution over output messages 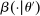 ; however, in
; however, in 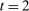 , she still chooses optimally whether to buy the good, which explains the term
, she still chooses optimally whether to buy the good, which explains the term 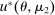 .
.
The three constraints in (OPT) provide us with a tractable representation of both the buyer's behavior and its impact on the mechanism offered in 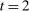 via the information that is generated about the buyer's type in
via the information that is generated about the buyer's type in 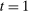 . Thus, instead of having to consider complicated mixed strategies on the part of the agent (see Laffont and Tirole (1988), Bester and Strausz (2001)), we have reduced the problem of characterizing the seller-optimal PBE outcome to the solution of a program (OPT) that combines elements of information design and mechanism design. Indeed, the solution to (OPT) can be leveraged to fully specify the PBE assessment that implements the seller's maximum revenue.22
. Thus, instead of having to consider complicated mixed strategies on the part of the agent (see Laffont and Tirole (1988), Bester and Strausz (2001)), we have reduced the problem of characterizing the seller-optimal PBE outcome to the solution of a program (OPT) that combines elements of information design and mechanism design. Indeed, the solution to (OPT) can be leveraged to fully specify the PBE assessment that implements the seller's maximum revenue.22
Furthermore, as we show below in Proposition 1, when Θ is finite, (OPT) can be further simplified: without loss of generality we can assume the seller employs mechanisms such that the support of β is finite for all 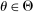 .
.
Proposition 1.Suppose Θ is finite. Fix 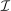 and let
and let 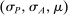 denote a canonical PBE assessment of
denote a canonical PBE assessment of 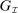 . Then a payoff-equivalent canonical PBE assessment exists such that for all
. Then a payoff-equivalent canonical PBE assessment exists such that for all 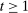 and all
and all 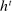 , the principal's choice of mechanism at
, the principal's choice of mechanism at 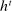 ,
, 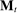 , satisfies that for all
, satisfies that for all 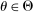 , the support of
, the support of 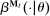 is finite.
is finite.
Most of the existing analysis of the model in Example 1 is performed for continuum type spaces; we thus revisit (OPT) when Θ is a continuum in Section 4.3. Before doing so, we first explain why it is impossible to endow the set of mechanisms with a measure structure so that the game is well-defined, and then develop a framework in Section 4.2 that is suitable to study mechanism design under limited commitment with continuum types spaces.
4 Continuum Type Spaces
Section 4 considers the case in which the set of types is an uncountable compact Polish space. This extension is important because much of the standard toolkit of mechanism design has been developed for continuum (and convex) type spaces, where the representation of incentive compatible mechanisms can be obtained using the envelope theorem. Section 4.1 reviews the issues raised by Aumann (1961), and hence the difficulties with having a well-defined mechanism-selection game when Θ is uncountable. In particular, we explain why the usual solution to this problem, namely, restricting the principal to choosing mechanisms in a suitably defined set, is not enough for the purpose of deriving a revelation principle. With little loss of continuity, the reader can skip to Section 4.2, where we propose a framework that allows us to sidestep the aforementioned issues and obtain the analogue of Theorem 1 when Θ is uncountable. We then apply our results to Example 1.
4.1 Choosing Functions at Random
To define the mechanism-selection game, a measurable structure on 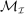 is needed to define (i) the principal's mixed strategies, (ii) the principal and the agent's expected payoffs from those mixed strategies, and (iii) the principal and the agent's strategies as measurable functions of the histories, which include the past choices of the mechanisms. Focusing on (i) and (ii), Aumann (1961, Theorem D) implies that no suitable measure structure on
is needed to define (i) the principal's mixed strategies, (ii) the principal and the agent's expected payoffs from those mixed strategies, and (iii) the principal and the agent's strategies as measurable functions of the histories, which include the past choices of the mechanisms. Focusing on (i) and (ii), Aumann (1961, Theorem D) implies that no suitable measure structure on 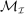 exists when the set of input messages is uncountable. Instead, Aumann (1964) circumvents the issue of defining a measurable structure on the set
exists when the set of input messages is uncountable. Instead, Aumann (1964) circumvents the issue of defining a measurable structure on the set  to define mixed strategies by relying on randomization devices. However, the construction in Aumann (1964) is insufficient for our purposes because the mechanisms chosen by the principal through period
to define mixed strategies by relying on randomization devices. However, the construction in Aumann (1964) is insufficient for our purposes because the mechanisms chosen by the principal through period  are part of the public histories. Thus, to define the principal and the agent's strategies as measurable functions of the histories, we again face the issue of defining a measurable structure on the set of mechanisms and with the negative answers in Aumann (1961).
are part of the public histories. Thus, to define the principal and the agent's strategies as measurable functions of the histories, we again face the issue of defining a measurable structure on the set of mechanisms and with the negative answers in Aumann (1961).
For this reason, the literature on competing principals (see, e.g., Attar, Campioni, Mariotti, and Pavan (2021a, 2021b)) follows a different approach: Theorem D in Aumann (1961) implies that the issues raised above would be mute if we restrict the principal to choosing mechanisms from a subset  of
of  , such that
, such that  is of bounded Borel class.23 For the purposes of deriving a revelation principle, this approach is again insufficient: Borel classes are not always closed under composition (Srivastava (2008)) and we obtain a canonical mechanism by composing the agent's strategy with the mechanism the principal employs in the mechanism-selection game. Unless the agent's strategy is continuous in her type, the induced canonical mechanism may be of a Borel class strictly larger than that of the original mechanism. Furthermore, different equilibria of the mechanism-selection game may necessitate canonical mechanisms of different Borel classes, which makes the task of defining the canonical game pointless: one would have to potentially consider a different canonical game for each equilibrium of each mechanism-selection game. Lastly, the restriction to a set of mechanisms of bounded Borel class is difficult to work with in applications: only payoffs from deviations to mechanisms within that class are well-defined and, in practice, verifying that only deviations to those mechanisms are being contemplated is difficult.
is of bounded Borel class.23 For the purposes of deriving a revelation principle, this approach is again insufficient: Borel classes are not always closed under composition (Srivastava (2008)) and we obtain a canonical mechanism by composing the agent's strategy with the mechanism the principal employs in the mechanism-selection game. Unless the agent's strategy is continuous in her type, the induced canonical mechanism may be of a Borel class strictly larger than that of the original mechanism. Furthermore, different equilibria of the mechanism-selection game may necessitate canonical mechanisms of different Borel classes, which makes the task of defining the canonical game pointless: one would have to potentially consider a different canonical game for each equilibrium of each mechanism-selection game. Lastly, the restriction to a set of mechanisms of bounded Borel class is difficult to work with in applications: only payoffs from deviations to mechanisms within that class are well-defined and, in practice, verifying that only deviations to those mechanisms are being contemplated is difficult.
Motivated by the importance of continuum type spaces, Section 4.2 proposes an approach to model mechanism-selection games that circumvents the above issues.
4.2 PBE-Feasible Outcomes
We develop a framework to characterize the outcomes that can be sustained under limited commitment, which we dub PBE-feasible outcomes and formally define below (Definition 5). By analogy with the mechanism-selection game, we keep the notation 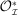 to denote PBE-feasible outcomes. Contrary to the mechanism-selection game,
to denote PBE-feasible outcomes. Contrary to the mechanism-selection game, 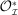 is now a correspondence describing the set of PBE-feasible outcomes for each period
is now a correspondence describing the set of PBE-feasible outcomes for each period 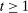 , each principal's belief
, each principal's belief 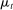 , and each sequence of allocations up to period t,
, and each sequence of allocations up to period t, 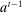 ,
, 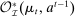 . The reason is that the definition of the set of PBE-feasible outcomes is recursive, and what is PBE-feasible in period t naturally depends on what is PBE-feasible in period
. The reason is that the definition of the set of PBE-feasible outcomes is recursive, and what is PBE-feasible in period t naturally depends on what is PBE-feasible in period 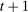 .
.
The discussion in Section 4.1 implies that the framework must sidestep the need to define the principal and the agent's “strategies” as measurable functions of the principal's past choices of mechanisms. There are (at least) two important roles measurability plays in the mechanism-selection game. First, it allows us to describe the agent's behavior along the path of the principal's strategy, which in turn allows us to evaluate the principal's payoff from a given strategy. Second, it allows us to describe how the agent's behavior changes when the principal deviates from the prescribed strategy, which in turn allows us to evaluate the principal's payoff from a deviation from the prescribed strategy. The comparison between these two payoffs determines whether the principal's strategy is sequentially rational.
Informally, the framework circumvents the aforementioned measurability issues as follows. The starting point of the analysis is that we no longer model the principal as a player. Instead, we describe the analogue of a principal's strategy in the mechanism-selection game via an extensive-form game for the agent, which describes the sequence of mechanisms the agent faces as a function of her participation decisions and the outcomes of the mechanisms (Definition 3). Importantly, in this extensive-form game the agent's strategy only depends on her type, her participation decisions, her input messages, and the outcomes of the mechanisms, but not on the mechanisms themselves. The principal's belief about the agent's type together with the agent's strategy define a distribution over the terminal nodes in this extensive form, which allows us to evaluate the principal's payoff from a particular sequence of mechanisms. The final component of the framework is how we define that a particular extensive form is sequentially rational for the principal; in other words, that the principal does not wish to revise the mechanisms that define the extensive form at any point in time (Definition 4). Here, we rely on two ideas. First, to determine whether the principal wishes to revise the mechanisms that define the extensive form, we only need to know the outcome distributions the principal expects he will face in the event of a deviation (equation (1)). Second, these outcome distributions can be defined without reference to a strategy of the agent that conditions on the sequence of mechanisms that has been offered so far.
We now formally define the set of PBE-feasible outcomes, 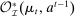 , for each period
, for each period 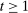 , and pair
, and pair  (Definition 5). Because the definition is recursive, we fix a period
(Definition 5). Because the definition is recursive, we fix a period 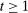 , and a pair
, and a pair  throughout. Definition 5 consists of three components, which we introduce first: (i) the sequence of mechanisms offered by the principal (Definition 3), (ii) optimal behavior by the agent within those mechanisms, and (iii) the outcome distributions the principal anticipates upon a deviation (equation (1)). For simplicity, we assume the principal has one set of input and output messages, that is,
throughout. Definition 5 consists of three components, which we introduce first: (i) the sequence of mechanisms offered by the principal (Definition 3), (ii) optimal behavior by the agent within those mechanisms, and (iii) the outcome distributions the principal anticipates upon a deviation (equation (1)). For simplicity, we assume the principal has one set of input and output messages, that is, 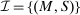 , and we use the shorthand notation
, and we use the shorthand notation 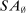 to denote the set
to denote the set 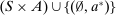 .
.
Dynamic Mechanisms
Instead of having the principal be a player in a game, we describe the analogue of the principal's strategy via a dynamic mechanism, defined as follows.
Definition 3. (Dynamic mechanisms)For  and
and 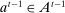 , a dynamic mechanism given
, a dynamic mechanism given 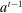 ,
, 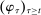 , is a sequence of measurable mappings
, is a sequence of measurable mappings 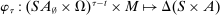 , such that for all
, such that for all 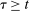 and all
and all 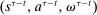 :
:
- 1.
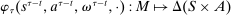 is a measurable function, and
is a measurable function, and - 2. for all
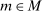 ,
, 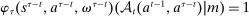 .
.
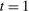 , a dynamic mechanism describes the mechanism the agent faces in period 1,
, a dynamic mechanism describes the mechanism the agent faces in period 1, 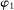 , the mechanism the agent faces in period 2 as a function of the agent's participation decision (i.e., whether
, the mechanism the agent faces in period 2 as a function of the agent's participation decision (i.e., whether 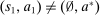 ), and the realization of the public randomization device,
), and the realization of the public randomization device, 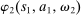 , and so on. Consider now
, and so on. Consider now 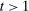 and suppose the allocation so far is
and suppose the allocation so far is 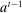 . Then we require that the dynamic mechanism only implements allocations that are feasible given
. Then we require that the dynamic mechanism only implements allocations that are feasible given 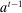 .
.
As we explain next, a dynamic mechanism defines an extensive-form game for the agent.
Agent-Extensive Form
Given 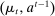 , a dynamic mechanism
, a dynamic mechanism 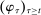 defines an extensive-form game for the agent,
defines an extensive-form game for the agent, 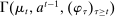 , as follows. First, nature draws the agent's type according to
, as follows. First, nature draws the agent's type according to 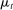 . Having observed her type, suppose that in stage
. Having observed her type, suppose that in stage  , the public history is
, the public history is 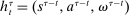 . Then, faced with
. Then, faced with 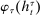 , the agent decides whether to participate, and conditional on participating, her reporting strategy. If the agent rejects
, the agent decides whether to participate, and conditional on participating, her reporting strategy. If the agent rejects 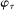 , the “output message” is ∅ and the allocation is
, the “output message” is ∅ and the allocation is 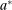 . Instead, if she accepts
. Instead, if she accepts 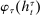 , she chooses an input message
, she chooses an input message 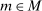 that determines the distribution from which the output message and the allocation are drawn,
that determines the distribution from which the output message and the allocation are drawn, 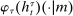 . In both cases, we proceed to stage
. In both cases, we proceed to stage 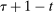 .
.
In the agent-extensive form 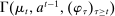 , there are two types of histories. The public history
, there are two types of histories. The public history 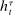 encodes the agent's participation in the mechanism, the realized output messages and allocations, and the realizations of the public randomization device. The private histories encode everything the agent knows: her payoff-relevant type θ, the public history
encodes the agent's participation in the mechanism, the realized output messages and allocations, and the realizations of the public randomization device. The private histories encode everything the agent knows: her payoff-relevant type θ, the public history 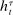 , and her past input messages. In a slight abuse of notation, we denote by
, and her past input messages. In a slight abuse of notation, we denote by 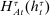 the set of agent histories consistent with
the set of agent histories consistent with 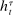 .
.
Importantly, we do not need to encode the mechanisms defining 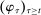 in the histories of the agent-extensive form, because the mechanisms are akin to a move by nature in the extensive form
in the histories of the agent-extensive form, because the mechanisms are akin to a move by nature in the extensive form 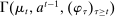 . It thus follows that in the agent-extensive form we can define the agent's strategy,
. It thus follows that in the agent-extensive form we can define the agent's strategy,  , as a measurable function of the private histories.
, as a measurable function of the private histories.
Finally, we note that the agent evaluates the payoffs of a strategy in 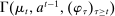 using
using 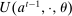 . We are now ready to define optimal play by the agent in
. We are now ready to define optimal play by the agent in 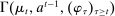 .
.
Agent-PBE
Together with the agent strategy  , we can also define a system of beliefs
, we can also define a system of beliefs  , which describes for each period
, which describes for each period 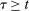 and for each public history
and for each public history 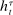 , the principal's beliefs over the private histories,
, the principal's beliefs over the private histories, 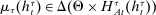 .
.
We say that 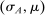 is an agent-PBE of the agent-extensive form
is an agent-PBE of the agent-extensive form 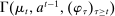 if the agent's strategy is sequentially rational (under payoffs
if the agent's strategy is sequentially rational (under payoffs 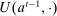 ) and the belief system satisfies Bayes' rule where possible. Although the belief system is not needed to test whether the agent's strategy is optimal in the extensive-form game, it is needed to test the optimality of the principal's choice of mechanism.
) and the belief system satisfies Bayes' rule where possible. Although the belief system is not needed to test whether the agent's strategy is optimal in the extensive-form game, it is needed to test the optimality of the principal's choice of mechanism.
Proposition B.1 applies verbatim, allowing us to conclude that for every agent-PBE 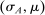 of
of 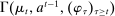 , an outcome equivalent
, an outcome equivalent 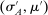 exists, in which the agent's strategy only conditions on her type and the public history. This property is responsible for the recursive nature of the set of PBE-feasible outcomes here and also in the mechanism-selection game. Hereafter, when we say agent-PBE, we mean one that satisfies the above property.
exists, in which the agent's strategy only conditions on her type and the public history. This property is responsible for the recursive nature of the set of PBE-feasible outcomes here and also in the mechanism-selection game. Hereafter, when we say agent-PBE, we mean one that satisfies the above property.
(Continuation) Outcome Distributions
An agent-PBE 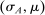 of
of 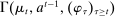 defines a distribution over
defines a distribution over 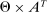 ,
, 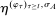 , that satisfies two conditions. First, the marginal on Θ is
, that satisfies two conditions. First, the marginal on Θ is 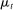 . Second, the distribution is supported on those tuples
. Second, the distribution is supported on those tuples 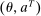 such that
such that 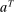 coincides with
coincides with 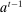 through
through  . (Appendix E.1 in the Online Supplementary Material contains the formal definition.)
. (Appendix E.1 in the Online Supplementary Material contains the formal definition.)
Furthermore, at any history 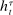 , the belief assessment together with the dynamic mechanisms and the agent's strategy, defines a continuation outcome,
, the belief assessment together with the dynamic mechanisms and the agent's strategy, defines a continuation outcome, 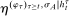 , whose marginal on Θ coincides with
, whose marginal on Θ coincides with 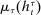 and assigns positive probability to those allocations that are consistent with
and assigns positive probability to those allocations that are consistent with 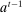 and
and 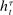 .
.
Principal's Sequential Rationality
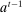 ,
, 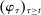 , and an agent-PBE
, and an agent-PBE 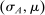 of
of 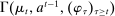 . Suppose that the principal considers offering mechanism
. Suppose that the principal considers offering mechanism  instead of
instead of  . In order to determine whether the principal wishes to deviate to
. In order to determine whether the principal wishes to deviate to 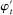 , we need to determine the outcome distributions that can follow
, we need to determine the outcome distributions that can follow 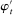 . We denote this set by
. We denote this set by  and is defined as follows:
and is defined as follows:
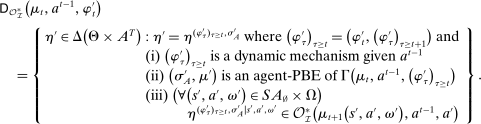 (1)
(1)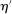 is in
is in 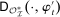 if it satisfies two properties. First,
if it satisfies two properties. First, 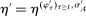 for a dynamic mechanism
for a dynamic mechanism 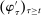 such that
such that 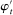 is the period t-mechanism and
is the period t-mechanism and 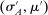 is an agent-PBE given
is an agent-PBE given 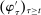 . Second, continuation outcomes are PBE-feasible. The reason that we are able to require that continuation outcomes are PBE-feasible is that whenever the agent does not condition her strategy on the payoff-irrelevant part of the private history the following holds: If
. Second, continuation outcomes are PBE-feasible. The reason that we are able to require that continuation outcomes are PBE-feasible is that whenever the agent does not condition her strategy on the payoff-irrelevant part of the private history the following holds: If 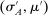 is an agent-PBE of
is an agent-PBE of 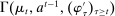 , then for all
, then for all 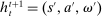 ,
, 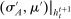 is an agent-PBE of
is an agent-PBE of 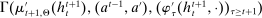 .
.While we can use the set 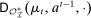 to test whether the principal has a deviation from
to test whether the principal has a deviation from 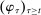 at the root of
at the root of 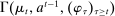 , Definition 4 also describes how we test for sequential rationality at later points in the agent-extensive form.
, Definition 4 also describes how we test for sequential rationality at later points in the agent-extensive form.
Definition 4. (Sequential rationality)Fix 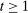 ,
, 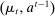 , a dynamic mechanism
, a dynamic mechanism 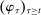 given
given 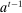 , and an agent-PBE
, and an agent-PBE 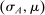 of
of 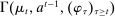 .
. 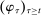 is sequentially rational given
is sequentially rational given 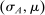 if the following hold:
if the following hold:
- 1. For all
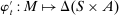 , a distribution
, a distribution 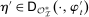 exists such that the principal prefers
exists such that the principal prefers 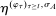 to
to 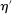 ; that is,
; that is, 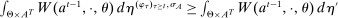 .
. - 2. For all
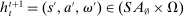 ,
, 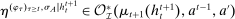 .
.
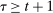 : the continuation outcome distribution induced by
: the continuation outcome distribution induced by 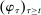 and
and 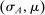 is PBE-feasible in the continuation.
is PBE-feasible in the continuation.
Definition 4 resembles the sequential rationality conditions in the mechanism-selection game, except for one important aspect: when we consider the outcomes the principal faces in the event of a deviation, we do not require that the agent's strategy is measurable in any way with respect to the history of mechanisms so far.24 By contrast, underlying the definition of the mechanism-selection game is the ability to measurably select as a function of 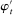 (in fact, as a function of the whole sequence of mechanisms that has been offered through period
(in fact, as a function of the whole sequence of mechanisms that has been offered through period  ) the outcomes that the principal faces in the event of a deviation.
) the outcomes that the principal faces in the event of a deviation.
We are now ready to define the set of PBE feasible outcomes at 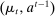 ,
, 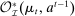 .
.
Definition 5. (PBE-feasible outcomes)Fix 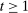 ,
, 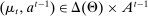 . The distribution
. The distribution 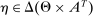 is PBE-feasible at (
is PBE-feasible at (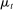 ,
,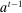 ) if a dynamic mechanism
) if a dynamic mechanism 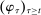 given
given 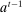 and an agent-PBE
and an agent-PBE 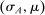 of
of 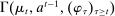 exist such that:
exist such that:
- 1. η is the outcome distribution induced by
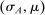 in
in 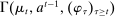 ,
, 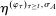 ,
, - 2.
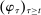 is sequentially rational given
is sequentially rational given 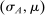 .
.
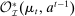 denotes the set of PBE-feasible outcomes at
denotes the set of PBE-feasible outcomes at 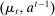 .
.
By varying 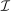 , we can define the set of PBE-feasible outcomes when the principal can offer mechanisms whose input and output messages are
, we can define the set of PBE-feasible outcomes when the principal can offer mechanisms whose input and output messages are 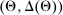 . Like in Theorem 1, our interest is in the canonical-PBE-feasible outcomes, that is, those outcomes that are induced by canonical dynamic mechanisms
. Like in Theorem 1, our interest is in the canonical-PBE-feasible outcomes, that is, those outcomes that are induced by canonical dynamic mechanisms 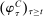 (Definition 1) and canonical-agent PBE of the extensive-form game
(Definition 1) and canonical-agent PBE of the extensive-form game 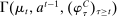 . In a slight abuse of notation, let
. In a slight abuse of notation, let 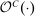 denote the correspondence of canonical-PBE-feasible outcomes when
denote the correspondence of canonical-PBE-feasible outcomes when 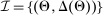 .
.
Theorem 2.For all 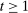 and pairs
and pairs 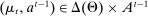 ,
, 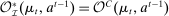 .
.
 and
and  . In particular, we are implicitly defining
. In particular, we are implicitly defining  by requiring that the continuation outcomes are drawn from the (continuation) set
by requiring that the continuation outcomes are drawn from the (continuation) set 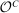 . However, in accounting for this difference, we illustrate how both sets can be defined in terms of an operator similar to that considered in Abreu, Pearce, and Stacchetti (1990), which in turn could be used in an application to characterize these sets.
. However, in accounting for this difference, we illustrate how both sets can be defined in terms of an operator similar to that considered in Abreu, Pearce, and Stacchetti (1990), which in turn could be used in an application to characterize these sets.
We conclude Section 4 by illustrating the framework in Section 4.2 within Example 1.
4.3 Example 1 Revisited
We now consider Example 1 under the assumption that the set of types is a continuum. Formally, let 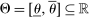 , for some finite
, for some finite 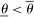 . In what follows, we use the standard cdf notation
. In what follows, we use the standard cdf notation 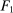 and
and 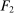 to denote the seller's prior and posterior beliefs, instead of
to denote the seller's prior and posterior beliefs, instead of 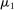 and
and 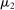 as in Section 3.1.
as in Section 3.1.
Seller's Program
We first argue that the program (OPT) continues to represent the seller's maximum revenue under a PBE-feasible outcome distribution. By Theorem 2, it continues to be without loss of generality to assume the seller chooses dynamic canonical mechanisms and to analyze the canonical agent-PBE of the game induced by the canonical dynamic mechanism. The only difference between the program (OPT) and the framework in Section 4.2 is that in (OPT) the seller only chooses the 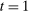 mechanism, instead of a dynamic mechanism. However, this distinction is inconsequential: One of the conditions in Definition 5 is that given the seller's belief
mechanism, instead of a dynamic mechanism. However, this distinction is inconsequential: One of the conditions in Definition 5 is that given the seller's belief  , the
, the  -outcome distribution is PBE-feasible in
-outcome distribution is PBE-feasible in  . It follows that the
. It follows that the  -mechanism chosen by the seller must maximize his revenue given his posterior belief about the buyer. Proposition 2 in Skreta (2006) implies the
-mechanism chosen by the seller must maximize his revenue given his posterior belief about the buyer. Proposition 2 in Skreta (2006) implies the 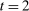 -mechanism is a posted price as a function of
-mechanism is a posted price as a function of 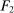 ,
, 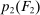 .
.
Virtual Surplus Representation
The assumption of a continuum of types allows us to apply standard mechanism design tools to represent the seller's payoff as a function of the allocation rule and the distribution over posteriors implied by the mechanism. To see this, let 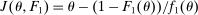 denote the buyer's virtual value.
denote the buyer's virtual value.
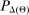 , and for each posterior he induces, a probability of trade
, and for each posterior he induces, a probability of trade 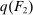 to solve
to solve
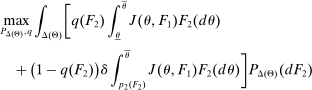 (2)
(2)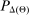 must be Bayes' plausible given
must be Bayes' plausible given 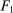 and (ii) a monotonicity condition, which states that, in expectation, higher types must trade with higher probability (see equation (18) in Appendix C). Equation (2) describes the seller's payoff in terms of the distribution over posteriors induced by the mechanism. If at posterior
and (ii) a monotonicity condition, which states that, in expectation, higher types must trade with higher probability (see equation (18) in Appendix C). Equation (2) describes the seller's payoff in terms of the distribution over posteriors induced by the mechanism. If at posterior 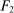 the seller sells the good (
the seller sells the good (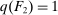 ), he obtains the expected virtual surplus, where the expectation is calculated using
), he obtains the expected virtual surplus, where the expectation is calculated using  , but the virtual values are calculated using
, but the virtual values are calculated using 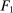 . This reflects that the probability with which the seller pays rents to a buyer of type θ is measured by the probability
. This reflects that the probability with which the seller pays rents to a buyer of type θ is measured by the probability 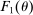 that buyer types below θ receive the good. Instead, if at
that buyer types below θ receive the good. Instead, if at 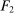 the seller does not sell the good (
the seller does not sell the good (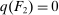 ) he obtains the (discounted) expected virtual surplus of selling the good at price
) he obtains the (discounted) expected virtual surplus of selling the good at price 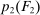 . Although the posted price in period 2 is optimal with respect to the posterior virtual values
. Although the posted price in period 2 is optimal with respect to the posterior virtual values 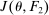 , it may not be for the prior virtual values. This reflects the conflict between the period 1 and period 2 sellers: if they hold different beliefs about the buyer's type, they pay rents with different probabilities and, therefore, may prefer different mechanisms.
, it may not be for the prior virtual values. This reflects the conflict between the period 1 and period 2 sellers: if they hold different beliefs about the buyer's type, they pay rents with different probabilities and, therefore, may prefer different mechanisms.Although the solution to the problem in equation (2) is beyond the scope of this paper,25 the virtual surplus representation of the seller's problem allows us to expand on what is known about the sale of a durable good under limited commitment. Skreta (2006) shows that, among the mechanisms in Bester and Strausz (2001), posted-prices are the optimal mechanism for the seller. Instead, when endowed with canonical mechanisms, Proposition 2 provides conditions under which the seller will profitably deviate from the optimal posted price mechanism. In other words, the outcome distribution induced by posted prices is not PBE-feasible.
Proposition 2. (Posted prices not PBE-feasible)Assume 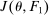 is strictly increasing and
is strictly increasing and 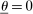 . Then
. Then 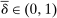 exists such that for all discount factors
exists such that for all discount factors 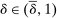 , the outcome distribution implemented by posted prices is not PBE-feasible.
, the outcome distribution implemented by posted prices is not PBE-feasible.
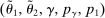 and works as follows. Pricing is nonuniform because in period 1 types above
and works as follows. Pricing is nonuniform because in period 1 types above 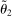 are served with probability 1 and pay
are served with probability 1 and pay 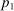 , while types in
, while types in 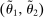 are rationed, that is, they are served with probability γ and pay
are rationed, that is, they are served with probability γ and pay  if they receive the good. The remaining types are not served in period 1 and pay nothing. It is obfuscated because when
if they receive the good. The remaining types are not served in period 1 and pay nothing. It is obfuscated because when 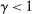 , the seller observes whether the good is sold in
, the seller observes whether the good is sold in 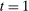 , but not whether the buyer's type is above or below
, but not whether the buyer's type is above or below 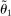 . Nonuniform pricing has been studied in the durable goods literature under commitment and limited capacity (see Loertscher and Muir (2021) and the references therein). Instead, Denicolo and Garella (1999) show that obfuscation may benefit a durable goods seller if he cannot commit to the sequence of posted prices.26 As we explain next, it is the combination of nonuniform pricing and obfuscation that makes this mechanism more attractive to the seller than the optimal posted-price mechanism.
. Nonuniform pricing has been studied in the durable goods literature under commitment and limited capacity (see Loertscher and Muir (2021) and the references therein). Instead, Denicolo and Garella (1999) show that obfuscation may benefit a durable goods seller if he cannot commit to the sequence of posted prices.26 As we explain next, it is the combination of nonuniform pricing and obfuscation that makes this mechanism more attractive to the seller than the optimal posted-price mechanism.
The proof of Proposition 2 shows the optimal posted-price mechanism is, in a sense, costly for the seller when the seller is patient: to avoid offering low prices in 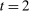 , the seller does not trade with buyer types with positive virtual values in
, the seller does not trade with buyer types with positive virtual values in 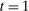 . Instead, by carefully designing the interval
. Instead, by carefully designing the interval 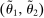 , the obfuscated nonuniform pricing mechanism allows the seller to serve these buyer types with positive probability in
, the obfuscated nonuniform pricing mechanism allows the seller to serve these buyer types with positive probability in 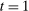 , without necessarily lowering the price in
, without necessarily lowering the price in 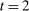 . The proof constructs a deviation to such a mechanism that guarantees that the unique best response for the buyer is to participate and truthfully report her type. It follows that in this setting the set of continuation outcomes described in equation (1) is not large enough to deter the seller from this deviation.
. The proof constructs a deviation to such a mechanism that guarantees that the unique best response for the buyer is to participate and truthfully report her type. It follows that in this setting the set of continuation outcomes described in equation (1) is not large enough to deter the seller from this deviation.
We conclude Section 4.3 by discussing the reason that, unlike Skreta (2006), other mechanisms within our class can outperform posted prices in a two-period setting.
Remark 2. (Comparison with [Skreta] ([2006]))To understand why in our two-period example the seller can do better than by using the optimal posted price mechanism, it is instructive to compare the incentive constraints in (OPT) with those implied by mechanisms where the seller observes the buyer's choice of input message as in, for instance, Laffont and Tirole (1988), Bester and Strausz (2001), Skreta (2006). Although not expressed in the language of type reports or beliefs, the incentive constraints in Skreta (2006) require that for each 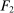 in the support of
in the support of 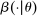 , the buyer prefers the tuple
, the buyer prefers the tuple 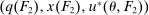 to any other tuple
to any other tuple 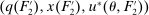 in the mechanism. In particular, the buyer must be indifferent between any two tuples that she chooses with positive probability. Contrast this with the incentive constraints in (OPT), where the buyer is not necessarily indifferent between the tuples
in the mechanism. In particular, the buyer must be indifferent between any two tuples that she chooses with positive probability. Contrast this with the incentive constraints in (OPT), where the buyer is not necessarily indifferent between the tuples 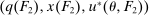 in the support of
in the support of 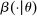 , although in expectation, the lottery she faces over such tuples under truth telling must be better than the one she faces by lying. Indeed, in the obfuscated nonuniform pricing mechanism, the seller exploits the weaker incentive constraints in (OPT): Buyer types in
, although in expectation, the lottery she faces over such tuples under truth telling must be better than the one she faces by lying. Indeed, in the obfuscated nonuniform pricing mechanism, the seller exploits the weaker incentive constraints in (OPT): Buyer types in 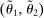 are not indifferent between receiving the good in period 1 at the rationing price and receiving the good in period 2.
are not indifferent between receiving the good in period 1 at the rationing price and receiving the good in period 2.
However, for longer horizons, the comparison of the seller's payoffs in the two models is not obvious because the larger set of canonical mechanisms also implies the seller has a larger set of deviations in our model than in the model in Skreta (2006).
The previous discussion highlights that under limited commitment, the principal may benefit from employing mechanisms where the output message (and hence, the allocation) does not reveal the input message that the agent submitted into the mechanism. Contrast this to the standard revelation principle for the case of commitment when the principal faces a privately informed agent (adverse selection): as we explained in the Introduction, it follows from the result in Myerson (1982) that it is without loss of generality in that case to consider mechanisms whereby the principal learns the input message from observing the realization of the output message. Instead, Myerson (1982) shows that adding “noise” to the communication may be essential when the principal also faces an agent whose actions are not contractible (moral hazard). Indeed, pooling in the same output message different types of the privately informed agent to incentivize the agent whose action is not contractible to follow the recommendation may be beneficial. Mechanism design with limited commitment is closer to the hybrid model of adverse selection and moral hazard in Myerson (1982) than it is to the model of pure adverse selection. Indeed, note that in a given period, the principal faces, in a sense, two agents whose incentives he needs to manage: the privately informed agent (adverse selection) and his future self, whose choice of mechanism is not contractible (moral hazard). That is, today's principal needs to elicit the agent's information while simultaneously ensuring his future behavior is sequentially rational. In the same way that output messages are key in the presence of moral hazard in Myerson (1982), they feature prominently in our framework.
Following Myerson (1982), it would have been natural to consider mechanisms where output messages encode a recommended sequence of mechanisms from tomorrow onward. However, the language of recommendations is self-referential because the set of output messages would refer to continuation mechanisms, which are themselves defined by a set of output messages. Instead, the language of posterior beliefs avoids this potential infinite-regress problem, allowing us to identify a canonical set of output messages for mechanism design with limited commitment.
5 Conclusions and Further Directions
This paper provides a revelation principle for dynamic mechanism-selection games in which the designer can only commit to short-term mechanisms. In doing so, it opens the door to the study of the implications of limited commitment in fundamental problems in economics and political economy, such as optimal taxation, redistribution, and the design of social insurance (Sleet and Yeltekin (2008), Farhi et al. (2012), Golosov and Iovino (2021)), or environmental regulation (Hiriart, Martimort, and Pouyet (2011)), which due to the difficulties with the revelation principle, have only been studied within simple informational environments, such as fully nonpersistent private information. Since our model allows for nonseparable payoffs and nontransferable utility, our results can be used in a broad range of applications.
A cornerstone of the analysis is the idea that a mechanism should encode not only the rules that determine the allocation, but also the information the designer obtains from the interaction with the agent. We expect that the idea that the mechanism's output messages should encode at the very least the principal's information about the agent is more far-reaching and carries to other forms of limited commitment, such as renegotiation with long-term mechanisms, where versions of the revelation principle have proved equally elusive. However, other aspects of our analysis may not carry immediately to the analysis of renegotiation: indeed, Proposition B.1 uncovered that PBE outcomes have a recursive structure. In games with time-separable payoffs, Proposition B.1 implies PBE payoffs can be characterized by relying on self-generating techniques as in Abreu, Pearce, and Stacchetti (1990) and Athey and Bagwell (2008), reducing the analysis of a complex dynamic game essentially to a series of static problems (see Doval and Skreta (2020) for an application).
At the same time, by highlighting the canonical role of beliefs as the signals employed by the mechanism, our work opens up a new avenue for research in information design. Indeed, as the analysis in Section 4.3 and our companion work, Doval and Skreta (2021), highlights, developing information design tools for continuum type spaces when the designer's payoff does not depend only on the posterior mean would contribute to our understanding of classical problems in mechanism design.
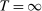 , and notation of the form
, and notation of the form 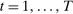 ,
, 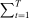 , or
, or 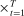 appears, we take this to mean
appears, we take this to mean 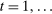 ,
,  , or
, or 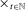 , respectively.
, respectively.
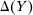 denote the set of all Borel probability measures over Y, endowed with the
denote the set of all Borel probability measures over Y, endowed with the 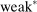 topology. Thus,
topology. Thus, 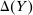 is also a Polish space (Aliprantis and Border (2006)). For any two measurable spaces, X and Y, a transition probability from X to Y is a measurable function
is also a Polish space (Aliprantis and Border (2006)). For any two measurable spaces, X and Y, a transition probability from X to Y is a measurable function 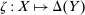 . When integrating under the measure
. When integrating under the measure 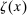 , we use the notation
, we use the notation 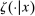 .
.
 is Polish, the public and private histories are Polish, because they are the (at most) countable product of Polish spaces.
is Polish, the public and private histories are Polish, because they are the (at most) countable product of Polish spaces.
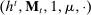 denotes the agent's decision to participate in mechanism
denotes the agent's decision to participate in mechanism  .
.
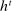 , item 3 implies this property also holds off the path of the equilibrium strategy starting at
, item 3 implies this property also holds off the path of the equilibrium strategy starting at 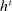 , for example, when the principal deviates and offers a mechanism not in the support of
, for example, when the principal deviates and offers a mechanism not in the support of  .
.
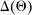 is in bijection with
is in bijection with 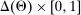 , so the number of messages is sufficient to encode both the beliefs and the suggested continuation play.
, so the number of messages is sufficient to encode both the beliefs and the suggested continuation play.
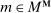 , the support of
, the support of 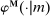 is finite. This simple proof mirrors the complete one in Appendix D.1 in the Online Supplementary Material, but it is technically simpler and more accessible.
is finite. This simple proof mirrors the complete one in Appendix D.1 in the Online Supplementary Material, but it is technically simpler and more accessible.
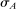 . This change to the mechanism actually makes the deviation less attractive, and hence, it “disincentivizes” the agent from deviating in the first place.
. This change to the mechanism actually makes the deviation less attractive, and hence, it “disincentivizes” the agent from deviating in the first place.
 among several prices. In that case, as in the literature on Bayesian persuasion, we determine the tie-breaking rule as a solution to the seller's problem in
among several prices. In that case, as in the literature on Bayesian persuasion, we determine the tie-breaking rule as a solution to the seller's problem in  (see (OPT)). Note that because of public randomization the selection from the set of optimal prices in
(see (OPT)). Note that because of public randomization the selection from the set of optimal prices in  at belief
at belief 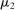 may be random. However, our notation does not account for this explicitly to simplify the presentation.
may be random. However, our notation does not account for this explicitly to simplify the presentation.
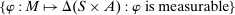 is not of bounded Borel class (Aumann (1961)).
is not of bounded Borel class (Aumann (1961)).
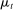 and the allocations so far
and the allocations so far 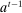 to describe what is PBE-feasible from period t onward. In a sense, the past mechanisms and output messages are bygones.
to describe what is PBE-feasible from period t onward. In a sense, the past mechanisms and output messages are bygones.
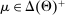 and θ is such that
and θ is such that 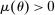 , then
, then 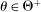 .
.
Appendix A: Collected Definitions and Notation
Appendix A introduces the necessary notation to define the payoffs from an assessment, and hence, the definition of perfect Bayesian equilibrium. It also collects notation that is used in the proofs. Throughout this section and also for most of Appendix B, we assume that Θ is finite and the mechanisms used by the principal have finite support and defer the proof of Theorem 1 for the general case to the Online Appendix.
Shorthand Notation
To simplify notation, we do not explicitly include the agent's decision to participate in the mechanism in the histories of the game. Instead, we follow the convention that if the agent does not participate, the input message is ∅, the output message is ∅, and the allocation is 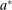 . With this convention in mind, we let
. With this convention in mind, we let 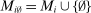 ,
, 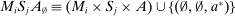 and
and 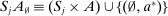 , denote the private and public outcomes in a given period when the principal uses a mechanism with labels
, denote the private and public outcomes in a given period when the principal uses a mechanism with labels 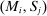 .
.
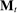 , let
, let 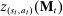 denote the tuple
denote the tuple 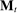 ,
, 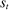 ,
, 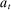 , which summarizes the period-t outcomes from offering
, which summarizes the period-t outcomes from offering 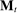 , where
, where 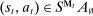 . Note that any public history at the beginning of period t can be written as
. Note that any public history at the beginning of period t can be written as 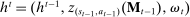 , with the convention that when
, with the convention that when  ,
, 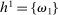 for some
for some 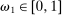 . Finally, given an assessment,
. Finally, given an assessment, 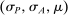 , it is useful to collapse the distribution on
, it is useful to collapse the distribution on 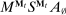 , defined by
, defined by
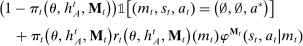 (A.1)
(A.1)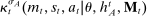 .
.Perfect Bayesian Equilibrium
 . The prior
. The prior  and the strategy profile
and the strategy profile 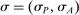 induce a probability distribution over the terminal histories
induce a probability distribution over the terminal histories 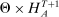 ,
, 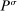 , via the Ionescu–Tulcea theorem (Pollard (2002)).27 Moreover, fixing t and
, via the Ionescu–Tulcea theorem (Pollard (2002)).27 Moreover, fixing t and 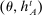 , the measure
, the measure 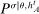 corresponds to the measure induced by drawing with probability 1
corresponds to the measure induced by drawing with probability 1 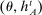 and then using the continuation strategy profile to determine the distribution over the continuation histories. Fix a public history
and then using the continuation strategy profile to determine the distribution over the continuation histories. Fix a public history 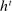 . The principal's payoff at
. The principal's payoff at 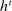 is given by
is given by

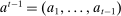 is the allocation through the beginning of period t that is consistent with
is the allocation through the beginning of period t that is consistent with 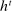 (with the convention that
(with the convention that  ). Note that the principal's payoff from offering
). Note that the principal's payoff from offering  at
at 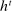 ,
, 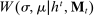 , depends on the belief system μ only through
, depends on the belief system μ only through 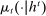 .
.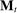 ,
, 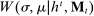 equals
equals
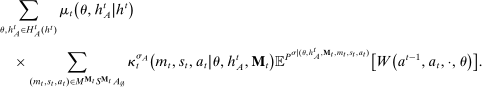
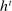 , together with mechanism
, together with mechanism 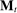 and the agent's strategy, define a distribution over the continuation public histories as follows:
and the agent's strategy, define a distribution over the continuation public histories as follows:
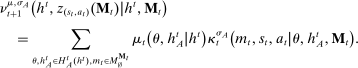 (A.2)
(A.2) as
as
 (A.3)
(A.3) , when the principal offers mechanism
, when the principal offers mechanism 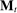 , is given by
, is given by
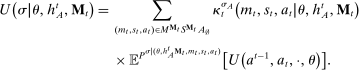 (A.4)
(A.4)Definition A.1.An assessment  is sequentially rational if for all
is sequentially rational if for all  and public histories
and public histories 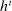 the following hold:
the following hold:
- 1. If
 is in the support of
is in the support of 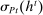 , then
, then 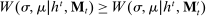 for all
for all 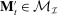 ,
, - 2. For all
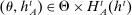 , and
, and  in
in  ,
, 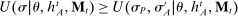 for all
for all 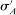 .
.
Definition A.2.An assessment 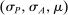 satisfies Bayes' rule where possible if for all public histories
satisfies Bayes' rule where possible if for all public histories 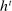 and mechanisms
and mechanisms 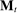 the following holds:
the following holds:
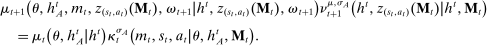 (A.5)
(A.5)Definition A.3.An assessment  is a perfect Bayesian equilibrium if it is sequentially rational and satisfies Bayes' rule where possible.
is a perfect Bayesian equilibrium if it is sequentially rational and satisfies Bayes' rule where possible.
Prunning
Given a mechanism 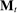 , let
, let  . The set
. The set 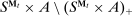 has zero probability regardless of the agent's strategy. Hence, if we remove from the tree those paths that are consistent with mechanism
has zero probability regardless of the agent's strategy. Hence, if we remove from the tree those paths that are consistent with mechanism 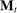 and
and 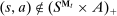 , this does not change the set of equilibrium outcomes. Hereafter, these histories are removed from the tree.
, this does not change the set of equilibrium outcomes. Hereafter, these histories are removed from the tree.
Principal Pure Strategies
Lemma D.1 in Online Appendix D.2 shows that without loss of generality, we can focus on PBE assessments of 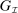 in which the principal plays a pure strategy. So in what follows, we focus on PBE assessments that satisfy Lemma D.1.
in which the principal plays a pure strategy. So in what follows, we focus on PBE assessments that satisfy Lemma D.1.
Appendix B: Proof of Theorem 1
The proof of Theorem 1 follows from the proof of Propositions B.1–B.2 below.
Proposition B.1.For every PBE assessment 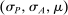 of
of 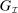 , an outcome-equivalent PBE assessment
, an outcome-equivalent PBE assessment 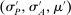 exists such that the agent's strategy only depends on her type and the public history.
exists such that the agent's strategy only depends on her type and the public history.
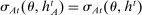 whenever
whenever 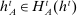 . Similarly, we write the belief system at history
. Similarly, we write the belief system at history 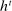 as inducing distributions over Θ and not over
as inducing distributions over Θ and not over 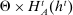 .
.
Proposition B.2.Fix 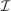 and let
and let 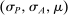 be a PBE assessment of
be a PBE assessment of 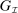 that satisfies Proposition B.1. Then an outcome-equivalent canonical PBE assessment
that satisfies Proposition B.1. Then an outcome-equivalent canonical PBE assessment 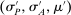 of
of 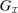 exists.
exists.
Proof of Proposition B.2.Let 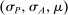 be as in the statement of Proposition B.2. Let
be as in the statement of Proposition B.2. Let 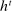 be a public history and let
be a public history and let 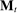 denote the mechanism that the principal offers at
denote the mechanism that the principal offers at 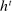 under
under 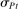 . Let
. Let 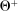 denote the support of the principal's beliefs at
denote the support of the principal's beliefs at 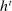 ,
, 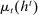 .
.
For types in 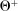 , use equation (3) to define an auxiliary mapping
, use equation (3) to define an auxiliary mapping 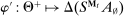 , as follows:
, as follows:
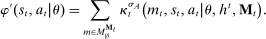 (B.6)
(B.6)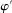 corresponds to the direct version of
corresponds to the direct version of 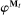 for
for 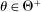 ; we use it in what follows to construct an alternative mechanism for the principal,
; we use it in what follows to construct an alternative mechanism for the principal, 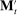 , that uses message sets
, that uses message sets 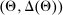 .
.Omitting the dependence on (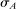 , μ), recall that
, μ), recall that 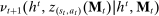 denotes the probability of history
denotes the probability of history 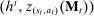 under the equilibrium strategy when the principal offers
under the equilibrium strategy when the principal offers  at
at 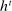 (equation (4)). Equation (4) implies we can write
(equation (4)). Equation (4) implies we can write 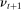 using
using 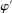 as follows:
as follows:
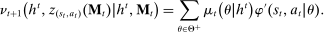
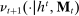 on
on 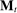 .
.The first step is to show that the distribution over continuation histories 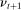 can be seen as inducing a distribution over posterior beliefs, allocations, and realizations of a public randomization device. To see this, for
can be seen as inducing a distribution over posterior beliefs, allocations, and realizations of a public randomization device. To see this, for 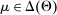 , let
, let 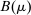 denote the set
denote the set
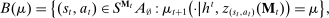
 denote the projection of
denote the projection of  onto
onto 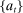 . In what follows, for any subset
. In what follows, for any subset 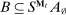 , we abuse notation and write
, we abuse notation and write 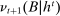 instead of
instead of 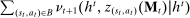 .
.Let 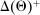 denote the smallest subset of
denote the smallest subset of 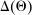 such that
such that 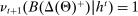 . That is,
. That is,  is the set of principal posterior beliefs that are pinned down via Bayes' rule. We can write the principal's payoff at history
is the set of principal posterior beliefs that are pinned down via Bayes' rule. We can write the principal's payoff at history 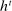 when he offers
when he offers 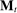 as follows:
as follows:
 (B.7)
(B.7)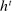 . The first is standard: we draw history (
. The first is standard: we draw history (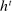 ,
,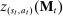 ) using the distribution induced by the equilibrium strategy,
) using the distribution induced by the equilibrium strategy, 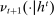 . The second is the one that delivers the canonical mechanisms: we first draw a belief μ using the distribution over continuation equilibrium beliefs induced by
. The second is the one that delivers the canonical mechanisms: we first draw a belief μ using the distribution over continuation equilibrium beliefs induced by 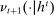 and then we draw an allocation
and then we draw an allocation 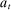 , conditional on the continuation equilibrium belief coinciding with μ. The principal's posterior belief μ and the allocation
, conditional on the continuation equilibrium belief coinciding with μ. The principal's posterior belief μ and the allocation 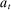 may still not be enough to pin down the continuation history, so we draw the output message
may still not be enough to pin down the continuation history, so we draw the output message 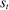 conditional on
conditional on 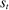 being consistent with
being consistent with 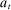 and μ.
and μ.The second step is to show that, conditional on the induced posterior belief μ, (i) the probability that the allocation is 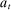 is independent of θ, and (ii) the probability that the output message is
is independent of θ, and (ii) the probability that the output message is 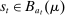 is independent of θ. To see this, note that for any belief
is independent of θ. To see this, note that for any belief 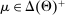 , for any
, for any 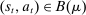 and for any θ such that
and for any θ such that 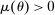 , we have28
, we have28
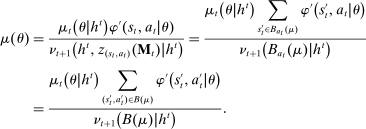 (B.8)
(B.8)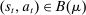 , (ii) he learns that
, (ii) he learns that 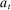 is the realized allocation, that is, he learns that
is the realized allocation, that is, he learns that 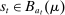 , or (iii) he learns that the output message and the allocation belong to
, or (iii) he learns that the output message and the allocation belong to 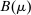 . Thus, for all θ in the support of μ, we have
. Thus, for all θ in the support of μ, we have
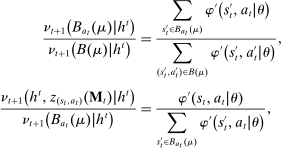 (B.9)
(B.9)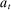 conditional on the induced belief being μ is independent of θ, and (ii) the probability that the output message is
conditional on the induced belief being μ is independent of θ, and (ii) the probability that the output message is 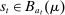 conditional on the allocation being
conditional on the allocation being 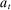 and the induced belief μ is independent of θ. It follows that for all
and the induced belief μ is independent of θ. It follows that for all 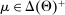 ,
, 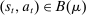 and for all θ in the support of μ, we can split the auxiliary mapping as follows:
and for all θ in the support of μ, we can split the auxiliary mapping as follows:
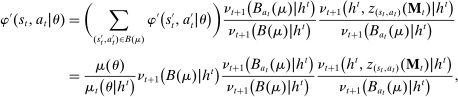
Thus, the agent's payoff at history  , when the principal offers mechanism
, when the principal offers mechanism  and her type is
and her type is  , can be written as follows:
, can be written as follows:
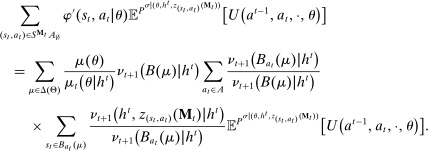 (B.10)
(B.10)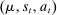 conditional on θ, whereas the principal's payoff is expressed in terms of the unconditional distribution. For this reason, the agent's payoff features the term
conditional on θ, whereas the principal's payoff is expressed in terms of the unconditional distribution. For this reason, the agent's payoff features the term 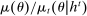 .
.We now define the canonical mechanism 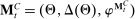 : First, for
: First, for 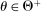 ,
,
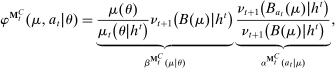
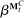 ,
, 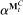 is well-defined because of the independence properties highlighted after equation (11). Second, if
is well-defined because of the independence properties highlighted after equation (11). Second, if 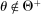 , let
, let 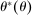 denote the solution to
denote the solution to
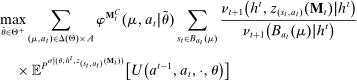 (B.11)
(B.11)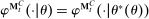 . Change the principal's strategy at
. Change the principal's strategy at 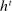 so that he offers
so that he offers 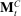 instead of
instead of 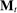 . Change the agent's strategy so that, conditional on participating, the agent truthfully reports her type,
. Change the agent's strategy so that, conditional on participating, the agent truthfully reports her type, 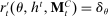 .
.For 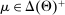 and allocation
and allocation 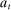 , enumerate the output messages in
, enumerate the output messages in 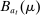 as
as  . (We omit the dependence of K on μ and
. (We omit the dependence of K on μ and 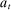 to simplify notation.) Define the sequence
to simplify notation.) Define the sequence 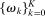 such that
such that 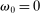 ,
, 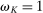 and for
and for  ,
,
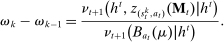
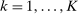 and
and 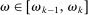 , let
, let 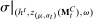 coincide with
coincide with 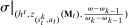 . Note these strategies imply the principal and the agent's payoffs remain the same as in the original equilibrium whenever
. Note these strategies imply the principal and the agent's payoffs remain the same as in the original equilibrium whenever 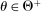 . Furthermore, modify the continuation strategies so that
. Furthermore, modify the continuation strategies so that 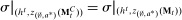 .
.For θ in 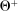 , set
, set 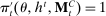 . For types not in
. For types not in 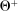 , use equation (13) to compute
, use equation (13) to compute 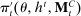 accordingly. Conditional on participating, the agent can guarantee at most the payoff from imitating the strategy followed by
accordingly. Conditional on participating, the agent can guarantee at most the payoff from imitating the strategy followed by 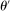 for some
for some 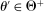 . This strategy was already feasible in the original PBE, so the agent has no new deviations. It follows that the new assessment is a PBE of the auxiliary game. Q.E.D.
. This strategy was already feasible in the original PBE, so the agent has no new deviations. It follows that the new assessment is a PBE of the auxiliary game. Q.E.D.
B.1 Proof of Proposition 1
Fix 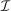 and let
and let 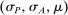 denote a canonical PBE of
denote a canonical PBE of 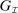 , like the one constructed in Proposition B.2. Fix a history
, like the one constructed in Proposition B.2. Fix a history 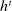 and let
and let 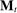 denote the mechanism the principal offers at
denote the mechanism the principal offers at 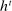 under
under 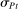 . Let
. Let  denote the support of
denote the support of 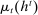 . To simplify notation, we use the shorthand notation
. To simplify notation, we use the shorthand notation 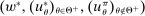 to denote the principal and the agent's payoff vector at
to denote the principal and the agent's payoff vector at 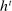 when the agent participates in
when the agent participates in 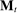 ,
, 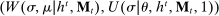 . Theorem 1 implies that for the principal and for
. Theorem 1 implies that for the principal and for 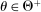 ,
,  and
and  are their equilibrium payoffs at
are their equilibrium payoffs at 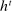 .
.
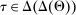 exists such that for all measurable subsets
exists such that for all measurable subsets 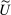 of
of 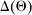 and for all
and for all 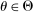 ,
,
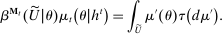
 is as in the proof of Proposition B.2 (recall equation (13)). Finally, note that the payoff of the agent of type θ from reporting
is as in the proof of Proposition B.2 (recall equation (13)). Finally, note that the payoff of the agent of type θ from reporting 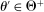 at history
at history 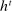 when the mechanism is
when the mechanism is 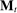 , and then following her equilibrium strategy is given by
, and then following her equilibrium strategy is given by
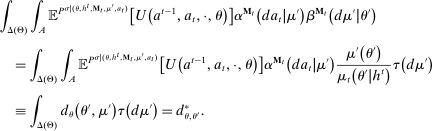
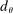 denotes that these are the payoffs that θ obtains from deviating to
denotes that these are the payoffs that θ obtains from deviating to 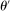 . The payoff
. The payoff 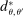 can be similarly defined for
can be similarly defined for 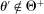 using
using 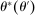 as in the definition of
as in the definition of 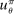 .
. . Define
. Define 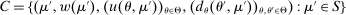 . Because Θ is finite, Rubin and Wesler (1958) implies that
. Because Θ is finite, Rubin and Wesler (1958) implies that 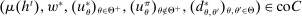 . Letting
. Letting 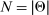 , Caratheodory's theorem implies
, Caratheodory's theorem implies 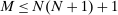 exists such that
exists such that 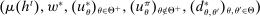 can be written as the convex combination of M elements of C. That is,
can be written as the convex combination of M elements of C. That is, 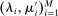 exist such that
exist such that 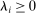 ,
, 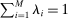 , and
, and
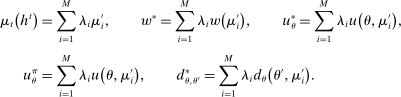
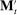 : For types in
: For types in 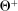 , let
, let 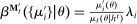 , and otherwise,
, and otherwise, 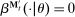 . For types not in
. For types not in 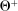 , let
, let 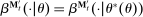 . Furthermore,
. Furthermore, 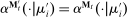 . Modify the PBE assessment so that the principal offers
. Modify the PBE assessment so that the principal offers 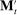 at
at 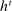 . Furthermore, modify the continuation strategies so that
. Furthermore, modify the continuation strategies so that 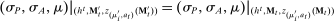 and
and 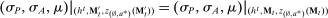 . Clearly, mechanism
. Clearly, mechanism  delivers the same payoff to the principal and the agent conditional on the agent participating and truthfully reporting her type. We now show it is optimal for the agent to truthfully report her type. Suppose the agent of type θ reports instead that her type is
delivers the same payoff to the principal and the agent conditional on the agent participating and truthfully reporting her type. We now show it is optimal for the agent to truthfully report her type. Suppose the agent of type θ reports instead that her type is 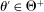 (the case
(the case 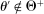 is similar). In this case, she obtains
is similar). In this case, she obtains
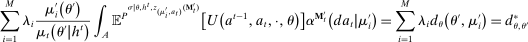
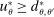 , then truth telling is still optimal. Thus, because the payoffs from participating and not participating are the same as in the original assessment for all types,
, then truth telling is still optimal. Thus, because the payoffs from participating and not participating are the same as in the original assessment for all types, 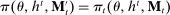 is a best response.
is a best response.Appendix C: Proofs of Section 4.3
Envelope Theorem
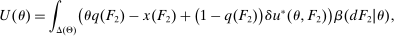 (C.12)
(C.12)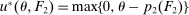 . Equation (15) defines the buyer's payoff when her type is θ and she deviates by first reporting
. Equation (15) defines the buyer's payoff when her type is θ and she deviates by first reporting  and then following
and then following 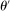 's strategy in
's strategy in  :
:
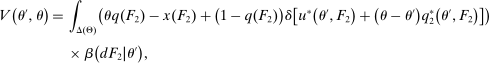 (C.13)
(C.13)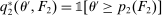 . The optimality of truth telling implies
. The optimality of truth telling implies 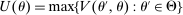 . We now establish that the family
. We now establish that the family 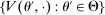 is equi-Lipschitz continuous. To see this, let θ,
is equi-Lipschitz continuous. To see this, let θ, 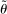 such that
such that 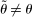 and consider
and consider
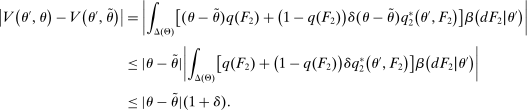
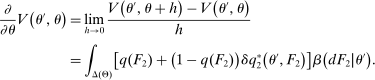
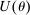 is then Lipschitz continuous because it is the maximum over a family of equi-Lipschitz continuous functions. Thus, it is differentiable almost everywhere. Theorem 1 in Milgrom and Segal (2002) implies that at any point of differentiability of
is then Lipschitz continuous because it is the maximum over a family of equi-Lipschitz continuous functions. Thus, it is differentiable almost everywhere. Theorem 1 in Milgrom and Segal (2002) implies that at any point of differentiability of 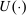 ,
,
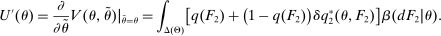
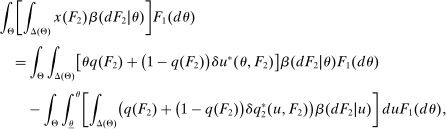 (C.14)
(C.14) . Recall from (OPT) that the seller's revenue is given by
. Recall from (OPT) that the seller's revenue is given by 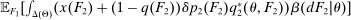 . Replacing the transfers (equation (16)) and integrating by parts, we obtain
. Replacing the transfers (equation (16)) and integrating by parts, we obtain
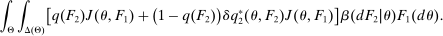 (C.15)
(C.15) defined as
defined as 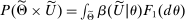 , for all measurable subsets
, for all measurable subsets  ,
, 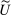 of Θ and
of Θ and 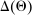 . Let
. Let 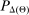 denote its marginal on
denote its marginal on 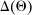 , Pollard (2002, Appendix F, Theorem 6) implies equation (17) equals
, Pollard (2002, Appendix F, Theorem 6) implies equation (17) equals
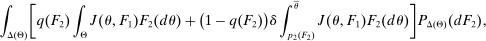
Monotonicity
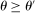 :
:
 (C.16)
(C.16)
Proof of Proposition 2.We first establish properties that the optimal posted-price mechanism satisfies. Let  denote the distribution of θ conditional on
denote the distribution of θ conditional on 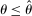 . Since
. Since 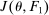 is strictly increasing, it follows that
is strictly increasing, it follows that 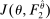 is also strictly increasing. Furthermore, since
is also strictly increasing. Furthermore, since 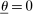 ,
, 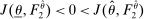 and there exists a unique
and there exists a unique 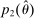 such that
such that 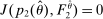 . It follows that
. It follows that 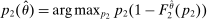 . The theorem of the maximum implies that
. The theorem of the maximum implies that 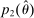 is continuous in
is continuous in  . Thus, the optimal posted-price mechanism solves
. Thus, the optimal posted-price mechanism solves
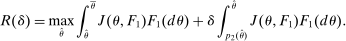 (C.17)
(C.17)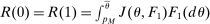 , where
, where  is the monopoly price, that is,
is the monopoly price, that is, 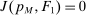 . For each
. For each 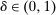 , let
, let 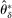 denote a solution to the problem in equation (19) and define
denote a solution to the problem in equation (19) and define
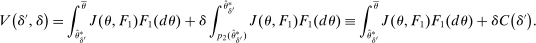
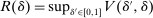 . Furthermore,
. Furthermore, 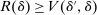 and
and 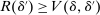 imply that if
imply that if  , then
, then 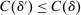 . Note that
. Note that 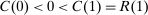 since the unique solution at
since the unique solution at 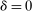 is to set
is to set 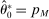 . Steps similar to those leading to the envelope representation of the buyer's payoffs imply that (i)
. Steps similar to those leading to the envelope representation of the buyer's payoffs imply that (i) 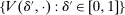 is equi-Lipschitz continuous, (ii) for all
is equi-Lipschitz continuous, (ii) for all 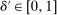 ,
, 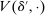 is differentiable on
is differentiable on 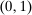 with derivative equal to
with derivative equal to 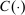 , and (iii) R is Lipschitz continuous and at any point of differentiability,
, and (iii) R is Lipschitz continuous and at any point of differentiability, 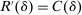 .
.We now show that 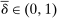 exists so that
exists so that 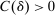 for
for 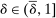 . Toward a contradiction, suppose that
. Toward a contradiction, suppose that 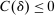 for all
for all 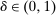 . Then R is decreasing on
. Then R is decreasing on  and because
and because 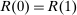 it follows that
it follows that 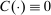 almost everywhere. Otherwise, a set
almost everywhere. Otherwise, a set 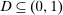 of nonzero Lebesgue measure exists such that
of nonzero Lebesgue measure exists such that 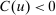 for
for  . Then
. Then
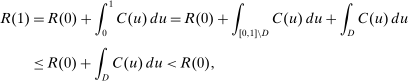
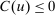 on
on  and the second by the definition of D. It follows that
and the second by the definition of D. It follows that  on
on  , and hence
, and hence 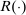 is constant and equal to the commitment payoff for all
is constant and equal to the commitment payoff for all 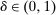 , a contradiction. Thus, a subset of
, a contradiction. Thus, a subset of 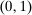 exists on which C is strictly positive and because C is increasing,
exists on which C is strictly positive and because C is increasing, 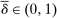 exists so that
exists so that 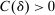 for
for 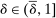 .
.Second, we use the above properties to construct a deviation for the seller. Define 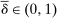 as above and let
as above and let 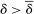 . We show
. We show 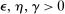 exist such that the seller can deviate to the following mechanism. Let
exist such that the seller can deviate to the following mechanism. Let 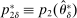 and define three posterior beliefs:
and define three posterior beliefs:
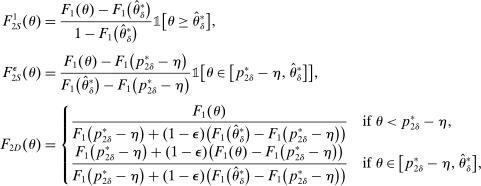
 and
and  . Furthermore, let
. Furthermore, let 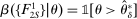 , and let
, and let
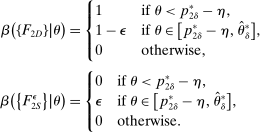
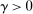 , define payments as follows:
, define payments as follows:
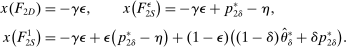
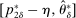 , and leaves the probability of trade for the remaining types unchanged; furthermore, he pays the buyer γϵ, regardless of her type. The value of η is chosen so that
, and leaves the probability of trade for the remaining types unchanged; furthermore, he pays the buyer γϵ, regardless of her type. The value of η is chosen so that 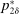 remains optimal in period 2.
remains optimal in period 2.In what follows, we first argue that for any agent-extensive form that is feasible given the above mechanism in period 1 and in any agent-assessment of that extensive form, the buyer must accept the above mechanism with probability 1. That, conditional on participating, truth telling is optimal is immediate. We then show that given ϵ we can always find η so that 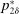 remains optimal in period 2. Finally, we show that for ϵ, γ small, the seller prefers the mechanism defined above to the optimal posted-price mechanism.
remains optimal in period 2. Finally, we show that for ϵ, γ small, the seller prefers the mechanism defined above to the optimal posted-price mechanism.
The buyer participates with probability 1. Note first that buyer types in 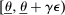 must accept the mechanism: the best price they can obtain in period 2 is
must accept the mechanism: the best price they can obtain in period 2 is 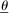 , whereas they obtain at least γϵ by participating in the mechanism offered by the seller. Since
, whereas they obtain at least γϵ by participating in the mechanism offered by the seller. Since 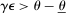 for all such types, they must accept the mechanism. It then follows that, conditional on rejecting the mechanism, the price is at least
for all such types, they must accept the mechanism. It then follows that, conditional on rejecting the mechanism, the price is at least 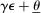 in period 2, so that it must be the case that types in
in period 2, so that it must be the case that types in 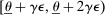 must also accept the mechanism. Proceeding inductively, it follows that the buyer accepts the mechanism with probability 1. Thus, Bayes' rule does not pin down beliefs conditional on nonparticipation, so that we can specify them arbitrarily: In particular, we can specify them so that the seller assigns probability 1 to
must also accept the mechanism. Proceeding inductively, it follows that the buyer accepts the mechanism with probability 1. Thus, Bayes' rule does not pin down beliefs conditional on nonparticipation, so that we can specify them arbitrarily: In particular, we can specify them so that the seller assigns probability 1 to  .
.
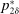 remains optimal in period 2. The virtual values under
remains optimal in period 2. The virtual values under 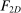 are given by
are given by
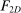 (i) are piecewise increasing in θ on
(i) are piecewise increasing in θ on 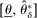 , (ii) are (weakly) negative on
, (ii) are (weakly) negative on 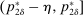 , and (iii) they jump down at
, and (iii) they jump down at 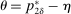 , whenever
, whenever 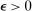 . Let
. Let 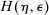 denote the limit from below of
denote the limit from below of 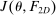 as
as 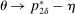 . That is,
. That is,
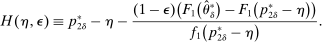
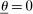 , it is immediate to show that for each
, it is immediate to show that for each 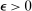 ,
, 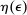 exists such that
exists such that 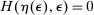 . Thus, for
. Thus, for 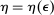 ,
, 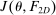 is (weakly) negative for types θ below
is (weakly) negative for types θ below 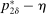 , and hence
, and hence 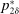 remains optimal. In what follows, it is important to note
remains optimal. In what follows, it is important to note 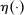 is increasing in ϵ and the definition of
is increasing in ϵ and the definition of 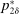 implies
implies 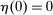 .
.The seller has a deviation. We now verify that for small enough ϵ, γ the seller prefers the above mechanism to the optimal posted price mechanism. Indeed, the difference in payoffs between the new mechanism and the optimal posted-price mechanism is as follows:
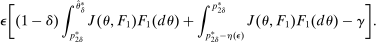
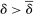 , small enough ϵ, γ exist such that the seller has a deviation. Q.E.D.
, small enough ϵ, γ exist such that the seller has a deviation. Q.E.D.



