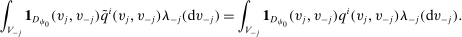Equivalence of Stochastic and Deterministic Mechanisms
Abstract
We consider a general social choice environment that has multiple agents, a finite set of alternatives, independent types, and atomless type distribution. We show that for any Bayesian incentive compatible mechanism, there exists an equivalent deterministic mechanism that (1) is Bayesian incentive compatible; (2) delivers the same interim expected allocation probabilities and the same interim expected utilities for all agents; and (3) delivers the same ex ante expected social surplus. This result holds in settings with a rich class of utility functions, multidimensional types, interdependent valuations, and in settings without monetary transfers. To prove our result, we develop a novel methodology of mutual purification, and establish its link with the mechanism design literature.
1 Introduction
Myerson (1981) provided the framework that has become the paradigm for the study of optimal auction design. Under a regularity condition, the optimal auction allocates the object to the bidder with the highest virtual value, provided that this virtual value is above the seller's opportunity cost. In other words, the optimal auction in Myerson's setting is deterministic.1
A natural conjecture is that the optimality of deterministic mechanisms generalizes beyond Myerson's setting. McAfee and McMillan (1988) claimed that under a general regularity condition on consumers' demand, stochastic delivery is not optimal for a multi-product monopolist. However, this result has been proven to be incorrect in settings with a single agent. Several papers have shown that a multi-product monopolist may find it beneficial to include lotteries as part of the selling mechanism; see, for example, Thanassoulis (2004), Manelli and Vincent (2006, 2007), Pycia (2006), Pavlov (2011), and more recently, Hart and Reny (2015) and Rochet and Thanassoulis (2017).2 In this paper, we prove a mechanism equivalence result that implies the optimality of deterministic mechanisms in remarkably general environments with multiple agents.
We consider a general social choice environment that has multiple agents, a finite set of alternatives, independent types, and atomless type distribution. We show that for any Bayesian incentive compatible mechanism, there exists an equivalent deterministic mechanism that (1) is Bayesian incentive compatible; (2) delivers the same interim expected allocation probabilities and the same interim expected utilities for all agents; and (3) delivers the same ex ante expected social surplus. In addition to the standard social choice environments with linear utilities and one-dimensional, private types, our result holds in settings with a rich class of utility functions, multidimensional types, interdependent valuations, and in settings without monetary transfers.
Our result implies that any mechanism, including the optimal mechanism (whether in terms of revenue or efficiency), can be implemented using a deterministic mechanism and nothing can be gained from designing more intricate mechanisms with possibly more complex randomization in the allocation rule. As pointed out in Hart and Reny (2015, p. 912), Aumann commented that it is surprising that randomization cannot increase revenue when there is only one good. Indeed, aforementioned papers in the screening literature establish that randomization helps when there are multiple goods. Nevertheless, we show that in a general social choice environment with multiple agents, the revenue maximizing mechanism can always be deterministically implemented. This is in sharp contrast with the results in the screening literature.
Our result has important implications beyond the revenue contrast. The mechanism design literature essentially builds on the assumption that a mechanism designer can credibly commit to any outcome of a mechanism. This requirement implies that any outcome of the mechanism must be verifiable before it can be employed. In this vein, a stochastic mechanism demands not only that a randomization device be available to the mechanism designer, but also that the outcome of the randomization device be objectively verified. As noted in Laffont and Martimort (2002, p. 67),
Our result implies that every mechanism can in fact be deterministically implemented, and thereby irons out the conceptual difficulties associated with stochastic mechanisms.4Ensuring this verifiability is a more difficult problem than ensuring that a deterministic mechanism is enforced, because any deviation away from a given randomization can only be statistically detected once a sufficient number of realizations of the contracts have been observed. … The enforcement of such stochastic mechanisms in a bilateral one-shot relationship is thus particularly problematic. This has led scholars to give up those random mechanisms or, at least, to focus on economic settings where they are not optimal.3
Along the lines of implementation, our paper is related to the literature of reduced form implementation (see, e.g., Border (1991) for the case of the single-unit auction and Cai, Daskalakis, and Weinberg (2018) for the case of multi-item auction). In many applications of mechanism design, it is convenient to work with interim expected allocation probabilities. The reduced form implementation literature asks what interim expected allocation probabilities can be implemented. Our result implies that whatever interim expected allocation probabilities that can be implemented can actually be implemented in a deterministic manner. As such, even if the mechanism designer does not have access to randomization devices or cannot commit to the outcomes induced by randomization devices, we can rest assured working with interim expected allocation probabilities.
This paper joins the strand of literature that studies mechanism equivalence. Though motivations vary, these results show that it is without loss of generality to consider the various subclasses of mechanisms. As in the case of dominant-strategy mechanisms (see Manelli and Vincent (2010) and Gershkov, Goeree, Kushnir, Moldovanu, and Shi (2013)) and symmetric auctions (see Deb and Pai (2017)), our findings imply that the requirement of deterministic mechanisms is not restrictive in itself.5
To prove the existence of an equivalent deterministic mechanism, we develop a new methodology of mutual purification and establish its link with the literature of mechanism design.6 The notion of mutual purification is both conceptually and technically different from the usual purification principle in the literature related to Bayesian games. We clarify these two different notions of purification in the next three paragraphs.
It follows from the general purification principle in Dvoretzky, Wald, and Wolfowitz (1950) that any behavioral-strategy Nash equilibrium in a finite-action Bayesian game with independent types and atomless type distribution corresponds to some pure-strategy Bayesian Nash equilibrium with the same payoff.7 In particular, independent types and atomless distributions allow the agents to replace their behavioral strategies by some equivalent pure strategies one-by-one.8 The point is that under the independent information assumption, any agent whose type has an atomless distribution could purify her own behavioral strategy regardless of whether the other agents' types have atomless distributions. Example 6 in the Supplemental Material (Chen et al. (2019)) illustrates this idea of self purification. Given a behavioral-strategy Nash equilibrium in a two-agent Bayesian game with independent information, there is an equivalent pure strategy for the agent whose type has an atomless distribution, while the other agent with an atom in her type space could not purify her behavioral strategy.
The general purification principle in Dvoretzky, Wald, and Wolfowitz (1950) is only applicable in the unconditional (ex ante) setting, and thus does not apply to this paper, as the notion of mechanism equivalence naturally requires us to study purification in the conditional (interim) setting. The purification result of this paper is based on the atomless distributions of types of the other agents. Example 7 in the Supplemental Material (Chen et al. (2019)) partially illustrates this idea of mutual purification. For a given randomized mechanism in a two-agent setting with independent information, the agent with an atom in her type space can achieve the same interim payoff by some deterministic mechanism, while there does not exist such a deterministic mechanism for the other agent whose type has an atomless distribution. In other words, our result becomes possible because each agent relies on the atomless distributions of types of the other agents rather than her own. This also explains why a similar result does not hold in the one-agent setting since there are no atomless distributions of types of the other agents for such a single agent to purify the relevant randomized mechanism. In addition, we emphasize that in the settings with multiple agents, the notion of mutual purification requires not only that each agent obtain the same interim payoff under some deterministic mechanism, but also that a single deterministic mechanism deliver the same interim payoffs for all the agents simultaneously.
From a methodological point of view, the general purification principle in Dvoretzky, Wald, and Wolfowitz (1950) is simply a version of the classical Lyapunov theorem about the convex range of an atomless finite-dimensional vector measure. Our purification result is technically different. First, the problem we consider is infinite-dimensional because we require the same interim expected allocation probabilities/utilities for the equivalent mechanism at the interim level with a continuum of types. Note that Lyapunov's theorem fails in an infinite-dimensional setting.9 Second, it is clearly impossible to obtain a purified deterministic mechanism that delivers the same interim expected allocation probabilities as the original stochastic mechanism, conditioned on the joint types of all the agents.10 However, our result on mutual purification shows that such an equivalence becomes possible when the conditioning operation is imposed on the individual types of every agent simultaneously, although the combination of the individual types of every agent is the joint types of all the agents. To the best of our knowledge, this paper is the first to consider the purification of a randomized decision rule that retains the same expected payoffs conditioned on the individual types of every agent in an economic model.
The assumption of atomless type distribution facilitates the development of the novel methodology of mutual purification, which lies at the core of our arguments. Thus, our paper also contributes to the Bayesian mechanism design literature in relying on specific aspects of agents' private information. These information aspects are often crucial in pinning down different properties of the optimal mechanism; see, for example, Myerson (1981) and Crémer and McLean (1988).
The rest of the paper is organized as follows. Section 2 introduces the model. Section 3 presents the mechanism equivalence result. Section 4 discusses the assumptions behind our equivalence result, the structures of the equivalence deterministic mechanisms, and the recent literature on the benefit of randomness in settings with multiple agents. Section 5 concludes. The appendices contain proofs and other technical results omitted from the main body of the paper, and examples delineating the limits of our mechanism equivalence result.
2 Model
2.1 Notation
We consider an environment with a finite set 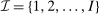 of risk-neutral agents (
of risk-neutral agents (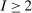 ) and a finite set
) and a finite set 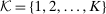 of social alternatives. The set of possible types
of social alternatives. The set of possible types 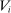 of agent i is a closed subset of finite-dimensional Euclidean space
of agent i is a closed subset of finite-dimensional Euclidean space 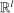 with generic element
with generic element 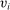 . The set of possible type profiles is
. The set of possible type profiles is 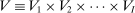 with generic element
with generic element 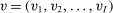 . We write
. We write 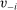 for a type profile of agent i's opponents; that is,
for a type profile of agent i's opponents; that is, 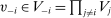 . The type profile v is distributed according to a probability distribution λ. For each agent
. The type profile v is distributed according to a probability distribution λ. For each agent 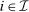 ,
, 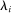 is the marginal distribution of λ on
is the marginal distribution of λ on 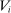 and is assumed to be atomless. Types are assumed to be independent. If
and is assumed to be atomless. Types are assumed to be independent. If 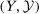 is a measurable space, then
is a measurable space, then 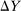 is the set of all probability measures on
is the set of all probability measures on 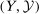 . If Y is a metric space, then we treat it as a measurable space with its Borel σ-algebra.
. If Y is a metric space, then we treat it as a measurable space with its Borel σ-algebra.
2.2 Mechanism
We consider direct mechanisms characterized by 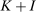 functions,
functions, 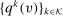 and
and 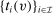 , where v is the profile of reports,
, where v is the profile of reports, 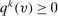 is the probability that alternative k is implemented satisfying
is the probability that alternative k is implemented satisfying 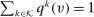 , and
, and 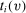 is the monetary transfer that agent i makes to the designer. Thus, we shall denote a mechanism by
is the monetary transfer that agent i makes to the designer. Thus, we shall denote a mechanism by 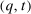 , where
, where 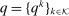 and
and 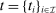 . By the revelation principle, it is without loss of generality to restrict attention to direct mechanisms.
. By the revelation principle, it is without loss of generality to restrict attention to direct mechanisms.
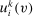 for agent i's gross utility in alternative k under the type profile v. Given a mechanism
for agent i's gross utility in alternative k under the type profile v. Given a mechanism 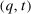 , we write
, we write
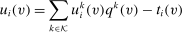
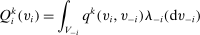
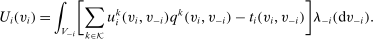
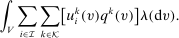
Definition 1.A mechanism is Bayesian incentive compatible (BIC) if, for all 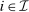 and
and 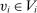 ,
,
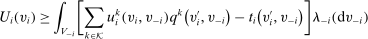
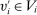 .
.A mechanism satisfies Bayesian individual rationality (BIR) if, for all 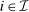 and
and 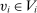 ,
,
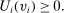
Definition 2.A mechanism 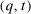 is deterministic at
is deterministic at 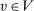 if
if 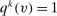 for some
for some 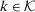 . A mechanism
. A mechanism 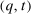 is deterministic if the mechanism is deterministic at all
is deterministic if the mechanism is deterministic at all 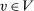 .
.
2.3 Mechanism Equivalence
We employ the following notion of mechanism equivalence in this paper.
Definition 3.Two mechanisms 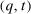 and
and 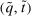 are equivalent if and only if they deliver the same interim expected allocation probabilities and the same interim expected utilities for all agents, and the same ex ante expected social surplus.
are equivalent if and only if they deliver the same interim expected allocation probabilities and the same interim expected utilities for all agents, and the same ex ante expected social surplus.
Remark 1.Our equivalence notion is stronger than the prevailing mechanism equivalence notions used in the literature. For example, Manelli and Vincent (2010) and Gershkov et al. (2013) defined two mechanisms to be equivalent if they deliver the same interim expected utilities for all agents and the same ex ante expected social surplus.11
To illustrate our notion of mechanism equivalence, it is best to consider an example. The example is deliberately kept simple. Our result is far more general and the proof is much more complex.
Example 1.Consider a single-unit auction with two bidders. Suppose that bidders' valuations for the object 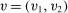 are uniformly distributed on the square
are uniformly distributed on the square 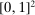 . Consider the following stochastic allocation rule
. Consider the following stochastic allocation rule 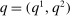 with
with
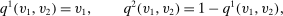
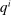 is the probability of bidder i getting the object for
is the probability of bidder i getting the object for 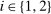 . In the construction of the equivalent deterministic mechanism below, the transfers are kept unchanged. Thus, for simplicity, we do not specify the transfer scheme t in the mechanism
. In the construction of the equivalent deterministic mechanism below, the transfers are kept unchanged. Thus, for simplicity, we do not specify the transfer scheme t in the mechanism 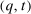 . The readers may think of t as an arbitrary transfer scheme such that
. The readers may think of t as an arbitrary transfer scheme such that 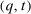 is BIC.
is BIC.The interim expected probability of bidder 1 getting the object is
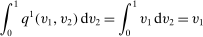
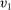 , and the interim expected probability of bidder 2 getting the object is
, and the interim expected probability of bidder 2 getting the object is
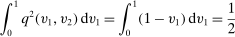
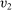 .
.It is easy to verify that the following deterministic mechanism 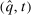 is equivalent in terms of interim expected allocation probabilities for all agents (Figure 1 provides a graphical illustration of the mechanism
is equivalent in terms of interim expected allocation probabilities for all agents (Figure 1 provides a graphical illustration of the mechanism  ). Since the transfers are kept unchanged, the deterministic mechanism
). Since the transfers are kept unchanged, the deterministic mechanism  is also equivalent in terms of interim expected utilities for all agents and ex ante expected social surplus:
is also equivalent in terms of interim expected utilities for all agents and ex ante expected social surplus:
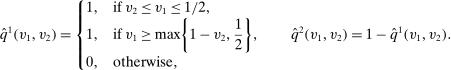
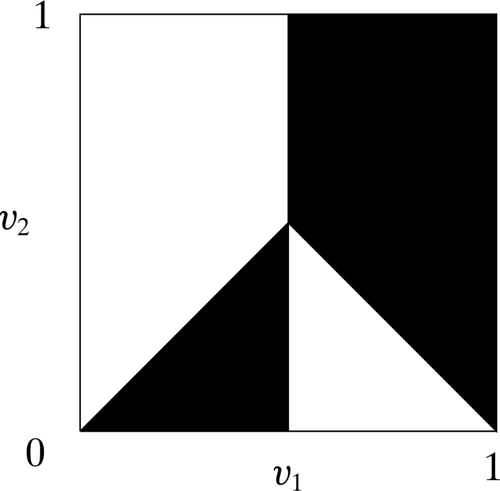
Bidder 1 is allocated the object in the shaded region, and bidder 2 is allocated the object in the unshaded region.
In Section 3, we show that for whatever stochastic mechanism that the designer may choose to use, however complicated, there always exists an equivalent mechanism that is deterministic.
3 Equivalence Result
This section presents our mechanism equivalence result. To make the logic of our arguments and the roles played by the various assumptions clear, we break down our analysis into two steps. In the first step, we show that for any allocation rule, there exists a deterministic allocation rule that delivers the same interim expected allocation probabilities for all agents. This step only requires the assumption of atomless distribution. While the assumption of independent types is not needed, for simplicity of exposition, we present this result in settings with independent types (see Remark 2 below for a detailed discussion). In the second step, under additional assumptions of independent types and separable payoffs, we show that for any BIC and BIR mechanism, there exists a deterministic mechanism that is BIC and BIR, delivers the same interim expected allocation probabilities and the same interim expected utilities for all agents, and delivers the same ex ante expected social surplus.
Interim Expected Allocation Probabilities
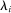 be atomless for all
be atomless for all 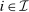 . Let
. Let
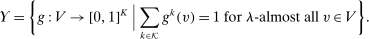
Theorem 1.For any allocation rule q, there exists a deterministic allocation rule 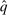 such that q and
such that q and 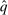 induce the same interim expected allocation probabilities for all agents. That is, for all
induce the same interim expected allocation probabilities for all agents. That is, for all 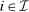 and
and 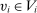 ,
,
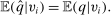 (1)
(1)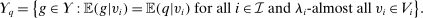
 is nonempty, convex, and weakly compact. Therefore, the set
is nonempty, convex, and weakly compact. Therefore, the set 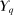 admits extreme points. Step (2) proceeds to show that all extreme points of
admits extreme points. Step (2) proceeds to show that all extreme points of 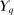 are deterministic at λ-almost all
are deterministic at λ-almost all 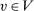 .14 Indeed, if
.14 Indeed, if 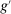 is not deterministic at λ-almost all
is not deterministic at λ-almost all 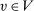 , then there exist distinct
, then there exist distinct 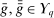 such that
such that 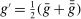 . Thus,
. Thus, 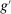 is not an extreme point of
is not an extreme point of 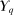 . The existence of
. The existence of 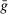 and
and 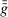 relies on the assumption that
relies on the assumption that 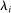 is atomless for all
is atomless for all 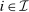 . Step (1) and Step (2) together imply that there exists
. Step (1) and Step (2) together imply that there exists 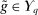 that is deterministic at λ-almost all
that is deterministic at λ-almost all 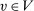 . Note that
. Note that 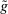 is not necessarily deterministic at all
is not necessarily deterministic at all 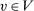 . Furthermore, such
. Furthermore, such 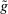 induces the same interim expected allocation probabilities for all
induces the same interim expected allocation probabilities for all 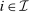 and λ-almost all
and λ-almost all 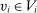 , but not for all
, but not for all 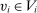 . Step (3) then constructs a deterministic allocation rule
. Step (3) then constructs a deterministic allocation rule 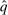 that induces the same interim expected allocation probabilities for all
that induces the same interim expected allocation probabilities for all 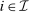 and
and 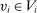 , by modifying
, by modifying 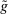 on sets of measure zero. The last step is (conceptually) straightforward.
on sets of measure zero. The last step is (conceptually) straightforward.Theorem 1 is not enough to show the mechanism equivalence result, as it only concerns the equivalence in terms of interim expected allocation probabilities for all agents. We now prove a generalization of Theorem 1, which is then invoked in Theorem 3 to prove the equivalence in terms of interim expected utilities for all agents.
Theorem 2.Let 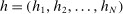 be an integrable function from V to
be an integrable function from V to 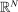 . For any allocation rule q, there exists a deterministic allocation rule
. For any allocation rule q, there exists a deterministic allocation rule  such that, for all
such that, for all 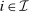 and
and 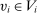 ,
,
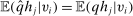 (2)
(2)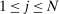 .
.
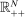 .15 Theorem 2 can be proved by applying similar arguments as in the proof of Theorem 1 to the following set:
.15 Theorem 2 can be proved by applying similar arguments as in the proof of Theorem 1 to the following set:
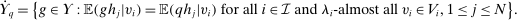
Remark 2.Theorem 1 and Theorem 2 above are established in the case of independent types. In settings with correlated types, let ρ denote the density function of λ with respect to 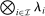 . Then, by Theorem 2, for any allocation rule q, there exists a deterministic allocation rule
. Then, by Theorem 2, for any allocation rule q, there exists a deterministic allocation rule 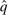 such that, for all
such that, for all 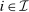 and
and 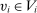 ,
,
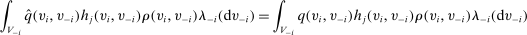
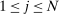 . Theorem 1 for the case of correlated types immediately follows by setting
. Theorem 1 for the case of correlated types immediately follows by setting  .
.
Mechanism Equivalence
Next, we present our mechanism equivalence result. For this result, we need additional assumptions of separate payoffs and independent types. We assume that all agents have separable payoffs in the following sense.
Definition 4.Agent 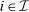 is said to have separable payoff if, for all
is said to have separable payoff if, for all 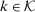 and
and 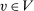 , her payoff function can be written as follows:
, her payoff function can be written as follows:
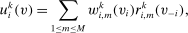
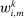 (resp.
(resp. 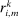 ) is
) is 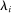 -integrable (resp.
-integrable (resp. 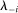 -integrable) on
-integrable) on 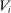 (resp. on
(resp. on 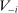 ) for
) for 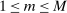 .
.
In words, the payoff of each agent i is a summation of finite terms, where each term is a product of two components: the first component only depends on agent i's own type, while the second component depends on the other agents' types. Note that this setup is sufficiently general to cover most applications. In particular, it includes the interdependent payoff function as in Jehiel and Moldovanu (2001), and obviously covers the widely adopted private value payoffs as a special case.
Theorem 3.Suppose that for each agent 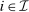 , her payoff function is separable. For any BIC and BIR mechanism
, her payoff function is separable. For any BIC and BIR mechanism 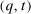 , there exists an equivalent deterministic mechanism
, there exists an equivalent deterministic mechanism 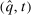 that is BIC and BIR. More explicitly,
that is BIC and BIR. More explicitly,
- (1) q and
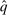 induce the same interim expected allocation probabilities for all
induce the same interim expected allocation probabilities for all 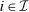 ;
; - (2)
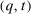 and
and 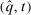 induce the same interim expected utilities for all
induce the same interim expected utilities for all 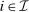 ; and
; and - (3)
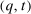 and
and 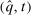 induce the same ex ante expected social surplus.
induce the same ex ante expected social surplus.
Remark 3.Theorem 3 has an interesting implication for the revelation principle. By the standard revelation principle, it is without loss of generality to consider only direct mechanisms that are BIC and BIR. Theorem 3 shows that for each such direct mechanism, there exists an equivalent deterministic mechanism that is BIC and BIR. Thus, it is without loss of generality to consider only direct deterministic mechanisms. For related discussions on deterministic mechanisms and the revelation principle, see Strausz (2003) and Jarman and Meisner (2017).16
Remark 4.Our approach is not constructive. While we know that there exists an equivalent deterministic mechanism, we do not know how to construct such an equivalent deterministic mechanism. We discuss the structures of the equivalent deterministic mechanisms in Section 4.2 and Section 4.3. We also provide a recipe for the construction of an approximately equivalent mechanism in Appendix D of the Supplemental Material (Chen et al. (2019)).
Proof of Theorem 3.Let h be a function from V to 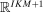 defined as follows. For each
defined as follows. For each 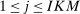 , there is a unique vector of integers
, there is a unique vector of integers 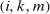 where
where 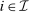 ,
, 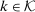 , and
, and 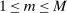 such that
such that 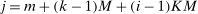 , and we let
, and we let 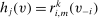 . Let
. Let 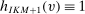 . By Theorem 2, for any BIC and BIR mechanism
. By Theorem 2, for any BIC and BIR mechanism 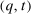 , there exists a deterministic allocation rule
, there exists a deterministic allocation rule 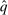 such that for any
such that for any 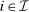 and
and 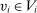 ,
,
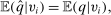 (3)
(3)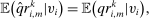 (4)
(4)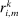 ,
, 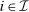 ,
, 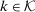 , and
, and 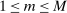 .
.By Equation (3), q and 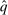 induce the same interim expected allocation probabilities for all agents. We proceed to verify that
induce the same interim expected allocation probabilities for all agents. We proceed to verify that 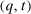 and
and 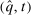 induce the same interim expected utilities for all agents. We calculate agent i's interim expected utility when her true type is
induce the same interim expected utilities for all agents. We calculate agent i's interim expected utility when her true type is 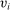 and she reports type
and she reports type 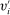 as follows:
as follows:
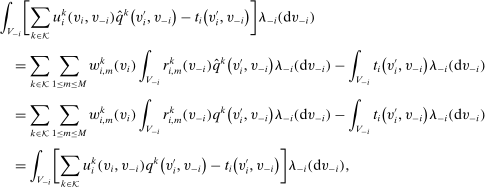
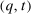 and
and 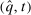 deliver the same interim expected utility for each agent, when each agent i has true type
deliver the same interim expected utility for each agent, when each agent i has true type 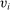 and misreports
and misreports 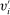 , for all
, for all 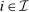 and
and 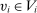 . Therefore, if
. Therefore, if 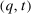 is BIC and BIR, then
is BIC and BIR, then 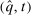 is BIC and BIR. Since the ex post transfers are kept unchanged, the arguments above also imply that both mechanisms deliver the same ex ante expected social surplus. More explicitly,
is BIC and BIR. Since the ex post transfers are kept unchanged, the arguments above also imply that both mechanisms deliver the same ex ante expected social surplus. More explicitly,
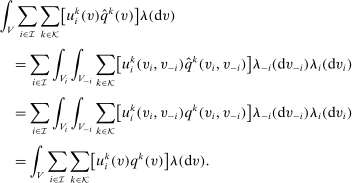
Remark 5.It is clear from the proof of Theorem 3 that the equivalent deterministic mechanism 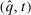 guarantees the same ex post monetary transfers and the same expected revenue. This implies our mechanism equivalence result also holds in settings without monetary transfers.
guarantees the same ex post monetary transfers and the same expected revenue. This implies our mechanism equivalence result also holds in settings without monetary transfers.
Remark 6.Say that a mechanism satisfies ex post individual rationality (EPIR) if, for all 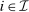 and
and 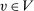 ,
, 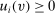 . For any stochastic BIC and BIR mechanism, if the assumptions of separable payoffs and independent types are satisfied, then there exists an equivalent deterministic mechanism that is BIC and EPIR. For this result, the ex post transfers may need to be adjusted. By Theorem 3, for any BIC and BIR mechanism
. For any stochastic BIC and BIR mechanism, if the assumptions of separable payoffs and independent types are satisfied, then there exists an equivalent deterministic mechanism that is BIC and EPIR. For this result, the ex post transfers may need to be adjusted. By Theorem 3, for any BIC and BIR mechanism 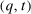 , there exists an equivalent deterministic mechanism
, there exists an equivalent deterministic mechanism 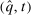 that is BIC and BIR. Since
that is BIC and BIR. Since 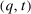 is BIR, the interim expected utility under
is BIR, the interim expected utility under 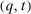 satisfies
satisfies
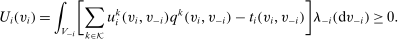
 as follows:
as follows:
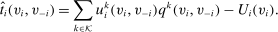
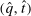 is an equivalent deterministic mechanism, and is BIC and EPIR.
is an equivalent deterministic mechanism, and is BIC and EPIR.
4 Discussions
In this section, we first discuss the assumptions behind our equivalence result in Section 4.1. We then move on to discuss the structures of the equivalent deterministic mechanisms. Here, our discussion is twofold. Section 4.2 illustrates by an example that, even in environments with linear utilities and independent, one-dimensional, private types, we cannot hope for a mechanism equivalence result between the class of BIC mechanisms and the class of DIC and deterministic mechanisms. On a more positive note, Section 4.3 shows that for any mechanism with a symmetric allocation rule, there exists an equivalent deterministic mechanism that preserves symmetry. Finally, Section 4.4 compares our results with the recent literature on the benefit of randomness in settings with multiple agents.
4.1 The Limits of the Equivalence Result
Here, we discuss the assumptions behind our equivalence result, including multiple agents, atomless distribution, separable payoffs, and independent types. The literature of multidimensional screening contains abundant examples illustrating that in the case of a single buyer, a multi-product monopolist may find it beneficial to include lotteries as part of the selling mechanism. Atomless distribution is an indispensable requirement for almost all purification results. Though separable payoff is a restriction, the setup is sufficiently general to cover most economic applications; see the discussion immediately after Definition 4 for details. While our result requires independence, it is worth mentioning that we only require independence across agents and we do not make any assumption regarding the correlation of the different coordinates of type 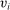 . For atomless distribution, separable payoffs, and independent types, we present examples in Appendix A.3 to illustrate that our mechanism equivalence result breaks down if each of these assumptions is violated.
. For atomless distribution, separable payoffs, and independent types, we present examples in Appendix A.3 to illustrate that our mechanism equivalence result breaks down if each of these assumptions is violated.
We wish to elaborate further on the requirement of multiple agents. While it is well known that lotteries could strictly improve revenue in the case of a single buyer, our equivalence result implies that the optimal mechanism is deterministic in the case of multiple agents. It is thus important to highlight and explain the differences between the case of a single agent with a multidimensional type and the case of multiple agents. In particular, the readers might wonder why, in the case of a single buyer with a two-dimension type 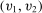 , the multi-product monopolist cannot use the agent's report along the second dimension to purify the allocation probability of good 1, and vice versa. The problem is that the incentive constraints would break down, since it is the same agent who controls the reports on both dimensions.
, the multi-product monopolist cannot use the agent's report along the second dimension to purify the allocation probability of good 1, and vice versa. The problem is that the incentive constraints would break down, since it is the same agent who controls the reports on both dimensions.
4.2 DIC and Deterministic Mechanisms
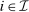 , for all
, for all 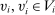 , and for all
, and for all 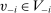 ,
,
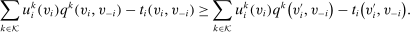
Example 2. (Example 1 Revisited)Suppose that there exists an equivalent mechanism 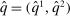 that is both DIC and deterministic. It follows that for each
that is both DIC and deterministic. It follows that for each 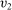 , there exists a threshold
, there exists a threshold 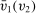 such that
such that 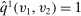 for all
for all 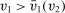 and
and 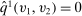 for all
for all 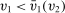 . Since the interim expected allocation probability of bidder 2 is
. Since the interim expected allocation probability of bidder 2 is  for all
for all 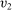 , it must be that
, it must be that 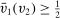 for all
for all 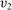 . By the arguments above, we have
. By the arguments above, we have 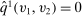 for all
for all 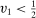 and
and 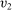 . Therefore, the interim expected allocation probability of bidder 1 is 0 for all
. Therefore, the interim expected allocation probability of bidder 1 is 0 for all 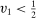 . We arrive at a contradiction.17
. We arrive at a contradiction.17
4.3 Application: Symmetric Auctions
Symmetric auctions received a lot of attention in the mechanism design literature (see, e.g., Border (1991) and Deb and Pai (2017)). Applying our results in Section 3, we show that for any mechanism with a symmetric allocation rule, there exists an equivalent deterministic mechanism that preserves symmetry. For simplicity of exposition, we prove this result in the single-unit auction setting.
Consider a single-unit auction with a finite set 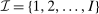 of risk-neutral bidders (
of risk-neutral bidders (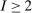 ). For all
). For all 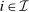 , agent i's valuation
, agent i's valuation 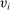 for the object is distributed according to
for the object is distributed according to 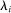 with support on
with support on 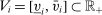 . The agents are ex ante symmetric; that is,
. The agents are ex ante symmetric; that is, 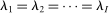 and
and 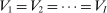 .
.
An allocation rule consists of 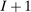 functions
functions 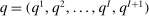 , where
, where 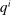 is the probability of bidder i getting the object for
is the probability of bidder i getting the object for 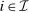 and
and 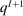 is the probability of the seller keeping the object. Let Ψ be the set of all permutations on
is the probability of the seller keeping the object. Let Ψ be the set of all permutations on 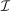 . An allocation rule q is said to be symmetric if
. An allocation rule q is said to be symmetric if 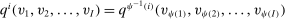 for all
for all 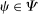 ,
, 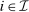 , and
, and 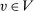 . Proposition 1 below shows that for any symmetric allocation rule, there exists a deterministic and symmetric allocation rule that induces the same interim expected allocation probabilities for all agents. This further implies that there exists an equivalent deterministic mechanism that preserves symmetry.
. Proposition 1 below shows that for any symmetric allocation rule, there exists a deterministic and symmetric allocation rule that induces the same interim expected allocation probabilities for all agents. This further implies that there exists an equivalent deterministic mechanism that preserves symmetry.
Proposition 1.For any symmetric allocation rule q, there exists a deterministic and symmetric allocation rule 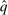 such that q and
such that q and 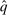 induce the same interim expected allocation probabilities for all agents.
induce the same interim expected allocation probabilities for all agents.
4.4 Benefit of Randomness Revisited
In a recent contribution, Chawla, Malec, and Sivan (2015) considered a multi-agent setting and focused on the case in which the agents' valuations are independent across both different agents' types and different coordinates of an agent's type. They established a constant factor upper bound for the benefit of randomness when the agents' values are independent. In the special case of multi-unit multi-item auctions, they showed that the revenue of any Bayesian incentive compatible, individually rational randomized mechanism is at most 33.75 times the revenue of the optimal deterministic mechanism. In this paper, we push this result to the extreme and show that the revenue maximizing auction can be deterministically implemented.18
5 Conclusion
We show that in a general social choice environment with multiple agents, for any mechanism, there exists an equivalent deterministic mechanism. On the one hand, our result implies that it is without loss of generality to work with stochastic mechanisms, even if the designer does not have access to a randomization device, or cannot fully commit to the outcomes induced by a randomization device. On the other hand, our result implies that the requirement of deterministic mechanisms is not restrictive in itself. Even if one is constrained to use only deterministic mechanisms, there is no loss of revenue or social welfare.
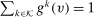 for λ-almost all
for λ-almost all 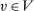 and thus is not necessarily an allocation rule.
and thus is not necessarily an allocation rule.
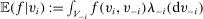 for any integrable function f defined on V.
for any integrable function f defined on V.
 , and show that all extreme points are deterministic. Despite the similarity in the general approach, the technical parts of proofs are dramatically different.
, and show that all extreme points are deterministic. Despite the similarity in the general approach, the technical parts of proofs are dramatically different.
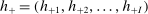 and
and 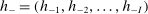 , where
, where 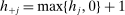 and
and 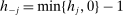 for all
for all 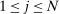 . Theorem 2 can thus be proved by considering
. Theorem 2 can thus be proved by considering 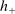 and
and 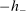 , respectively, as
, respectively, as 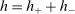 .
.
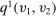 is nondecreasing in
is nondecreasing in 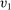 for all
for all 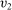 and that
and that 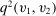 is nondecreasing in
is nondecreasing in 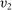 for all
for all 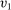 . As such, there exists a transfer scheme t such that
. As such, there exists a transfer scheme t such that 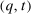 is DIC. Thus, our discussion here also implies that the equivalence of DIC mechanisms and mechanisms that are both DIC and deterministic does not hold, even in the single-unit auction setting.
is DIC. Thus, our discussion here also implies that the equivalence of DIC mechanisms and mechanisms that are both DIC and deterministic does not hold, even in the single-unit auction setting.
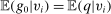 directly, we work with integrals involving bounded measurable mapping p to avoid working with multiple null sets for the sequence of functions
directly, we work with integrals involving bounded measurable mapping p to avoid working with multiple null sets for the sequence of functions 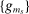 in
in 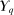 .
.
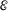 as follows:
as follows:
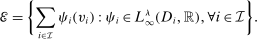
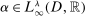 is a solution to the system of equations (5) if and only if
is a solution to the system of equations (5) if and only if 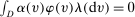 for any
for any 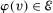 . Thus, our objective is to show that
. Thus, our objective is to show that 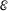 is not dense in
is not dense in 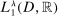 . Note that the set
. Note that the set 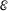 is the collection of all the integrable and additively separable functions, while
is the collection of all the integrable and additively separable functions, while 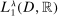 is the collection of all the integrable multivariate functions. The key idea of the proof is hence to identify a multivariate bounded measurable function α that cannot be approximated by additively separable functions. If D is a measurable rectangle
is the collection of all the integrable multivariate functions. The key idea of the proof is hence to identify a multivariate bounded measurable function α that cannot be approximated by additively separable functions. If D is a measurable rectangle 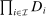 , then one can simply take α to be the product
, then one can simply take α to be the product 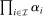 , where the univariate bounded measurable function
, where the univariate bounded measurable function 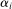 is nontrivial and has zero integral on
is nontrivial and has zero integral on 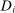 . Because D is a general Borel measurable set without any product structure that allows for such a direct separation of variables, the proof for the general case is rather involved.
. Because D is a general Borel measurable set without any product structure that allows for such a direct separation of variables, the proof for the general case is rather involved.
Appendix A
A.1 Proof of Theorem 1
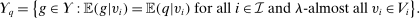
We first show that  is nonempty, convex, and weakly compact. Then, by the Krein–Milman theorem (see Royden and Fitzpatrick (2010, p. 296)),
is nonempty, convex, and weakly compact. Then, by the Krein–Milman theorem (see Royden and Fitzpatrick (2010, p. 296)), 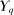 admits extreme points.
admits extreme points.
Lemma 1.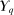 is nonempty, convex, and weakly compact.
is nonempty, convex, and weakly compact.
Proof.Clearly, 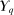 is nonempty and convex. For weak compactness, it suffices to show that
is nonempty and convex. For weak compactness, it suffices to show that 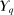 is norm closed in
is norm closed in 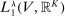 , where
, where 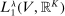 is the
is the 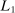 space of all integrable mappings from V to
space of all integrable mappings from V to 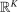 under the probability measure λ. Since
under the probability measure λ. Since 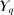 is convex, by Mazur's theorem (see Royden and Fitzpatrick (2010, p. 292)),
is convex, by Mazur's theorem (see Royden and Fitzpatrick (2010, p. 292)), 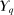 is also weakly closed in
is also weakly closed in 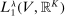 . Since
. Since 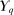 is bounded, it is uniformly integrable. By Theorem 12 in Royden and Fitzpatrick (2010, p. 412),
is bounded, it is uniformly integrable. By Theorem 12 in Royden and Fitzpatrick (2010, p. 412), 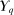 is weakly compact in
is weakly compact in 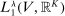 .
.
In what follows, we show that 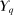 is norm closed in
is norm closed in 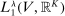 . Consider any sequence
. Consider any sequence 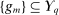 such that
such that 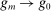 in norm in
in norm in 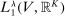 . We show that
. We show that 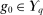 . By the Riesz–Fischer theorem (see Royden and Fitzpatrick (2010, p. 398)), there exists a subsequence
. By the Riesz–Fischer theorem (see Royden and Fitzpatrick (2010, p. 398)), there exists a subsequence 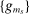 of
of 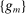 such that
such that 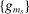 converges to
converges to 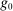 λ-almost everywhere. Since
λ-almost everywhere. Since 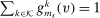 for λ-almost all v,
for λ-almost all v, 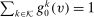 for λ-almost all v. Therefore,
for λ-almost all v. Therefore, 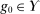 .
.
Given any 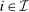 , let
, let 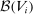 be the Borel σ-algebra of the set
be the Borel σ-algebra of the set 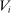 . For each
. For each  , and for any
, and for any 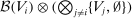 -measurable bounded mapping
-measurable bounded mapping 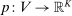 ,
,
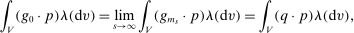
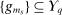 . By the arbitrary choice of bounded measurable mapping p, we obtain that
. By the arbitrary choice of bounded measurable mapping p, we obtain that 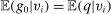 for λ-almost all
for λ-almost all 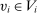 , which implies that
, which implies that 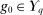 .19 □
.19 □Step (2) We show that all extreme points of 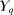 are deterministic for λ-almost all
are deterministic for λ-almost all 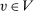 . Then, there exists
. Then, there exists 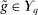 that is deterministic for λ-almost all
that is deterministic for λ-almost all 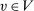 .
.
Lemma 2.All extreme points of 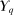 are deterministic for λ-almost all
are deterministic for λ-almost all 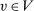 .
.
Proof.We prove the proposition by contraposition. We show that if 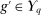 is not deterministic for λ-almost all
is not deterministic for λ-almost all 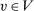 , then
, then 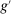 is not an extreme point of
is not an extreme point of 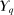 . Suppose that
. Suppose that 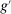 is not deterministic for λ-almost all
is not deterministic for λ-almost all 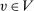 . Then, there exists
. Then, there exists
- (1)
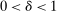 ;
; - (2) a Borel measurable set
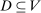 with
with 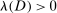 ; and
; and - (3) indices
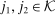
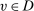 ,
,
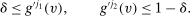
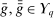 such that
such that 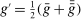 . This establishes that
. This establishes that 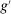 is not an extreme point of
is not an extreme point of 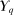 .
.For any 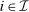 , let
, let 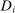 be the projection of D on
be the projection of D on 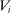 . For any
. For any 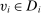 , let
, let 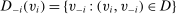 . Consider the following system of equations where
. Consider the following system of equations where 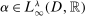 are the unknown:
are the unknown:
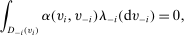 (5)
(5)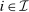 and
and 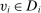 .
.Since 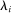 is atomless for all
is atomless for all 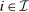 , one can show that besides the trivial solution that
, one can show that besides the trivial solution that 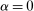 , the system of equations (5) also has a nontrivial bounded solution α. The proof of this claim is technical and is contained in Appendix B of the Supplemental Material (Chen et al. (2019)).20
, the system of equations (5) also has a nontrivial bounded solution α. The proof of this claim is technical and is contained in Appendix B of the Supplemental Material (Chen et al. (2019)).20
Without loss of generality, we assume that 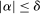 . Since α is defined on D, we extend the domain of α to V by setting
. Since α is defined on D, we extend the domain of α to V by setting 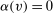 whenever
whenever 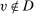 . We construct
. We construct 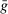 and
and 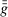 as follows: for all
as follows: for all 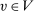 ,
,
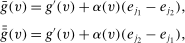
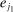 and
and 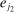 are the standard basis vectors in
are the standard basis vectors in 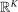 .
.We proceed to verify that 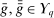 . To see that
. To see that 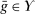 , note that
, note that
- (1)
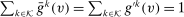 for λ-almost all
for λ-almost all 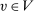 ;
; - (2) if
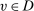 , then
, then 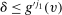 ,
, 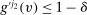 , which implies that
, which implies that 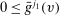 ,
, 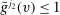 ;
; - (3) if
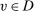 , then
, then 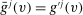 for
for 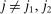 ; and
; and - (4) if
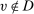 , then
, then 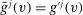 as
as 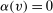 .
.
Next, we show that 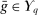 . Fix any
. Fix any 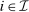 . We obtain that for
. We obtain that for 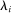 -almost all
-almost all 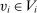 ,
,

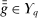 . Since
. Since 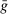 and
and 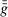 are distinct and
are distinct and 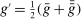 ,
, 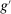 is not an extreme point of
is not an extreme point of 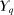 . □
. □Step (3) Fix 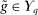 that is deterministic for λ-almost all
that is deterministic for λ-almost all 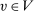 . Note that (1)
. Note that (1) 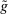 is deterministic for λ-almost all
is deterministic for λ-almost all 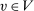 , but not for all
, but not for all 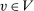 ; and (2)
; and (2) 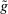 induces the same interim expected allocation probabilities for all
induces the same interim expected allocation probabilities for all 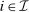 and
and 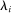 -almost all
-almost all 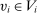 , but not for all
, but not for all 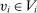 . We now construct a deterministic allocation rule
. We now construct a deterministic allocation rule 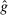 that induces the same interim expected allocation probabilities for all
that induces the same interim expected allocation probabilities for all 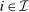 and
and 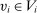 , by modifying
, by modifying 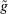 on sets of measure zero.
on sets of measure zero.
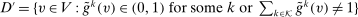 . Since
. Since 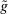 is deterministic for almost all
is deterministic for almost all 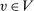 ,
, 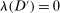 . Define a new allocation rule
. Define a new allocation rule 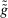 as follows:
as follows:
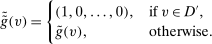
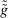 is deterministic for all
is deterministic for all 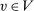 . Note that
. Note that 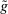 and q induce the same interim expected allocation probabilities for all
and q induce the same interim expected allocation probabilities for all 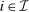 and
and 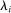 -almost all
-almost all 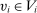 (the relevant null sets could be very different from the null set
(the relevant null sets could be very different from the null set 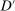 ). Since
). Since 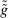 is modified from
is modified from 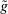 on the null set
on the null set 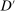 ,
, 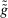 and q induce the same interim expected allocation probabilities for all
and q induce the same interim expected allocation probabilities for all 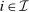 and
and 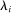 -almost all
-almost all 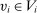 . That is, for all
. That is, for all 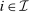 and
and 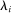 -almost all
-almost all 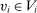 ,
,
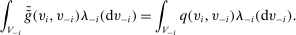 (6)
(6)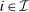 , let
, let 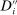 be the subset of
be the subset of 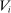 such that Equation (6) does not hold. Then,
such that Equation (6) does not hold. Then, 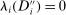 . By Proposition 10.7.6 in Bogachev (2007), for each
. By Proposition 10.7.6 in Bogachev (2007), for each 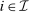 , there exists a deterministic allocation rule
, there exists a deterministic allocation rule 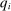 on
on 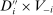 such that for all
such that for all 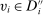 ,
,
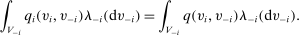 (7)
(7)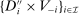 may not be disjoint, we construct an allocation rule
may not be disjoint, we construct an allocation rule 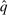 by taking a suitable decomposition of
by taking a suitable decomposition of 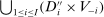 as follows:
as follows:
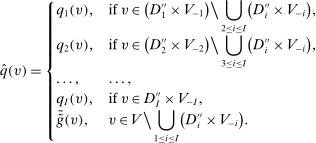
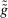 and
and 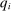 for all
for all 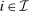 that
that 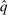 is deterministic for all
is deterministic for all 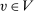 . We now proceed to verify that
. We now proceed to verify that 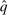 and q induce the same interim expected allocation probabilities for all
and q induce the same interim expected allocation probabilities for all 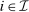 and
and 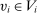 .
.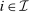 and
and 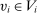 . If
. If 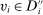 , by the definition of
, by the definition of 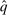 ,
,
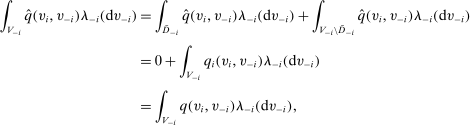
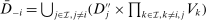 . The second line follows from that
. The second line follows from that 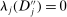 for all
for all 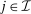 , and the third line follows from (7).
, and the third line follows from (7).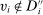 , by the definition of
, by the definition of 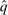 ,
,
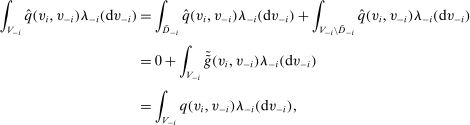
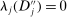 for all
for all 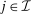 , and the third line follows from (6).
, and the third line follows from (6).A.2 Proof of Proposition 1
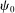 be the identity mapping on
be the identity mapping on 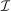 . For each
. For each 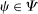 , define
, define
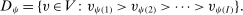
- 1. for distinct
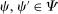 ,
, 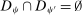 ;
; - 2.
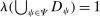 ;
; - 3.
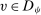 for some ψ if and only if
for some ψ if and only if  .
.
The structure of the proof is as follows. For an arbitrary symmetric allocation rule q, Step (1) constructs a deterministic allocation rule 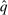 , Step (2) shows that
, Step (2) shows that 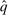 is symmetric, and Step (3) shows that q and
is symmetric, and Step (3) shows that q and 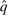 induce the same interim expected allocation probabilities for all agents.
induce the same interim expected allocation probabilities for all agents.
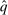 so that it is identical with
so that it is identical with 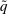 on
on 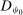 . By symmetry, we know that the values of
. By symmetry, we know that the values of 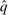 on
on 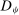 are completely determined by its values on
are completely determined by its values on 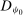 via the permutation ψ. More specifically, the deterministic allocation rule
via the permutation ψ. More specifically, the deterministic allocation rule 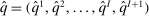 is defined as follows: for
is defined as follows: for 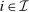 ,
,
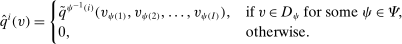
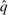 is symmetric. That is, for all
is symmetric. That is, for all 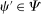 ,
, 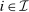 , and
, and 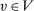 ,
,
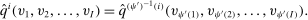
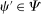 . We first consider the case in which
. We first consider the case in which 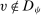 for all
for all 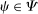 . Then
. Then

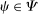 . It follows from the definition of
. It follows from the definition of 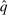 that for all
that for all 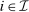 ,
,
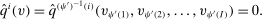
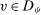 for some
for some 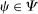 . For notational simplicity, we relabel
. For notational simplicity, we relabel 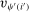 by
by 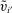 for all
for all 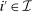 . Let
. Let 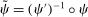 . Since
. Since
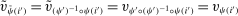
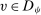 , we have
, we have 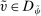 . Therefore, for all
. Therefore, for all 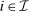 ,
,
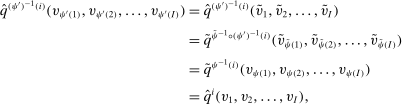
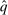 and the fact that
and the fact that 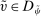 , the third equality holds because
, the third equality holds because 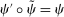 and
and 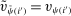 for all
for all 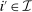 , and the last equality follows from the definition of
, and the last equality follows from the definition of 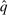 and the fact that
and the fact that 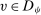 .
.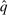 and q induce the same interim expected allocation probabilities for all agents. For all
and q induce the same interim expected allocation probabilities for all agents. For all 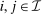 and
and 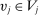 , we have
, we have
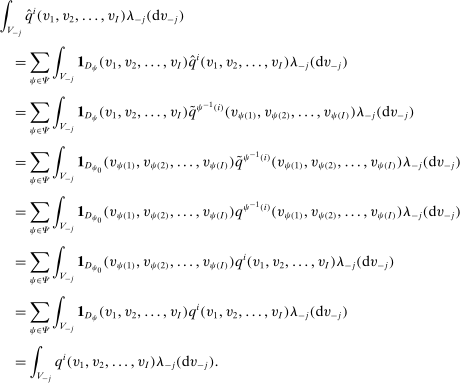
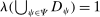 . The second equality follows from the definition of
. The second equality follows from the definition of 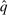 . The third and sixth equalities hold since
. The third and sixth equalities hold since 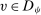 if and only if
if and only if  . The fourth equality follows from (8). The fifth equality follows from the symmetry of q.
. The fourth equality follows from (8). The fifth equality follows from the symmetry of q.A.3 The Limits of the Equivalence Result
For atomless distribution, separable payoffs, and independent types, we present examples here to illustrate that our mechanism equivalence result breaks down if each of these assumptions is violated. Recall that our approach of proving the existence of equivalent deterministic mechanism keeps the ex post transfers unchanged. In the same vein, we also require that the transfers be kept unchanged in the examples on separable payoffs and independent types.
To prove that there exists a deterministic allocation rule that delivers the same interim expected allocation probabilities for all agents, we do not require the assumption of independent types. We invoke additional assumptions of separable payoffs and independent types to establish that the equivalent deterministic mechanism is BIC. When types are correlated, our approach no longer works. However, under certain conditions, one can invoke the Crémer–McLean type arguments to approximately satisfy the incentive constraints by adjusting transfers. Indeed, by combining the results in McAfee and Reny (1992) and Miller, Pratt, Zeckhauser, and Johnson (2007), one can show that under the conditions in their papers, there exists a deterministic mechanism that is approximately equivalent.
Example 3. (Atomless Distribution)Consider a setting with two agents. Suppose that 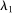 has an atom
has an atom 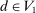 with
with 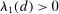 . Note that the assumption of atomless distribution is violated. Consider the following mapping
. Note that the assumption of atomless distribution is violated. Consider the following mapping 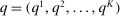 :
:
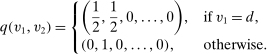
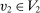 ,
,
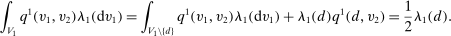 (9)
(9)We claim that there does not exist a deterministic allocation rule that delivers the same interim expected allocation probabilities for all agents. Suppose, to the contrary, such a deterministic allocation rule 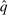 exists. For all
exists. For all 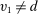 ,
,
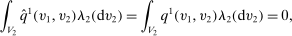
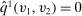 for
for 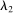 -almost all
-almost all 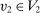 .
.By Fubini's theorem (see Royden and Fitzpatrick (2010, p. 416)), for 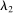 -almost all
-almost all 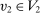 ,
, 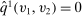 for
for 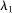 -almost all
-almost all 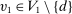 . Therefore, for
. Therefore, for 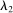 -almost all
-almost all 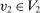 ,
,
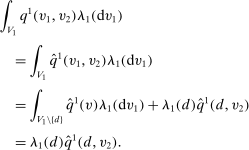 (10)
(10)It follows from (9) and (10) that 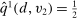 for
for 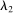 -almost all
-almost all 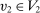 , which contradicts the assumption that
, which contradicts the assumption that  is either 0 or 1.
is either 0 or 1.
Example 4. (Separable Payoff)Consider a single-unit common value auction with two bidders. The bidders' valuations for the object 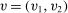 are uniformly distributed on the square
are uniformly distributed on the square 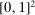 . Let λ denote the uniform distribution on the square
. Let λ denote the uniform distribution on the square 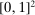 . Each agent's payoff is 1 if she gets the object and
. Each agent's payoff is 1 if she gets the object and 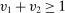 , and 0 otherwise. More succinctly, the payoff function of bidder i is
, and 0 otherwise. More succinctly, the payoff function of bidder i is 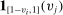 if she gets the object and 0 otherwise. Note that the assumption of separable payoffs is violated.
if she gets the object and 0 otherwise. Note that the assumption of separable payoffs is violated.
Consider the allocation rule 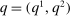 with
with 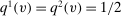 for all v, where
for all v, where 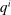 is the probability of bidder i getting the object for
is the probability of bidder i getting the object for 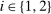 . We claim that there does not exist a BIC and deterministic allocation rule that delivers the same interim expected utilities for all bidders. Suppose, to the contrary, such a BIC and deterministic allocation rule
. We claim that there does not exist a BIC and deterministic allocation rule that delivers the same interim expected utilities for all bidders. Suppose, to the contrary, such a BIC and deterministic allocation rule 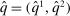 exists. Then the payoff of bidder 1 for any
exists. Then the payoff of bidder 1 for any 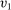 is
is
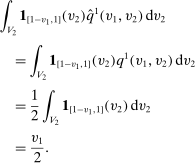
Since 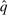 is BIC, for
is BIC, for 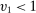 , agent 1 has an incentive to truthfully report her type than to misreport
, agent 1 has an incentive to truthfully report her type than to misreport 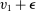 (where
(where  is sufficiently small such that
is sufficiently small such that 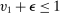 ). That is,
). That is,
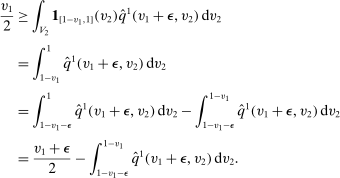
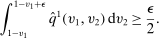
Fix any 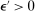 ; consider the region
; consider the region
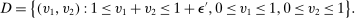
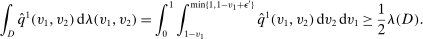 (11)
(11) (12)
(12)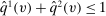 for all v, we have
for all v, we have
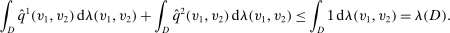 (13)
(13)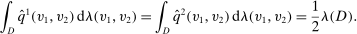
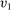 , for all
, for all  such that
such that 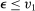 ,
,
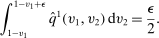
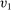 , for any
, for any 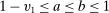 ,
,
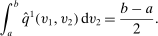
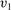 ,
, 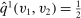 for almost all
for almost all 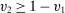 . We arrive at a contradiction.
. We arrive at a contradiction.
Example 5. (Independent Types)Consider a single-unit auction with two bidders. Let 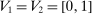 be endowed with the joint distribution λ, which has density
be endowed with the joint distribution λ, which has density 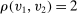 if
if 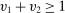 and 0 otherwise. The payoff function of bidder i is 1 if she gets the good and 0 otherwise. Note that the assumption of independent types is violated.
and 0 otherwise. The payoff function of bidder i is 1 if she gets the good and 0 otherwise. Note that the assumption of independent types is violated.
Consider the allocation rule 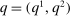 with
with 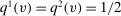 for all v, where
for all v, where 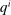 is the probability of bidder i getting the object for
is the probability of bidder i getting the object for 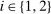 . We claim that there does not exist a BIC and deterministic allocation rule that delivers the same interim expected utilities for all bidders. Suppose, to the contrary, such a BIC and deterministic allocation rule
. We claim that there does not exist a BIC and deterministic allocation rule that delivers the same interim expected utilities for all bidders. Suppose, to the contrary, such a BIC and deterministic allocation rule 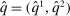 exists. Then the payoff of bidder 1 for any
exists. Then the payoff of bidder 1 for any 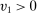 is
is
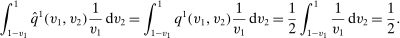
Since 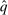 is BIC, for any
is BIC, for any 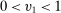 , agent 1 has an incentive to truthfully report her type than to misreport
, agent 1 has an incentive to truthfully report her type than to misreport 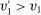 . We have
. We have
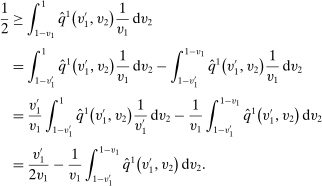
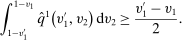
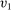 ,
, 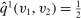 for almost all
for almost all 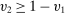 . We arrive at a contradiction.
. We arrive at a contradiction.


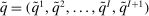 such that for all
such that for all 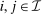 and
and 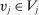 ,
,