Transition of Firing Patterns in a Complex Neural Network

1. Introduction

In nature, many real systems can be described by complex networks, where nodes represent dynamical individuals and links represent interactions between individuals. Some works have been dedicated to the studies of complex networks in the last decade [1–4]. In particular, the small-world network, a prominent type of complex networks introduced by Watts and Strogatz [5, 6], has been realized extensively for describing the structure of many real-world networks [7–10].

The brain consists of a large number of neurons connected to each other by synapses, which can be depicted by a complex network. In the cortex and other brain regions, the connectivity of neurons is mainly local, where the long-distance projections are comparatively sparse, forming together a small-world brain network [11]. The neurons communicate with each other through electrical impulse. For a neuron stimulated by an external stimulus from its connected neurons, it fires an electrical discharge through its axon which through synapses transmits charges to the dendrites of other neurons. Neuronal firing activities are crucial to the information processing. Based on the time intervals inside neural firings, neural information is coded and transmitted [12], and different firing patterns are displayed in the firing neurons including spiking, bursting, chaos, and so on [13]. Therefore, various neuronal firing patterns and their generation and transition, which is basic for the understanding the origins of different neural coding and information processing strategies, have always been a significant research subject [14–18].

Previous studies of small-world network mostly focused on the network topological properties and various mechanisms to determine the topological structure, however, more recent works have shifted to the investigation of the influences of the network topology on dynamical behaviors [19–23]. For instance, Kwon and Moon. have shown that small-world connections could lead to an enhancement of temporal coherence and of spatial synchronization in coupled excitable neurons [19]. Lin and Chen. have found that there were different avalanche dynamical behaviors for different density of short paths in small-world neural network [20]. In reference [21], the effects of the topology on the synchronization properties of the Hindmarsh–Rose neural network have been investigated. Additionally, in nervous system, there exists optimal network topology randomness at which the spiking oscillations show the best regularity [22, 23]. All these studies have indicated that small-world network topology plays an essential role in dynamics of nervous systems. However, studies on the dependence of generation and transition of various neural firing patterns in neural networks on the random long-range connections are still few in the previous literatures. Specifically, for the purpose of the present work, we are wondering how the network topologies influence the generation and transition of various neural firing patterns.

In this paper, we mainly study the effects of topological randomness on the firing patterns in a network composed of Hindmarsh–Rose (HR) neurons. We show that random long-range connections can induce the transitions of neural firing patterns when the number of random connections is greater than a threshold value. Furthermore, we introduce the average transition ratio λ to quantitatively study the transition degree of firing patterns of the neural network. The influences of coupling strength on such transition behavior of neural firing patterns are also considered. For any transition of firing patterns, the threshold value decreases with coupling strength increasing.

2. Model

The model used in this paper consists of N = 500 HR neurons that form a small-world network, which is constructed as follows. First, constructing a regular ring, where each neuron connects to its K = 2 nearest neighbors. then, links are randomly added between nonnearest neurons. To measure the effects of shortcuts on the neural firing patterns, we introduce a controlling parameter p defined as the ratio of the number of shortcuts M to the total number of all possible additional connections: p = 2M/[N(N − 3)]. The parameter p controls the topology of neural network that can take different values between 0 and 1: for p = 0, the network becomes the original regular network, and conversely for p = 1, it turns to globally coupled network. Additionally, lots of network realizations present for a given p. The dynamics of each HR neuron are given by [24]:

In this paper, by using the fourth-order Runge-Kutta method with a fixed time step of 0.001, equations (1) are numerically integrated. One notes that each neuron in the network is identical except for different initial conditions. To qualitatively measure dynamical behavior of neural network, the interspike intervals (ISIs) of neural firing for each HR neural are calculated: $$, where $$ is the time of the kth pulse in the ith neuron, and the threshold value of x_i(t) is set at x_i  = 1.0.

3. Results and Discussion

To begin, we fix the coupling strength g = 0.0002, and take separately the external current I_ext = 1.400, 1.950, and 2.456, where the firing pattern of each neuron in the network is corresponding to period-1, period-2, and period-3, respectively. The patterns of ISIs of an arbitrary individual neuron in the HR neural network as the variation of p at different levels of the external current I_ext are plotted in Figure 2. We can see that, no matter which I_ext we apply to the system, ISIs turn into high-period firing pattern from low-period firing pattern when the parameter p is greater than a threshold, indicating the occurrence of the transition of neural firing patterns. Figure 2(a) depicts the transition of firing patterns from period-1 to period-2 for arbitrary single neuron in the network. Also, Figures 2(b) and 2(c) show the transition from period-2 to period-3 at I_ext = 1.950, and the transition from period-3 to period-4 at I_ext = 2.456, respectively. The corresponding phase diagrams are displayed from left pannel to right pannel in Figure 3, respectively. This indicates that the transitions of neural firing patterns can be induced by adjusting the network topological structure.

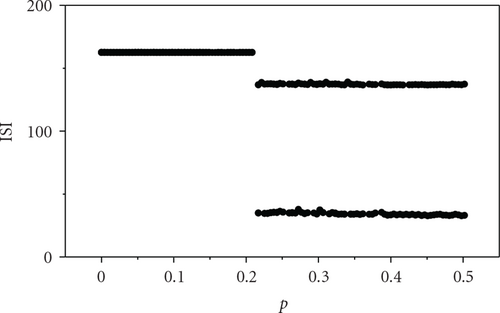
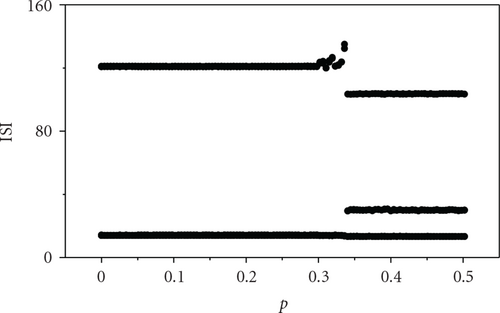
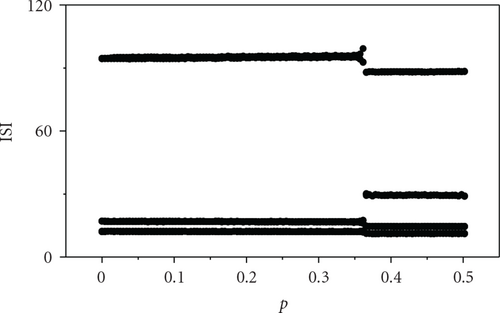
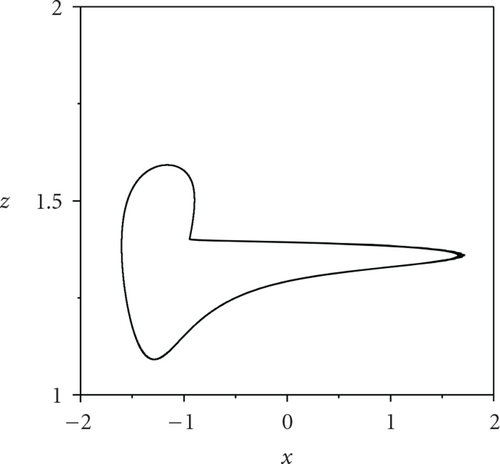
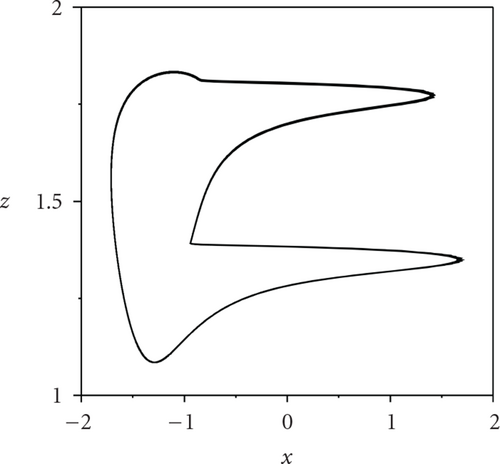
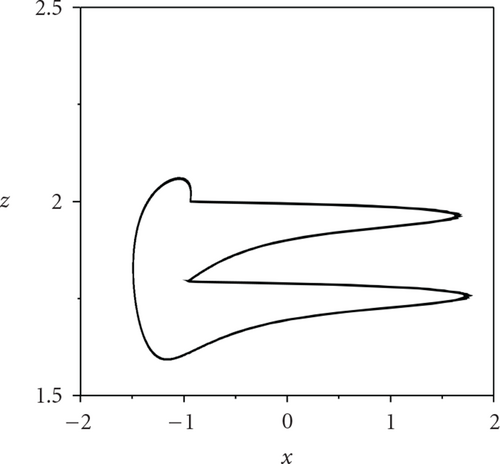
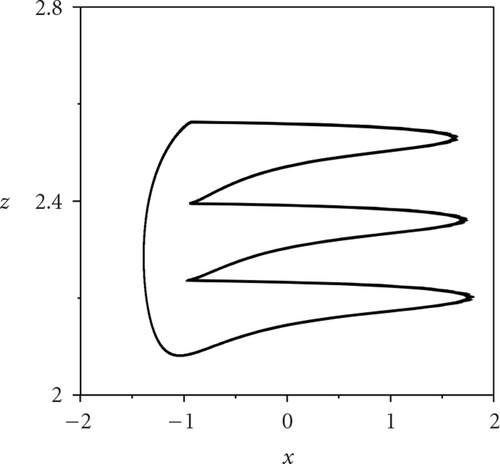
To quantitatively study the transition degree of firing patterns of the neural network, we introduce the average transition ratio λ which is defined as follows:

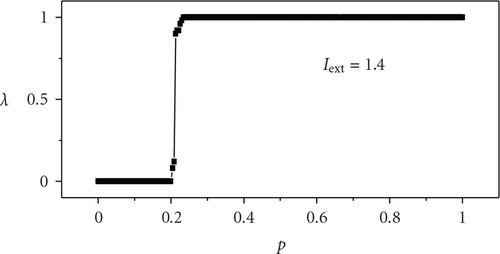
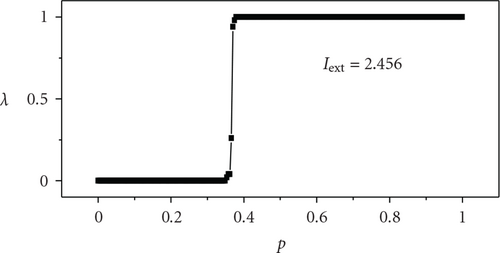
In Figure 4, the average transition ratio λ versus the parameter p at different external current I_ext is plotted. When I_ext is set as 1.40 (the period-1 state), one can find that there exist two critical points corresponding to the parameter p, that is, the system maintains in the period-1 state when p < p_c1 ≈ 0.20. However, when p increases a bit from 0.20, few neurons still locate in the period-1 firing state, but a larger portion of neurons begin to behave period-2 firing state, thus λ increases steeply from 0 to 1. If p increases further, and reaches another critical value p_c2 ≈ 0.23, all the neurons in the network turn into period-2 state from period-1state. This indicates the occurrence of the transition of firing pattern of neural network. Such trend is shown in Figure 4(a). Also, if the level of the external stimulation is changed, that is, I_ext is set at 1.95 (transition from period-2 to period-3) and 2.456 (transition from period-3 to period-4), respectively, similar results can be obtained and are shown in Figures 4(b) and 4(c). These phenomena imply that the nervous system may have the ability to make the optimal response to the change of stimulation by a corresponding adjustment of the shortcuts.

We now consider the effects of coupling strength g on the transition of neural firing patterns. Here, the average threshold value 〈P_c〉 is introduced as a measure which is defined as follow:

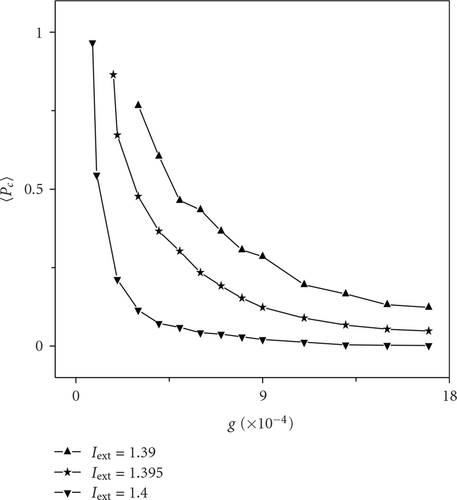
To check the effect of system size, we have also calculated the patterns of ISIs of neural network as the variation of p at different external current I_ext for the other three system size levels N = 100, 400, 800 with g   =   0.0002 (figures not shown). We find that for different values of N, the nervous system undergoes the transitions of neural firing patterns as well, and the variation of λ versus p is almost unchanged, as well as the evolution of 〈P_c〉 with changing g. These indicate that the variation of appropriate system size takes slight effect on neural firing patterns.

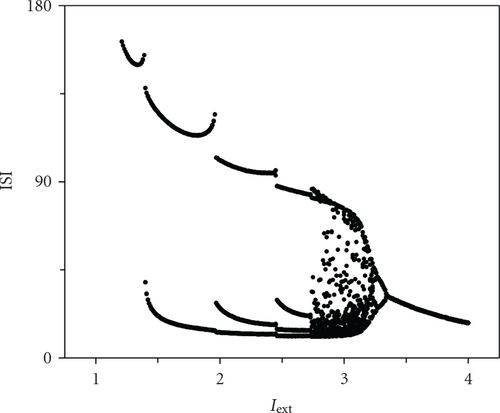
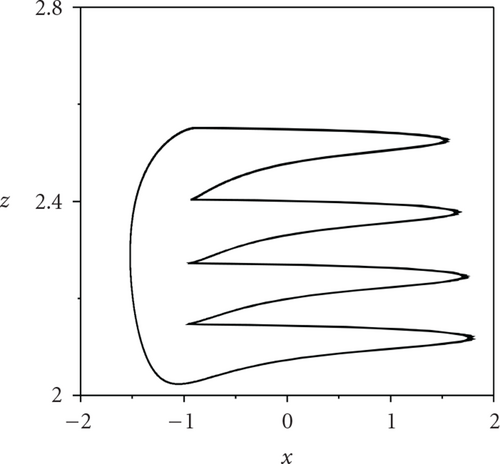
How does explain the occurrence of the transition of firing patterns induced by random long-range connections in the complex neural network? Maybe, it has inherent relevance to the bifurcation feature of a single neuron and interneuronal interaction through gap junctions. In Figure 1, one can see that, for a single HR neuron subject to an external stimulus current I_ext closed to the bifurcation point, some external fluctuations can make the neurons stay at different activity intensity state and lead to the occurrence of transitions. When the parameter p is relatively small, the system shows rather bad synchronization such that neurons behave incoherent firing [27]. For any neuron in the network, it may receive many incoherent inputs from its neighbor neurons, which leads to counteract coupling interactions between different neurons, and thus low-period firing pattern is still maintained. On the other hand, with the increment of p, the interaction between neurons will be strengthened. A small portion of HR neurons begin to make coherent firing activities such that each neuron can obtain some coherent synaptic inputs [28, 29]. As a result, coupling term in the right hand of (1) plays a similar role in enhancing the external current I_ext. When p is larger than a critical value p_c, coupling interaction is strong enough to ensure the emergence of the transition of firing patterns. At last, coupling strength can lower the critical value p_c, which can be easily understood from the above analysis.

From the biological point of view, our result exhibits its importance and reasonability since (i) in neurobiological system, the neurons are connected to each other by synapses. Despite that most synapses just connect close by neurons, a few of them also can be long range and connect to a neuron. So, a number of long-range shortcuts among neurons are reasonable and realistic; (ii) for a single HR neuron subject to an external stimulus current, the neuron sustains obvious persistent firing as the amplitude of the stimulus varies [26]. Thus the studies of the connection between the topological structure of neural network and neural firing patterns may play a significant role in unveiling the mechanism of neural coding and information processing in neurobiological systems. Synaptic plasticity is one of the most functions in real neural network, where new synaptic connections can be generated, and old synaptic connections among neurons can be also pruned. Our findings exhibit the network topology can induce the transitions of neural firing patterns. Therefore, we may speculate that there should be a link between synaptic plasticity and the problems of neural coding and signal transmission.

4. Conclusion

In summary, we investigate the effects of the network topology on the firing patterns in a network composed of HR neurons. It is found that shortcuts can induce the transitions of neural firing patterns when the number of random shortcuts is greater than a threshold. Our findings imply that, on the one hand, shortcuts may play a constructive role in the transition process among different firing patterns of nervous system, thus, the neural network system may have the ability to make the optimal response to the change of stimulation by a corresponding self-adjustment of topological randomness [21]; on the other hand, our results may be useful in comprehending the real mechanism in neural coding and information transmission in neurobiological systems and have interesting implications for understanding the dynamical behaviors in some living neuronal systems.