Scholarly Research Exchange
Volume 2009, Issue 1 856320
Research Article
Open Access

Dynamic Stability of Axially Accelerating Viscoelastic Plate

Yin-Feng Zhou, 

Corresponding Author

Yin-Feng Zhou

School of Sciences, Xi′an University of Technology, Xi′an 710048, China xaut.edu.cn

Search for more papers by this author
Zhong-Min Wang, 

Zhong-Min Wang

School of Sciences, Xi′an University of Technology, Xi′an 710048, China xaut.edu.cn

Search for more papers by this author
First published: 17 March 2009
https://doi.org/10.3814/2009/856320

Abstract

The transverse vibration of an axially accelerating viscoelastic plate is investigated. The governing equation is derived from the two-dimensional viscoelastic differential constitutive relation while the resulting equation is discretized by the differential quadrature method (DQM). By introducing state vector, the first-order state equation with periodic coefficients is established and then it is solved by Runge-Kutta method. Based on the Floquet theory, the dynamic instability regions and dynamic stability regions for the accelerating plate are determined and the effects of the system parameters on dynamic stability of the plate are discussed.

1. Introduction

Transmission belts, band saw blades, elevator cables, magnetic types, paper webs are some technological examples of axially moving continua. There are comprehensive studies on such systems [1–5]. In recent years, much attention has been paid to parametric vibration of traveling systems and transverse parametric vibration of axially accelerating systems has been extensively analyzed [6, 7]. Pakdemirli et al. [8] conducted a stability analysis using the Floquet theory for sinusoidal transporting velocity function. Oz [9] used the method of multiple scales to calculate analytically the stability boundaries of an axially moving beam with the velocity as a simple harmonic function. Based on the second-term Galerkin discretization, Chen et al. [10] analyzed the stability of axially accelerating linear beams. Chen and Yang [11] studied transverse stability of axially moving viscoelastic beams with the speed that is harmonically fluctuating about a constant mean value.

All above-mentioned researchers considered elastic beams or viscoelastic strings and viscoelastic beams; however, the literature that is specially related to axially accelerating viscoelastic plates is relatively limited. To address the lack of research in this aspect, the present investigation is devoted to analytical study of axially accelerating viscoelastic plate.

In this paper, we take the axially accelerating viscoelastic plate as research object; the axially moving speed of the plate is a constant mean speed with small harmonic variations. The partial differential equation of motion was discretized by DQM, then the stability analysis was made using the Floquet theory and effects of the system parameters on dynamic stability of the plate are discussed.

2. The Governing Equation

Consider a uniform axially moving viscoelastic plate, with density ρ, the length a, width b, and thickness h in the x,  y, and z directions, respectively. The plate move with the time-dependent axial speed v(t), as shown in Figure 1.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The axially accelerating viscoelastic plate.
Assuming that the material of the plate obeys elastic behavior in dilatation and the Kelvin-Voigt law in distortion, the constitutive equations are as follows [12]:
()
where G is shear elastic modulus, K is bulk elastic modulus, and η is viscosity coefficient. sij and eij are deviatoric tensor of stress and deviatoric tensor of strain, σii and εii are spherical tensor of stress and spherical tensor of strain.
The speed of the plate in the x direction is v(t), in the direction of transverse displacement w(x, y, t) is , that is to say
()
where the differential operator is
()
the transverse acceleration of the axially moving plate can be obtained as
()
The geometry equations of viscoelastic plate are the same as the elastic plates. Based on the thin plate theory and the constitutive equations of the viscoelastic material in Laplace domain [13], the differential equation of motion of axially moving viscoelastic plate constituted by the Kelvin-Voigt model in time domain is
()
where A1 = 3K + 4G,  A2 = 4η,  A3 = 2G(6K + 2G),  A4 = 8Gη + 12Kη,  A5 = 4η2, shear elastic modulus G = E/(2(1 + μ)), bulk elastic modulus K = E/(3(1 − 2μ)), μ is the Poisson ratio.

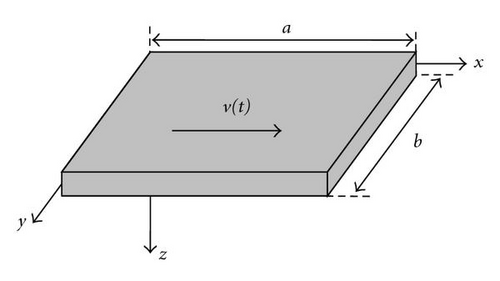
The speed in the x direction is assumed to be a small simple harmonic variation about the constant mean speed, namely, v(t) = v0 + v1sinωt.

Introduce the dimensionless variables and parameters:
()
where H is dimensionless delay time, c and c1 are dimensionless axially moving speed, ϕ is aspect ratio of the plate, and τ is dimensionless time.
Substituting (6) into (5), one obtains
()
The boundary conditions of the plate with four edges simply supported are as follows:
()
The boundary conditions of the plate with two opposite edges simply supported and other two edges clamped are as follows:
()

3. Discretization of the Governing Equation by Differential Quadrature Method

The basic idea of the DQ method is to approximate the partial derivatives of a function with respect to a spatial variable at any discrete point as the weighted linear sum of the function values at all the discrete points chosen in the solution domain of spatial variable [14]. Consider smooth function f(x, y, t) in region 0 ≤ x ≤ a,  0 ≤ y ≤ b, the partial derivative of the rth order with respect to x of it at the point (xi, yi, t), the partial derivative of the sth order with respect to y, the mixed partial derivative of the sth order with respect to y and the rth order with respect to x are defined as follows, respectively [15]:
()
()
()
where and are weight coefficients, and they are defined by
()
()
in the case of r = 2, 3, …, N − 1;  s = 2, 3, …, M − 1, then
()
()
where N,  M is the number of nodes in x and y directions, respectively, in this paper M = N.
There are two key points in the successful application of the differential quadrature method, one is how to determine the weighting coefficients and the other is how to select the grid points. The natural and simplest choice of the grid points is equally spaced points in the direction of the coordinate axes of the computational domain. It was demonstrated that nonuniform grid points give a better results with the same number of equally spaced grid points [16]. In this paper, we choose these set of grid points in terms of natural coordinate directions ξ and ψ for the plate with four edges simply supported and the plate with two opposite edges simply supported and other edges clamped, respectively, as
()
()
According to the DQ method procedures, the governing differential equation (7) with their associated boundary conditions can be discretized into the following forms:
()
()
()
Equation (19) and boundary conditions (20) or (21) can be written into the matrix form
()
where matrices [Q],  [R],  [C],  [K] involve such parameters as dimensionless delay time H, dimensionless axially moving speed c,  c1, aspect ratio ϕ of the plate, and dimensionless time τ, furthermore, these matrices have the same period. So the system of (22) is a third-order partial differential equation containing periodic time-varying coefficient.

4. Dynamic Stability Analysis

Introducing the state vector , then substituting it into (22) gives
()
where
()
IN×N is Nth-order identity matrix, and G3N×3N(τ + T) = G3N×3N(τ), that is to say, G3N×3N(τ) is periodic expression, T is the periodic of the function in the axially accelerating speed.
Based on the Floquet theory, the solution matrix to express (23) is supposed as matrix U, namely,
()
Because G(τ + T) = G(τ), so U(τ + T) is also the solution matrix to (20), moreover, the relation between U(τ + T) and U(τ) is
()
where A(τ) is nonsingular matrix.
Introducing transformation
()
then (26) can be expressed as
()
The nonsingular matrix P can make matrix B has the Jordan canonical form, the matrix B and matrix A are similar matrices, then they have the same eigenvalues. The eigenvalues of matrix A can be obtained by
()
When (29) has different roots, matrix B will be diagonal matrix as
()
So (28) can be rewritten as the following component form:
()
From format (31), we can obtain
()
so when t → ∞, that is, n → ∞
()
It can be seen if |λi| < 1, the system is stable, in case of, |λi| > 1 the system is unstable, when |λi| = 1 the system is critical condition of stability and instability.

It is known from the analysis mentioned above that the eigenvalues of the dynamic stability equation must be calculated before determining the dynamic instability region.

We can use initial condition U(0) = I to calculate the basic solution of (25) in a vibrational periodic. From (26), one can get A = U(τ), then solving (29), the eigenvalues are obtained. We can adopt the Runge-Kutta method to get the matrix A.

5. Results and Discussion

Numerical examples are presented to examine the effects of the dimensionless delay time, the aspect ratio, and the mean axial speed on the instability region.

5.1. The Plate with Four Edges Simply Supported (ssss)

Figure 2 shows the effect of the dimensionless delay time for ϕ = 1,  c = 2, and H = 10−4 (dotted line), 10−3 (solid line). Obviously, the larger the dimensionless delay time, the smaller the instability region.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The effect of the dimensionless delay time on the instability boundary.

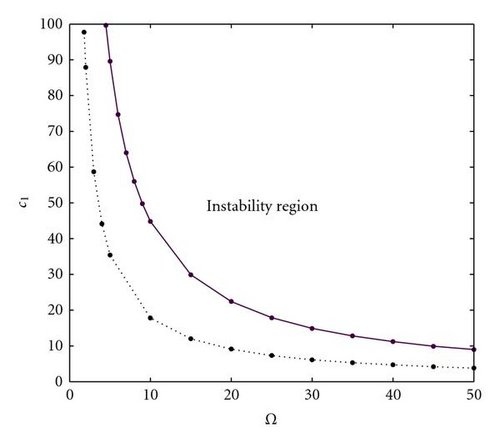
Figure 3 depicts the effect of the aspect ratio for H = 10−3,  c = 2, and ϕ = 0.5 (dashed line), 1 (solid line). It indicates that with the increase of aspect ratio, the instability region decreases.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The effect of the aspect ratio on the instability boundary.

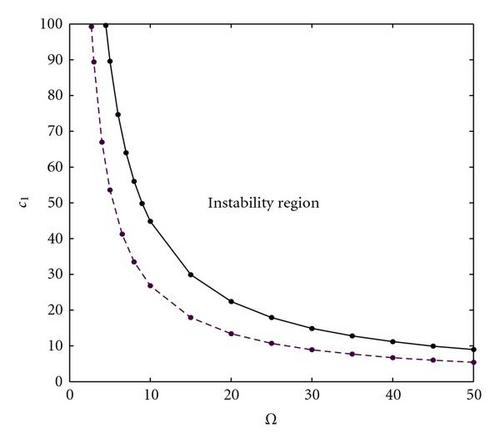
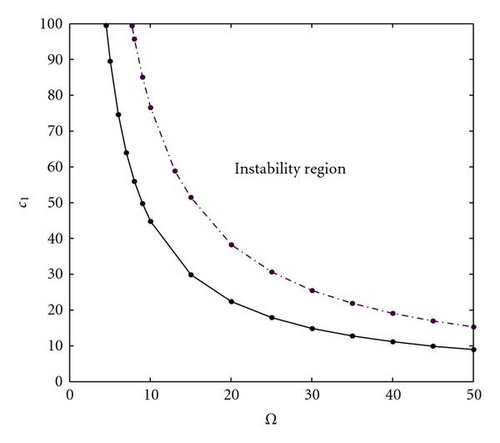
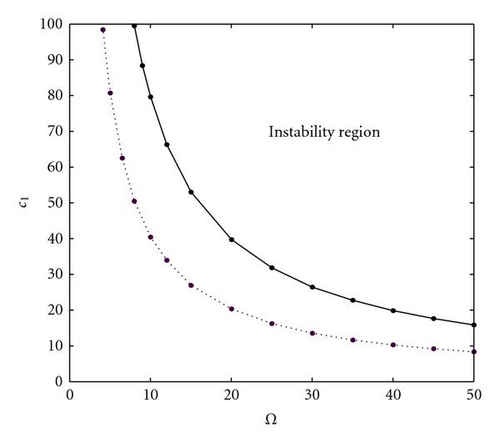
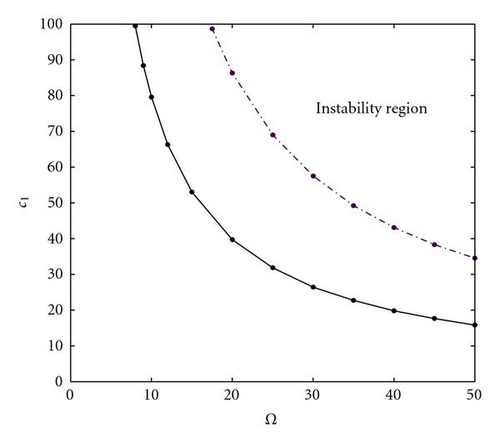
Figure 4 illustrates the effect of the mean axial speed for H = 10−3,  ϕ = 1, and c = 2 (solid line), 5 (dash-dotted line).It can be seen that the larger the mean axial speed, the smaller the stable region.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The effect of the mean axial speed on the instability boundary.

5.2. The Plate with Two Opposite Edges Simply Supported and Other Two Edges Clamped (cscs)

Figures 5, 6, and 7 demonstrate, respectively, the effects of the dimensionless delay time, the aspect ratio, and the mean axial speed on the instability region for the plate with two opposite edges simply supported and other two edges clamped. In Figure 5, ϕ = 1,  c = 2, and H = 10−4 (dotted line), 10−3 (solid line). In Figure 6, H = 10−3,  c = 2, and ϕ = 0.5 (dashed line), 1 (solid line). In Figure 7, H = 10−3, ϕ = 1, and c = 2 (solid line), 5 (dash-dotted line). Similar to the trends for the plate with four edges simply supported, the larger the dimensionless delay time, the larger the aspect ratio and the smaller the mean axial speed, which lead to the smaller the instability region. That is, the increasing dimensionless delay time, the increasing aspect ratio, and the decreasing mean axial speed make the instability boundaries move toward the increasing direction of c1 in plane (Ω, c1) and the instability regions become small.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
The effect of the dimensionless delay time on the instability boundary.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
The effect of the aspect ratio on the instability boundary.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
The effect of the mean axial speed on the instability boundary.

6. Conclusions

Dynamic stability of axially moving viscoelastic plate is studied in this paper. The axially moving speed of the viscoelastic plate is assumed as harmonically fluctuating about a constant mean value. The differential quadrature method is applied to the partial-differential equation governing the transverse parametric vibration.

The results of the present investigation indicate that, for the SSSS plate and the CSCS plate considered in the paper, (1) with the increase of the delay time H, the instability region decreases, (2) with the increase of the aspect ratio ϕ, the stability region decreases, (3) with the increase of the mean axial speed c, the instability region increases. In addition, for the same parameters, the instability region of CSCS plate is smaller than that of SSSS plate.

Acknowledgment

The research is supported by the National Natural Science Foundation of China (Project no. 10872163).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.