This paper investigates the forces acting on a cutter-oscillator during free longitudinal orthogonal turning under regenerative self-oscillation conditions. The cutter-oscillator had single degree of freedom in the direction of cutting thickness variation, while the workpiece was rigid and made of AISI 1045 steel. Cutting parameters such as cutting speed, feed rate, and depth of cut, as well as the cutter-oscillator’s additional mass, were varied. Two main groups of forces influencing the cutter-oscillator were identified. The first group consists of cutting forces generated during chip formation and friction between the tool edge, chip, and cutting surface. These forces depend on the equilibrium between the shear plane and the tool’s contact surfaces. The second group arises from the dynamic behavior of the cutter-oscillator and includes elastic, inertial, and damping forces. These are governed by the cutter-oscillator’s mass and its response to cutting loads. An important feature of the system is the mutual interaction between these force groups, forming feedback loops that complicate analysis and control. Under regenerative self-oscillations, the cutter-oscillator’s deflections are affected by a combination of forces whose individual contributions cannot be isolated. As a result, conventional dynamometers, which have their own elastic properties, are unsuitable for capturing the true dynamics of the cutting process in such conditions. Cutter-oscillators, by contrast, provide a more accurate representation of the cutting forces under self-oscillation. The oscillogram of the cutter edge deflection serves as a reliable and reproducible indicator of both static and dynamic cutting conditions. This approach aids in better understanding of the process mechanics, contributes to the optimization of cutting parameters, and enhances overall manufacturing efficiency.

1. Introduction

The study of the dynamics of the cutting process and the resulting forces is one of the key tasks in the field of metal machining and mechanical engineering. Forces acting on cutting tools directly affect the quality of machining, dimensional accuracy, tool wear resistance, and economic efficiency of production processes. Therefore, predicting cutting forces is an essential part for optimizing the cutting process.

In order to effectively analyze such processes, it is necessary to understand the nature of the occurrence of dynamic forces, as well as to possess methods of their accurate measurement and control. The dynamic nature of forces during cutting occurs in the presence of vibrations. The main type of vibration during turning is regenerative self-oscillation (SO), which occurs under conditions when there is waviness in the longitudinal section of the cut layer on the free cutting surface from the previous revolution of the part. In the presence of a phase shift between the waves on the cutting surface during the previous and current revolutions of the part, an oscillation in the thickness of the cut allowance occurs, which is the source of the regenerative SO.

2. Literature Review

The most convenient scheme for studying regenerative SO during turning is the scheme of free orthogonal cutting [1]. The condition of free orthogonal cutting is convenient in that in the orthogonal plane, located perpendicular to the direction of the cutting edge (CE), the system of forces is flat and the same for each point of CE. Let us consider the system of forces for this turning scheme (Figure 1), in which the part will be considered absolutely rigid, and the cutter will act as an oscillator. To simplify the system of forces, we will use a cutting insert with a rake angle equal to 0° and the principal approach angle of the CE equal to 90°.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

System of forces acting on the cutter at rake angle γ = 0° in orthogonal plane (π_O).

If the direction of the CE coincides with the y-axis (the principal approach angle of the CE equal to 90°), then in this direction, there will be no radial force F_y acting on the cutter. Then the resulting cutting force F will be determined only by its two components: in the x-axis—the longitudinal (thrust) force F_x, and in the z-axis—the tangential (cutting) force F_z. It is impossible to directly measure the resulting cutting force F, since it has an indefinite magnitude and direction of action. Therefore, its magnitude and direction are calculated by measuring the components F_x and F_z with a dynamometer according to formula [2]:

\begin{matrix} F = \sqrt{F_{z}^{2} + F_{x}^{2}} . \end{matrix}

()

During cutting, the CE of the lathe cutting tool simultaneously contacts the rake surface with the layer to be cut (chip) at a length km (Figure 1), thus generating the force of chip formation—F_rs. At contact of the flank surface of the cutter with the cutting surface on the section of length kg, a force acting on the flank surface of the cutter (wear force) appears—F_fs [3]. Each of these forces acts on the cutter independently of each other [4]. Therefore, their total action is considered as a sum of forces [5], which determines the resulting cutting force:

\begin{matrix} \bar{F} = \bar{F_{r s}} + \bar{F_{f s}} . \end{matrix}

()

The chip formation force and the force acting on the flank surface can also be decomposed into components acting along the x-axis and along the z-axis. In this case, the horizontal component of the chip formation force

F_{χ}^{r s}

is equal to the friction force F_fr between the chip and the rake surface of the cutter (

F_{χ}^{r s} = F_{f r}

), and the vertical component is equal to the normal force N (

F_{z}^{r s} = N

). As for the force on the flank surface of the cutter, in this case, the horizontal component of the force

F_{χ}^{f s}

is equal to the normal force, and the vertical component

F_{z}^{f s}

is equal to the friction force between the cutting surface and the flank surface of the cutter. Then the components of the resulting cutting force along the z-axis will be:

\begin{matrix} F_{z} = F_{z}^{r s} + F_{z}^{f s} . \end{matrix}

()

And the components of the resulting cutting force along the x-axis will be:

\begin{matrix} F_{χ} = F_{χ}^{r s} + F_{χ}^{f s} . \end{matrix}

()

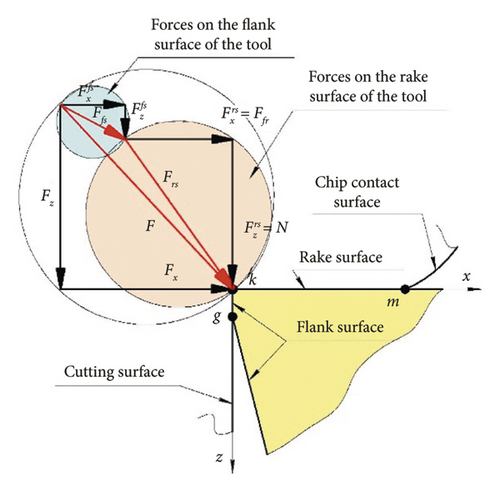
To study cutting as a physical process, the system of forces is considered separately: only on the rake surface, due to the process of chip formation, and on the flank surface, due to its friction with the cutting surface [6]. The forces acting on the cutter from the flank surface F_fs are significantly less than the forces acting on the rake surface of the cutter F_rs. Moreover, the actions of these forces are independent of each other. Therefore, to simplify the system of forces, the cutting force on the flank surface F_fs is usually not taken into account (F = F_rs). It role becomes significant only in cases of cutting with small cutting thicknesses.

To study the forces acting on the cutter under vibration cutting conditions, numerical and analytical methods [7, 8], modeling, artificial intelligence technologies [9, 10], and experimental methods [11, 12] are used. In experimental studies, dynamometers of different designs are used to study forces [12, 13]. Cutting forces have good sensitivity to vibration. Modern designs of dynamometers for measuring the components of cutting forces F_x, F_y, and F_z allow these measurements practically eliminating the mutual influence of forces on different axes [14]. However, due to their complex design, the dynamometers reflect their own elastic system (ES) in the investigation rather than the cutting process [15].

The most suitable devices for investigating cutting forces under regenerative SO conditions are single-degree-of-freedom (SDOF) cutter-oscillators, whose direction of force measurement aligns with the direction of change in shear thickness (x-axis) [15, 16].

However, despite the extensive body of research dedicated to the dynamics of the cutting process under regenerative SO conditions, many studies have not sufficiently addressed the simplification of the ES of the cutter-oscillator in order to constrain its vibrations solely to the direction of variation in chip thickness—the primary source of regenerative SO. Such simplification makes it possible to isolate the specific force system responsible for exciting vibration of the cutter-oscillator in that direction.

On the other hand, the measurement instruments used in existing studies to investigate the dynamic components of the forces acting on the cutter-oscillator often fail to provide the required level of accuracy and data reproducibility.

The objective of this study is to analyze the force system responsible for the oscillations of SDOF cutter-oscillator during turning under conditions of regenerative SO.

The scientific novelty of this work lies in the assessment of the contribution of each component of the force system to the overall dynamics of the cutting process, as well as in the establishment of an objective and accurate method for measuring the dynamic component of all types of forces acting on the cutter-oscillator during turning under regenerative SO conditions.

3. Analysis of the System of Forces Acting on a Cutter-Oscillator With SDOF

Figure 2 shows the scheme of forces, in the orthogonal plane (π_O) in free orthogonal cutting, proposed by Merchant [17, 18] and studied in detail by Zorev [19]. The physical basis of this scheme is the position of the chip equilibrium between the acting forces on the conventional shear plane kn with length l and the contact surface of the chip with the tool km with length C (Figure 2). The stress-strain state of the chip-forming zone is assumed to be flat. Therefore, increasing the width of the cut layer a, located along the CE (point k), proportionally increases the chip-forming force F_rs = F, but does not change the stress-strain state at each point of the CE. In order to maintain the chip equilibrium conditions, equal forces with opposite directions act on the chip from both sides. Shear force F_s and normal force F_n act in the shear zone, and friction force F_fr and normal force N act in the tool contact zone.

The force F_s in the shear plane is equal to:

\begin{matrix} F_{s} = a \cdot l \cdot τ, \end{matrix}

()

where а is the width of the cutting layer, τ is the shear tangent stress of the processed material, and l is the length of shear plane.

\begin{matrix} l = \frac{h_{0}}{\sin ϕ}, \end{matrix}

()

where h₀ is the nominal cutting thickness and ϕ is the angle of inclination of the shear plane.

In continuous, vibration-free cutting, the chip formation force is expressed as a relationship:

\begin{matrix} F = F_{r s} = \frac{F_{s}}{\cos (ϕ + μ)} = \frac{h_{0} a τ}{\sin ϕ \cdot \cos (ϕ + μ)}, \end{matrix}

()

where μ is the angle of action of force F with respect to the velocity vector. Replacing equations (6) in (7) is possible only for vibration-free cutting conditions.

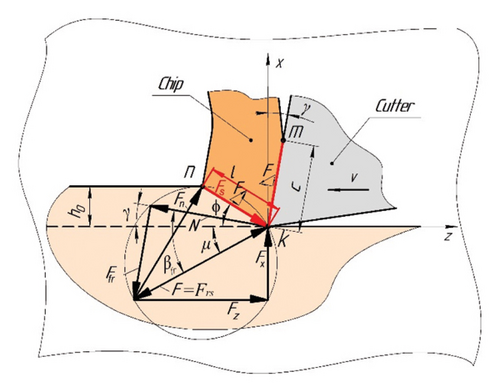
If the system of forces shown in Figure 2 is applied to a cutter-oscillator, which is absolutely rigid, i.e., immobile from the action of forces in the chip-forming zone (Figure 3(a)), then reactions R_x and R_z, equal to the forces F_x and F_z, but oppositely directed, appear at the points where the cutter-oscillator is fixed.

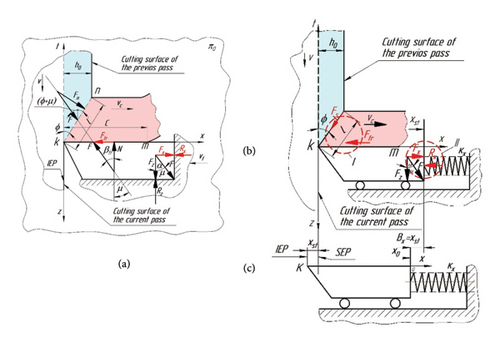
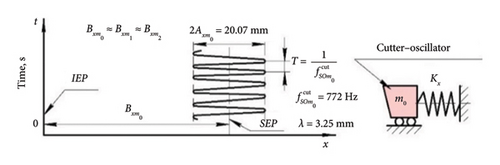
Under static loading, the deformation of an elastic element of the cutter-oscillator is related to the loading force by Hooke’s law [20]. From Figure 3 shows that the CE (point k) of the cutter-oscillator has two equilibrium positions. Initial equilibrium position (IEP) (Figure 3(c)), when there is no cutting process. The of static equilibrium position (SEP) (Figure 3(b)), when the forces F_x and F_z act on the cutter-oscillator during the cutting process, but the CE is displaced only along the x-axis by the value x_st = B_x (B_x—static deflection of the cutter-oscillator), since there is only SDOF.

Figure 3(a) shows that the force F_x and the reaction R_x change according to different laws when the cutting thickness h changes and the cutting edge moves along x.

The cutting force is expressed by the dependence [21]:

\begin{matrix} F_{x} = C_{p x} {\cdot a \cdot h}^{0.75}, \end{matrix}

()

where the coefficient C_px depends on cutting conditions and h is the cutting thickness.

A reaction of the cutter-oscillator [20, 22]:

\begin{matrix} R_{x} = k_{x} \cdot x, \end{matrix}

()

where k_x is the stiffness of the elastic element and x is the deformation value. All dynamometers for measuring static cutting forces are based on this principle [13, 14].

Figures 4(a) and 4(c) show that the zero value of the reaction of the cutter-oscillator R_x = 0 starts from the IEP and increases in proportion to the increase in its displacement along the x-axis during cutting until the equilibrium between F_x and R_x, i.e., the SEP, occurs.

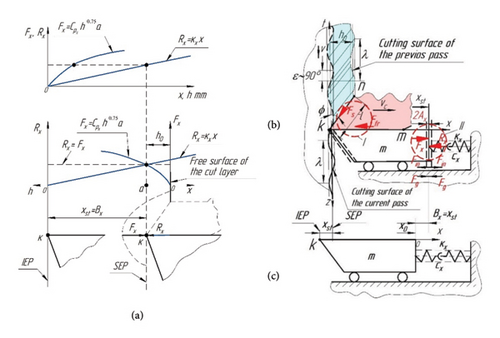
The zero value of the force F_x = 0 is located at the point of contact of the CE (point k) with the free surface of the layer to be cut and increases according to the power law with the increase of the cutting thickness h. Thus, it can be stated that during cutting, there are two zones in which the conditions of force equilibrium are maintained (Figures 4(b) and 4(c)): the zone between the shear plane and the contact surface of the cutter and the zone between the force F_x and the elastic reaction R_x.

During continuous cutting along the “vibration trace” (Figures 4(b) and 4(c)) on the cutting surface, chip formation occurs as a result of shear deformations under the shear angle ϕ along the length l, as well as during cutting without vibration (Figure 2). However, in the presence of a wave on the cutting surface from the previous revolution, the length of the shear plane will be variable and therefore the force F_s in the shear plane calculated by equation (5) will also be variable [23].

It has been experimentally established that the frequency of oscillation of the length of shear plane is equal to the frequency of oscillation of CE of the cutter-oscillator along the x-axis $f_{S O}^{cut}$ [23]. Therefore, the shear force F_s will also oscillate with frequency $f_{S O}^{cut}$ . Based on the statement about the preservation of the chip equilibrium condition, we can assume that the force F_x will also start oscillating with frequency $f_{S O}^{cut}$ , but with some delay. The oscillation of force F_x should cause the oscillation of cutter-oscillator reaction R_x. But since the moving cutter-oscillator has a mass, there are additional inertia forces $F_{i n} = m \ddot{x}$ and damping forces $F_{g} = C_{x} \dot{x}$ , at the appearance of which the conditions of static cutting become dynamic.

4. Materials and Methods

The forces acting on the cutter-oscillator were investigated during longitudinal turning of a rigid part made of AISI 1045 steel (Figure 5). The research was carried out on a CNC lathe mod. Zenitech WL 320 (Figure 6(a)). The design of the cutter-oscillator (Figure 6(b)) provided for the possibility of installing an additional mass to the head of cutter-ocsillator to change the natural frequency of oscillation in the range from f = 150 to f = 1250 Hz.

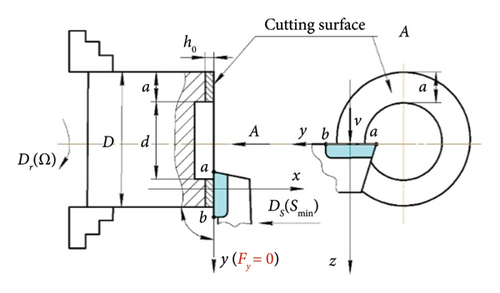
During turning process, the cutting modes were varied: cutting speed v = 100…300 m/min, feed S = h₀ = 0.1…0.3 mm/rev, and depth of cut t = a = 1…2 mm. The cutting insert had a principal approach angle of φ = 90°, a rake angle of γ = 8°, and a clearance angle of α = 8° and was made of HS123 carbide.

The cutter-oscillator with SDOF provided movement of CE in the direction that coincided with the direction of the force F_x [15]. The displacement of CE was measured with a Schneider Electronics XS4-P12AB110 sensor. The analog-to-digital converter mod. LCard E14-0 converted the sensor signal into a digital oscillogram form and transmitted it to a personal computer (Figure 7).

5. Results

5.1. Results of Investigation of Inertia Forces Under Cutting Conditions With Vibration

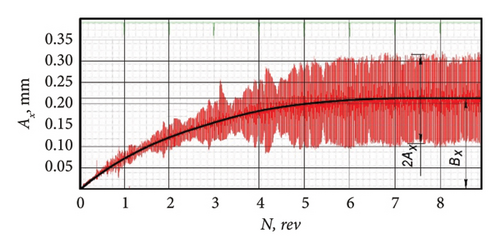
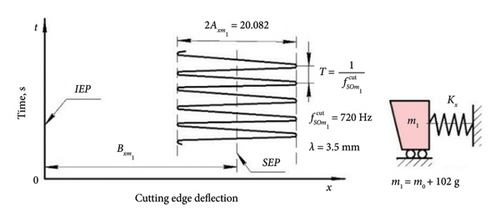
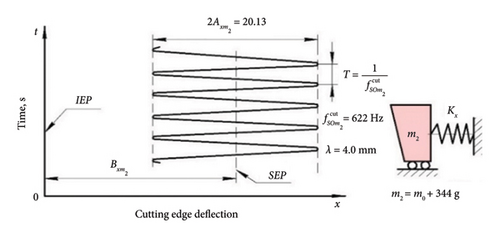
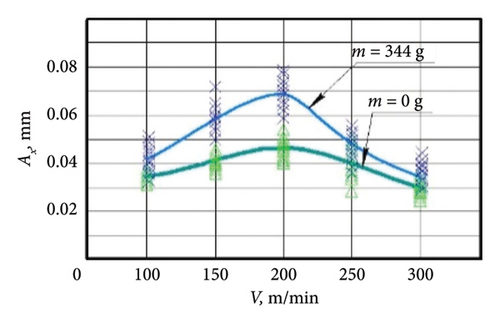
In the course of experimental studies, the results of the influence of the mass of the cutter-oscillator on its dynamic behavior (50 experiments for each value of additional mass) were obtained. The turning was carried out at a constant cutting speed corresponding to the regenerative SO zone. The width of the flank surface wear area was kept in the range of 0.10…0.15 mm to ensure constant damping conditions. Additional weights m₁ = 102 g and m₂ = 344 g were attached to the head of the cutter-oscillator. The stiffness of the cutter ES was constant in all cases. The experimental results are summarized in Table 1 and Figures 8 and 9.

Table 1. Experimental results (v = 150 m/min, S = 0.2 mm/rev, t = 1 mm).

Additional mass, m, g	Diameter D, mm	Spindle speed, Ω, rpm	Static deflection, B_x, mm	Amplitude, A_x, mm	Frequency $f_{S O}^{cut}$ , Hz	Wavelength, λ, mm
0	132.5	360.4	0.082	0.051	762.7	3.3
0	120.5	396.2	0.08	0.061	772.3	3.2
0	106.5	448.3	0.081	0.07	769.2	3.3
0	78.5	608.2	0.079	0.075	769.8	3.3
0	44.5	1073	0.077	0.077	767	3.3
102	128	373	0.074	0.084	722	3.5
102	102	468.1	0.075	0.078	716.9	3.5
102	80	596.8	0.078	0.081	724.8	3.5
102	44	1085.1	0.078	0.082	720.1	3.5
102	30	1591.5	0.078	0.084	711.5	3.5
344	132.5	360.4	0.079	0.093	594.5	4.2
344	112.5	424.4	0.077	0.095	593.9	4.2
344	94.2	505.3	0.079	0.093	622.1	4
344	56.5	845.1	0.075	0.11	617.9	4.1
344	32.5	1469.1	0.074	0.107	631.9	4

5.2. Results of Investigation of Friction Forces on the Flank Surface of the Cutter-Oscillator Under Cutting Conditions With Vibration

The results of the experimental study of the influence of friction forces on the flank surface of the cutter-oscillator on the dynamics of the cutting process are presented in Table 2 and Figure 10.

Table 2. The average vibration amplitude (S = 0.2 mm/rev, t = 1 mm, m = 0 g).

Cutting speed, v, m/min	Width of the wear area on the flank surface, h_f
Cutting speed, v, m/min	0–0.05 mm	0.1–0.15 mm	0.25–0.25 mm	0.3–0.5 mm
50	0.016	0.007	0.006	0.000
75	0.028	0.014	0.012	0.001
100	0.038	0.020	0.014	0.002
125	0.053	0.026	0.018	0.003
150	0.067	0.036	0.021	0.003
175	0.084	0.042	0.025	0.005
200	0.100	0.050	0.028	0.006
225	0.117	0.060	0.030	0.007
250	0.143	0.050	0.024	0.006
275	0.158	0.043	0.022	0.004
300	0.175	0.030	0.013	0.003
325	0.188	0.020	0.009	0.002
350	0.200	0.008	0.005	0.000

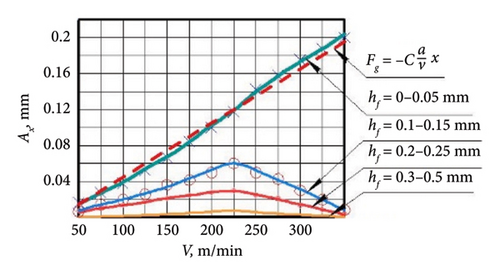
The red dashed line (Figure 10) shows the results obtained by Altintas et al. [24] for the case of negative damping caused by friction on the flank surface of the cutter with force F_g. Figure 11 shows the results of the study of the effect of additional mass on the vibration amplitude for a cutter-oscillator with area of wear of the CE.

6. Discussion

The cutter-oscillator was displaced under the action of the static component of the cutting force by the value x_st = B_x in the SEP relative to which it performed oscillatory motion with amplitude A_x. 4 types of forces simultaneously affected the cutter-oscillator: cutting force, elastic reaction force, inertia force, and damping force. Physically, all these forces have different nature of origin and directions of action. Therefore, when cutting under regenerative SO conditions, there is a case of action of forces of mixed nature (Figure 12). It is known that if forces of mixed character can develop in mechanical systems, they are not decomposable into the sum of these forces. In particular, this applies to cutter-oscillating systems [25].

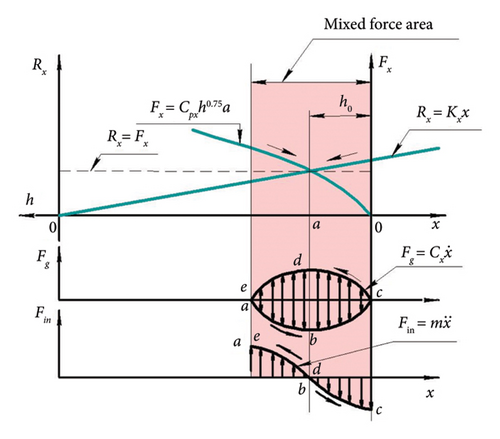
Since the cutter-oscillator has mass, on the wave of oscillatory motion (Figure 13), starting from the SEP position, the inertia force F_in increases, reaching its maximum value at points a, c, and e, where the acceleration has maximum values. However, the CE oscillation occurs in the medium of the sheared material, so naturally there is resistance to oscillatory motion, the value of which depends on the speed of oscillatory motion. With increasing speed, the resistance increases. Therefore, in points b and d, the speed of the maximum resistance (damping) force F_g will be maximum. And the direction of action of the force F_g will be opposite to the direction of motion of the cutter-oscillator.

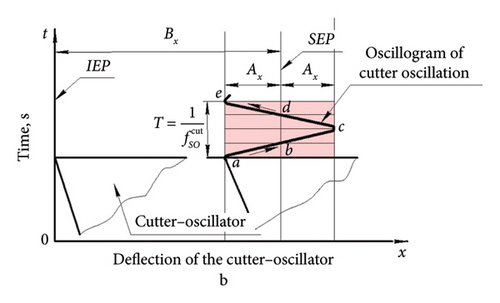
In this case, measuring the values of simultaneously acting forces is practically impossible. But, it is enough to simply measure and memorize graphically the law of motion of the cutter-oscillator from the simultaneous action of all these types of forces as an oscillogram of the deflection of CE (Figure 13). The deflection of the cutter-oscillator is completely determined by the oscillogram of its oscillations, which consists of two parts: a constant part, which is determined by the deviation of B_x from the IEP, and a variable part, which is determined by oscillations with amplitude relative to the SEP. The primary source of oscillation is the oscillation of the shear force due to the oscillation of the length of the conditional shear plane, when cutting along the “vibration trace” located on the free surface of the cut layer (Figure 4(b)). But, since the force F_s is related to the friction force F_fr by the condition of preservation of the chip equilibrium, naturally the oscillation of the force F_s will cause the oscillation of the force F_fr. If the rake angle CE is 0°, then the friction force F_fr is equal to the cutting force in the direction of the x-axis F_x, while F_fr acts on the chip, and F_x acts on the cutter. Therefore, the oscillation of force F_tr will be equal to the oscillation of force F_x. But the force F_x is balanced by the elastic reaction force R_x. In this case, the oscillations along the force chain are transmitted from the oscillations of force F_s to the oscillations of forces F_x and R_x. And the force F_x acts in the direction of pushing the cutter out of the cutting zone, and the reaction force R_x acts in the direction of returning the cutter to the cutting zone.

As a result of studies of the effect of inertia force on cutting dynamics (Figures 8 and 9), it was found that:

1.
Changing the mass of the cutter-oscillator has practically no effect on the static deflection B_x, which depends mainly on the rigidity of the cutter-oscillator.
2.
The vibration characteristics of the cutter-oscillator deflection in the form of amplitude A_x and frequency SO $f_{S O}^{cut}$ depend significantly on the mass. The amplitude increases and the frequency decreases because mass is a characteristic of inertia.

The obtained results are in full agreement with the theory of mechanical vibrations [11, 26]. They allow us to assert the possibility of effective application of the proposed methodology to study the physical basis of cutting dynamics under conditions of loading by forces of mixed character.

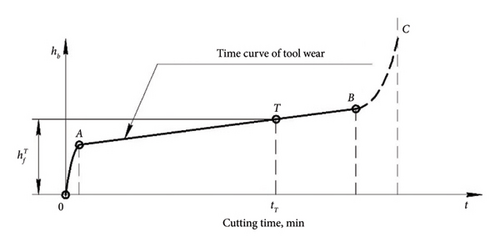
Figure 14 shows the conditions of contact of the flank surface of the oscillator cutter with the cutting surface when cutting without vibration. At the beginning of cutting (Figure 14(a)), the geometry of the flank surface is estimated by the clearance angle α and the cutting-edge radius ρ_c. As a result of the elastic recovery, the cutting surface is above the shear line by the value Δх, so the flank surface is in contact with the cutting surface for a length of Δz. However, due to the very high pressure in the CE area (point K), a flank wear land h_f appears on the flank surface within a short time (Figure 14(b)) [27]. The flank wear land of the cutter is affected by the normal force and the friction force from the cutting surface, which are added to the forces acting from the side of the chips on the rake surface. The change in the size of the flank wear land is shown as a wear curve (Figure 14(c)) [28].

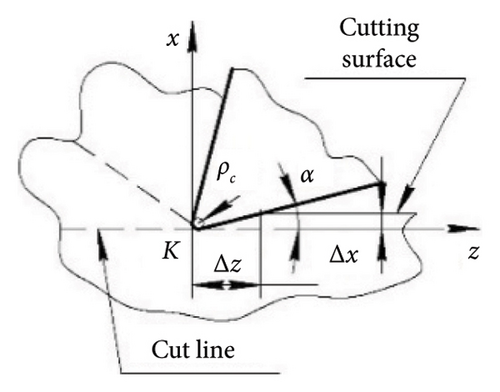
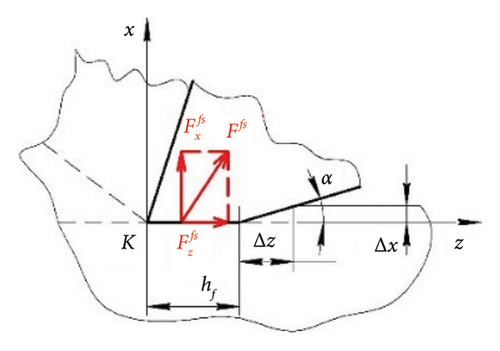
The effect of the friction force on the flank surface in regenerative SO has been studied quite well [29]. The cutting surface formed by the cutter during regenerative SO is wavy, which is usually depicted as a sinusoid. Figure 15 shows one wave of length λ, at different points of which the conditions of contact of the flank surface of the cutter with the cutting surface are shown. At each point A, B, C and D, the cutting plane (π_C), tangent to the cutting surface, is shown. The actual clearance angle α lies between the flank surface of the cutter and the cutting plane (π_C). At points A and C, the clearance angle α is equal to the nominal value. But at point B, the value of the clearance angle becomes minimal α_min or even negative, which sharply increases friction and makes it impossible for the flank surface to penetrate the cutting surface. At point D, the clearance angle has a maximum value α_max and the flank surface of the cutter does not contact the cutting surface. Thus, at point B, the cutting plane (π_C) has the maximum angle of inclination σ_max. With decreasing wavelength λ, the angle of inclination σ_max should increase and, naturally, the clearance angle α will decrease, increasing the damping capacity of the flank surface.

The results of the study of the influence of friction forces on the flank surface showed that with a decrease in cutting speed, the wavelength on the cutting surface will decrease, the inclination angle of the cutting plane (π_C) will increase, and the damping force F_g will increase. The wavelength on the cutting surface depends on the cutting speed according to the formula:

\begin{matrix} λ = \frac{1000 v}{60 f_{S O}^{c u t}}, \end{matrix}

()

where

f_{S O}^{cut}

is the frequency of cutter-oscillator during turning in the direction of the x-axis and v is the cutting speed.

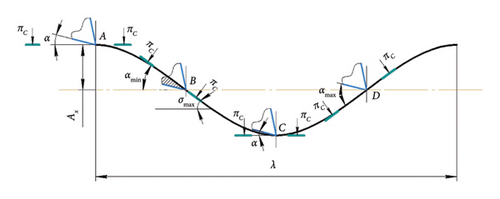
The obtained experimental results fully confirm the existing provisions of cutting dynamics [29, 30].

Altintas et al. [24] proposed a formula for determining the damping force:

\begin{matrix} F_{g} = - C \frac{a}{v} \dot{x} . \end{matrix}

()

According to this equation, with increasing cutting speed, the damping force decreases proportionally, and the oscillation amplitude increases.

The results of the experimental verification of this statement (Figure 10) showed that the condition equation (11) is satisfied only if there is no flank wear land h_f on the flank surface of the cutter. But such a condition is maintained for a short time during the running-in period of the cutter—section of AO (Figure 14(c)). With an increase in the size of the area on the flank wear land h_f > 0.05 mm, the vibration excitation intensity sharply decreases and has a different pattern. This pattern has a certain cutting speed v = 225 m/min at which maximum vibrations are observed. Above and below this cutting speed, the regenerative SO decreases and thereby highlights the speed range in which the regenerative SOs are excited.

The size of the wear land on the flank surface of the cutter has a greater effect on the damping of regenerative SO compared to the effect of friction on the flank surface of the cutter caused by a decrease in the actual clearance angle during cutting along “wave trace.” This is due to the fact that with an increase in the wear land on the flank surface of the cutter, the forces of resistance to the penetration CE into the cut allowance sharply increase.

7. Conclusions

Analysis of the system of forces arising during cutting showed that there are two groups of forces. The first group includes forces that arise directly during cutting. Chip formation and friction of the cutter against the chip and the cutting surface occur. The second group includes forces that are caused by the movement of a part or tool that has mass.

Each group of forces is determined by certain equilibrium conditions. The first group of forces is determined from the condition of equilibrium of the chip between the conditional plane of shear and the line of contact of the chip with the cutter. The second group of forces is determined from the conditions of equilibrium between the cutting force and the forces of elasticity, inertia, and damping of the cutter-oscillator. There is a direct and inverse relationship between these two groups of forces.

When cutting under regenerative SO conditions, mixed forces act on the cutter-oscillator, the contribution of which to the deflection of the CE cannot be estimated as the sum of these forces. Therefore, in this case, the oscillogram of the cutting tool deflections, as the law of its movement from the action of all types of forces, is an objective, well-reproducible criterion for assessing both static and dynamic conditions of the cutting process.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

All authors have read and agreed to the published version of the manuscript.

Funding

No funding was received for this research.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Mazur M. P., Vnukov Y. M., Hrabchenko A. I. et al., Osnovy Teorii Rizannia Materialiv, 2010, Novyi Svit-2000, Lviv.
Google Scholar
2 Duarte L., Dellinger N., Dellinger G., Ghenaim A., and Terfous A., Experimental Investigation of the Dynamic Behaviour of a Fully Passive Flapping Foil Hydrokinetic Turbine, Journal of Fluids and Structures. (2019) 88, 1–12, https://doi.org/10.1016/j.jfluidstructs.2019.04.012, 2-s2.0-85064935734.
10.1016/j.jfluidstructs.2019.04.012
Web of Science® Google Scholar
3 Yiǧit K. and Tuǧrul Ö., An Analytical-Thermal Modeling Approach for Predicting Forces, Stresses and Temperatures in Machining With Worn Tools, Manufacturing Engineering Division. (2005) 16, no. 1, 489–498, https://doi.org/10.1115/IMECE2005-81035, 2-s2.0-33646014437.
10.1115/IMECE2005-81035
Google Scholar
4 Childs T. H. C., Arrazola P. J., Azpitarte L. et al., Physical Modelling With Experimental Validation of High Ductility Metal Cutting Chip Formation Illustrated by Copper Machining, International Journal of Machine Tools and Manufacture. (2022) 173, https://doi.org/10.1016/j.ijmachtools.2021.103847.
10.1016/j.ijmachtools.2021.103847
Web of Science® Google Scholar
5 Milutinović M. and Tanović L., Сutting Forces in Hard Turning Comprising Tool Flank Wear and Its Implication for the Friction Between Tool and Workpiece, Tehnički Vjesnik. (2016) 23, no. 5, 1373–1379, https://doi.org/10.17559/TV-20140903224947, 2-s2.0-84991628225.
10.17559/TV-20140903224947
Google Scholar
6 Yaonan C., Xiaoyu G., Rui G., and Mengda L., Modeling of Dynamic Cutting Force Considering Flank Wear and Analysis of Tool Wear Mechanism in Milling 508III Steel, Integrated Ferroelectrics. (2022) 233, 1–18, https://doi.org/10.1080/10584587.2023.2191501.
10.1080/10584587.2023.2191501
Google Scholar
7 Castorena-Minor H. D., Saldivar B., and Bueno C., Critical Depth of Cut in Turning Processes: Time and Frequency Domain Approaches, IFAC-PapersOnLine. (2024) 58, no. 27, 148–153, https://doi.org/10.1016/j.ifacol.2024.10.315.
10.1016/j.ifacol.2024.10.315
Google Scholar
8 Wang A., Zhou B., and Jin W., Dynamics of the Regenerative Turning Chatter With Little Mass Eccentricity, International Journal of Non-linear Mechanics. (2024) 166, https://doi.org/10.1016/j.ijnonlinmec.2024.104851.
10.1016/j.ijnonlinmec.2024.104851
Web of Science® Google Scholar
9 Sun H., Jin H., Zhuo Y., Ding Y., Guo Z., and Han Z., Investigation on a Chatter Detection Method Based on Meta Learning for Machining Multiple Types of Workpieces, Journal of Manufacturing Processes. (2024) 131, 1815–1832, https://doi.org/10.1016/j.jmapro.2024.09.091.
10.1016/j.jmapro.2024.09.091
Web of Science® Google Scholar
10 Kounta C. A. K. A., Arnaud L., Kamsu-Foguem B., and Tangara F., Deep Learning for the Detection of Machining Vibration Chatter, Advances in Engineering Software. (2023) 180, https://doi.org/10.1016/j.advengsoft.2023.103445.
10.1016/j.advengsoft.2023.103445
Web of Science® Google Scholar
11 Nakagawa J., Farahani N. D., and Altintas Y., Identification and Effect of Chip Shear Band on Chatter Vibration in the Turning of Nickel Alloy 718, CIRP Journal of Manufacturing Science and Technology. (2023) 44, 82–90, https://doi.org/10.1016/j.cirpj.2023.05.004.
10.1016/j.cirpj.2023.05.004
Web of Science® Google Scholar
12 Yan S. and Sun Y., Enhancing Tool Dynamics and Stability in Internal Turning With an Adjustable Clamping Device Under Variable Cutting Conditions, Mechanical Systems and Signal Processing. (2024) 208, https://doi.org/10.1016/j.ymssp.2023.111007.
10.1016/j.ymssp.2023.111007
Web of Science® Google Scholar
13 Li K., He S., Liu H., Mao X., Li B., and Luo B., Bayesian Uncertainty Quantification and Propagation for Prediction of Milling Stability Lobe, Mechanical Systems and Signal Processing. (2020) 138, https://doi.org/10.1016/j.ymssp.2019.106532.
10.1016/j.ymssp.2019.106532
Web of Science® Google Scholar
14 Emami M. and Karimipour A., Theoretical and Experimental Study of the Chatter Vibration in Wet and MQL Machining Conditions in Turning Process, Precision Engineering. (2021) 72, 41–58, https://doi.org/10.1016/j.precisioneng.2021.04.006.
10.1016/j.precisioneng.2021.04.006
Web of Science® Google Scholar
15 Vnukov Y., Tryshyn P., Kozlova O., and Dyadya S., Cutter-Oscillator With Single-Degree-of-Freedom for the Study of Cutting Vibrations, Strojnícky časopis—Journal of Mechanical Engineering. (2024) 74, no. 1, 169–180, https://doi.org/10.2478/scjme-2024-0017.
10.2478/scjme-2024-0017
Google Scholar
16 Christopher M., Sam T., and Neil D., Chatter, Process Damping, and Chip Segmentation in Turning: A Signal Processing Approach, Journal of Sound and Vibration. (2009) 329, no. 23, 4922–4935, https://doi.org/10.1016/j.jsv.2010.05.025, 2-s2.0-77955428687.
10.1016/j.jsv.2010.05.025
Google Scholar
17 Merchant M., Mechanics of the Metal Cutting Process. I. Orthogonal Cutting and a Type 2 Chip, Journal of Applied Physics. (1945) 16, no. 5, 267–275, https://doi.org/10.1063/1.1707586, 2-s2.0-36849140209.
10.1063/1.1707586
Web of Science® Google Scholar
18 Monroy Vazquez K. P., Giardini C., and Ceretti E., L. Laperrière and G. Reinhart, Cutting Force Modeling, CIRP Encyclopedia of Production Engineering, 2014, Springer, https://doi.org/10.1007/978-3-642-20617-7_6399.
10.1007/978-3-642-20617-7_6399
Google Scholar
19 Zorev N. N., Some Issues of Metal Cutting Mechanics (in Russian), 1956, Moscow.
Google Scholar
20 Liu P. and Yan P., A Modified Pseudo-Rigid-Body Modeling Approach for Compliant Mechanisms With Fixed-Guided Beam Flexures, Mechanical Sciences. (2017) 8, no. 2, 359–368, https://doi.org/10.5194/ms-8-359-2017, 2-s2.0-85038366201.
10.5194/ms-8-359-2017
Web of Science® Google Scholar
21 Tlusty J. and Spacek L., Samobuzené Kmity v Obráběcích Strojích, 1954, ČSAV.
Google Scholar
22 Divjak A., Modrić D., Kovačić I., and Cviljušac V., Anisotropic Mechanical Properties of Materials in Stereolithographic, Additive Manufacturing January Technical Gazette. (2020) 27, no. 6, 1748–1753, https://doi.org/10.17559/TV-20190507160151.
10.17559/TV-20190507160151
Google Scholar
23 Tryshyn P., Vnukov Y., Dyadya S., and Kozlova O., Experimental Verification of the Impact of Phase Shift Between Neighboring Waves on the Intensity of Regenerative Oscillations During Continuous Cutting in Grabchenko’s International Conference on Advanced Manufacturing Processes VI. Interpartner 2024, Lecture Notes in Mechanical Engineering. (2025) Springer, 342–357, https://doi.org/10.1007/978-3-031-82746-4_31.
10.1007/978-3-031-82746-4_31
Google Scholar
24 Altintas Y., Eynian M., and Onozuka H., Identification of Dynamic Cutting Force Coefficients and Chatter Stability With Process Damping, CIRP Annals. (2008) 57, no. 1, 371–374, https://doi.org/10.1016/j.cirp.2008.03.048, 2-s2.0-43649090981.
10.1016/j.cirp.2008.03.048
Web of Science® Google Scholar
25 Panovko Y. H., Fundamentals of the Applied Theory of Vibration and Impact L.,, 1976, Mashyno-Stroenye.
Google Scholar
26 Li K., He S., Li B., Liu H., Mao X., and Shi C., A Novel Online Chatter Detection Method in Milling Process Based on Multiscale Entropy and Gradient Tree Boosting, Mechanical Systems and Signal Processing. (2020) 135, https://doi.org/10.1016/j.ymssp.2019.106385.
10.1016/j.ymssp.2019.106385
Web of Science® Google Scholar
27 Necati U. and Aslantas A., Experimental Evaluation of Tool Wear and Surface Roughness Under Different Conditions in High-Speed Turning of Ti6Al4V Alloy, Journal of Materials and Manufacturing. (2023) 2, no. 1, 1–10, https://doi.org/10.5281/zenodo.8020503.
10.5281/zenodo.8020503
Google Scholar
28 Colantonio L., Equeter L., Dehombreux P., and Ducobu F., A Systematic Literature Review of Cutting Tool Wear Monitoring in Turning by Using Artificial Intelligence Techniques, Machines. (2021) 9, no. 12, https://doi.org/10.3390/machines9120351.
10.3390/machines9120351
Web of Science® Google Scholar
29 Tlusty G., Manufacturing Process and Equipment, 2000, Prentice Hall.
Google Scholar
30 Schmitz T. L. and Smith K. S., Machining Dynamics, Frequency Response to Improved Productivity. (2019) 2nd edition, Springer.
Google Scholar

All articles

Study of the System of Forces Acting on the Cutter-Oscillator Under Conditions of Turning With Vibration

Abstract

1. Introduction

2. Literature Review

3. Analysis of the System of Forces Acting on a Cutter-Oscillator With SDOF

4. Materials and Methods

5. Results

5.1. Results of Investigation of Inertia Forces Under Cutting Conditions With Vibration

5.2. Results of Investigation of Friction Forces on the Flank Surface of the Cutter-Oscillator Under Cutting Conditions With Vibration

6. Discussion

7. Conclusions

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Study of the System of Forces Acting on the Cutter-Oscillator Under Conditions of Turning With Vibration

Abstract

1. Introduction

2. Literature Review

3. Analysis of the System of Forces Acting on a Cutter-Oscillator With SDOF

4. Materials and Methods

5. Results

5.1. Results of Investigation of Inertia Forces Under Cutting Conditions With Vibration

5.2. Results of Investigation of Friction Forces on the Flank Surface of the Cutter-Oscillator Under Cutting Conditions With Vibration

6. Discussion

7. Conclusions

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information