The increasing scale and capacity of wind turbines, driven by advancements in wind power technology, present significant challenges in managing fatigue loads and vibrations. To address these challenges, we have designed an eddy current tuned rolling cylinder damper (ECTRCD) which incorporates eddy current–induced damping into the traditional tuned rolling cylinder damper (TRCD) and optimised the parameters including the radius ratio, mass ratio, frequency ratio and damping ratio. The optimal frequency ratio is observed between 0.9 and 1, with the damping ratio around 0.05 and the radius ration of 1/6. On the contrary, the optimal damping performance improves as the mass ratio increases. Additionally, the reduction ratio of the equivalent fatigue load is 17.7% by the ECTRCD with the optimal parameters (a radius ratio of 1/6, a mass ratio of 1.2%, a frequency ratio of 0.943 and a damping ratio of 0.059). Compared with the TRCD, the enhancement in this value is modest, with only a 1% improvement. Nevertheless, the displacement at the tower top in the side-to-side direction is significantly mitigated, particularly under high wind speeds. This finding underscores the potential of the ECTRCD as a promising alternative to conventional TRCDs, offering enhanced damping performance and improved structural stability.

1. Introduction

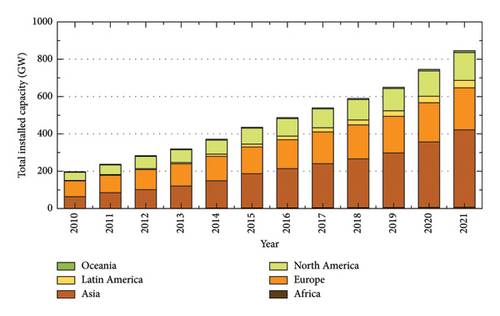
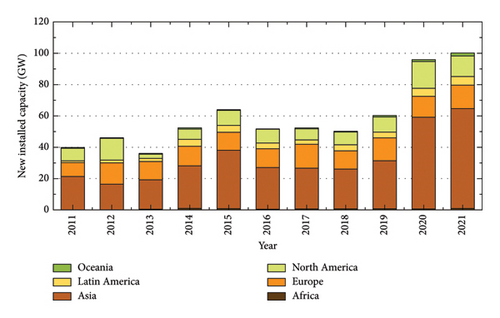
Wind energy represents a clean and renewable power source, distinctly advantageous over fossil fuels due to its nonemissive nature and minimal contribution to climate change. Utilising wind power significantly reduces dependency on fossil fuels and lowers greenhouse gas emissions, thus playing a crucial role in mitigating climate change impacts. Recent statistics from the World Wind Energy Association (WWEA) [1] highlight the rapid development of the global wind power industry over the past decade. Specifically, global installed wind capacity has surged from 197 GW in 2010 to 846 GW in 2021, now contributing 7% to the total electricity supply in Figure 1(a). Furthermore, the annual increase in installed capacity has shown a marked upward trend, with 59.3 GW added in 2019, rising to 100.2 GW in 2021, nearly doubling and exhibiting signs of stabilisation in Figure 1(b).

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

(a) The total installed capacity and (b) new installed capacity.

The rapid advancement of the wind power industry has led to an increase in the size and capacity of wind turbines, posing significant challenges in managing their vibration and fatigue loads. To enhance structural performance, dampers are commonly installed on high-rise buildings, towers and wind turbines to mitigate structural vibrations. Zuo, Bi and Hao [2] have reviewed the latest technologies for vibration control in wind turbines, highlighting the prevalence of passive dampers, such as tuned mass dampers (TMDs) [3, 4], tuned liquid dampers (TLDs) [5], tuned rolling ball dampers (TRBDs), tuned rolling cylinder dampers (TRCD) [6] and energy absorbing dampers [7].

The TMD has been widely adopted for controlling wind turbine vibrations. Both active [8–12] and semiactive [13] TMDs, alongside their passive counterparts [14–18], have been widely employed to address vibrations in turbine towers. Compared with the active and semiactive TMD, the passive TMDs are more robust, simple and cost-effective. Ghassempour, Failla and Arena [14] demonstrated the effectiveness of TMDs in mitigating wind turbine vibrations and proposed that tuning the TMD frequency to match varying wind conditions could enhance performance. Chen et al. [19] leveraging the artificial fish swarm algorithm (AFSA) within a pile–soil coupling framework, successfully optimised TMD parameters, lowering the tower’s natural frequency from 0.26 to 0.235 Hz. Similarly, optimisation techniques such as AFSA [20], particle swarm optimisation (PSO) [21] and iterative linear matrix inequalities [22] have been utilised to refine TMD configurations, taking into account model uncertainties and physical constraints. Several other improved TMDs [23–26] are also designed, to suppress bidirectional vibrations in wind turbine towers. The adaptive-passive TMDs [27–29] are proposed to reduce the vibration induced by winds and other external excitations. Despite these advancements of TMD, issues such as spring fractures and oil leakage still exist. Such failures not only diminish the effectiveness of vibration mitigation but also risk secondary damage to the main structure.

As an alternative to the conventional TMD, TRCD comprising primarily a rolling oscillator and its track, dispense with the need for additional spring stiffness and oil pump damping systems. Unlike pendulum-type TMDs, TRCDs adjust their operating frequency through modifications to the track radius, thereby eliminating the conventional suspension system. This design not only enhances space efficiency but also better meets the vibration reduction needs of structures of varying sizes, improving overall system flexibility, efficiency and applicability. The concept of the ball vibration absorber (BVA), first introduced by Priner [30] for mitigating pedestrian bridge vibrations, has since evolved with Matta [31] proposing uniform and discrete isomorphic BVA types. These designs were validated through experimental and numerical analyses, demonstrating BVA’s simplicity, cost-effectiveness, compactness and ease of maintenance. Legeza [32] further investigated the dynamic behaviour of homogeneous rolling balls within a spherical guide rail, deriving motion equations and calculating structural vibration responses under linear viscous forces. The exceptional characteristics of BVA as a passive vibration mitigation measure have promoted extensive research [33–35]. Based on these principles, Zhang et al. [36] and Li, Fu and Kong [37] developed TRCDs, replacing balls with rolling cylinders, resulting in a two-dimensional simplified model TRCD. Tsuda and Saeki [38] advanced this work by exploring TRCD parameters, establishing the relationship between damper structural features and vibration reduction performance and providing foundational guidelines for TRCD design. Wang, Liu and Ma [6] evaluated TRCD performance in wind turbine vibration control under real wind conditions, concluding that optimal performance is achieved when the roller’s moment of inertia is minimised. Meanwhile, Sarkar and Chakraborty [39, 40] designed a semiactive tuned liquid column damper with optimal parameters for mitigating wind turbine tower vibrations. However, TRCD relies on rolling friction for energy dissipation, which may not provide sufficient damping for systems with high vibration energy.

Eddy current damping is a phenomenon where a conductive material moving through a magnetic field generates electric currents that resist motion and help dampen vibrations. This technique can be integrated with traditional dampers to enhance vibration control efficacy. As early as 1995, Larose, Larsen and Svensson [41] designed a unidirectional eddy current TMD (ECTMD) for bridge vibration control, although practical applications were limited. Leng et al. [42] investigated the performance of magnetorheological elastomer (MRE)-based TMDs for wind turbine vibration control. Chen et al. [43] reviewed the efficacy of TMDs in vortex-induced vibration control and developed an eddy current device to replace traditional oil pump systems. They employed genetic algorithms to optimise the design parameters of the multiple tuned mass damper (MTMD), finding that permanent magnets arranged with the same polarity and a magnetic circuit design with a magnetic guiding outer cylinder resulted in the highest eddy current density and damping efficiency. Lou et al. [44] introduced an omnidirectional cantilever beam-type ECTMD for lattice tower structures, demonstrating its effectiveness in mitigating both along-wind and crosswind vibrations. Eddy current damping has been widely utilised to enhance the performance of TMDs. However, its application to improve the performance of TRCDs remains unexplored.

To solve the current challenges, the present study introduces a novel eddy current tuned rolling cylinder damper (ECTRCD) and evaluates its performance in vibration control of wind turbine. The key contributions of this research are as follows:

1.
A novel ECTRCD is designed, and the parameters including radius ratio, mass ratio, frequency ratio, damping ratio are optimised to improve the vibration mitigation performance.
2.
A comparative comparison of the vibration control performance between the traditional TRCD and the ECTRCD is carried out.
3.
An investigation into the impact of the optimised ECTRCD on the fatigue loads and vibrations of wind turbines is carried out.

This study is organised as follows: Section 2 outlines the numerical models employed, including the wind condition and wind turbine model. Section 3 details the damper models, including the TRCD, the eddy current damping model and the proposed ECTRCD. Section 4 presents the wind turbine verification, parameter optimisation for both the TRCD and ECTRCD in controlling wind turbine vibrations and the performance of both dampers. Finally, the conclusions of this study are summarised in Section 5.

2. Numerical Models

2.1. Wind Condition

The Weibull distribution is widely used for simulating actual wind speeds, and it is an important tool for analysing and describing wind power resource characteristics. This distribution was proposed by Weibull [45] in 1951, and the probability density function of the Weibull distribution can be expressed as follows:

()

where v represents wind speed, k is the shape parameter, which determines the shape of the wind speed distribution, and C is the scale parameter, which is related to the average wind speed. The cumulative distribution function of the Weibull distribution can be derived from the probability density function:

()

where C_w is the cumulative distribution probability of wind speed and V_ave is the annual average wind speed.

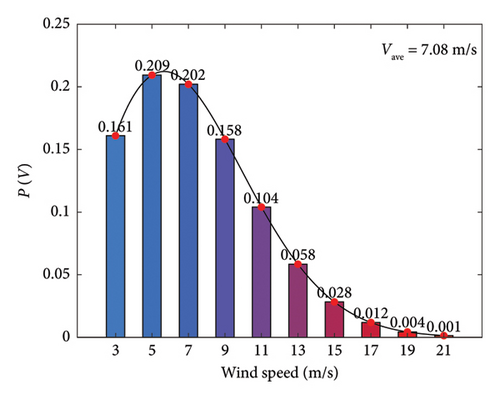
The Weibull parameters can be determined by the long-term observation data in a special region. In this study, the annual average wind speed design value for the actual operating wind field is 7.08 m/s, and the shape parameter is k = 2. The scale parameter is C = 7.99. According to IEC 61400-13 (2015) [46], statistical wind speed values are selected at intervals of 2 m/s, including 3, 5, 7, 9, 11, 13, 15, 17, 19 and 21 m/s. The occurrence probabilities of each wind speed are calculated based on equation (1), as shown in Figure 2. It can be observed from the figure that the maximum occurrence probability for a wind speed of 5 m/s is approximately 0.209.

In this study, the vertical wind speed profile is modelled using a power law with an exponent of 0.2. The wind speed at hub height serves as the reference, enabling the derivation of the corresponding vertical distribution of wind speed.

2.2. Aerodynamic Forces

The Kaimal turbulence spectrum recommended in the IEC 61400-1 [47] is adopted to generate the wind field over the whole rotor. The Kaimal turbulence spectrum can be expressed as follows:

()

where τ shows the standard deviation of velocity component, L represents the integral scale parameter of velocity component, V is the wind velocity, and f is the frequency.

The fluctuating wind speed in time domain can be obtained using the harmonic superposition method and the Shinozuka theory. The fluctuating wind speed can be expressed as follows:

()

where Δω is the circular frequency increment, k is the simulation point, k = 1, 2, …, n, N is the division number of pulsating wind frequency, f_ml is the double index frequency, f_ml = (l − 1)Δf + (m/n)Δf, in which Δf is the frequency increment, H(f) is obtained by Cholesky decomposition of S(f),

; θ(f) is the phase angle of H(f), θ(f) = arctan{Im[H(f)]/Re[H(f)]}; Φ(f) is a random initial phase in the range of (0, 2π).

The blade element momentum (BEM) theory is widely used to evaluate aerodynamic forces on blades. The local lift and drag forces on each blade element can be expressed as follows:

()

where ρ represents the air density, P_N and P_T refer to the lift and drag coefficients of blade, B and c are the number of blades and chord length of blade, dR shows the thickness of blade element, and V_r presents the relative wind speed on the blade element and it can be expressed as follows:

()

where δ and δ^′ represent the axial and tangential induction factors, R is the radial distance of the element from the hub centre, and Ω is the rotor velocity.

2.3. Wind Turbine Model

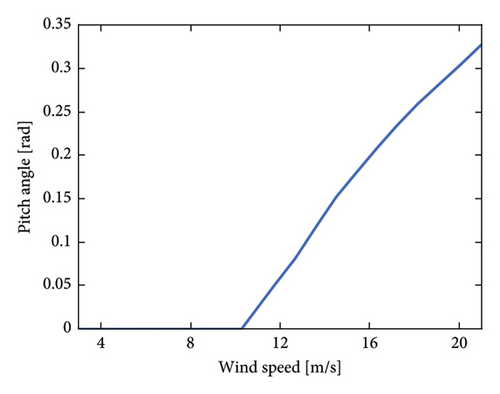
An onshore wind turbine Org-H155-4.5 MW is adopted in this study. The basic dynamic parameters of the wind turbine are shown in Table 1. It is noted that the hub height and rotor diameter are 94.5 and 155 m, respectively. The cut-in, rated and cut-off wind speeds are 3, 10.2 and 22 m/s. The relationship between the wind turbine’s pitch angle and wind speed is illustrated in Figure 3, serving as the basis for implementing the pitch control strategy. The Cartesian coordinate system is defined as shown in Figure 4.

Table 1. Basic information of the Org-H155-4.5 MW wind turbine.

Terms	Values
Hub height	94.5 m
Rotor diameter	155.0 m
Rated power	4500 kW
Cut-in wind speed	3.0 m/s
Rated wind speed	10.2 m/s
Cut-off wind speed	22.0 m/s

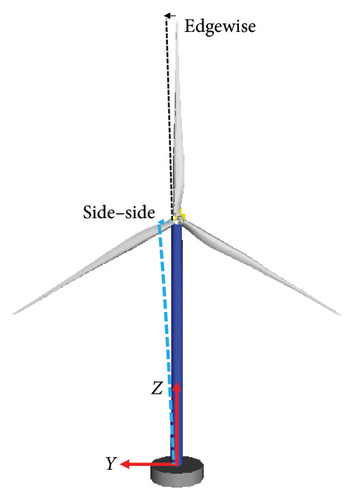
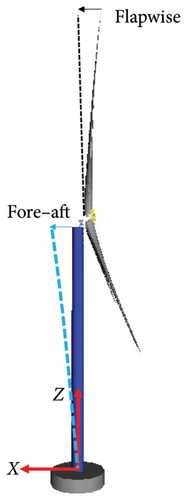
The commercial multibody simulation software Simpack [48] is adopted, and the detailed description of the process of constructing wind turbine model is presented in this study. In this model, a linear elastic material is used, and the relevant modelling is completed by referencing the material properties defined under the tower panel in the GH-Bladed model. The sectional properties at various heights are set according to the tower geometric model data in the GH-Bladed model. The tower is modelled using the linear SIMBEAM approach, specifying the height and sequence of each section. The initial damping ratio is defined as 0.02, as defined by Wang, Liu and Ma [6]. The tower base is fixed on the ground without any displacement during operation. In Simpack, an RBL file for blade modelling is first created based on the blade properties, and the automated modelling of the blade is completed using the utilities function page. The additional mass on the blade is defined using the same method as for the tower. The blade is fixedly connected to the hub unit, restricting relative displacement between the blade root and the connecting unit in all six degrees of freedom. The yaw system was set up and installed on the tower top which moves with the displacement of top tower. A rigid nacelle with a predefined mass and moment of inertia is built on the tower top, which is fixed on the yaw system. The gearbox and generator are built in the nacelle as rigid bodies, being able to rotate around the x-axis. Three blades are flexible bodies and installed at the hub. The blade pitching can be simulated by rotating around the z-axis. The initial damping ratios of blade in the flapwise and edgewise directions are 0.4 and 0.007, respectively, and the first six mode shapes are considered. Various inflow wind conditions generated by the TurbSim module are used, and aerodynamic loads are added using the AeroDyn V13 force element. The blade pitching and rotor angular velocity are controlled by the control element. The blades rotate under different inflow conditions to generate electricity and the blade and tower vibrates during operation. The numerical model in Simpack is shown in Figure 4.

3. Damper Models

3.1. TRCD

The TRCD typically consists of a rolling cylinder, a rolling cylindrical track and a track support system, as shown in Figure 5. The track (represented by the black arc in Figure 5) is fixed to the main structure through the support system (represented by the blue line in Figure 5). When the main structure vibrates under external excitations, the rolling cylinder (represented by the red circle in Figure 5) moves freely on the track. The motion of the rolling cylinder provides additional damping to the main structure. Therefore, after installing the TRCD, the vibration of the main structure can be controlled and its vibration damping ratio can be improved.

As shown in Figure 5, four main parameters can be used to describe the TRCD, namely, the rolling cylinder radius r, the track radius R, the rolling cylinder mass m and the moment of inertia relative to its centre J. The motion of the rolling cylinder can be divided into two parts, including the translational motion along the tangent direction of the track and the rotational motion around its centre of cylinder. Therefore, the total kinetic energy of the TRCD can be expressed as follows:

()

where T_{TRCD,translate} and T_TRCD,rotate represent the translational kinetic energy along the tangent direction of the track and the rotational kinetic energy around its centre of cylinder, respectively.

For T_{TRCD,translate}, the rolling cylinder translates along the track with a velocity of

, and the horizontal and vertical velocities of the rolling cylinder can be calculated as

and

, respectively. The expression can be obtained as follows:

()

To calculate T_TRCD,rotate, the angular velocity of the rolling cylinder as a function of θ should be determined. Specifically, by applying sufficient friction coefficient between the rolling cylinder and the track, no relative sliding motion occurs between them when the rolling cylinder moves. In Figure 5, the rolling cylinder moves away from its equilibrium position by θ, and the angle β between the original contact point and the current contact point can be divided into two parts, including the angles induced by rotational and translational motions of the rolling cylinder, represented by β = α + θ. Therefore, α which is caused by the rotational motion of the rolling cylinder can be calculated as α = β − θ. Meanwhile, as mentioned earlier, there is no relative sliding motion between the rolling cylinder and the track. Therefore, as shown in Figure 5, there exists s₁ = s₂, where s₁ and s₂ are the distances moved by the rolling cylinder on the track surface and the rolling cylinder surface, respectively, and can be expressed as follows:

()

Thus, the expression for T_TRCD,rotate can be calculated.

()

Combining the above equations, the total kinetic energy of the TRCD can be obtained:

()

The potential energy of the TRCD can be expressed as follows:

()

Subsequently, consider a linear viscous damping term in the TRCD system in the form of

, where c represents the damping coefficient of the TRCD reference to the degree of freedom θ. Based on the Euler–Lagrange equation, the equation of motion of the TRCD without external excitations can be derived as follows:

()

Taking l = R − r, solving the above equation for undamped vibration yields the natural frequency of the TRCD.

()

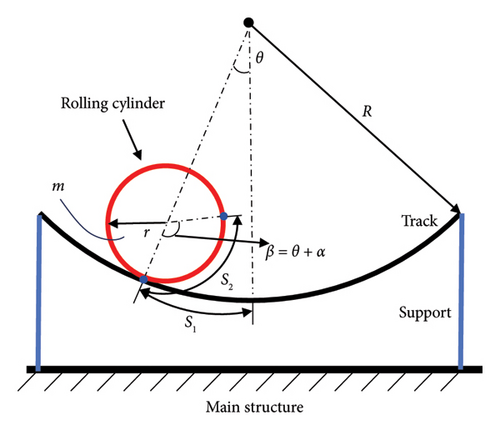
From the above equations, it is noted that the natural frequency of the TRCD is mainly determined by the gravitational acceleration g and the length of the pendulum l = R − r. The longer the pendulum length, the smaller the natural frequency of the TRCD.

Finally, the formulas for the mass ratio μ, frequency ratio ν and damping ratio ξ are expressed as follows:

()

3.2. Eddy Current Damping Model

In low-speed electromagnetic systems, the calculation of electromagnetic forces on conductors within a magnetic field often relies on magnetic circuit theory. Magnetic circuit theory is widely applied in engineering for determining linear electromagnetic forces and provides a foundational framework for approximating the effects of low-speed linear eddy current damping.

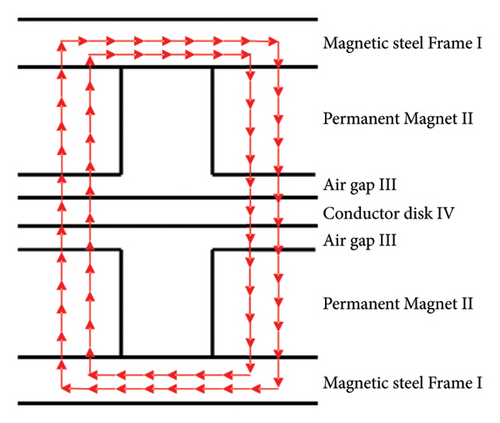
To explore the application of magnetic circuit theory in generating linear damping forces, we designed a rolling disk eddy current damper, as illustrated in Figure 6. This design accounts for the high linear velocity at the disk’s edge, where maximising the radius intersecting magnetic field lines enhances the eddy current damping force. To achieve this, the magnetic steel is strategically positioned along the outermost circumference with alternating poles and specific spacing to optimise magnetic performance. Additionally, magnetic steel is symmetrically arranged on both sides of the disk with opposing polarities to maintain balance. For analytical clarity, the cylindrical disk is unfolded radially, producing a schematic of its circumference and radial configuration, as depicted in Figure 7.

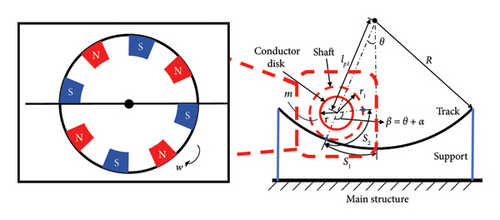
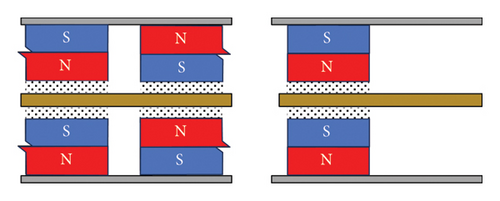
As illustrated in Figure 8, the cylindrical disk features a symmetrical structure on both sides, comprising the magnetic steel frame, the permanent magnet, the air gap and the conductor disk. According to magnetic circuit theory, the high magnetic permeability of the steel frames confines the magnetic flux between the central magnetic steel and the conductor disk. When the conductor disk moves relative to the magnetic steel, Kirchhoff’s law allows the disk to be conceptualised as composed of numerous rotating current elements. After half a cycle of motion, the magnetic field reverses direction, inducing a current that is dissipated as internal energy through the material’s resistance, resulting in energy loss. By considering half-cycle units and analysing half of the adjacent magnetic poles, the magnetic circuit projection on the circular arc surface, as shown in Figure 8, is derived, with arrows indicating the direction of magnetic flux.

Based on the magnetic flux direction indicated in Figure 8, a complete magnetic circuit can be constructed by taking half of the adjacent magnetic poles as the analysis unit. The calculation and analysis of this magnetic circuit are analogous to the treatment of conductivity, current and voltage in an electrical circuit. A magnetic circuit is defined as a closed loop through which magnetic flux flows, and the governing equation for the magnetic circuit can be expressed as

()

where ϕ is the total magnetic flux in the circuit,

represents the magnetic reluctance, analogous to electrical resistance, describing the opposition to magnetic flux, and F is the total magnetomotive force, determined by integrating the magnetic field strength over the length of the circuit.

()

Based on these principles, the key parameters of the magnetic circuit in Figure 8 are analysed. Given the circuit’s symmetry, the magnetic flux passes through a sequence of one magnetic steel frame, one magnetic steel segment, one air gap and half of the conductor disk as it traverses 1/4 of the region. For this analysis, the magnetic circuit is confined to half the projected area of the magnetic steel, denoted as A = A_m/2, and the thickness of the magnetic steel is taken as t_m. The remaining magnetic flux density is given by B_re, and the magnetic potential across the loop is calculated by

()

where μ₀ is the permeability of free space. Since the magnetic steel frames primarily confine the magnetic flux and are composed of high-permeability ferromagnetic material, their contribution to magnetic reluctance is negligible. Assuming the air gap between the magnetic steel and the conductor disk has a thickness t_a, and the conductor disk has a thickness t_c, the total magnetic reluctance of the circuit is given by

()

where μ_rm is the relative permeability of the magnetic material. The magnetic flux density B in the loop is then determined as

()

Using the Lorentz force equation, the tangential damping force acting on the conductor disk is derived as

()

where σ is the electrical conductivity of the conductor disk, R is the radius of the rolling disk, t_c is the thickness of the conductor disk in the magnetic field direction, r_m is the radial length of the permanent magnet, θ_m is the combined circumference angle of all permanent magnets, t_m is the thickness of the permanent magnet, t_a is the air gap thickness, and B_re is the remaining magnetic flux density of the permanent magnet. From the formula, it can be seen that the magnitude of the damping force is directly proportional to the rotation speed of the conductor, exhibiting linearity under low-speed conditions.

3.3. ECTRCD

Based on the traditional TRCD model, the ECTRCD is designed where the electromagnetic damping mechanism enhances overall energy dissipation, making the ECTRCD more effective across a broader frequency range compared to the TRCD, which relies solely on rolling friction. The transmission component is uniquely engineered to allow variable velocities of the rolling cylinder during rotation, creating speed differentials at different positions along the cylinder. The structure of the ECTRCD includes a conductor disk, magnetic steel and magnetic disks in Figure 9. The conductor disk, along with the conical shaft, forms part of the rolling cylinder oscillator. Magnetic steel, mounted on the magnetic disk in alternating N and S poles along the circumference, generates electromagnetic damping through its interaction with the conductor disk. The conductor disk and magnetic disks are separated by an air gap, ensuring that when the rolling cylinder rotates, the magnetic disks remain stationary, causing relative motion between the conductor and magnetic steel. This motion induces eddy currents, producing electromagnetic damping torque.

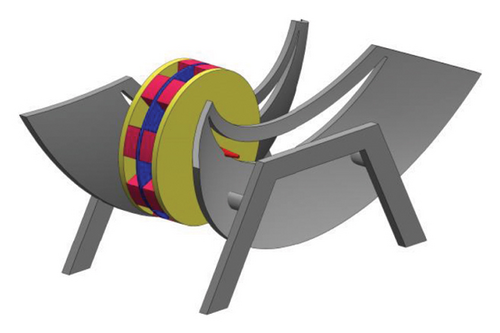
The ECTRCD’s design transforms horizontal vibrations of the main structure into rotational motion of the rolling cylinder via the support track, as seen in conventional TRCD systems. The electromagnetic torques convert the kinetic energy of the rolling cylinder into internal energy, effectively dissipating the vibration energy of the primary structure and mitigating its vibrational response.

The ECTRCD introduces several key improvements over the traditional TRCD:

1.
The conventional rolling cylinder is replaced by a combination of a rolling cylinder and conductor disk, increasing rotational inertia through the enhanced mass and radius of the conductor disk, while also enabling electromagnetic damping.
2.
An electromagnetic system, consisting of magnetic steel and magnetic disks, is added around the conductor disk. As the rolling cylinder system rotates, relative motion between the conductor disk and magnetic steel induces currents, providing additional damping.
3.
The conical roller and arc-shaped guide track are designed to enable speed variation across different positions. The greater the overall rotation angle of the rolling cylinder system relative to the guide track, the faster the conductor disk rotates, enhancing the system’s performance.

The theoretical model of the ECTRCD, simplified as shown in Figure 10, adheres to the fundamental design principles of a TRCD, comprising a rolling cylinder, a rolling cylinder track and a track support system. To enhance the rotational inertia of the wheel and accommodate electromagnetic damping, an auxiliary cylinder body supports the rolling cylinder. Additionally, a magnetic field is introduced between the auxiliary cylinder and the rolling cylinder.

As shown in Figure 10, the radius of the auxiliary support cylinder is denoted as r₁, which corresponds to the axis radius, while the distance from the axis centre to the centre of the guide track is represented as l_p1 = R − r₁. For T_{TRCD,translate}, the rolling cylinder translates tangentially along the track at a speed of

()

Taking into consideration the variation in the axis, equation (10) is modified as follows:

()

By integrating the above two formulas, the following equation is obtained:

()

The equivalent rotational inertia of the rolling cylinder system with respect to the relevant degree θ is expressed as follows:

()

For the rolling cylinder, the rotational inertia J_d = (1/2)m_dr², when substituted into equation (25), we can yield

()

where τ is the ratio of the conductor disk radius r to the axis cylinder radius r₁, denoted as τ = r/r₁. According to equation (26), the larger the value of τ, the larger the value of J_TRCD,e. Therefore, τ can be used as a variable to directly control the equivalent rotational inertia of the rolling cylinder.

Using the simplified values, equations (11) and (12) are corrected to obtain the kinetic and potential energy expressions for the ECTRCD:

()

Incorporating the linear viscous damping term

arising from friction in the guide track plane and the linear damping term

due to electromagnetic damping in the rolling cylinder’s rotational degree of freedom,

and

satisfy the following relationship:

()

Applying the Euler–Lagrange equation, the motion equation for the ECTRCD without external excitation is derived as

()

Solving this equation, the natural frequency of the ECTRCD can be determined as

()

Consequently, the expressions for the mass ratio μ, frequency ratio ν and damping ratio ξ are obtained as follows:

()

4. Results and Discussion

4.1. Verification of Wind Turbine Model

To assess the accuracy of the wind turbine model, key structural parameters of the tower and blades were calculated and compared against those of the GH-Bladed model [49]. A comparison of the first six blade mode frequencies and the first four tower mode frequencies reveals a maximum error of 1.6% in Table 2, demonstrating strong consistency in dynamic characteristics between the two models, thereby validating the reliability of the Simpack model for subsequent analyses.

Table 2. Comparisons of results obtained by Simpack and GH-Bladed.

Parameters	Simpack (Hz)	GH-Bladed (Hz)	Relative error (%)
Blade 1^st order mode	0.428	0.427	0.2
Blade 2^nd order mode	0.696	0.695	0.5
Blade 3^rd order mode	1.165	1.164	0.08
Blade 4^th order mode	1.955	1.957	0.2
Blade 5^th order mode	2.371	2.374	0.13
Blade 6^th order mode	4.000	3.995	0.13
Tower 1^st order mode	0.261	0.260	0.4
Tower 2^nd order mode	0.266	0.262	1.6
Tower 3^rd order mode	1.464	1.462	0.14
Tower 4^th order mode	1.470	1.468	0.27

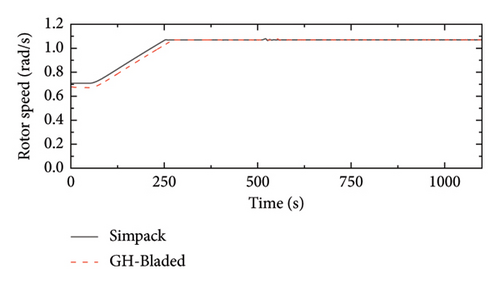
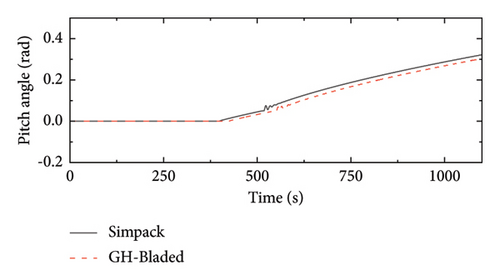
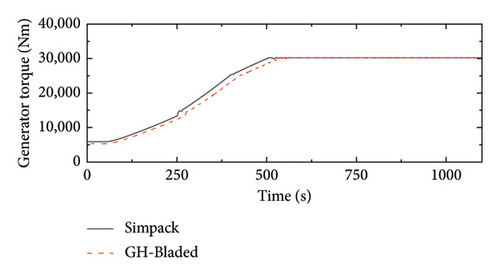
To further verify the Simpack model’s accuracy, a comparison of key state variables, including the rotor speed, the blade pitch angle and the generator torque, between the Simpack and GH-Bladed models, employs a linearly varying wind scenario. In this case, the wind speed starts at 5 m/s and increases linearly to 20 m/s over a period of 1100 s. The results for these variables were found to be in exact agreement, confirming the accuracy of the control system representation in the Simpack model in Figure 11.

4.2. Parameter Optimisation of TRCD for Vibration Control of Wind Turbine

To optimise parameters of the TRCD, the reduction ratio of the equivalent fatigue load (EFL), denoted as γ, is chosen as the optimisation objective and calculated according to equation (34). In this study, the EFL at the tower base moment is determined using the rainflow counting method:

()

where EFL₀ and EFL refer to the equivalent fatigue loads of the wind turbine without and with dampers, respectively.

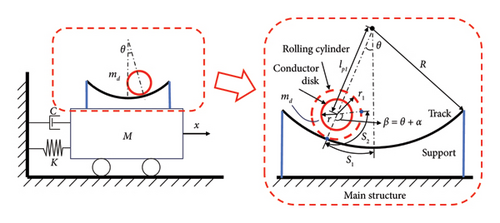
The TRCD system consists of an oscillating cylinder with a mass of m_d and a two-dimensional curved guide track with a radius R. The arc surface of the curved guide track is coaxially aligned with the arc surface of the oscillating cylinder, allowing the cylinder to roll freely along its axis of rotation. Figure 12 illustrates the basic TRCD model and its installation in Simpack.

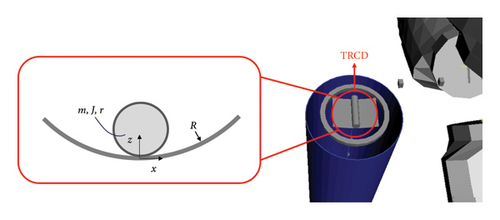
The oscillating cylinder is a rigid structure with a geometric dimension of r × h and a material density ρ_d. The rotational inertia about the axis is given by 1/2ρ_dhπr⁴. The 18-force element (Unilateral Spring-Damper Cmp) in Simpack is used to model the normal contact force between the cylinder and the track, which constrains the cylinder’s motion within the guide track. Additionally, the 100-force element (Nonlinear Friction Cmp) is employed to simulate the frictional force at the contact point between the cylinder and the track. Assuming the damping coefficient of the TRCD is c_d, the friction damping force is constructed between the centre of the arc and the rotational reference point using the 43-damping force element (Bushing Cmp), in line with the theoretical derivation.

Using the derived formulas, the dimensionless parameters, namely, the mass ratio μ, frequency ratio ν and damping ratio ξ, are constructed across a gradient grid, as detailed in Table 3. The grid designates the following ranges: the mass ratio varies from 0.2% to 1.2%, in steps of 0.2%; the frequency ratio spans from 0.7 to 1.6, with increments of 1/15; and the damping ratio covers values from 0.01 to 0.2, with increments of 0.02. These settings yield 6, 10 and 10 values for each parameter, respectively, producing a total of 600 parameter combinations. To achieve the optimisation objective of minimising EFL, such as the tower base bending moment, simulations are conducted under 10 different wind speed scenarios for each combination. This approach results in a comprehensive analysis encompassing 6000 distinct operating conditions in the TRCD parameter study.

Table 3. Parameter variation for TRCD and ECTRCD.

Parameter	μ (%)	ν	ξ
Range	0.2∼1.2	0.7∼1.6	0.01∼0.2
Step	0.2	1/15	0.02

The cloud map illustrating vibration reduction performance across various parameters is presented in Figure 13. The optimal performance is achieved with a mass ratio of 1.2%, a frequency ratio of 0.934 and a damping ratio of 0.056. At a constant mass ratio, the relationship between vibration reduction performance, frequency ratio and damping ratio is distinctly nonlinear, generally increasing initially before tapering off. The optimal frequency ratio is observed between 0.9 and 1, with the damping ratio around 0.05. A comparative analysis of the damper’s vibration reduction effect across different mass ratios shows an initial increase followed by gradual convergence. The incremental improvements in vibration reduction performance for successive mass ratios are −0.002, 0.028, 0.0037, 0.009 and 0.003, respectively, with the peak performance occurring at a mass ratio of 1.2%. Beyond this threshold, further increases in mass yield negligible improvements, indicating a saturation effect in the TRCD system’s vibration reduction capacity.

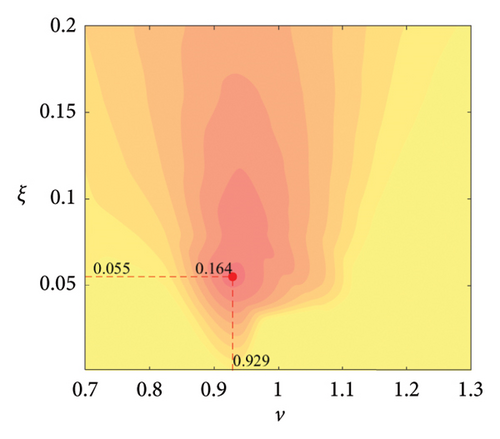
4.3. Parameter Optimisation of ECTRCD for Vibration Control of Wind Turbine

Similar to the TRCD, the ECTRCD comprises a rolling cylinder oscillator and a two-dimensional curved guide track. The oscillator is further subdivided into a supporting shaft and a rotating disk, with the mass and moment of inertia of the supporting shaft set to 0.001 to avoid computational instability and reduce its influence on the simulation outcomes. The rotating disk is rigidly attached to the supporting shaft. A detailed schematic of the system configuration is presented in Figure 14, illustrating the overall structural layout and component integration.

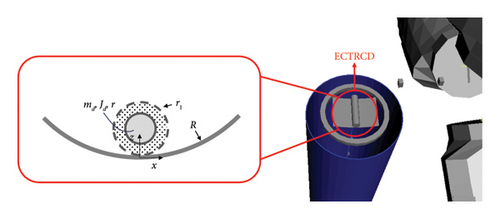
Similar to the friction damping force, the eddy current damping force is applied between the reference points of the rolling cylinder and the supporting structure using the 43-damping force element (Bushing Cmp) in Simpack with the damping coefficient c_e. The eddy current damping coefficient c_e can be derived by equation (33) once the damping ratio is specified. Additionally, for the ECTRCD system, the friction damping force is negligible, effectively rendering the friction damping coefficient c_d is zero.

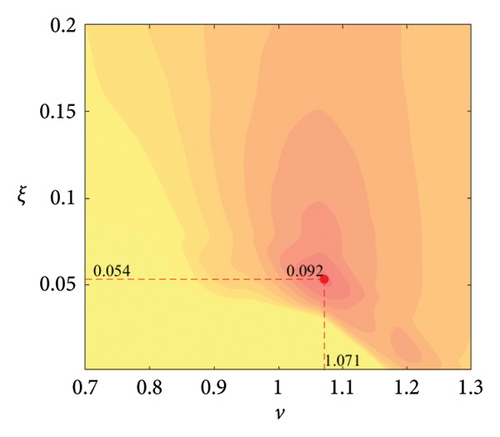
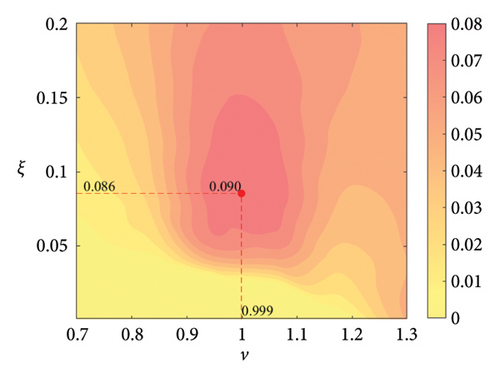
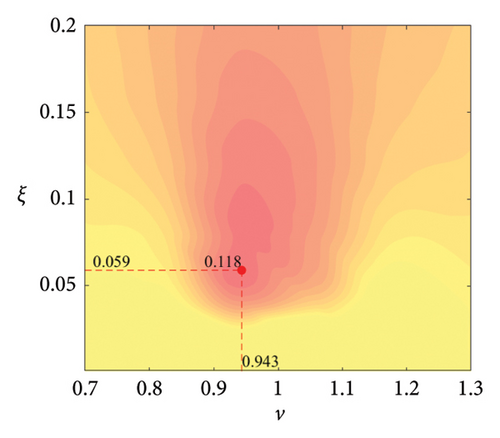
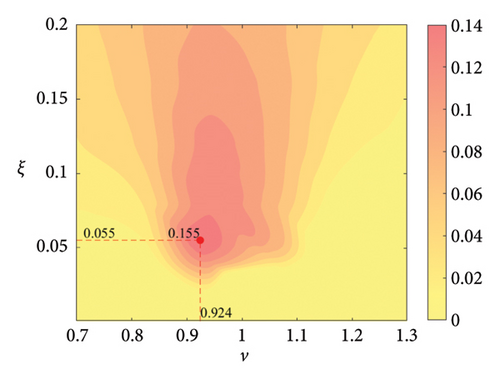
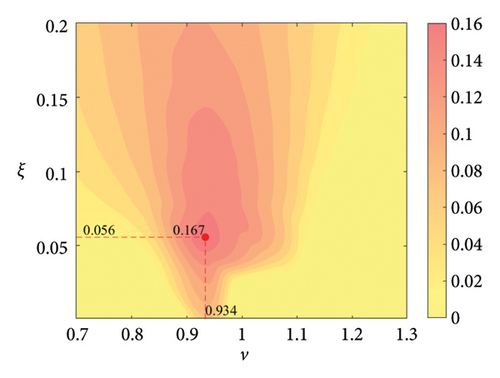
The parameter settings for the ECTRCD are detailed in Table 3, where multiple parameters are evaluated. The radius ratio τ is varied across values of 1/6, 1/3, 3 and 6, with the rolling cylinder radius denoted as r₁. For each τ, the parameter configuration mirrors that of the TRCD, resulting in a total of 600 distinct parameter combinations. Using the EFL of the tower base bending moment as the optimisation objective, 10 wind speed scenarios are assessed for each parameter combination. Consequently, for each radius ratio, a total of 6000 operating conditions are analysed in the ECTRCD parameter study. The results of this optimisation are illustrated in Figures 15, 16, 17, 18.

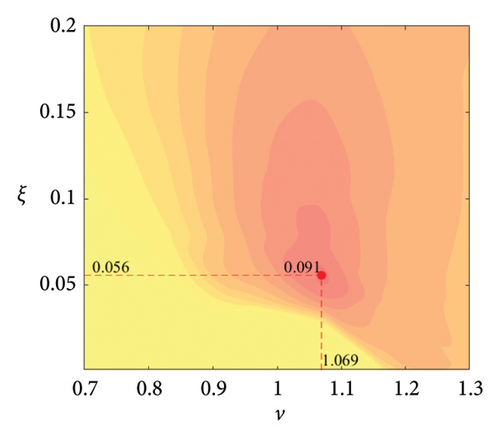
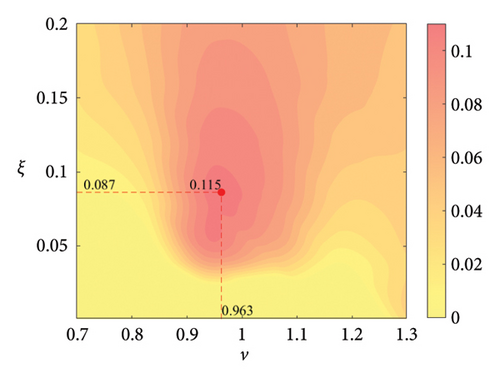
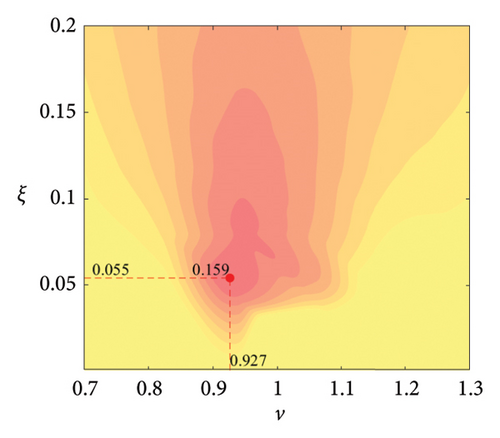
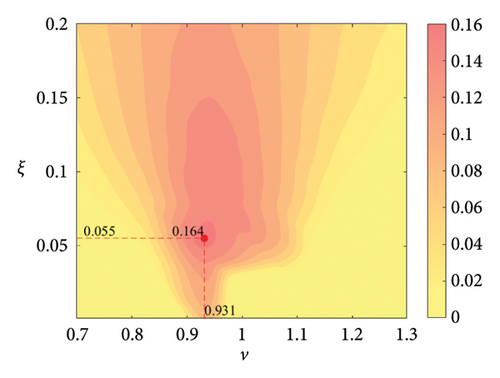
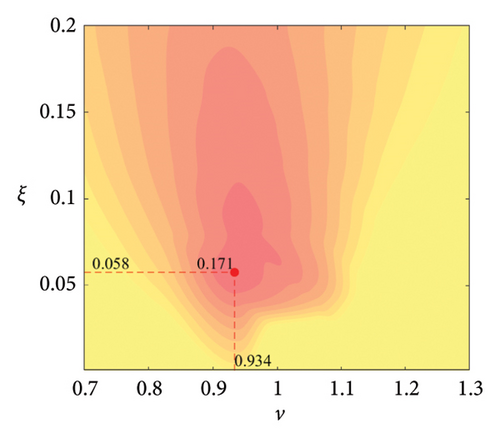
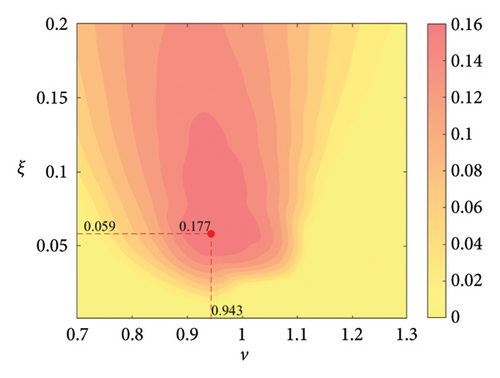
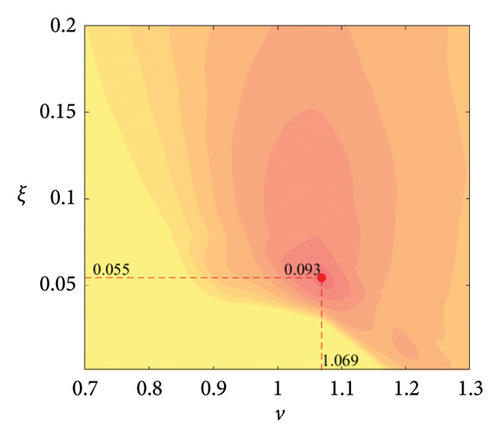
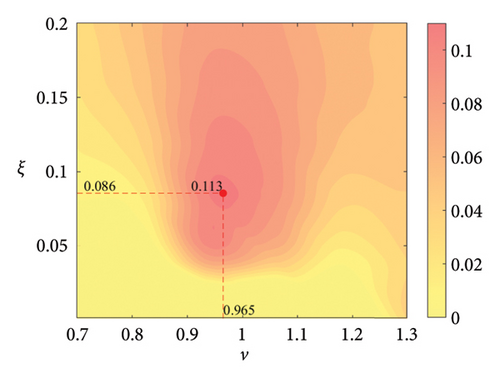
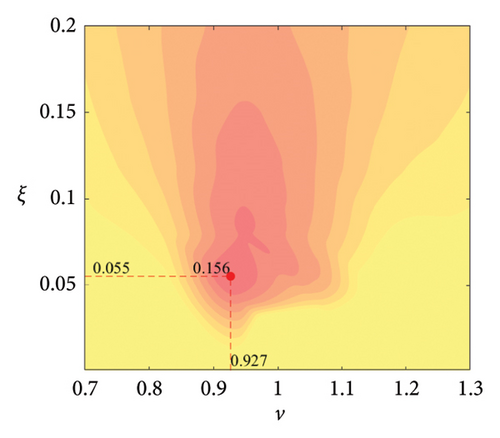
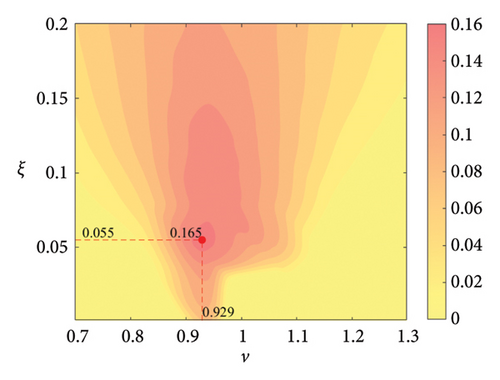
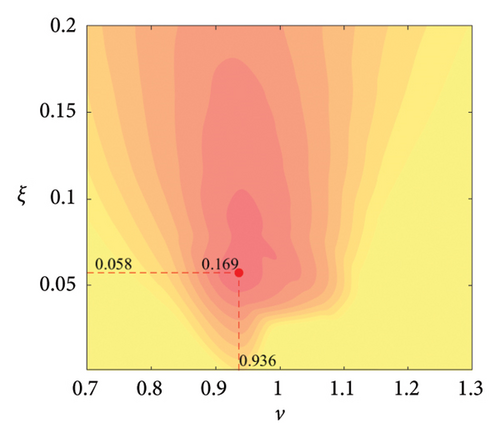
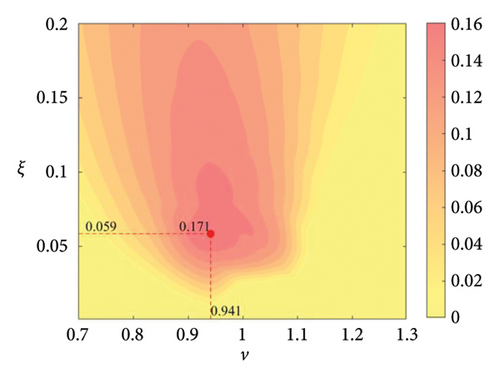
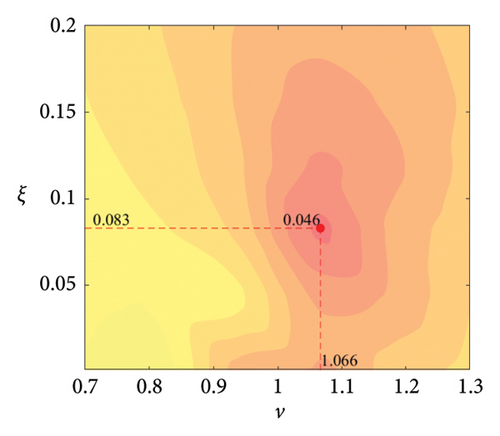
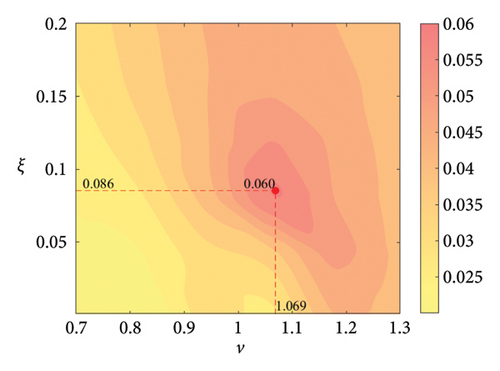
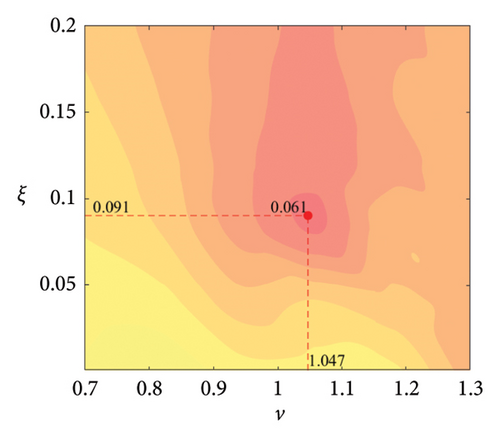
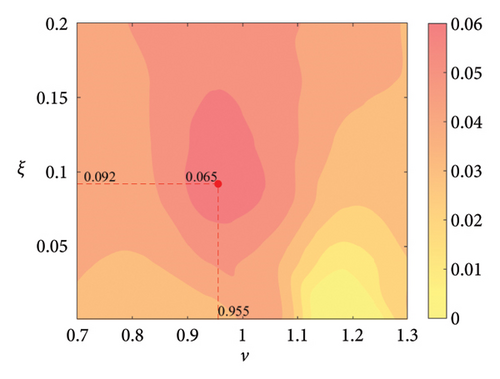
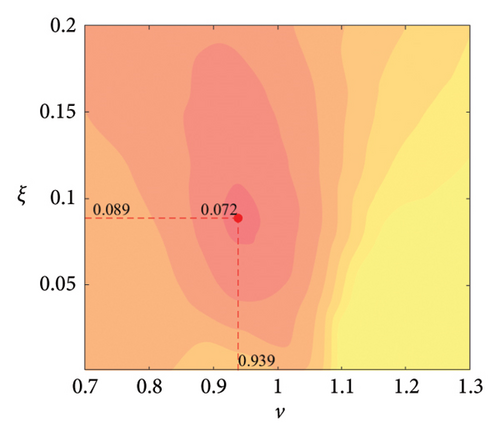
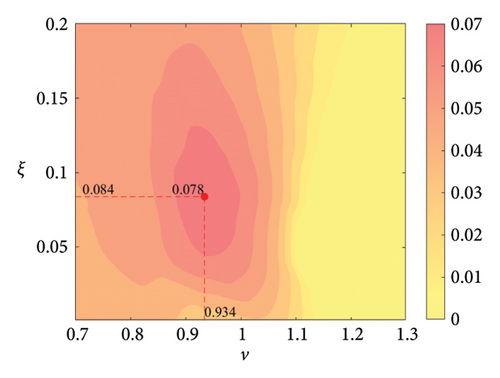
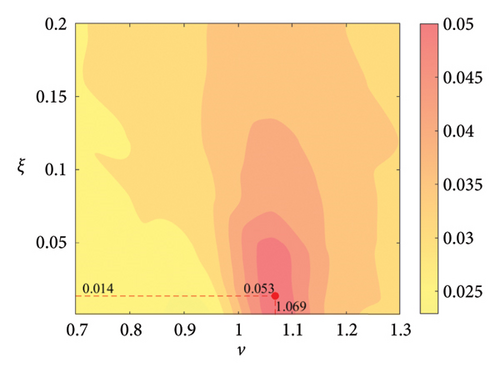
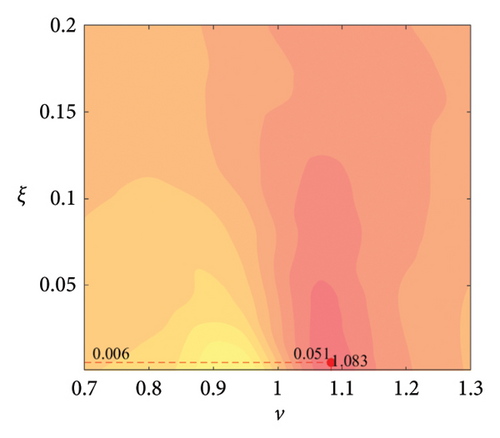
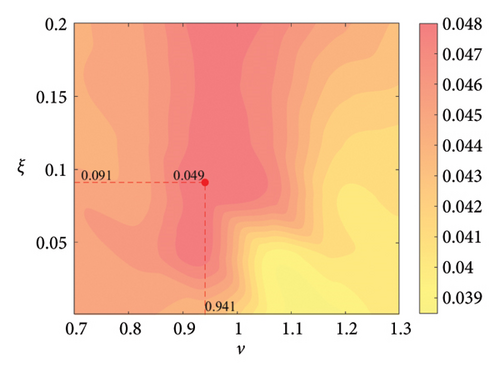
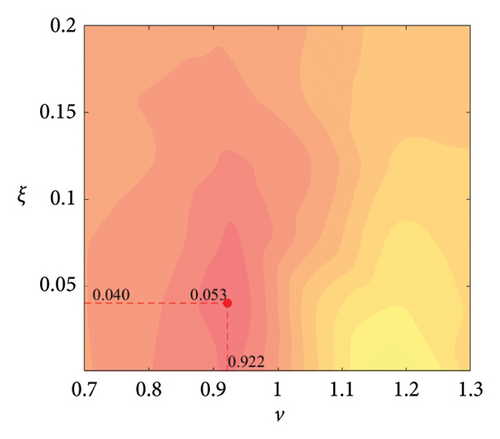
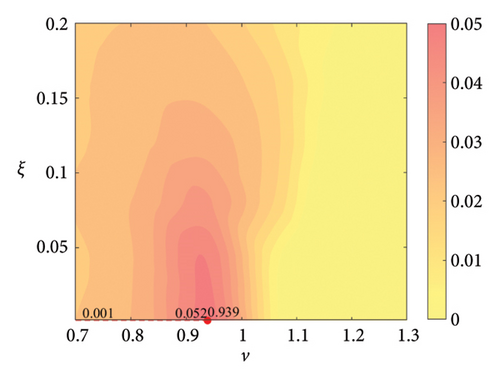
For each τ value, optimal parameter configurations for maximising damping performance can be identified. For instance, with a radius ratio of 1/6, a mass ratio of 1.2%, a frequency ratio of 0.943 and a damping ratio of 0.059, the ECTRCD achieves an optimal damping efficacy of 17.7%. Additional optimal configurations are presented in Figures 15, 16, 17, 18. Similar to the behaviour observed in the TRCD, the damping performance exhibits a nonlinear trend with respect to the frequency ratio ν, and damping ratio ξ, initially increasing before reaching a peak and subsequently declining as the parameters continue to rise. The optimal frequency ratio fluctuates notably between 0.9 and 1.1, while the damping ratio displays even greater variability.

A comparison of the optimal damping efficacy across different mass ratios indicates that, like the TRCD, the damping performance increases initially and then plateaus as the mass ratio is further augmented. Furthermore, when comparing the optimal damping performance of the ECTRCD across different radius ratios, the results show values of 17.7%, 17.1%, 7.8% and 5.3% for radius ratios of 1/6, 1/3, 3 and 6, respectively. This demonstrates a clear trend as the radius ratio increases, the damping efficacy of the ECTRCD decreases. The increase in radius ratio leads to a higher moment of inertia of the rotating disk, consistent with findings from previous studies, such as those in [6], regarding optimised TRCD designs.

The ECTRCD outperforms the TRCD in damping efficacy, offering a more refined design space through the adjustment of the radius ratio τ. This highlights the role of eddy current damping in enhancing the overall performance of the ECTRCD. Specifically, reducing the radius ratio while keeping mass and frequency ratios constant increases the guide track radius and amplifies the rotational amplitude of the rolling column oscillator around the track centre. This elevated rotational velocity of the rolling cylinder oscillator generates a stronger eddy current damping force, further improving the system’s overall damping efficiency.

4.4. Comparisons of the Performance of Two Different Dampers

The optimised damper parameters, including those for the TRCD and ECTRCD across various radius ratios, were selected for further analysis. In accordance with the [50], a comprehensive simulation under normal power generation conditions was conducted. The lateral shear force and base moment of the wind turbine tower were extracted for comparison. During lateral load calculations, adjustments were made to the installation orientation of the damper to ensure optimal performance. As the simulation in Simpack covers the full operational process of the wind turbine, from startup to stable operation, the initial 50 s of data was excluded to eliminate transient effects. To provide a more precise assessment of the dampers’ impact on wind turbine load response, the wind speed for the primary simulation condition was set at 11 m/s, near the rated speed of the turbine. Additional comparisons were performed under low (3 m/s) and high (21 m/s) wind speed conditions, corresponding to the cut-in and cut-out speeds of the turbine, respectively.

4.4.1. Forces at the Tower Base

Figures 19 and 20 depict the lateral shear force and moment at the tower base under various wind conditions with different damper configurations. The data demonstrate that the installation of dampers substantially influences aerodynamic loads in both the fore–aft and side-to-side directions across different wind speeds. In the fore–aft direction, dampers effectively reduce peak forces, highlighting their capacity to mitigate the primary structure’s vibrational response. However, the variations between curves are relatively minor due to two primary factors: first, the substantial forces in the fore–aft direction mean that while dampers mitigate load fluctuations induced by gusts, the static load from the wind field remains significant and less affected over time. Second, the inherent structural and aerodynamic damping already present in the wind turbine contributes to the overall damping, rendering the additional effect of the dampers comparatively limited.

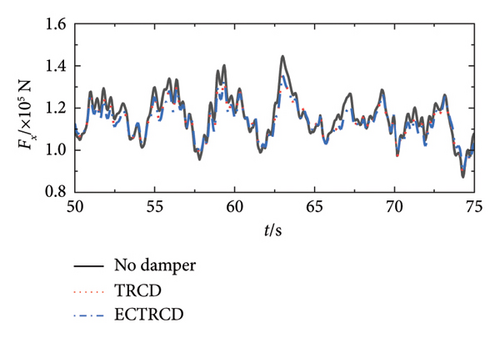
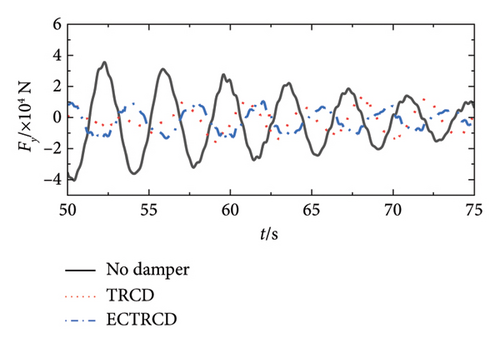
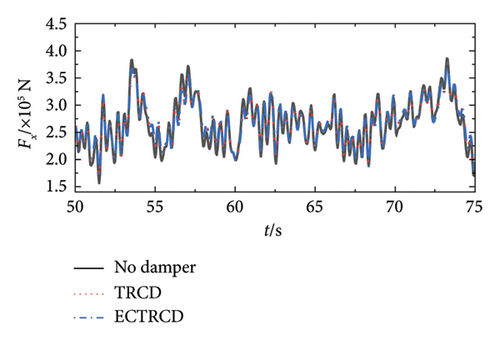
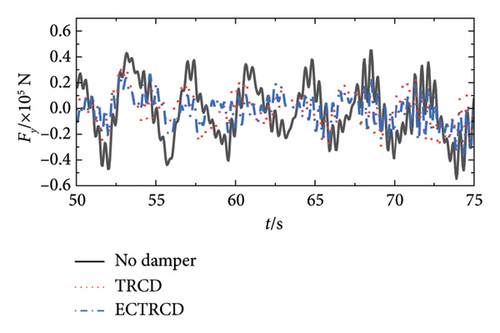
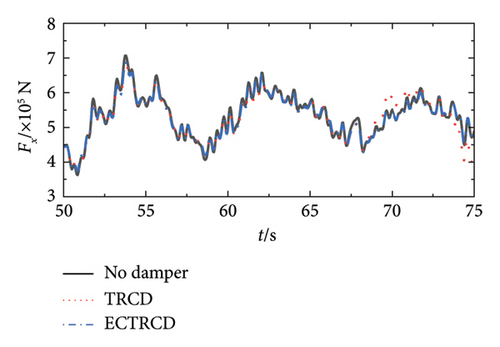
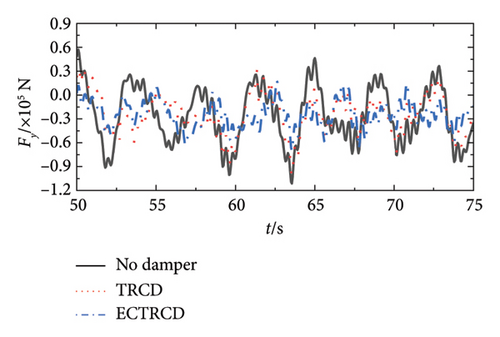
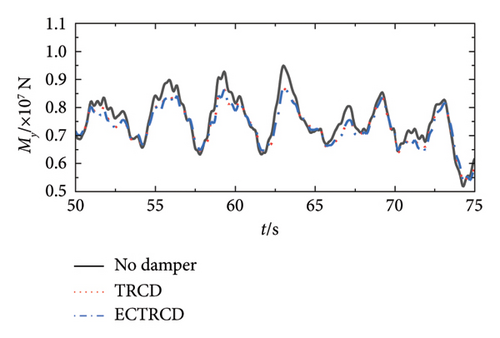
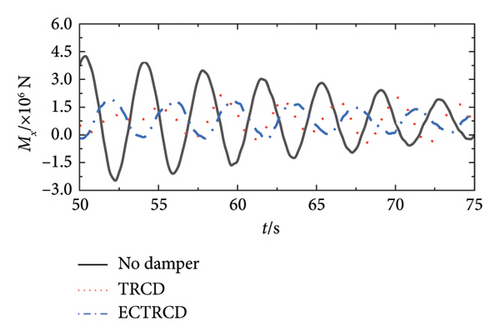
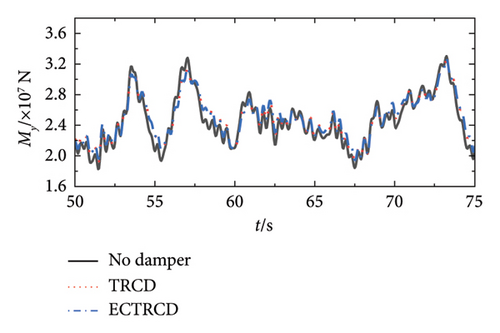
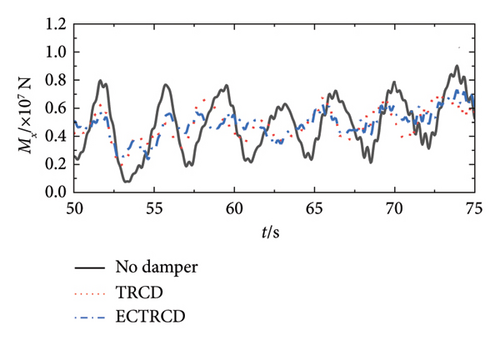
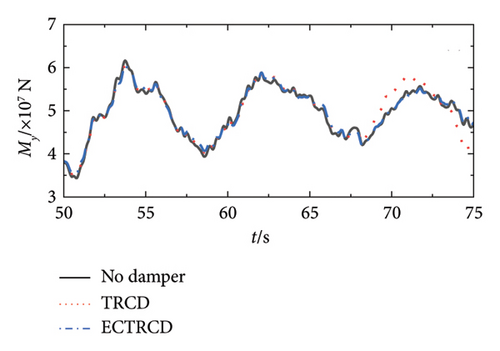
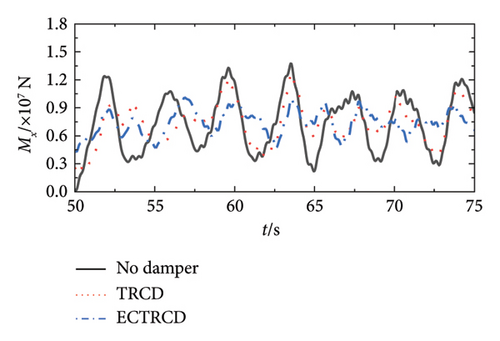
Conversely, the impact of dampers on forces and moments in the side-to-side direction is more pronounced. Figures 19 and 20 reveal that different dampers not only reduce peak loads but also modify the lateral vibration characteristics of the wind turbine, including changes in load vibration frequency. This more pronounced effect arises because the wind turbine’s lateral stiffness and damping are relatively low, allowing for greater influence from the dampers. Additionally, since the turbine’s lateral orientation is perpendicular to the wind direction, the aerodynamic damping is minimal, making the turbine’s vibration characteristics highly sensitive to adjustments in the damper’s parameters.

4.4.2. Equivalent Fatigue Loads

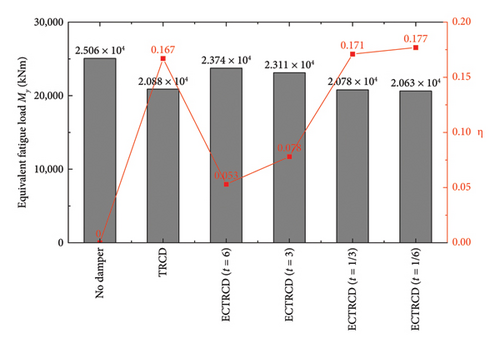
The rainflow counting method, as outlined in [51], is utilised to compute the EFL. Leveraging the previously optimised damper parameters, the EFL of the wind turbine tower’s base bending moment is analysed under the optimal vibration reduction settings for each damper, with results illustrated in the histogram shown in Figure 21. The data reveal that the ECTRCD, when considering the radius ratio of 1/6, demonstrates a nearly 6% improvement in vibration reduction performance compared to the TRCD. Moreover, the efficacy of vibration reduction with the ECTRCD enhances as the radius ratio decreases. Notably, a sharp decline in performance occurs when the radius ratio is larger than 1, with the damper’s effectiveness decreasing by 32.1% as the radius ratio shifts from 3 to 6.

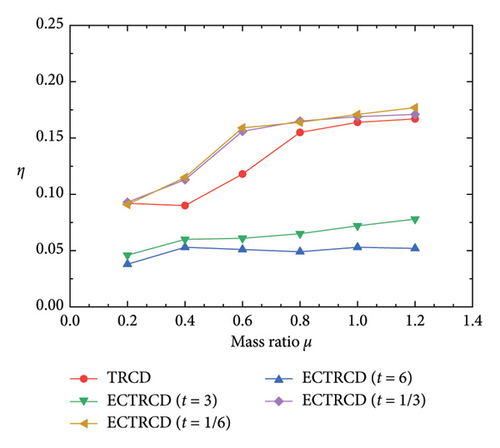
The optimal vibration reduction performance η for each damper configuration, evaluated across different mass ratios, is statistically analysed, and the resulting curve is presented in Figure 22. This analysis shows that the vibration reduction performance of the dampers initially increases with the mass ratio before stabilising, consistent with the findings from the parameter optimisation analysis. For the ECTRCD, however, when the radius ratio exceeds 1, changes in mass have a negligible effect. This indicates a potential design limitation in the ECTRCD under these conditions, where the increased mass does not adequately address the reduced guide track radius and the elevated moment of inertia of the roller, resulting in a relatively flat performance curve.

4.4.3. Dynamic Response of the Top Tower

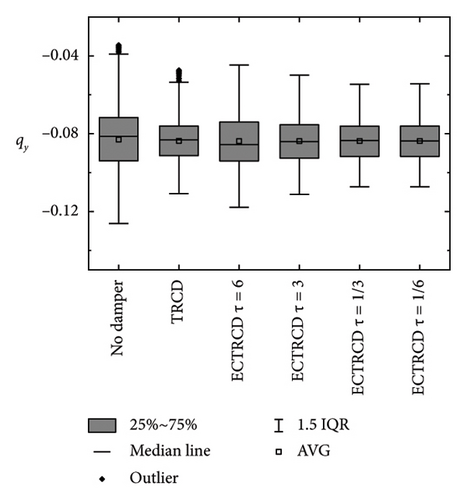
The displacement response at the top of the wind turbine tower under various wind conditions and damper configurations is presented in Figure 23. The data clearly show that the addition of dampers affects the displacement to varying extents when compared to the undamped turbine. In the fore–aft direction, dampers are particularly effective at reducing the peak displacement without notably altering the vibration frequency, underscoring their role in mitigating the dynamic response of the primary structure. The displacement initially rises and then declines with increasing wind speed, peaking near the rated wind speed, which is consistent with engineering predictions. Similar to the aerodynamic loads, the structural and aerodynamic damping intrinsic to the turbine and the wind field diminish the additional damping provided by the dampers, leading to a reduced impact on the dynamic response at higher wind speeds.

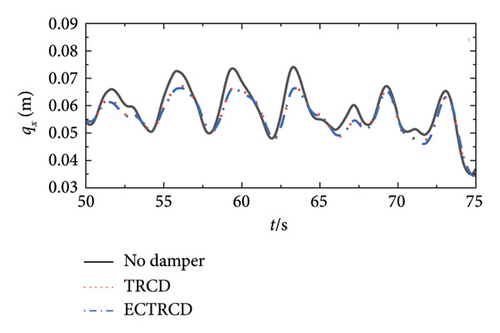
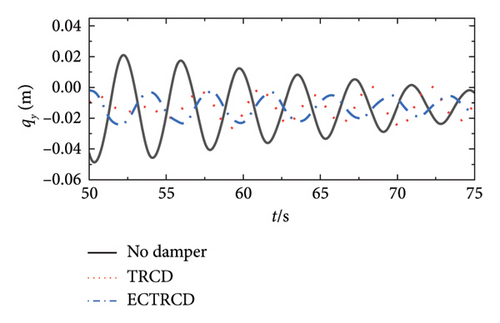
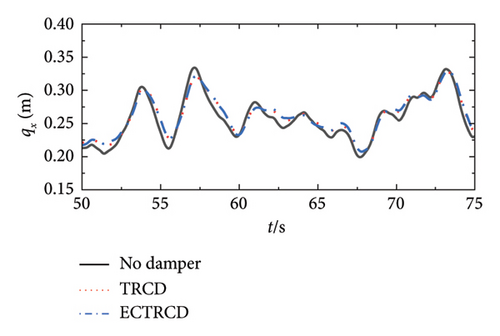
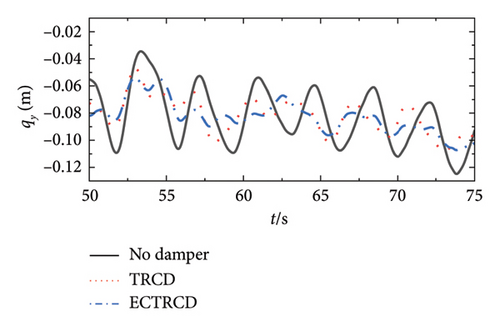
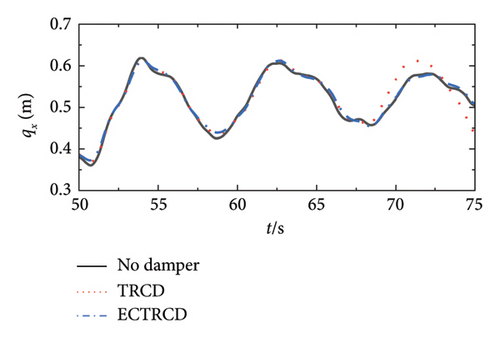
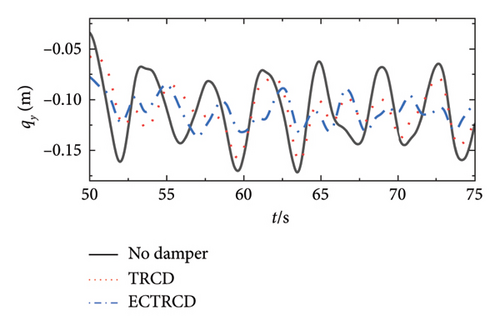
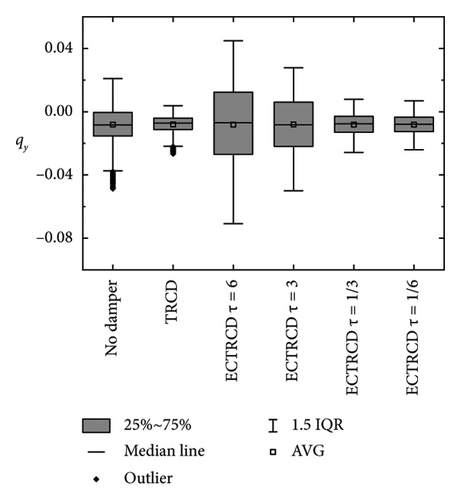
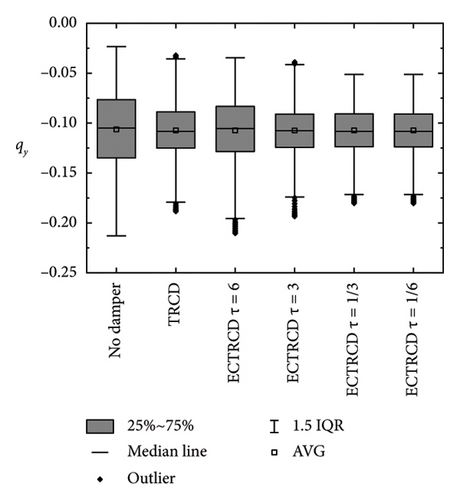
Conversely, the dampers exert a more pronounced influence on the lateral displacement. As illustrated on the right side of Figure 23, the presence of various dampers not only lowers the peak displacement but also modifies the vibration characteristics, including the frequency of lateral displacement. Unlike in the fore–aft direction, lateral vibrations of the turbine steadily increase with wind speed, which proves it is effective for the vibration mitigation of wind turbine tower in the side-to-side direction.

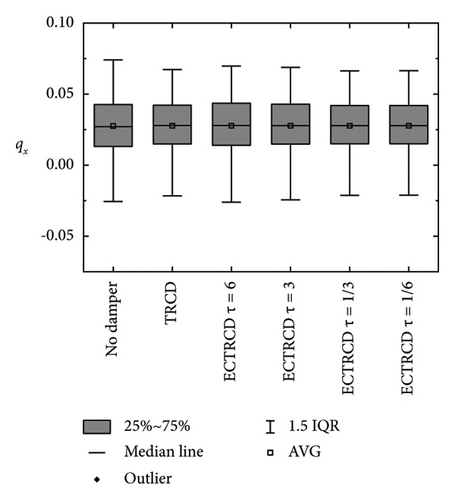
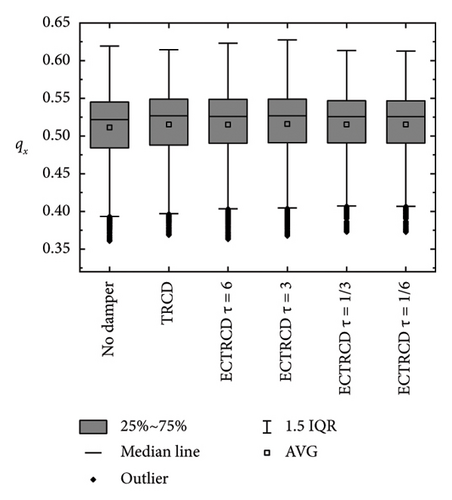
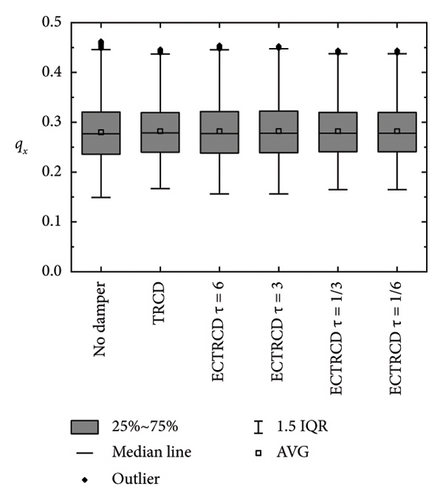
Box plots illustrating the displacement at the tower top in the fore–aft and side-to-side directions are presented in Figures 24 and 25, respectively. In the fore–aft direction, the interquartile range (IQR) is notably narrower following the implementation of the damper, demonstrating its effectiveness, particularly under high wind speed conditions. The performance of the TRCD and the ECTRCD with a radius ratio of 1/6 is observed to be comparable in this direction. In contrast, in the side-to-side direction, the ECTRCD with a radius ratio of 1/6 exhibits superior performance, as indicated by a significantly narrower IQR compared to the TRCD. These findings suggest that the ECTRCD outperforms the TRCD in controlling vibrations in the side-to-side direction, particularly under high wind speeds.

5. Concluding Remarks and Future Works

This study presents the design of a novel ECTRCD aimed at mitigating fatigue loads and vibrations in wind turbines. To achieve optimal vibration control performance, the parameters were optimised. The vibration control efficacy was compared with that of the traditional TRCD, revealing superior performance of the ECTRCD. The aerodynamic loads and dynamic response of the wind turbine, incorporating the optimised parameters, are detailed. The key findings are summarised as follows:

1.
The damping performance of the ECTRCD is influenced by the radius ratio, mass ratio, frequency ratio and damping ratio. The optimal frequency ratio is observed between 0.9 and 1, with the damping ratio around 0.05. As this radius ratio τ increases, the damping performance deteriorates due to the increased moment of inertia of the rolling cylinder and the reduced radius of the guide track arc. When the radius ratio changes from 6 to 1/6, the optimal damping performance improves from 5.3% to 17.7%, an enhancement by a factor of 3.34.
2.
The reduction ratio of the EFL is 16.7% using the TRCD with the optimised parameters (a mass ratio of 1.2%, a frequency ratio of 0.934 and a damping ratio of 0.056). This value can be improved to be 17.7% by the ECTRCD with the optimal parameters (a radius ratio of 1/6, a mass ratio of 1.2%, a frequency ratio of 0.943 and a damping ratio of 0.059). Compared with the TRCD, the EFL is further reduced by 1%.
3.
The ECTRCD, with optimised parameters, significantly affects the aerodynamic load and displacement of the wind turbine in the side-to-side direction, altering both the vibration amplitude and frequency, thus enhancing the vibration characteristics of the wind turbine. Conversely, the impact of the damper on the load or displacement in the fore–aft direction is less pronounced, being substantially influenced by the aerodynamic damping of the wind field and the structural damping of the wind turbine.

This study focuses exclusively on linear damping. However, in practical applications, nonlinear friction damping in the TRCD and nonlinear eddy current damping in the ECTRCD are inherently present. Future investigations should account for these nonlinear damping forces to enhance the model’s realism and applicability.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Zhenqing Liu: supervision, project administration, methodology and conceptualisation. Chao Wang: investigation, software, formal analysis and visualisation. Dongqin Zhang: writing – original draft preparation, writing – review and editing, and visualisation. All authors agree to be accountable for the content and conclusions of the article.

Funding

In this paper, the authors did not receive funding from any institution or company.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 GWPS, Global Wind Power Statistics by 2021—Wind Energy International Platform, 2021, https://library.wwindea.org/global-wind-power-statistics/.
Google Scholar
2 Zuo H., Bi K., and Hao H., A State-of-the-Art Review on the Vibration Mitigation of Wind Turbines, Renewable and Sustainable Energy Reviews. (2020) 121, https://doi.org/10.1016/j.rser.2020.109710.
10.1016/j.rser.2020.109710
Web of Science® Google Scholar
3 Luo M., Jin X., Yue Y., and Chen Y., Bidirectional Vibration Control for Fully-Coupled Floating Offshore Wind Turbines, Ocean Engineering. (2024) 292, https://doi.org/10.1016/j.oceaneng.2023.116523.
10.1016/j.oceaneng.2023.116523
Web of Science® Google Scholar
4 Lu D., Wang W., and Li X., Experimental Study of Structural Vibration Control of 10-MW Jacket Offshore Wind Turbines Using Tuned Mass Damper Under Wind and Wave Loads, Ocean Engineering. (2023) 288, https://doi.org/10.1016/j.oceaneng.2023.116015.
10.1016/j.oceaneng.2023.116015
Web of Science® Google Scholar
5 Ding H., Altay O., and Wang J. T., Lateral Vibration Control of Monopile Supported Offshore Wind Turbines With Toroidal Tuned Liquid Column Dampers, Engineering Structures. (2023) 286, https://doi.org/10.1016/j.engstruct.2023.116107.
10.1016/j.engstruct.2023.116107
Web of Science® Google Scholar
6 Wang Y., Liu Z., and Ma X., Improvement of Tuned Rolling Cylinder Damper for Wind Turbine Tower Vibration Control Considering Real Wind Distribution, Renewable Energy. (2023) 216, https://doi.org/10.1016/j.renene.2023.119078.
10.1016/j.renene.2023.119078
Web of Science® Google Scholar
7 Zhao Z., Dai K., Lalonde E. R. et al., Studies on Application of Scissor-Jack Braced Viscous Damper System in Wind Turbines Under Seismic and Wind Loads, Engineering Structures. (2019) 196, https://doi.org/10.1016/j.engstruct.2019.109294, 2-s2.0-85067396788.
10.1016/j.engstruct.2019.109294
Web of Science® Google Scholar
8 Fitzgerald B., Sarkar S., and Staino A., Improved Reliability of Wind Turbine Towers With Active Tuned Mass Dampers (ATMDs), Journal of Sound and Vibration. (2018) 419, 103–122, https://doi.org/10.1016/j.jsv.2017.12.026, 2-s2.0-85041539008.
10.1016/j.jsv.2017.12.026
Web of Science® Google Scholar
9 Hu Y., Chen M. Z. Q., and Li C., Active Structural Control for Load Mitigation of Wind Turbines via Adaptive Sliding-Mode Approach, Journal of the Franklin Institute. (2017) 354, no. 11, 4311–4330, https://doi.org/10.1016/j.jfranklin.2017.04.002, 2-s2.0-85018421155.
10.1016/j.jfranklin.2017.04.002
Web of Science® Google Scholar
10 Brodersen M. L., Bjørke A. S., and Høgsberg J., Active Tuned Mass Damper for Damping of Offshore Wind Turbine Vibrations, Wind Energy. (2017) 20, no. 5, 783–796, https://doi.org/10.1002/we.2063, 2-s2.0-84995952520.
10.1002/we.2063
Web of Science® Google Scholar
11 Fitzgerald B. and Basu B., Structural Control of Wind Turbines With Soil Structure Interaction Included, Engineering Structures. (2016) 111, 131–151, https://doi.org/10.1016/j.engstruct.2015.12.019, 2-s2.0-84952926979.
10.1016/j.engstruct.2015.12.019
Web of Science® Google Scholar
12 Long T., Yang Q., Wang Q., Huang G., Zhou X., and Yang Y., Active Vibration Control of Wind Turbine Using Virtual TMD Algorithm Based on Aerodynamic-Structure-Servo Coupling Model, Structural Control and Health Monitoring. (2023) 2023, no. 1, 1–26, https://doi.org/10.1155/2023/6618783.
10.1155/2023/6618783
Web of Science® Google Scholar
13 Wang L., Zhou Y., and Shi W., Random Crowd-Induced Vibration in Footbridge and Adaptive Control Using Semi-Active TMD Including Crowd-Structure Interaction, Engineering Structures. (2024) 306, https://doi.org/10.1016/j.engstruct.2024.117839.
10.1016/j.engstruct.2024.117839
Web of Science® Google Scholar
14 Ghassempour M., Failla G., and Arena F., Vibration Mitigation in Offshore Wind Turbines via Tuned Mass Damper, Engineering Structures. (2019) 183, 610–636, https://doi.org/10.1016/j.engstruct.2018.12.092, 2-s2.0-85060131180.
10.1016/j.engstruct.2018.12.092
Web of Science® Google Scholar
15 Tong X., Zhao X., and Zhao S., Load Reduction of a Monopile Wind Turbine Tower Using Optimal Tuned Mass Dampers, International Journal of Control. (2017) 90, no. 7, 1283–1298, https://doi.org/10.1080/00207179.2015.1124143, 2-s2.0-85019598015.
10.1080/00207179.2015.1124143
Web of Science® Google Scholar
16 Yang J. J. and He E. M., Coupled Modeling and Structural Vibration Control for Floating Offshore Wind Turbine, Renewable Energy. (2020) 157, 678–694, https://doi.org/10.1016/j.renene.2020.05.075.
10.1016/j.renene.2020.05.075
Web of Science® Google Scholar
17 Zhang H., Wen B., Tian X. et al., Experimental Study on Mitigating Vibration of Floating Offshore Wind Turbine Using Tuned Mass Damper, Ocean Engineering. (2023) 288, https://doi.org/10.1016/j.oceaneng.2023.115974.
10.1016/j.oceaneng.2023.115974
Web of Science® Google Scholar
18 Mitra A., Giridharan Y., and Chakraborty A., Wavelet Linear Quadratic Regulator-Based Gain Scheduling for Optimal Fore-Aft Vibration Control of Horizontal Axis Wind Turbine Tower Using Active Tuned Mass Damper, Structural Control and Health Monitoring. (2022) 29, no. 11, https://doi.org/10.1002/stc.3055.
10.1002/stc.3055
PubMed Web of Science® Google Scholar
19 Chen Y., Jin X., Liu H., Li F., and Luo M., Large Scale Wind Turbine TMD Optimization Based on Blade-Nacelle-Tower-Foundation Coupled Model, Ocean Engineering. (2021) 239, https://doi.org/10.1016/j.oceaneng.2021.109764.
10.1016/j.oceaneng.2021.109764
Web of Science® Google Scholar
20 He J., Jin X., Xie S. Y., Cao L., Lin Y., and Wang N., Multi-Body Dynamics Modeling and TMD Optimization Based on the Improved AFSA for Floating Wind Turbines, Renewable Energy. (2019) 141, 305–321, https://doi.org/10.1016/j.renene.2019.04.005, 2-s2.0-85064506954.
10.1016/j.renene.2019.04.005
Web of Science® Google Scholar
21 Dong X., Ren S., Jia Y., and Yu T., Parameter Optimization and Vibration Reduction Effect of One C-Shaped Particle Damping-Tuned Mass Damper for Offshore Wind Turbine, Ocean Engineering. (2024) 305, https://doi.org/10.1016/j.oceaneng.2024.117856.
10.1016/j.oceaneng.2024.117856
Web of Science® Google Scholar
22 Verma M., Nartu M. K., and Subbulakshmi A., Optimal TMD Design for Floating Offshore Wind Turbines Considering Model Uncertainties and Physical Constraints, Ocean Engineering. (2022) 243, https://doi.org/10.1016/j.oceaneng.2021.110236.
10.1016/j.oceaneng.2021.110236
Web of Science® Google Scholar
23 Jahangiri V., Sun C., and Kong F., Study on a 3D Pounding Pendulum TMD for Mitigating Bi-Directional Vibration of Offshore Wind Turbines, Engineering Structures. (2021) 241, https://doi.org/10.1016/j.engstruct.2021.112383.
10.1016/j.engstruct.2021.112383
Web of Science® Google Scholar
24 Chen J., Zhao Y., Cong O., and He M. J., Vibration Control Using Double-Response Damper and Site Measurements on Wind Turbine, Structural Control and Health Monitoring. (2018) 25, no. 9, https://doi.org/10.1002/stc.2200, 2-s2.0-85051137960.
10.1002/stc.2200
Web of Science® Google Scholar
25 Liu G., Lei Z., and Wang H., Investigation and Optimization of a Pre-Stressed Tuned Mass Damper for Wind Turbine Tower, Structural Control and Health Monitoring. (2022) 29, no. 3, https://doi.org/10.1002/stc.2894.
10.1002/stc.2894
PubMed Web of Science® Google Scholar
26 Lei Z., Liu G., Zhang X., Yang Q., and Law S. S., Three-Dimensional Prestressed Tuned Mass Damper for Passive Vibration Control of Coupled Multiple DOFs Offshore Wind Turbine, Structural Control and Health Monitoring. (2023) 2023, no. 1, 1–27, https://doi.org/10.1155/2023/8897653.
10.1155/2023/8897653
Web of Science® Google Scholar
27 Wang L., Shi W., Li X., Zhang Q., and Zhou Y., An Adaptive-Passive Retuning Device for a Pendulum Tuned Mass Damper Considering Mass Uncertainty and Optimum Frequency, Structural Control and Health Monitoring. (2019) 26, no. 7, https://doi.org/10.1002/stc.2377, 2-s2.0-85066893105.
10.1002/stc.2377
PubMed Web of Science® Google Scholar
28 Wang L., Nagarajaiah S., Shi W., and Zhou Y., Study on Adaptive-Passive Eddy Current Pendulum Tuned Mass Damper for Wind-Induced Vibration Control, The Structural Design of Tall and Special Buildings. (2020) 29, no. 15, https://doi.org/10.1002/tal.1793.
10.1002/tal.1793
Web of Science® Google Scholar
29 Wang L., Shi W., and Zhou Y., Adaptive-Passive Tuned Mass Damper for Structural Aseismic Protection Including Soil–Structure Interaction, Soil Dynamics and Earthquake Engineering. (2022) 158, https://doi.org/10.1016/j.soildyn.2022.107298.
10.1016/j.soildyn.2022.107298
Web of Science® Google Scholar
30 Pirner M., Actual Behaviour of a Ball Vibration Absorber, Journal of Wind Engineering and Industrial Aerodynamics. (2002) 90, no. 8, 987–1005, https://doi.org/10.1016/S0167-6105(02)00215-5, 2-s2.0-0036677301.
10.1016/S0167-6105(02)00215-5
Web of Science® Google Scholar
31 Matta E., Ball Vibration Absorbers With Radially-Increasing Rolling Friction, Mechanical Systems and Signal Processing. (2019) 132, 353–379, https://doi.org/10.1016/j.ymssp.2019.06.033, 2-s2.0-85068499924.
10.1016/j.ymssp.2019.06.033
Web of Science® Google Scholar
32 Legeza V. P., Rolling of a Heavy Ball in a Spherical Recess of a Translationally Moving Body, International Applied Mechanics. (2002) 38, no. 6, 758–764, https://doi.org/10.1023/A:1020445215419, 2-s2.0-0036392979.
10.1023/A:1020445215419
Web of Science® Google Scholar
33 Chen J. and Georgakis C. T., Tuned Rolling-Ball Dampers for Vibration Control in Wind Turbines, Journal of Sound and Vibration. (2013) 332, no. 21, 5271–5282, https://doi.org/10.1016/j.jsv.2013.05.019, 2-s2.0-84880167853.
10.1016/j.jsv.2013.05.019
Web of Science® Google Scholar
34 Li J., Zhang Z., and Chen J., Experimental Study on Vibration Control of Offshore Wind Turbines Using a Ball Vibration Absorber, Energy and Power Engineering. (2012) 4, no. 3, 153–157, https://doi.org/10.4236/epe.2012.43021.
10.4236/epe.2012.43021
Google Scholar
35 Zhang Z. L., Chen J. B., and Li J., Theoretical Study and Experimental Verification of Vibration Control of Offshore Wind Turbines by a Ball Vibration Absorber, Structure and Infrastructure Engineering. (2014) 10, no. 8, 1087–1100, https://doi.org/10.1080/15732479.2013.792098, 2-s2.0-84901274034.
10.1080/15732479.2013.792098
Web of Science® Google Scholar
36 Zhang Z., Li J., Nielsen S. R. K., and Basu B., Mitigation of Edgewise Vibrations in Wind Turbine Blades by Means of Roller Dampers, Journal of Sound and Vibration. (2014) 333, no. 21, 5283–5298, https://doi.org/10.1016/j.jsv.2014.06.006, 2-s2.0-84903750377.
10.1016/j.jsv.2014.06.006
Web of Science® Google Scholar
37 Li S., Fu L., and Kong F., Seismic Response Reduction of Structures Equipped With a Voided Biaxial Slab-Based Tuned Rolling Mass Damper, Shock and Vibration. (2015) 2015, 1–15, https://doi.org/10.1155/2015/760394, 2-s2.0-84934312339.
10.1155/2015/760394
Web of Science® Google Scholar
38 Tsuda R. and Saeki M., Efficiency of Vibrational Energy Dissipation by Tuned Rolling-Cylinder Dampers, Journal of Sound and Vibration. (2019) 463, https://doi.org/10.1016/j.jsv.2019.114977, 2-s2.0-85072838906.
10.1016/j.jsv.2019.114977
Web of Science® Google Scholar
39 Sarkar S. and Chakraborty A., Optimal Design of Semiactive MR-TLCD for Along-Wind Vibration Control of Horizontal Axis Wind Turbine Tower, Structural Control and Health Monitoring. (2018) 25, no. 2, https://doi.org/10.1002/stc.2083, 2-s2.0-85041011808.
10.1002/stc.2083
Web of Science® Google Scholar
40 Sarkar S. and Chakraborty A., Development of Semi-Active Vibration Control Strategy for Horizontal Axis Wind Turbine Tower Using Multiple Magneto-Rheological Tuned Liquid Column Dampers, Journal of Sound and Vibration. (2019) 457, 15–36, https://doi.org/10.1016/j.jsv.2019.05.052, 2-s2.0-85066479302.
10.1016/j.jsv.2019.05.052
Web of Science® Google Scholar
41 Larose G. L., Larsen A., and Svensson E., Modelling of Tuned Mass Dampers for Wind-Tunnel Tests on a Full-Bridge Aeroelastic Model, Journal of Wind Engineering and Industrial Aerodynamics. (1995) 54–55, 427–437, https://doi.org/10.1016/0167-6105(94)00058-L, 2-s2.0-0029240106.
10.1016/0167-6105(94)00058-L
Web of Science® Google Scholar
42 Leng D., Wang R., Yang Y., Li Y., and Liu G., Study on a Three-Dimensional Variable-Stiffness TMD for Mitigating Bi-Directional Vibration of Monopile Offshore Wind Turbines, Ocean Engineering. (2023) 281, https://doi.org/10.1016/j.oceaneng.2023.114791.
10.1016/j.oceaneng.2023.114791
Web of Science® Google Scholar
43 Chen Z., Huang Z., Wang J., and Niu H., Basic Requirements of Tuned Mass Damper for Bridges and the Eddy Current TMD, Journal of Hunan University. (2013) 40, no. 8.
Google Scholar
44 Lou W., Wen Z., Chen Y., and Huang M., Wind Tunnel Study on Bidirectional Vibration Control of Lattice Towers With Omnidirectional Cantilever-type Eddy Current TMD, Applied Sciences. (2019) 9, no. 15, https://doi.org/10.3390/app9152978, 2-s2.0-85070673530.
10.3390/app9152978
Google Scholar
45 Johnson N. L., Kotz S., and Balakrishnan N., Wiley Series in Probability and Mathematical Statistics: Applied Probability and Statistics, 1994, 2nd edition, John Wiley & Sons, New York.
Google Scholar
46 IEC 61400-13, IEC 61400-13:2015 Wind Turbines—Part 13: Measurement of Mechanical Loads, 2015.
Google Scholar
47 IEC 61400-1, IEC 61400-1:2019 Wind Energy Generation Systems—Part 1: Design Requirements, 2019.
Google Scholar
48 Dassault Systems, SIMPACK 2021 Simpack Assistant, 2021.
Google Scholar
49 Bossanyi E., GH Bladed Theory Manual, 2003, GH & Partners Ltd.
Google Scholar
50 IEC 61400-1, Wind Turbine Generator Systems Part1, Safety Requirements, 2019.
Google Scholar
51 Zhang D., Liu Z., Li W., Zhang J., Cheng L., and Hu G., Fluid-Structure Interaction Analysis of Wind Turbine Aerodynamic Loads and Aeroelastic Responses Considering Blade and Tower Flexibility, Engineering Structures. (2024) 301, https://doi.org/10.1016/j.engstruct.2023.117289.
10.1016/j.engstruct.2023.117289
Web of Science® Google Scholar

All articles

Study on Vibration Control of Wind Turbine With an Optimised Eddy Current Tuned Rolling Cylinder Damper

Abstract

1. Introduction

2. Numerical Models

2.1. Wind Condition

2.2. Aerodynamic Forces

2.3. Wind Turbine Model

3. Damper Models

3.1. TRCD

3.2. Eddy Current Damping Model

3.3. ECTRCD

4. Results and Discussion

4.1. Verification of Wind Turbine Model

4.2. Parameter Optimisation of TRCD for Vibration Control of Wind Turbine

4.3. Parameter Optimisation of ECTRCD for Vibration Control of Wind Turbine

4.4. Comparisons of the Performance of Two Different Dampers

4.4.1. Forces at the Tower Base

4.4.2. Equivalent Fatigue Loads

4.4.3. Dynamic Response of the Top Tower

5. Concluding Remarks and Future Works

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Study on Vibration Control of Wind Turbine With an Optimised Eddy Current Tuned Rolling Cylinder Damper

Abstract

1. Introduction

2. Numerical Models

2.1. Wind Condition

2.2. Aerodynamic Forces

2.3. Wind Turbine Model

3. Damper Models

3.1. TRCD

3.2. Eddy Current Damping Model

3.3. ECTRCD

4. Results and Discussion

4.1. Verification of Wind Turbine Model

4.2. Parameter Optimisation of TRCD for Vibration Control of Wind Turbine

4.3. Parameter Optimisation of ECTRCD for Vibration Control of Wind Turbine

4.4. Comparisons of the Performance of Two Different Dampers

4.4.1. Forces at the Tower Base

4.4.2. Equivalent Fatigue Loads

4.4.3. Dynamic Response of the Top Tower

5. Concluding Remarks and Future Works

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information