The current application of vibration-based damage detection is constrained by the low spatial resolution of signals obtained from contact sensors and an overreliance on hand-engineered damage indices. In this paper, we propose a novel vision-aided framework featuring convolutional multihead self-attention neural network (CMSNN) to deal with damage detection tasks. To meet the requirement of spatially intensive measurements, a computer vision algorithm called optical flow estimation is employed to provide informative enough mode shapes. As a downstream process, a CMSNN model is designed to autonomously learn high-level damage representations from noisy mode shapes without any manual feature design. In contrast to the conventional approach of solely stacking convolutional layers, the model is enhanced by combining a convolutional neural network (CNN)–based multiscale information extraction module with an attention-based information fusion module. During the training process, various scenarios are considered, including measurement noise, data missing, multiple damages, and undamaged samples. Moreover, the parameter transfer strategy is introduced to enhance the universality of the application. The performance of the proposed framework is extensively verified via datasets based on numerical simulations and two laboratory measurements. The results demonstrate that the proposed framework can provide reliable damage detection results even when the input data are corrupted by noise or incomplete.

1. Introduction

Engineering structures are susceptible to various levels of damage due to harsh environments and complex loads [1, 2]. To guarantee the integrity and safety of structures, studies on structural health monitoring (SHM) have been pursued. In the field of SHM, vibration signals are frequently used to assess structural conditions [3]. Several vibration-based methods are developed to detect damage, such as those based on frequency response function [4–6], modal damping [7–9], characteristic frequency [10–12], and mode shape [13–16]. Among these methods, mode shape-based methods are well suited to the task of detecting damage, leveraging their comprehensive spatial dynamic information.

Accurate mode shape measurement is vital for mode shape-based damage detection, as it directly influences the precision of damage localization. Currently, mode shape acquisition methods fall into two broad categories: contact and noncontact techniques. Contact methods based on contact sensors are the most adopted [17–19]. However, contact methods inevitably induce mass-loading effects and offer only sparse and discrete monitoring points, resulting in low spatial measurement resolution [20, 21]. This is typically insufficient for mode shape-based damage detection. Noncontact methods, such as scanning laser vibrometer (SLV)–based and vision-based techniques, can collect vibration signals without requiring sensors to be physically mounted on structures. Yang et al. placed nineteen measurement points on an aluminum beam and utilized SLV to capture its mode shapes [22]. Pan et al. measured the mode shapes of carbon-epoxy curved plates under free conditions using SLV [23]. Xin et al. utilized high-speed videos processed with a phase-based computer vision algorithm to measure the mode shapes of beams [24]. Chen et al. applied complex-valued steerable pyramid filter banks to analyze digital videos of structural motion and extract mode shapes of a pipe [25]. Despite providing denser measurement points, the use of SLV is costly and time-consuming. In contrast, vision-based methods, which offer lower costs, higher efficiency, and high-spatial-resolution measurements, are gaining increasing attention [26–28].

On the other hand, there is currently a lack of universally applicable mode shape-based index for revealing damage. Roy presented detailed mathematical derivations showing that the maximum difference in mode shape slopes occurs at the damage location [29]. Pooya et al. introduced the difference between mode shape curvature and its estimation as an indicator of damage location [30]. Cao et al. proposed a damage index combining wavelet transform technique and mode shape curvature to detect multiple cracks in beam structures [31]. Xiang et al. adopted modal curvature utility information entropy index (MCUIE) to catch the damage-induced discontinuity in mode shapes [32]. Cui et al. identified fatigue cracks by calculating spatially distributed wavelet entropy of mode shapes [33]. Although different damage indices have been presented and verified, it is important to note that these hand-engineered indices face many challenges. The formulation of a hand-engineered damage index necessitates an analysis of dynamic characteristics both before and after damage has occurred. This process heavily relies on domain-specific expert knowledge. Moreover, it is not feasible to universally apply a specific damage index in realistic complex noisy environments, even for identical structures. Therefore, a model that requires no manual intervention and is robust to noise, as well as capable of dealing with extreme cases of partial data missing, is desirable.

In recent years, data-driven methods based on deep neural network (DNN) have revolutionized numerous scientific domains [34]. One significant advantage of DNNs is their capacity to autonomously learn high-level feature representations from massive samples without manual feature engineering, which allows for end-to-end prediction [35]. Scholars have made efforts to utilize DNN-based methods to realize damage detection. Oh et al. used a convolutional neural network (CNN) to model the interrelation of dynamic displacement response between healthy and damaged states [36]. Lei et al. proposed a CNN model to identify structural damage from transmission functions of vibration response [37]. Tang et al. developed a CNN-based data anomaly detection method imitating human vision and decision making [38]. He et al. combined CNN with fast Fourier transform (FFT) to identify damage conditions [39]. Guo et al. utilized a model composed of stacked CNN modules to extract damage features from raw mode shapes [40]. Nevertheless, most DNN-based methods rely solely on CNN for their network architecture. This limits their model improvement to merely stacking network layers to increase trainable parameters, rather than enhancing feature extraction capabilities.

To overcome the above deficiencies, in this paper, we propose a novel vision-aided framework with convolutional multihead self-attention neural network (CMSNN) to deal with damage detection tasks. A computer vision algorithm named optical flow estimation is first employed to conduct high-spatial-resolution vibration measurements. Then, the CMSNN model, composed of two distinct types of modules, is designed to perform multiscale damage information (DI) extraction and fusion autonomously. To meet the requirement of generating massive labeled samples for model training, a numerical simulation strategy is adopted to construct datasets of damaged mode shapes, accounting for measurement noise, multiple damages, and undamaged samples. Moreover, the results of numerical simulations and experiments show that the proposed framework can accurately detect structural damage from raw data with strong robustness and remains effective across various scenarios.

The rest of the paper is organized as follows. Section 2 presents the theory of optical flow estimation and the architecture design of the CMSNN model. Section 3 describes the strategy for the CMSNN model training. The performance of the CMSNN model is numerically evaluated in Section 4, and the proposed framework is experimentally verified in Section 5. Section 6 concludes the paper with a summary of findings and suggests potential future research directions.

2. Methodology

In this section, the principles of the proposed damage detection framework are described in detail. Figure 1 provides a visual representation of the specific process of the framework.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Flowchart of the proposed framework for structural damage detection.

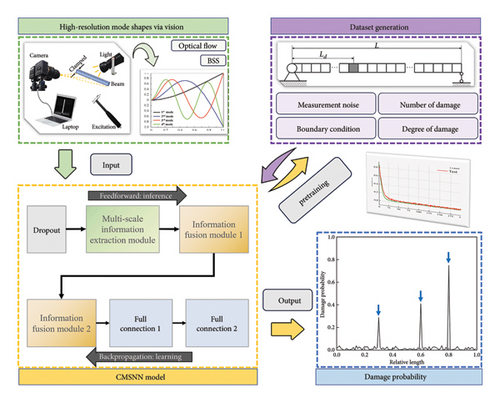
2.1. High-Spatial-Resolution Mode Shapes via Vision

It is well accepted that the video recording process is a projection of structural motion onto the image plane. The aim of optical flow estimation is to compute reliable estimates of the motion field from time-varying image intensity. The initial step in estimating optical flow involves assuming that pixel intensities are consistently translated from one frame to the next

()

where I(x, y, t) is the image intensity at spatial location (x, y) and time t, dx, and dy are the pixel shift in the x and y directions, respectively, and dt is the interframe time.

Considering the high frame rate of video sampling and the typically small vibration amplitude, the pixel motion from one frame to the next is sufficiently minor. Thus, we can expand the right-hand side of equation (1) by applying the first-order Taylor series approximation:

()

By substituting equation (2) into equation (1), the following equation can be obtained:

()

where I_x and I_y are the horizontal and vertical image intensity gradients, respectively, I_t is the difference of the image intensities between the 2 frames, and u and v are the optical flow embedded with vibration signals in the horizontal and vertical direction.

Equation (3) is known as the optical flow equation. It is underdetermined, which implies that the two variables (u, v) cannot be recovered uniquely from a single gradient constraint. To address this issue, it is reasonable to assume that neighboring pixels in a small region around the measured pixel share the same optical flow. Let the number of neighboring pixels be k. The equation system below holds since the neighboring pixels are subject to the same motion

()

where p₁, p₂, …, p_k are the neighboring pixels of the measured pixel.

For simplicity, we can express equation (4) as a matrix multiplication

()

Equation (5) is overdetermined since the value of k used is generally much greater than 2. To identify the solution that minimizes the constraint errors, the least-squares optimization method is employed to provide the most accurate optical flow estimation:

()

In practice, optical flow vectors are calculated to track the locations of pixels across video frame sequences, thereby providing the vibration signals associated with those pixels. Notably, each tracked pixel can serve as a measuring point, which allows for high-spatial-resolution vibration measurements. In this paper, blind source separation (BSS) technique is adopted to extract high-spatial-resolution mode shapes from the obtained vibration signals. The comprehensive explanations and derivations of BSS are available in [41].

2.2. CMSNN Model for DI Extraction and Fusion

In this paper, a novel CMSNN model is proposed to autonomously learn high-level feature representations from obtained noisy mode shapes, obviating the need for explicit manual feature design. In particular, the architecture of the CMSNN model mainly consists of two principal functional modules: the CNN-based multiscale information extraction module and the attention mechanism–based information fusion module.

2.2.1. Multiscale Information Extraction Module

The architecture design of the multiscale information extraction module is depicted in Figure 2. In this module, convolutional layers are used to extract multiscale damage features from the raw mode shape data. The input mode shape vector comprises 100 components, indicating that the mode shapes obtained via simulations and vision-aided experiments both equally contain 100 sample points.

Unlike operations of conventional CNN, which simply stack multiple convolutional layers on top of each other to deepen the network, we introduce four sets of cascade convolutional filters with varying kernel sizes (specifically, 1 × 3, 1 × 5, 1 × 7, and 1 × 9) to extract semantic information of damage in parallel. Smaller kernels are used to capture finer details of damage, whereas larger kernels provide greater noise robustness through their larger receptive fields. This approach leads to a more lightweight module and allows for DI extraction from multiple scales. The mathematical representation of the process can be described as follows:

()

where DI_i,j denotes the jth DI vector at scale i, ψ denotes the input mode shape vector, F_i,j denotes the jth convolutional kernel at scale i, b_i,j denotes the jth bias parameter at scale i, n_ci denotes the number of convolution kernels at scale i, and σ denotes the activation function.

Inspired by the earlier work in [42], the parametric rectified linear unit (PReLU) is adopted here as the activation function for the convolutional layer, which can be written as follows:

()

where α is the trainable parameter that controls the slope of the function.

It is worth noting that a pooling layer has not been included in order to retain DI to the maximum extent possible. At the end of the module, channel concatenation is performed on the DI across all scales to generate a highly integrated damage information map (DIM) for further information fusion, which can be described as follows:

()

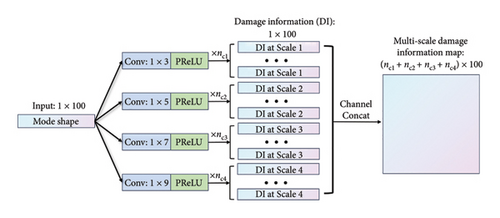
2.2.2. Information Fusion Module

The attention mechanism is fundamentally analogous to the human vision mechanism focusing on the key features and attenuating the impact of noise interference during the training process [43], making it particularly well suited to the damage detection task. The primary objective of the information fusion module is to achieve an efficient fusion of multiscale DI using an architecture based on multihead self-attention mechanisms. Figure 3 provides a visual representation of this architecture.

In order to capture the dependencies between each sequence and other sequences of the input matrix, the multihead self-attention mechanism establishes mapping relationships between queries, keys, values, and outputs in different embedding spaces. In this study, the DIM extracted by the multiscale information extraction module is used as the input matrix, and the DI across all scales in the DIM are the sequences to be analyzed. The input DIM is first mapped into h groups of matrices through linear projection, with each group comprising three distinct matrices:

()

where Q_i, K_i, and V_i are the query matrix, key matrix, and value matrix belonging to the ith head,

, and

are trainable linear projection matrices of the ith head, h is the number of heads, and d_e = 100/h is the dimension of embedding space.

For each group of matrices, the computation of scaled dot-product attention is then performed according to equation (11):

()

where SoftMax is the normalized exponential function. Its detailed description can be found in [44].

Finally, the multihead attention of DI is acquired by horizontally concatenating the h scaled dot-product attention:

()

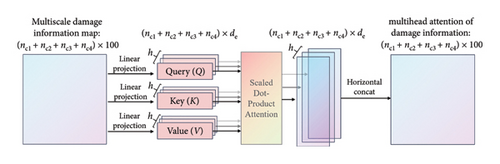
The multihead attention obtained has established an adaptive correlation of DI between different scales in multiple embedding spaces. It is important to note that this is an efficient and robust process of information fusion, not limited by the spacing of the scales.

2.2.3. CMSNN Model Construction

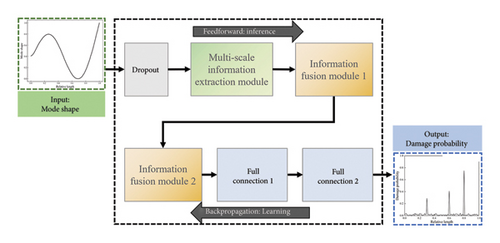
During the verification stage, a series of experiments were conducted to assess the performance of different module combinations and hyperparameter settings. Figure 4 illustrates the overall architectural configuration that yielded the optimal results, and Table 1 lists the detailed configuration of each module.

Table 1. Detailed configuration of the proposed CMSNN model.

Module type	Kernel size	Kernel number	Stride	Padding	Head number	Activation function	Output size
Multiscale information extraction module	1 × 3	32	1	1	/	PReLU	32 × 100
	1 × 5	32	1	2	/	PReLU	32 × 100
	1 × 7	32	1	3	/	PReLU	32 × 100
	1 × 9	32	1	4	/	PReLU	32 × 100

Information fusion module 1	/	/	/	/	4	PReLU	128 × 100

Information fusion module 2	/	/	/	/	2	PReLU	128 × 100

Full connection 1	/	/	/	/	/	PReLU	1 × 1000

Full connection 2	/	/	/	/	/	Sigmoid	1 × 100

The mode shape fed into the CMSNN model is initially processed by a dropout layer to randomly freeze input nodes. This simulates data-missing scenarios while simultaneously avoiding overfitting. Subsequently, the damage semantic information is extracted from various scales through the multiscale information extraction module to construct the DIM. Following this, two information fusion modules are stacked to perform attention computation on the DIM in multiple embedding spaces, achieving efficient and robust information fusion. Finally, the high-level attention feature is flattened and fed into two stacked fully connected layers to provide the damage probability distribution.

3. Training Strategy

3.1. Dataset Generation

Constructing datasets through video stream acquisition and optical flow estimation undoubtedly results in significant computational overheads and wasted storage space. Accordingly, we adopt a numerical simulation strategy to generate a large number of labeled samples for model training. The strategy is divided into two steps.

The first step involves generating undamaged samples using the theoretical formula for the mode shape of beam-like structures. Equations (13) and (14) list the theoretical formulas of mode shapes under three different boundary conditions:

()

where l denotes the length of the beam, C denotes a constant, and the specific values of βl for mode shapes of different orders are listed in Table 2.

Table 2. Specific values of βl for mode shapes of different orders.

Boundary condition	First mode shape	Second mode shape	Third mode shape
Clamped–free (C–F)	1.875104	4.694091	7.854757
Clamped–clamped (C–C)	4.730041	7.853205	10.995608
Clamped–pinned (C–P)	3.926602	7.068583	10.210176

Second, the finite element method (FEM) is employed to model Euler–Bernoulli beams with single or multiple damages to generate damaged samples. Considering that localized damage to a structure can lead to a reduction in the material’s bearing capacity, structural damage is simulated here using the stiffness degradation method, which can be described by the following formula:

()

where

and

are the elastic modulus of the ith element in damage and undamaged beam, respectively, and d_i is the degree of damage of the ith element.

The label for each sample is designed as a vector with n components (n should be equal to the dimension of the mode shape and n = 100 in this work). The value of each component represents the damage probability of the corresponding beam element, which can be calculated as

()

where P_i is the value of the ith component of the label.

In the process of dataset generation, various factors are taken into account, including boundary conditions, measurement noise, number of damages, and degree of damages, to allow the CMSNN model to learn a more intrinsic representation of the DI. The range of possible choices at random for each of these factors is shown in Table 3, and the detailed allocation of samples for the dataset is shown in Table 4.

Table 3. The range of possible choices for various factors.

Boundary condition	Number of damages	Degree of damages	Signal-to-noise ratio (dB)
{C-F, C-C, C-P}	{1, 2, 3}	(0, 1)	(60, 120)

Table 4. Allocation of samples for the dataset.

Sample use	Damaged samples	Undamaged samples	Total samples
Train	10,000	2000	12,000
Validate	2500	500	3000
Test	1000	200	1200

3.2. Loss Function

Since the prediction of our CMSNN model is the continuous damage probability distribution rather than the discrete judgment of finite structural conditions, the regression model rather than the classification model is more appropriate for our damage detection task. In this study, the mean square error (MSE, also known as L2 loss) is chosen as the loss function, which can be written as

()

where P and

are the prediction result and true label, respectively, and n is the dimension of the label vector.

To minimize the loss value, we use Adam [45] as the optimization method to optimize the network weights, as it can adaptively change the learning rate according to the current gradient. The two momentum parameters for Adam are set to β₁ = 0.9 and β₂ = 0.999.

3.3. Training Results

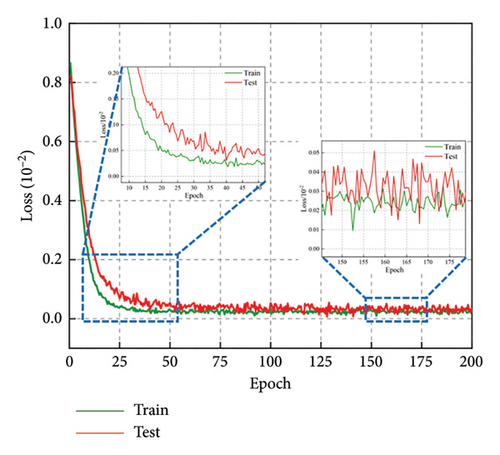
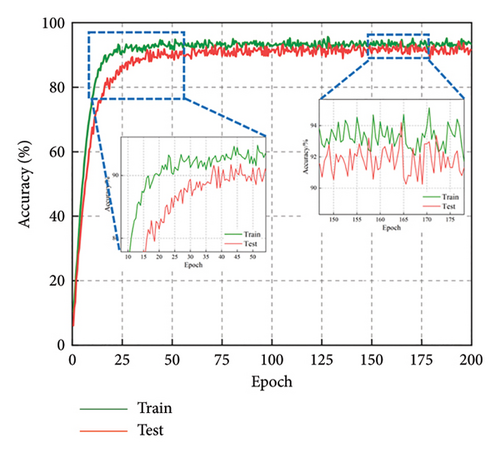
The CMSNN model is implemented on the PyTorch (Version 1.11.0) platform. All modules are initialized from scratch with random weights. The training and testing processes are conducted on the same hardware (CPU: Intel Xeon Platinum 8375C, GPU: NVIDIA GeForce RTX 3090, RAM: 128 GB). We trained the proposed network with the generated dataset for 200 epochs using a batch size of 128, with detailed records of loss and accuracy values. The convergence history of the CMSNN model is plotted in Figure 5. The plots reveal that the loss and accuracy curves exhibit an inflection point around the 30th epoch, signifying the model’s quick convergence in the initial 30 epochs to meet the task’s predictive demands. Following 200 epochs of training, the accuracy on both the training set and testing set reaches 0.9, demonstrating that the CMSNN model presents an excellent ability for the prediction task.

4. Model Evaluation

4.1. Noise Floor Evaluation

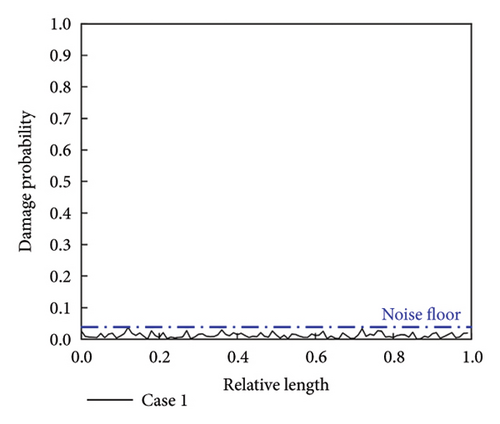
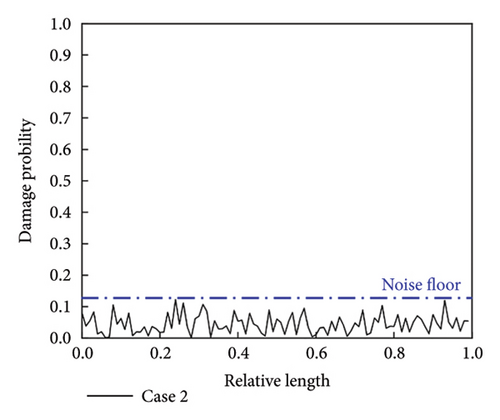
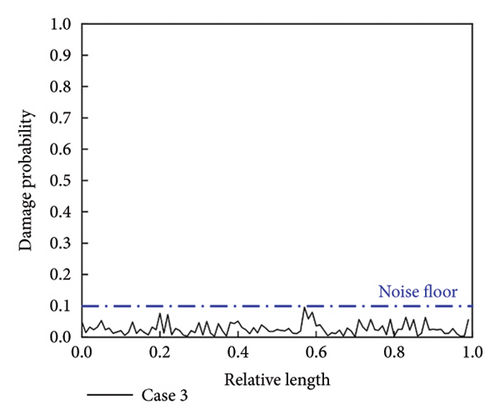
The noise floor is an important indicator of a model’s performance. In the context of our damage detection task, the noise floor level is reflected in the predicted damage probability distribution for undamaged samples. We first randomly chose three cases to evaluate the noise floor level of the CMSNN model. The specific settings of these cases are presented in Table 5.

Table 5. Settings of three cases for noise floor evaluation.

Case	Mode shape	Boundary condition	Signal-to-noise ratio (dB)
1	First order	C-C	105
2	Second order	C-F	69
3	Third order	C-P	82

By feeding the mode shapes into the CMSNN model, the predicted damage probability distributions for three undamaged cases are obtained, as shown in Figure 6. It is presented that the predicted damage probability distributions lack localized peaks, indicating the absence of damage. Despite increased fluctuations in the damage probability distribution curve in noisier cases (i.e., lower signal-to-noise ratio), the damage probability remains at a low level. This suggests that the CMSNN model can deal well with undamaged states and possesses a low noise floor.

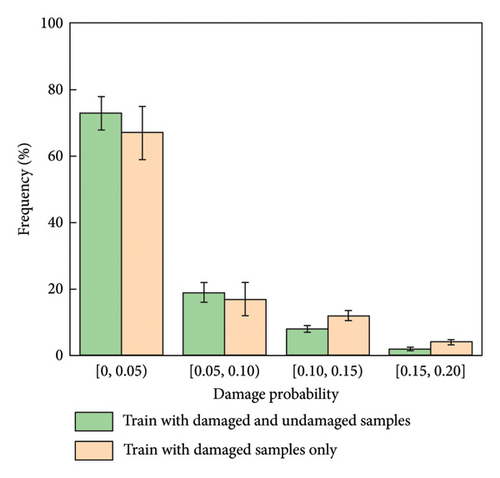
Moreover, it is important to recognize that this good performance benefits from the incorporation of a proportion of undamaged samples within our dataset. To verify this inference, we remove the undamaged samples from the dataset and retrain the network. On a batch of 512 undamaged samples, the model trained with damaged samples only is compared to the model trained with both damaged and undamaged samples. Figure 7 demonstrates the frequency distribution pattern of damage probability predicted by the two models for all samples, where the height of the column denotes the mean of the frequencies and the height of the error bar denotes the standard deviation of the frequencies. As demonstrated in plots, the model trained with both damaged and undamaged samples achieves a lower and more stable predicted damage probability distribution for the undamaged case, indicating a lower noise floor.

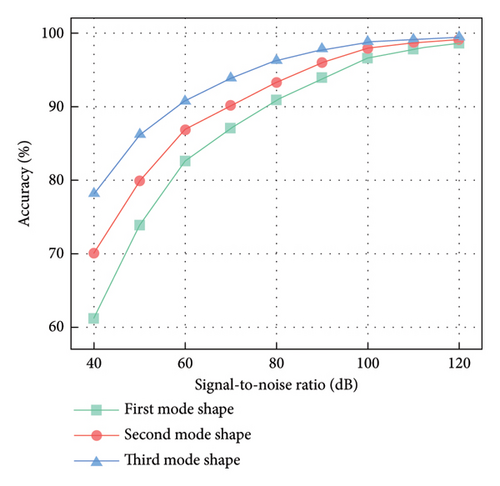
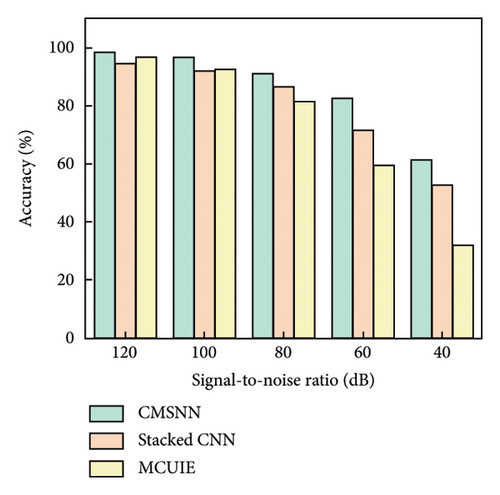
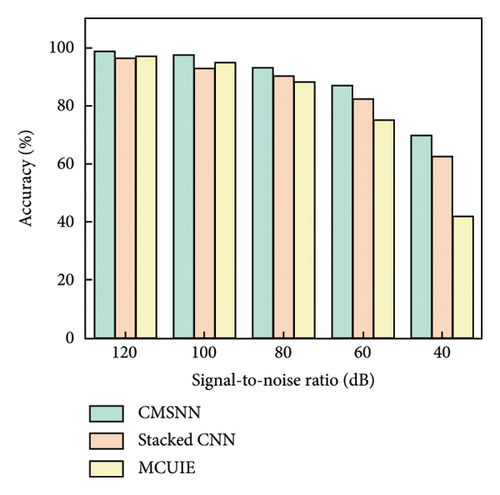
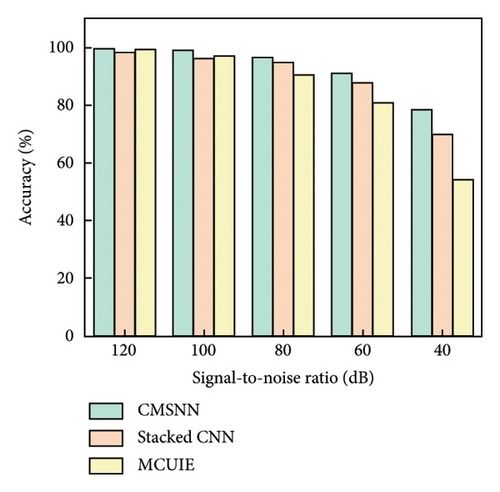
4.2. Noise Immunity Test

To perform the noise immunity test, the Monte Carlo method is employed to evaluate the detection capability of the CMSNN model at various noise levels. Each noise level comprises 512 samples, including random boundary conditions, measurement noise, number of damages, and degree of damages. To evaluate the performance of the CMSNN model, the accuracy of detection is introduced, which is defined as

()

where N_correct and N_total are the number of correctly detected damage locations and total damage locations, respectively.

Figure 8 shows the results of the accuracy assessments. It can be observed that the higher order mode shape demonstrates greater robustness to noise compared to the lower order mode shape. Although the damage features are inevitably blurred by noise, the proposed model maintains satisfactory detection accuracy. The model can achieve an accuracy of over 90% when the signal-to-noise ratio exceeds 80 dB, and an accuracy of over 80% when the signal-to-noise ratio is above 60 dB. When the signal-to-noise ratio falls below 60 dB, the model’s detection accuracy drops more rapidly, as the model has not yet learned from samples with these noise levels. Nevertheless, the accuracy can reach over 60% at the signal-to-noise ratio of 40 dB, suggesting that the model has learned a more fundamental representation of the DI.

4.3. Data Missing Test

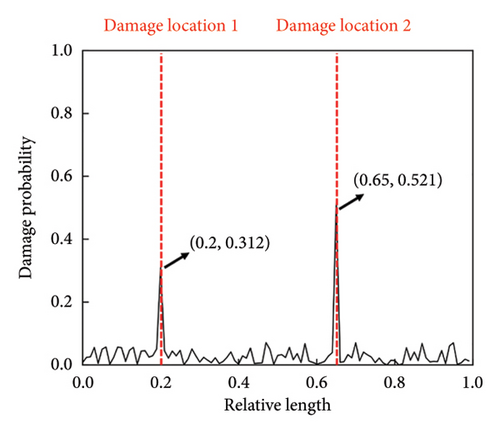
Considering the limitations of measurement and data storage, the issue of missing data sometimes arises in practice. To evaluate the capability of the CMSNN model to deal with data-missing scenarios, three cases are randomly selected. In each case, we introduce 20% and 30% stiffness reductions at the relative lengths of 0.2 and 0.65, respectively. The data missing is simulated by replacing the original value of the missing location with zero. The settings of these cases are given in Table 6.

Table 6. Settings of three cases for data missing test.

Case	Mode shape	Boundary condition	Missing ratio (%)
1	First order	C-F	5
2	Second order	C-C	8
3	Third order	C-P	10

The detection results of the three cases are shown in Figure 9. It is presented that the damage locations can be correctly detected even when incomplete data are provided as input. This indicates that the proposed model is capable of extracting effective DI in the data-missing scenarios.

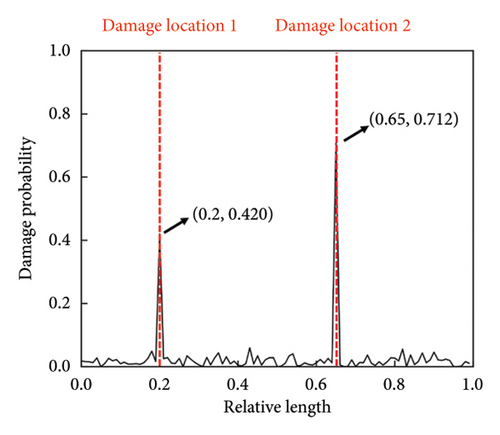
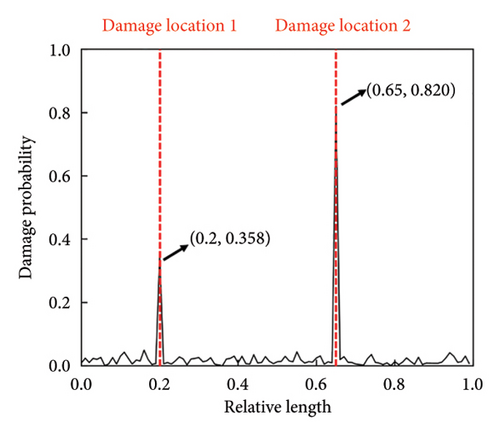
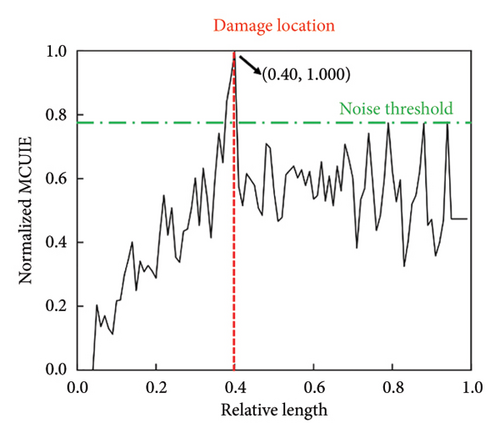
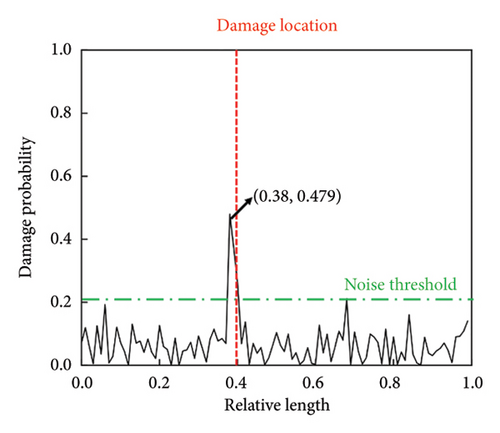
4.4. Compared With Other Methods

To showcase the efficacy of the proposed CMSNN model, a comparative analysis is conducted with two alternative damage detection methods: the MCUIE-based method [32] and the stacked CNN-based method [40]. For this comparison, a cantilever beam sample is selected, where a 20% stiffness reduction is introduced at a relative length of 0.4. As a representative case, we performed the comparison on the second mode shape in a noisy environment with a signal-to-noise ratio of 60 dB. To compare the detection effectiveness of different methods, the degree of differentiation is introduced here, which is defined as

()

where A_damage and A_noise are the amplitude of the damage location and the noise threshold, respectively.

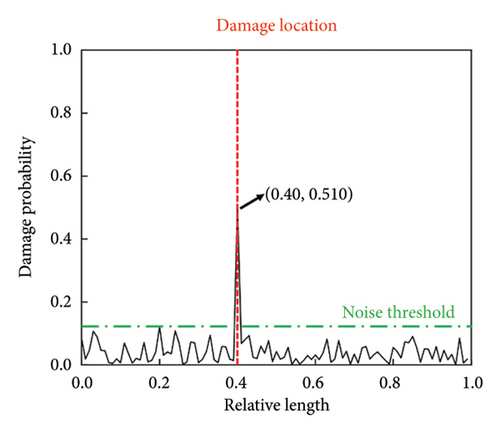
The detection results of the three methods are illustrated in Figure 10. Although both the MCUIE-based and stacked CNN-based methods are capable of damage detection, each exhibits certain limitations. The MCUIE-based method, while sensitive to damage, is prone to noise interference. Its sensitivity to local mutations in the MCUIE can lead to false positives, where noise is mistakenly identified as damage features, and it achieves a degree of differentiation of only 1.28. On the other hand, the stacked CNN-based method is more robust against noise, but it still exhibits significant fluctuations in nondamaged regions, with a low degree of differentiation of 2.34. This can make it challenging to set an accurate noise threshold for damage detection and may introduce ambiguity in localizing the damage. In contrast, the proposed CMSNN model demonstrates a marked improvement, effectively detecting damage with a high degree of differentiation reaching 4.22. This superior performance highlights the CMSNN model’s ability to discern damage features with greater precision, even in the presence of noise, and to provide a clearer distinction between damaged and nondamaged regions.

Furthermore, to quantitatively assess the detection accuracy of the various methods under statistical conditions, we conducted Monte Carlo experiments. The outcomes of the Monte Carlo simulations are presented in Figure 11. The proposed CMSNN model exhibits a superior level of noise immunity relative to the other two methods under consideration, highlighting its reliability and stability in detecting damage even in the presence of significant noise.

5. Experimental Verifications

This section details the experiments conducted to further validate the proposed damage detection framework with real-world data, which comprises two distinct parts. Concretely, the first part involves performing damage detection on a beam with multiple damages to validate the method’s effectiveness in practical situations. In the second part, a practical strategy, called parameter transfer, is introduced and applied to the method for further damage detection in a laminated plate.

5.1. Damage Detection for the Through-Hole Beam

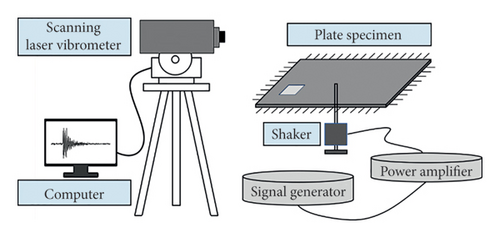
The schematic diagram of the vision-aided experimental system is displayed in Figure 12(a). The experiment is carried out on an aluminum alloy 6061 beam specimen with three through-holes. The three through-holes are introduced into the specimen by a drilling machine, with internal diameters of 4, 4, and 5 mm, respectively. Figure 12(b) illustrates the dimensions of the specimen and the location of damages. The beam’s vibration video is collected during the experiment process using a high-speed camera (Revealer 5F04, full resolution: 2320 × 1718 pixels, pixel size: 7 × 7 μm, maximum frame rate: 52,800 fps, responsivity: ISO 6400). Based on the finite element analysis, the first three modal frequencies of the beam are calculated as 19.73, 123.71, and 346.39 Hz. In accordance with the Nyquist sampling theorem, it is imperative that the sampling frequency exceeds twice the frequency of the signal being identified to ensure that the discrete signals can accurately reconstruct the original continuous signals without the introduction of aliasing. For modal shape identification, which is crucial for damage detection, a more conservative sampling frequency is indeed preferable. Given that an elevated sampling frequency can enhance the fidelity of the vibration data, the frame rate of the camera is set to 3000 frames per second (fps).

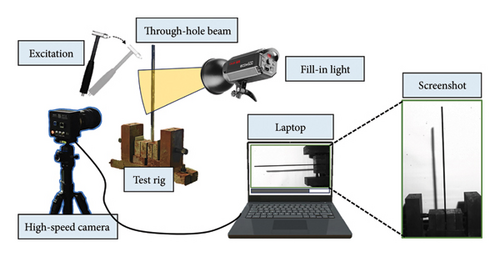
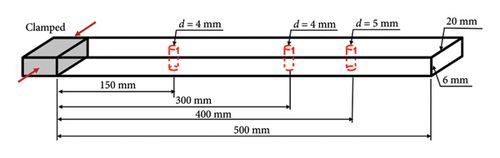
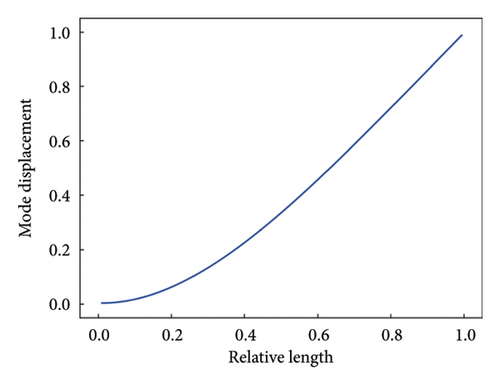
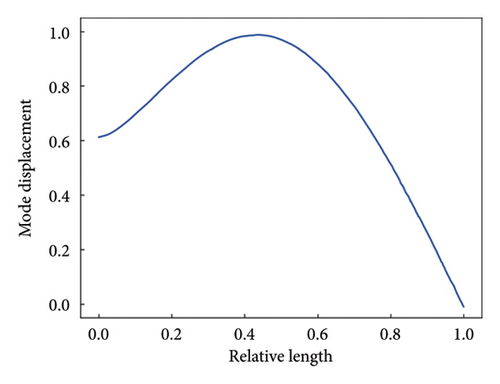
A total of 100 pixel points are uniformly selected along the length direction of the target beam to be tracked by optical flow estimation, acting as 100 virtual sensors without mass loading effects. Based on the high-spatial-resolution measurement, the first three mode shapes are identified, which are shown in Figure 13. The detection results are shown in Figure 14. In actual scenarios, although vision-aided technology can be a useful solution to the limitation of measurement resolution, it cannot be ignored that the measurement noise is still present in the obtained mode shapes due to various factors like lighting conditions and image resolution. Benefiting from the efficient CNN-based DI extraction and robust attention-based information fusion of the CMSNN model, the exact locations of damage are all indicated at the peak of the predicted damage probability distribution.

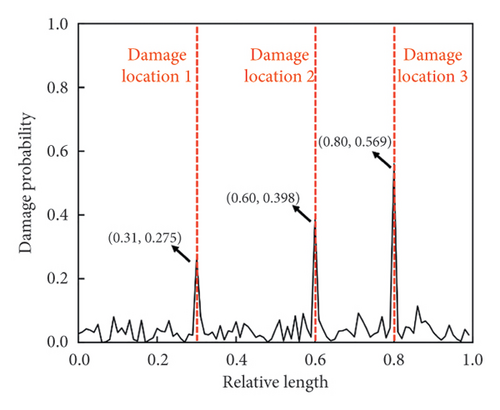
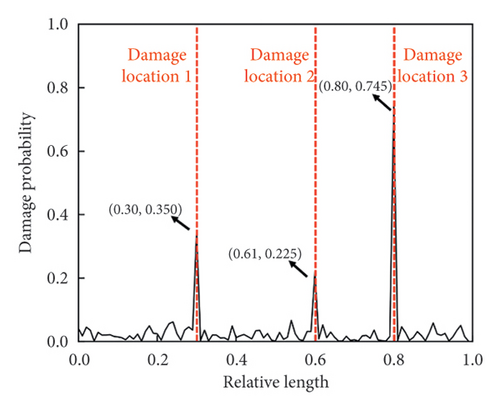
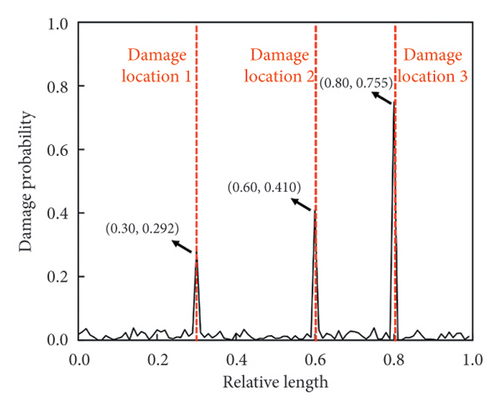
5.2. Application of Parameter Transfer Strategy

In the field of SHM, it is a common issue that the length of the input signal (or the number of sampling points) varies due to the differences in the measuring approaches and target objects. Conventional methods suggest resolving this issue by interpolating the input signal to meet the signal length requirement or by retraining the network model. However, data interpolation can result in loss of information from the source signal, and retraining the network from scratch can be both time-consuming and computationally intensive.

Inspired by the domain of transfer learning, a practical strategy named parameter transfer is introduced here. The CNN-based multiscale information extraction module can extract essential DI from input mode shape signals after training without strict length requirements for input signals. This makes it a generic extractor for DI without needing to be retrained. That is, in various damage detection scenarios, the proposed model can be employed to address the detection task by fixing the parameters of the generic multiscale information extraction module and only retraining the information fusion module with explicit constraints on the signal length.

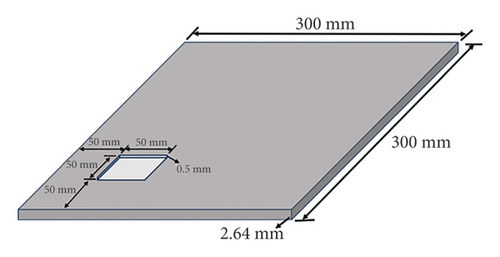
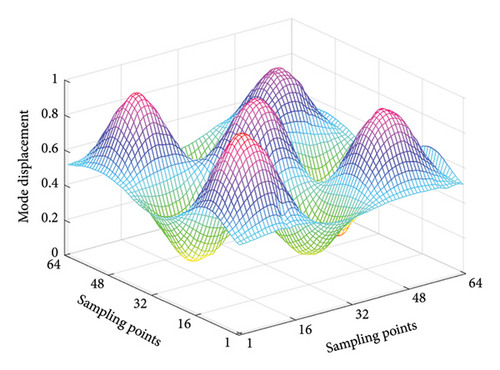
In order to verify the detection capability of the proposed framework with parameter transfer, an experimental investigation is performed based on the publicly available Damage Assessment Benchmark, as detailed in reference [46]. The schematic diagram of the experimental system is shown in Figure 15(a). This benchmark includes data measured from vibration tests of composite structures. The study focuses on the case of a damaged laminated plate specimen, which is a square plate made of 12-layered grass fiber-reinforced epoxy-based laminated composite. It has a length of 300 mm and a thickness of 2.64 mm, and all four sides are fixed. The spatial surface damage is machined with a milling machine to a depth of 0.5 mm. Figure 15(b) shows the dimensions and location of the damage. The first four mode shapes are obtained using an SLV (Polytec PSV-400) with a resolution of 64 × 64 sampling points, which are demonstrated in Figure 16.

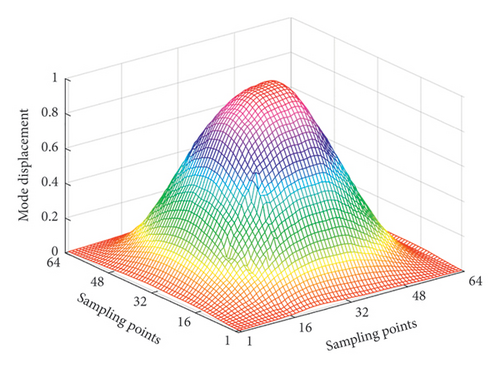
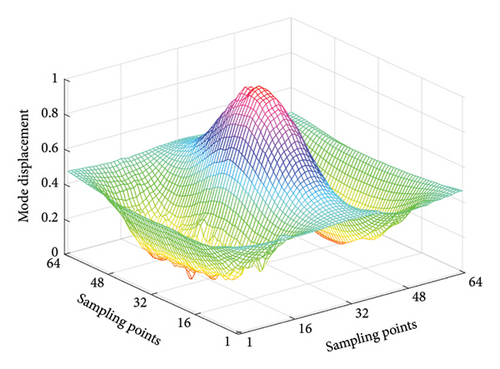
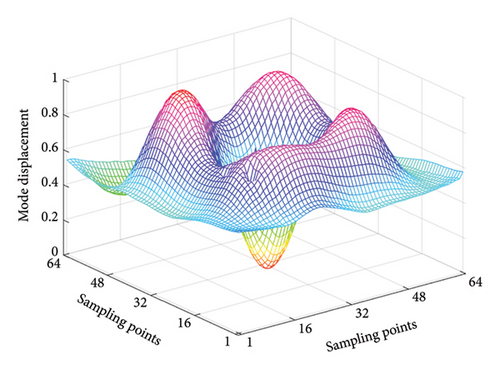
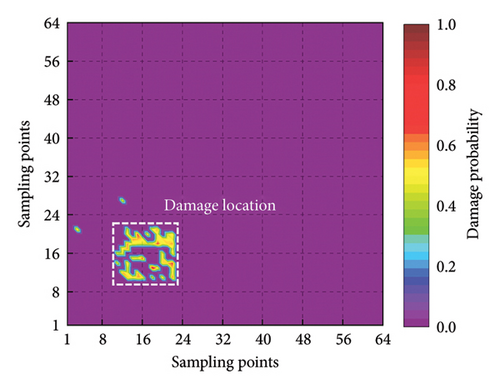
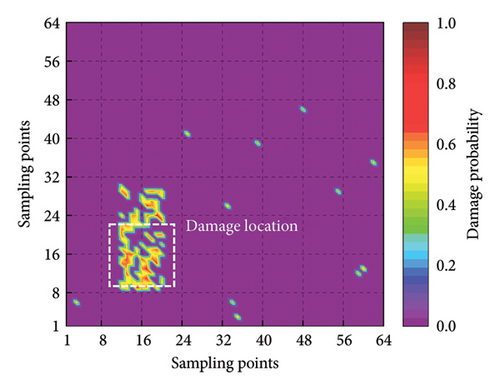
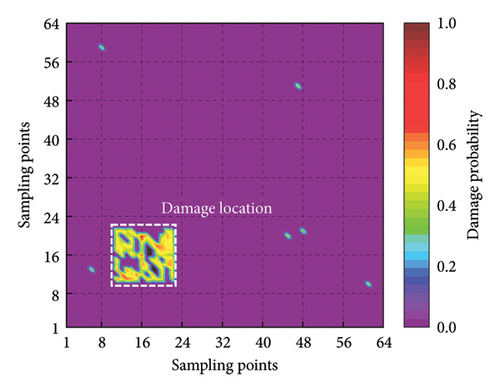
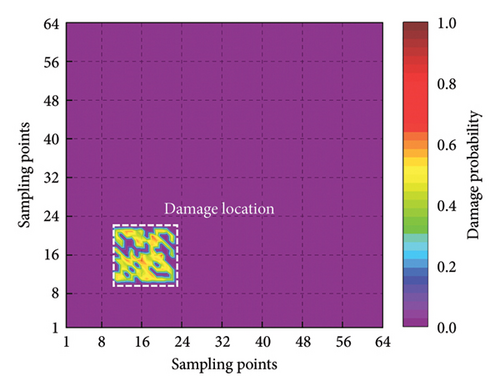
In the experimental process, the weights of the multiscale information extraction module in the CMSNN model are frozen and only the weights of the information fusion module are retrained. To analyze the two-dimensional plate using the proposed model, we input the mode shape data of the plate row by row and column by column. This enables the predicted damage probability spatial distribution in two different directions to be obtained. The final damage probability spatial distribution is calculated by taking a weighted average of the two aforementioned spatial distributions. To enhance the intuitiveness of the results, positions with a damage probability of less than 0.3 are set to zero. The detection results are presented in Figure 17, which clearly demonstrates the damaged area.

6. Conclusions

This study proposes a novel vision-aided framework with CMSNN to deal with damage detection tasks. The performance of the proposed framework is evaluated through numerical and experimental analysis across a variety of scenarios. The principal conclusions of this paper are summarized as follows:

1.
The utilization of optical flow estimation algorithm enables the acquisition of mode shapes of target structures at a high spatial resolution without mass-loading effects, which is suitable and informative enough for damage detection tasks.
2.
A novel CMSNN model is designed to autonomously learn high-level feature representations from noisy mode shapes, eliminating the need for explicit manual feature design. The model combines a CNN-based multiscale information extraction module with an attention-based information fusion module, thereby enhancing its capabilities.
3.
During the design and training process, the CMSNN model considers a range of scenarios, including measurement noise, data missing, and undamaged samples. This ensures that the proposed framework can provide reliable detection results even when the input data are corrupted by noise or incomplete.
4.
The results of experiments demonstrate that the proposed framework accurately detects damages in actual scenarios. Furthermore, the application of the parameter transfer strategy minimizes retraining effort while preserving the capacity for damage detection, which increases versatility.

Despite the laboratory success of this paper, there are some potential challenges. The excessive compression artifacts and lighting variations of experimental videos under undesirable conditions may affect the accuracy of optical flow estimation and alter the noise distribution compared to the training dataset, which impacts the overall performance of the CMSNN model. In future work, real-world data will be further combined with simulation-generated dataset for training to improve generalization and address the challenges. Moreover, the interpretability of the proposed model will be studied using visualization techniques to guide the understanding of damage features. The combination of data-driven models and physics-based methods promises to provide a more comprehensive approach to damage detection.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the Basic Research Project Group (No. 514010106-302).

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Saidin S. S., Jamadin A., Abdul Kudus S., Mohd Amin N., and Anuar M. A., An Overview: The Application of Vibration-Based Techniques in Bridge Structural Health Monitoring, International Journal of Concrete Structures and Materials. (2022) 16, no. 1, https://doi.org/10.1186/s40069-022-00557-1.
10.1186/s40069-022-00557-1
Web of Science® Google Scholar
2 Xu Y. and Brownjohn J. M., Review of Machine-Vision Based Methodologies for Displacement Measurement in Civil Structures, Journal of Civil Structural Health Monitoring. (2018) 8, no. 1, 91–110, https://doi.org/10.1007/s13349-017-0261-4, 2-s2.0-85041514243.
10.1007/s13349-017-0261-4
Web of Science® Google Scholar
3 Hou R. and Xia Y., Review on the New Development of Vibration-Based Damage Identification for Civil Engineering Structures: 2010–2019, Journal of Sound and Vibration. (2021) 491, https://doi.org/10.1016/j.jsv.2020.115741.
10.1016/j.jsv.2020.115741
Web of Science® Google Scholar
4 Esfandiari A., Nabiyan M. S., and Rofooei F. R., Structural Damage Detection Using Principal Component Analysis of Frequency Response Function Data, Structural Control and Health Monitoring. (2020) 27, no. 7, https://doi.org/10.1002/stc.2550.
10.1002/stc.2550
Web of Science® Google Scholar
5 Mao H., Tang W., Huang Y. et al., The Construction and Comparison of Damage Detection Index Based on the Nonlinear Output Frequency Response Function and Experimental Analysis, Journal of Sound and Vibration. (2018) 427, 82–94, https://doi.org/10.1016/j.jsv.2018.04.028, 2-s2.0-85046827263.
10.1016/j.jsv.2018.04.028
Web of Science® Google Scholar
6 Bagherahmadi S. A. and Seyedpoor S. M., Structural Damage Detection Using a Damage Probability Index Based on Frequency Response Function and Strain Energy Concept, Structural Engineering & Mechanics. (2018) 67, no. 4, 327–336, https://doi.org/10.12989/sem.2018.67.4.327, 2-s2.0-85051967169.
10.12989/sem.2018.67.4.327
Web of Science® Google Scholar
7 Kouris L. A. S., Penna A., and Magenes G., Seismic Damage Diagnosis of a Masonry Building Using Short-Term Damping Measurements, Journal of Sound and Vibration. (2017) 394, 366–391, https://doi.org/10.1016/j.jsv.2017.02.001, 2-s2.0-85012024040.
10.1016/j.jsv.2017.02.001
Web of Science® Google Scholar
8 Cao M., Sha G., Gao Y., and Ostachowicz W., Structural Damage Identification Using Damping: a Compendium of Uses and Features, Smart Materials and Structures. (2017) 26, no. 4, https://doi.org/10.1088/1361-665X/aa550a, 2-s2.0-85016156270.
10.1088/1361-665X/aa550a
Web of Science® Google Scholar
9 Montalvão D., Ribeiro A., and Duarte-Silva J., A Method for the Localization of Damage in a CFRP Plate Using Damping, Mechanical Systems and Signal Processing. (2009) 23, no. 6, 1846–1854, https://doi.org/10.1016/j.ymssp.2008.08.011, 2-s2.0-67349277096.
10.1016/j.ymssp.2008.08.011
Web of Science® Google Scholar
10 Zhou X. Q., Xia Y., and Weng S., L1 Regularization Approach to Structural Damage Detection Using Frequency Data, Structural Health Monitoring. (2015) 14, no. 6, 571–582, https://doi.org/10.1177/1475921715604386, 2-s2.0-84948738452.
10.1177/1475921715604386
Web of Science® Google Scholar
11 Wang L., Lie S. T., and Zhang Y., Damage Detection Using Frequency Shift Path, Mechanical Systems and Signal Processing. (2016) 66, 298–313, https://doi.org/10.1016/j.ymssp.2015.06.028, 2-s2.0-84955720713.
10.1016/j.ymssp.2015.06.028
CAS Web of Science® Google Scholar
12 Sha G., Radzieński M., Cao M., and Ostachowicz W., A Novel Method for Single and Multiple Damage Detection in Beams Using Relative Natural Frequency Changes, Mechanical Systems and Signal Processing. (2019) 132, 335–352, https://doi.org/10.1016/j.ymssp.2019.06.027, 2-s2.0-85068465315.
10.1016/j.ymssp.2019.06.027
Web of Science® Google Scholar
13 Svendsen B. T., Øiseth O., Frøseth G. T., and Rønnquist A., A Hybrid Structural Health Monitoring Approach for Damage Detection in Steel Bridges under Simulated Environmental Conditions Using Numerical and Experimental Data, Structural Health Monitoring. (2023) 22, no. 1, 540–561, https://doi.org/10.1177/14759217221098998.
10.1177/14759217221098998
Web of Science® Google Scholar
14 Zamani Kouhpangi M., Yaghoubi S., and Torabipour A., Improved Structural Health Monitoring Using Mode Shapes: An Enhanced Framework for Damage Detection in 2D and 3D Structures, Engineer. (2023) 4, no. 2, 1742–1760, https://doi.org/10.3390/eng4020099.
10.3390/eng4020099
Google Scholar
15 Nguyen D. H. and Abdel Wahab M., Damage Detection in Slab Structures Based on Two-Dimensional Curvature Mode Shape Method and Faster R-CNN, Advances in Engineering Software. (2023) 176, https://doi.org/10.1016/j.advengsoft.2022.103371.
10.1016/j.advengsoft.2022.103371
Web of Science® Google Scholar
16 Sheng Z., Zhang K., Ge Z. et al., Defects Localization Using the Data Fusion of Laser Doppler and Image Correlation Vibration Measurements, Optics and Lasers in Engineering. (2023) 160, https://doi.org/10.1016/j.optlaseng.2022.107293.
10.1016/j.optlaseng.2022.107293
Web of Science® Google Scholar
17 Poozesh P., Sarrafi A., Mao Z., Avitabile P., and Niezrecki C., Feasibility of Extracting Operating Shapes Using Phase-Based Motion Magnification Technique and Stereo-Photogrammetry, Journal of Sound and Vibration. (2017) 407, 350–366, https://doi.org/10.1016/j.jsv.2017.06.003, 2-s2.0-85021712223.
10.1016/j.jsv.2017.06.003
Web of Science® Google Scholar
18 Reynders E., Degrauwe D., De Roeck G., Magalhães F., and Caetano E., Combined Experimental-Operational Modal Testing of Footbridges, Journal of Engineering Mechanics. (2010) 136, no. 6, 687–696, https://doi.org/10.1061/(ASCE)EM.1943-7889.0000119, 2-s2.0-77953994667.
10.1061/(ASCE)EM.1943-7889.0000119
Web of Science® Google Scholar
19 Duvnjak I., Damjanović D., Bartolac M., and Skender A., Mode Shape-Based Damage Detection Method (MSDI): Experimental Validation, Applied Sciences. (2021) 11, no. 10, https://doi.org/10.3390/app11104589.
10.3390/app11104589
Google Scholar
20 Sofi A., Jane Regita J., Rane B., and Lau H. H., Structural Health Monitoring Using Wireless Smart Sensor Network–An Overview, Mechanical Systems and Signal Processing. (2022) 163, https://doi.org/10.1016/j.ymssp.2021.108113.
10.1016/j.ymssp.2021.108113
Web of Science® Google Scholar
21 Baqersad J., Poozesh P., Niezrecki C., and Avitabile P., Photogrammetry and Optical Methods in Structural Dynamics–A Review, Mechanical Systems and Signal Processing. (2017) 86, 17–34, https://doi.org/10.1016/j.ymssp.2016.02.011, 2-s2.0-84958559406.
10.1016/j.ymssp.2016.02.011
Web of Science® Google Scholar
22 Yang Z. B., Chen X. F., Xie Y., and Zhang X. W., The Hybrid Multivariate Analysis Method for Damage Detection, Structural Control and Health Monitoring. (2016) 23, no. 1, 123–143, https://doi.org/10.1002/stc.1758, 2-s2.0-84955195689.
10.1002/stc.1758
Web of Science® Google Scholar
23 Pan J., Zhang Z., Wu J., Ramakrishnan K. R., and Singh H. K., A Novel Method of Vibration Modes Selection for Improving Accuracy of Frequency-Based Damage Detection, Composites Part B: Engineering. (2019) 159, 437–446, https://doi.org/10.1016/j.compositesb.2018.08.134, 2-s2.0-85054920622.
10.1016/j.compositesb.2018.08.134
Web of Science® Google Scholar
24 Xin C., Qin M., He M., and Xu Z., An Approach for Damage Detection in Noisy Environments Using DOG Multi-Scale Space and Fractal Dimension, Nondestructive Testing and Evaluation. (2023) 38, no. 5, 767–797, https://doi.org/10.1080/10589759.2023.2170372.
10.1080/10589759.2023.2170372
Web of Science® Google Scholar
25 Chen J. G., Wadhwa N., Cha Y. J., Durand F., Freeman W. T., and Buyukozturk O., Modal Identification of Simple Structures With High-Speed Video Using Motion Magnification, Journal of Sound and Vibration. (2015) 345, 58–71, https://doi.org/10.1016/j.jsv.2015.01.024, 2-s2.0-84924497350.
10.1016/j.jsv.2015.01.024
Web of Science® Google Scholar
26 Huang J., Shao X., Yang F., Zhu J., and He X., Measurement Method and Recent Progress of Vision-Based Deflection Measurement of Bridges: a Technical Review, Optical Engineering. (2022) 61, no. 07, https://doi.org/10.1117/1.OE.61.7.070901.
10.1117/1.OE.61.7.070901
PubMed Web of Science® Google Scholar
27 Yu L. and Pan B., Overview of High-Temperature Deformation Measurement Using Digital Image Correlation, Experimental Mechanics. (2021) 61, no. 7, 1121–1142, https://doi.org/10.1007/s11340-021-00723-8.
10.1007/s11340-021-00723-8
Web of Science® Google Scholar
28 Feng D. and Feng M. Q., Computer Vision for SHM of Civil Infrastructure: From Dynamic Response Measurement to Damage Detection–A Review, Engineering Structures. (2018) 156, 105–117, https://doi.org/10.1016/j.engstruct.2017.11.018, 2-s2.0-85034238493.
10.1016/j.engstruct.2017.11.018
Web of Science® Google Scholar
29 Roy K., Structural Damage Identification Using Mode Shape Slope and Curvature, Journal of Engineering Mechanics. (2017) 143, no. 9, https://doi.org/10.1061/(ASCE)EM.1943-7889.0001305, 2-s2.0-85024366278.
10.1061/(ASCE)EM.1943-7889.0001305
Web of Science® Google Scholar
30 Pooya S. M. H. and Massumi A., A Novel and Efficient Method for Damage Detection in Beam-like Structures Solely Based on Damaged Structure Data and Using Mode Shape Curvature Estimation, Applied Mathematical Modelling. (2021) 91, 670–694, https://doi.org/10.1016/j.apm.2020.09.012.
10.1016/j.apm.2020.09.012
Web of Science® Google Scholar
31 Cao M., Radzieński M., Xu W., and Ostachowicz W., Identification of Multiple Damage in Beams Based on Robust Curvature Mode Shapes, Mechanical Systems and Signal Processing. (2014) 46, no. 2, 468–480, https://doi.org/10.1016/j.ymssp.2014.01.004, 2-s2.0-84898066222.
10.1016/j.ymssp.2014.01.004
Web of Science® Google Scholar
32 Xiang C. S., Li L. Y., Zhou Y., and Yuan Z., Damage Identification Method of Beam Structure Based on Modal Curvature Utility Information Entropy, Advances in Civil Engineering. (2020) 2020, https://doi.org/10.1155/2020/8892686.
10.1155/2020/8892686
Web of Science® Google Scholar
33 Cui S., Maghoul P., Liang X., Wu N., and Wang Q., Structural Fatigue Crack Localisation Based on Spatially Distributed Entropy and Wavelet Transform, Engineering Structures. (2022) 266, https://doi.org/10.1016/j.engstruct.2022.114544.
10.1016/j.engstruct.2022.114544
Web of Science® Google Scholar
34 Avci O., Abdeljaber O., Kiranyaz S., Hussein M., Gabbouj M., and Inman D. J., A Review of Vibration-Based Damage Detection in Civil Structures: From Traditional Methods to Machine Learning and Deep Learning Applications, Mechanical Systems and Signal Processing. (2021) 147, https://doi.org/10.1016/j.ymssp.2020.107077.
10.1016/j.ymssp.2020.107077
Web of Science® Google Scholar
35 Lecun Y., Bengio Y., and Hinton G., Deep Learning, Nature. (2015) 521, no. 7553, 436–444, https://doi.org/10.1038/nature14539, 2-s2.0-84930630277.
10.1038/nature14539
CAS PubMed Web of Science® Google Scholar
36 Oh B. K., Lee S. H., and Park H. S., Damage Localization Method for Building Structures Based on the Interrelation of Dynamic Displacement Measurements Using Convolutional Neural Network, Structural Control and Health Monitoring. (2020) 27, no. 8, https://doi.org/10.1002/stc.2578.
10.1002/stc.2578
Web of Science® Google Scholar
37 Lei Y., Zhang Y., Mi J., Liu W., and Liu L., Detecting Structural Damage under Unknown Seismic Excitation by Deep Convolutional Neural Network with Wavelet-Based Transmissibility Data, Structural Health Monitoring. (2021) 20, no. 4, 1583–1596, https://doi.org/10.1177/1475921720923081.
10.1177/1475921720923081
Web of Science® Google Scholar
38 Tang Z., Chen Z., Bao Y., and Li H., Convolutional Neural Network-based Data Anomaly Detection Method Using Multiple Information for Structural Health Monitoring, Structural Control and Health Monitoring. (2019) 26, no. 1, https://doi.org/10.1002/stc.2296, 2-s2.0-85057834773.
10.1002/stc.2296
PubMed Web of Science® Google Scholar
39 He Y., Chen H., Liu D., and Zhang L., A Framework of Structural Damage Detection for Civil Structures Using Fast Fourier Transform and Deep Convolutional Neural Networks, Applied Sciences. (2021) 11, no. 19, https://doi.org/10.3390/app11199345.
10.3390/app11199345
Google Scholar
40 Guo T., Wu L., Wang C., and Xu Z., Damage Detection in a Novel Deep-Learning Framework: a Robust Method for Feature Extraction, Structural Health Monitoring. (2020) 19, no. 2, 424–442, https://doi.org/10.1177/1475921719846051, 2-s2.0-85066839064.
10.1177/1475921719846051
Web of Science® Google Scholar
41 Nagarajaiah S. and Yang Y., Modeling and Harnessing Sparse and Low-rank Data Structure: a New Paradigm for Structural Dynamics, Identification, Damage Detection, and Health Monitoring, Structural Control and Health Monitoring. (2017) 24, no. 1, https://doi.org/10.1002/stc.1851, 2-s2.0-84959419287.
10.1002/stc.1851
Web of Science® Google Scholar
42 He K., Zhang X., Ren S., and Sun J., Delving Deep into Rectifiers: Surpassing Human-Level Performance on Imagenet Classification, Proceedings of the IEEE International Conference on Computer Vision, March 2015, https://doi.org/10.1109/iccv.2015.123, 2-s2.0-84973911419.
10.1109/iccv.2015.123
Google Scholar
43 Vaswani A., Shazeer N., Parmar N. et al., Attention Is All You Need, Advances in Neural Information Processing Systems. (2017) 30.
Google Scholar
44 Jia F., Lei Y., Lu N., and Xing S., Deep Normalized Convolutional Neural Network for Imbalanced Fault Classification of Machinery and its Understanding via Visualization, Mechanical Systems and Signal Processing. (2018) 110, 349–367, https://doi.org/10.1016/j.ymssp.2018.03.025, 2-s2.0-85044123126.
10.1016/j.ymssp.2018.03.025
Web of Science® Google Scholar
45 Kingma D. P. and Ba J., Adam: A Method for Stochastic Optimization, 2014, https://doi.org/10.48550/arXiv.1412.6980.
10.48550/arXiv.1412.6980
Google Scholar
46 Katunin A., Nondestructive Damage Assessment of Composite Structures Based on Wavelet Analysis of Modal Curvatures: State-of-the-art Review and Description of Wavelet-based Damage Assessment Benchmark, Shock and Vibration. (2015) 2015, no. 2015, 1–19, https://doi.org/10.1155/2015/735219, 2-s2.0-84948397180.
10.1155/2015/735219
Web of Science® Google Scholar

All articles

Vision-Aided Damage Detection With Convolutional Multihead Self-Attention Neural Network: A Novel Framework for Damage Information Extraction and Fusion

Abstract

1. Introduction

2. Methodology

2.1. High-Spatial-Resolution Mode Shapes via Vision