Throttle valves are widely used in piping processes including oil and gas energy. Quick and accurate control of the position of the valve and reducing the dependency on the initial conditions of the valve not only leads to a decrease in energy consumption but also takes advantage of increasing the productivity of the generator and saving the fuel entered into the turbine. In this article, a newly proposed fuzzy-regulated fixed-time terminal sliding mode control (TSMC) is performed for the nonlinear second-order electronic throttle valve (ETV) system in the presence of uncertainty and external disturbances. In addition, a fuzzy rule base is applied to regulate the coefficients of the switching control law to improve the convergence of state variables to the sliding surface and reduce the chattering phenomenon. The proposed method is compared with the fixed-time TSMC and backstepping sliding mode control methods, and the results show that the designed controller works well in reducing the chattering phenomenon by 38.66% and reducing overshoot by 75.46%. Also, increasing the convergence speed of the transient response to 0.33 s, reducing the tracking error, improving system robustness, and getting free from initial conditions are some advantages of the proposed method.

1. Introduction

Since throttle valve industrial equipment is widely used as a flow regulator of fluids such as steam and gas in piping processes [1], it has attracted the attention of many researchers. The fields of research related to throttle valves are controller design, friction and corrosion [2, 3], operational and economic analysis, and fluid structure analysis [4–8]. This study focused on the first field of research, which is controller design. Because electronic or pneumatic throttle valves exhibit nonlinear dynamic behavior and external loads that affect the state of the valve, it has become a challenging issue in engineering science. To increase the performance of the turbine, controllers and actuators are applied to convert electrical or pneumatic signals into mechanical ones to change the position of the valve quickly and accurately, which leads to managing energy consumption and increasing the efficiency of the generator which produces the energy. In addition, it helps reduce the fuel input to the turbine. When the load on the generator decreased, the fuel decrease command was applied to the throttle valve positioner. In this case, the controller must change the position of the valve quickly and accurately to maintain a constant frequency of 50 Hz. By doing this, the consumption of fuel input to the turbine, which can be either gas or steam, is reduced, and it is also prevented from exiting the turbine with an overspeed alarm and the loss of stable energy production for the subscribers. In recent years, many control methods have been used to accurately control electronic throttle valves so that the system can follow the reference signal with acceptable accuracy. A proportional–integral–derivative (PID) controller to adjust the throttle valve using the moth flame optimization algorithm was proposed in [9]. Reference [10] utilizes a fractional-order PID controller whose controller coefficients are modified by the gray wolf optimization algorithm. Owing to the effectiveness of sliding mode controllers (SMCs) against disturbances and uncertainties, the combination of PID controllers with SMC has been proposed in recent years [11, 12]. Recently, hybrid controllers have been used to combine the advantages of each controller. These nonlinear hybrid control approaches, including adaptive backstepping integral SMC, are used for speed control of direct current (DC) motors with multiple inputs and multiple outputs [13]. The proposed method performed well against load disturbances and uncertainties. In [14–17], adaptive SMCs were utilized to control the valve position. The control strategy in [17] includes a recursive full-order TSMC based on the bilimit homogeneous property, which effectively suppresses the chattering phenomenon. Reference [18] proposed a fixed-time sliding-mode observer-based controller for uncertain nonlinear double integrator systems. A new form of a sliding mode observer in combination with a SMC is designed to estimate unknown parameters and states. In [19], a fuzzy adaptive fixed-time SMC method was proposed to track the trajectories of a high-order nonlinear system that faces mismatched external disturbances and uncertainties. Additionally, a fixed-time state observer was applied to estimate the unmeasured states. Reference [20] proposed a continuous fixed-time SMC for servo motors. In [21], a robust fixed-time SMC is defined, which is cooperating with a fixed-time sliding mode observer to solve the tracking problem in flexible joint robot-attached drones. First, the underactuated robot is modeled, and then, based on the availability of the measured states, a cascaded system is constructed to estimate the unmeasurable variables in a fixed time. In [22], a TSMC was proposed which guarantees finite-time convergence and achieves acceptable robustness against lumped disturbances. A cascaded finite-time sliding mode observer was also constructed to estimate the states and reduce the peaking phenomenon. Changing the parameters of the system owing to long-term operation causes a chattering phenomenon in the control signal [23]. Although the sliding mode control method is not sensitive to changes in parameters and external disturbances [24], it usually suffers from chattering. In [25], the use of neural networks for system training was suggested, which depends on information, and the chattering phenomenon was also clearly observed. Backstepping control based on Kalman filters was proposed in [26] to reject the disturbance and suppress noise in throttle valve control. Backstepping control based on barrier functions has also been proposed to ensure the stability of the entire nonlinear system [27]. In Table 1, the control strategies that have been recently used for throttle valve control are reviewed. As we have proposed an improved SMC, this review focuses on this field of research.

Table 1. Review of electronic throttle valve control methods.

Controlling method	Reference	Advantage	Disadvantage
Classic SMC	Li et al. (2015) [28] Pan et al. (2001) [29] Dagci et al. (2002) [30] Kang et al. (2005) [31]	•Simplicity in implementation •Simple control structure •Low computational effort •Robustness •Acceptable tracking accuracy •Simple Lyapunov-based stability proof	•Chattering phenomenon •Low convergence speed •Unbounded convergence time during sliding phase •Dependence on initial conditions

Integral SMC	Li et al. (2017) [32]	•Robustness •Chattering reduction	•Complex design •Low convergence speed

TSMC	Hu et al. (2021) [33] Long et al. (2023) [34]	•Robustness •Finite-time stability •High convergence speed	•Dependence on initial conditions •Adjustment of controlling parameters •Singularity problem

Adaptive SMC	Bai (2018) [16] Hu et al. (2018) [17] Feng et al. (2023) [35] Qiu et al. (2023) [36]	•Robustness •Adaptability in changing operating conditions •Suitable for issues with unknown dynamics or unknown parameters with slow variations •Simple Lyapunov-based stability proof	•Chattering phenomenon •Singularity problem •Poor convergence speed •Complex calculations •It is not applicable for systems with fast parametric variations

Fuzzy control and fuzzy SMC	Yang et al. (2018) [37] Gritli et al. (2018) [38]	•Robustness •Proper performance in cases of chaos and nonlinear, time-varying issues •Good performance in controlling and approximating uncertainties •Compatible with soft computing algorithms •Flexible control of complex systems without need to know the exact system model	•Dependency on human experience •No principled method for membership functions •Stability analysis

Extended PID	Ghani et al. (2022) [11] Wang et al. (2016) [12] Mercorelli (2009) [39] Samarraie (2012) [40]	•Common in the industry •Proper tracking ability •Simple structure of PID controller •Practical implementation •Manual and automatic control	•Tuning is limited to only three different parameters •Weak performance in disturbance rejection •Be sensitive to noise and measurement errors

Dynamic optimization	Gritli et al. (2016) [41] Saerens et al. (2009) [42]	•Cost function minimization •Ability to combine with fuzzy and PID methods	•It is usually offline •Curse of dimensions •The probability of convergence to local minimums

Neural network–based feedback tuning methods	Amico et al. (2023) [25]	•High accuracy of calculations •Fast learning of system behavior •Suitable for controlling complex and nonlinear systems •Suitable for problems with unknown dynamics	•Data dependence •Probability-based performance •Overfitting problem •The need for detailed network training •The need to determine the exact structure of the network

Reinforcement learning	Siraskar (2021) [43] Bischoff et al. (2013) [44]	•Low computational effort •Learning through interaction with the environment •Appropriate learning speed •Excellence in dynamic and uncertain environments •There are several approaches to dealing with problems •No need for an exact model	•Complexity of training •Unpredictable behavior during the initial learning stage •The possibility of falling into nonoptimal solutions if there is no interaction between exploration and exploitation

Barrier Lyapunov function–based adaptive control	Wang et al. (2021) [27]	•Use of barrier Lyapunov function to ensure transient and steady-state performance •No singularity problem •Simplicity in implementation	•Controller limits •Difficult design

The Sliding mode control method and its related developments are suitable controllers for ETV due to their accuracy and robustness. In this paper, a fixed-time TSMC which is adjusted by fuzzy rules is proposed. TSMC proposes finite-time convergence regarding their nonlinear sliding surface. Considering that throttle valve industrial equipment is very sensitive and is used in sustainable energy supply, the state variables must reach equilibrium in a fixed time which is not dependent on the initial conditions of the system. In addition, in this study, fuzzy rules were used for adjusting the switching law. The presence of chattering phenomena and chaotic movements in the control signal applied to an electronic throttle dynamical system leads to challenges such as increased energy consumption, more control effort, reduced valve life, and increased valve friction, and as a result, it will increase controlling costs [45]. External disturbances in throttle valves are inevitable owing to their installation in industrial environments. These disturbances are usually caused by the valve which is sometimes stuck to the valve body, corrosion of the valve plate, vibration of other devices [43], and measurement noises. Therefore, robustness has been investigated and emphasized in this article to guarantee stability in the presence of uncertainties and disturbances. As the throttle valve is installed in the power plant, vibrations are one of the most significant disturbances that affect the position of the valve. In addition, the throttle may wear on the valve body which causes uncertainty in the parameters. Inevitable electrical noise, caused by generators and power cables, sometimes enters the shield and affects sensitive equipment. Accordingly, the main motivation in this study is to design a controller which is resistant to the mentioned uncertainties and external disturbances and reaches equilibrium in a fixed time that is independent of the initial conditions of the system. The designed controller was tested on the dynamics of the electronic throttle valve system. Because the presence of the chattering phenomenon in the control signal causes substantial damage to industrial equipment, the chattering phenomenon is reduced by the proposed fuzzy rule base. To design the proposed control structure, in the second section, a dynamic model of an ETV system with unknown nonlinear terms and disturbances is presented. In Section 3, a robust control approach for an ETV system based on fixed-time TSMC and a fuzzy inference system is presented. The Lyapunov stability proof is investigated to guarantee the stability of the designed fixed-time controller. Adjusting the parameters and using the fixed-time sliding surface, the control objectives such as convergence speed, system consistency, and chattering reduction are investigated. Finally, the simulation and results of the designed controller are analyzed.

2. Mathematical Model and Preliminaries

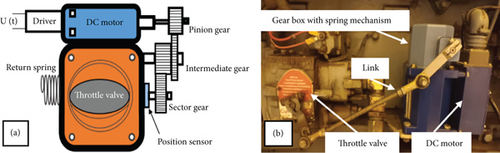
According to Figure 1, ETV consists of a DC drive (powered by a chopper), a gearbox, a valve plate, a double return spring, and a position sensor [38]. The DC motor is responsible for adjusting the valve plate angle to control the amount of fuel entering [46] the internal combustion engine manifold or the turbine [31]. The goal is to follow the reference opening command with the plate. The presence of friction and uncertainty in the nonlinear dynamic equations of the throttle makes the use of nonlinear control methods attractive. Owing to the disturbance in the system, the use of advanced sliding mode control methods is suggested. In Table 2, the parameters of the system are introduced, and the parameters that affect the dynamic equations of the system are quantified.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

(a) Electromechanical structure of the throttle valve. (b) Throttle valve installed on diesel.

Table 2. Parameters’ definition and values of ETV parameters.

Symbol	Description	Value	Unit
k_t	Constant torque of the engine	0.016	N·m/A
R_a	Armature resistance	2.8	Ω
k_ch	Chopper gain constant	2.4	—
k_v	Electromotive force constant	0.016	V·s/rad
k_pre	Spring tightening torque coefficient	0.107	N·m
J	Inertia coefficient on the engine side	0.00115	kg · m²
k_l		16.95	—
k_tf	Coulomb friction coefficient	0.0048	N·m
k_f	Sliding friction coefficient	0.0004	V·m·s/rad
k_sp	Spring elastic coefficient	0.0247	V·m/rad
θ₀	Default gas plate opening angle	2	Degree
l_d	Upper band of external disturbance	2.2	N·m
L_a	Inductance of the armature	—	—
i_a	Armature current of a DC motor	—	—
θ	Position and opening angle of the throttle valve	—	—
	Angular velocity of a motor	—	—
u	Input control voltage applied to the motor	—	—
m_s	Throttle return spring torque	—	—
m_f	Frictional torque	—	—
m_g	Unknown gear backlash torque	—	—

The system dynamic is defined as follows [28, 32]:

(1)

(2)

(3)

(4)

The parameters and states are listed in Table 2. The system’s sampling time was chosen to be very low and set to T = 5 ms according to the dominant time constant of the linear ETV model. Considering the following inequality, the armature current dynamics can be neglected, and Equation (1) can be simplified to Equation (6):

(5)

(6)

According to Equations (2)–(6), the throttle valve model is defined in Equation (7):

(7)

(8)

Defining x₁ = θ and

and considering d(t) as an external disturbance, Equation (7) can be rewritten in the following standard form:

(9)

In Equation (9),

is the vector of system state variables, f(x, t) is the nonlinear function, and u is the input control signal. g ≠ 0 is the input control signal coefficient which is defined in Table 3. Also, function d(t) as |d(t)| ≤ l_d. In Equation (9), the uncertainty is considered to be d(t) = k₃m_g + l_d(t). The f(x, t) function is obtained based on Equations (7), (8), and (9) as follows [27, 31]:

(10)

Table 3. Dynamic model details.

Symbol	Formula
ζ₂₁
ζ₂₂
k₁
k₂
k₃
g	(k_tk_ch/k_lJR_a)

In throttle valve, d(t) denotes the unwanted vibrations of turbines, and accordingly, l_d which is its related upper bound is considered to be l_d = 2.2 N · m where l_d = SUP(d(t)). In Table 3, the details of parameters related to throttle valve system dynamics are presented.

3. Controller Design

For the ETV system (9), a fixed-time terminal control law was designed such that the system trajectory converged to the origin in a fixed time. In addition, because chattering removal is very important in this industrial equipment, the fuzzy switching law was used to reduce chattering and adjust the controller parameters. These goals must be achieved in the presence of external disturbances and system uncertainties.

3.1. Design of Fixed-Time TSMC

In this section, a controller using a fixed-time TSMC approach is proposed. The proposed rule provides fast convergence and accurate tracking, independent of the initial conditions.

3.1.1. Mathematical Preliminaries

In this section, some basic definitions and lemmas are proposed to clarify the stability of the proposed controller.

Definition 1. Consider the following nonlinear system [18]:

(11)

where x ∈ ℝⁿ is the vector of state variables and f : ℝⁿ⟶ℝⁿ is a nonlinear function. t∈[t₀, ∞), and t₀ ∈ ℝ₊ ∪ {0}. The initial condition of the system is defined as x(t₀) = x₀.

Definition 2. The equilibrium point of the nonlinear system defined in (11) is globally finite-time stable if for any solution x(t, x₀) of the system, the following conditions hold:

•
It is globally asymptotically stable and any solution x(t, x₀) of (11) reaches equilibrium at some finite-time moment.
•
It is stable in the sense of Lyapunov.
•
For any ε > 0, there exists a δ(ε) > 0 such that ‖x(t, x₀) ‖ < ε for any ‖x₀‖ < δ and t ≥ 0.
•
It is finite-time convergent: x(t, x₀) = 0, ∀t ≥ T(x₀).
•
There exists a settling function T, such that .

Definition 3 (fixed-time stability). The equilibrium point of the nonlinear system defined in (11) is fixed-time stable if and only if [47, 48]

•
It is globally finite-time stable.
•
The settling time T(x₀) should be bounded according to the initial conditions. In other words, the upper bound of the settling time T_max > 0 is independent of the initial conditions, that is, ∃T > 0 such that T(x₀) ≤ T_max for ∀x₀ ∈ ℝⁿ.

According to Definition 3, settling time is always independent of the initial conditions of the system and its value is bounded in constant time control methods.

Lemma 1 ([49]). Consider the following system:

(12)

where α, β > 0 and m, n, q, p are positive odd integers satisfying 0 < n < m, 0 < p < q < 2p. Then, the equilibrium of (12) is fixed-time stable and the settling time T is bounded as follows:

(13)

Remark 1. As illustrated in Lemma 1, the settling time function has a limited upper bound which is independent of the initial conditions. In other words, it is only related to the design parameters m, n, q, p, α, and β. Consequently, the convergence time to the equilibrium points can be guaranteed.

Lemma 2 ([50]). For nonlinear system (12), assume that a continuously differentiable and radially infinite Lyapunov function V(x): ℝⁿ⟶ℝ₊ exists such that for each α, β > 0 and 0 < p < 1, q > 1 the following conditions hold. Then, the origin will be fixed-time stable, and the upper limit of the convergence time is calculated according to Equation (13) and is independent of the initial conditions:

(14)

Then, the equilibrium points are globally fixed-time stable for the system in (11) and the settling time function is bounded as T(x₀) ≤ 1/(α(1 − p)) + 1/(β(q − 1)).

3.2. Design and Stability Analysis

To design the fixed-time TSMC, the following steps are considered.

The following assumptions have been taken into account for the design of the controller.

Assumption 1. It is assumed that vibrations generated by various mechanical equipment in the throttle system introduce uncertainties or disturbances into the dynamic model of the nonlinear system.

Assumption 2. In the design of the control law, due to issues such as equipment corrosion, it is assumed that the throttle system model has parameters with a limited range of variation.

Assumption 3. The upper bound of external disturbances is limited by known positive constants.

Assumption 4. It is assumed that the position and opening angle of the throttle valve, denoted by θ, can be measured.

Assumption 5. When using the TSMC rules, the position and opening angle of the throttle valve are assumed to be constant. The designed controller ensures the convergence of the sliding mode behavior in a constant time, independent of the initial conditions, even in the presence of finite uncertainties. As a result, the tracking errors are expected to converge to zero in a constant time interval.

Assumption 6. Given the existence of delicate apparatus within the throttle system, the extent of variations in control signals is deemed restricted to avert potential harm to the equipment during practical application.

•
The sliding surface is defined as follows [47, 51, 52]:

(15)

Here, m, n, p, q are odd positive integers.

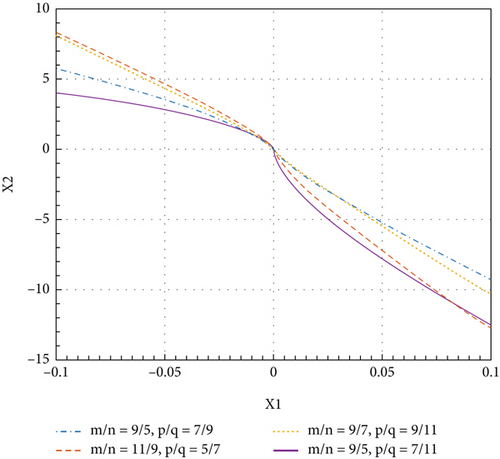
The figure below shows the sliding surface in the fixed-time TSMC according to Equation (15). As shown in Figure 2, the choice of control parameters affects the behavior of the sliding surface and ultimately affects the performance and stability of the system. The fractional power 0 < p/q < 1 and m/n > 1 affects how quickly the system state reaches the sliding surface and then the system converges to the desired state. It should be noted that if larger values are chosen for the parameters, the convergence rate will be faster, but it may lead to chattering phenomenon. In addition, the parameters should be chosen in such a way that fixed-time convergence is guaranteed.

The sliding surface introduced in (14) can be defined based on the tracking errors e(t) = x₁(t) − x_d(t) and

, where x_d(t) is the input reference signal applied to the system. The state variables are defined according to the error as follows:

The sliding surface based on the tracking errors is defined as follows.

The control signal based on the tracking error is defined as follows:

(16)

•
Sliding phase

In sliding phase, the following relation is considered:

(17)

Remark 2. According to Lemma 1, the system defined in (17) is fixed-time stable. In other words, the states converge to the origin in a fixed time [47].

•
Reaching phase

u should be designed in such a way that states reach the sliding surface in a fixed time.

The controller is considered to be

, where

is the nominal part of controller and should guarantee the system maintenance on sliding surface which is equal to

(18)

Substituting (9) in (18) yields

(19)

The nominal controller is selected as follows:

(20)

Theorem 1. For nonlinear system (9), the following controller is a fixed-time stabilizing controller:

(21)

terms are added to the controller to guarantee the stability. The controlling parameters are defined as follows:

(22)

Proof 1. To prove the stability, the following Lyapunov function is considered:

(23)

Derivation of (23) yields

(24)

Substituting controller (21) in (24) yields

(25)

(26)

Considering (μ + l_d)|s| ≥ sd(t), it is concluded that which proves the system stability.

Theorem 2. System (9) is fixed-time stable considering the controller defined in (21).

Proof 2. To prove the fixed-time stability, the following Lyapunov function is considered:

(27)

y is defined as follows:

(28)

Consequently, it yields

(29)

According to Lemma 2, the system is fixed-time stable.

3.3. Improving the Controller Efficiency by Fuzzy Defining of Coefficients

The proposed control law includes a nominal control and a switching control part [53]. In this section, the switching gain of the control law (denoted by μ) can be selected with the help of fuzzy rules [54]. This coefficient has a direct effect on the chattering phenomenon and the convergence time to the sliding surface. So, the proper adjustment of the coefficient will lead to an efficient controller. In fact, fuzzy rules detect the position of the sliding surface and, based on that, select the switching coefficient in such a way that the controller response quickly moves toward maintaining the desired conditions and a robust and adaptive controller with high performance is created [55]. Accordingly, the proposed controller is defined as below:

(30)

where u_sw is the fuzzy rule base for μ determination defined as follows:

(31)

(32)

(33)

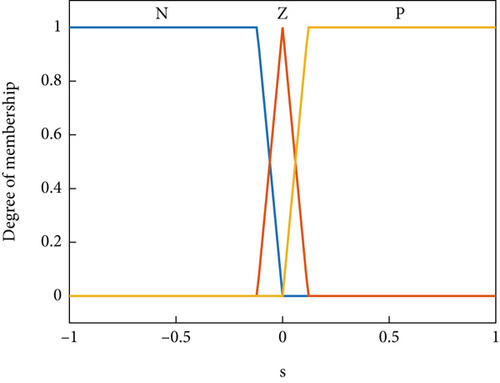
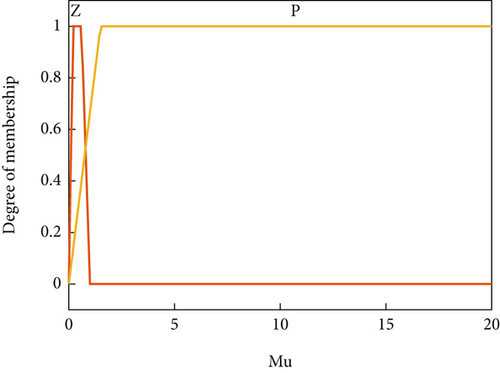
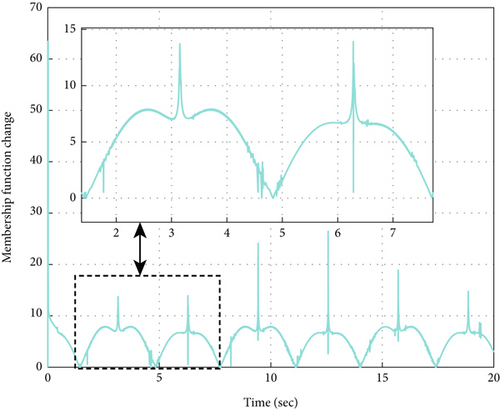
In control law (30), to reduce the chatter phenomenon and ensure Lyapunov stability, the switching control gain (μ) is selected in a fuzzy manner. Figures 3 and 4 show the membership functions related to the input s and the output μ.

3.4. Backstepping SMC Controller Design

Backstepping SMC controller is widely used for controlling nonlinear systems [56]. For example, the backstepping controller is applied to a six-degree-of-freedom (DOF) robotic manipulator model and is designed to perform well in the face of actuator and sensor errors [57]. In this paper, to analyze the performance of fixed-time fuzzy TSMC, the proposed method is compared with the backstepping SMC controller. The mathematical equations of the backstepping SMC method are expressed in Theorem 3.

Theorem 3. For System (9), the stable backstepping SMC controller is presented as follows [56, 58]:

(34)

Proof 3. The error equation is considered as follows:

(35)

To prove the stability, the following Lyapunov function is considered.

First step:

(36)

To guarantee , x₂ must be chosen as follows:

(37)

The sliding surface is selected as follows:

(38)

Equation (36) is rewritten as follows:

(39)

The sliding surface is derived as follows:

(40)

Second step:

The Lyapunov function v₂ is defined as follows:

(41)

The derivative of the Lyapunov function v₂ is as follows:

(42)

For , the control signal u is chosen as follows:

(43)

By inserting the designed control signal into Equation (42), is guaranteed as follows:

(44)

The values c₁ = c₂ = 5 are selected.

4. Simulation Results

In this section, the fuzzy fixed-time TSMC is implemented to the ETV. All simulations in this paper are performed in the MATLAB/Simulink (R2024a) environment with ordinary differential equation (ODE45) solver. The simulation platform is a laptop running with 4 GB memory and Intel(R) Core (TM) i7-13700H, 64-bit operating system. The initial condition of the states is x₀ = [0.2,0.1], and the desired reference signal is x_d = 0.9 sin(t). The parameters related to the throttle valve system are listed in Table 2. Also, since the ETV is installed in a stressful environment next to the turbine and generator, the vibration of other devices is considered as an external bounded disturbance. It should be noted that if the vibration exceeds the limit, the turbine and generator will be shut down. In this section, uncertainty and external disturbances are added to the system by using multiple harmonics:

(45)

Figure 5 shows the external disturbance.

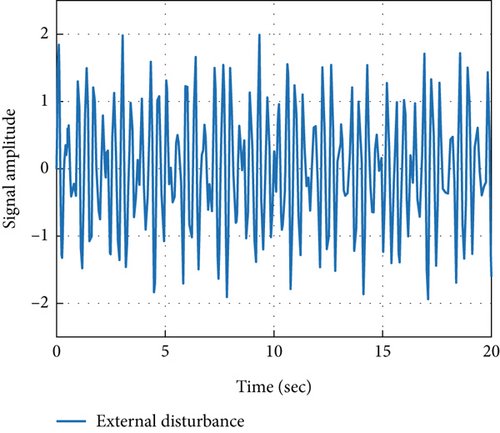
Figure 6 shows the block diagram of the controller, designed for the throttle valve.

The controlling parameters are considered to be as follows:

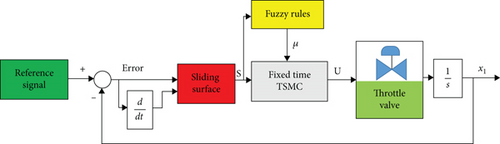
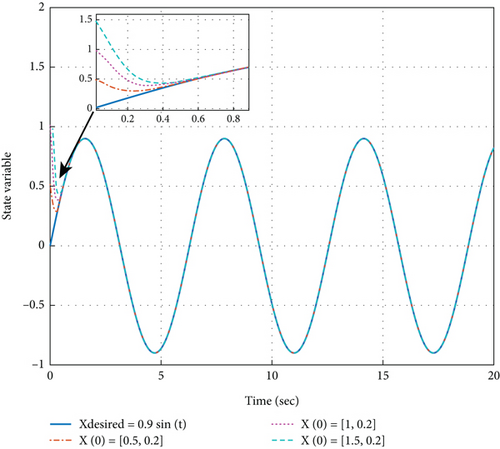
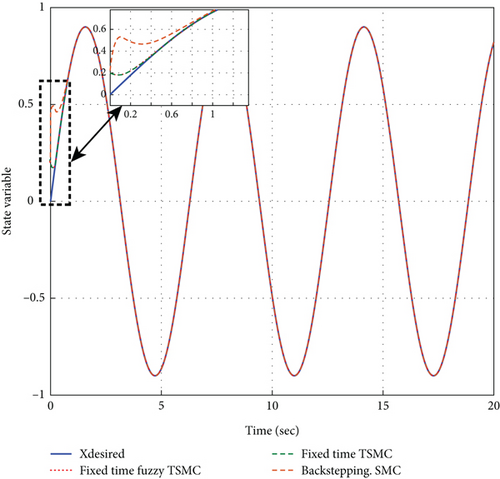
Figure 7 shows the success of the designed fixed-time TSMC for the ETV system in terms of convergence speed, accuracy, and especially independence from initial conditions x(0) = [0.5,0.2], [1,0.2], [1.5,0.2]. According to the values of the above parameters and Equation (13), the upper bound of the convergence time in reaching phase is 1.6 s and the upper bound of the convergence time in sliding phase is 1.15 s. As seen in Figure 7, the state variable converges to the reference signal in 0.54 s.

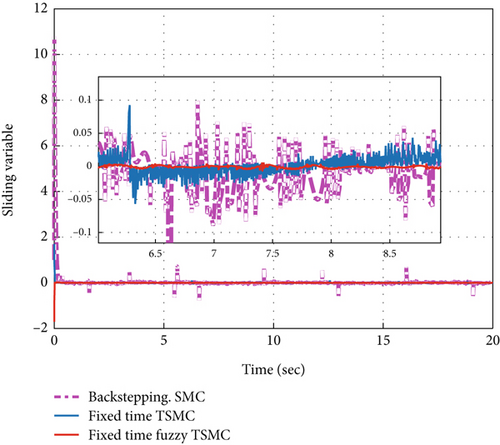
Use of the controller derived from a fixed-time TSMC strategy will damage the highly sensitive electronic throttle due to excessive chattering. Also, in the backstepping SMC method, the control signal has a lot of chattering. As seen in Figure 8, in the proposed fixed-time fuzzy TSMC signal, the chattering is effectively reduced.

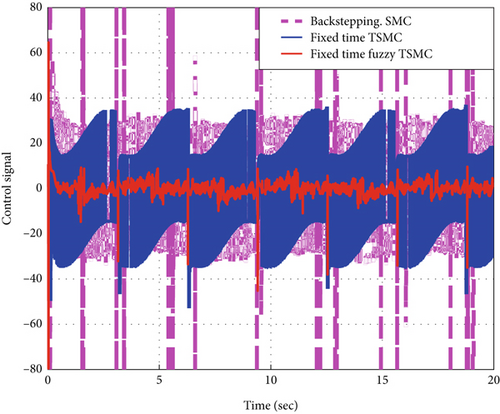
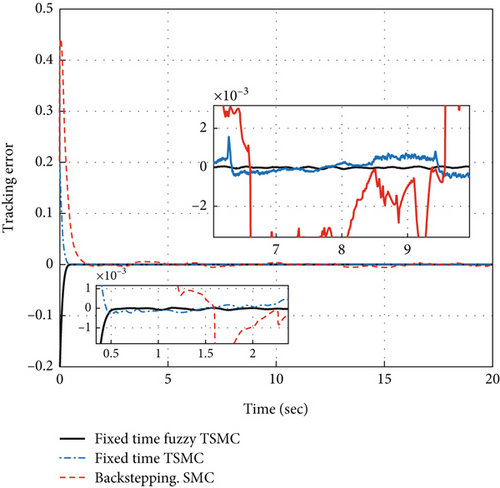
As can be seen in Figure 9, in both the fixed-time TSMC and fixed-time fuzzy TSMC methods, the convergence speed is reasonable and less than 0.33 s compared to [33]. The convergence speed in the backstepping SMC method is 6 s. The error performance indexes have been defined in Table 4. Considering Table 5 and Figures 8 and 9, it is clear that the method based on the fuzzy switching law has been very successful in reducing chattering, overshoot, and mean square error (MSE) index. All three methods have shown acceptable performance in reducing steady-state error. How the fuzzy term μ changes in the fixed-time fuzzy terminal sliding mode method can be seen in Figure 10. In Figure 11, it is clearly seen that in fixed-time fuzzy TSMC, the sliding variable has very few fluctuations and the system modes are attracted to the sliding surface, which leads to the reduction of the chattering phenomenon. Figure 12 shows how the tracking error signal becomes zero. In the fixed-time fuzzy terminal sliding mode method, the tracking error oscillates much less around the zero baseline and is clearly more accurate than in other methods. The evaluation results of the methods used in this article are presented in Table 5. Also, in order to accurately check the error reduction in different methods, the analysis of error values is illustrated in Table 6.

Table 4. Formulas related to error criteria.

Error criterion	Criterion formula
Mean square error (MSE)
Integral square error (ISE)
Integral absolute error (IAE)
Integral time weighted square error (ITSE)
Integral time weighted absolute error (ITAE)

Table 5. Performance analysis of control strategies.

Response specification	Steady-state error	Convergence time (s)	Overshoot (u)	Peak-to-peak controller variations
Fixed time TSMC	3.24e − 4	0.4	34.96	87.85
Fixed time fuzzy TSMC	2.3449e − 4	0.33	8.58	53.89
Backstepping SMC	0.0011	1.5	80	160

Table 6. Performance error index analysis for control strategies.

Response specification	ISE	IAE	ITSE	ITAE	MSE
Fixed time TSMC	0.0025	0.0257	1.3483e − 4	0.0390	3.31e − 8
Fixed time fuzzy TSMC	0.0024	0.0271	1.4530e − 4	0.0621	1.75e − 4
Backstepping SMC	0.0397	0.1882	0.0051	0.5035	7.22e − 4

In Table 5, three control methods are compared, analyzed, and investigated in terms of some performance indexes. As it is clear from Table 5, the amount of steady-state error in the fixed-time fuzzy TSMC method is less than in other methods. Using the fixed-time fuzzy TSMC method, the system states converge to the equilibrium points of the system in 0.33 seconds that is guaranteed. Considering the fixed-time fuzzy TSMC method, it is clear that the chattering of the control signal is reduced by 38.66%, and the overshoot of the control signal is reduced by 75.46% compared to the fixed-time TSMC method.

Table 6 shows that the fixed-time TSMC and the fixed-time fuzzy TSMC methods have efficient performance. To discuss the results more clearly, they are analyzed in comparison with [33–35] results. In [33], an adaptive fixed-time full-order SMC is proposed for throttle valve control. Comparing the simulation results shows that our proposed fuzzy fixed-time TSMC performs more effectively in reducing chattering and convergence time. In [34], a fast nonsingular TSMC is proposed, which converges in 0.52 s. So our method performs more effectively in the sense of reducing convergence time. Reference [35] proposes an adaptive second-order fixed-time SMC, which is developed with disturbance observer compensation techniques. In comparison with this, our proposed method leads to less tracking error and controller vibrations.

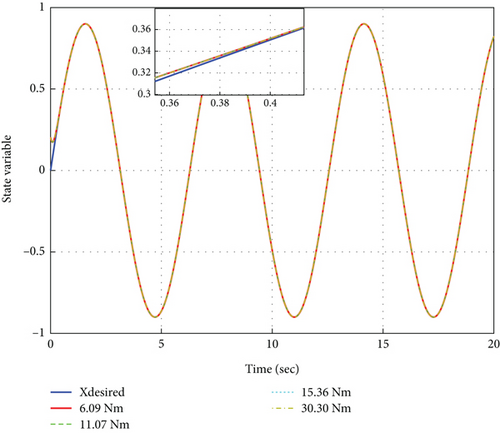
In Table 7, the amplitude of the disturbances becomes stronger and more destructive. Table 7 shows that with increasing the upper bound of the disturbance l_d(t), the convergence time of the state variables to the equilibrium points remains constant and it is clearly shown that the fixed-time fuzzy TSMC method is a robust method. Also, with increasing the amplitude of the disturbance, the ISE error index in all modes is 0.0024.

Table 7. Robustness of the fixed-time fuzzy TSMC method.

The upper bound of disturbance (Nm)	Convergence time (s)	ISE
6.09	0.36	0.0024
11.07	0.36	0.0024
15.36	0.36	0.0024
30.30	0.36	0.0024

Figure 13 indicates that although the upper boundary of the disturbance (l_d) increases and the disturbance intensifies, the fixed-time fuzzy TSMC method remains robust, the disturbance does not affect the system performance, and the proposed method has an effective performance in rejecting the disturbance. It can be seen from Figure 13, under all scenarios concerning the upper boundary of the disturbance, the system states converge very favorably to the input reference signal in a time constant of 0.36 s.

5. Conclusion

In this article, the problem of fuzzy fixed-time TSMC for the sensitive industrial equipment of ETV, which is a class of second-order nonlinear systems in the presence of uncertainty and external disturbances, is discussed. Although the proposed fixed-time TSMC has performed well in terms of fixed-time convergence, it suffers from chattering phenomena. Accordingly, a fuzzy regulation law has been added to the controller to reduce the chattering and prevent the erosion of industrial system parts. Fuzzy fixed-time TSMC is designed to achieve acceptable performance in terms of chattering and controlling effort reduction. Proof of fixed-time stability, discussed by the Lyapunov stability theorem, shows that the state variables of the system converge to the origin in a fixed time. The results of numerical simulations show the proper performance of the designed controller in reducing the chattering phenomenon to an acceptable level and improving the convergence speed of the transient response, reducing the error index and being resistant to external disturbances. It should be mentioned that, on the one hand, this paper considers some implementation limitations such as vibrations, friction of throttle with the valve body which causes parametric uncertainty, and the electrical noise caused by generators and power cables and penetrated into the shield; on the other hand, some other practical considerations such as input delay are neglected. So it will be beneficial to evaluate the efficiency of the proposed controlling method experimentally and analyze the technical conditions and the performance of the controller against the presence of noise in future works. It is also possible to take advantage of time-varying multisurface SMCs to improve controller efficiency.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

There is no funding or financial support related to this manuscript.

Open Research

Data Availability Statement

All the data used in the simulations are included in the text of the article.

References

1 Zhang Y., Tang Z., Hanguang L., Qi J., Yao M., Wang S., Zhai C., and Peng H., Method for Predicting Service Life of Cage Throttle Valves, Journal of Failure Analysis and Prevention. (2023) 23, 1907–1917, https://doi.org/10.1007/s11668-023-01764-y.
10.1007/s11668-023-01764-y
Web of Science® Google Scholar
2 Rong Z., Zhao C., Zihan Z., Qiyu H., Pengbo H., and Kuan S., Simulation and Optimization Design of Tubular Throttle Valve Based on SolidWorks, International Journal of Frontiers in Engineering Technology. (2023) 5, no. 6, 9–14, https://doi.org/10.25236/IJFET.2023.050602.
10.25236/IJFET.2023.050602
Google Scholar
3 Hu G., Zhang P., Wang G., Zhu H., Li Q., Zhao S., Qiao K., and Wang T., Performance Study of Erosion Resistance on Throttle Valve of Managed Pressure Drilling, Journal of Petroleum Science and Engineering. (2017) 156, 29–40, https://doi.org/10.1016/j.petrol.2017.05.011, 2-s2.0-85019605989.
10.1016/j.petrol.2017.05.011
CAS Web of Science® Google Scholar
4 Tecza J. and Chochua G., Analysis of Fluid-Structure Interaction in a Steam Turbine Throttle Valve, Turbo Expo: Power for Land, Sea, and Air. (2010) 7, 2329–2338, https://doi.org/10.1115/GT2010-23788, 2-s2.0-82055200402.
10.1115/GT2010-23788
Google Scholar
5 Zhang Z., Sun B., Wang Z., Mu X., and Sun D., Multiphase Throttling Characteristic Analysis and Structure Optimization Design of Throttling Valve in Managed Pressure Drilling, Energy. (2023) 262, 125619, https://doi.org/10.1016/j.energy.2022.125619.
10.1016/j.energy.2022.125619
Web of Science® Google Scholar
6 Bordjane M. and Chalet D., Numerical Investigation of Throttle Valve Flow Characteristics for Internal Combustion Engines, Journal of Multidisciplinary Engineering Science and Technology (JMEST). (2015) 2, no. 12, 3532–3541.
Google Scholar
7 Zhang C., Li C., Jia W., Xie H., and He J., Numerical Study on the Differences in Condensation Characteristics in Throttle Valves With Different Structures, Cryogenics. (2023) 133, 103696, https://doi.org/10.1016/j.cryogenics.2023.103696.
10.1016/j.cryogenics.2023.103696
CAS Web of Science® Google Scholar
8 Smołka K., Wiśniewski P., Majkut M., and Dykas S., Operational and Economic Analysis of a Velox-Type Combined Heat & Power Plant With a Throttle Valve, Proceedings of the MATEC Web of Conferences, 2021, 345, EDP Sciences, 1–12, https://doi.org/10.1051/matecconf/202134500028.
Google Scholar
9 Naik K. P., Pradhan R., and Majhi S. K., Speed Control of Hybrid Electric Vehicle by Using Moth Flame Optimization, Proceedings of the International Conference on Communications and Cyber Physical Engineering 2018, 2023, Springer Nature Singapore, 847–859, https://doi.org/10.1007/978-981-19-8086-281.
10.1007/978-981-19-8086-2_81
Google Scholar
10 Youssef O. and Shalaby R., Optimizing Automotive Electronic Throttle Control With a Modified Grey Wolf Algorithm, Proceedings of the 2023 5th Novel Intelligent and Leading Emerging Sciences Conference (NILES), 2023, IEEE, 222–227, https://doi.org/10.1109/NILES59815.2023.10296740.
10.1109/NILES59815.2023.10296740
Google Scholar
11 Ghani M. F., Ghazali R., Jaafar H. I., Soon C. C., Sam Y., and Has Z., Improved Third Order PID Sliding Mode Controller for Electrohydraulic Actuator Tracking Control, Journal of Robotics and Control (JRC). (2022) 3, no. 2, 219–226, https://doi.org/10.18196/jrc.v3i2.14236.
10.18196/jrc.v3i2.14236
Google Scholar
12 Wang H., Liu L., He P., Yu M., Do M. T., Kong H., and Man Z., Robust Adaptive Position Control of Automotive Electronic Throttle Valve Using PID-Type Sliding Mode Technique, Nonlinear Dynamics. (2016) 85, 1331–1344, https://doi.org/10.1007/s11071-016-2763-8, 2-s2.0-84962634401.
10.1007/s11071-016-2763-8
Web of Science® Google Scholar
13 Afifa R., Ali S., Pervaiz M., and Iqbal J., Adaptive Backstepping Integral Sliding Mode Control of a MIMO Separately Excited DC Motor, Robotics. (2023) 12, no. 4, 105–121, https://doi.org/10.3390/robotics12040105.
10.3390/robotics12040105
Web of Science® Google Scholar
14 Chen L., Wang Y., Zhao J., Ding S., Gao J., and Chen H., A Novel Adaptive Control Scheme for Automotive Electronic Throttle Based on Extremum Seeking, IEEE Transactions on Circuits and Systems I: Regular Papers. (2023) 70, no. 6, 2599–2611, https://doi.org/10.1109/TCSI.2023.3258465.
10.1109/TCSI.2023.3258465
Web of Science® Google Scholar
15 Feng Y., Long Y., Yao C., and Song E., Adaptive Second-Order Fixed-Time Sliding Mode Controller With a Disturbance Observer for Electronic Throttle Valves, Sensors. (2023) 23, no. 18, https://doi.org/10.3390/s23187676, 37765733.
10.3390/s23187676
PubMed Web of Science® Google Scholar
16 Bai R., Adaptive Sliding-Mode Control of an Automotive Electronic Throttle in the Presence of Input Saturation Constraint, IEEE/CAA Journal of Automatica Sinica. (2018) 5, no. 4, 878–884, https://doi.org/10.1109/JAS.2018.7511147, 2-s2.0-85048326895.
10.1109/JAS.2018.7511147
Web of Science® Google Scholar
17 Hu Y., Wang H., Yazdani A., and Man Z., Adaptive Full Order Sliding Mode Control for Electronic Throttle Valve System With Fixed-Time Convergence Using Extreme Learning Machine, Neural Computing and Applications. (2021) 34, 5241–5253, https://doi.org/10.1007/s00521-021-06365-0.
10.1007/s00521-021-06365-0
Web of Science® Google Scholar
18 Hosseinabadi P. A., Abadi A. S. S., Schwartz H., Pota H., and Mekhilef S., Fixed-Time Sliding Mode Observer-Based Controller for a Class of Uncertain Nonlinear Double Integrator Systems, Asian Journal of Control. (2023) 25, no. 5, 3456–3473.
10.1002/asjc.3052
Web of Science® Google Scholar
19 Abadi A. S. S., Hosseinabadi P. A., and Mekhilef S., Fuzzy Adaptive Fixed-Time Sliding Mode Control With State Observer for A Class of High-Order Mismatched Uncertain Systems, International Journal of Control, Automation and Systems. (2020) 18, 1–17, https://doi.org/10.1007/s12555-019-0650-z.
10.1007/s12555-019-0650-z
Web of Science® Google Scholar
20 Hou H., Yu X., Xu L., Rsetam K., and Cao Z., Finite-Time Continuous Terminal Sliding Mode Control of Servo Motor Systems, IEEE Transactions on Industrial Electronics. (2019) 67, no. 7, 5647–5656, https://doi.org/10.1109/TIE.2019.2931517.
10.1109/TIE.2019.2931517
Google Scholar
21 Rsetam K., Cao Z., Wang L., Al-Rawi M., and Man Z., Practically Robust Fixed-Time Convergent Sliding Mode Control for Underactuated Aerial Flexible Joint Robots Manipulators, Drones. (2022) 6, no. 12, https://doi.org/10.3390/drones6120428.
10.3390/drones6120428
Google Scholar
22 Rsetam K., Cao Z., and Man Z., Design of Robust Terminal Sliding Mode Control for Underactuated Flexible Joint Robot, IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2021) 52, no. 7, 4272–4285, https://doi.org/10.1109/TSMC.2021.3096835.
10.1109/TSMC.2021.3096835
Web of Science® Google Scholar
23 Anjum M. B., Khan Q., Ullah S., Hafeez G., Fida A., Iqbal J., and Albogamy F. R., Maximum Power Extraction From a Standalone Photo Voltaic System via Neuro-Adaptive Arbitrary Order Sliding Mode Control Strategy With High Gain Differentiation, Applied Sciences. (2022) 12, no. 7, https://doi.org/10.3390/app12062773.
10.3390/app12062773
Google Scholar
24 Wu X., Li L., Wang X., Chen X., and Cheng S., Nonlinear Controller Design and Testing for Chatter Suppression in an Electric-Pneumatic Braking System With Parametric Variation, Mechanical Systems and Signal Processing. (2020) 135, 106401, https://doi.org/10.1016/j.ymssp.2019.106401.
10.1016/j.ymssp.2019.106401
Web of Science® Google Scholar
25 D’Amico W., Farina M., and Panzani G., Advanced Control Based on Recurrent Neural Networks Learned Using Virtual Reference Feedback Tuning and Application to an Electronic Throttle Body (With Supplementary Material), 2021, Electrical Engineering and Systems Science, Systems and Control, https://arxiv.org/abs/2103.02567.
Google Scholar
26 Li W., Su J., and Li S., Adaptive Augmented Kalman Filter-Based Control for Electronic Throttle Systems With Disturbances and Noises, Proceedings of the 42nd Chinese Control Conference (CCC), 2023, IEEE, https://doi.org/10.23919/CCC58697.2023.10240635.
10.23919/CCC58697.2023.10240635
Google Scholar
27 Wang D., Liu S., He Y., and Shen J., Barrier Lyapunov Function-Based Adaptive Back-Stepping Control for Electronic Throttle Control System, Mathematics. (2021) 9, no. 4, 326–340, https://doi.org/10.3390/math9040326.
10.3390/math9040326
Web of Science® Google Scholar
28 Li Y., Yang B., Zheng T., Li Y., Cui M., and Peeta S., Extended-State-Observer-Based Double-Loop Integral Sliding-Mode Control of Electronic Throttle Valve, IEEE Transactions on Intelligent Transportation Systems. (2015) 16, no. 5, 2501–2510, https://doi.org/10.1109/TITS.2015.2410282, 2-s2.0-84959506359.
10.1109/TITS.2015.2410282
Web of Science® Google Scholar
29 Pan Y., Dagci O., and Ozguner U., Variable Structure Control of Electronic Throttle Valve, IVEC2001. Proceedings of the IEEE International Vehicle Electronics Conference 2001. IVEC 2001 (Cat. No.01EX522), 2001, IEEE, 103–108, https://doi.org/10.1109/IVEC.2001.961734, 2-s2.0-84963759233.
Google Scholar
30 Dagci O. H., Pan Y., and Ozguner U., Sliding Mode Control of Electronic Throttle Valve, Proceedings of the 2002 American Control Conference (IEEE Cat. No.CH37301), 2002, 3, IEEE, 1996–2001, https://doi.org/10.1109/ACC.2002.1023928.
10.1109/ACC.2002.1023928
Google Scholar
31 Kang S., Yoon M., and Sunwoo M., Traction Control Using a Throttle Valve Based on Sliding Mode Control and Load Torque Estimation, Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering. (2015) 219, no. 5, 645–653, https://doi.org/10.1243/095440705X11059, 2-s2.0-19544368309.
10.1243/095440705X11059
Google Scholar
32 Li Y., Yang B., Zhang X., Wu Q., and Zheng T., Extended State Observer–Based Intelligent Double Integral Sliding Mode Control of Electronic Throttle Valve, Advances in Mechanical Engineering. (2017) 9, no. 12, https://doi.org/10.1177/1687814017737981, 2-s2.0-85039775627, 168781401773798.
10.1177/1687814017737981
Web of Science® Google Scholar
33 Hu Y., Wang H., He S., Zheng J., Ping Z., Shao K., Cao Z., and Man Z., Adaptive Tracking Control of an Electronic Throttle Valve Based on Recursive Terminal Sliding Mode, IEEE Transactions on Vehicular Technology. (2021) 70, no. 1, 251–262, https://doi.org/10.1109/TVT.2020.3045778.
10.1109/TVT.2020.3045778
Web of Science® Google Scholar
34 Long Y., Yao C., and Song E., Design and Experimental Analysis of an Adaptive Second-Order Fast Non-Singular Terminal Sliding Mode Controller for Electronic Throttle With Disturbance, IEEE Access. (2023) 11, 57854–57866, https://doi.org/10.1109/ACCESS.2023.3284686.
10.1109/ACCESS.2023.3284686
Web of Science® Google Scholar
35 Barman S. and Sinha M., A Novel Nonsingular Fast Fixed-Time Sliding Mode Control and Its Application to Satellite Attitude Control, Robust and Nonlinear Control. (2025) 35, no. 6, 2184–2198, https://doi.org/10.1002/rnc.7787.
10.1002/rnc.7787
Web of Science® Google Scholar
36 Qiu Z., Zhang J., Su Q., Li H., Xu B., and Wang J., Adaptive Sliding Mode Control Based on the Immersion and Invariance Principle for the Accurate Spool Control of Proportional Servo Valve, Fluid Power Systems Technology, 2023, American Society of Mechanical Engineers, https://doi.org/10.1115/FPMC2023-111998.
10.1115/FPMC2023-111998
Google Scholar
37 Yang B., Liu M., Kim H., and Cui X., Luenberger-Sliding Mode Observer Based Fuzzy Double Loop Integral Sliding Mode Controller for Electronic Throttle Valve, Journal of Process Control. (2018) 61, 36–46, https://doi.org/10.1016/j.jprocont.2017.11.004, 2-s2.0-85035361002.
10.1016/j.jprocont.2017.11.004
CAS Web of Science® Google Scholar
38 Gritli W., Gharsallaoui H., Benrejeb M., and Borne P., Electronic Throttle Valve Takagi-Sugeno Fuzzy Control Based on Nonlinear Unknown Input Observers, International Journal of Computers Communications & Control. (2018) 13, no. 5, 808–823, https://doi.org/10.15837/ijccc.2018.5.3281.
10.15837/ijccc.2018.5.3281
Web of Science® Google Scholar
39 Mercorelli P., Robust Feedback Linearization Using an Adaptive PD Regulator for a Sensorless Control of a Throttle Valve, Mechatronics. (2009) 19, no. 8, 1334–1345, https://doi.org/10.1016/j.mechatronics.2009.08.008, 2-s2.0-70849114086.
10.1016/j.mechatronics.2009.08.008
Web of Science® Google Scholar
40 AL-Samarraie S. A. and Abbas Y. K., Design of Electronic Throttle Valve Position Control System Using Nonlinear PID Controller, International Journal of Computer Applications. (2012) 59, no. 15, 27–34, https://doi.org/10.5120/9625-4273.
10.5120/9625-4273
Google Scholar
41 Gritli W., Gharsallaoui H., and Benrejeb M., PID-Type Fuzzy Scaling Factors Tuning Using Genetic Algorithm and Simulink Design Optimization for Electronic Throttle Valve, Proceedings of the 2016 International Conference on Control, Decision and Information Technologies (CoDIT), 2016, IEEE, 216–221, https://doi.org/10.1109/CoDIT.2016.7593563, 2-s2.0-84995519549.
10.1109/CoDIT.2016.7593563
Google Scholar
42 Saerens B., Vandersteen J., Persoons T., Swevers J., Diehl M., and Bulck E. V. D., Minimization of the Fuel Consumption of a Gasoline Engine Using Dynamic Optimization, Applied Energy. (2009) 86, no. 9, 1582–1588, https://doi.org/10.1016/j.apenergy.2008.12.022, 2-s2.0-63449128406.
10.1016/j.apenergy.2008.12.022
CAS Web of Science® Google Scholar
43 Siraskar R., Reinforcement Learning for Control of Valves, Machine Learning with Applications. (2021) 4, 100030–100047, https://doi.org/10.1016/j.mlwa.2021.100030.
10.1016/j.mlwa.2021.100030
Web of Science® Google Scholar
44 Bischoff B., Nguyen-Tuong D., Koller T., Markert H., and Knoll A., H. Blockeel, K. Kersting, S. Nijssen, and F. Železný, Learning Throttle Valve Control Using Policy Search, Machine Learning and Knowledge Discovery in Databases. ECML PKDD 2013. Lecture Notes in Computer Science, 2013, 8188, Springer, https://doi.org/10.1007/978-3-642-40988-2_4, 2-s2.0-84886463721.
10.1007/978-3-642-40988-2_4
Google Scholar
45 Chang S. C., Stability Analysis and Chaos Control of Electronic Throttle Dynamical System, Mathematical Problems in Engineering. (2021) 2021, 14, https://doi.org/10.1155/2021/5286043, 5286043.
10.1155/2021/5286043
Web of Science® Google Scholar
46 Gharsallaoui H., Gritli W., Benrejeb M., and Borne P., RST Switching Bi-Controller Based Flatness for an Electronic Throttle Valve, International Journal of Computers Communications & Control. (2023) 18, no. 5, https://doi.org/10.15837/ijccc.2023.5.5630.
10.15837/ijccc.2023.5.5630
Web of Science® Google Scholar
47 Zuo Z., Non-Singular Fixed-Time Terminal Sliding Mode Control of Non-Linear Systems, IET Control Theory and Applications. (2015) 9, no. 4, 545–552, https://doi.org/10.1049/iet-cta.2014.0202, 2-s2.0-84924435769.
10.1049/iet-cta.2014.0202
Web of Science® Google Scholar
48 Ni J., Fixed-Time Terminal Sliding Mode Tracking Protocol Design for High-Order Multiagent Systems With Directed Communication Topology, ISA Transactions. (2022) 124, 444–457, https://doi.org/10.1016/j.isatra.2020.02.022, 32115190.
10.1016/j.isatra.2020.02.022
PubMed Web of Science® Google Scholar
49 Zuo Z. and Tie L., Distributed Robust Finite-Time Nonlinear Consensus Protocols for Multi-Agent Systems, International Journal of Systems Science. (2014) 47, no. 6, 1366–1375, https://doi.org/10.1080/00207721.2014.925608, 2-s2.0-84995360041.
10.1080/00207721.2014.925608
Google Scholar
50 Polyakov A., Nonlinear Feedback Design for Fixed-Time Stabilization of Linear Control Systems, IEEE Transactions on Automatic Control. (2011) 57, no. 8, 2106–2110, https://doi.org/10.1109/TAC.2011.2179869, 2-s2.0-84864747003.
10.1109/TAC.2011.2179869
Web of Science® Google Scholar
51 Tian Y., Cal Y., and Deng Y., A Fast Nonsingular Terminal Sliding Mode Control Method for Nonlinear Systems With Fixed-Time Stability Guarantees, IEEE Access. (2020) 8, 60444–60454, https://doi.org/10.1109/ACCESS.2020.2980044.
10.1109/ACCESS.2020.2980044
Web of Science® Google Scholar
52 Zhang J., Yu S., Wu D., and Yan Y., Nonsingular Fixed-Time Terminal Sliding Mode Trajectory Tracking Control for Marine Surface Vessels With Anti-Disturbances, Ocean Engineering. (2020) 217, https://doi.org/10.1016/j.oceaneng.2020.108158.
10.1016/j.oceaneng.2020.108158
Web of Science® Google Scholar
53 Irfan S., Zhao L., Ullah S., Javaid U., and Iqbal J., Differentiator-and Observer-Based Feedback Linearized Advanced Nonlinear Control Strategies for an Unmanned Aerial Vehicle System, Drones. (2024) 8, no. 10, 527–564, https://doi.org/10.3390/drones8100527.
10.3390/drones8100527
Web of Science® Google Scholar
54 Liu J. and Wang X., Advanced Sliding Mode Control for Mechanical Systems: Design, Analysis and MATLAB Simulation, 2012, Springer.
Google Scholar
55 Saleem O., Hamza A., and Iqbal J., A Fuzzy-Immune-Regulated Single-Neuron Proportional–Integral–Derivative Control System for Robust Trajectory Tracking in a Lawn-Mowing Robot, Computers. (2024) 13, no. 11, 301–337, https://doi.org/10.3390/computers13110301.
10.3390/computers13110301
Web of Science® Google Scholar
56 Rabbani M. and Moghaddam R. K., A Newly Proposed Super-Twisting Backstepping Sliding Mode Controller, International Journal of Nonlinear Analysis and Applications. (2025) 16, no. 4, 295–309, https://doi.org/10.22075/ijnaa.2023.30984.4532.
10.22075/ijnaa.2023.30984.4532
Google Scholar
57 Awan Z. S., Ali K., Iqbal J., and Mehmood A., Adaptive Backstepping Based Sensor and Actuator Fault Tolerant Control of a Manipulator, Journal of Electrical Engineering & Technology. (2019) 14, 2497–2504, https://doi.org/10.1007/s42835-019-00277-9.
10.1007/s42835-019-00277-9
Web of Science® Google Scholar
58 Moghaddam R. K. and Rabbani M., Methods of Developing Sliding Mode Controllers: Design and MATLAB Simulation, 2025, Wiley-IEEE Press.
Google Scholar

All articles

A Newly Proposed Fixed-Time Terminal Sliding Mode Controller for a Class of Nonlinear Systems: Throttle Valve Study

Abstract

1. Introduction

2. Mathematical Model and Preliminaries