The nanofluids and their advanced models (ternary and tetra nanofluids) possess an outstanding thermal mechanism and attract engineers and industrialists with their prominent features. Tetra nanofluids have high thermal conductivity; thus, by inserting nanoparticles in the base fluids, the effective thermal conductivity of heat transfer fluids is enhanced. A framework has now been illuminated throughout this work to scrutinize the behavior of chemical reactions and radiation on water-based magnetohydrodynamics (MHD) biviscous Bingham flow of tetra nanofluid (Al₂O₃–Fe₃O₄–TiO₂–Cu/H₂O) over an accelerated plate through a porous medium in the presence of slip conditions, heat source/sink, and viscous dissipation. The overall physical problem is designed in the form of a nonlinear partial differential equation, which is then altered into a highly nonlinear ordinary differential equation via a proper dimensionless variable. These equations are solved analytically, along with the associated boundary conditions. The flow, energy, and mass problems were examined analytically, especially the heat transport phenomena performed for both prescribed surface temperature (PST) and prescribed heat flux (PHF) cases, and mass transfer was also evaluated in two different cases, namely prescribed surface concentration (PSC) and prescribed mass flux (PMF) cases, and then, these solutions were demonstrated in terms of the confluent hypergeometric function. There were plots showing how the different variables affected the velocity of flow, energy, concentration, skin friction, and rate of heat transmission. The dual solution is found for velocity, temperature, and concentration profiles. The finding discloses that the performance of the magnetic parameter, the biviscous Bingham fluid parameter, and the slip parameters experience a slowdown in the impact of their corresponding velocities in cases of stretching boundaries. For both boundary conditions, the magnitude of the magnetic field parameter increases with increasing temperature and the concentration profile in the second solution, whereas a reverse trend is observed in the first solution.

1. Introduction

The investigation of non-Newtonian liquids has drawn a lot of attention due to their wide range of engineering and industry applications, especially in the extraction of crude oil and petroleum products, the fabrication of plastic substances, and syrup drugs, but their flow features cannot be accomplished by a single constitutive equation. Hence, different NN models have been proposed to depict the flow behavior. Among the several NN liquids, some exhibit yield stress, namely the Bingham plastic model, the Herschel–Bulkley fluid model, and the Casson model. However, when the velocity gradient approaches zero, the apparent viscosity of these fluid models changes.

A Bingham fluid is a non-Newtonian viscoplastic fluid that possesses a yield strength that must be outstripped before the fluid will flow. In many geological and industry materials, Bingham fluids are used as a general mathematical basis of mudflow in drilling engineering, including in the handling of slurries and granular suspensions. Bingham fluid is named after Eugene C. Bingham, who declared its mathematical explanation. We have considered biviscous Bingham fluid for this current study. In the early twentieth century, Bingham [1] introduced the concept of Bingham fluid. In the year 1916, he developed the mathematical model for this fluid, hence the name Bingham fluid. Several substances are prepared as Bingham fluids, including oil drilling mud, volcanic lava, paints, dental paste, and ceramics. In its first approximation, blood is considered as a Bingham fluid due to its yield stress. Later, Nakamura and Sawada [2] carried out a thorough examination of the regularized Bingham fluid model by contrasting its rheological features with those of the Casson liquid model. They found that the regularized (biviscous) Bingham model and the Casson fluid model are very similar outside of the low shear rate region. The regularized (biviscous) Bingham fluid has a relatively large yield stress compared with the Casson model. Recently, Basavarajappa et al. [3] presented the impact of nonlinear convection on the multilayer motion of biviscous Bingham fluid due to vertical slab, and they highlighted that this research has significant uses in industries and engineering. Dandapat et al. [4] analytically studied the 2D motion of biviscosity fluid flow through an unstable stretching sheet. Srivastava [5] discussed the laminar movement of NN fluid past a rotating disk. Islam et al. [6] conducted a numerical investigation of unstable, viscous, and incompressible Bingham fluid flow along parallel plates.

Pure liquids such as water, oil, and ethylene glycol with lower thermal conductivity are restrained in the flow phenomenon of the liquid. To enhance the thermal conductivity of base/pure liquid, scientists have implemented several methods and strategies. Choi and Eastman [7] were the first to develop the technique of suspending small particles. This type of fluid is known as a nanofluid, which is employed in industry for cooling purposes. Examples of applications for nanofluids include coolant for vehicle engines, power plant equipment, various electronic gadgets, and manufacturing operations. Recently, many studies on nanofluid flow have been carried out by various experts, with a primary emphasis on heat transmission. Mahabaleshwar et al. [8] probed the laminar flow of incompressible Casson nanoparticles over a stretching or shrinking surface. Ghosh et al. [9] conducted research on the bioconvection of a viscoelastic Casson nanoparticle moving across a stretching surface. Afterward, researchers revealed that the distribution of two distinct kinds of nanoparticles in a pure fluid enhances the properties of thermal flow much more. They referred to this fluid as a hybrid nanofluid. Waini et al. [10] described the impact of transpiration on heat transmission and HNF motion through a stretching/shrinking sheet for steady shear flow. After that, Kamis et al. [11] highlighted the heat transport in blood fluid-based copper and alumina nanoparticles along an unstable penetrable stretching material.

In recent times, researchers have found that a pure liquid’s thermal conductivity is effectively enhanced by suspending three distinct kinds of nanoparticles in it. These liquids are known as trihybrid nanofluids. Sahoo et al. [12] used a tnf with various nanoparticle structures to examine the irreversibility and thermal flow. This work concludes that the growth of entropy in tnf has increased from 12.24% upon increasing the concentration from 1% to 3%. Priyadharshini et al. [13] explored the fabrication of tnf nanoparticles (Cu), (TiO₂), and (SiO₂) floating in water across a symmetrically stretched sheet. A tnf nanofluid incorporating convective heat transport along a stretched sheet was portrayed by Manjunatha et al. [14]. According to several studies [15, 16], trihybrid nanofluids have significantly superior heat flow features than other hybrid or conventional nanofluids. Certainly, a great deal of study is being performed regarding the development of contemporary nanofluids. These liquids were also named tetra hybrid nanofluid. Because THNFs have several linked parts, they are more effective at transporting heat. This affects the entire system cumulatively. Researchers from all around the world looked into THNFs because they advance to heat more rapidly than other hybrid nanofluids. Sajid et al. [17, 18] examine the impact of tetra hybrid nanofluid on the cross-fluid flow when it is exposed to a Riga plate with a catalysis reaction influence on it.

In recent years, magnetohydrodynamics (MHD) fluid flow has drawn the interest of researchers because of its variable heat transfer rate. Additionally, the MHD phenomenon is important in moderating the rate of cooling and extracting molten metal from different nonmetallic contaminants. MHD flow of fluid has a broad application in manufacturing and industrial applications. Fluid properties, such as velocity, temperature, and concentration, may change when an external magnetic field is present because of the Lorentz drag force it exerts on the fluid. Kopp et al. [19] presented the 3D Casson flow of a tnf nanoparticle across a permeable, continuously stretching, or shrinking surface in the context of an external magnetic field. Khan et al. [20] reported on the motion of THNFs and Casson fluid with dust particles and heat transport among parallel surfaces. Teh et al. [21] computationally depicted an alumina (Al₂O₃) and copper (Cu) hybrid nanofluid in three dimensions traveling across a stretching/shrinking sheet. Kumaresan [22] presented an exact solution for unsteady MHD BL flow of silver nanoparticles over an exponentially permeable accelerated moving vertical plate in the presence of radiation, heat source/sink, and chemical reaction. Many researchers [23–25] researched the movement of MHD nanoparticles via various geometries. Maranna [26] deliberated the impact of Navier’s slip and radiation on MHD nanofluid flow over a porous stretching/shrinking sheet.

Thermal radiation is a heat transfer process that propagates heat energy across fluid particles. The impact of radiation on MHD flow exhibits a significant character in engineering, and many industrial processes require greater temperatures, such as the production of paper plates, the cooling of metallic objects, the development of electric chips, and petroleum pumps. Maranna et al. [26] deliberated the analytical study on MHD nanoparticles (Ag/Cu) across penetrable stretching/shrinking surfaces in the presence of slip and radiation. They concluded that the copper particle has more acceleration compared with silver nanoparticles. Mahabaleshwar et al. [27] discussed the role of radiation and suction/injection on dusty trinanoparticle (Ag + SWCNT + graphene) motion over a permeable stretching/shrinking sheet. Later on, Adnan et al. [28] investigated the stationary point flow of tetra nanoparticles (Al₂O₃–CuO–TiO₂–Ag)/water through a vertically aligned cylinder under the porosity effect in the presence of MHD and radiation. In recent years, several researchers [29–31] have inspected various aspects of the relevance of radiation and MHD on nanoparticle flow.

The research on the application of heat generation/absorption on MHD flow continues to motivate investigators in different fields because of its applicability in industries. In fluid transport, heat generation plays the role of elevating the fluid’s thermal conductivity, which elevates the fluid’s temperature. Heat absorption, however, drops the fluid’s thermal conductivity, which lowers the fluid’s temperature. Maranna et al. [32] dealt with the radiation effect on viscoelastic trinanoparticle streams over a shrinking porous medium in the presence of heat generation or absorption. Shobha et al. [33] illustrated the entropy development in the Williamson nanofluid moving in a vertical perforated channel subjected to nonlinear thermal radiation and a heat source or sink. Ilya et al. [34] explored the erratic hydromagnetic mixed convective motion across an electrically conducting cone submerged in a porous material in the presence of thermal buoyancy, magnetic field, and heat source/sink phenomena.

During the acceleration of liquid particles, a portion of the fluid’s kinetic energy is converted to thermal energy by its viscosity. This process is referred to as viscous dissipation as it is irreversible and induced by viscosity. Brickman et al. [35] first took into account the implications of viscous dissipation. He observed the Newtonian fluid’s temperature variation in a straight circular tube and determined the effects originated in the close area. Mahabaleshwar et al. [36] portrayed the radiation and energy dissipation effects on MHD micropolar fluid flow through an elongating or contracting sheet in the presence of suction or injection. Muyungi et al. [37] addressed the flow of nanofluids (Al₂O₃–Cu) across a porous medium when the slip phenomenon is present. During the recent years, the other research work can be seen in [38–41].

Many studies have investigated the impact of chemical reactions on heat and mass transfer issues due to their significance in hydrometallurgical sectors and chemical technology, including the manufacturing of pulp and shielded cables, curing of polymers, cleaning, and chemical processing of materials. First or higher chemical reaction orders are possible. Vanitha et al. [42] analyzed the flow properties of a micropolar liquid injected with ternary nanoparticles along a stretching or shrinking surface when exposed to radiation and chemical processes. Mumtaz et al. [43] explored the 2D motion of an altered hybrid nanoparticle along a curved stretching sheet under the action of magnetic and electrical fields. Ketchate et al. [44] explored the stability characterization of a ferrofluid with magnetic nanoparticles with blood as the base liquid. This work integrates the impact of chemical reaction and radiation. More studies related to the chemical reaction effect on NFs are found in [25, 45–50].

A review of the currently available literature sheds light on research gaps and inadequate research. As far as the author’s knowledge, there has been no study on 2D biviscous Bingham tetra hybrid nanoparticles flowing past a permeable accelerated plate while considering the MHD, radiation, viscous dissipation, heat source/sink, suction/injection, slip condition, and chemical reaction into account. To fill this gap, the novelty of the current research is to analytically examine the effect of radiation, heat source/sink, viscous dissipation, slip condition, and chemical reaction on MHD tetra hybrid nanoparticle (Al₂O₃–Fe₃O₄–TiO₂–Cu) flow over a permeable accelerated plate. Water is recycled as a base liquid. Additionally, the non-Newtonian biviscous Bingham model is taken into account. The governing PDEs have been simplified to a set of ODEs through appropriate similarity transformations, and then, analytical solutions have been derived. Two distinct boundary conditions are examined for heat and mass transfer, and solutions are determined using the hypergeometric function. Furthermore, we plotted graphs to show the effect of pertinent parameters on the action of the variables of state such as momentum, energy, skin friction, concentration, and heat gradient, and then, we reviewed them physically.

2. Model Development

2.1. Model Statement and Geometry

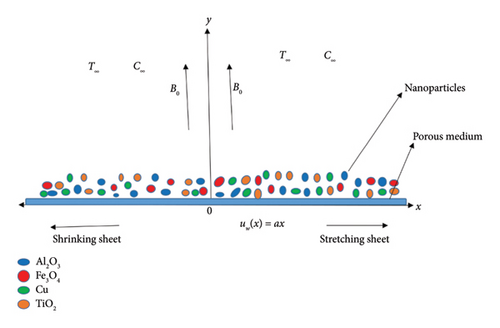
This study considers a steady 2D laminar boundary layer MHD flow of a biviscous Bingham tetra nanoparticle over a permeable stretching/shrinking sheet. The nanoparticle is composed of Al₂O₃, Fe₃O₄, TiO₂, and Cu in a water-based fluid. The velocity of the sheet is u_w(x) = ax. The flow is restricted to y > 0. Fluid moves in a path perpendicular to the direction in which magnetic force B₀ is applied. The coordinates (x, y) are employed so that x is along the sheet surface and y is considered to be perpendicular to it. Figure 1 portrays a simplified schematic depiction of the fluid flow. The problem incorporates the magnetic field, permeable medium, heat generation/absorption, viscous dissipation, concentration, and chemical reaction effects. The far temperature and concentration at the walls are T_∞ and C_∞, respectively.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Geometric illustration of the flow problem.

The rheological expression for biviscous Bingham fluid is given as follows [3, 51]:

(1)

In the above equation, p_y is the yield stress of the biviscous Bingham fluid, μ_b is the plastic dynamic viscosity, π = e_ij and e_ij denote the (i, j)th element of deformation rate, and π_c is the critical value of this product based on the non-Newtonian model.

The expression for the biviscous Bingham fluid p_y yield stress is

(2)

A biviscous Bingham fluid flow happens when π > π_c, and it is possible to propose that

(3)

By inserting equation (2) into (3), we obtain

(4)

The convection factor in the momentum equation can be interpreted as follows based on the information described earlier:

(5)

For tetra nanoparticles, we interpret the expression as ν_tetra(1 + (1/β))(∂²u/∂y²).

The main leading flow equations, constructed in the usual notation [17, 36, 52–54], are as follows.

The continuity equation is as follows:

(6)

The momentum equation is as follows:

(7)

The energy equation is as follows:

(8)

The concentration equation is as follows:

(9)

With the radiative heat transition term rearranged using the Rosseland estimate [55–57], we attain

(10)

Here, σ^∗ is known as the Stefan–Boltzmann coefficient and k^∗ is the mean absorption constant. With Taylor’s expansion of T⁴ about T_∞ and ignoring higher-order terms, we have

(11)

By inserting equation (11) in (8), we yield

(12)

Accordingly, the prescribed boundary conditions are stated [36, 58] by

(13)

where (u, v) denotes the velocity fundamental quantities, with the direction of (x, y) axis, respectively. μ_tetra, ρ_tetra, σ_tetra, κ_tetra, and

represent the dynamic viscosity, density, electrical, and thermal conductivity and heat capacitance of tetra nanoparticles. K denotes the permeability, β is the biviscous Bingham liquid, Q₀ is the heat generation/absorption coefficient, K^∗ symbolizes the reaction rate constant, and v_w represents the mass transfer velocity. The remaining other parameters are described in the nomenclature section.

2.2. Conversion of Leading Equations

To convert the given equation to dimension-free form, the following set of similar variables will be incorporated [58] as follows:

(14)

By incorporating equation (14) into (7), (8), (9), and (13), we obtain

(15)

(16)

(17)

and boundary conditions (13) are altered as

(18)

where Q is the heat generation/absorption parameter, where Q > 0 stands for the heat generation and Q < 0 stands for the heat absorption; d reflects the stretching/shrinking parameter, such that d > 0 stands for the stretching and d < 0 stands for the shrinking parameter, respectively; V_c depicts the mass transpiration parameter, in which V_c > 0 implies the suction, V_c < 0 represents the injection, and V_c = 0 conveys no permeability; and

and λ₂ = A₂(a/ν_f) are the first- and second-order velocity slip parameters.

Mathematical models of thermophysical properties of advanced tetra hybrid nanoparticles are depicted as follows [17, 18, 28].

Dynamic viscosity is given as follows:

(19)

Density is given as follows:

(20)

Heat capacity is given as follows:

(21)

Thermal conductivity is given as follows:

(22)

Electrical conductivity is given as follows:

(23)

Here, , and σ_f are forceful dynamic viscosity, density, heat capability, thermal conductivity, and electrical conductivity of the base fluid. ρ_s1, ρ_s2, ρ_s3, and ρ_s4, , κ_s1, κ_s2, κ_s3, and κ_s4, σ_s1, σ_s2, σ_s3, and σ_s4 are the densities, capacities, heat conductivities, and electrical conductivities of the used nanoparticles. ϕ₁, ϕ₂, ϕ₃, and ϕ₄ are the solid volume fractions of the first, second, third, and fourth nanoparticles.

3. Analytical Procedure

3.1. Solution for Momentum

In addition to the findings outlined in [26] and the genuine exponential-type physical solutions depicted, the general shape of the solution is as follows:

(24)

Inserting equation (24) into (15) gives the following biquadratic algebraic equations in terms of α:

(25)

where

(26)

The relevant four-root algebraic equation (25) is exactly demonstrated properly by

(27)

and

(28)

with the dummy variables:

(29)

It should be noted that because the square roots may provide complex values, the solutions provided in equations (27) and (28) may or may not exist based on the values of the pertinent physical parameters. Note that, according to α₂, there is only one solution for d > 0. Moreover, for d < 0 given by the α₄, there is another solution that arises.

After extracting the proper roots (positively) from equations (27) and (28), after differentiating (19), the velocity profile for d becomes

(30)

The physical meaning of the skin friction ratio is offered directly by

(31)

3.2. Solution for Energy

The energy equation (16) can be rewritten as

(32)

To obtain a precise solution for equation (16), we incorporate an intermediate variable:

(33)

and equation (32) becomes

(34)

where

(35)

and

(36)

Both boundary conditions take the forms:

(37)

Equation (34) constitutes a nonhomogeneous BVP. Denoting the solution of equation (34) by

(38)

here θ_c(ζ) is the complementary function and θ_p(ζ) is the particular solution of equation (34).

Considering the homogeneous part of equation (34):

(39)

Consequently, the power solutions of equation (39) are evaluated through the Frobenius approach:

(40)

Following the derivative of the first- and second-order equations (40) wrt ζ, equation (40) is defined as

(41)

If r = 0, then the lowest (r − 1) term of the above equation (41) yields

(42)

The value of the δ becomes

(43)

Therefore, for the prescribed surface temperature (PST) case, the complementary solution of equation (39) is

(44)

and here is the particular solution form as obtained as follows:

(45)

where

(46)

Thus, the solution of equation (34) becomes

(47)

In light of the PST case, the ultimate solution of the energy equation in terms of η is expressed in hypergeometric function:

(48)

For the prescribed heat flux (PHF) case, the solution of equation (32) is

(49)

For both PST and PHF cases, equations (48) and (49) provide exact solutions for the energy equation.

3.3. Solution for Mass

Equation (17) can be expressed in the following form:

(50)

To determine the exact solutions for the aforementioned equation (50), we initiate a variable transformation technique:

(51)

Thus, equation (50) can be written as

(52)

where

(53)

with BCs taking the forms:

(54)

Therefore, for the prescribed surface concentration (PSC) case, the solution in terms of η becomes

(55)

where

(56)

Finally, the solution for the prescribed mass flux (PMF) case is

(57)

In this part, we achieved an exact solution for both energy and mass equations in terms of hypergeometric function. Move on to the next part, where we have to discuss the present issues and their results.

4. Graphical Description

In this work, we utilized the four different types of nanoparticles (Al₂O₃+Fe₃O₄+TiO₂+Cu/H₂O) in base fluid H₂O that flows over a permeable stretching/shrinking sheet with a slip model. In the analytical inspection of the present mathematical model, we deliberated the impression of controlled dimensionless parameters on innumerable values on and θ^′(0) displayed through graphically. The primary goal of the present study is to explore the use of THNF to boost the thermal transfer rate. It has been observed that THNF is more efficient for improving the rate of heat transfer. The thermophysical characteristics of the H₂O and present nanoparticles are provided in Table 1, where the Prandtl number of the base fluid is kept at 6.2. We adopt constant values for the controlling parameters throughout the computation: 0.01 ≤ ϕ₁ + ϕ₂ + ϕ₃ + ϕ₄ ≤ 0.1, 0.5 ≤ M ≤ 24, −1 ≤ V_c ≤ 2, 0.1 ≤ β ≤ 2, −1.5 ≤ λ₁ ≤ 1, −3 ≤ λ₂ ≤ 1, 0.1 ≤ Da⁻¹ ≤ 2, 0.1 ≤ N_r ≤ 0.4, 0.1 ≤ E_c ≤ 4, 0.2 ≤ S_c ≤ 4, 0.02 ≤ K ≤ 10, 0.1 ≤ λ ≤ 4, and −0.37 ≤ Q ≤ 0.37 are employed to achieve the desired accuracy and convergence. The preparation of tetra nanoparticles is shown in Figure 2.

Table 1. The thermophysical characteristics of water and tetra hybrid nanoparticles [17, 18, 59].

Properties	Water	Al₂O₃	Fe₃O₄	TiO₂	Cu
Density ρ(kgm⁻³)	997.1	3970	5180	4250	8933
Specific heat (Jkg⁻¹K⁻¹)	4180	765	670	686.5	385
Heat conductivity (Wm⁻¹K⁻¹)	0.613	40	9.7	8953	401
Electrical conductivity (Ωm)⁻¹	5.5 × 10⁶	5.96 × 10⁷	2.5 × 10⁻⁴	2.6 × 10⁶	5.96 × 10⁷
Prandtl number Pr	6.7	—	—	—	—

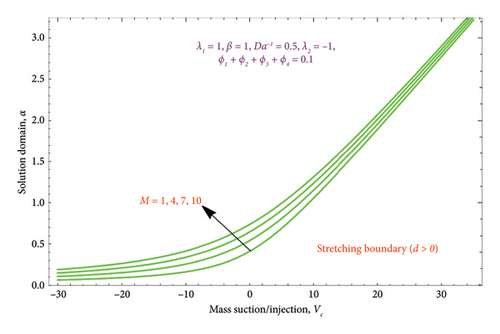
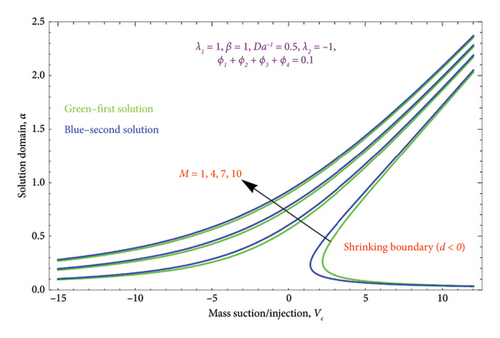
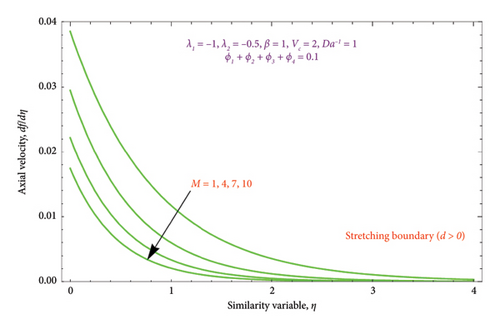
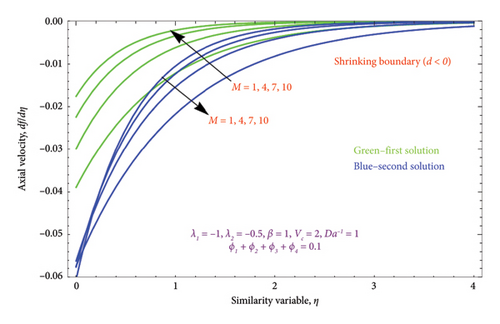
The region of solution for α and the consequence of magnetic strength M are shown in Figures 3(a) and 3(b), which depict the d > 0 and the d < 0, respectively. Raising M influences the value of α to rise as well. Additionally, as predicted by equation (20), there are several solutions for d = −1 and a unique solution for d = 1, and the area of multiple solutions spreads as M grows. Figures 4(a) and 4(b) demonstrate the key characteristics of magnetic number M on the velocity profile. For d > 0, it is observed in Figure 4(a) that as the velocity component declines, it enhances the magnetic number M. Physically, due to the presence of a magnetic field, an opposing sort of force (such as Lorentz force) will be developed in the nanoparticle flow. This force tends to lower the nanoparticle velocity. Figure 4(b) is drawn to witness the effect of M on dimensionless velocity profile (df/dη). Curves indicate that the strength of the (df/dη) in the first solution expands as the entities of M rise; however, in the second solution, they behave oppositely.

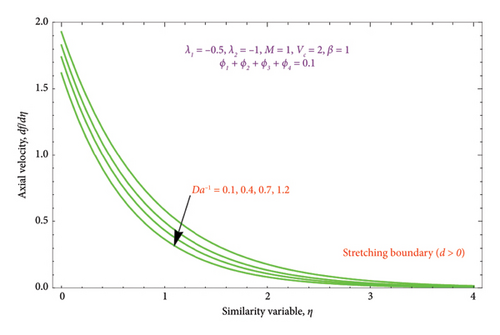
Figures 5(a) and 5(b) are drawn to analyze the upshot of Da⁻¹ on the velocity profile (df/dη). For d > 0, it is noted from Figure 5(a) that the magnitude of the Da⁻¹ rises by lowering the fluid velocity. It happens because there is a porous medium in the flow field, which retards the fluid velocity more and, as a result, thins the boundary layer. Similarly, from Figure 5(b), it can be seen that dimensionless velocity increases by increasing the strength of the Da⁻¹ in the first solution. The second solution shows the opposite behavior. As the Da⁻¹ parameter rises, decreasing velocity profiles and BL are seen. This could be because of the incorporation of nanoparticles into the biviscous Bingham fluid and the resistance force of the porous matrix, which will slow down the flow.

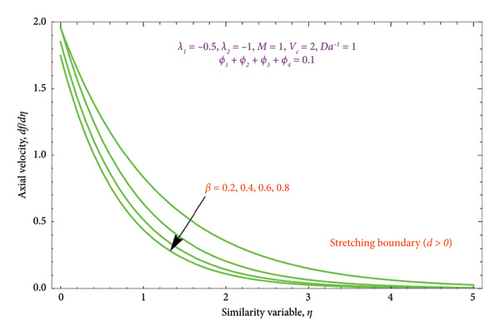
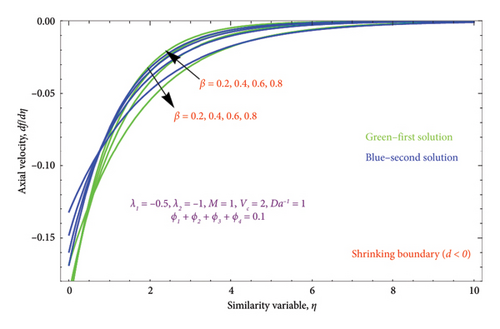
Figures 6(a) and 6(b) depict the performance of the biviscous Bingham fluid parameter β on the velocity profile for both cases of d > 0 and d < 0. It is evident from Figure 6(a) that rises in quantity of β lowers the thickness of BL. As a result, the nanoparticle movements decelerate away from the surface, resulting in a thinner BL as β rises. The dual character of the solution for various values of β is displayed in Figure 6(b). For the second solution, it is found that the BL thickness of the velocity function falls gradually as the Bingham parameter rises, but for the first solution, it exhibits a slightly rising behavior.

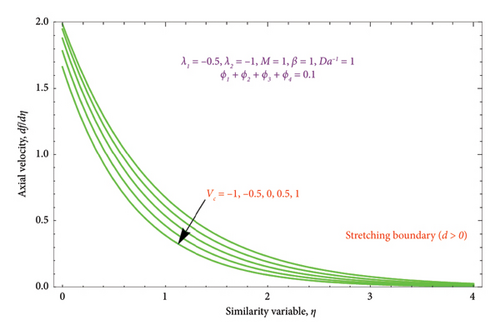
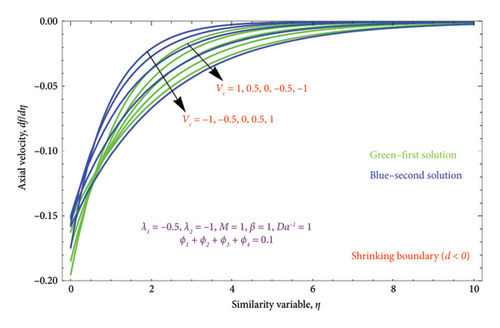
Figures 7(a) and 7(b) are constructed for the variation of the mass suction/injection parameter V_c on the dimensionless velocity profile. Figure 7(a) shows that the nature of the flow velocity declines when the strength of the V_c rises. As a result, the low pressure at the inlet face permits liquid to pass through the media. This is because elevated V_c parameters affect both the BL and momentum BL thicknesses. The suction V_c = 0.5, 1 depicts the thinner effect, whereas V_c = −1, −0.5 signifies the thicker effect on velocity. Figure 7(b) displays the dual nature solution for variation of V_c on the velocity profile. It is observed that the BL thickness of velocity has slight deceleration with improving the V_c values in the first solution, whereas the BL thickness of the velocity function reveals a sharp acceleration in Solution 2.

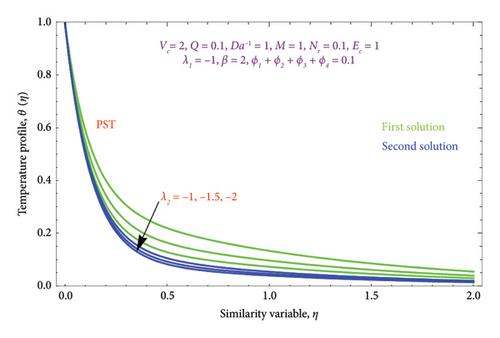
Figures 8(a) and 8(b) and 9(a) and 9(b) are plotted to analyze the effects of the first-order λ₁ and second-order λ₂ slips on the velocity profile. From Figures 8(a) and 9(a), it can be easily noticed that the nanoparticle velocity reduces when entities of |λ₁| and |λ₂| escalate. Hence, the hydrodynamic BL diminishes. In turn, there is a decline in local velocity. The phenomenon occurs because of the physical nature of surface slip, which results in higher slip attendance and lower fluid penetration of the d > 0. Moreover, Figure 8(b) reveals that rising values of |λ₁| resulted in a reduction in the momentum BL thickness and velocity profile for both solutions. Finally, the dual velocity profile for several values of |λ₂| is displayed in Figure 9(b). It is observed from Figure 9(b) that the BL thickness rises with enhancing the |λ₂| values for the first solution. In contrast, the second solution demonstrates the crossing over as it climbs with |λ₂|.

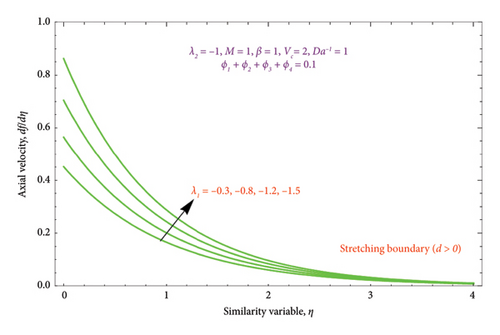
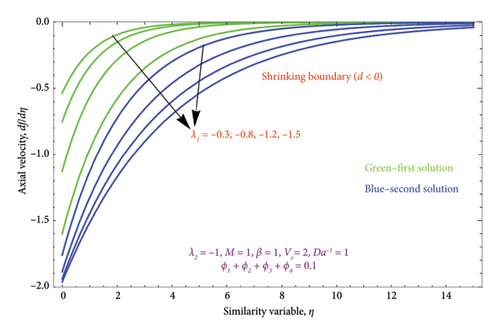
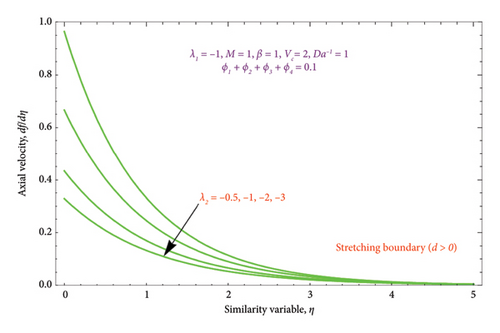
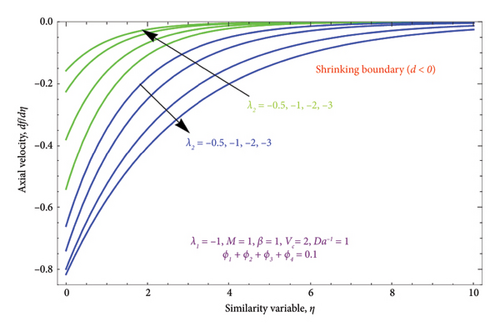
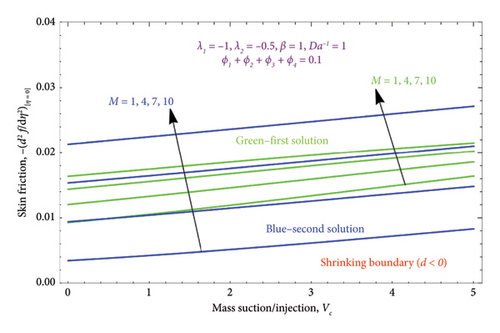
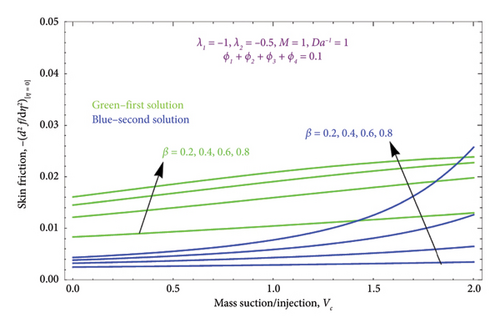
Figure 10 displays the variation of the skin friction profile versus suction/injection parameter V_c for several values controlling parameter M when d < 0. It depicts that the magnitude of the skin friction profile is directly proportional to the M; when M enhances, it also improves the magnitude of the skin friction profile in both solutions. Moreover, Figure 11 is drawn with various values of the biviscous Bingham parameter β on the skin friction profile, while other parameters are kept fixed. From this figure, we observed a massive enhancement in values of β, which enhances the skin friction profile.

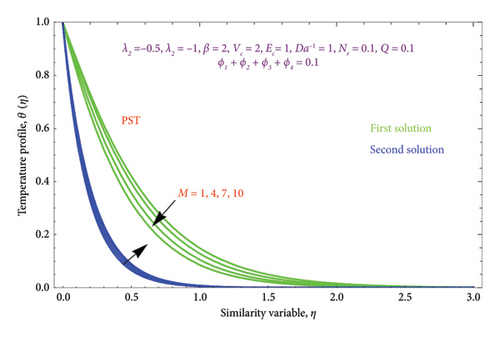
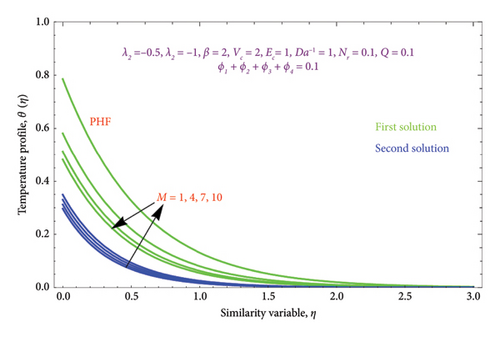
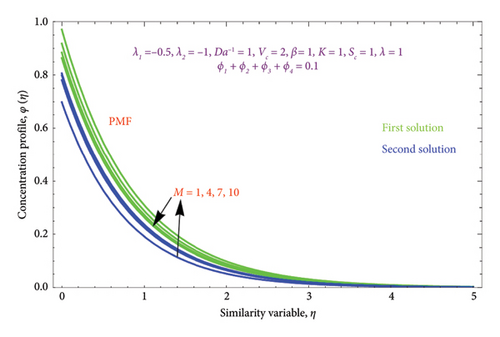
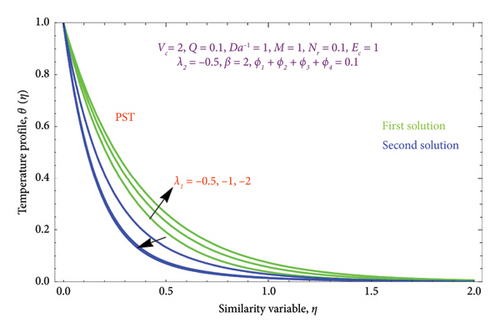
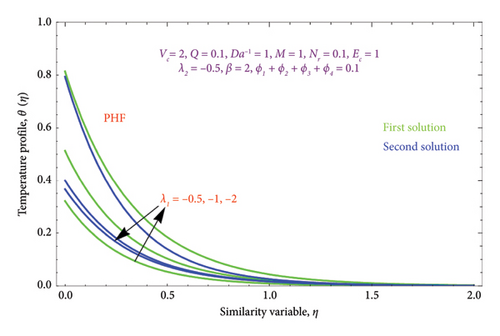
Figures 12(a) and 12(b) and 13(a) and 13(b) illustrated the variation of M on θ(η) with PST and PHF conditions as well as φ(η) profile along with PSC and PMF, respectively, while other parameters are kept fixed. It is seen from Figure 12 that the magnitude of the M escalates with rises in the θ(η) profile in the second solution of both conditions. This can be attributed to the fact that the extra energy needed to move the fluid against the M, which allows the fluid’s temperature to increase. As demonstrated in Figures 12(a) and 12(b) of both BCs, the work is turned into heat energy, which heats the liquid and advances the thermal BL thickness, while the reverse effect occurs in the first solution. Furthermore, we see a growing trend in φ(η) profile by uplifting the values of M in the second solution, whereas the opposite trend was observed in the first solution as exhibited in Figures 13(a) and 13(b).

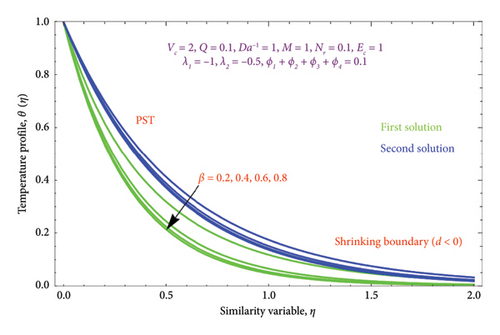
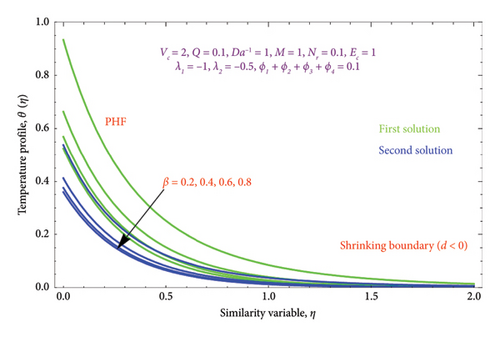
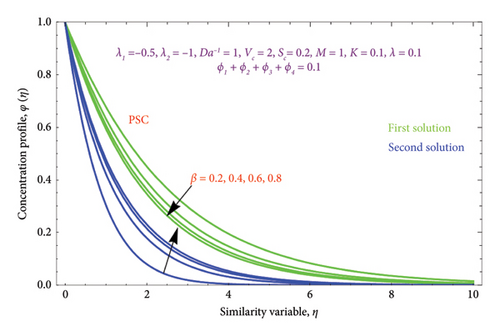
Figures 14(a) and 14(b) and 15(a) and 15(b) reveal the characteristics of β on θ(η) and φ(η) profiles. From Figures 14(a) and 14(b), it is noted that the θ(η) profiles are belittled for incrementing the values of the β. The (Al₂O₃–Fe₃O₄–TiO₂–Cu/H₂O) Bingham nanoparticles yield stress strength that degrades with raising β values, which in turn improves the plastic dynamic viscosity and, as a result, reduces the thickness of the thermal BL in both solutions. Here, we report that the thermal BL thickness of the Bingham tetra nanoparticles is higher than that of the Newtonian liquid. It can be observed that the Bingham tetra nanoparticles behave like a Newtonian liquid when the β (β⟶∞) increases. Consequently, lowering stress boosts fluid flow and diminishes heat transmission. Enhancement in the values of the β reduces the thickness of the φ(η) profile in the first solution, while opposite effects as observed in the second solution are displayed in Figures 15(a) and 15(b).

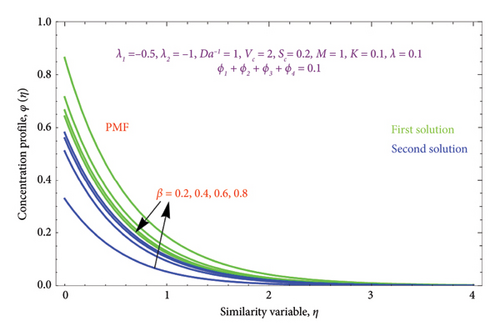
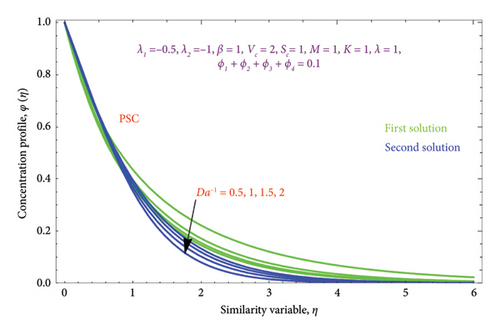
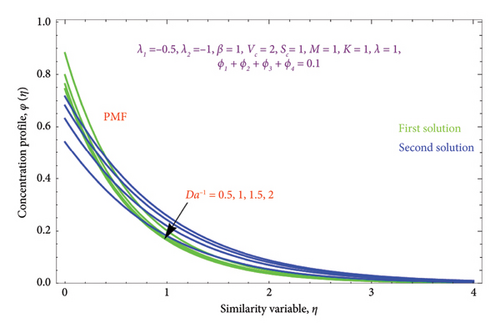
Figures 16(a) and 16(b) and 17(a) and 17(b) present with different values of Da⁻¹ on θ(η) and φ(η) profiles, accordingly. From these figures, it is found that as the Da⁻¹ rises, the fluid temperature and concentration fall in both solutions. This is because a resistive force induced by the Da⁻¹ drops the fluid’s thermal diffusivity and concentration. It indicates an upsurge in the permeable structure of the pores.

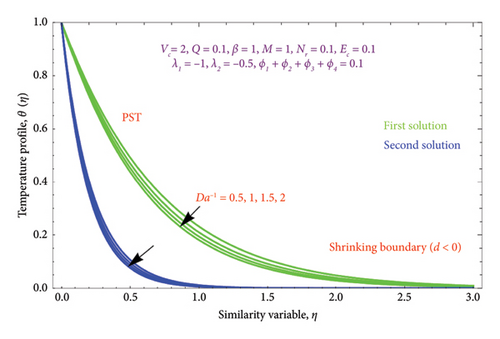
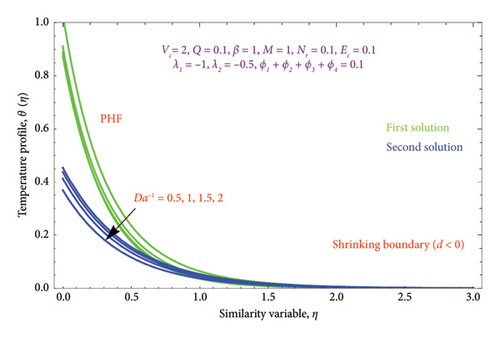
Figures 18(a) and 18(b) and 19(a) and 19(b) interpret the influence of first-order λ₁ and second-order λ₂ slips on θ(η) profile, respectively. From Figures 18(a) and 18(b), we detect an accelerating value of |λ₁| with an increment in thermal BL thickness in the first solution, whereas reverse impact occurs in the second solution. It can be clearly examined that dimensionless thermal and concentration fields declined by raising the values |λ₂| enlightened in Figures 19(a) and 19(b) and 20(a) and 20(b). The upsurges in quantities of first-order slip |λ₁| with enhancing the thickness of the φ(η) profile are interpreted in Figures 21(a) and 21(b).

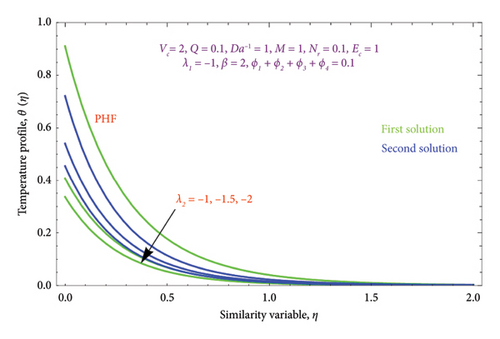
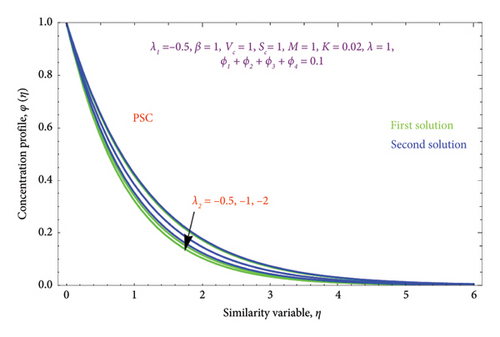
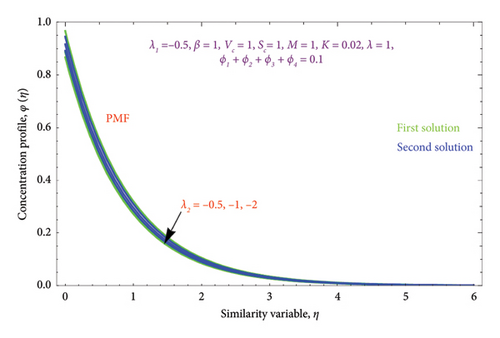
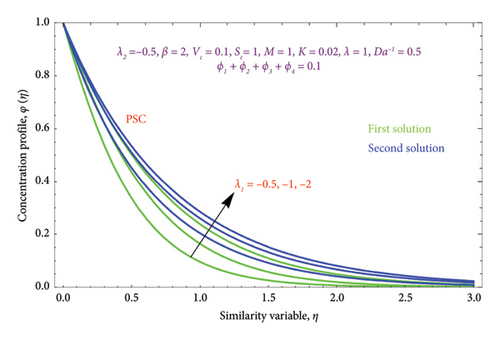
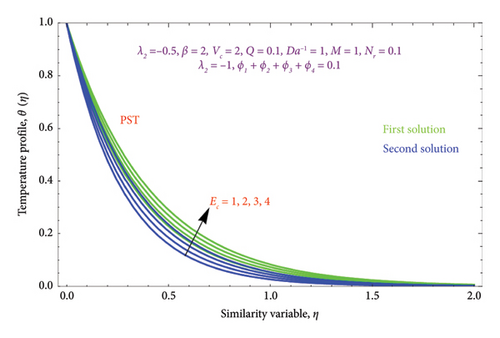
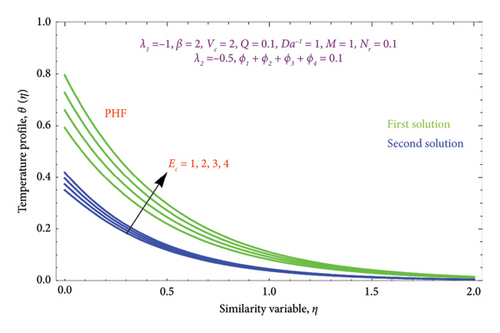
Figures 22(a) and 22(b) are plotted to know the essence of E_c on θ(η) profile for both PST and PHF conditions. We see that the ascending values of the E_c number boost the thermal field in the porous regime in both solutions. The E_c reflects the amount of mechanical energy that turns into heat energy, or heat dissipation, through internal friction. As a result, rising E_c values will result in more thermal energy entering the flow and heating the regime. There is a noticeable temperature overshoot close to the wall for all nonzero values of E_c; as E_c rises, this overshoot somewhat moves into the BL.

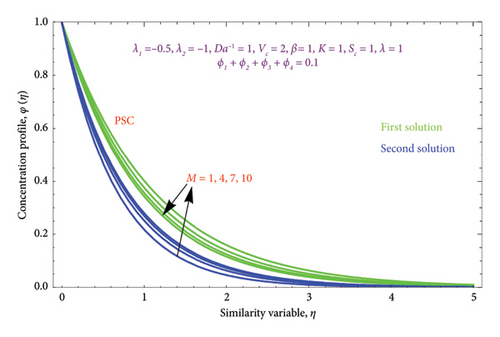
Figures 23(a) and 23(b) are sketched to know the characteristics of S_c on φ(η) profile for both scenarios of PSC and PMF conditions. As the S_c rises, the solute diffusivity decreases, allowing the solutal action to penetrate the solution relatively shallower. Consequently, as S_c expands, the concentration diminishes in both solution branches. Therefore, for lower concentrations of S_c, the solute BL is thicker and vice versa. Figures 24(a) and 24(b) are prepared to demonstrate the effect of heat source/sink Q parameter on θ(η) profile with cases PST and PHF. It is noticed from Figure 24 that the temperature field grows as Q rises in both solutions. Growing Q really allows the thin film’s kinetic energy to escalate, which boosts internal heat.

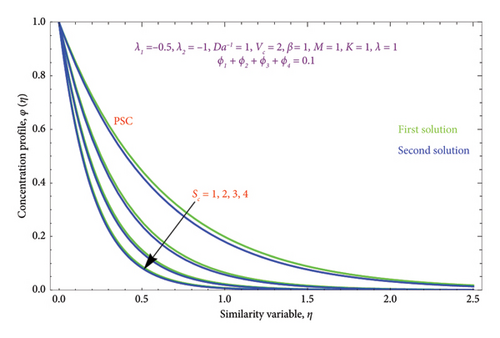
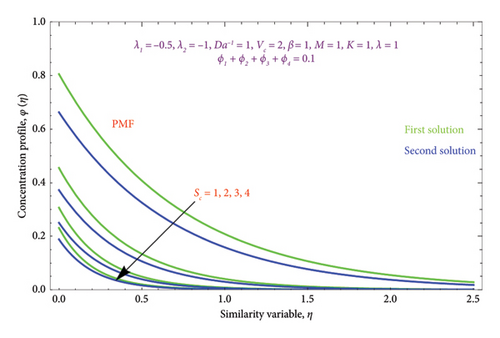
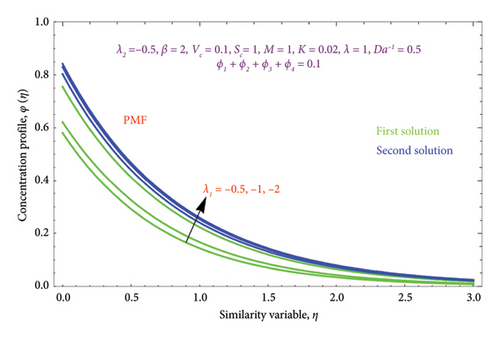
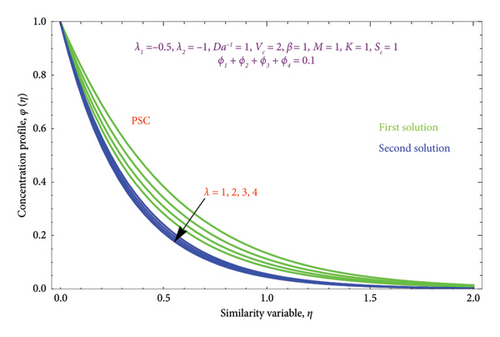
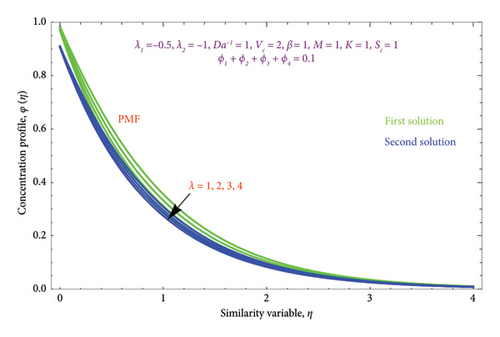
Figure 25 depicts the effect of λ on φ(η) profile with PSC and PMF cases. It is evident from the figure that the φ(η) profile and the λ parameter are inversely related in both solutions. Physically, when λ > 0, it indicates that mass is moving outward from the porous stretched sheet and into the surrounding area.

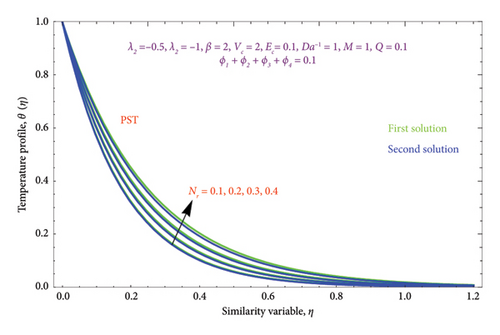
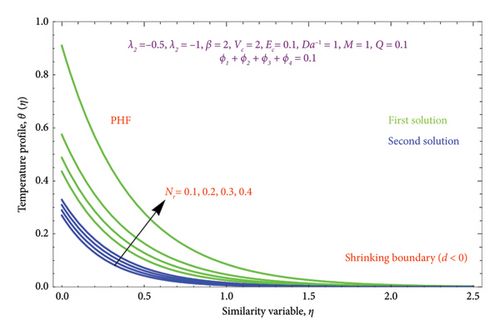
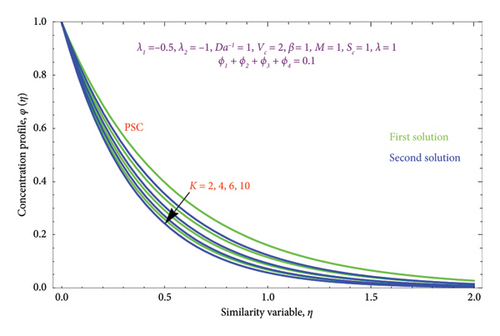
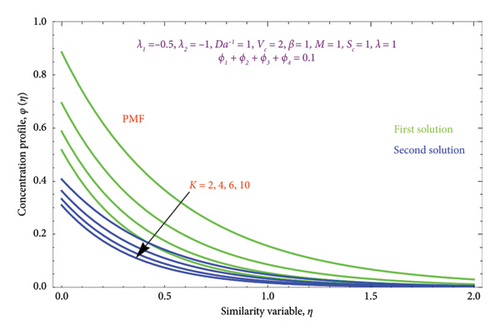
Figures 26(a) and 26(b) are plotted to perceive the impact of N_r on θ(η) profile with PST and PHF conditions. The figure indicates that there is a growing impression of N_r on θ(η) in both solutions. It is well known that the process of radiation and heat transmission generates energy through fluid particles, leading the flow to produce more heat. It is noteworthy to emphasize that the impact of radiation increases with N_r⟶∞ and can be neglected when N_r = 0. The inclusion of the chemical effect parameter K on φ(η) profile is illustrated in Figures 27(a) and 27(b) with PSC and PMF conditions. It has been shown that concentration declines as the chemical reaction K grows in both solutions. This is valid since chemical molecule diffusivity diminishes with greater K values.

5. Final Remarks

Throughout the research, our main attention has been devoted to describing the ramifications of a chemical reaction and radiation on MHD biviscous Bingham tetrananoparticles (Al₂O₃–Fe₃O₄–TiO₂–Cu/H₂O) flowing past a permeable stretching/shrinking sheet subjected to slip BCs. Furthermore, the phenomena of resultant thermal transfer are explored by accounting for radiation, heat dissipation, and heat source/sink impacts. Proposing pertinent similarity transformations on PDEs leads to the development of nonlinear ODEs and is solved analytically. Energy and mass equations are presented in hypergeometric function form. The energy equation is determined with two thermal BL constraints, namely PST and PHF. Additionally, the concentration trends are contrasted using the PSC and PMF BCs. The impact of various parameters on momentum, skin friction, energy, Nusselt number, and concentration profiles is addressed and presented by means of plots. It should be noted that the limiting cases of the current analysis are in good agreement with the existing literature found in Table 2. The findings derived from the discussion are outlined as follows:

•
For the d < 0, two solutions are found.
•
For d > 0, an upsurges in magnitude of M, Da⁻¹, β, V_c, |λ₁|, and |λ₂| yield declines in (df/dη) profile and increment in M and β values with increases in profile.
•
For d < 0, an enrichment in strength of M, Da⁻¹, β, V_c, and |λ₂| is observed in the first solution, whereas opposite trends are observed in the second solution of the (df/dη) profile. While |λ₁| goes up, it reduces the thickness of momentum BL in both solutions.
•
The growth in M and β enhances the θ(η) and φ(η) BL thicknesses in the second solution, whereas a reverse criterion is observed in the first solution, while Da⁻¹ value rises with a decline in the θ(η) and φ(η) profiles in both solution branches.
•
In θ(η) profile, the upward trend is observed in E_c, Q, and N_r quantities with improvement in θ(η). BL is thicker in PST than PHF, whereas φ(η) reduces with increases in entities of S_c, λ, and K in both PSC and PMF conditions.

Table 2. Comparison of the present study and related works by other authors.

Related works by other authors	Fluids	Value of α
Maranna et al. [26]	Non-Newtonian	f(η) = A + B exp(−αη),
Maranna et al. [26]	Non-Newtonian	A = V_c + (d/α + λ₁α² − λ₂α³), with B = (−d/α + λ₁α² − λ₂α³), α⁴ − pα³ + qα² + rα + t = 0
Sadighi et al. [58]	Non-Newtonian
Present work	Non-Newtonian	f(η) = V_c + d((1 − e^−αη)/α(1 + λ₁α − λ₂α²)), ξ₁α⁴ − ξ₂α³ − ξ₃α² + ξ₄α + ξ₅ = 0

It should be noted that the limiting cases of the current analysis are as follows:

•
{Results present work}⟶{Results of Sadighi [58]}.

Nomenclature

a: Constant
A, A₁, A₂: Constants
b₀, b₁, b₂: Constants
B₀: Magnetic field Am⁻¹
C: Concentration function
C_w: Wall concentration
C_∞: Ambient concentration
Da⁻¹: ( = μ_f/ρ_fKa) Inverse Darcy number
E_c: Eckert number
f: Dimensionless function
H: Hypergeometric function
h₁, h₂: Constants
K: Permeability (N/A²)
K_c: ( = (K^∗/a)) Chemical reaction parameter (mol/s)
k^∗: Mean absorption coefficient (m/s³)
k: Constant
M: Magnetic field (kgm⁻¹s⁻¹A⁻¹)
m, m₁, n, n₁: Constants
N_r: Radiation parameter m²s⁻³
Pr: Prandtl number
q_r: Radiative heat flux (kgm²s⁻³)
Q: Heat generation/absorption
p, q: Constants
T: Fluid temperature K
T_w: Wall temperature K
T_∞: Far temperature K
S_c: ( = (ν_f/D)) Schmidt number
S₁, S₂, S₃, S₄: Constants

Greek symbol

α: Solution domain
ξ, ξ₁, ξ₂, ξ₃, ξ₄: Constants
ζ: Constants
μ_f: Dynamic viscosity (kg/ms)
ρ_f: Density of base fluid (kg/m³)
σ_f: Electrical conductivity (S/m)
σ^∗: Stefan–Boltzmann constant (Wm⁻²K)
κ_f: Thermal conductivity (W/mK)

Abbreviations

PDEs: Partial differential equations
ODEs: Ordinary differential equations
MHD: Magnetohydrodynamics
nf: Nanofluid
tnf: Ternary nanofluid
THNFs: Tetrahybrid nanofluids
NN: Non-Newtonian
BL: Boundary layer
PST: Prescribed surface temperature
PHF: Prescribed heat flux
PSC: Prescribed surface concentration
PMF: Prescribed mass flux

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was funded by the National Research Foundation of Korea (Grant Number NRF2022-R1A2C2002799). The work of the author H. N. Huang is partially supported under Grant No. MOST 110-2115-M-029-002 and nice hospitality.

Acknowledgements

This work was funded by the Grant NRF2022-R1A2C2002799 of the National Research Foundation of Korea. The author T. Maranna acknowledged the financial assistance received from the Karnataka Science and Technology Society (KSTePS) under the program of Karnataka DST-Ph.D. Fellowship for Science and Engineering: DST/KSTePS/Ph.D. Fellowship/MP-07:2023-24. The work of the author H. N. Huang was partially supported under Grant No. MOST 110-2115-M-029-002 and nice hospitality.

Open Research

Data Availability Statement

Data that support the findings of this study are available from the corresponding authors upon reasonable request.

References

1 Bingham E. C., Fluidity and Plasticity, 1922, McGraw-Hill Book Company, Inc.
Google Scholar
2 Nakamura M. and Sawada T., Numerical Study on the Laminar Pulsatile Flow of Slurries, Journal of Non-newtonian Fluid Mechanics. (1987) 22, no. 2, 191–206, https://doi.org/10.1016/0377-0257(87)80035-6, 2-s2.0-0013764010.
10.1016/0377-0257(87)80035-6
CAS Web of Science® Google Scholar
3 Basavarajappa M., Myson S., and Vajravelu K., Study of Multilayer Flow of a Bi-viscous Bingham Fluid Sandwiched Between Hybrid Nanofluid in a Vertical Slab With Nonlinear Boussinesq Approximation, Physics of Fluids. (2022) 34, no. 12, https://doi.org/10.1063/5.0123131.
10.1063/5.0123131
Web of Science® Google Scholar
4 Dandapat B. S., Singh S. K., and Maity S., Thin Film Flow of Bi-Viscosity Liquid Over an Unsteady Stretching Sheet: An Analytical Solution, International Journal of Mechanical Sciences. (2017) 130, 367–374, https://doi.org/10.1016/j.ijmecsci.2017.06.027, 2-s2.0-85021066190.
10.1016/j.ijmecsci.2017.06.027
Web of Science® Google Scholar
5 Srivastava S. K., Laminar Flow of a Bingham Fluid over a Rotating Disk, International Journal Mathematics Invention. (2014) 2, 1–7.
Google Scholar
6 Islam M. M., Mollah M. T., Khatun S., Ferdows M., and Alam M. M., Unsteady Viscous Incompressible Bingham Fluid Flow through a Parallel Plate, Inventions. (2019) 4, no. 3, https://doi.org/10.3390/inventions4030051, 2-s2.0-85073474212.
10.3390/inventions4030051
Google Scholar
7 Choi S. U. and Eastman J. A., Enhancing Thermal Conductivity of Fluids and With Nanoparticles, ASME Intenat Mech. (1995) 66, 99–105.
Google Scholar
8 Mahabaleshwar U. S., Maranna T., and Sofos F., Analytical Investigation of an Incompressible Viscous Laminar Casson Fluid Flow Past a Stretching/shrinking Sheet, Scientific Reports. (2022) 12, no. 1, https://doi.org/10.1038/s41598-022-23295-6.
10.1038/s41598-022-23295-6
Web of Science® Google Scholar
9 Ghosh R., Agbaje T. M., Mondal S., and Shaw S., Bio-Convective Viscoelastic Casson Nanofluid Flow Over a Stretching Sheet in the Presence of Induced Magnetic Field with Cattaneo-Christov Double Diffusion, International Journal of Biomathematics. (2022) 15, no. 03, https://doi.org/10.1142/s1793524521500996.
10.1142/S1793524521500996
Web of Science® Google Scholar
10 Waini I., Ishak A., and Pop I., Transpiration Effects on Hybrid Nanofluid Flow and Heat Transfer over a Stretching/Shrinking Sheet With Uniform Shear Flow, Alexandria Engineering Journal. (2020) 59, no. 1, 91–99, https://doi.org/10.1016/j.aej.2019.12.010.
10.1016/j.aej.2019.12.010
Web of Science® Google Scholar
11 Kamis N. I., Basir Md.F. Md., Shafie S., Khairuddin T. K. A., and Jiann L. M., Suction Effect on an Unsteady Hybrid Nanofluid Film Past a Stretching Sheet with Heat Transfer Analysis, IOP Conf. Mater. Sci. Eng.(2021) 1078.
Google Scholar
12 Sahoo R. R., Heat Transfer and Second Law Characteristics of Radiator With Dissimilar Shape Nanoparticle-Based Ternary Hybrid Nanofluid, Journal of Thermal Analysis and Calorimetry. (2021) 146, no. 2, 827–839, https://doi.org/10.1007/s10973-020-10039-9.
10.1007/s10973-020-10039-9
CAS Web of Science® Google Scholar
13 Priyadharshini P., Archana M. V., Shah N. A., and Alshehri M. H., Ternary Hybrid Nanofluid Flow Emerging on a Symmetrically Stretching Sheet Optimization with Machine Learning Prediction Scheme, Symmetry. (2023) 15, no. 6, https://doi.org/10.3390/sym15061225.
10.3390/sym15061225
PubMed Web of Science® Google Scholar
14 Manjunatha S., Puneeth V., Gireesha B. J., and Chamkha A., Theoretical Study of Convective Heat Transfer in Ternary Nanofluid Flowing Past a Stretching Sheet, J. Appl. Comput. Mech.(2021) 8, 1279–1286.
Web of Science® Google Scholar
15 Shah N. A., Wakif A., El-Zahar E. R., Thumma T., and Yook S. J., Heat Transfers Thermodynamic Activity of a Second-Grade Ternary Nanofluid Flow over a Vertical Plate with Atangana-Baleanu Time-Fractional Integral, Alexandria Engineering Journal. (2022) 61, no. 12, 10045–10053, https://doi.org/10.1016/j.aej.2022.03.048.
10.1016/j.aej.2022.03.048
Web of Science® Google Scholar
16 Dezfulizadeh A., Aghaei A., Joshaghani A. H., and Najafizadeh M. M., An Experimental Study on Dynamic Viscosity and Thermal Conductivity of Water-Cu-SiO2- MWCNT Ternary Hybrid Nanofluid and the Development of Practical Correlations, Powder Technology. (2021) 389, 215–234, https://doi.org/10.1016/j.powtec.2021.05.029.
10.1016/j.powtec.2021.05.029
CAS Web of Science® Google Scholar
17 Sajid T., Jamshed W., Algarni S. et al., Catalysis Reaction Influence on 3D Tetra Hybrid Nanofluid Flow via Oil Rig Solar Panel Sheet: Case Study towards Oil Extraction, Case Studies in Thermal Engineering. (2023) 49, https://doi.org/10.1016/j.csite.2023.103261.
10.1016/j.csite.2023.103261
Web of Science® Google Scholar
18 Sajid T., Gari A. A., Jamshed W. et al., Case Study of Autocatalysis Reactions on Tetra Hybrid Binary Nanofluid Flow via Riga Wedge: Biofuel Thermal Application, Case Studies in Thermal Engineering. (2023) 47, https://doi.org/10.1016/j.csite.2023.103058.
10.1016/j.csite.2023.103058
Web of Science® Google Scholar
19 Kopp M. I., Mahabaleshwar U. S., and Perez L. M., Exact Solution of the MHD Three-Dimensional Casson Flow of a Ternary Hybrid Nanofluid over a Porous Stretching/Shrinking Surface With Mass Transpiration, Journal of Physical Studies. (2023) 27, 1–11.
10.30970/jps.27.2402
Google Scholar
20 Khan D., Hussien M. A., Elsiddieg A. M. A., Lone S. A., and Hassan A. M., Exploration of Generalized Two-phase Free Convection Magnetohydrodynamic Flow of Dusty Tetra-Hybrid Casson Nanofluid Between Parallel Microplates, Nanotechnology Reviews. (2023) 12, no. 1, https://doi.org/10.1515/ntrev-2023-0102.
10.1515/ntrev-2023-0102
Web of Science® Google Scholar
21 Teh Y. Y. and Ashgar A., Three Dimensional MHD Hybrid Nanofluid Flow With Rotating Stretching/Shrinking Sheet and Joule Heating, CFD Letters. (2021) 13, no. 8, 1–19, https://doi.org/10.37934/cfdl.13.8.119.
10.37934/cfdl.13.8.119
Google Scholar
22 Kumaresan E., Vijaya Kumar A. G., and Rushi Kumar B., An Exact Solution on Unsteady MHD Free Convection Chemically Reacting Silver Nanofluid Flow Past an Exponentially Accelerated Vertical Plate Through Porous Medium, IOP Conference Series: Materials Science and Engineering. (2017) 263, https://doi.org/10.1088/1757-899x/263/6/062018, 2-s2.0-85037810247.
10.1088/1757-899X/263/6/062018
Google Scholar
23 Kamran A., Azhar E., and Atif S. M., Magnetic Dipole Interactions With Tangent Hyperbolic Ferromagnetic Fluid Over a Moving Plate: A Numerical Study, Numerical Heat Transfer, Part B: Fundamentals. (2024) 1–17, https://doi.org/10.1080/10407790.2023.2300687.
10.1080/10407790.2023.2300687
Web of Science® Google Scholar
24 Vishalakshi A. B., Mahabaleshwar U. S., and Sarris I. E., An MHD Fluid Flow over a Porous Stretching/shrinking Sheet With Slips and Mass Transpiration, Micromachines. (2022) 13, no. 1, https://doi.org/10.3390/mi13010116.
10.3390/mi13010116
PubMed Web of Science® Google Scholar
25 Azhar E., Kamran A., and Atif S. M., Exploring the Dynamics of Natural Convective Prandtl Fluid Flow Subjected to Induced Magnetic Field, Waves in Random and Complex Media. (2022) 1–17, https://doi.org/10.1080/17455030.2022.2089931.
10.1080/17455030.2022.2089931
Web of Science® Google Scholar
26 Maranna T., Sachhin S. M., Mahabaleshwar U. S., and Hatami M., Impact of Navier’s Slip and MHD on Laminar Boundary Layer Flow With Heat Transfer for Non-Newtonian Nanofluid Over a Porous Media, Scientific Reports. (2023) 13, no. 1, https://doi.org/10.1038/s41598-023-39153-y.
10.1038/s41598-023-39153-y
PubMed Web of Science® Google Scholar
27 Mahabaleshwar U. S., Maranna T., Perez L. M., Bognar G. V., and Oztop H. F., An Impact of Radiation on Laminar Flow of Dusty Ternary Nanofluid over Porous Stretching/Shrinking Sheet With Mass Transpiration, Results in Engineering. (2023) 18, https://doi.org/10.1016/j.rineng.2023.101227.
10.1016/j.rineng.2023.101227
PubMed Web of Science® Google Scholar
28 Abbas W., Bani-Fwaz M. Z., and Asogwa K. K., Thermal Efficiency of Radiated Tetra-Hybrid Nanofluid [(Al₂O₃-CuO-TiO₂-Ag)/water]_tetra under Permeability Effects Over Vertically Aligned Cylinder Subjected to Magnetic Field and Combined Convection, Science Progress. (2023) 106, 1–17.
Google Scholar
29 Maranna T., Mahabaleshwar U. S., Ravichandra Nayakar S. N., Sarris I. E., and Souayeh B., An Influence of Radiation and Magnetohydrodynamic Flow of Hybrid Nanofluid Past a Stretching/shrinking Sheet With Mass Transpiration, Zeitschrift für Angewandte Mathematik und Mechanik. (2023) 103, no. 12, https://doi.org/10.1002/zamm.202300140.
10.1002/zamm.202300140
Web of Science® Google Scholar
30 Mohana C. and Rushi Kumar B., Nanoparticle Shape Effects on MHD Cu-Water Nanofluid Flow over a Stretching Sheet With Thermal Radiation and Heat Source/sink, International Journal of Modern Physics B. (2023) 38, no. 10, https://doi.org/10.1142/s0217979224501510.
10.1142/s0217979224501510
Web of Science® Google Scholar
31 Mohana C. M. and Kumar B. R., Nanoparticle Shape Effects on Hydromagnetic Flow of Cu-Water Nanofluid over a Nonlinear Stretching Sheet in a Porous Medium with Heat Source, Thermal Radiation, and Joule Heating, ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik. (2024) 104, no. 1, https://doi.org/10.1002/zamm.202300188.
10.1002/zamm.202300188
Web of Science® Google Scholar
32 Maranna T., Mahabaleshwar U. S., Perez L. M., and Manca O., Flow of Viscoelastic Ternary Nanofluid Over a Shrinking Porous Medium With Heat Source/sink and Radiation, Thermal Science and Engineering Progress. (2023) 40, https://doi.org/10.1016/j.tsep.2023.101791.
10.1016/j.tsep.2023.101791
Web of Science® Google Scholar
33 Shobha K. C. and Patil Mallikarjun B., Effect of Non-Linear Thermal Radiation on Flow of Williamson Nanofluid in a Vertical Porous Channel with Heat Source or Sink by Using Adomian Decomposition Method, Journal Nanofluids. (2022) 11, no. 1, 39–47, https://doi.org/10.1166/jon.2022.1822.
10.1166/jon.2022.1822
Google Scholar
34 Ilya A., Ashraf M., Ali A., Shah Z., Kumam P., and Thounthong P., Heat Source and Sink Effects on Periodic Mixed Convection Flow Along the Electrically Conducting Cone Inserted in Porous Medium, PLoS One. (2021) 23.
Google Scholar
35 Brinkman H. C., Heat Effects in Capillary Flow, I, Applied Scientific Research. (1951) 2, no. 1, 120–124, https://doi.org/10.1007/bf00411976, 2-s2.0-34250592892.
10.1007/BF00411976
Web of Science® Google Scholar
36 Mahabaleshwar U. S., Vishalakshi A. B., and Hatami M., MHD Micropolar Fluid Flow over a Stretching/shrinking Sheet With Dissipation of Energy and Stress Work Considering Mass Transpiration and Thermal Radiation, International Communications in Heat and Mass Transfer. (2022) 133, https://doi.org/10.1016/j.icheatmasstransfer.2022.105966.
10.1016/j.icheatmasstransfer.2022.105966
Web of Science® Google Scholar
37 Muyungi W. N., Mkwizu M. H., and Masanja V. G., The Effect of Navier Slip and Skin Friction on Nanofluid Flow in a Porous Pipe, Engineering, Technology & Applied Science Research. (2022) 12, no. 2, 8342–8348, https://doi.org/10.48084/etasr.4763.
10.48084/etasr.4763
Web of Science® Google Scholar
38 Aslani K. E., Mahabaleshwar U. S., Sakanaka P. H., and Sarris I. E., Effect of Partial Slip and Radiation on Liquid Film Fluid Flow over an Unsteady Porous Stretching Sheet with Viscous Dissipation and Heat Source/Sink, Journal of Porous Media. (2021) 24, no. 11, 1–15, https://doi.org/10.1615/jpormedia.2021035873.
10.1615/JPorMedia.2021035873
Web of Science® Google Scholar
39 Padmaja K. and Rushi Kumar B., Viscous Dissipation and Chemical Reaction Effects on MHD Nanofluid Flow Over a Vertical Plate in a Rotating System, ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik. (2023) 103, no. 9, https://doi.org/10.1002/zamm.202200471.
10.1002/zamm.202200471
Web of Science® Google Scholar
40 Atif S. M., Hussain S., and Sagheer M., Effect of Viscous Dissipation and Joule Heating on MHD Radiative Tangent Hyperbolic Nanofluid With Convective and Slip Conditions, Journal of the Brazilian Society of Mechanical Sciences and Engineering. (2019) 41, no. 4, https://doi.org/10.1007/s40430-019-1688-9, 2-s2.0-85063473905.
10.1007/s40430-019-1688-9
Web of Science® Google Scholar
41 Atif S. M., Shah S., and Kamran A., Effect of MHD on Casson Fluid With Arrhenius Activation Energy and Variable Properties, Scientia Iranica. (2021) 0, no. 0, 3570–3581, https://doi.org/10.24200/sci.2021.57873.5452.
10.24200/sci.2021.57873.5452
Google Scholar
42 Vanitha G. P., Mahabaleshwar U. S., Hatami M., and Yang X., Heat and Mass Transfer of Micropolar Liquid Flow Due to Porous Stretching/Shrinking Surface With Ternary Nanoparticles, Scientific Reports. (2023) 13, no. 1, https://doi.org/10.1038/s41598-023-29469-0.
10.1038/s41598-023-29469-0
Web of Science® Google Scholar
43 Mumtaz M., Islam S., Ullah H., and Shah Z., Chemically Reactive MHD Convective Flow and Heat Transfer Performance of Ternary Hybrid Nanofluid Past a Curved Stretching Sheet, Journal of Molecular Liquids. (2023) 390, https://doi.org/10.1016/j.molliq.2023.123179.
10.1016/j.molliq.2023.123179
Web of Science® Google Scholar
44 Njingang Ketchate C. G., Tiam Kapen P., Madiebie-Lambou I. et al., Chemical Reaction, Dufour and Soret Effects on the Stability of Magnetohydrodynamic Blood Flow Conveying Magnetic Nanoparticle in Presence of Thermal Radiation: A Biomedical Application, Heliyon. (2023) 9, no. 1, https://doi.org/10.1016/j.heliyon.2023.e12962.
10.1016/j.heliyon.2023.e12962
PubMed Google Scholar
45 Vanitha G. P., Mahabaleshwar U. S., and Shadloo M., An Impact of Richardson Number on Mixed Convective Flow of Nanoparticles With Heat and Mass Transfer, International Communications in Heat and Mass Transfer. (2022) 139, https://doi.org/10.1016/j.icheatmasstransfer.2022.106441.
10.1016/j.icheatmasstransfer.2022.106441
Web of Science® Google Scholar
46 Padmaja K. and Kumar B. R., Higher Order Chemical Reaction Effects on Cu−H2O Nanofluid Flow over a Vertical Plate, Scientific Reports. (2022) 12.
Web of Science® Google Scholar
47 Humane P. P., Patil V. S., and Patil A. B., Effects of Radiation and Chemical Reaction on MHD Casson Nanofluid Flow Past a Porous Stretching Surface, Computational Thermal Sciences: International Journal. (2023) 15, no. 5, 1–15, https://doi.org/10.1615/computthermalscien.2023038739.
10.1615/ComputThermalScien.2023038739
Web of Science® Google Scholar
48 Atif S. M., Ganie A. H., Khan I., Andualem M., and Safaei M., Unsteady MHD Tangent Hyperbolic Nanofluid Past a Wedge Filled With Gyrotactic Micro-organism, Mathematical Problems in Engineering. (2022) 2022, 1–14, https://doi.org/10.1155/2022/4025831.
10.1155/2022/4025831
Web of Science® Google Scholar
49 Atif S. M., Khan W. A., Abbas M., and Rashid U., Biconvection Magnetohydrodynamic Tangent Hyperbolic Nanofluid Flow With Quartic Chemical Reaction Past a Paraboloid Surface, Computer Modeling in Engineering and Sciences. (2021) 130, 205–220.
10.32604/cmes.2022.017304
Google Scholar
50 Atif S. M., Kamran A., and Shah S., MHD Micropolar Nanofluid with Non-fourier and Non-fick’s Law, International Communications in Heat and Mass Transfer. (2021) 122, https://doi.org/10.1016/j.icheatmasstransfer.2021.105114.
10.1016/j.icheatmasstransfer.2021.105114
Web of Science® Google Scholar
51 Mahabaleshwar U. S., Sachhin S. M., Perez L. M., and Oztop H. F., An Impact of Inclined MHD on Biviscosity Bingham Hybrid Nanofluid Flow Over Porous Stretching/shrinking Sheet with Heat Transfer, Journal of Molecular Liquids. (2024) 398, https://doi.org/10.1016/j.molliq.2024.124244.
10.1016/j.molliq.2024.124244
Web of Science® Google Scholar
52 Mahabaleshwar U., Maranna T., Perez L. M., and Ravichandra Nayakar S., An Effect of Magnetohydrodynamic and Radiation on Axisymmetric Flow of Non-Newtonian Fluid Past a Porous Shrinking/stretching Surface, Journal of Magnetism and Magnetic Materials. (2023) 571, https://doi.org/10.1016/j.jmmm.2023.170538.
10.1016/j.jmmm.2023.170538
Web of Science® Google Scholar
53 Sajid T., Jamshed W., Eid M. R. et al., Magnetized Cross Tetra Hybrid Nanofluid Passed a Stenosed Artery With Nonuniform Heat Source (Sink) and Thermal Radiation: Novel Tetra Hybrid Tiwari and Das Nanofluid Model, Journal of Magnetism and Magnetic Materials. (2023) 569, https://doi.org/10.1016/j.jmmm.2023.170443.
10.1016/j.jmmm.2023.170443
Web of Science® Google Scholar
54 Venkateswarlu B. and Satya Narayana P. V., Chemical Reaction and Radiation Absorption Effects on the Flow and Heat Transfer of a Nanofluid in a Rotating System, Applied Nanoscience. (2015) 5, no. 3, 351–360, https://doi.org/10.1007/s13204-014-0324-3, 2-s2.0-84963559804.
10.1007/s13204-014-0324-3
CAS Web of Science® Google Scholar
55 Mahabaleshwar U. S., Maranna T., Mishra M., Hatami M., and Sunden B., Radiation Effect on Stagnation Point Flow of Casson Nanofluid Past a Stretching Plate/cylinder, Scientific Reports. (2024) 14, no. 1, https://doi.org/10.1038/s41598-024-51963-2.
10.1038/s41598-024-51963-2
Web of Science® Google Scholar
56 Atif S. M., Hussain S., and Sagheer M., Heat and Mass Transfer Analysis of Time-dependent Tangent Hyperbolic Nanofluid Flow Past a Wedge, Physics Letters A. (2019) 383, no. 11, 1187–1198, https://doi.org/10.1016/j.physleta.2019.01.003, 2-s2.0-85060128464.
10.1016/j.physleta.2019.01.003
CAS Web of Science® Google Scholar
57 Mahabaleshwar U. S., Maranna T., Sachin G. M., Buonomo B., and Manca O., Effect of MHD and Radiation on Biviscous Bingham Fluid Flow on Marangoni Boundary for Heat Source/sink with Chemical Reaction, Case Studies in Thermal Engineering. (2024) 61, https://doi.org/10.1016/j.csite.2024.105105.
10.1016/j.csite.2024.105105
Web of Science® Google Scholar
58 Sadighi S., Afshar H., Jabbari M., and Ahmadi Danesh Ashtiani H., Heat and Mass Transfer for MHD Nanofluid Flow on a Porous Stretching Sheet with Prescribed Boundary Conditions, Case Studies in Thermal Engineering. (2023) 49, https://doi.org/10.1016/j.csite.2023.103345.
10.1016/j.csite.2023.103345
Web of Science® Google Scholar
59 Maheswari C., Ramana R. M., Shaw S. M., Dharmaiah G., and Noeiaghdam S., Numerical Investigation on MHD Forchheimer Flow of Fe₃O₄-H₂O, Cu- H₂O, and Ag- H₂O Nanofluids over Permeable Stretching Sheet with Radiation, Results Eng. (2023) 18.
10.1016/j.rineng.2023.101194
PubMed Web of Science® Google Scholar

Citing Literature

All articles

An Analytical Inspection on Effect of Chemical Reaction and Radiation on MHD Biviscous Bingham Tetra Nanofluid Flow With Accelerated Plate

Abstract

1. Introduction

2. Model Development

2.1. Model Statement and Geometry

2.2. Conversion of Leading Equations

3. Analytical Procedure

3.1. Solution for Momentum

3.2. Solution for Energy

3.3. Solution for Mass

4. Graphical Description

5. Final Remarks

Nomenclature

Greek symbol

Abbreviations

Conflicts of Interest

Funding

Acknowledgements

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

An Analytical Inspection on Effect of Chemical Reaction and Radiation on MHD Biviscous Bingham Tetra Nanofluid Flow With Accelerated Plate

Abstract

1. Introduction

2. Model Development

2.1. Model Statement and Geometry

2.2. Conversion of Leading Equations

3. Analytical Procedure

3.1. Solution for Momentum

3.2. Solution for Energy

3.3. Solution for Mass

4. Graphical Description

5. Final Remarks

Nomenclature

Greek symbol

Abbreviations

Conflicts of Interest

Funding

Acknowledgements

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Related

Information