Volume 2025, Issue 1 8816146

Research Article

Open Access

Integrated Neural Network Analysis of Machining Characteristics in Dry-Turned Al7075/FA_0.9SiC_0.9 Hybrid Composite Using PCD Inserts

Sunil Setia,

Sunil Setia

School of Mechanical Engineering , Lovely Professional University , Phagwara , Punjab , India , lpu.in

Search for more papers by this author

Jarnail Singh,

Jarnail Singh

Department of Mechanical Engineering , University Centre for Research and Development , Chandigarh University , Mohali , India , chandigarhuniversity.ac.in

Search for more papers by this author

Sant Ram Chauhan,

Sant Ram Chauhan

Department of Mechanical Engineering , National Institute of Technology , Hamirpur , India , nita.ac.in

Search for more papers by this author

Nikunj Rachchh,

Nikunj Rachchh

Department of Mechanical Engineering , Faculty of Engineering & Technology , Marwadi University Research Center , Marwadi University , Rajkot , Gujarat , India

Search for more papers by this author

Raman Kumar,

Raman Kumar

orcid.org/0000-0002-5040-7920

University School of Mechanical Engineering , Rayat Bahra University , Kharar , Punjab , India

Faculty of Engineering , Sohar University , Sohar , Oman , soharuni.edu.om

Search for more papers by this author

Abhijit Bhowmik,

Corresponding Author

Abhijit Bhowmik

[email protected]

orcid.org/0000-0001-9409-0972

Department of Additive Manufacturing , Mechanical Engineering , SIMATS , Saveetha Institute of Medical and Technical Sciences , Thandalam , Chennai , India , saveetha.com

Research and Innovation Cell , Bahra University , Distt. Solan, HP , Waknaghat , India , bahrauniversity.edu.in

Search for more papers by this author

Sunil Setia,

Sunil Setia

School of Mechanical Engineering , Lovely Professional University , Phagwara , Punjab , India , lpu.in

Search for more papers by this author

Jarnail Singh,

Jarnail Singh

Department of Mechanical Engineering , University Centre for Research and Development , Chandigarh University , Mohali , India , chandigarhuniversity.ac.in

Search for more papers by this author

Sant Ram Chauhan,

Sant Ram Chauhan

Department of Mechanical Engineering , National Institute of Technology , Hamirpur , India , nita.ac.in

Search for more papers by this author

Nikunj Rachchh,

Nikunj Rachchh

Department of Mechanical Engineering , Faculty of Engineering & Technology , Marwadi University Research Center , Marwadi University , Rajkot , Gujarat , India

Search for more papers by this author

Raman Kumar,

Raman Kumar

orcid.org/0000-0002-5040-7920

University School of Mechanical Engineering , Rayat Bahra University , Kharar , Punjab , India

Faculty of Engineering , Sohar University , Sohar , Oman , soharuni.edu.om

Search for more papers by this author

Abhijit Bhowmik,

Corresponding Author

Abhijit Bhowmik

[email protected]

orcid.org/0000-0001-9409-0972

Department of Additive Manufacturing , Mechanical Engineering , SIMATS , Saveetha Institute of Medical and Technical Sciences , Thandalam , Chennai , India , saveetha.com

Research and Innovation Cell , Bahra University , Distt. Solan, HP , Waknaghat , India , bahrauniversity.edu.in

Search for more papers by this author

First published: 03 July 2025

https://doi.org/10.1155/je/8816146

Academic Editor: Fabio La Foresta

Share a link

Email
Wechat
Bluesky

Abstract

This study presents a comprehensive analysis of the machinability characteristics of an aluminum-based hybrid nanocomposite (Al7075 reinforced with 0.9 wt.% fly ash and 0.9 wt.% SiC) fabricated using an ultrasonically assisted stir-casting technique. Dry turning operations were performed using polycrystalline diamond (PCD) inserts to evaluate the influence of key input parameters—cutting speed, feed rate, depth of cut, and tool nose radius—on output machining regimes, namely, cutting force components and tool tip temperature. The results revealed that increasing cutting speed reduces the cutting force while elevating the tool tip temperature. Conversely, an increase in feed rate, depth of cut, and nose radius leads to a rise in both force components and temperature. A full factorial artificial neural network (ANN) model was developed to predict these output responses accurately. The ANN model demonstrated high prediction accuracies with errors of 11.50%, 15.88%, and 9.89% for the main cutting force, thrust force, and tool tip temperature, respectively, in the validation set. These findings confirm the model’s reliability in forecasting machining behavior, offering valuable insights for optimizing the dry machining of hybrid composites.

1. Introduction

Lightweight, inexpensive materials with high specific strength are in high demand in industries like aerospace, sports, and automobiles [1]. The demand from various sectors can be met by metal matrix composites (MMCs) [2]. Machining operation creates the vast majority of components used in the manufacturing sector. Aluminum alloy is prioritized by aerospace and automotive engineers for its superior thermal stability, mechanical qualities, and low cost compared to other lightweight alloys [3].

Particulates like SiC, B₄C, Al₂O₃, TiO₂, and SiN have been studied extensively over the past two decades to improve the specific mechanical properties of MMCs [4–7]. Particles with sizes on the order of a micron and a nanometer are the focus of these investigations. These experiments have shown that nanoscale particles can significantly impact the properties of MMCs compared to their microscale counterparts [8–10]. Using hard-phased nanosized ceramic reinforcement typically raises composite material costs [4]. Using industrial and bio waste ashes like rice husks, coconut shells, walnut shells, and fly ash (FA) can additionally increase the composite materials’ individual qualities [11–15]. Therefore, the cost of reinforcing particles can be decreased, as these materials are easily available and may cause environmental problems (pollution) if not utilized. Thermal power facilities produce FA as a by-product; it consists of the thermally stable phases of alumina and silicate [16]. Composites benefit greatly from the low density and high hot hardness of FA particles, resulting in superior specific strength [17, 18].

In the manufacturing industry, the machining process plays a crucial role in developing the components. Due to hard phase reinforcements, MMCs are relatively difficult to cut, resulting in a high machining cost [19, 20]. Among the several types of machining, turning is the most significant. It is required to optimize the machine variables associated with the turning operation to reduce machining costs [21]. Numerous studies have been undertaken to establish a database of optimal combinations of tools, workpieces, and machine variables [22–25].

Regression correlations have been derived utilizing methodologies such as the gray relational analysis (GRA), intuitionistic fuzzy logic, dimensional analysis (DA), artificial neural networks (NNs) (ANNs), adaptive neuro-fuzzy inference system (ANFIS), dimensional exponential model (DEM) and response surface method (RSM) [7, 24, 26–32]. By exploiting these correlations, optimal input regime values can be identified [27, 33]. Optimization of EDM parameters for Al/B₄C composites using Taguchi and GRA improved MRR, tool wear rate (TWR), and Ra, with pulse on time and input current (IP) being the most influential factors [24]. In other research, an integrated TOPSIS-ANFIS approach was applied to optimize WEDM parameters for Al/GrCp10 MMC, leading to significant improvement in machining performance [30]. Furthermore, the cutting operation of wire EDM of a novel Al/Gr/Cp5 MMC was optimized using an integrated ANFIS and RSM, identifying pulse-on time as the most critical factor with a minimum surface roughness of 1.8655 microns, demonstrating strong predictive accuracy (R² = 0.9624) and effective process optimization [29]. Additionally, the EDM operation of Al/Cu/Ni alloys was optimized using an ANFIS, where IP and pulse-on time were the most significant factors affecting TWR, achieving excellent prediction accuracy (R² = 0.9999) and minimizing TWR to 0.0388 mm³/min [34]. This study investigates the effect of EDM parameters on surface roughness of Al/Cu/Ni alloy using DEM, RSM, and ANFIS models, finding ANFIS most accurate. The IP was identified as the most influential parameter in determining surface quality [31]. Further, another study models and predicts WEDM performance for Al/SiCp MMC using DA and ANN, finding ANN models more accurate. Pulse-on time was identified as the most influential factor affecting surface roughness and material removal rate [35]. Additionally, the development and performance evaluation of Al/SiC/coconut and bagasse ash composites using integrated DA and ANFIS found DA models more accurate for predicting MRR, with feed rate (FR) being the most critical parameter [12]. Furthermore, an intuitionistic fuzzy divergence approach was used to classify the mechanical stress states of steel plates subjected to biaxial loads based on eddy current maps, improving classification accuracy and reducing uncertainty significantly [36]. Previous research demonstrates that the ANN model can successfully handle problems such as the mathematical relations between input and output variables, which is crucial for machining processes to obtain the optimum set of variables [37]. The ANN model is, therefore, useful for constructing prediction models associated with machining regimes. Various researchers have investigated the suitability of different combinations of workpieces and cutting tools for the machining of aluminum matrix composites (AMCs). Among these investigations, it has been consistently determined that the use of a polycrystalline diamond (PCD) tool yields the most favorable results [38–40]. PCD tools have shown superior performance over conventional tungsten carbide (WC) tools for machining AMCs reinforced with SiC particles. PCD tools, due to their very high hardness (around 80–85 GPa) and excellent abrasion resistance, achieve significantly longer tool life up to 30 times higher compared to WC tools, which wear rapidly due to the hardness of SiC reinforcements [41, 42]. While WC tools experience severe flank and crater wear even at moderate cutting speeds (CSs), PCD tools mainly exhibit minor crater wear with negligible flank damage. The formation of a stable built-up edge (BUE) on PCD tools acts as a protective barrier against abrasive forces, further extending tool life [43]. Additionally, PCD allows high-speed dry machining, maintains better surface integrity, and results in lower cutting forces and specific power consumption, making it the preferred cutting tool material for precision machining of MMCs compared to WC [42].

Although extensive studies exist on machining AMCs with conventional reinforcements, limited work focuses on hybrid composites reinforced with nanosized SiC and industrial waste like FA. Additionally, the combined influence of cutting parameters and tool nose radius (NR) on cutting forces and tool-tip temperature, especially using PCD tools under dry turning, remains underexplored. Further, the use of ANN for accurate predictive modeling in this context has not been sufficiently addressed. The present study is an in-depth experimental investigation of Al7075 alloy reinforced with a hybrid mix of SiC and FA nanosized (≤ 100 nm) particles. In this experiment, we considered three levels of FR, CS, and depth of cut (DoC) to examine how they affect the machining process. For turning PCD tool has been considered with two different NR of 0.4 and 0.8 mm. It has been revealed how these cutting variables affect the value of required cutting force components (main cutting force (F_x) and thrust force (F_t)) and the temperature at the tool’s tip (T_t). Further, ANNs are used to create regression correlations between input and output variables. The created model has been trained using 21 different combinations, and six trials have validated it. The validation sets demonstrate a significant level of concurrence between the observed values and the experimental values, thus indicating the high accuracy of the ANN models. The created model can also predict output regimes within the allowed operational range relative to input regimes.

2. Machinability Study

Experiments were carried out in a dry machining condition using a computer numerical control machine (manufactured by Baltiboi). For experimentation, the composite material was fabricated by considering industrial waste (FA and SiC) particulates with ≤ 100 nm size, each having a 0.9 weight percentage. Nanocomposite was fabricated by using an ultrasonically assisted stir-casting process. Composite specimens, with dimensions of ϕ10 mm and 10 mm in height, were made specifically for the purpose of scanning electron microscopy (SEM) examination. The SEM analysis of the specimens affirms the homogeneous dispersion of FA and silicon carbide particles within the Al7075 matrix. The turning operation was conducted on an Al7075 alloy and a hybrid nano (≤ 100 nm) composite (Al7075/SiC_0.9CS_0.9). The PCD CCGW090304 insert with a 6° rake, 7° clearance angle, and 0.4 and 0.8 mm NR was utilized for the experiments. Three cutting regimes (CS, FR, and DoC) are chosen after assessing the tool’s and machine’s capabilities. A full factorial experimental design has been chosen to improve the accuracy of the ANN model, Table 1. Various machine and tool variables are considered in the machining experiment, Tables 2 and 3. A Kistler 9257B quartz three-component universal dynamometer was utilized to evaluate the cutting forces. The temperature is detected with a radiation sensor (1°C–1200°C) focused directly on the tip of the tool, as unveiled in Figure 1.

Table 1. ANN nomenclature and architecture used for modeling.

	ANN nomenclature	Value/type
	Number of input layers	1
	Number of output layers	1
	Number of hidden layers	1
	Number of neurons in the input layer	3
	Number of neurons in a hidden layer	5
	Number of neurons in the output layer	1
	Network training algorithm	Levenberg–Marquardt backpropagation
	Activation function used in a hidden layer	Hyperbolic tangent function (tansig)
	Activation function used in the output layer	Pure linear function (purelin)
	Number of epochs	1000
	Training goal	0.001

Table 2. Comparison of experimental and ANN values for training runs.

Exp. no.	CS	FR	DOC	Tool material	Nose radius	Al7075/FA_0.9 SiC_0.9
Exp. no.	m/min	mm/rev	mm		mm	Exp. Fx (N)	ANN Fx (N)	%age error	Exp. Ft (N)	ANN Ft (N)	%age error	Exp. Tt (°C)	ANN Tt (°C)	%age error
1	60	0.14	0.2	PCD	0.4	46	46.0043	0.0093	8	8.01124	6.8165	64	63.999713	0.0004
2	120	0.14	0.2	PCD	0.4	37	37.01942	0.0525	7	6.99259	7.5783	105	104.99995	0.0001
3	180	0.14	0.2	PCD	0.4	34	34.00769	0.0226	5	5.0003	0.006	117	117.0001	0.0001
4	120	0.18	0.2	PCD	0.4	43	42.98837	0.0270	7	7.0234	0.3343	123	123.0001	0.0001
5	180	0.18	0.2	PCD	0.4	38	37.96845	0.0830	5	4.99964	0.0072	126	125.99944	0.0004
6	60	0.22	0.2	PCD	0.4	55	55.00393	0.0071	9	9.0285	0.3167	95	94.999906	0.2743
7	180	0.22	0.2	PCD	0.4	44	43.99948	0.0012	7	6.99848	0.0217	145	144.99889	0.0008
8	60	0.14	0.3	PCD	0.4	53	53.01328	0.0251	9	9.01747	3.8879	70	69.999166	0.0012
9	120	0.14	0.3	PCD	0.4	45	45.04997	0.1110	8	8.01254	0.1567	107	107.00017	0.0002
10	60	0.18	0.3	PCD	0.4	65	64.99991	0.0001	12	11.9994	0.0053	90	90.0004	0.0004
11	120	0.18	0.3	PCD	0.4	58	57.98918	0.0187	10	9.99278	3.4514	120	120.00006	0.0001
12	180	0.18	0.3	PCD	0.4	52	51.96642	0.0646	8	7.99214	3.3598	131	131.00031	0.0002
13	60	0.22	0.3	PCD	0.4	73	72.99397	0.0083	14	13.9492	3.3275	100	100.00021	0.0002
14	120	0.22	0.3	PCD	0.4	67	67.00599	0.0089	11	10.993	4.695	128	127.99941	0.0005
15	180	0.22	0.3	PCD	0.4	65	64.97014	0.0459	9	8.99793	2.6198	153	152.99877	0.0008
16	120	0.14	0.4	PCD	0.4	71	71.05417	0.0763	11	11.0064	0.0584	117	116.99962	0.0003
17	180	0.14	0.4	PCD	0.4	65	65.02047	0.0315	10	9.99137	5.1723	135	134.99985	0.0001
18	60	0.18	0.4	PCD	0.4	89	88.97926	0.0233	14	13.9938	0.044	91	91.000616	0.0007
19	180	0.18	0.4	PCD	0.4	74	74.01215	0.0164	11	10.9829	4.5995	135	135.00012	0.0001
20	60	0.22	0.4	PCD	0.4	103	102.9087	0.0886	17	16.9501	2.7278	101	101.00115	0.0011
21	120	0.22	0.4	PCD	0.4	89	89.01031	0.0116	13	12.9975	0.0194	134	133.99958	0.0003
22	60	0.14	0.2	PCD	0.8	60	59.99946	0.0009	14	14.0373	2.3126	103	102.88399	0.1126
23	120	0.14	0.2	PCD	0.8	47	47.07237	0.1540	12	11.9886	4.2491	149	148.91306	0.2191
24	180	0.14	0.2	PCD	0.8	46	46.00312	0.0068	11	11.0235	4.9855	180	179.98662	0.0074
25	120	0.18	0.2	PCD	0.8	60	60.76647	1.2775	14	13.9027	2.0004	170	170.04266	0.0251
26	180	0.18	0.2	PCD	0.8	58	57.41849	1.0026	13	13.0252	4.2019	201	201.02002	0.0100
27	60	0.22	0.2	PCD	0.8	82	81.16276	1.0210	19	19.0215	0.9295	115	115.02697	0.0235
28	180	0.22	0.2	PCD	0.8	67	66.99601	0.0060	13	13.0064	1.4665	222	222.08679	0.0391
29	60	0.14	0.3	PCD	0.8	90	89.99428	0.0064	19	18.9979	0.011	108	108.13234	0.1225
30	120	0.14	0.3	PCD	0.8	70	69.49177	0.7260	15	14.9931	1.1342	151	151.07968	0.0528
31	60	0.18	0.3	PCD	0.8	99	99.80554	0.8137	21	20.9701	0.048	111	110.99929	0.0006
32	120	0.18	0.3	PCD	0.8	84	83.11355	1.0553	16	16.0696	0.4347	176	176.00003	0.0000
33	180	0.18	0.3	PCD	0.8	60	61.13794	1.8966	15	14.9756	0.1629	209	208.94996	0.0239
34	60	0.22	0.3	PCD	0.8	110	109.7848	0.1956	31	31.0006	0.3996	116	115.88937	0.0954
35	120	0.22	0.3	PCD	0.8	100	99.88903	0.1110	26	25.9877	1.9126	189	189.08264	0.0437
36	180	0.22	0.3	PCD	0.8	90	90.20711	0.2301	19	18.9969	0.2788	228	227.90865	0.0401
37	120	0.14	0.4	PCD	0.8	81	81.51308	0.6334	18	18.0134	1.9434	158	157.97903	0.0133
38	180	0.14	0.4	PCD	0.8	77	76.65751	0.4448	17	16.9783	2.8986	186	186.01263	0.0068
39	60	0.18	0.4	PCD	0.8	145	145.1764	0.1217	28	27.9993	0.4639	115	114.98868	0.0098
40	180	0.18	0.4	PCD	0.8	111	110.5042	0.4466	20	20.0023	1.4664	211	211.03736	0.0177
41	60	0.22	0.4	PCD	0.8	147	146.9587	0.0281	37	36.9988	0.0034	119	119.08097	0.0680
42	120	0.22	0.4	PCD	0.8	134	134.3474	0.2592	27	27.0044	0.0906	193	192.89928	0.0522

Table 3. Comparison of experimental and ANN values for validation runs.

Exp. no.	CS	FR	DOC	Tool material	Nose radius					Al7075/FA _0.9 SiC_0.9
Exp. no.	m/min	mm/rev	mm		mm	Exp. Fx (N)	ANN Fx (N)	%age error	Exp. Ft (N)	ANN Ft (N)	%age error	Exp. Tt (°C)	ANN Tt (°C)	%age error
1	60	0.18	0.2	PCD	0.4	53	48.3997	8.68	8	8.566369	7.08	84	86.7705	3.30
2	120	0.22	0.2	PCD	0.4	50	51.4052	2.81	8	8.709094	11.09	123	121.011	1.62
3	180	0.14	0.3	PCD	0.4	40	37.7931	5.52	7	6.617455	5.46	125	120.723	3.42
4	60	0.14	0.4	PCD	0.4	74	75.7238	2.33	13	12.37844	0.97	74	81.3212	9.89
5	120	0.18	0.4	PCD	0.4	76	81.5484	7.30	12	13.32626	15.88	125	128.832	3.07
6	180	0.22	0.4	PCD	0.4	85	77.9064	8.35	11	11.75572	2.40	159	158.764	0.15
7	60	0.18	0.2	PCD	0.8	75	74.0102	1.32	15	16.83145	10.92	107	117.142	9.48
8	120	0.22	0.2	PCD	0.8	79	69.9851	11.41	15	14.29211	4.72	181	187.15	3.40
9	180	0.14	0.3	PCD	0.8	60	57.5555	4.07	15	13.96145	3.71	178	180.948	1.66
10	60	0.14	0.4	PCD	0.8	110	103.692	5.73	22	24.65481	12.27	112	115.856	3.44
11	120	0.18	0.4	PCD	0.8	114	127.107	11.50	23	24.77937	7.74	185	179.394	3.03
12	180	0.22	0.4	PCD	0.8	132	124.844	5.42	24	23.73084	1.12	233	236.585	1.54

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Experimental setup.

3. Results and Discussion

3.1. Effect of Variation of Machining Variables on Output Regimes

3.1.1. Effect of Variation of CS on Output Variables

Increasing the CS from 60 to 180 m/min results in a decrease in the cutting forces (F_x and F_t), as shown in Tables 2 and 3. Figure 2c illustrates that when the value of the CS increases, so does the value of the T_t.

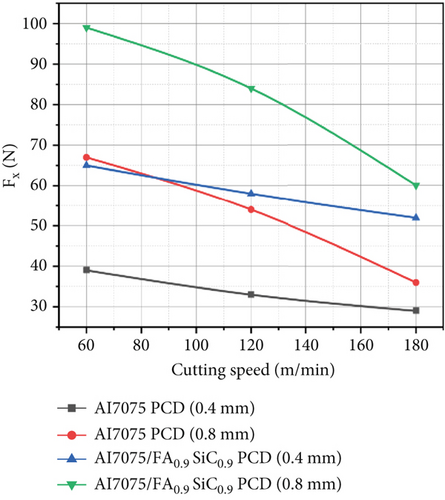
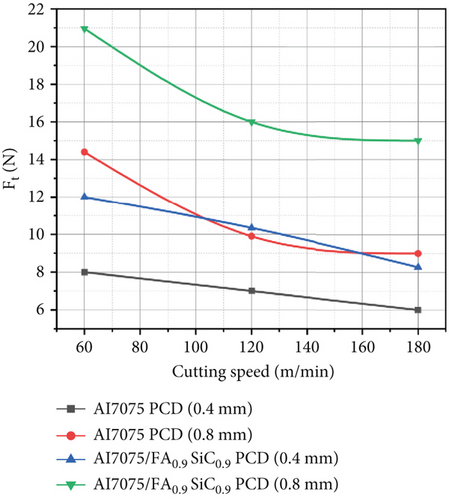
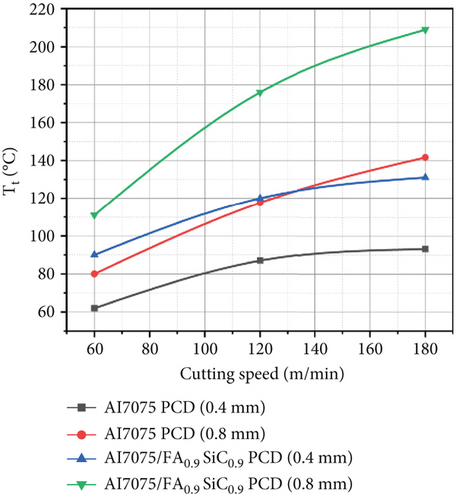
The Al7075/FA_0.9SiC_0.9 composite shows maximum values of main cutting force of 147 N at CS of 60 m/min, FR of 0.22 mm/rev, DoC of 0.4 mm, and NR of 0.8 mm, with a T_t of 119°C. At 180 m/min CS, 0.14 mm/rev FR, and 0.2 mm DoC, with a corresponding T_t of 117°C, the minimum cutting force components are 34 N (F_x).

Matrix material undergoes thermal softening due to the elevated temperature along the shear plane zone. In the shear plane zone, it reduces the cutting force needed to dislodge the matrix material [23, 26]. Furthermore, Figure 2a,b demonstrates a decreasing trend in the F_x and F_t as the CS increases.

3.1.2. Effect of Variation of FR on Output Variables

The experimental findings indicate that the shear plane angle and the uncut chip thickness exhibit an increment as the FR value increases [44]. The elevation of the shear plane angle results in an augmented concentration of stress along the cutting edge and rake face, thereby leading to an escalation in the necessary shearing force within the matrix phase [45]. With an increase in FR, the cross-section and fracture resistance of the sheared chip increase, requiring more cutting forces to remove the material.

In addition, as the FR increases from 0.14 to 0.22 mm/rev, F_x, F_t, and T_t exhibit an increasing trend, as seen in Table 2 and Figures 3 and 4. The matrix phase’s plastic strain increases as the T_t rises. Increasing the FR results in an elevation of the maximum shear stress necessary for crack initiation and propagation. Consequently, this leads to an augmentation in both the cutting force and temperature.

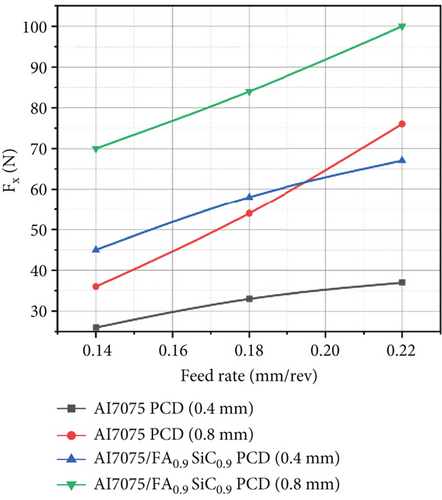
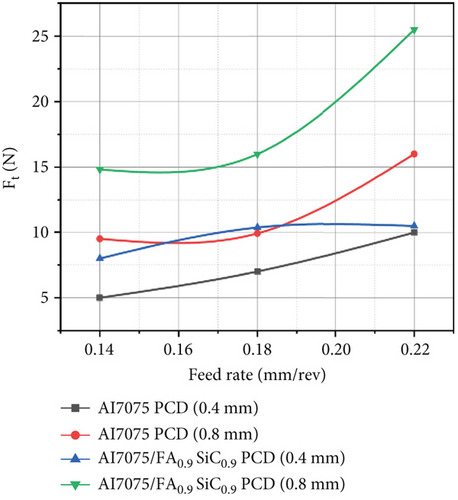
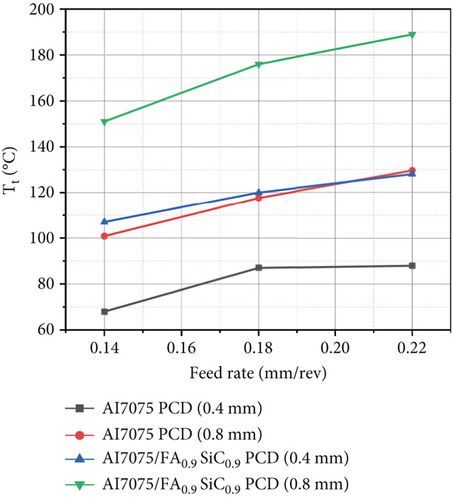
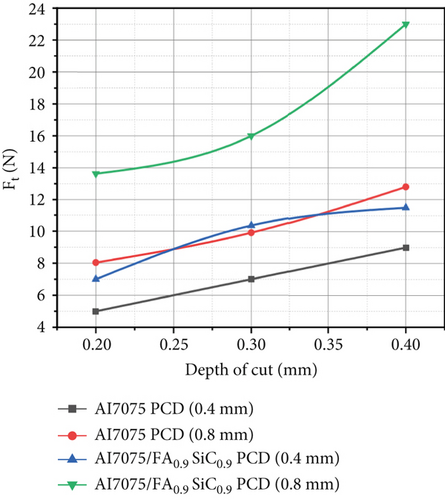
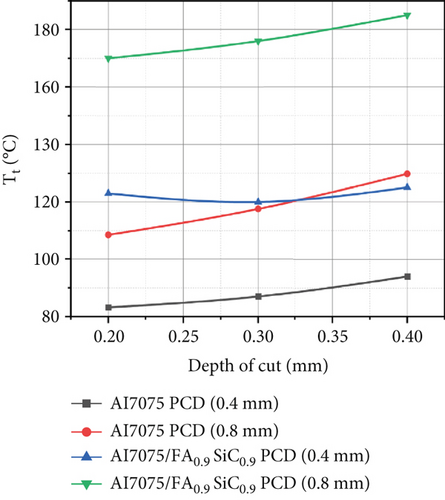
3.1.3. Effect of Variation of DoC on Output Variables

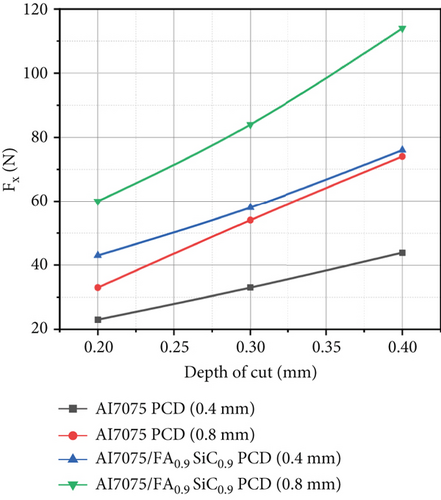
Figure 4a demonstrates that when the value of the DoC increases, the principal cutting forces increase due to the increase in chip load. The cross-sectional area of the chip and the amount of material removed will rise as the DoC is raised. As the DoC increases, the tool will penetrate deeper into the workpiece, thereby leading to an enlarged contact area between the tool and the workpiece [23].

This raises the friction between the two surfaces, hence increasing the cutting force and temperature, as shown in Figure 4b,c. It increases resistance to deformation and fracture, requiring more forces at the tool and the workpiece interface to overcome this resistance.

In response to an increase in force value, the temperature along the interfacial region of the tool chip rises. As the DoC increases, the shear plane angle tends to increase. This effect tends to increase the cutting forces required for deformation. In Figure 4c, it is observed that an increase in the shearing plane angle and material resistance during shearing results in an upward trend in the cutting temperature.

3.1.4. Effect of Variation of Tool NR on Output Variables

The tool NR impacts the shearing of metal in turning operations. Experiments on Al7075 alloy and nanocomposite by PCD tool have been conducted considering two different NR, 0.4 and 0.8 mm. It is depicted from Figures 2, 3, and 4 that with a tool NR of 0.4 mm, the values of F_x, F_t, and T_t are less as compared to the NR of 0.8 mm. As with a tool NR of 0.4 mm, shearing stress concentrations along the tooltip and shearing plane are higher. This can lead to increased deformation and improved material flow, resulting in a better surface finish. Moreover, a larger tool NR (0.8 mm) will reduce shearing stress at the tool-workpiece interface, so higher forces are required to fracture the material. Further, a larger tool NR changes the direction of cutting forces, leading to an increase in cutting force perpendicular to the direction of cutting, which can increase the shear plane angle, which is a cause of an increase in cutting forces and temperature along the shear plane. Additionally, as the tool NR increases from 0.4 to 0.8 mm, the shear plane angle increases, which will cause an increase in the size of the chip and make it more difficult to control. A smaller NR concentrates cutting forces at the tip, while a larger NR distributes cutting forces more evenly along the cutting edge. This can reduce the risk of tool breakage and wear, but it can also result in a poor surface finish due to reduced material flow.

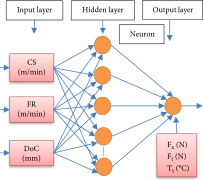
3.2. ANN Modeling

ANNs can perform mathematical mapping (regression) between input and output regimes [46]. In ANN architecture, neurons in the hidden and output layers function as information transmission sources [46]. For each link in these layers, a particular weight is assigned to improve the signal to be processed. Applying an activation function to the input signal determines the output signal of the neuron. Training NNs necessitates the selection of a suitable design, as training process efficiency and convergence are the major objectives at this stage [46]. This indicates that the training architecture is employed to ascertain the network weights necessary for establishing the input-to-output mapping. The error correction process utilizes a multilayer feed-forward network and an error-back propagation algorithm [47]. Since there is no rule for selecting the appropriate number of regulating parameters (epochs and neurons) in the hidden layer, the Levenberg–Marquardt backpropagation (LMBP) training algorithm was implemented, utilizing different configurations of neurons and epochs. The optimal values of neurons and epochs were determined to be 5 and 1000, respectively, by reducing the validation set prediction error (Tables 2 and 3). Three types of ANN layers are created: input, output, and hidden. Input factors for the machinability behavior study include CS (meters per second), FR (millimeters per revolution), and DoC (millimeters). Five neurons execute a nonlinear hyperbolic tangent function in hidden layers (tansig). One neuron is utilized in the output layer, which includes the F_x, F_t, and T_t. For training purposes, the LMBP feed-forward algorithm is used (Table 1). Comparing experimental values to those predicted by an ANN and determining the square root of the average error, the final architecture of the ANN is finalized. When the estimated mean square error hits a predefined threshold of 0.001 or when a predetermined iteration value of 1000 epochs is reached, the network training process is terminated. Initially, experimental data are classified into training and validation sets. The first group consists of the training data set (Table 2). The second group consists of the validation data set (Table 3). However, a NN model with 5 neurons and 1000 epochs is built, and training and validation run experimental values are compared.

3.2.1. Model for Main Cutting Force (F_x) for PCD Tool With Variation in Tool Geometry

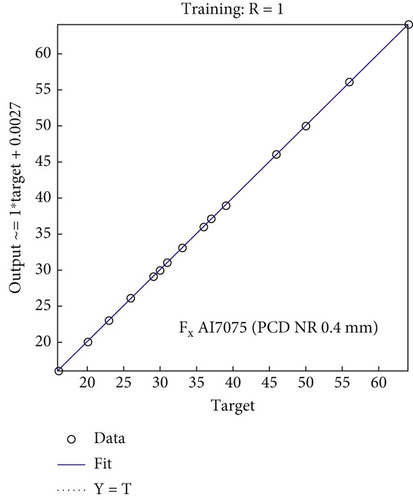
It is observed from Tables 2 and 3 that the maximum percentage errors between ANN model and the experimental data for training runs of F_x of Al7075 and Al7075/FA_0.9SiC_0.9 vary from 0% to 0.39% and 0% to 1.89%, respectively, for PCD tool materials (0.4 and 0.8 mm NR). Table 3 illustrates the maximum percentage errors for Al7075 and Al7075/FA_0.9SiC_0.9 in the validation set. The range of maximum percentage errors for Al7075 is from 0.1% to 9.48%, whereas for Al7075/FA_0.9SiC_0.9, it ranges from 1.32% to 11.50%. For validation experiments, the regression model can predict with 88.50% accuracy. Figures 5a, 5d, 5g, 5j, 6a, and 6b depict a comparative analysis of the observed F_x values against their corresponding estimated values, utilizing a NN, for both the training and validation datasets. The resemblance between the predicted model values and the experimental values of F_x is apparent. Consequently, it is evident that a substantial concurrence exists between the estimated and observed values of F_x, thereby substantiating the models’ validity.

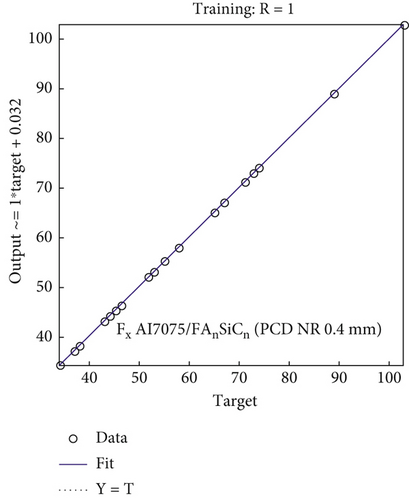
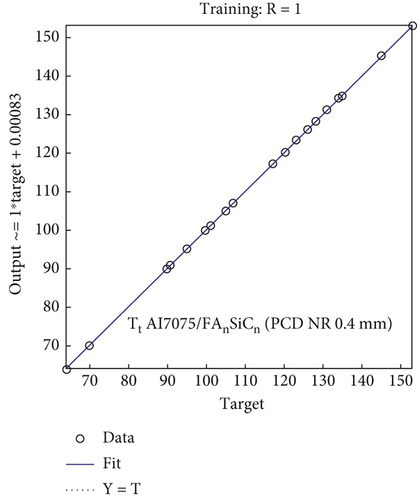
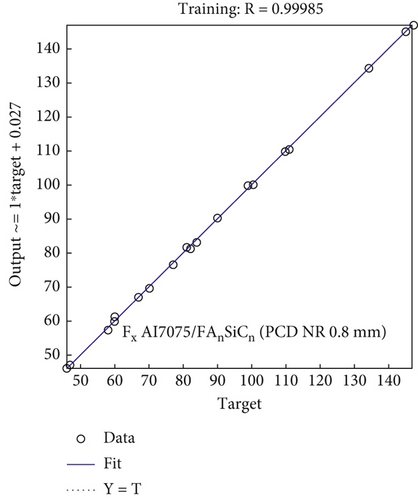
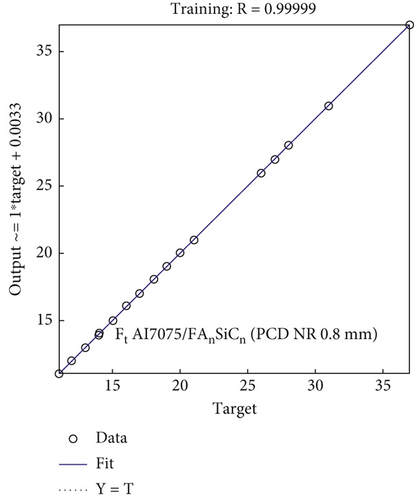
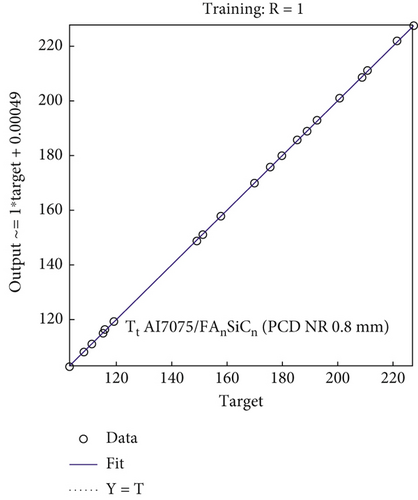
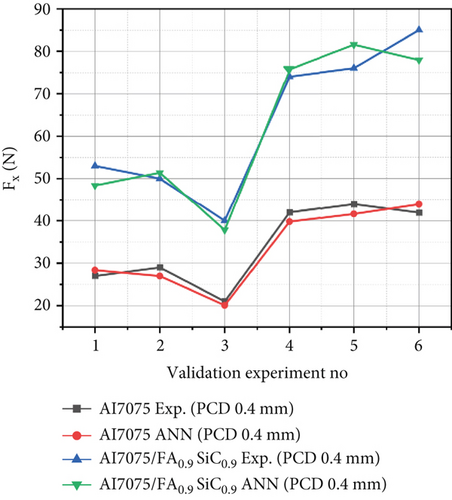
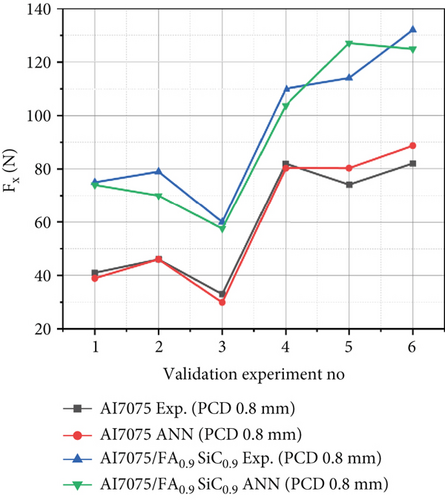
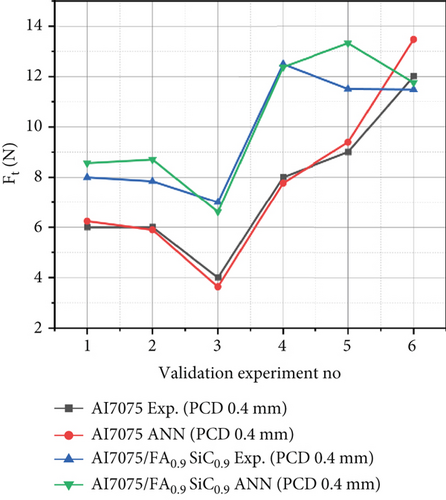
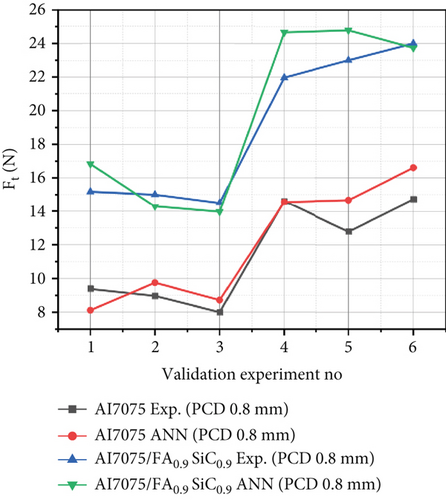
3.2.2. Model for Thrust Force (F_t) for PCD Tool With Variation in Tool Geometry

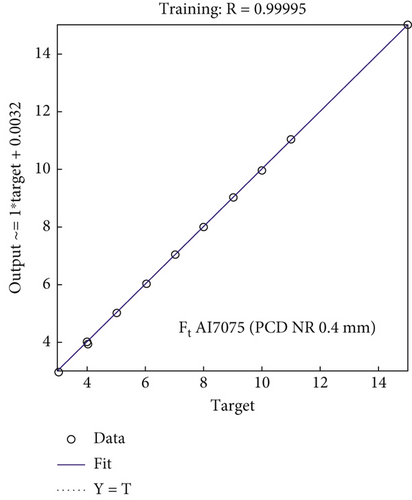
According to the data presented in Table 2, the maximum percentage errors observed between the experimental results and the ANN model during the training process for F_t values of Al7075 and Al7075/FA_0.9SiC_0.9 range from 0% to 6.40% and 0% to 7.58%, respectively. These observations were obtained when employing the PCD tool. In Table 3, the validation set reveals that the maximum percentage errors for Al7075 and Al7075/FA_0.9SiC_0.9 are observed to range from 0.32% to 14.54% and from 0.97% to 15.88%, respectively. Based on the training and validation experiments conducted, the regression model demonstrates predictive capabilities with an accuracy of 92.42% and 84.12%, respectively. These results indicate a strong agreement between the estimated values of cutting force and the corresponding experimental measurements. Figures 5b, 5e, 5h, 5k, 6c, and 6d) show the comparison between the experimental versus estimated values of F_t for training and validation sets obtained using a NN. The observed data demonstrate a notable resemblance between the predicted values and the experimental values of F_t. This indicates a substantial level of agreement between the estimated and observed values of F_t, thereby substantiating the validity of the models utilized.

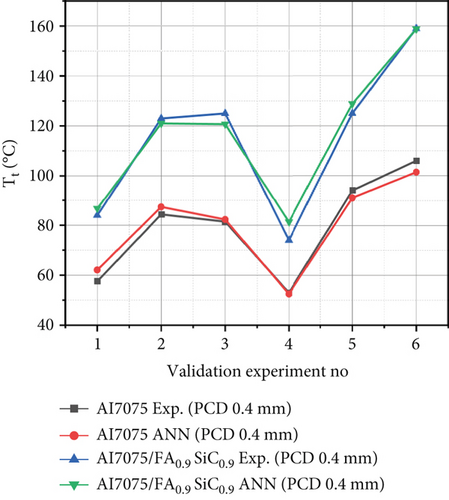
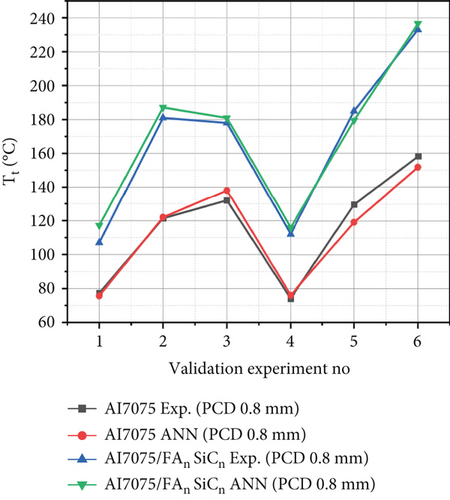
3.2.3. Model for Tool Tip Temperature (T_t) for PCD Tool With Variation in Tool Geometry

According to the data presented in Table 2, the comparative analysis reveals that the highest percentage discrepancies between the empirical observations and ANN models for the training iterations of T_t for Al7075 and Al7075/FA_0.9SiC_0.9, using the PCD tool, range from 0% to 3.38% and from 0% to 0.27%, respectively.

For the validation iterations, it is perceived from Table 3 that the maximum percentage errors for Al7075, Al7075/FA_0.9SiC_0.9 are 0.46%–8.10% and 0.15%–9.89%, respectively. In the training and validation experiments, the regression model demonstrates predictive accuracies of 96.62% and 90.11%, respectively.

This indicates a strong correspondence between the estimated and experimentally determined cutting force values. Figures 5c, 5f, 5i, 5l, 6e, and 6f) show the comparison between the experimental versus estimated values of T_t for training and validation sets obtained using NNs.

The close proximity between the predicted values of the model and the experimental value of T_t indicates a notable correlation. Thus, it is apparent that there exists a substantial concurrence between the estimated and observed values of T_t, thereby validating the credibility of the models.

The research demonstrated that key machining parameters, including CS, FR, DoC, and tool NR, significantly influence cutting forces (F_x, F_t) and tool tip temperature (T_t) during machining processes. Specifically, an increase in CS led to a reduction in cutting forces, while tool tip temperature showed a proportional relation with CS. Both FR and DoC were found to increase cutting forces and tool tip temperature due to enhanced material removal and frictional effects. Additionally, an increase in tool NR resulted in higher forces and temperatures, attributed to the greater contact area and resistance encountered during machining. The study further utilized ANNs, utilizing the LMBP algorithm, to predict the cutting forces and tool tip temperature with high accuracy. The ANN model exhibited a strong correlation between predicted and experimental values, confirming its effectiveness for machining performance prediction. Furthermore, the research revealed that hybrid Al7075/FA_0.9SiC_0.9 composites required more energy for machining compared to the base Al7075 material, indicating the necessity of optimized machining strategies for composite materials. Overall, the findings emphasize the critical role of machining parameters in influencing tool performance and material behavior, highlighting the potential of ANN-based models for enhancing predictive capabilities in machining operations.

4. Conclusions

In this study, CS, FR, DoC, and tool NR varied during turning operations using a PCD tool to investigate their effects on key output parameters—namely, cutting force components and tool tip temperature. An ANN model was developed using the LMBP algorithm to predict these responses. The key findings of the study are summarized as follows:

•
The tool tip temperature exhibits an increasing trend with higher CSs, while the cutting force components (F_x and F_t) tend to decrease.
•
An increase in FR, DoC, and tool NR leads to a corresponding rise in cutting force components and tool tip temperature.
•
Hybrid MMCs demand higher shearing and cutting forces compared to the Al7075 alloy, indicating greater machining resistance.
•
The developed ANN models demonstrated strong predictive performance, achieving maximum prediction accuracies of 98.11%, 92.42%, and 96.62% for F_x, F_t, and T_t, respectively, during training. For the validation set, the prediction accuracies were 88.50%, 84.12%, and 90.11% for the same parameters.

Overall, the proposed ANN-based model exhibits a high level of reliability and effectiveness in forecasting machining outcomes under varying process parameters.

Conflicts of Interest

The authors have nothing to report.

Funding

No funding was received for this manuscript.

Acknowledgments

The current study was conducted within the state-of-the-art Advanced Manufacturing Lab at the Department of Mechanical Engineering, NIT Hamirpur.

Open Research

Data Availability Statement

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.

References

1 Tisza M. and Czinege I., Comparative Study of the Application of Steels and Aluminium in Lightweight Production of Automotive Parts, International Journal of Lightweight Materials and Manufacture. (2018) 1, no. 4, 229–238, https://doi.org/10.1016/j.ijlmm.2018.09.001.
10.1016/j.ijlmm.2018.09.001
Google Scholar
2 Singh L., Singh B., and Saxena K. K., Manufacturing Techniques for Metal Matrix Composites (MMC): An Overview, Advances in Materials and Processing Technologies. (2020) 6, no. 2, 441–457, https://doi.org/10.1080/2374068X.2020.1729603.
10.1080/2374068X.2020.1729603
Web of Science® Google Scholar
3 Zhu L., Li N., and Childs P. R. N., Light-Weighting in Aerospace Component and System Design, Propulsion and Power Research. (2018) 7, no. 2, 103–119, https://doi.org/10.1016/j.jppr.2018.04.001, 2-s2.0-85048939787.
10.1016/j.jppr.2018.04.001
Web of Science® Google Scholar
4 Setia S. and Chauhan S. R., Investigating the Machinability Behaviour of Al7075/SiC5CS5 Hybrid Composite With the Variation of Tool Geometry, Materials Today: Proceedings. (2024) 113, 185–192, https://doi.org/10.1016/j.matpr.2023.08.110.
10.1016/j.matpr.2023.08.110
CAS Google Scholar
5 Chand S., Chandrasekhar P., Sarangi R. K., and Nayak R. K., Influence of B4C Particles on Processing and Strengthening Mechanisms in Aluminum Metal Matrix Composites-A Review, Materials Today: Proceedings. (2019) 18, 5356–5363, https://doi.org/10.1016/j.matpr.2019.07.562.
10.1016/j.matpr.2019.07.562
CAS Google Scholar
6 Atta M., Megahed M., and Saber D., Using ANN and OA Techniques to Determine the Specific Wear Rate Effectors of A356 Al-Si/Al2O3 MMC, Neural Computing and Applications. (2022) 34, no. 17, 14373, https://doi.org/10.1007/s00521-022-07215-3.
10.1007/s00521-022-07215-3
Web of Science® Google Scholar
7 Phate M. R., Toney S. B., and Phate V. R., Multi-Parametric Optimization of WEDM Using Artificial Neural Network (ANN)-Based PCA for Al/SiCp MMC, Journal of The Institution of Engineers (India): Series C. (2021) 102, no. 1, 169–181, https://doi.org/10.1007/s40032-020-00615-1.
10.1007/s40032-020-00615-1
Google Scholar
8 Zhou D., Qiu F., Wang H., Jiang Q., and Metall A., Manufacture of Nano-Sized Particle-Reinforced Metal Matrix Composites: A Review, Acta Metallurgica Sinica (English Letters). (2014) 27, no. 5, 798–805, https://doi.org/10.1007/s40195-014-0154-z, 2-s2.0-84908877763.
10.1007/s40195-014-0154-z
CAS Web of Science® Google Scholar
9 Safi M., Hassanzadeh-Aghdam M. K., and Mahmoodi M. J., Effects of Nano-Sized Ceramic Particles on the Coefficients of Thermal Expansion of Short SiC Fiber-Aluminum Hybrid Composites, Journal of Alloys and Compounds. (2019) 803, 554–564, https://doi.org/10.1016/j.jallcom.2019.06.314, 2-s2.0-85068088588.
10.1016/j.jallcom.2019.06.314
CAS Web of Science® Google Scholar
10 Mahato A. and Mondal S., Fabrication and Microstructure of Micro and Nano Silicon Carbide Reinforced Copper Metal Matrix Composites/Nanocomposites, Silicon. (2021) 13, no. 4, 1097–1105, https://doi.org/10.1007/s12633-020-00491-5.
10.1007/s12633-020-00491-5
CAS Web of Science® Google Scholar
11 Wang L., Xu P., Yin H., Yue Y., Kang W., Liu J., and Fan Y., Fracture Resistance Biomechanisms of Walnut Shell with High-Strength and Toughening, Advanced Science. (2023) 10, no. 27, https://doi.org/10.1002/advs.202303238.
10.1002/advs.202303238
Web of Science® Google Scholar
12 Mote M., Phate M., and Sathe A., Manufacturing and Performance Evaluation of Al/SiC/Coconut & Bagasse Ash Composite Using Novel Integrated Dimensional Analysis (DA) and Adaptive Neuro Fuzzy Inference System (ANFIS) Techniques, International Journal on Interactive Design and Manufacturing (IJIDeM). (2024) 18.
PubMed Google Scholar
13 Rajan T. P. D., Pillai R. M., Pai B. C., Satyanarayana K. G., and Rohatgi P. K., Fabrication and Characterisation of Al–7Si–0.35Mg/fly Ash Metal Matrix Composites Processed by Different Stir Casting Routes, Composites Science and Technology. (2007) 67, no. 15-16, 3369–3377, https://doi.org/10.1016/j.compscitech.2007.03.028, 2-s2.0-35248836895.
10.1016/j.compscitech.2007.03.028
CAS Web of Science® Google Scholar
14 Mandal A. K. and Sinha O. P., New-Generation Aluminum Composite With Bottom Ash Industrial Waste, JOM. (2018) 70, no. 6, 811–816, https://doi.org/10.1007/s11837-018-2774-7, 2-s2.0-85042210654.
10.1007/s11837-018-2774-7
CAS Web of Science® Google Scholar
15 Balasubramanian K., Nataraj M., and Duraisamy P., Machinability Analysis and Application of Response Surface Approach on CNC Turning of LM6/SiCp Composites, Materials and Manufacturing Processes. (2019) 34.
Web of Science® Google Scholar
16 Ranjbar N. and Kuenzel C., Cenospheres: A Review, Fuel. (2017) 207, 1–12, https://doi.org/10.1016/j.fuel.2017.06.059, 2-s2.0-85021139261.
10.1016/j.fuel.2017.06.059
CAS Web of Science® Google Scholar
17 Ghosal S. and Self S. A., Particle Size-Density Relation and Cenosphere Content of Coal Fly Ash, Fuel. (1995) 74, no. 4, 522–529, https://doi.org/10.1016/0016-2361(95)98354-H, 2-s2.0-0029288688.
10.1016/0016-2361(95)98354-H
CAS Web of Science® Google Scholar
18 Narayan S. and Rajeshkannan A., Hardness, Tensile and Impact Behaviour of Hot Forged Aluminium Metal Matrix Composites, Journal of Materials Research and Technology. (2017) 6, no. 3, 213–219, https://doi.org/10.1016/j.jmrt.2016.09.006, 2-s2.0-85010015829.
10.1016/j.jmrt.2016.09.006
CAS Web of Science® Google Scholar
19 Kar K. K., Composite Materials: Processing, Applications, Characterizations, 2016, Springer.
Google Scholar
20 Sekhar R. and Singh T. P., Mechanisms in Turning of Metal Matrix Composites: A Review, Journal of Materials Research and Technology. (2015) 4, no. 2, 197–207, https://doi.org/10.1016/j.jmrt.2014.10.013, 2-s2.0-84927753404.
10.1016/j.jmrt.2014.10.013
Web of Science® Google Scholar
21 Basavarajappa S., Chandramohan G., Rao K., Radhakrishanan R., and Krishnaraj V., Turning of Particulate Metal Matrix Composites—Review and Discussion, Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture. (2006) 220, no. 7, 1189–1204, https://doi.org/10.1243/09544054JEM304, 2-s2.0-34548150804.
10.1243/09544054JEM304
CAS Web of Science® Google Scholar
22 El-Gallab M. and Sklad M., Machining of Al/SiC Particulate Metal-Matrix Composites: Part I: Tool Performance, Journal of Materials Processing Technology. (1998) 83, no. 1-3, 151–158.
10.1016/S0924-0136(98)00054-5
Web of Science® Google Scholar
23 Shoba C., Ramanaiah N., and Nageswara Rao D., Effect of reinforcement on the cutting Forces While Machining Metal Matrix Composites–An Experimental Approach, Engineering Science and Technology, An International Journal. (2015) 18, no. 4, 658–663, https://doi.org/10.1016/j.jestch.2015.03.013, 2-s2.0-85017352750.
10.1016/j.jestch.2015.03.013
Google Scholar
24 Phate M. R., Toney S. B., and Phate V. R., Multi-Response Optimization and Analysis of Al/B4Cp EDM Using Grey Relational Analysis, Journal of Mechanical Engineering (JMechE). (2022) 19, no. 1, 39–55, https://doi.org/10.24191/jmeche.v19i1.19685.
10.24191/jmeche.v19i1.19685
Google Scholar
25 Rudrapati R., Effects of Welding Process Conditions on Friction Stir Welding of Polymer Composites: A Review, Composites Part C. (2022) 8, 100269, https://doi.org/10.1016/j.jcomc.2022.100269.
10.1016/j.jcomc.2022.100269
CAS Google Scholar
26 Muthusamy Subramanian A. V., Nachimuthu M. D. G., and Cinnasamy V., Assessment of Cutting Force and Surface Roughness in LM6/SiC p Using Response Surface Methodology, Journal of Applied Research and Technology. (2017) 15, no. 3, 283–296, https://doi.org/10.1016/j.jart.2017.01.013, 2-s2.0-85020714527.
10.1016/j.jart.2017.01.013
Google Scholar
27 Priyadarshi D. and Sharma R. K., Optimization for Turning of Al-6061-SiC-Gr Hybrid Nanocomposites Using Response Surface Methodologies, Materials and Manufacturing Processes. (2016) 31, no. 10, 1342–1350, https://doi.org/10.1080/10426914.2015.1070427, 2-s2.0-84959056080.
10.1080/10426914.2015.1070427
CAS Web of Science® Google Scholar
28 Rajeswari B. and Amirthagadeswaran K. S., Experimental Investigation of Machinability Characteristics and Multi-Response Optimization of End Milling in Aluminium Composites Using RSM Based Grey Relational Analysis, Measurement. (2017) 105, 78–86, https://doi.org/10.1016/j.measurement.2017.04.014, 2-s2.0-85017591649.
10.1016/j.measurement.2017.04.014
Web of Science® Google Scholar
29 Phate M., Toney S., and Phate V., Response Surface Modelling and Effective Application of Adaptive Neuro-Fuzzy Inference System to Analyze Surface Roughness of Al/Gr/Cp5 MMC Machined Using WEDM, Australian Journal of Mechanical Engineering. (2023) 21, no. 2, 653–667, https://doi.org/10.1080/14484846.2021.1913852.
10.1080/14484846.2021.1913852
Web of Science® Google Scholar
30 Phate M., Toney S., Phate V., and Tatwawadi V., Multi-Response Optimization of Al/GrCp10 MMC Performance in WEDM Using Integrated TOPSIS-ANFIS Approach, Journal of The Institution of Engineers (India): Series D. (2022) 103, no. 1, 249–261, https://doi.org/10.1007/s40033-021-00302-0.
10.1007/s40033-021-00302-0
CAS Google Scholar
31 Phate M., Toney S., and Phate V., Modelling and Investigating the Impact of EDM Parameters on Surface Roughness in EDM of Al/Cu/Ni Alloy, Australian Journal of Mechanical Engineering. (2022) 20, no. 5, 1226–1239, https://doi.org/10.1080/14484846.2020.1790478.
10.1080/14484846.2020.1790478
Web of Science® Google Scholar
32 Tan Y., Yang D., and Sheng Y., Discrete Element Method (DEM) Modeling of Fracture and Damage in the Machining Process of Polycrystalline SiC, Journal of the European ceramic society. (2009) 29, no. 6, 1029–1037, https://doi.org/10.1016/j.jeurceramsoc.2008.07.060, 2-s2.0-60649084372.
10.1016/j.jeurceramsoc.2008.07.060
CAS Web of Science® Google Scholar
33 Thakre A. A. and Soni S., Modeling of Burr Size in Drilling of Aluminum Silicon Carbide Composites Using Response Surface Methodology, Engineering Science and Technology, An International Journal. (2016) 19, no. 3, 1199–1205, https://doi.org/10.1016/j.jestch.2016.02.007, 2-s2.0-85017344759.
10.1016/j.jestch.2016.02.007
Google Scholar
34 Phate M., Bendale A., Toney S., and Phate V., Prediction and Optimization of Tool Wear Rate During Electric Discharge Machining of Al/Cu/Ni Alloy Using Adaptive Neuro-Fuzzy Inference System, Heliyon. (2020) 6, no. 10, e05308, https://doi.org/10.1016/j.heliyon.2020.e05308, 33163650.
10.1016/j.heliyon.2020.e05308
CAS PubMed Web of Science® Google Scholar
35 Phate M. R. and Toney S. B., Modeling and Prediction of WEDM Performance Parameters for Al/SiCp MMC Using Dimensional Analysis and Artificial Neural Network, Engineering Science and Technology, an International Journal. (2019) 22, no. 2, 468–476, https://doi.org/10.1016/j.jestch.2018.12.002, 2-s2.0-85058945004.
10.1016/j.jestch.2018.12.002
Web of Science® Google Scholar
36 Versaci M., Angiulli G., La F., Laganà F., and Palumbo A., Intuitionistic Fuzzy Divergence for Evaluating the Mechanical Stress State of Steel Plates Subject To Bi-Axial Loads, Integrated Computer-Aided Engineering. (2024) 31, no. 4, 363–379, https://doi.org/10.3233/ICA-230730.
10.3233/ICA-230730
Web of Science® Google Scholar
37 Naresh Babu M. and Muthukrishnan N., Investigation on Surface Roughness in Abrasive Water-Jet Machining by the Response Surface Method, Materials and Manufacturing Processes. (2014) 29, no. 11-12, 1422–1428, https://doi.org/10.1080/10426914.2014.952020, 2-s2.0-84908042408.
10.1080/10426914.2014.952020
CAS Google Scholar
38 Andrewes C. J. E., Feng H., and Lau W. M., Machining of an Aluminum/SiC Composite Using Diamond Inserts, Journal of Materials Processing Technology. (2000) 102, no. 1-3, 25–29, https://doi.org/10.1016/S0924-0136(00)00425-8, 2-s2.0-0033741074.
10.1016/S0924-0136(00)00425-8
Web of Science® Google Scholar
39 Ding X., Liew W. Y. H., and Liu X. D., Evaluation of Machining Performance of MMC With PCBN and PCD Tools, Wear. (2005) 259, no. 7-12, 1225–1234, https://doi.org/10.1016/j.wear.2005.02.094, 2-s2.0-19944394247.
10.1016/j.wear.2005.02.094
CAS Web of Science® Google Scholar
40 El-Gallab M. and Sklad M., Machining of Al/SiC Particulate Metal Matrix Composites: Part II: Workpiece Surface Integrity, Journal of Materials Processing Technology. (1998) 83, no. 1-3, 277–285.
10.1016/S0924-0136(98)00072-7
Web of Science® Google Scholar
41 Muthukrishnan N., Murugan M., and Prahlada Rao K., Machinability Issues in Turning of Al-SiC (10p) Metal Matrix Composites, International Journal of Advanced Manufacturing Technology. (2008) 39, no. 3-4, 211–218, https://doi.org/10.1007/s00170-007-1220-8, 2-s2.0-52649160316.
10.1007/s00170-007-1220-8
Web of Science® Google Scholar
42 Muthukrishnan N., Murugan M., and Rao K. P., An Investigation on the Machinability of Al-SiC Metal Matrix Composites Using PCD Inserts, International Journal of Advanced Manufacturing Technology. (2008) 38, no. 5-6, 447–454, https://doi.org/10.1007/s00170-007-1111-z, 2-s2.0-49449105826.
10.1007/s00170-007-1111-z
Web of Science® Google Scholar
43 Beristain J., Gonzalo O., and Sandá A., Machinability of Al-SiC Metal Matrix Composites Using WC, PCD and MCD Inserts, Revista De Metalurgia. (2014) 50, 1–6.
10.3989/revmetalm.006
Web of Science® Google Scholar
44 Setia S. and Chauhan S. R., Comparative Analysis and Optimization of FEM and RSM Based Regression Model with Experimental Results for the Dry Turning of SiCp- Al7075 Composite, Silicon. (2021) 13, no. 12, 4681–4701, https://doi.org/10.1007/s12633-020-00711-y.
10.1007/s12633-020-00711-y
CAS Web of Science® Google Scholar
45 Setia S. and Chauhan S. R., Experimental Investigation and Comparison of Output Cutting Regimes with Finite Element Machining Models for SiCp Based Al7075 Composite, Silicon. (2022) 14, no. 3, 883–892, https://doi.org/10.1007/s12633-020-00887-3.
10.1007/s12633-020-00887-3
CAS Web of Science® Google Scholar
46 Mahender T., Balasundar I., Gupta A. V. S. S. K. S., and Raghu T., Metamodels to Describe the High Temperature Deformation Behaviour of Al 2014+2wt%Tib2Composite, Advances in Materials and Processing Technologies. (2022) 8, no. sup4, 2097–2109, https://doi.org/10.1080/2374068X.2022.2035967.
10.1080/2374068X.2022.2035967
Google Scholar
47 Tsai K. M. and Wang P. J., Predictions on Surface Finish in Electrical Discharge Machining Based Upon Neural Network Models, International Journal of Machine Tools and Manufacture. (2001) 41, no. 10, 1385–1403, https://doi.org/10.1016/S0890-6955(01)00028-1, 2-s2.0-0035427810.
10.1016/S0890-6955(01)00028-1
Web of Science® Google Scholar

All articles

Integrated Neural Network Analysis of Machining Characteristics in Dry-Turned Al7075/FA_0.9SiC_0.9 Hybrid Composite Using PCD Inserts

Abstract

1. Introduction

2. Machinability Study

3. Results and Discussion

3.1. Effect of Variation of Machining Variables on Output Regimes

3.1.1. Effect of Variation of CS on Output Variables

3.1.2. Effect of Variation of FR on Output Variables

3.1.3. Effect of Variation of DoC on Output Variables

3.1.4. Effect of Variation of Tool NR on Output Variables

3.2. ANN Modeling

3.2.1. Model for Main Cutting Force (F_x) for PCD Tool With Variation in Tool Geometry

3.2.2. Model for Thrust Force (F_t) for PCD Tool With Variation in Tool Geometry

3.2.3. Model for Tool Tip Temperature (T_t) for PCD Tool With Variation in Tool Geometry

4. Conclusions

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Integrated Neural Network Analysis of Machining Characteristics in Dry-Turned Al7075/FA0.9SiC0.9 Hybrid Composite Using PCD Inserts

Abstract

1. Introduction

2. Machinability Study

3. Results and Discussion

3.1. Effect of Variation of Machining Variables on Output Regimes

3.1.1. Effect of Variation of CS on Output Variables

3.1.2. Effect of Variation of FR on Output Variables

3.1.3. Effect of Variation of DoC on Output Variables

3.1.4. Effect of Variation of Tool NR on Output Variables

3.2. ANN Modeling

3.2.1. Model for Main Cutting Force (Fx) for PCD Tool With Variation in Tool Geometry

3.2.2. Model for Thrust Force (Ft) for PCD Tool With Variation in Tool Geometry

3.2.3. Model for Tool Tip Temperature (Tt) for PCD Tool With Variation in Tool Geometry

4. Conclusions

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Related

Information

Integrated Neural Network Analysis of Machining Characteristics in Dry-Turned Al7075/FA_0.9SiC_0.9 Hybrid Composite Using PCD Inserts

3.2.1. Model for Main Cutting Force (F_x) for PCD Tool With Variation in Tool Geometry

3.2.2. Model for Thrust Force (F_t) for PCD Tool With Variation in Tool Geometry

3.2.3. Model for Tool Tip Temperature (T_t) for PCD Tool With Variation in Tool Geometry