This study addresses a critical gap in traffic flow modeling by developing a macroscopic framework that simultaneously accounts for taillight signaling effects and deteriorated road conditions—a common but understudied scenario in developing regions. Building on the observation that reduced road quality and limited visibility significantly alter driver behavior, particularly in response to preceding vehicles’ taillights, we formulate a model that captures these complex interactions neglected by classical approaches. Through systematic mathematical analysis, we first demonstrate that the vector–matrix formulation yields a strictly hyperbolic and anisotropic system, characterized by finite-speed wave propagation along distinct characteristic fields. We then establish the model’s theoretical foundations by conducting a linear stability analysis that quantitatively links traffic stability to key parameters including driver sensitivity, headway, and road condition factors. Numerical simulations validate our analytical framework, revealing how small initial density perturbations evolve into characteristic traffic wave phenomena: shock formations, rarefaction waves, and stop-and-go clusters. These results not only confirm the model’s ability to reproduce realistic traffic patterns under infrastructure constraints but also provide mechanistic insights into the emergence of congestion in poor road conditions. By integrating taillight dynamics with road quality effects, this work advances macroscopic traffic theory while offering practical tools for traffic management in low-maintenance road networks.

1. Introduction

Taillights are crucial for vehicle and occupants safety, especially in low-visibility conditions. They are mandatory components of vehicle design for driving on public highways, serving as signals to inform other road users about a vehicle’s location, speed, and intentions. Numerous micro [1–3], lattice-based [4–7], lane changing [8, 9], and macro [10–20] models have been proposed to address various aspects of vehicular traffic flow, including the effects of taillight signaling [21–23]. In particular, Zhang et al. [21] presented an enhanced car-following model to analyze the impact of the preceding vehicle’s taillight on driving behavior. Their findings revealed that drivers could anticipate future headway by using visual cues from nearby vehicles, thereby adjusting their acceleration based on the discrepancy between expected and actual headway.

By converting microvariables into macrovariables, Zhai and Wu [23] introduced dynamic velocity equations that incorporate both the driver’s memory time and the taillight of the preceding vehicle. Through nonlinear stability analysis, the authors derived a modified KdV–Burgers equation to characterize the properties of density wave propagation and evolution near the neutral stability curve. Their findings suggest that memory time negatively impacts traffic flow stability, whereas the presence of the preceding vehicle’s taillight helps alleviate congestion and conserve energy. Subsequently, Zhai and Wu [22] developed a continuous traffic flow model that considers the combined effect of headway variation and the taillight of the preceding vehicle. The flow of traffic jams near steady conditions was similarly explained using the density wave solution obtained by solving the KdV–Burgers equation. Additionally, Li and Ma [24] proposed a lattice model that considers the effects of taillights and velocity variation on traffic flow stability. Through a phase diagram analysis, they observed that both taillight effects and velocity variation positively influence traffic flow stability. This finding was validated by examining the spatiotemporal evolution of density wave profiles. It was also discovered that low-speed estimates and high critical densities negatively impact traffic flow stability, while the opposite conditions have a positive effect.

While these studies advance our understanding of taillight-informed driver behavior, another critical factor affecting traffic flow, particularly in low- and middle-income regions, is the condition of the road surface itself. Deteriorated roads, characterized by potholes, cracks, and uneven textures, introduce sudden variations in vehicle speed, elevate reaction times, and often disrupt uniform traffic progression [25, 26]. Drivers encountering such conditions tend to reduce speed either preemptively or in response to the behavior of leading vehicles, especially when visibility is low.

The aforementioned models, however, are limited in their ability to directly study various complex traffic phenomena caused by these diverse road conditions, as they do not explicitly account for these factors. Nevertheless, some efforts have been made to address the impact of road surfaces in traffic modeling. These efforts include the discrete velocity model proposed by [27], a traffic flow model that accommodates both good and bad road conditions by [28], and a car-following model that considers driving resistance [29].

Using discrete theory, Delitala and Tosin [27] developed a mathematical model for vehicle traffic to explore the influence of road conditions on traffic flow. However, this study focused solely on the mathematical aspects of how road conditions affect traffic flow and did not conduct numerical tests to demonstrate whether the model can qualitatively reproduce these effects. More precisely, the study did not investigate how road conditions impact the fundamental diagram, the formation and evolution of shock and rarefaction waves, traffic flow stability, or other traffic phenomena. Moreover, the study exclusively examines the traffic scenario in which a zero equilibrium speed is reached under the worst road conditions and derives the anticipation term of the proposed model for both the worst and best road conditions. Furthermore, the car-following model proposed by [29] examined how driving resistance influences car-following behavior. This model assumed that variations in road conditions would have qualitatively similar effects on traffic flow, with only minor variations in the values of certain parameters. Based on the findings of [28, 29], Tang et al. [30] introduced a new model based on empirical data that considers various road conditions in car-following behavior. Initially, the authors analyzed the impact of road conditions on uniform flow from both analytical and numerical perspectives. The results confirmed that road conditions have a significant effect on uniform flow. Specifically, good road conditions were found to increase velocity and flow, with improvements becoming more pronounced as road conditions improve. Conversely, poor road conditions were associated with decreased velocity and flow.

In 2014, Tang et al. [31] formulated a similar model that considers varying road conditions. The analytical and numerical findings indicate that poor road conditions decelerate traffic, while good road conditions can enhance the speed and flow of uniform traffic. Besides, the numerical results demonstrate that poor road conditions lead to steeper shock waves and reduced traffic flow stability, whereas good road conditions can mitigate shock waves and improve stability. The qualitative agreement with empirical findings suggests that the proposed model accurately describes the impacts of road conditions on traffic flow. To investigate the effects of road, institutional, and weather conditions on traffic flow, Golovnin [32] proposed a data-driven approach for traffic flow characterization. The author utilized detailed information on road conditions along with macroscale traffic flow parameters. The study focused on profiling weather-sensitive traffic flow speed and intensity using data from the city of Aarhus, Denmark. The results highlighted the effectiveness of this approach in predicting traffic flow dynamics under varying road conditions.

A second-order macroscopic traffic model introduced by [25] considers road surface irregularities that disrupt smooth vehicular flow. The study investigated how pothole size, along with flow rate severity and vehicle speed, affects driver reaction time to these irregularities. Also, a local cluster analysis was conducted to examine the effects of minor disturbances on traffic flow. The findings revealed that, except in low and high jam density scenarios where amplifications dissipate rapidly, the amplification on road surfaces with wider cracks is less severe compared to those with smaller potholes. While potholes are visible road features, their relationship with macroscopic traffic factors remains a subject of debate. Existing literature on potholes has primarily emphasized detection methods [33–43]. However, some recent studies, such as [26], have begun to model the effects of road surface irregularities on traffic dynamics, focusing on pothole-induced congestion. Despite these advancements, current models largely overlook the interaction between deteriorated road conditions and adaptive driver behavior, including responses to taillight signals. This study proposes a new macroscopic traffic flow model to explore how taillight signaling influences driver behavior and its implications for traffic flow dynamics, especially in the context of poor road conditions. The proposed model integrates these critical elements, which have been largely disregarded in traditional traffic flow models.

The remaining sections are organized as follows: Section 2 outlines the model derivation process, followed by a discussion of linear stability analysis in Section 3. Section 4 provides a detailed analysis of the model, focusing on nonlinear traffic phenomena. The final section summarizes the findings, draws conclusions, and suggests avenues for future research.

2. Model Derivation and Properties

The two main classifications of vehicular models are microscopic and macroscopic equations. Microscopic models delve into a detailed analysis of individual driver-vehicle behavior, while macroscopic models provide an aggregate analysis of traffic flow. Microscopic models can be aggregated into macroscopic models, offering a broader perspective on traffic dynamics.

This derivation begins from a microscopic car-following framework, where each vehicle adjusts its speed based on its distance and relative velocity with respect to the preceding vehicle. Classical car-following models [44, 45] assume that such adjustments are smooth and primarily based on headway or speed difference. However, more recent studies have highlighted the role of additional visual cues such as the activation of taillights on driver response, especially during deceleration. Building on the formulation proposed in [21], we adopt a velocity adjustment rule that includes both optimal velocity and relative speed terms, along with a taillight-induced disturbance term as

()

where u_n(t) is the velocity of vehicle n at time t and Δu_n(t) = u_n+1(t) − u_n(t), the relative speed with respect the vehicle n + 1. x_n(t) denote the position of the n-th vehicle at time t and Δx_n(t) = x_n+1(t) − x_n(t), its relative position with respect to n + 1-th vehicle. U(Δx_n(t)) denotes the optimal velocity function of the n-th vehicle determined by the speed of the vehicle headway. The functions Ψ_n(t) and Φ_n(t) are used to determine if the leading car slows down and the disturbance generated by the taillight of the leading vehicle, respectively, and are written as

in which d_v indicates the distance maintained between a following vehicle and the preceding vehicle in a free flow traffic situation and x_o is the distance between vehicles whenever the behavior of the leading vehicle, particularly the visibility of its taillights, can influence the driving behavior of the following vehicle. K_n+1 is the acceleration of the leading vehicle at time t. Φ₀ is a parameter associated with each driver’s unique characteristics, and H is defined by

where κ and λ are the sensitivity coefficients but κ is equivalent to the inverse of the relaxation time τ.

We now derive a macroscopic model from (1) using the following transform notations:

and the total derivative can be expressed as

using Taylor series expansion: u(x + d_v, t) = u(x, t) + (∂u(x, t)/∂x)d_v. This implies that the relative speed of vehicle n at time t reduces to

Let us introduce ρ(x, t) and u(x, t) as the macroscopic density and velocity, respectively, and set h≔1/ρ as the mean headway with u_e(ρ) the density-dependent steady state speed. Then, Equation (1) can be aggregated as

which also simplifies to

()

To account for the preceding vehicle’s taillight on a bad road, we introduce a source term into the velocity equation of (2) as

()

The last term in Equation (3) is adopted from [25] to explain all abnormalities on the roadway. The constants α and β represent the depth and width of potholes, whereas ρ_crit is the critical density and T is the driver’s physiological reaction time. Since second-order macroscopic traffic flow models comprise a continuity equation and a dynamic velocity equation, the macroscopic model proposed in this study is ultimately formulated as follows:

()

where M = Φ_otanh(1 − d_v/x_o). The variables ρ and u are unknown variables.

To examine the structural properties of the waves and characteristic fields present in them, System (4) and (5) are cast into vector form as

()

so that

Here, note that C(ψ) is simply the Jacobian of the flux function if Equation (6) is written in the conservative form and ψ is a vector of the conserved variables. Since the mathematical structure of System (6) is solely determined by its homogeneous part, we set D(ψ) = 0 in subsequent analysis to determine the characteristic field of the system. The speed of waves present in the system are derived from the eigenvalues of the Jacobian matrix and are determined by solving

for h. The eigenvalues are

It can be inferred from the above that the system is strictly hyperbolic as long as λ ≠ M and d_v ≠ 0. Strict hyperbolicity guarantees the existence of two distinct characteristic curves along which traffic information, such as traffic jams and shock waves, propagates. These curves are governed by the relations:

Thus, the wave speed remains lower than the vehicle speed, thereby preserving the anisotropic nature of traffic flow, where drivers respond only to the conditions ahead of them.

Let us refer to the waves associated with h₁ and h₂ eigenvalues as the h₁-wave and h₂-wave characteristic fields, respectively. By computing the gradient vector of each eigenvalue with respect to the conserved variables and evaluating the dot product of the resulting vector with the corresponding right eigenvector, we discover that h₁-wave is genuinely nonlinear, while the h₂-wave is linearly degenerate for the homogeneous part of (6). This can also be confirmed from the right eigenvectors of h₁ and h₂ which are given by [−ρ/d_v(λ + M), μ] and [ν, 0], respectively, for some real nonzero constants ν and μ.

It is well known that Cauchy problems of hyperbolic systems admit differentiable solutions only up to a finite time, beyond which the solution develops severe irregularities [46, 47]. These irregular solutions—typically shock waves, rarefaction waves, or contact discontinuities—are collectively referred to as weak solutions. For (6), let us briefly consider a special initial data, namely, the Riemann data, characterized by constant states (ρ_L, u_L) and (ρ_R, u_R) on the left and right of x = 0, respectively. In general, a genuinely nonlinear wave is classified as a shock wave if it satisfies the Rankine–Hugoniot jump condition with a finite speed of propagation and meets the Lax admissibility criteria. On the other hand, a linearly degenerate wave is a rarefaction wave if the generalized Riemann invariants are all constant and a corresponding “diverging” entropy condition is also satisfied. Furthermore, a contact wave discontinuity arises for a linearly degenerate field only if the characteristics on both sides of the wave are parallel. [48].

For System (6), both eigenvalues are functions of only u and the Riemann invariants of h₂-wave is not well defined. In contrast, the Riemann invariant across h₁-wave is given by u + d_v(λ + M)lnρ = const. Thus, any solution of a generalized Riemann problem arises only from changes in the flow speed and not from perturbations in density of vehicles on the road. Consequently, h₂-wave is further classified as contact discontinuity with a propagation speed of (ρ_Ru_R − ρ_Lu_L)/(ρ_R − ρ_L). On the other hand, h₁-wave is a rarefaction, a shock wave, or is represented by a contact discontinuity given that u_L < u_R, u_L > u_R, or u_L = u_R, respectively. See Section 4 for detailed exposition.

Additional Riemann variables can be obtained by combining the associated eigenvector of h₁ and h₂ to form the matrix W and its inverse W⁻¹ as

A similarity matrix M is used to diagonalize the system

Multiplying Equation (6) by W⁻¹ gives

()

Assuming a slight change in δψ, the derivative with respect to time is ∂ψ/∂t, and the derivative with respect to the spatial variable is ∂ψ/∂x. The Riemann variables are then inferred from these modifications as δz = W⁻¹δψ and inversely as δψ = Wδz. Thus, ∂z = W⁻¹δψ can be expanded as

Expanding the above into separate equations will result in

By integrating both sides, we obtain the wave propagation paths for this model as

Thus, the propagation of z₁ is along the characteristic u(x, t), whereas the propagation of z₂ is along the characteristic u(x, t) − d_v(λ + M).

3. Stability Condition of the Proposed Model

Stop-and-go waves and phantom congestion are indicators of traffic instability. This section identifies the parameter conditions that lead to nonstationary flow. Given that ρ_e and u_e represent the solutions to our proposed model, any slight deviation from the steady state can be mathematically expressed as

Following from the above, we obtain the underlying linearized continuity equation as

()

Similarly, the linearized dynamic velocity equation is given by

()

With the assumption that ρ_e ~ ρ_crit, Equations (9) reduces to

()

We assume that the disturbance δρ(x, t), δu(x, t) can be mimicked using the simple wave equation.

()

s and ω are the wave number and speed, respectively, and growth rate Λ. Slight changes in Λ could lead to phantom traffic jam when Λ > 0. Substituting (11) and its derivatives into the continuity,

and the momentum equation

()

The linearized continuity and dynamic velocity equation are rearranged as

()

Equations (13) and (14) are simplified using matrix notation as

where

Let

and

, this gives the result

From the homogeneous part, the characteristic equation is

where

The solution to the characteristic polynomial is obtained as

which can be expanded as

then

where

Following from [49, 50]

hence,

()

Equation (15) can be separated into real and imaginary parts. Therefore,

This implies that

Based on the given parameters, if Rε(Λ₁) is positive, then Rε(Λ₂) will also be positive because Rε(Λ₁) exceeds Rε(Λ₂). Conversely, if Rε(Λ₁) is negative, then the stability of the new model will be achieved. Thus,

which can be simplified as

()

From the previous analysis, we observe that

These real and imaginary terms are substituted into Equation (16).

expanding and simplifying

This implies

Thus, the stability condition is

()

The stability of the proposed model depends on specific conditions, underscoring the importance of identifying and monitoring these conditions to prevent instability. Understanding the steady-state conditions of the proposed model enables more accurate predictions and more efficient regulation of traffic flow, leading to reduced congestion and improved road safety. These findings are crucial for devising effective strategies to mitigate oscillatory traffic and congestion, with significant implications for traffic management.

4. Numerical Simulation

The performance of the proposed model in simulating contraction and dissolution waves is investigated, focusing on how these waves are realistically captured. Also, the model’s ability to exemplify local cluster effects is explored. First, Equations (4) and (5) are transformed into a discretized form using an upwind finite difference scheme. These are expressed as

()

For

()

and for

()

where c_w = (λ + M)d_v.

At the position (i, j), the variables and correspond to the density and velocity, and the spatial increment is denoted by Δx, while the time increment is denoted by Δt.

4.1. Traffic Wave Dynamics

Traffic waves depict fluctuations in vehicle flow along a roadway, marking abrupt shifts between congested and free-flowing traffic conditions. Unlike physical waves in water, these traffic waves represent changes in vehicle speed and density that propagate along the road. Understanding traffic wave profiles is crucial for accurately modeling traffic behavior, especially in scenarios such as traffic jams, merging lanes, or sudden changes in road conditions. To demonstrate these concepts, we conduct a numerical simulation of a Riemann-type problem based on Equations (4) and (5) using constant initial states that specify the distributions of density and velocity at t = 0. The Riemann-type initial condition provides a snapshot of the traffic flow at the outset, allowing the simulation to advance and accurately replicate the behavior of shock waves and rarefaction waves. The initial profile is defined as follows:

()

where ρ_l and u_l represent the upstream density and velocity, respectively, and ρ_r and u_r represent the downstream density and velocity, respectively. These values are to be selected to represent two distinct traffic regimes: a low-density free-flow state and a high-density congested state. This contrast creates a sharp density gradient, which is known to trigger the formation and propagation of nonlinear traffic waves such as shock and rarefaction waves. Such initial configurations are commonly used to test a model’s ability to capture the wave patterns arising from abrupt transitions between flow regimes.

The speed–density Equation (22) was chosen for adaptation in the simulation, as proposed by [51, 52]. This equation, which delineates the relationship between speed and density, is deemed suitable for modeling the traffic flow dynamics under consideration.

()

The free flow velocity is represented by u_f, where ρ_m denotes the maximum density and c_m signifies the kinematic wave velocity. The parameter values used in the simulation are shown in Table 1. These values, derived from real traffic experiments, are standard references in traffic research.

Table 1. Parameter values.

Parameter	Value
u_f	25.00
τ	3.00
c_m	11.00
α	0.20
d_v	4. 00
ρ_crit	0.38
λ	0.60
ρ_m	1.00
x₀	6.00
β	1.40
T	1.00
Φ_o	0.10

The plot in Figure 1 illustrates an initial profile defined by upstream and downstream densities and velocities. The upstream initial density is set at 0.3900 vehicles per meter (ρ_l), while the downstream initial density is 0.3700 vehicles per meter (ρ_r). The corresponding upstream velocity (u_l) and downstream velocity (u_r) are determined based on these densities. The traffic wave depicted in Figure 1 represents a scenario where the upstream and downstream density values are close to the critical density. An immediate drop in downstream density is observed, followed by a stabilization phase. This is accompanied by an initial increase in speed as fewer vehicles reduce congestion. The speed increase eventually stabilizes as traffic adjusts to the new conditions, leading to a constant speed downstream. Simultaneously, the upstream wave profiles propagate forward gradually. This movement reflects how transitions at one point in traffic affect the entire flow downstream.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Traffic wave dynamics with the initial density profile ρ_l = 0.3900 and ρ_r = 0.3700.

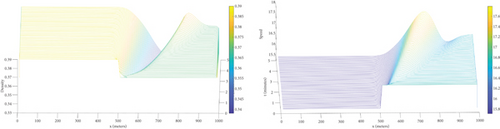
In Figure 2, the upstream initial density is set at 0.7500 vehicles per meter (ρ_l), while the downstream initial density is 0.1500 vehicles per meter (ρ_r). This scenario represents a significant disparity between upstream and downstream density values relative to the critical density. This scenario represents a significant disparity between upstream and downstream density values relative to the critical density to observe the behavior of the vehicles approaching the midpoint. With relatively few vehicles downstream, those nearing this point experience an increase in speed. This acceleration occurs because reduced congestion downstream facilitates smoother and faster traffic flow as vehicles approach the midpoint. Further analysis of the plot reveals the gradual dissolution of the vehicle queue over time. This dissolution is a crucial aspect of traffic dynamics, demonstrating how changes in traffic density can lead to the easing of congestion as vehicles redistribute themselves along the road network. The insights from our rarefaction plot not only illustrate these intricate traffic dynamics but also align with real-world observations. In practice, similar behaviors are often observed, where traffic waves dissolve as vehicles adjust their speeds and positions.

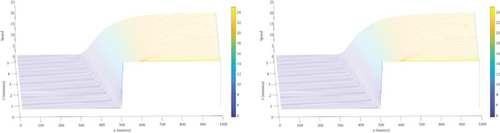
In Figure 3, the upstream initial density is set at 0.3700 vehicles per meter (ρ_l), and the downstream initial density is set at 0.3900 vehicles per meter (ρ_r). Observations from the plot reveal a dynamic pattern in downstream density. Initially, as vehicles from the upstream region enter the downstream section, the density increases. This rise in density leads to a corresponding drop in downstream speed, as the higher vehicle count results in congestion and slower traffic flow. Over time, the downstream density decreases as vehicles from the shock region move downstream. This drop in density leads to stabilization, where the downstream density reaches an equilibrium point. This stabilization is reflected in a constant downstream speed as traffic adjusts to the new conditions following the shock. Meanwhile, the propagation of upstream wave profiles gradually advances, demonstrating how changes in traffic conditions at one point in the road network can influence traffic patterns upstream.

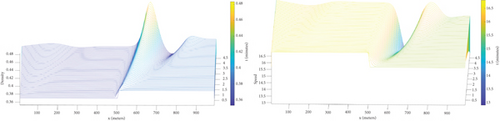
In Figure 4, the plot analysis examines a traffic wave scenario where upstream and downstream density values are significantly different from the critical density. In this case, the relatively light density upstream merges with the somewhat moving traffic downstream. This dynamic results in only a minor queue buildup, as the lighter upstream traffic integrates smoothly with the downstream flow without causing significant congestion. Further observation reveals a decrease in downstream density over time. This decline occurs because the light upstream traffic merges with the downstream flow, leading to fewer vehicles in this section. As a result, the reduction in density corresponds to an increase in downstream speed, as the decreased congestion facilitates smoother and faster traffic flow. Moreover, no substantial queue buildup is observed due to the efficient merging of traffic from the upstream and downstream sections. This scenario reflects real-world conditions where light traffic merging with a slightly moving flow does not typically lead to significant congestion or queue formation.

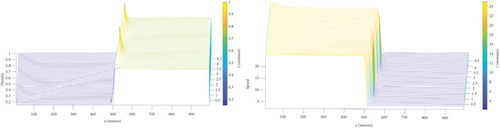
4.2. Cluster Analysis

Delving into the stop-and-go behavior observed in traffic flow, especially in response to minor disruptions, reveals that this phenomenon involves the clustering of vehicles, leading to a wave-like pattern of acceleration and braking. This behavior highlights how even small disturbances can cause vehicles to intermittently speed up and slow down, resulting in inefficiencies in traffic flow. To simulate this, the initial density equation proposed by [53] will be incorporated.

()

with the boundary conditions

The amplitude of a localized disturbance is indicated by Δρ₀ = 0.2. The road length is denoted by L. The initial constant density is represented by ρ₀, which serves as a variable parameter to measure the amplification of the perturbation. The speed–density equation follows the proposition by [54].

The simulation results for the cluster effect are illustrated in Figures 5 and 6. These plots visually demonstrate how minor variations in initial traffic density can lead to significant fluctuations in traffic flow patterns. The observed cluster effect highlights the importance of considering initial conditions when modeling traffic flow, especially in scenarios with wide variations in traffic densities. The simulations reveal substantial fluctuations in traffic density, ranging from 0.11 to 0.46, showcasing the sensitivity of traffic flow dynamics to initial density values. These variations underscore the diverse nature of road networks and how small changes in the initial density profile can significantly impact traffic flow patterns. As the initial density increases from lower to higher values, the disturbance in the wave profiles intensifies. This disturbance is characterized by the emergence of multiple local clusters and pockets of varying densities along the road, indicating regions of higher congestion or slower traffic flow interspersed with areas of smoother flow. However, once the initial density exceeds a certain threshold, the impact of the disturbance diminishes. Beyond this point, traffic flow tends toward uniformity, resulting in a more consistent density profile along the road network.

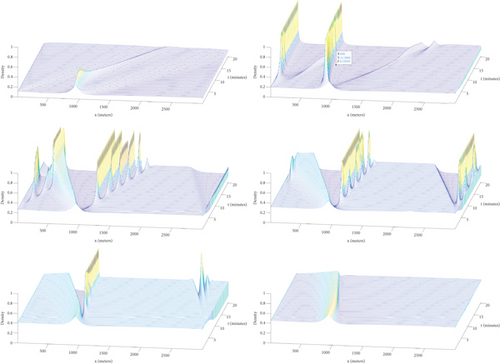
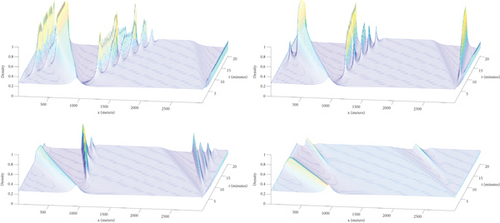
The plots depicted in Figure 6 illustrate how varying values of Δ influence density profile amplifications. As Δ values increase from lower to higher levels, a notable decrease in the amplitude of density profiles for traffic clusters is observed. Larger intervehicle distances correspond to diminished amplitudes in these density profiles. This suggests that traffic congestion and clustering decrease as vehicles are spaced farther apart. Essentially, greater intervehicle distances result in smoother traffic flow and lower amplitude fluctuations in density profiles. In addition, for smaller Δ values, the influence of the taillight effect on traffic flow is evident. In these cases, the taillight effect significantly impacts the traffic density downstream of the disturbance, leading to noticeable changes in density profiles. However, for larger Δ values, the impact of the taillight effect on traffic flow diminishes. This suggests that at higher perturbation levels, traffic flow patterns are influenced more by other factors, with the taillight effect having a lesser impact on flow dynamics.

5. Conclusion

This study presents a significant advancement in understanding traffic dynamics in challenging road environments by introducing a novel macroscopic traffic flow model that incorporates taillight signaling and deteriorated road conditions. By drawing on insights from both microscopic and macroscopic modeling, we derive a system of equations that captures the interaction between vehicle behavior and infrastructure degradation. The model accounts for taillight-induced deceleration and variable road surface quality, thereby enhancing realism in low-visibility and poorly maintained environments.

We analytically established that the proposed model is strictly hyperbolic and anisotropic. The associated wave structure reveals two distinct characteristic fields: one linearly degenerate and one genuinely nonlinear. A linear stability analysis yields an explicit stability criterion, which relates stability thresholds to key physical and behavioral parameters such as driver sensitivity, road condition metrics, and vehicle headway.

Simulation results demonstrate the model’s ability to replicate realistic traffic phenomena. These include the emergence and propagation of shock waves, rarefaction patterns, and stop-and-go clusters under different density profiles. The model also captures the formation of localized traffic disturbances and highlights how minor variations in initial density can trigger significant dynamic effects. This confirms both the sensitivity and internal consistency of the framework.

To assess real-world applicability, the model was tested under synthetic conditions mimicking deteriorated road scenarios common in many developing regions. The speed–density relations used are empirically grounded, and the resulting traffic profiles are qualitatively consistent with field observations. In future work, we aim to calibrate the model using empirical data from West African road networks, particularly Ghana.

These contributions—ranging from theoretical derivation and structural classification to realistic simulation and contextual applicability—emphasize the model’s potential as a tool for analyzing and managing traffic flow under infrastructure-constrained conditions.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

G.O.F., G.K.G., and K.A.G. contributed to the conceptualization and supervision of the study. G.O.F. and K.A.G. conducted the formal analysis. G.O.F., G.K.G., and R.O. were responsible for the investigation and validation of results and prepared the original draft. G.O.F., G.K.G., K.A.G., and R.O. contributed to writing, review, and editing. All authors have reviewed and approved the final version of the manuscript.

Funding

No funding was received for this manuscript

Open Research

Data Availability Statement

Data sharing is not applicable to this article as no new data were created or analyzed in this study.

References

1 Hossain M. A. and Tanimoto J., A Microscopic Traffic Flow Model for Sharing Information From a Vehicle to Vehicle by Considering System Time Delay Effect, Physica A: Statistical Mechanics and its Applications. (2022) 585, 126437, https://doi.org/10.1016/j.physa.2021.126437.
10.1016/j.physa.2021.126437
Web of Science® Google Scholar
2 Yu S., Chen Y., Song L., Xuan Z., and Li Y., Modelling and Mitigating Secondary Crash Risk for Serial Tunnels on Freeway via Lighting-Related Microscopic Traffic Model With Inter-Lane Dependency, International Journal of Environmental Research and Public Health. (2023) 20, no. 4, https://doi.org/10.3390/ijerph20043066, 36833757.
10.3390/ijerph20043066
PubMed Google Scholar
3 Zhai C., Wu W., and Xiao Y., Cooperative Car-Following Control With Electronic Throttle and Perceived Headway Errors on Gyroidal Roads, Applied Mathematical Modelling. (2022) 108, 770–786, https://doi.org/10.1016/j.apm.2022.04.010.
10.1016/j.apm.2022.04.010
Web of Science® Google Scholar
4 Xiao Y., Wu W., Zhai C., Zhai M., and Zhang J., Analysis of Empirical Lane-Changing Rate Effect on Multi-Lane Traffic on Curved Roads, Chinese Journal of Physics. (2025) 95, 260–274, https://doi.org/10.1016/j.cjph.2025.01.041.
10.1016/j.cjph.2025.01.041
Web of Science® Google Scholar
5 Zhai C., Wu W., and Xiao Y., The Jamming Transition of Multi-Lane Lattice Hydrodynamic Model With Passing Effect, Chaos, Solitons & Fractals. (2023) 171, 113515, https://doi.org/10.1016/j.chaos.2023.113515.
10.1016/j.chaos.2023.113515
Web of Science® Google Scholar
6 Zhai C., Zhang R., Peng T., Zhong C., and Xu H., Heterogeneous Lattice Hydrodynamic Model and Jamming Transition Mixed With Connected Vehicles and Human-Driven Vehicles, Physica A: Statistical Mechanics and its Applications. (2023) 623, 128903, https://doi.org/10.1016/j.physa.2023.128903.
10.1016/j.physa.2023.128903
Web of Science® Google Scholar
7 Zhai C., Wu W., Zhang J., and Xiao Y., Congested Traffic Patterns of Mixed Lattice Hydrodynamic Model Combining the Perceptual Range Differences With Passing Effect, Chinese Journal of Physics. (2024) 92, 1174–1187, https://doi.org/10.1016/j.cjph.2024.10.022.
10.1016/j.cjph.2024.10.022
Web of Science® Google Scholar
8 Chen S., Piao L., Zang X., Luo Q., Li J., Yang J., and Rong J., Analyzing Differences of Highway Lane-Changing Behavior Using Vehicle Trajectory Data, Physica A: Statistical Mechanics and its Applications. (2023) 624, 128980, https://doi.org/10.1016/j.physa.2023.128980.
10.1016/j.physa.2023.128980
Web of Science® Google Scholar
9 Li J., Ling M., Zang X., Luo Q., Yang J., Chen S., and Guo X., Quantifying Risks of Lane-Changing Behavior in Highways With Vehicle Trajectory Data Under Different Driving Environments, International Journal of Modern Physics C. (2024) 35, no. 11, 2450141, https://doi.org/10.1142/S0129183124501419.
10.1142/S0129183124501419
Web of Science® Google Scholar
10 Fosu G. O., Oduro F. T., and Caligaris C., Multilane Analysis of a Viscous Second-Order Macroscopic Traffic Flow Model, SN Partial Differential Equations and Applications. (2021) 2, no. 1, 1–17, https://doi.org/10.1007/s42985-020-00054-8.
10.1007/s42985-020-00054-8
Google Scholar
11 Jafaripournimchahi A., Cai Y., Wang H., Sun L., Tang Y., and Babadi A. A., A Viscous Continuum Traffic Flow Model Based on the Cooperative Car-Following Behaviour of Connected and Autonomous Vehicles, IET Intelligent Transport Systems. (2023) 17, no. 5, 973–991, https://doi.org/10.1049/itr2.12320.
10.1049/itr2.12320
Web of Science® Google Scholar
12 Khan Z. H., Gulliver T. A., Imran W., Khattak K. S., Altamimi A. B., and Qazi A., A Macroscopic Traffic Model Based on Relaxation Time, Alexandria Engineering Journal. (2022) 61, no. 1, 585–596, https://doi.org/10.1016/j.aej.2021.06.042.
10.1016/j.aej.2021.06.042
Web of Science® Google Scholar
13 Mohan R. and Ramadurai G., Multi-Class Traffic Flow Model Based on Three Dimensional Flow–Concentration Surface, Physica A: Statistical Mechanics and its Applications. (2021) 577, 126060, https://doi.org/10.1016/j.physa.2021.126060.
10.1016/j.physa.2021.126060
Web of Science® Google Scholar
14 Ngoduy D., Noise-Induced Instability of a Class of Stochastic Higher Order Continuum Traffic Models, Transportation Research Part B: Methodological. (2021) 150, 260–278, https://doi.org/10.1016/j.trb.2021.06.013.
10.1016/j.trb.2021.06.013
Web of Science® Google Scholar
15 Qaiser T., Altamimi A. B., Khan F. A., Alsaffar M., Alreshidi A., Khattak K. S., Khan Z. H., and Khan W., A New Macroscopic Traffic Flow Characterization Incorporating Traffic Emissions, Applied Sciences. (2023) 13, no. 9, https://doi.org/10.3390/app13095545.
10.3390/app13095545
Google Scholar
16 Qiao D., Dai B., Lin Z., Guo M., Zhang X., Zhang P., and Cheng F., Study on Vehicle Fuel Consumption and Exhaust Emissions Based on a New Viscous Macroscopic Traffic Flow Model, Journal of Transportation Engineering, Part A: Systems. (2023) 149, no. 2, 04022137, https://doi.org/10.1061/JTEPBS.TEENG-7506.
10.1061/JTEPBS.TEENG-7506
Web of Science® Google Scholar
17 Wang Z. and Zhu W. X., Modeling and Stability Analysis of Traffic Flow Considering Electronic Throttle Dynamics on a Curved Road With Slope, Physica A: Statistical Mechanics and its Applications. (2022) 597, 127225, https://doi.org/10.1016/j.physa.2022.127225.
10.1016/j.physa.2022.127225
Web of Science® Google Scholar
18 Zhai C., Wu W., and Xiao Y., Non-Lane-Discipline-Based Continuum Model Considering the Effect of Lateral Gaps and Electronic Throttle Dynamics, Chinese Journal of Physics. (2023) 83, 253–269, https://doi.org/10.1016/j.cjph.2023.03.013.
10.1016/j.cjph.2023.03.013
Web of Science® Google Scholar
19 Zhai C. and Wu W., A Continuum Model With Traffic Interruption Probability and Electronic Throttle Opening Angle Effect Under Connected Vehicle Environment, European Physical Journal B. (2020) 93, no. 3, 1–12, https://doi.org/10.1140/epjb/e2020-100492-6.
10.1140/epjb/e2020-100492-6
Web of Science® Google Scholar
20 Zhai C. and Wu W. T., An Extended Continuum Model With Consideration of the Self-Anticipative Effect, Modern Physics Letters B. (2018) 32, no. 31, 1850382, https://doi.org/10.1142/S0217984918503827, 2-s2.0-85054433728.
10.1142/S0217984918503827
CAS Web of Science® Google Scholar
21 Zhang J., Tang T. Q., and Yu S. W., An Improved Car-Following Model Accounting for the Preceding Car’s Taillight, Physica A: Statistical Mechanics and Its Applications. (2018) 492, 1831–1837, https://doi.org/10.1016/j.physa.2017.11.100, 2-s2.0-85035355646.
10.1016/j.physa.2017.11.100
Web of Science® Google Scholar
22 Zhai C. and Wu W., A Continuous Traffic Flow Model Considering Predictive Headway Variation and Preceding Vehicle’s Taillight Effect, Physica A: Statistical Mechanics and its Applications. (2021) 584, 126364, https://doi.org/10.1016/j.physa.2021.126364.
10.1016/j.physa.2021.126364
Web of Science® Google Scholar
23 Zhai C. and Wu W., A New Continuum Model With Driver’s Continuous Sensory Memory and Preceding Vehicle’s Taillight, Communications in Theoretical Physics. (2020) 72, no. 10, 105004, https://doi.org/10.1088/1572-9494/aba24c.
10.1088/1572-9494/aba24c
Web of Science® Google Scholar
24 Li Z. and Ma C., Stability Analysis of the New Traffic Flow Lattice Model Considering Taillight Effect and Speed Deviation, Journal of Advanced Transportation. (2022) 2022, no. 1, 11, 1716827, https://doi.org/10.1155/2022/1716827.
10.1155/2022/1716827
Web of Science® Google Scholar
25 Fosu G. O., Opong J. M., Owusu B. E., and Naandam S. M., Modeling Road Surface Potholes Within the Macroscopic Flow Framework, Mathematics in Applied Sciences and Engineering. (2022) 3, no. 2, 106–118, https://doi.org/10.5206/mase/14625.
10.5206/mase/14625
Web of Science® Google Scholar
26 Khan Z. H., Altamimi A. B., Imran W., Alsaffar M., Khattak K. S., and Alfaisal F. F., Macroscopic Traffic Modelling on the Impact of Road Surface Potholes: Development and Numerical Solution, IEEE Access. (2024) 12, 81718–81735, https://doi.org/10.1109/ACCESS.2024.3411303.
10.1109/ACCESS.2024.3411303
Web of Science® Google Scholar
27 Delitala M. and Tosin A., Mathematical Modeling of Vehicular Traffic: A Discrete Kinetic Theory Approach, Mathematical Models and Methods in Applied Sciences. (2007) 17, no. 6, 901–932, https://doi.org/10.1142/S0218202507002157, 2-s2.0-34249789588.
10.1142/S0218202507002157
Web of Science® Google Scholar
28 Bellouquid A. and Delitala M., Asymptotic Limits of a Discrete Kinetic Theory Model of Vehicular Traffic, Applied Mathematics Letters. (2011) 24, no. 5, 672–678, https://doi.org/10.1016/j.aml.2010.12.004, 2-s2.0-79551486464.
10.1016/j.aml.2010.12.004
Web of Science® Google Scholar
29 Li C. Y., Tang T. Q., Huang H. J., and Shang H. Y., A New Car-Following Model With Consideration of Driving Resistance, Chinese Physics Letters. (2011) 28, no. 3, 038902, https://doi.org/10.1088/0256-307X/28/3/038902, 2-s2.0-79952519202.
10.1088/0256-307X/28/3/038902
Web of Science® Google Scholar
30 Tang T. Q., Li P., Wu Y. H., and Huang H. J., A Macro Model for Traffic Flow With Consideration of Static Bottleneck, Communications in Theoretical Physics. (2012) 58, no. 2, 300–306, https://doi.org/10.1088/0253-6102/58/2/23, 2-s2.0-84864910645.
10.1088/0253-6102/58/2/23
Web of Science® Google Scholar
31 Tang T. Q., Caccetta L., Wu Y. H., Huang H. J., and Yang X. B., A Macro Model for Traffic Flow on Road Networks With Varying Road Conditions, Journal of Advanced Transportation. (2014) 48, no. 4, 304–317, https://doi.org/10.1002/atr.215, 2-s2.0-84902472521.
10.1002/atr.215
Web of Science® Google Scholar
32 Golovnin O., Data-Driven Profiling of Traffic Flow With Varying Road Conditions, CEUR Workshop Proceedings, 2019, Institute of Physics Publishing (IOP), 149–157.
10.18287/1613-0073-2019-2416-149-157
Google Scholar
33 Arjapure S. and Kalbande D., Review on Analysis Techniques for Road Pothole Detection, Soft Computing: Theories and Applications: Proceedings of SoCTA 2018, 2020, Springer, 1189–1197.
10.1007/978-981-15-0751-9_109
Google Scholar
34 Bansal K., Mittal K., Ahuja G., Singh A., and Gill S. S., DeepBus: Machine Learning Based Real Time Pothole Detection System for Smart Transportation Using IoT, Internet Technology Letters. (2020) 3, no. 3, e156, https://doi.org/10.1002/itl2.156.
10.1002/itl2.156
Web of Science® Google Scholar
35 Dharneeshkar J., Aniruthan S., Karthika R., and Parameswaran L., Deep Learning Based Detection of Potholes in Indian Roads Using YOLO, Proceedings of the 2020 International Conference on Inventive Computation Technologies (ICICT), 2020, IEEE, 381–385, https://doi.org/10.1109/ICICT48043.2020.9112424.
Google Scholar
36 Asad M. H., Khaliq S., Yousaf M. H., Ullah M. O., and Ahmad A., Pothole Detection Using Deep Learning: A Real-Time and AI-on-the-Edge Perspective, Advances in Civil Engineering. (2022) 2022, no. 1, 9221211, https://doi.org/10.1155/2022/9221211.
10.1155/2022/9221211
Web of Science® Google Scholar
37 Audu-war S. O., Anigbogu S. O., Anigbogu K. S., Anigbogu G. N., and Asogwa D. C., Pothole Detection Using Image Surveillance System: A Review, World Journal of Advanced Engineering Technology and Sciences. (2023) 9, no. 2, 214–222, https://doi.org/10.30574/wjaets.2023.9.2.0210.
10.30574/wjaets.2023.9.2.0210
Google Scholar
38 Bučko B., Lieskovská E., Zábovská K., and Zábovský M., Computer Vision Based Pothole Detection Under Challenging Conditions, Sensors. (2022) 22, no. 22, https://doi.org/10.3390/s22228878, 36433474.
10.3390/s22228878
PubMed Web of Science® Google Scholar
39 Chougule S. and Barhatte A., Smart Pothole Detection System Using Deep Learning Algorithms, International Journal of Intelligent Transportation Systems Research. (2023) 21, no. 3, 483–492, https://doi.org/10.1007/s13177-023-00363-3.
10.1007/s13177-023-00363-3
Web of Science® Google Scholar
40 Jakubec M., Lieskovská E., Buˇcko B., and Zábovská K., Comparison of CNN-Based Models for Pothole Detection in Real-World Adverse Conditions: Overview and Evaluation, Applied Sciences. (2023) 13, no. 9, https://doi.org/10.3390/app13095810.
10.3390/app13095810
Google Scholar
41 Ma N., Fan J., Wang W., Wu J., Jiang Y., Xie L., and Fan R., Computer Vision for Road Imaging and Pothole Detection: A State-of-the-Art Review of Systems and Algorithms, Transportation safety and Environment. (2022) 4, no. 4, tdac026, https://doi.org/10.1093/tse/tdac026.
10.1093/tse/tdac026
Web of Science® Google Scholar
42 Pandey A. K., Iqbal R., Maniak T., Karyotis C., Akuma S., and Palade V., Convolution Neural Networks for Pothole Detection of Critical Road Infrastructure, Computers and Electrical Engineering. (2022) 99, 107725, https://doi.org/10.1016/j.compeleceng.2022.107725.
10.1016/j.compeleceng.2022.107725
Web of Science® Google Scholar
43 Singh P., Kamal A. E., Bansal A., and Kumar S., Road Pothole Detection From Smartphone Sensor Data Using Improved LSTM, Multimedia Tools and Applications. (2024) 83, no. 9, 26009–26030, https://doi.org/10.1007/s11042-023-16177-0.
10.1007/s11042-023-16177-0
Web of Science® Google Scholar
44 Bexelius S., An Extended Model for Car-Following, Transportation Research. (1968) 2, no. 1, 13–21, https://doi.org/10.1016/0041-1647(68)90004-X, 2-s2.0-0041503216.
10.1016/0041-1647(68)90004-X
Web of Science® Google Scholar
45 Gipps P. G., A Behavioural Car-Following Model for Computer Simulation, Transportation Research Part B: Methodological. (1981) 15, no. 2, 105–111, https://doi.org/10.1016/0191-2615(81)90037-0, 2-s2.0-0019558539.
10.1016/0191-2615(81)90037-0
Web of Science® Google Scholar
46 Dafermos C. M., Hyperbolic Conservation Laws in Continuum Physics, 2005, Springer.
10.1007/3-540-29089-3
Google Scholar
47 Bressan A., Hyperbolic Systems of Conservation Laws, Oxford Lecture Series in Mathematics and its Applications. (1999) 12, no. 1, https://doi.org/10.5209/rev_REMA.1999.v12.n1.17204.
10.5209/rev_REMA.1999.v12.n1.17204
Google Scholar
48 Toro E. F., Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction, 2013, Springer Science & Business Media.
Google Scholar
49 Helbing D. and Johansson A., On the Controversy Around Daganzo’s Requiem for and Aw-Rascle’s Resurrection of Second-Order Traffic Flow Models, European Physical Journal B. (2009) 69, no. 4, 549–562, https://doi.org/10.1140/epjb/e2009-00182-7, 2-s2.0-67650224266.
10.1140/epjb/e2009-00182-7
CAS Web of Science® Google Scholar
50 Fosu G. O. and Oduro F. T., Two Dimensional Anisotropic Macroscopic Second-Order Traffic Flow Model, Journal of Applied Mathematics and Computational Mechanics. (2020) 19, no. 2, 59–71, https://doi.org/10.17512/jamcm.2020.2.05.
10.17512/jamcm.2020.2.05
Web of Science® Google Scholar
51 Del Castillo J. M. and Benitez F., On the Functional Form of the Speed-Density Relationship—I: General Theory, Transportation Research Part B: Methodological. (1995) 29, no. 5, 373–389, https://doi.org/10.1016/0191-2615(95)00008-2, 2-s2.0-0029391007.
10.1016/0191-2615(95)00008-2
Google Scholar
52 Fosu G. O., Akweittey E., Opong J. M., and Otoo M. E., Vehicular Traffic Models for Speed-Density-Flow Relationship, Journal of Mathematical Modeling. (2020) 8, no. 3, 241–255, https://doi.org/10.22124/jmm.2020.15409.1370.
10.22124/jmm.2020.15409.1370
Google Scholar
53 Herrmann M. and Kerner B. S., Local Cluster Effect in Different Traffic Flow Models, Physica A: Statistical Mechanics and Its Applications. (1998) 255, no. 1-2, 163–188, https://doi.org/10.1016/S0378-4371(98)00102-2, 2-s2.0-0032098844.
10.1016/S0378-4371(98)00102-2
Google Scholar
54 Kerner B. S. and Konhäuser P., Structure and Parameters of Clusters in Traffic Flow, Physical Review E. (1994) 50, no. 1, 54–83, https://doi.org/10.1103/PhysRevE.50.54, 2-s2.0-0002562202, 9961944.
10.1103/PhysRevE.50.54
CAS PubMed Web of Science® Google Scholar

All articles

Modeling Vehicular Traffic Flow With Taillight Effect on Deteriorated Roads

Abstract

1. Introduction

2. Model Derivation and Properties

3. Stability Condition of the Proposed Model

4. Numerical Simulation

4.1. Traffic Wave Dynamics

4.2. Cluster Analysis

5. Conclusion

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Modeling Vehicular Traffic Flow With Taillight Effect on Deteriorated Roads

Abstract

1. Introduction

2. Model Derivation and Properties

3. Stability Condition of the Proposed Model

4. Numerical Simulation

4.1. Traffic Wave Dynamics

4.2. Cluster Analysis

5. Conclusion

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information