Volume 2025, Issue 1 2404681

Research Article

Open Access

Optimization Design of Nonpulsating, Equal Contact Stress Guide Curves for Internal Curve Radial Piston Motors

Hongbin Qiang,

Corresponding Author

Hongbin Qiang

[email protected]

orcid.org/0000-0003-0749-7171

School of Mechanical Engineering , Jiangsu University of Technology , Changzhou , China , just.edu.cn

Jiangsu Provincial Engineering Research Center for Advanced Fluid Power and Equipment , Jiangsu University of Technology , Changzhou , China , just.edu.cn

Search for more papers by this author

Jiajun Shao,

Jiajun Shao

School of Mechanical Engineering , Jiangsu University of Technology , Changzhou , China , just.edu.cn

Search for more papers by this author

Shaopeng Kang,

Shaopeng Kang

School of Mechanical Engineering , Jiangsu University of Technology , Changzhou , China , just.edu.cn

Jiangsu Provincial Engineering Research Center for Advanced Fluid Power and Equipment , Jiangsu University of Technology , Changzhou , China , just.edu.cn

Search for more papers by this author

Kailei Liu,

Kailei Liu

orcid.org/0000-0002-3503-9891

School of Mechanical Engineering , Jiangsu University of Technology , Changzhou , China , just.edu.cn

Jiangsu Provincial Engineering Research Center for Advanced Fluid Power and Equipment , Jiangsu University of Technology , Changzhou , China , just.edu.cn

Search for more papers by this author

Dongming Li,

Dongming Li

Department of Transmission Business , Jiangsu Hengli Hydraulic Co. , Ltd , Changzhou , China

Search for more papers by this author

Xiansheng Ke,

Xiansheng Ke

Department of Transmission Business , Jiangsu Hengli Hydraulic Co. , Ltd , Changzhou , China

Search for more papers by this author

Hongbin Qiang,

Corresponding Author

Hongbin Qiang

[email protected]

orcid.org/0000-0003-0749-7171

School of Mechanical Engineering , Jiangsu University of Technology , Changzhou , China , just.edu.cn

Jiangsu Provincial Engineering Research Center for Advanced Fluid Power and Equipment , Jiangsu University of Technology , Changzhou , China , just.edu.cn

Search for more papers by this author

Jiajun Shao,

Jiajun Shao

School of Mechanical Engineering , Jiangsu University of Technology , Changzhou , China , just.edu.cn

Search for more papers by this author

Shaopeng Kang,

Shaopeng Kang

School of Mechanical Engineering , Jiangsu University of Technology , Changzhou , China , just.edu.cn

Jiangsu Provincial Engineering Research Center for Advanced Fluid Power and Equipment , Jiangsu University of Technology , Changzhou , China , just.edu.cn

Search for more papers by this author

Kailei Liu,

Kailei Liu

orcid.org/0000-0002-3503-9891

School of Mechanical Engineering , Jiangsu University of Technology , Changzhou , China , just.edu.cn

Jiangsu Provincial Engineering Research Center for Advanced Fluid Power and Equipment , Jiangsu University of Technology , Changzhou , China , just.edu.cn

Search for more papers by this author

Dongming Li,

Dongming Li

Department of Transmission Business , Jiangsu Hengli Hydraulic Co. , Ltd , Changzhou , China

Search for more papers by this author

Xiansheng Ke,

Xiansheng Ke

Department of Transmission Business , Jiangsu Hengli Hydraulic Co. , Ltd , Changzhou , China

Search for more papers by this author

First published: 29 April 2025

https://doi.org/10.1155/jama/2404681

Academic Editor: Qiankun Song

Share a link

Email
Wechat
Bluesky

Abstract

To address the issues of short lifespan and high pulsation rates in existing radial piston hydraulic motors, this study focused on the design and optimization of the guide curve based on contact stress analysis. Initially, a thorough mechanical analysis and mathematical modeling of the piston rollers were conducted, taking into account friction forces. Using a six-action, eight-piston motor as a case study, the movement patterns of the pistons were extensively analyzed, and the corresponding torque was calculated. An extended acceleration zone approach was employed to develop a mathematical model of the guide curve, aimed at achieving constant contact stress without pulsation. Finally, the nondominated sorting genetic algorithm (NSGA-II) was utilized to optimize the lifespan of the guide, resulting in a guide curve that ensures a longer operational lifespan and low pulsation rate. This design method for the guide curve offers a critical reference for optimizing the design of internal curve radial piston motors, which require stringent control over both lifespan and pulsation rates.

1. Introduction

Hydraulic actuation is a crucial element in various machinery and equipment [1, 2]. Radial piston hydraulic motors are extensively utilized in hydraulic transmission systems for ships, ports, construction, and metallurgical machinery due to their high mechanical and volumetric efficiencies, as well as their ability to provide substantial torque at low speeds [3, 4]. Furthermore, these motors are recognized for their exceptional low-speed stability and minimal noise levels. Within these motors, the cam ring serves as a vital component of the internal curve motor, and the design of the guide rail’s curve is pivotal for the motor’s overall performance and durability. A poorly designed guide rail curve can result in heightened noise levels, frequent impacts, and accelerated wear, consequently diminishing the motor’s lifespan [5, 6]. The configuration of the guide rail’s curve directly impacts the trajectory of the piston roller’s movement, thereby impacting critical parameters such as the distribution of contact stress and the guide rail’s longevity.

Recent studies have extensively focused on enhancing the design of guide rail curves; however, there are still deficiencies in the existing methods. The concept of equal contact stress in guide rail curves was first introduced by Yang et al. [7]. Wang et al. and Huang et al. [8, 9] utilized the Hertz theory and force analysis of the piston subassembly to establish differential equations for determining maximum equal contact stresses. These equations were then solved using MATLAB to obtain numerical solutions for evaluating various performance aspects of the guide rails. However, these studies did not address the pulsation issues that occur during the overall motion of the pistons. Liu et al. developed a guide rail curve that could eliminate piston pulsation by considering the concept of equal contact stress. However, this analysis did not account for the friction effects, thereby restricting the practical utility of the model.

Firth and Cunningham [10] implemented a trapezoidal acceleration curve in the guide rail design to minimize the flexible impact between the roller and the guide rail, albeit leading to a slight increase in the maximum contact stress. Li and Wang [11] employed a cosine acceleration curve for the guide rail design, resulting in higher acceleration in the oil inlet zone, which elevated the contact stress at the initial curve and consequently rendered the inner side of the guide rail more susceptible to pitting and spalling. Likewise, there are designs that opt for a sinusoidal acceleration curve for the guide rail, characterized by acceleration values defined by a sine function, effectively enhancing the acceleration by π/2 compared to a constant acceleration curve. Sinusoidal acceleration curves, in comparison to cosine acceleration curves, exhibit a smaller rise near the beginning of the acceleration zone and reduced curvature, thereby effectively mitigating contact stress between guide rails. However, this design’s drawback is the generation of relatively larger pulsations.

Yu et al. [12] proposed the concept of utilizing a high-order differentiable and continuously closed curve, known as the modified cardioid, for the purpose of guide rail curve design. This approach has been effective in mitigating internal shocks within the motor system, particularly in engines with an odd number of pistons. Engines with an even number of pistons exhibit a higher pulsation rate in comparison to those with an odd number. Zhang et al. [13] employed the genetic algorithm (GA) to develop higher-order curves. The resultant guide rail curves offer seamless transitions in velocity, acceleration, reaction forces, and maximum contact stress, thereby eliminating impacts and showcasing a lower pulsation rate than the modified cardioid. However, the process of solving the associated equations is complex, and challenges related to pulsation persist.

An et al. [14] explored the impact of guide rail curve cam angle allocation on contact stress, velocity, and acceleration. The study effectively addressed issues related to the inability to allocate nonpulsating cam angles or the failure to generate zero-speed zones at low angle allocation coefficients. This development helped mitigate the design constraints of curves and prevented the shock associated with oil shut-off during flow distribution. Zhang et al. [15] developed a quasiactual mechatronic instrument capable of replicating real-world operating conditions to test roller-piston friction pairs in hydraulic motors, addressing the lack of cost-effective testing tools for wear and reliability analysis. Xin et al. [16, 17] introduced a novel design of generalized elliptical stator curves for double-ball piston hydraulic motors and performed a comprehensive analysis of the motor’s performance characteristics. Zhang et al. [18] proposed a self-compensation oil distributor (SCOD) for hydraulic motors, which reduces oil leakage and power loss by autoadjusting interface spacing through balancing pistons and floating seal sleeves, ensuring efficient operation. Gao et al. [19, 20] focused on the design and analysis of stator curves for six-action, ten-piston water hydraulic motors. Zhang et al. [21] developed a composite thermal lubrication model for hybrid journal bearings, incorporating four thermal effects and actual surface roughness, to evaluate friction and temperature characteristics under low-speed, heavy-load conditions, with experimental validation.

Given the critical importance of designing guide rail curves that ensure a long service life and eliminate pulsation in piston motors, this paper employs multiple research methodologies. Firstly, a thorough mechanical analysis and mathematical modeling of piston rollers are conducted to deeply explore the conditions for achieving equal contact stress in guide rails. Subsequently, the motion laws of hydraulic motor pistons are discussed in detail, and the torque of the piston rollers is calculated. Using a six-action, eight-piston motor as a case study, methods to eliminate torque pulsation by increasing the equal acceleration zone are examined. Ultimately, a multiobjective optimization of lifespan and torque for the nonpulsating, equal-stress guide rail curve model is performed.

The nondominated sorting genetic algorithm (NSGA-II) is a robust decision space exploration tool derived from GA framework, specifically designed for addressing multiobjective optimization problems (MOOPs) [22]. This algorithm effectively distinguishes between superior and inferior solutions by employing rapid nondominated sorting, maintains population diversity through the concept of crowding distance, incorporates an elitism strategy to improve search efficiency, and offers easily adjustable parameter settings for seamless implementation. The NSGA-II is particularly well suited for tackling complex multiobjective problems. The application of the NSGA-II in obtaining Pareto optimal solutions resulted in the development of a nonpulsating, equal-stress guide rail curve for radial piston hydraulic motors, leading to enhanced longevity and torque output. This technological development significantly advances both the theoretical understanding and practical implementation in the design of radial piston motors.

2. Equal Contact Stress Guide Rail Curve Analysis

Under the impact of hydraulic pressure, the roller’s movement along the curved guide rail can lead to fluctuations in contact stress, resulting in pitting and spalling on the inner side of the guide rail. To address this issue, the study proposes dividing the guide rail curve in the oil inlet zone into two segments for design considerations. The first segment is the equal contact stress curve, which is intended to ensure consistent contact stress distribution. This design strategy is aimed at improving the wear resistance of the guide rail.

2.1. Single-Piston Contact Stress Analysis

Under the impact of the hydraulic cylinder’s propulsion, the roller travels along the curved trajectory defined by the guide rail. The guide rail applies a reaction force on the roller, inducing its rotation. The specific orientation of this force is illustrated in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Force analysis of roller assembly.

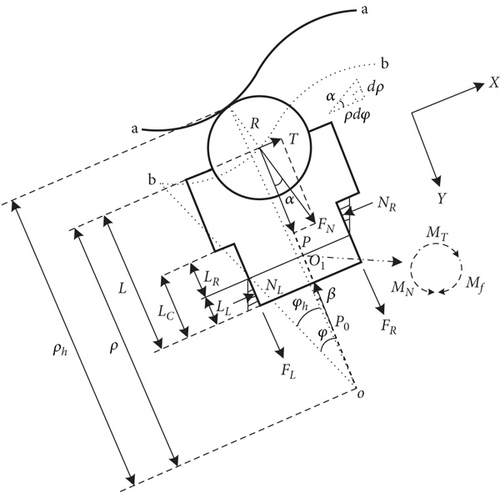
In Figure 1, the curve “a-a” represents the actual guide rail curve at the contact points between the roller and the guide rail, while the curve “b-b” represents the theoretical guide rail curve depicting the motion trajectory of the roller’s center. The theoretical guide rail curve “b-b” provides a more precise reflection of the roller’s motion state [23]. Therefore, this study primarily focuses on the theoretical guide rail curve “b-b” and derives the actual guide rail curve “a-a” through an outward extrapolation. The distance from the roller center to the rotor center ρ is referred to as the polar radius. The distance to the guide rail is ρ_h. The total piston length L is the distance from the roller center to the bottom of the piston, while the effective piston length L_C is the part of the piston in contact with the rotor.

The angular velocity of the roller ρ^′ is determined as follows:

(1)

The angular acceleration ρ^″ of the roller is obtained as follows:

(2)

The main forces acting on the roller during its motion are detailed as follows:

The reaction force exerted by the guide rail on the roller is F_N. This force can be decomposed into two components: the radial force P and the tangential force T according to the pressure angle α:

(3)

The hydraulic pressure at the bottom of the hydraulic cylinder is P₀. The static pressure of the hydraulic oil within the piston cylinder bore is p, and the diameter of the piston cylinder’s bottom is d:

(4)

As the roller moves, the normal pressures acting on the piston are N_R and N_L. The slope of the exerted force is q:

(5)

The frictional forces encountered by the piston during its entry and exit are F_R and F_L, respectively, with f denoting the coefficient of friction:

(6)

Using o₁ as the reference point for torque balance, the following equation can be derived:

(7)

The torque components of the tangential force M_T, the normal pressure M_N, and the frictional force M_f are calculated as follows:

(8)

By combining Equations (7) and (8), the solution is obtained as follows:

(9)

By combining Equations (5), (6), and (9), the solution is given as follows:

(10)

In the simplified model of the piston roller, the piston assembly is subjected to different forces along the X- and Y-directions. Along the X-direction, it experiences the tangential component of force T and the normal pressures N_R and N_L on both sides. Along the Y-direction, it is subjected to the radial component of force P, friction forces F_R and F_L, and the hydraulic oil pressure P₀ at the bottom of the piston.

The force balance equation in the X-direction is determined as follows:

(11)

The force balance equation in the Y-direction is calculated as follows:

(12)

The equation for calculating the pressure angle α is given as follows:

(13)

By solving simultaneous Equations (11)–(13), the following results can be derived:

(14)

By integrating the practical working conditions of the roller with the Hertzian contact theory [24–26], the line contact existing between the roller and the inner surface of the guide rail is simplified to a contact scenario resembling that of two cylinders [27]. Figure 2 depicts the contact interaction between the roller and the guide rail, with the maximum contact stress between the two elastic bodies being determined as follows:

(15)

where ρ^∗ is the equivalent curvature radius of the guide rail, E^∗ is the equivalent elastic modulus, and μ₁ and μ₂ are Poisson’s ratios of the rolling element and the rolling material, respectively, while E₁ and E₂ are the elastic moduli of the rolling element and the raceway material, respectively.

(16)

where R_C is the radius of curvature of the guide rail curve at a given point.

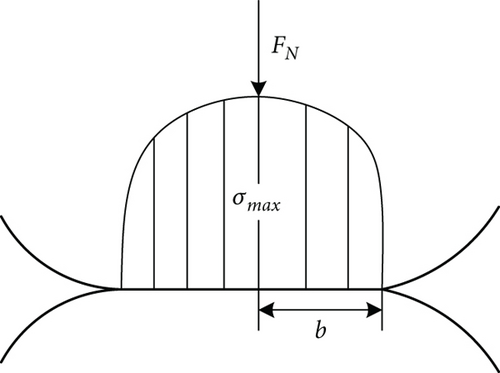
2.2. Solution for Equal Contact Stress Conditions

To maintain the maximum contact stress σ_max constant on the guide rail, the following condition must be met:

(17)

Therefore, to obtain the curve of equal contact stress, it is essential to solve the following equation:

(18)

Assigning specific values to each variable as follows

(19)

Subsequently, the following equations can be derived below:

(20)

2.3. Mathematical Modeling and Analysis

To simplify the computation process, it is recommended to utilize the mathematical software MATLAB for solving the equations. It can be initially set as follows:

(21)

Consequently, the original differential equations for the equal contact stress curve can be transformed as follows:

(22)

The paper uses a six-action, eight-piston radial piston hydraulic motor as a case study, presenting the initial values of the pertinent parameters in Table 1.

Table 1. Initial parameters for equal contact stress guide rail curve.

Parameter	Meaning	Value
ρ (m)	Polar radius	0.05622
ρ^′ (m/s)	Angular velocity	0
ρ^″ (m/s²)	Angular acceleration	0.142
ρ^‴ (m/s³)	Angular jerk	0.005
f	Coefficient of friction	0.08
L_C0 (m)	Initial effective length of the piston	0.02218
L (m)	Total length of the piston	0.031
R (m)	Radius of the roller	0.01
p (Pa)	Static hydraulic pressure	3∗10⁷
l (m)	Width of the roller	0.02
E₁ (Pa)	Young’s modulus of the guide rail material	2.16∗10⁵
9 (Pa)	Young’s modulus of the roller material	2.19∗10⁵
μ₁	Poisson’s ratio of the guide rail material	0.3
μ₂	Poisson’s ratio of the roller material	0.3

In MATLAB, the solver for the system of differential equations based on Equations (21) and (22) should be programmed initially. Subsequently, utilizing the initial values provided in Table 1, all the necessary initial values for the system of differential equations for the equal contact stress curve should be calculated. Following this, the system of equations should be solved using MATLAB’s implicit differential equation solver ode15i, with the specified range set. The numerical solution of the curve is illustrated in Figure 3.

The solver ode15i’s adaptive step size setting during the solution process results in uneven angles in the numerical solution of the curve. To calculate the nonpulsating torque curve’s next step, the uniform polar radius ρ, along with its first and second derivatives (i.e., ρ^′ and ρ^″), is required. Initially, a fitting method is utilized to process ρ, followed by derivative operations on the fitted curve to derive ρ^′ and ρ^″. However, discrepancies were observed between ρ^′ and ρ^″ obtained from the derivative operations and the original curve. Consequently, it was decided to fit the curve ρ and its derivatives ρ^′ and ρ^″, separately. Through an examination of residual plots before and after fitting, it was determined that a seventh-degree polynomial offers the best fit. Figure 4 illustrates the comparison before and after the fitting process.

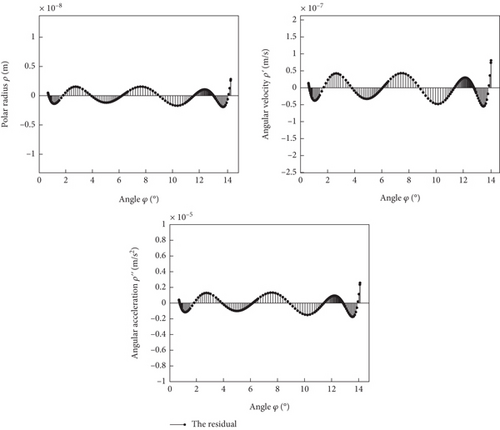
The coefficient values for the fitting equations are detailed as follows: For ρ, the coefficients of the fitting equation are 1.907, −0.982, 0.414, 0.025, 0.020, 0.066, −0.0016, and 0.056; for ρ^′, the coefficients of the fitting equation are 39.5, −22.2, 7.01, −0.339, 0.346, 0.048, 0.133, and −0.001; and for ρ^″, the coefficients of the fitting equation are 1113, −725, 229, −32.4, 5.52, 0.665, 0.106, and 0.133.

3. Nonpulsating Equal-Stress Guide Rail Curve Analysis

The guide rail curve in the initial section employs an equal contact stress design approach primarily to improve the wear resistance of the inner side of the guide rail. However, this guide rail curve with equal contact stress may lead to excessive torque pulsation. Consequently, in the subsequent section, the guide rail curve is formulated utilizing a no-torque-pulsation technique, which is integrated with the equal contact stress curve from the preceding section to mitigate the impact of pulsation. This design method is intended to enhance the stability of the piston motion.

3.1. Multipiston Nonpulsating Motion Strategy

Figure 5a illustrates a schematic diagram of the guide rail curve for a six-action, eight-piston radial piston hydraulic motor. In this diagram, Piston Number 1 is positioned at the initiation of the return oil zone, while Piston Number 3 is located at the commencement of the oil inlet zone. The guide rail curve is then unfolded, with the shaded zone denoting the oil inlet zone and the unshaded portion representing the return oil zone. These two zones collectively form a piston action zone, with a dimension of 2π/x. Subsequently, the positions of the pistons are distributed and depicted on the unfolded curve diagram, with each piston being separated by a distance of 2π/y (Figure 5b).

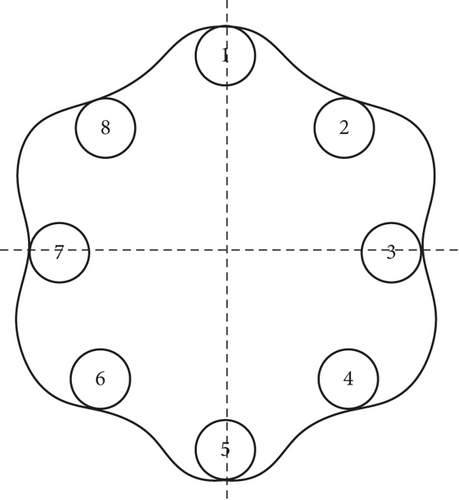
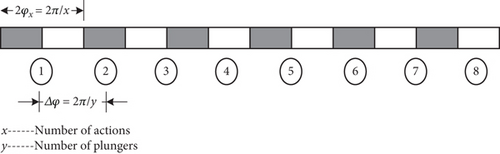
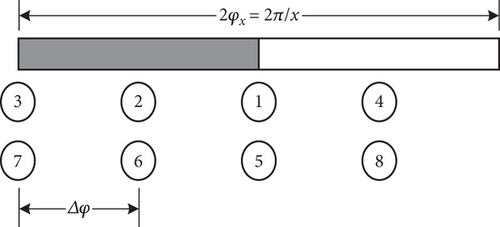
In Figure 5b, Piston Number 3 and Piston Number 7 occupy identical positions within the piston action zone. Similarly, Pistons Number 2 and Number 6, Number 1 and Number 5, and Number 4 and Number 8 are also situated at corresponding locations along the action curve. Consequently, these four pairs of pistons can be accommodated within a single action angle, with each pair separated by 2π/x/4 = 15^° (Figure 5c), where Δφ is the periodic angle. When the piston motor advances by one periodic angle, all pistons revert to their initial positions. In essence, the movement of the pistons undergoes continuous variations with Δφ as the period. Therefore, this study focuses only on examining the alterations of pistons within one action angle.

Figure 6 illustrates the segmentation of the guide rail curve within a single action angle. The left side φ_x is the oil inlet zone, while the right side φ_x is the oil outlet zone, with each piston separated by Δφ. The guide rail curve is symmetrically divided within one action angle. Moving from left to right, the curve in the oil inlet zone consists of the zero-speed zone, equal contact stress zone, constant acceleration zone, pulsation compensation zone, and another zero-speed zone. As one piston reaches the beginning of the zero-speed zone, another piston is precisely positioned at the midpoint of the constant acceleration zone. Subsequently, as the former piston regresses by angular size of the zero-speed zone φ₀ into the equal contact stress zone, the latter piston enters the pulsation compensation zone. When the former piston transitions from the equal contact stress zone back into the constant acceleration zone, the latter piston moves from the pulsation compensation zone to φ₀. This zoning strategy ensures that pulsations in piston motion are effectively minimized.

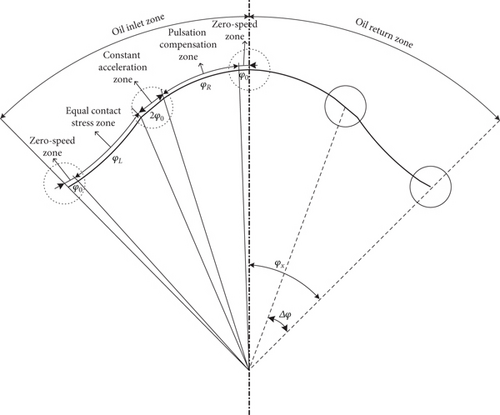
The zero-speed zone is established to prevent oil transfer occurrences when the piston transits the interface between the oil return zone and the oil inlet zone. Inadequate sizing of φ₀ can result in oil crossover, while an excessively large zone may cause oil entrapment and consequential operational issues. Typically, φ₀ is configured within the range of 0.5°–1.5°. In this study, φ₀ is designated as 1°. Within the zero-speed zone, the guide rail curve is configured in an arc shape, ensuring that both ρ^′ and ρ^″ of the piston are maintained at zero within this zone.

In the equal contact stress zone, when the piston roller approaches the oil inlet position, high-pressure oil exerts force on the piston, causing it to move outward along the bore wall. In this process, ρ^′ of the piston initially begins at zero and then rapidly increases, while ρ^″ also starts from zero and experiences a sudden rise. Consequently, there is a significant change in the contact stress. Therefore, the area of equal contact stress plays a crucial role in determining the lifespan of the motor’s guide rail. The dimension of this zone is expressed as φ_x/2 − φ₀ = 14^°.

In the constant acceleration zone, the piston roller experiences uniform acceleration. Within this zone, ρ^′ of the piston remains constant, while ρ^″ is zero. This design of the curve guarantees that when the piston in this zone synchronizes with another piston in the zero-speed zone, the motion pulsation remains at zero, and the contact stress also undergoes a sudden decrease. The length of the constant acceleration zone is established as twice that of φ₀, which, in this case, is set at 2°.

In the pulsation compensation zone, the piston roller experiences deceleration, causing its ρ^′ to gradually decrease until it reaches zero. Consequently, the contact stress between the roller and the guide rail decreases as well. The main purpose of the pulsation compensation zone is to collaborate with the equal contact stress zone to guarantee that the pulsation in the piston’s movement remains at zero.

Within the first half of the action angle range (0, φ_x), the trajectory of the roller center’s motion in the zero-speed zone is symbolized as ρ₀(φ). The trajectory of the roller center’s motion in the zone of equal contact stress is indicated as ρ₁(φ), in the area of constant acceleration as ρ₂(φ), in the pulsation compensation zone as ρ₃(φ), and in the other zero-speed zone as ρ₀(φ) + h.

Therefore, the trajectory of the roller center’s motion in the oil inlet zone can be depicted as Figure 7.

The expression equation is given as follows:

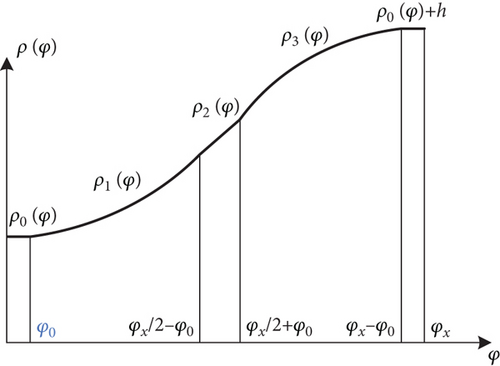
In the constant acceleration zone, the curve is depicted as a sloping straight line. At the onset of the constant acceleration zone, the polar radius and ρ^′ are equivalent to those at the endpoint of the equal contact stress zone, given their adjacency.

The equation is expressed as follows:

(23)

3.2. Nonpulsating Guide Rail Curve Analysis

Based on Equations (3), (6), and (12), the radial force on the piston roller can be calculated as follows:

(24)

Further analysis reveals that the forces exerted on the roller can be represented by the following equation:

(25)

Consequently, the tangential force T_F on the roller can be expressed as follows:

(26)

Assuming the polar radius of the roller center is ρ_i, the instantaneous torque for each piston can be represented as follows:

(27)

Considering that multiple pistons are operating in the oil inlet zone, the total torque of the hydraulic motor can be expressed as follows:

(28)

The pulsation rate of the hydraulic motor is defined as follows:

(29)

where M_av = pV/2π = pd²hxy/8 is the average output torque of the motor.

Therefore, to ensure that the output torque pulsation rate is zero, the total torque M in the oil inlet zone must remain constant. By assuming the condition as follows

(30)

Therefore, the condition for achieving nonpulsating torque output is given as follows:

(31)

Subsequently, the following equation can be derived below:

(32)

In Figure 5, two sets of pistons exhibiting identical motion patterns are in operation. For the purposes of this study, the initial set of pistons is chosen. In a full cycle, the sequence of pistons from left to right is as follows: Piston Number 3, Piston Number 2, Piston Number 1, and Piston Number 4 (Figure 5c). When determining the output torque, it is essential to aggregate the torque fluctuations of the pistons within the oil inlet zone.

For Piston Number 3, as it transitions to the equal contact stress zone, its phase angle falls within the range of (φ₀, φ_x/2 − φ₀). In this interval, the polar radius variation can be described by the following equation:

The corresponding torque pulsation calculation is given as follows:

(33)

When Piston Number 3 is located within the zone of equal contact stress, Piston Number 4 is situated in the pulsation compensation zone, characterized by a phase angle of (φ_x/2 + φ₀ ~ φ_x − φ₀). The equation governing the variation in polar radius within this zone is expressed as follows:

The corresponding torque pulsation is expressed as follows:

(34)

Through the aforementioned analysis, by substituting Equations (33) and (34) into the no-torque pulsation Equation (31), the subsequent equation can be deduced as follows:

(35)

Furthermore, the differential equation for the velocity balancing zone can be derived as follows:

(36)

Given that the velocity balancing zone is contiguous to the constant acceleration zone, the polar radius and ρ^′ at the initiation of the velocity balancing zone are equivalent to those at the conclusion of the constant acceleration zone. This relationship can be explicitly expressed as follows:

(37)

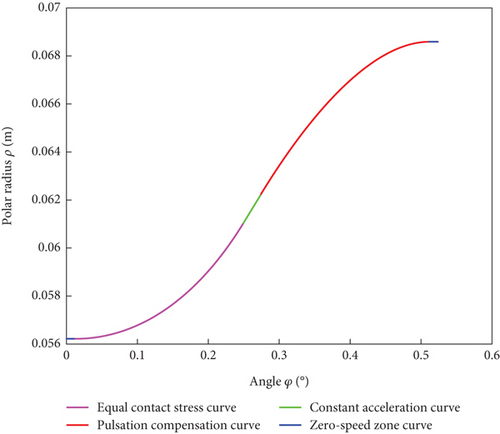
Finally, by using the ode45 solver in MATLAB, it is possible to solve the guide rail curve within the range of (φ_x/2 + φ₀ ~ φ_x − φ₀), which is denoted as ρ₃(φ).

Therefore, this study has effectively resolved the entire theoretical curve within a half action angle (Figure 8).

3.3. Calculation and Solution of Actual Guide Rail Curves

In Figure 1, the curve formed at the contact point between the roller and the guide rail, when the roller moves along the guide rail, is referred to as the actual curves ρ_h with the phase angle φ_h. The angle between the polar radius of the roller center and the polar radius at the guide rail contact point is β. Its calculation is expressed as follows:

(38)

Consequently, the mathematical expression for ρ_h is given as follows:

(39)

The equation for calculating φ_h is given as follows:

(40)

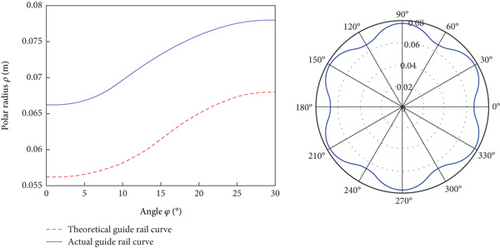
After solving in MATLAB, the representation of the actual curve can be obtained (Figure 9).

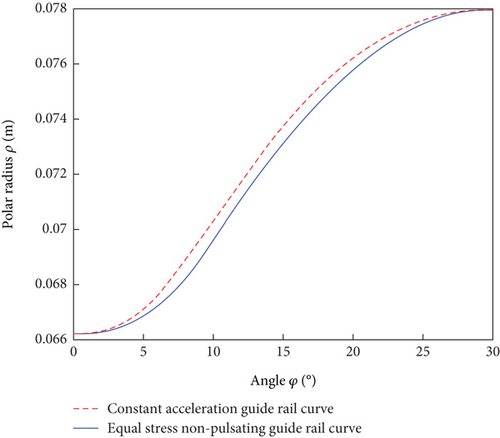
3.4. Comparison With the Constant Acceleration Guide Rail Curve

Based on Yu et al. [28], this study developed a constant acceleration guide rail curve with an equivalent φ₀ and displacement compared to the previously proposed nontorque pulsating guide rail curve with equal contact stress (Figure 10). The comparison of contact stress levels is illustrated in Figure 11. The analysis reveals that the maximum contact stress of the guide rail curve proposed in this research is approximately 300 MPa lower than that of the constant acceleration guide rail curve. Consequently, the service life extended from 1400 to nearly 3400 h. The equation for estimating the lifespan is given as follows:

(41)

where z = 8 is the number of pistons in a single row of the motor, n = 100 is the rated speed, [σ_c] = 3800 is the allowable contact stress for the guide rail material, and σ_c is the actual calculated contact stress.

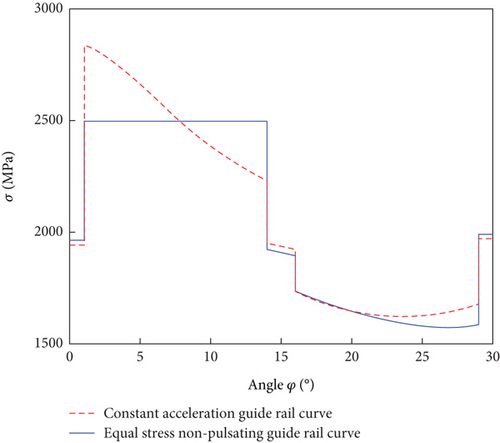
4. Multiobjective Optimization

MOOPs present challenges due to conflicting optimized objectives. Finding an optimal solution that fulfills all objectives is typically complex from a mathematical perspective. In contrast to analytical and classical numerical methods that necessitate precise mathematical computations or predetermined initial search values, intelligent optimization algorithms, as heuristic algorithms, have the capability to identify global optimal solutions [29].

When addressing multiobjective optimization challenges, it is essential to initially establish a clear definition of the design variables, objective functions, and constraints. This includes objectives such as maximizing output and minimizing costs. Subsequently, a suitable algorithm, such as GA or particle swarm optimization (PSO), should be chosen. These algorithms have the capability to produce a range of solutions that constitute a Pareto front. This front encompasses diverse optimization results within the objective space.

4.1. Multiobjective Optimization Strategy Modeling

Through the analysis of the equal-stress nonpulsating guide rail curve model, it has been determined that a reduction in ρ^″ can lead to a decrease in the contact stress σ, consequently prolonging the lifespan L_h of the guide rail. However, a decrease in ρ^″ may result in a reduction in the starting torque M_T, thereby impacting the startup efficiency. Conversely, an increase in ρ^″ has the potential to improve M_T, but it also raises the contact stress σ, thereby shortening L_h. Therefore, it is imperative to strike a balance between these two factors by adjusting the parameters of the equal-stress nonpulsating guide rail curve to achieve an extended L_h and enhanced startup efficiency. While the optimization objectives of maximizing L_h and maximizing starting M_T are inherently conflicting and cannot be simultaneously optimized, they can be approximated to optimal conditions through compromise and coordination. Consequently, this study introduces multiobjective optimization algorithms to approach this desired equilibrium.

The multiobjective optimization model for this study aims to maximize L_h and starting M_T while adhering to the constraints of the guide rail curve. The specific mathematical model description is expressed as follows:

Subject to:0 ≤ ρ^″ ≤ 0.23, 0.5 ≤ φ₀ ≤ 1.5, 392 ≤ V ≤ 408, where F₁ and F₂ are the lifespan and starting torque of the equal-stress nonpulsating guide rail curve, respectively, ρ^″ is the angular acceleration of the guide rail curve, φ₀ is the angular size of the zero-speed zone, and V is the displacement.

Since ρ^″ and φ₀ impact the motion stroke of the piston roller, they consequently determine the displacement of the motor, which is specified at 400 mL with a permissible error margin of ±2%.

4.2. NSGA-II Optimization

To enhance both longevity and initial torque, this study utilizes the NSGA-II for multiobjective optimization. In contrast to conventional algorithms, the NSGA-II offers benefits by integrating nondominated sorting and crowding distance mechanisms. These characteristics empower the algorithm to efficiently recognize and uphold a collection of Pareto optimal solutions, where no solution outperforms another. Additionally, the NSGA-II’s elitism approach, which conserves superior parents and offspring from the prior generation, effectively upholds high-quality solutions, thereby improving the algorithm’s robustness and convergence speed. The workflow of the NSGA-II is depicted in Figure 12, with the main steps described as follows:

1.
The population is initialized, and algorithm parameters are set.
2.
Calculate the population’s objective values and violations, and normalize the violations.
3.
The population’s objective values and violations are calculated, followed by the normalization of these violations.
4.
Selection, crossover, and mutation are performed on the current population to generate new offspring.
5.
The objective values and violations of the new offspring are evaluated, and they are then merged with the parent generation to form an intermediate population.
6.
Nondominated sorting and crowding distance calculations are conducted on the intermediate population to select the next generation.

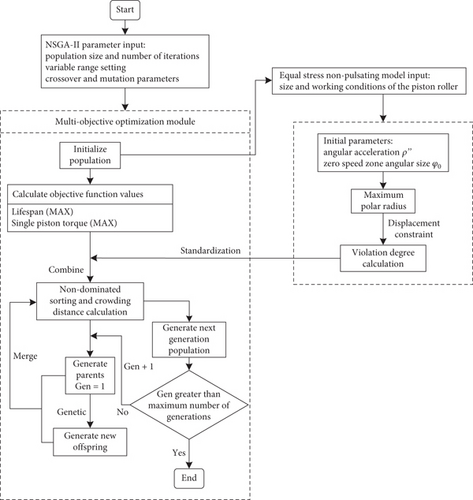
In this algorithm, the utilization of simulated binary crossover (SBX) and polynomial mutation strategies is employed. Parents are selected optimally through a binary tournament selection process to generate superior offspring effectively. The specific parameter settings for this algorithm are outlined in Table 2.

Table 2. Parameter settings for the NSGA-II.

Parameter	Value
Population size	100
Number of iterations	300
Crossover distribution index	10
Mutation distribution index	60
Mutation probability	60

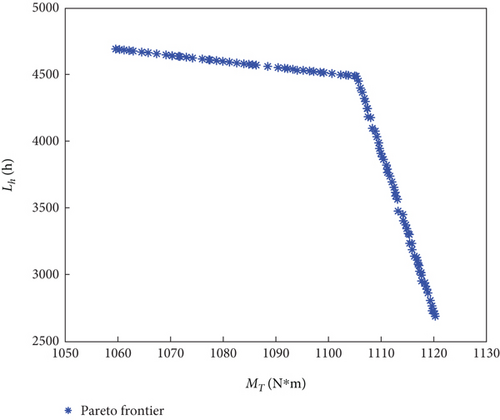
4.3. Optimization Results and Pareto Frontier Analysis

After the completion of the optimization algorithm, a collection of Pareto optimal solutions was derived for the equal contact stress nonpulsating guide rail curve model, considering L_h and M_T. The particular Pareto front is depicted in Figure 13.

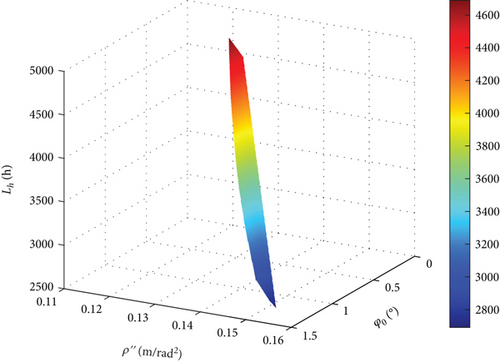
Within a zero-speed zone (Figure 14), φ₀ is approximately 1.5°, leading the system to converge to a local optimum. As ρ^″ decreases, the system progressively moves away from the local optimum, leading to an extended L_h, accompanied by a gradual decrease in M_T.

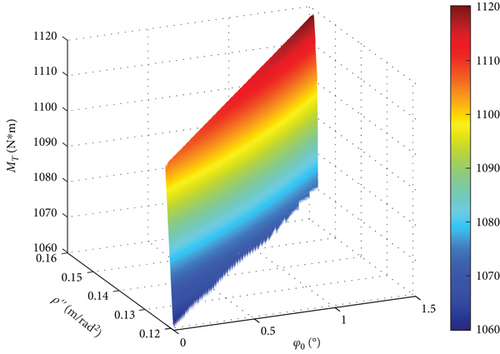
4.4. Entropy Weighting Method for Pareto Solution Selection

The entropy weight method is a decision analysis technique rooted in the concept of information entropy. It is predominantly employed to ascertain the weights of different evaluation indicators. Information entropy serves as a statistical metric that measures the level of chaos within data. The fundamental premise is that indicators with higher variability convey more information and possess lower certainty, thereby warranting a reduced weight in the analysis as follows:

For MOOPs, the entropy weight method serves as a tool for the objective evaluation and comparison of the significance of various objectives. Consequently, it offers a rational mechanism for distributing weights in multiobjective optimization.

Firstly, the objective values are standardized as follows:

After standardization, the entropy of each objective is calculated to assess the dispersion of the data as follows:

where p_ij is the proportional value of the i solution on the j objective.

The weight of each objective is determined based on the entropy values. This calculation of weights serves to indicate the significance of each objective within the comprehensive evaluation. The weight equation is expressed as follows:

where k is the total number of objectives.

Finally, the calculated weights are used to score each solution to determine the optimal solution. The scoring equation is expressed as follows:

Based on Score_i, the optimization solution with the highest Score_i is selected. The comparison of the equal-stress nonpulsating guide rail curve parameters before and after optimization is shown in Table 3.

Table 3. Comparison of optimization parameters.

		Initial value	Optimized solution
Variable	9	1	0.1
Variable	ρ^″	0.142	0.124
Objective function value	L_h	3412	4370
Objective function value	M_T	1088	1106

Table 3 illustrates that following optimization using the NSGA-II, the optimized values satisfy the constraints. The optimized solution’s lifespan increased from 3412 to 4370 h, marking a 28% enhancement compared to the initial values. Additionally, the maximum torque per piston rose from 1088 to 1106 Nm, reflecting a 1.65% increase.

4.5. Comparison of Optimization Results

Figure 15 depicts a comparison of single-piston torque and contact stress in the oil inlet zone before and after optimization. The analysis indicates that following the optimization process, there was a negligible increase in torque, while the contact stress reduced by approximately 100 MPa. Consequently, the lifespan of the component extended by nearly 1000 h.

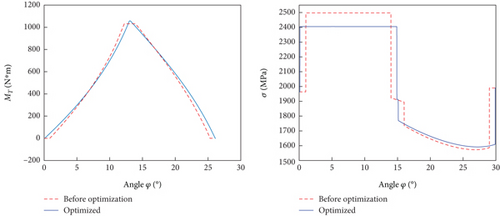
Figure 16 presents the torque generated by individual pistons as the motor rotor undergoes a 60° rotation. With the rotor’s 60° rotation, four pistons have contributed to generating torque. Analysis of the torque overlay reveals that the overall torque postoptimization has risen by 60 N·m in comparison to the preoptimization state.

The torque pulsation of a motor, excluding external factors such as leakage, friction, and hydraulic compression, is primarily dependent on the guide rail curve. The equation for calculating the motor’s torque pulsation rate is expressed as follows:

where M_Tmax is the maximum superimposed torque, M_Tmin is the minimum superimposed torque, and M_Tavg is the average superimposed torque.

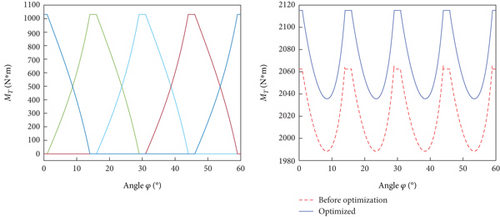
The calculation results indicate that the torque pulsation rate was δ = 3.76% before optimization and slightly increased to δ = 3.80% after optimization. This change is minimal and remains within the acceptable range of ±2%.

5. Conclusion

This paper proposes a groundbreaking guide rail curve design that integrates equal contact stress distribution and nonpulsating torque characteristics. The design effectively mitigates key issues in radial piston hydraulic motors, such as excessive pulsation and limited lifespan, paving the way for enhanced motor reliability and efficiency.

Through an in-depth analysis of piston motion and force dynamics, the study introduces a zoning strategy that incorporates zero-speed zones, equal contact stress zones, and pulsation compensation zones. This ensures stable piston motion, reduced wear, and minimized stress fluctuations.

By employing the NSGA-II, a multiobjective optimization framework was established to balance conflicting objectives, such as extending guide rail lifespan and maximizing torque output. The optimized design achieved a lifespan increase of over 28% and improved torque consistency, validating the effectiveness of the proposed approach.

This study offers a robust theoretical foundation and practical guidance for the design and optimization of internal curve radial piston motors. Its contributions are particularly valuable for high-demand applications, such as construction machinery, marine equipment, and heavy-duty hydraulic systems, where precise control and enhanced durability are critical.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the National Natural Science Foundation of China (grant number 51805228), the Natural Science Research of Jiangsu Higher Education Institutions of China (grant numbers 22KJB460021, 23KJA460006), and the Changzhou Leading Innovative Talents Introduction and Cultivation Project (grant numbers CQ20210093, CQ20220089).

Open Research

Data Availability Statement

Research data are not shared.

References

1 Dasgupta K., Mandal S. K., and Pan S., Dynamic Analysis of a Low Speed High Torque Hydrostatic Drive Using Steady-State Characteristics, Mechanism and Machine Theory. (2012) 52, 1–17, https://doi.org/10.1016/j.mechmachtheory.2011.12.004, 2-s2.0-84859600437.
10.1016/j.mechmachtheory.2011.12.004
Web of Science® Google Scholar
2 Mehta V. and Rath S. N., 3D Printed Microfluidic Devices: A Review Focused on Four Fundamental Manufacturing Approaches and Implications on the Field of Healthcare, Bio-Design and Manufacturing. (2021) 4, no. 2, 311–343, https://doi.org/10.1007/s42242-020-00112-5.
10.1007/s42242-020-00112-5
Web of Science® Google Scholar
3 Olsson H. and Ukonsaari J., Wear Testing and Specification of Hydraulic Fluid in Industrial Applications, Tribology International. (2003) 36, no. 11, 835–841, https://doi.org/10.1016/S0301-679X(03)00101-4, 2-s2.0-0141458100.
10.1016/S0301-679X(03)00101-4
CAS Web of Science® Google Scholar
4 Pettersson U. and Jacobson S., Textured Surfaces for Improved Lubrication at High Pressure and Low Sliding Speed of Roller/Piston in Hydraulic Motors, Tribology International. (2007) 40, no. 2, 355–359, https://doi.org/10.1016/j.triboint.2005.11.024, 2-s2.0-33748789841.
10.1016/j.triboint.2005.11.024
CAS Web of Science® Google Scholar
5 Liu Y., Gu L., Yang B., Wang S., and Yuan H., A New Evaluation Method on Hydraulic System Using the Instantaneous Speed Fluctuation of Hydraulic Motor, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. (2018) 232, no. 15, 2674–2684, https://doi.org/10.1177/0954406217722576, 2-s2.0-85045447203.
10.1177/0954406217722576
Web of Science® Google Scholar
6 Liu Y., Deng Y., Fang M., Li D., and Wu D., Research on the Torque Characteristics of a Seawater Hydraulic Axial Piston Motor in Deep-Sea Environment, Ocean Engineering. (2017) 146, 411–423, https://doi.org/10.1016/j.oceaneng.2017.10.004, 2-s2.0-85032701107.
10.1016/j.oceaneng.2017.10.004
Web of Science® Google Scholar
7 Yang G. L., Huang Z. X., Li X. B., and Zhao J., Effect of Argument Distribution on Performance of Larger Displacement Radial Piston Pump, Chinese Hydraulics & Pneumatics. (2016) no. 6, 1–7, https://doi.org/10.11832/j.issn.1000-4858.2016.06.001.
10.11832/j.issn.1000-4858.2016.06.001
Google Scholar
8 Wang Q., Liu L., Gong C. Y., Qu C., and Yi Y. L., Contact Nonlinear Analysis of Hydraulic Differential Spiral of Horizontal Spiral Filter Centrifuge Based on Ansys, Machine Tool & Hydraulics. (2014) 42, no. 23, 144–149, https://doi.org/10.3969/j.issn.1001-3881.2014.23.036.
10.3969/j.issn.1001-3881.2014.23.036
Google Scholar
9 Huang F., Huang F. P., and Shen M. H., Accurate Drawing of Internal Curves of Contact Stress in Radial Piston Hydraulic Motors, Machine Tool & Hydraulics. (2013) 41, no. 19, 148–150, https://doi.org/10.3969/j.issn.1001-3881.2013.19.042.
10.3969/j.issn.1001-3881.2013.19.042
CAS Google Scholar
10 Firth D. and Cunningham S., Improvements in Ball Piston Hydrostatic Motors or Pumps, 1970, U.K. Patent, GB1196901A. https://patents.google.com/patent/GB1122441A/en.
Google Scholar
11 Li F. C. and Wang J., Similarity Design Calculation of Performance Parameters of Cosine Inner Curve Piston Hydraulic Motor, Hydraulics Pneumatics & Seals. (2010) 30, no. 1, 20–25, https://doi.org/10.3969/j.issn.1008-0813.2010.01.009.
10.3969/j.issn.1008-0813.2010.01.009
Google Scholar
12 Yu H. Y., Zhong H. T., and Li S., The Analysis on the Flow Pulsation of Radial Piston Motor With the Modified Heart-Shaped Curve as Inner Curve, Journal of Harbin Institute of Technology. (2012) 44, no. 3, 44–48, https://doi.org/10.11918/j.issn.0367-6234.2012.03.009.
10.11918/j.issn.0367-6234.2012.03.009
Google Scholar
13 Zhang X. L., Zhang J. H., Zhang H. J., and Xu B., Optimized Design of Cam Ring Curve of Cam Lobe Radial-Piston Motor, Journal of Huazhong University of Science and Technology (Natural Science Edition). (2021) 49, no. 10, 30–35, https://doi.org/10.13245/j.hust.211005.
10.13245/j.hust.211005
Google Scholar
14 An G. C., Hu Z. H., and Dong H. Q., Design and Analysis of Guide Curve of Radial Piston Motor With Low Amplitude Angle Distribution Coefficient, Journal of Jilin University (Engineering and Technology Edition). (2023) 55, no. 2, 485–493.
Google Scholar
15 Zhang X., Zhang J., Zeng D., Zhao J., Xu B., and Zhang C., A Quasi-Actual Mechatronic Instrument for Realistically Testing Roller-Piston Friction Pairs, IEEE/ASME Transactions on Mechatronics. (2024) 29, no. 2, 1240–1248, https://doi.org/10.1109/TMECH.2023.3301117.
10.1109/TMECH.2023.3301117
Web of Science® Google Scholar
16 Xin J. B., Ke Z. R., and Wu Y., Analysis and Design on Curved Guide Orbit of Generalized Elliptic Stator for Radial Double Ball Plunger Motor, Chinese Hydraulics & Pneumatics. (2018) 10, 87–91, https://doi.org/10.11832/j.issn.1000-4858.2018.10.015.
10.11832/j.issn.1000-4858.2018.10.015
Google Scholar
17 Xin J. B., Ke Z. R., Le G. P., and Wu Y., Output Characteristics of Radial Ball Piston Motor Using Generalized Elliptic Equation Curve Guide, Chinese Hydraulics & Pneumatics. (2019) 6, 47–52, https://doi.org/10.11832/j.issn.1000-4858.2019.06.009.
10.11832/j.issn.1000-4858.2019.06.009
Google Scholar
18 Zhang X., Zhang J., Han M., Fang Y., Zhang H., Li S., Xu B., and Zhang C., Design and Optimization of Self-Compensation Oil Distributor for Hydraulic Motors, IEEE/ASME Transactions on Mechatronics. (2024) 29, no. 3, 2103–2114, https://doi.org/10.1109/TMECH.2023.3316360.
10.1109/TMECH.2023.3316360
Web of Science® Google Scholar
19 Gao D. R., Wang Z. Q., and Zhao Y. N., Analysis of Stator Curve Characteristics of Radial Low-Speed High-Torque Water Hydraulic Motor, Journal of Machine Design. (2012) 29, no. 9, 29–35, https://doi.org/10.3969/j.issn.1001-2354.2012.09.007.
10.3969/j.issn.1001-2354.2012.09.007
Google Scholar
20 Man J. X., Zhao J. Y., Wang Y. F., and Huang D., Working Characteristics of Crankshaft Swing Cylinder Water Hydraulic Motor With Flow Distribution Valve, Transactions of the Chinese Society for Agricultural Machinery. (2022) 54, no. 1, 450–458, https://doi.org/10.6041/j.issn.1000-1298.2023.01.047.
10.6041/j.issn.1000-1298.2023.01.047
Google Scholar
21 Zhang C., Zhang X., Dong P., Zhang H., Zheng Z., Zhang J., and Xu B., Composite Thermal Oil Film Lubrication Model for Hybrid Journal Bearings, Tribology International. (2024) 194, 109556, https://doi.org/10.1016/j.triboint.2024.109556.
10.1016/j.triboint.2024.109556
Web of Science® Google Scholar
22 Verma S., Pant M., and Snasel V., A Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems, IEEE Access. (2021) 9, 57757–57791, https://doi.org/10.1109/ACCESS.2021.3070634.
10.1109/ACCESS.2021.3070634
Web of Science® Google Scholar
23 Zhang C., Tan H., Fang Y., Zhang X., Yang Y., Duan Y., Han M., Cui S., Xu B., and Zhang J., Deformation Pre-Compensated Optimization Design of Cam Ring for Low Pulsation Hydraulic Motors, Journal of Zhejiang University-Science A. (2023) 24, no. 2, 130–145, https://doi.org/10.1631/jzus.A2200552.
10.1631/jzus.A2200552
Web of Science® Google Scholar
24 Johnson K. L., Normal Contact of Elastic Solids – Hertz Theory, Contact Mechanics, 1985, Cambridge University Press, 84–106, https://doi.org/10.1017/CBO9781139171731.005.
10.1017/CBO9781139171731.005
Google Scholar
25 Kong F., Huang W., Jiang Y., Wang W., and Zhao X., A Vibration Model of Ball Bearings With a Localized Defect Based on the Hertzian Contact Stress Distribution, Shock and Vibration. (2018) 2018, no. 1, 5424875, https://doi.org/10.1155/2018/5424875, 2-s2.0-85045726625.
10.1155/2018/5424875
Web of Science® Google Scholar
26 Sánchez M. B., Pleguezuelos M., and Pedrero J. I., Approximate equations for the meshing stiffness and the load sharing ratio of spur gears including Hertzian effects, Mechanism and Machine Theory. (2017) 109, 231–249, https://doi.org/10.1016/j.mechmachtheory.2016.11.014, 2-s2.0-85002799849.
10.1016/j.mechmachtheory.2016.11.014
Web of Science® Google Scholar
27 Nakhatakyan F. G. and Kosarev O. I., An Analytical Method for Solving a Problem of Cylinder-to-Cylinder Contacts at Misalignment, Journal of Machinery Manufacture and Reliability. (2012) 41, no. 2, 137–140, https://doi.org/10.3103/S1052618812020124, 2-s2.0-84859772683.
10.3103/S1052618812020124
Google Scholar
28 Yu S., Pan Y., Sun Y. W., Nie S. L., and Yi F. L., Study on the Design Method of Stator Curve and Self-Locking Problem of Water Hydraulic Motor, Machine Tool & Hydraulics. (2023) 51, no. 2, 69–75, https://doi.org/10.3969/j.issn.1001-3881.2023.02.011.
10.3969/j.issn.1001-3881.2023.02.011
Google Scholar
29 Cui Y., Geng Z., Zhu Q., and Han Y., Multi-Objective Optimization Methods and Application in Energy Saving, Energy. (2017) 125, 681–704, https://doi.org/10.1016/j.energy.2017.02.174, 2-s2.0-85014926378.
10.1016/j.energy.2017.02.174
Web of Science® Google Scholar

All articles

Optimization Design of Nonpulsating, Equal Contact Stress Guide Curves for Internal Curve Radial Piston Motors

Abstract

1. Introduction

2. Equal Contact Stress Guide Rail Curve Analysis

2.1. Single-Piston Contact Stress Analysis