Weak Population–Empowered Large-Scale Multiobjective Immune Algorithm
Abstract
The multiobjective immune optimization algorithms (MOIAs) utilize the principle of clonal selection, iteratively evolving by replicating a small number of superior solutions to optimize decision vectors. However, this method often leads to a lack of diversity and is particularly ineffective when facing large-scale optimization problems. Moreover, an overemphasis on elite solutions may result in a large number of redundant offspring, reducing evolutionary efficiency. By delving into the causes of these issues, we find that a key factor is that existing algorithms overlook the role of weak solutions during the evolutionary process. With this in mind, we propose a weak population–empowered large-scale multiobjective immune algorithm (WP–MOIA). The core of this algorithm is to construct, in addition to the traditional elite population, a cooperative evolutionary population based on a portion of the remaining solutions, referred to as the weak population. During the evolution, both populations work together: the elite population maximizes its advantageous status for local searches, focusing on exploitation, while the weak population seeks greater variation to escape its disadvantaged position, engaging in broader exploration. At the same time, the sizes of both populations are dynamically adjusted to collaboratively maintain the balance of evolution. Through comparisons with nine state-of-the-art multiobjective evolutionary algorithms (MOEAs) and four powerful MOIAs on 30 benchmark problems, the proposed algorithm demonstrates superior performance in both small-scale and large-scale multiobjective optimization problems (MOPs), and exhibits better convergence efficiency. Especially in large-scale MOPs, the new algorithm’s performance nearly surpasses all 13 advanced algorithms being compared.
1. Introduction
Due to the inherent complexity and uncertainty of MOPs, traditional deterministic methods often fail to generate satisfactory solution sets within a reasonable time. To address this issue, numerous studies have utilized evolutionary algorithms that leverage the population-based search characteristics to iteratively explore the optimal solution set. This approach makes it possible to identify multiple Pareto optimal solutions simultaneously in a single operation, significantly enhancing the efficiency of solution generation. Although evolution-inspired algorithms [5–7] have been proven to be powerful tools for tackling multiobjective optimization challenges, existing multiobjective evolutionary algorithms (MOEAs) rarely consider the scalability of decision variables in MOPs. In practical applications, MOPs with a large number of decision variables, such as ratio error estimation [8], complex dispatching model optimization [9], energy hub system planning [10], and community detection [11], are also widely prevalent. Typically, if n ≥ 100 in equation (1), the MOPs are called large-scale MOPs [12]. As the number of decision variables increases linearly, the size of the search space will increase exponentially, leading to the algorithm converging prematurely to local optima or vast areas [13], or even failing to converge [14].
Compared to other nature-inspired algorithms, multiobjective immune optimization algorithms (MOIAs) inspired by the biological immune system, exhibit superior convergence characteristics. This is attributed to their use of the clonal selection principle to enhance the selection of high-quality parents. At its core, the approach involves mass cloning and the proliferation of a select subset of the most competitive parental solutions, those with better convergence and diversity, to form a breeding population. This population then serves as the foundation for iteratively evolving superior individuals. This mechanism is believed to be beneficial for the better preservation and utilization of advantageous genes, maintenance of population diversity, and enhancement of convergence speed [15]. The nondominated neighbor immunization algorithm (NNIA) is recognized as the first real-coded MOIA [16]. It selects individuals based on their crowding degree, clones a portion of superior nondominated individuals, and proceeds with a heuristic search. Subsequent MOIAs have also adopted similar clonal selection mechanisms to generate an evolutionary population, aiming to allocate the task of producing superior offspring to less crowded search areas [17, 18]. However, the extensive use of repetitive parental solutions inevitably leads to the production of redundant offspring [19] and the dilemma of difficulty in escaping local optima [20], which also makes the search in large-scale decision variable spaces exceedingly challenging.
Re-examining the actual biological immune system, we observe that during the early development phase of immune B cells, diversity is generated through methods such as V(D)J recombination, forming B cell receptors (BCRs) with distinct antigen recognition capabilities. In the germinal center response, B cells undergo a process of somatic hypermutation (HM) and affinity selection, enhancing their binding ability to antigens. Mature B cells enter the lymphatic system and circulate in the blood. When a B cell recognizes a specific antigen through its BCR, it becomes activated. B cells with high affinity are selected and amplified at a higher probability, producing a large number of cells with the same specificity. B cells with lower affinity expand at a lower rate or are eliminated, but they are not completely eliminated. The presence of low-affinity B cells is crucial for maintaining the diversity of the entire B cell pool and, together with high-affinity B cells, maintaining the immune system’s broad recognition and response capabilities. Unfortunately, to the best of our knowledge, the role of low-affinity immune cells in the evolution is almost completely ignored in MOIAs.
- 1.
We introduce an innovative approach to population segmentation, which delineates a concrete strategy for extracting both an elite and a weak subpopulation from the original population. In addition, we propose a dynamic resizing method for these subpopulations. This method enables the adaptive adjustment of the sizes of the elite and weak subpopulations throughout the evolutionary process, ensuring an equilibrium between exploration and exploitation.
- 2.
To facilitate the coevolution of the two subpopulations, we have tailored distinct evolutionary inclinations and corresponding strategies for each. This approach not only capitalizes on the exploitation of superior solutions but also enables the weak solutions to achieve self-transcendence. It is instrumental in escaping local optima and conducting extensive searches across the solution space.
- 3.
To further enhance the algorithm’s capability in dealing with large-scale MOPs, a cluster-based population selection scheme was designed, complemented by ideal point-driven guidance. The proposed algorithm has demonstrated excellent performance on 30 test cases, including DTLZ and ZDT problems with decision variables not larger than 50, as well as large-scale MOPs with decision variables of 300 and 1000. When compared with 13 advanced algorithms, it has achieved optimal results in over 86% of these cases.
The remainder of this paper is organized as follows: Section 2 introduces some related research work and existing issues. Section 3 provides a detailed description of our newly designed algorithm, WP–MOIA. Section 4 presents the experimental results and comparative analysis of WP–MOIA with competitive MOEAs, MOIAs, and variants of WP–MOIA. Finally, in Section 5, the paper is summarized and future work plans are discussed.
2. Related Works and Motivation
2.1. Related Works
To address large-scale MOPs, a series of targeted MOEAs that have been proposed can be categorized into three major types based on their implementation strategies. The first type tackles large-scale MOPs by employing a divide-and-conquer strategy from the perspective of decision variables. This category includes MOEAs based on collaborative coevolution (CC) and those based on decision variable analysis (DVA). An example of the former is the third-generation generalized differential evolution (DE) based on CC (CCGDE3) [21], while the reformulated DVA algorithm (LERD) [22] exemplifies the latter. However, MOEAs based on decision variables not only require substantial effort for analyzing decision variables but also risk a significant decline in optimization performance if the separation of decision variables is incorrect.
The second type embodies the philosophy of dimensionality reduction, transforming the original large-scale MOPs into a lower-dimensional counterpart. Representative algorithms in this category include optimization strategies based on dimension reduction (DRMOS) [23] and the large-scale multiobjective optimization framework (LSMOF) based on problem transformation [24]. MOEAs based on dimensionality reduction require the design of a problem transformation function to ensure that the loss of information after transformation is as minimal as possible. However, finding an excellent problem transformation function for large-scale MOPs is exceedingly difficult.
The third category involves utilizing efficient and innovative search strategies to enhance convergence performance. Typical algorithms in this category include the evolutionary algorithm based on a competitive swarm optimizer (LMOCSO) [25] and the adaptive offspring generation evolutionary algorithm (DGEA) [26]. These MOEAs directly seek the optimal solution in the original decision space. However, as the dimension of the decision variables increases, the volume and complexity of the search space grow exponentially. Searching in such a vast space, populations can easily lose their way, leading to convergence outcomes that are far from satisfactory.
As one of the heuristic optimization algorithms, MOIAs have shown significant effects in solving MOPs in recent years. It has achieved excellent performance in a large number of application scenarios, such as multirobot patrol strategies [27], internet of things service response decision-making [28], network intrusion detection [29], and others. This algorithm is primarily inspired by mechanisms such as elitist clonal selection and affinity maturation in the biological immune system, offering a novel perspective and approach to addressing complex multiobjective optimization challenges.
In terms of elitist clonal selection, as this characteristic of 10 has a stronger advantage in convergence than in diversity, a number of strategies have been proposed to mitigate this issue. For instance, the hybrid evolutionary framework for MOIAs (HEIA) [30], the vertical distance–based MOIA (VD–MOIA) [31], and the MOIA with dynamic population strategy (MOIA–DPS) [32] each employ methods such as evolving the cloned population in subgroups, using vertical distance instead of crowding distance for selecting cloning parents, and dynamically adjusting the size of the cloned population to achieve this goal. However, these strategies have all focused solely on elite solutions, overlooking the role of weak solutions. This makes solving large-scale multiobjective problems still face the challenge of the distribution of evolutionary parents remaining relatively concentrated.
On the other hand, due to the significant influence of evolutionary operators on the maturation of population affinity, studies also have been carried out in this field. For example, the MOIA based on adaptive dynamic mutation strategy (MOIA–ADMS) [33] and the nondominated immune-endocrine short feedback algorithm (NISFA) [27]. These two schemes, respectively, utilize an adaptive evolutionary strategy pool and mutation hormone guidance, facilitating the convergence of generated solutions toward the true PF. However, when confronted with the vast decision variable space of large-scale MOPs, merely relying on the refinement of evolutionary operators for elite solutions to approach the PF remains a low-probability event. Constructing a separate breakout population, simultaneously increasing its proportion at appropriate junctures, and augmenting it with a higher mutation rate will significantly enhance the probability of locating the PF within expansive spaces.
In summary, although existing MOIAs have made commendable progress on MOPs with a small number of decision variables, to the best of our knowledge, there have been few successful applications of MOIAs to large-scale MOPs. The primary reason is due to the double-edged sword effect of the clonal selection mechanism. During each evolutionary process, elitist clonal selection identifies a small number of superior individuals, generates a large number of clones for these individuals, and then uses these cloned individuals as parents for further evolution. This mechanism is feasible for small-scale MOPs, as it accelerates the search process towards high-quality solutions and effectively improves convergence efficiency. However, when facing large-scale MOPs, the explosive growth of the solution space makes it more difficult to select the most promising elite solutions. Moreover, cloning only a small number of elite solutions (e.g., 20% of the entire population) as the starting point for evolution can easily lead to a loss of diversity in the vast solution space. This will confine the evolution to several local regions and prevent comprehensive exploration of the entire solution space.
Taking NNIA as an example, it adopts a nondominated neighbor–based selection technique, the core of which is to select only a minority of isolated nondominated individuals in the population, and then clone them proportionally based on their crowding distance, using this as the basis for iterative evolution. This method performs well when solving small-scale MOPs. However, on large-scale MOPs, the extremely large solution space means that the individuals in the initial population are almost randomly dispersed throughout the space. In this case, the probability that the few isolated nondominated individuals selected by NNIA based on crowding distance are close to the true PF is very low. In this case, when these cloned individuals are used as parents for evolution, they struggle to provide effective guidance. As a result, the population repeatedly moves within a local space far from the true PF, making it difficult to achieve a breakthrough. Even a significant increase in the number of evolutionary iterations is difficult to improve the situation. This phenomenon is more clearly observed in the comparative experiments presented later in the article.
2.2. Motivation
Due to the widespread extensive search and convergence challenges faced by MOEAs when dealing with large-scale MOPs, our goal is to leverage the convergence advantages of MOIAs and enhance their exploratory capabilities to address these issues. In applying MOIAs to large-scale MOPs, we harness the potential of the WP, a factor often overlooked in existing research, to achieve breakthrough searches and maintain diversity, thereby compensating for the inherent limitations of MOIAs and making them suitable for large-scale MOPs. This strategy is inspired by the real immune system, where, unlike cloned superior individuals, uncloned weak individuals contribute differently to the evolution of the entire population by introducing greater variability, enhancing the population’s exploratory ability. This is particularly crucial for maintaining population diversity in the early stages of evolution. Next, once an excellent decision variable space has been located, how to maintain the population’s persistence and proximity is also very important. To this end, we aim to guide the directional evolution of the elite population (EP) by continuously updating idealized reference points and then combining clustering methods to select the outstanding next generation. Based on the above ideas, we propose WP–MOIA, an algorithm that for the first time emphasizes the important role of the WP in the optimization process. It takes the dynamic collaboration between the elite and WPs as its core, and through customized guidance mechanisms, evolutionary operators, and population selection strategies, maintains a balance between diversity and convergence. This allows WP–MOIA to be effective in dealing with large-scale MOPs while also maintaining effectiveness for small-scale MOPs. Experimental results have verified the feasibility of our approach.
3. Proposed Algorithm
To better illustrate our approach, Figure 1 presents the overall framework of WP–MOIA. In Step 1, the algorithm generates an initial population randomly and initializes the reference point, known as the ideal point, based on the existing population. In Step 2, we first identify all nondominated solutions in the population and compute their affinities. We then clone and replicate a portion of the high-ranking superior solutions to form the EP. For the remaining solutions outside the superior solutions, a WP is constructed using random elimination. It should be noted that the sizes of both populations are dynamically adjusted over the course of evolution but their total size remains consistent with that of the initial population. In Step 3, the EP and WP evolve separately. The EP tends to exploit by moving towards the excellent regions guided by the ideal point, utilizing an evolutionary operator that combines DE, polynomial mutation (PM), and vector restriction (VR). Meanwhile, the WP focuses on exploration, primarily responsible for global search, employing HM and filling the gaps between the two populations, using DE without crossover (DE). In Step 4, the evolved populations are used to update the ideal point, and the newly generated solutions are merged with the original population. Clustering is then performed on this merged population, with the number of clusters equal to the size of the original population. Subsequently, within each cluster, the solution closest to the ideal point is selected to be retained as the next-generation individual. When the algorithm reaches its termination condition, the final population is output as the result of the algorithm. Further details about the algorithm will be explained in the following sections.
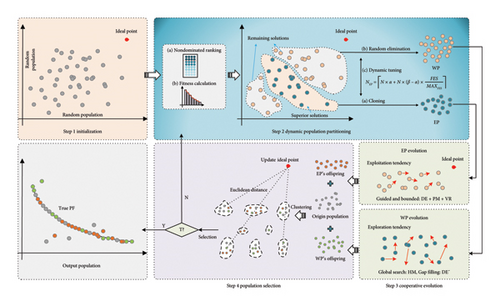
3.1. Initialization
-
Algorithm 1: Initialization.
- 1.
Input:N, n, m, Pop = Ø
- 2.
for i = 1 toNdo//initialize the population
- 3.
for j = 1 tondo
- 4.
randomly generate a decision variable xi,j using equation (2)
- 5.
end
- 6.
Pop = merge xi into Pop
- 7.
end
- 8.
for k = 1 tomdo//initialize the ideal point
- 9.
generate using equation (3)
- 10.
end
- 11.
Output: Pop, Z∗
3.2. Dynamic Population Partitioning
At the beginning of each iteration, the population is divided to prepare for the evolutionary phase. We first identify all nondominated solutions to form a population through nondominated sorting and then calculate the shift-based crowding distance for all nondominated solutions. This method of calculating crowding distance was initially proposed by the authors in [34] and has been used in multiple MOPs [14, 19]. We use this crowding distance as the fitness value for the solutions and rank them accordingly.
3.2.1. Cloning
3.2.2. Random Elimination
The pseudocode for dynamic population partitioning is detailed in Algorithm 2. Upon completion of this algorithm, the original population is bifurcated into two distinct new populations: EP and WP.
-
Algorithm 2: Population partitioning.
- 1.
Input: Pop, ρ
- 2.
Popsort = NDSort(Pop)//nondominated sorting
- 3.
Pdp = collect all nondominated solutions in Popsort
- 4.
CalFitness(Pdp) and sort by fitness
- 5.
Select the top Nc solutions in Pdp
- 6.
Calculate the size NEP using equation (5)
- 7.
Calculate the value qi for Nc solutions using equation (4)
- 8.
EP = clone superior solutions using equation (6)
- 9.
WPt = remove the cloned solutions from Pop
- 10.
WP = select N − NEP different solutions using equation (7)
- 11.
Output:EP, WP
3.3. Evolution
Postpartitioning, considering the distinct characteristics of the EP and WP, we have designed evolution tasks with different inclinations for these two populations. The EP is more inclined towards exploitation, while the WP leans more towards exploration. However, it is important to highlight that this inclination does not mean that a population solely performs one task and completely abandons others, but it rather focuses more on certain tasks. In addition, based on our designed partitioning strategy, the sizes of the two populations will be continuously adjusted during the evolutionary process to balance their spheres of influence.
3.3.1. EP Evolution
- a.
We define the best solutions in the EP as those with the top 10% closest Euclidean distance to the ideal point. The Euclidean distance DistEuc for an objective corresponding to the solution xi from the ideal point Z∗ is calculated as
() -
Our method differs from the traditional approach of selecting the best solutions based on crowding distance, offering a more effective driving force to guide the solutions towards the ideal point. This will prompt the EP to rapidly converge towards the discovered high-quality solution space while maintaining good diversity.
- b.
We impose restrictions on the range of DE vectors to better meet the evolution task of the EP. The method of restriction is similar to that in literature [35], which limits the mutation scale to within half of the range between the upper and lower bounds. However, the generation method of our difference vector differs from [35], resulting in a different distribution. Let vi,j = Fpm × (xpbest,j − xi,j + xr1,j − xr2,j), then equation (10) provides the variation limits for vi,j as
()
After evolution, offspring that are completely identical are kept only once, and those identical to the parent are also removed, consequently making room for a greater number of effective solutions. All newly generated valid offspring are placed into EPnext. The pseudocode for the EP evolution is shown in Algorithm 3.
-
Algorithm 3:EP evolution.
- 1.
Input:EP, Z∗
- 2.
Calculate DistEuc from EP solutions to Z∗ using equation (9)
- 3.
xpbset = randomly select a solution from the top 10%
- 4.
Choose three distinct parent xi, xr1, xr2 from EP
- 5.
fori = 1 toNEPdo
- 6.
forj = 1 tondo
- 7.
ifr < CR
- 8.
vi,j = Fpm × (xpbest,j − xi,j + xr1,j − xr2,j)
- 9.
ifvi,j exceeds the limit
- 10.
adjust vi,j using equation (10)
- 11.
end
- 12.
Calculate the new variable li,j using equation (8)
- 13.
end
- 14.
Correct the out-of-bounds variables using equation (11)
- 15.
end
- 16.
EPnext = merge the offspring li
- 17.
end
- 18.
Remove duplicate solutions from EPnext
- 19.
Output:EPnext
3.3.2. WP Evolution
- a.
Global search: The first evolutionary strategy employs HM. HM is a typical immune evolutionary mutation method, which has a significantly higher mutation rate than the normal mutation rate [36]. By increasing the mutation rate of individuals, HM enables them to escape from local optimal solutions and explore a broader search space. We have adopted a very efficient static HM method, as shown in the following equation:
() -
In this scenario, both rand and γ are uniformly distributed random numbers generated within the range [0, 1].
- b.
Gap filling: The second evolutionary strategy still relies on DE, but without the crossover operation to reduce complexity. Its primary task is to guide weak solutions towards elite solutions and to search the periphery and the gaps of the two subpopulations. The specific evolution method is shown in the following equation:
() -
where xEP and xWP are two individuals randomly selected from the EP and WP, respectively. This direction vector will guide the evolution of the population towards higher fitness. For values that exceed the upper and lower bounds, they are adjusted to these bounds. In addition, as with the EP, duplicate offspring are eliminated. Algorithm 4 displays the pseudocode for the evolution of WP.
-
Algorithm 4:WP evolution.
- 1.
Input:WP, EP
- 2.
fori = 1 toNWPdo
- 3.
if rand < 0.5//HM
- 4.
for j = 1 tondo
- 5.
ifγ < 0.5
- 6.
Calculate the new variable li,j using equation (12)
- 7.
end
- 8.
end
- 9.
else //DE without the crossover operation
- 10.
choose a parent xEP from EP
- 11.
choose a parent xWP from WP
- 12.
for j = 1 tondo
- 13.
Calculate the new variable li,j using equation (13)
- 14.
end
- 15.
end
- 16.
WPnext = merge the offspring li
- 17.
end
- 18.
Output:WPnext
3.4. Population Selection
First, we update the ideal point based on the new offspring generated from the EP and WP; if lower values are found for any objective, then the corresponding objective value of the ideal point is updated. Then, we merge these offspring with the original population to form a temporary population U. Subsequently, this population undergoes an updation process that starts with a nondominated sorting to identify all nondominated solutions. If the number of nondominated solutions exceeds N, a truncation operation is executed among the nondominated solutions to retain only N nondominated solutions. Conversely, if there are fewer, all are retained, and a truncation operation is executed among the dominated solutions, retaining only the number of solutions needed to make up N, ensuring the next generation’s size remains consistent.
The algorithm’s population truncation operation is based on clustering, which is a commonly used technique in MOPs [37, 38]. The use of clustering for individual selection is conducive to maintaining the diversity of the population, especially when dealing with large-scale MOPs, and it has the advantages of being simple and fast. WP–MOIA utilizes hierarchical clustering methods for clustering operations. The number of clusters is set equal to the number of solutions to be retained, thereby avoiding the introduction of additional parameters. After clustering, the Euclidean distance of each individual within the clusters to the ideal point is calculated, and the solution closest to the ideal point is selected for the next generation. This approach further reinforces the guiding role of the ideal point, ensuring that solutions close to the optimal regions are preserved. The pseudocode for population selection is illustrated in Algorithm 5.
-
Algorithm 5: Population selection.
- 1.
Input:EPnext, WPnext, Pop
- 2.
Update the ideal point Z∗
- 3.
U = merge EPnext, WPnext and Pop
- 4.
NDSort(U)
- 5.
Und = obtain all nondominated solutions in U
- 6.
If size(Und) > N
- 7.
Perform clustering on Und into N clusters
- 8.
Pop = add the solution closest to Z∗ in each cluster
- 9.
else
- 10.
Perform clustering on U−Und into N− size(Und) clusters
- 11.
Pop = add Und and the solution closest to Z∗ in each cluster
- 12.
end
- 13.
Output: Pop
3.5. The Complete WP–MOIA
Algorithm 6 provides the complete procedure for WP–MOIA. The algorithm begins with the initialization of the population Pop and the ideal point Z∗. Subsequently, without reaching the maximum number of evaluation limits, it continuously optimizes the population through iteration. In each iteration, the current population is divided into two subpopulations: EP and WP. The sizes of these two subpopulations are dynamically adjusted, with the ratio of EP to the total population being smaller in the early stages of evolution and gradually increasing, while WP follows the opposite trend. Then, different evolutionary strategies are applied to evolve these two subpopulations. EP mainly focuses on exploitation, utilizing the neighborhood of existing solutions, while WP focuses on exploration, aiming for breakthroughs. The dynamic change in population size ensures a balance between diversity and convergence. The current population and its evolved offspring are merged and duplicates removed, serving as the basis for selecting a new population. We use cluster analysis and ideal point guidance to update the population, selecting the solution closest to the ideal point within each cluster to enter the next generation. New individuals generated in each iteration are evaluated, making the number of FES gradually accumulate until it reaches or exceeds the preset MAXFES. At this point, the algorithm outputs the final selected solution set as the result.
-
Algorithm 6: WP–MOIA.
- 1.
Initialize the Pop and the Z∗ using Algorithm 1
- 2.
While FES ≤ MAXFES
- 3.
Divide Pop into EP and WP using Algorithm 2
- 4.
EPnext = evolve EP using Algorithm 3
- 5.
WPnext = evolve WP using Algorithm 4
- 6.
Select the offspring population Pop using Algorithm 5
- 7.
FES = FES + size (EPnext) + size (EPnext)
- 8.
end
4. Experiments and Discussion
To validate the effectiveness of the WP–MOIA algorithm, we conducted a comparative analysis with nine state-of-the-art MOEAs and four formidable MOIAs across 30 benchmark problems, which include both small-scale and large-scale MOPs. Our study also delves into the influence of the dynamic partitioning factor on the proposed algorithm, highlighting the importance of the WP and the rationale behind the co-operative coevolution of subtasks. The experiments presented herein were all conducted utilizing the PlatEMO platform [39].
4.1. Benchmark Problems and Metrics
Widely recognized benchmark problems, including the ZDT series (ZDT1-ZDT4, and ZDT6) [40], the DTLZ series (DTLZ1–DTLZ7) [41], and the LSMOP series (LSMOP1–LSMOP9) [42], were utilized for the performance evaluation of algorithms. These problems offer a diverse range of PF characteristics, such as concave, convex, planar, degenerate, and piecewise features, facilitating a comprehensive assessment. The optimization objectives follow the default settings in the PlatEMO platform. Specifically, ZDT1–ZDT4 and ZDT6 are designed as biobjective problems, while the remaining problems, including the DTLZ series and LSMOP series, are three-objective problems. To assess the performance of WP–MOIA on both small-scale and large-scale MOPs, the following decision variable settings were adopted: ZDT1–ZDT3 have 30 decision variables, ZDT4 and ZDT6 have 10, DTLZ1 has 7, DTLZ2–DTLZ3 have 12, DTLZ4–DTLZ6 have 24, and DTLZ7 has 22. These constitute a small-scale benchmark test suite. The LSMOP series was used to evaluate WP–MOIA’s ability to handle large-scale complex optimization challenges. Each LSMOP problem was tested with 300 and 1000 decision variables. For clarity, LSMOP problem names are annotated with their respective dimensions, e.g., LSMOP1 (300) and LSMOP1 (1000).
MOPs aim to identify a solution set that closely approximates the true PF and strive to ensure an even distribution of solutions. To compare the performance of various algorithms, this paper employed two established metrics: the inverted generation distance (IGD) [43] and hypervolume (HV) [44]. The IGD quantifies the average distance between the algorithm’s approximate Pareto set and the actual PF, with a lower value indicating closer proximity. The HV metric evaluates the size of the objective space covered by the solution set, with a larger value signifying better coverage. Thus, a smaller IGD value and a larger HV value are indicative of superior algorithm performance. Both metrics reflect the diversity and convergence of the solution set. However, it is worth noting that the two indicators are not always consistent. For example, a solution set may have a poor IGD value but maintain a good HV value. This indicates that these solutions may be concentrated in certain boundary regions of the objective space, even if the distribution in the central region is relatively sparse. This is because the HV metric focuses on the overall volume coverage of the solution set in the objective space, rather than the overall uniformity of the solution set [45]. Conversely, when a solution set has a good IGD value but a poor HV value, it always means that the optimization process has successfully found a solution set that is close to the PF and uniformly distributed, but the coverage of these solutions in the objective space is relatively limited. To ensure the reliability of the algorithm performance, each algorithm is run 30 times, yielding the mean and standard deviation results.
4.2. Parameter Settings
In the present study, comparative experiments were conducted using 13 representative algorithms, including nine state-of-the-art MOEAs and four competitive MOIAs. Our aim is to examine the effectiveness of WP–MOIA from three perspectives: small-scale MOPs, large-scale MOPs, and the improvement over traditional MOIAs. For this purpose, we can classify these algorithms into three groups. The first group includes four MOEAs: DEA–GNG [46], LMPFE [47], PREA [48], and MOEA/D-UR [49]. This group of algorithms is used to compare with WP–MOIA on a wide range of multiobjective problems. Among them, DEA–GNG and LMPFE are proficient in handling irregular PFs, PREA is suitable for various types of PFs, and MOEA/D-UR is skilled at solving problems with complex geometric structures. The second group comprises five MOEAs that have been specifically optimized for large-scale MOPs: LERD [22], DGEA [26], S3–CMA–ES [50], IMMOEAD [51], and IMTCMO–BS [52]. The selection of these algorithms is intended to assess WP–MOIA’s capability in dealing with large-scale MOPs. In view of this, as far as we know, there are currently no effective MOIAs specifically tailored for large-scale MOPs. Therefore, we selected four general MOIAs: NNIA [16], MOIA–DCSS [53], ADE–MOIA [54], and MaIA [19]. The choice of this group of algorithms aims to verify that WP–MOIA can not only continue the excellent performance of MOIAs on small-scale MOPs but also break through the limitations of traditional MOIAs, significantly enhancing their capabilities on large-scale MOPs. It is worth mentioning that among the above algorithms, LMPFE and S3–CMA–ES employ a grouping strategy, while MOIA–DCSS and ADE–MOIA are based on DE. These characteristics endow these algorithms with features similar to those of WP–MOIA, enhancing their comparability with WP–MOIA and further facilitating the comparative evaluation of the performance of WP–MOIA.
Considering the characteristics of different algorithms, to achieve the optimal performance of each algorithm, all algorithms’ parameters were set according to the recommendations given in the relevant literature, with unspecified parameters set to the default values in PlatEMO. The core parameter settings for the aforementioned 13 algorithms are provided in Table 1. For WP–MOIA, the newly introduced parameters, α and β, which are used for dynamically adjusting the population size, were empirically set to 0.4 and 0.85, respectively. The crossover rate CR is set to 0.15 across all four test problem suites for consistency. However, for the LSMOP problems, setting the CR to 1 will yield better results. In addition, ρ was set to 0.2, and the PM rate was Pm = 1/n, with the distribution index being ηm = 20. To ensure fairness in our comparisons, the population size N for all algorithms was standardized to 100, and the maximum number of evaluations was set to 10,000.
| Algorithms | Parameter values |
|---|---|
| DEA–GNG | ∈a = 0.2, ∈n b = 0.01, α = 0.5, δ = 0.9 |
| LMPFE | fPFE = 0.1, K = 5, θ = 0.8 |
| PREA | Ps = 0.7 |
| MOEA/D-UR | K = 10, δ = 0.9, nr = 2, T = 0.1 |
| LERD | ns = 3, nb = 10, gen = 20 |
| DGEA | r = 10 |
| S3–CMA–ES | M = 5, λ = 20, ∆ = 1e−6, RT = 400 |
| IMMOEAD | K = 10, L = 3, T = 0.05N |
| IMTCMO–BS | g = 50 |
| NNIA | nA = 20, Pc = 1, ηc = 15, Pm = 1/n, ηm = 20 |
| MOIA–DCSS | nA = 20, ηc = 20, δ = 0.9, nr = 2, Pmin = 0.15 |
| ADE–MOIA | nA = 20, Fm = 0.5, CR = 0.55, p = 10 |
| MaIA | nA = 0.2N, Pc = 1, ηc = 20, Pm = 1/n, ηm = 20 |
4.3. Experimental Results
4.3.1. Results of 14 Algorithms on Small-Scale MOPs
Tables 2 and 3 display the IGD values of 14 comparative algorithms on the ZDT and DTLZ benchmark suites, with the number of decision variables for each problem being less than 100. The first item in each row of the tables is the name of the problem, with the number of decision variables indicated in parentheses. The remaining items represent the average IGD value and its standard deviation, with the standard deviation given in parentheses. These data are derived from the results of 30 independent runs. In addition, the Wilcoxon’s rank sum test is applied at a 0.05 significance level, following the recommendation in reference [55]. The symbols “+, −, and ≈” signify that the algorithm’s performance is better, worse, or similar to that of WP–MOIA, respectively. The optimal outcomes for each problem are distinctively highlighted with a dark gray background, while the second-best results are marked with a light gray background.
| Problem | DEA–GNG | LMPFE | MOEA/D-UR | PREA | LERD | S3–CMA–ES | DGEA | IMMOEAD | IMTCMO–BS | WP–MOIA |
|---|---|---|---|---|---|---|---|---|---|---|
| ZDT1 | 1.3425e − 2 (4.81e − 3)− | 1.0717e − 2 (2.19e − 3)− | 1.4181e − 2 (3.54e − 3)− | 1.5211e − 1 (1.20e − 1)− | 1.1194e − 2 (2.85e − 3)− | 1.8540e − 1 (1.28e − 1)− | 9.1592e − 1 (2.75e − 1)− | 9.4261e − 2 (4.44e − 2)− | 3.1347e − 2 (3.07e − 2)− | 4.3022e − 3 (1.36e − 4) |
| ZDT2 | 2.7661e − 2 (3.86e − 2)− | 4.5392e − 2 (7.20e − 2)− | 2.7183e − 2 (4.33e − 2)− | 4.2546e − 1 (7.99e − 2)− | 2.8649e − 1 (6.10e − 1)− | 3.5563e − 1 (1.50e − 1)− | 3.3890e − 1 (3.42e − 1)− | 6.1384e − 2 (2.57e − 2)− | 6.4379e − 2 (1.13e − 1)− | 4.2847e − 3 (9.62e − 5) |
| ZDT3 | 1.3080e − 2 (7.04e − 3)− | 1.4785e − 2 (1.04e − 2)− | 1.8547e − 2 (7.65e − 3)− | 7.4824e − 2 (5.72e − 2)− | 1.4807e − 1 (1.24e − 1)− | 1.6669e − 1 (1.01e − 1)− | 8.7319e − 1 (2.35e − 1)− | 7.5243e − 2 (5.68e − 2)− | 3.7237e − 2 (2.96e − 2)≈ | 6.8510e − 3 (6.28e − 4) |
| ZDT4 | 5.7135e + 1 (1.12e + 1)− | 5.5104e + 1 (9.39e + 0)− | 4.6801e + 1 (9.91e + 0)− | 9.1896e + 1 (1.66e + 1)− | 1.0383e + 1 (8.36e + 0)− | 5.6054e + 2 (4.12e + 1)− | 1.6827e + 2 (4.87e + 1)− | 1.5435e + 2 (2.99e + 1)− | 2.1845e + 2 (2.93e + 1)− | 4.4161e − 3 (1.42e − 4) |
| ZDT6 | 3.0933e + 0 (2.29e − 1)− | 3.1074e + 0 (2.22e − 1)− | 2.3614e + 0 (3.02e − 1)− | 4.9126e + 0 (2.66e − 1)− | 6.5252e − 2 (1.53e − 1)− | 6.2639e + 0 (1.49e − 1)− | 6.1443e + 0 (3.59e − 1)− | 6.2994e + 0 (1.37e − 1)− | 1.8103e + 0 (1.98e + 0)≈ | 3.5311e − 3 (8.70e − 5) |
| DTLZ1 | 1.2638e − 1 (1.51e − 1)− | 2.1493e − 1 (2.35e − 1)− | 1.4861e − 1 (1.83e − 1)− | 4.3197e − 1 (3.31e − 1)− | 7.2979e − 1 (8.44e − 1)− | 3.4028e + 1 (4.73e + 0)− | 1.7281e + 1 (1.10e + 1)− | 3.5151e + 0 (1.22e + 0)− | 1.1136e + 0 (4.85e − 1)− | 2.0420e − 2 (2.99e − 4) |
| DTLZ2 | 5.5668e − 2 (6.90e − 4)+ | 5.3591e − 2 (4.49e − 4) + | 5.7887e − 2 (1.54e − 3)≈ | 5.7530e − 2 (9.05e − 4)≈ | 6.6295e − 2 (1.57e − 3)− | 5.8082e − 2 (9.05e − 4) ≈ | 1.0310e − 1 (1.35e − 2)− | 8.0771e − 2 (2.28e − 3)− | 6.3620e − 2 (1.42e − 3)− | 5.8219e − 2 (1.45e − 3) |
| DTLZ3 | 7.8832e + 0 (4.93e + 0)− | 7.5726e + 0 (4.19e + 0)− | 6.5293e + 0 (3.89e + 0)− | 1.2588e + 1 (4.47e + 0)− | 2.0780e + 1 (2.62e + 1)− | 2.3053e + 2 (3.57e + 1) | 9.2874e + 1 (5.61e + 1)− | 6.0882e + 1 (1.49e + 1)− | 3.0789e + 1 (1.20e + 1)− | 1.5778e − 1 (2.76e − 1) |
| DTLZ4 | 2.3311e − 1 (2.61e − 1)− | 2.9159e − 1 (3.12e − 1)≈ | 2.4609e − 1 (2.29e − 1) ≈ | 4.3512e − 1 (3.01e − 1)− | 4.7121e − 1 (4.89e − 1)− | 5.6763e − 1 (1.01e − 1)− | 5.0595e − 1 (1.52e − 1)− | 2.5097e − 1 (1.40e − 1)− | 1.1334e − 1 (9.78e − 3)≈ | 1.6556e − 1 (9.81e − 2) |
| DTLZ5 | 7.7723e − 3 (1.03e − 3)− | 8.0819e − 3 (9.12e − 4)− | 1.0061e − 2 (1.01e − 3)− | 9.4088e − 3 (2.59e − 3)− | 2.9882e − 2 (5.17e − 3)− | 9.3429e − 3 (2.78e − 3)− | 1.6055e − 1 (5.10e − 2)− | 4.6144e − 2 (6.47e − 3)− | 3.6239e − 2 (4.67e − 3)− | 5.6298e − 3 (4.65e − 4) |
| DTLZ6 | 1.3584e + 0 (1.02e + 0)− | 1.3486e + 0 (9.42e − 1)− | 1.0057e + 0 (8.49e − 1)− | 1.0259e + 0 (7.55e − 1)− | 2.3970e − 2 (6.45e − 4)− | 1.2730e + 1 (7.74e − 1)− | 6.4788e + 0 (1.42e + 0)− | 1.1709e + 1 (5.14e − 1)− | 1.1119e − 1 (2.71e − 1)≈ | 4.4207e − 3 (7.89e − 5) |
| DTLZ7 | 8.8279e − 2 (7.77e − 2)− | 1.3987e − 1 (1.26e − 1)− | 1.0926e − 1 (8.57e − 3)− | 1.7594e − 1 (1.79e − 1)− | 7.5081e − 1 (1.78e − 1)− | 2.1612e − 1 (2.42e − 1)− | 2.4120e + 0 (1.23e + 0)− | 2.0310e − 1 (1.36e − 2)− | 2.8199e − 1 (2.79e − 1)− | 6.1952e − 2 (2.74e − 3) |
| +/−/≈ | 1/11/0 | 1/10/1 | 0/10/2 | 0/11/1 | 0/12/0 | 0/11/1 | 0/12/0 | 0/12/0 | 0/8/4 |
| Problem | NNIA | MOIA–DCSS | ADE–MOIA | MaIA | WP–MOIA |
|---|---|---|---|---|---|
| ZDT1 | 1.0301e − 2 (2.18e − 3)− | 4.3181e − 1 (1.26e − 1)− | 5.0300e − 3 (2.98e − 4)− | 4.7209e − 3 (2.78e − 4)− | 4.3022e − 3 (1.36e − 4) |
| ZDT | 2.9473e − 2 (4.50e − 2)− | 7.9934e − 1 (1.71e − 1)− | 1.0358e − 1 (5.35e − 1)− | 2.8860e − 2 (7.83e − 2)− | 4.2847e − 3 (9.62e − 5) |
| ZDT3 | 1.4133e − 2 (2.14e − 2)≈ | 4.6922e − 1 (8.98e − 2)− | 5.4900e − 3 (2.09e − 4)+ | 1.7651e − 2 (1.62e − 2)− | 6.8510e − 3 (6.28e − 4) |
| ZDT4 | 6.4618e + 1 (1.16e + 1)− | 1.4774e + 2 (2.42e + 1)− | 8.4481e + 1 (3.06e + 1)− | 4.1217e + 1 (1.08e + 1)− | 4.4161e − 3 (1.42e − 4) |
| ZDT6 | 3.1136e + 0 (4.30e − 1)− | 5.8464e + 0 (2.29e − 1)− | 1.8533e − 2 (3.67e − 2)− | 9.7525e − 1 (2.06e − 1)− | 3.5311e − 3 (8.70e − 5) |
| DTLZ1 | 5.9295e − 1 (8.09e − 1)− | 5.7548e − 1 (8.59e − 1)− | 2.6296e − 1 (3.47e − 1)− | 1.1081e − 1 (1.24e − 1)− | 2.0420e − 2 (2.99e − 4) |
| DTLZ2 | 7.0226e − 2 (3.03e − 3)− | 7.6728e − 2 (1.23e − 3)− | 6.6592e − 2 (1.84e − 3)− | 7.5453e − 2 (3.08e − 3)− | 5.8219e − 2 (1.45e − 3) |
| DTLZ3 | 8.8278e + 0 (5.13e + 0)− | 1.3954e + 1 (1.82e + 1)− | 1.9507e + 1 (1.37e + 1)− | 4.3936e + 0 (3.56e + 0)− | 1.5778e − 1 (2.76e − 1) |
| DTLZ4 | 1.5811e − 1 (2.67e − 1)+ | 2.4029e − 1 (5.40e − 2)− | 6.9668e − 2 (2.55e − 3)+ | 4.2589e − 1 (2.80e − 1)− | 1.6556e − 1 (9.81e − 2) |
| DTLZ5 | 8.0040e − 3 (7.41e − 4)− | 2.0790e − 2 (3.94e − 3)− | 9.3385e − 3 (9.37e − 4)− | 1.0417e − 2 (1.19e − 3)− | 5.6298e − 3 (4.65e − 4) |
| DTLZ6 | 4.5482e + 0 (1.22e + 0)− | 4.2699e − 1 (5.61e − 1)− | 6.8187e − 3 (4.33e − 4)− | 7.6242e − 1 (7.41e − 1)− | 4.4207e − 3 (7.89e − 5) |
| DTLZ7 | 1.2618e − 1 (1.47e.1)− | 4.9083e − 1 (1.09e − 1)− | 7.8539e − 2 (4.62e − 3)− | 2.1908e − 1 (1.72e − 1)− | 6.1952e − 2 (2.74e − 3) |
| +/−/≈ | 1/10/1 | 0/12/0 | 2/10/0 | 0/12/0 |
The IGD metrics show that WP–MOIA outperforms nine MOEAs and four MOIAs, achieving the best performance on 10 out of 12 problems and the second-best on one problem. Among the MOEAs, LMPFE obtains the optimal result on DTLZ2, and IMTCMO–BS achieves the best on DTLZ4. However, WP–MOIA still maintains the same accuracy as LMPFE on DTLZ2 and achieves the second-best on DTLZ4. WP–MOIA also outperforms other MOEAs by at least an order of magnitude on all problems in the ZDT series and on DTLZ1, DTLZ3, and DTLZ6. In the MOIAs, ADE–MOIA achieves the optimal result on ZDT3 and DTLZ4, while WP–MOIA achieves the second-best on ZDT3 and outperforms MOIAs by at least an order of magnitude on ZDT2, ZDT4, ZDT6, DTLZ1, and DTLZ3.
To further analyze these results, Figures 2(a) and 2(b), respectively, present the nondominated solutions corresponding to the median IGD values obtained from 30 independent runs of the 14 algorithms on ZDT2 and DTLZ3. On ZDT2, WP–MOIA successfully generated the most uniformly distributed set on the true PF, while MOIA–DCSS failed to find high-quality approximate solutions close to the PF. The solution sets obtained by other algorithms show a certain degree of compromise. It is noteworthy that the solutions of S3–CMA–ES, DGEA, IMMOEAD, and IMTCMO–BS are all relatively far from the PF, indicating that large-scale MOPs may encounter difficulties when dealing with small-scale MOPs. On DTLZ3, WP–MOIA also achieved the best-distributed set of solutions, while those obtained by other algorithms were far from the true PF. Due to the complex interactions between decision variables, this problem exhibits a higher degree of complexity, requiring more effective exploration of the decision space. WP–MOIA, through the large mutation strategy implemented by its WP, greatly enhances its exploration ability, giving it a significant advantage on DTLZ3. This also proves the importance of the WP in driving the evolution of the entire population.

Tables 4 and 5 give the HV values for 14 comparative algorithms on the ZDT and DTLZ benchmark suites. This metric shows results similar to those of the IGD, with WP–MOIA achieving the best performance on 10 out of 12 problems when compared to MOEAs and 8 best and 3 second-best performances when compared to MOIAs. Although there is some discrepancy between the two metrics on ZDT3, DTLZ2, and DTLZ5, WP–MOIA still achieves an accuracy level of the same order as the optimal solutions on these three problems. These results confirm WP–MOIA’s capability in addressing small-scale MOPs.
| Problem | DEA–GNG | LMPFE | MOEA/D-UR | PREA | LERD | S3–CMA–ES | DGEA | IMMOEAD | IMTCMO–BS | WP–MOIA |
|---|---|---|---|---|---|---|---|---|---|---|
| ZDT1 | 7.0538e − 1 (4.39e − 3)− | 7.0866e − 1 (3.04e − 3)− | 7.0422e − 1 (4.29e − 3)− | 6.1082e − 1 (7.14e − 2)− | 7.0827e − 1 (3.82e − 3)− | 5.0906e − 1 (1.04e − 1)− | 4.3534e − 2 (1.25e − 1)− | 6.1560e − 1 (2.99e − 2)− | 6.8117e − 1 (4.25e − 2)− | 7.1955e − 1 (3.07e − 4) |
| ZDT2 | 4.1172e − 1 (3.88e − 2)− | 3.9622e − 1 (6.45e − 2)− | 4.1361e − 1 (4.34e − 2)− | 1.2220e − 1 (3.53e − 2)− | 3.4554e − 1 (1.63e − 1)− | 1.2661e − 1 (7.46e − 2)− | 2.1012e − 1 (1.82e − 1)− | 3.5452e − 1 (3.42e − 2)− | 3.7308e − 1 (8.01e − 2)− | 4.4422e − 1 (2.82e − 4) |
| ZDT3 | 5.9323e − 1 (1.77e − 2)− | 6.0437e − 1 (3.09e − 2)+ | 5.9205e − 1 (9.02e − 3)− | 6.6036e − 1 (7.77e − 2)+ | 6.4519e − 1 (4.13e − 2)+ | 5.0108e − 1 (3.93e − 2)− | 6.7457e − 2 (9.52e − 2)− | 5.8201e − 1 (2.89e − 2)− | 5.7704e − 1 (2.06e − 2)− | 5.9927e − 1 (5.13e − 4) |
| ZDT4 | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 7.1917e − 1 (3.28e − 4) |
| ZDT6 | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 3.3867e − 1 (1.08e − 1)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 2.0736e − 1 (1.97e − 1) ≈ | 3.8799e − 1 (2.76e − 4) |
| DTLZ1 | 5.9846e − 1 (3.03e − 1)− | 4.7333e − 1 (3.40e − 1)− | 5.6636e − 1 (3.29e − 1)− | 2.3182e − 1 (2.96e − 1)− | 2.7862e − 1 (3.43e − 1)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 1.6086e − 2 (8.81e − 2)− | 8.3073e − 1 (4.88e − 3) |
| DTLZ2 | 5.4727e − 1 (2.81e − 3)− | 5.5694e − 1 (1.06e − 3)+ | 5.5721e − 1 (1.63e − 3)+ | 5.5718e − 1 (7.91e − 4)+ | 5.3779e − 1 (3.32e − 3)− | 5.5879e − 1 (1.11e − 3)+ | 4.4724e − 1 (2.61e − 2)− | 4.9200e − 1 (7.86e − 3)− | 5.2883e − 1 (2.49e − 3)− | 5.5306e − 1 (2.47e − 3) |
| DTLZ3 | 3.2373e − 4 (1.77e − 3)− | 0.0000e + 0 (0.00e + 0)− | 5.6272e − 3 (3.08e − 2)− | 0.0000e + 0 (0.00e + 0)− | 5.1067e − 2 (1.51e − 1)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 4.7991e − 1 (1.74e − 1) |
| DTLZ4 | 4.7079e − 1 (1.19e − 1)≈ | 4.3991e − 1 (1.49e − 1)≈ | 4.7145e − 1 (1.01e − 1)≈ | 3.7973e − 1 (1.50e − 1)− | 3.7850e − 1 (1.70e − 1)− | 1.7455e − 1 (5.49e − 2)− | 1.1559e − 1 (8.86e − 2)− | 3.3068e − 1 (1.06e − 1)− | 4.6068e − 1 (1.25e − 2)≈ | 4.9148e − 1 (5.84e − 2) |
| DTLZ5 | 1.9632e − 1 (8.72e − 4)− | 1.9513e − 1 (8.71e − 4)− | 1.9505e − 1 (8.82e − 4)− | 1.9530e − 1 (1.06e − 3)− | 1.8109e − 1 (4.30e − 3)− | 1.9330e − 1 (3.39e − 3)− | 5.6378e − 2 (2.65e − 2)− | 1.5541e − 1 (9.62e − 3)− | 1.6649e − 1 (4.17e − 3)− | 1.9800e − 1 (6.09e − 4) |
| DTLZ6 | 1.2512e − 2 (3.77e − 2)− | 2.9627e − 2 (6.08e − 2)− | 3.8355e − 2 (6.73e − 2)− | 1.7038e − 2 (3.97e − 2)− | 1.9033e − 1 (3.06e − 4)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 1.7475e − 1 (5.59e − 2)− | 1.9955e − 1 (2.04e − 4) |
| DTLZ7 | 2.6343e − 1 (9.45e − 3)− | 2.5554e − 1 (1.36e − 2)− | 2.6204e − 1 (2.18e − 3)− | 2.4472e − 1 (1.74e − 2)− | 2.0170e − 1 (1.28e − 2)− | 2.3389e − 1 (5.45e − 2)− | 1.8214e − 2 (4.63e − 2)− | 1.7153e − 1 (7.32e − 3)− | 2.2669e − 1 (1.93e − 2)− | 2.7858e − 1 (9.79e − 4) |
| +/−/≈ | 0/11/1 | 2/9/1 | 1/10/1 | 2/10/0 | 1/11/0 | 1/11/0 | 0/12/0 | 0/12/0 | 0/10/2 |
| Problem | NNIA | MOIA–DCSS | ADE–MOIA | MaIA | WP–MOIA |
|---|---|---|---|---|---|
| ZDT1 | 7.0966e − 1 (3.06e − 3)− | 2.5896e − 1 (1.08e − 1)− | 7.1877e − 1 (3.30e − 4)− | 7.1830e − 1 (5.90e − 4)− | 7.1955e − 1 (3.07e − 4) |
| ZDT2 | 4.1144e − 1 (4.45e − 2)− | 6.8671e − 3 (2.98e − 2)− | 4.2803e − 1 (8.08e − 2)− | 4.2260e − 1 (6.51e − 2)− | 4.4422e − 1 (2.82e − 4) |
| ZDT3 | 6.0993e − 1 (4.19e − 2)+ | 2.7439e − 1 (6.87e − 2)− | 5.9905e − 1 (2.95e − 4)− | 6.0489e − 1 (4.34e − 2)+ | 5.9927e − 1 (5.13e − 4) |
| ZDT4 | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e − 0)− | 0.0000e + 0 (0.00e − 0)− | 0.0000e + 0 (0.00e − 0)− | 7.1917e − 1 (3.28e − 4) |
| ZDT6 | 0.0000e + 0 (0.00e − 0)− | 0.0000e + 0 (0.00e − 0)− | 3.7187e − 1 (4.37e − 2)− | 0.0000e + 0 (0.00e − 0)− | 3.8799e − 1 (2.76e − 4) |
| DTLZ1 | 2.8087e − 1 (3.51e − 1)− | 3.5044e − 1 (3.48e − 1)− | 4.1606e − 1 (3.50e − 1)− | 6.1981e − 1 (3.00e − 1)− | 8.3073e − 1 (4.88e − 3) |
| DTLZ2 | 5.3515e − 1 (4.86e − 3)− | 5.1947e − 1 (2.94e − 3)− | 5.3531e − 1 (3.83e − 3)− | 5.5556e − 1 (2.66e − 3)+ | 5.5306e − 1 (2.47e − 3) |
| DTLZ3 | 3.9356e − 3 (2.16e − 2)− | 5.9121e − 2 (1.54e − 1)− | 0.0000e + 0 (0.00e + 0)− | 8.5857e − 3 (3.45e − 2)− | 4.7991e − 1 (1.74e − 1) |
| DTLZ4 | 4.8544e − 1 (1.34e − 1)≈ | 4.3891e − 1 (3.25e − 2)− | 5.2547e − 1 (4.32e − 3)≈ | 3.9204e − 1 (1.42e − 1)− | 4.9148e − 1 (5.84e − 2) |
| DTLZ5 | 1.9642e − 1 (5.73e − 4)− | 1.8633e − 1 (2.12e − 3)− | 1.9538e − 1 (7.27e − 4) | 1.9891e − 1 (2.75e − 4)+ | 1.9800e − 1 (6.09e − 4) |
| DTLZ6 | 0.0000e + 0 (0.00e + 0)− | 1.3195e − 1 (7.76e − 2)− | 1.9898e − 1 (1.90e − 4)− | 6.7448e − 2 (8.67e − 2)− | 1.9955e − 1 (2.04e − 4) |
| DTLZ7 | 2.5515e − 1 (1.28e − 2)− | 6.8597e − 2 (2.94e − 2)− | 2.6965e − 1 (1.99e − 3)− | 2.6025e − 1 (2.05e − 2)− | 2.7858e − 1 (9.79e − 4) |
| +/−/≈ | 1/10/1 | 0/12/0 | 0/11/1 | 3/9/0 |
4.3.2. Results of 14 Algorithms on Large-Scale MOPs
Tables 6, 7, 8, and 9 provide detailed data on the average values of IGD and HV performance metrics obtained from 30 independent runs of 14 algorithms on the LSMOP series. These data showcase WP–MOIA’s strong competitiveness in handling challenging LSMOP benchmark problems with 300 and 1000 decision variables. WP–MOIA outperformed the other 13 comparison algorithms in almost all assessment items, failing to achieve the best results only in a few specific scenarios (i.e., the HV value assessment of LSMOP6 at 300 decision variables and LSMOP2, LSMOP6, and LSMOP7 at 1000 decision variables). Specifically, in the IGD indicator, WP–MOIA achieved a comprehensive lead, obtaining the best results without exception. The rank-sum test analysis based on the IGD values shows that only the IMTCMO–BS algorithm had a comparable performance to WP–MOIA on LSMOP9 with 1000 decision variables. When examining the IGD values at 300 and 1000 decision variables separately, it can be seen that WP–MOIA performed even better at the higher dimension (1000 decision variables), not only consolidating its significant advantage on LSMOP5–LSMOP7 and LSMOP9 but also extending this advantage to LSMOP1, LSMOP3, and LSMOP4, fully demonstrating its strong ability to guide the population close to the true PF in high-dimensional decision spaces.
| Problem | DEA–GNG | LMPFE | MOEA/D-UR | PREA | LERD | S3–CMA–ES | DGEA | IMMOEAD | IMTCMO–BS | WP–MOIA |
|---|---|---|---|---|---|---|---|---|---|---|
| LSMOP1 (300) | 3.7692e + 0 (4.11e − 1)− | 4.9017e + 0 (5.97e − 1)− | 1.9866e + 0 (3.72e − 1)− | 3.0008e + 0 (2.84e − 1)− | 1.7316e + 0 (3.49e − 1)− | 4.7662e + 1 (3.53e + 1)− | 9.7572e − 1 (2.08e − 1)− | 6.5658e + 0 (7.70e − 1) | 2.1372e + 0 (1.60e + 0) | 6.3351e − 1 (3.36e − 2) |
| LSMOP2 (300) | 9.1133e − 2 (1.93e − 3)− | 8.9306e − 2 (7.78e − 4)− | 9.1691e − 2 (5.73e − 4)− | 9.3505e − 2 (9.62e − 4)− | 9.4768e − 2 (1.51e − 3)− | 5.7957e − 1 (1.35e − 1)− | 8.7790e − 2 (1.94e − 3)− | 1.0331e − 1 (8.17e − 4)− | 9.9216e − 2 (7.16e − 4)− | 8.0699e − 2 (8.32e − 4) |
| LSMOP3 (300) | 1.6480e + 1 (8.10e + 0)− | 1.3413e + 1 (7.55e − 1)− | 7.9053e + 0 (3.61e + 0)− | 1.0110e + 1 (6.43e − 1)− | 1.1156e + 1 (1.21e + 0)− | 3.0594e + 4 (2.15e + 4)− | 2.1390e + 0 (2.84e + 0)− | 2.0359e + 1 (8.46e + 0)− | 2.6951e + 1 (3.35e + 1)− | 8.5915e − 1 (6.24e − 3) |
| LSMOP4 (300) | 2.4437e − 1 (3.35e − 3)− | 2.4183e − 1 (4.56e − 3)− | 2.6069e − 1 (4.03e − 3)− | 2.3695e − 1 (2.97e − 3)− | 2.4646e − 1 (8.43e − 3)− | 1.0567e + 0 (3.47e − 1)− | 2.3785e − 1 (1.46e − 2)− | 2.8886e − 1 (2.61e − 3)− | 2.7127e − 1 (3.29e − 2)− | 2.0806e − 1 (4.73e − 3) |
| LSMOP5 (300) | 9.6982e + 0 (1.21e + 0)− | 1.0898e + 1 (1.51e + 0)− | 2.1793e + 0 (5.74e − 1)− | 5.7470e + 0 (7.60e − 1)− | 3.5800e + 0 (7.84e − 1)− | 7.8258e + 1 (5.95e + 1)− | 1.4204e + 0 (6.43e − 1)− | 5.8693e + 0 | 5.2090e + 0 (4.51e + 0)− | 5.3984e − 1 (4.48e − 3) |
| (9.53e − 1)− | ||||||||||
| LSMOP6 (300) | 1.1646e + 3 (3.63e + 2)− | 1.4853e + 3 (5.64e + 2)− | 1.9038e + 2 (7.70e + 1)− | 1.8296e + 3 (7.10e + 2)− | 8.0054e + 2 (1.02e + 3)− | 5.6657e + 5 (5.30e + 5)− | 2.6609e + 2 (3.41e + 2)− | 3.1805e + 3 (1.08e + 3)− | 8.6890e + 2 (9.97e + 2)− | 1.2663e + 0 (1.05e − 2) |
| LSMOP7 (300) | 4.1110e + 3 (2.56e + 3)− | 1.6076e + 0 (3.60e − 2)− | 1.2461e + 0 (8.98e − 2)− | 1.5220e + 0 (2.94e − 2)− | 1.4128e + 0 (5.93e − 2)− | 4.4287e + 5 (5.14e + 5)− | 1.1336e + 0 (9.39e − 2)− | 2.9524e + 1 (9.13e + 1)− | 1.7191e + 3 (4.62e + 3)− | 9.3315e − 1 (1.57e − 2) |
| LSMOP8 (300) | 9.1029e − 1 (7.23e − 2)− | 8.5805e − 1 (7.36e − 2)− | 7.2631e − 1 (1.40e − 1)− | 9.2749e − 1 (8.95e − 2)− | 6.2712e − 1 (2.10e − 1)− | 3.8445e + 1 (2.72e + 1)− | 6.5618e − 1 (1.24e − 1)− | 6.9647e − 1 (8.80e − 2)− | 6.3160e − 1 (3.37e − 1)≈ | 3.4522e − 1 (2.75e − 2) |
| LSMOP9 (300) | 1.9712e + 1 (2.33e + 0)− | 1.8205e + 1 (2.70e + 0)− | 1.3110e + 1 (2.91e + 0)− | 2.3551e + 1 | 1.5116e + 1 (6.22e + 0)− | 2.6455e + 2 (1.13e + 2)− | 4.1074e + 1 (1.03e + 1)− | 3.9391e + 1 (7.09e + 0)− | 1.9128e + 1 (1.32e + 1)− | 5.8862e − 1 (1.71e − 4) |
| (3.27e + 0)− | ||||||||||
| LSMOP1 (1000) | 7.7301e + 0 (3.51e − 1)− | 8.8129e + 0 (3.39e − 1)− | 5.4914e + 0 (4.56e − 1)− | 5.7916e + 0 (2.77e − 1)− | 1.9618e + 0 (2.59e − 1)− | 4.9524e + 1 (3.14e + 1)− | 1.0151e + 0 (1.61e − 1)− | 9.9599e + 0 (4.06e − 1)− | 2.2204e + 0 (1.84e + 0)− | 7.6362e − 1 (2.59e − 2) |
| LSMOP2 (1000) | 5.2632e − 2 (6.64e − 4)− | 5.4011e − 2 (3.89e − 4)− | 5.5006e − 2 (5.48e − 4)− | 5.9300e − 2 (1.68e − 3)− | 5.4207e − 2 (2.79e − 4)− | 5.3808e − 1 (1.16e − 1)− | 5.2611e − 2 (3.50e − 4)− | 7.1939e − 2 (3.08e − 3)− | 5.4216e − 2 (3.75e − 4)− | 5.2182e − 2 (6.26e − 4) |
| LSMOP3 (1000) | 4.1299e + 1 (3.15e + 1)− | 1.7925e + 1 (1.46e + 0)− | 1.2804e + 1 (1.05e + 0)− | 1.4351e + 1 (6.91e − 1)− | 1.1453e + 1 (9.24e − 1)− | 3.1004e + 4 (2.25e + 4)− | 2.7538e + 0 (2.95e + 0)− | 1.0352e + 2 (1.03e + 2)− | 4.8265e + 1 (4.42e + 1)− | 8.6579e − 1 (2.78e − 2) |
| LSMOP4 (1000) | 1.1427e − 1 (7.69e − 4)− | 1.1270e − 1 (9.80e − 4)− | 1.1701e − 1 (1.23e − 3)− | 1.1704e − 1 (1.73e − 3)− | 1.1294e − 1 (3.03e − 3)− | 6.5458e − 1 (1.74e − 1)− | 1.0469e − 1 (5.34e − 3)− | 1.3315e − 1 (2.63e − 3)− | 1.2345e − 1 (6.44e − 3)− | 9.1372e − 2 (1.50e − 3) |
| LSMOP5 (1000) | 1.6645e + 1 (7.29e − 1)− | 1.9317e + 1 (7.92e − 1)− | 6.9593e + 0 (6.79e − 1)− | 1.1824e + 1 (7.38e − 1)− | 4.1737e + 0 (6.20e − 1)− | 7.3715e + 1 (5.67e + 1)− | 1.5541e + 0 (7.25e − 1)− | 1.5387e + 1 (1.00e + 0)− | 7.3765e + 0 (6.15e + 0)− | 5.4075e − 1 (3.42e − 4) |
| LSMOP6 (1000) | 7.9641e + 3 (1.36e + 3)− | 1.2365e + 4 (1.91e + 3)− | 3.7444e + 3 (8.70e + 2)− | 7.6771e + 3 (1.05e + 3)− | 1.3745e + 3 (9.78e + 2)− | 4.6885e + 5 (5.72e + 5)− | 3.2422e + 2 (3.30e + 2)− | 2.0425e + 4 (4.45e + 3)− | 2.2961e + 3 (2.47e + 3)− | 1.3533e + 0 (9.88e − 2) |
| LSMOP7 (1000) | 1.3979e + 4 (8.69e + 3)− | 1.1013e + 0 (3.26e − 3)− | 1.0449e + 0 (6.13e − 2)− | 6.0355e + 2 (3.30e + 3)− | 1.0599e + 0 (1.23e − 2)− | 4.9390e + 5 (5.32e + 5)− | 9.8006e − 1 (4.98e − 2)− | 7.0446e + 2 (1.27e + 3)− | 4.2444e + 3 (9.08e + 3)− | 8.6150e − 1 (2.26e − 3) |
| LSMOP8 (1000) | 3.1056e + 0 (2.28e + 0)− | 9.5785e − 1 (2.07e − 4)− | 5.7650e − 1 (8.22e − 3)− | 9.5978e − 1 (2.86e − 2)− | 7.0093e − 1 (1.15e − 1)− | 4.8535e + 1 (3.44e + 1)− | 6.0949e − 1 (8.34e − 2)− | 6.3750e − 1 (3.94e − 2)− | 6.6674e − 1 (4.54e − 1)− | 3.4553e − 1 (2.39e − 2) |
| LSMOP9 (1000) | 4.0262e + 1 (3.25e + 0)− | 4.0118e + 1 (2.63e + 0)− | 5.0565e + 1 (5.31e + 0)− | 4.7407e + 1 (2.73e + 0)− | 2.4778e + 1 (7.06e + 0)− | 3.1216e + 2 (1.40e + 2)− | 6.2423e + 1 (1.58e + 1)− | 9.8399e + 1 (6.09e + 0)− | 1.7590e + 1 (2.39e + 1)− | 7.9774e − 1 (2.76e − 1) |
| +/−/≈ | 0/18/0 | 0/18/0 | 0/18/0 | 0/18/0 | 0/18/0 | 0/18/0 | 0/18/0 | 0/18/0 | 0/17/1 |
| Problem | NNIA | MOIA–DCSS | ADE–MOIA | MaIA | WP–MOIA |
|---|---|---|---|---|---|
| LSMOP1 (300) | 5.2039e + 0 (6.40e − 1)− | 1.9492e + 0 (1.98e − 1)− | 4.6520e + 0 (7.21e − 1)− | 3.0060e + 0 (5.57e − 1)− | 6.3351e − 1 (3.36e − 2) |
| LSMOP2 (300) | 1.1321e − 1 (4.31e − 3)− | 9.6612e − 2 (1.68e − 3)− | 1.1159e − 1 (2.99e − 3)− | 9.3491e − 2 (2.10e − 3)− | 8.0699e − 2 (8.32e − 4) |
| LSMOP3 (300) | 1.3789e + 1 (1.59e + 0)− | 1.0271e + 1 (9.83e − 1)− | 1.3114e + 1 (9.66e − 1)− | 8.3835e + 0 (1.55e + 0)− | 8.5915e − 1 (6.24e − 3) |
| LSMOP4 (300) | 2.9446e − 1 (1.06e − 2)− | 2.5014e − 1 (4.84e − 3)− | 3.0520e − 1 (4.76e − 3)− | 2.4673e − 1 (6.37e − 3)− | 2.0806e − 1 (4.73e − 3) |
| LSMOP5 (300) | 1.5426e + 1 (1.54e + 0)− | 3.9140e + 0 (5.81e − 1)− | 1.4322e + 1 (1.39e + 0)− | 6.6912e + 0 (1.71e + 0)− | 5.3984e − 1 (4.48e − 3) |
| LSMOP6 (300) | 6.7453e + 3 (2.77e + 3)− | 4.1014e + 2 (2.86e + 2)− | 4.2664e + 3 (1.40e + 3)− | 2.9116e + 3 (1.20e + 3)− | 1.2663e + 0 (1.05e − 2) |
| LSMOP7 (300) | 1.6555e + 0 (3.85e − 2)− | 1.4007e + 0 (2.82e − 2)− | 1.5719e + 0 (2.97e − 2)− | 1.3027e + 0 (6.03e − 2)− | 9.3315e − 1 (1.57e − 2) |
| LSMOP8 (300) | 9.3140e − 1 (7.16e − 2)− | 5.9771e − 1 (1.87e − 2)− | 8.2816e − 1 (9.61e − 2)− | 7.6552e − 1 (8.61e − 2)− | 3.4522e − 1 (2.75e − 2) |
| LSMOP9 (300) | 3.0274e + 1 (5.14e + 0)− | 1.4179e + 1 (1.71e + 0)− | 8.9519e + 0 (2.06e + 0)− | 1.9428e + 1 (3.98e + 0)− | 5.8862e − 1 (1.71e − 4) |
| LSMOP1 (1000) | 8.9471e + 0 (6.28e − 1)− | 2.1752e + 0 (1.93e − 1)− | 9.7650e + 0 (8.34e − 1)− | 5.3037e + 0 (4.29e − 1)− | 7.6362e − 1 (2.59e − 2) |
| LSMOP2 (1000) | 7.4445e − 2 (4.19e − 3)− | 6.8144e − 2 (3.89e − 4)− | 6.9456e − 2 (2.97e − 3)− | 5.5363e − 2 (8.38e − 4)− | 5.2182e − 2 (6.26e − 4) |
| LSMOP3 (1000) | 1.9962e + 1 (3.48e + 0)− | 1.1348e + 1 (8.91e − 1)− | 1.9674e + 1 (2.36e + 0)− | 1.2387e + 1 (9.05e − 1)− | 8.6579e − 1 (2.78e − 2) |
| LSMOP4 (1000) | 1.4166e − 1 (5.25e − 3)− | 1.1612e − 1 (1.87e − 3)− | 1.3759e − 1 (3.25e − 3)− | 1.1217e − 1 (1.80e − 3)− | 9.1372e − 2 (1.50e − 3) |
| LSMOP5 (1000) | 1.9612e + 1 (9.53e − 1)− | 4.5425e + 0 (4.26e − 1)− | 1.7013e + 1 (1.53e + 0)− | 1.1853e + 1 (1.41e + 0)− | 5.4075e − 1 (3.42e − 4) |
| LSMOP6 (1000) | 3.1078e + 4 (9.14e + 3)− | 1.3641e + 3 (8.74e + 2)− | 1.8054e + 4 (5.68e + 3)− | 1.1212e + 4 (2.07e + 3)− | 1.3533e + 0 (9.88e − 2) |
| LSMOP7 (1000) | 1.1092e + 0 (3.79e − 3)− | 1.0737e + 0 (3.08e − 3)− | 1.1027e + 0 (3.58e − 3)− | 1.0795e + 0 (4.01e − 3)− | 8.6150e − 1 (2.26e − 3) |
| LSMOP8 (1000) | 9.5068e − 1 (2.72e − 2)− | 5.5263e − 1 (1.21e − 2)− | 9.1590e − 1 (7.99e − 2)− | 9.2742e − 1 (4.19e − 2)− | 3.4553e − 1 (2.39e − 2) |
| LSMOP9 (1000) | 5.7766e + 1 (4.38e + 0)− | 2.6511e + 1 (1.82e + 0)− | 5.0709e + 1 (3.43e + 0)− | 6.4054e + 1 (4.67e + 0)− | 7.9774e − 1 (2.76e − 1) |
| +/−/≈ | 0/18/0 | 0/18/0 | 0/18/0 | 0/18/0 |
| Problem | DEA–GNG | LMPFE | MOEA/D-UR | PREA | LERD | S3–CMA–ES | DGEA | IMMOEAD | IMTCMO–BS | WP–MOIA |
|---|---|---|---|---|---|---|---|---|---|---|
| LSMOP1 (300) | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 3.0303e − 3 (1.66e − 2)− | 0.0000e + 0 (0.00e + 0)− | 3.5088e − 2 (5.84e − 2)− | 0.0000e + 0 (0.00e + 0)− | 4.8503e − 2 (4.61e − 2)− | 1.1851e − 1 (2.07e − 2) |
| LSMOP2 (300) | 7.4304e − 1 (4.55e − 3)− | 7.7179e − 1 (8.65e − 4)− | 7.6564e − 1 (1.64e − 3)− | 7.6834e − 1 (1.06e − 3)− | 7.6465e − 1 (1.70e − 3)− | 2.0672e − 1 (6.51e − 2)− | 7.6993e − 1 (2.96e − 3)− | 7.1756e − 1 (5.79e − 3)− | 7.6117e − 1 (1.59e − 3)− | 7.8047e − 1 (2.44e − 3) |
| LSMOP3 (300) | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 7.2728e − 2 (3.70e − 2)− | 0.0000e + 0 (0.00e + 0)− | 4.8485e − 2 (4.61e − 2)− | 9.0911e − 2 (4.62e − 6) |
| LSMOP4 (300) | 5.4738e − 1 (9.27e − 3)− | 5.7342e − 1 (6.57e − 3)− | 5.4947e − 1 (5.21e − 3)− | 5.8199e − 1 (3.98e − 3)− | 5.6846e − 1 (1.27e − 2)− | 2.3109e − 2 (4.91e − 2)− | 5.6717e − 1 (1.95e − 2)− | 4.8348e − 1 (6.41e − 3)− | 5.4606e − 1 (5.02e − 2)− | 6.3056e − 1 (5.22e − 3) |
| LSMOP5 (300) | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 1.0497e − 2 (5.75e − 2)− | 0.0000e + 0 (0.00e + 0)− | 6.9241e − 2 (1.09e − 1)− | 0.0000e + 0 (0.00e + 0)− | 1.5665e − 1 (1.70e − 1)− | 3.4657e − 1 (3.19e − 4) |
| LSMOP6 (300) | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 6.9061e − 4 (2.21e − 3)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0) |
| LSMOP7 (300) | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0) |
| LSMOP8 (300) | 2.7984e − 2 (3.84e − 3)− | 2.8251e − 2 (7.35e − 4)− | 4.6376e − 2 (4.09e − 3)− | 3.0606e − 2 (7.71e − 4)− | 9.2748e − 2 (1.07e − 1)− | 0.0000e + 0 (0.00e + 0)− | 6.3479e − 2 (5.94e − 2)− | 3.3197e − 2 (2.71e − 3)− | 2.2208e − 1 (1.77e − 1)≈ | 3.7164e − 1 (9.04e − 4) |
| LSMOP9 (300) | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 4.8616e − 2 (6.99e − 2)− | 1.9186e − 1 (2.63e − 4) |
| LSMOP1 (1000) | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 2.1157e − 2 (3.90e − 2)− | 0.0000e + 0 (0.00e + 0)− | 5.3988e − 2 (4.49e − 2)− | 9.6823e − 2 (4.78e − 3) |
| LSMOP2 (1000) | 7.9081e − 1 (5.95e − 3)− | 8.1650e − 1 (3.88e − 4)+ | 8.1157e − 1 (1.76e − 3)− | 8.1267e − 1 (1.27e − 3)− | 8.1629e − 1 (3.61e − 4)+ | 2.5576e − 1 (5.81e − 2)− | 8.1786e − 1 (5.32e − 4)+ | 7.6667e − 1 (8.15e − 3)− | 8.1658e − 1 (3.03e − 4)+ | 8.1397e − 1 (2.73e − 3) |
| LSMOP3 (1000) | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 4.8485e − 2 (4.61e − 2)− | 0.0000e + 0 (0.00e + 0)− | 2.4247e − 2 (3.91e − 2)− | 8.7879e − 2 (1.66e − 2) |
| LSMOP4 (1000) | 7.1309e − 1 (7.33e − 3)− | 7.4251e − 1 (1.16e − 3)− | 7.3273e − 1 (2.55e − 3)− | 7.3830e − 1 (2.27e − 3)− | 7.4269e − 1 (3.61e − 3)− | 1.5068e − 1 (8.81e − 2)− | 7.4762e − 1 (7.44e − 3)− | 6.7778e − 1 (8.81e − 3)− | 7.3464e − 1 (1.06e − 2)− | 7.6987e − 1 (2.48e − 3) |
| LSMOP5 (1000) | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 4.8636e − 2 (6.94e − 2)− | 0.0000e + 0 (0.00e + 0)− | 1.3110e − 1 (1.60e − 1)− | 3.4601e − 1 (4.12e − 4) |
| LSMOP6 (1000) | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 1.6799e − 3 (4.75e − 3)+ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0) |
| LSMOP7 (1000) | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 1.1630e − 3 (2.77e − 3)+ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 1.8502e − 5 (1.01e − 4) |
| LSMOP8 (1000) | 1.1351e − 2 (2.39e − 2)− | 6.8786e − 2 (3.72e − 4)− | 7.3076e − 2 (7.12e − 4)− | 6.7047e − 2 (1.28e − 2)− | 7.3032e − 2 (9.11e − 4)− | 2.4781e − 3 (1.05e − 2)− | 8.3834e − 2 (2.22e − 2)− | 6.2269e − 2 (7.99e − 3)− | 2.2318e − 1 (1.64e − 1)− | 3.9505e − 1 (4.27e − 4) |
| LSMOP9 (1000) | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 9.7498e − 2 (7.01e − 2)− | 1.7442e − 1 (2.19e − 2) |
| +/−/≈ | 0/14/4 | 1/13/4 | 0/14/4 | 0/14/4 | 1/13/4 | 0/14/4 | 3/13/2 | 0/14/4 | 1/12/5 |
| Problem | NNIA | MOIA–DCSS | ADE–MOIA | MaIA | WP–MOIA |
|---|---|---|---|---|---|
| LSMOP1 (300) | 0.0000e + 0 (0.00e − 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 1.1851e − 1 (2.07e − 2) |
| LSMOP2 (300) | 7.4324e − 1 (4.16e − 3)− | 7.2790e − 1 (2.08e − 3)− | 7.4527e − 1 (3.26e − 3)− | 7.6134e − 1 (3.30e − 3)− | 7.8047e − 1 (2.44e − 3) |
| LSMOP3 (300) | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 9.0911e − 2 (4.62e − 6) |
| LSMOP4 (300) | 4.8942e − 1 (1.24e − 2)− | 5.3717e − 1 (5.11e − 3)− | 4.8270e − 1 (8.33e − 3)− | 5.6159e − 1 (7.78e − 3)− | 6.3056e − 1 (5.22e − 3) |
| LSMOP5 (300) | 0.0000e + 0 (0.00e − 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 3.4657e − 1 (3.19e − 4) |
| LSMOP6 (300) | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0) |
| LSMOP7 (300) | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0) |
| LSMOP8 (300) | 2.6948e − 2 (9.31e − 4)− | 4.0344e − 2 (2.77e − 3)− | 2.8596e − 2 (7.68e − 4)− | 3.3412e − 2 (2.17e − 3)− | 3.7164e − 1 (9.04e − 4) |
| LSMOP9 (300) | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 1.9186e − 1 (2.63e − 4) |
| LSMOP1 (1000) | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 9.6823e − 2 (4.78e − 3) |
| LSMOP2 (1000) | 7.9893e − 1 (3.20e − 3)− | 7.7439e − 1 (9.29e − 4)− | 8.0257e − 1 (2.84e − 3)− | 8.0858e − 1 (3.31e − 3)− | 8.1397e − 1 (2.73e − 3) |
| LSMOP3 (1000) | 0.0000e + 0 (0.00e +0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 8.7879e − 2 (1.66e − 2) |
| LSMOP4 (1000) | 7.0409e − 1 (5.42e − 3)− | 7.0868e − 1 (2.11e − 3)− | 7.1061e − 1 (3.25e − 3)− | 7.4160e − 1 (2.17e − 3)− | 7.6987e − 1 (2.48e − 3) |
| LSMOP5 (1000) | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 3.4601e − 1 (4.12e − 4) |
| LSMOP6 (1000) | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0) |
| LSMOP7 (1000) | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 1.8502e − 5 (1.01e − 4) |
| LSMOP8 (1000) | 6.7751e − 2 (4.21e − 4)− | 7.8742e − 2 (2.38e − 3)− | 6.8059e − 2 (4.55e − 4)− | 7.0301e − 2 (2.80e − 4)− | 3.9505e − 1 (4.27e − 4) |
| LSMOP9 (1000) | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e + 0)− | 1.7442e − 1 (2.19e − 2) |
| +/−/≈ | 0/14/4 | 0/14/4 | 0/14/4 | 0/14/4 |
Similarly, the results reflected by the rank-sum test based on HV show a high degree of consistency with those indicated by the IGD metrics. Although WP–MOIA is slightly inferior in a few problems (including three problems of DGEA and one problem each of LMPFE, LERD, and IMTCMO–BS), its overall performance remains excellent. To conduct a more in-depth exploration of the reasons for the discrepancies between the two metrics, we selected the experimental case where the contrast between the metrics was most significant as an example. Specifically, we took the performance of WP–MOIA and DGEA on LSMOP6 as an example for illustration. Experimental observations show that the solution set generated by WP–MOIA is uniformly distributed along an arc parallel to the PF and is closer to it. This situation gives it a better IGD value than DGEA. In contrast, although the solution set generated by DGEA is more scattered and relatively concentrated in one direction of the PF, it covers a larger volume of the objective space, causing WP–MOIA to lag behind in the HV metric. This indicates that WP–MOIA excels at finding high-quality solution sets that are close to the PF and uniformly distributed, but there is still room for improvement in exploring and covering a more comprehensive PF. Nevertheless, compared to MOIAs, WP–MOIA still maintains a completely dominant advantage. This achievement fully proves the contribution of WP–MOIA in enhancing the ability of MOIAs to handle large-scale MOPs.
Figure 3 presents the final nondominated solutions corresponding to the median IGD values obtained from 30 runs of all comparative algorithms on LSMOP8 with 1000 decision variables. It can be observed that WP–MOIA achieved good convergence but the distribution of solutions was not sufficiently uniform. Overall, other algorithms failed to yield satisfactory results. Among them, DEA–GNG, LMPFE, PREA, and LERD exhibited relatively uniform solution distributions but were far from the true PF. IMTCMO–BS and DGEA were closer to the true PF, but the solutions were more concentrated in a small region, which is consistent with the result analysis in Section 4.1 for poor IGD and better HV values. The performance of the four MOIAs lagged considerably behind that of WP–MOIA. This reaffirms the effectiveness of the improvements made by WP–MOIA in addressing large-scale MOPs.
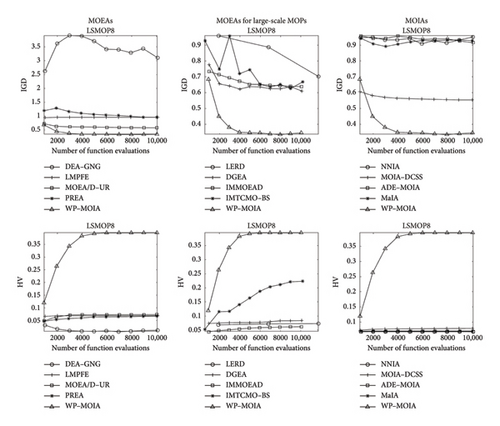
To compare the evolutionary efficiency of different algorithms, we plotted the average IGD and HV values for LSMOP8 with 1000 decision variables in Figure 4, showing how these metrics change as the number of function evaluations increases. To avoid line clutter, we divided the 14 algorithms into 3 groups: MOEAs, MOEAs for large-scale MOPs, and MOIAs. It should be noted that we excluded S3–CMA–ES because it was unable to produce valid data points within the default number of evaluations. In addition, due to the population evaluation mechanism in LERD, its last data point’s horizontal coordinate exceeds the right boundary of the evaluation count, indicating that this algorithm actually performs more evaluations than other algorithms in comparative experiments. From the Figure 4, we can clearly see that WP–MOIA not only achieves the final best value but also exhibits faster convergence. The rapid evolutionary capability is mainly attributed to the specially designed strategy using a dual-population evolution, especially the WP for broad search to quickly update the ideal point, followed by guiding an increasingly larger proportion of the EP to evolve towards it. In the Figure 4, we also observe that algorithms specifically designed for large-scale MOPs (LERD, DGEA, IMMOEAD, and IMTCMO–BS) do not necessarily outperform other algorithms that have not been specifically optimized. This is why we included a variety of algorithm categories in our comparisons. In the MOIAs series, we can see that apart from WP–MOIA, the other algorithms hardly decrease (or increase) their IGD (or HV) values as the number of evaluations increases. This suggests that these MOIAs are largely unable to gradually find solutions closer to the true PF in very high-dimensional search spaces. This suggests that these MOIAs are largely incapable of gradually finding solutions closer to the true PF in very high-dimensional search spaces. Summarizing the analysis above, we can reasonably conclude that WP–MOIA has outstanding capabilities in dealing with large-scale MOPs.
4.3.3. Analysis of Newly Introduced Parameters
WP–MOIA introduces two new parameters, α and β, which dynamically regulate the relative proportions of EP and WP during the evolutionary process, aiming for dynamic collaborative evolution between the two subpopulations. This mechanism is designed to harness the power of the WP and balance the levels of exploration and exploitation of the entire population. To validate the effectiveness of the proposed method, Tables 10, 11, 12, and 13 present the IGD and HV values obtained by variants of WP–MOIA with different configurations of α and β.
| Problem | WP–MOIA1 | WP–MOIA2 | WP–MOIA3 | WP–MOIA4 | WP–MOIA |
|---|---|---|---|---|---|
| ZDT1 | 1.3660e − 2 (9.06e − 3)− | 2.3540e − 2 (5.14e − 3)− | 4.4229e − 3 (1.35e − 4)− | 4.3429e − 3 (1.61e − 4)≈ | 4.3022e − 3 (1.36e − 4) |
| ZDT2 | 2.4283e − 2 (2.06e − 2)− | 1.5177e − 2 (2.39e − 3)− | 4.3148e − 3 (1.20e − 4)≈ | 4.2819e − 3 (1.25e − 4)≈ | 4.2847e − 3 (9.62e − 5) |
| ZDT3 | 2.9955e − 2 (1.58e − 2)− | 1.7585e − 2 (4.54e − 3)− | 6.7586e − 3 (4.66e − 4)≈ | 6.5008e − 3 (5.31e − 4)+ | 6.8510e − 3 (6.28e − 4) |
| ZDT4 | 1.6464e + 1 (1.10e + 1)− | 1.2909e + 1 (4.57e + 0)− | 4.4149e − 3 (1.67e − 4)≈ | 4.0719e − 2 (1.98e − 1)− | 4.4161e − 3 (1.42e − 4) |
| ZDT6 | 1.8035e − 1 (1.70e − 1)− | 1.8556e + 0 (8.10e − 2)− | 3.5391e − 3 (9.20e − 5)≈ | 3.6401e − 3 (7.09e − 4)≈ | 3.5311e − 3 (8.70e − 5) |
| DTLZ1 | 1.3523e − 1 (1.05e − 1)− | 1.1733e − 1 (1.85e − 1)− | 5.4813e − 2 (1.18e − 1)− | 2.0466e − 2 (3.55e − 4)≈ | 2.0420e − 2 (2.99e − 4) |
| DTLZ2 | 1.9387e − 1 (1.73e − 2)− | 5.5011e − 2 (1.05e − 3)+ | 5.9126e − 2 (1.32e − 3)− | 5.9007e − 2 (1.73e − 3)≈ | 5.8219e − 2 (1.45e − 3) |
| DTLZ3 | 5.3247e − 1 (4.17e − 1)− | 3.7500e + 0 (3.18e + 0)− | 5.3309e − 1 (9.68e − 1)− | 9.2260e − 2 (1.75e − 1)≈ | 1.5778e − 1 (2.76e − 1) |
| DTLZ4 | 5.6768e − 1 (5.48e − 2)− | 7.4880e − 2 (1.14e − 2)+ | 1.4684e − 1 (8.15e − 2)≈ | 1.3388e − 1 (6.66e − 2)≈ | 1.6556e − 1 (9.81e − 2) |
| DTLZ5 | 2.5130e − 1 (4.60e − 2)− | 5.1115e − 3 (4.21e − 4)+ | 7.0831e − 3 (1.86e − 3)− | 6.0674e − 3 (1.21e − 3)≈ | 5.6298e − 3 (4.65e − 4) |
| DTLZ6 | 2.9918e − 2 (6.70e − 2)− | 1.0596e + 1 (2.81e − 1)− | 4.4957e − 3 (9.11e − 5)− | 4.3890e − 3 (7.64e − 5)≈ | 4.4207e − 3 (7.89e − 5) |
| DTLZ7 | 1.4644e − 1 (5.18e − 2)− | 6.8917e − 2 (3.56e − 3)− | 6.2746e − 2 (2.42e − 3)≈ | 6.3120e − 2 (2.25e − 3)− | 6.1952e − 2 (2.74e − 3) |
| +/−/≈ | 0/12/0 | 3/9/0 | 0/6/6 | 1/2/9 |
| Problem | WP–MOIA1 | WP–MOIA2 | WP–MOIA3 | WP–MOIA4 | WP–MOIA |
|---|---|---|---|---|---|
| ZDT1 | 7.0774e − 1 (9.67e − 3)− | 6.9089e − 1 (6.84e − 3)− | 7.1951e − 1 (2.59e − 4)≈ | 7.1935e − 1 (3.40e − 4)− | 7.1955e − 1 (3.07e − 4) |
| ZDT2 | 4.0614e − 1 (3.27e − 2)− | 4.2470e − 1 (3.48e − 3)− | 4.4427e − 1 (2.45e − 4)≈ | 4.4403e − 1 (2.95e − 4)− | 4.4422e − 1 (2.82e − 4) |
| ZDT3 | 6.1520e − 1 (2.48e − 2)+ | 5.8746e − 1 (4.39e − 3)− | 5.9915e − 1 (4.05e − 4)≈ | 5.9886e − 1 (3.09e − 4)− | 5.9927e − 1 (5.13e − 4) |
| ZDT4 | 0.0000e + 0 (0.00e + 0)− | 0.0000e + 0 (0.00e − 0)− | 7.1917e − 1 (4.16e − 4)≈ | 6.9472e − 1 (1.31e − 1)− | 7.1917e − 1 (3.28e − 4) |
| ZDT6 | 2.4430e − 1 (1.30e − 1)− | 0.0000e + 0 (0.00e + 0)− | 3.8786e − 1 (3.27e − 4)≈ | 3.8782e − 1 (6.16e − 4)≈ | 3.8799e − 1 (2.76e − 4) |
| DTLZ1 | 5.8096e − 1 (2.09e − 1)− | 6.4404e − 1 (3.06e − 1)− | 7.7077e − 1 (2.03e − 1)≈ | 8.2820e − 1 (4.31e − 3)− | 8.3073e − 1 (4.88e − 3) |
| DTLZ2 | 3.0719e − 1 (2.59e − 2)− | 5.4040e − 1 (4.47e − 3)− | 5.5257e − 1 (1.96e − 3)≈ | 5.5269e − 1 (1.78e − 3)≈ | 5.5306e − 1 (2.47e − 3) |
| DTLZ3 | 2.1308e − 1 (1.33e − 1)− | 5.8885e − 2 (1.41e − 1)− | 3.9743e − 1 (2.39e − 1)≈ | 5.2860e − 1 (1.02e − 1)≈ | 4.7991e − 1 (1.74e − 1) |
| DTLZ4 | 4.3366e − 2 (4.42e − 2)− | 5.3303e − 1 (1.34e − 2)+ | 4.9962e − 1 (4.75e − 2)≈ | 5.1023e − 1 (4.11e − 2)≈ | 4.9148e − 1 (5.84e − 2) |
| DTLZ5 | 1.8827e − 2 (1.54e − 2)− | 1.9819e − 1 (6.40e − 4)≈ | 1.9678e − 1 (1.64e − 3)− | 1.9766e − 1 (1.31e − 3)≈ | 1.9800e − 1 (6.09e − 4) |
| DTLZ6 | 1.8116e − 1 (3.96e − 2)− | 0.0000e + 0 (0.00e + 0)− | 1.9954e − 1 (2.37e − 4)≈ | 1.9961e − 1 (1.80e − 4)≈ | 1.9955e − 1 (2.04e − 4) |
| DTLZ7 | 2.5420e − 1 (1.09e − 2)− | 2.5865e − 1 (4.51e − 3)− | 2.7869e − 1 (9.10e − 4)≈ | 2.7795e − 1 (1.43e − 3)≈ | 2.7858e − 1 (9.79e − 4) |
| +/−/≈ | 1/11/0 | 1/10/1 | 0/1/11 | 0/5/7 |
| Problem | WP–MOIA1 | WP–MOIA2 | WP–MOIA3 | WP–MOIA4 | WP–MOIA |
|---|---|---|---|---|---|
| LSMOP1 (300) | 8.1655e − 1 (1.98e − 2)− | 2.4204e + 0 (3.94e − 1)− | 6.5265e − 1 (3.36e − 2)− | 6.5537e − 1 (2.68e − 2)− | 6.3351e − 1 (3.36e − 2) |
| LSMOP2 (300) | 7.8025e − 2 (9.99e − 4)+ | 8.8715e − 2 (7.63e − 4)− | 8.0466e − 2 (1.12e − 3)≈ | 7.9963e − 2 (1.06e − 3)+ | 8.0699e − 2 (8.32e − 4) |
| LSMOP3 (300) | 8.6071e − 1 (1.46e − 5)≈ | 1.4762e + 1 (4.03e + 0)− | 8.6072e − 1 (3.39e − 16)≈ | 8.6071e − 1 (1.33e − 5)≈ | 8.5915e − 1 (6.24e − 3) |
| LSMOP4 (300) | 2.1206e − 1 (4.48e − 3)− | 2.4709e − 1 (3.75e − 3)− | 2.1168e − 1 (5.13e − 3)− | 2.0839e − 1 (3.15e − 3)≈ | 2.0806e − 1 (4.73e − 3) |
| LSMOP5 (300) | 5.4674e − 1 (1.49e − 2)− | 6.4686e + 0 (1.82e + 0)− | 5.4060e − 1 (5.60e − 4)≈ | 5.4071e − 1 (4.14e − 4)≈ | 5.3984e − 1 (4.48e − 3) |
| LSMOP6 (300) | 1.2903e + 0 (4.77e − 2)− | 3.1227e + 3 (3.19e + 3)− | 1.2831e + 0 (6.80e − 2)≈ | 1.2656e + 0 (4.24e − 3)≈ | 1.2663e + 0 (1.05e − 2) |
| LSMOP7 (300) | 9.6987e − 1 (2.51e − 2)− | 1.6020e + 1 (2.18e + 1)− | 9.4222e − 1 (1.26e − 2)− | 9.4311e − 1 (1.15e − 2)− | 9.3315e − 1 (1.57e − 2) |
| LSMOP8 (300) | 3.4695e − 1 (2.30e − 2)≈ | 7.1081e − 1 (8.54e − 2)− | 3.2944e − 1 (2.54e − 2)+ | 3.4662e − 1 (2.59e − 2)≈ | 3.4522e − 1 (2.75e − 2) |
| LSMOP9 (300) | 1.4483e + 0 (2.08e − 1)− | 1.8235e + 1 (4.01e + 0)− | 5.8870e − 1 (3.75e − 4)≈ | 6.5683e − 1 (1.89e − 1)− | 5.8862e − 1 (1.71e − 4) |
| LSMOP1 (1000) | 8.2828e − 1 (1.44e − 2)− | 4.8290e + 0 (3.87e − 1)− | 7.6596e − 1 (3.10e − 2)≈ | 7.6180e − 1 (3.22e − 2)≈ | 7.6362e − 1 (2.59e − 2) |
| LSMOP2 (1000) | 4.9802e − 2 (7.14e − 4)+ | 5.0581e − 2 (5.82e − 4)+ | 5.0429e − 2 (5.97e − 4)+ | 5.0288e − 2 (6.88e − 4)+ | 5.2182e − 2 (6.26e − 4) |
| LSMOP3 (1000) | 8.6072e − 1 (3.39e − 16)≈ | 2.2069e + 1 (1.08e + 1)− | 8.6427e − 1 (1.95e − 2)≈ | 8.6072e − 1 (6.93e − 7)≈ | 8.6579e − 1 (2.78e − 2) |
| LSMOP4 (1000) | 9.0892e − 2 (1.12e − 3)≈ | 1.1070e − 1 (1.10e − 3)− | 9.0552e − 2 (1.56e − 3)+ | 9.0099e − 2 (1.36e − 3)+ | 9.1372e − 2 (1.50e − 3) |
| LSMOP5 (1000) | 5.4712e − 1 (1.72e − 2)− | 1.1126e + 1 (1.79e + 0)− | 5.4068e − e − 1 (3.61e − 4)+ | 5.4073e − 1 (3.43e − 4)+ | 5.4075e − 1 (3.42e − 4) |
| LSMOP6 (1000) | 1.3253e + 0 (2.24e − 2)≈ | 7.1374e + 3 (4.73e + 3)≈ | 1.3333e + 0 (7.40e − 2)+ | 1.3283e + 0 (6.92e − 2)+ | 1.3533e + 0 (9.88e − 2) |
| LSMOP7 (1000) | 8.6929e − 1 (6.77e − 3)− | 4.2893e + 1 (5.45e + 1)− | 8.6145e − 1 (5.31e − 3)≈ | 8.5713e − 1 (2.18e − 2)≈ | 8.6150e − 1 (2.26e − 3) |
| LSMOP8 (1000) | 3.2115e − 1 (3.06e − 2)+ | 5.6390e − 1 (6.13e − 3)− | 3.2011e − 1 (3.77e − 2)+ | 3.4347e − 1 (2.74e − 2)≈ | 3.4553e − 1 (2.39e − 2) |
| LSMOP9 (1000) | 1.4981e + 0 (1.37e − 1)− | 4.3898e + 1 (5.80e + 0)− | 8.4604e − 1 (2.90e − 1)≈ | 1.0932e + 0 (2.95e − 1)− | 7.9774e − 1 (2.76e − 1) |
| +/−/≈ | 3/10/5 | 1/17/0 | 6/3/9 | 5/4/9 |
| Problem | WP–MOIA1 | WP–MOIA2 | WP–MOIA3 | WP–MOIA4 | WP–MOIA |
|---|---|---|---|---|---|
| LSMOP1 (300) | 1.0645e − 1 (7.68e − 3)− | 0.0000e + 0 (0.00e + 0)− | 1.0485e − 1 (9.94e − 3)− | 1.0314e − 1 (1.31e − 2)− | 1.1851e − 1 (2.07e − 2) |
| LSMOP2 (300) | 7.8504e − 1 (2.38e − 3)+ | 7.5562e − 1 (5.94e − 3)− | 7.8263e − 1 (1.63e − 3)+ | 7.8086e − 1 (2.45e − 3)≈ | 7.8047e − 1 (2.44e − 3) |
| LSMOP3 (300) | 9.0910e − 2 (3.35e − 6)≈ | 0.0000e + 0 (0.00e + 0)− | 9.0909e − 2 (7.06e − 17)≈ | 9.0910e − 2 (4.71e − 6)≈ | 9.0911e − 2 (4.62e − 6) |
| LSMOP4 (300) | 6.2358e − 1 (4.50e − 3)− | 5.5614e − 1 (4.93e − 3)− | 6.2619e − 1 (4.98e − 3)− | 6.3083e − 1 (3.15e − 3)≈ | 6.3056e − 1 (5.22e − 3) |
| LSMOP5 (300) | 3.3538e − 1 (2.21e − 2)− | 0.0000e + 0 (0.00e + 0)− | 3.4650e − 1 (2.60e − 4)≈ | 3.4648e − 1 (3.19e − 4)≈ | 3.4657e − 1 (3.19e − 4) |
| LSMOP6 (300) | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0) |
| LSMOP7 (300) | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0) |
| LSMOP8 (300) | 3.6625e − 1 (1.18e − 2)≈ | 3.8626e − 2 (6.53e − 3)− | 3.7163e − 1 (8.67e − 4)≈ | 3.7194e − 1 (9.11e − 4)≈ | 3.7164e − 1 (9.04e − 4) |
| LSMOP9 (300) | 1.0031e − 1 (2.08e − 2)− | 0.0000e + 0 (0.00e + 0)− | 1.9180e − 1 (4.20e − 4)≈ | 1.8551e − 1 (1.65e − 2)− | 1.9186e − 1 (2.63e − 4) |
| LSMOP1 (1000) | 1.0224e − 1 (6.37e − 3)+ | 0.0000e + 0 (0.00e + 0)− | 1.0015e − 1 (8.68e − 3)≈ | 9.9279e − 2 (8.51e − 3)≈ | 9.6823e − 2 (4.78e − 3) |
| LSMOP2 (1000) | 8.1992e − 1 (1.28e − 3)+ | 7.9958e − 1 (5.72e − 3)− | 8.1842e − 1 (1.54e − 3)+ | 8.1604e − 1 (2.93e − 3)+ | 8.1397e − 1 (2.73e − 3) |
| LSMOP3 (1000) | 9.0909e − 2 (7.06e − 17)≈ | 0.0000e + 0 (0.00e + 0)− | 8.7879e − 2 (1.66e − 2)≈ | 9.0909e − 2 (2.52e − 7)≈ | 8.7879e − 2 (1.66e − 2) |
| LSMOP4 (1000) | 7.7161e − 1 (2.03e − 3)+ | 7.2736e − 1 (6.46e − 3)− | 7.7113e − 1 (2.29e − 3)+ | 7.7030e − 1 (2.48e − 3)≈ | 7.6987e − 1 (2.48e − 3) |
| LSMOP5 (1000) | 3.3291e − 1 (2.38e − 2)− | 0.0000e + 0 (0.00e + 0)− | 3.4660e − 1 (2.49e − 4)+ | 3.4642e − 1 (4.03e − 4)+ | 3.4601e − 1 (4.12e − 4) |
| LSMOP6 (1000) | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0) |
| LSMOP7 (1000) | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 0.0000e + 0 (0.00e + 0)≈ | 1.8502e − 5 (1.01e − 4) |
| LSMOP8 (1000) | 3.9107e − 1 (1.12e − 2)≈ | 7.2442e − 2 (9.35e − 4)− | 3.9521e − 1 (4.01e − 4)≈ | 3.9516e − 1 (4.45e − 4)≈ | 3.9505e − 1 (4.27e − 4) |
| LSMOP9 (1000) | 9.5207e − 2 (1.35e − 2)− | 0.0000e + 0 (0.00e + 0)− | 1.7057e − 1 (2.41e − 2)≈ | 1.4603e − 1 (2.87e − 2)− | 1.7442e − 1 (2.19e − 2) |
| +/−/≈ | 4/6/8 | 0/14/4 | 4/2/12 | 2/3/13 |
In the aforementioned WP–MOIA, α is set to 0.4, representing an initial proportion of 40% for EP in the entire population. Meanwhile, β is set to 0.85, indicating that, according to equation (5), once the maximum number of function evaluations is reached, the EP proportion will progressively increase to a maximum ratio of 85%, as depicted in Figure 5. To ensure integral individual values, a ceiling operation is applied in equation (5), causing a stepped increment in the growth of the EP proportion. This configuration implies that initially, the WP accounts for a majority of the whole population, biasing the overall population towards exploration. However, as the optimization process advances, the population increasingly favors exploitation while still retaining a certain level of exploration.
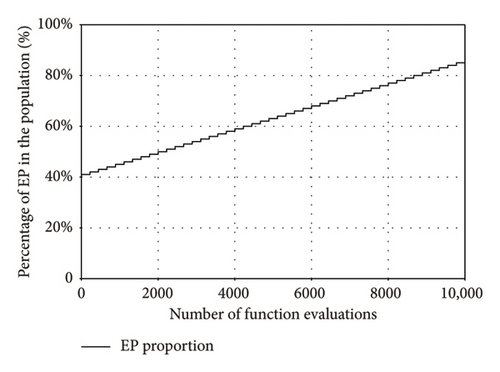
In WP–MOIA1, both α and β are set to 0, indicating that the algorithm relies solely on the evolution of the WP, with no contribution from EP. In WP–MOIA2, both α and β are set to 1, which means the algorithm entirely depends on the evolution of the EP, completely excluding the empowerment of the WP, effectively conducting an experiment of dissolving the WP. For WP–MOIA3, both α and β are set to 0.5, implying that throughout the whole evolutionary process, the EP and WP maintain the same size, working collaboratively in a static manner without any dynamic change in their roles as the evolutionary process unfolds. In WP–MOIA4, α is set to 0, while β is set to 1, meaning the EP starts from empty and gradually comes to dominate the entire evolutionary population, while the WP starts as the sole occupant of the evolutionary population and progressively diminishes to empty. This setup allows for dynamic coordination between the two subpopulations. From the overall results, it is observed that WP–MOIA achieved better results on the ZDT series, DTLZ series, and LSMOP series with 300 decision variables, while WP–MOIA3 and WP–MOIA4 obtained better results on the LSMOP series with 1000 decision variables. Between WP–MOIA1, which relies solely on WP evolution, and WP–MOIA2, which relies solely on EP evolution, the former performed better on large-scale MOPs, while the latter performed better on small-scale MOPs.
In the following, we analyze the reasons for the aforementioned performance individually. On small-scale MOPs, the solution space is much smaller than that of large-scale MOPs. Under these circumstances, WP–MOIA2, which uses the EP for fine search based on the superior solutions, is more effective than WP–MOIA1, which tends to explore through large mutations. Therefore, it performs better on small-scale MOPs. On the other hand, for large-scale MOPs, the search space for solutions grows substantially, and at this point, the drawback of WP–MOIA1, which relies solely on the search for superior solutions, becomes evident. Its probability of finding Pareto optimal solutions is quite low, which is also a challenge currently faced by MOIAs when solving large-scale MOPs. Conversely, WP–MOIA2 utilizes the WP for a broad search, resulting in better performance on large-scale MOPs. However, both WP–MOIA1 and WP–MOIA2 perform less effectively compared to the cooperative coevolutionary approaches of WP–MOIA3, WP–MOIA4, and WP–MOIA.
Analyzing the performance of WP–MOIA3, WP–MOIA4, and WP–MOIA on small-scale MOPs, WP–MOIA shows the best results, followed by WP–MOIA4, while WP–MOIA3 performs the worst. This indicates that the dynamic collaboration of starting with a large proportion of exploration and gradually shifting to exploitation-dominated is effective. However, on large-scale MOPs, WP–MOIA’s performance changes from the best with 300 decision variables to the worst with 1000 decision variables. The reason for this lies in the settings of parameters α and β. For WP–MOIA, α is set to 0.4 and β to 0.85; for WP–MOIA4, α is set to 0 and β to 1; and for WP–MOIA3, both α and β are set to 0.5. This means that the proportion of the WP, representing the broad search of the entire population, decreases from 60% to 15%, from 100% to 0, and remains unchanged at 50%, respectively. Since the search space for 300 decision variables is much smaller than that for 1000 decision variables, a relatively smaller search population proportion is appropriate; hence, WP–MOIA achieves optimal results on LSMOP with 300 decision variables. However, when facing LSMOP with 1000 decision variables, it shows insufficient search capability. At this point, it is necessary to further increase the proportion of WP in the evolutionary population. WP–MOIA4 in its early stage and WP–MOIA3 in its later stage have a higher WP proportion than WP–MOIA, which is why they achieve better results on problems with 1000 decision variables. The performance of WP–MOIA3, WP–MOIA4, and WP–MOIA across different scale problems not only demonstrates that our approach of dual population (corresponding to different evolutionary tasks) collaborative evolution and dynamically adjusting population proportions (i.e., task dominance) is correct but also suggests that we can set different α and β for different problems to achieve better optimization effects.
Due to the complexity of the optimization problems and the influence of the population, α and β values that perform well on one MOP may not yield good results on others. To analyze the selection strategy for these parameters, we set α to 0.1, 0.2, 0.3, 0.4, and 0.5 and β to 0.5, 0.6, 0.7, 0.8, and 0.9, resulting in 25 different combinations of α and β. Experiments were conducted on ZDT1 and LSMOP1 (300) to further observe their effects, as shown in Figures 6 and 7.
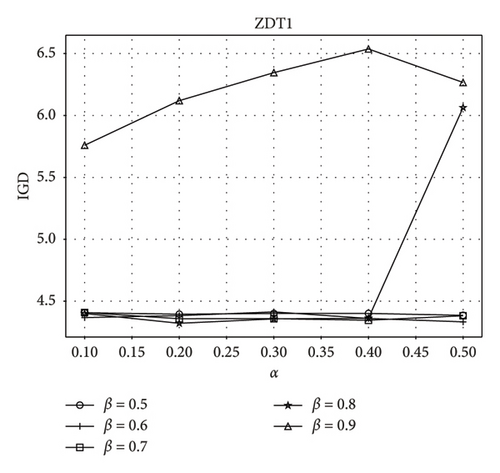

From Figure 6, we can see that on ZDT1, the optimal result is achieved when (α = 0.2, β = 0.8), while the result is poor when β = 0.9 or (α = 0.5, β = 0.8), with other combinations yielding similar results. For the LSMOP1 (300) in Figure 7, the best result is obtained when (α = 0.3, β = 0.7), but the worst result occurs when (α = 0.5, β = 0.8), with the results from other combinations overlapping, also demonstrating the more complex nature of large-scale MOPs. According to equation (5), α determines the initial size of EP, while β determines the final size that EP reaches as the evolutionary process progresses. In our design, the EP tends to exploit, while the WP, obtained after random elimination excluding EP, tends to explore. Overall, selecting a smaller α is appropriate, as all the worst values (i.e., the largest IGD) occur when α = 0.5, and this would result in a smaller size of the WP at the beginning of evolution, limiting the population’s exploration ability. For the selection of β, when β = 0.9, the results are relatively poor regardless of the value of α, indicating that an overly large β is also detrimental, as a certain size of the WP is still needed in the later stages of evolution to maintain exploration ability. The selection of α and β further highlights the value of the WP proposed in this paper. From the optimal results, we can see that small-scale MOPs require a larger β than large-scale ones, due to their smaller search space. However, the α for large-scale MOPs is larger than that for small-scale ones, seemingly indicating that for large-scale problems, a greater emphasis should be placed on the balance between exploitation and exploration. This may be because in the vast solution space, more focus is needed on utilizing existing excellent solutions. The above analysis will guide us to select the appropriate pair of α and β more quickly to address different MOPs. Although due to the complexity of the problems, multiple attempts may still be needed to find the suitable parameter pair; fortunately, in this paper, we achieved significant results using only one pair of α and β for all comparative experiments, highlighting the effectiveness and robustness of our algorithm.
5. Conclusion
For large-scale MOPs, extensive search in vast decision variable spaces while maintaining good convergence is a critical challenge. MOIAs, with their distinctive principle of clonal selection, continuously strengthen the influence of superior individuals during evolution, achieving good convergence. This lays the foundation for their application in solving large-scale MOPs. However, clonal selection also leads to the risk of overconcentration of parents in MOIAs, which may result in a lack of diversity. To leverage the strengths of MOIAs to address the challenges faced by large-scale multiobjective optimization algorithms, it is necessary to overcome the shortcomings of MOIAs. For this purpose, this paper proposes the WP–MOIA algorithm. Its main innovation lies in the first utilization of the power of WPs and the realization of coevolution between WPs and EPs. To achieve this, we designed new methods for subpopulation division and dynamic adjustment of population size. Empowered by the WPs, WP–MOIA greatly enhances its ability to explore large spaces and improves the deficiency in diversity, while maintaining good convergence. Combined with customized population evolution, guidance, and selection strategies, WP–MOIA has achieved success in solving large-scale MOPs.
Experimental results comparing WP–MOIA with nine state-of-the-art MOEAs (including five specifically optimized for large-scale MOPs) and four competitive MOIAs on 30 benchmark problems (including 12 small-scale and 18 large-scale MOPs) show that WP–MOIA obtained the best results in 27 cases in the IGD metric and in 22 cases in the HV metric. This fully demonstrates that WP–MOIA is highly effective not only in handling large-scale MOPs but also small-scale MOPs. A comparison of the evolutionary curves of all algorithms on large-scale MOPs reveals that WP–MOIA enhances exploration capabilities while inheriting the convergence advantages of MOIAs. Ablation and comparative experiments based on various combinations of newly introduced parameters not only prove the rationality of the proposed ideas but also provide insights into how to apply WP–MOIA to solve different MOPs.
Inspired by the experimental results, further testing the ability of WP–MOIA to handle a more diverse range of problem types will be our next research focus. In addition, optimizing the search and guidance mechanisms by drawing on ideas from other excellent algorithms, along with maintaining a more uniformly distributed offspring population during evolution, will be explored as key research directions. Furthermore, we will explore applying this novel approach to solve real-world problems.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This work was supported in part by the National Natural Science Foundation of China (Grant nos. U24A20239, 62032002, and 62402300); in part by the Sichuan Provincial Science and Technology Department Regional Innovation Cooperation Key Project (Grant no. 2025YFHZ0265); in part by the Youth Science Foundation of Sichuan (Grant no. 2025ZNSFSC1474); in part by the China Postdoctoral Science Foundation (Grant no. 2024M752211); in part by the Key Laboratory of Data Protection and Intelligent Management, Ministry of Education (Grant no. SCUSACXYD202301); and in part by the Sichuan Province Science and Technology Innovation Seedling Project (Grant no. MZGC20240056).
Open Research
Data Availability Statement
The data generated during the current study are available from the corresponding author upon reasonable request.




