Volume 2025, Issue 1 4453536

Research Article

Open Access

Assessing the Fluctuation of Indoor Thermal Conditions in Naturally Ventilated Classrooms Through K-Means Clustering

Corresponding Author

Sen Miao

[email protected]

orcid.org/0000-0003-0266-9405

Department of Project and Construction Engineering , Group of Construction Research and Innovation (GRIC) , Polytechnic University of Catalonia , Terrassa , Barcelona , Spain , upc.edu

Search for more papers by this author

Marta Gangolells,

Marta Gangolells

orcid.org/0000-0001-7921-595X

Department of Project and Construction Engineering , Group of Construction Research and Innovation (GRIC) , Polytechnic University of Catalonia , Terrassa , Barcelona , Spain , upc.edu

Search for more papers by this author

Blanca Tejedor,

Blanca Tejedor

orcid.org/0000-0002-2064-0617

Department of Project and Construction Engineering , Group of Construction Research and Innovation (GRIC) , Polytechnic University of Catalonia , Terrassa , Barcelona , Spain , upc.edu

Search for more papers by this author

Sen Miao,

Corresponding Author

Sen Miao

[email protected]

orcid.org/0000-0003-0266-9405

Department of Project and Construction Engineering , Group of Construction Research and Innovation (GRIC) , Polytechnic University of Catalonia , Terrassa , Barcelona , Spain , upc.edu

Search for more papers by this author

Marta Gangolells,

Marta Gangolells

orcid.org/0000-0001-7921-595X

Department of Project and Construction Engineering , Group of Construction Research and Innovation (GRIC) , Polytechnic University of Catalonia , Terrassa , Barcelona , Spain , upc.edu

Search for more papers by this author

Blanca Tejedor,

Blanca Tejedor

orcid.org/0000-0002-2064-0617

Department of Project and Construction Engineering , Group of Construction Research and Innovation (GRIC) , Polytechnic University of Catalonia , Terrassa , Barcelona , Spain , upc.edu

Search for more papers by this author

First published: 11 March 2025

https://doi.org/10.1155/ina/4453536

Academic Editor: Faming Wang

Share a link

Email
Wechat
Bluesky

Abstract

For naturally ventilated classrooms, windows should be constantly open to maintain good indoor air quality during class times. However, it is unknown whether this would result in significant fluctuations in the indoor thermal environment, while the effects of ventilation rate and window operation are still unclear. Therefore, this study assesses the fluctuation of indoor thermal conditions under natural ventilation during class periods, based on the K-means clustering and statistical analysis of data collected in a large measurement campaign in Spanish schools. The results showed that regardless of the heating mode, the indoor thermal parameters remained stable in most cases. High fluctuations were observed only in a few cases: 15% for indoor temperature, 6% for relative humidity, and 3% for indoor air velocity. The variability of the indoor thermal parameters within an hour was less than 1°C for indoor temperature, 3% for relative humidity, and 0.1 m/s for indoor air velocity. Ventilation rate and window operation were found to be related to the fluctuation of the indoor temperature and air velocity, rather than the relative humidity. These findings shed light on the thermal conditions in naturally ventilated classrooms and have practical implications for the implementation of natural ventilation protocols in schools.

1. Introduction

The primary goal of educational buildings is to provide a conducive learning environment. Related research highlighted the significance of indoor air quality and thermal comfort for students’ well-being and learning performance [1, 2]. For most educational buildings, natural ventilation is the main and often the only way to maintain indoor air quality [3]. Relevant field studies in naturally ventilated schools have reported poor indoor air quality problems, particularly during the heating season. The main cause was often found to be the improper operation of windows [4–8].

Some previous studies believed that occupants are reluctant to open windows mainly for comfort reasons, as the exchange of indoor and outdoor air may affect indoor thermal conditions [9, 10]. Accordingly, relevant research suggested ventilating the classroom during class breaks to avoid potential discomfort issues [5, 11]. However, some other studies indicated that natural ventilation may not compromise the comfort of occupants, as long as it is not excessively cold outside [12–14]. Recent studies have also shown that ventilating only during the class break cannot effectively renew the stale air in the classroom because the required ventilation rates may not always be achieved due to the uncertainty of natural ventilation. As a result, it is necessary to open windows at all times to ensure continuous natural ventilation during class periods [15, 16].

In fact, many field studies have reported that inadequate ventilation and poor indoor air quality occur not only during cold seasons but also during mild outdoor weather and when classrooms are overheated in winter [7, 17–20]. Related studies have pointed out that window operation behavior depends on a variety of factors, such as the occupants’ perception of indoor environmental quality, their accessibility to the windows, and their knowledge of indoor air quality and ventilation. It has also been revealed that students often adapt passively to the indoor environment, whereas teachers tend to take more initiative in operating windows [21–23]. Sanguinetti et al. [22] discovered that teachers were more satisfied with indoor environmental quality in classrooms with poorer ventilation. They proposed that the possible reason may be the temperature fluctuations associated with higher ventilation rates. However, such speculation needs to be verified by further investigation.

In recent years, a large number of studies have investigated the indoor thermal environment of naturally ventilated educational buildings. However, to the author’s best knowledge, existing studies have mainly focused on the overall assessment of the indoor temperature and relative humidity in terms of compliance with standards over the entire measurement period rather than on the variation of relevant indoor thermal parameters under natural ventilation during single class periods. Moreover, current studies often lack in-depth analysis of window and door operations and ventilation rates. These overlooked aspects indicate the gaps that need to be addressed on such topics: it is still unknown whether encouraging natural ventilation during the class would result in significant fluctuations in the indoor thermal environment, and the relationship between window and door operations, ventilation rates, and the variation of indoor thermal parameters is still unclear.

Therefore, the objective of this study is to assess the fluctuation of indoor thermal conditions of the classrooms under natural ventilation during single class periods. The assessment was performed by combining statistical analysis with K-means clustering techniques based on a large-scale measurement campaign conducted in naturally ventilated schools.

Certainly, the results of this study have clear practical implications. On one hand, it reveals the dynamic changes of the indoor thermal environment under natural ventilation and its influential factors, providing valuable insights for the planning and design of natural ventilation in schools. On the other hand, the study provides a new perspective for analyzing the environmental monitoring time series data by combining conventional statistical analysis with the machine learning technique of K-means clustering. This provides a useful reference for relevant researchers.

Following this introduction, Section 2 describes the methodology, Section 3 analyzes and discusses the obtained results, and Section 4 summarizes the conclusions and recommendations.

2. Methodology

This section describes the methodology of this research step by step, including the field measurement campaign for data collection (Section 2.1), the processing of the measurement data (Section 2.2), and the analysis of the processed data (Section 2.3).

2.1. Field Measurement Campaign

This research is part of the IAQ4EDU project [24]. From April 2022 to January 2023, the project investigated 32 naturally ventilated classrooms in 16 primary and secondary schools in Catalonia, Spain. These representative samples of buildings and classrooms were selected with the help of the Catalan government and the management staff of schools. These representative samples of buildings and classrooms were selected with the help of the Catalan government and management staff of schools, which were built in different years and located in various geographical areas. All investigated classrooms are naturally ventilated and equipped with radiators but without any cooling facilities (fans or air conditioners). Appendix A summarizes the characteristics of these schools and classrooms. A detailed introduction of the IAQ4EDU research project, the measurement campaign, and the general analysis results can be found in previous publications [7, 25]. This section only highlights the most relevant information for this study.

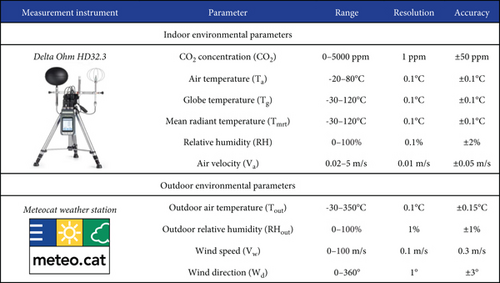
During the measurement campaign, indoor environmental parameters were measured using the Delta Ohm-HD32.2 microclimate station. Following the criteria of ISO 7726 [26], ASTM D6245-18 [27], and ASHRAE 55 [28], the measurement instrument was placed in the center of the classroom at a height of 1.1 m and located 2 m away from any disturbances such as students, windows, doors, walls, and radiators. The outdoor environmental parameters were gathered by Meteocat urban weather stations located in the city of the schools [29]. The measurement data were recorded and organized at 1-min intervals. Figure 1 summarizes the measured indoor and outdoor environmental parameters and the technical specifications of the measurement equipment.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Indoor and outdoor environmental parameter measurement equipment.

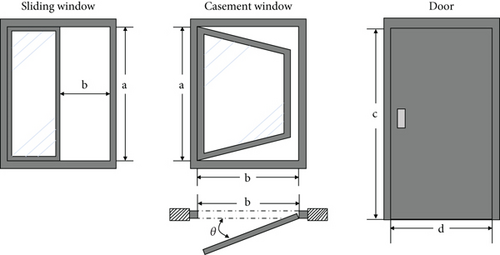
The researchers stayed in the classrooms with the teachers and students at all times to collect data on occupancy and window/door operation, such as the number of occupants, their gender, age, and activity. Following the requirements of the Catalan government, the researchers were not allowed to interfere with the activity and behavior of the occupants in the classrooms. Therefore, the operation of the windows and doors was completely dependent on their willingness. The researchers recorded each time when the occupants operated the windows and doors and calculated the change in the opening area of the windows and doors. Most of the classrooms have sliding windows, and only four classrooms have casement windows (Figure 2). In all cases, the windows are connected to the outdoors, and the doors are connected to the corridor. The effective opening area of the window (OA_window) was calculated using Equations (1) and (2) [30]. The door was found to be usually either fully open or closed, so the opening area of the door (OA_door) depends on its opening state and was calculated through Equation (3). Accordingly, the total opening area of windows and doors was calculated using Equation (4).

The opening area of the window:

Sliding window:

(1)

Casement window:

(2)

The opening area of the door:

(3)

The total opening area of windows and doors:

(4)

where OA_window denotes the opening area of windows (square meter); OA_door is the opening area of doors (square meter); OA_total is the total opening area of windows and doors (square meter); and a, b, c, d, and θ are defined in Figure 2.

2.2. Processing of Measurement Data

Firstly, several required parameters need to be further calculated based on the measured environmental parameters (Figure 1), including operative temperature (T_op), ventilation rate (Q_vent), and air change rate per hour (ACH).

The operative temperature (T_op) can be calculated using Equations (5) and (6) [31]:

(5)

(6)

where T_op is the operative temperature (degrees Celsius), V_a is the indoor air velocity (meters per second), T_a is the indoor air temperature (degrees Celsius), and T_mrt is the mean radiant temperature (degrees Celsius) given by the measurement instrument.

The ventilation rate (Q_vent) can be calculated using the transient mass balance method (Equation (7)). Related studies have shown that this method has the highest accuracy in ventilation rate estimation, especially for rooms with changing occupancy [32, 33]. Raw measurement data of CO₂ concentration often contain noise that affects the precision of the estimated ventilation rate [33, 34]. Hence, a 5-min moving average filter was applied to filter the CO₂ measurement noise, as suggested by related studies [35, 36]. In addition, a common challenge in ventilation rate estimation is that the exact CO₂ generation rate of the occupants is often impossible to know. Relevant studies usually assume an estimated constant value for all students [6, 18, 37]. To further ensure the accuracy of the calculated ventilation rate, the CO₂ generation rate of the students used in this study was taken from Persily and Jonge [38], depending on their gender and age. Since the investigated classrooms have different volumes, the ventilation rate (Q_vent) needs to be converted to the ACH for analysis, according to Equation (8).

(7)

(8)

where C_t is the indoor CO₂ concentration (parts per million) at time t; C_t+1 is the indoor CO₂ concentration at time t + 1; Δt is the measurement interval (1 min in this study); C_out is the outdoor CO₂ concentration, taken as 420 ppm according to IDAEA (2021); N_t is the number of occupants at time t; G_p is the CO₂ generation rate of occupants (cubic meters per minute); V is the volume of the classroom (cubic meters); Q_vent is the calculated ventilation rate (cubic meters per minute); and ACH is the air change rate per hour (times per hour).

After calculating the required parameters, the obtained data need to be further cleaned, considering that the objective of this research is to assess the variation of indoor thermal parameters under natural ventilation during single class periods. The obtained data were segmented with a length of 60 min, considering the typical duration of the class in schools. The cleaning of the data followed two fundamental principles. Within the 60-min period, (1) classrooms have a constant and stable occupancy, and (2) windows and/or doors are always open to ensure continuous natural ventilation.

Finally, based on more than 460 h of raw measurement data, a total of 125 time series data with a length of 60 min were obtained after the above processing and cleaning process. Each 60-min time series contains 16 parameters shown in Table 1. These data were organized into a dataset for further analysis.

Table 1. Parameters of obtained time series dataset.

Parameter	Abbreviation	Unit
Indoor thermal parameters
Indoor air temperature	T_a	°C
Mean radiant temperature	T_mrt	°C
Globe temperature	T_g	°C
Operative temperature	T_op	°C
Indoor relative humidity	RH_in	%
Indoor air velocity	V_a	m/s
Outdoor thermal parameters
Outdoor air temperature	T_out	°C
Outdoor relative humidity	RH_out	%
Wind speed	V_w	m/s
Wind direction	W_d	°
Ventilation-related parameters
Air change rate	ACH	Times/hour
Total opening area	OA_total	m²
Window opening area	OA_window	m²
Door opening area	OA_door	m²
Window operation frequency^a	F_window	Times
Door operation frequency^b	F_door	Times

^aThe number of times that occupants operated the window in this 60-min period.
^bThe number of times that occupants operated the door in this 60-min period.

2.3. Analysis of the Processed Data

Figure 3 presents a schematic diagram of the data analysis process in this study.

In the first step, the variation of the indoor thermal parameters (Table 1) was examined from the perspective of variability and fluctuation. The variability of the indoor thermal parameter can be characterized by the difference (Diff) between its maximum and minimum values during each 60-min period (Equation (9)). The fluctuation of the indoor thermal parameter can be characterized by the standard deviation (SD) of each time series (Equation (10)).

(9)

(10)

where X denotes the indoor thermal parameter, X_i is the number of the ith value of the parameter, X_max is the maximum value of the parameter within the 60-min period, X_min is the minimum value of the parameter within the 60-min period, and

is the mean value of the parameter during the 60-min period.

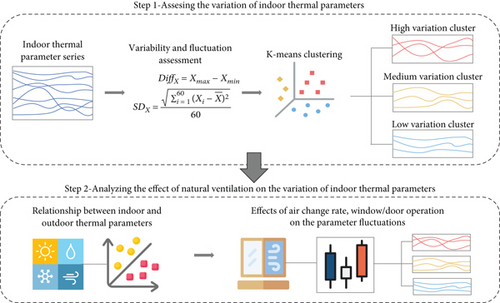
Then, the level of the variation was assessed using a clustering technique. Clustering is an unsupervised machine learning technique that assigns the data (observations) with similar features into the same cluster for comparative analysis of different clusters. K-means is one of the most widely used clustering algorithms. It automatically identifies the most representative clusters given the expected number of clusters. The centroid characterizes the main features of each cluster with the mean value. This makes it more intuitive and more interpretable than other algorithms such as hierarchical clustering or density-based clustering [39, 40]. For each indoor thermal parameter, 125-time series were clustered based on their SD into three groups that correspond to the different levels of variation, namely, (1) low variation cluster, (2) medium variation cluster, and (3) high variation cluster. The proportion of data contained in each cluster represents the observed probability of each variation level of the indoor thermal parameter.

In the second step, a more in-depth analysis was conducted to investigate the effect of natural ventilation on the fluctuation of indoor thermal parameters. Firstly, the relationship between indoor thermal parameters and outdoor environmental parameters, air change rate, and window/door operation was examined using a correlation test and regression. Then, based on the identified clusters, the effects of air change rate, the opening area, and the operation frequency of windows and doors were analyzed. Given the characteristics of the measurement data, the correlation was examined by the Spearman correlation test, and the Kruskal–Wallis H test was used to examine the statistical significance of the observed differences between clusters. These statistical tests are nonparametric and do not require a normal distribution of the analyzed data. The statistical significance involves three typical levels depending on the p value, namely, ^∗∗∗p < 0.001, ^∗∗p < 0.01, and ^∗p < 0.05.

The calculation and analysis were performed on the Google Colab platform using Python 3.7.3. The Python packages of NumPy and Pandas were used for data processing. The statsmodels package was used for the statistical analysis. The Scikit-learn package was used for K-means clustering. Matplotlib and Seaborn packages were used for visualization.

3. Results and Discussion

This section analyzes and discusses the obtained results, following the defined methodology in Section 2.3, including the overview of measured parameters (Section 3.1), the variation of indoor thermal parameters (Section 3.2), the effect of natural ventilation on indoor thermal parameter variation (Section 3.3), and further discussion and limitation (Section 3.4).

3.1. Overview of Measured Parameters

Table 2 shows the descriptive statistics of all the measured parameters listed in Table 1. In terms of the indoor and outdoor thermal parameters, the outdoor air temperature (T_out) ranged from 0.40°C to 35.20°C, with an average of 19.24°C. Due to the heating of the classroom, the minimum indoor temperature was higher than the outdoor temperature. The indoor air temperature (T_a) ranged from 18.22°C to 33.57°C, with a mean of 24.38°C. The statistical values of mean radiant temperature (T_mrt), globe temperature (T_g), and operative temperature (T_op) were very close to that of indoor air temperature (T_a). The outdoor relative humidity (RH_out) ranged widely, from 23.0% to 100.0%, with an average of 57.3%. The indoor relative humidity (RH_in) was much lower, ranging from 24.7% to 67.8%, with a mean of 47.6%. The outdoor wind was mainly from the south (191°), with a speed ranging from 0.24 to 8.2 m/s and 2.64 m/s on average. In contrast, indoor air velocity (V_a) ranged from 0 to 0.625 m/s, but with a very low mean of only 0.028 m/s.

Table 2. Descriptive statistics of the measured parameters.

Parameters	T_a (°C)	T_mrt (°C)	T_g (°C)	T_op (°C)	RH_in (%)	V_a (m/s)	T_out (°C)	RH_out (%)
Count	7500	7500	7500	7500	7500	7500	7500	7500
Mean	24.38	24.14	24.20	24.26	47.6	0.028	19.24	57.3
Std	3.56	3.61	3.60	3.59	9.4	0.053	6.80	17.8
Min	18.22	17.29	17.58	17.81	24.7	0.000	0.40	23.0
25%	21.61	21.25	21.36	21.45	40.4	0.001	13.62	45.3
Median	23.47	23.03	23.14	23.25	48.0	0.008	17.75	53.8
75%	27.01	26.89	26.90	26.96	56.0	0.031	24.25	69.0
Max	33.57	33.70	33.70	33.63	67.8	0.625	35.20	100.0
Parameters	V_w (m/s)	W_d (°)	ACH (times/h)	OA_total (m²)	OA_window (m²)	OA_door (m²)	F_window (times)	F_door (times)
Count	7500	7500	7500	7500	7500	7500	7500	7500
Mean	2.64	191	7.1	3.54	2.24	1.30	0.7	0.9
Std	1.30	83	5.8	2.20	1.99	0.94	1.0	1.3
Min	0.24	14	0.0	0.21	0.00	0.00	0.0	0.0
25%	1.74	132	2.6	1.70	0.59	0.00	0.0	0.0
Median	2.43	188	5.8	3.21	1.56	1.66	0.0	0.0
75%	3.27	257	9.9	4.96	3.50	1.71	1.0	2.0
Max	8.20	358	43.1	9.48	7.69	3.74	5.0	6.0

Regarding ventilation-related parameters, the ACH ranged from 0 to 43.1 (times/h), with a mean of 7.1 (times/h). The mean ACH was slightly higher than observed values in relevant studies (e.g., [3, 6, 41–43]) because this study focused on the period under continuous natural ventilation rather than the whole measurement period. The opening area of the windows (OA_window) and doors (OA_door) varied widely because the operation was completely dependent on the occupants. The total opening area (OA_total₎ ranged from 0.21 to 9.48 m², with an average of 3.54 m², meaning that one window and one door were fully open in general. On average, occupants operated windows or doors less than one time within an hour.

3.2. Variation of Indoor Thermal Parameters

This section analyzes the variation of indoor thermal parameters in terms of variability (Section 3.2.1), fluctuation (Section 3.2.2), and the clustering of the indoor thermal parameters (Section 3.2.3).

Figure 4 visualizes the overview of all 125-time series of each indoor thermal parameter. Notably, 46.4% of the data were measured during the heating mode and 53.6% during the nonheating mode.

3.2.1. Variability of Indoor Thermal Parameters

The variability of each indoor thermal parameter during the 60-min period was examined and summarized in Table 3. With respect to the variability of the indoor temperature, air temperature (T_a), mean radiant temperature (T_mrt), globe temperature (T_g), and operative temperature (T_op), they had very close statistical values. The Kruskal–Wallis H test showed that there was no statistical difference in terms of their variability between the heating and nonheating modes (p = 0.498 > 0.05). According to ISO 7730 [44] and ASHRAE 55 (2020) standards, the operative temperature is used to characterize the comfort of the occupants. Within the 60-min periods under continuous natural ventilation, the difference between the maximum and minimum values of the operative temperature ranged from 0.22°C to 2.45°C, with a mean of only 0.97°C. For indoor relative humidity (RH_in), the difference between the maximum and minimum values within the 60-min periods ranged from 0.2% to 11%, and the average was only 3.4%. Although the Kruskal–Wallis H test revealed a statistically significant difference between the heating and nonheating modes ( ^∗p < 0.05), the difference was rather small, with less than 1% in the mean and median values. Relevant standards such as ISO 7730 [44] specify a comfort band of 2°C for the operative temperature and 10% for the relative humidity. The maximum variability of these parameters within the 60-min period was slightly higher than the specified values, but the mean variability was much lower. The variability of the indoor air velocity (V_a) within the 60-min periods ranged from 0.002 to 0.579 m/s, with a mean of only 0.073 m/s. In comparison, the indoor air velocity (V_a) during the nonheating periods had a larger variability, as reflected in its higher median and mean values. The Kruskal–Wallis H test confirmed the statistical significance of such a difference between the two modes ( ^∗∗p < 0.01). The main reason for this difference is that occupants were more willing to open windows during the nonheating season, resulting in larger window opening areas and higher air change rates in the classrooms (this will be further discussed in Section 3.3). However, the indoor air velocity (V_a) remained relatively stable in most cases, with a small variability of 0.073 m/s. For 97.7% of the time, the value was lower than the cooling effect threshold of 0.20 m/s specified in the ASHRAE 55 standard [28].

Table 3. Variability of indoor thermal parameters during the 60-min period.

Parameter	T_a (°C)	T_mrt (°C)	T_g (°C)	T_op (°C)	RH_in (%)	V_a (m/s)
All scenarios (100%)
Count	125	125	125	125	125	125
Mean	1.05	0.98	0.96	0.97	3.4	0.073
Std	0.54	0.51	0.50	0.50	2.3	0.089
Min	0.24	0.21	0.20	0.22	0.2	0.002
25%	0.60	0.63	0.61	0.59	1.8	0.021
Median	0.95	0.90	0.85	0.89	2.8	0.051
75%	1.40	1.27	1.30	1.30	4.0	0.083
Max	2.80	2.54	2.45	2.45	11.0	0.579
Heating mode (46.4%)
Count	58	58	58	58	58	58
Mean	1.10	1.03	0.99	1.01	2.9	0.068
Std	0.54	0.57	0.53	0.52	2.0	0.107
Min	0.25	0.21	0.20	0.22	0.7	0.002
25%	0.61	0.65	0.62	0.60	1.6	0.017
Median	0.96	0.89	0.92	0.92	2.6	0.024
75%	1.48	1.44	1.42	1.41	3.2	0.065
Max	2.49	2.54	2.45	2.45	9.3	0.579
Nonheating mode (53.6%)
Count	67	67	67	67	67	67
Mean	1.01	0.94	0.93	0.94	3.8	0.078
Std	0.54	0.46	0.47	0.48	2.4	0.070
Min	0.24	0.21	0.20	0.24	0.2	0.002
25%	0.59	0.62	0.61	0.59	2.3	0.030
Median	0.93	0.90	0.81	0.83	3.1	0.060
75%	1.39	1.20	1.25	1.24	5.2	0.092
Max	2.80	2.26	2.32	2.36	11.0	0.368

3.2.2. Fluctuation of Indoor Thermal Parameters

The fluctuation of each indoor thermal parameter during the 60-min period was examined and shown in Table 4. Similar to the case of variability, the fluctuation of indoor temperature parameters was very close in statistical values. The SD of the operative temperature (T_op) series ranged from 0.05°C to 0.75°C, with a mean of 0.29°C. The Kruskal–Wallis H test confirmed that there was no statistical difference in terms of the fluctuation between the heating and nonheating modes (p = 0.455 > 0.05). The SD of the relative humidity series ranged from 0.07% to 3.91%, with a mean of 0.97%. A statistical difference between the heating and nonheating modes was found by the Kruskal–Wallis H test ( ^∗p < 0.05), though the difference was only 0.2% in the mean and median values. For indoor air velocity series, the SD was between 0.025 and 0.161 m/s, with 0.019 m/s on average. The Kruskal–Wallis H test showed that there was a statistical difference between the heating and nonheating modes ( ^∗∗∗p < 0.001). The indoor air velocity (V_a) during the nonheating periods had more fluctuations, as the median value was more than twice that of the heating periods.

Table 4. Fluctuation of indoor thermal parameters during the 60-min period.

Parameter	T_a (°C)	T_mrt (°C)	T_g (°C)	T_op (°C)	RH_in (%)	V_a (m/s)
All scenarios (100%)
Count	125	125	125	125	125	125
Mean	0.30	0.29	0.28	0.28	1.0	0.019
Std	0.17	0.15	0.15	0.16	0.7	0.025
Min	0.05	0.06	0.06	0.05	0.1	0.000
25%	0.17	0.17	0.16	0.16	0.5	0.005
Median	0.27	0.25	0.24	0.26	0.8	0.012
75%	0.42	0.38	0.37	0.37	1.2	0.021
Max	0.94	0.81	0.77	0.76	3.9	0.161
Heating mode (46.4%)
Count	58	58	58	58	58	58
Mean	0.32	0.31	0.30	0.30	0.8	0.018
Std	0.17	0.17	0.17	0.16	0.5	0.031
Min	0.07	0.06	0.06	0.06	0.2	0.000
25%	0.18	0.16	0.16	0.17	0.4	0.004
Median	0.29	0.27	0.24	0.26	0.7	0.006
75%	0.43	0.44	0.44	0.44	1.0	0.016
Max	0.72	0.81	0.77	0.76	2.8	0.161
Nonheating mode (53.6%)
Count	67	67	67	67	67	67
Mean	0.29	0.27	0.27	0.27	1.1	0.020
Std	0.17	0.13	0.14	0.15	0.8	0.018
Min	0.05	0.06	0.06	0.05	0.1	0.000
25%	0.17	0.17	0.15	0.16	0.6	0.008
Median	0.25	0.25	0.24	0.25	0.9	0.015
75%	0.40	0.36	0.36	0.36	1.5	0.023
Max	0.94	0.61	0.69	0.73	3.9	0.102

3.2.3. Clustering of Indoor Thermal Parameters

Figure 5 visualizes the low, medium, and high variation clusters of each indoor thermal parameter identified by the K-means clustering technique. The results showed that under continuous natural ventilation, the indoor temperature generally remained stable in most cases. Only 10% of the observations for indoor air temperature (T_a) were classified into the high variance cluster, while this figure was close to 20% for mean radiant temperature (T_mrt). The operative temperature (T_op) was calculated based on the indoor air temperature and mean radiant temperature. In more than 50% of the cases, the operative temperature had a very small variability within the 60-min periods, with only 0.57°C on average. Such a change in temperature is even barely noticeable to the occupants. In 15% of the cases, the operative temperature had more fluctuations, but the variability was less than 2°C. Indoor relative humidity (RH_in) even remained stable in more than 70% of cases, with a small variability of 2.2% within the 60-min periods. The variability was observed to be close to 10% in only 6% of the cases. In addition, the indoor air velocity (V_a) was lower than 0.150 m/s in 80% of the cases, and the variability was smaller than 0.040 m/s. Only in about 3% of the cases did the variation reach higher than 0.20 m/s on average (0.434 m/s).

3.3. Effect of Natural Ventilation on Indoor Thermal Parameter Variations

This section analyzes and discusses the effects of outdoor thermal parameters (Section 3.3.1), air change rate (Section 3.3.2), and window/door operation (Section 3.3.3) on indoor thermal parameters.

3.3.1. Outdoor Thermal Parameters

Under natural ventilation, indoor thermal parameters were mainly influenced by the outdoor parameters. The Spearman correlation test showed that the indoor temperature was strongly correlated with the outdoor temperature (Spearman^’s correlation coefficient = 0.81, ^∗∗∗p < 0.001), while the indoor relative humidity was moderately correlated with the outdoor relative humidity (correlation coefficient = 0.64, ^∗∗∗p < 0.001). In contrast, the correlation between indoor air velocity and outdoor wind speed was found to be very weak (correlation coefficient = 0.10, ^∗∗∗p < 0.001).

The regression between indoor and outdoor thermal parameters (Figure 6) showed that the indoor temperature was highly dependent on the outdoor temperature during the nonheating season, with an R² higher than 0.8 in general. During the heating season, it depended mainly on the temperature setting of the heating system and was therefore not affected by the outdoor temperature (R² < 0.01). The situation was slightly different in the case of indoor relative humidity (RH_in), as the regression had similar R² in heating and nonheating modes. The R² was found to be lower than that of the temperature. This is because the relative humidity varies greatly depending on the geographical location. The measurement of urban weather stations could not precisely characterize the outdoor relative humidity conditions around the school buildings [45].

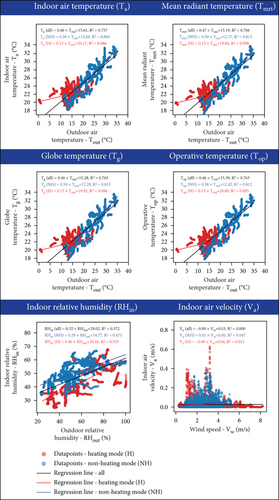
Notably, the regression results showed that the indoor air velocity (V_a) was almost independent of the outdoor wind speed (R² < 0.1). The main reason is that the exchange of indoor and outdoor air under natural ventilation depends on both buoyancy (temperature gradient) and wind effects. The natural wind is of high uncertainty, while the wind-driven ventilation depends not only on the window opening area but also on the building facade orientation and the incident wind direction [6, 46, 47]. Accordingly, the measured outdoor wind may not accurately reflect the local wind conditions outside the classroom windows. Nonetheless, the indoor air velocity remained at a very low value for most of the time, as previously mentioned, suggesting that the observed indoor air velocity was mainly driven by the buoyancy effect rather than the wind effect.

3.3.2. Air Change Rate

Table 5 summarizes the descriptive statistics of the ACH. The Kruskal–Wallis H test revealed a statistical difference ( ^∗∗∗p < 0.001) in ACH between the heating and nonheating modes. The natural ventilation rate is determined by both buoyancy and wind effects and is therefore influenced by the outdoor–indoor temperature difference, outdoor wind speed, and incident wind direction [46]. Theoretically, the outdoor–indoor temperature difference was larger during the heating period, providing favorable conditions for high ventilation rates. However, the average ACH in the nonheating mode was 9.3 times/h, which is twice as high as the value in the heating mode (4.6 times/h). However, regardless of the heating mode, the mean ACH met the minimum requirement of four times per hour for classrooms, as specified in the EN16798-1 [48] standard.

Table 5. Descriptive statistics of the air change rate.

Scenario	All scenarios (100%)	Heating mode (46.4%)	Nonheating mode (53.6%)
Mean	7.1	4.6	9.3
Std	5.8	3.3	6.5
Min	0.0	0.0	0.0
25%	2.6	1.9	3.9
50%	5.8	4.0	8.1
75%	9.9	6.8	13.5
Max	43.1	21.5	43.1

The ACH difference between heating and nonheating periods is mainly due to the fact that the occupants were less willing to open the windows for ventilation during the cold season. Figure 7 shows the relationship between the outdoor and indoor temperature difference and the opening area of the window and door. As seen, the opening area of the window and door increased with the decrease in outdoor and indoor temperature difference, reflecting the increased willingness of the occupants to ventilate in mild weather.

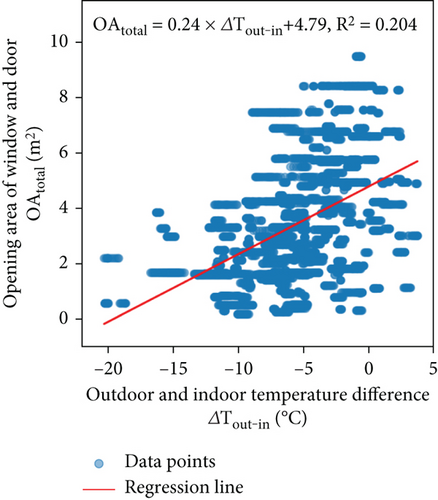
The Spearman correlation test showed that ACH had a relatively weak correlation with the indoor temperature (Spearman^’s correlation coefficient = 0.36, ^∗∗∗p < 0.001) and a moderate correlation with the indoor air velocity (correlation coefficient = 0.53, ^∗∗∗p < 0.001). In contrast, no correlation was found for the indoor relative humidity (correlation coefficient = −0.004, ^∗∗∗p < 0.001). The ACH of each cluster of indoor temperature, relative humidity, and air velocity is shown in Figure 8. Since all the indoor temperature parameters had similar results, the operative temperature (T_op) was used for visualization. The Kruskal–Wallis H test confirmed the statistical differences in the ACH between these clusters ( ^∗∗∗p < 0.001). It was observed that for operative temperature, the ACH of the low, medium, and high variation clusters gradually reduced, with an average of 7.8, 6.6, and 5.6 times per hour, respectively. This suggests that regardless of the heating mode, high air change rates promote the exchange of indoor and outdoor air more efficiently, thus keeping the indoor temperature relatively stable with smaller fluctuations. However, such an effect was not observed for relative humidity (RH_in). The average ACH of each relative humidity cluster was 7.3, 6.4, and 7.5 times per hour, respectively. No evidence was obtained to show that ACH caused the fluctuation of relative humidity. For indoor air velocity (V_a), the average ACH of low, medium, and high variation clusters was 6.6, 8.3, and 12.2 times per hour, respectively. This indicates that high air change rates were associated with high variations of indoor air velocity, which was mainly driven by the outdoor wind.

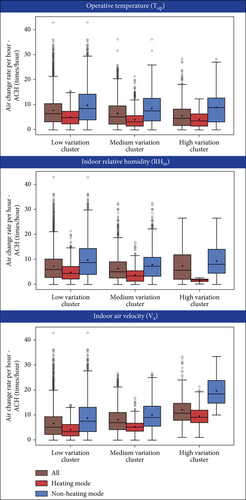
3.3.3. Window and Door Operation

Table 6 summarizes the descriptive statistics of the opening area of windows and doors. The Kruskal–Wallis H test revealed statistical differences ( ^∗∗∗p < 0.001) in the opening areas between the heating and nonheating modes. As seen, the main difference in the opening area between the heating and nonheating modes was the window opening area, which ultimately determined the total opening area. The window opening area in the nonheating mode was more than twice that of the heating mode.

Table 6. Descriptive statistics of opening area of windows and doors.

Parameter	Window opening area (OA_window) (m²)			Door opening area (OA_door) (m²)			Total opening area (OA_total) (m²)
Scenario	All	H	NH	All	H	NH	All	H	NH
Mean	2.24	1.33	3.03	1.30	1.33	1.27	3.54	2.66	4.29
Std	1.99	1.40	2.08	0.94	0.97	0.92	2.20	1.82	2.23
Min	0.00	0.00	0.00	0.00	0.00	0.00	0.21	0.21	0.28
25%	0.59	0.39	1.16	0.00	0.00	0.00	1.70	1.47	2.43
50%	1.56	0.93	2.88	1.66	1.66	1.67	3.21	2.18	4.02
75%	3.50	1.65	4.89	1.71	1.69	1.84	4.96	3.32	5.77
Max	7.69	5.80	7.69	3.74	3.39	3.74	9.48	7.46	9.48

Abbreviations: H, heating mode; NH, nonheating mode.

The operation of the windows was found to be correlated with the fluctuation of indoor temperature in terms of the window operation frequency (Spearman^’s correlation coefficient = 0.11, ^∗∗∗p < 0.001) and the change (SD) in the window opening area (correlation coefficient = 0.10, ^∗∗∗p < 0.001). Such correlations were not found with the door operation. For relative humidity (RH_in), no correlation was found with both window and door operations. In contrast, the fluctuation of the indoor air velocity (V_a) was weakly correlated with the change in the opening area of the window (correlation coefficient = 0.15, ^∗∗∗p < 0.001) and the door (correlation coefficient = 0.09, ^∗∗∗p < 0.001), but no correlation was found with their operation frequency.

Figure 9 shows the operation frequency and the change in the opening areas of each indoor thermal parameter cluster. The Kruskal–Wallis H test confirmed that the differences between these clusters are statistically significant ( ^∗∗∗p < 0.001). The temperature fluctuation was mainly caused by the operation of the window rather than the door. As observed, the window operation frequency and the change in the window opening area gradually increased from the low variation cluster to the high variation cluster. The mean window operation frequency of each cluster was 0.6, 0.7, and 0.9 times, respectively, while the average changes in the window opening area were 0.20, 0.21, and 0.34 m². This suggests that the more frequently the window was operated and the larger the change in the window opening area, the more likely it is to cause fluctuations in the indoor temperature.

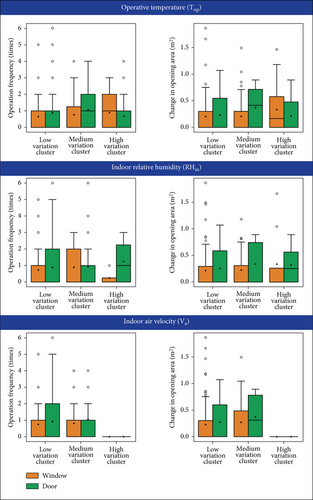
The reason is that the window is directly connected to the outdoors, and the opening of the window is the key factor affecting and achieving high ACH. Figure 10 shows that the correlation between ACH and door opening area was very low (R² < 0.05). The door usually has a limited area and is connected to the corridor. The ACH that can be achieved by the door is thereby limited. In contrast, the regression equation of the window opening area has the highest slope and R². The windows have larger total areas and are directly connected to the outdoors. Hence, increasing the window opening area improves the air exchange rate more effectively. For indoor relative humidity, no evidence was observed to suggest that relative humidity fluctuations were caused by the window and door operation. Considering that the relative humidity had small fluctuations in most of the cases and only 6.4% of the cases had a high variation, it is speculated that these large humidity fluctuations were caused by certain occasional events or disturbances of the occupants’ behavior. As the opening of windows and doors enables the exchange of indoor and outdoor air, larger changes in their opening area could lead to more fluctuations in indoor air velocity. Notably, the evidence was mainly observed in the comparison between the low and the medium variation clusters under indoor air velocity (Figure 9), as only 3% of the observations were classified into the high variation cluster, which was not enough to demonstrate such a trend.

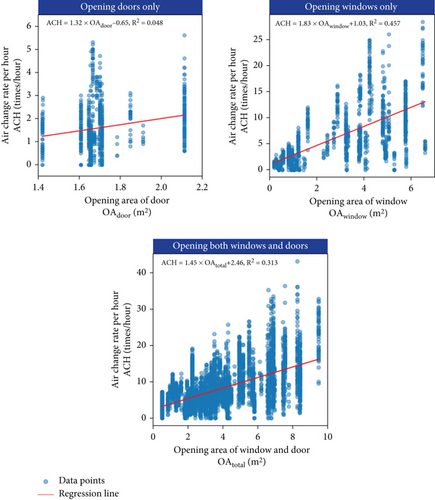
3.4. Further Discussion and Limitations

The practical implications of this study should be discussed. The results in the above sections suggest that, regardless of the heating mode, opening windows and doors to provide continuous natural ventilation did not cause dramatic fluctuations in the indoor thermal environment during single class periods. In most cases, the indoor thermal parameters remained quite stable, and the variations were hardly even noticeable. Obvious fluctuations caused by the window operation were observed in a few cases, but these variations were within the comfort band specified in the related standards and are therefore not very likely to cause a drastic and intolerable sense of discomfort to the occupants.

The limitation of the reported results should also be discussed to help future research. The investigation and analysis of this research are based on the physical measurement of the indoor thermal environment, which may not reflect the subjective feelings of all the occupants in the classrooms. For instance, students sitting close to the windows may have different sensations than those sitting far from the window. Therefore, future research is recommended to conduct a more in-depth investigation when feasible.

However, encouraging natural ventilation during class should not be considered a bad option, concerning the negative impact of poor indoor air quality on students’ health. As existing research highlighted, ventilating during the class may be inevitable because short breaks between classes cannot effectively refresh the stale indoor air, particularly during flu seasons. Previous studies in the Mediterranean climate have indicated that an outdoor temperature of 16°C can be considered a reference for the implementation of natural ventilation, while this value can be 12°C with the heating of the classroom [12, 14]. Although ventilating during the heating season may inevitably lead to some energy waste, it can be considered an emergency countermeasure for the health and well-being of the students.

4. Conclusions and Recommendations

This study investigated the variation of indoor thermal parameters under continuous natural ventilation during class times, based on a total of 125 groups of 60-min time series data collected from a large field measurement campaign in naturally ventilated educational buildings in Spain.

The results showed that regardless of the heating mode, the indoor thermal parameters remained stable in most cases. The variability of the indoor temperature was less than 1°C within an hour on average, while the figure was 3.4% for relative humidity. For nearly 98% of the time, the indoor air velocity was lower than 0.20 m/s. These values are much lower than the comfort band specified in the related standards. Obvious fluctuations were observed in a few cases, with merely 15.2% for indoor temperature, 6.4% for relative humidity, and 3.2% for indoor air velocity. Under natural ventilation, indoor thermal parameters were mainly influenced by the outdoor conditions. The air change rate and window operation were found to be related to the fluctuation of the indoor temperature and air velocity rather than the relative humidity. High air change rates promote the exchange of indoor and outdoor air more efficiently and maintain stable indoor temperatures, while frequent window operation and large changes in the window opening area were found to result in the fluctuation of indoor temperature and air velocity.

The findings of this study have practical implications for the implementation of ventilation protocols in naturally ventilated schools. In winter, occupants tend to be less willing to open windows for ventilation due to comfort reasons, but this may be inevitable during the flu season. The study found that the thermal conditions of the classroom remained relatively stable under natural ventilation regardless of the heating mode, which may be owing to the mild weather of the Mediterranean climate. The indoor thermal conditions are mainly influenced by the outdoor weather. When the outdoor temperature is appropriate (e.g., above 16°C), the classroom can be continuously ventilated to ensure good indoor air quality. A periodic ventilation strategy can be considered when the outdoor weather is too cold, while continuous ventilation should be implemented during the flu season for the safety of the students. Heating can maintain stable indoor thermal conditions for the basic needs of the students. Although this may result in certain energy loss, it can be considered an emergency measure for schools without HVAC systems.

Considering the limitation of this study, future research is recommended to conduct a further investigation based on both objective and subjective surveys. Besides, as the study was conducted in Mediterranean schools, future studies are recommended to investigate schools in different climates for a comparative study.

Nomenclature

T_a: indoor air temperature
T_mrt: mean radiant temperature
T_g: globe temperature
T_op: operative temperature
RH_in: indoor relative humidity
V_a: indoor air velocity
T_out: outdoor air temperature
RH_out: outdoor relative humidity
V_w: wind speed
W_d: wind direction
ACH: air change rate per hour
OA_total: total opening area
OA_window: window opening area
OA_door: door opening area
F_window: window operation frequency
F_door: door operation frequency

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research is part of the R&D Project IAQ4EDU (Reference No. PID2020-117366RB-I00) funded by the State Research Agency (Agencia Estatal de Investigación) of Spain (Reference No. MCIN/AEI/10.13039/501100011033). The study was supported by the Catalan University and Research Grants Management Agency (Agència de Gestió d’Ajuts Universitaris i de Recerca) under their research group support program (2021 SGR 00341). The author Sen Miao is funded by the China Scholarship Council (CSC) as a full-time PhD student (Reference No. 202208390065).

Appendix A

Table A1. Characteristics of investigated classrooms.

School code	Educational level	Construction year	Classroom code	Student age	Room floor	Facade orientation	Volume (m³)	Floor area (m²)	Number of windows	Total window area (m²)	Number of doors	Total door area (m²)
BP1	Primary	1975	I4	5	1	SE	145.88	48.38	4	7.00	2	3.39
BP1	Primary	1975	4T	9	2	SE	144.28	48.13	4	6.62	1	1.67
BP2	Primary	1987	I4	5	0	NW	180.20	60.90	3	4.20	1	1.66
BP2	Primary	1987	4T	9	1	NE	165.04	55.85	6	3.61	1	1.84
BP3	Primary	1980	4TA	9	2	W	145.75	49.54	4	6.60	1	1.67
BP3	Primary	1980	4TB	9	2	E	150.31	51.32	3	4.92	1	1.69
LP1	Primary	2007	I4	5	0	SW	190.09	59.38	1	1.16	2	3.74
LP1	Primary	2007	4T	9	1	SE	146.90	51.55	5	5.58	1	1.65
LP2	Primary	1976	I4	5	0	NW	169.29	56.92	2	2.46	2	3.19
LP2	Primary	1976	4T	9	1	NW	169.14	56.12	4	5.94	1	1.63
TP1	Primary	1980	I4	5	0	S&E	249.29	87.63	8	3.93	1	1.84
TP1	Primary	1980	4T	9	1	W	173.17	58.88	4	4.15	2	3.42
TP2	Primary	2010	I4	5	0	S	154.68	58.44	3	2.09	2	3.90
TP2	Primary	2010	4T	9	1	N	135.36	52.36	4	3.01	1	1.42
GP1	Primary	2006	I4	5	0	SW	164.81	58.71	3	3.87	2	3.61
GP1	Primary	2006	4T	9	1	NW	133.45	47.54	3	3.33	1	1.61
GP2	Primary	1993	I4	5	0	SE	147.67	49.09	1	0.34	2	3.42
GP2	Primary	1993	4T	9	0	SE	197.04	48.52	2	2.27	1	2.11
BS1	Secondary	1975	1E	12	2	NW	136.69	51.39	12	4.81	1	1.42
BS1	Secondary	1975	4E	16	4	NW	138.03	51.22	11	2.99	1	1.42
LS1	Secondary	1953	1E	12	1	SW	148.20	49.68	4	2.36	1	1.72
LS1	Secondary	1953	4E	16	2	SW	152.53	51.05	4	2.30	1	1.85
LS2	Secondary	2016	1E	12	2	N	154.02	53.48	4	7.69	1	1.79
LS2	Secondary	2016	4E	16	1	N	154.22	53.57	4	7.69	1	1.79
TS1	Secondary	1986	1E	12	0	W	176.37	59.41	2	9.38	1	1.67
TS1	Secondary	1986	4E	16	1	W	176.58	59.18	2	8.14	1	1.67
TS2	Secondary	2012	1E	12	1	SE	156.34	52.45	4	5.06	1	1.70
TS2	Secondary	2012	4E	16	2	SE	158.72	51.38	4	5.06	1	1.71
GS1	Secondary	2008	1E	12	1	SW	135.20	50.35	4	6.49	1	1.91
GS1	Secondary	2008	4E	16	0	NE	139.84	50.05	4	6.50	1	1.92
GS2	Secondary	1956	1E	12	2	SW	114.28	41.98	1	1.18	1	1.62
GS2	Secondary	1956	4E	16	1	NE	148.33	50.21	4	4.53	1	1.61

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Jia L., Han J., Chen X., Li Q., Lee C., and Fung Y., Interaction between thermal comfort, indoor air quality and ventilation energy consumption of educational buildings: a comprehensive review, Buildings. (2021) 11, no. 12, https://doi.org/10.3390/buildings11120591.
10.3390/buildings11120591
Web of Science® Google Scholar
2 Singh M. K., Ooka R., Rijal H. B., Kumar S., Kumar A., and Mahapatra S., Progress in thermal comfort studies in classrooms over last 50 years and way forward, Energy and Buildings. (2019) 188, 149–174, https://doi.org/10.1016/j.enbuild.2019.01.051, 2-s2.0-85061833024.
10.1016/j.enbuild.2019.01.051
Web of Science® Google Scholar
3 Aguilar A. J., Ruiz D. P., Martínez-Aires M. D., and de la Hoz Torres M. L., D. Bienvenido-Huertas and J. Durán-Álvarez, Indoor environment in educational buildings: Assessing natural ventilation, Building engineering facing the challenges of the 21st century, 2023, 345, Springer, Singapore, Lecture notes in civil engineering, https://doi.org/10.1007/978-981-99-2714-2_24.
10.1007/978-981-99-2714-2_24
Google Scholar
4 Fisk W. J., The ventilation problem in schools: literature review, Indoor Air. (2017) 27, no. 6, 1039–1051, https://doi.org/10.1111/ina.12403, 2-s2.0-85026489615.
10.1111/ina.12403
CAS PubMed Web of Science® Google Scholar
5 Heracleous C. and Michael A., Experimental assessment of the impact of natural ventilation on indoor air quality and thermal comfort conditions of educational buildings in the Eastern Mediterranean region during the heating period, Journal of Building Engineering. (2019) 26, 100917, https://doi.org/10.1016/j.jobe.2019.100917, 2-s2.0-85072708367.
10.1016/j.jobe.2019.100917
Web of Science® Google Scholar
6 Korsavi S. S., Montazami A., and Mumovic D., Ventilation rates in naturally ventilated primary schools in the UK; contextual, occupant and building-related (COB) factors, Building and Environment. (2020) 181, 107061, https://doi.org/10.1016/j.buildenv.2020.107061.
10.1016/j.buildenv.2020.107061
Web of Science® Google Scholar
7 Miao S., Gangolells M., and Tejedor B., A comprehensive assessment of indoor air quality and thermal comfort in educational buildings in the Mediterranean climate, Indoor Air. (2023) 2023, no. 1, 6649829, https://doi.org/10.1155/2023/6649829.
10.1155/2023/6649829
Web of Science® Google Scholar
8 Pereira L. D., Raimondo D., Corgnati S. P., and Gameiro da Silva M., Assessment of indoor air quality and thermal comfort in Portuguese secondary classrooms: methodology and results, Building and Environment. (2014) 81, 69–80, https://doi.org/10.1016/j.buildenv.2014.06.008, 2-s2.0-84903833326.
10.1016/j.buildenv.2014.06.008
Web of Science® Google Scholar
9 Alonso A., Llanos J., Escandón R., and Sendra J. J., Effects of the COVID-19 pandemic on indoor air quality and thermal comfort of primary schools in winter in a Mediterranean climate, Sustainability. (2021) 13, no. 5, https://doi.org/10.3390/su13052699.
10.3390/su13052699
Web of Science® Google Scholar
10 Ma F., Zhan C., Xu X., and Li G., Winter thermal comfort and perceived air quality: a case study of primary schools in severe cold regions in China, Energies. (2020) 13, no. 22, https://doi.org/10.3390/en13225958.
10.3390/en13225958
Web of Science® Google Scholar
11 Monge-Barrio A., Bes-Rastrollo M., Dorregaray-Oyaregui S., González-Martínez P., Martin-Calvo N., López-Hernández D., Arriazu-Ramos A., and Sánchez-Ostiz A., Encouraging natural ventilation to improve indoor environmental conditions at schools. Case studies in the north of Spain before and during COVID, Energy and Buildings. (2022) 254, 111567, https://doi.org/10.1016/j.enbuild.2021.111567.
10.1016/j.enbuild.2021.111567
Web of Science® Google Scholar
12 Duarte R., da Glória Gomes M., and Moret Rodrigues A., Classroom ventilation with manual opening of windows: findings from a two-year-long experimental study of a Portuguese secondary school, Building and Environment. (2017) 124, 118–129, https://doi.org/10.1016/j.buildenv.2017.07.041, 2-s2.0-85026821812.
10.1016/j.buildenv.2017.07.041
Web of Science® Google Scholar
13 Lovec V., Premrov M., and Leskovar V. Ž., Practical impact of the COVID-19 pandemic on indoor air quality and thermal comfort in kindergartens. A case study of Slovenia, International Journal of Environmental Research and Public Health. (2021) 18, no. 18, https://doi.org/10.3390/ijerph18189712, 34574634.
10.3390/ijerph18189712
PubMed Web of Science® Google Scholar
14 Miranda M. T., Romero P., Valero-Amaro V., Arranz J. I., and Montero I., Ventilation conditions and their influence on thermal comfort in examination classrooms in times of COVID-19. A case study in a Spanish area with Mediterranean climate, International Journal of Hygiene and Environmental Health. (2022) 240, 113910, https://doi.org/10.1016/j.ijheh.2021.113910, 34968975.
10.1016/j.ijheh.2021.113910
CAS PubMed Web of Science® Google Scholar
15 Ding E., Zhang D., Hamida A., García-Sánchez C., Jonker L., de Boer A. R., Bruijning P. C. J. L., Linde K. J., Wouters I. M., and Bluyssen P. M., Ventilation and thermal conditions in secondary schools in the Netherlands: effects of COVID-19 pandemic control and prevention measures, Building and Environment. (2023) 229, 109922, https://doi.org/10.1016/j.buildenv.2022.109922, 36575741.
10.1016/j.buildenv.2022.109922
PubMed Web of Science® Google Scholar
16 Makaveckas T., Bliūdžius R., Alavočienė S., Paukštys V., and Brazionienė I., Investigation of microclimate parameter assurance in schools with natural ventilation systems, Buildings. (2023) 13, no. 7, https://doi.org/10.3390/buildings13071807.
10.3390/buildings13071807
Web of Science® Google Scholar
17 Babich F., Torriani G., Corona J., and Lara-Ibeas I., Comparison of indoor air quality and thermal comfort standards and variations in exceedance for school buildings, Journal of Building Engineering. (2023) 71, 106405, https://doi.org/10.1016/j.jobe.2023.106405.
10.1016/j.jobe.2023.106405
Web of Science® Google Scholar
18 Gil-Baez M., Lizana J., Becerra Villanueva J. A., Molina-Huelva M., Serrano-Jimenez A., and Chacartegui R., Natural ventilation in classrooms for healthy schools in the COVID era in Mediterranean climate, Building and Environment. (2021) 206, 108345, https://doi.org/10.1016/j.buildenv.2021.108345.
10.1016/j.buildenv.2021.108345
Web of Science® Google Scholar
19 Hama S., Kumar P., Tiwari A., Wang Y., and Linden P. F., The underpinning factors affecting the classroom air quality, thermal comfort and ventilation in 30 classrooms of primary schools in London, Environmental Research. (2023) 236, Part 2, 116863, https://doi.org/10.1016/j.envres.2023.116863, 37567379.
10.1016/j.envres.2023.116863
PubMed Google Scholar
20 Mohamed S., Rodrigues L., Omer S., and Calautit J., Overheating and indoor air quality in primary schools in the UK, Energy and Buildings. (2021) 250, 111291, https://doi.org/10.1016/j.enbuild.2021.111291.
10.1016/j.enbuild.2021.111291
Web of Science® Google Scholar
21 Korsavi S. S., Montazami A., and Mumovic D., Indoor air quality (IAQ) in naturally-ventilated primary schools in the UK: occupant-related factors, Building and Environment. (2020) 180, 106992, https://doi.org/10.1016/j.buildenv.2020.106992.
10.1016/j.buildenv.2020.106992
Web of Science® Google Scholar
22 Sanguinetti A., Outcault S., Pistochini T., and Hoffacker M., Understanding teachers’ experiences of ventilation in California K-12 classrooms and implications for supporting safe operation of schools in the wake of the COVID-19 pandemic, Indoor Air. (2022) 32, no. 2, e12998, https://doi.org/10.1111/ina.12998, 35170085.
10.1111/ina.12998
PubMed Web of Science® Google Scholar
23 Torriani G., Lamberti G., Fantozzi F., and Babich F., Exploring the impact of perceived control on thermal comfort and indoor air quality perception in schools, Journal of Building Engineering. (2023) 63, 105419, https://doi.org/10.1016/j.jobe.2022.105419.
10.1016/j.jobe.2022.105419
Web of Science® Google Scholar
24 IAQ4EDU project, Optimal ventilation strategies for balancing indoor air quality, comfort and energy use in educational buildings, 2021, Funded by State Research Agency of Spain (Agencia Estatal de Investigación), reference number PID2020-117366RB-I00. Available at: http://iaq4edu.upc.edu/en.
Google Scholar
25 Miao S., Gangolells M., and Tejedor B., Improving the thermal comfort model for students in naturally ventilated schools: insights from a holistic study in the Mediterranean climate, Building and Environment. (2024) 258, 111622, https://doi.org/10.1016/j.buildenv.2024.111622.
10.1016/j.buildenv.2024.111622
Web of Science® Google Scholar
26 ISO, EN ISO 7726: ergonomics of the thermal environment–instruments for measuring physical quantities, 2001, International Organization for Standardization (ISO), Geneva.
Google Scholar
27 ASTM, ASTM D6245-18. Standard guide for using indoor carbon dioxide concentrations to evaluate indoor air quality and ventilation, 2018, American Society for Testing and Materials (ASTM), Pennsylvania.
Google Scholar
28 ASHRAE, ASHRAE 55: Thermal environment conditions for human occupancy, 2020, The American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE), Atlanta.
Google Scholar
29 Meteocat, Meteorological data API, 2023, Available at: https://apidocs.meteocat.gencat.cat/documentacio/. Accessed on 31 March 2022.
Google Scholar
30 Li Y. and Li X., Natural ventilation potential of high-rise residential buildings in northern China using coupling thermal and airflow simulations, Building Simulation. (2015) 8, no. 1, 51–64, https://doi.org/10.1007/s12273-014-0188-1, 2-s2.0-84919921752.
10.1007/s12273-014-0188-1
Web of Science® Google Scholar
31 Kumar S., Singh M. K., Mathur A., Mathur J., and Mathur S., Evaluation of comfort preferences and insights into behavioural adaptation of students in naturally ventilated classrooms in a tropical country, India, Building and Environment. (2018) 143, 532–547, https://doi.org/10.1016/j.buildenv.2018.07.035, 2-s2.0-85050695613.
10.1016/j.buildenv.2018.07.035
Web of Science® Google Scholar
32 Batterman S., Review and extension of CO₂-based methods to determine ventilation rates with application to school classrooms, International Journal of Environmental Research and Public Health. (2017) 14, no. 2, https://doi.org/10.3390/ijerph14020145, 2-s2.0-85011957116, 28165398.
10.3390/ijerph14020145
PubMed Web of Science® Google Scholar
33 Remion G., Moujalled B., and El Mankibi M., Review of tracer gas-based methods for the characterization of natural ventilation performance: comparative analysis of their accuracy, Building and Environment. (2019) 160, 106180, https://doi.org/10.1016/j.buildenv.2019.106180, 2-s2.0-85067202756.
10.1016/j.buildenv.2019.106180
Web of Science® Google Scholar
34 Kabirikopaei A. and Lau J., Uncertainty analysis of various CO₂-based tracer-gas methods for estimating seasonal ventilation rates in classrooms with different mechanical systems, Building and Environment. (2020) 179, 107003, https://doi.org/10.1016/j.buildenv.2020.107003.
10.1016/j.buildenv.2020.107003
Google Scholar
35 Kang J. and Hwang K. I., A comprehensive real-time indoor air-quality level indicator, Sustainability. (2016) 8, no. 9, https://doi.org/10.3390/su8090881, 2-s2.0-84990923858.
10.3390/su8090881
PubMed Web of Science® Google Scholar
36 Mohammadshirazi A., Kalkhorani V. A., Humes J., Speno B., Rike J., Ramnath R., and Clark J. D., Predicting airborne pollutant concentrations and events in a commercial building using low-cost pollutant sensors and machine learning: a case study, Building and Environment. (2022) 213, 108833, https://doi.org/10.1016/j.buildenv.2022.108833.
10.1016/j.buildenv.2022.108833
Web of Science® Google Scholar
37 Johnson D. L., Lynch R. A., Floyd E. L., Wang J., and Bartels J. N., Indoor air quality in classrooms: environmental measures and effective ventilation rate modeling in urban elementary schools, Building and Environment. (2018) 136, 185–197, https://doi.org/10.1016/j.buildenv.2018.03.040, 2-s2.0-85044579033.
10.1016/j.buildenv.2018.03.040
Web of Science® Google Scholar
38 Persily A. and Jonge L., Carbon dioxide generation rates for building occupants, Indoor Air. (2017) 27, no. 5, 868–879, https://doi.org/10.1111/ina.12383, 2-s2.0-85025615554, 28321932.
10.1111/ina.12383
CAS PubMed Web of Science® Google Scholar
39 Gangolells M., Casals M., Ferré-Bigorra J., Forcada N., Macarulla M., Gaspar K., and Tejedor B., Office representatives for cost-optimal energy retrofitting analysis: a novel approach using cluster analysis of energy performance certificate databases, Energy and Buildings. (2020) 206, 109557, https://doi.org/10.1016/j.enbuild.2019.109557.
10.1016/j.enbuild.2019.109557
Web of Science® Google Scholar
40 Saxena A., Prasad M., Gupta A., Bharill N., Patel O. P., Tiwari A., Er M. J., Ding W., and Lin C. T., A review of clustering techniques and developments, Neurocomputing. (2017) 267, 664–681, https://doi.org/10.1016/j.neucom.2017.06.053, 2-s2.0-85021901708.
10.1016/j.neucom.2017.06.053
Web of Science® Google Scholar
41 Asif A. and Zeeshan M., Indoor temperature, relative humidity and CO₂ monitoring and air exchange rates simulation utilizing system dynamics tools for naturally ventilated classrooms, Building and Environment. (2020) 180, 106980, https://doi.org/10.1016/j.buildenv.2020.106980.
10.1016/j.buildenv.2020.106980
Web of Science® Google Scholar
42 Shrestha M., Rijal H. B., Kayo G., and Shukuya M., An investigation on CO₂ concentration based on field survey and simulation in naturally ventilated Nepalese school buildings during summer, Building and Environment. (2022) 207, 108405, https://doi.org/10.1016/j.buildenv.2021.108405.
10.1016/j.buildenv.2021.108405
Web of Science® Google Scholar
43 Vignolo A., Gómez A. P., Draper M., and Mendina M., Quantitative assessment of natural ventilation in an elementary school classroom in the context of COVID-19 and its impact in airborne transmission, Applied Sciences. (2022) 12, no. 18, https://doi.org/10.3390/app12189261.
10.3390/app12189261
Google Scholar
44 ISO, EN ISO 7730: ergonomics of the thermal environment - analytical determination and interpretation of thermal comfort using calculation of the PMV and PPD indices and local thermal comfort criteria, 2005, International Organization for Standardization (ISO), Geneva.
Google Scholar
45 Miao S., Gangolells M., and Tejedor B., Data-driven model for predicting indoor air quality and thermal comfort levels in naturally ventilated educational buildings using easily accessible data for schools, Journal of Building Engineering. (2023) 80, 108001, https://doi.org/10.1016/j.jobe.2023.108001.
10.1016/j.jobe.2023.108001
Web of Science® Google Scholar
46 Larsen T. S. and Heiselberg P., Single-sided natural ventilation driven by wind pressure and temperature difference, Energy and Buildings. (2008) 40, no. 6, 1031–1040, https://doi.org/10.1016/j.enbuild.2006.07.012, 2-s2.0-38949126224.
10.1016/j.enbuild.2006.07.012
Web of Science® Google Scholar
47 Tang Y., Li X., Zhu W., and Cheng P. L., Predicting single-sided airflow rates based on primary school experimental study, Building and Environment. (2016) 98, 71–79, https://doi.org/10.1016/j.buildenv.2015.12.021, 2-s2.0-84953234663.
10.1016/j.buildenv.2015.12.021
Web of Science® Google Scholar
48 CEN, EN 16798-1: 2019, Part 1: Indoor environmental input parameters for design and assessment of energy performance of buildings addressing indoor air quality, thermal environment, lighting and acoustics, 2019, European Committee for Standardization (CEN), Brussels.
Google Scholar

All articles

Assessing the Fluctuation of Indoor Thermal Conditions in Naturally Ventilated Classrooms Through K-Means Clustering

Abstract

1. Introduction

2. Methodology

2.1. Field Measurement Campaign

2.2. Processing of Measurement Data

2.3. Analysis of the Processed Data

3. Results and Discussion

3.1. Overview of Measured Parameters

3.2. Variation of Indoor Thermal Parameters

3.2.1. Variability of Indoor Thermal Parameters

3.2.2. Fluctuation of Indoor Thermal Parameters

3.2.3. Clustering of Indoor Thermal Parameters

3.3. Effect of Natural Ventilation on Indoor Thermal Parameter Variations

3.3.1. Outdoor Thermal Parameters

3.3.2. Air Change Rate

3.3.3. Window and Door Operation

3.4. Further Discussion and Limitations

4. Conclusions and Recommendations

Nomenclature

Conflicts of Interest

Funding

Appendix A

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley