This study examined the multidimensional fractional diffusion equations that characterize the density dynamics in a diffusing medium utilizing the exact and analytical Aboodh transform decomposition method (ATDM). The Caputo–Fabrizio (CF) derivative is utilized to account for the fractional derivative that is being employed here. The suggested method handles nonlinear terms by combining the Adomian decomposition method (ADM) with the Aboodh transform (AT) and Adomian polynomials. Since the AT can only be applied to linear equations, ADM is a helpful technique for estimating solutions to nonlinear differential equations. In nonlinear systems, multidimensional diffusion problems which account for the production of stripes in two-dimensional systems are important. Additionally, we used MATLAB to compute numerical and graphical data that illustrate how the close-form analytical solution compares to the precise solution. Promising and appropriate for addressing multidimensional diffusion problems with fractional derivatives are the obtained results. The key benefit is that our devised approach does not depend on presumptions or constraints on variables that skew the actual issue. Overcoming fluctuating constraints that can make it difficult to discover the answer and represent the problem depends much on this technique. In the domains of science and technology, the approach presented in this work offers exceptional computational accuracy and convenience of use for analyzing and resolving intricate phenomena associated with CF fractional nonlinear partial differential equations.

1. Introduction

A query from L’Hospital to Gottfried Wilhelm Leibniz in 1695 served as the inspiration for the development of the current, much debated notion of fractional calculus (FC). L’Hospital insisted on obtaining data regarding the derivative of order α = 1/2, laying the groundwork for a potent FC. Many scholars from other fields have recently been captivated by the discovery of symmetry-related FC, which enables them to contribute their unique viewpoints to solving practical issues. Due to its capacity to accurately characterize a wide range of nonlinear events, FC has drawn the attention of numerous authors in recent years. Differential equations of fractional order are extensions of conventional differential equations that show intrinsic and nonlocal effects on material properties. Reputable academics who have developed ground-breaking definitions and established the field of FC have thoroughly researched and explicated the idea of FC.

According to recent research, FC is more useful than classical calculus for solving the majority of challenging real-world issues. Over time, the application of FC in applied studies has grown and extended. Recent research has shown that nonlocal fractional operators exist even in the absence of a unique kernel, and has even predicted their occurrence. In addition, some fractional derivatives that are classified as local or nonlocal are defined differently than others, but they are distinguished by their capacity to characterize models. Among the most significant benefits offered by fractional derivatives are the exceptional memory and inheritance qualities displayed by numerous materials and processes.

The Caputo–Fabrizio (CF) derivative varies from standard fractional derivatives such as Riemann–Liouville (RL) and Caputo in numerous key areas, including kernel structure, memory effect, and physical interpretability [1, 2]. Nonlocal fractional derivatives offer a straightforward way to describe these properties along various processes. As a result, nonlocal fractional derivatives are definitely preferable to their local counterparts from a physical and practical standpoint. Particularly in cases involving nonlocal events, FC is applied in numerical techniques for differential equation solution. Engineering and physical processes have been most aptly modeled and described using fractional differential equations. Systems requiring precise modeling of damping are modeled faithfully using fractional differential models. Fractional derivatives can explain mechanisms displaying abnormal diffusion or wave propagation in several physical models. When modeling difficult materials, including viscoelastic materials, where conventional derivatives fall short in capturing the behavior, they are very helpful.

As a result, the CF derivative shows promise in handling this issue. With multiple applications in biology [3–7], electrodynamics [8], mechanics [9–11], nanotechnology [12], biotechnology [13], chaos theory [14], and many other fields [15–17], integral transforms are without a doubt one of the most practical and efficient methods in theoretical and applied mathematics. Different physical models have been solved in recent years using a variety of integral transforms, including the Sumudu transform (SMT) [18, 19], Shehu transform (ST) [20–22], Elzaki transform (ET) [23, 24], Laplace transform (LT) [25, 26], Aboodh transform method [27–29], differential transform method (DTM) [30–35] and these techniques include Adomian decomposition method (ADM) [36–38].

In this paper, we apply the Aboodh transform decomposition method (ATDM) to obtain analytical and numerical solutions of the CF fractional multidimensional diffusion equations. The advantage of this technique is that it uses two powerful methods together to obtain exact and approximate analytical solutions for nonlinear equations. It is worth mentioning strongly that the proposed method can reduce the computational volume compared to classical methods while maintaining high accuracy of the numerical result; dimensionality reduction implies an improvement in the performance of the approach. This work aims to examine the use of ATDM in the numerical resolution of multidimensional fractional diffusion equations, taking into account recent technical advancements and contrasting the findings with a contemporary methodology. The primary aim of this study is to provide the Aboodh Adomian transform technology. The second purpose is to implement the newly created hybrid method to address multidimensional fractional diffusion problems for the first time. A significant quantity of hitherto unexamined responses from the literature is identified, and their extensive graphical characteristics are illustrated. The primary aim of this study is to employ a novel hybrid technique, the ATDM, to get new numerical solutions for multidimensional fractional diffusion problems. Recently, there have been significant studies in the literature on the applications of FC [39–54]. This work significantly expands the scope and utility of fractional differential equations in scientific and engineering contexts by addressing the constraints of current numerical methods and fractional operators. It also establishes a framework that is both robust and adaptable for the resolution of multidimensional diffusion problems.

The motivation of this paper is to extend the application of ATDM to derive analytical approximate solutions of the fractional differential multidimensional diffusion equation. The suggested approach, which combines the integral transform power of the Aboodh transform with the recursive structure of the Adomian decomposition, allows for the efficient and easy derivation of precise and approximation analytical solutions to complicated nonlinear fractional systems. This paper addresses a significant gap by expanding the use of this hybrid technique to a class of multidimensional diffusion problems regulated by the CF derivative.

(1)

Subject to the initial conditions:

(2)

The current document is structured as follows: A summary of several fundamental definitions is given in Section 2. The study’s methodology is presented in Section 3. Three issues are answered in Section 4 to show how the methodology is applied. The results are presented in Section 5 and are further examined and commented. The primary findings are finally summarized in Section 6.

2. Preliminaries

Here, we present some basic definitions of CF that are important to our research.

Definition 1. CF fractional derivative [55] of order

(3)

and P(α) is the normalization constant, which is contingent upon a, where P(0) = P(1) = 1.

Definition 2. The Caputo fractional derivative [56–58] of , with α > 0 representing the order of the derivative:

(4)

It is defined as.

Definition 3. The functions in set , as delineated, are examined by a novel transformation for exponential functions referred to as the Aboodh transformation [27–29].

(5)

Aboodh transform of function

(6)

It is defined as.

Definition 4. The inverse Aboodh transform of a function , t ∈ (0, ∞) if then

(7)

Theorem 1. Below are the Aboodh transformations for some special cases of the function [27–29].

(8)

(9)

(10)

(11)

Definition 5. Laplace Transform of CF fractional derivative [59–61]:

(12)

for n = 0

(13)

3. Methods and Materials

We analyze the broader nonhomogeneous nonlinear fractional partial differential equation to elucidate the Aboodh decomposition method.

(14)

with the initial condition

(15)

where R is the remaining linear operator less than N is the nonlinear operator and g(x, t) is the nonhomogeneous term.

Solution (14). Let’s use the Aboodh transformation for both sides of the problem.

(16)

(17)

(18)

Now, replacing the unknown function Ψ(x, t) by an infinite series of Ψ_m’s i.e.,

(19)

and the nonlinear component by an endless sequence of the Adomian polynomials B_m’s, which are provided by

(20)

where

(21)

Equation (18), after substituting equations (19) and (18) into it, is (17). Let’s calculate the inverse Aboodh transform of each expression;

(22)

(23)

Equation (23) in the equation n = 0, 1, 2, … using their values;

(24)

3.1. Analysis of Convergence

Take into consideration all continuous functions on [0, T] with supremum norm and their Banach space C[0, T]. We take into consideration Ψ(x, t), Ψ_n(x, t) ∈ C[0, T] throughout this section.

Theorem 2. The Aboodh transform of the CF fractional derivative [61, 62] of order α, denoted as A{h(s)}, where h(t) is the function in question;

(25)

Theorem 3 (Uniqueness theorem [63–65]). The solution for the nonlinear fractional differential equation (1) derived via ATDM is unique for 0 < ϱ < 1.

Proof 1. The solution of nonlinear FPDEs equation (1) is presented as

(26)

(27)

Here,

(28)

Assuming Ψ and Φ are two distinct solutions of (1), we can derive the following using the previously given equation.

(29)

Currently, the Aboodh transform is obtained by employing the convolution theorem like this:

(30)

where δ = (∂/(∂x))(Ψ − Φ) Subsequently, applying the integral mean-value theorem, it results in

(31)

Therefore, |Ψ − Φ| = 0, as 0 < ϱ < 1. Consequently, Ψ = Φ. This demonstrates the solution’s distinctiveness.

Theorem 4 (Convergence theorem [63–66]). Assume that X is a Banach space and H : X⟶X is a nonlinear mapping. If the inequality

(32)

If it exists, then H possesses a fixed point according to Banach’s fixed point theorem [43]. Moreover, for the arbitrary selection of Ψ₀ and Ψ₁ in X, the sequence generated by the A-ADM converges to a fixed point of H.

(33)

Proof 2. Consider a Banach space (C[J], ‖.‖) comprising all continuous functions on J, with the norm defined as ‖h(ξ)‖ = max_ξ∈J|h(ξ)|.

We now illustrate that the sequence {Ψ_n} constitutes a Cauchy sequence within the Banach space:

(34)

Currently, the convolution theorem for Laplace transform is employed to provide the following:

(35)

Next, we obtain the result by employing the integral mean value theorem [43].

(36)

Let m = n + 1, then we have

(37)

Utilizing the triangular inequality, it generates the following:

(38)

Because γ ∈ (0, 1), so 1 − ϱ^m−n−1 < 1, then we have

(39)

Although ‖Ψ₁ − Ψ₀‖ < ∞, as m approaches infinity, ‖Ψ_m − Ψ_n‖ approaches zero. Consequently, the sequence {Ψ_n} is a Cauchy sequence in C[J], and is therefore convergent.

4. Applications of ATDM

In this section, we apply the Aboodh transform decomposition approach to multidimensional fractional diffusion equations [67], in particular the nonlinearity is controlled by using Adomian polynomials. The solutions and absolute errors will then be compared with exact solution by evaluating the accuracy of the proposed method.

Example 1.

(40)

Ψ(x, 0) = e^x is the CF fractional partial differential equation. Determine the initial condition and solve it using the Aboodh transform decomposition approach.

Solution (40). In the event that both sides of the equation undergo the Aboodh transformation;

(41)

(42)

(43)

(44)

B_n ve C_n Adomian polynomials.

Let’s substitute the definitions in (44) in (43);

(45)

Solution (41). If the equation’s inverse Aboodh transformation is applied

(46)

(47)

Solution (47). In the equation, n = 0, 1, 2, … using the values;

(48)

(49)

Let’s substitute the expressions (49) in (48)

(50)

(51)

(52)

Let’s substitute the expressions (52) in (51)

(53)

(54)

(55)

Let’s substitute the definitions in (55) in (54)

(56)

(57)

(58)

is found as.

If we examine the convergence by choosing t = 1, x = 1, α = 1

(59)

(60)

(61)

It converges because its values are less than 1 [68, 69].

For α = 1 in equation (58);

(62)

the exact solution is obtained.

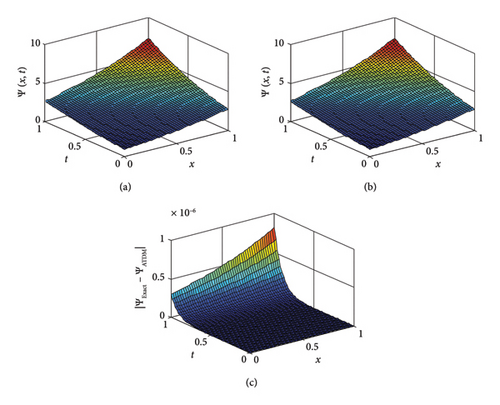
For fractional derivative values α = 1, Figure 1 displays the exact solution, the 3D graphs of the resulting absolute error, and the results obtained from the ATDM method. It is evident that the results obtained are entirely consistent.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

3D graphical representation for Ψ(x, t). (a) The exact solution, (b) the approximate solution, (c) absolute error when α = 1 of Example 1.

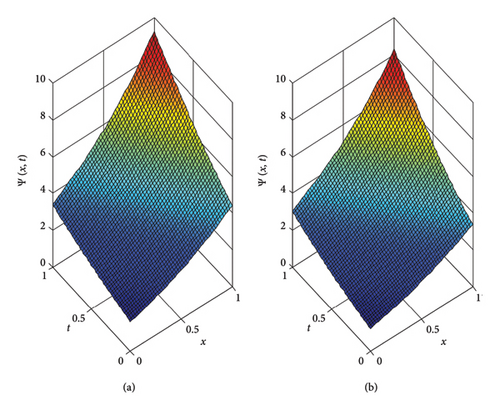
The results obtained from the ATDM method for fractional derivative values α = 0.6 and 0.8 are shown in Figure 2. It is seen that the maximum value of Ψ(x, t) increases when the α value decreases from 0.8 to 0.6.

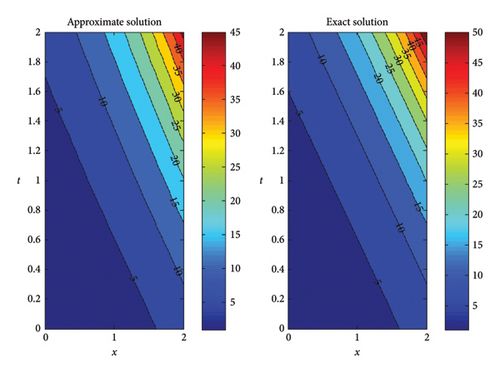
Contour diagrams of exact and approximate solutions for α = 1, x ∈ [0, 2] and t ∈ [0, 2] values are depicted in Figure 3. The graphs show that the results are extremely similar.

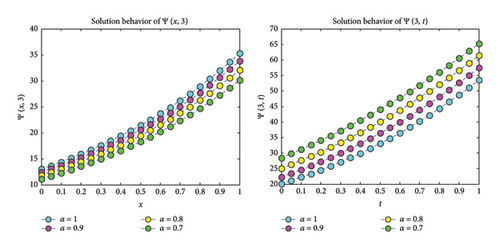
In Figure 4, when we look at Ψ(x, 3) in the x ∈ [0, 1] range, it is observed that as the order of the fractional derivative decreases, the Ψ(x, 3) solutions decrease. On the contrary, when we look at Ψ(3, t) in the t ∈ [0, 1] range, it is observed that as the order of the fractional derivative decreases, the Ψ(3, t) solutions increase.

In Table 1, the values for different values of (x, t) and α = 0.85 and 1 are calculated, and the exact solution is compared with the proposed ATDM method at α = 1, and the results obtained are extremely promising.

Table 1. The fractional value at α = 0.85 and absolute error of ATDM at α = 1 for Example 1.

(x, t)	α = 0.85	α = 1	Exact	\|Ψ_Ex.−Ψ_ATDM\|
(1, 0.5)	5.166936999	4.481689068	4.481689070	0.2000000000 10⁻⁸
(1, 1)	8.058119957	7.389056028	7.389056099	0.7100000000 10⁻⁷
(1, 1.5)	12.07857912	12.18248724	12.18249396	0.6720000000 10⁻⁵
(1, 2)	17.43698509	20.08537004	20.08553692	0.0001668800000
(1, 2.5)	24.34200848	33.11341112	33.11545196	0.002040840000
(2, 0.5)	14.04519096	12.18249396	12.18249396	0
(2, 1)	21.90424105	20.08553674	20.08553692	0.1800000000 10⁻⁶
(2, 1.5)	32.83298214	33.11543369	33.11545196	0.00001827000000
(2, 2)	47.39863973	54.59769642	54.59815003	0.0004536100000
(2, 2.5)	66.16843934	90.01158374	90.01713130	0.005547560000

Example 2.

(63)

Using the Aboodh transform decomposition approach, the CF fractional partial differential equation Ψ(x, y, 0) = sin x cos y may be solved given the initial condition.

Solution (63). Let us take the Aboodh transformation of both sides of the equation.

(64)

(65)

(66)

Let’s substitute the definitions in (66) in (65)

(67)

(67) If the inverse Aboodh transformation of the equation is taken;

(68)

Solution (68). In the equation, n = 0, 1, 2, … using their values;

(69)

(70)

Let’s substitute the expressions (70) in (69)

(71)

(72)

(73)

Let’s substitute the expressions (73) in (72)

(74)

(75)

(76)

Let’s substitute the expressions (76) in (75)

(77)

(78)

(79)

is found as.

If we examine the convergence by choosing t = 1, x = 1, y = 1, α = 1

(80)

(81)

(82)

It converges because its values are less than 1 [68, 69].

For α = 1 in equation (79);

(83)

the exact solution is obtained.

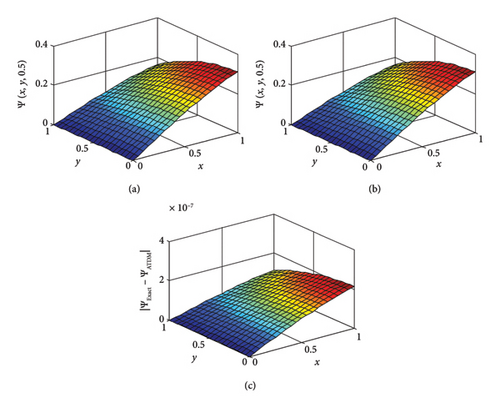
For fractional derivative parameters α = 1 and t = 0.5, Figure 5 illustrates the precise solution, the three-dimensional representations of the resultant absolute error, and the outcomes derived from the ATDM approach. The data obtained are unequivocally consistent.

In Figure 6, when the α value diminishes from 1 to 0.7 inside the interval x ∈ [0, 1], it is observed that the Ψ(x, 4, 4) solutions decline as the order of the fractional derivative lowers. As the alpha value diminishes from 1 to 0.7 within the interval y ∈ [0, 1], the Ψ(4, y, 4) solutions are observed to decline with the reduction in the order of the fractional derivative. As the alpha value diminishes from 1 to 0.7 within the interval t ∈ [0, 1], the Ψ(4, 4, t) solutions are observed to decline with a reduction in the order of the fractional derivative.

In Table 2, values for α = 0.85 and 1 are computed and the precise solution is compared with the ATDM approach suggested for α = 1 and the resulting results show great agreement when t changes in the range of [0, 1].

Table 2. The A_ADM results for fifth order Ψ(x, y, t) with x = 0.3, y = 0.3 for Example 2.

t	α = 0.85	α = 1	Exact solution	\|Ψ_Ex − Ψ_ATDM\|
0.1	0.1834314950	0.2311450788	0.2311450787	0.1000000000 10⁻⁹
0.2	0.1508807502	0.1892455844	0.1892455844	0
0.3	0.1163718256	0.1549411794	0.1549411798	0.4000000000 10⁻⁸
0.4	0.07851767673	0.1268551010	0.1268551088	0.7800000000 10⁻⁷
0.5	0.03593125898	0.1038601075	0.1038601788	0.7130000000 10⁻⁶
0.6	−0.01277447132	0.08503308842	0.08503352239	0.4339700000 10⁻⁵
0.7	−0.06898655893	0.06961756571	0.06961955981	0.1994100000 10⁻⁵
0.8	−0.1340920473	0.05699221715	0.05699967465	0.7457500000 10
0.9	−0.2094779817	0.04664355553	0.04666738654	0.00002383101000
1	−0.2965314059	0.03814075272	0.03820802452	0.00006727180000

Example 3.

(84)

Utilizing the ATDM, solve the CF fractional multidimensional partial differential equation for the initial condition Ψ(x, y, z, 0) = sin x sin y sin z.

Solution (84). Let us take the Aboodh transformation of both sides of the equation.

(85)

(86)

(87)

Let’s substitute the definitions in (87) in (86)

(88)

Solution (88). If the inverse Aboodh transformation of the equation is taken;

(89)

Solution (89). In the equation, n = 0, 1, 2, … using their values;

(90)

(91)

Let’s substitute the expressions (91) in (90)

(92)

(93)

(94)

Let’s substitute the expressions (94) in (93)

(95)

(96)

(97)

Let’s substitute the expressions (93) in (92)

(98)

(99)

(100)

is found as.

If we examine the convergence by choosing t = 1, x = 1, y = 1, z = 1, α = 1

(101)

(102)

(103)

It converges because its values are less than 1 [68, 69].

For α = 1 in equation (96)

(104)

the exact solution is obtained.

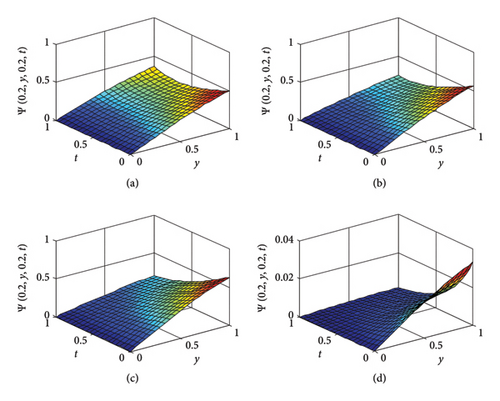
The 3D graphs of Ψ(0.2, y, 0.2, t) are depicted in Figure 7 for α values of 0.8, 0.9, and 1, as well as for x values of 0.2 and z values of 0.2. It has been noted that the solutions increase in tandem with the alpha fractional derivative value.

5. Results and Discussions

In this paper, we presented Tables 1 and 2, which show that the simulation results obtained with the proposed technique are close to the exact solution for fractional order diffusion equations. Figure 1 shows the nature of the 3D plots of the approximate exact solution and absolute error of Example 1. Figure 2 examines the 3D nature of the approximate solution for different values of α. Contour plots of the exact and approximate solutions are given in Figure 3. Figure 4 presents the 2D plots of the approximate solution plots of Ψ(x, 3) and Ψ(3, t) for different values of α. Figure 5 shows the nature of the 3D plots of the approximate exact solution and absolute error of Example 2. Figure 6 presents the 2D plots of the approximate solution plots of Ψ(x, 4, 4), Ψ(4, y, 4) and Ψ(4, 4, t) for different values of alpha. Figure 7 depicts the dynamic behavior of the approximate and exact solutions of Example 3 at x = 0.20 and z = 0.20. From the graphical solutions, we observe that the approximate solutions closely match the exact solutions at α = 1.

6. Conclusion

In this study, we effectively employed a hybrid technique known as ATDM to investigate the multidimensional fractional order diffusion problem with the CF derivative. The existence and uniqueness of the proposed approach are established by the fixed point theorem. We solved three types of fractional order diffusion equations to demonstrate the accuracy and effectiveness of the proposed scheme. The results of the approximate solutions that are obtained using the ATDM are exceedingly similar to the exact solution. The results show how reliable and accurate the suggested technique is computationally. The proposed method is highly applicable to a diverse array of engineering disciplines due to its capacity to simulate memory effects, nonlocal properties, and multivariate diffusion processes. The method equips engineers with a potent instrument to design and optimize systems, thereby advancing both theoretical comprehension and practical innovation, spanning from thermal management and fluid flow to biomedical engineering and environmental modeling. The ATDM is distinguished by its capacity to provide precise, analytical solutions with minimal computational effort, while simultaneously effectively addressing complex multidimensional fractional diffusion problems. In contrast to conventional numerical or analytical methods, it is a potent instrument due to its robustness, versatility, and efficiency. The significance of ATDM in the advancement of FC and its applications is illustrated by these advantages.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

Open access funding was provided and organized under the TUBITAK-Ulakbim + Wiley UAE agreement.

Open Research

Data Availability Statement

Data sharing is not applicable to this article as no new data were created or analyzed in this study.

References

1 Caputo M. and Fabrizio M., A New Definition of Fractional Derivative without Singular Kernel, Progress in Fractional Differentiation and Applications. (2015) 1, 73–58.
Google Scholar
2 Caputo M. and Fabrizio M., Applications of New Time and Spatial Fractional Derivatives With Exponential Kernels, Progress in Fractional Differentiation and Applications. (2016) 2, 1–11.
10.18576/pfda/020101
Google Scholar
3 Dubey R. S. and Goswami P., On the Existence and Uniqueness Analysis of Fractional Blood Glucose-Insulin Minimal Model, International Journal of Modeling, Simulation, and Scientific Computing. (2023) 18.
Google Scholar
4 Alzaid S. S., Alkahtani B. S. T., Sharma S., and Dubey R. S., Numerical Solution of Fractional Model of HIV-1 Infection in Framework of Different Fractional Derivatives, Journal of Function Spaces. (2021) 2021.
10.1155/2021/6642957
Google Scholar
5 Jafari H., Goswami P., Dubey R. S., Sharma S., and Chaudhary A., Fractional SIZR Model of Zombie Infection, International Journal of Mathematics and Computer in Engineering. (2023) 1, no. 1, 91–104.
10.2478/ijmce-2023-0007
Google Scholar
6 Gour M. M., Yadav L. K., Purohit S. D., and Suthar D. L., Homotopy Decomposition Method to Analysis Fractional Hepatitis B Virus Infection Model, Applied Mathematics in Science and Engineering. (2023) 31, no. 1.
10.1080/27690911.2023.2260075
Google Scholar
7 Dubey R. S., Baleanu D., Mishra M. N., and Goswami P., Solution of Modified Bergman Minimal Blood Glucose-Insulin Model Using Caputo-Fabrizio Fractional Derivative, CMES, Computer Modeling in Engineering and Sciences. (2021) 128, no. 3, 1247–1263.
10.32604/cmes.2021.015224
Google Scholar
8 Nasrolahpour H., A Note on Fractional Electrodynamics, Communications in Nonlinear Science and Numerical Simulation. (2013) 18, 2589–2593.
10.1016/j.cnsns.2013.01.005
Google Scholar
9 Drapaca C. S. and Sivaloganathan S., A Fractional Model of Continuum Mechanics, Journal of Elasticity. (2012) 107, 105–123.
10.1007/s10659-011-9346-1
Google Scholar
10 Mainardi F., Fractional Calculus and Waves in Linear Viscoelasticity, 2010, Imperial College Press.
10.1142/p614
Google Scholar
11 Agarwal R., Yadav M. P., Balenu D., and Purohit S. D., Existence and Uniqueness of Miscible Flow Equation Through Porous Media With a Non Singular Fractional Derivative, AIMS Mathematics. (2020) 5, no. 2, 1062–1073.
10.3934/math.2020074
Google Scholar
12 Baleanu D., Guvenc Z. B., and Machado J. A. T., New Trends in Nanotechnology and Fractional Calculus Applications, 2010, Springer.
10.1007/978-90-481-3293-5
Google Scholar
13 Kumar D., Seadwy A. R., and Joarder A. K., Modified Kudryashov Method via New Exact Solutions for Some Conformable Fractional Differential Equations Arising in Mathematical Biology, Chinese Journal of Physics. (2018) 56, no. 1, 75–85.
10.1016/j.cjph.2017.11.020
Google Scholar
14 Baleanu D., Wu G. C., and Zeng S. D., Chaos Analysis and Asymptotic Stability of Generalized Caputo Fractional Differential Equations, Chaos, Solitons & Fractals. (2017) 102, 99–105.
10.1016/j.chaos.2017.02.007
Google Scholar
15 Alhamzi G., Dubey R. S., Alkahtani B. S. T., and Saini G. L., Analytical Solutions for a Generalized Nonlinear Local Fractional Bratu-Type Equation in a Fractal Environment, Fractal Fraction. (2024) 8, no. 1.
Google Scholar
16 Dubey R. S. and Goswami P., Mathematical Model of Diabetes and Its Complication Involving Fractional Operator Without Singular Kernel, Discrete and Continuous Dynamical Systems. (2021) 14, no. 17, 2151–2161.
10.3934/dcdss.2020144
Google Scholar
17 Yadav M. P. and Agarwal R., Numerical Investigation of Fractional-Fractal Boussinesq Equation, Chaos: An Interdiscip, Journal of Nonlinear Science. (2019) 29.
Google Scholar
18 Kiliman A. and Gadain H. E., On the Applications of Laplace and Sumudu Transforms, Journal of the Franklin Institute. (2010) 347, 848–862.
10.1016/j.jfranklin.2010.03.008
Google Scholar
19 Dubey R. S., Alkahtani B. S. T., and Atangana A., Analytical Solution of Space-Time Fractional Fokker-Plank Equation by Homotopy Perturbation Sumudu Transform Method, Mathematical Problems in Engineering. (2015) 2015.
10.1155/2015/780929
Google Scholar
20 Liaqat M. I., Khan A., Alqudah M. A., and Abdeljawad T., Adapted Homotopy Perturbatıon Method with Shehu Transform for Solving Conformable Fractional Nonlinear Partial Differential Equations, Fractals. (2023) 31, no. 02, https://doi.org/10.1142/S0218348X23400273.
10.1142/S0218348X23400273
Google Scholar
21 Liaqat M. I., Khan A., Alam M., Pandit M. K., Etemad S., and Rezapour S., Approximate and Closed-form Solutions of Newell-Whitehead-Segel Equations via Modified Conformable Shehu Transform Decomposition Method, Mathematical Problems in Engineering. (2022) https://doi.org/10.1155/2022/6752455.
10.1155/2022/6752455
Google Scholar
22 Bektaş U. and Anaç H., Q-homotopy Shehu Analysıs Transform Method of Timefractional Coupled Burgers Equations, Eskişehir Technical Unıversity Journal of Science and Technology A-Applied Sciences and Engineering. (2023) 24, no. 3, https://doi.org/10.18038/estubtda.1312725.
10.18038/estubtda.1312725
Google Scholar
23 Neamaty A., Agheli B., and Darzi R., Applications of Homotopy Perturbation Method and Elzaki Transform Forsolving Nonlinear Partial Differential Equations of Fractional Order, Journal of Nonlinear Evolution Equations and Applications. (2016) 6, 91–104.
Google Scholar
24 Agarwal G., Yadav L. K., Albalawi W., Abdel-Aty A. H., Nisar K. S., and Shefeeq T., Two Analytical Approaches for Space-And Time-Fractional Coupled Burgers Equations via Elzaki Transform, Fractional Differentiation and Applications. (2022) 8, no. 1, 177–190.
10.18576/pfda/080111
Google Scholar
25 Kumar S., A New Analytical Modelling for Fractional Telegraph Equation via Laplace Transform, Applied Mathematical Modelling. (2014) 38, 3154–3163.
10.1016/j.apm.2013.11.035
Google Scholar
26 Kazem S., Exact Solution of Some Linear Fractional Differential Equations by Laplace Transform, International Journal of Nonlinear Science. (2013) 16, 3–11.
Google Scholar
27 Aboodh K. S., Application of New Transform “Aboodh Transform” to Partial Differential Equations, Global Journal of Pure and Applied Mathematics. Number. (2014) 2, 249–254.
Google Scholar
28 Aboodh K. S., The New Integral Transform Aboodh Transform, Global Journal of Pure and Applied Mathematics. Number. (2013) 1, 35–43.
Google Scholar
29 Al-aati A. and Al-sharai W. M., Application of Double Aboodh-Shehu Decomposition Method to Solve Linear and Nonlinear System of Partial Differential Equations, Turkish Journal of Mathematics and Computer Science. (2024) 16, no. 1, 217–228.
10.47000/tjmcs.1372574
Google Scholar
30 Anaç H., Merdan M., Bekiryazıcı Z., and Kesemen T., Bazı Rastgele Kısmi Diferansiyel Denklemlerin Diferansiyel Dönüşüm Metodu Ve Laplace-Padé Metodu Kullanarak Çözümü. Gümüşhane Üniv. Bilim, Enstitüsü Derg. (2019) 9, no. 1, 108–118, https://doi.org/10.17714/gumusfenbil.404332.
10.17714/gumusfenbil.404332
Google Scholar
31 Ayaz F., Solutions of the System of Differential Equations by Differential Transform Method, Applied Mathematics and Computation. (2004) 147, no. 2, 547–567.
10.1016/S0096-3003(02)00794-4
Web of Science® Google Scholar
32 Kangalgil F. and Ayaz F., Solitary Wave Solutions for the KdV and MkdV Equations by Differential Transform Method, Chaos, Solitons & Fractals. (2009) 41, no. 1, 464–472.
10.1016/j.chaos.2008.02.009
Google Scholar
33 Merdan M., A New Application of Modified Differential Transformation Method for Modeling the Pollution of A System of Lakes, Selcuk Journal of Applied Mathematics. (2010) 11, no. 2, 27–40.
Google Scholar
34 Merdan M., Numerical Solution of the Fractional-Order Vallis Systems Using Multi-Step Differential Transformation Method, Applied Mathematical Modelling. (2013) 6025–6036, https://doi.org/10.1016/j.apm.2012.11.007, 2-s2.0-84874565219.
10.1016/j.apm.2012.11.007
Google Scholar
35 Merdan M. and Merdan K., On the Fractional-Order Distributed of a Self-Developing Market Economy via Multi-Step Differential Transformation Method, IJRRAS. (2012) 13, no. 1, 110–125.
Google Scholar
36 Wazwaz A.-M., A Reliable Modification of Adomian Decomposition Method, Applied Mathematics and Computation. (1999) 77-86.
Google Scholar
37 Adomian G., A Review of the Decomposition Method in Applied Mathematics, Journal of Mathematical Analysis and Applications, 135, 501–544, https://doi.org/10.1016/0022-247X(88)90170-9, 2-s2.0-0041185368.
10.1016/0022-247X(88)90170-9
Google Scholar
38 Bellman R. E. and Adomian G., Partial Differential Equations: New Methods for Their Treatment and Solution, 1985, D.Reidel.
10.1007/978-94-009-5209-6
Google Scholar
39 Ganie A. H., Mofarreh F., and Khan A., A Fractional Analysis of Zakharov–Kuznetsov Equations With the Liouville–Caputo Operator, Axioms. (2023) 12.
10.3390/axioms12060609
PubMed Google Scholar
40 Yépez-Martínez H. and Gómez-Aguilar J. F., A New Modified Definition of Caputo–Fabrizio Fractional-Order Derivative and Their Applications to the Multi Step Homotopy Analysis Method (MHAM), Journal of Computational and Applied Mathematics. (2019) 346, 247–260.
10.1016/j.cam.2018.07.023
Google Scholar
41 Raghavendrana P., Gunasekara T., Balasundaram H., Santrac S. S., Majumderc D., and Baleanu D., Solving Fractional Integro-Differential Equations by Aboodh Transform, Journal of Mathematics and Computer Science. (2024) 32, 229–240.
Google Scholar
42 AlBaidani M. M., Aljuaydi F., Alharthi N. S., Khan A., and Ganie A. H., Study of Fractional Forced KdV Equation With Caputo–Fabrizio and Atangana–Baleanu–Caputo Differential Operators, AIP Advances. (2024) 14.
10.1063/5.0185670
Google Scholar
43 Awadalla M., Ganie A. H., Fathima D., Khan A., and Alahmadi J., A Mathematical Fractional Model of Waves on Shallow Water Surfaces: The Korteweg-De Vries Equation, AIMS Mathematics. (2024) 9, no. 5, 10561–10579.
10.3934/math.2024516
Google Scholar
44 Ganie A. H., Zidan A. M., Shah R., Akgül A., and Hassani M. K., Analysis of Some Dynamical Systems by Combination of Two Different Methods, Scientific Reports. (2024) 14.
Google Scholar
45 Ganie A. H., Mallik S., AlBaidani M. M., Khan A., and Shah M. A., Novel Analysis of Nonlinear Seventh Order Kaup-Kupershmidt Equation via the Caputo Operator, Research Squar. (2024) https://doi.org/10.21203/rs.3.rs-3919656/v1.
10.21203/rs.3.rs-3919656/v1
Google Scholar
46 Yasmin H., Alderremy A. A., Shah R., Ganie A. H., and Aly S., Iterative Solution of the Fractional Wu-Zhang Equation under Caputo Derivative Operator, Frontiers in Physics. (2024) 12.
10.3389/fphy.2024.1333990
PubMed Google Scholar
47 Ganie A. H., Mofarreh F., and Khan A., A Novel Analysis of the Time-Fractional Nonlinear Dispersive K(m,n,1) Equations Using the Homotopy Perturbation Transform Method and Yang Transform Decomposition Method, AIMS Mathematics. (2024) 9, no. 1, 1877–1898.
10.3934/math.2024092
Google Scholar
48 Jawarneh Y., Yasmin H., Ganie A. H., Al-Sawalha M. M., and Ali A., Unification of Adomian Decomposition Method and ZZ Transformation for Exploring the Dynamics of Fractional Kersten-Krasil’shchik Coupled KdV-mKdV Systems, AIMS Mathematics. (2024) 9, no. 1, 371–390.
10.3934/math.2024021
Google Scholar
49 Khan H., Gomez-Aguılar J. F., Abdeljawad T., and Khan A., Existence Results and Stability Crıterıa for ABC-Fuzzy-Volterra Integro-Differential Equation, Fractals. (2020) 28, no. 8 2040048.
10.1142/S0218348X20400484
Google Scholar
50 Khan A., Abdeljawad T., and Alqudah M. A., Neural Networking Study of Worms in a Wireless Sensor Model in the Sense of Fractal Fractional, AIMS Mathematics. (2023) 8, no. 11, 26406–26424.
10.3934/math.20231348
Google Scholar
51 Khan A., Abdeljawad T., and Khan H., A Numerical Scheme for the Generalized ABC Fractional Derivative Based on Lagrange Interpolation Polynomial, Fractals. (2022) 30, no. 5.
10.1142/S0218348X22401806
Google Scholar
52 Khan A. and Abdeljawad T., On Existence Results of Coupled Pantograph Discrete Fractional Order Difference Equations with Numerical Application, Results in Control and Optimization. (2023) 13.
10.1016/j.rico.2023.100307
Google Scholar
53 Khan A., Khan H., Gómez-Aguilar J. F., and Abdeljawad T., Existence and Hyers-Ulam Stability for a Nonlinear Singular Fractional Differential Equations With Mittag-Leffler Kernel, Chaos, Solitons & Fractals. (2019) 127, 422–427.
10.1016/j.chaos.2019.07.026
Google Scholar
54 Khan A., Shah K., Abdeljawad T., and Amacha I., Fractal Fractional Model for Tuberculosis: Existence and Numerical Solutions, Scientific Reports. (2024) 14.
Google Scholar
55 Caputo M. and Fabrizio M., A New Definition of Fractional Derivative without Singular Kernel, Progress in Fractional Differentiation and Applications.(2015) 73-85.
Google Scholar
56 Losada J. and Nieto J., Properties of a New Fractional Derivative Without Singular Kernel, Progress in Fractional Differentiation and Applications. (2015) 87-92.
Google Scholar
57 Samko S. G., Kilbas A. A., and Marichev O. I., Fractional Integrals and Derivatives: Theory and Applications, 1993, Gordon and Breach Science Publishers.
Google Scholar
58 Bhangale N., Kachhia B., and Gómez-Aguilar J. F., A New Iterative Method with ρ Laplace Transform for Solving Fractional Differential Equations with Caputo Generalized Fractional Derivative, Engineering with Computers. (2022) 2125–2138.
10.1007/s00366-020-01202-9
Google Scholar
59 Caputo M. and Fabrizio M., Applications of New Time and Spatial Fractional Derivatives With Exponential Kernels, Progress in Fractional Differentiation and Applications. (2016) 2, 1–11.
10.18576/pfda/020101
Google Scholar
60 Mboro Nchama G. A., Properties of Caputo-Fabrizio Fractional Operators, New Trends in Mathematical Sciences. (2020) 1, no. 8, 001–025.
10.20852/ntmsci.2020.393
Google Scholar
61 Benattia M. E. and Belghaba K., Application of the Aboodh Transform for Solving Fractional Delay Differential Equations, Universal Journal of Mathematics and Applications. (2020) 3, no. 3, 93–101.
10.32323/ujma.702033
Google Scholar
62 Ziane D., Belgacem R., and Bokhari A., A New Modified Adomian Decomposition Method for Nonlinear Partial Differential Equations, Open Journal of Mathematical Analysis.(2019) 3, no. 2, 81–90.
10.30538/psrp-oma2019.0041
Google Scholar
63 Veeresha P., Prakasha D. G., and Baskonus H. M., Solving Smoking Epidemic Model of Fractional Order Using a Modified Homotopy Analysis Transform Method, The Mathematical Scientist. (2019) 13, no. 2, 115–128.
10.1007/s40096-019-0284-6
Google Scholar
64 Kumar D., Singh J., and Baleanu D., A New Analysis for Fractional Model of Regularized Long-Wave Equation Arising in Ionacoustic Plasma Waves, Mathematical Methods in the Applied Sciences. (2017) 40, no. 15, 5642–5653.
10.1002/mma.4414
Google Scholar
65 Magreñán Á.A., A New Tool to Study Real Dynamics: the Convergence Plane, Applied Mathematics and Computation. (2014) 248, 215–224.
10.1016/j.amc.2014.09.061
Google Scholar
66 Şahin Y., Merdan M., and Açıkgöz P., The Novel Numerical Solutions for Caputo-Fabrizio Fractional Newell–Whitehead–Segel Equation by Using Aboodh-ADM, Research Square. (2024) https://doi.org/10.21203/rs.3.rs-4287125/v1.
10.21203/rs.3.rs-4287125/v1
Google Scholar
67 Yadav S. K., Purohit M., Gour M. M., Yadav L. K., and Mishra M. N., Hybrid Technique for Multi-Dimensional Fractional Diffusion Problems Involving Caputo-Fabrizio Derivative, International Journal of Mathematics for Industry, https://doi.org/10.1142/S2661335224500205.
10.1142/S2661335224500205
Google Scholar
68 Bildik N., General Convergence Analysis for the Perturbation Iteration Technique, Turkish Journal of Mathematics and Computer Science. (2017) 6, 1–9.
Google Scholar
69 Odibat Z. M., A Study on the Convergence of Variational Iteration Method, Mathematical and Computer Modelling. (2010) 51, 1181–1192.
10.1016/j.mcm.2009.12.034
Google Scholar

All articles

New Numerical Solutions for Caputo–Fabrizio Fractional Differential Multidimensional Diffusion Problems

Abstract

1. Introduction

2. Preliminaries

3. Methods and Materials

3.1. Analysis of Convergence

4. Applications of ATDM

5. Results and Discussions

6. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

New Numerical Solutions for Caputo–Fabrizio Fractional Differential Multidimensional Diffusion Problems

Abstract

1. Introduction

2. Preliminaries

3. Methods and Materials

3.1. Analysis of Convergence

4. Applications of ATDM

5. Results and Discussions

6. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information