International Journal of Differential Equations

Volume 2025, Issue 1 8813408

Research Article

Open Access

A Comparative Study of Linearization Techniques With Adaptive Block Hybrid Method for Solving First-Order Initial Value Problems

Salma Ahmedai,

Corresponding Author

Salma Ahmedai

[email protected]

orcid.org/0000-0001-7250-7714

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Pietermaritzburg , South Africa , ukzn.ac.za

Department of Modeling and Computing for Mathematics , Al Neelain University , Khartoum , Sudan , neelain.edu.sd

Search for more papers by this author

Precious Sibanda,

Precious Sibanda

orcid.org/0000-0003-2115-4642

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Pietermaritzburg , South Africa , ukzn.ac.za

Search for more papers by this author

Sicelo Goqo,

Sicelo Goqo

orcid.org/0000-0003-1383-068X

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Pietermaritzburg , South Africa , ukzn.ac.za

Search for more papers by this author

Osman Noreldin,

Osman Noreldin

orcid.org/0000-0002-8736-0601

Department of Mathematical Sciences , University of Zululand , Zululand , South Africa , unizulu.ac.za

Search for more papers by this author

Salma Ahmedai,

Corresponding Author

Salma Ahmedai

[email protected]

orcid.org/0000-0001-7250-7714

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Pietermaritzburg , South Africa , ukzn.ac.za

Department of Modeling and Computing for Mathematics , Al Neelain University , Khartoum , Sudan , neelain.edu.sd

Search for more papers by this author

Precious Sibanda,

Precious Sibanda

orcid.org/0000-0003-2115-4642

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Pietermaritzburg , South Africa , ukzn.ac.za

Search for more papers by this author

Sicelo Goqo,

Sicelo Goqo

orcid.org/0000-0003-1383-068X

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Pietermaritzburg , South Africa , ukzn.ac.za

Search for more papers by this author

Osman Noreldin,

Osman Noreldin

orcid.org/0000-0002-8736-0601

Department of Mathematical Sciences , University of Zululand , Zululand , South Africa , unizulu.ac.za

Search for more papers by this author

First published: 01 July 2025

https://doi.org/10.1155/ijde/8813408

Academic Editor: Jaume Giné

Share a link

Email
Wechat
Bluesky

Abstract

This paper investigates linearization methods used in the development of an adaptive block hybrid method for solving first-order initial value problems. The study focuses on Picard, linear partition, simple iteration, and quasi-linearization methods, emphasizing their role in enhancing the performance of the adaptive block hybrid method. The efficiency and accuracy of these techniques are evaluated through solving nonlinear differential equations. The study provides a comparative analysis focusing on convergence properties, computational cost, and the ease of implementation. Nonlinear differential equations are solved using the adaptive block hybrid method, and for each linearization method, we determine the absolute error, maximum absolute error, and number of iterations per block for different initial step-sizes and tolerance values. The findings indicate that the four techniques demonstrated absolute errors, ranging from O(10⁻¹²) to O(10⁻²⁰). We noted that both the Picard and quasi-linearization methods consistently achieve the highest accuracy in minimizing absolute errors and enhancing computational efficiency. Additionally, the quasi-linearization method required the fewest number of iterations per block to achieve its accuracy. Furthermore, the simple iteration method required fewer number of iterations than the linear partition method. Comparing minimal CPU time, the Picard method required the least. These results address a critical gap in optimizing linearization techniques for the adaptive block hybrid method, offering valuable insights that enhance the precision and efficiency of methods for solving nonlinear differential equations.

1. Introduction

Nonlinear differential equations arise in various fields of science and engineering, and obtaining accurate solutions to these problems remain a challenging task to researchers. Numerical methods are essential for solving nonlinear differential equations that lack analytical solutions [1]. Many numerical methods allow for iterative refinement and visualization of solutions, making them valuable for practical applications in science and engineering [2].

Block hybrid methods (BHMs) have emerged as promising numerical methods, combining the strengths of multistep and one-step methods to provide efficient and stable numerical schemes [3]. It is widely recognized that BHMs are capable of efficiently solving initial value problems (IVPs) and boundary value problems (BVPs) [4, 5]. The theoretical properties of the BHM, such as convergence order, zero-stability, and consistency, to ensure their convergence have been investigated [6]. Many researchers are focusing on improving BHM to enhance the efficiency and convergence when solving differential equations [7, 8]. The goal is to develop more accurate and robust BHMs that can handle a wider range of problems, including nonlinear IVPs. For example, some of the key areas being explored include deriving new k-step hybrid block methods with higher orders of accuracy and better stability properties [9]. Other innovations include incorporating off-grid points within the block to improve the approximation solutions [10] and employing different basis functions, such as Hermite polynomials, to construct the continuous linear multistep methods that form the foundation of the BHM [11]. Focusing on these aspects, researchers aim to develop BHMs that are not only more accurate but are also computationally efficient and reliable for solving differential equations.

One technique used to improve the BHM is to utilize variable step-sizes instead of a fixed step-size scheme [12]. This adaptive technique offers several advantages, such as improving the accuracy of the solution by adjusting the step-size to achieve the desired level of precision without wasting computational time or introducing unnecessary errors [13]. Adaptive techniques can enhance the efficiency of the method by avoiding unnecessary evaluations of the function or its derivatives, and thereby saving time and memory [14]. The variable step-size scheme can improve the stability of the method by using smaller step-sizes when needed to avoid numerical instability or divergence that may occur with a fixed step-size approach [15]. There are several existing methods for introducing adaptivity in numerical methods [16]. One such technique is the use of embedded methods that use two approximations of different orders at each step, and the difference is taken as an estimate of the local error [17, 18]. Examples of these include the Runge–Kutta–Fehlberg method, the Dormand–Prince method, and the Cash–Karp method [19–21].

Several researchers have investigated different strategies for implementing the adaptive block hybrid method (ABHM) for solving nonlinear differential equations [22]. Some ABHMs employ two different approximations, each of a different order of accuracy, at each step [23]. The difference between these two approximations is then used as a local error estimate at that step. This error estimates the key that allows the method to adaptively adjust the step-size to maintain a desired accuracy in the computation [24]. Singh et al. [23] presented an efficient optimized adaptive hybrid block method for IVPs. The authors utilized three off-step points within the one-step block. Two of the off-step points were optimized to minimize the local truncation errors (LTEs) of the main method. The adaptive method was tested on several well-known systems and it compared favorably with other numerical methods in the literature. Rufai et al. [25] proposed an adaptive hybrid block method for solving first-order IVPs of ordinary differential equations and partial differential equation problems. The method was formulated in a variable step-size and implemented with an adaptive step-size strategy to maintain the error within a specified tolerance. It was demonstrated that the method was more efficient than some other existing numerical methods used in solving the differential equations in the study.

A key aspect of enhancing the accuracy of a numerical approximation is the choice of the linearization technique [26]. Linearization is necessary to transform the nonlinear problem into a form that can be easily solved [27]. Linearization methods are therefore important for the purpose of transforming nonlinear differential equations into linear equations that are easier to solve using numerical techniques [28]. The choice of the linearization method can impact the stability of the numerical scheme, its accuracy, and computational efficiency [29]. Some well-known linearization techniques include the Taylor series linearization which involves expanding the nonlinear function in a Taylor series around a point of interest and truncating higher-order terms. This is straightforward but may require small step-sizes for accuracy [30]. Newton’s method uses an iterative technique where the nonlinear equation is approximated by a linear one at each iteration step [31]. It is highly accurate but can be computationally intensive [32].

ABHMs have gained prominence due to their flexibility in adjusting step-sizes and ability to handle stiff equations. However, the performance of numerical methods is significantly influenced by the linearization techniques used [33]. Despite extensive work on linearization techniques, there remains a need for a comprehensive survey that evaluates these methods in the context of ABHMs for first-order IVPs. This paper aims to fill this gap by presenting an evaluation of linearization methods when used with the ABHM, assessing their strengths and weaknesses. We outline the following questions.

•
What are the existing linearization methods used with ABHM, and what are their strengths and weaknesses?
•
How can linearization techniques be implemented with the ABHM, and how does the performance compare with other numerical methods?

The Picard method (PM) is based on the Picard–Lindelöf theorem, which ensures the existence and uniqueness of solutions for IVPs [34–36]. The PM starts with an initial guess which is then refined iteratively by integrating the nonlinear function over the interval of interest [37, 38]. The PM is a straightforward method that may however not always converge as it relies on the assumption that the nonlinear function is locally Lipschitz continuous, which is not always the case [39]. The PM converges linearly, meaning that the error in the solution decreases at a constant rate [40]. This can lead to a slow convergence rate, especially for problems with complex nonlinearities. The PM was utilized with the BHM to solve second-order IVPs by Rufai et al. [9].

There are several local and piece-wise linearization schemes for IVPs, the use of which depend on the algorithm employed in the numerical implementation [41–44]. The piece-wise linearization approach is useful for handling nonlinearities locally, making the overall problem more tractable [45]. The linear partition method (LPM) linearization scheme is a modified piece-wise linearization approach that allows for flexibility in handling the nonlinearities [46]. The LPM is a direct scheme and is particularly useful for solving stiff differential equations. The LPM used to linearize first-order IVPs and combined with the BHM by Shateyi [5]. Similarly, the simple iteration method (SIM) technique is a piece-wise linearization approach that is easy to implement and is very effective for IVPs [47]. Ahmedai Abd Allah et al. [47] proposed a SIM and used it with the BHM to solve third-order IVPs. The SIM works similar to fixed-point iteration [48].

The quasi-linearization method (QLM) transforms the nonlinear equations into a sequence of linear problems [49]. This method is similar to Newton’s method for root-finding but applied to differential equations [50]. At each iteration, the method linearized the nonlinear terms around the current solution estimate, resulting in a linear differential equation that can be solved to update the solution. The QLM converges quadratically, making it very efficient for problems where a good initial guess is available [51]. It is particularly effective for strongly nonlinear problems where other linearization methods might not converge [52]. Motsa [53] implemented the BHM with the QLM to solve first-order IVPs.

2. Implementation of the BHM

We describe the derivation of the ABHM for solving the first-order IVPs of the following form:

()

where the prime denotes the derivative with respect to the independent variable t. We divide the interval [0, t_F] into N blocks with variable step-size h as

()

The intrastep points introduced as equally spaced grid points defined as

()

Here, m is the number of intrastep points and

()

Approximating the solution in each block I_r using Lagrange interpolating polynomials, we obtain

()

Similarly, we approximate the first derivative by

()

where a_r,k are m + 2 unknown coefficients. We collocate at the unknown nodes

and assume that the approximated solutions (5)–(6) satisfy equation (1). The coefficients a_r,k are obtained from a system of m + 2 equations with m + 2 unknowns generated from

()

where

, f_r = f(t_r, y_r), and y_r = y(t_r). Equations (6)–(7) can be written in matrix notation as

()

We solve equation (8) to obtain a_r,k. Substituting a_r,k into equation (5) and evaluating the result at collocation points (3), we obtain the approximate solution as

()

where α_i,j are known constants. Equation (10) can be written in the matrix form as

()

where A and B are matrices of size m × m, and Y_r, Y_r+p, F_r, and F_r+p are vectors of size m × 1.

3. Theoretical Analysis

In this section, we investigate the order, error constant, linear stability, order star, and zero stability analysis of the BHM.

3.1. LTE and Consistency

To determine the accuracy of the BHM, we evaluated the LTE. To analyze the LTE within each block, we introduced the linear operator

, which represents the difference between the exact solution and the numerical approximation. Using equation (10), the LTE is analyzed using the linear operator

defined as

()

We consider that y(t) is sufficiently differentiable. Expanding the terms y(t_r + hp_i) and y^′(t_r + hp_i) by using Taylor series about t_r to obtain

()

where C_i,0, C_i,1, …, C_i,q are constant. The method is said to be order q if

()

where

. The vector

is the error constant of the method [54]. In equation (12), applying Taylor series about t_r leads to

()

where K is a positive integer. Expanding equation (16) gives

()

Following [55], equation (17) may be written as

()

From equation (18), we deduced that the error constant vector is defined as

()

Also from equation (18), the leading term in the LTE is proportional to O(h^m+2). A method has order q if the LTE satisfies

()

Comparing equations (18) and (20) yields q = m + 1 as the order of the BHM. Following [56, 57], a block method is consistent if its order q ≥ 1. This condition is satisfied since m ≥ 2.

3.2. Zero Stability and Convergence

Zero stability ensures that the numerical solution remains bounded as the number of steps increases [58]. For the BHM, writing equation (10) in the matrix form and setting h⟶0, the system reduces to

()

Equation (21) gives the following characteristic equation:

()

The roots of the characteristic equation, called the characteristic roots, must satisfy all roots of ρ(λ) ≤ 1. Furthermore, any roots must have multiplicity one. This ensures that the method is zero stable, which is a prerequisite for convergence. Hence, the BHMs developed in this study are zero-stable. Since these methods exhibit both zero-stability and consistency, Dahlquist’s theorem implies that they are convergent [54].

3.3. Absolute Stability

We applied the method to the scalar linear test equation given in [59]. Following this procedure, we define

()

Substituting equation (23) into equation (10) yields

()

Equation (24) can be reduced to the matrix form as presented in [60]. Thus, we have

()

where

is the stability function, and I is the identity matrix of size m × m. Table 1 presents the stability functions for the BHM for different values, specifically m = 2, 3, 4, 5.

Table 1. Stability functions for the BHM with varying values of m and corresponding equally spaced grid points.

m	p_j	Stability function
2	0, (1/2), 1	(24 − z²)/(2(z² − 6z + 12))
3	0, (1/3), (2/3), 1	(−z³ + 3z² + 54z − 324)/(3(z³ − 11z² + 54z − 108))
4	0, (1/4), (1/2), (3/4), 1	(−3z⁴ + 20z³ + 240z² − 3840z + 15360)/(4(3z⁴ − 50z³ + 420z² − 1920z + 3840))
5	0, (1/5), (2/5), (3/5), (4/5), 1	(−12z⁵ + 130z⁴ + 1125z³ − 37500z² + 337500z − 1125000)/(5(12z⁵ − 274z⁴ + 3375z³ − 25500z² + 112500z − 225000))

Following [61, 62], we define the region of absolute stability R as

()

Figure 1 shows the absolute stability regions of the BHM for different values of (m = 2, 3, 4, 5). The shaded areas represent the set of complex values z = hλ where the stability condition is satisfied.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The absolute stability regions of the BHM for various values of m. (a) m = 2. (b) m = 3. (c) m = 4. (d) m = 5.

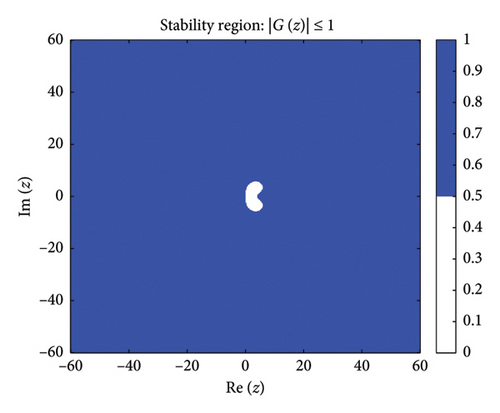
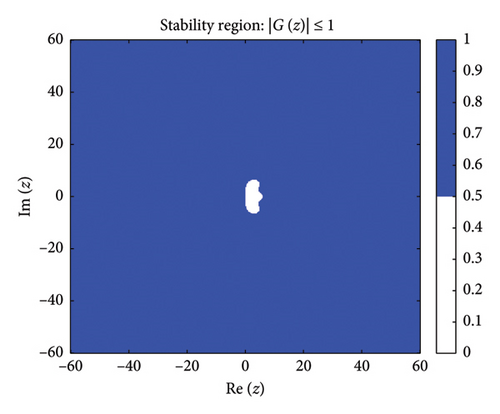
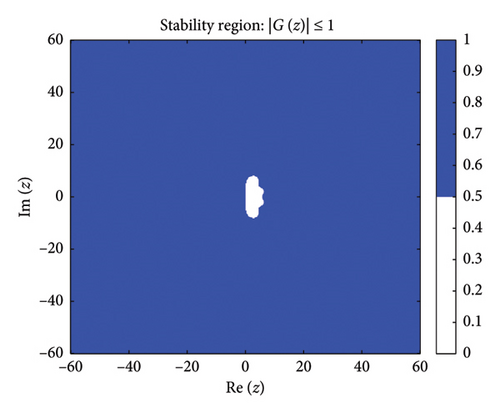
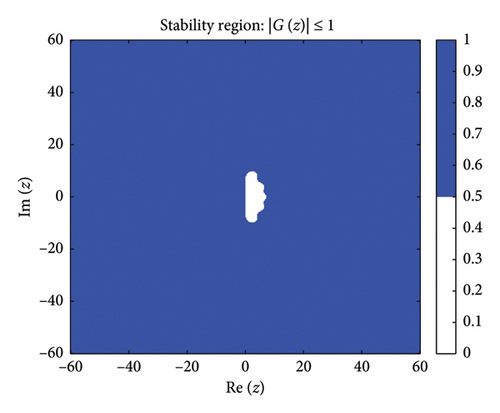
Definition: Following [63], a numerical method for solving ordinary differential equations is A-stable if its region of absolute stability contains the entire left half-plane of .

Figure 1 shows the absolute stability regions for m = 2, 3, 4, 5, confirming the A-stability of the BHM as the entire left-half complex plane is covered.

Definition: Following [64], a numerical method is L-stable if it satisfies both.

1.
Its region of absolute stability contains the entire left half-plane.
2.
Its stability function satisfies
()
From Table 1, we compute the asymptotic behavior of each stability function as z⟶∞, which yields
()
Since none of the stability functions satisfy , the BHM is not L-stable for any m ≥ 2, despite being A-stable (as shown in Figure 1).

3.4. Order Stars

Order star theory is a crucial tool for assessing the stability and accuracy of numerical methods for ordinary differential equations [65]. Order stars provide a means to evaluate the stability of numerical methods in relative terms [66]. Given a numerical method with stability function

, where

and

are polynomials. To analyze the stability properties, order stars partition the complex plane into three distinct regions based on comparing the stability function

of a method with the exact solution

as in [67]. We considered the first type of the order stars, which defined the three regions as

()

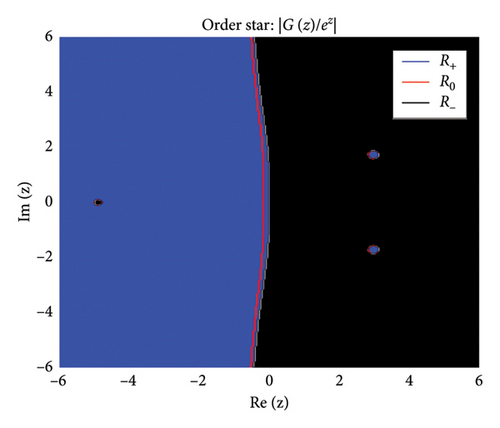
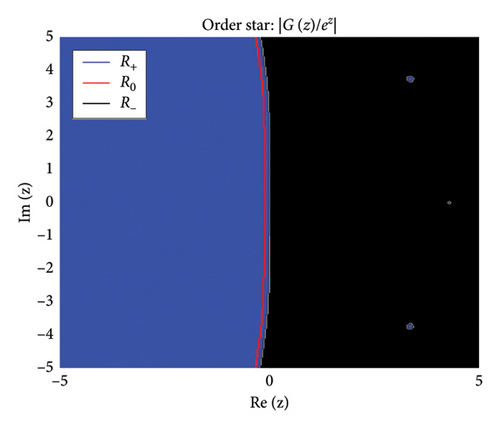
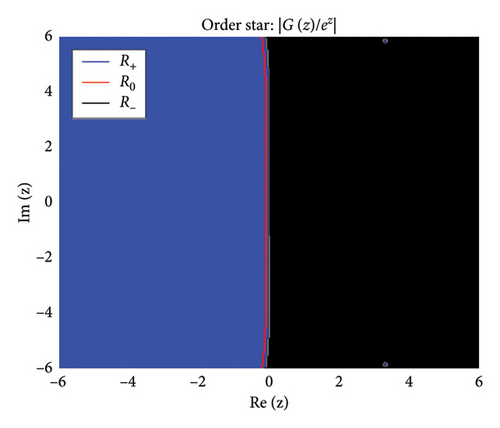
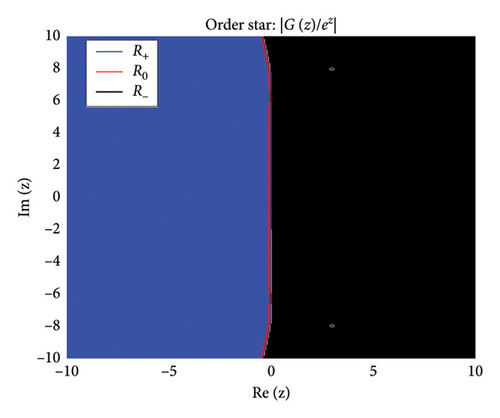
The zeros of (roots of ) appear as points where stable regions contract, indicating strong damping properties, while poles (roots of ) act as sources of instability where unstable regions diverge. Figures 2 and 3 show the structure of the three regions, zeros, and poles of the BHM, respectively.

Definition: Following [68], a numerical method is said to be A-acceptable if its stability function

satisfies the following conditions:

•
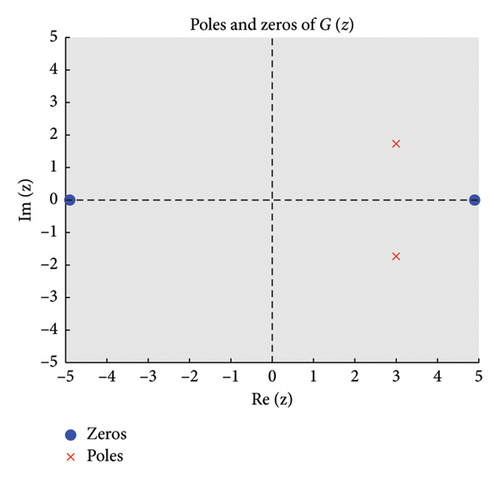
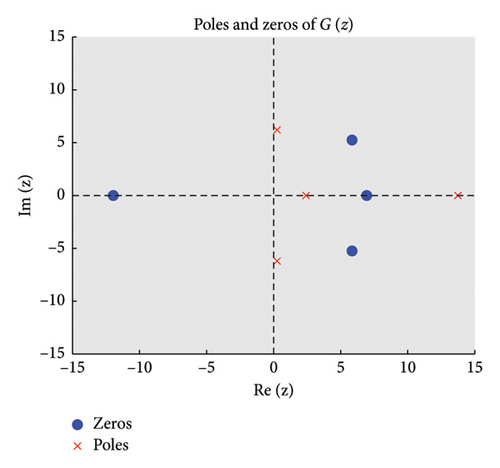
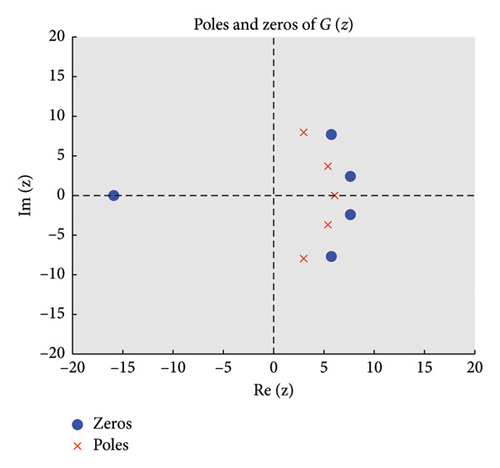
The growth region R₊ does not intersect the imaginary axis.
•
There are no poles of in the left half of the complex plane, i.e., Re(z) < 0.

These conditions ensure that the numerical method exhibits stable behavior. Figure 2 shows the order stars stability region for the scheme. It is observed that the region contains the entire left half of the complex plane for all values of (m = 2, 3, 4, 5). It is also noted that R₊ does not intersect the imaginary axis, and no poles are found in the left of the complex plane (as shown in Figure 3). Thus, we conclude that the method is A-acceptable.

4. The Adaptive Scheme

An important factor to take into account is the derivation of the adaptive scheme, which is crucial for error estimation [69]. To achieve this, we calculate the error between two different versions of the BHM in equation (10) evaluated at specific points

. One version of the higher order method is associated with a LTE of order O(h^q+1), while the other is a lower order method with a LTE of order O(h^q). To demonstrate the integration of adaptivity into the BHM, we consider a method derived from the evaluated points. We use the equally spaced intrastep points when m = 5, as

()

We evaluate equation (10) at the collocation points in equation (30). The resulting equations can be written in the matrix form:

()

where the matrices A and B of size 5 × 5 are defined as

()

whereas the vectors Y_r+p, Y_r, F_r+p, and F_r of size (5 × 1) are

()

In this case, the LTE from equation (18) are given in Table 2.

Table 2. Truncation errors for the block hybrid method when m = 5.

p_j	p₁	p₂	p₃	p₄	p₅
Local truncation error	−(863y⁽⁷⁾(t_r)h⁷)/4725000000	−(37y⁽⁷⁾(t_r)h⁷)/295312500	−(29y⁽⁷⁾(t_r)h⁷)/175000000	−(8y⁽⁷⁾(t_r)h⁷)/73828125	−(11y⁽⁷⁾(t_r)h⁷)/37800000

An adaptive counterpart of the main method y_r+1 can be constructed utilizing the method of undetermined coefficients on an equation with identical grid points, except at p₅ = 1. This expression has a LTE in Table 3.

Table 3. Truncation errors for the block hybrid method when m = 5 excluding p₅.

p_j	p₁	p₂	p₃	p₄	p₅
Local truncation error	(3y⁽⁶⁾(t_r)h⁶)/2500000	(y⁽⁶⁾(t_r)h⁶)/1406250	(3y⁽⁶⁾(t_r)h⁶)/25000000	−(8y⁽⁷⁾(t_r)h⁷)/73828125	(19y⁽⁶⁾(t_r)h⁶)/900000

The adaptive pair is given as

()

where y_r+1 and

correspond to the higher order and lower order methods, respectively. The error estimation function, denoted as EST, is expressed as

()

The local error, subsequently utilized in ascertaining the optimal step-size for the ensuing step, is thus approximated as

()

For the step-size of the successive time step, we use the formula proposed by authors in [23].

()

where σ and Tol₁ are the safety factor and the first user-defined tolerance, respectively, with the condition σ ∈ (0, 1). Furthermore, we evaluate the subsequent conditional structure in the implementation of the ABHM as

•
If ‖EST‖ < Tol₁, we accept the procured values and increase the step-size by h_new = 2h_old, to forward the integration process.
•
If ‖EST‖ ≥ Tol₁, we recalibrate the current step-size employing the criterion in equation (38) and recalculate.

By the above methodology, we ensure a reliable error estimation and optimize the step-size for each integration block in the ABHM.

4.1. Error Estimation

To assess the convergence of the method, we evaluated the absolute error (AE) and absolute error estimate (AEE) between two consecutive iterations. Suppose Y(t) is the approximate solution. The AE is defined as

()

We compute the AEE between two consecutive iterations using the following:

()

This provides a measure of how much the solution changes between iterations, indicating the convergence behavior of the method.

We evaluate in Algorithm 1 the following conditional stopping procedure in the ABHM where Tol₂ represents the second user-defined tolerance. Within each block, the method iterates until the error AEE falls below Tol₂. Once the AEE converges to within an acceptable criteria, the procedure advances to the next block or concludes the computation. By applying this conditional structure, we ensure that the accuracy of our solutions is systematically improved within each block, thereby enhancing control and precision in the numerical computations. The pseudo-code loops through the steps until convergence or the maximum number of iterations is reached.

Algorithm 1: ABHM algorithm pseudo-code.

Step 1: Input IVP f(t, y), tolerance levels Tol₁, Tol₂, initial step-size h₀, safety factor σ, and max iterations.
Step 2: Initialize Y_r+p, F_r+p, Y_r, F_r.
Step 3: While not converged (AEE < Tol₂) or max iterations not reached, do Steps 4–11:
Step 4: Compute using the ABHM equation.
Step 5: Compute y_r+1 and using adaptive pair equations.
Step 6: Compute the error estimate EST,
if‖EST‖ < Tol₁then
(a) Accept the current .
(b) Set h_new = 2 × h_old.
else
(c) Set .
end if
Step 10: Update Y_r+p and F_r+p with h_new.
Step 11: Update h_old to h_new.
Step 12: Return Y_r+p.

5. Linearization Techniques

In this section, we discuss various linearization approaches, namely, PM, LPM, SIM, and QLM, that must be applied to linearized equation (1) before using ABHM equation (10). ABHM equation (10) is a powerful numerical approach for solving differential equations, offering accuracy and efficiency by adapting to the problem’s behavior. However, the nonlinear nature of many IVPs necessitates an initial linearization step to facilitate the application of the ABHM. These techniques transform nonlinear IVPs into linear equations, which are easier to solve. Consider that f is a nonlinear function and F is the linearized form of f. The linear and nonlinear terms are evaluated as known and unknown terms at iteration s and s + 1, respectively.

5.1. PM

Applying the PM scheme to equation (1), the linearization of f is presented as follows:

()

where

. Substituting equation (41) into equation (10) gives

()

Equation (42) may be written in the matrix notation as

()

Equation (43) represents the Picard adaptive block hybrid method (PM-ABHM) equations.

5.2. LPM

For the LPM scheme, we define

()

where

and

are the linear and nonlinear terms, respectively. Substituting equation (44) into equation (10) yields

()

where

and

. Equation (45) can be written as

()

Equation (46) has the matrix form

()

where L_r+p is a matrix of size m × m, and N_r+p is a vector of size m × 1. The approximate solutions are found using the linear partition adaptive block hybrid method (LPM-ABHM)

()

where inv denotes the inverse of the matrix, and

is a nonsingular matrix.

5.3. SIM

In the SIM implementation, we consider the nonlinear term

as a combination of known (at iteration s) and unknown (at iteration s + 1) of y at a particular iteration as

()

where

. Thus, by substituting equation (49) into generalized BHM equation (10), and solving for

, we have

()

where

, and

. The simple iteration adaptive block hybrid method (SIM-ABHM) can be written in the matrix form

()

where the matrix

is of size m × m, and the vector

is of size m × 1. Then, the approximate solutions are

()

where

is a nonsingular matrix.

5.4. QLM

In QLM, we define the nonlinear function F(y, y^′) as

()

Expanding equation (53) using Taylor series approximation around

and

, we obtain

()

Assuming that the difference between the current and previous iteration

and

are small and the terms with higher order

are negligible gives

()

Upon the application of QLM to equation (1), we derive the linearized form

()

where

and

. With this approximation, equation (10) becomes

()

where

, and

The quasi-linearization adaptive block hybrid method (QLM-ABHM) equations in the matrix notation are given by

()

The matrix Φ_r+p is of size m × m, and the vector Ψ_r+p is of size m × 1. The approximate solutions are found by solving the equation

()

where

is a nonsingular matrix.

6. Numerical Results and Discussion

In this section, we present and analyze the numerical results obtained by implementing the ABHM on various first-order IVPs with particular focus on demonstrating the effectiveness and accuracy of the adaptive BHM, particularly when utilizing several linearization schemes in the case m = 5 and σ = 0.9. All computational experiments have been performed using MATLAB R2021b.

6.1. Example 1

Consider the Riccati equation

()

where the exact solution is given by

()

We define the function f = −y² + 2y + 1. The ABHM is implemented using four linearization techniques

•
PM: .
•
LPM: .
•
SIM: .
•
QLM: .

Figure 4 shows the numerical and exact solutions for equation (60). It can be observed that the approximate and exact solutions coincide.

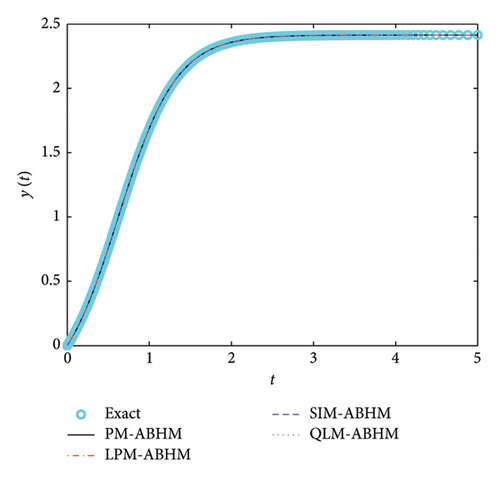
Figure 5 shows the AE for different linearization techniques with varying initial step-sizes and the first user-defined tolerance. As shown in Figure 5(a), the PM-ABHM, LPM-ABHM, SIM-ABHM, and QLM-ABHM achieve an AE ranging from O(10⁻¹³) to O(10⁻¹⁷) for h₀ = 10⁻¹ and Tol₁ = 10⁻⁸. Figure 5(b) presents the AE for these methods with h₀ = 10⁻² and Tol₁ = 10⁻¹⁰, where all methods maintain an AE between O(10⁻¹³) and O(10⁻¹⁹).

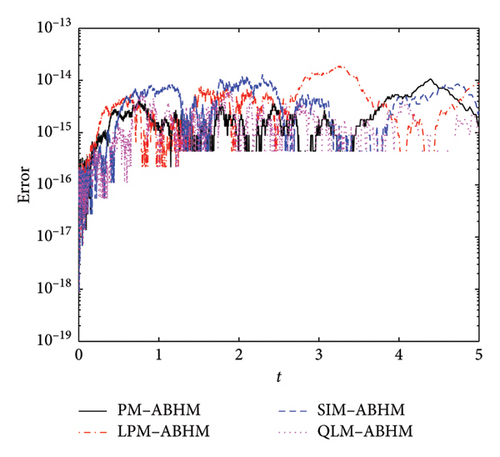
Table 4 compares the maximum AE for different linearization schemes of the ABHM at Tol₂ = 10⁻¹³ with varying h₀ and Tol₁. From Table 4, it is evident that the PM-ABHM, SIM-ABHM, and QLM-ABHM achieve a maximum AE of order O(10⁻¹⁵), while the LPM-ABHM records a maximum AE of order O(10⁻¹⁴) for h₀ = 10⁻¹ and Tol₁ = 10⁻⁸. For h₀ = 10⁻² and Tol₁ = 10⁻¹⁰, QLM-ABHM maintains a maximum AE of order O(10⁻¹⁵), while the PM-ABHM, LPM-ABHM, and SIM-ABHM achieve a maximum AE of order O(10⁻¹⁴). The results show that QLM-ABHM outperforms the other methods, with LPM-ABHM having the highest maximum AE. Table 4 reveals that PM-ABHM is the fastest for both h₀ = 10⁻¹ and h₀ = 10⁻².

Table 4. Comparison of maximum absolute errors for different linearization schemes of the ABHM at Tol₂ = 10⁻¹³ for various initial step-sizes and first user-defined tolerances for Example 1.

t_F	h₀	Tol₂	PM-ABHM	LPM-ABHM	SIM-ABHM	QLM-ABHM
5	10⁻¹	10⁻⁸	6.2172 × 10⁻¹⁵	1.5543 × 10⁻¹⁴	6.6613 × 10⁻¹⁵	5.3291 × 10⁻¹⁵
CPU time in seconds			0.012192	0.082196	0.088391	0.052143

5	10⁻²	10⁻¹⁰	1.0658 × 10⁻¹⁴	1.8652 × 10⁻¹⁴	1.2879 × 10⁻¹⁴	6.6613 × 10⁻¹⁵
CPU time in seconds			0.061403	0.255753	0.263201	0.189779

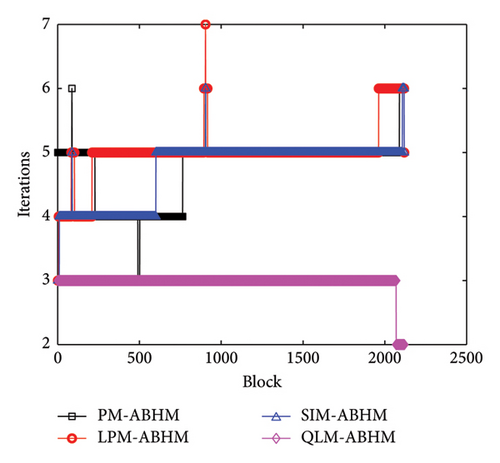
Figure 6 shows the number of iterations per block for different linearization schemes with varying initial step-sizes and the first user-defined tolerance. Figure 6(a) illustrates the performance of the PM, LPM, SIM, and QLM schemes for h₀ = 10⁻¹ and Tol₁ = 10⁻⁸. We observe that the maximum number of iterations required is 10 for LPM-ABHM, while the PM-ABHM and SIM-ABHM schemes require a maximum of eight iterations, and QLM-ABHM requires between three to four iterations. As shown in Figure 6(b), for smaller initial step-sizes and the first user-defined tolerance, the number of iterations per block is reduced to seven for LPM-ABHM. However, the PM-ABHM and SIM-ABHM schemes decrease to six iterations, while QLM-ABHM decreases to between two to three iterations. This indicates that smaller initial step-sizes and the first user-defined tolerance decrease the number of iterations per block, leading to rapid convergence of the ABHM.

6.2. Example 2

Consider a special case of the Riccati equation [5]

()

The exact solution for this case is given by

()

We define f = (1/t²)y² + (1/t)y + 1, and its linearized forms are expressed as follows:

•
PM: .
•
LPM: .
•
SIM: .
•
QLM: .

Figure 7 depicts the numerical and exact solution using PM-ABHM, LPM-ABHM, SIM-ABHM, and QLM-ABHM, respectively. We note that the numerical solutions match the exact solution.

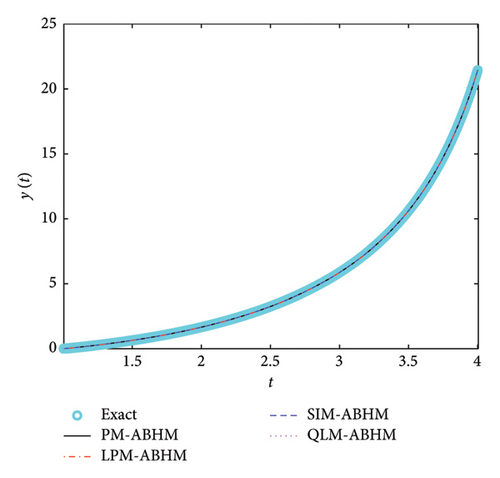
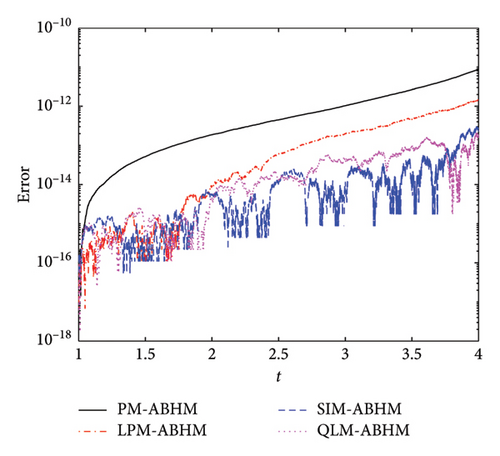
Figure 8 and Table 5 present a comparison of the AE and the maximum AE achieved using the PM-ABHM, LPM-ABHM, SIM-ABHM, and QLM-ABHM, respectively, for different initial step-sizes and second user-defined tolerances. Figure 8(a) shows that for h₀ = 10⁻¹ and Tol₂ = 10⁻¹², all methods achieve an AE between O(10⁻¹¹) and O(10⁻¹⁷). Similarly, Figure 8(b) shows that for h₀ = 10⁻³ and Tol₂ = 10⁻¹⁴, the AE ranges from O(10⁻¹²) to O(10⁻¹⁷). These results indicate that smaller initial step-sizes and second user-defined tolerances lead to higher precision.

Table 5. Comparison of the maximum absolute error for the ABHM with Tol₁ = 10⁻¹³ using the Picard, linear partition, simple iteration, and quasi-linearization methods for Example 2.

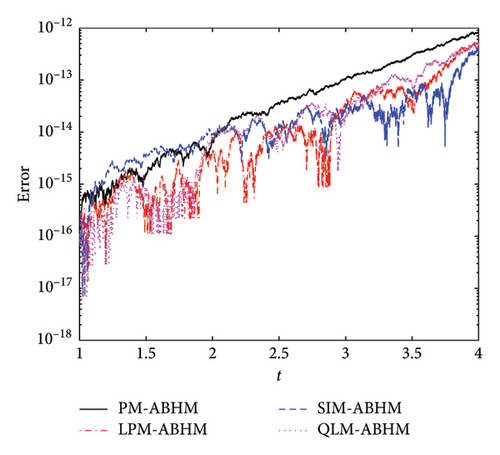
t_F	h₀	Tol₂	PM-ABHM	LPM-ABHM	SIM-ABHM	QLM-ABHM
4	10⁻¹	10⁻¹²	8.8143 × 10⁻¹²	1.4779 × 10⁻¹²	3.0198 × 10⁻¹³	2.1672 × 10⁻¹³
CPU time in seconds			0.079389	0.408207	0.362927	0.309272

4	10⁻³	10⁻¹⁴	8.5620 × 10⁻¹³	5.0449 × 10⁻¹³	4.2633 × 10⁻¹³	5.4001 × 10⁻¹³
CPU time in seconds			0.121848	0.467590	0.447170	0.297296

From Table 5, it is evident that the maximum AE improves with smaller h₀ and Tol₂ for all methods, although the improvement is marginal. Regarding CPU time, the PM-ABHM and QLM-ABHM are faster compared to the LPM-ABHM and SIM-ABHM.

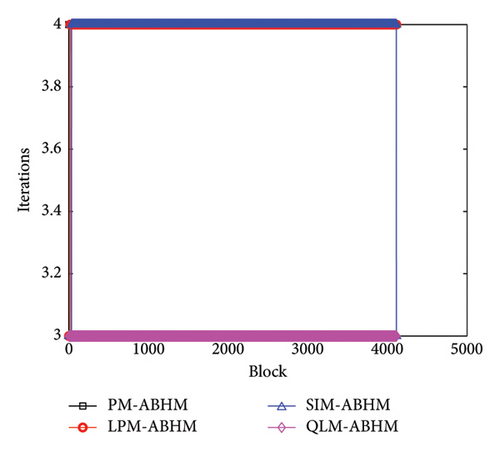
Figure 9 compares the number of iterations per block required for all methods with varying h₀ and Tol₂. Figure 9(a) shows the performance of the PM, LPM, SIM, and QLM for h₀ = 10⁻¹ and Tol₂ = 10⁻¹². We observe that the maximum number of iterations required is four for PM-ABHM, while LPM-ABHM and SIM-ABHM require between three and four iterations, and the QLM-ABHM scheme requires three iterations. As shown in Figure 9(b), when h₀ = 10⁻³ and Tol₂ = 10⁻¹⁴, the number of iterations increases by one for all methods.

6.3. Example 3

We examine the logistic differential equation presented in [70].

()

where ω_e is representing the growth rate, ω_f is a factor that modulates the effect of the carrying capacity, and y₀ is the initial population size. The exact solution is given by

()

By applying the ABHM with α = 0.98, ω_e = 2, and ω_f = 1, we define f = ω_e y − ω_f y ln(y). The linearized forms of f are as follows:

•
PM: .
•
LPM: .
•
SIM: .
•
QLM: .

In Figure 10, the numerical and exact solutions for Example 3 are presented using PM-ABHM, LPM-ABHM, SIM-ABHM, and QLM-ABHM, respectively. It is evident from Figure 10 that the approximate solutions match the exact solutions.

Figure 11 presents the AE for the four techniques for different values of the second user-defined tolerance. Figures 11(a) and 11(b) show that the AE for PM-ABHM, LPM-ABHM, SIM-ABHM, and QLM-ABHM is less than or equal to O(10⁻¹³) for Tol₂ = 10⁻¹² and Tol₂ = 10⁻¹⁴, respectively. It can be observed that for the same initial step-size but different Tol₂, the AE remains within the same order.

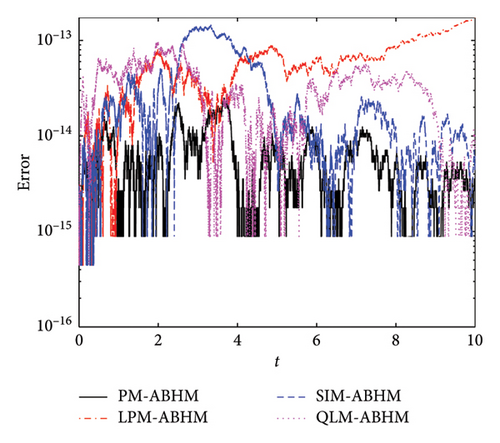
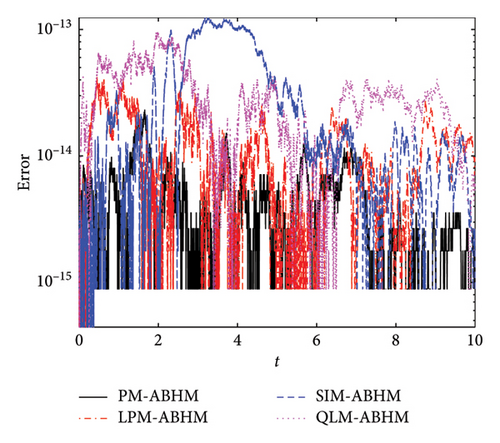
Table 6 compares the maximum AEs for the ABHMs. For Tol₂ = 10⁻¹², PM-ABHM and QLM-ABHM achieve O(10⁻¹⁴) error, while LPM-ABHM and SIM-ABHM have O(10⁻¹³). For Tol₂ = 10⁻¹⁴, all methods except SIM-ABHM achieve O(10⁻¹⁴). The PM-ABHM and QLM-ABHM are faster than LPM-ABHM and SIM-ABHM.

Table 6. Maximum absolute error for Example 4 using the PM-ABHM, LPM-ABHM, SIM-ABHM, and QLM-ABHM with Tol₁ = 10⁻¹².

t_F	h₀	Tol₂	PM-ABHM	LPM-ABHM	SIM-ABHM	QLM-ABHM
10	10⁻²	10⁻¹²	2.4869 × 10⁻¹⁴	1.7408 × 10⁻¹³	1.4477 × 10⁻¹³	9.5923 × 10⁻¹⁴
CPU time in seconds			0.303831	1.071535	1.089501	0.917177

10	10⁻²	10⁻¹⁴	2.3093 × 10⁻¹⁴	4.1744 × 10⁻¹⁴	1.2434 × 10⁻¹³	9.5923 × 10⁻¹⁴
CPU time in seconds			0.324150	1.252072	1.112535	0.979220

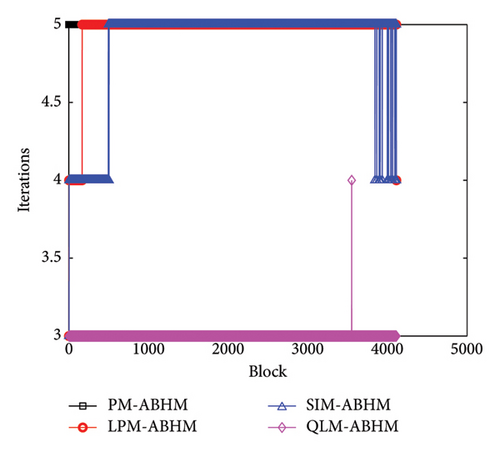
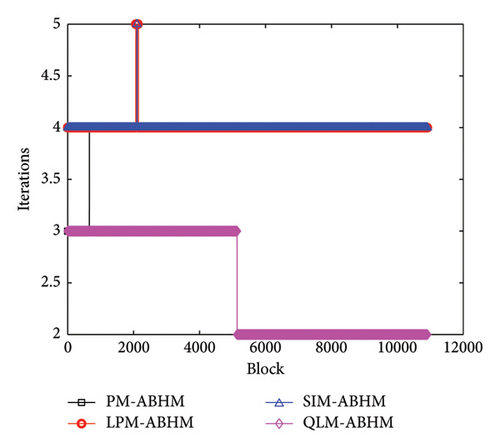
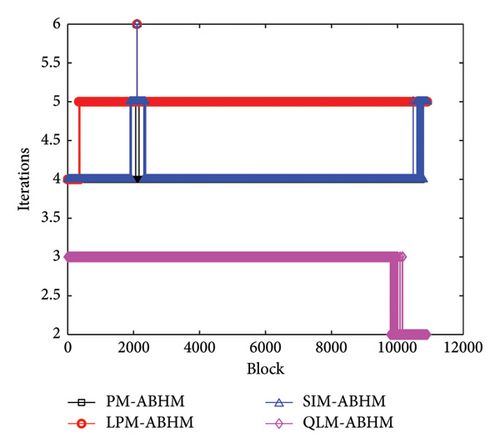
Figure 12 shows the number of iterations per block using PM-ABHM, LPM-ABHM, SIM-ABHM, and QLM-ABHM for different values of Tol₂. In Figure 12(a), the PM requires between three and four iterations, while LPM-ABHM and SIM-ABHM require between four and five iterations, and QLM-ABHM requires between two and three iterations for Tol₂ = 10⁻¹². In Figure 12(b), for Tol₂ = 10⁻¹⁴, the number of iterations for PM-ABHM, LPM-ABHM, and SIM-ABHM increases by one, while QLM-ABHM maintains the same number of iterations.

6.4. Example 4

We analyze the nonlinear IVP

()

The exact solution is

()

Defining f = −(1/3)y − e^ty⁴, we apply the ABHM with the following linearization techniques

•
PM: .
•
LPM: .
•
SIM: .
•
QLM: .

We depicted the exact and numerical solutions for Example 4 in Figure 13. It is evident that the numerical solutions closely align with the exact solution.

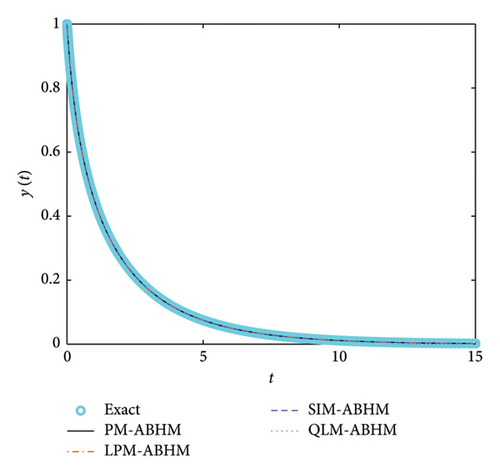
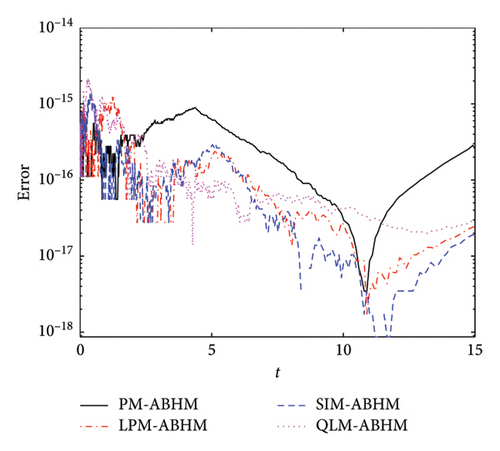
Figure 14 presents the AE for the PM-ABHM, LPM-ABHM, SIM-ABHM, and QLM-ABHM with varying initial step-sizes and the first user-defined tolerance. Figure 14(a) shows that the AE for these methods ranges from O(10⁻¹⁴) to O(10⁻¹⁸) for h₀ = 10⁻¹ and Tol₁ = 10⁻⁸. In Figure 14(b), the AE for all four methods ranges from O(10⁻¹⁴) to O(10⁻¹⁹). We noted that smaller initial step-sizes and the first user-defined tolerance result in improved AE.

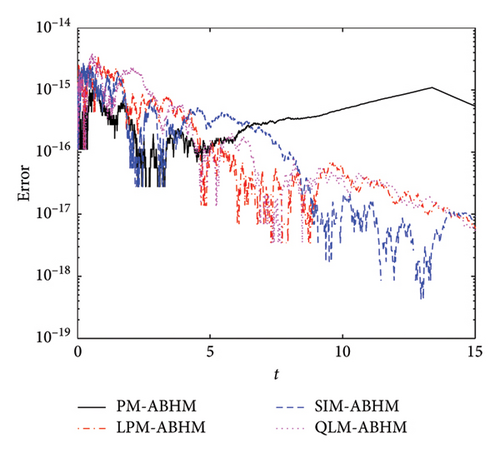
A comparison of the maximum AEs is shown in Table 7. The PM-ABHM achieves a maximum AE of O(10⁻¹⁶), while the LPM-ABHM, SIM-ABHM, and QLM-ABHM achieve maximum errors of O(10⁻¹⁵) for h₀ = 10⁻¹ and Tol₁ = 10⁻⁸. For h₀ = 10⁻³ and Tol₁ = 10⁻¹⁰, all methods reach a maximum AE of O(10⁻¹⁵). The PM-ABHM consistently provides the smallest maximum AE across varying initial step-sizes and first user-defined tolerances, demonstrating its superior accuracy. The CPU times for each method differ, with PM-ABHM being the fastest.

Table 7. Comparison of maximum absolute errors and CPU times for the PM-ABHM, LPM-ABHM, SIM-ABHM, and QLM-ABHM with Tol₂ = 10⁻¹⁴ for Example 4.

t_F	h₀	Tol₁	PM-ABHM	LPM-ABHM	SIM-ABHM	QLM-ABHM
15	10⁻¹	10⁻⁸	8.8818 × 10⁻¹⁶	1.2768 × 10⁻¹⁵	1.3323 × 10⁻¹⁵	2.2204 × 10⁻¹⁵
CPU time in seconds			0.048587	0.129061	0.114315	0.071829

15	10⁻³	10⁻¹⁰	1.3323 × 10⁻¹⁵	3.3307 × 10⁻¹⁵	2.6645 × 10⁻¹⁵	3.7748 × 10⁻¹⁵
CPU time in seconds			0.131735	0.388458	0.396925	0.297469

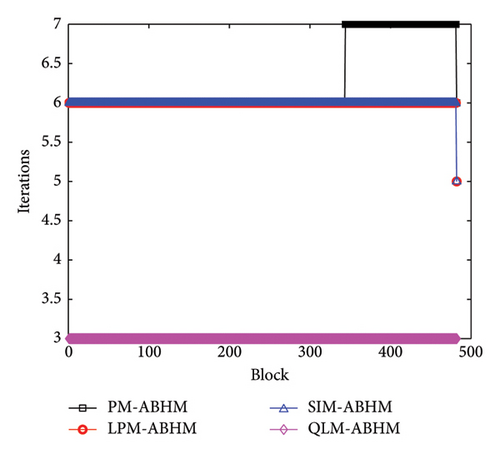
Figure 15 shows the number of iterations per block for the four methods with different initial step-sizes and first user-defined tolerance values. In Figure 15(a), the PM-ABHM requires six to seven iterations, while LPM-ABHM and SIM-ABHM need five to six, and QLM-ABHM only three iterations per block for h₀ = 10⁻¹ and Tol₁ = 10⁻⁸. For h₀ = 10⁻³ and Tol₁ = 10⁻¹⁰, as shown in Figure 15(b), the number of iterations decreases by one for PM-ABHM, LPM-ABHM, and SIM-ABHM, while QLM-ABHM requires only three iterations.

6.5. Example 5

We consider the nonlinear Krogh’s problem [22].

()

where β₁ = 0.2, β₂ = 0.2, β₃ = 0.3, and β₄ = 0.4. The exact solution is

()

Let us define

and explore the following linearization of f_i as

•
PM: .
•
LPM: .
•
SIM: .
•
QLM: .

We present the numerical and exact solutions in Figure 16. Figure 16 shows that the graphs of the approximate and exact solutions coincide.

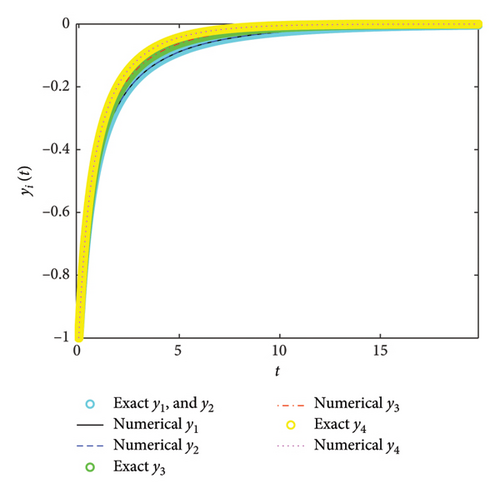
Figure 17 presents a comparative analysis of the AEs for the four implemented methods. We used h₀ = 10⁻², Tol₁ = 10⁻¹², Tol₂ = 10⁻¹², and t_F = 20. Figure 17(a) illustrates the AE for the PM-ABHM. The PM demonstrates a high initial error O(10⁻¹⁴) that decreases consistently, achieving errors as low as O(10⁻²⁰). Figure 17(b) depicts the AE for the LPM-ABHM. The LPM shows a similar trend of error reduction over time. The LPM-ABHM achieves errors in the range of O(10⁻¹³) to O(10⁻¹⁷). Figure 17(c) shows the AE for the SIM-ABHM. The SIM scheme manages to reduce the errors reaching O(10⁻¹⁸). Figure 17(d) presents the AE for the QLM-ABHM. The QLM technique shows a more consistent reduction in errors compared to the SIM. The error graphs decrease, reaching values between O(10⁻¹³) and O(10⁻¹⁹). It is evident that all four methods are capable of achieving low AEs.

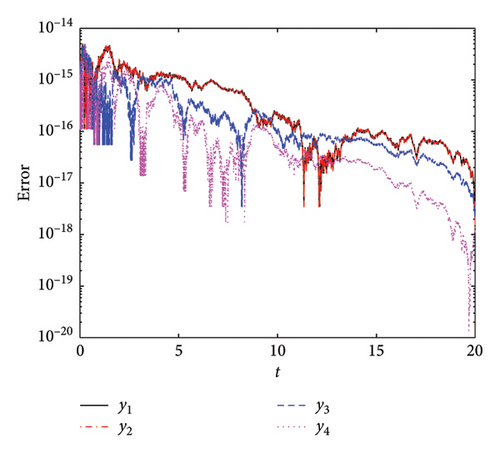
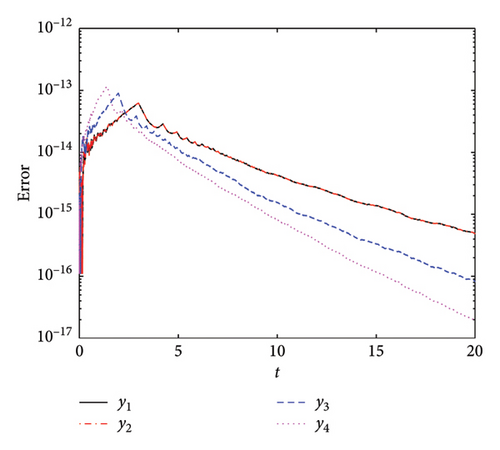
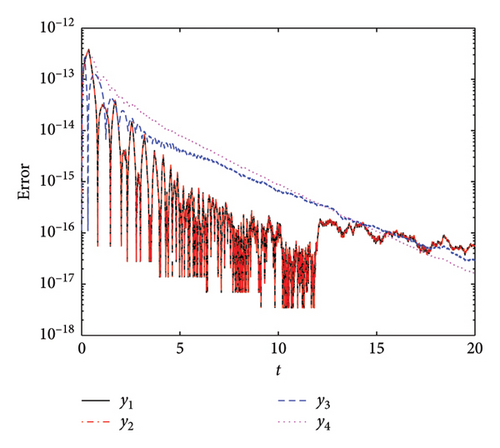
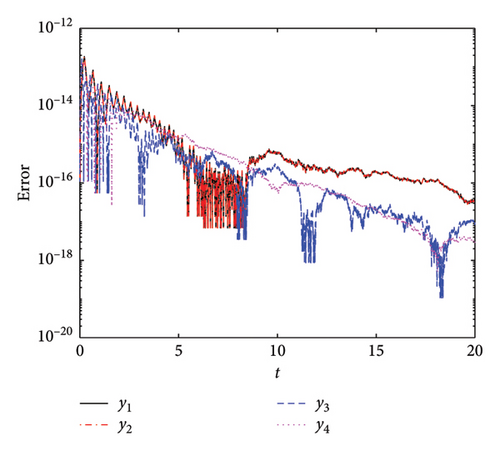
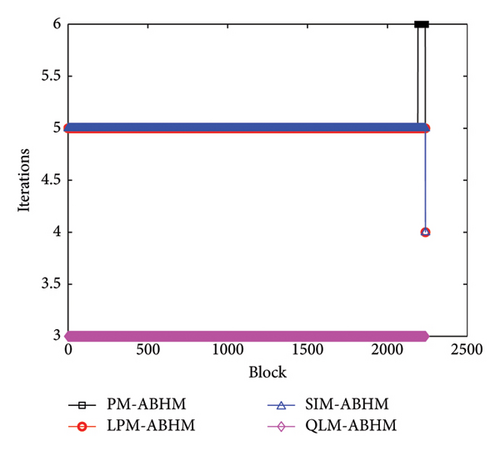
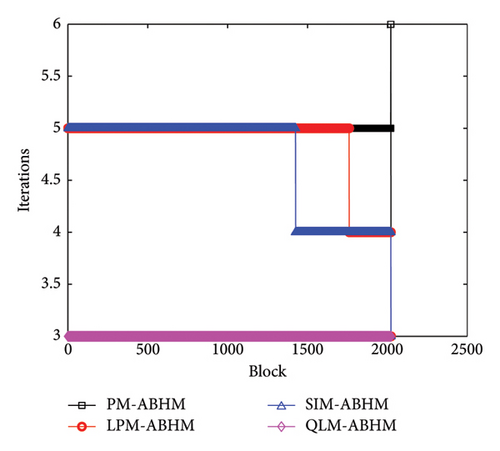
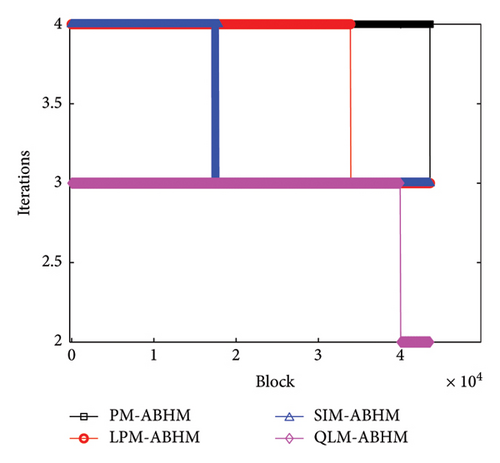
Figure 18 illustrates the number of iterations per block for the PM-ABHM, LPM-ABHM, SIM-ABHM, and QLM-ABHM at various Tol₁ values in Example 5. In Figure 18(a), for Tol₁ = 10⁻¹⁰, the PM-ABHM required five to six iterations per block, while the LPM-ABHM and SIM-ABHM maintained around four and five iterations, respectively. The QLM-ABHM consistently performs better, requiring only three iterations. In Figure 18(b), for Tol₁ = 10⁻¹⁴, the PM-ABHM, LPM-ABHM, and SIM-ABHM were reduced to three and four iterations per block, respectively. The QLM-ABHM remains the most efficient, maintaining around two to three iterations.

6.6. Example 6

The Brusselator is an oscillating system that models an autocatalytic chemical reaction, described by the following system of nonlinear differential equations [23, 71].

()

where μ and ν are constants. We define the functions f₁ = μ + Y²Z − (ν + 1)Y and f₂ = νY − Y²Z. The corresponding linearization techniques are implemented as follows:

•
PM:
()
•
LPM:
()
•
SIM:
()
•
QLM:
()

Figure 19 shows that the numerical solutions obtained by PM-ABHM, LPM-ABHM, SIM-ABHM, and QLM-ABHM demonstrate strong consistency with the reference solution computed using the ode45 MATLAB solver, as no exact solutions are available. This close agreement validates the effectiveness of the proposed methods in accurately solving Example 6.

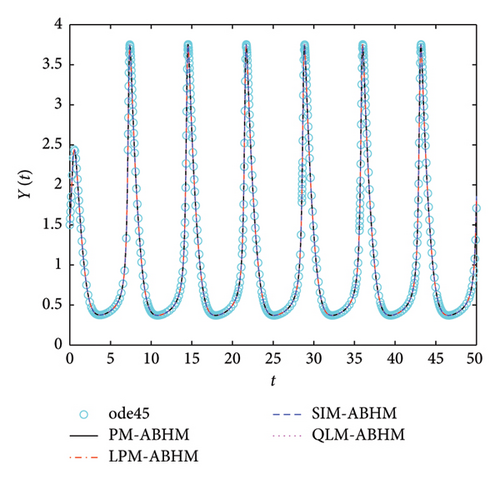
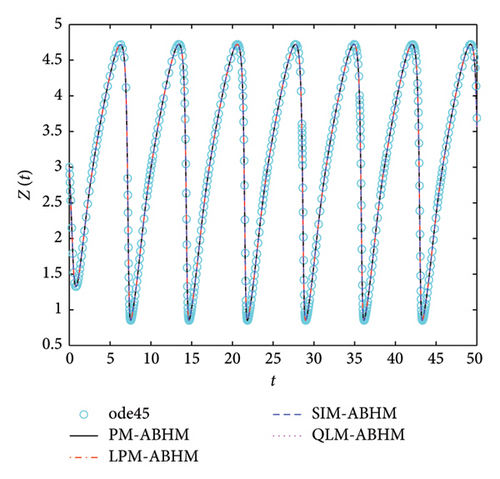
Table 8 gives a comparison of the maximum AE using the PM-ABHM, LPM-ABHM, SIM-ABHM, and QLM-ABHM at t_F = 20 with various ABHMs [23, 71]. The results indicate that PM-ABHM, LPM-ABHM, SIM-ABHM, and QLM-ABHM consistently achieve the lowest errors across different h₀ and Tol₁, outperforming Opthbm and EMOHM. Additionally, PM-ABHM demonstrates the best computational efficiency in terms of CPU time.

Table 8. Comparison of the maximum absolute error using the PM-ABHM, LPM-ABHM, SIM-ABHM, QLM-ABHM, Opthbm [23], and EMOHM [71] at t_F = 20 with Tol₂ = 10⁻¹⁴ for Example 6.

h₀	Tol₁	PM-ABHM	LPM-ABHM	SIM-ABHM	QLM-ABHM	EMOHM [71]	Opthbm [23]
10⁻³	10⁻⁶	1.3412 × 10⁻¹¹	1.3421 × 10⁻¹¹	1.3413 × 10⁻¹¹	1.3408 × 10⁻¹¹	1.53089 × 10⁻⁹	1.2513 × 10⁻⁸
CPU		0.059026	0.300385	0.314092	0.325632	—	0.077

10⁻⁴	10⁻⁷	1.7031 × 10⁻¹³	1.6931 × 10⁻¹³	1.7025 × 10⁻¹³	1.6875 × 10⁻¹³	—	9.6196 × 10⁻¹⁰
CPU		0.102599	0.450135	0.597188	0.515766	—	0.107

10⁻¹	10⁻¹⁰	5.8287 × 10⁻¹⁵	1.1324 × 10⁻¹⁴	1.2434 × 10⁻¹⁴	7.6050 × 10⁻¹⁵	—	—
CPU		0.698620	2.923950	3.880332	3.542907	—	—

7. On the Application of the ABHM

We consider convection in a fluid layer that is heated from below [72, 73].

()

where Y, Z, and W are the convective amplitudes, Pr is the Prandtl number, Ra is the Rayleigh number, and a is the wave number. We used Pr = 10, Ra = 27π⁴/4, and

. We implemented the ode45 solver in MATLAB to solve equations (76)–(78) and compared it with the numerical solutions obtained using the ABHM. Figure 20 shows that the ode45 solutions align with the PM-ABHM, LPM-ABHM, SIM-ABHM, and QLM-ABHM solutions.

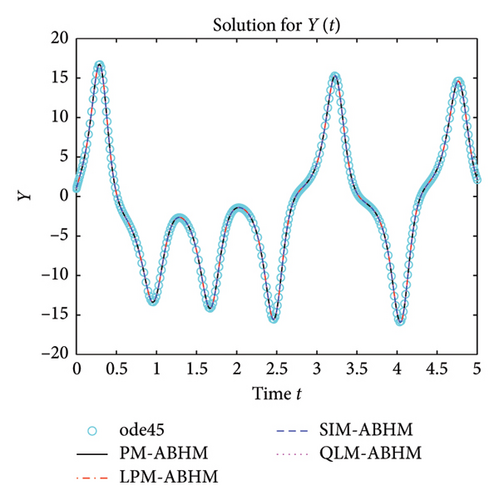
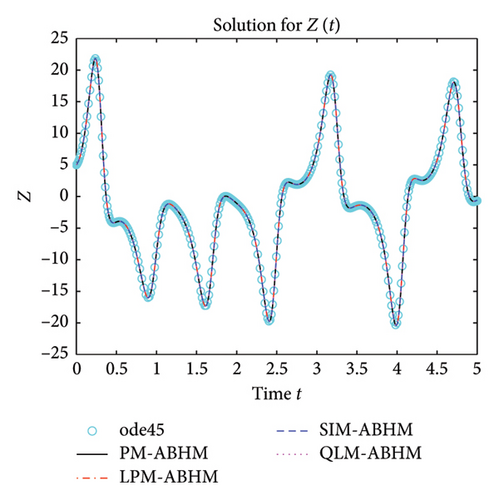
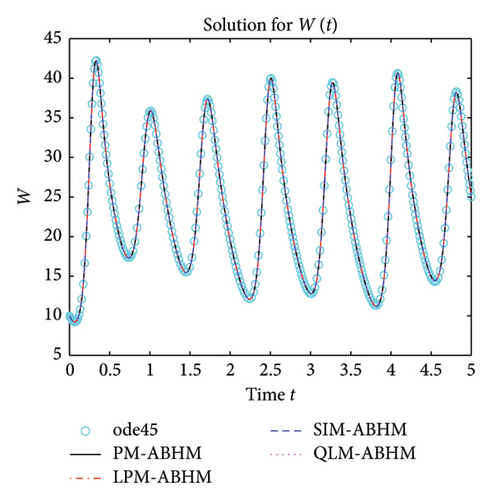
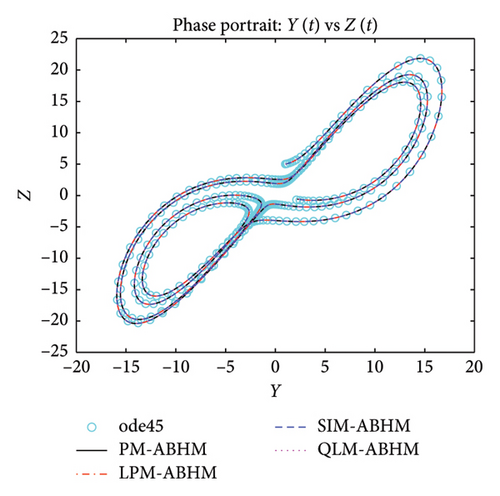
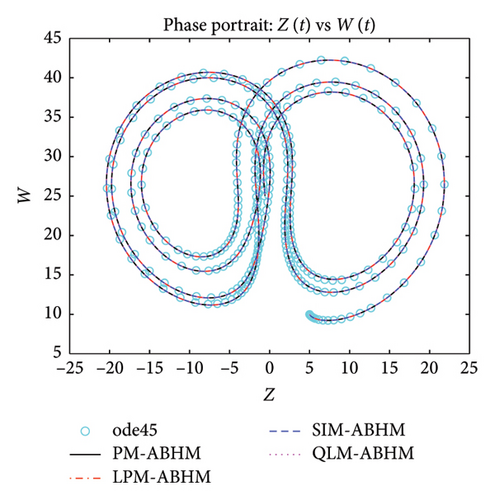
8. Conclusion

In this study, we conducted a comprehensive investigation of the performance of the ABHM along with four linearization techniques for solving first-order IVP under various initial step-sizes and user-defined tolerance values. We used PM, LPM, SIM, and QLM to linearize the differential equations. We evaluated the AE, maximum AE, and the number of iterations per block for each method. This represents a significant step forward in optimizing linearization techniques for ABHM, addressing a critical gap in the numerical analysis of nonlinear differential equations. The key findings of our study are as follows.

•
For the same initial step-size, all methods exhibit comparable effectiveness, indicating their suitability for high precision.
•
By choosing the initial step-size and first user-defined tolerance small enough, we observed that the number of iterations per block required was reduced in all ABHMs.
•
The PM-ABHM and QLM-ABHM consistently achieve the highest accuracy and efficiency, making them highly effective for applications demanding high precision.
•
The QLM-ABHM, despite requiring the fewest iterations, achieves high accuracy and efficiency.
•
The SIM-ABHM is slightly better than the LPM-ABHM in terms of accuracy and the number of iterations required per block.
•
In terms of CPU time required, we noted that the PM-ABHM and QLM-ABHM are faster than SIM-ABHM and LPM-ABHM.

The insights gained from this work not only enhance the theoretical understanding of ABHM but also provide practical guidelines for selecting effective linearization methods. Future research could further implement the rational optimal grid points within ABHMs, combined with linearization techniques. Also, it could focus on implementing these methods to solve higher-order initial and BVPs, as well as enhancing their performance through more efficient tolerance settings. Additionally, developing new linearization techniques that surpass existing methods in terms of efficiency would represent a significant contribution.

Nomenclature

EST: Error estimation function
Tol₁: First user-defined tolerance
Tol₂: Second user-defined tolerance

Greek symbols

σ: Safety factor

Abbreviations

AE: Absolute error
AEE: Absolute error estimate
ABHM: Adaptive block hybrid method
BHM: Block hybrid method
IVP: Initial value problem
PM: Picard method
SIM: Simple iteration method
LPM: Linear partition method
LTE: Local truncation error
QLM: Quasi-linearization method

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funding was received for this manuscript.

Acknowledgments

The authors are grateful to the University of KwaZulu-Natal and University of Zululand. The authors sincerely thank the editors and reviewers for their valuable and constructive feedback.

Open Research

Data Availability Statement

The data that support the findings of this study are available within the article.

References

1 Eriksson K., Computational Differential Equations, 1996, Cambridge University Press.
Google Scholar
2 Hamming R., Numerical Methods for Scientists and Engineers, Courier Corporation. (2012) .
Google Scholar
3 Shampine L. F. and Watts H., Block Implicit One-Step Methods, Mathematics of Computation. (1969) 23, no. 108, 731–740, https://doi.org/10.1090/s0025-5718-1969-0264854-5, 2-s2.0-0040307896.
10.1090/S0025-5718-1969-0264854-5
Web of Science® Google Scholar
4 Majid Z. A., Phang P. S., and Suleiman M., Application of Block Method for Solving Nonlinear Two Point Boundary Value Problem, Advanced Science Letters. (2012) 13, no. 1, 754–757, https://doi.org/10.1166/asl.2012.3767, 2-s2.0-84863302949.
10.1166/asl.2012.3767
Google Scholar
5 Shateyi S., On the Application of the Block Hybrid Methods to Solve Linear and Non-Linear First Order Differential Equations, Axioms. (2023) 12, no. 2, https://doi.org/10.3390/axioms12020189.
10.3390/axioms12020189
PubMed Web of Science® Google Scholar
6 Orakwelu M. G., Otegbeye O., and Mambili-Mamboundou H., A Class of Single-Step Hybrid Block Methods With Equally Spaced Points for General Third-Order Ordinary Differential Equations, Journal of the Nigerian Society of Physical Sciences. (2023) https://doi.org/10.46481/jnsps.2023.1484.
10.46481/jnsps.2023.1484
Google Scholar
7 Brugnano L. and Trigiante D., Solving Differential Equations by Multistep Initial and Boundary Value Methods, 1998, CRC Press.
Google Scholar
8 Jator S. N., Solving Second Order Initial Value Problems by a Hybrid Multistep Method Without Predictors, Applied Mathematics and Computation. (2010) 217, no. 8, 4036–4046, https://doi.org/10.1016/j.amc.2010.10.010, 2-s2.0-78649956840.
10.1016/j.amc.2010.10.010
Web of Science® Google Scholar
9 Rufai U. O., Sibanda P., and Goqo S. P., A One-Step Multi-Derivative Hybrid Block Method With Modified-Picard Iteration for the Solution of Second Order IVP, Engineering Letters. (2023) 31, no. 4.
Google Scholar
10 Biala T., Jator S., Adeniyi R., and Ndukum P., Block Hybrid Simpson’s Method With Two Offgrid Points for Stiff System, International Journal of Nonlinear Science. (2015) 20, no. 1, 3–10.
Google Scholar
11 Adeyefa E. O., Omole E. O., Shokri A., and Yao S. W., Hermite Fitted Block Integrator for Solving Second-Order Anisotropic Elliptic Type PDEs, Fractal and Fractional. (2022) 6, no. 9, https://doi.org/10.3390/fractalfract6090497.
10.3390/fractalfract6090497
Web of Science® Google Scholar
12 Qureshi S., Akanbi M. A., Shaikh A. A. et al., A New Adaptive Nonlinear Numerical Method for Singular and Stiff Differential Problems, Alexandria Engineering Journal. (2023) 74, 585–597, https://doi.org/10.1016/j.aej.2023.05.055.
10.1016/j.aej.2023.05.055
Web of Science® Google Scholar
13 Ajani Rufai M., Mazzia F., and Ramos H., An Adaptive Optimized Nyström Method for Second-Order IVPs, Mathematical Methods in the Applied Sciences. (2023) 46, no. 6, 7543–7556, https://doi.org/10.1002/mma.8983.
10.1002/mma.8983
Web of Science® Google Scholar
14 Ramos H. and Rufai M. A., A New One-Step Method With Three Intermediate Points in a Variable Step-Size Mode for Stiff Differential Systems, Journal of Mathematical Chemistry. (2023) 61, no. 4, 673–688, https://doi.org/10.1007/s10910-022-01427-7.
10.1007/s10910-022-01427-7
CAS Web of Science® Google Scholar
15 Qureshi S. and Ramos H., L-Stable Explicit Nonlinear Method With Constant and Variable Step-Size Formulation for Solving Initial Value Problems, International Journal of Nonlinear Sciences and Numerical Stimulation. (2018) 19, no. 7-8, 741–751, https://doi.org/10.1515/ijnsns-2017-0267, 2-s2.0-85055663710.
10.1515/ijnsns-2017-0267
Web of Science® Google Scholar
16 Holsapple R., Iyer R., and Doman D., Variable Step-Size Selection Methods for Implicit Integration Schemes for ODEs, International Journal of Numerical Analysis and Modeling. (2007) 4, no. 2, 210–240.
Web of Science® Google Scholar
17 Bangerth W. and Rannacher R., Adaptive Finite Element Methods for Differential Equations, 2003, Springer Science & Business Media.
10.1007/978-3-0348-7605-6
Google Scholar
18 Eriksson K., Estep D., Hansbo P., and Johnson C., Introduction to Adaptive Methods for Differential Equations, Acta Numerica. (1995) 4, 105–158, https://doi.org/10.1017/s0962492900002531, 2-s2.0-0009522795.
10.1017/S0962492900002531
Google Scholar
19 Polla G., Comparing Accuracy of Differential Equation Results Between Runge-Kutta Fehlberg Methods and Adams-Moulton Methods, Applied Mathematical Sciences. (2013) 7, 5115–5127, https://doi.org/10.12988/ams.2013.36314, 2-s2.0-84886256863.
10.12988/ams.2013.36314
Google Scholar
20 Chowdhury A., Clayton S., and Lemma M., Numerical Solutions of Nonlinear Ordinary Differential Equations by Using Adaptive Runge-Kutta Method, Journal of Advances in Mathematics. (2019) 17, 147–154, https://doi.org/10.24297/jam.v17i0.8408.
10.24297/jam.v17i0.8408
Google Scholar
21 Nüßlein S., Ranocha H., and Ketcheson D. I., Positivity-Preserving Adaptive Runge–Kutta Methods, Communications in Applied Mathematics and Computational Science. (2021) 16, no. 2, 155–179, https://doi.org/10.2140/camcos.2021.16.155.
10.2140/camcos.2021.16.155
Web of Science® Google Scholar
22 Mehrkanoon S., Majid Z. A., and Suleiman M., A Variable Step Implicit Block Multistep Method for Solving First-Order ODEs, Journal of Computational and Applied Mathematics. (2010) 233, no. 9, 2387–2394, https://doi.org/10.1016/j.cam.2009.10.023, 2-s2.0-73249123695.
10.1016/j.cam.2009.10.023
Web of Science® Google Scholar
23 Singh G., Garg A., Kanwar V., and Ramos H., An Efficient Optimized Adaptive Step-Size Hybrid Block Method for Integrating Differential Systems, Applied Mathematics and Computation. (2019) 362, https://doi.org/10.1016/j.amc.2019.124567, 2-s2.0-85068584676.
10.1016/j.amc.2019.124567
Web of Science® Google Scholar
24 Singla R., Singh G., Ramos H., and Kanwar V., An Efficient Optimized Adaptive Step-Size Hybrid Block Method for Integrating W= F (T, W,w) Directly, Journal of Computational and Applied Mathematics. (2023) 420, https://doi.org/10.1016/j.cam.2022.114838.
10.1016/j.cam.2022.114838
Web of Science® Google Scholar
25 Rufai M. A., Carpentieri B., and Ramos H., A New Hybrid Block Method for Solving First-Order Differential System Models in Applied Sciences and Engineering, Fractal and Fractional. (2023) 7, no. 10, https://doi.org/10.3390/fractalfract7100703.
10.3390/fractalfract7100703
Web of Science® Google Scholar
26 Moin P., Fundamentals of Engineering Numerical Analysis, 2010, Cambridge University Press.
10.1017/CBO9780511781438
Google Scholar
27 Ramos J. I., Piecewise-Linearized Methods for Initial-Value Problems With Oscillating Solutions, Applied Mathematics and Computation. (2006) 181, no. 1, 123–146, https://doi.org/10.1016/j.amc.2006.01.020, 2-s2.0-33749685537.
10.1016/j.amc.2006.01.020
Web of Science® Google Scholar
28 Moser J., A New Technique for the Construction of Solutions of Nonlinear Differential Equations, Proceedings of the National Academy of Sciences. (1961) 47, no. 11, 1824–1831, https://doi.org/10.1073/pnas.47.11.1824.
10.1073/pnas.47.11.1824
CAS PubMed Google Scholar
29 Farthing M. W. and Ogden F. L., Numerical Solution of Richards’ Equation: A Review of Advances and Challenges, Soil Science Society of America Journal. (2017) 81, no. 6, 1257–1269, https://doi.org/10.2136/sssaj2017.02.0058, 2-s2.0-85040601139.
10.2136/sssaj2017.02.0058
CAS Web of Science® Google Scholar
30 Kazantzis N. and Kravaris C., Time-Discretization of Nonlinear Control Systems via Taylor Methods, Computers and Chemical Engineering. (1999) 23, no. 6, 763–784, https://doi.org/10.1016/s0098-1354(99)00007-1, 2-s2.0-0033153174.
10.1016/s0098-1354(99)00007-1
CAS Web of Science® Google Scholar
31 Ortega J. M. and Rheinboldt W. C., Iterative Solution of Nonlinear Equations in Several Variables, 2000, SIAM.
10.1137/1.9780898719468
Google Scholar
32 Sherman A. H., On Newton-Iterative Methods for the Solution of Systems of Nonlinear Equations, SIAM Journal on Numerical Analysis. (1978) 15, no. 4, 755–771, https://doi.org/10.1137/0715050.
10.1137/0715050
Web of Science® Google Scholar
33 Kunkel P., Differential-Algebraic Equations: Analysis and Numerical Solution, 2006, European Mathematical Society.
10.4171/017
Google Scholar
34 Nevanlinna O., Remarks on Picard-Lindelöf Iteration: Part I, BIT Numerical Mathematics. (1989) 29, no. 2, 328–346, https://doi.org/10.1007/bf01952687, 2-s2.0-0001065602.
10.1007/bf01952687
Google Scholar
35 Ramos J. I., On the Variational Iteration Method and Other Iterative Techniques for Nonlinear Differential Equations, Applied Mathematics and Computation. (2008) 199, no. 1, 39–69, https://doi.org/10.1016/j.amc.2007.09.024, 2-s2.0-41949128327.
10.1016/j.amc.2007.09.024
Web of Science® Google Scholar
36 Makarov E. and Spitters B., The Picard Algorithm for Ordinary Differential Equations in Coq, Interactive Theorem Proving: 4th International Conference, ITP 2013, Rennes, France, July 22-26, 2013. Proceedings 4, 2013, Springer, 463–468.
10.1007/978-3-642-39634-2_34
Google Scholar
37 Beaudoin Y., The Iterative Solution of a Nonlinear Equation Using the Integral-Equation Formulations of an Imbedding, 1984.
Google Scholar
38 Traub J. F., Iterative Methods for the Solution of Equations, 1982, American Mathematical Soc.
Google Scholar
39 Junkins J. L., Bani Younes A., Woollands R. M., and Bai X., Picard Iteration, Chebyshev Polynomials and Chebyshev-Picard Methods: Application in Astrodynamics, Journal of the Astronautical Sciences. (2013) 60, no. 3-4, 623–653, https://doi.org/10.1007/s40295-015-0061-1.
10.1007/s40295-015-0061-1
Web of Science® Google Scholar
40 Paniconi C. and Putti M., A Comparison of Picard and Newton Iteration in the Numerical Solution of Multidimensional Variably Saturated Flow Problems, Water Resources Research. (1994) 30, no. 12, 3357–3374, https://doi.org/10.1029/94wr02046, 2-s2.0-0028666563.
10.1029/94WR02046
Web of Science® Google Scholar
41 Jimenez J. C. and Carbonell F., Rate of Convergence of Local Linearization Schemes for Initial-Value Problems, Applied Mathematics and Computation. (2005) 171, no. 2, 1282–1295, https://doi.org/10.1016/j.amc.2005.01.118, 2-s2.0-31144450407.
10.1016/j.amc.2005.01.118
Web of Science® Google Scholar
42 Jimenez J. C. and Carbonell F., Rate of Convergence of Local Linearization Schemes for Random Differential Equations, BIT Numerical Mathematics. (2009) 49, no. 2, 357–373, https://doi.org/10.1007/s10543-009-0225-0, 2-s2.0-67349195512.
10.1007/s10543-009-0225-0
Web of Science® Google Scholar
43 Motsa S. S., A New Piecewise-Quasilinearization Method for Solving Chaotic Systems of Initial Value Problems, Open Physics. (2012) 10, no. 4, 936–946, https://doi.org/10.2478/s11534-011-0124-2, 2-s2.0-84864081385.
10.2478/s11534-011-0124-2
Google Scholar
44 Lin M. H., Carlsson J. G., Ge D., Shi J., and Tsai J. F., A Review of Piecewise Linearization Methods, Mathematical Problems in Engineering. (2013) 2013, no. 1, 1–8, https://doi.org/10.1155/2013/101376, 2-s2.0-84888860141.
10.1155/2013/101376
Web of Science® Google Scholar
45 Garcia-Lopez C., Piecewise-Linearized and Linearized θ-Methods for Ordinary and Partial Differential Equations, Computers and Mathematics With Applications. (2003) 45, no. 1-3, 351–381, https://doi.org/10.1016/s0898-1221(03)80023-8, 2-s2.0-0037287147.
10.1016/s0898-1221(03)80023-8
Google Scholar
46 Khumalo F. B., Motsa S. S., and Magagula V. M., A Bivariate Spectral Linear Partition Method for Solving Nonlinear Evolution Equations, Mathematical Methods in the Applied Sciences. (2024) 47, no. 7, 6607–6621, https://doi.org/10.1002/mma.9940.
10.1002/mma.9940
Web of Science® Google Scholar
47 Ahmedai Abd Allah S. A., Sibanda P., Goqo S. P., Rufai U. O., Sithole Mthethwa H., and Noreldin O. A., A Block Hybrid Method With Equally Spaced Grid Points for Third-Order Initial Value Problems, Applied Math. (2024) 4, no. 1, 320–347, https://doi.org/10.3390/appliedmath4010017.
10.3390/appliedmath4010017
Google Scholar
48 Otegbeye O. and Ansari M. S., A Finite Difference Based Simple Iteration Method for Solving Boundary Layer Flow Problems, AIP Conference Proceedings, 2022, AIP Publishing.
Google Scholar
49 Kalaba R., Some Aspects of Quasilinearization, International Symposium on Nonlinear Differential Equations and Nonlinear Mechanics, 1963, Elsevier, 135–146.
10.1016/B978-0-12-395651-4.50020-9
Google Scholar
50 Bellman R. E. and Kalaba R. E., Quasilinearization and Nonlinear Boundary-Value Problems, 1965.
Google Scholar
51 Banks H. T. and GroomeG. M.Jr., Convergence Theorems for Parameter Estimation by Quasilinearization, Journal of Mathematical Analysis and Applications. (1973) 42, no. 1, 91–109, https://doi.org/10.1016/0022-247x(73)90122-4, 2-s2.0-0002301024.
10.1016/0022-247x(73)90122-4
Web of Science® Google Scholar
52 Mandelzweig V. and Tabakin F., Quasilinearization Approach to Nonlinear Problems in Physics With Application to Nonlinear ODEs, Computer Physics Communications. (2001) 141, no. 2, 268–281, https://doi.org/10.1016/s0010-4655(01)00415-5, 2-s2.0-0035976505.
10.1016/S0010-4655(01)00415-5
CAS Web of Science® Google Scholar
53 Motsa S., Overlapping Grid-Based Optimized Single-Step Hybrid Block Method for Solving First-Order Initial Value Problems, Algorithms. (2022) 15, no. 11, https://doi.org/10.3390/a15110427.
10.3390/a15110427
Web of Science® Google Scholar
54 Henrici P., Discrete Variable Methods in Ordinary Differential Equations, 1962, Wiley.
Google Scholar
55 Butcher J. C., Implicit Runge-Kutta Processes, Mathematics of Computation. (1964) 18, no. 85, 50–64, https://doi.org/10.2307/2003405.
10.1090/S0025-5718-1964-0159424-9
Web of Science® Google Scholar
56 Areo E. and Rufai M., A New Uniform Fourth Order One-Third Step Continuous Block Method for the Direct Solutions of Y = F (X, Y, Y), British Journal of Mathematics and Computer Science. (2016) 15, no. 4, 1–12, https://doi.org/10.9734/bjmcs/2016/24310.
10.9734/bjmcs/2016/24310
Google Scholar
57 Areo E. A. and Omojola M. T., A New One-Twelfth Step Continuous Block Method for the Solution of Modeled Problems of Ordinary Differential Equations, American Journal of Computational Mathematics. (2015) 05, no. 04, 447–450, https://doi.org/10.4236/ajcm.2015.54039.
10.4236/ajcm.2015.54039
Google Scholar
58 Lambert J. D., Computational Methods in Ordinary Differential Equations, 1973, Wiley.
Google Scholar
59 Dahlquist G., Convergence and Stability in the Numerical Integration of Ordinary Differential Equations, Mathematica Scandinavica. (1956) 4, 33–53, https://doi.org/10.7146/math.scand.a-10454.
10.7146/math.scand.a-10454
Google Scholar
60 Ramos H., Kalogiratou Z., Monovasilis T., and Simos T., An Optimized Two-Step Hybrid Block Method for Solving General Second Order Initial-Value Problems, Numerical Algorithms. (2016) 72, no. 4, 1089–1102, https://doi.org/10.1007/s11075-015-0081-8, 2-s2.0-84948988921.
10.1007/s11075-015-0081-8
PubMed Web of Science® Google Scholar
61 Watts H. A. and Shampine L., A-Stable Block Implicit One-Step Methods, BIT Numerical Mathematics. (1972) 12, no. 2, 252–266, https://doi.org/10.1007/bf01932819, 2-s2.0-0001643419.
10.1007/BF01932819
Google Scholar
62 Prothero A. and Robinson A., On the Stability and Accuracy of One-Step Methods for Solving Stiff Systems of Ordinary Differential Equations, Mathematics of Computation. (1974) 28, no. 125, 145–162, https://doi.org/10.2307/2005822.
10.1090/S0025-5718-1974-0331793-2
Google Scholar
63 Dahlquist G. G., A Special Stability Problem for Linear Multistep Methods, BIT Numerical Mathematics. (1963) 3, no. 1, 27–43, https://doi.org/10.1007/bf01963532, 2-s2.0-11044230975.
10.1007/bf01963532
Google Scholar
64 Wanner G. and Hairer E., Solving Ordinary Differential Equations II, 1996, Springer.
Google Scholar
65 Wanner G., Hairer E., and Nørsett S. P., Order Stars and Stability Theorems, BIT Numerical Mathematics. (1978) 18, 475–489.
10.1007/BF01932026
Google Scholar
66 Emmanuel F. S., Soomro A., Qureshi S., and Hincal E., A New Family of L-Stable Block Methods With Relative Measure of Stability, International Journal of Applied nonlinear Science. (2022) 1, no. 1, 1–222, https://doi.org/10.1504/ijans.2022.10047786.
10.1504/ijans.2022.10047786
Google Scholar
67 Ferreira J., Meira S., Meneguette Jr M., and Nogueira J., Linear Multistep Methods and Order Stars: Some Properties, TEMA: Tendências em Matemática Aplicada e Computacional. (2008) 9, no. 2, 233–242, https://doi.org/10.5540/tema.2008.09.02.0233.
10.5540/tema.2008.09.02.0233
Google Scholar
68 Ramos H., Qureshi S., and Soomro A., Adaptive Step-Size Approach for Simpson’s-Type Block Methods With Time Efficiency and Order Stars, Computational and Applied Mathematics. (2021) 40, no. 6, https://doi.org/10.1007/s40314-021-01605-4.
10.1007/s40314-021-01605-4
Web of Science® Google Scholar
69 Dahlke S., Dahmen W., Hochmuth R., and Schneider R., Stable Multiscale Bases and Local Error Estimation for Elliptic Problems, Applied Numerical Mathematics. (1997) 23, no. 1, 21–47, https://doi.org/10.1016/s0168-9274(96)00060-8, 2-s2.0-0031069391.
10.1016/s0168-9274(96)00060-8
Web of Science® Google Scholar
70 Cufaro Petroni N., De Martino S., and De Siena S., Logistic and θ-Logistic Models in Population Dynamics: General Analysis and Exact Results, Journal of Physics A: Mathematical and Theoretical. (2020) 53, no. 44, https://doi.org/10.1088/1751-8121/abb277.
10.1088/1751-8121/abb277
Google Scholar
71 Singla R., Singh G., Ramos H., and Kanwar V., Development of a Higher-Order A-Stable Block Approach With Symmetric Hybrid Points and an Adaptive Step-Size Strategy for Integrating Differential Systems Efficiently, Symmetry. (2023) 15, no. 9, https://doi.org/10.3390/sym15091635.
10.3390/sym15091635
PubMed Web of Science® Google Scholar
72 Rayleigh L. L. I. X., LIX. On Convection Currents in a Horizontal Layer of Fluid, When the Higher Temperature Is on the Under Side, The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science. (1916) 32, no. 192, 529–546, https://doi.org/10.1080/14786441608635602.
10.1080/14786441608635602
Google Scholar
73 Noreldin O., Mondal S., and Sibanda P., Thermal Instability of Double-Diffusive Natural Convection in an Inclined Open Square Cavity, Acta Technica Czech Science Advanced Views. (2018) 63, no. 3, 385–406.
Google Scholar

All articles

A Comparative Study of Linearization Techniques With Adaptive Block Hybrid Method for Solving First-Order Initial Value Problems

Abstract

1. Introduction

2. Implementation of the BHM

3. Theoretical Analysis

3.1. LTE and Consistency

3.2. Zero Stability and Convergence

3.3. Absolute Stability

3.4. Order Stars

4. The Adaptive Scheme

4.1. Error Estimation

5. Linearization Techniques

5.1. PM

5.2. LPM

5.3. SIM

5.4. QLM

6. Numerical Results and Discussion

6.1. Example 1

6.2. Example 2

6.3. Example 3

6.4. Example 4

6.5. Example 5

6.6. Example 6

7. On the Application of the ABHM

8. Conclusion

Nomenclature

Greek symbols

Abbreviations

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Related

Information