International Journal of Differential Equations

Volume 2025, Issue 1 1943008

Research Article

Open Access

Spectral Optimized Multiderivative Hybrid Block Method for Fitzhugh–Nagumo Equations

Uthman O. Rufai,

Corresponding Author

Uthman O. Rufai

[email protected]

orcid.org/0000-0001-7638-9153

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Scottsville, Pietermaritzburg , 3209 , South Africa , ukzn.ac.za

Search for more papers by this author

Precious Sibanda,

Precious Sibanda

orcid.org/0000-0003-2115-4642

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Scottsville, Pietermaritzburg , 3209 , South Africa , ukzn.ac.za

Search for more papers by this author

Sicelo P. Goqo,

Sicelo P. Goqo

orcid.org/0000-0003-1383-068X

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Scottsville, Pietermaritzburg , 3209 , South Africa , ukzn.ac.za

Search for more papers by this author

Salma A. A. Ahmedai,

Salma A. A. Ahmedai

orcid.org/0000-0001-7250-7714

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Scottsville, Pietermaritzburg , 3209 , South Africa , ukzn.ac.za

Search for more papers by this author

Adeyinka S. Adeyemo,

Adeyinka S. Adeyemo

orcid.org/0000-0003-3140-5652

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Scottsville, Pietermaritzburg , 3209 , South Africa , ukzn.ac.za

Search for more papers by this author

Uthman O. Rufai,

Corresponding Author

Uthman O. Rufai

[email protected]

orcid.org/0000-0001-7638-9153

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Scottsville, Pietermaritzburg , 3209 , South Africa , ukzn.ac.za

Search for more papers by this author

Precious Sibanda,

Precious Sibanda

orcid.org/0000-0003-2115-4642

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Scottsville, Pietermaritzburg , 3209 , South Africa , ukzn.ac.za

Search for more papers by this author

Sicelo P. Goqo,

Sicelo P. Goqo

orcid.org/0000-0003-1383-068X

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Scottsville, Pietermaritzburg , 3209 , South Africa , ukzn.ac.za

Search for more papers by this author

Salma A. A. Ahmedai,

Salma A. A. Ahmedai

orcid.org/0000-0001-7250-7714

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Scottsville, Pietermaritzburg , 3209 , South Africa , ukzn.ac.za

Search for more papers by this author

Adeyinka S. Adeyemo,

Adeyinka S. Adeyemo

orcid.org/0000-0003-3140-5652

School of Mathematics , Statistics and Computer Science , University of KwaZulu-Natal , Scottsville, Pietermaritzburg , 3209 , South Africa , ukzn.ac.za

Search for more papers by this author

First published: 17 June 2025

https://doi.org/10.1155/ijde/1943008

Academic Editor: Md. Kamrujjaman

Share a link

Email
Wechat
Bluesky

Abstract

The Fitzhugh–Nagumo equation, a key model for excitable systems in biology and neuroscience, requires efficient numerical methods due to its nonlinear nature. A spectral optimized multiderivative hybrid block method is proposed, constructed using a multistep collocation and interpolation technique with an approximated power series as the basis function. Incorporating two optimal intra-step points, the method demonstrates improved accuracy, with its consistency, convergence, and absolute stability rigorously analyzed. By combining the optimized multiderivative hybrid block method in time with a spectral collocation method in space, the approach demonstrates potency and flexibility in solving partial differential equations. Prior to using the spectral method, the partial differential equation is linearized using a linear partition technique. Numerical experiments confirm the accuracy and efficiency of the method compared to existing methods, demonstrating the potential of the method as a robust framework for solving partial differential equations requiring both high accuracy and stability.

1. Introduction

Nonlinear PDEs are extensively utilized for describing complex physical occurrences in diverse scientific fields, including fluid mechanics. These nonlinear models have also found importance in areas like biology and economics (see [1, 2]). One well-known example is the Fitzhugh–Nagumo (F-N) equation, which was developed by previous researchers [3, 4].

()

where 0 ≤ δ ≤ 1 and w(x, t) denotes the dependent function that relies on both the time variable t and the space variable x. Equation (1) has various applications in physics, applied mathematics and mathematical modeling of complex physical and biological systems (see [5–8]). This equation incorporates both the diffusion and non-linearity, which is governed by the term w(1 − w)(w − δ).

The F-N equation with diffusion arose as a special case of the famed Hodgkin–Huxley model, which earned the Nobel Prize in 1963. Nagumo’s work [4] paved the way for extensive research in neuroscience, leading to the development of various extended forms of the F-N model. This system is widely used to describe how a voltage of neuron changes over time and space and is given by

()

where Λ, ε, and Δ are real parameters. The functions w(x, t) and y(x, t), represent the voltage potential (fast variable) and the recovery variable (slow variable), respectively. This model is well-established in neurodynamics [9, 10]. An exact solution to the F-N model (2) was presented in [9].

Several methods have been investigated for the direct solution of equation (1), such as the adomian decomposition method (ADM) [11], variational iteration method (VIM) [12, 13], shifted Legendre polynomial (SLP) [14] and differential transform method (DTM) [15], including the Haar wavelet method presented in [16]. According to [17], analytical solutions for PDEs related to Nagumo reaction-diffusion have been derived using the variational method. Additionally, the homotopy analysis technique has effectively been utilized to provide approximate solutions for the standard F-N equation [18]. Furthermore, the approximate conditional symmetry method as proposed in [19], has been utilized to find approximate solutions for the perturbation of equation (1). Exact solutions have also been obtained using the first integral method [20] and Jacobi elliptic function [21]. While some of these methods require many terms for accurate analytical solutions, others face challenges in determining a suitable initial guess.

Among the diverse array of approaches used to solve PDEs (see [22–24]), the nonstandard finite difference (NSFD) techniques have recently emerged as one of the most effective approaches [25]. The exact finite-difference method (see [26–29]) is a special NSFD scheme. These methods produce reliable results across a wide range of initial and boundary conditions (BCs). However, they can be computationally demanding and prone to numerical instability.

Spectral methods are a class of numerical techniques that approximate solutions to differential equations (DEs). The three traditional spectral methods are the Galerkin, Tau and collocation methods [30]. Spectral techniques have attracted interest due to their computational efficiency and the relative simplicity with which they are used to solve nonlinear DEs [31, 32]. These methods are based on expanding the solution to the equation in terms of a set of basis functions like polynomial kind or Fourier basis [33]. Spectral collocation methods (SCMs), such as the Lagrange pseudo-spectral approach [34], the uniform Haar wavelets and quasilinearization process [35], and the Chebyshev SCMs (see [36–38]), have been presented for solving time-dependent DEs, including nonlinear and stochastic Burgers’ equation. The reaction-diffusion Brusselator system and several nonlinear Burgers’ type equations were effectively solved numerically utilizing the differential quadrature method (DQM) [39, 40]. Motsa et al. [41] introduced the bivariate SCM with the use of Chebyshev and Lagrange cardinal polynomials. This approach involves applying SCM to the time variable to transform the PDE into an ODE, followed by the spatial direction to form systems of linear equations and simplifying the solution process. Initially applied to evolutionary parabolic PDEs, this method has been adapted in [42] to solve various classes of PDEs with two independent variables. The precision of SCMs relies on the choice of grid points and the type of basis functions used to construct the interpolating polynomial [43]. However, their effectiveness decreases when applied to PDEs over extended time intervals. By using fewer grid points, SCMs not only enhance accuracy but also significantly reduce computational costs [44]. The ongoing pursuit of greater precision and computational efficiency continues to drive the development of new techniques. Spectral methods have been combined with other numerical techniques to enhance performance when utilized to solve various types of DEs. One such approach, presented in [45], integrates the finite difference method for time discretization with the spectral method for spatial discretization to solve DEs. Despite the advancements, existing methods often struggle to balance high accuracy, stability, and computational efficiency for nonlinear PDEs like the F-N equation.

Hybrid block method (HBM) has been utilized to solve equation (1) by transforming it into an equivalent system of ordinary DEs through the method of lines [46]. It was noted that as the value of time increases, the error also increases, indicating that shorter time is required to achieve more accurate solution approximations. The Hermite block method introduced in [47] was developed using Hermite polynomials as basis functions to solve second-order nonlinear elliptic PDEs, aiming to enhance numerical accuracy and efficiency. Olaoluwa Omole et al. [48] employed an implicit block method to solve PDEs, achieving greater precision and faster convergence.

Another approach is the multiderivative (MDHBMs), which offer a significant advancement in computational techniques for solving DEs. These methods incorporate higher-order derivatives in the formulation to enhance accuracy and stability without significantly increasing computational complexity [49–51]. By utilizing second or higher-order derivative terms, multiderivative methods reduce truncation errors and improve the convergence rates [51–53]. By merging the strengths of linear multistep methods and block techniques, these methods can efficiently solve both linear and nonlinear problems. Kayode et al. [52] introduced a predictor-corrector technique utilizing higher derivative to solve IVPs. To achieve optimal accuracy in block hybrid methods (BHMs), various optimized BHMs for the numerical integration of IVPs have been presented in [54–57]. A one-step optimized HBM for solving systems of IVPs was presented in [58]. An efficient optimized HBM for integrating second-order IVPs was presented in [59]. Recently, Yakubu and Sibanda [60] used a power series polynomial as a basis function to develop an optimized second-derivative HBM to maximize accuracy when utilized to solve IVPs. While these methods have shown promise for initial value problems (IVPs), their application to nonlinear PDEs have not been extensively studied. This gap highlights the need for innovative numerical techniques to tackle nonlinear PDEs with greater efficiency and accuracy.

To address these challenges, this study introduces a spectral optimized MDHBM (SOMDHBM) for solving the F-N equations (1) and (2). By combining the high accuracy of spectral methods with the stability and computational efficiency of multiderivative hybrid block techniques, the SOMDHBM offers a robust framework for solving nonlinear and diffusive characteristics of the equation. The F-N equation is first linearized using a linear partition mapping technique before applying the SOMDHBM. The effectiveness of the SOMDHBM is validated through numerical experiments, demonstrating the accuracy and efficiency compared to existing techniques such as the polynomial DQM (PDQM) [61], compact finite difference block method (CFDBM) [49], ADM [11], VIM [12, 13], DTM [15], exact finite-difference and NSFD scheme [62], İnan et al. [63] and exponential finite difference method (ExpFDM) [64].

2. Derivation of the Method

In this section, the SOMDHBM is developed for a parabolic PDE of the form

()

with the initial and BCs

()

where ℵ_a(t) and ℵ_b(t) are time-dependent functions or constants. The dot and the prime denote partial differentiation with respect to t and x, respectively. The SOMDHBM is derived from the combination of OMDHBM and the SCM, with an appropriate linear transformation to convert x ∈ [a, b] to

. We develop the OMDHBM for the DEs of the form

()

where the dot denotes the first-derivative of w with respect to the time t. The solution w(t) of equation (5) is approximated at four collocation points

()

in the closed interval [t_n, t_n+1], h is the chosen step-size, p_i is the collocation parameters, i = 0, 1, …, 3 and n is the grid index. The following points will be utilized

()

where p₀ = 0 and p₃ = 1. The points p₁ = c and p₂ = 1 − c are inter-step points. These choices will ensure that the method is stable and achieves higher accuracy. The solution w(t) will be approximated by a power series polynomial of the form

()

where the unknown coefficients η_n,j is obtained through a system of five equations with five unknowns generated from the equations

()

with the initial condition

()

The Mathematica 13.0 code presented in Algorithm 1, for equations (8)–(10), is used to determine the unknown coefficients η_n,j.

Algorithm 1: Mathematica code for obtaining the coefficients η_n,j.

1.
Define Points: p_i = {0, c, 1 − c, 1}; Set: J = Length[p];
2.
Collocate: , for i = 0, …, J;
3.
Set:
;
, for i = 1, …, J;
, for i = J;
4.
Identify Unknowns: Unknowns = Table[η_n,i, {i, 0, J + 1}];
5.
Apply Initial Condition: Initial = (W/.t⟶t_n) = = w_n;
6.
Combine All Equations: AllEquations = Join[W’, W”, {Initial}];
7.
Solve for Unknowns:
Solutions = Simplify[Flatten[Solve[AllEquations, Unknowns]]];

Substituting η_n,j in the continuous approximation (8) and evaluating at the collocation points (6). The method obtained is given below:

()

The method can also be presented in the form

()

and in matrix form

()

where

()

3. Analysis of the Method

In this section, we present the truncation error, order, zero-stability and absolute stability of the OMDHBM.

3.1. Local Truncation Error (LTE)

The LTE for the OMDHBM (14) is expressed as

()

This result was derived by assuming w(t) to be a sufficiently differentiable function, applying

()

using Taylor’s series to expand (18) around t_n, to obtain

()

where

are constants. The OMDHBM have order

()

According to [57, 65], expanding equation (19) using the Taylor series, we obtain

()

Expanding equation (21), we obtain

()

where μ = 3 and K ≥ μ + 3 is a positive integer. This can be expressed as

()

According to [57, 65], it is noted that

()

Substituting (24) into (23), we obtain

()

Using equation (25), the error constant is

()

To determine a suitable value for c, we optimize the LTE in equation (13). This decision is driven by the fact that at the end of the interval [t_n, t_n+1], only w_n+1 is required to proceed with computations in the next block. This approach effectively increases the order of accuracy in each equation. The value of c in the LTE corresponding to w_n+1 is

()

and is the root of −1 + 5c − 5c², which can be calculated by equating to zero. We obtained

()

Substituting (28) in (27), the optimized truncation error (27) becomes

()

The truncation errors for the method (11)–(13) are given below:

()

The error constant is

()

which indicates that OMDHBM has an order of

3.2. Zero Stability

The zero stability of the OMDHBM can be determined by considering the matrix (15) as h⟶0. In this limit, the matrix (15) reduces to

()

The characteristics polynomial is defined as

()

By equating ρ(λ) = 0, the roots of the polynomials are λ = 0 and λ = 1. Thus, following [66], the OMDHBM is zero stable. Since the order of the OMDHBM is greater than 1 (), the method is consistent. When the method is zero stable and consistent, this leads to the conclusion that the method converges.

3.3. Proof of Absolute Stability

A stable numerical method is affirmed when errors introduced in a single time step do not amplify in subsequent time steps. According to [57, 67], a region of absolute stability for a method is described by

()

A method is considered A-stable if the absolute stability region contains the entire left side of the plane

and L-stable, if

. The test equations

()

are applied to the matrix equation (15) to give

()

where

is a matrix given by

()

By computing the eigenvalues of the matrix

, a stability function

can be deduced as

()

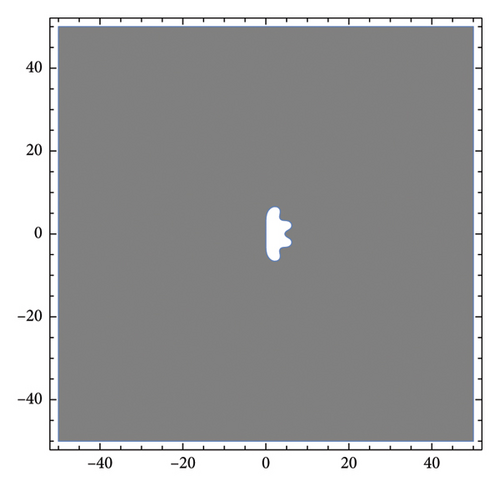
As shown in Figure 1, the stability region for the OMDHBM is the shaded area, which encompasses the entire left side of the plane (A-stable), while the unshaded area is the unstable region. It is evident that the method is not L-stable since . A-stable method is more suitable for a wider range of problems compared to methods with limited regions of absolute stability. It ensures stability regardless of the step size.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Stability region of the method.

4. Implementation

In this section, we discuss the extension of OMDHBM to solve parabolic PDEs (3). Equation (3) is solved using the OMDHBM with respect to t and the SCM in x after transforming x ∈ [a, b] to

using a linear transformation of

()

as suggested in [68]. This transformation ensures that the domain of x is mapped onto the interval [−1, 1]. The spectral approach replaces the continuous derivatives

with discrete approximations at specific grid points, represented as a matrix vector product. The discretized derivatives are expressed as

()

where

and T represent matrix transpose. The matrix D = 2D/(b − a), where D is the Chebyshev differentiation matrix [68]. The collocation points used are the Gauss-Lobatto collocation points defined on the interval [−1, 1] as

()

The application of the spectral method is best described for linear PDEs which can be expressed in general form

()

where α(x, t) and γ_σ(x, t) are known functions. For nonlinear PDEs, the equations are linearized before applying the SCM. Utilizing the SCM with N_x + 1 collocation points on equation (3) gives equation (5) of the form

()

with BCs given by

()

Utilizing the OMDHBM on equation (43) gives

()

where

()

Equation (45) can be defined as

()

where i = 1, 2, 3. In matrix form, equation (47) becomes

()

where

()

where

and

are diagonal matrices.

()

where I is an identity matrix of order N_x + 1, N_x is the number of intervals and

()

The given expression in (48) is expressed compactly as

()

This can also be expressed in the form

()

where R_n+1 = W_n + A₀F_n + C₁Ψ_n+1 + B₁K_n+1 + B₁Θ_n+1Ψ_n+1.

The BCs for the PDE are imposed on the first and last row of each E₁ and the corresponding row entry of R_n+1 in (53) as follows:

()

The next section discusses the applications of the SOMDHBM on the F-N equations (1) and (2).

5. Applications in F-N Equations

Prior to applying the method, the F-N equations are linearized using a linear partition technique. The core concept behind this linearization approach is to evaluate all linear terms at the present iteration level (r + 1) and all nonlinear terms at the previous iteration level (r). The difference between the iterations is assumed to be very small. The details of the linear partition technique are provided in [44, 69]. The linearized form of the F-N equation (1) is

()

The second-derivative with respect to t is

()

The SOMDHBM is applied using the parameters from equation (55)

()

and from equation (56)

()

where I is (N_x + 1) × (N_x + 1) identity matrix and N_x is the number of intervals. The step-by-step implementation of the SOMDHBM for solving the F-N equations is presented in Algorithm 2. All numerical simulations were performed using MATLAB 2016a on a 64 bit Windows system with an Intel(R) Core i5 processor (2 physical cores, 4 logical cores, 2.50 GHz), 8GB RAM. The computations were executed using 2 logical cores, as assigned by MATLAB due to hyper-threading.

Algorithm 2: Algorithmic implementation of the SOMDHBM.

Input: Parameter δ, step size h, number of spatial points N_x, number of iterations R
1.
Generate Chebyshev collocation points and compute D, D₁, D₂ over spatial domain [a, b];
2.
Define the time grid N_t with step size h over an interval [0, T];
3.
Define initial condition w(x, 0);
4.
Define boundary functions w(a, t), w(b, t), and exact solution w(x, t);
5.
Define first-derivative parameters: Φ, Ψ;
6.
Define second-derivative parameters: Θ, Ω, K;
7.
Forn = 1 to N_t:
a. Initialize guesses: W_r(:, n + i) ← W(:, n) for i = 0 to 3;
b. Forr = 1 to R:
i. Fori = 0 to 3:
- Evaluate Ψ, Φ, Θ, Ω, K at t_n + h·points(i + 1);
ii. Fori = 1 to 3:
- Forj = 1 to 3:
∗ Assemble coefficient matrices E_i,j, A_i,j, C_i,j, B_i,j;
∗ Impose boundary conditions on rows 1 and N_x + 1 of E_i,j;
- Adjust diagonals in E_i,i for boundary rows;
iii. Flatten block matrices into matrix system: E₁·W = W_n + A₀·F_n + C₁·Ψ + B₁·K + B₁·Θ·Ψ;
iv. Apply boundary values in RHS vector;
v. Solve the linear system for W_n+i,r;
vi. Compute error: ∥W_n+3,r − exact(x, t_n + h·points(4))∥_∞;
c. Update solution: W(:, n + 1) ← W_r(:, n + 3);
Output: Final numerical solution W

Example 1. Consider the F-N equation (1) in [62], subject to the BCs

()

and the IC

()

The exact solution of (1) is

()

where

()

The BCs are imposed on the first and last rows of equation (53) in the form of equation (54). For different values of δ, the SOMDHBM for the current problem is evaluated and compared to the calculated absolute error for accuracy and efficiency. The absolute error is defined as

()

where

and

represent the exact and numerical solutions, respectively.

When δ = 0.01, N_x = 50, h = 0.01 and fifteen iterations, Table 1 shows a comparison of the absolute error (AE_n) in the computed solutions for the F-N equation (1) obtained using ADM [11], VIM [12, 13], DTM [15], NSFD [62] and SOMDHBM. The results demonstrate that SOMDHBM consistently achieves the lowest AE_n error across all test cases, with errors significantly lower than those obtained using other methods. For instance, at x = 0.1 and t = 1.0, the SOMDHBM achieves an AE_n error in the order of 10⁻¹³, whereas NSFD produces errors around 10⁻¹² and ADM, VIM and DTM yield errors in the range of 10⁻⁶ to 10⁻⁵. This confirms the high accuracy of SOMDHBM, as it outperforms all compared methods. The NFEval column in table indicates the number of function evaluations required by SOMDHBM. The values show that SOMDHBM maintains its high accuracy while using a relatively small number of function evaluations. Based on the observed numerical results, the SOMDHBM is highly competitive with existing methods and demonstrates efficiency in finding solutions for the F-N equation (1).

When δ = 0.001, N_x = 50, h = 0.01 and fifteen iterations, Table 2 presents the AE_n error for different values of x and t in the F-N (1), comparing the performance of the SOMDHBM and NSFD [62]. The data reveal that SOMDHBM consistently produces more accurate results than NSFD, achieving significantly lower AE_n error. At all tested spatial points (x = 0.2, 0.5, 0.8), the AE_n error of SOMDHBM remain within the order of 10⁻¹⁵, while NSFD exhibits errors in the order of 10⁻¹⁴, which are approximately ten times larger. This trend is observed across different time steps, confirming that SOMDHBM maintains its precision over time. The NFEval for SOMDHBM increases as t progresses, from 1800 at t = 0.3 to 5400 at t = 0.9. This suggests that while computational effort increases over time, SOMDHBM retains its superior accuracy. These results show that the SOMDHBM not only improves accuracy compared to NSFD but also provides a stable and efficient approach for solving the F-N (1).

The numerical results demonstrate that the SOMDHBM accurately captures the propagation of traveling wavefronts, which represent electrical signals, across a spatial domain over time. The extremely low error magnitudes (on the order of 10⁻¹⁵) indicate that SOMDHBM preserves sharp wave profiles, essential for realistic simulations of nerve activity. The ability of the method to handle small δ values (which correspond to near-threshold excitability) shows its robustness in modeling sensitive nerve dynamics.

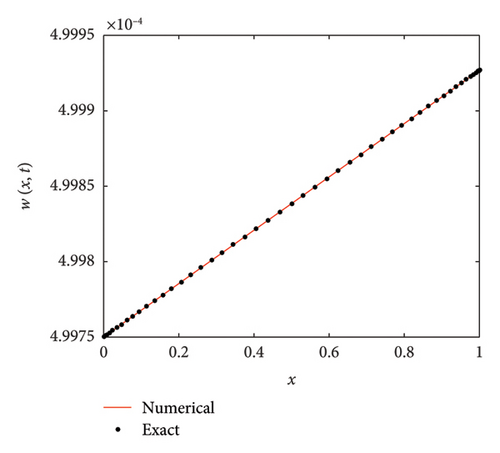
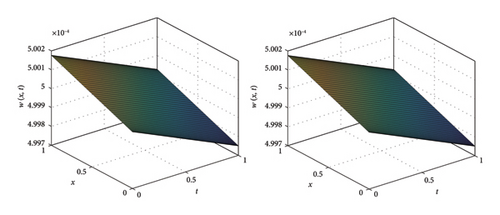
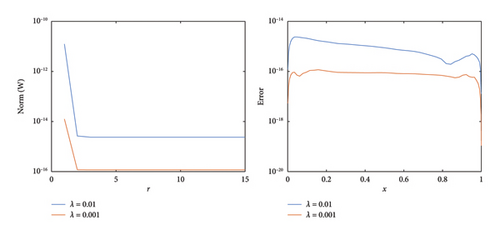
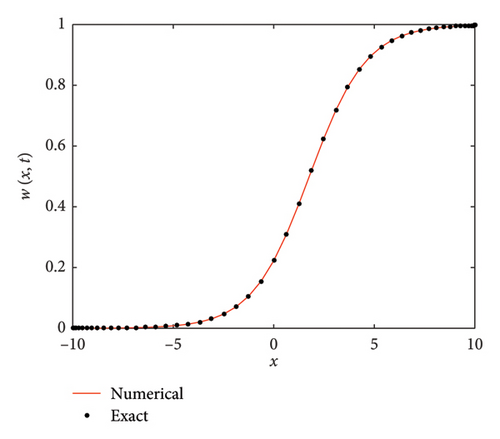
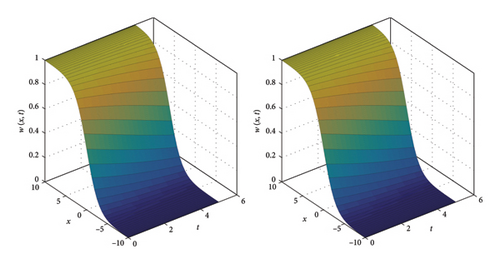
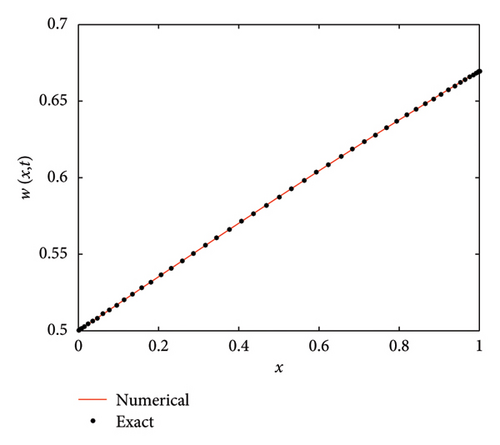
The numerical and exact solutions of (1) for δ = 0.001 with h = 0.01 are compared and presented in Figure 2. The graph shows that the numerical solution aligns closely with the exact solution throughout the entire domain, highlighting the effectiveness of the SOMDHBM. Figure 3 shows the exact solution alongside the numerical solution. The convergence and error profile of the numerical solution for SOMDHBM when δ = 0.01, 0.001, h = 0.01 and N_x = 50 are illustrated in Figure 4. As the δ decreases, the SOMDHBM converges faster.

Table 1. AE_n of the solution for F-N equation compared with ADM, VIM, DTM and NSFD, with δ = 0.01N_x = 50 and h = 0.01.

x	t	SOMDHBM	NFEval	NSFD [62]	ADM [11]	VIM [12, 13]	DTM [15]
0.1	0.05	3.4425E − 13	300	5.0915E − 12	2.4853E − 06	2.4880E − 06	2.4875E − 06
	0.1	1.3896E − 13	600	7.4482E − 12	4.9728E − 06	4.9750E − 06	4.9750E − 06
	1.0	2.0949E − 13	6000	1.1137E − 12	4.9744E − 05	4.9750E − 05	4.9750E − 05

0.5	0.05	6.9701E − 15	300	1.1430E − 11	2.4763E − 06	2.4875E − 06	2.4875E − 06
	0.1	6.5494E − 15	600	1.8999E − 11	4.9638E − 06	4.9750E − 06	4.9750E − 06
	1.0	6.2910E − 15	6000	3.0936E − 11	4.9738E − 05	4.9749E − 05	4.9749E − 05

0.9	0.05	3.1650E − 15	300	5.0915E − 12	2.4674E − 06	2.4875E − 06	2.4874E − 06
	0.1	3.3081E − 15	600	7.4481E − 12	4.9549E − 06	4.9750E − 06	4.9750E − 06
	1.0	3.4564E − 15	6000	7.8174E − 12	4.9730E − 05	4.9789E − 05	4.9749E − 05

Table 2. AE_n of the solution for F-N equation compared with NSFD, with N_x = 50, δ = 0.001 and h = 0.01.

t	SOMDHBM				NSFD [62]
t	x = 0.2	x = 0.5	x = 0.8	NFEval	x = 0.2	x = 0.5	x = 0.8
0.3	4.6113E − 15	6.0347E − 16	4.2761E − 16	1800	1.8987E − 14	1.9838E − 14	1.9974E − 14
0.5	4.4390E − 15	5.8384E − 16	4.2696E − 16	3000	2.9530E − 14	3.0978E − 14	3.1209E − 14
0.9	4.2354E − 15	5.2259E − 16	4.2577E − 16	5400	1.8987E − 14	1.9838E − 14	1.9974E − 14

Example 2. Consider the F-N (1) in [49], subject to the BCs

()

and the IC

()

The exact solution is

()

By imposing the BCs from Example 2 on (53) in the form of (54), we analyze the numerical accuracy and efficiency of different methods. With a = −10, b = 10, δ = 0.75, N_x = 50, h = 0.02 over fifteen iterations, Table 3 presents the maximum absolute error (ME_∞), error norm (EN₂), computation time and number of function evaluations (NFEval) for different values of t in the F-N equation (1). The table compares the performance of SOMDHBM, PDQM [61] and CFDBM [49].

The numerical results show that SOMDHBM consistently achieves the lowest ME_∞ error ranging from 10⁻⁹ to 10⁻⁸, while PDQM exhibits much higher errors, reaching values as large as 10⁻³ to 10⁻⁴. Similarly, the EN₂ norm for SOMDHBM remains significantly smaller than that of PDQM, confirming the effectiveness of the SOMDHBM. Compared to CFDBM, SOMDHBM achieves at least one order of magnitude lower error across all time steps. The SOMDHBM demonstrates higher computational efficiency by achieving lower computation times while maintaining superior accuracy.

The CPU time for SOMDHBM remains below 0.2 s even for large values of t, whereas PDQM requires significantly longer processing time, reaching 0.55 s at t = 5.0. This indicates that SOMDHBM not only produces more accurate results but also operates with significantly lower computation time, making it suitable for long-term and large-scale simulations in applied fields like neuroscience and chemical reaction-diffusion systems. The numerical findings confirm that the SOMDHBM outperforms PDQM and CFDBM in both accuracy and efficiency, making it a highly effective method for solving the F-N equation (1). The maximum absolute error is calculated using the following equation:

()

and the error norm is

()

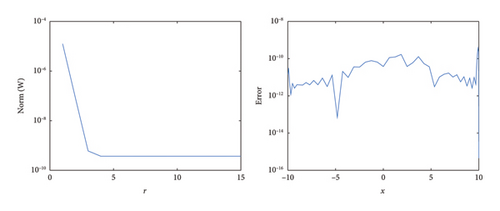
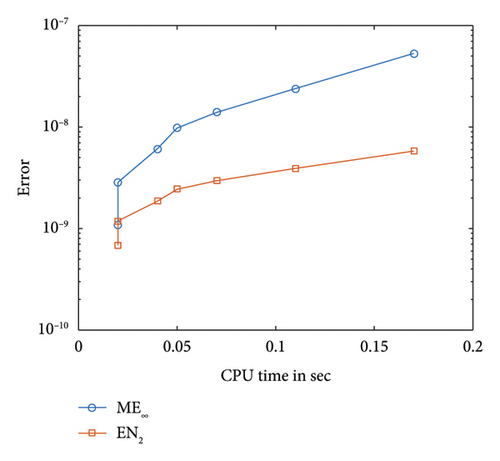
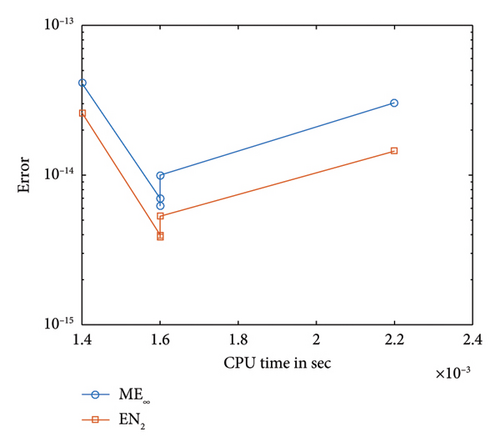
Figure 5 illustrates the comparison between the numerical and exact solutions of the F-N equation (1) for δ = 0.75 with a step-size of h = 0.02. Figure 6 presents a proximity of the exact solution against the numerical solution. The convergence and corresponding error profile of the SOMDHBM are displayed in Figure 7, indicating that the numerical method is accurate and that convergence is achieved after the 3rd iteration. The efficiency curves in Figure 8 illustrate the relationship between CPU time and error measures (ME_∞ and EN₂) for the SOMDHBM. The plot suggests that as CPU time increases, the error decreases, indicating the accuracy of the method improves with more computational effort.

Table 3. ME_∞ and EN₂ of the solutions for Example 2 with δ = 0.75, N_x = 50 and h = 0.02.

t	SOMDHBM				CFDBM [49]		PDQM [61]
t	ME_∞	EN₂	CPU time	NFEval	ME_∞	ME_∞	EN₂	CPU time
0.2	1.0905E − 09	6.8424E − 10	0.02	600	5.4996E − 08	4.7416E − 05	2.3012E − 06	0.10
0.5	2.8575E − 09	1.1878E − 09	0.02	1500	1.0653E − 07	1.2312E − 04	5.5695E − 06	0.10
1.0	6.1097E − 09	1.8586E − 09	0.04	3000	1.5822E − 07	2.6261E − 04	1.1864E − 05	0.18
1.5	9.7815E − 09	2.4373E − 09	0.05	4500	1.9190E − 07	4.2096E − 04	1.9400E − 05	0.24
2.0	1.3928E − 08	2.9581E − 09	0.07	6000	2.1710E − 07	5.9999E − 04	2.8162E − 05	0.31
3.0	2.3928E − 08	3.9140E − 09	0.11	9000	2.5517E − 07	1.0324E − 03	4.9735E − 04	0.35
5.0	5.3186E − 08	5.7975E − 09	0.17	15,000	3.1252E − 07	2.3050E − 03	1.1395E − 04	0.55

Example 3. Consider the F-N equation (1), as presented in [49], subject to the BCs

()

and the IC

()

The exact solution is

()

where

()

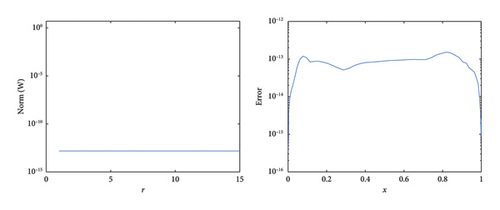
Table 4 displays the absolute error (AE_n) and computation time for different values of x at t = 0.04 over one iteration for N = 10 in equation (1). It compares the performance of the SOMDHBM with CFDBM [49], İnan et al. [63] and ExpFDM [64]. The results indicate that SOMDHBM achieves the highest accuracy, with AE_n error ranging from 10⁻¹⁵ to 10⁻¹⁶, while CFDBM produces errors on the order of 10⁻⁹ to 10⁻⁸. Although CFDBM is more accurate than İnan et al. and ExpFDM, SOMDHBM still outperforms CFDBM by at least six orders of magnitude across all spatial points. The SOMDHBM, like CFDBM, converges in just one iteration, whereas İnan et al. and ExpFDM require eight iterations, reinforcing the computational efficiency of the SOMDHBM.

Table 5 further supports these findings by presenting the NFEval, ME_∞ error and EN₂ norm for SOMDHBM. The results show that ME_∞ and EN₂ remain stable across all x, with values between 10⁻¹⁴ and 10⁻¹⁵, confirming that SOMDHBM maintains its accuracy across the domain. Overall, the numerical findings confirm that SOMDHBM surpasses CFDBM, İnan et al., and ExpFDM in both accuracy and efficiency, making it an optimal approach for solving the F-N equation (1). Its ability to capture sharp gradients and preserve wave profiles with minimal iterations also makes it ideal for real-time simulations and high-fidelity modeling, enhancing its practical relevance in both theoretical and applied contexts.

Figure 9 compares the numerical solution to the exact solution of the F-N equation (1) when δ = 0.5, h = 0.02 over fifteen iterations. Figure 10 shows the closeness of the exact solution and the numerical solution. The convergence and corresponding error profile of the SOMDHBM are depicted in Figure 11. The efficiency curves in Figure 12 show the relationship between CPU time, ME_∞ and EN₂ for the SOMDHBM. The graph shows that the method efficiently reduces computational errors with minimal processing time.

Table 4. AE_n of the solution for Example 3, with δ = 0.5, t = 0.04 and N = 10.

x	SOMDHBM	CPU time	CFDBM [49]	İnan et al. [63]	ExpFDM [64]
0.2	4.3299E − 15	0.0014	1.72E − 08	2.00E − 07	3.00E − 06
0.4	7.7716E − 16	0.0016	4.63E − 09	5.00E − 07	1.00E − 05
0.6	7.7716E − 16	0.0016	1.63E − 09	7.00E − 07	2.00E − 05
0.8	1.2212E − 15	0.0016	7.26E − 09	6.00E − 07	4.00E − 05
1	3.1086E − 15	0.0022	0	0	0
Iterations	1		1	8	8

Table 5. ME_∞ and EN₂ of the solution for Example 3, with δ = 0.5, t = 0.04 and N = 10.

SOMDHBM
x	ME_∞	EN₂	NFEval
0.2	4.1078E − 14	2.6128E − 14	40
0.4	6.9944E − 15	3.9893E − 15	40
0.6	6.2172E − 15	3.8373E − 15	40
0.8	9.9920E − 15	5.3106E − 15	40
1	3.0420E − 14	1.4457E − 14	40
Iteration	1

Example 4. Consider the F-N equation (2), with the exact solutions given by

()

where

()

as presented in [9, 10].

With parameters A₁ = 1, A₂ = 1, ε = 0.3, Λ = 1.03, Δ = 2, N_x = 50, and h = 0.1, Table 6 presents the accuracy and efficiency of the SOMDHBM in solving a nonlinear neuronal PDE system. The method achieves very high accuracy, with ME_∞ and EN₂ remaining extremely small (around 10⁻¹³ to 10⁻¹²) across time steps. The errors increase slowly and smoothly, indicating good long-term stability. Computationally, the method is efficient, with CPU time rising moderately and the number of function evaluations increasing linearly. Overall, SOMDHBM is shown to be accurate, stable, and reliable for solving complex neurodynamic systems.

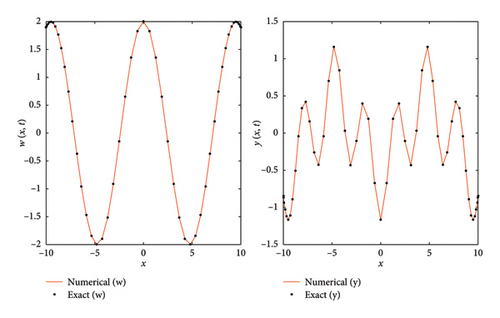
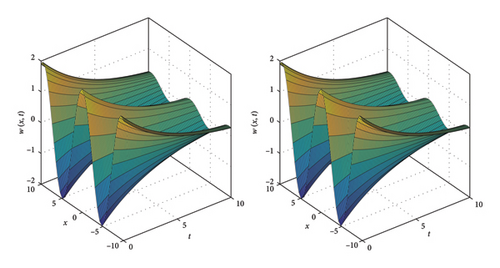
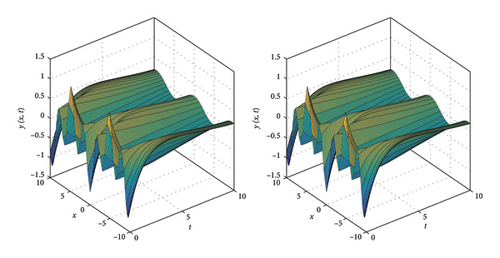
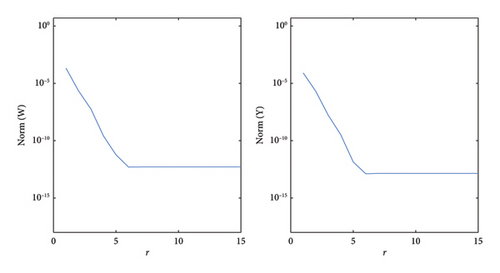
Figures 13, 14, and 15 illustrate the comparison between the numerical and exact solutions of the variables w and y for Example 4, using parameters N_x = 50, h = 0.1 and t = 10. Figure 13 displays both the numerical and exact solutions of w and y over the spatial domain x ∈ [−10, 10]., demonstrating a close agreement and validating the accuracy of SOMDHBM. Figures 14 and 15 separately present the numerical and exact solutions for w and y, respectively. The near-perfect alignment between the numerical and exact profiles confirms the reliable performance of the method for each component. Figure 16 illustrates the convergence behavior of the numerical solutions w and y over fifteen iterations. After approximately the sixth iteration, the norms of both solutions decrease rapidly and nearly exponentially, confirming strong stability and rapid convergence of the SOMDHBM.

Table 6. ME_∞ and EN₂ of the SOMDHBM solutions for Example 4 with N_x = 50 and h = 0.1.

t	w		y		CPU time	NFEval
t	ME_∞	EN₂	ME_∞	EN₂	CPU time	NFEval
1.0	6.8345E − 13	9.2908E − 13	9.2584E − 13	1.4409E − 12	0.31	750
2.0	1.1466E − 12	1.1409E − 12	2.4992E − 12	2.6659E − 12	0.40	1500
3.0	1.2450E − 12	1.1523E − 12	3.9191E − 12	3.3491E − 12	0.29	2250
4.0	1.5676E − 12	1.2269E − 12	4.9390E − 12	3.6615E − 12	0.45	3000
5.0	2.2278E − 12	1.4265E − 12	5.5462E − 12	3.7777E − 12	0.46	3750
6.0	3.1541E − 12	1.7283E − 12	5.9411E − 12	3.8094E − 12	0.56	4500
7.0	4.3344E − 12	2.1448E − 12	6.2205E − 12	3.8135E − 12	0.66	5250
8.0	5.7888E − 12	2.8069E − 12	6.4206E − 12	3.8143E − 12	0.88	6000
9.0	8.0435E − 12	4.0106E − 12	6.6980e − 12	3.8204E − 12	0.89	6750
10.0	1.1832E − 11	6.1989E − 12	7.6159E − 12	3.8380E − 12	0.89	7500

6. Conclusions

In this study, the efficiency and accuracy of the SOMDHBM were demonstrated for the F-N equation over large space and time intervals. The method utilized the optimized MDHBM in time and the SCM in space to solve F-N equation, a widely studied model in neuroscience and mathematical biology. The SOMDHBM results were compared with those obtained from the ADM, İnan et al. [63], CFDBM, ExpFDM, DTM, NSFD, PDQM and VIM scheme. Details of the numerical results were presented and it was evident from the numerical experiments that the SOMDHBM solutions performed better than other schemes in terms of accuracy, computation efficiency and agrees with the exact solutions. Future work may extend this approach to higher-dimensional or stochastic versions of the F-N model, or apply it to other nonlinear PDEs arising in applied sciences.

Nomenclature

ADM: Adomian decomposition method
AE: Absolute error
BCs: Boundary conditions
BHM: Block hybrid method
CFDBM: Compact finite difference block method
CPU time: Computation time
DQM: Difference quadrature method
DTM: Differential transform method
EN₂: Error norm
ExpFDM: Exponential finite difference method
F-N: Fitzhugh–Nagumo
HBM: Hybrid block method
IC: Initial condition
MDHBM: Multiderivative hybrid block method
ME_∞: Maximum absolute error
NFEval: Number of function evaluations
NSFD: Nonstandard finite difference
OMDHBM: Optimized multiderivative hybrid block method
PDQM: Polynomial differential quadrature method
SCM: Spectral collocation method
SOMDHBM: Spectral optimized multiderivative hybrid block method
VIM: Variational iteration method

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research was funded by the University of KwaZulu-Natal, South Africa.

Acknowledgments

The authors are grateful to the University of Kwazulu-Natal, South Africa, for assistance.

Open Research

Data Availability Statement

The data that support the findings of this study are available within the article.

References

1 Wazwaz A., Partial Differential Equations and Solitary Waves Theory, 2010, Springer Science & Business Media.
Google Scholar
2 Murray J. D., Spatial Models and Biomedical Applications, Mathematical Biology. (2003) .
10.1007/b98869
Google Scholar
3 FitzHugh R., Impulses and Physiological States in Theoretical Models of Nerve Membrane, Biophysical Journal. (1961) 1, no. 6, 445–466, https://doi.org/10.1016/s0006-3495(61)86902-6, 2-s2.0-53349102813.
10.1016/S0006-3495(61)86902-6
CAS PubMed Web of Science® Google Scholar
4 Nagumo J., Arimoto S., and Yoshizawa S., An Active Pulse Transmission Line Simulating Nerve Axon, Proceedings of the IRE. (1962) 50, no. 10, 2061–2070, https://doi.org/10.1109/jrproc.1962.288235, 2-s2.0-6344238035.
10.1109/JRPROC.1962.288235
Web of Science® Google Scholar
5 Abbasbandy S., Soliton Solutions for the Fitzhugh–Nagumo Equation With the Homotopy Analysis Method, Applied Mathematical Modelling. (2008) 32, no. 12, 2706–2714, https://doi.org/10.1016/j.apm.2007.09.019, 2-s2.0-50249115553.
10.1016/j.apm.2007.09.019
Web of Science® Google Scholar
6 Abdusalam H. A., Analytic and Approximate Solutions for Nagumo Telegraph Reaction Diffusion Equation, Applied Mathematics and Computation. (2004) 157, no. 2, 515–522, https://doi.org/10.1016/j.amc.2003.08.050, 2-s2.0-4444331927.
10.1016/j.amc.2003.08.050
Web of Science® Google Scholar
7 Aronson D. G. and Weinberger H. f., Multidimensional Nonlinear Diffusion Arising in Population Genetics, Advances in Mathematics. (1978) 30, no. 1, 33–76, https://doi.org/10.1016/0001-8708(78)90130-5, 2-s2.0-49349119963.
10.1016/0001-8708(78)90130-5
Web of Science® Google Scholar
8 Browne P., Momoniat E., and Mahomed F. M., A Generalized Fitzhugh–Nagumo Equation, Nonlinear Analysis: Theory, Methods & Applications. (2008) 68, no. 4, 1006–1015, https://doi.org/10.1016/j.na.2006.12.001, 2-s2.0-36749063849.
10.1016/j.na.2006.12.001
Web of Science® Google Scholar
9 Ramji S. S. A., Eddy K., and Mujahid A., Uncountable Infinite Exact Solutions to the Fitzhugh-Nagumo Model, 2024.
Google Scholar
10 Shahid A. M., Abbas M., and Kwessi E., Nonstandard Nearly Exact Analysis of the Fitzhugh–Nagumo Model, Symmetry. (2024) 16, no. 5, https://doi.org/10.3390/sym16050585.
10.3390/sym16050585
PubMed Web of Science® Google Scholar
11 Hashim I., Noorani M. S. M., and Batiha B., A Note on the Adomian Decomposition Method for the Generalized Huxley Equation, Applied Mathematics and Computation. (2006) 181, no. 2, 1439–1445, https://doi.org/10.1016/j.amc.2006.03.011, 2-s2.0-33750481227.
10.1016/j.amc.2006.03.011
Web of Science® Google Scholar
12 Batiha B., Noorani M. S. M., and Hashim I., Numerical Simulation of the Generalized Huxley Equation by He’s Variational Iteration Method, Applied Mathematics and Computation. (2007) 186, no. 2, 1322–1325, https://doi.org/10.1016/j.amc.2006.07.166, 2-s2.0-33947705255.
10.1016/j.amc.2006.07.166
Web of Science® Google Scholar
13 Batiha B., Noorani M. S. M., and Hashim I., Application of Variational Iteration Method to the Generalized Burgers–Huxley Equation, Chaos, Solitons and Fractals. (2008) 36, no. 3, 660–663, https://doi.org/10.1016/j.chaos.2006.06.080, 2-s2.0-37349130963.
10.1016/j.chaos.2006.06.080
Web of Science® Google Scholar
14 Uma D., Jafari H., Raja Balachandar S., Venkatesh S. G., and Vaidyanathan S., An Approximate Solution for Stochastic Fitzhugh–Nagumo Partial Differential Equations Arising in Neurobiology Models, Mathematical Methods in the Applied Sciences. (2025) 48, no. 3, 2980–2998, https://doi.org/10.1002/mma.10471.
10.1002/mma.10471
Web of Science® Google Scholar
15 Biazar J. and Mohammadi F., Application of Differential Transform Method to the Generalized Burgers–Huxley Equation, Applications and Applied Mathematics: International Journal. (2010) 5, no. 2.
Google Scholar
16 Hariharan G. and Kannan K., Haar Wavelet Method for Solving Fitzhugh-Nagumo Equation, International Journal of Mathematical and Statistical Sciences. (2010) 2, no. 2, 59–63.
Google Scholar
17 Van Gorder R. A., Vajravelu K., and Vajravelu K., A Variational Formulation of the Nagumo Reaction: Diffusion Equation and the Nagumo Telegraph Equation, Nonlinear Analysis: Real World Applications. (2010) 11, no. 4, 2957–2962, https://doi.org/10.1016/j.nonrwa.2009.10.016, 2-s2.0-77955769869.
10.1016/j.nonrwa.2009.10.016
Web of Science® Google Scholar
18 Van G. and Robert A., Gaussian Waves in the Fitzhugh–Nagumo Equation Demonstrate One Role of the Auxiliary Function H.
Google Scholar
19 Shih M., Momoniat E., and Mahomed F. M., Approximate Conditional Symmetries and Approximate Solutions of the Perturbed Fitzhugh–Nagumo Equation, Journal of Mathematical Physics. (2005) 46, no. 2, https://doi.org/10.1063/1.1839276, 2-s2.0-17044384563.
10.1063/1.1839276
Web of Science® Google Scholar
20 Li H. and Guo Y., New Exact Solutions to the Fitzhugh–Nagumo Equation, Applied Mathematics and Computation. (2006) 180, no. 2, 524–528, https://doi.org/10.1016/j.amc.2005.12.035, 2-s2.0-33748956490.
10.1016/j.amc.2005.12.035
Web of Science® Google Scholar
21 Nucci M. C. and Clarkson P. A., The Nonclassical Method Is More General Than the Direct Method for Symmetry Reductions. An Example of the Fitzhugh-Nagumo Equation, Physics Letters A. (1992) 164, no. 1, 49–56, https://doi.org/10.1016/0375-9601(92)90904-z, 2-s2.0-0001870614.
10.1016/0375-9601(92)90904-Z
Web of Science® Google Scholar
22 Bhrawy A. H., An Efficient Jacobi Pseudospectral Approximation for Nonlinear Complex Generalized Zakharov System, Applied Mathematics and Computation. (2014) 247, 30–46, https://doi.org/10.1016/j.amc.2014.08.062, 2-s2.0-84907494463.
10.1016/j.amc.2014.08.062
Web of Science® Google Scholar
23 Bhrawy A. H., A Jacobi Spectral Collocation Method for Solving Multi-Dimensional Nonlinear Fractional Sub-Diffusion Equations, Numerical Algorithms. (2016) 73, no. 1, 91–113, https://doi.org/10.1007/s11075-015-0087-2, 2-s2.0-84949604683.
10.1007/s11075-015-0087-2
Web of Science® Google Scholar
24 Bhrawy A. H., Doha E. H., Ezz-Eldien S. S., and Abdelkawy M. A., A Numerical Technique Based on the Shifted Legendre Polynomials for Solving the Time-Fractional Coupled Kdv Equations, Calcolo. (2016) 53, 1–17, https://doi.org/10.1007/s10092-014-0132-x, 2-s2.0-84959146510.
10.1007/s10092-014-0132-x
Web of Science® Google Scholar
25 Mickens R. E., Advances in the Applications of Nonstandard Finite Diffference Schemes, 2005, World Scientific.
10.1142/5884
Google Scholar
26 Roeger L. I. W. and Mickens R. E., Exact Finite-Difference Schemes for First Order Differential Equations Having Three Distinct Fixed-Points, Journal of Difference Equations and Applications. (2007) 13, no. 12, 1179–1185, https://doi.org/10.1080/10236190701466439, 2-s2.0-36249026248.
10.1080/10236190701466439
Web of Science® Google Scholar
27 Roeger L. I. W., Exact Finite-Difference Schemes for Two-Dimensional Linear Systems With Constant Coefficients, Journal of Computational and Applied Mathematics. (2008) 219, no. 1, 102–109, https://doi.org/10.1016/j.cam.2007.07.015, 2-s2.0-45249111149.
10.1016/j.cam.2007.07.015
Web of Science® Google Scholar
28 Roeger L. I. W., Exact Nonstandard Finite-Difference Methods for A Linear System-the Case of Centers, Journal of Difference Equations and Applications. (2008) 14, no. 4, 381–389, https://doi.org/10.1080/10236190701607669, 2-s2.0-40849124321.
10.1080/10236190701607669
Web of Science® Google Scholar
29 Rucker S., Exact Finite Difference Scheme for an Advection-Reaction Equation, Journal of Difference Equations and Applications. (2003) 9, no. 11, 1007–1013, https://doi.org/10.1080/1023619031000146931, 2-s2.0-0141792573.
10.1080/1023619031000146931
Web of Science® Google Scholar
30 Doha E. H., Dumitru B., Bhrawy A. H., and Abdelkawy M. A., A Jacobi Collocation Method for Solving Nonlinear Burgers-Type Equations, Abstract and Applied Analysis 2013. (2013) 1.
Google Scholar
31 Hussaini M. Y., Craig L. S., and Thomas A. Z., Spectral Methods for Partial Differential Equations, 1983.
Google Scholar
32 Trefethen L. N., Finite Difference and Spectral Methods for Ordinary and Partial Differential Equations, 1996.
Google Scholar
33 Davis P. J., Interpolation and Approximation, Courier Corporation. (1975) .
Google Scholar
34 Khater A. H., Temsah R. S., and Callebaut D. k., Numerical Solutions for Some Coupled Nonlinear Evolution Equations by Using Spectral Collocation Method, Mathematical and Computer Modelling. (2008) 48, no. 7-8, 1237–1253, https://doi.org/10.1016/j.mcm.2008.02.001, 2-s2.0-49749124630.
10.1016/j.mcm.2008.02.001
Web of Science® Google Scholar
35 Jiwari R., A Haar Wavelet Quasilinearization Approach for Numerical Simulation of Burgers’ Equation, Computer Physics Communications. (2012) 183, no. 11, 2413–2423, https://doi.org/10.1016/j.cpc.2012.06.009, 2-s2.0-84864445832.
10.1016/j.cpc.2012.06.009
CAS Web of Science® Google Scholar
36 Kamrani M. and Hosseini S. M., Spectral Collocation Method for Stochastic Burgers Equation Driven by Additive Noise, Mathematics and Computers in Simulation. (2012) 82, no. 9, 1630–1644, https://doi.org/10.1016/j.matcom.2012.03.007, 2-s2.0-84861611189.
10.1016/j.matcom.2012.03.007
Web of Science® Google Scholar
37 Sun Y. and Li B. W., Chebyshev Collocation Spectral Method for One-Dimensional Radiative Heat Transfer in Graded Index Media, International Journal of Thermal Sciences. (2009) 48, no. 4, 691–698, https://doi.org/10.1016/j.ijthermalsci.2008.07.003, 2-s2.0-58549090306.
10.1016/j.ijthermalsci.2008.07.003
CAS Google Scholar
38 Sun Y. and Li B. W., Chebyshev Collocation Spectral Approach for Combined Radiation and Conduction Heat Transfer in One-Dimensional Semitransparent Medium With Graded Index, International Journal of Heat and Mass Transfer. (2010) 53, no. 7-8, 1491–1497, https://doi.org/10.1016/j.ijheatmasstransfer.2009.11.047, 2-s2.0-74549195771.
10.1016/j.ijheatmasstransfer.2009.11.047
Web of Science® Google Scholar
39 Mittal R. C. and Jiwari R., Numerical Solution of Two-Dimensional Reaction-Diffusion Brusselator System, Applied Mathematics and Computation. (2011) 217, no. 12, 5404–5415, https://doi.org/10.1016/j.amc.2010.12.010, 2-s2.0-79551629810.
10.1016/j.amc.2010.12.010
Web of Science® Google Scholar
40 Mittal R. C. and Jiwari R., A Differential Quadrature Method for Numerical Solutions of Burgers’-Type Equations, International Journal of Numerical Methods for Heat and Fluid Flow. (2012) 22, no. 7, 880–895, https://doi.org/10.1108/09615531211255761, 2-s2.0-84866976370.
10.1108/09615531211255761
Web of Science® Google Scholar
41 Motsa S. S., Magagula V. M., and Sibanda P., A Bivariate Chebyshev Spectral Collocation Quasilinearization Method for Nonlinear Evolution Parabolic Equations, The Scientific World Journal. (2014) 2014, no. 1, 1–13, https://doi.org/10.1155/2014/581987, 2-s2.0-84931331766.
10.1155/2014/581987
Google Scholar
42 Rezazadeh A., Mahmoud M., and Majid D., Space–Time Spectral Collocation Method for One-Dimensional PDE Constrained Optimization, International Journal of Control. (2020) 93, no. 5, 1231–1241.
10.1080/00207179.2018.1501161
Google Scholar
43 Shadrin A., Error Bounds for Lagrange Interpolation, Journal of Approximation Theory. (1995) 80, no. 1, 25–49, https://doi.org/10.1006/jath.1995.1003, 2-s2.0-0001871037.
10.1006/jath.1995.1003
Web of Science® Google Scholar
44 Khumalo F. B., Motsa S. S., and Magagula V. M., A Bivariate Spectral Linear Partition Method for Solving Nonlinear Evolution Equations, Mathematical Methods in the Applied Sciences. (2024) 47, no. 7, 6607–6621, https://doi.org/10.1002/mma.9940.
10.1002/mma.9940
Web of Science® Google Scholar
45 Huang J., Nie N., and Tang Y., A Second Order Finite Difference-Spectral Method for Space Fractional Diffusion Equations, Science China Mathematics. (2014) 57, no. 6, 1303–1317, https://doi.org/10.1007/s11425-013-4716-8, 2-s2.0-84900504953.
10.1007/s11425-013-4716-8
Web of Science® Google Scholar
46 Rufai M. A., Kosti A. A., Anastassi Z. A., and Carpentieri B., A New Two-Step Hybrid Block Method for the FitzHugh–Nagumo Model Equation, Mathematics (Basel). (2023) 12, no. 1, https://doi.org/10.3390/math12010051.
10.3390/math12010051
Google Scholar
47 Adeyefa E. O., Omole E. O., and Shokri A., Numerical Solution of Second-Order Nonlinear Partial Differential Equations Originating From Physical Phenomena Using Hermite Based Block Methods, Results in Physics. (2023) 46, https://doi.org/10.1016/j.rinp.2023.106270.
10.1016/j.rinp.2023.106270
Web of Science® Google Scholar
48 Olaoluwa Omole E., Olusheye Adeyefa E., Iyabo Apanpa K., Iyadunni Ayodele V., Emmanuel Amoyedo F., and Emadifar H., Unveiling the Power of Implicit Six-Point Block Scheme: Advancing Numerical Approximation of Two-Dimensional PDEs in Physical Systems, PLoS One. (2024) 19, no. 5, https://doi.org/10.1371/journal.pone.0301505.
10.1371/journal.pone.0301505
PubMed Web of Science® Google Scholar
49 Mehta A., Singh G., and Ramos H., Numerical Solution of Time Dependent Nonlinear Partial Differential Equations Using a Novel Block Method Coupled With Compact Finite Difference Schemes, Computational and Applied Mathematics. (2023) 42, no. 4, https://doi.org/10.1007/s40314-023-02345-3.
10.1007/s40314-023-02345-3
Web of Science® Google Scholar
50 Rufai M. A. and Ramos H., A Variable Step-Size Fourth-Derivative Hybrid Block Strategy for Integrating Third-Order IVPs, With Applications, International Journal of Computer Mathematics. (2022) 99, no. 2, 292–308, https://doi.org/10.1080/00207160.2021.1907357.
10.1080/00207160.2021.1907357
Web of Science® Google Scholar
51 Rufai U. O., Sibanda P., and Goqo S. P., A One-Step Multi-Derivative Hybrid Block Method With Modified-Picard Iteration for the Solution of Second Order IVP, Engineering Letters. (2023) 31, no. 4.
Google Scholar
52 Kayode S. J., Olabode B. T., and Ige O. S., Four-Step Multi-Derivative Predictor Corrector Method for the Solution of Second Order Ordinary Differential Equations, World Scientific News. (2023) 176, 133–144.
Google Scholar
53 Rufai U. O., Sibanda P., and Goqo S., An Overlapping Adaptive Step-Size Multi-Derivative Hybrid Block Method for Higher Order Initial Value Problems, Computational Methods for Differential Equations. (2025) .
Google Scholar
54 Ramos H., Kalogiratou Z., Monovasilis T., and Simos T. E., An Optimized Two-Step Hybrid Block Method for Solving General Second Order Initial-Value Problems, Numerical Algorithms. (2016) 72, no. 4, 1089–1102, https://doi.org/10.1007/s11075-015-0081-8, 2-s2.0-84948988921.
10.1007/s11075-015-0081-8
PubMed Web of Science® Google Scholar
55 Ramos H., An Optimized Two-Step Hybrid Block Method for Solving rst-Order Initial-Value Problems in ODEs, Differential Geometry-Dynamical Systems. (2017) 19.
Google Scholar
56 Kashkari B. S. and Alqarni S., Optimization of Two-Step Block Method With Three Hybrid Points for Solving Third Order Initial Value Problems, The Journal of Nonlinear Science and Applications. (2019) 12, no. 07, 450–469, https://doi.org/10.22436/jnsa.012.07.04.
10.22436/jnsa.012.07.04
Google Scholar
57 Motsa S., Overlapping Grid-Based Optimized Single-Step Hybrid Block Method for Solving First-Order Initial Value Problems, Algorithms. (2022) 15, no. 11, https://doi.org/10.3390/a15110427.
10.3390/a15110427
Web of Science® Google Scholar
58 Singh G., Garg A., Kanwar V., and Ramos H., An Efficient Optimized Adaptive Step-Size Hybrid Block Method for Integrating Differential Systems, Applied Mathematics and Computation. (2019) 362, https://doi.org/10.1016/j.amc.2019.124567, 2-s2.0-85068584676.
10.1016/j.amc.2019.124567
Web of Science® Google Scholar
59 Singla R., Singh G., Ramos H., and Kanwar V., An Efficient Optimized Adaptive Step-Size Hybrid Block Method for Integrating Directly, Journal of Computational and Applied Mathematics. (2023) 420, https://doi.org/10.1016/j.cam.2022.114838.
10.1016/j.cam.2022.114838
Google Scholar
60 Yakubu S. D. and Sibanda P., One-Step Family of Three Optimized Second-Derivative Hybrid Block Methods for Solving First-Order Stiff Problems, Journal of Applied Mathematics. (2024) 2024, no. 1, https://doi.org/10.1155/2024/5078943.
10.1155/2024/5078943
Web of Science® Google Scholar
61 Jiwari R., Gupta R. K., and Kumar V., Polynomial Differential Quadrature Method for Numerical Solutions of The Generalized Fitzhugh–Nagumo Equation with Time-Dependent Coefficients, Ain Shams Engineering Journal. (2014) 5, no. 4, 1343–1350, https://doi.org/10.1016/j.asej.2014.06.005, 2-s2.0-84919483705.
10.1016/j.asej.2014.06.005
Google Scholar
62 Namjoo M. and Zibaei S., Numerical Solutions of Fitzhugh–Nagumo Equation by Exact Finite-Difference and NSFD Schemes, Computational and Applied Mathematics. (2018) 37, no. 2, 1395–1411, https://doi.org/10.1007/s40314-016-0406-9, 2-s2.0-85047428132.
10.1007/s40314-016-0406-9
Web of Science® Google Scholar
63 İnan B., Ali K. K., Saha A., and Ak T., Analytical and Numerical Solutions of the Fitzhugh–Nagumo Equation and Their Multistability Behavior, Numerical Methods for Partial Differential Equations. (2021) 37, no. 1, 7–23, https://doi.org/10.1002/num.22516.
10.1002/num.22516
Web of Science® Google Scholar
64 Manaa S. A., Easif F. H., and Faris A. S., The Finite Difference Methods for FitzHugh-Nagumo Equation, Journal of Mathematics. (2015) 11, no. 2, 51–55.
Google Scholar
65 Ahmedai Abd Allah S. A. A., Sibanda P., Goqo S. P., Rufai U. O., Sithole Mthethwa H., and Noreldin O. A. I., A Block Hybrid Method With Equally Spaced Grid Points for Third-Order Initial Value Problems, AppliedMath. (2024) 4, no. 1, 320–347, https://doi.org/10.3390/appliedmath4010017.
10.3390/appliedmath4010017
Google Scholar
66 Ola Fatunla S., Block Methods for Second Order Odes, International Journal of Computer Mathematics. (1991) 41, no. 1–2, 55–63, https://doi.org/10.1080/00207169108804026, 2-s2.0-84948885570.
10.1080/00207169108804026
Web of Science® Google Scholar
67 Singla R., Singh G., Ramos H., and Kanwar V., A Family of A-Stable Optimized Hybrid Block Methods for Integrating Stiff Differential Systems, Mathematical Problems in Engineering. (2022) 1.
Google Scholar
68 Trefethen L. N., Spectral Methods in MATLAB, 2000, Society for Industrial and Applied Mathematics.
10.1137/1.9780898719598
Google Scholar
69 Motsa S. S., On the Optimal Auxiliary Linear Operator for the Spectral Homotopy Analysis Method Solution of Nonlinear Ordinary Differential Equations, Mathematical Problems in Engineering. (2014) 2014, no. 1, https://doi.org/10.1155/2014/697845, 2-s2.0-84907257065.
10.1155/2014/697845
Web of Science® Google Scholar

All articles

Spectral Optimized Multiderivative Hybrid Block Method for Fitzhugh–Nagumo Equations

Abstract

1. Introduction

2. Derivation of the Method

3. Analysis of the Method

3.1. Local Truncation Error (LTE)

3.2. Zero Stability

3.3. Proof of Absolute Stability

4. Implementation

5. Applications in F-N Equations

6. Conclusions

Nomenclature

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Spectral Optimized Multiderivative Hybrid Block Method for Fitzhugh–Nagumo Equations

Abstract

1. Introduction

2. Derivation of the Method

3. Analysis of the Method

3.1. Local Truncation Error (LTE)

3.2. Zero Stability

3.3. Proof of Absolute Stability

4. Implementation

5. Applications in F-N Equations

6. Conclusions

Nomenclature

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Related

Information