This work presents a theoretical comparative analysis of wireless optical nanolinks with different cylindrical plasmonic nanoantennas fed by a Gaussian beam. The nanolinks considered are Yagi–Uda-loop/dipole, Yagi–Uda/dipole and dipole/dipole, where the operating wavelength is λ = 1153 nm. The numerical analysis of these nanolinks was performed by the linear moment method with an equivalent surface impedance of the conductors. With this method, the following parameters were evaluated by each nanlolink: current along the antennas, near field distributions and the power transmission in the receiving antenna. The results show that the Yagi–Uda-loop/dipole nanolink presents an improvement of approximately 5 dB in relation to the dipole/dipole nanolink and 3.2 dB in relation to the Yagi–Uda/dipole nanolink.

1. Introduction

In recent years, optical nanoantennas have been the subject of great interest in the scientific community thanks to their ability to amplify, manipulate, and confine optical fields beyond the diffraction limit of light [1]. Due to these characteristics, they offer unique opportunities for applications in more efficient photovoltaic devices [2], optical sensors [3, 4], optical circuits [5], fiber optics [6], and wireless optical nanolinks [7–11], which can be used, for example, to interconnect different devices in an integrated nanophotonic circuit.

Optical wireless communications have recently emerged as a promising alternative for chip-scale interconnects, particularly through the use of plasmonic nanoantennas that allow subwavelength field confinement and highly directional radiation. Among the proposed architectures, Yagi–Uda nanoantennas stand out as efficient optical analogs of traditional radio-frequency antennas, offering high directivity and front-to-back ratios [12]. In [12], Maksymov et al. provided a comprehensive review of the design and application of these antennas in the optical regime, emphasizing the necessity to adapt classical design strategies due to plasmonic resonance effects. Building on this foundation, Damasceno et al. [13] proposed a systematic optimization strategy for chip-scale Yagi–Uda nanoantennas, considering variations in the length and spacing of metallic elements. Furthermore, Damasceno et al. [14] introduced reconfigurable magnetoplasmonic nanoantennas whose emission direction can be controlled magnetically, enabling active and tunable links on integrated platforms. Another significant contribution came from Elsaid et al. [15], who proposed rhombic nanoantennas with broadband response and high efficiency at 1550 nm, making them attractive candidates for optical telecommunication systems. In addition, Solís et al. [16] demonstrated that matched directive nanoantennas significantly outperform omnidirectional structures and plasmonic waveguides by reducing absorption losses and improving coupling efficiency. Despite these advances, comparative studies involving different plasmonic nanoantenna topologies in wireless nanolinks excited by spatially confined optical beams, such as Gaussian beams, remain scarce, a gap this work aims to address.

This work presents a comparative analysis of nanolinks formed by transmitting and receiving cylindrical plasmonic nanoantennas, where the transmitting antennas are fed by a Gaussian beam, which is a more realistic power source, with a wavelength equal to λ = 1153 nm. The antennas used in the links are Yagi–Uda-loop, Yagi–Uda, and dipole, where the first consists of a Yagi–Uda antenna coupled to a cylindrical parasitic loop. These nanoantennas have already been analyzed in isolated situations, being fed by a voltage source. However, this work investigates these nanoantennas for the first time in wireless nanolinks and fed by a Gaussian beam.

Three nanolinks are analyzed: Yagi–Uda-loop/dipole, Yagi–Uda/dipole and dipole/dipole, where the dipole is the receiving antenna in all cases. The analysis of these electromagnetic problems was performed by the linear Method of Moments (MoMs), in the same way as was done in [17, 18]. The results show the current along the antennas and the near field distributions. Also, the relation between the power received by the load connected in the terminals of the receiving antenna and the Gaussian beam power is investigated as a function of the distance between transmitter and receiver. This relation we call here transmission power. Section 2 presents the theoretical development, Section 3 shows the numerical results, and Section 4 discusses the conclusions.

2. Theoretical Development

2.1. Geometries of the Nanolinks

Three models of nanolinks are investigated, each with different antenna configurations for transmission and reception: the first model consists of Yagi–Uda-loop/dipole antennas, with a Yagi–Uda-loop antenna for transmission and a dipole for reception (Figure 1(a)); the second model is composed of Yagi–Uda/dipole antennas, with a Yagi–Uda antenna for transmission and a dipole for reception (Figure 1(b)); and the third model employs dipole/dipole antennas, where both the transmitting and receiving antennas are of the dipole type (Figure 1(c)).

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Geometries of the four YU nanoantennas models in study. (a) Yagi–Uda-loop/dipole, (b) Yagi–Uda/dipole, and (c) dipole/dipole.

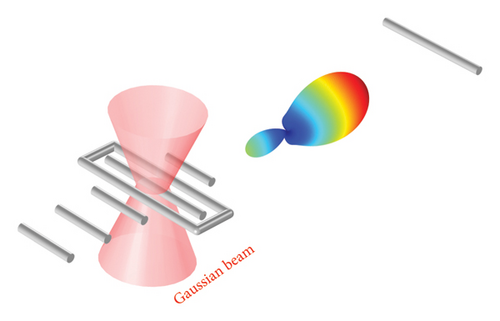
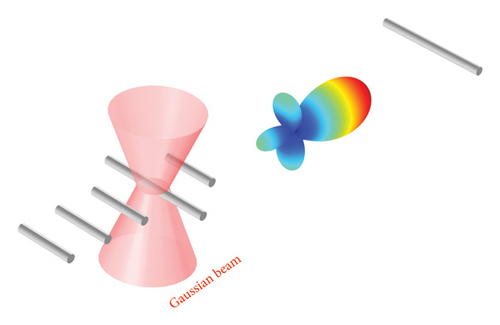
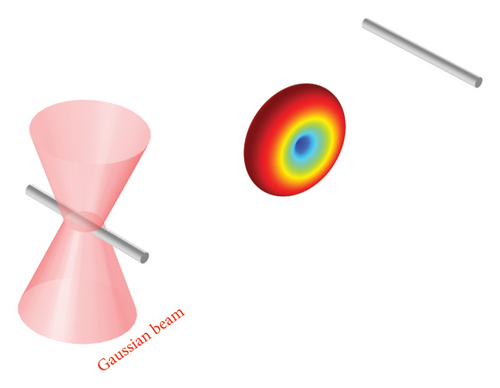
Figure 2(a) shows the geometry of the Yagi–Uda-loop/dipole nanolink. A Gaussian beam is used to feed the nanoantenna located on the left side (Yagi–Uda-loop antenna), which acts as the transmitter. This antenna converts the near field receiving from the Gaussian beam into optical radiation (scattered field), which propagates through free space. The nanoantenna positioned on the right serves as the receiver (dipole antenna), capturing the radiation emitted by the transmitting antenna and converting it into received power across the load Z_C.

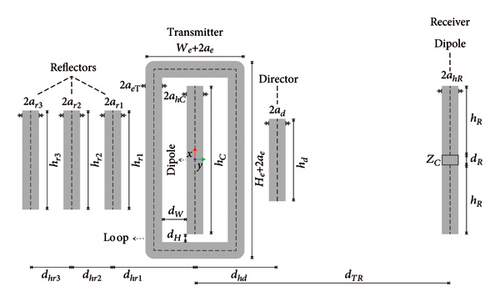
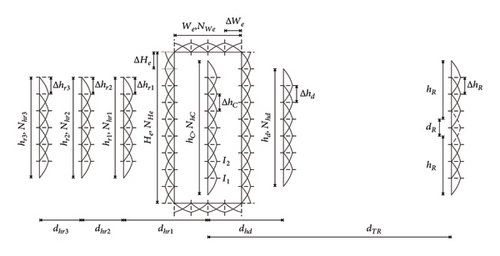
The antennas are made by cylindrical gold conductors positioned in free space. The transmitting nanoantenna is composed by one central dipole, one director, three reflectors, and a rectangular loop (Figure 2(a), left side). The central dipole is located in the z = 0 plane, along the x axis and centered at the origin, with length h_C and radius a_hC. The director has length h_d and radius a_d. The reflectors (first, second, and third) have lengths h_r1, h_r2, and h_r3 and radii a_r1, a_r2, and a_r3, respectively.

The rectangular loop has length H_e + 2a_e, width W_e + 2a_e, radius a_e, and the parameters d_W and d_H are the distances between the surfaces of the dipole and the loop. The parameters d_hd, d_hr1, d_hr2, and d_hr3 are the distances between the elements of the Yagi–Uda antenna (Figure 2(a) left). The receiving antenna is a dipole (Figure 2(a) right), located in the plane z = 0 and displaced by a distance d_TR with respect to the axis of the dipole of the transmitting antenna, of total length 2h_R + d_R, radius a_hR, and size d_R of the center gap where the load Z_C is connected.

The geometry of the Yagi–Uda/dipole and dipole/dipole nanolinks is based on the Yagi–Uda-loop/dipole link model (Figure 2(a)), with simplifications. The geometry of the Yagi–Uda/dipole link is the same as the Yagi–Uda-Loop/dipole, but without the loop element. The geometry of the dipole/dipole link uses only simple dipoles in transmission and reception, removing the reflectors, the director, and the loop element.

2.2. MoMs Model

To analyze the nanolink configurations depicted in Figure 1, we employ the linear MoMs to solve the one-dimensional integral equation governing the electric field. The solution is obtained using a linear approximation of the longitudinal current, with sinusoidal basis functions and rectangular pulse testing functions, as described in [17].

The nanoantennas are modeled using gold as the conducting material, whose complex permittivity is described by the Lorentz–Drude model [19]. A detailed implementation of this model, including the specific parameters used for gold in the optical frequency range, can be found in [17].

Metallic losses are accounted for via the surface impedance Z_s, which is approximated by modeling the conductor as a cylindrical waveguide operating in the fundamental TM₀₁ mode. Under this approximation, the surface impedance is expressed as follows [20]:

()

where

and

, J₀ and J₁ are the Bessel functions of the first kind of order zero and one, respectively, ω is the angular frequency of operation, k₀ is the propagation constant in air, µ₀ is the magnetic permeability of air, ε₀ is the electrical permittivity of air, and a is the radius of the cylindrical conductor.

The integral equation of the scattering problem is obtained by the following boundary condition on the surface of the conductor

, where

is a unit vector tangential to the surface of the conductor,

is the scattered electric field due to the linear current I induced in the conductor,

is the external electric field incident on the conductor due to the Gaussian beam, and I is the longitudinal current induced at a given point of the nanoantenna. The scattered field is given by

()

where

is the free-space Green’s function and

is the distance between the source and the observation points. For MoM application, the nanolink in Figure 2(a) is discretized (see Figure 2(b)), where N_hC, N_He, N_We, N_hd, N_hr1, N_hr2, N_hr3, and N_hR are the numbers of straight line segments in h_C, H_e, W_e, h_d, h_r1, h_r2, h_r3, and h_R – 0.5d_R, respectively, with discretization sizes Δh_C = h_C/N_hC, ΔH_e = H_e/N_He, ΔW_e = W_e/N_We, Δh_d = h_d/N_hd, Δh_r1 = h_r1/N_hr1, Δh_r2 = h_r2/N_hr2, Δh_r3 = h_r3/N_hr3, and Δh_R = (h_R–0.5d_R)h_r3/N_R (solid line segment in the receiving antenna dipole), respectively. The load has two segments at the center of the receiving antenna dipole, with size Δd_R (segment with dashed line in the receiving antenna dipole). The total number of straight segments of the nanolink are N_t = N_hC + N_He + N_We + N_hd + N_hr1 + N_hr2 + N_hr3 + 2N_hR and the number of sinusoidal basis functions are N = N_t −1. For the stability of the method, the convergence condition Δh_C > 2a_hC, ΔH_e > 2a_e, ΔW_e > 2a_e, Δh_d > 2a_hd, Δh_r1 > 2a_hr1, Δh_r2 > 2a_hr2, Δh_r2 > 2a_hr2, and Δh_R > 2a_hR is used. Then, the current in each segment is approximated by sinusoidal basis functions. The expansion constants are shown in Figure 2(b), where each constant defines a triangular sinusoidal current. To determine these constants, rectangular pulse test functions with unit amplitude are used and the conventional test procedure [17] is performed, where the following linear system is obtained:

()

where V_m is the voltage across a generic segment m, the elements of Z_mn represent the mutual impedance between different points m and n on the antenna surface,

. The solution of system (3) gives the current along the elements forming the nonalinks. With these results, it is possible to calculate the near and far field distributions and other parameters.

2.3. Gaussian Beam

The incident electric field

that feeds the transmitting antennas is an ideal Gaussian beam. This type of wave is obtained by solving the Helmholtz scalar wave equation with the paraxial approximation [21]. The magnetic vector potential of a Gaussian beam polarized on the x axis and propagating in the +z direction is given by

()

where

, P is the beam power, w is the beam radius (beam waist) at a given position along the z-axis, w₀ is the minimum beam waist (i.e., the waist at the focal plane, where z = 0), R is the radius of curvature of the phase front, and ϕ is the beam phase. The three main parameters that define the Gaussian beam are the power P, the minimum waist radius w₀, and the operating wavelength λ. Using the vector potential described in equation (4), the x-component of the electric field E_x can be derived from Maxwell’s equations, as shown in [21].

3. Numerical Results

In this section, we initially discuss the accuracy of the MoM code developed in MATLAB, based on the mathematical model presented in Section 2, by comparing a simulation example performed using the MoM and the Comsol Multiphysics software [22]. Subsequently, we analyze the proposed nanoantennas alone and later the wireless nanolinks. The numerical results for the isolated nanoantennas and wireless nanolinks are presented considering their excitation by a Gaussian beam with a wavelength of λ = 1153 nm.

3.1. Theoretical Validation of the MoM Model

To verify the theoretical accuracy of MoM, this section presents a simulation example, performed by MoM and the Comsol Multiphysics software [22], of a cylindrical gold nanorod located in free space, positioned along the x-axis and centered at the origin. The nanoantenna of length h_C and radius a_hC = 27 nm is illuminated by an ideal Gaussian beam (power source) polarized on the x-axis and propagating in the +z direction. The beam has radius w, beam waist w₀, power P, and operating wavelength λ. The Gaussian beam model is shown in detail in chapter 9 of reference [21]. In this example, a fixed Gaussian beam was used, with power P = 10⁻¹² W, wavelength λ = 1153 nm, and beam waist w₀ = 340 nm.

Figure 3 shows the variation of the current amplitude at the center (I_C) of the cylindrical nanobar as a function of the length h_C and radius a_hC = 27 nm, simulated by MoM and Comsol software. The figure shows good agreement between the two methods, which reflects excellent accuracy and convergence of MoM. The difference between the results occurs because MoM uses a 1D current element approximation for the cylindrical conductor, while Comsol uses 3D elements.

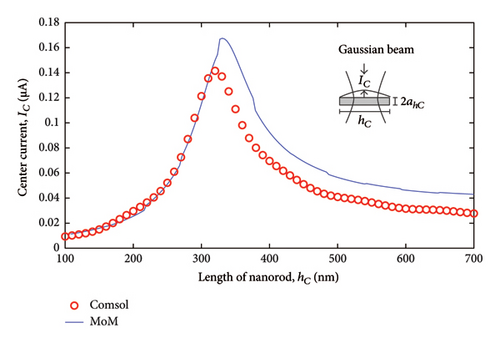
MoM discretizes only the conductor and Comsol discretizes the conductor and the domain around the conductor. Therefore, MoM uses a smaller number of elements, which results in computational gains in terms of memory and processing time.

Other comparisons of results between the MoM model and the Comsol software for cylindrical structures are found in [17, 18, 23, 24]. In [23], the structure is a dipole-loop nanoantenna fed by a two-wire optical transmission line; in [24], a dipole fed by a voltage source; in [18], an optical nanocircuit fed by a Gaussian beam; and in [17], are nanobar and nanodipole fed by a plane wave and optical nanocircuit fed by a voltage source.

3.2. Transmitting Antennas

In this section, the Yagi–Uda-loop, Yagi–Uda, and dipole antennas are analyzed separately. For this analysis, the antenna parameter values are those shown in Table 1, where with these values the main resonance is around 260 THz (λ ≈ 1153 nm). The parameters of the transmitting antennas are based on [25], where the author used the optimization method called adaptive fuzzy GAPSO, to find the best geometry for the nanoantennas.

Table 1. Geometric parameters of the transmitting nanoantennas.

Dipole					1^streflector
Length (h_C)			Radius (a_hC)		Length (h_r1)	Distance (d_r1)	Radius (a_r1)
550 nm			27 nm		285 nm	291 nm	30 nm
Director					2^ndreflector
Length (h_d)		Distance (d_d)		Radius (a_d)	Length (h_r2)	Distance (d_r2)	Radius (a_r2)
254 nm		267 nm		29 nm	281 nm	283 nm	30 nm
Rectangular loop					3^ndreflector
d_W	d_H	Length (H_e)	Width (W_e)	Radius (a_e)	Length (h_r3)	Distance (d_r3)	Radius (a_r3)
50 nm	20 nm	630 nm	194 nm	20 nm	280 nm	290 nm	28 nm

The excitation beam used to feed the transmitting antennas is focused on the transmitting dipole with polarization along the dipole axis (x-axis), the propagation direction is +z, the beam axis is along the z axis, and the minimum beam waist (w₀) is located at z = 0, which is the plane of the nanoantennas. In all analyses a fixed Gaussian beam will be used, with power P = 10⁻¹²W, wavelength λ = 1153 nm, and beam waist w₀ = 340 nm. The beam parameters are based on [18].

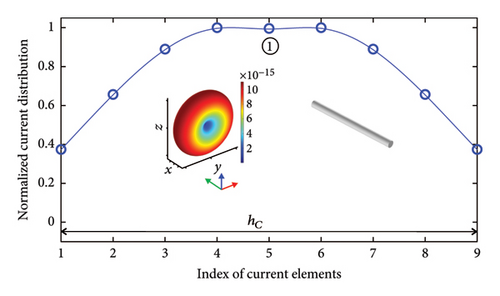
Figure 4 presents the results of current distribution and 3D far-field radiation (radiation intensity) diagram for the isolated nanodipole (Figure 4(a)), Yagi–Uda (Figure 4(b)), and Yagi–Uda-loop (Figure 4(c)). For the isolated nanodipole (Figure 4(a)), it is possible to observe the 3D diagram with the conventional omnidirectional radiation pattern of the dipole and the expected current distribution, presenting the half-wavelength λ/2 format.

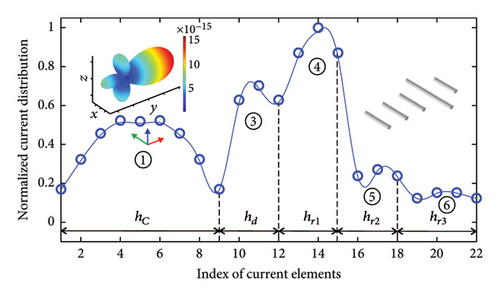
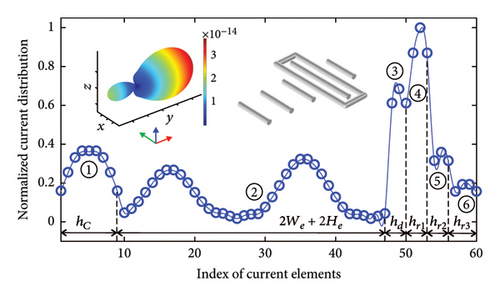
In the case of the isolated Yagi–Uda nanoantenna (Figure 4(b)), the directional radiation diagram is observed, with the main lobe (+y direction) and three small side lobes. In the current distribution, some limits are drawn to identify the current of each element of the Yagi–Uda nanoantenna, from left to right, they are dipole (h_C), director (h_d), reflector 1 (h_r1), reflector 2 (h_r2), and reflector 3 (h_r3).

In the case of the Yagi–Uda-loop nanoantenna (Figure 4(c)), the directional radiation diagram is observed, with the main lobe (+y direction), and a small secondary lobe in the −y direction. In the current distribution, some limits are drawn to identify the current of each element of the Yagi–Uda-loop nanoantenna, from left to right, they are dipole (h_C), loop (2W_e + 2H_e), director (h_d), reflector 1 (h_r1), reflector 2 (h_r2), and reflector 3 (h_r3). It can be observed that all elements of the Yagi–Uda-loop antenna have a dipolar current distribution pattern, approaching half a wavelength λ/2. In addition, the current amplitude is smaller in the reflectors furthest from the dipole.

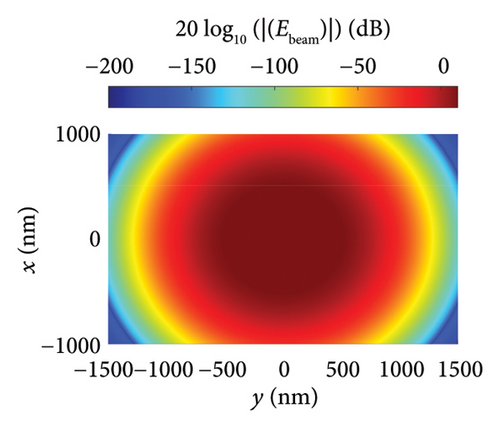
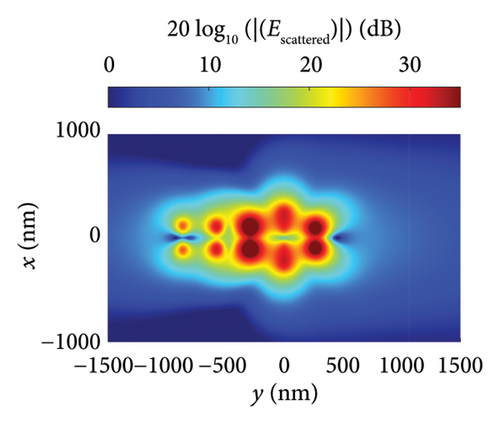
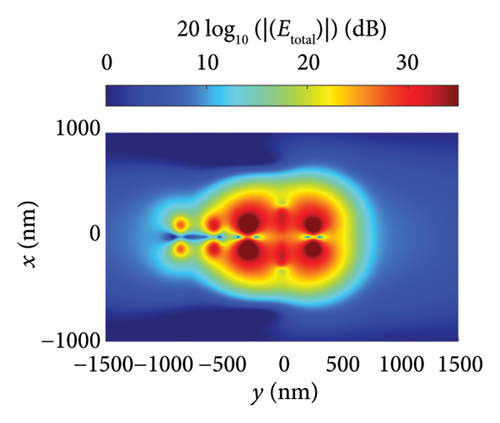
Figures 5(a), 5(b), and 5(c) illustrate the distribution of the incident, scattered, and total near fields, respectively, for the isolated nanodipole. Similarly, Figures 6(a), 6(b), and 6(c) present the distribution of the incident, scattered, and total near fields for the Yagi–Uda nanoantenna. Figures 7(a), 7(b), and 7(c) show the same field distributions for the Yagi–Uda-loop nanoantenna. It can be observed in Figures 5(b), 5(c), 6(b), 6(c), 7(b), and 7(c) that regions with higher electric field intensity are located near the nanoantennas, indicating strong coupling between the Gaussian beam and the transmitting nanoantennas. In other words, the Gaussian beam is effectively exciting these nanostructures.

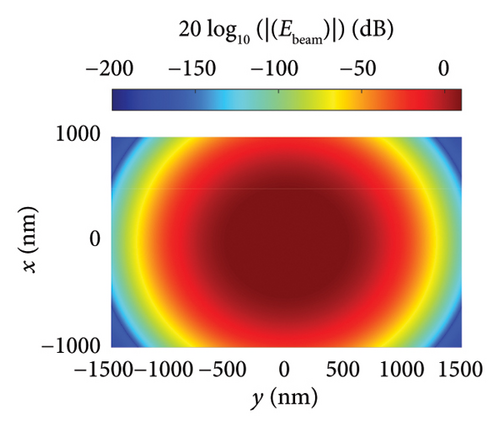
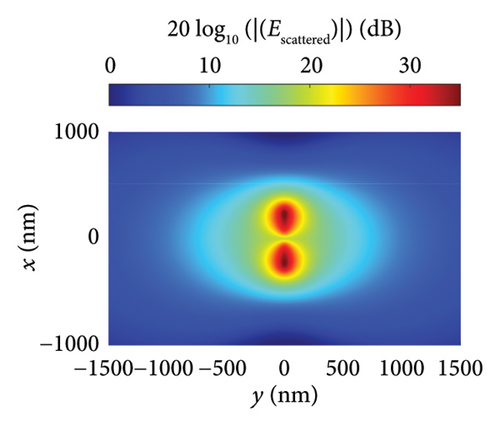
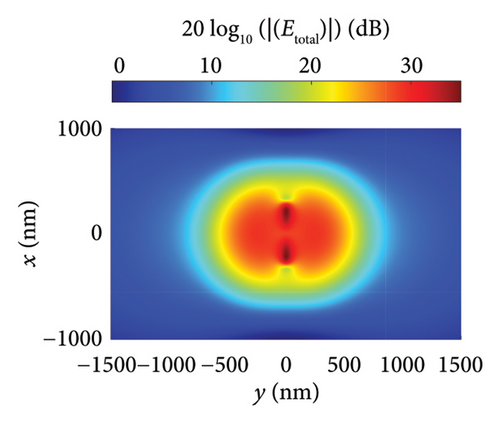
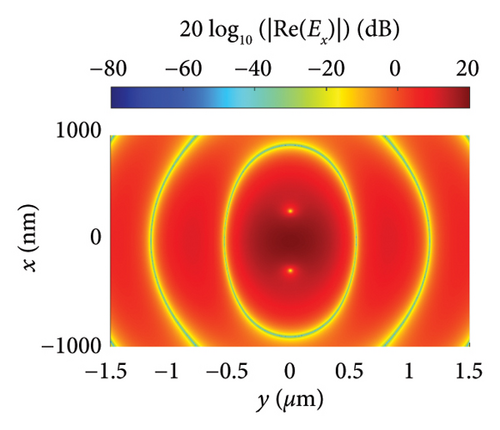
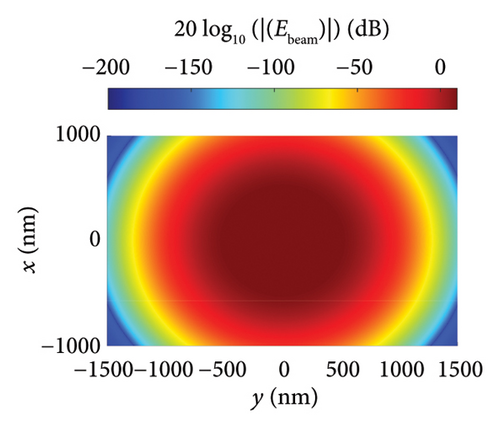
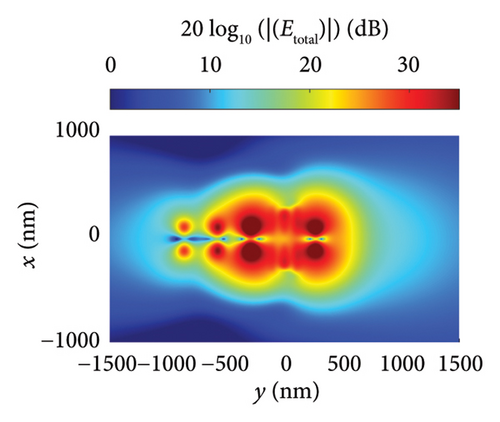
Figures 5(d), 6(d), and 7(d) show the magnitude and phase of the near-field electric field distribution, E = 20 log₁₀ (|Re (E_x)|), for the dipole, Yagi–Uda, and Yagi–Uda-loop antennas, respectively, in the z = a_hC + 20 nm plane. In this result, a more spherical wavefront is observed in Figure 7(d) mainly due to the loop, which has a more spherical geometry in this plane.

3.3. Wireless Optical Nanolinks

This section presents the results obtained in the analysis of the dipole/dipole nanolink (Figure 2(a), without director, reflectors, and loop), Yagi–Uda/dipole (Figure 2(a) without the loop), and Yagi–Uda-loop/dipole (Figure 2(a)). The parameters used for the transmitting antennas are the same as in the previous section and for the receiving antennas, the parameters used were h_R = 260 nm, d_R = 30 nm, and a_dR = 27 nm. For each nanolink, a load Z_C = 50 Ω was used and connected to the terminals of the receiving dipole antenna.

The power transfer between transmitter–receiver links can be investigated by calculating the power transmission (or power transfer function). This parameter can be calculated approximately using the Friis analytical transmission equation [26], as was done in [7, 9, 10], or more precisely by the numerical model of MoM [8, 17, 23]. The definition of this parameter is the ratio between the power delivered to the load Z_C and the power delivered to the transmitting antenna. In MoM, this power can be given by P_ZC/P_in = (0, 5) |I_C| Re (Z_C)/(10⁻¹²), where the P_in used was the power of the Gaussian beam (P_in = 10⁻¹² W). The calculation of transmission power using the MoM model offers significant advantages over other methods, such as the finite difference time domain (FDTD) and the finite element method (FEM). In these methods, analyzing large distances would be computationally impractical, as it would require an enormous amount of memory to discretize the entire analysis domain. In contrast, the MoM overcomes this limitation by discretizing only the geometry of the antenna, significantly reducing computational demands [23].

Figure 8 shows the power transmission behavior, as a function of distance, for the dipole/dipole, Yagi–Uda/dipole, and Yagi–Uda-loop/dipole nanolinks. In addition, the figure also presents the power transmission characteristics of a bifilar cylindrical optical transmission line (OTL), which connects the transmitting and receiving nanoantennas shown in Figure 2(a), but without the inclusion of directors, reflectors, or the loop element, thus forming a basic optical nanocircuit. The transmitting nanoantenna is excited by the same Gaussian beam used in the wireless nanolinks. The OTL has a conductor radius of 15 nm and a total length of 5 μm.

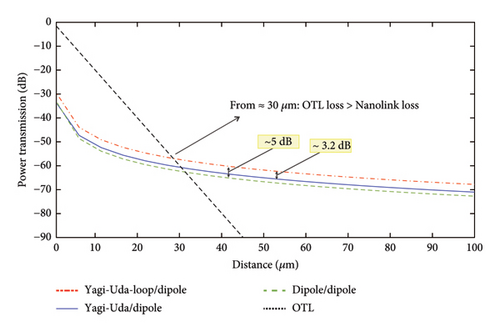
The losses in the OTL are estimated using the same methodology described in [18] and further supported by [27]. In this approach, the loss constant α, which remains approximately constant for the dominant propagation mode in the OTL, is determined by the average slope of the current amplitude in decibels (dB) as a function of distance along the transmission line. Mathematically, this is expressed as α = ΔI/ΔL, where ΔI represents the average current decay in dB over a distance ΔL. For the configuration analyzed, the estimated value of α was approximately 0.0019954 dB/nm for an OTL of length L = 5 μm.

Figure 8 shows that wireless optical nanolinks can have lower loss compared with wired nanolinks, from a certain distance, which for the considered cases is from 30 μm. This shows that optical nanolinks based on nanoantennas are more suitable than OTL for communication at distances above approximately 30 μm. In addition, the Yagi–Uda-loop/dipole nanolink presents an improvement of approximately 5 dB compared with the dipole/dipole nanolink and 3.2 dB compared with the Yagi–Uda/dipole nanolink. The Yagi–Uda/dipole nanolink presents an improvement of 1.7 dB compared with the dipole/dipole nanolink.

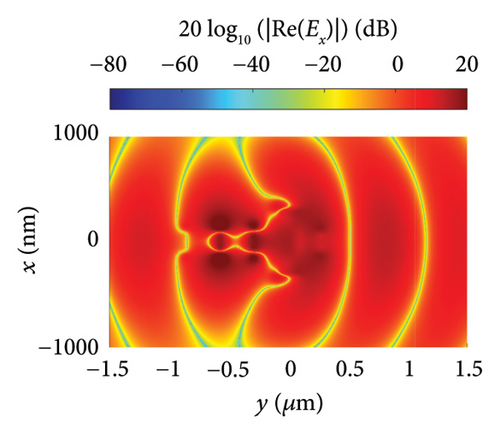
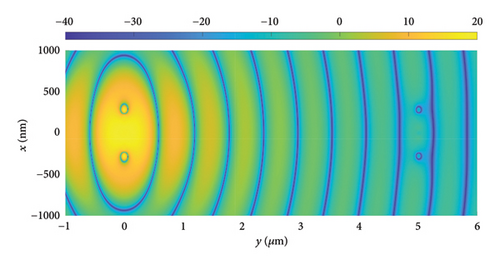
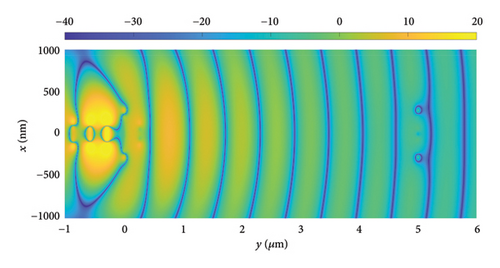
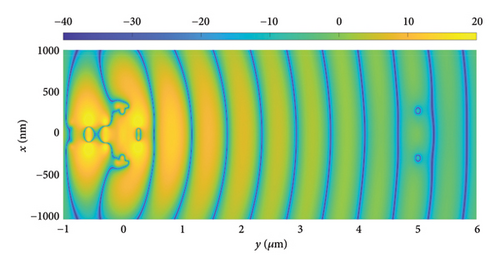
Figure 9 shows the near-field electric field distribution, E = 20 log10 (|Re (E_x)|), of the dipole/dipole (Figure 9(a)), Yagi–Uda/dipole (Figure 9(b)), and Yagi–Uda-loop/dipole (Figure 9(c)) nanolinks, in the z = a_hC + 20 nm plane, for a distance between the transmitting and receiving antennas of 5 μm. In the three nanolinks shown in this figure, one can observe the electric field propagating from the transmitting antennas to the receiving antennas. Furthermore, the decay of the electric field intensity of the wave front with distance is observed. We observe that the case of Yagi–Uda-loop/dipole (Figure 9(c)) presents higher field intensities near de receiving antennas. This is in accordance with the best power transmission presented in Figure 8.

4. Conclusions

This work presented a comparative analysis of nanolinks formed by Yagi–Uda-loop, Yagi–Uda, and dipole plasmonic nanoantennas fed by Gaussian beam. The linear MoMs with equivalent surface impedance were used to model the scattering problems, where a simulation example was compared with finite element calculations and a good agreement was observed. The results obtained were the near field and current distributions for the three isolated antennas and three nanolinks and the transmission power of the proposed nanolinks. The results showed that the Yagi–Uda-loop/dipole case presents an improvement of approximately 5 dB in relation to the dipole/dipole case and 3.2 dB in relation to the Yagi–Uda/dipole case. Also, we proved that the wireless nanolinks analyzed present better transmission over distances larger than 30 μm, when compared with wired nanolinks of bifilar OTL type. This result is of great importance for future applications in wireless communication at the nanoscale. In future works, nanolinks with Yagi–Uda-loop in both transmitter and receiver can be used to improve the power transmission.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by Fundação Amazônia Paraense de Amparo à Pesquisa; Pró-Reitoria de Pesquisa e Pós-Graduação, Universidade Federal do Pará.

Acknowledgments

The authors would like to thank the Brazilian agencies Amazon Foundation for Studies and Research Support (FAPESPA) and the Pro-Rectory of Research and Postgraduate Studies of the Federal University of Pará (PROPESP/UFPA) for providing funding for this research work.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Novotny L. and Van Hulst N., Antennas for Light, Nature Photonics. (2011) 5, no. 2, 83–90, https://doi.org/10.1038/nphoton.2010.237, 2-s2.0-79551607809.
10.1038/nphoton.2010.237
CAS Web of Science® Google Scholar
2 Santos M. S., Lameirinhas R., Torres J. P., Fernandes J. F., and Bernardo C., Nanostructures for Solar Energy Harvesting, Micromachines. (January 2023) 14, no. 2, 1–24.
10.3390/mi14020364
Web of Science® Google Scholar
3 Roggero U. F. S., Zapata-Herrera M., García-Etxarri A., Seifert A., and Hernández-Figueroa H. E., Plasmonic Nanoantennas for Biosensing and Monitoring of Cell Activity, Proceedings of the 2024 International Conference on Optical MEMS and Nanophotonics (OMN), 2024, San Sebastian, Spain, 1–2, https://doi.org/10.1109/omn61224.2024.10685249.
10.1109/omn61224.2024.10685249
Google Scholar
4 Marques Lameirinhas R. A., Bernardo C. P. C. V., Torres J. P. N., Baptista A., and Marques Martins M. J., Plasmonic Nanoantennas to Exploit Extraordinary Optical Transmission in Biosensing, Proceedings of the 2024 IEEE 22nd Mediterranean Electrotechnical Conference (MELECON), 2024, Porto, Portugal, 674–677, https://doi.org/10.1109/melecon56669.2024.10608535.
10.1109/melecon56669.2024.10608535
Google Scholar
5 Bechhofer A. R., Nirantar S., Daniel L., Berggren K. K., and Keathley P. D., Circuit Model for Nanoscale Optical Frequency Electronics, Proceedings of the 2023 IEEE 36th International Vacuum Nanoelectronics Conference (IVNC), 2023, Cambridge, 22–24, https://doi.org/10.1109/ivnc57695.2023.10188885.
10.1109/ivnc57695.2023.10188885
Google Scholar
6 Gao Q., Ren F., and Wang A. X., Direct and Efficient Optical Coupling into Plasmonic Integrated Circuits From Optical Fibers, IEEE Photonics Technology Letters. (June 2016) 28, no. 11, 1165–1168, https://doi.org/10.1109/lpt.2016.2533583, 2-s2.0-84963804411.
10.1109/lpt.2016.2533583
Web of Science® Google Scholar
7 Alù A. and Engheta N., Wireless at the Nanoscale: Optical Interconnects Using Matched Nanoantennas, Physical Review Letters. (2010) 104, no. 21, 213902–213904, https://doi.org/10.1103/physrevlett.104.213902, 2-s2.0-77953091276.
10.1103/physrevlett.104.213902
PubMed Web of Science® Google Scholar
8 de Souza J. L. and da Costa K. Q., Broadband Wireless Optical Nanolink Composed by Dipole-Loop Nanoantennas, IEEE Photonics Journal. (April 2018) 10, no. 2, 1–8, https://doi.org/10.1109/jphot.2018.2810842, 2-s2.0-85043392554.
10.1109/jphot.2018.2810842
Web of Science® Google Scholar
9 Alves A. A. C. et al., Plasmonic Nanoantennas for 6g Intra/inter-Chip Optical-Wireless Communications, Proceedings of the 2020 2nd 6G Wireless Summit (6G SUMMIT), 2020, Levi, Finland, 1–4.
Google Scholar
10 Elsaid M., Mahmoud K. R., Hussein M., Hameed M. F. O., and Obayya S. S. A., Improvement of Sectoral Horn Nanoantenna Based on Arc Directors for Point to Point Communications, Optical and Quantum Electronics. (2021) 53, no. 3, 141–15, https://doi.org/10.1007/s11082-021-02788-0.
10.1007/s11082-021-02788-0
Web of Science® Google Scholar
11 da Costa K., de Sousa G., Amaral P., Souza J., Garcia T., and Santos P., Wireless Optical Nanolinks With Yagi-Uda and Dipoles Plasmonic Nanoantennas, Nanoplasmonics. IntechOpen. (2019) 2019.
Google Scholar
12 Maksymov I. S., Staude I., Miroshnichenko A. E., and Kivshar Y. S., Optical Yagi-Uda Nanoantennas, Nanophotonics. (2012) 1, no. 1, 65–81, https://doi.org/10.1515/nanoph-2012-0005, 2-s2.0-84867189357.
10.1515/nanoph-2012-0005
Web of Science® Google Scholar
13 Damasceno G. H. B., Carvalho W. O. F., and Mejía-Salazar J. R., Design of Plasmonic Yagi–Uda Nanoantennas for Chip-Scale Optical Wireless Communications, Sensors. (2022) 22, 1–13.
10.3390/s22197336
Web of Science® Google Scholar
14 Damasceno G. H. B., Carvalho W. O. F., Cerqueira SodréA.Jr, Oliveira O. N. J., and Mejía-Salazar J. R., Magnetoplasmonic Nanoantennas for On-Chip Reconfigurable Optical Wireless Communications, ACS Applied Materials & Interfaces. (2023) 15, no. 6, 8617–8623, https://doi.org/10.1021/acsami.2c19376.
10.1021/acsami.2c19376
CAS PubMed Web of Science® Google Scholar
15 Elsaid M., Mahmoud K. R., Hameed M. F. O., Obayya S. S. A., and Hussein M., Broadband Directional Rhombic Nanoantenna for Optical Wireless Communications Systems, Journal of the Optical Society of America B. (2020) 37, no. 4, https://doi.org/10.1364/josab.383458.
10.1364/josab.383458
PubMed Google Scholar
16 Solís D. M., Taboada J. M., Obelleiro F., and Landesa L., Optimization of an Optical Wireless Nanolink Using Directive Nanoantennas, Optics Express. (2013) 21, no. 2, https://doi.org/10.1364/oe.21.002369, 2-s2.0-84874070831.
10.1364/oe.21.002369
PubMed Web of Science® Google Scholar
17 Costa K. and Dmitriev V., Simple and Efficient Computational Method to Analyze Cylindrical Plasmonic Nanoantennas, International Journal of Antennas and Propagation. (2014) 2014, 1–8, https://doi.org/10.1155/2014/675036, 2-s2.0-84900327911.
10.1155/2014/675036
Web of Science® Google Scholar
18 Costa K., Dmitriev V., Souza J., and Silvano G., Analysis of Nanodipoles in Optical Nanocircuits Fed by Gaussian Beam, International Journal of Antennas and Propagation. (2014) 2014, 1–12, https://doi.org/10.1155/2014/429425, 2-s2.0-84904126028.
10.1155/2014/429425
Web of Science® Google Scholar
19 Novotny L. and Hecht B., Principles of Nano-Optics, 2006, Cambridge University Press.
10.1017/CBO9780511813535
Google Scholar
20 Hanson G. W., On the Applicability of the Surface Impedance Integral Equation for Optical and Near Infrared Copper Dipole Antennas, IEEE Transactions on Antennas and Propagation. (2006) 54, no. 12, 3677–3685, https://doi.org/10.1109/tap.2006.886516, 2-s2.0-36849032346.
10.1109/tap.2006.886516
Web of Science® Google Scholar
21 Zhang K. and Li D., Electromagnetic Theory for Microwaves and Optoelectronics, 2007, 2nd edition, Springer.
Google Scholar
22 COMSOL Inc., COMSOL Multiphysic 4.4a, 2013, COMSOL Inc, https://www.comsol.com/.
Google Scholar
23 de Souza J. L., da Costa K. Q., Dmitriev V., and Bamberg F., Broadband Dipole-Loop Combined Nanoantenna Fed by Two-Wire Optical Transmission Line, International Journal of Antennas and Propagation. (2017) 2017, 1–13, https://doi.org/10.1155/2017/4903747, 2-s2.0-85015715332.
10.1155/2017/4903747
Web of Science® Google Scholar
24 Da Costa K. Q. and Dmitriev V., Radiation and Absorption Properties of Gold Nanodipoles in Transmitting Mode, Microwave and Optical Technology Letters. (2015) 57, no. 1, 1–6, https://doi.org/10.1002/mop.28489, 2-s2.0-84912039230.
10.1002/mop.28489
Web of Science® Google Scholar
25 Santos P., Dmitriev V., and da Costa K., Optimization of Modified Yagi-Uda Nanoantenna Arrays Using Adaptive Fuzzy GAPSO, International Journal of Antennas and Propagation. (2021) 2021, https://doi.org/10.1155/2021/8874385.
10.1155/2021/8874385
Web of Science® Google Scholar
26 Balanis C. A., Antenna Theory-Analysis and Design, 2005, 3rd edition, Wiley-Interscience.
Google Scholar
27 Huang J.-S., Feichtner T., Biagioni P., and Hecht B., Impedance Matching and Emission Properties of Nanoantennas in an Optical Nanocircuit, Nano Letters. (2009) 9, no. 5, 1897–1902, https://doi.org/10.1021/nl803902t, 2-s2.0-66449126209.
10.1021/nl803902t
CAS PubMed Web of Science® Google Scholar

All articles

Optical Nanolinks With Yagi–Uda-Loop and Dipole Antennas Fed by Gaussian Beam

Abstract

1. Introduction