Research on the Design and Simulation of Missile Intelligent Agent Autopilot Integrated With Deep Reinforcement Learning
Abstract
This paper proposes an innovative method for missile autopilot design based on the deep deterministic policy gradient (DDPG) algorithm. Under the framework of deep reinforcement learning, by integrating the missile’s dynamic characteristics to optimize the reward function and network structure, an adaptive control model capable of adapting to complex flight conditions was constructed. The effective integration of the autopilot and guidance system was achieved in the Simulink simulation environment, and the model’s validity and robustness in complex dynamic environments were verified. This research provides a new technological approach for the intelligent design of missile autopilots.
1. Introduction
As a critical actuator in missile guidance systems, the autopilot plays an essential role in achieving precise missile guidance and control. It controls missile attitude and trajectory by receiving command signals from the guidance system and driving the missile’s aerodynamic control surfaces or thrust vector devices [1]. Throughout the flight, the autopilot must maintain missile flight stability, suppress disturbances from external interference, and rapidly and accurately execute guidance commands to ensure precise target engagement [2]. However, traditional autopilot design methods, such as gain-scheduled PID control or sliding mode control (SMC), typically rely on linearized models of nonlinear dynamics. This simplification can lead to model errors under extreme conditions, such as high-maneuver flight or in thin atmospheres, which significantly degrades control performance. Furthermore, traditional methods exhibit limited robustness to unmodeled dynamics and parameter perturbations, struggling to cope with complex and variable flight environments [3].
To overcome these limitations, this study proposes an intelligent autopilot design method based on the DDPG algorithm. DDPG is a model-free reinforcement learning (RL) algorithm that learns an optimal control policy through direct interaction with the environment, enabling it to adapt to complex nonlinear dynamics and uncertainties. Unlike traditional approaches that depend on predefined control laws, DDPG utilizes an actor–critic network to adjust its control policy in real time. It particularly excels in continuous action spaces, providing smooth and adaptive rudder deflection commands to achieve precise target tracking and enhance system robustness. Figure 1a,b contrast the traditional PID control loop, which relies on a fixed control law, with the DDPG control loop, which dynamically optimizes its behavior through learning.
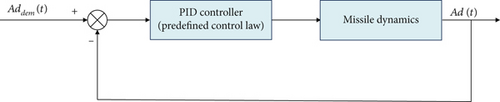
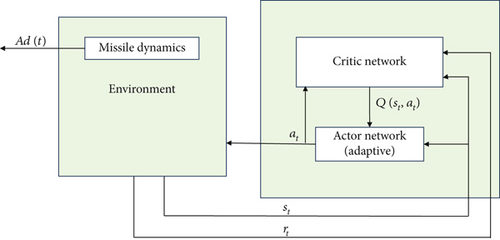
The innovation of this work lies in the integration of the DDPG algorithm with the Simulink simulation environment to build an end-to-end adaptive control model. Its effectiveness has been validated in complex dynamic environments. To systematically present this study, the paper is structured as follows. Section 2 reviews related work, Section 3 introduces the missile dynamics model, Section 4 details the DDPG algorithm principles, Section 5 describes the DDPG-based autopilot design, Section 6 validates performance through simulations, and Section 7 summarizes contributions and outlines future directions.
2. Correlational Research
Traditional autopilot design methods include optimal control [4], SMC [5], nonlinear model predictive control [6], and other techniques [7, 8]. In Xu et al. [9] researchers redesigned a three-loop missile autopilot based on linear quadratic regulator optimal control theory, optimizing controller parameters through performance index functions to enhance system response speed, tracking accuracy, and robustness. The study by Wang et al. [10] transformed the attitude dynamics of nonlinear rotating glide missiles into constant linear closed-loop systems by introducing fixed-time convergence disturbance observers and higher order fully actuated system methods, while effectively addressing disturbance estimation and chattering issues through integral sliding mode techniques. This method significantly improved trajectory tracking precision and system robustness, providing new insights for high-precision control of complex aircraft, particularly demonstrating significant engineering value in addressing strong uncertainties and nonlinear disturbances. The research by Liao and Bang [11] constructed a missile autopilot system using nonlinear SMC and introduced saturation functions to avoid control chattering, a common issue in SMC. Furthermore, the paper thoroughly investigated the impact of boundary layer thickness on system response performance, suggesting that selecting a smaller boundary layer thickness can significantly improve control precision and system response speed, thereby achieving a more rational SMC autopilot design. While these methods have been widely applied in engineering practice, it is noteworthy that traditional control methods typically require linearization of nonlinear dynamic models. Although this simplification enables the application of classical control theory, it inevitably introduces model errors. Particularly under extreme conditions, such as high-maneuver flight or high-altitude thin atmosphere, the deviation between linearized models and actual systems may significantly affect control performance [12]. Moreover, the presence of unmodeled dynamics, parameter perturbations, and external disturbances adds additional complexity to the application of traditional control methods [13].
To address these limitations, this study proposes DDPG-based autopilot design is a model-free approach that learns optimal control strategies through direct interaction with the environment, effectively adapting to complex nonlinear dynamics and uncertainties. DDPG’s advantage in continuous action spaces makes it particularly suitable for missile control, providing smooth and adaptive rudder deflection commands to achieve precise target tracking while enhancing system adaptability and robustness. Traditional control methods rely on linearized models and predefined parameters, whereas DDPG achieves adaptive control through RL. Figure 1a,b illustrates the comparison between the traditional PID control loop and the DDPG control loop, with the former depending on fixed control laws and the latter dynamically adjusting strategies via the actor–critic network.
RL, a significant branch of machine learning, has shown great potential in control system design due to its unique learning mechanisms [14]. This approach transcends the traditional control theory’s reliance on precise system models, instead obtaining optimal control strategies through continuous interaction between agents and their environment [15, 16]. During the learning process, agents progressively develop task-specific capabilities by experimenting with various control actions and observing the resulting reward signals. This autonomous learning characteristic makes it particularly suitable for control systems with complex dynamics that are difficult to model accurately [17, 18]. Deep reinforcement learning (DRL) combines the perceptual capabilities of deep learning (DL) with the decision-making abilities of RL, enabling it to handle problems involving high-dimensional state and action spaces. Compared to traditional control algorithms, DRL exhibits superior adaptability, robustness, and real-time decision-making capabilities.
Several studies have proposed innovative RL and DRL methods for various control systems. The study by Wu and Li [19] proposed a RL method based on multiagent deep deterministic policy gradient (MADDPG) by incorporating multiagent collaborative learning and aggregation policy design. This approach reduces the complexity of environment modeling and training while improving the precision and adaptability of autonomous driving decision-making. According to Chopra and Roy [20], an end-to-end autonomous driving control strategy learning method was developed using the deep Q-network (DQN) algorithm within DRL. This method employs deep neural networks to map raw sensor inputs directly to control outputs, achieving an integrated perception–control strategy optimization. Based on visual servo control, Mitakidis et al. [21] developed a visual servo control strategy for target tracking of multirotor UAVs using the DDPG algorithm. By employing an actor–critic structured controller, this method directly maps the position information of the target in the image plane to the UAV’s control commands. The study by Kim et al. [22], based on collaborative robot balancing tasks, proposed an optimized robot control strategy using DRL algorithms. By employing DQN, the study designed a control method capable of autonomously learning balance and collaboration, thereby enhancing the adaptability and coordination ability of robots in dynamic environments. In Crowder et al. [23], an improved RL control method was proposed for motion control in human musculoskeletal models. By adjusting the learning rate in the RL algorithm, improving the policy network to enhance control precision, and expanding the state and action spaces of the model, the study significantly improved RL algorithm performance in controlling arm movements in humans. The study by Bousnina and Guerassimoff [24] proposed an intelligent energy optimization management method for smart grids based on DDPG. The optimization problem for multienergy systems was modeled as a partially observable Markov decision process (POMDP), and the DDPG algorithm was utilized to achieve real-time optimization of multi-energy scheduling in continuous state and action spaces. RL and DRL have been widely applied in various control engineering problems, including autonomous vehicles [25–27], robotic [28], healthcare [29], and smart grids [30].
It is worth noting that research on the application of DRL in missile autopilot design is relatively scarce, in stark contrast to its immense application potential. The study by Shin et al. [31] designed an autopilot method based on the DDPG algorithm, innovatively combining domain knowledge with data-driven algorithms. By utilizing a fixed three-loop autopilot structure, the method improved learning efficiency and generalization capability. A key aspect of this approach was the redesign of the reward function with reference inputs, which simplified the tuning of multiobjective optimization weights. Additionally, normalization techniques were introduced, significantly enhancing training convergence speed and stability. The proposed algorithm demonstrated excellent robustness and relative stability, meeting gain and phase margin requirements. The study by Candeli et al. [32] proposed a DDPG-based missile autopilot design method that restructured the autopilot problem within the RL framework. The agent was trained on a linearized model, and experiments validated the effectiveness of this method under varying flight conditions and aerodynamic coefficient uncertainties. The results showed that the model-free, data-driven approach could achieve the desired closed-loop response without requiring a precise system model. The study by Fan et al. [33] presented a two-loop autopilot design method using the TD3 algorithm. Control parameters were optimized through the DRL model to ensure performance across the entire flight envelope. Furthermore, an online adaptive adjustment of control parameters was achieved using a multilayer perceptron (MLP) neural network.
Based on the inspiration from the aforementioned related studies and the limitations of the existing technologies, this paper has the following characteristics in the design of the missile autopilot: it successfully integrates the DDPG algorithm with the missile guidance system within the Simulink simulation environment and constructs a DDPG-based autopilot model. Unlike traditional control methods such as gain-scheduling-based control strategies, which require parameter tuning at specific local state points, this design achieves end-to-end control strategy learning by building an agent model. The agent uses the missile’s angle of attack, body-axis angular velocity, actual control surface deflection angle, and commanded normal acceleration as input states, outputting control commands for the control surface deflection angle. The DDPG-based autopilot design method within the Simulink environment not only holds theoretical innovation significance but also offers engineering application value. By leveraging Simulink’s powerful simulation capabilities, the method simplifies the complexity of algorithm implementation, providing a feasible technical pathway for the engineering application of DRL in missile guidance systems. Through training, the DDPG controller can autonomously adjust control strategies under varying flight conditions and uncertainties, improving the system’s adaptability and robustness.
3. Missile Dynamics Model
To validate the effectiveness of the proposed autopilot system and simulate the missile dynamics, this study employs a simplified two-degree-of-freedom (2-DoF) nonlinear model proposed in the literature. This model effectively describes the longitudinal dynamics of a tail-fin-controlled missile. In this study, the 2-DoF nonlinear model was chosen because it effectively balances model complexity and computational efficiency while meeting the practical demands of missile autopilot design. Compared to a full 6-DoF model, the 2-DoF model focuses on longitudinal dynamics, simplifying the modeling of lateral and roll channels and thereby reducing computational load. The model is established based on the following fundamental assumptions:
Assumption: The pitch, yaw, and roll channels are decoupled, meaning the coupling effects between the channels are ignored.
Here, σ(t) represents the actual tail fin deflection angle, σc(t) is the commanded tail fin deflection angle, Ad(t) is the commanded normal acceleration, σv(t) is the fin deflection rate, α(t) is the angle of attack, q(t) is the pitch rate, and M(t) is the Mach number.
| Parameter | Value | Unit |
|---|---|---|
| Reference area | 0.041 | m2 |
| Reference length | 0.228 | m |
| Mass | 204 | kg |
| Moment of inertia | 247.6 | kg·m2 |
| Thrust | 10,000 | N |
| Initial velocity | 1049.6 | m/s |
| Maximum fin deflection | ± 0.524 | rad |
| Maximum fin rate | 8.727 | rad/s |
| Axial force coefficient | −0.3 | — |
| Maximum load factor | 40 | m/s2 |
| Seeker time constant | 0.05 | s |
| Maximum gimbal angle | ± 0.611 | rad |
4. Deep Deterministic Policy Gradient Algorithm
In the field of RL, the core challenge lies in enabling intelligent systems to improve their performance through continuous interaction with the environment. The system needs to continuously explore and learn in an unknown environment to derive an optimal behavioral policy. Specifically, this learning process can be described using a POMDP. At each time step, the system acquires information about the current environment and selects its next action at+1. For ease of study, the system’s perception of the environment, represented as state st, is taken as the focus of research. Figure 2 shows the basic structural diagram of the actor–critic framework.

DDPG is a model-free, deterministic policy algorithm, which is an off-policy method based on the actor–critic architecture. This algorithm combines the feature extraction capability of deep neural networks with the decision-making ability of RL, making it particularly suitable for control problems in continuous action spaces. Therefore, given the challenges of continuous action spaces, nonlinear dynamics, and uncertainties in missile autopilot design, this study adopts the DDPG algorithm to address these issues. DDPG’s model-free nature enables it to learn optimal control strategies through direct environmental interaction, while its strength in continuous action spaces provides smooth and adaptive control commands for the missile. Its core components include four neural networks:
Actor network: Outputs the deterministic action policy;
Critic network: Evaluates the state-action value function;
Target actor: Used to compute the target policy;
Target critic: Used to compute the target Q-value.
-
Algorithm 1: Deep deterministic policy gradient (DDPG).
-
Initialization:
-
Randomly initialize Actor network μ(st|θu) and Critic network Q(s, a|θQ)
-
Create target network copies: θu′⟵θu, θ′⟵θ
-
Initialize experience replay buffer D
-
Initialize OU noise process N
-
For episode = 1 to M do:
-
Obtain initial observation state s1
-
For t = 1 to T do:
-
Select action
-
Execute action at, observe reward rt and new state st+1
-
Store transition sample (st, at, rt, st+1) in replay buffer D
-
Sample N transitions (si, ai, ri, si+1) randomly from D
-
Calculate target Q value: yi = ri + γQ′(si+1, μ′(si+1|θu′)|θQ′)
-
Update Critic network: minimize
-
Update Actor network: using policy gradient ∇θμJ
-
Soft update target networks:
-
-
End For
-
End For
5. Design of an Autonomous Pilot Based on DDPG
This section provides a detailed explanation of the missile autopilot design scheme based on the DDPG algorithm. It focuses on the structure of the control system, the design of the deep neural network architecture, and the specifics of the reward function during the training phase. Figure 3 illustrates the input states and output control commands of the DDPG agent in the Simulink environment.
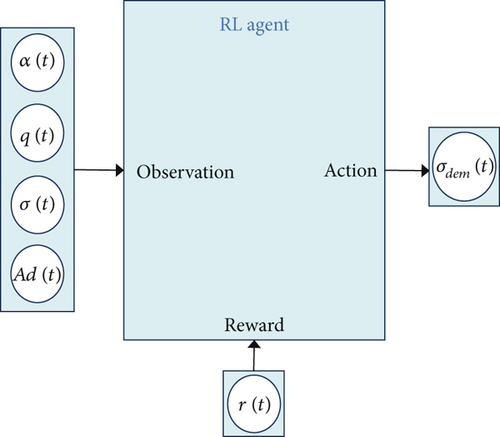
These four state variables form a complete state description, fully capturing the missile’s pitch channel motion characteristics. This state description not only reflects the system’s critical dynamic properties but also avoids an excessively high-dimensional state space.
To achieve effective policy learning, this study designs two deep neural networks based on fully connected layers: an actor network and a critic network. The network architectures were determined through iterative experiments to balance model performance with the constraints of onboard computational resources. The specific structures are as follows: The Actor network is responsible for mapping the four-dimensional state vector to a deterministic control command. It consists of an input layer, three fully connected hidden layers, and an output layer. After normalization, the input state vector passes sequentially through hidden layers with 512, 256, and 128 neurons, all of which use the Leaky ReLU activation function. The output layer is a single-neuron, fully connected layer that uses a tanh activation function to constrain the action output to the range of (−1, 1), thereby satisfying the physical constraints of the actuator and corresponding to the normalized rudder command. The critic network, which evaluates the state-action value function, features a dual-path architecture. The state path processes the four-dimensional state vector through two fully connected hidden layers of 512 and 256 neurons, both using the ReLU activation function. The action path processes the one-dimensional action from the actor network through a fully connected layer containing 256 neurons with a ReLU activation function. These two feature streams are then merged via element-wise addition and passed through a final hidden layer to produce a single scalar Q-value.
Here , , , and is the input value of the normalized neural network, where α ∈ [αmin, αmax], q ∈ [qmin, qmax], σ ∈ [σmin, σmax], and Ad ∈ [Admin, Admax].
The Adam optimizer with L2 regularization is used to train both the actor and critic networks, preventing overfitting. Since hyperparameter settings have a significant impact on the performance of the DDPG algorithm, Table 2 lists the hyperparameter configurations suitable for the application scenario of this study.
| Parameter | Value |
|---|---|
| Agent sampling time | 0.01 |
| Maximum allowed steps (per episode) | 400 |
| Maximum allowed episodes | 5000 |
| Experience buffer size | 106 |
| Minibatch size | 256 |
| Actor network learning rate | 1 × 10−4 |
| Critic network learning rate | 2 × 10−4 |
| Discount factor | 0.95 |
| Gradient clipping threshold | 1 |
| Exploration noise standard deviation | 0.15 |
| Exploration noise decay rate | 5 × 10−6 |
The reward function implements a comprehensive evaluation of control performance across multiple dimensions. Specifically, when the missile’s acceleration is accurately guided and maintained near the reference value, the control strategy receives positive rewards, directly reflecting the requirement for control precision. Conversely, if the missile’s motion exceeds the predetermined lateral acceleration range, penalties are imposed to ensure system safety. Regarding dynamic characteristics, the incorporation of a quadratic term for missile angular velocity in the reward function effectively constrains overshoot, while the quadratic terms of actuator deflection angle and its rate of change are used to limit control input magnitude. Notably, considering the system’s non-minimum phase characteristics, an additional error penalty term is introduced to suppress undershoot phenomena. Due to inherent conflicts between various control system performance indicators (such as rise time versus overshoot), this paper achieves a balanced compromise control strategy by adjusting weight coefficients Ti for different terms in the reward function.
In this paper, the DDPG algorithm is employed for training in the design of missile autopilots. The environment is based on a 2-DoF nonlinear missile model, with training episodes designed for various flight conditions.
Within each training episode, the target acceleration reference value is generated as a random step signal, with final values uniformly sampled from the interval [−1 and 1 g] to simulate random maneuver requirements under real flight conditions. Each episode has a maximum simulation time of 1.5 s or terminates early if the missile’s lateral acceleration Ad(t) exceeds the predetermined range.
6. Simulation Verification and Result Analysis
This chapter verifies the performance of the proposed controller through numerical simulation. Based on the training methods described in Section 5, the DDPG agent underwent training. The parameter values in the reward function are specifically set as Table 3.
| U1 | U2 | U3 | T1 | T2 | T3 | T4 | T5 |
|---|---|---|---|---|---|---|---|
| 150 | 3 | 25 | 3.2 | 0.2 | 0.01 | 100 | 25 |
In this section, we first analyze the training process and convergence of the agent and then conduct nonlinear simulation verification of the DDPG controller, analyzing its control performance and robustness under parametric uncertainties. Further analysis of control performance is presented in Section 6.2. Section 6.3 provides comparative test results between the designed DDPG-based autopilot and traditional controllers based on gain scheduling.
6.1. Training Process and Convergence Analysis
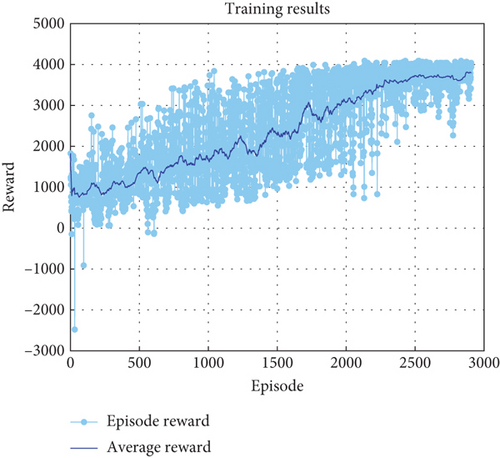
To evaluate the learning effectiveness and convergence performance of the designed DDPG agent, we recorded the change in its reward values during the training process. The training environment and associated parameters are set as described in Sections 3 and 5. Figure 4 presents the reward curve of the DDPG agent. In the initial exploration phase, the average reward is low and the episode reward exhibits large fluctuations, indicating that the agent is primarily interacting with the environment through random exploration without having formed an effective control policy. As training progresses, the agent gradually learns from experience, and the average reward shows a general upward trend. This suggests that the agent is progressively mastering the skills to obtain higher rewards and that its control policy is continuously being optimized. Around Episodes 2500–3000, the growth rate of the average reward slows down, and the reward level tends to stabilize and converge. Although the episode reward still fluctuates within a certain range, the stability of the average reward indicates that the DDPG algorithm has learned a relatively optimal control policy. This convergence trend, combined with the randomized generation of the target acceleration reference value during training, helps to enhance the controller’s generalization capability and avoid overfitting to specific operating conditions. Subsequent sections will validate the performance of the trained controller.
6.2. Controller Verification
As shown in Figure 5, through 30 Monte Carlo simulation experiments with a 1-g step command under ± 20% uncertainties in aerodynamic parameters Cn and Cm, it demonstrates that even with 20% uncertainties in aerodynamic parameters Cn and Cm, the designed DDPG controller can maintain good tracking performance. From the time-domain response curves in Figure 5a, it can be observed that although there are certain differences in overshoot and adjustment time across different simulations, the control system consistently maintains closed-loop stability. This performance characteristic is not derived from explicit robustness training but rather reflects the controller’s inherent adaptability. To further improve control precision under system parameter uncertainties, robustness indicators could be explicitly introduced as optimization objectives during the training phase.
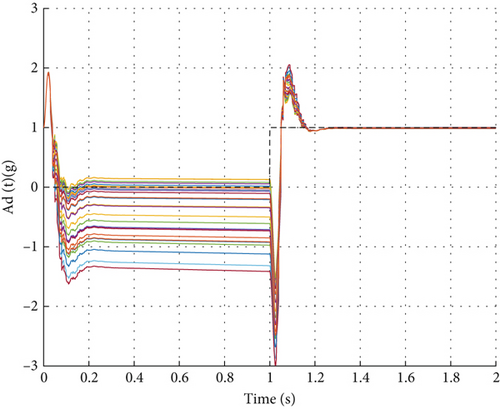
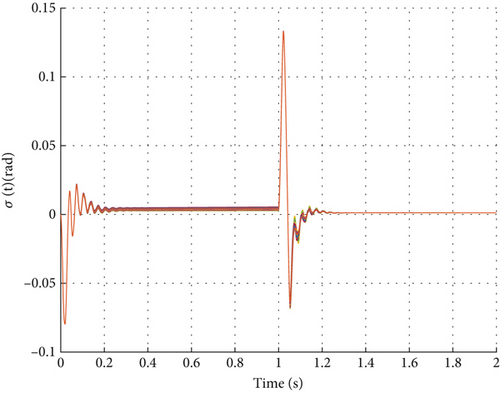
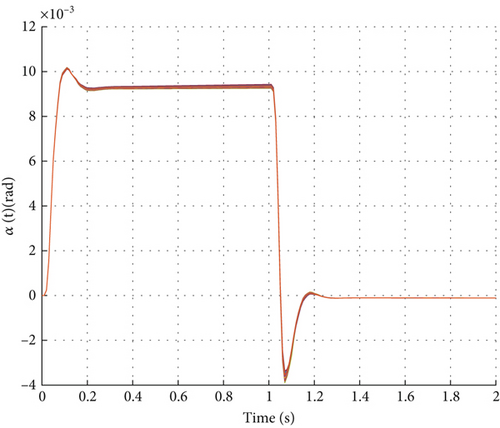
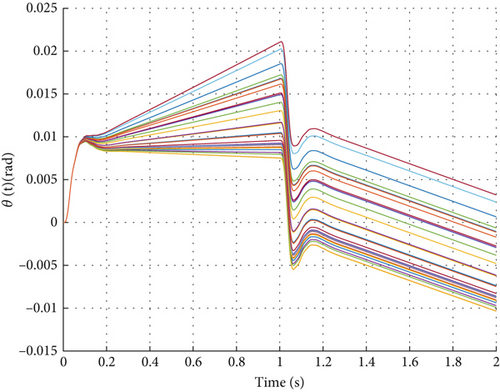
6.3. Comparative Analysis With Model-Based Control Strategies
To better discuss the advantages of the proposed DDPG-based autopilot in missile lateral acceleration tracking, its closed-loop response is compared with an autopilot based on a gain scheduling control strategy.
The design of the gain scheduling-based autopilot is founded on the missile’s linearized model. Through linearized dynamic equations under different flight conditions, numerous linearized missile models are constructed to ensure good control performance and robustness across a wide flight envelope. This controller has been tuned to exhibit similar overshoot characteristics to the DDPG controller for step responses with final values randomly selected from the interval [−1 and 1 g].
As shown in Figure 6, the system executes three distinct step commands with final values randomly sampled from the interval [−4 and 4 g]. In terms of overall control performance, while both controllers exhibit comparable undershoot following the step inputs, the DDPG controller demonstrates a shorter settling time. Additionally, it performs well in terms of overshoot and response speed; the control process involves slight overshoot and effectively tracks changes in the target value.
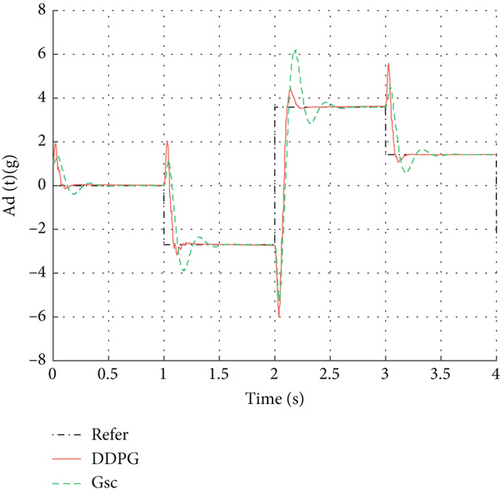
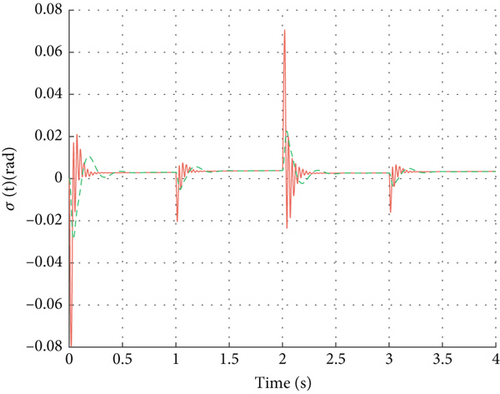
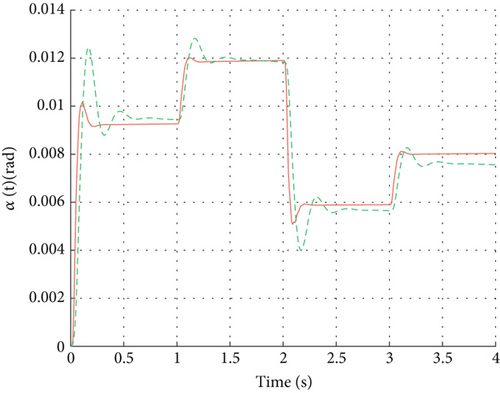
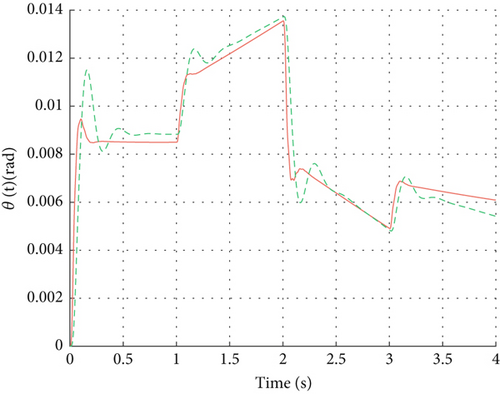
Figure 6b shows that the rudder commands of DDPG exhibit steeper changes at certain moments compared to those of the gain-scheduled control strategy. This phenomenon arises because DDPG learns to adjust rudder angles more aggressively to respond quickly to changes in target acceleration and minimize tracking errors. Nevertheless, owing to DDPG’s capability in continuous action spaces, its control signals remain continuous rather than discrete jumps, thus still considered smooth. As shown in Figure 6a, the normal acceleration curve of DDPG demonstrates smaller tracking errors and faster response speeds, validating its superiority in precision.
Figure 7 shows the system response to reference signals calculated from tracking moving targets. Although the RL controller did not use such reference signals as training samples, the response results maintain high consistency with the target reference signals, demonstrating excellent tracking performance. Particularly during phases of large dynamic changes, the DDPG controller can quickly adjust system states, maintaining small tracking errors and good system stability. Under the same conditions, while the alternative control strategy can also achieve reference signal tracking, its response process exhibits notable overshoot and oscillation, with somewhat insufficient dynamic performance especially during moments of dramatic signal changes.
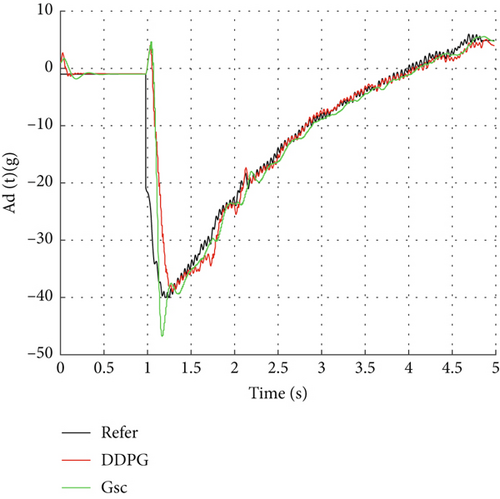
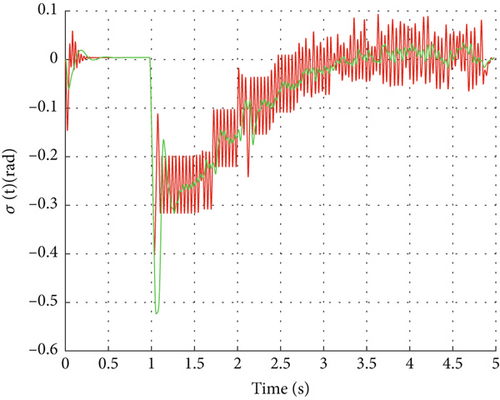
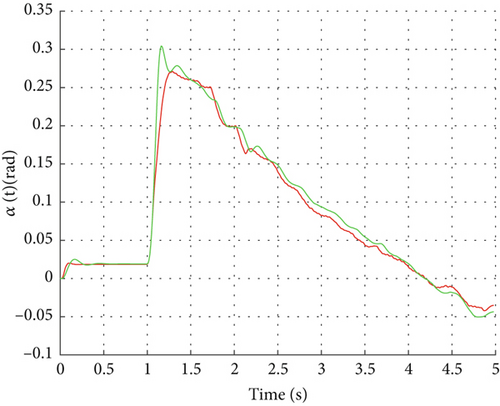
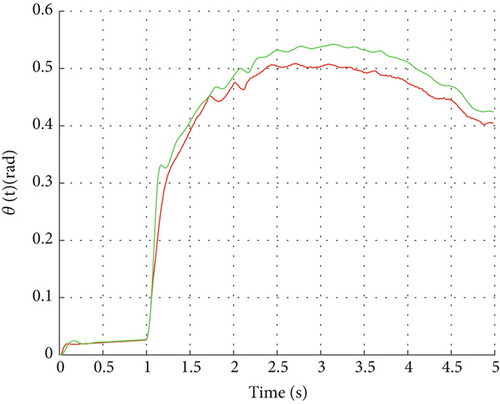
Overall, the DDPG controller demonstrates good robustness and adaptability when facing unseen reference signals. Unlike gain scheduling-based control strategies that require constructing numerous linearized missile models based on linearized dynamic equations under different flight conditions, the DDPG strategy does not rely on complex system modeling and can be implemented through data-driven methods alone. This further proves the effectiveness and advantages of model-free data-driven methods in robust autopilot design. Although this study has verified the effectiveness and robustness of the DDPG controller through Simulink simulation, we are aware that relying solely on numerical simulation is not sufficient to fully prove the feasibility of this method in an actual flight environment. Preliminary hardware-related work, such as hardware-in-the-loop (HIL) simulation, has been planned as a future expansion after the current work matures and overcomes the existing limitations, in order to further verify the application effect of the DDPG algorithm in missile autopilots.
7. Conclusion and Prospect
This paper successfully implements the integration of the DDPG algorithm with missile guidance systems in the Simulink simulation environment, constructing a DDPG-based autopilot model. Unlike traditional gain scheduling control strategies that require parameter tuning at local state points, this research achieves end-to-end control strategy learning through the construction of an agent model. The agent takes missile angle of attack, body axis angular velocity, actual rudder angle, and commanded normal acceleration as input state variables, outputting control command rudder angles. Furthermore, the DDPG autopilot design method based on the Simulink environment presents both theoretical innovation and practical engineering value. By leveraging Simulink’s powerful simulation capabilities, the complexity of algorithm implementation is significantly reduced. Through offline training, the generated controller can autonomously adjust control strategies when facing different flight conditions and uncertainties, effectively enhancing system adaptability and robustness. In simulation verification, this paper evaluates controller performance through various test scenarios, including aerodynamic coefficient uncertainty ranges, different reference input signals, and nonlinear disturbance conditions. Results show that the proposed method achieves high-precision target tracking in complex flight environments while exhibiting considerable robustness and adaptability. Moreover, comparative experiments with traditional gain scheduling controllers further illustrate the advantages of data-driven methods in performance indicators such as dynamic response, overshoot, and response time. In the verification section of the article’s controller, the direction for improving robustness is pointed out. Future research can consider introducing specific robustness indicators as optimization objectives in the training stage to further enhance the robustness of the controller in specific scenarios. Furthermore, future research will explore the deployment of the DDPG controller onto a hardware platform, and its performance will be validated through HIL testing to advance the engineering application of the method. We acknowledge that hardware deployment may present challenges such as computational latency, sensor noise, and actuator constraints, which we plan to address by optimizing the neural network architecture and introducing robust filtering techniques. These considerations will be further investigated in subsequent work to ensure transparency regarding the research scope and to provide a clear roadmap for practical application.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This research received no external funding.
Open Research
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.




