International Journal of Aerospace Engineering

Volume 2025, Issue 1 8850329

Research Article

Open Access

General Modeling for Space Robot Proximity Relative Motion by Using Dual Operator With Hybrid Coordinates

Peiji Wang,

Peiji Wang

Institute of Space Science and Applied Technology , Harbin Institute of Technology , Shenzhen , China , hit.edu.cn

Search for more papers by this author

Xianliang Zhang,

Corresponding Author

Xianliang Zhang

[email protected]

orcid.org/0000-0001-5966-6884

School of Mathematics and Statistics , Taishan University , Tai’an , China , tsu.edu.cn

Search for more papers by this author

Min Yang,

Min Yang

School of Mathematics and Statistics , Taishan University , Tai’an , China , tsu.edu.cn

Search for more papers by this author

Weiren Wu,

Weiren Wu

Institute of Space Science and Applied Technology , Harbin Institute of Technology , Shenzhen , China , hit.edu.cn

Lunar Exploration and Space Program Center , China National Space Administration , Beijing , China , cnsa.gov.cn

Search for more papers by this author

Peiji Wang,

Peiji Wang

Institute of Space Science and Applied Technology , Harbin Institute of Technology , Shenzhen , China , hit.edu.cn

Search for more papers by this author

Xianliang Zhang,

Corresponding Author

Xianliang Zhang

[email protected]

orcid.org/0000-0001-5966-6884

School of Mathematics and Statistics , Taishan University , Tai’an , China , tsu.edu.cn

Search for more papers by this author

Min Yang,

Min Yang

School of Mathematics and Statistics , Taishan University , Tai’an , China , tsu.edu.cn

Search for more papers by this author

Weiren Wu,

Weiren Wu

Institute of Space Science and Applied Technology , Harbin Institute of Technology , Shenzhen , China , hit.edu.cn

Lunar Exploration and Space Program Center , China National Space Administration , Beijing , China , cnsa.gov.cn

Search for more papers by this author

First published: 19 March 2025

https://doi.org/10.1155/ijae/8850329

Academic Editor: Chuang Liu

Share a link

Email
Wechat
Bluesky

Abstract

With the increasing demand for space missions, task robots have evolved from rigid bodies to rigid-flexible coupling in close-range approach missions, such as flexible module in-orbit assembly missions and flexible spacecraft formation missions proposed in recent years. This poses a challenge to the dynamic modeling of space proximity tasks that are more concise, efficient, and have engineering practicality. In this paper, a six-degree-of-freedom representation of space robot proximity relative dynamics is developed by using the algebra of dual numbers, whether the space robot is a rigid body or a rigid-flexible coupling system. The main work of this paper lies in the following three aspects: First, this paper develops a six-dimensional screw representation of dual number–based general dynamics that allows model parameters (dual inertia operator) to be directly matched with space robot engineering parameters (mass and moment of inertia) to replace its classical three-dimensional motor form. This work improves the convenience of the engineering application of the general model. Second, by combining hybrid coordinate modeling methods with dual algebra, the general expression is extended from the motion of a rigid body to a flexible body; on this basis, the integrated dynamic model of the rigid-flexible coupling space robot is developed. This effort solves the problem of compact representation and computational efficiency of relative dynamic models between two rigid-flexible coupling space robots. Third, the derivative rule of a space robot with time-varying configuration is provided; this work enables the general model to be applied to certain specific scenarios, such as space robot proximity missions under the premise of rotating solar panels, rotating optical lenses, or other rotating structures. Based on the above relative dynamics, a PD controller is adopted, and the successful application of the proposed models is verified.

1. Introduction

In the 19th century, Clifford first introduced dual numbers in Ref. [1]. At first, the application of dual numbers to rigid body kinematics was subsequently generalized by Study and Brodsky and Shoham in their principle of transference [2, 3]. In 1999, the general representation of rigid body dynamics was provided by Brodsky and Shoham by using motor transformation rules and a dual inertia operator [3]. In Ref. [3], the dual number–based dynamic equations are represented in Newton–Euler form. Compared with the classical Newton–Euler equation, the main advantage of the dual number–based equation is the compactness of representation. That is, the classical dynamic models are derived using two equations: one that accounts for the three degree-of-freedom (DOF) translational dynamics and the other that captures the three-DOF rotational dynamics. The dynamic model based on dual numbers describes the six-DOF motion of a rigid body with one equation by using a three-dimensional dual motor; therefore, it is defined as an integrated model [4–6]. Wang et al. [7] extended the above-integrated model to describe the attitude and orbital motion of a rigid space robot and further proposed a three-dimensional motor model of space robot proximity six-DOF relative motion. However, the dynamic equation derived by Wang et al. [7] is a centroid-relative dynamic model instead of a general model; that is, the origin of the reference coordinate system is set at the center-of-mass (COM) of a space robot and can describe the relative motion between the COM of rigid space robots. Wang et al. [8, 9] further investigated the control methods of space robot formation flying (SFF) missions based on the centroid relative dynamic model. This model was followed to solve the guidance, navigation, and control (GNC) problems of the space robot proximity cooperative missions, such as SFF, on-orbit assembly, and space debris capture, in Refs. [10–18].

However, the integrated model proposed in Ref. [3] is represented as a three-dimensional motor form, whose dual inertia operator is related to the moment of inertia relative to the arbitrary axis of the rigid body. In aerospace engineering, the space robot’s moment of inertia is always given relative to the principal axis of inertia. This leads to a problem where the parameters of the general model cannot be directly obtained with engineering parameters. The extended dynamic equation proposed in Ref. [7] is a model for special operating conditions and does not have universal applicability. In addition, it is not intuitive to express the six-DOF relative motion as a three-dimensional motor form for scholars without a foundation in studying dual algebra, which is not conducive to the promotion and application of the model. This paper proposes the six-dimensional screw representation of dual vector, dual inertia, and dual force to replace its three-dimensional motor form and develops a six-dimensional screw representation of dual number–based dynamics to describe the six-DOF motion of a rigid space robot. Compared with the dual motor form, the six-dimensional screw representation allows the model parameter (dual inertia operator) to be directly matched with space robot engineering parameters (mass and moment of inertia), which greatly improves the convenience of the engineering application of the general model.

In recent years, there has been an attempt to apply dual numbers to rigid-flexible coupling space robot dynamics [19]. However, in the above investigation, the integrated model was expressed as a simple symbol transformation of classical Newton–Euler equations, which does not reflect the advantages of the dual number in physical description and mathematical computation. The recently introduced dual momentum of a flexible body [20, 21] suggested a solution to this problem by developing a dual vector, dual momentum, dual inertia operator, dual coupling coefficient operator, and dual-modal coordinates of a flexible body. On this basis, the centroid relative dynamic model between the rigid-flexible coupling space robot was derived from Zhang et al.’s paper [20–22]. This paper expands on the results reported in Refs. [20–22] and gives a more general expression for the relative dynamic equation. The relative dynamic equations between the rigid-flexible coupling space robot with a time-varying configuration are further derived. This relative dynamic model can solve the description problem of relative motion between space robots with rotating flexible components, such as solar panels.

In summary, this paper mainly focuses on the general dynamic modeling for proximity relative motion of space robots. In the first part, this paper combines the advantage of the results reported in Brodsky and Shoham [3] and Wang et al. [7] and proposes a six-dimensional screw representation of dual number–based general dynamics for the proximity relative motion of space robots. Then, the six-dimensional screw representation is expanded to the general relative dynamic modeling between two rigid-flexible space robots, preserving the advantages of compactness and computational efficiency of the dual number. In addition, the application of the general dynamics to the time-varying configuration space robot is explored in this paper.

The paper is organized as follows. In Section 2, the general model between rigid space robots is provided. Section 3 proposes the general model between rigid-flexible coupling space robots. Section 4 develops the integrated dynamics between space robots with time-varying configurations. Section 5 provides a PD controller. Numerical simulation is presented in Section 6 to verify the dynamics developed in this paper. Finally, the paper is concluded in Section 7.

2. General Representation of Six-DOF Relative Motion Between Rigid Space Robot

This section considers the earth-orbiting space robot’s six-DOF motion. Although Brodsky and Shoham [3] and Wang et al. [7–9] have focused on this work [3, 7–9] during the past 20 years, their investigations have some representation contradictions. The main contribution of Brodsky and Shoham [3] is the construction of the general model for a rigid body. However, the general model in Ref. [3] is represented in three-dimensional motor form. The specific form of which is as follows:

()

Obviously, the operation of the above model is not easy, and for scholars who are not familiar with dual operation, the application of the above model poses certain difficulties. On this basis, Wang et al. [7–9] developed a six-dimensional screw representation of the dynamics of a rigid body, and it is expressed as

()

Equation (2) can be directly solved through screw operations, making it more suitable for engineering promotion. However, the six-dimensional screw representation provided by Wang et al. is the centroid dynamic equation that replaces rigid body dynamics with the motion of the COM, not a general model. This paper develops a six-dimensional screw general dynamic model instead of Brodsky and Shoham’s three-dimensional motor representation and Wang et al.’s centroid dynamic equation.

Remark 1. In a dual number–based model, the motion of a rigid space robot is equivalent to that of a system of particles rather than a single COM. That is, in the modeling process, we not only care about the mass of the space robot but also the size of the space robot. Space robot size is an important parameter for dynamics modeling. Since the space robot has volume, the origin of the body-fixed coordinate system (BFCS) of the rigid space robot can be set at an arbitrary point on the space robot, not necessarily the point of COM. The general representation of rigid space robot dynamics enables the calculation of the dual vector and the dual force with respect to the BFCS, in which the origin is set at an arbitrary point on the space robot.

Remark 2. The derivation of the dynamic equation in this paper is carried out with respect to the BFCS. That is, the representation of the space robot rotational equation and the translational equation are unified not only in the same mathematical framework but also in the same reference coordinate system.

As shown in Figure 1, in this section, the following two coordinate systems are used: Ψ_I, the standard earth-centered, inertial, Cartesian right-hand coordinate system. Ψ_B, the BFCS of a rigid space robot B, with its origin in an arbitrary point, k, of the space robot, and axes pointing along the principal axes of inertia. The following notations are employed: denotes the components of x expressed in the BFCS of space robot B with its origin in an arbitrary point k.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Dual vector of a rigid space robot.

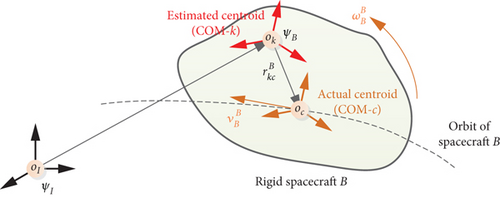
2.1. General Representation of a Rigid Particle by Using Six-Dimensional Dual Screw

A rigid space robot is equivalent to a system of particles. As shown in Figure 1, assuming the rigid space robot B is a system composed of N particles with equal mass. In order to clearly express the six-dimensional screw form of dual vector and dual momentum, we start our discussion by deriving the dual velocity and dual momentum of a rigid particle relative to the COM of a rigid space robot B. That is, in the next derivation, we set the state quantities of COM of space robot B as the known parameters, and the state quantities of other particles of the rigid space robot are derived from the above-known parameters.

The symbols of the known parameters are defined as follows:

1.
, the attitude angular velocity of space robot B, is defined as the angular velocity of Ψ_B relative to Ψ_I in terms of components along the BFCS of space robot B. is used as a known parameter for deriving the dual velocity of rigid particles in this paper.
2.
, the orbital velocity of space robot B, is defined as the linear velocity of the COM of space robot B relative to the origin of Ψ_I in terms of components along the BFCS of space robot B. is used as another known parameter for deriving the dual velocity of rigid particles.

Based on the above two known parameters, the attitude angular velocity of an arbitrary particle, i, in terms of components along the axes of Ψ_B can be expressed as

()

Then, the orbital velocity of i is obtained.

()

where

is the position vector from the COM of space robot B to particle i. “×” denotes cross multiplication of vector.

Furthermore, the dual velocity of i is obtained.

()

where ε is the dual unit with multiplication rule ε ≠ 0 and ε² = 0.

Representing Equation (5) in six-dimensional screw form, the dual velocity can further be expressed as

()

Introducing Equations (3) and (4) into Equation (5) and representing it in six-dimensional screw form, we obtain

()

where I_3×3 ∈ ℝ^3×3 denotes the third-order identity matrix.

is the position vector from i to the COM of space robot B. 0_3×3 is the third-order zero matrix.

denotes the cross-product matrix of

. Note that

Let

()

where

is an Hermitian matrix expressed in six-dimensional screw form.

Introducing Equation (8) into Equation (7), one can obtain

()

where

According to the operation rules of dual number [3], based on Equation (7), the dual momentum of i in terms of components along the axes of Ψ_B is

()

where

denotes the position vector from k to i.

is the dual mass operator of i. m_i is the mass of i.

Substituting Equation (6) into Equation (10), the dual momentum of i can specifically be expressed as

()

2.2. General Representation of a Rigid Space Robot by Using Six-Dimensional Dual Screw

By performing linear superposition operation on Equation (11), the dual momentum of rigid space robot B with respect to Ψ_B is obtained.

()

Substituting Equation (11) into Equation (12), the specific expression of dual momentum of rigid space robot B is obtained.

()

Let

()

where m_B ∈ ℝ is the mass of the space robot. J_B ∈ ℝ^3×3 is the moment of inertia of the space robot. In this paper, the moment of inertia with respect to the COM, J_B, is adopted instead of the moment of inertia with respect to point k derived in Ref. [3]. Since J_B is a constant matrix, the moment of inertia with respect to point k is a time-varying matrix.

Substituting Equation (14) into Equation (13), one can obtain

()

Representing Equation (15) in matrix form

()

Equation (16) can further be expressed as

()

Equation (17) is the general representation of the dual momentum of a rigid space robot.

is the dual inertia operator of space robot B expressed in six-dimensional screw form

()

Obviously, Equation (18) includes mutually canceling terms.

()

is represented as a six-dimensional matrix in this paper instead of a three-dimensional matrix proposed in Ref. [3] to describe the six-DOF of a rigid space robot. m_B and J_B are common parameters in aerospace engineering missions. Therefore, the general representation of the dual momentum of a rigid space robot in a six-dimensional screw form is obtained.

2.3. General Representation of a Rigid Space Robot Dynamics in Newton–Euler Form

The dynamic equation of a rigid space robot can be derived as follows:

()

where

is the dual velocity of the BFCS with its origin in an arbitrary point k and

The derivation of Equation (19) is carried out with respect to the BFCS of space robot B, as explained in Remark 2. The selection of a reference coordinate system is crucial for derivative operations of Equation (21). This is also the difference between the dual screw dynamics modeling method and the traditional Newton–Euler method. The traditional Newton–Euler equation can use different reference coordinate systems for translational motion and rotational motion. For example, the reference coordinate system for the CW equation is the orbital coordinate system, while the Euler attitude equation uses the BFCS as the reference. The reference coordinate system for the six-DOF motion of the dual screw method must be unified, which reflects the idea of integrated modeling.

The rigid body dynamic equation is obtained by substituting Equation (17) into Equation (21).

()

where

denotes the dual force acting on the point k of space robot B.

and

denote the force and torque acting on the point k. The dual force can be further expressed as

()

denotes the dual force acting on the COM of space robot B.

Equation (22) can also be equivalent to the following equation:

()

where

Equations (22) and (24) are the general representation of rigid space robot dynamics. They are represented in a six-dimensional screw instead of a three-dimensional motor proposed in Ref. [3]. Note that all of the dual vectors are represented with respect to the BFCS of the rigid space robot, and the origin of the BFCS is located at an arbitrary point, k, of the rigid space robot. If the origin of the BFCS is located at the COM of the rigid space robot, this leads to a much simpler expression.

()

2.4. General Representation of Relative Dynamics Between Rigid Space Robot

This subsection considers a two-earth-orbiting-space robot proximity cooperative mission, including a leader space robot A and an operator space robot B. In this subsection, a new BFCS of space robot A is adopted. Ψ_A, the BFCS of a rigid space robot A, with its origin in an arbitrary point, p, of space robot A, and axes pointing along the principal axes of inertia. The following notations are employed: denotes the components of x expressed in the BFCS of space robot A with its origin in an arbitrary point p.

According to Ref. [7–9], dual quaternion is used to describe the relative state. The relative six-DOF state between space robots A and B is

()

where

is a dual quaternion, representing the six-DOF motion state of space robot B relative to space robot A. q_BA ∈ ℝ^4×1 is the real part, representing the relative attitude quaternion between two space robots.

is the dual part.

is the quaternion representation of screw

, specifically represented as

is the relative position vector from the origin of the BFCS of space robot B to the origin of the BFCS of space robot A.

Taking the first derivative of

, then, the relative kinematic equation is obtained.

()

where

is the dual quaternion representation of screw

, specifically represented as

;

denotes the dual velocity of the BFCS of space robot B relative to the BFCS of space robot A.

Furthermore,

can be derived as follows:

()

where

and

denote the dual velocity of space robot A expressed in BFCS of space robot B and BFCS of space robot A, respectively. E_x{⋅} is the vector operation for converting dual quaternions into screws, for example,

The general dynamic model is derived by taking the first derivative of

()

If the origins of Ψ_A and Ψ_B are located at the COM of the rigid space robot, this leads to a much simpler expression.

()

Equation (30) is defined as the centroid relative dynamic equation.

3. General Representation of Six-DOF Relative Motion Between Rigid-Flexible Coupling Space Robot

A typical rigid-flexible coupling space robot consists of a rigid body and a flexible body, as shown in Figure 2. This section uses the same two coordinate systems as Section 2, and the origin of Ψ_B is set at an arbitrary point, k, in the rigid part of space robot B. In addition, a new coordinate system, floating coordinate system Ψ_F is used in the derivation of the dynamic model in this section. Ψ_f, the floating coordinate system of the rigid-flexible space robot B, with its origin in the connection point between the rigid part and flexible part, f, and axes pointing along the principal axes of BFCS.

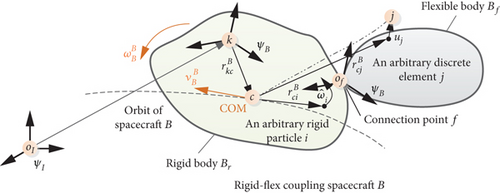
The first challenge of this section is the derivation of the dual momentum of the flexible body by using hybrid coordinates. Since we use dual number representation, the six-dimensional screw expression of vibration motion, a coupling matrix is needed. On this basis, the cross-coupling dynamics between attitude-orbit coupling and rigid-flexible coupling of a rigid-flexible combination space robot are developed. Finally, the relative dynamic equations between rigid-flexible coupling space robots are provided.

3.1. General Representation of a Flexible Body by Using Dual Operator With Hybrid Coordinates

As shown in Figure 2, selecting the flexible body B_f as the object, by using Ψ_f and Ψ_B as reference coordinate systems, the dual velocity and dual momentum of B_f are derived with hybrid coordinates.

First, based on the finite-element principle [23, 24], a continuous infinite DOF problem of the flexible body B_f is equivalent to a discrete finite DOF problem of a system of discrete elements, j. As shown in Figure 2, the attitude angular velocity of an arbitrary discrete element j, in terms of components along the axes of Ψ_f, is

()

Note that the premise for Equation (31) to hold is that the space robot configuration is stable. At this point, Ψ_f coincides with Ψ_B. And, Equation (31) can further be expressed as

()

The translational velocity of the discrete element j can be obtained.

()

where

and

are elastic position of j with respect to Ψ_f and Ψ_B, respectively.

and

are the first derivative of

and

, respectively.

and

denote vector from the COM to j with respect to Ψ_f and Ψ_B, respectively.

Considering that the initial three-axis orientation of Ψ_f coincides with that of Ψ_B, and there is no relative rotation between the above two coordinate systems. In order to match the rigid body dynamics derived in Section 2, we plan to construct the rigid-flexible coupling dynamics model in Ψ_B.

Representing Equations (32) and (33) in six-dimensional screw form with respect to Ψ_B, one can obtain

()

where the dual velocity

The dual momentum of j relative to k is

()

where

is the dual mass of j.

Introducing Equation (34) into Equation (35), the dual momentum of j can further be expressed as

()

Equation (36) is the complete expression of the dual momentum of a discrete finite element j. According to Refs. [23, 24], in order to represent the dual momentum with a hybrid coordinate system, the small deformation assumption needs to be adopted. That is, in Equation (36), is much smaller than and can be ignored in calculations.

Based on a small deformation assumption, Equation (36) can further be expressed as

()

Comparing Equation (37) with Equation (11), which represents the dual momentum of a rigid particle, we find that three new items, , , and , are needed to describe six-DOF motion of an arbitrary discrete element of the flexible body.

Based on the finite-element principle, the dual momentum of the flexible body B_f can be expressed as

()

Introducing Equation (37) into Equation (38), one can obtain

()

where

and

denote mass and moment of inertia of the flexible body B_f, respectively. The definition of

, and

correspond to the definition of

, and J_B in Equation (14), respectively.

According to Refs. [23, 24], representing Equation (39) with modal coordinates, one can obtain

()

where Φ_j ∈ ℝ^3×N is the matrix of eigenvectors of j. η ∈ ℝ^N×1 is the vibration mode of the flexible body.

Meanwhile, the translational and rotational rigid-flexible coupling coefficients are defined as follows:

()

Substituting Equations (40) and (41) into Equation (39) and representing Equation (39) in six-dimensional screw form, the dual momentum of B_f can further be expressed as

()

Equation (38) can further be expressed as

()

where

()

denote the dual inertia operator, dual rigid-flexible coupling coefficient operator, and dual vibration mode of the flexible body, respectively.

Two coordinate systems, Ψ_f and Ψ_B, are used in Equation (30). Through the above work, the dual momentum of the flexible body B_f is represented in a six-dimensional screw form with hybrid coordinates. Note that, due to the stable configuration of rigid-flexible coupling space robots, Ψ_f and Ψ_B always coincide. Therefore, the variables derived in this subsection can be represented in either the floating coordinate system or the BFCS.

3.2. General Representation of Dynamics by Using Dual Operator With Hybrid Coordinates

According to Equation (17), the dual momentum of a rigid body B_r is

()

where

denotes dual inertia operator of rigid body B_r.

Considering a typical rigid-flexible coupling space robot consisting of a rigid platform B_r and a flexible component B_f, as shown in Figure 2. And, dual momentum of B_r and B_f are both derived with respect to the same coordinate system Ψ_B. So, the dual momentum of the rigid-flexible coupling space robot in terms of components along the axes of Ψ_B is

()

The dual inertia operator of the rigid-flexible coupling space robot B is defined as

()

Similarly, assuming that the COM and moment of inertia of a rigid-flexible coupling space robot are minimally affected by system motion (including attitude, orbital motion, and flexible body vibration), the following equation holds

()

Substituting Equation (48) into Equation (47), the dual inertia operator of the rigid-flexible coupling space robot B can be transformed into the following form:

()

where

and

Taking the first derivative of Equation (46), the six-dimensional screw representation dynamic equation of the rigid-flexible coupling space robot is obtained.

()

where

Note that all of the dual vectors are represented with respect to the BFCS of the rigid-flexible coupling space robot, and the origin of the BFCS is located at an arbitrary point, k, on the rigid-flexible coupling space robot. If the origin of the BFCS is located at the COM of the rigid-flexible coupling space robot, this leads to a much simpler expression

()

The vibration function of the rigid-flexible coupling space robot refers to Equation (31) in Ref. [21].

3.3. General Representation of Relative Dynamics by Using Dual Operator With Hybrid Coordinates

Similarly, this subsection considers a two-earth-orbiting-space robot proximity cooperative mission including a leader space robot A and an operator space robot B [25–28], and the follower space robot B is a rigid-flexible coupling system. The definition of BFCS of leader space robot A is the same as that in Subsection 2.4. Then, the relative kinematic equation between space robot B and A is

()

where

;

denotes the dual velocity of the BFCS of space robot B relative to the BFCS of space robot A.

A general representation of the relative dynamic equation is obtained.

()

If the origins of Ψ_A and Ψ_B are located at the COM of the rigid space robot, this leads to a much simpler expression.

()

Equation (54) is defined as the centroid relative dynamic equation.

4. General Representation of Six-DOF Relative Motion Between Space Robot With Time-Varying Configuration

In Section 3, dynamic equations of rigid-flexible coupling space robots with a stable configuration are developed. The dynamic equations proposed in Section 3 are applicable to the working conditions of space robots in which flexible components are firmly connected with rigid platforms, such as some radar satellites and optical satellites. However, in most cases, there is relative rotation between the flexible component and the rigid platform. For example, solar panels sometimes rotate around the platform, and optical lenses rotate around the platform in some working conditions. In view of the above scenario, it is necessary to develop a six-dimensional screw representation of the six-DOF motion of the rigid-flexible coupling space robot with a time-varying configuration. This section focuses on the above issues.

4.1. General Representation of Space Robot With Time-Varying Configuration

As shown in Figure 2, we assume that the flexible body B_f rotates around a rigid body B_r through connection point f, and the relative rotation angular velocity is ω_f. As in Section 3, we first derive the attitude angular velocity of a discrete finite element j on the flexible body B_f.

()

In Equation (55), the attitude angular velocity is represented with respect to the BFCS Ψ_B.

The translational velocity of j with respect to the BFCS Ψ_B can be expressed as

()

where

denotes the position vector from COM to connection point f.

denotes the position vector from point the f to j.

Note that, in practical engineering, r_fj and u_j are usually measured in the floating coordinate system Ψ_f. That is,

and

are directly obtainable quantities. However, in the process of deriving dynamic equations, in order to unify the reference coordinate system, the following coordinate transformations need to be performed.

()

where

is coordinate transformation matrix from Ψ_f to Ψ_B. In hybrid coordinate modeling methods, a large amount of coordinate transformation operations are required.

Based on Equations (55) and (56), the dual velocity of j relative to the COM representing in six-dimensional screw form can be obtained.

()

The dual momentum of j relative to k is

()

The elastic displacement

can be neglected in the calculation of Equation (59). Subsequently, Equation (59) can be written in the explicit form

()

Comparing with Equation (39), we find that three new items, , , and , are taken to describe the dual momentum of a discrete element.

Carry out integral operation on Equation (60) and express it in six-dimensional screw form, the dual momentum of B_f can be transformed into the following expression form:

()

where

()

Equation (61) can further be expressed as

()

where

is defined as the dual velocity of the flexible body B_f relative to the rigid body B_r.

Through Equations (61) and (63), we find that the dual momentum representation of the flexible body B_f is extremely complex. In the following, a special case is considered. Assume that the COM of the space robot is at the connection point f, then the dual momentum of B_f will lead to a much simpler expression

()

Taking the first derivative of Equation (64), we obtain

()

where

, since the origin k of Ψ_B, is set in the rigid part of space robot B.

Let

()

where

is the interaction force between B_f and B_r.

According to Equation (45), the dual momentum of a rigid body B_r is

()

Taking the first derivative of Equation (67), we obtain

()

4.2. General Representation of Dynamics of Space Robot With Time-Varying Configuration

Based on the dual momentum equation of the flexible body B_f and the rigid body B_r (Equations (65), (66), and (68)), the dual momentum of the space robot, which consists of a flexible body and a rigid body, is obtained.

()

Compared with Equation (46), it can be found that the derivation rule of Equation (69) has changed. For a configuration time-varying system, it is necessary to first solve the derivative of the dual momentum of each subsystem and then perform the sum operation. The operation order cannot be reversed since the dual velocity of each subsystem is different. However, the order of addition and derivation can be reversed for a configuration-stabilized system.

Substituting Equations (65), (66), and (68) into Equation (69), a dynamic equation of a space robot with a time-varying configuration is obtained.

()

where

4.3. General Representation of Relative Dynamics of Space Robot With Time-Varying Configuration

This subsection considers a two-earth-orbiting space robot proximity cooperative mission including a leader space robot A and an operator space robot B, and the follower space robot B is a rigid-flexible coupling system with time-varying configuration. The definition of BFCS of leader space robot A is the same as that in Sections 2.4 and 3.3. Then, the relative kinematic equation between space robots B and A is

()

A general representation of the relative dynamic equation is obtained.

()

If the origins of Ψ_A and Ψ_B are located at the COM of the rigid space robot, this leads to a much simpler expression.

()

5. Dual Number–Based Controller

Since the general representation of the space robot proximity relative dynamics consists of three equations, Equations (30), (54), and (73), the controller adopted in this paper should be universal. Considering the above factors, in this section, a PD controller proposed in Ref. [9] is adopted.

()

where

is the dual control force acting on the follower.

and

are both positive dual scalars with that

and

, and

denotes the vector part of the

is a dual function with that

()

where

and

. λ_i and

are positive scalar constants, φ_i(t) > 0,

for t ≥ 0.

, c, and c^′ are positive scalar constants.

Controller (74) has achieved good results in proximity collaborative tasks of rigid space robots, such as space robot formation, rendezvous, and docking. This paper mainly uses this controller to demonstrate the evolutionary trajectory of the proposed dynamic model.

6. Simulations and Results

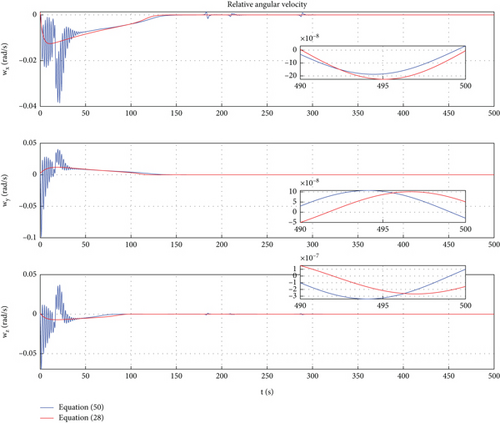
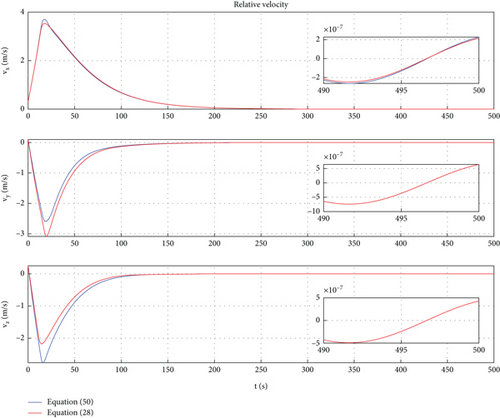
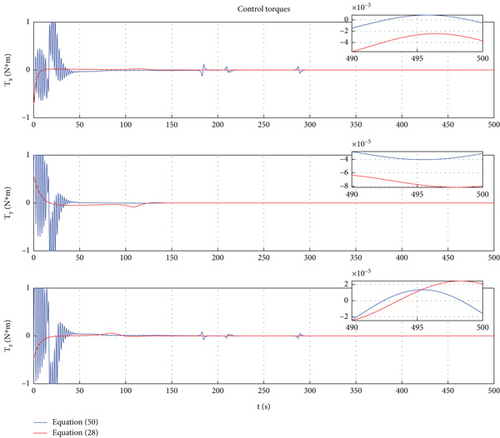
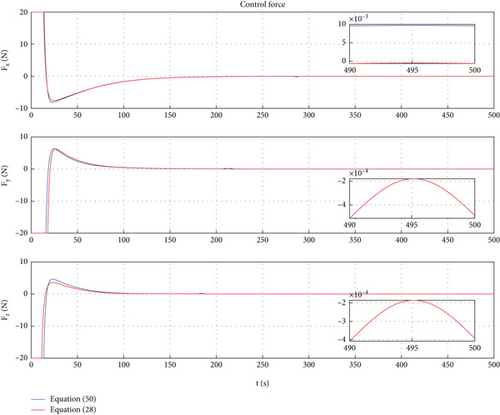
In this section, three sets of numerical simulations are provided. The purpose of the first set of simulations is to verify the engineering application significance of the general representation dynamic model. Since one of the main innovations of this paper is to develop the general representation of the dual number–based dynamic model, and the difference between the general model and the centroid model is whether the origin of the reference coordinate system is set at the centroid, the first set of simulations mainly compares the description deviation of the above two models. The second set of simulations is provided to show the relative motion results in the space robot formation proximity mission [29–37] of the two models, Equations (30) and (54). Since the general representation of relative motion between rigid-flexible space robots is another innovation of this paper, the purpose of this simulation is to verify the correctness of Equation (54). In the third simulation, relative dynamics models, Equations (30) and (54), are implemented for the motion between space robots. A PD controller is presented, and the simulation results are provided.

6.1. Case 1: Description Deviation Between General Dynamics and Centroid Dynamics

At present, the centroid dynamics model is commonly used to describe the six-DOF motion of space robots. However, in aerospace engineering, it is not an easy task to accurately locate the centroid of a space robot in real time, since the centroid of a space robot changes with fuel consumption. That is, there is a deviation between the motion described by the centroid dynamics equation and the true value. This subsection is designed to present the magnitude of the deviation through simulation.

The simulation idea of this subsection is designed as follows. As shown in Figure 3, assume that the COM of the space robot B calibrated by engineering is at point k in a certain period of time, and the six-DOF motion can be described by Equation (22). However, in fact, the COM of the space robot B is at point c, at which six-DOF motion can be described by Equation (25). The position deviation between the two is . The space robot B is orbiting the earth in an elliptical orbit. The orbital parameters are shown in Table 1.

Table 1. Orbital parameters of space robot B.

Semimajor axis	Inclination	Argument of periapsis	Longitude of the ascending node	Mean anomaly at epoch	Eccentricity
a_L = 6998455m	I_L = 45^∘	ω_L = 0^∘	Ω_L = 0^∘	f_L = 30^∘	e_L = 0.02

The initial state of space robot B is as follows:

The mass and moment of inertia of space robot B are

Considering the gravity () and the gravity gradient moment (), the influence of other forces and noises is neglected.

Four sets of values for the position vector are taken, which are , , , and . Based on the above conditions, simulation results are shown in Figures 4, 5, 6, and 7. Figure 4 shows the orbit of space robot B under four initial conditions. Figures 5 and 6 are the orbital velocity and position under four initial conditions, respectively. Figure 7 shows the description deviation among four initial conditions; the red line represents the description deviation between and ; the green line represents the description deviation between and ; the blue line represents the description deviation between and .

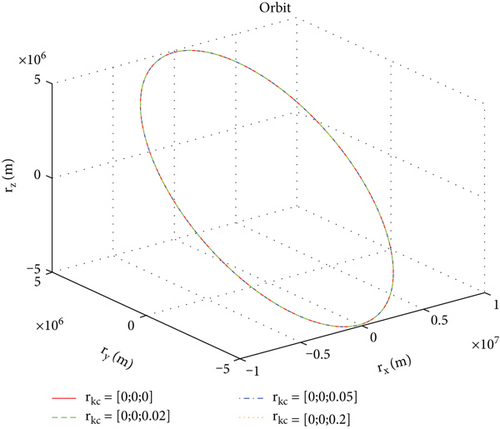
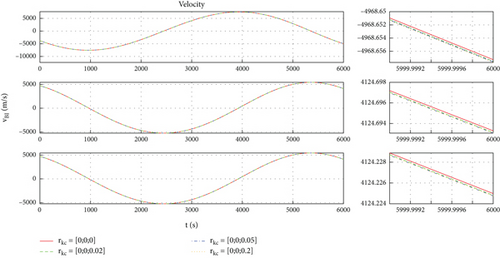
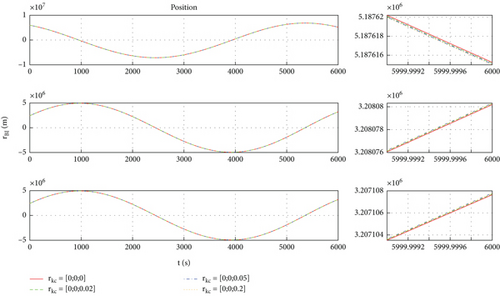
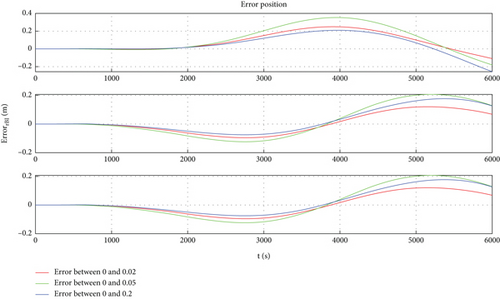
As shown in Figure 4, the orbits of the space robot B basically coincide under the four initial conditions. The simulation results are consistent with the physical phenomena, which proves the correctness of the general model. Through Figures 5, 6, and 7, one can find that there is a description deviation between the general model and centroid model, and the position description offset reaches about 0.4 m. It can be concluded that the model description error is one of the important error sources for the mission with high requirements for space robot position accuracy.

6.2. Case 2: Description Deviation of Dynamics Between Rigid Space Robot and Rigid-Flexible Space Robot

In this subsection, simulation results are provided to explicitly present the six-DOF proximity relative motions of the space robot described by two dynamic models, Equations (30) and (54). Simulation scenarios are designed to be a proximity leader–follower SFF mission. The rigid leader space robot A was assumed to deploy on the 500 km circular orbit. Initial states of space robot A are as follows.

Due to the fact that the simulation in this case compares the curve trajectories of Models (30) and (54), where Model (30) is the model for the proximity collaboration task of a rigid body space robot and Model (54) is the model for the proximity collaboration task of a rigid-flexible coupling space robot, two sets of mass characteristic parameters should be set for the follower space robot. In Model (30), the mass and moment of inertia of follower space robot B are the same as in Case 1. In Model (54), the mass characteristic parameters of follower space robot B are shown (Table 2), and the fundamental frequency of the flexible body of space robot B is set as 0.174 Hz. In addition, the mass and moment of inertia of leader space robot A are the same as those of follower space robot B.

Table 2. Parameters of space robot B.

Symbol	Value	Unit
	80	kg
	20	kg
J_B	diag{50, 45, 50}	kg·m²
B_tran	[1.55 − 1.55 0.225]^T	—
B_rot	20 − 5 1.5	—
ξ	0.005	—
Λ	1.727	—

Relative initial states between space robot B and space robot A are set as follows:

Considering the effects of earth’s gravity and gravitational gradient torque, ignoring other interferences, the simulation results are shown in Figures 8, 9, 10, and 11.

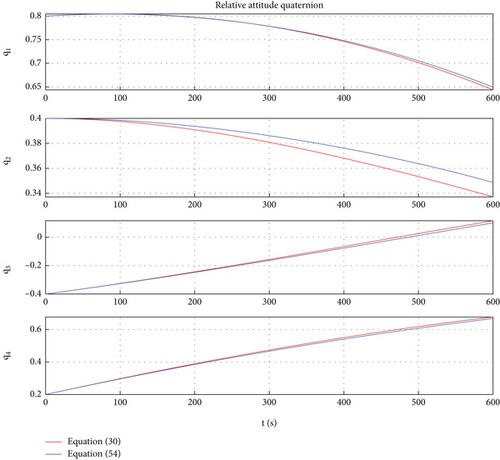
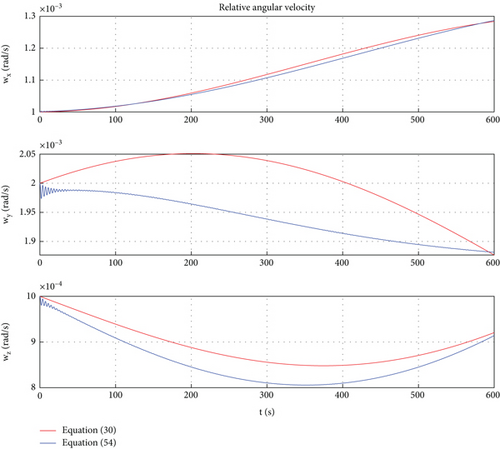
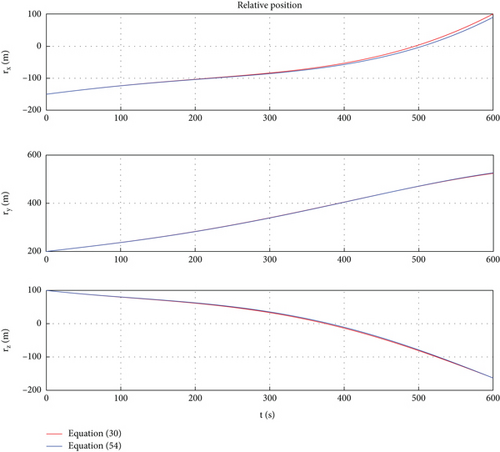
In Figures 8, 9, 10, and 11, the red lines represent the relative dynamic evolution trajectory of the space robot described by model (30), while the blue lines represent the relative dynamic evolution trajectory of the space robot described by model (54). From Figures 8, 9, 10, and 11, we can discover that the relative translational and rotational trajectory between follower space robot B and leader space robot A changes under the influence of the earth’s gravity and gravitational gradient torque. Overall, the trends of relative translational and rotational changes between space robots described by the two models tend to be similar. From Figures 8 and 9, one can find that under the action of gravitational gradient torque, the relative attitude between the rigid-flexible coupling space robots described by Model (54) generates an angular acceleration maneuver, which leads to vibration of the flexible body. Therefore, there is a deviation between the relative attitude curve described by Model (54) and Model (30). The above simulation results are consistent with the characteristics of the objects described by Models (54) and (30). In addition, from Figures 8, 9, 10, and 11, one can conclude that in the case of small space robot attitude and orbital maneuvers (caused only by gravity and gravitational gradient torque), the relative attitude and orbital errors caused by the rigid-flexible coupling effect are within a reasonable range.

6.3. Case 3: Description of Deviation of Dynamics Between Rigid Space Robot and Rigid-Flexible Space Robot Under Control

In this subsection, relative dynamics models, Equations (30) and (54), are implemented for the motion between space robots. A PD controller is presented, and the controller gains are shown in Table 3. The parameters of the follower and leader space robots are the same as in Case 2. Based on the above simulation conditions, the control objective is that

can be reached in the presence of external disturbances.

Table 3. Controller gains.

Symbol	Value
K_p	10
	10
K_d	500
	500
c	0.6
c^′	0.8
λ₁	0.3
λ₂	0.3
λ₃	0.3
	2
	2
	2
δ₁	0.005
δ₂	0.005
δ₃	0.005
	0.002
	0.002
	0.002

In this case, a PD control is applied to achieve motion control of Dynamic Models (30) and (54). In Ref. [9], the PD controller has been proven to have good control performance in proximity relative motion control of rigid space robots. In this paper, one can find that the PD controller also has excellent control performance for the relative motion of a rigid-flexible coupling space robot under the interference of flexible body vibration. Of course, the emergence of the excellent control effect mentioned above requires ensuring frequency band isolation between the control bandwidth and vibration. From Figures 12, 13, 14, 15, 16, and 17, we can find that two sets of control error curves deviated under the influence of flexible vibration but eventually converged to the desired value. And the changes of control force and control torque are within the achievable range of the actuator engineering.

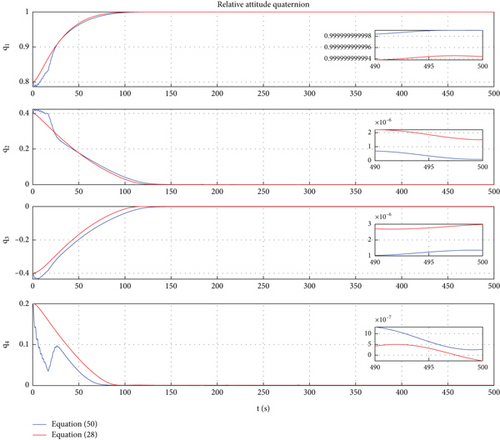
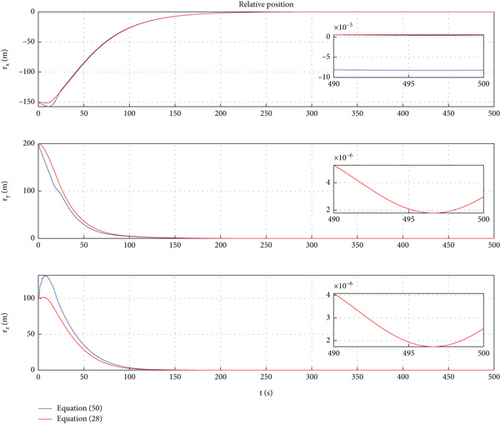
7. Conclusions

This paper conducts innovative research on the dynamic modeling of space robots for proximity collaborative tasks. Three problems of general representation of space robot relative motion based on dual numbers are solved. At first, a six-dimensional screw representation of dual number–based dynamics is developed. With this six-dimensional screw representation, all six-DOF relative dynamic equations between rigid space robots, rigid-flexible space robots, and time-varying configuration space robots are naturally embedded into the dual screw space. Second, the general representation of the relative dynamic equation between rigid-flexible space robots is proposed. Third, the general representation of the relative dynamic model between space robots with time-varying configurations is provided. Simulation results show that compared with the classical centroid dynamic model, the general model proposed in this paper has higher precision for the scenario in which space robots have variable dynamic parameters. In addition, the general model proposed in this article has a compact representation and can be directly used for controller design. It proves the engineering application value of the general representation of the relative dynamic model. Furthermore, the model and conclusions studied in this paper can provide a fundamental theory for the dynamic modeling of multirigid-flexible coupling robots, such as space crawling robots.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funding was received for this manuscript.

Open Research

Data Availability Statement

Data sets generated during the current study are available from the corresponding author upon reasonable request.

References

1 Clifford W. K., Preliminary Sketch of Bi-Quaternions, Proceedings of the London Mathematical Society. (1871) s1-4, no. 1, 381–395, https://doi.org/10.1112/plms/s1-4.1.381, 2-s2.0-84960556043.
10.1112/plms/s1-4.1.381
Google Scholar
2 E. Study, Von den Bewegungen und Umlegungen: I. und II. Abhandlung, Mathematische Annalen. (1891) 39, no. 4, 441–565, https://doi.org/10.1007/BF01199824, 2-s2.0-0042906634.
10.1007/BF01199824
Google Scholar
3 Brodsky V. and Shoham M., Dual Numbers Representation of Rigid Body Dynamics, Mechanism and Machine Theory. (1999) 34, no. 5, 693–718, https://doi.org/10.1016/S0094-114X(98)00049-4, 2-s2.0-0032659155.
10.1016/S0094-114X(98)00049-4
Web of Science® Google Scholar
4 Wu Y., Hu X., Hu D., and Li T., Strapdown Inertial Navigation System Algorithms Based on Dual Quaternions, IEEE Transactions on Aerospace and Electronic Systems. (2005) 41, no. 1, 110–132, https://doi.org/10.1109/TAES.2005.1413751, 2-s2.0-18844456799.
10.1109/TAES.2005.1413751
Web of Science® Google Scholar
5 Gan D., Liao Q., Wei S., and Dai J., Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. (2008) 222, no. 8, 1593–1598.
10.1243/09544062JMES1082
Google Scholar
6 Perez A. and McCarthy J., Dual Quaternion Synthesis of Constrained Robotic Systems, Journal of Mechanical Design. (2004) 126, no. 3, 425–435, https://doi.org/10.1115/1.1737378, 2-s2.0-4344672026.
10.1115/1.1737378
Web of Science® Google Scholar
7 Wang J., Liang H., Sun Z., Zhang S., and Liu M., Finite-Time Control for Spacecraft Formation With Dual-Number-Based Description, Journal of Guidance, Control, and Dynamics. (2012) 35, no. 3, 950–962, https://doi.org/10.2514/1.54277, 2-s2.0-84861512879.
10.2514/1.54277
Web of Science® Google Scholar
8 Wang J. and Sun Z., 6-DOF Robust Adaptive Terminal Sliding Mode Control for Spacecraft Formation Flying, Acta Astronautica. (2012) 73, 76–87, https://doi.org/10.1016/j.actaastro.2011.12.005, 2-s2.0-84856442176.
10.1016/j.actaastro.2011.12.005
Web of Science® Google Scholar
9 Wang J., Liang H., Sun Z., Wu S., and Zhang S., Relative Motion Coupled Control Based on Dual Quaternion, Aerospace Science and Technology. (2013) 25, no. 1, 102–113, https://doi.org/10.1016/j.ast.2011.12.013, 2-s2.0-84875148154.
10.1016/j.ast.2011.12.013
Web of Science® Google Scholar
10 Zhang F. and Duan G., Integrated Relative Position and Attitude Control of Spacecraft in Proximity Operation Missions, International Journal of Automation and Computing. (2012) 9, no. 4, 342–351, https://doi.org/10.1007/s11633-012-0654-0, 2-s2.0-84865545391.
10.1007/s11633-012-0654-0
Google Scholar
11 Lee U. and Mesbahi M., Constrained Autonomous Precision Landing via Dual Quaternions and Model Predictive Control, Journal of Guidance, Control and Dynamics. (2017) 40, no. 2, 292–308, https://doi.org/10.2514/1.G001879, 2-s2.0-85014194981.
10.2514/1.G001879
Web of Science® Google Scholar
12 Sun C., Xiao Y., Sun Z., and Ye D., Dual Quaternion Based Close Proximity Operation for In-Orbit Assembly via Model Predictive Control, International Journal of Aerospace Engineering. (2021) 2021, no. 1, 1305095, https://doi.org/10.1155/2021/1305095.
10.1155/2021/1305095
Web of Science® Google Scholar
13 Xu H., Ye Y., Yang Z., and Yang Y., Dual-Quaternion Based Distributed Coordination Control of Six-DOF Spacecraft Formation With Collision Avoidance, Aerospace Science and Technology. (2017) 67, 443–455, https://doi.org/10.1016/j.ast.2017.04.011, 2-s2.0-85018907111.
10.1016/j.ast.2017.04.011
Google Scholar
14 Henry D., Zenteno-Torres J., Cieslak J., De Loza A., and Dávila J., A 6-DOF Sliding Mode Fault Tolerant Control Solution for In-Orbit Autonomous Rendezvous, Aerospace Science and Technology. (2021) 118, 107050, https://doi.org/10.1016/j.ast.2021.107050.
10.1016/j.ast.2021.107050
Web of Science® Google Scholar
15 Dong H., Hu Q., and Ma G., Dual-Quaternion Based Fault-Tolerant Control for Spacecraft Formation Flying With Finite-Time Convergence, ISA Transactions. (2016) 61, 87–94, https://doi.org/10.1016/j.isatra.2015.12.008, 2-s2.0-84954304605, 26775087.
10.1016/j.isatra.2015.12.008
PubMed Web of Science® Google Scholar
16 Dong H., Hu Q., Friswell M., and Ma G., Dual-Quaternion-Based Fault-Tolerant Control for Spacecraft Tracking With Finite-Time Convergence, IEEE Transations on Control Systems Technology. (2017) 25, no. 4, 1231–1242, https://doi.org/10.1109/TCST.2016.2603070, 2-s2.0-85027707435.
10.1109/TCST.2016.2603070
Web of Science® Google Scholar
17 Li L., Yuan L., Wang L., Zheng R., Wu Y., and Wang Y., Recent Advances in Precision Measurement & Pointing Control of Spacecraft, Chinese Journal of Aeronautics. (2021) 34, no. 10, 191–209, https://doi.org/10.1016/j.cja.2020.11.018.
10.1016/j.cja.2020.11.018
Web of Science® Google Scholar
18 Zhuang M., Tan L., Li K., and Song S., Fixed-Time Position Coordinated Tracking Control for Spacecraft Formation Flying With Collision Avoidance, Chinese Journal of Aeronautics. (2021) 34, no. 11, 182–199, https://doi.org/10.1016/j.cja.2020.12.024.
10.1016/j.cja.2020.12.024
Web of Science® Google Scholar
19 Yang Y., Jing W., and Zhang Z., “A New Method for Orbit and Attitude Coupling Control Problem of Flexible Spacecraft Based on Dual Quaternions”, [in Chinese], Journal of Astronautics. (2016) 37, no. 8, 946–956.
Google Scholar
20 Zhang X., Zhu W., Wu X., Song T., Xie Y., and Zhao H., Dynamics and Control for In-Space Assembly Robots With Large Translational and Rotational Maneuvers, Acta Astronautica. (2020) 174, 166–179, https://doi.org/10.1016/j.actaastro.2020.04.063.
10.1016/j.actaastro.2020.04.063
Web of Science® Google Scholar
21 Zhang X., Zhu W., Xie Y., Wu X., and Guo J., Cross-Coupling Relative Dynamics for On-Orbit Assembly in Rotating Frame of Reference, Applied Mathematical Modelling. (2023) 116, 372–392, https://doi.org/10.1016/j.apm.2022.11.037.
10.1016/j.apm.2022.11.037
Web of Science® Google Scholar
22 Deng C., Shi Z., Liu S., and Zhang X., General Representation of Dual Screw in Hybrid Coordinate and Its Application in Dynamic Modeling of Rigid-Flexible Multibody Spacecraft, Journal of Vibration Engineering & Technologies. (2025) 13, no. 2, https://doi.org/10.1007/s42417-024-01585-9.
10.1007/s42417-024-01585-9
Web of Science® Google Scholar
23 Likins P., Modal Method for Analysis of Free Rotations of Spacecraft, AIAA Journal. (1967) 5, no. 7, 1304–1308, https://doi.org/10.2514/3.4188, 2-s2.0-85007721208.
10.2514/3.4188
Web of Science® Google Scholar
24 Likins P. and Wirsching P., Use of Synthetic Modes in Hybrid Coordinate Dynamic Analysis, AIAA Journal. (1968) 6, no. 10, 1867–1872, https://doi.org/10.2514/3.4894, 2-s2.0-85007724398.
10.2514/3.4894
Web of Science® Google Scholar
25 Liu C., Yue X., Zhang J., and Shi K., Active Disturbance Rejection Control for Delayed Electromagnetic Docking of Spacecraft in Elliptical Orbits, IEEE Transactions on Aerospace and Electronic Systems. (2022) 58, no. 3, 2257–2268, https://doi.org/10.1109/TAES.2021.3130830.
10.1109/TAES.2021.3130830
Web of Science® Google Scholar
26 Liu C., Yue X., Shi K., and Sun Z., Spacecraft Attitude Control: A Linear Matrix Inequality Approach, 2022, Elsevier, Amsterdam.
Google Scholar
27 Lyu B., Liu C., and Yue X., Integrated Predictor-Observer Feedback Control for Vibration Mitigation of Large-Scale Spacecraft With Unbounded Input Time Delay, Proceedings of the IEEE Transactions on Aerospace and Electronic Systems, 2024, IEEE, 1–12, https://doi.org/10.1109/TAES.2024.3505851.
10.1109/TAES.2024.3505851
Google Scholar
28 Yu W., Liu C., and Yue X., Reinforcement Learning-Based Decision-Making for Spacecraft Pursuit-Evasion Game in Elliptical Orbits, Control Engineering Practice. (2024) 153, 106072, https://doi.org/10.1016/j.conengprac.2024.106072.
10.1016/j.conengprac.2024.106072
Web of Science® Google Scholar
29 Jiang R., Ye D., Xiao Y., Sun Z., and Zhang Z., Orbital Interception Pursuit Strategy for Random Evasion Using Deep Reinforcement Learning, Space Science & Technology. (2023) 3, https://doi.org/10.34133/space.0086.
10.34133/space.0086
Web of Science® Google Scholar
30 Xu L., Zhang G., Qiu S., and Cao X., Optimal Multi-Impulse Linear Rendezvous via Reinforcement Learning, Space Science & Technology. (2023) 3, https://doi.org/10.34133/space.0047.
10.34133/space.0047
Web of Science® Google Scholar
31 Li D., Li Y., Liu X., Yang B., Huang X., Yang Y., Wang B., and Li S., Pseudospectral Convex Programming for Free-Floating Space Manipulator Path Planning, Space Science & Technology. (2023) 3, https://doi.org/10.34133/space.0030.
10.34133/space.0030
Web of Science® Google Scholar
32 Zhang J., Cai Y., Xue C., Xue Z., and Cai H., LEO Mega Constellations: Review of Development, Impact, Surveillance, and Governance, Space Science & Technology. (2022) 17, 9865174, https://doi.org/10.34133/2022/9865174.
10.34133/2022/9865174
Google Scholar
33 Wang B., Li S., Mu J., Hao X., Zhu W., and Hu J., Research Advancements in Key Technologies for Space-Based Situational Awareness, Space Science & Technology. (2022) 31, 9802793, https://doi.org/10.34133/2022/9802793.
10.34133/2022/9802793
Google Scholar
34 Zhou W., Xing Z., Bai W., and Deng C., Route Planning Algorithm for Autonomous Underwater Vehicles Based on the Hybrid of Particle Swarm Optimization Algorithm and Radial Basis Function, Transactions of the Institute of Measurement and Control. (2019) 41, no. 4, 942–953, https://doi.org/10.1177/0142331218785708, 2-s2.0-85052590446.
10.1177/0142331218785708
Web of Science® Google Scholar
35 Xing Z., Cheng Y., Zhou W., Wu X., Deng C., and Li S., RTS Filtering With a Combined View Time Comparison Algorithm for GNSS Navigation System, Proceedings of the 2018 37th Chinese Control Conference (CCC), 2018, IEEE.
10.23919/ChiCC.2018.8482766
Google Scholar
36 Zhou W., Xing Z., and Cui H., Analysis of a Stochastic Cooperation-Competition Model, Advances in Difference Equations. (2018) 74, 1–22.
Google Scholar
37 Xing Z., Cui H., and Zhang J., Dynamics of a Stochastic Intraguild Predation Model, Applied Sciences-Basel. (2016) 6, no. 4, https://doi.org/10.3390/app6040118, 2-s2.0-84967235588.
10.3390/app6040118
Web of Science® Google Scholar

All articles

General Modeling for Space Robot Proximity Relative Motion by Using Dual Operator With Hybrid Coordinates

Abstract

1. Introduction

2. General Representation of Six-DOF Relative Motion Between Rigid Space Robot

2.1. General Representation of a Rigid Particle by Using Six-Dimensional Dual Screw

2.2. General Representation of a Rigid Space Robot by Using Six-Dimensional Dual Screw

2.3. General Representation of a Rigid Space Robot Dynamics in Newton–Euler Form

2.4. General Representation of Relative Dynamics Between Rigid Space Robot

3. General Representation of Six-DOF Relative Motion Between Rigid-Flexible Coupling Space Robot

3.1. General Representation of a Flexible Body by Using Dual Operator With Hybrid Coordinates

3.2. General Representation of Dynamics by Using Dual Operator With Hybrid Coordinates

3.3. General Representation of Relative Dynamics by Using Dual Operator With Hybrid Coordinates

4. General Representation of Six-DOF Relative Motion Between Space Robot With Time-Varying Configuration

4.1. General Representation of Space Robot With Time-Varying Configuration

4.2. General Representation of Dynamics of Space Robot With Time-Varying Configuration

4.3. General Representation of Relative Dynamics of Space Robot With Time-Varying Configuration

5. Dual Number–Based Controller

6. Simulations and Results

6.1. Case 1: Description Deviation Between General Dynamics and Centroid Dynamics

6.2. Case 2: Description Deviation of Dynamics Between Rigid Space Robot and Rigid-Flexible Space Robot

6.3. Case 3: Description of Deviation of Dynamics Between Rigid Space Robot and Rigid-Flexible Space Robot Under Control

7. Conclusions

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

General Modeling for Space Robot Proximity Relative Motion by Using Dual Operator With Hybrid Coordinates

Abstract

1. Introduction

2. General Representation of Six-DOF Relative Motion Between Rigid Space Robot

2.1. General Representation of a Rigid Particle by Using Six-Dimensional Dual Screw

2.2. General Representation of a Rigid Space Robot by Using Six-Dimensional Dual Screw

2.3. General Representation of a Rigid Space Robot Dynamics in Newton–Euler Form

2.4. General Representation of Relative Dynamics Between Rigid Space Robot

3. General Representation of Six-DOF Relative Motion Between Rigid-Flexible Coupling Space Robot

3.1. General Representation of a Flexible Body by Using Dual Operator With Hybrid Coordinates

3.2. General Representation of Dynamics by Using Dual Operator With Hybrid Coordinates

3.3. General Representation of Relative Dynamics by Using Dual Operator With Hybrid Coordinates

4. General Representation of Six-DOF Relative Motion Between Space Robot With Time-Varying Configuration

4.1. General Representation of Space Robot With Time-Varying Configuration

4.2. General Representation of Dynamics of Space Robot With Time-Varying Configuration

4.3. General Representation of Relative Dynamics of Space Robot With Time-Varying Configuration

5. Dual Number–Based Controller

6. Simulations and Results

6.1. Case 1: Description Deviation Between General Dynamics and Centroid Dynamics

6.2. Case 2: Description Deviation of Dynamics Between Rigid Space Robot and Rigid-Flexible Space Robot

6.3. Case 3: Description of Deviation of Dynamics Between Rigid Space Robot and Rigid-Flexible Space Robot Under Control

7. Conclusions

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information