International Journal of Aerospace Engineering
Volume 2025, Issue 1 7686417
Research Article
Open Access

Reinforcement Learning-Based UAV Swarm Fission–Fusion Approach With Real-World Data-Integrated Validation

Xiaorong Zhang, 

Xiaorong Zhang

School of Electronic Information Engineering , Beihang University , Beijing , China , buaa.edu.cn

ShenYuan Honors College , Beihang University , Beijing , China , buaa.edu.cn

Search for more papers by this author
Dacheng Qi, 

Dacheng Qi

School of Electronic Information Engineering , Beihang University , Beijing , China , buaa.edu.cn

Search for more papers by this author
Wenrui Ding, 

Wenrui Ding

School of Institute of Unmanned System , Beihang University , Beijing , China , buaa.edu.cn

Search for more papers by this author
Xinrui Zhang, 

Xinrui Zhang

School of Electronic Information Engineering , Beihang University , Beijing , China , buaa.edu.cn

Search for more papers by this author
Qingyi Liu, 

Qingyi Liu

School of Electronic Information Engineering , Beihang University , Beijing , China , buaa.edu.cn

Search for more papers by this author
Yufeng Wang, 

Corresponding Author

Yufeng Wang

School of Institute of Unmanned System , Beihang University , Beijing , China , buaa.edu.cn

Search for more papers by this author
First published: 14 May 2025
https://doi.org/10.1155/ijae/7686417
Academic Editor: Mohammad Rezwan Habib

Abstract

The motion of unmanned aerial vehicle (UAV) swarms is a complex research area due to the involvement of various system components, including perception, control, and decision-making policies. However, compared to static flight behaviors, the fission–fusion motion of UAV swarms in response to multiple unknown dynamic disturbances has received relatively less attention. This paper proposes a reinforcement learning–based UAV swarm fission–fusion approach with real-world data integrated validation for the swarm’s fission-fusion behavior in response to multiple unknown dynamic disturbances, along with a system validation method utilizing real-world data. The proposed approach effectively integrates fission–fusion dynamics with perception and control to enable UAV swarms to function robustly in the presence of such disturbances. First, we develop a self-organized control framework that facilitates the coordinated motion of multiple UAV swarms. Second, we introduce a reinforcement learning–based fission–fusion confrontation algorithm designed to minimize resource consumption while effectively responding to multiple unknown dynamic disturbances. Finally, we present a real-world data-based validation system based on AirSim, which allows comprehensive evaluation of UAV swarm performance in actual environments. Simulation results demonstrate that when UAV swarms operate in environments with multiple unknown disturbances, they can successfully perform self-organized fission-fusion motion, effectively protecting the parent-swarm from the impact of multiple unknown dynamic disturbances.

1. Introduction

In recent years, the UAV swarm systems have emerged as a key area of research in UAV technology. Studies have shown that the collective capabilities of a swarm significantly surpass the sum of the individual capabilities of its constituent units [1–3]. In nature, many organisms rely on swarming behavior to enhance their survival and adaptive capabilities [4–6].

With the progress in swarm behavior research, scholars have come to recognize, from an evolutionary perspective, that a complete swarm behavior includes both fusion and fission dynamics [7–9]. Fusion behavior refers to the process where individuals within a specific area self-organize and aggregate without collisions, often through global or local information exchange, ultimately moving as a single, coordinated swarm [7]. In contrast, fission behavior occurs when, under various internal or external conditions, certain individuals within the swarm systematically separate from the parent swarm, forming smaller, organized subswarms that move independently [9]. Consequently, swarm motion often involves transitions between a unified swarm and multiple subswarms, integrating both fusion and fission behaviors. This fission–fusion behavior offers distinct advantages in biological swarms. For example, bat swarms employ fission–fusion dynamics to improve foraging efficiency [10], while fish and bird swarms use it to strengthen defense mechanisms and evade predators [11, 12].

Inspired by the fission–fusion behavior observed in biological swarms, researchers have progressively incorporated this concept into UAV swarm research. For example, Song et al. [13, 14] and Akcakoca et al. [15] successfully implemented swarm obstacle avoidance in static environments through fission-fusion motion, while Dai et al. [16] and Chen et al. [17] applied fission–fusion dynamics to enhance task execution efficiency within swarms. Additionally, Bernardeschi et al. [18, 19] and Wang et al. [20] further explored the use of fission–fusion motion in dynamic environment to address fission–fusion behavior under single dynamic interference. However, these studies mainly focus on fission–fusion motion in static environments or under single dynamic interferences, with relatively few addressing fission–fusion behavior in environments affected by multiple unknown dynamic disturbances. This gap primarily exists because multiple dynamic disturbances significantly increase the complexity of designing effective control strategies for UAV swarms. The unpredictability of dynamic interferences adds further challenges to path optimization. As a result, achieving effective swarm flight in environments with multiple dynamic interferences remains a critical challenge that requires urgent attention.

In real-world flight operations, UAV swarms are often subjected to various environmental factors that can disrupt performance, such as unknown dynamic disturbances, weather changes, and fluctuations in lighting conditions. These factors frequently interact with one another, collectively affecting the flight dynamics of the swarm. However, current validation methods for UAV swarms are primarily conducted in controlled, interference-free environment and mainly focus on verifying swarm control mechanisms [21, 22]. These methods often overlook how environmental conditions may impact UAV perception and other critical capabilities. As a result, most existing approaches are not directly applicable to real-world flight scenarios [22–24]. Furthermore, conducting flight experiments in real-world environments is both expensive and logistically complex. Therefore, developing a systematic validation framework for UAV swarms based on real environmental data is crucial. Such a framework would not only reduce validation costs but also enhance validation efficiency, thereby facilitating the advancement of UAV swarm technology.

Building on the previous discussion, this paper focuses on developing a fission-fusion approach for UAV swarms operating in environment characterized by multiple unknown dynamic disturbances, along with a validation system that utilizes real-world environmental data. A reinforcement learning–based UAV swarms fission–fusion approach with real-world data validation is proposed. First, a self-organized fission–fusion control framework is established. Next, a reinforcement learning–based algorithm for swarm fission–fusion confrontation is introduced to address the challenges posed by multiple dynamic disturbances, enabling adaptive swarm fission-fusion behaviors in response to various unknown disturbances. Finally, a real-world data-based–integrated validation system based on AirSim is developed to evaluate the effectiveness of the proposed algorithm.

The contributions of this study are as follows:
  • •

    Proposed a self-organized fission–fusion control framework for UAV swarms, enabling the swarm to transition self-organized from a single swarm to multiswarms.

  • •

    Developed a reinforcement learning–based fission–fusion swarms confrontation algorithm, achieving self-organized adversarial motion of subswarms against multiple unknown dynamic disturbances with minimal resource consumption, thereby protecting the parent-swarm from the impact of these disturbances.

  • •

    Proposed a real-world data-based–integrated validation system based on AirSim, allowing for low-cost UAV swarm algorithm validation based on real environmental data.

  • •

    Designed a set of systematic evaluation indicators, and the effectiveness of the proposed algorithm is demonstrated through simulation.

The remainder of this paper is organized as follows: Section 2 establishes the self-organized fission-fusion control framework. Section 3 describes the reinforcement learning–based fission–fusion swarms confrontation algorithm to address challenges in environments with multiple unknown dynamic disturbances. Section 4 introduces the real-world data-based–integrated validation system based on AirSim. Section 5 outlines the evaluation indicators developed for the proposed algorithm and assesses its effectiveness through metric analysis. Finally, Section 6 provides a summary of the overall work presented in this paper.

2. Self-Organized Fission–Fusion Control Framework

2.1. UAV Models

This paper studies a UAV swarm composed of quadrotor UAVs. It is assumed that each UAV is equipped with an autopilot system that includes three control loops for speed, yaw angle, and altitude. Therefore, the UAV model can be simplified as [25]:
()
where represents the spatial coordinates of UAV i; and denote the heading angle and its input; and represent the horizontal speed and its input; and indicate the altitude and its input; and , , , and denote the autopilot control parameters.
The constraints on the quadrotor UAV model are as follows:
()
where is the maximum values of horizontal velocity, g is the acceleration of gravity, ϕmax denotes the maximum lateral overload, and hmax represents the maximum rate of change in altitude and hmin the minimum rate.

2.2. Kinematic Models for UAV Swarms

Consider two UAV swarm systems as , which are not in a subordinate relationship. The UAV swarms are controlled by a double integrator as follows:
()
where represents the spatial coordinates of UAV i in swarm , is the velocity vector of UAV i, represents the mass of the individual UAV, indicates the control acceleration input, is the environmental influences, and is the random disturbances. To achieve fission–fusion motion in the UAV swarm, a new kinematic model for fission–fusion behavior is proposed as follows:
()
where represents the inertial term, ηine denotes the inertial parameters, is the position coordination term, represents the velocity coordination term, and is the navigation force, which corresponds to the swarm’s initial mission objective. represents the state of the UAV. Control of the swarm state is achieved through changes in .
The position coordination term is defined as follows:
()
where ℴpos denotes the swarm position synergy coefficient, is the number of UAV of swarm , represents the expected distance between individuals within the swarm, and is the position coordination decay coefficient. is the distance between the dynamic disturbance and UAV within the swarm, and εinvader is the elasticity coefficient, which increases the spacing between individuals in the swarm as they approach the dynamic disturbance, thereby reducing the likelihood of interference.
The velocity coordination term is defined as follows:
()
where ℴvel is the velocity synergy coefficient, utra represents the interference term for dynamic disturbances, and ulure denotes the entrapment term generated in response to dynamic disturbances. The velocity differentiation of the UAV swarm is achieved through the velocity coordination term, enabling fission–fusion motion.

2.3. Mapping Relationship Between Swarm UAV Model and Kinematic Model

The input for swarm control is obtained from the command outputs of the autopilot control of UAV i.
()
()
where , , and are the input control ratio of swarm.
The above results can be further converted into position and velocity vectors, which are then used as inputs to the swarm control model:
()
()

3. Reinforcement Learning–Based Fission–Fusion Swarm Confrontation Algorithm

3.1. UAV Swarm Fission–Fusion Confrontation Algorithm

To enhance the complexity of interference scenarios, we equipped the dynamic disturbances with tracking capabilities and set their initial states as unknown. To address these challenges, this section presents a UAV swarm fission-fusion confrontation algorithm that achieves self-organized fission–fusion trapping motions to counter multiple unknown dynamic disturbances with minimal resource consumption, thus safeguarding the parent swarm from their impact. The detailed process is outlined in Algorithm 1.

    Algorithm 1: UAV swarm fission–fusion confrontation algorithm.

  • input: The set of interactions of UAV i at moment t:; Individual UAVs closest to dynamic disturbances: which distance size: ; The number of individuals in the swarm: ; The number of UAVs available in the subswarm at moment t: ; The number of target UAVs in the subswarm at time t: ; The set of subswarm at time t: ; The perceptual range of an individual UAV: Rradius; The number of dynamic disturbances: Ninv; Confrontation range δinduction−area

  • output: , ulure, utra

  • function fission-fusion control

  • for ninv⟵1 : Ninv then

  •    if && then

  •       get the

  •       get

  •       get

  •       get   

  •       if then

  •          get

  •          get

  •          get

  •       end if

  •    end if

  •    if then

  •       return

  •    end if

  • end for

  • if then

  •    get

  • else

  •    get ulure⟵Algorithm 2

  • end if

  • return utra, ulure

  • end function

3.2. Reinforcement Learning–Based Confrontation Algorithm

To prevent disruptions to the parent swarm, the path of the subswarm is designed using traditional optimization methods, which rely on mathematical functions and require the collection of known data before task execution. However, real-time scheduling in confrontation scenarios encounters dynamic environmental parameters that constantly change. Traditional methods struggle to adapt quickly to these fluctuations. With the advancement of artificial intelligence, deep reinforcement learning (DRL) has been introduced to optimization problems, benefiting from its ability to continuously adapt and improve through interaction with the environment. Among various DRL algorithms, the proximal policy (P) optimization (PPO) algorithm was selected due to its high sample efficiency, stability, and ease of implementation. Unlike other models such as soft actor-critic (SAC) and Deep Q-Network (DQN), PPO is less sensitive to hyperparameter tuning, making it more reliable in dynamic and uncertain environments. Additionally, PPO is known for its capability to handle both discrete and continuous action spaces (As), which makes it particularly well-suited for the complex, multidimensional nature of UAV swarm tasks. By restricting the optimization gradient, PPO ensures stable convergence, allowing for efficient multiobjective optimization in real-world scenarios.

The subswarm trajectory is designed to avoid interrupting the parent swarm. With PPO-based intelligence, the signal-to-interference-plus-noise ratio (SINR) of the parent swarm can be enhanced while minimizing energy consumption and communication costs.

To address the specific challenge of UAV swarm confrontation, it is essential to define the decision-making actions, P functions, reward (R) functions, and state spaces (Ss) for the UAVs. These components are crucial in the reinforcement learning framework, guiding the swarm’s behavior and decision-making in dynamic environments. The four standard elements of decision-making—S, A, R, and P—serve as the foundation for modeling the swarm’s interactions with its environment and optimizing its decision-making process. The S represents the set of all possible configurations the swarm might encounter, including UAV positions and external influences like interference from other UAVs or enemy aircraft. The A defines the set of feasible actions the UAVs can take, which, in this case, corresponds to their movement and positioning in a continuous 3-dimensional space, allowing for coordinated maneuvers. The R function quantifies the swarm’s success by assigning positive Rs for achieving desirable outcomes like avoiding interference or maintaining optimal formation, while negative Rs or penalties are given for undesirable behaviors such as energy wastage or failure to avoid obstacles. The P function dictates how the swarm chooses actions based on the current state, using learned strategies to optimize performance. By clearly defining these elements and integrating them into the reinforcement learning framework, the UAV swarm can autonomously adapt to various dynamic challenges, making real-time decisions that improve its overall effectiveness in confrontation situations.

The optimization function is shown as follows:
()
where xmax refers to the cost function and ymax refers to the risk function. xsub and ysub refer to location of subswarm at current time, with coordinate increment controlled by velocity v and direction angled θ.The objective function consists both communication equality represented by SINR value and costs.
Costs involves communication costs and energy costs. Communication costs depends on communication power, while the second item depending on mass and velocity.
()
Risk value also matters in this optimization, including collision risk rc and interference risk ri. Both items are influenced by relative distance between UAVs. The closer the UAVs are, the higher risks occurs, with the calculation generalized as follows:
()
where d is the distance variable and others are undominated parameters.
The SINR also depends on distance, and the total objective function at time t is shown as follows:
()
where pt refers to transmission power, pn refers to noise power, and pi refers to interference power with minimum interference distance di.

Based on the above optimization equation, the UAV strategy can be continuously optimized during the reinforcement learning training process, enhancing the effectiveness of the confrontation.

4. Real-World Data-Based–Integrated Validation System Based on AirSim

AirSim [26] is a simulation platform developed by Microsoft Research in 2017, designed to create a virtual environment closely approximating real-world conditions. This platform enables researchers to share code and explore innovative concepts in aerial AI development and simulation. Based on AirSim, we constructed a swarm validation system utilizing real-world data and designed a real data acquisition UAV platform to collect visual data. The overall system framework is shown in Figure 1.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Framework of integrated validation system.

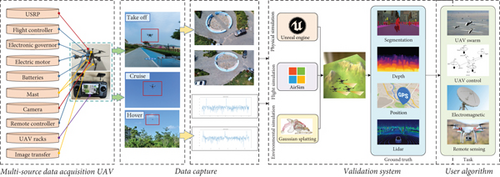
In the “multisource data acquisition UAV” section of the figure, the red lines represent the channel data acquisition unit (USRP) and the visual data collection camera. The blue lines indicate the UAV’s power system, including the motors, flight controller, frame, and propellers. The yellow lines represent the transmission links and antennas used for data transmission, while the purple lines represent the UAV control handle.

4.1. Real World Capture and Reconstruction

The reconstruction of real-world environments is a critical component of our validation system framework, essential for ensuring its applicability and reliability. To strengthen this aspect, we developed a UAV platform specifically designed for real data acquisition and created two independent yet standardized workflows dedicated to data collection and scene reconstruction. These workflows are intended to enhance both the systematic implementation and operational efficiency of the system. This section provides an in-depth discussion of these methods, outlining their architecture, functionalities, and integration into the overall validation framework. The aim is to clearly demonstrate how each workflow contributes to the ultimate goal of advancing our complete validation process.

4.1.1. 3D Reconstruction Based on 2D Image

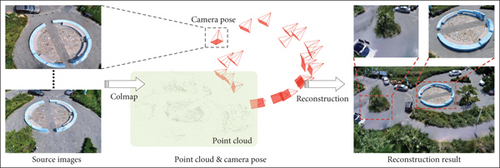
After constructing a multisource data acquisition UAV platform to capture target scenes from multiple angles and altitudes, thereby obtaining accurate two-dimensional visual data of the target scene, the next step is to perform three-dimensional reconstruction using these 2D images. Recent studies have proposed a variety of methods, among which neural radiance fields (NeRFs) [27] and Gaussian splatting [28] have received considerable attention. This section will outline the specific steps involved in three-dimensional scene reconstruction using the Gaussian splatting technique.

The Gaussian splatting method incorporates two reconstruction approaches: volume reconstruction based on 3D Gaussian point clouds and surface reconstruction based on 2D grids. Both methods require initialization using multiview images of the scene. In practical applications, quadcopter UAVs are particularly effective for capturing comprehensive and detailed images of large-scale scenes, while high-resolution smartphone cameras are more suitable for photographing smaller objects. These images are initially processed with “Colmap” software to estimate camera poses and generate a sparse point cloud, which serves as the foundation for more detailed reconstruction. The Gaussian splatting method then refines these data points, improving the accuracy of the reconstruction and ensuring consistency in data quality, ultimately producing a highly realistic simulated environment.

This technique is notably advantageous due to its rapid processing and low computational requirements, capable of rendering scenes at speeds exceeding 100 frames per second. Therefore, it is well-suited for real-time applications in dynamic virtual simulations and interactive environments. The complete reconstruction process is illustrated in Figure 2.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Reconstruction pipeline for real-time scene rendering using Gaussian splatting.

4.1.2. 3D Reconstruction Based on Remote Sensing

For large-scale scene reconstruction with a limited number of images and perspectives, the methods discussed in Section 4.1.1 are associated with a high computational workload and pose challenges for real-time execution. In contrast, this section presents an alternative approach that leverages remote sensing for preliminary reconstruction, offering a viable substitute for the techniques outlined in Section 4.1.1 in less critical areas. This alternative approach simplifies the process while ensuring the effectiveness of the results.

Advancements in satellite technology and oblique photography have enabled the 3D reconstruction of numerous urban areas, including downtown Los Angeles. As illustrated in Figure 3, key image features are matched with corresponding 3D data, offering sufficient information for applications such as flight simulation, despite certain limitations in finer details.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
3D reconstruction of urban using satellite and oblique photography.

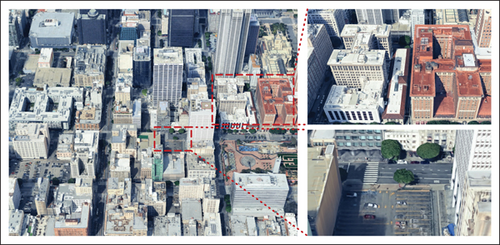
For large-scale scene reconstruction using oblique photography, UAVs simplify the process of capturing images from multiple angles, as higher altitudes reduce the number of required images. Subsequently, clear images must be carefully selected, with blurred ones discarded, followed by necessary adjustments such as distortion correction, image segmentation, and other enhancements to improve the efficiency and accuracy of subsequent processing. These refined images are then imported into Contextcapture software for 3D reconstruction.

Additionally, satellite imagery and elevation data can be directly utilized to reconstruct scenes. For this purpose, the use of Cesium software is highly recommended. Cesium offers preregistered elevation data and satellite imagery, as well as plugins that are compatible with various platforms. By inputting specific latitude and longitude coordinates, scenes can be directly integrated.

4.2. Flight Simulation Based on Physics Engine

To further enhance the realism and interactivity of the virtual environment, we utilize Unreal Engine 5.12, developed by Epic Games, to simulate lighting and physical effects. Renowned for its robust rendering capabilities and extensive development toolkit, Unreal Engine has garnered widespread acclaim from developers and artists alike. The platform offers a rich array of resources, significantly reducing the time and effort required for environment creation. Moreover, Unreal Engine provides a comprehensive visual development environment, offering users a more intuitive and efficient workflow, which further optimizes scene construction.

In flight simulation, the aerodynamic model of the aircraft plays a pivotal role in ensuring the authenticity and accuracy of the flight experience. This study utilizes AirSim to model a quadrotor UAV. AirSim is designed with a focus on high fidelity and precision, which guarantees that the simulation closely replicates real-world flight dynamics. By using this model, researchers are able to observe flight behaviors that more accurately reflect real-world conditions, thereby improving the reliability of the flight simulation system.

4.3. UAV Swarm Simulation

The simulation of UAV swarms is another essential component of this system, specifically designed to facilitate the flight validation of UAV swarms. The system allows for precise monitoring of each UAV’s position and motion state within the swarm, while also enabling the observation of relative positions and interactions between UAVs. By providing real-time data and visual feedback, the system supports effective strategic planning and coordination among the UAVs, thereby improving mission efficiency and safety. This functionality is critical for assessing the effectiveness of swarm algorithms.

4.3.1. Coordinates and Coordinate Systems

The simulation system employs a dual-coordinate framework that includes both a global coordinate system and a simulation coordinate system. The global coordinate system serves as the primary reference for environmental design and modifications, while the simulation coordinate system is used for the positioning and movement of objects within the simulation. This dual-coordinate approach ensures a clear distinction between environmental design tasks and the dynamic operations of the simulation.

The origin of the global coordinate system does not impact the progress of the simulation and can be flexibly chosen according to the modeling requirements. However, the orientation of the global coordinate system’s axes is inherited by the simulation coordinate system, making it crucial to carefully consider the axis directions to meet the specific needs of the simulation. In Unreal Engine, adjusting the orientation of the coordinate system is a routine operation, which allows for flexible configuration of the global coordinate system during the early stages of simulation environment setup. Subsequently, rotational adjustments can be made to achieve optimal axis alignment before the simulation begins. In Unreal Engine, this can be accomplished by using the PlayerStart component, which defines the origin of the simulation coordinate system. Furthermore, the orientation of the coordinate axes can be directly aligned with the global coordinate system’s direction.

The transformation between these two coordinate systems is expressed as follows:
()
where represents the coordinates of the object within the global coordinate system, denotes the origin of the simulation coordinate system within the global coordinate system, and is the coordinate of the same object within the simulation coordinate system.

4.3.2. Swarm Control Mode

In our simulation system, the configuration file specifies the relative offset for the UAV. When the UAV is commanded via an API to navigate to a particular location, its actual target position is the predefined location adjusted by the relative offset. Initially, Airsim places the UAV at the origin of the simulation’s coordinate system, thereby defining its initial position based on the relative offset. Regarding UAV flight control mechanisms, two primary methods are employed: speed-based control and waypoint-based control. Speed-based control governs the UAV’s velocity along the three coordinate axes, whereas waypoint-based control dictates the UAV’s trajectory by setting a series of target points. It is important to note that the waypoint-based control method requires adjustments to accommodate any coordinate offsets specified in the configuration file. Additionally, the API does not support control of adversarial UAVs; these UAVs operate autonomously within a defined range and are capable of automatically tracking the nearest detected target.

5. Simulation Experiments

The effectiveness of the proposed UAV swarm fission–fusion method is validated in this section through both numerical simulations and a real-world data-based–integrated validation system based on AirSim.

5.1. Evaluation Indicators

Polarization Index. The polarization index ℸ is used to measure the cohesion and stability of the swarm. This index represents the consistency of swarm velocity by comparing the differences in direction and magnitude of individual velocities within the swarm. The closer the polarization index is to 1, the greater the consistency of the swarm. However, in this study, the polarization index is significantly influenced by dynamic indices and environmental random variables. Therefore, a threshold ℸthreshold is set, and when the polarization index exceeds this threshold, the swarm is considered to have a high degree of cohesion and stability.
()
Differentiation Index. Since the polarization index only reflects the aggregation degree of the swarm and cannot adequately assess the degree of differentiation within the swarm, a differentiation index ℷ is introduced to evaluate swarm differentiation [26]. When the differentiation index reaches 1, it indicates that the UAV swarm has achieved complete speed differentiation; when it reaches 0.5, it indicates that no speed differentiation has occurred within the swarm. Similar to the polarization index, a threshold ℷthreshold is also set for the differentiation index to address dynamic interferences and random disturbances in the environment.
()
Counterpoint Accuracy. The adversarial accuracy is used to measure the extent to which the UAV swarm is affected by multiple dynamic disturbances. A higher adversarial accuracy indicates that the swarm is more severely impacted by disturbances, while a lower adversarial accuracy suggests that the swarm has not been significantly affected by dynamic interferences. The adversarial accuracy is defined as follows:
()
where ϰatt denotes the direction of the interference.

5.2. Simulation Parameters

The simulation parameters are as follows (Table 1).

Table 1. Simulation parameters and their values.
Parameter Physical implications Value
The autopilot control parameters 0.70
3.32
0.5
1.26
  
The maximum values of horizontal velocity 0.86 m/s
  
ϕmax Maximum lateral overload 1.72
  
hmax The maximum altitude rate 0.2
  
hmin The minimum altitude rate 1.0
  
g The acceleration of gravity 9.8 m/s2
  
The random disturbances 0.03
  
ηine The inertial parameters 0.8
  
The navigation force (1,1,0)
  
ℴpos The swarm position synergy coefficient 0.97
  
The expected distance 0.3
  
The position coordination decay coefficient 0.03
  
εinvader The elasticity coefficient 0.2
  
ℴvel The velocity synergy coefficient 0.97
  
The input control ratio of swarm 0.2
0.2
0.15
  
xmax The cost function 10
  
ymax The risk function 10
  
pt The transmission power 12
  
pn The noise power 15
  
pi The interference power 13
  
δinduction−area The confrontation range 10

5.3. Simulation Analysis

5.3.1. Dynamic Disturbance Environment Construction

The motion model for dynamic disturbances is defined as follows:
()
where represents the velocity vector of dynamic disturbance i; is the motion inertia coefficient of the dynamic disturbance; , , , and ϑ are random values of 0 or 1, where the random value changes to 1 during the capture confrontation process. When this happens, the dynamic disturbance completely detaches from the subswarms and starts retracking the mother swarm until a subswarm follows it and reenters the capture range δinduction−area. ϑ then returns to 0. To validate the effectiveness of the algorithm, assume that the dynamic disturbance has already sensed the swarm and begins to move toward the swarm’s location to perform interference movements. Additionally, when either the mother swarm or a subswarm enters the dynamic disturbance’s range, it is considered a failure of the swarm capture.

5.3.2. Numerical Simulation

Figure 4 presents the simulation results of the fission–fusion dynamics of a UAV swarm in an environment subject to unknown dynamic disturbances. Figure 4a illustrates the entire fission–fusion process. During the simulation, multiple unknown dynamic disturbances are randomly generated and begin to interfere with the swarm as they approach it. When a disturbance enters the swarm’s perception range, the swarm autonomously organizes into two distinct swarms: a parent-swarm consisting of 15 UAVs and a subswarm made up of 5 UAVs. As the interception process unfolds, the subswarm employs the proposed reinforcement learning–based adversarial algorithm to counter the dynamic disturbances. Upon completing the adversarial task, the subswarm autonomously returns to the parent–swarm, rejoining it to form a stable formation and continuing toward the original target direction. Figure 4b shows the random initial positions of all UAVs. Figure 4c demonstrates how the UAVs quickly organize into a stable swarm following random initialization. In Figure 4d, as multiple unknown disturbances enter the swarm’s perception range, the swarm self-organizes into two stable subswarms and initiates adversarial maneuvers using the reinforcement learning–based swarm adversarial algorithm. Figure 4e shows the subswarm beginning its return to the parent-swarm after successfully completing the adversarial task. Finally, Figure 4f illustrates the subswarm merging with the parent–swarm to reform a stable swarm and flight toward the initial target direction.

Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
(a–f) Motion process of UAV swarm fission–fusion under multiple unknown dynamic disturbances.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
(a–f) Motion process of UAV swarm fission–fusion under multiple unknown dynamic disturbances.
Details are in the caption following the image
Figure 4 (c)
Open in figure viewerPowerPoint
(a–f) Motion process of UAV swarm fission–fusion under multiple unknown dynamic disturbances.
Details are in the caption following the image
Figure 4 (d)
Open in figure viewerPowerPoint
(a–f) Motion process of UAV swarm fission–fusion under multiple unknown dynamic disturbances.
Details are in the caption following the image
Figure 4 (e)
Open in figure viewerPowerPoint
(a–f) Motion process of UAV swarm fission–fusion under multiple unknown dynamic disturbances.
Details are in the caption following the image
Figure 4 (f)
Open in figure viewerPowerPoint
(a–f) Motion process of UAV swarm fission–fusion under multiple unknown dynamic disturbances.

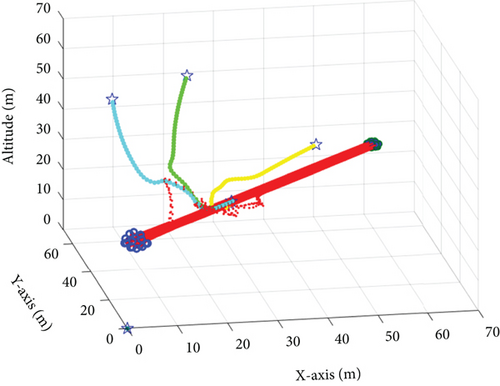
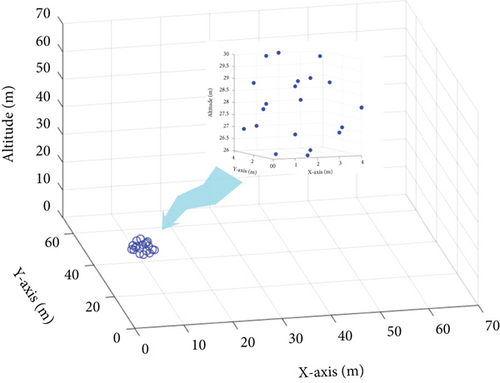
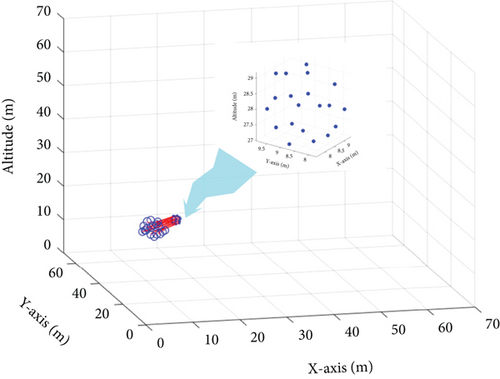
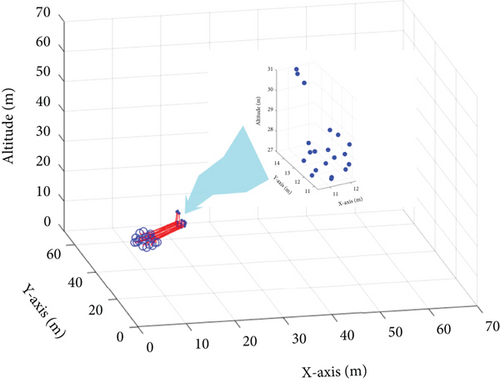
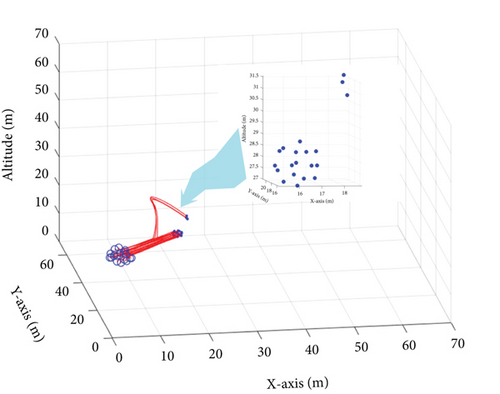
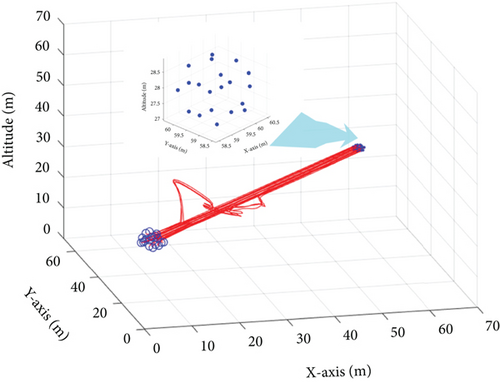
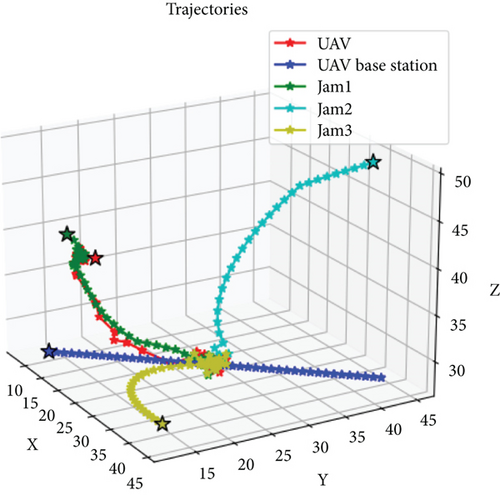
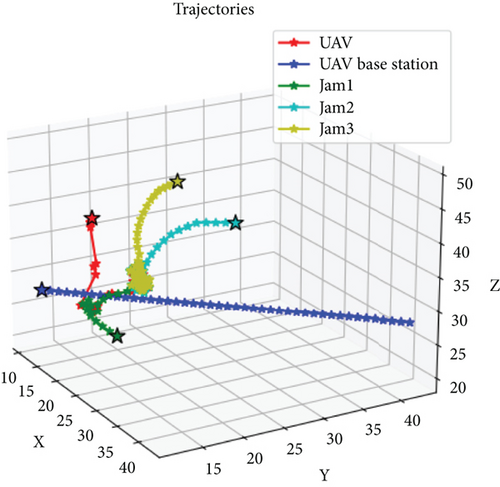
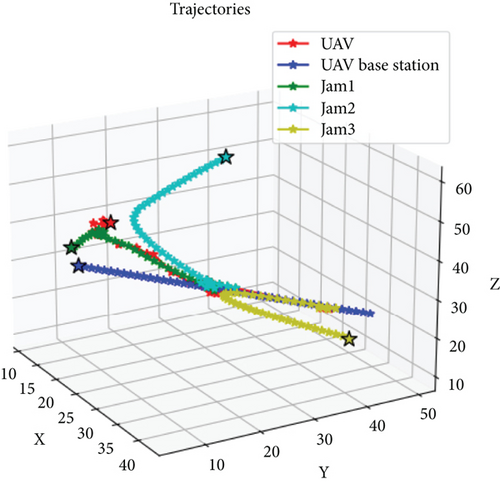
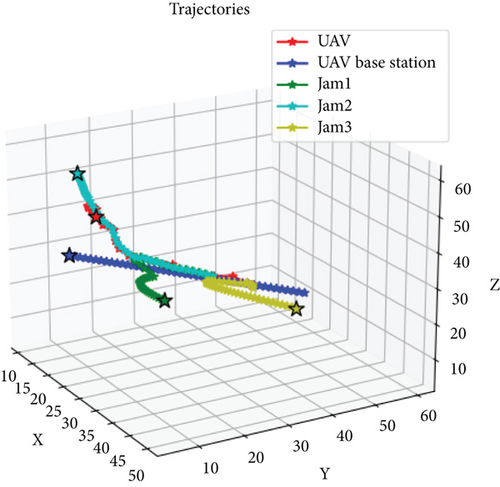
Figure 5 illustrates the trajectories of several subswarms planned using the proposed PPO algorithm. In the simulation, the time interval is set to 1 s, and three unknown dynamic disturbances are randomly generated in the three-dimensional environment. In the PPO computation process, we incorporate constraints related to the penalty value of dynamic disturbances, path Rs, and the distance between dynamic disturbances and the mother swarm. These constraints are consistent with the descriptions in Section 3.2. Additionally, according to Algorithm 2, the goal of the UAV swarm is to achieve subswarms capture while ensuring that dynamic disturbances are kept at a distance from the mother swarm, all while minimizing the capture path. The results demonstrate that the subswarms are able to execute effective countermeasures with minimal resource consumption, thereby shielding the parent swarm from the impact of the disturbances. The results demonstrate that the subswarms are able to execute effective countermeasures with minimal resource consumption, thereby shielding the parent swarm from the impact of the disturbances.

Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
(a–d) Demonstration of path planning with different initial positions.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
(a–d) Demonstration of path planning with different initial positions.
Details are in the caption following the image
Figure 5 (c)
Open in figure viewerPowerPoint
(a–d) Demonstration of path planning with different initial positions.
Details are in the caption following the image
Figure 5 (d)
Open in figure viewerPowerPoint
(a–d) Demonstration of path planning with different initial positions.
    Algorithm 2: PPO reinforcement learning algorithm.

  • Initialize policy network π(θ) and value network V(θ)

  • Initialize replay buffer

  • for each iteration do

  •    for each environment step do

  •       Collect action At ~ π(θ) for state St

  •       Execute action At and observe reward Rt and next state St+1

  •       Store (St, At, Rt, St+1) in replay buffer

  •       Compute advantages Vt using Generalized Advantage Estimation (GAE)

  •    end for

  •    for each epoch do

  •       Shuffle replay buffer

  •       for each minibatch do

  •          Compute the ratio: ra = π (At/St)/πold (At/St) (15)

  •          Compute surrogate loss: L(θ) = Et[min (ra  ∗  Vt, clip(ra, 1-ε, 1 + ε) ∗  VT)] (16)

  •          Compute value loss: (17)

  •          Update policy network by maximizing L(θ)

  •          Update value network by minimizing LV(θ)

  •          Update old policy πold = π(θ)

  •       end for

  • end for

  • end for

  • end function

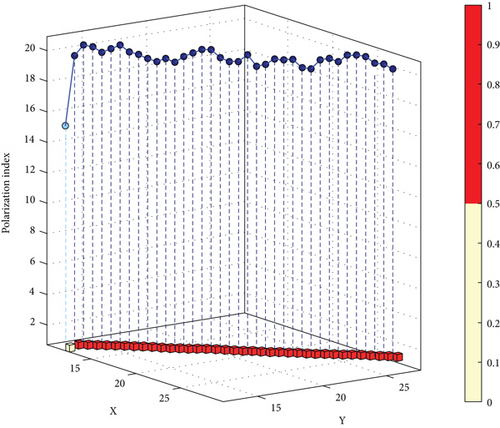
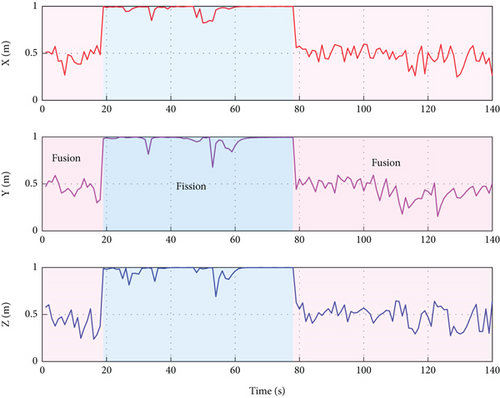
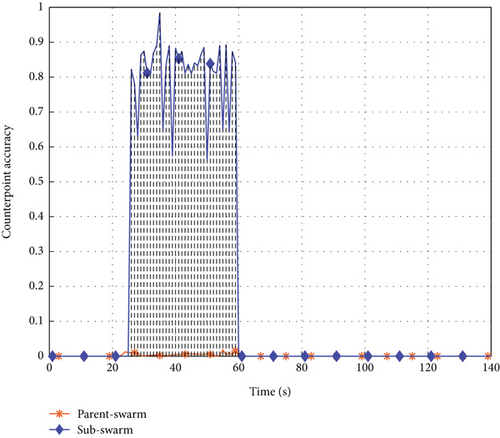
Figure 6 illustrates the changes in polarization index, differentiation index, and counterpoint accuracy during swarm motion. In Figure 6a, the polarization index indicates that the parent–swarm quickly achieved cohesive motion from its initial state, forming a stable configuration. After dispersive motion, the polarization index of the parent-swarm stabilizes around 1, suggesting that multiple dynamic disturbances had no direct impact on the parent swarm’s state. Figure 6b shows the variations in the differentiation index, demonstrating that the parent-swarm remains stable from 0 to 34 s, after which it rapidly fission into two swarms. These two swarms maintain stable configurations until 60 s, after which the subswarm rapidly fuses with the parent–swarm, reforming a unified and stable formation. This outcome confirms the effectiveness of the UAV swarm’s fission–fusion behavior. Figure 6c presents the results for counterpoint accuracy. Throughout the process, the parent swarm remains unaffected by dynamic disturbances, while the subswarm is significantly influenced by multiple dynamic disturbances, highlighting the effectiveness of the subswarm’s counterpoint maneuvering.

Details are in the caption following the image
Figure 6 (a)
Open in figure viewerPowerPoint
The results of evaluation indicators. (a) Polarization index. (b) Differentiation index. (c) Counterpoint accuracy.
Details are in the caption following the image
Figure 6 (b)
Open in figure viewerPowerPoint
The results of evaluation indicators. (a) Polarization index. (b) Differentiation index. (c) Counterpoint accuracy.
Details are in the caption following the image
Figure 6 (c)
Open in figure viewerPowerPoint
The results of evaluation indicators. (a) Polarization index. (b) Differentiation index. (c) Counterpoint accuracy.

5.3.3. Real-World Data-Based–Integrated Validation System Based on AirSim Simulation

In this section, we use the IPCVSA to evaluate the UAV Swarm Self-Organized Fission–Fusion Control Framework.
  • a.

    Experimental settings

All real-world data-based–integrated validation system based on AirSim experiments was run on a high-performance computing system with an NVIDIA GeForce RTX 4090 GPU, an Intel Xeon Silver 4310 CPU, and Windows 10 (64-bit). The simulations consistently maintained at least 144 FPS for smooth performance. Unreal Engine 5.2.1 and Colosseum (AirSim’s successor for Unreal 5) were used for physics simulation.
  • b.

    Validation system

Real-world data-based–integrated validation system based on AirSim is a visualization and verification platform shown in Figure 7. The left side displays the visual flight interface with engine-rendered effects, including UAV, ground station, and enemy views. The right side presents key locations on a satellite map, real-time swarm attitude, and live images from the swarm, indicating flight status.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Real-world data-based–integrated validation system based on AirSim.
Swarm performance is evaluated across five dimensions related to the cluster’s state, with results displayed in the central verification section. The middle section focuses on electromagnetic signal verification, illustrating local radio interference levels affecting UAV clusters across locations.
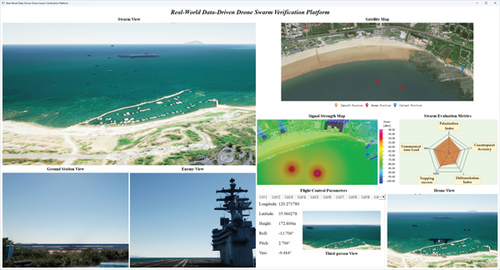
  • c.

    Swarm simulation

In this simulation, a script was developed for sea reconnaissance using UAV swarm formations. The enemy is assumed to deploy two fixed-wing UAVs for aerial reconnaissance, programmed to track the nearest target upon detection. To complete the mission, our UAV swarm splits into two subswarms to divert enemy UAVs from the main swarm, allowing it sufficient time and space for reconnaissance. Once the main swarm completes its task, it signals the subswarms to prepare for regrouping, at which point the subswarms disengage from enemy tracking. Figure 8 presents the detailed simulation steps.

Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Simulation steps.

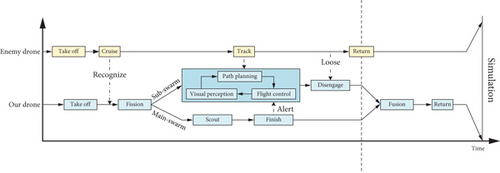
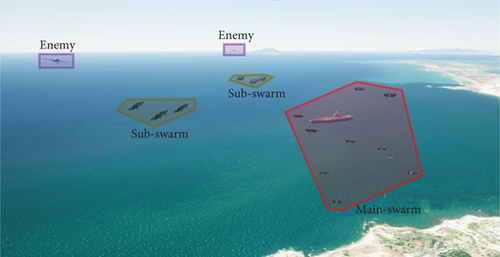
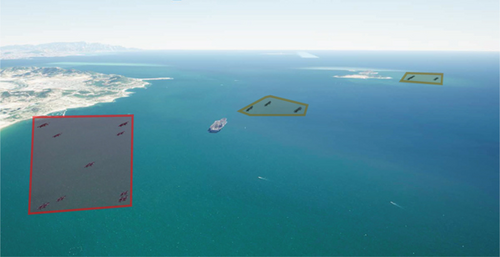
Figure 9 illustrates the complete simulation process. Initially, all UAVs take off from designated positions and fly toward the target sea area in a unified swarm. Upon detecting two enemy UAVs, the swarm splits into two subswarms to lure the enemy away from the main group. After the main swarm completes its reconnaissance mission, the subswarms exit the sensitive sea area to avoid tracking and eventually rejoin the main swarm.

Details are in the caption following the image
Figure 9 (a)
Open in figure viewerPowerPoint
Visual depiction of critical simulation stages: (a) takeoff, (b) swarm flight, (c) fission, (d) decoying enemy aircraft, and (e, f) Fusion.
Details are in the caption following the image
Figure 9 (b)
Open in figure viewerPowerPoint
Visual depiction of critical simulation stages: (a) takeoff, (b) swarm flight, (c) fission, (d) decoying enemy aircraft, and (e, f) Fusion.
Details are in the caption following the image
Figure 9 (c)
Open in figure viewerPowerPoint
Visual depiction of critical simulation stages: (a) takeoff, (b) swarm flight, (c) fission, (d) decoying enemy aircraft, and (e, f) Fusion.
Details are in the caption following the image
Figure 9 (d)
Open in figure viewerPowerPoint
Visual depiction of critical simulation stages: (a) takeoff, (b) swarm flight, (c) fission, (d) decoying enemy aircraft, and (e, f) Fusion.
Details are in the caption following the image
Figure 9 (e)
Open in figure viewerPowerPoint
Visual depiction of critical simulation stages: (a) takeoff, (b) swarm flight, (c) fission, (d) decoying enemy aircraft, and (e, f) Fusion.
Details are in the caption following the image
Figure 9 (f)
Open in figure viewerPowerPoint
Visual depiction of critical simulation stages: (a) takeoff, (b) swarm flight, (c) fission, (d) decoying enemy aircraft, and (e, f) Fusion.

6. Conclusions

In recent years, there has been significant attention on research related to UAV swarm motion methodologies and validation systems, particularly focusing on self-organized fission–fusion swarm behaviors and systematic validation methods. This paper presents a reinforcement learning–based approach for UAV swarm fission–fusion with real-world data integrated validation. First, we introduce the Self-Organized Fission–Fusion Control Framework, which enables multi-UAV self-organized fission-fusion control. Next, to address multiple unknown dynamic disturbances, we develop a reinforcement learning–based confrontation algorithm designed to counter these disturbances with minimal resource expenditure. We then present a real-world data-based integrated validation system, utilizing the AirSim platform, to allow UAV systems to undergo swarm flight validation in realistically reconstructed environments. Finally, we conduct simulations using both a digital simulation and the real-world data-based integrated validation system to evaluate the proposed algorithms, demonstrating the effectiveness and applicability of both the algorithms and the simulation platform.

It is worth noting that although the proposed algorithms have been validated within the system presented in this paper, further in-depth research on similar algorithms would require researchers to specifically construct swarm flight environments to ensure the validity and reliability of comparative experiments. However, this approach would still be more convenient and efficient than conducting actual swarm flight experiments. At the same time, this control framework enables multidivision and fusion control of UAV swarms, and future work can focus on further optimizing the number of subswarms and the number of individuals within each subswarm.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Xiaorong Zhang and Dacheng Qi contributed equally to this work and co-first authors.

Funding

This research was funded by the National Natural Science Foundation of China (Grant No. U20B2042).

Acknowledgments

The authors have nothing to report.

    Data Availability Statement

    Data is available on request from the authors.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.