To provide autonomous and accurate time service for deep space missions, a pulsar observation–based timekeeping method is documented in this paper, which utilizes pulsars as the time information source. Firstly, the pulsar observation noise is remodeled as the combination of the Gaussian noise and colored noise, and the detailed expression of the colored noise is presented in the paper. An improved Grey model (GM) is proposed to describe the onboard clock evolution, which models the grey action quantity as a time-varying coefficient and attenuates the dependence of the model on the initial state. On the basis of the modified observation noise model and GM, an unscented Kalman filtering (UKF) is adopted to estimate the onboard clock error. Numerical experiments are conducted to analyze the validity of the proposed method and the impact of spacecraft positioning error and pulsar selection on the proposed method. The proposed method offers an autonomous solution for onboard timekeeping in deep space missions.

1. Introduction

For space navigation and communication, time information is one of the key parameters [1]. For near-Earth timekeeping, it mainly relies on the Earth-based time standard and Global Positioning System (GPS) [2]. GPS is not only a reliable time source but also a time transfer system, making it suitable for time synchronization and frequency distribution. Earth-based time reference also plays an important role in deep space application. The Novel Time Synchronization Techniques for Deep Space Probes (Syndee) project developed by the European Space Agency (ESA) proposed two novel clock synchronization methods for deep space probe. Both methods depend on the accurate Earth time reference [3]. For Deep Space Network (DSN) frequency and time standards, Jet Propulsion Laboratory (JPL) developed the DSN Frequency and Timing Subsystem (FTS) for NASA’s deep space activities. Its “central clock” is realized and maintained on ground [4]. However, reliance on Earth-based system can present challenges, including latency, constraints on availability, substantial construction, and maintenance cost. Thus, autonomous time reference becomes a preferable choice for deep space applications.

For autonomous time reference, highly precise and stable onboard clock is a viable option. Mercury ion clock is based on the 40.5-GHz ground-state hyperfine transition of trapped ¹⁹⁹Hg+, providing continuous and high-stability time information [5, 6]. Using spin-polarized, ultracold atomic ytterbium, optical lattice clocks are a new type of atomic clocks benefitting from the emergence of ultrastable laser technique [7, 8]. These novel clocks show excellent stability and accuracy but have significant deficiencies. The construction of these clocks necessitates complicated instruments, strict circumstance, and high construction cost. An alternative autonomous time reference is pulsar timing. Pulsars are highly magnetized neutron stars rotating around their rotation axis with signals emitting from their poles. Continuous observation indicates that the pulsar rotation frequency shows high stability over long time interval. Consequently, pulsars are regarded as high-stability celestial clocks in deep space [9]. Compared with terrestrial clocks, pulsar timing standard indicates high autonomy, wide cover range (the solar system and even beyond), and good continuity. Researchers have studied the implementation of pulsar timing [10–12], the origins of pulsar timing error [13, 14], and the correction and compensation of pulsar time residual [15, 16]. Furthermore, several projects are carried out to verify the feasibility of pulsar timing, including the “International Pulsar Timing Array” project by Australia and Europe [17] and the X-ray Timing system and Station Explorer for X-ray Timing and Navigation Technology (SEXTANT) project by America [18, 19]. Recently, studies are conducted on pulsar-based timekeeping. A server satellite parked in a stable distant retrograde orbit (DRO) utilized X-ray Pulsar-based Navigation (XPNAV) to determine its orbital position and velocity and maintain its onboard timing autonomously [20]. The possibility of establishing time scales with high-stability performance by combining pulsars and atomic clocks was discussed in [21, 22]. The authors in [23] discussed the impact of different data spans on the accuracy of pulsar timing model parameters. The authors in [24] intended to utilize millisecond pulsar timing to enhance and maintain a space-time benchmark for future deep space application. Those research lays a solid foundation for pulsar timekeeping theory and technical application. However, there is a paucity of detailed research on the pulsar timekeeping at spacecraft for deep space missions. Timekeeping onboard a spacecraft is of great engineering value. The establishment of a local time reference at the spacecraft would increase the autonomy of the spacecraft and reduces the dependence on the Earth support. Consequently, the autonomy and exploration range of deep space missions would be enhanced.

To establish an autonomous time standard for deep space missions, a pulsar observation–based timekeeping method is documented in this paper. With pulsar timing observation, the onboard clock error can be corrected by pulsar time residual observation. However, due to various factors including the free precession motion and glitches of pulsars, the interstellar dispersion, and the spin noise intrinsic to pulsar [25, 26], pulsar time residual is influenced by timing noise, which cannot be simply modeled as Gaussian noise. This paper proposes a model that combines both Gaussian noise and colored noise to present the pulsar time observation noise. An improved Grey model (GM) is adopted for indicating the clock evolution process. With the pulsar timing observation model and the clock evolution model, unscented Kalman filtering (UKF) method is utilized to estimate the onboard clock error.

2. Basic Model

2.1. Pulsar Timing Observation Model

At the solar system barycenter (SSB), a pulsar phase evolution model is established based on long-duration pulsar observation, which is used to predict the time of arrival (TOA) of pulsar pulses at the SSB. A polynomial function is used to express the pulsar phase evolution [27]:

()

where t₀ is the reference epoch, φ(t₀) is the initial phase at t₀, f is the pulsar spin frequency, and f^(k) is the derivative of the kth order of the pulsar spin frequency. Generally, a second-order expression of Equation (1) is sufficient to describe the pulsar phase evolution:

()

where ε(t) represents the high-order terms that are ignored. With Equation (2), the pulse arrival time can be predicted.

Let t_obs be the pulse arrival time observed at the spacecraft and t_SSB be the TOA at SSB for the same pulse. μ_s denotes the gravitational constant of the Sun. D₀ is the distance between the barycenter of the Sun and the pulsar, and b is the vector pointing from the Sun center to SSB. The time transfer from the spacecraft to SSB can be presented as

()

where n_i is the pulse emission direction vector of the ith pulsar, r_SSB is the vector pointing from SSB to the spacecraft location, c is the speed of light, δt is the onboard clock error, and v is the observation noise. The third term at the right of Equation (3) is the geometric delay. The fourth term reflects the parallax effects. The fifth term is caused by the Sun’s gravity field, that is, the Shapiro delay effect. Let

denote the TOA predicted by the phase evolution model and e the pulsar time residual. Then, the pulsar timing residual can be expressed as

()

Based on the above analysis, the pulsar timing observation equation can be written as

()

where v is the observation noise. Let

denote the observation variable and assume that m pulsars are observed. Then, the observation equation can be described as

()

where H is the observation matrix,

, and V is the observation noise matrix defined as

. v_i is the observation noise.

2.2. Pulsar Timing Observation Noise Model

Given the existence of the rotational irregularities, interstellar dispersion, and other unpredicted factors, the pulsar observation is influenced by a mixed noise, which cannot be simply described by a Gaussian noise model. In this paper, the pulsar observation noise is modeled as the combination of the observation error noise n_O and the timing noise n_t

()

where n_O is a Gaussian white noise and n_t is a colored noise.

denotes the standard variance of n_O of the ith pulsar.

can be calculated based on the pulsar parameters [28]:

()

where F_i,x is the flux intensity, B_X is the background radiation flux, p_i,f is the pulsed fraction. The pulsed fraction defines the percentage of the source flux that is pulsed, t_obs is the observation interval, A is the detector area, and d_i is the duty cycle defined as d_i = W_i/P_i. W_i is the width of the pulse, and P_i is the pulse period.

To express the colored timing noise n_t, m-order autoregressive model (AR model) is introduced, which is expressed by [29]

()

where ψ_k−j is the autoregressive parameter that indicates the influence of the past values on current value, s_k−m is the observation value at k − m, and ρ_k is the error term at k. ψ_k−j reflects the “degree of correlation” of the noise. In the paper, the first-order AR model is utilized to express the correlated timing noise:

()

where ρ_k is a Gaussian white noise with zero mean value and a variance of

. With the relation expressed by Equation (11), the timing noise at k + 1 is correlated with the noise at k and has no correlation with previous values.

Assume m pulsars are observed, and

denotes the correlated timing noise.

is the noise for the ith pulsar. Equation (11) can be rewritten as

()

where

and

Various methods are available for expressing the level of n_t. Of all the methods, a method related to the frequency drift and the derivative of the frequency drift shows fine performance in estimating the timing noise, which can be described as

()

where C, α₁, β₁, and γ₁ are the fitting parameters of the model estimated with a large number of pulsars over a long time duration [30]; T is the time span; v_f is the frequency; and

is the first derivative of v. While C, α₁, β₁, and γ₁ are fitted using a large volume of pulsar observation data,

is a universal and averaged model reflecting the averaged level of the timing noise for a large amount of pulsars. In this paper, the level of n_t is expressed by

As the pulsar observation noise is modeled as a combination of Gaussian noise and colored noise, the observation equation is redefined as

()

where ρ_k is a Gaussian white noise ingredient of pulsar timing noise. N_O,k+1 and N_O,k are Gaussian noises of pulsar observation error noise. Let G = ρ_k + N_O,k+1 − Ψ_kN_O,k. G is a Gaussian noise with zero mean value.

2.3. Onboard Clock Evolution Model Based on Improved GM

For the evolution of atomic clocks, multiple models have been proposed in available literatures, including the polynomial model, the GM, the periodic model, and the autoregressive integrated moving average (ARIMA) model. Among these models, the GM has the advantage of being able to use small amounts of data to express the evolution process. Theoretically, a minimum of four sets of data are required for establishing a GM. With small amounts of data required, a GM can be dynamically adjusted with new data observed, which consequently increases the short-term and long-term prediction accuracy.

The definition of traditional GM for clock evolution can be described as follows:

()

where ξ_k+1 is the estimated clock error at k + 1, ξ₁ is the initial clock error, u is the grey action quantity, and a is the developing coefficient. u and a are generally regarded as constants.

As demonstrated in Equation (15), GM depends greatly on the initial clock error ξ₁. As time elapses, the model error increases owing to the aforementioned dependence. In addition, as the real model undergoes minor alterations over time, the grey action quantity u is not necessarily a constant [31]. Thus, to reduce the dependence on the initial state and to consider the time-varying property of the model, the clock evolution model is modified.

()

where ξ_k is the estimated clock error at k, the grey action quantity is modeled as a time-varying coefficient, and b₂ is a constant parameter. With the modification, the model is independent of the initial error and dynamically adjusts over time. Let ξ = [ξ, u]^T be the state variable. The clock evolution model can be expressed as

()

where Φ_k is the state transition matrix. Based on Equation (18), the state transition equation can be written as

()

where

is the process noise. w_ξ and w_u are Gaussian, and the covariance matrix of W_p is

3. Pulsar Observation–Based Timekeeping Using UKF

As discussed in the preceding section, the clock evolution model is a nonlinear model. To facilitate the pulsar observation–based timekeeping, an UKF is adopted.

Unscented transform (UT) is the basis of UKF. The principle of UT can be described as follows.

Firstly, 2n + 1 sigma points are established.

()

where ξ is a random variable vector,

is the mean value of ξ, P_ξ is the covariance matrix of ξ, ( )_i indicates the ith row of the result, and κ is the scale parameter that influences the approximation accuracy. In Equation (20), the Cholesky decomposition of P_ξ is required. Factors like observation error and state model turbulence make P_ξ lose its positive definite. To solve this problem, a singular value decomposition (SVD) method is introduced [32]. According to the SVD theory, the SVD of P_ξ can be expressed by

()

Then, Equation (20) is modified.

()

With SVD, the loss of the positive definite of P_ξ is solved and the stability of the filtering algorithm is guaranteed.

Then, the sigma points are transformed through the nonlinear model, that is,

()

Φ_i is the state transition matrix. The weighted mean value

and variance of Y are calculated using the following equation:

()

where

and

are the weighted parameters.

and

are calculated using Equation (25):

()

where α is generally a positive constant less than 1, λ is a scale parameter that is set to 0 or 3 − n, and β is the state distribution parameter, which is often set to be 0. α and λ affect the estimation accuracy of the mean value, and β influences the estimation accuracy of the covariance.

Based on the principle of UT, pulsar observation-based UKF can be conducted:

1.
Calculating the sigma points

()

where

is the optimal estimation at k − 1.

2.
Obtaining the state transition of the sigma points

()

The weighted mean value

and covariance

are calculated by

()

where Q_w is the covariance matrix of the process noise of the clock evolution. The observation result can be expressed by

()

3.
Updating the covariance matrix and the gain

The estimation performance of

is expressed by the covariance matrix, P_z,k:

()

In addition, the cross-covariance matrix P_xz,k is also defined and calculated:

()

The gain can be calculated based on P_z,k and P_xz,k:

()

4.
Estimating the states

Then, the state estimation can be described by

()

Update the covariance matrix of

()

4. Simulation and Analysis

4.1. Simulation Conditions

For the simulation experiments, pulsar parameters used are listed in Table 1. The pulsar parameters are obtained from the Australia Telescope National Facility (ATNF) Pulsar Catalogue and Reference [27]. The area of the x-ray pulsar detector is set to be 10,000 cm². The average background noise flux intensity is set to 5e−3 ph/(cm²·s) [27].

Table 1. Pulsar parameters.

Pulsars	Period (s)	Frequency (s⁻¹)	Frequency drift (s⁻²)	Flux intensity (ph/cm²·s)	Pulse width (s)	Pulsed fraction (%)
B1937+21	1.558e−3	641.928	−4.291e−16	4.99e−5	3.82e−5	86
B1821-24	3.050e−3	327.406	−1.735e−13	1.93e−4	5.50e−5	98
B0531+21	3.339e−2	29.947	−3.775e−10	1.54	3.0e−3	70

To measure the level of the timing noise, a model is presented in Section 2.2. According to reference [30], the timing noise model parameters are set as follows: C₂ = exp(1.5), α₁ = −1.4, β₁ = 0.9, γ₁ = 2.0, and T = 5. It should be noted that the timing noise model is an averaged model suitable for a large number of pulsars. Equation (13) is employed to express the timing noise intensity.

4.2. Clock Evolution Simulation

The performance of the proposed timekeeping method is analyzed in this section. For comparison, a comparative experiment with the second-order polynomial model is also carried out. All the experiment conditions are the same except the clock evolution model. For the purpose of simulation, the initial clock error is set to be 4e−5 s. The filtering interval is set to 100 s. The pulsars used in the simulation are B1937+21 and B1821-24. Besides, the position errors of the spacecraft are obtained from the augmentation method described in the preceding paper accomplished by the authors [33].

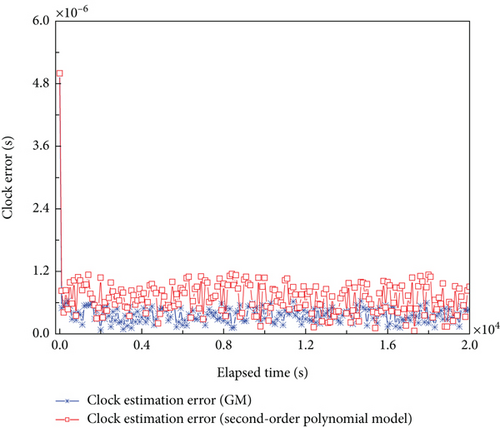
The performance of the proposed method and that of the second-order polynomial model in estimating clock error is presented in Figure 1. From the figure, it is known that with the proposed model and UKF filtering algorithm, the clock error remains at a relatively low level instead of increasing with time. Through UKF filtering, the observed pulsar time information is utilized to correct the clock evolution process. With new information from pulsar observation used, the clock error is dynamically corrected at the spacecraft. Compared with the estimation results of the second-order polynomial model, the proposed method shows better performance in clock error estimation.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Filtering result of the pulsar observation–based timekeeping method (GM and second-order polynomial model).

4.3. Influence of the Positioning Errors

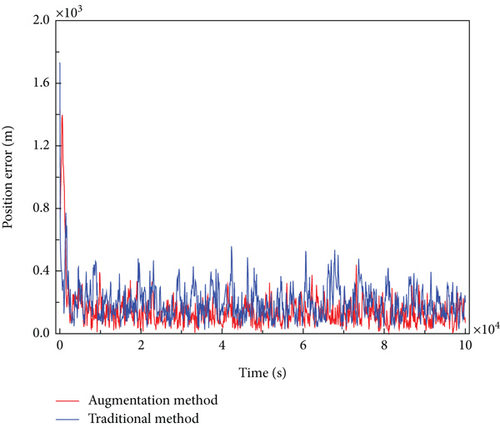
In this section, the influence of the positioning errors of the spacecraft on the pulsar-based timekeeping method is simulated and analyzed. The pulsars utilized are the same as those of Section 4.2, and the positioning errors utilized are the results obtained from the previous paper accomplished by the authors [33]. For comparison, the positioning errors from both the augmentation method and the traditional filtering method are employed in the simulation, which is indicated in Figure 2. In Figure 2, the positioning error level is evaluated by , where r is the real positioning vector and is the estimated positioning vector. The mean positioning estimation error of the augmentation method is approximately 124 m, while the traditional method is around 200 m.

As demonstrated in Figure 3, the clock estimation error of the proposed method is shown to be contingent on the magnitude of the positioning error.

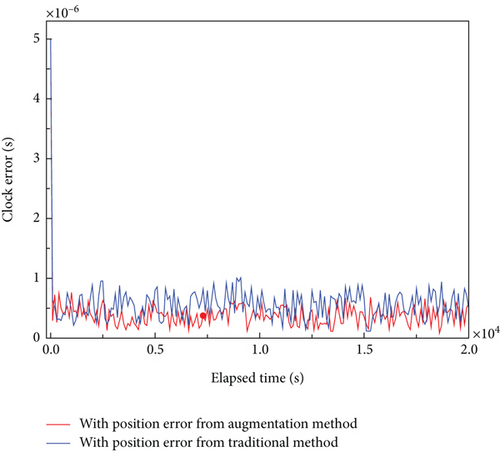
Figure 3 shows the clock estimation error of the proposed method under different positioning errors. The figure demonstrates that with a more accurate positioning estimation, the clock estimation shows better performance. With a more accurate position estimation result, the time transfer from the spacecraft to SSB would be more accurate. Consequently, an improvement in the accuracy of time transfer would result in an enhancement in the estimation of the clock.

4.4. Influence of the Pulsar Selection

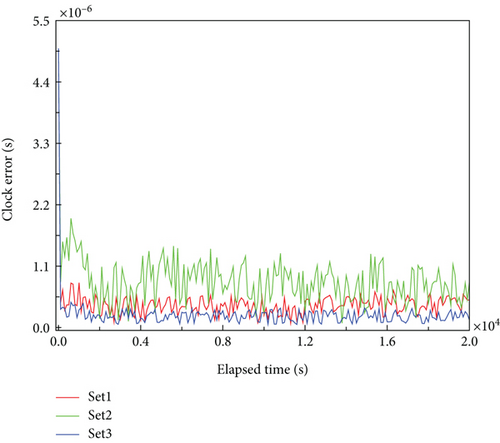
As different pulsars exhibit varying signal intensity and parameters, the selection of pulsars also influences the performance of the pulsar-based timekeeping method. For comparison, three sets of pulsar selection are chosen. In Set 1, B1937+21 and B1821-24 are observed. In Set 2, B1937+21 and B0531+21 are used. Set 3 utilizes B1821-24 and B0531+21. The parameters of the pulsars are listed in Table 1, and the other parameters employed in the simulation are identical to those outlined in Section 4.2.

As illustrated in Figure 4, the estimation performance is contingent on the selection of pulsars. Set 1 and Set 3 show similar performance. Conversely, Set 2 demonstrates the poorest estimation results compared with Set 1 and Set 3. These results underscore the significance of selecting the appropriate pulsars for clock error estimation, emphasizing the necessity for the establishment of a comprehensive and well-managed pulsar database for pulsar-based timing applications.

5. Conclusions

A pulsar observation–based method for onboard timekeeping in deep space is documented in this paper. The method realizes onboard clock error correction using pulsar observation information. The proposed method utilizes pulsar observation for the establishment of an onboard timekeeping method. Initially, the pulsar observation noise is remodeled as the combination of Gaussian noise and colored noise. The detailed model and noise level of the colored noise are presented in the paper. Furthermore, a modified GM is established to describe the onboard clock evolution, which models the grey action quantity as a time-varying coefficient and reduces the dependence of the model on the initial state. Utilizing the aforementioned modified pulsar observation noise and the GM clock evolution model, UKF is employed to estimate the onboard clock error. Numerical simulation indicates the validity of the proposed method. The simulation results also demonstrate the impact of the positioning errors of the spacecraft and the pulsar selection on the clock error estimation performance. The pulsar-based timekeeping method is distinguished by its autonomy, universality, and continuity, thus providing a novel timekeeping option for deep space missions.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the National Natural Science Foundation of China (62103245 and 62273213), the Natural Science Foundation of Shandong Province (ZR2020MF095), and Taishan Scholarship Construction Engineering.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 National Research Council of the National Academies, NASA Space Technology Roadmaps and Priorities: Restoring NASA’s Technological Edge and Paving the Way for a New Era in Space, 2012, NASA Technical Reports, National Academies Press, https://doi.org/10.17226/13354.
Google Scholar
2 Lewandowski W., Azoubib J., and Klepczynski W. J., GPS: primary tool for time transfer, Proceedings of the IEEE. (1999) 87, no. 1, 163–172, https://doi.org/10.1109/5.736348, 2-s2.0-0032715746.
10.1109/5.736348
Web of Science® Google Scholar
3 Re E., Di Cintio A., Busca G., Giunta D., and Sanchez M., Novel time synchronization techniques for deep space probes, 2009 IEEE International Frequency Control Symposium Joint with the 22nd European Frequency and Time forum, 2009, Besancon, France, 205–210, https://doi.org/10.1109/FREQ.2009.5168170, 2-s2.0-70449487109.
10.1109/FREQ.2009.5168170
Google Scholar
4 Tjoelker R. L., Time and Frequency Activities at the NASA Jet Propulsion Laboratory, 2007, Jet Propulsion Laboratory, Pasadena, CA, USA, https://www.ion.org/publications/abstract.cfm?articleID=10578.
Google Scholar
5 Tjoelker R. L., Prestage J. D., Burt E. A., Chen P., Chong Y. J., Chung S. K., Diener W., Ely T., Enzer D. G., Mojaradi H., Okino C., Pauken M., Robison D., Swenson B. L., Tucker B., and Wang R., Mercury ion clock for a NASA technology demonstration mission, EEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. (2016) 63, no. 7, 1034–1043, https://doi.org/10.1109/TUFFC.2016.2543738, 2-s2.0-84978699337, 27019481.
10.1109/TUFFC.2016.2543738
PubMed Web of Science® Google Scholar
6 Yi L., Burt E. A., and Tjoelker R. L., Mercury lamp studies in support of trapped ion frequency standards, 2015 Joint Conference of the IEEE International Frequency Control Symposium & the European Frequency and Time Forum, April 2015, Denver, CO, USA, https://doi.org/10.1109/FCS.2015.7138820, 2-s2.0-84943232179.
10.1109/FCS.2015.7138820
Google Scholar
7 Hinkley N., Sherman J. A., Phillips N. B., Schioppo M., Lemke N. D., Beloy K., Pizzocaro M., Oates C. W., and Ludlow A. D., An atomic clock with 10^–18 instability, Science. (2013) 341, no. 6151, 1215–1218, https://doi.org/10.1126/science.1240420, 2-s2.0-84883791947.
10.1126/science.1240420
CAS PubMed Web of Science® Google Scholar
8 Lu X., Yin M., Li T., Wang Y., and Chang H., Demonstration of the frequency-drift-induced self-comparison measurement error in optical lattice clocks, Japanese Journal of Applied Physics. (2020) 59, no. 7, 070903, https://doi.org/10.35848/1347-4065/ab98d8.
10.35848/1347-4065/ab98d8
CAS Web of Science® Google Scholar
9 Manchester R. N., Pulsar timing and its applications, Journal of Physics: Conference Series. (2017) 932, 012002, https://doi.org/10.1088/1742-6596/932/1/012002, 2-s2.0-85039425135.
10.1088/1742-6596/932/1/012002
Google Scholar
10 Chen P. T., Speyer J. L., and Majid W. A., Frequency stability analysis of pulsar-aided clocks, Navigation. (2019) 66, no. 3, 621–632, https://doi.org/10.1002/navi.325, 2-s2.0-85070752367.
10.1002/navi.325
Web of Science® Google Scholar
11 Sun H. F., Sun X., Fang H. Y., Shen L. R., Cong S. P., Liu Y. M., Li X. P., and Bao W. M., Building X-ray pulsar timing model without the use of radio parameters, Acta Astronautica. (2018) 143, 155–162, https://doi.org/10.1016/j.actaastro.2017.11.014, 2-s2.0-85037157257.
10.1016/j.actaastro.2017.11.014
Web of Science® Google Scholar
12 Huang L., Shuai P., Zhang X., and Chen S., A new explorer mission for soft X-ray timing - observation of the Crab pulsar, Acta Astronautica. (2018) 151, 63–67, https://doi.org/10.1016/j.actaastro.2018.05.060, 2-s2.0-85048192576.
10.1016/j.actaastro.2018.05.060
Web of Science® Google Scholar
13 Hobbs G., Coles W., Manchester R. N., Keith M. J., Shannon R. M., Chen D., Bailes M., Bhat N. D. R., Burke-Spolaor S., Champion D., Chaudhary A., Hotan A., Khoo J., Kocz J., Levin Y., Oslowski S., Preisig B., Ravi V., Reynolds J. E., Sarkissian J., van Straten W., Verbiest J. P. W., Yardley D., and You X. P., Development of a pulsar-based time-scale, Monthly Notices of the Royal Astronomical Society. (2012) 427, no. 4, 2780–2787, https://doi.org/10.1111/j.1365-2966.2012.21946.x, 2-s2.0-84885244830.
10.1111/j.1365-2966.2012.21946.x
Web of Science® Google Scholar
14 Melatos A. and Link B., Pulsar timing noise from superfluid turbulence, Monthly Notices of the Royal Astronomical Society. (2014) 437, no. 1, 21–31, https://doi.org/10.1093/mnras/stt1828, 2-s2.0-84890021910.
10.1093/mnras/stt1828
Web of Science® Google Scholar
15 Rodin A. E. and Chen D., Optimal filtration and a pulsar time scale, Astronomy Reports. (2011) 55, no. 7, 622–628, https://doi.org/10.1134/S1063772911070055, 2-s2.0-79959915638.
10.1134/S1063772911070055
Web of Science® Google Scholar
16 Wang Y., Zheng W., Sun S., and An X., Algorithm for the pulsar timing system with the system bias, Journal of National University of Defense Technology. (2013) 35, no. 2, 12–16, http://journal.nudt.edu.cn/gfkjdxxben/article/abstract/201302003?st=article_issue.
Google Scholar
17 Hobbs G., Guo L., Caballero R. N., Coles W., Lee K. J., Manchester R. N., Reardon D. J., Matsakis D., Tong M. L., Arzoumanian Z., Bailes M., Bassa C. G., Bhat N. D. R., Brazier A., Burke-Spolaor S., Champion D. J., Chatterjee S., Cognard I., Dai S., Desvignes G., Dolch T., Ferdman R. D., Graikou E., Guillemot L., Janssen G. H., Keith M. J., Kerr M., Kramer M., Lam M. T., Liu K., Lyne A., Lazio T. J. W., Lynch R., McKee J. W., McLaughlin M. A., Mingarelli C. M. F., Nice D. J., Osłowski S., Pennucci T. T., Perera B. B. P., Perrodin D., Possenti A., Russell C. J., Sanidas S., Sesana A., Shaifullah G., Shannon R. M., Simon J., Spiewak R., Stairs I. H., Stappers B. W., Swiggum J. K., Taylor S. R., Theureau G., Toomey L., van Haasteren R., Wang J. B., Wang Y., and Zhu X. J., A pulsar-based time-scale from the International Pulsar Timing Array, Monthly Notices of the Royal Astronomical Society. (2020) 491, no. 4, 5951–5965, https://doi.org/10.1093/mnras/stz3071.
10.1093/mnras/stz3071
Web of Science® Google Scholar
18 Sheikh S. I., Hanson J. E., Graven P. H., and Pines D. J., Spacecraft navigation and timing using X-ray pulsars, Navigation. (2011) 58, no. 2, 165–186, https://doi.org/10.1002/j.2161-4296.2011.tb01799.x, 2-s2.0-80052326145.
10.1002/j.2161-4296.2011.tb01799.x
Google Scholar
19 Mitchell J. W., Hassouneh M. A., Winternitz L. M., Valdez J. E., Ray P. S., Arzoumanian Z., and Gendreau K. C., Station explorer for X-ray timing and navigation technology architecture overview, Proceedings of the 27th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2014), September 2014, Tampa, FL, USA, 3194–3200, https://www.ion.org/publications/abstract.cfm?articleID=12401.
Google Scholar
20 Liu J., Wang W., Zhang H., Shu L., and Gao Y., Autonomous orbit determination and timekeeping in lunar distant retrograde orbits by observing X-ray pulsars, Navigation. (2021) 68, no. 4, 687–708, https://doi.org/10.1002/navi.451.
10.1002/navi.451
CAS Web of Science® Google Scholar
21 Liu Y., Xu B., Zheng Z., Chen Z., and Zhu X., Research on the joint timekeeping of pulsars and atomic clocks based on Vondrak-Cepek filtering, Monthly Notices of the Royal Astronomical Society. (2023) 521, no. 2, 2553–2559, https://doi.org/10.1093/mnras/stad613.
10.1093/mnras/stad613
CAS Web of Science® Google Scholar
22 Zhu X., Zhang Z., Zhao C., Li B., Tong M., Gao Y., and Yang T., Research on establishing a joint time-scale of pulsar time and atomic time based on a wavelet analysis method, Monthly Notices of the Royal Astronomical Society. (2024) 529, no. 2, 1082–1090, https://doi.org/10.1093/mnras/stae331.
10.1093/mnras/stae331
Web of Science® Google Scholar
23 Wang L., Zhang Z., Zhao C., Li Z., and Tong M., Study on the one-year accuracy of pulsar time-scale, Research in Astronomy and Astrophysics. (2025) 25, no. 1, https://doi.org/10.1088/1674-4527/ada05f.
10.1088/1674-4527/ada05f
Web of Science® Google Scholar
24 Zhou Q., Wei Z. Q., Yan L. L., Sun P. F., Liu S. W., Feng L. P., Jiang K., Wang Y. D., Zhu Y. X., Liu X. G., Ming F., Zhang F., and He Z. N., Space/ground based pulsar timescale for comprehensive PNT system, Acta Physica Sinica. (2021) 70, no. 13, 139701, https://doi.org/10.7498/aps.70.20210288.
10.7498/aps.70.20210288
Web of Science® Google Scholar
25 Coles W., Hobbs G., Champion D. J., Manchester R. N., and Verbiest J. P. W., Pulsar timing analysis in the presence of correlated noise, Monthly Notices of the Royal Astronomical Society. (2011) 418, no. 1, 561–570, https://doi.org/10.1111/j.1365-2966.2011.19505.x, 2-s2.0-81055156773.
10.1111/j.1365-2966.2011.19505.x
Web of Science® Google Scholar
26 Lyne A. G., Shemar S. L., and Graham Smith F., Statistical studies of pulsar glitches, Monthly Notices of the Royal Astronomical Society. (2000) 315, no. 3, 534–542, https://doi.org/10.1046/j.1365-8711.2000.03415.x, 2-s2.0-0042350959.
10.1046/j.1365-8711.2000.03415.x
Web of Science® Google Scholar
27 Emadzadeh A. A. and Speyer J. L., On modeling and pulse phase estimation of X-ray pulsars, IEEE Transactions on Signal Processing. (2010) 58, no. 9, 4484–4495, https://doi.org/10.1109/TSP.2010.2050479, 2-s2.0-77955592785.
10.1109/TSP.2010.2050479
Web of Science® Google Scholar
28 Sheikh S. I., The Use of Variable Celestial X-Ray Sources for Spacecraft Navigation, 2005, University of Maryland, College Park, Ann Arbor.
Google Scholar
29 Salas J. D., Applied Modeling of Hydrologic Time Series, 1980, Water Resources Publication, Michigan.
Google Scholar
30 Shannon R. M. and Cordes J. M., Assessing the role of spin noise in the precision timing of millisecond pulsars, Astrophysical Journal. (2010) 725, no. 2, 1607–1619, https://doi.org/10.1088/0004-637X/725/2/1607, 2-s2.0-78650094663.
10.1088/0004-637X/725/2/1607
Web of Science® Google Scholar
31 Kedong Y., Yan G., and Xuemei L., Improved grey prediction model based on exponential grey action quantity, Journal of Systems Engineering and Electronics. (2018) 29, no. 3, 560–570, https://doi.org/10.21629/JSEE.2018.03.13, 2-s2.0-85049743908.
10.21629/JSEE.2018.03.13
Google Scholar
32 Cilden D., Soken H. E., and Hajiyev C., Nanosatellite attitude estimation from vector measurements using SVD-aided UKF algorithm, Metrology and Measurement Systems. (2017) 24, no. 1, 113–125.
10.1515/mms-2017-0011
Web of Science® Google Scholar
33 Song S., Xu L., Zhang H., and Bai Y., Novel X-ray communication based XNAV augmentation method using X-ray detectors, Sensors. (2015) 15, no. 9, 22325–22342, https://doi.org/10.3390/s150922325, 2-s2.0-84940987520, 26404295.
10.3390/s150922325
PubMed Web of Science® Google Scholar

All articles

On an Autonomous Pulsar Observation–Based Timekeeping Method for Deep Space

Abstract

1. Introduction