International Journal of Aerospace Engineering

Volume 2025, Issue 1 5555968

Research Article

Open Access

Effect of a Nonlinear Energy Sink on the Nonlinear Panel Flutter Suppression Under Variable Temperature Rise and Airflow Yawed Angle

Zhou Jian

orcid.org/0000-0001-5621-329X

State Key Laboratory for Strength and Vibration of Mechanical Structures , School of Aerospace Engineering , Xi’an Jiaotong University , Xi’an , China , xjtu.edu.cn

Search for more papers by this author

Guo Yilin,

Guo Yilin

orcid.org/0009-0006-6884-4121

State Key Laboratory for Strength and Vibration of Mechanical Structures , School of Aerospace Engineering , Xi’an Jiaotong University , Xi’an , China , xjtu.edu.cn

Search for more papers by this author

Gao Zehao,

Gao Zehao

orcid.org/0009-0007-3708-7073

State Key Laboratory for Strength and Vibration of Mechanical Structures , School of Aerospace Engineering , Xi’an Jiaotong University , Xi’an , China , xjtu.edu.cn

Search for more papers by this author

Xu Minglong,

Corresponding Author

Xu Minglong

[email protected]

orcid.org/0009-0000-3340-4632

State Key Laboratory for Strength and Vibration of Mechanical Structures , School of Aerospace Engineering , Xi’an Jiaotong University , Xi’an , China , xjtu.edu.cn

Search for more papers by this author

Zhou Jian,

Zhou Jian

orcid.org/0000-0001-5621-329X

State Key Laboratory for Strength and Vibration of Mechanical Structures , School of Aerospace Engineering , Xi’an Jiaotong University , Xi’an , China , xjtu.edu.cn

Search for more papers by this author

Guo Yilin,

Guo Yilin

orcid.org/0009-0006-6884-4121

State Key Laboratory for Strength and Vibration of Mechanical Structures , School of Aerospace Engineering , Xi’an Jiaotong University , Xi’an , China , xjtu.edu.cn

Search for more papers by this author

Gao Zehao,

Gao Zehao

orcid.org/0009-0007-3708-7073

State Key Laboratory for Strength and Vibration of Mechanical Structures , School of Aerospace Engineering , Xi’an Jiaotong University , Xi’an , China , xjtu.edu.cn

Search for more papers by this author

Xu Minglong,

Corresponding Author

Xu Minglong

[email protected]

orcid.org/0009-0000-3340-4632

State Key Laboratory for Strength and Vibration of Mechanical Structures , School of Aerospace Engineering , Xi’an Jiaotong University , Xi’an , China , xjtu.edu.cn

Search for more papers by this author

First published: 13 June 2025

https://doi.org/10.1155/ijae/5555968

Academic Editor: Mohammad Rezwan Habib

Share a link

Email
Wechat
Bluesky

Abstract

This study investigates the nonlinear aeroelastic response behaviors and robustness of a square isotropic panel with a nonlinear energy sink (NES) considering temperature rise and airflow yawed angle. Considering uniform temperature rise, the nonlinear aerothermoelastic equations for a three-dimensional (3D) isotropic panel with an NES were derived using the von Karman large deformation theory and the piston theoretical aerodynamic force with airflow yawed angle and then discretized using the Galerkin method. The fourth-order Runge–Kutta method was used to solve the aerothermoelastic equations for the panel response, and the effect of temperature rise and airflow yawed angle on the NES suppression ability was examined. The numerical results revealed the appearance of a buckling region due to the temperature rise; however, the NES had no impact on the boundary of this region. The suppression ability of the NES gradually weakened and disappeared completely as temperature increased. Furthermore, within a small angular range, the NES suppression ability increased with the increasing airflow yawed angle. For a large airflow yawed angle, the NES not only lost its suppression ability but also made the panel aeroelastic response worse.

1. Introduction

Panel flutter is an aeroelastically induced self-excited vibration of the flight vehicle skin exposed on one side to supersonic airflow [1]. Under supersonic airflow conditions, the panel experiences high-speed airflow effects with varying yawed angles [2], along with aerodynamic heating [3, 4]. Panel flutter usually appears as a limited amplitude oscillation due to the geometric nonlinearity of the panel. However, continuous large-amplitude oscillations can lead to panel fatigue and affect flight safety [5]. Therefore, panel flutter suppression is a crucial aspect when designing aerospace vehicles.

A significant amount of research on panel flutter control has been carried out. Scott and Weisshaar [6] and Sadri et al. [7] improved the panel flutter boundary using piezoceramic actuators. Moon and Hwang [8, 9] employed the LQR method to control the aeroelastic response for a composite flat panel and obtained the actuator and sensor locations using genetic algorithms for best control effects. Kim et al. [10] developed an active controller to control panel aeroelastic response by using aeroelastic modes. Hasheminejad and Motaaleghi [11] studied the flutter suppression of a sandwich cylindrical panel by using a tunable electrorheological fluid (ERF) mid-layer considering yawed supersonic airflow. Li [12] investigated the effect of active mass and stiffness on suppressing the panel aeroelastic response and revealed that increasing the feedback control gains can improve the active aeroelastic properties for the lower order modes. Chai et al. [13] utilized the MFC actuator and sensor to control panel flutter with time-dependent boundary conditions.

The abovementioned active control methods exhibit effective control of nonlinear aeroelastic panel response. However, these systems require additional sensors and actuators, and the stability of closed-loop systems is affected by the signal transmission delay. Passive control technology, by contrast, is simple in structure, robust, and consumes no energy, so it has been widely adopted as a means of suppressing panel flutter [14], especially in the form of dynamic vibration absorbers. However, traditional dynamic vibration absorbers are designed with linear stiffness. So, only when the frequency is equal to or close to the natural frequency of the main system does the vibration absorption effect become obvious. The vibration absorption frequency is also relatively narrow. This limits the scope of the development and application of this kind of solution. However, a dynamic vibration absorber called a nonlinear energy sink (NES), consisting of a small mass, a cubic stiffness, and a linear damping, has a wide frequency band and a highly efficient vibration absorption mechanism, displaying great potential for passive suppression [15–17].

NES have been widely studied for vibration suppression in beam structures under forced loads, such as harmonic/impact excitations [18–22]. NES can also suppress self-excited system responses. Lee et al. [23] suppressed the limit cycle oscillations of a van der Pol oscillator using an NES. They subsequently adopted an NES to suppress wing flutter and revealed the suppression mechanism using energy–frequency and time-frequency analyses [24, 25]. Yan et al. [26] studied transonic wing flutter suppression by using an NES. Zhang et al. [27] combined a piezoelectric energy harvester and an NES to suppress the aeroelastic response of an airfoil with two-degree-of-freedom. Guo et al. [28] introduced an NES to suppress the vibration of the airfoil with freeplay and enhance the reliability. NES has also been used to suppress other self-excited system vibrations, such as fluid-conveying pipes [29, 30], rotor blades [31], and a long-span bridges [32].

Relatively, fewer works exist on the panel flutter response suppressing using an NES. Zhang et al. [33] used an NES to rapidly restore the static state of the panel postperturbations in the supersonic airflow. Pacheco et al. [34] suppressed panel aeroelastic response using an NES and established the important suppression mechanism via the energy-based method. Zhou et al. [35, 36] studied the NES parameter effect on the suppression ability for the nonlinear aeroelastic response of a 2D panel and 3D panel. Wang et al. [37] designed an NES to suppress the nonlinear aeroelastic responses of graphene platelet–reinforced composite lattice sandwich plates. However, the temperature rise and airflow yawed angle, which will affect the NES suppression ability seriously, are not considered in the above studies.

In this study, we investigated the effect of the temperature rise and airflow yawed angle on the NES suppression ability of the panel aeroelastic response. The rest of the article is structured as follows: The nonlinear aerothermoelastic equations for a 3D isotropic panel with an NES under yawed supersonic flow are derived in Section 2; the validation and effectiveness analyses are demonstrated in Sections 3 and 4; and finally, Section 5 presents the primary conclusions of the study.

2. Nonlinear Aerothermoelastic Formulation

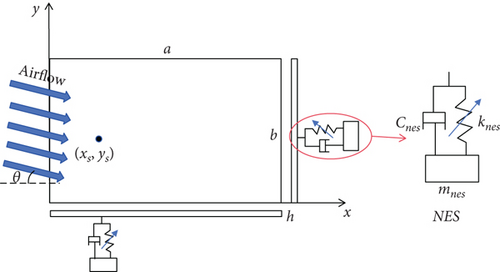
Figure 1 shows a 3D isotropic panel model with an NES under yawed supersonic flow, where a, b, and h are, respectively, the length, width, and thickness of the panel; m_nes, k_nes, and c_nes are, respectively, the mass, nonlinear stiffness, and damping of the NES. The NES is installed at (x_s, y_s) with θ being the airflow yawed angle with the x-axis.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

A 3D isotropic panel model with an NES under yawed supersonic flow.

2.1. Constitutive Equations

According to the von Karman large deformation theory, the nonlinear strain–displacement relation of the panel is

()

where

Considering a uniform temperature rise, ΔT, the stress–strain relationship becomes

()

where α is the thermal expansion coefficient, H = [1 1 0]^T, and

, where υ is Poisson’s ratio. The force and moment resultant vectors can be then obtained as

()

D = Eh³/12(1 − υ²) is the panel bending stiffness, N_T = EhαΔT/(1 − υ), and E is elastic modulus.

2.2. Aerothermoelastic Equations

The panel kinetic (T) and potential energies (U)can be expressed as

()

The panel is subjected to an external NES and aerodynamic loading, which leads to the variation in the work done to the panel expressed as

()

where

()

and , where Ma is the Mach number; ρ_∞ and U_∞ are the airflow density and velocity, respectively; w_s is the panel displacement at (x_s, y_s); s is the NES displacement; and is the Dirac function.

By adopting Hamilton’s principle, the nonlinear aerothermoelastic equations of the panel with an NES can be expressed as

()

which provides

()

To solve Equation (9), the following consistency equation must be adopted:

()

Using Equation (3), we can obtain ε₀ as

()

By combining Equations (10) and (11), we can obtain

()

Let us assume {N_x, N_y, N_xy} = {∂²ϕ/∂y², ∂²ϕ/∂x², −∂²ϕ/∂x∂y}h, where ϕ is the airy stress and adopt the NES motion equation from [34]. The final nonlinear aerothermoelastic equations for a 3D isotropic panel with an NES under yawed supersonic flow are then obtained as

()

2.3. Galerkin’s Discretization Method

Let us define the following dimensionless variables:

and introduce them into Equations (13)–(15), we obtain:

()

where

, and

are the unknown variables. Further, we have

The solution of the airy stress,

, can be divided as

()

is a homogeneous solution and is a particular solution.

Introducing Equation (19) into Equation (17), we have

()

Under simply supported boundary conditions, the panel displacement discretized using the Galerkin method can be expressed as

()

By combining Equations (21) and (22), the following equation can be obtained:

()

where the coefficients A, B, C₁, C₂, C₃, and C₄ are derived in Appendix A. Let us assume

()

where P₁, P₂, P₃, and P₄ are obtained by substituting Equations (23) and (24) into Equation (21) (Appendix B). The homogeneous solution,

, takes the following form:

()

The following boundary conditions need to be satisfied:

()

Further, β₁ and β₂ can be obtained as

()

, T_cr = π²h²/[12(1 + υ)αa²] is the critical temperature [4], and β₃ = 0 when considering a uniform temperature rise of the panel. Thus, we obtain

()

Combining Equations (16), (18), (19), (22), (24), and (29) and integrating Equation (16) over panel length and width after multiplying throughout with sin(rπξ)sin(gπη), we can obtain a set of coupled ordinary nonlinear differential equations as

()

where A^∗, B^∗, C^∗, F^∗, and

are shown in Appendix C. The above equations were solved using the fourth-order Runge–Kutta (RK4) method to obtain the coefficient, q_rg, which allows the panel displacement response calculations.

3. Validations

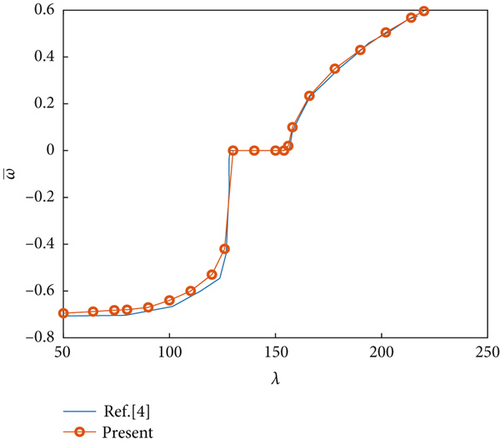
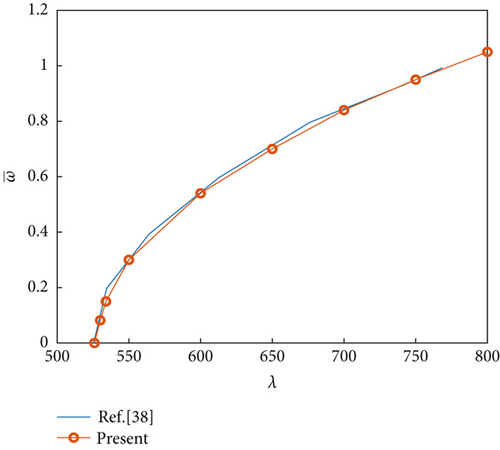
Following our previous work [36], we only needed to verify the introduction of the temperature rise and airflow yawed angle variables into the aeroelastic equations. The present panel aeroelastic response results were in good agreement with that of panels with a/b = 0.5, ΔT/T_cr = 3, and θ = 0 in [4] and a/b = 1, ΔT/T_cr = 0, and θ = 45^° in [38] under temperature rise and airflow yawed angle conditions (Figure 2). This verified the validity of the proposed model, which can be used for further research on the effects of an NES on nonlinear panel aeroelastic response suppression.

4. Numerical Results and Discussions

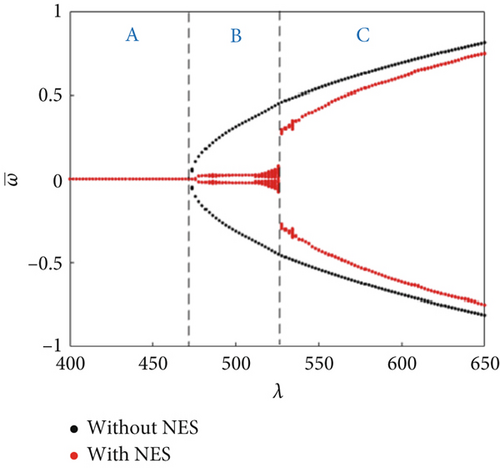
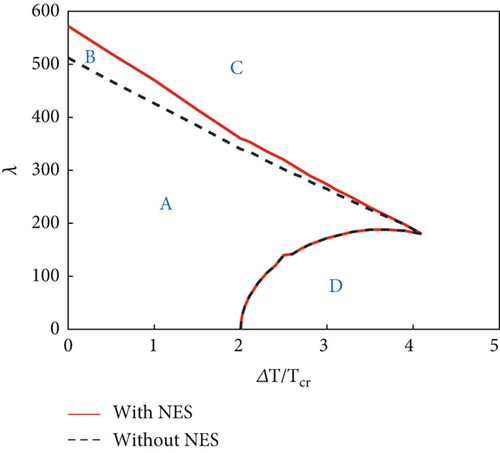
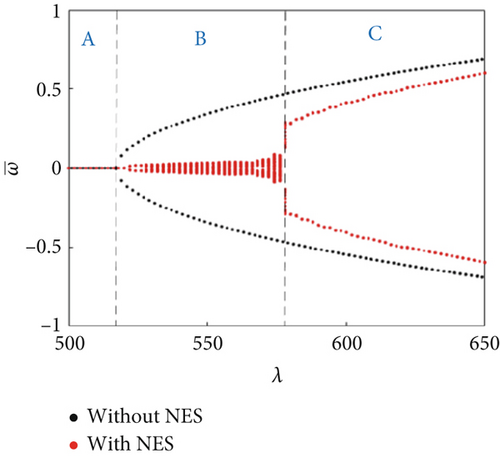
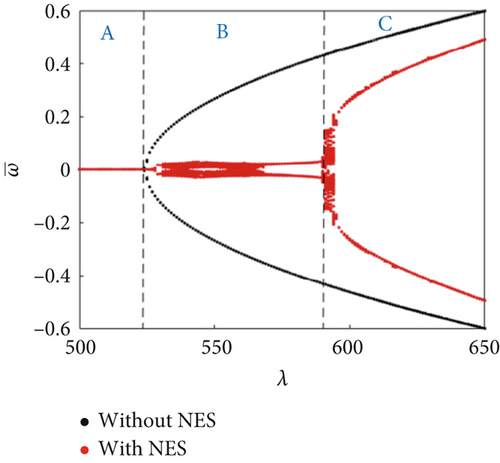
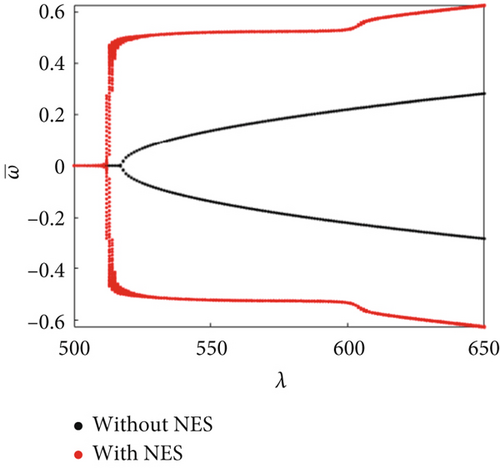
In this study, the NES parameters of the NES installed at and were set as , , and . The panel dimensions were a/b = 1 and h = 1/300a. The bifurcation diagrams were obtained using steady amplitude response data at and . For ΔT/T_cr = 0.5 and θ = 15^°, the bifurcation characteristics were compared with and without the presence of an NES under changing dynamic pressure (Figure 3). The bifurcation characteristic diagram can be divided into three regions: (A) static equilibrium region: In this region, regardless of the presence/absence of the NES, the panel aeroelastic response eventually converges to the static equilibrium, with a faster convergence in the presence of an NES (Figure 4a). (B) NES suppression region: In this region, the aeroelastic response amplitudes of the panel with an NES are much smaller than those without an NES. The panel aeroelastic response is suppressed by the NES unique performance: permanent resonance capture (PRC) and recurrent transient resonance capture (TRC), as shown in Figure 4b,c. (C) Flutter response region: In this region, the NES performance deteriorates, and the panel exhibits a large amplitude vibration response (Figure 4d). The NES suppression region is not only affected by the NES parameters [36] but is also related to the temperature rise of the panel and the airflow yawed angle (discussed later).

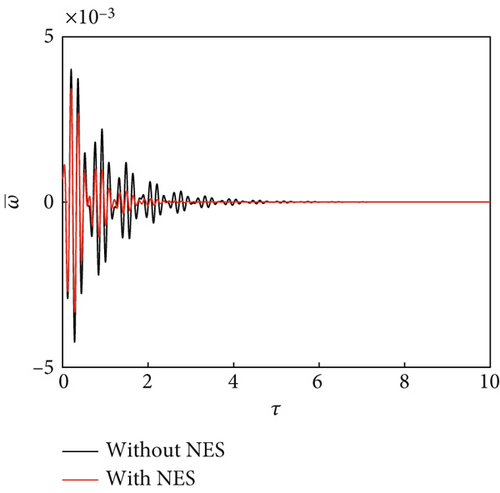
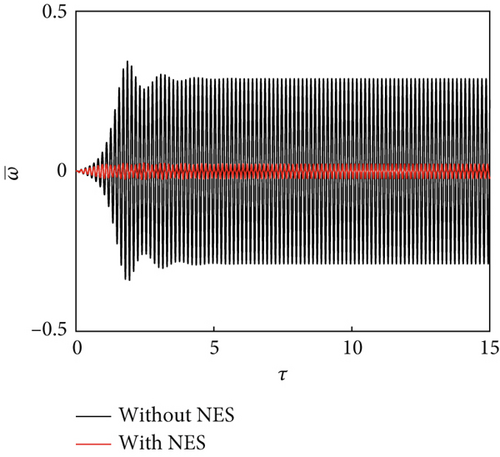
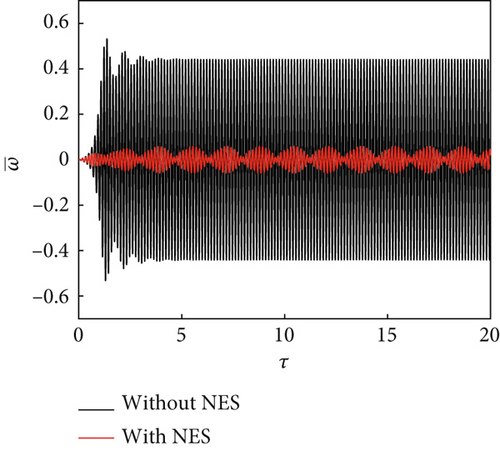
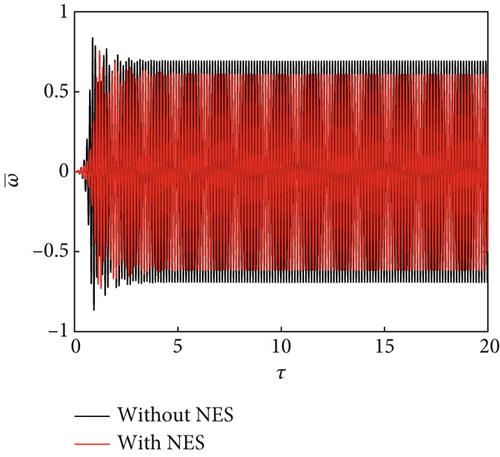
4.1. Effect of Temperature Rise

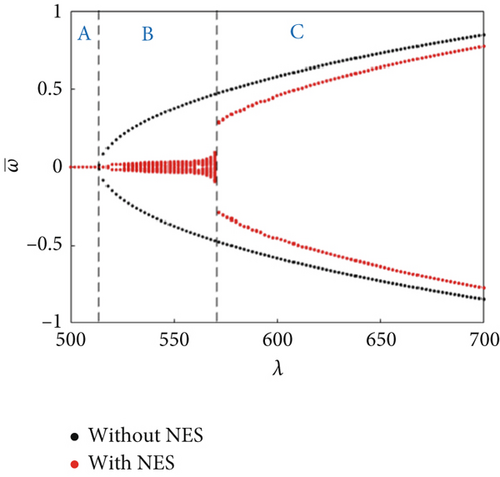
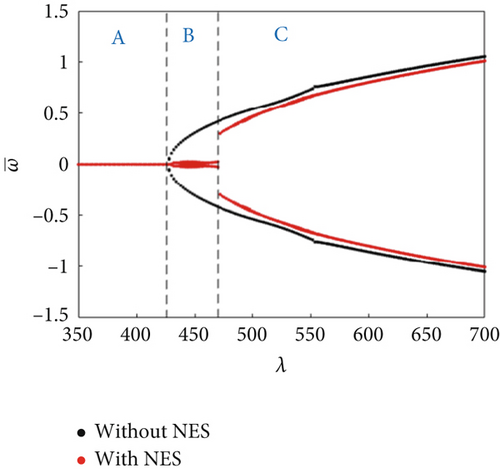
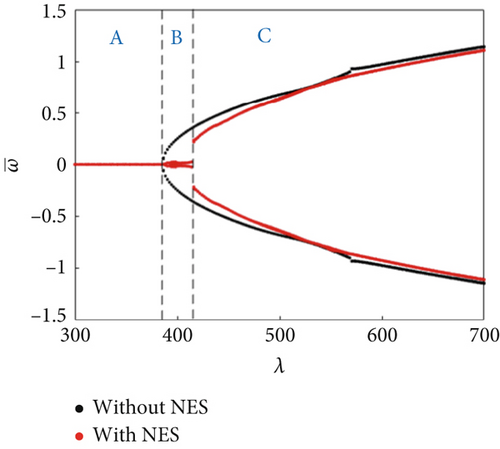
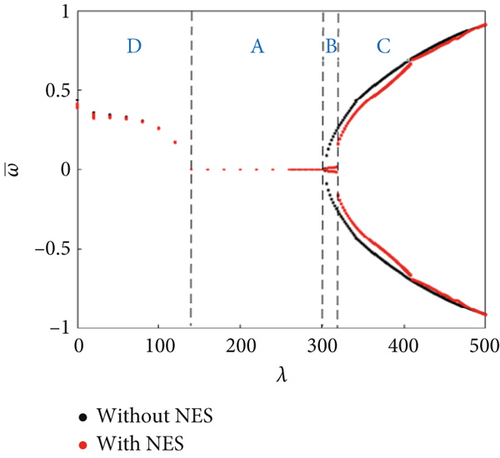
The bifurcation characteristics with/without an NES were further compared under dynamically varying pressure for ΔT/T_cr = 0.0, 1.0, 1.5, and 2.5 (Figure 5). The dynamic pressure ranges of the NES suppression region under the above four temperature rise values were obtained as 512 ≤ λ ≤ 570, 426 ≤ λ ≤ 470, 384 ≤ λ ≤ 414, and 302 ≤ λ ≤ 318, respectively. It shows that the static equilibrium region decreased with the increasing temperature rise, indicating that the flutter critical dynamic pressure decreased. The NES suppression region also decreased with increasing temperature rise, suggesting that the NES gradually loses performance under temperature rise conditions. Additionally, a buckling region (Region D) appeared for a high ΔT/T_cr (Figure 5d). In this region, the buckling response amplitude and boundary of the buckling region are basically the same, indicating that the NES did not affect the buckling region. Overall, the panel response suppression ability of the NES will gradually weakened with increasing temperature rise till it disappeared completely (Figure 6).

4.2. Effect of Airflow Yawed Angle

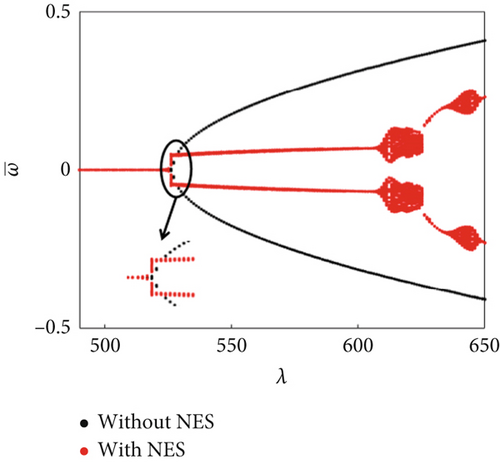
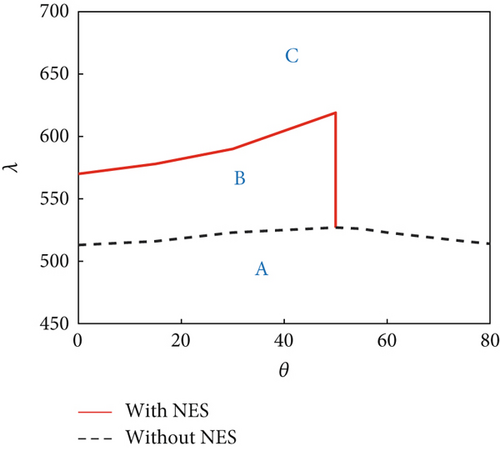
The bifurcation characteristics with/without an NES under changing dynamic pressure were further compared for θ = 15^°, 30°, 55°, and 75° (Figure 7). For θ = 15^° and θ = 30^°, the dynamic pressure ranges of the NES suppression region were 513 ≤ λ ≤ 570 and 516 ≤ λ ≤ 578, respectively. The NES suppression region slightly increased with the increasing airflow yawed angle. However, when the airflow angle increases to θ = 55^°, as shown in Figure 7c, although the NES has a good suppression effect in a large dynamic pressure range, the flutter critical dynamic pressure reduced unexpectedly, as shown in the enlarged part in Figure 7c. Therefore, the NES suppression performance lost its significance in this case. As θ was further increased, the flutter critical dynamic pressure of the panel reduced, while the aeroelastic response amplitude increased (Figure 7d), that is, the panel aeroelastic response deteriorated. We have plotted the effect of airflow yawed angle on the suppression region, as shown in Figure 8. From the figure, it revealed that the NES had good suppression ability for 0^° ≤ θ ≤ 50^°, and the NES suppression region also increases with the increase of the airflow yawed angle. If the airflow yawed angle is too large, the NES will not only lose its suppression ability but also make the panel aeroelastic response worse.

5. Conclusions

This study provides critical insights into the effectiveness of NES in suppressing panel flutter under varying temperature rise and airflow yawed angle conditions. The findings offer actionable guidance for engineers designing aerospace structures, particularly in optimizing NES performance for real-world operational environments. The primary conclusions are presented as follows:

1.
The study reveals that temperature rise significantly diminishes the NES suppression ability. As the temperature increases, the NES suppression region shrinks, and the flutter critical dynamic pressure decreases. Notably, at high temperatures, a buckling region emerges where the NES has no effect on the buckling response amplitude.
2.
The airflow yawed angle exhibits a dual effect on NES performance. Within a moderate range (0^° ≤ θ ≤ 50^°), the NES suppression region expands slightly with increasing angle, suggesting enhanced performance. However, beyond this range, the flutter critical dynamic pressure drops abruptly, and the panel’s aeroelastic response deteriorates. Engineers should prioritize NES deployment in applications where the yawed angle remains within the effective range.

In summary, this work not only advances the theoretical understanding of NES-based flutter suppression but also delivers practical recommendations for aerospace engineers. By addressing the interplay between temperature, airflow angle, and NES dynamics, the study equips designers with the knowledge to enhance flight safety and structural reliability in supersonic applications.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research was supported by the Natural Science Basic Research Program of Shaanxi (2023-JC-QN-0019).

Acknowledgments

This study was funded by the Natural Science Basic Research Program of Shaanxi (Program No. 2023-JC-QN-0019).

Appendix A

A, B, C₁, C₂, C₃, and C₄:

Appendix B

P₁, P₂, P₃, and P₄:

where m = i, n = j, and P₁ = 0.

Appendix C

A^∗, B^∗, C^∗, F^∗, and

Open Research

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Dowell E. H., Aeroelasticity of Plates and Shells, 1975, Noordhoff International Publishing.
Google Scholar
2 Guo X. Y. and Mei C., Using Aeroelastic Modes for Nonlinear Panel Flutter at Arbitrary Supersonic Yawed Angle, AIAA Journal. (2003) 42, no. 2, 272–279.
10.2514/2.1940
Google Scholar
3 Guo X. Y. and Mei C., Application of Aeroelastic Modes on Nonlinear Supersonic Panel Flutter at Elevated Temperatures, Computers& Structures. (2006) 84, no. 24-25, 1619–1628, https://doi.org/10.1016/j.compstruc.2006.01.041, 2-s2.0-33746864521.
10.1016/j.compstruc.2006.01.041
Web of Science® Google Scholar
4 Xie D., Xu M., Dai H. H., and Dowell E. H., Proper Orthogonal Decomposition Method for Analysis of Nonlinear Panel Flutter With Thermal Effects in Supersonic Flow, Journal of Sound and Vibration. (2015) 337, 263–283, https://doi.org/10.1016/j.jsv.2014.10.038, 2-s2.0-84916623534.
10.1016/j.jsv.2014.10.038
Web of Science® Google Scholar
5 Garrick I. E. and Reed Iii W. H., Historical Development of Aircraft Flutter, Journal of Aircraft. (1981) 18, no. 11, 897–912, https://doi.org/10.2514/3.57579, 2-s2.0-0019633695.
10.2514/3.57579
Web of Science® Google Scholar
6 Scott R. and Weisshaar T., Panel Flutter Suppression Using Adaptive Material Actuators, Journal of Aircraft. (1994) 31, no. 1, 213–222, https://doi.org/10.2514/3.46476, 2-s2.0-0028195864.
10.2514/3.46476
Web of Science® Google Scholar
7 Sadri A. M., Wright J. R., and Wynne R. J., LQG Control Design for Panel Flutter Suppression Using Piezoelectric Actuators, Smart Materials and Structures. (2002) 11, no. 6, 834–839, https://doi.org/10.1088/0964-1726/11/6/302, 2-s2.0-0036962020.
10.1088/0964-1726/11/6/302
Google Scholar
8 Moon S. H. and Hwang J. S., Panel Flutter Suppression With an Optimal Controller Based on the Nonlinear Model Using Piezoelectric Materials, Composite Structures. (2005) 68, no. 3, 371–379, https://doi.org/10.1016/j.compstruct.2004.04.002, 2-s2.0-11144231425.
10.1016/j.compstruct.2004.04.002
Web of Science® Google Scholar
9 Moon S. H., Finite Element Analysis and Design of Control System With Feedback Output Using Piezoelectric Sensor/Actuator for Panel Flutter Suppression, Finite Elements in Analysis and Design. (2006) 42, no. 12, 1071–1078, https://doi.org/10.1016/j.finel.2006.04.001, 2-s2.0-33745430717.
10.1016/j.finel.2006.04.001
Web of Science® Google Scholar
10 Kim M., Li Q. Q., and Mei C., Active Control of Nonlinear Panel Flutter Using Aeroelastic Modes and Piezoelectric Actuators, AIAA Journal. (2008) 46, no. 3, 733–743, https://doi.org/10.2514/1.33803, 2-s2.0-43649107662.
10.2514/1.33803
CAS Web of Science® Google Scholar
11 Hasheminejad S. M. and Motaaleghi M. A., Aeroelastic Analysis and Active Flutter Suppression of an Electro-Rheological Sandwich Cylindrical Panel Under Yawed Supersonic Flow, Aerospace Science and Technology. (2015) 42, 118–127, https://doi.org/10.1016/j.ast.2015.01.004, 2-s2.0-84922062402.
10.1016/j.ast.2015.01.004
Web of Science® Google Scholar
12 Li F. M., Active Aeroelastic Flutter Suppression of a Supersonic Plate With Piezoelectric Material, International Journal of Engineering Science. (2012) 51, 190–203, https://doi.org/10.1016/j.ijengsci.2011.10.003, 2-s2.0-84155170909.
10.1016/j.ijengsci.2011.10.003
Web of Science® Google Scholar
13 Chai Y. Y., Song Z. G., and Li F. M., Active Aerothermoelastic Flutter Suppression of Composite Laminated Panels With Time-Dependent Boundaries, Composite Structures. (2017) 179, 61–76, https://doi.org/10.1016/j.compstruct.2017.07.053, 2-s2.0-85026229613.
10.1016/j.compstruct.2017.07.053
Web of Science® Google Scholar
14 Hai Z., Dengqing C., and Gang L., Suppression of Supersonic Flutter of Laminated Composite Panel Using Dynamic Absorber Device and Its Optimal Design [in Chinese], Journal of Aerospace Power. (2013) 28, no. 10, 2202–2208.
Google Scholar
15 Gendelman O., Manevitch L. I., Vakakis A. F., and Closkey R. M., Energy Pumping in Nonlinear Mechanical Oscillators: Part I-Dynamics of the Underlying Hamiltonian Systems, Journal of Applied Mechanics. (2001) 68, no. 1, 34–41, https://doi.org/10.1115/1.1345524, 2-s2.0-14944348772.
10.1115/1.1345524
Web of Science® Google Scholar
16 Vakakis A. F. and Gendelman O., Energy Pumping in Nonlinear Mechanical Oscillators: Part II-Resonance Capture, Journal of Applied Mechanics. (2001) 68, no. 1, 42–48, https://doi.org/10.1115/1.1345525, 2-s2.0-0002298634.
10.1115/1.1345525
Web of Science® Google Scholar
17 Vakakis A. F., Inducing Passive Nonlinear Energy Sinks in Vibrating Systems, Journal of Vibration and Acoustics. (2001) 123, no. 3, 324–332, https://doi.org/10.1115/1.1368883, 2-s2.0-0000721176.
10.1115/1.1368883
Web of Science® Google Scholar
18 Georgiades F. and Vakakis A. F., Dynamics of a Linear Beam With an Attached Local Nonlinear Energy Sink, Communications in Nonlinear Science and Numerical Simulation. (2007) 12, no. 5, 643–651, https://doi.org/10.1016/j.cnsns.2005.07.003, 2-s2.0-33845771741.
10.1016/j.cnsns.2005.07.003
Web of Science® Google Scholar
19 Ahmadabadi Z. N. and Khadem S. E., Nonlinear Vibration Control of a Cantilever Beam by a Nonlinear Energy Sink, Mechanism and Machine Theory. (2012) 50, 134–149, https://doi.org/10.1016/j.mechmachtheory.2011.11.007, 2-s2.0-84855983895.
10.1016/j.mechmachtheory.2011.11.007
Web of Science® Google Scholar
20 Parseh M., Dardel M., and Ghasemi M. H., Performance Comparison of Nonlinear Energy Sink and Linear Tuned Mass Damper in Steady-State Dynamics of a Linear Beam, Nonlinear Dynamics. (2015) 81, no. 4, 1981–2002, https://doi.org/10.1007/s11071-015-2120-3, 2-s2.0-84938960361.
10.1007/s11071-015-2120-3
Web of Science® Google Scholar
21 Zhang Y. W., Yuan B., Fang B., and Chen L. Q., Reducing Thermal Shock-Induced Vibration of an Axially Moving Beam via a Nonlinear Energy Sink, Nonlinear Dynamics. (2017) 87, no. 2, 1159–1167, https://doi.org/10.1007/s11071-016-3107-4, 2-s2.0-84990852187.
10.1007/s11071-016-3107-4
Web of Science® Google Scholar
22 Wang Y. R., Feng C. K., and Chen S. Y., Damping Effects of Linear and Nonlinear Tuned Mass Dampers on Nonlinear Hinged-Hinged Beam, Journal of Sound and Vibration. (2018) 430, 150–173, https://doi.org/10.1016/j.jsv.2018.05.033, 2-s2.0-85047853300.
10.1016/j.jsv.2018.05.033
Web of Science® Google Scholar
23 Lee Y. S., Vakakis A. F., Bergman L. A., and Mcfarland D. M., Suppression of Limit Cycle Oscillations in the Van der Pol Oscillator by Means of Passive Non-Linear Energy Sinks, Structural Control and Health Monitoring. (2006) 13, no. 1, 41–75, https://doi.org/10.1002/stc.143, 2-s2.0-33144472123.
10.1002/stc.143
Web of Science® Google Scholar
24 Lee Y. S., Vakakis A. F., Bergman L. A., Mcfarland D. M., and Kerschen G., Suppression Aeroelastic Instability Using Broadband Passive Targeted Energy Transfers, Part 1: Theory, AIAA Journal. (2007) 45, no. 3, 693–711, https://doi.org/10.2514/1.24062, 2-s2.0-34047260407.
10.2514/1.24062
Web of Science® Google Scholar
25 Lee Y. S., Kerschen G., Mcfarland D. M., Bergman L. A., and Vakakis A. F., Suppressing Aeroelastic Instability Using Broadband Passive Targeted Energy Transfers, Part 2: Experiments, AIAA Journal. (2007) 45, no. 10, 2391–2400, https://doi.org/10.2514/1.28300, 2-s2.0-36049032787.
10.2514/1.28300
Web of Science® Google Scholar
26 Yan Z. M., Ragab S. A., and Hajj M. R., Passive Control of Transonic Flutter With a Nonlinear Energy Sink, Nonlinear Dynamics. (2018) 91, no. 1, 577–590, https://doi.org/10.1007/s11071-017-3894-2, 2-s2.0-85032689037.
10.1007/s11071-017-3894-2
Web of Science® Google Scholar
27 Zhang H., Li Z. Y., Yang Z. C., and Zhou S. X., Flutter Suppression of an Airfoil Using a Nonlinear Energy Sink Combined With a Piezoelectric Energy Harvester, Communications in Nonlinear Science and Numerical Simulation. (2023) 125, 107350, https://doi.org/10.1016/j.cnsns.2023.107350.
10.1016/j.cnsns.2023.107350
Web of Science® Google Scholar
28 Guo W. L., Xu Y., Liu Q., Lenci S., and Li G. N., Reliability of Hypersonic Airfoil With Freeplay and Stochasticity via Nonlinear Energy Sink, AIAA Journal. (2024) 62, no. 9, 3258–3270, https://doi.org/10.2514/1.J064048.
10.2514/1.J064048
Web of Science® Google Scholar
29 Khazaee M., Khadem S. E., Moslemi A., and Abdollahi A., A Comparative Study on Optimization of Multiple Essentially Nonlinear Isolators Attached to a Pipe Conveying Fluid, Mechanical Systems and Signal Processing. (2020) 141, 106442, https://doi.org/10.1016/j.ymssp.2019.106442.
10.1016/j.ymssp.2019.106442
Web of Science® Google Scholar
30 Chang X. P. and Hong X. X., Stability and Nonlinear Vibration Characteristics of Cantilevered Fluid-Conveying Pipe With Nonlinear Energy Sink, Thin-Walled Structures. (2024) 205, 111987, https://doi.org/10.1016/j.tws.2024.111987.
10.1016/j.tws.2024.111987
Web of Science® Google Scholar
31 Ebrahimzade N., Dardel M., and Shafaghat R., Investigating the Aeroelastic Behaviors of Rotor Blades With Nonlinear Energy Sinks, AIAA Journal. (2018) 56, no. 7, 2856–2869, https://doi.org/10.2514/1.J056530, 2-s2.0-85049129715.
10.2514/1.J056530
Web of Science® Google Scholar
32 Vaurigaud B., Manevitch L. I., and Lamarque C. H., Passive Control of Aeroelastic Instability in a Long Span Bridge Model Prone to Coupled Flutter Using Targeted Energy Transfer, Journal of Sound and Vibration. (2011) 330, no. 11, 2580–2595, https://doi.org/10.1016/j.jsv.2010.12.011, 2-s2.0-79952538699.
10.1016/j.jsv.2010.12.011
Web of Science® Google Scholar
33 Zhang Y. W., Zhang H., Hou S., Xu K. F., and Chen L. Q., Vibration Suppression of Composite Laminated Plate With Nonlinear Energy Sink, Acta Astronautica. (2016) 123, 109–115, https://doi.org/10.1016/j.actaastro.2016.02.021, 2-s2.0-84961639770.
10.1016/j.actaastro.2016.02.021
Web of Science® Google Scholar
34 Pacheco D. R. Q., Marques F. D., and Ferreira A. J. M., Panel Flutter Suppression With Nonlinear Energy Sinks: Numerical Modeling and Analysis, International Journal of Non-Linear Mechanics. (2018) 106, 108–114, https://doi.org/10.1016/j.ijnonlinmec.2018.08.009, 2-s2.0-85053766104.
10.1016/j.ijnonlinmec.2018.08.009
Web of Science® Google Scholar
35 Zhou J., Xu M. L., and Xia W., Passive Suppression of Panel Flutter Using a Nonlinear Energy Sink, International Journal of Aerospace Engineering. (2020) 2020, 14, https://doi.org/10.1155/2020/8896744, 8896744.
10.1155/2020/8896744
Web of Science® Google Scholar
36 Zhou J., Xu M. L., Yang Z. C., and Gu Y. S., Suppression of Panel Flutter Response in Supersonic Airflow Using a Nonlinear Vibration Absorber, International Journal of Non-Linear Mechanics. (2021) 133, 103714, https://doi.org/10.1016/j.ijnonlinmec.2021.103714.
10.1016/j.ijnonlinmec.2021.103714
Web of Science® Google Scholar
37 Wang Y. W., Zhang Z. P., and Zhang W., Suppression of Nonlinear Aeroelastic Responses of Graphene Platelet-Reinforced Composite Lattice Sandwich Plates Using a Nonlinear Energy Sink, Nonlinear Dynamics. (2024) 112, no. 15, 12925–12939, https://doi.org/10.1007/s11071-024-09738-x.
10.1007/s11071-024-09738-x
Web of Science® Google Scholar
38 Abdel-Motagaly K., Guo X. Y., Duan B., and Mei C., Active Control of Nonlinear Panel Flutter Under Yawed Supersonic Flow, AIAA Journal. (2005) 43, no. 3, 671–680, https://doi.org/10.2514/1.13840, 2-s2.0-15944382007.
10.2514/1.13840
Web of Science® Google Scholar

All articles

Effect of a Nonlinear Energy Sink on the Nonlinear Panel Flutter Suppression Under Variable Temperature Rise and Airflow Yawed Angle

Abstract

1. Introduction