International Transactions on Electrical Energy Systems
Volume 2025, Issue 1 6575682
Research Article
Open Access

A Novel Data Driven Model for Voltage Stability Status Prediction and Instability Mitigation

F. Kh. Alabbas, 

F. Kh. Alabbas

Center of Excellence for Power System Automation and Operation , Iran University of Science and Technology (IUST) , Tehran , Iran , iust.ac.ir

Search for more papers by this author
M. Khalilifar, 

M. Khalilifar

Center of Excellence for Power System Automation and Operation , Iran University of Science and Technology (IUST) , Tehran , Iran , iust.ac.ir

Search for more papers by this author
S. M. Shahrtash, 

S. M. Shahrtash

Center of Excellence for Power System Automation and Operation , Iran University of Science and Technology (IUST) , Tehran , Iran , iust.ac.ir

Search for more papers by this author
D. A. Khaburi, 

Corresponding Author

D. A. Khaburi

Center of Excellence for Power System Automation and Operation , Iran University of Science and Technology (IUST) , Tehran , Iran , iust.ac.ir

Search for more papers by this author
First published: 11 May 2025
https://doi.org/10.1155/etep/6575682
Academic Editor: Reza Hamidi

Abstract

An intelligent power system is either a system that is smartly designed from zero to 100, or a system that was not smartly designed but currently uses all its facilities to be smartly operated in different sectors. This paper presents a novel data-driven model for real time voltage instability diagnosis and instability mitigating. The method combines deep recurrent neural techniques to forecast future voltage stability and mathematical morphology (MM) tools to pinpoint the specific on-load tap changers (OLTCs) contributing to instability and issuing blocking commands to prevent their operation and consequently instability. The approach for voltage stability assessment is centralized, using real-time data, while the method for voltage instability mitigation is localized, focusing on real-time voltage magnitude related to the secondary side of the load transformer. The network was trained and tested on the Nordic32 test system. Results show that the method accurately predicted the stability status just one second after a disturbance, and successfully mitigated all voltage instability events related to load restoration by blocking only the OLTCs that were effective in causing instability. This selective approach provides a significant selectivity index and improves the system resiliency index.

1. Introduction

Voltage stability refers to the ability of a power system to maintain steady voltages at all the buses in the system after being subjected to a disturbance from a given initial operating condition and can be categorized in two distinct types: short-term voltage stability and long-term voltage stability [1]. Short term pertains to the dynamics of fast acting load components, while long term voltage stability is associated with slower acting equipment such as tap-changing transformers, thermostatically controlled loads, and generator current limiters. Long term voltage stability typically manifests as a gradual decline in voltage levels at specific network buses, resulting from a loss of long-term equilibrium [1–4].

In order to ensure safe operation during disturbances, system operators must be able to quickly be aware of the situation. They need to determine:
  • i.

    Is the system still stable?

  • ii.

    If not, how much time is left before instability occurs?

  • iii.

    If it becomes unstable, what actions can be taken to prevent instability?

In the context of a literature review, the responses to the following fundamental questions are addressed as outlined below:
  • i.

    The initial question is addressed through the utilization of real-time voltage stability assessment algorithms, commonly referred to as voltage security assessment (VSA). It can be stated that the evaluation of voltage stability status is a highly sought-after research topic among scholars in the field [2–18]. In [6], 29 voltage instability indices have been reviewed by giving their equations, critical values, and assumptions, but without any implementation of the reviewed voltage stability indices (VSIs). In [7], in addition to presenting an improved voltage instability index, 17 line instability indices have been reviewed by giving their equations, critical values, and assumptions, where despite giving the performance of reviewed VSIs against different PF, different R/X ratios, different voltages at the sending bus and different directions of load increase through static simulations, no quantitative results were given regarding the accuracy of the algorithms in discriminating between stable scenarios and unstable scenarios. It ends with the conclusion that their proposed index seems to be a more proper index than the other reviewed line stability index. The obvious drawback of this indicator is that it gives an indication of the instability occurrence. In [8], 6 voltage instability indices have been reviewed by giving their accuracy, machine learning (ML) algorithm, and test system; again, without any implementation of the reviewed VSIs. It ends with the advice that future research work should be applied to large scale networks, as well. In [9], 59 papers where ML techniques have been employed in online detecting the voltage stability status of power systems have been reviewed by explaining their methods, inputs, outputs, and test systems used, without any implementation of the reviewed algorithms. It concludes with this general recommendation that although the implementation of ML techniques in online voltage stability assessment reduces the possibility of blackouts, there is still a need to improve these techniques to become more compatible with online applications. In [10], 66 voltage instability indices have been reviewed by giving their equations, critical values, and assumptions, but it does not deal with the implementation of the reviewed VSIs. One of the primary challenges in real-time voltage stability assessment tools that rely on measured variables is the timing of instability detection. In many cases, instability is detected too close to the actual event, leaving insufficient time for effective mitigation. Methods based on continuous load flow calculations face additional limitations, such as a low rate of correctly identifying stable conditions and reduced operator sensitivity when distinguishing between actual unstable conditions and stable conditions that are incorrectly classified as unstable. Furthermore, the reliance on network simulation results—rather than measured variables—for voltage instability detection introduces inaccuracies in control models of network equipment, which is another significant drawback of existing methods. In this paper, these challenges are addressed by leveraging ML capabilities and utilizing measured data from network equipment. This approach enables the accurate prediction of both stable and unstable network conditions within a short time frame after each disturbance. By combining advanced ML techniques with real-time data, we overcome the limitations of traditional methods, providing a more reliable and timely solution for voltage stability assessment. Furthermore, this paper emphasizes the need for more precise stability indices in voltage stability assessment. While existing review articles have made valuable contributions, ongoing research continues to focus on developing advanced algorithms that can be effectively implemented in control room environments. These efforts aim to push the boundaries of current methodologies and deliver practical, real-time solutions for voltage stability monitoring and control, addressing the gaps in existing approaches.

  • ii.

    Although the topic of this review part is not related to the work of this paper, but for the completeness of the voltage stability content review, this part is included, the second question arises whenever the answer to the first one is that the system is in imminent occurrence of voltage instability. In this situation, the operator needs to recognize how close the system is to the time of instability occurrence. Unlike voltage stability assessment algorithms, time to instability prediction algorithms has not received as much focus in voltage stability research [19–24]. In [19], the probability distribution function of the time to instability with a large computational burden has been proposed for uncertain but known load consumption. In [20], for an operating point close to a bifurcation point, a proximity to instability indices has been measured when the stochastic fluctuations of loads are taken into account. Virtual acceleration procedures were presented in [21, 22] to accelerate simulation time and forecast the occurrence of voltage instability. Despite their reasonable accuracy, none of these algorithms fall into the just after disturbance (JAD) category. In [23, 24], voltage instability inception time is estimated using the JAD approach and a k-nearest neighbor learning algorithm.

  • iii.

    The final question is addressed by developing and implementing real-time emergency voltage stability controls to prevent a power system from collapsing due to imminent voltage instability [25, 26]. The emergency controls may involve: reactive shunt element switching and generation rescheduling [27–30], modified control of on-load tap changer (OLTC) [31–34], and as a last resort, load shedding [35–37]. When considering the implementation cost on consumers and the network, as well as feasibility in terms of time and efficiency, the control of OLTC receives more attention in cases where instability is caused by load restoration. Emergency LTC control measures such as tap blocking, voltage set point reduction, lowering the reference voltage, adjusting the dead band of the distribution side voltage, and tap reversing are commonly used to mitigate voltage instability. In [31], a decentralized approach of tap changer blocking and load shedding to counter voltage instability is suggested. Although the results indicate the effectiveness of this method in maintaining stability, the selectivity of the approach has not been thoroughly investigated. In [32], a centralized scheme is proposed to prevent voltage instability by blocking OLTCs. However, limitations of this scheme include the need for remote access to each individual tap mechanism, detecting instability near occurrence, and not guaranteeing voltage stability.

Through an analysis of the strengths and limitations of prior research in this domain, it is apparent that voltage stability represents a complex and multifaceted issue shaped by a wide array of influencing factors. While the concept has been explored since 1985, researchers continue to investigate fundamental challenges, such as the accurate identification of stability status. These ongoing efforts seek to capitalize on advancements in computational sciences and monitoring technologies to develop more robust and practical tools, thereby enhancing the operational intelligence and reliability of power systems.

In this paper, a simple platform for voltage stability status prediction and voltage instability prevention (VIP) based on selective OLTCs blocking is proposed, which can be used as an Early Enough Instability Status Assessment unit in situational awareness platforms in control rooms. The main motivations for this work are:
  • •

    Developing a novel data driven model for voltage stability status prediction with overall accuracy over 97% and instability mitigation with a guarantee of preventing voltage instability events caused by load restoration.

  • •

    Providing the voltage stability assessment results just one second after the disturbance.

  • •

    Developing a simple mathematical morphology (MM)-based module for voltage instability mitigation (VIM) in a local manner.

  • •

    Achieving an acceptable index for selectivity by identifying OLTCs contributes to instability and sending block signal to them.

The rest of this paper is organized as follows. Proposed methodology is given in Section 2, and the simulation, Results, and Discussion are reported in Section 3. The paper concludes in Section 4, and further work is given in Section 5.

2. Proposed Methodology

The main idea of this study is that by utilizing raw data on the contributions of generators, loads, and transmission lines to instability, deep learning (DL) algorithms can identify patterns in stability status. This prediction of future stability status is crucial for making decisions regarding OLTCs and preventing instability by addressing load restoration. The implementation of the proposed model for detecting voltage stability status and mitigating instability is illustrated in Figure 1. The proposed platform consists of three parts: the Disturbance Detection (DD) module, the VIP module, and the VIM module. The roles of each module are given as follows.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Proposed data driven model for voltage stability prediction and voltage instability mitigation.

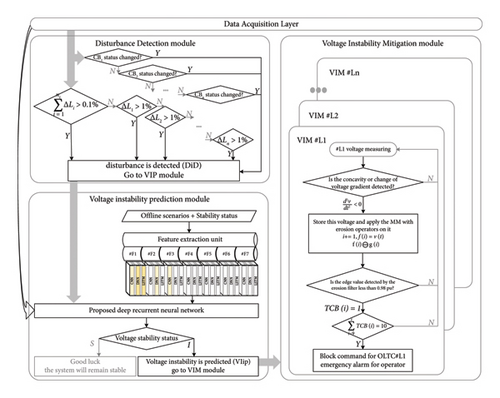
2.1. DD Module

The DD module monitors the statuses of all circuit breakers and all load demands and detects the disturbance:
  • -

    If there is a change in the state of any of the circuit breakers, or

  • -

    If the demand on a load bus increases by at least 1% (ΔLi > 1%), or

  • -

    If the total network load increases by 0.1% ()

This module utilizes statuses of circuit breakers and the current and voltage magnitude data of each load obtained from Phasor Measurement Units (PMUs) installed on load buses.

2.2. VIP Module

VIP module is activated when the DD module identifies any disturbances. It is important to note that there is no distinction among the various types of disturbances. VIP module consists of two preliminary unit:
  • 1.

    The Off-line training unit provides a dataset of time-domain simulation results for DL techniques. The output of this unit is the stability status, while the input consists of a feature set extracted directly from variables measured by PMUs on different buses within a second after the load disturbance. When using ML systems, selecting appropriate features is crucial for successful performance. In the context of voltage instability detection, factors such as the availability of required variables, their impact on instability occurrence, and their operational time need to be considered. For example, the slow response of OLTCs to transformers plays a critical role in stability, and while the tap position of transformers is an available variable, its time constant for the initial operation is approximately 30 s. Monitoring this variable immediately after a disturbance may not be useful due to the long waiting time involved.

  •  

    In this study, seven sets of raw variables are created (feature detentions are given is annex):

    • •

      Characteristics related to the generators include generated active power, reactive power, excitation current, and terminal voltage magnitude (#F1).

    • •

      Characteristics related to the loads include bus voltage magnitudes, reactive and active power consumption of loads (#F2).

    • •

      Characteristics related to the lines include voltage magnitudes and reactive and active power at sending/receiving buses of transmission lines (#F3).

    • •

      Characteristics related to the generators and loads (#F4).

    • •

      Characteristics related to the generators and lines (#F5).

    • •

      Characteristics related to the loads and lines (#F6).

    • •

      Characteristics related to the generators, loads, and lines (#F7).

  •  

    The learning algorithms utilized in this study to classify the network’s stability state are Convolutional Neural Network (CNN), Deep NN (DNN), and Long Short-Term Memory (LSTM) as the well-known classes of NNs used for future prediction problems.

    • i.

      A CNN is a specialized kind of NN for processing data that has a known grid-like topology. The operation of a CNN block is summarized by [38]:

      ()

    •  

      Here,

      • -

        x is the input data and ∗ means covolutin operation

      • -

        b and w, are respectively biases, and the convolutional kernel (filter)

      • -

        f( ) is the activation function

    • ii.

      A DNN is a type of NN architecture that consists of multiple layers of nodes, commonly known as hidden layers. The operation of a DNN block is summarized by [38]:

      ()

    •  

      Here,

      • -

        xi is the input from input layer or the output from the previous hidden layer

      • -

        ∗ means convolution operation

      • -

        bi, wi are respectively bias of hidden neuron i, and the weight of the connection from input neuron xi to hidden neuron ith

      • -

        f( ) is the activation function

    • iii.

      LSTM is a type of Recurrent NN (RNN) that is capable of learning long-term dependencies between data points in a sequence. The operation of an LSTM block at a time t is summarized by [38]:

      ()

    •  

      Here,

      • -

        f(t) is the activation vector of the forget gate at time step t

      • -

        σ is the sigmoid activation function

      • -

        bf, Uf, Wf are respectively biases, input weights, and recurrent weights for the forget gates

      • -

        x(t) is the current input vector and h(t) is the current hidden layer vector, containing the outputs of all the LSTM cells at time step t

      • -

        s(t) is the state unit at time step t

      • -

        b, U and W respectively denote the biases, input weights, and recurrent weights into the LSTM cell

      • -

        g(t) is the external input gate at time step t

      • -

        bg, Ug, Wg are respectively biases, input weights, and recurrent weights for the external input gates

      • -

        h(t) is the hidden state at time step t

      • -

        q(t) is the output gate at time step t

      • -

        bo, Uo, Wo are respectively biases, input weights, and recurrent weights for the output gates

  •  

    Detailed information about the networks’ architecture, is given in the annex.

  • 2.

    Real-time measurements are applied to the trained network to determine the future stability status of the network. The performance of the proposed VIP module is evaluated based on the following statistical metrics:

    • -

      Precision measures the accuracy of the positive predictions (i.e., the proportion of predicted unstable cases that are actually unstable).

      ()

    •  

      Where TP means the actual Unstable states which correctly predicts as Unstable states. FP means the actual Stable states which incorrectly predicts as Unstable states.

    • -

      Recall (Reliability) measures the ability of the model to correctly identify all unstable cases (i.e., the proportion of actual unstable cases that are correctly predicted as unstable).

      ()

    •  

      Where FN means the actual Unstable states which incorrectly predicts as Stable states.

    • -

      Specificity (Selectivity) measures the ability of the model to correctly identify stable cases (i.e., the proportion of actual stable cases that are correctly predicted as stable).

      ()

    •  

      Where TN means the actual Stable states which correctly predicts as Stable states.

    • -

      The False Positive Rate (FPR) measures the proportion of stable cases incorrectly predicted as unstable.

      ()

    • -

      The False Negative Rate (FNR) measures the proportion of unstable cases incorrectly predicted as stable.

      ()

    • -

      Accuracy measures the overall correctness of the model (i.e., the proportion of correctly predicted stable and unstable cases out of all cases).

      ()

2.3. VIM Module

Most power system loads are voltage-dependent, meaning that a system voltage drop following a disturbance results in reduced load demand, potentially easing stress on the system and preventing instability. However, the operation of OLTCs to address instability may restore load voltages to their rated values, increasing stress on the system. Therefore, smart management to predict the operation of these equipment and then evaluate their impact on voltage stability status is crucial to improve operational conditions, both in normal and abnormal situations.

The proposed VIM module focuses on OLTCs operation prediction and selecting the effective tap changers to block in order to prevent instability. This module is activated upon receiving an instability detection message from the VIP module. The VIM module identifies transformers where tap changer operation leads to instability utilizing local voltage information on the secondary side of the transformers within a one-second information window, in each window, the algorithm identifies the concavity point and stores this point and the applies the MM with erosion and dilation operators on it as follows:
()
Here,
  • -

    v(t) is the load voltage magnitude at t

  • -

    f(i) and g(i) are the input signal and structuring element, respectively

  • -

    ⊕ and ⊖ are the dilation and erosion operators, respectively

  • -

    τ is the time shift

  • -

    max and min are the maximum and minimum operators, respectively

MM is a time-domain processing tool that focuses on the form, shape, and size of a signal waveform in the time domain. A flat Structural Element (SE) with a length of 3, SE = [0, 0, 0], is selected. If the edge value detected by the erosion filter is below 0.98 pu (the lower limit of the tap changers’ dead band), the Tap Changer Block (TCB) variable is set to one, and the difference between the dilation and erosion values is recorded. If the sum of the TCB variable over 10 consecutive windows (approximately 10 s) reaches 10, a blocking command is issued to the tap changer.
()

Given the approximate 30 s time delay for the initial operation of tap changers, there is sufficient time to make a reliable decision and implement a blocking command. Alongside the ability to execute the algorithm locally, central monitoring allows for assessing the emergency tool’s performance at each substation from the control center. By receiving data from PMUs in the control center, operators can rank the loads contributing to instability based on their involvement in the first ten-second time window following an event.

3. Simulation, Results, and Discussion

The proposed algorithm for predicting stability assessment and mitigating instability was applied to the Nordic32 test system as shown in Figure 2. This test system which is similar to the Swedish and Nordic power systems comprises 74 buses, 52 lines (including 30 double-circuit lines), 20 generators (incorporating all Online Exciter Limiters (OELs), Automatic Voltage Regulators (AVRs), Power System Stabilizers (PSSs), and governors), and 22 loads at distribution levels (all load transformers are equipped with OLTCs, the details of modeling is given in the annex). The Nordic32 system is introduced in PES-TR19 as a test system for voltage stability analysis [39].

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
One-line diagram of the Nordic32 test system [39].

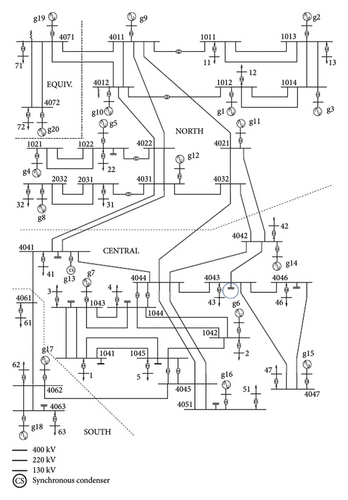
In this work, operational scenarios were developed by modifying loading conditions, both individually and collectively, relative to the base operating point. Changes in generation were implemented in two ways: (i) uniform increases across nonslack power plants and (ii) random increases across power plants. A key consideration in constructing these operating points was to ensure that simulations began from a stable operating condition by applying appropriate adjustments to the tap changer controller settings.

Additionally, 389 load disturbance scenarios were generated through time-domain simulations, comprising 219 scenarios representing long-term voltage instability cases and 170 scenarios representing long-term voltage stability cases. These scenarios encompassed 22 distinct classes of load disturbances. The disturbances were examined in two forms: (i) individual load increases and (ii) load increases across multiple regions. These diverse scenarios were designed to thoroughly evaluate the system’s robustness under a wide range of operational conditions.

3.1. Simulation and Computation Tools

Time domain simulation is performed by DIgSILENT software, which can model the dynamic behavior of the power system. Developing voltage stability prediction algorithms based on deep RNNs is done through Python and run on Google Collaboratory. Implementation of local VIM by utilizing MM is carried out in MATLAB.

3.2. VIP Module

In this section, the results of utilizing the proposed VIP module are investigated for three types of DL networks.

Detailed information about the networks’ architecture, including the number of layers, types of layers, number of neurons, activation functions, dropout rates, and batch normalization can be found in Tables A1, A2, A3 in the annex. In this work, 80% of the data has been used for training models and the remaining 20% for testing models, Adam’s optimization function and categorical_crossentropy loss function have been used to train networks and the learning rate in all models under training is equal to 0.02.

The performance of the proposed DL networks are evaluated using seven categories of feature sets with different dimensions as follows: (F1) characteristics related to the generators are 80, (F2) characteristics related to the loads are 66, (F3) characteristics related to the lines are 312, (F4) characteristics related to the generators and loads are 146 (F5) characteristics related to the generators and lines are 392, (F6) characteristics related to the loads and lines are 377, and (F7) characteristics related to the generators, loads, and lines are 438. The results are presented in Tables 1, 2, 3, 4 and analyzed below based on the evaluation metrics included confusion matrix, precision, recall, specificity, FPR, FNR, and accuracy.

Table 1. Confusion table of employing proposed three DL networks for seven categories of features extracted at the first second after disturbance.
Feature type Actual state CNN DNN LSTM
Predicted unstable Predicted stable Predicted unstable Predicted stable Predicted unstable Predicted stable
F1 Unstable 219 0 215 4 219 0
Stable 6 164 0 170 13 158
  
F2 Unstable 215 4 219 0 215 4
Stable 7 163 12 158 7 163
  
F3 Unstable 210.24 8.103 210 9 214.62 4.38
Stable 7 163 7 163 39 141
  
F4 Unstable 211 8 211 8 215 4
Stable 14 156 14 156 6 164
  
F5 Unstable 219 0 211 8 215 4
Stable 6 164 7 163 13 157
  
F6 Unstable 215 4 200 19 219 0
Stable 13 157 0 170 37 133
  
F7 Unstable 219 0 208 12 215 4
Stable 19 151 7 163 29 141
Table 2. Prediction results of employing proposed CNN network for seven categories of features extracted at the first second after disturbance.
Feature type Precision (%) Recall (%) Specificity (%) FPR (%) FNR (%) Accuracy (%)
F1 97.3 100.0 96.5 3.5 0.0 98.5
F2 96.8 98.2 95.9 4.1 1.8 97.2
F3 96.8 96.3 95.9 4.1 3.7 96.1
F4 93.8 96.3 91.8 8.2 3.7 94.3
F5 97.3 100.0 96.5 3.5 0.0 98.5
F6 94.3 98.2 92.4 7.6 1.8 95.6
F7 92.0 100.0 88.8 11.2 0.0 95.1
Table 3. Prediction results of employing proposed DNN network for seven categories of features extracted at the first second after disturbance.
Feature type Precision (%) Recall (%) Specificity (%) FPR (%) FNR (%) Accuracy (%)
F1 100.0 98.2 100.0 0.0 1.8 99.0
F2 94.8 100.0 92.9 7.1 0.0 96.9
F3 96.8 95.9 95.9 4.1 4.1 95.9
F4 93.8 96.3 91.8 8.2 3.7 94.3
F5 96.8 96.3 95.9 4.1 3.7 96.1
F6 100.0 91.3 100.0 0.0 8.7 95.1
F7 96.7 94.5 95.9 4.1 5.5 95.1
Table 4. Prediction results of employing proposed LSTM network for seven categories of features extracted at the first second after disturbance.
Feature type Precision (%) Recall (%) Specificity (%) FPR (%) FNR (%) Accuracy (%)
F1 94.4 100.0 92.4 7.6 0.0 96.7
F2 96.8 98.2 95.9 4.1 1.8 97.2
F3 84.6 98.0 78.3 21.7 2.0 89.1
F4 97.3 98.2 96.5 3.5 1.8 97.4
F5 94.3 98.2 92.4 7.6 1.8 95.6
F6 85.5 100.0 78.2 21.8 0.0 90.5
F7 88.1 98.2 82.9 17.1 1.8 91.5
The confusion matrices in Table 1 provide a detailed breakdown of the predictions made by the three DL networks for each feature set. Key observations include:
  • i.

    CNN: Achieved perfect prediction for unstable cases in feature sets F1, F5, and F7, with 100% accuracy for VIP. However, it exhibited minor misclassifications in stable cases, particularly for feature sets F4 and F7.

  • ii.

    DNN: Demonstrated strong performance across multiple feature sets. It achieved 100% precision and specificity for feature sets F1 and F6, along with perfect prediction for unstable cases in feature set F2.

  • iii.

    LSTM: Delivered robust performance for feature sets F1, F2, and F4, achieving high recall (98.2%–100%) and specificity (92.4%–96.5%). However, its performance varied significantly for other feature sets, particularly F3 and F6, where specificity dropped considerably.

To achieve better accuracy in predicting voltage stability status, this study investigated the effect of DL networks and compared the performance of solo and combined feature sets. The performance metrics for each DL network (CNN, DNN, and LSTM) are summarized in Tables 2, 3, 4. The results reveal the following key findings:
  • i.

    Solo feature sets F1 and F2 consistently outperformed other feature sets, including F7, in terms of accuracy, recall, and specificity, making them the most reliable choices for voltage stability prediction.

  • ii.

    Feature sets F1 and F5 consistently yielded the best results across all networks, suggesting their effectiveness for voltage stability prediction, while feature sets F3 and F6 posed challenges, particularly for LSTM, due to higher FPR and FNR.

  • iii.

    For applications that prioritize the detection of unstable cases, feature sets F1, F5, and F7 are the most effective, with the best performances achieved by F1 in CNN (100% recall and 98.5% accuracy) and F1 in LSTM (100% recall and 96.7% accuracy).

  • iv.

    For achieving balanced performance with high recall and specificity, feature sets F2 and F4 are recommended, with the best performance demonstrated by F2 in DNN (100% precision, 98.2% recall, and 99.0% accuracy).

  • v.

    CNN and DNN outperformed LSTM in terms of accuracy and robustness across most feature sets, with CNN achieving the highest accuracy (98.5%) for feature sets F1 and F5, and DNN achieving the highest precision and specificity for feature sets F1 and F6.

  • vi.

    CNN excelled in recall and accuracy, making it suitable for applications where minimizing false negatives is critical; DNN demonstrated high precision and specificity, making it ideal for scenarios where false positives must be minimized; and LSTM showed potential for certain feature sets (e.g., F1, F2, F4) but struggled with others, indicating limitations in handling complex or noisy data.

The results demonstrate the robustness of the proposed DL networks under diverse operational scenarios. CNN and DNN consistently delivered reliable predictions, even for challenging feature sets, while LSTM showed variability in performance. This highlights the importance of selecting appropriate feature sets and network architectures for voltage stability prediction tasks.

3.3. VIM Results

In this section, the results of employing the proposed emergency tool to effectively manage the performance of OLTCs within the Nordic32 network are presented and compared with outcomes of the traditional method of blocking all tap changer transformers. Disturbances in this work are categorized as follows:
  • i.

    Disturbances in which the network’s stability status remains unaffected by load restoration, resulting in a stable final system status. In these scenarios, whether all OLTCs are active or if some or all of them are blocked, network stability is maintained. Both the proposed method and the general approach of blocking all OLTCs yield the same stable outcome in these situations. The disturbances falling into this category are outlined in Table 5.

  •  

    If there is a failure in the telecommunication system and the loss of the VIP-message, the stability status remains unaffected, and depending on the severity of the disturbance, the load restoration at various substations may be delayed.

  • ii.

    Disturbances in which the network’s stability status relies on load restoration and the operation of OLTCs. In such disturbances, the normal operation of OLTCs leads to long-term instability, whereas sending block commands to all OLTCs or intelligently blocking the OLTCs involved in instability based on the proposed algorithm ensures long-term stability. The success rate of the proposed algorithm in preventing instability is evaluated by comparing it with the all OLTCs blocking algorithm for disturbances in this category, as detailed in Table 6. The table indicates that the proposed algorithm’s reliability in preventing instability is on par with the all OLTCs blocking method, with both achieving a success rate of 100%.

  • iii.

    Disturbances in which the network’s stability status remains unaffected by load restoration, resulting in system instability. In these scenarios, irrespective of OLTC performance, the power system loses its stable state and becomes unstable. This indicates that the network experiences instability regardless of whether all OLTCs are active or blocked. Also, even blocking the OLTCs will not delay the instability time. An investigation into the type of instability in these disturbances reveals they are related to short-term voltage instability and transient stability.

Table 5. Incidents leading to stability in different conditions for the use of tap changers of Nordic32 test network load transformers.
Load ΔL < (%) With all OLTCs Blocking all OLTCs Blocking effective OLTCs (proposed)
Load1 25 Stable Stable Stable
Load11 200 Stable Stable Stable
Load12 200 Stable Stable Stable
Load13 200 Stable Stable Stable
Load2 53 Stable Stable Stable
Load22 200 Stable Stable Stable
Load3 61 Stable Stable Stable
Load31 200 Stable Stable Stable
Load32 200 Stable Stable Stable
Load4 26 Stable Stable Stable
Load41 52 Stable Stable Stable
Load42 62 Stable Stable Stable
Load43 27 Stable Stable Stable
Load46 45 Stable Stable Stable
Load47 200 Stable Stable Stable
Load5 29 Stable Stable Stable
Load51 26 Stable Stable Stable
Load61 55 Stable Stable Stable
Load62 100 Stable Stable Stable
Load 63 52 Stable Stable Stable
Load71 200 Stable Stable Stable
Load72 200 Stable Stable Stable
Table 6. Incidents leading to instability in load transformer tap changer operating conditions and stability in load transformer tap changer blocking conditions on the Nordic32 test network.
Load ΔL ≥ (%) ΔL ≤ (%) With all OLTCs Blocking all OLTCs Blocking effective OLTCs (proposed)
Load1 25 50 Unstable Stable Stable
Load2 53 61 Unstable Stable Stable
Load3 61 125 Unstable Stable Stable
Load4 26 63 Unstable Stable Stable
Load41 52 102 Unstable Stable Stable
Load42 62 140 Unstable Stable Stable
Load43 27 64 Unstable Stable Stable
Load46 45 90 Unstable Stable Stable
Load5 29 70 Unstable Stable Stable
Load51 26 71 Unstable Stable Stable
Load61 55 124 Unstable Stable Stable
Load62 100 200 Unstable Stable Stable
Load 63 52 100 Unstable Stable Stable

3.4. Reliability Index and Selectivity of the Proposed Algorithm

  • i.

    The reliability index of the proposed VIM module in identifying OLTCs that influence instability can be evaluated by comparing the network’s stability state when blocking all OLTCs. As shown in Tables 4 and 5, the performance of the proposed algorithm in preventing instability was found to be comparable to the method of blocking all OLTCs (representing the maximum capability of OLTCs in mitigating instability) across all scenarios examined. Therefore, the proposed algorithm demonstrates a high level of reliability in its performance.

  • ii.

    The selectivity index of the proposed VIM module is assessed by determining the necessity of sending a block signal to each identified OLTC, contributing to instability. Table 7 presents a list of transformers that received the blocking command for OLTC operation in 20 critical disturbance cases. Unlike the method of blocking all OLTCs, where every OLTC is blocked, the proposed algorithm adjusts the number of blocking commands based on the type and impact of each disturbance. For instance, in certain events such as the second row in Table 7, blocking only one transformer (L2) can effectively prevent instability.

The selectivity evaluation involves removing the block command from transformers with minimal contribution to instability. Results indicate that in new decision-making condition, the system’s stability status transitions from stable (when OLTCs identified as instability causes are blocked, as per Table 7) to unstable.

Table 7. A comparison of performance indicators of two tap changer blocking methods for load transformers at the instability limit.
  ΔL (%) No. of OLTCs with blocking command List of OLTCs with blocking command
Blocking all OLTCs Proposed method
Load1 50 All 22 OLTCs 9 {‘Load1,’ ‘Load3,’ ‘Load5,’ ‘Load4,’ ‘Load51,’ ‘Load42,’ ‘Load43,’ ‘Load46,’ ‘Load47′}
Load2 61 1 {Load2}
Load3 125 10 {‘Load3,’ ‘Load1,’ ‘Load5,’ ‘Load4,’ ‘Load42,’ ‘Load51,’ ‘Load43,’ ‘Load46,’ ‘Load41,’ ‘Load22’}
Load4 63 15 {‘Load4,’ ‘Load3,’ ‘Load1,’ ‘Load5,’ ‘Load42,’ ‘Load43,’ ‘Load41,’ ‘Load31,’ ‘Load51,’ ‘Load46,’ ‘Load22,’ ‘Load47,’ ‘Load61,’ ‘Load11,’ ‘Load12’}
Load41 102 16 {‘Load41,’ ‘Load31,’ ‘Load22,’ ‘Load42,’ ‘Load61,’ ‘Load4,’ ‘Load5,’ ‘Load3,’ ‘Load1,’ ‘Load11,’ ‘Load43,’ ‘Load46,’ ‘Load47,’ ‘Load12,’ ‘Load51,’ ‘Load32’}
Load42 140 15 {‘Load42,’ ‘Load22,’ ‘Load31,’ ‘Load4,’ ‘Load41,’ ‘Load5,’ ‘Load43,’ ‘Load46,’ ‘Load1,’ ‘Load3,’ ‘Load47,’ ‘Load11,’ ‘Load51,’ ‘Load61,’ ‘Load12’}
Load43 64 16 {‘Load43,’ ‘Load42,’ ‘Load46,’ ‘Load47,’ ‘Load4,’ ‘Load31,’ ‘Load22,’ ‘Load41,’ ‘Load1,’ ‘Load3,’ ‘Load5,’ ‘Load51,’ ‘Load61,’ ‘Load11,’ ‘Load12,’ ‘Load32’}
Load46 90 16 {‘Load43,’ ‘Load42,’ ‘Load46,’ ‘Load47,’ ‘Load4,’ ‘Load31,’ ‘Load22,’ ‘Load41,’ ‘Load1,’ ‘Load3,’ ‘Load5,’ ‘Load51,’ ‘Load61,’ ‘Load11,’ ‘Load12,’ ‘Load32’}
Load5 70 16 {‘Load5,’ ‘Load1,’ ‘Load3,’ ‘Load4,’ ‘Load42,’ ‘Load51,’ ‘Load43,’ ‘Load41,’ ‘Load46,’ ‘Load22,’ ‘Load61,’ ‘Load31,’ ‘Load47,’ ‘Load2,’ ‘Load11,’ ‘Load62’}
Load51 71 18 {‘Load51,’ ‘Load5,’ ‘Load1,’ ‘Load3,’ ‘Load4,’ ‘Load42,’ ‘Load43,’ ‘Load41,’ ‘Load46,’ ‘Load31,’ ‘Load47,’ ‘Load22,’ ‘Load61,’ ‘Load2,’ ‘Load62,’ ‘Load11,’ ‘Load12,’ ‘Load32’}
Load61 124 18 {‘Load61,’ ‘Load41,’ ‘Load31,’ ‘Load22,’ ‘Load62,’ ‘Load42,’ ‘Load4,’ ‘Load5,’ ‘Load1,’ ‘Load3,’ ‘Load43,’ ‘Load11,’ ‘Load46,’ ‘Load63,’ ‘Load47,’ ‘Load51,’ ‘Load12,’ ‘Load32’}
Load62 200 19 {‘Load62,’ ‘Load61,’ ‘Load22,’ ‘Load31,’ ‘Load41,’ ‘Load42,’ ‘Load4,’ ‘Load5,’ ‘Load1,’ ‘Load3,’ ‘Load43,’ ‘Load11,’ ‘Load46,’ ‘Load63,’ ‘Load47,’ ‘Load51,’ ‘Load12,’ ‘Load32,’ ‘Load13’}
Load 63 100 19 {‘Load63,’ ‘Load31,’ ‘Load22,’ ‘Load41,’ ‘Load61,’ ‘Load42,’ ‘Load62,’ ‘Load4,’ ‘Load5,’ ‘Load3,’ ‘Load1,’ ‘Load43,’ ‘Load46,’ ‘Load11,’ ‘Load47,’ ‘Load51,’ ‘Load12,’ ‘Load32,’ ‘Load13’}

An illustrative example of this evaluation is presented for disturbances related to load L2 in the second row of Table 7, showcasing the sensitivity index of the proposed algorithm without the need for simulation.

For a disturbance magnitude of ΔL3 = 120%, voltage profiles of significant loads during instability are depicted in the following figures:
  • 1.

    In the first scenario (Figure 3), no emergency actions are taken, resulting in instability.

  • 2.

    In the second scenario (Figure 4), all OLTCs are blocked, leading to system stability.

  • 3.

    The third scenario implements the proposed VIM algorithm, where only identified OLTCs contributing to instability are blocked (Figure 5), resulting in stability.

  • 4.

    In the last scenario, all effective OLTCs according to the proposed VIM algorithm are blocked except for the OLTC of load 22 (the least effective load in the list of effective loads for this disturbance). As shown in Figure 6, the stability status of this scenario shifts to instability, but the time to instability is delayed compared to the first scenario.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Voltage profiles of loads influencing instability and tap changer performance for a 120% increase in load L3 (ΔL3 = 120%), all tap changers active-final state is instability.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Voltage profiles of loads influencing instability for a 120% increase in load L3 (ΔL3 = 120%), all tap changers are blocked-final state is stability.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Voltage profiles of loads influencing instability and tap changer performance for a 120% increase in load L3 (ΔL3 = 120%), effective tap changers are blocked and noneffective tap changers are active (proposed method)-final state is stability.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Voltage profiles of loads influencing instability and tap changer performance for a 120% increase in load L3 (Δ;L = 120%), all effective tap changers are blocked except load 22-final state is instability.

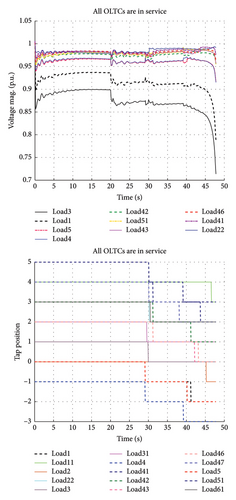
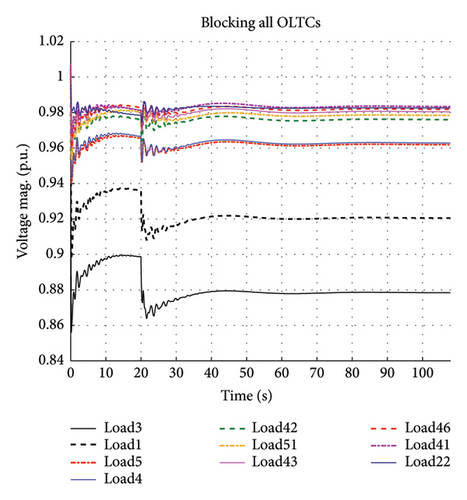
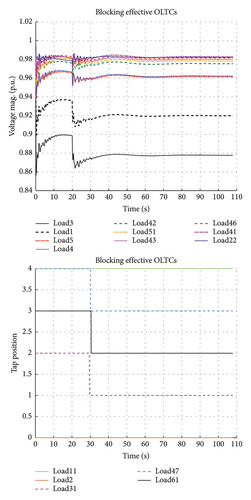
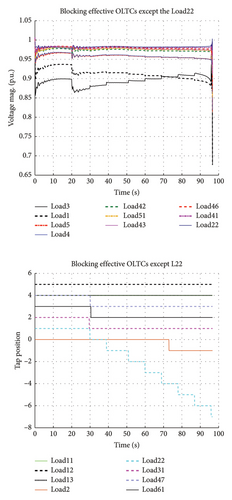
Through these scenarios, the selectivity index of the proposed algorithm is confirmed.

3.5. Computation Time

Computation time is a critical factor in real-time applications, as it directly impacts the practicality of deploying ML models. The execution time of a program depends on several factors, including:
  • •

    CPU clock speed and the instruction set architecture.

  • •

    The number of processes running concurrently on the system.

  • •

    Memory I/O access times.

  • •

    Network I/O access times (where applicable).

In this study, all experiments were conducted on a single-core virtual server equipped with hyper-threaded Xeon processors operating at 2.3 GHz and 12.7 GB of RAM. This setup was chosen to simulate realistic computational constraints and evaluate the efficiency of the proposed models.

To provide a comprehensive analysis, we measured two key metrics for each model:
  • 1.

    CPU Time: The total time the program actively uses the CPU for processing.

  • 2.

    Wall Time: The actual elapsed time from the start to the end of the program execution, as measured by a clock.

Wall time includes delays caused by factors such as memory access, I/O operations, and context switching between processes, while CPU time reflects the actual computational workload. These metrics help assess the efficiency of the models and their suitability for real-time applications.

Tables 8, 9, 10 summarize the training and testing times for the DNN, CNN, and LSTM models across different feature sets. As shown, the CPU time for testing is consistently below 200 milliseconds, and the wall time is below 300 milliseconds for all models and feature sets. These results demonstrate the computational efficiency of the proposed models and their potential for deployment in real-time scenarios.

Table 8. CNN model computation times.
Feature type Training time (s) Testing time (s)
CPU time Wall time CPU time Wall time
F1 24.1 25.4 0.113 0.137
F2 33.9 37.4 0.133 0.161
F3 23 23.8 0.153 0.177
F4 35.3 38 0.133 0.17
F5 25.7 27.5 0.14 0.249
F6 31.7 35.4 0.137 0.167
F7 77 84 0.184 0.207
Table 9. DNN model computation times.
Feature type Training time (s) Testing time (s)
CPU time Wall time CPU time Wall time
F1 30 32.2 0.179 0.288
F2 32.4 33.5 0.155 0.179
F3 29.7 31 0.144 0.172
F4 32.5 33 0.149 0.176
F5 30.2 32.9 0.128 0.159
F6 31.7 32.5 0.137 0.178
F7 43.4 49.7 0.184 0.203
Table 10. LSTM model computation times.
Feature type Training time (s) Testing time (s)
CPU time Wall time CPU time Wall time
F1 42.7 46.6 0.14 0.18
F2 45.6 50.4 0.132 0.159
F3 42.1 46.2 0.14 0.181
F4 51.4 53.6 0.152 0.176
F5 44.2 46.9 0.143 0.173
F6 42.5 48.9 0.145 0.161
F7 73 88 0.187 0.27

4. Conclusion

This paper introduces a novel approach for predicting voltage stability and mitigating instability during load restoration. The VIP module uses real-time data, achieving over 97% accuracy within one second of a disturbance, suitable for online use. The VIM module employs real-time voltage data to prevent instability by blocking OLTCs locally, successfully mitigating all load restoration-related instability events with high selectivity.

5. Further Work

It is important to note that the proposed VIM module may not be sufficient to address non-long-term voltage instability in the third type of disturbances that are not influenced by OLTC performance. Stability in these cases of instability may only be achieved through appropriate load shedding schemes. Given the importance of this issue within stability discussions, many researchers have examined this field. Given the importance of this issue within stability discussions, many researchers have examined this field. A technical report by EPRI titled “Voltage Instability Load Shedding” has been published to develop a new control scheme to enhance the conventional under voltage load shedding (UVLS) in [40], an adaptive wide-area load shedding scheme has been presented in [41] to preserve PSS, and an emergency control strategy has been proposed in [42, 43] for UVLS to provide voltage stability are examples of highlighting the latest advancements in the area. Building on the existing work of others, further research could explore a novel scheme to mitigate this complicated type of instability.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funding was received for this research.

Appendix A

Feature Definition. To have a proper ML-based classifier, defining the proper inputs is one of the first steps. In this study, seven categories of inputs are defined.

Definition of Generator features:
()
Definition of Load features:
()
Definition of Line features:
()
Definition of Generator and Load features:
()
Definition of Generator and Line features:
()
Definition of Load and Line features:
()
Definition of Generator, Load and Line features:
()

Here, Pgi(t) and Pgi−pre are the pre- and postdisturbance value of active power of the ith generator at the end of window. Qgi(t) and Qgi−pre are the pre- and postdisturbance value of reactive power of the ith generator at the end of window. Ugi(t) and Ugi−pre are the pre- and postdisturbance value of terminal voltage magnitude of the ith generator at the end of window. igi(t) and igi−pre are the pre- and postdisturbance value of excitation current of the ith generator at the end of window. PLj(t) and PLj−pre are the pre- and postdisturbance value of active power of the jth load at the end of window. QLj(t) and QLj−pre are the pre- and postdisturbance value of reactive power of the jth load at the end of window. ULj(t) and ULj−pre are the pre- and postdisturbance value of bus voltage magnitude of the jth load at the end of window. Pse_z(t) and Pse_z−pre are the pre- and postdisturbance value of active power of the sending end of the zth line at the end of window. Pre_z(t) and Pre_z−pre are the pre- and postdisturbance value of active power of the receiving end of the zth line at the end of window. Qse_z(t) and Qse_z−pre are the pre- and postdisturbance value of reactive power of the sending end of the zth line at the end of window. Qre_z(t) and Qre_z−pre are the pre- and postdisturbance value of reactive power of the receiving end of the zth line at the end of window. Use_z(t) and Use_z−pre are the pre- and postdisturbance value of voltage magnitude of the sending end of the zth line at the end of window. Ure_z(t) and Ure_z−pre are the pre- and postdisturbance value of voltage magnitude of the receiving end of the zth line at the end of window. Ng, NLo, and NLi are the number of generators, loads, and lines, respectively.

DL Network Architecture. All parameters related to the proposed DL networks are given in the following tables.

Table A1. The proposed CNN network architecture.
Layer Number of filters Kernel size Activation function
1st hidden layer/Conv1D 256 2 Relu
2nd hidden layer/Conv1D 128 2 Relu
3rd hidden layer/MaxPooling1D — 2 —
4th hidden layer/Conv1D 32 2 Relu
5th hidden layer/flatten      
  
Layer Number of neurons Activation function Dropout Batch normalization
  
6th hidden layer/dense 64 Relu 0.2 ✓
7th hidden layer/dense 32 Relu 0.1 ✓
Output layer/dense 2 Softmax — ×
Batch size 32
Epoch 100
Table A2. The proposed DNN network architecture.
Layer Number of neurons Activation function Dropout Batch normalization
1st hidden layer/dense 250 Relu — ×
2nd hidden layer/dense 500 Relu 0.2 ✓
3rd hidden layer/dense 600 Relu 0.3 ✓
4th hidden layer/dense 140 Relu — ×
Output/layer dense 2 Softmax — ×
Batch size 32
Epoch 100
Table A3. The proposed LSTM network architecture.
Layer/type Number of neurons Activation function Dropout Batch normalization
1st hidden layer/LSTM 150 — 0.2 ✓
2nd hidden layer/LSTM 250 — 0.2 ✓
3rd hidden layer/LSTM 90 — — ×
4th hidden layer/dense 64 Relu 0.2 ×
5th hidden layer/dense 32 Relu — ✓
Output layer/dense 2 SoftMax — —
Batch size 32
Epoch 100

Hyperparameter Selection. Hyperparameters are crucial in designing ML models, as their proper tuning significantly impacts model performance. Unlike model parameters (e.g., weights in NNs), which are learned during training, hyperparameters are set prior to training.

However, there is no universal rule for selecting hyperparameters, as their optimal values depend on the specific problem, dataset, and model architecture. In this work, hyperparameters were initialized based on general recommendations, prior experience, and iterative trial-and-error methods.

OLTCs Modeling [37]. All OLTCs are modeled to monitor load voltage, work in the range of [0.88 1.2] and keep the voltage in the dead band [0.99 1.01] pu by using 33 tap positions with the step of 0.01 pu, via predefined time delays. When the load voltage leaves its dead band at time t0, the first tap change take place at time t0 + τ1 and the subsequent changes will be take place after t0 + τ1 + kτ2. The delay is reset to τ1 if the load voltage enter to the dead band. The values of τ1 and τ2 for all OLTCs are given in Table A4.

Table A4. OLTC delays [39].
Transformer Delays
τ1 τ2
11-1011 30 8
12-1012 30 9
13-1013 30 10
22-1022 30 11
1-1041 29 12
2-1042 29 8
3-1043 29 9
4-1044 29 10
5-1045 29 11
31-2031 29 12
32-2032 31 8
41-4041 31 9
42-4042 31 10
43-4043 31 11
46-4046 31 12
47-4047 30 8
51-4051 30 9
61-4061 30 10
62-4062 30 11
63-4063 30 12
71-4071 31 9
72-4072 31 11

Data Availability Statement

Data will be made available on request.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.