Optimal Multienergy Management for Networked Electricity–Hydrogen Hybrid Charging Stations: A Vehicle-Level Auction Approach
Abstract
Electricity and hydrogen have emerged as viable alternatives to traditional fossil fuels, playing a crucial role in clean and sustainable transportation solutions. The rapid growth of hydrogen vehicles (HVs) and electric vehicles (EVs) has significantly increased the demand for electricity–hydrogen hybrid charging stations (HCSs). Compared to the existing literature that predominantly focuses on optimal energy management from a system-level perspective, this paper explores power management in multiple HCSs and multienergy trading between HCSs and vehicles. In the proposed energy trading mechanism, the EVs and HVs are enabled to strategically submit their offer prices to maximize their utilities. Based on these prices, the aggregator allocates electricity and hydrogen and determines the final payments for the vehicles, aiming to maximize social welfare within the system, subject to the operational constraints of the HCSs. The theory of the Vickrey–Clarke–Groves (VCG) mechanism is employed to design the energy trading mechanism. Furthermore, we introduce the concept of information rents to address potential budget imbalances for the aggregator, enhancing the economic stability of the system. We also provide theoretical proofs for the properties of the proposed mechanism, which include truthfulness, individual rationality, and social welfare maximization. Simulation results demonstrate the effectiveness of the proposed mechanism and verify its three properties.
1. Introduction
In the burgeoning fields of sustainable transportation and energy systems, an electricity–hydrogen hybrid charging station (HCS) emerges as a pivotal innovation, synergizing the strengths of both electric vehicle (EV) charging and hydrogen vehicle (HV) fueling systems [1]. These stations not only demonstrate unparalleled versatility in accommodating a diverse array of clean energy vehicles but also optimize infrastructure utilization, enhancing the efficiency of energy resource deployment [2–4]. HCSs play a crucial role in enabling long-distance travel, addressing a critical bottleneck in the adoption of sustainable transportation solutions [5]. Moreover, their resilience to fluctuations in the electricity grid guarantees a steady and reliable refueling option, a vital component in boosting energy security and dependability [6].
Electricity–hydrogen HCSs are mostly equipped with renewable energy generation units, water electrolyzers, and hydrogen tanks [7]. By intelligently coordinating the distribution and storage of both electric and hydrogen energy, HCSs enhance the overall performance and reliability of multienergy supply [8]. There are a number of existing works focusing on the optimization of joint electricity–hydrogen management. For instance, an optimal scheduling model for hydrogen fueling stations is proposed in [9], where the stations serve the transportation sector and respond to the demand response signals issued by the electricity market. In [10], a real-time co-optimization scheme is proposed to coordinate the management of renewable generation, hydrogen fueling, and EV charging, with an aim to reduce network loss and increase EV comfort levels. In [11], optimal scheduling for a microgrid with hydrogen fueling stations is investigated, taking into account the uncertainty of renewable energy power, electrical loads, and hydrogen loads. The authors in reference [12] propose a coordinated planning methodology of an electricity–hydrogen–integrated energy system to reduce the carbon emissions of new energy and hydrogen equipment, considering the demands from both EVs and HVs. In [13], two-stage energy management for multiple hydrogen-based multienergy microgrids is studied with the consideration of electricity and hydrogen trading among subsystems.
Some related works emphasize the energy and information interaction between electricity systems and hydrogen systems from a multiplayer perspective. For example, a cooperative framework is proposed in [14] to manage the operation of wind turbines and hydrogen fueling stations, including their energy trading and benefit sharing in the cooperation. Furthermore, the cooperation between wind farms and hydrogen refueling is discussed in [15] with risk migration under the uncertainty of wind power and electricity prices. In [16], the influence of hydrogen energy service providers’ decisions on electricity prices is investigated, and hydrogen production and transportation are coordinated to minimize the providers’ costs. The multienergy trading of a hydrogen provider with renewable energy resources is studied in [17], where the provider can earn from both the electricity and hydrogen markets through flexible electricity–hydrogen conversion. Recently, some studies explored the carbon emission reduction potential in electricity-hydrogen coordination. In [18], joint planning of electricity and transportation systems is studied, considering energy demands from EVs and HVs and aiming to reduce the total carbon emission in both systems. An economic dispatch model for an electricity–hydrogen integrated system is proposed in [19], where the carbon equilibrium in the optimal dispatch decisions is explored. In [20], a price-based mechanism is developed to optimize the electricity–hydrogen operation for the goal of low-carbon and economic management in energy and transportation systems.
Electricity–hydrogen HCSs are energy refueling infrastructures specialized for EVs and HVs. Optimization of energy management in HCSs considering the temporal and spatial characteristics of vehicle refueling demands can enhance HCS operating efficiency, sustainability, and economy and also contribute to grid stability and wider adoption of clean transportation solutions. In [21], the optimal operation method for electricity–hydrogen HCSs is designed to reduce the usage costs of energy storage systems and increase their usage efficiency. In [22], the optimal sizing of a stand-alone microgrid is discussed, and the microgrid with renewable energy sources, energy storage, and hydrogen charging stations (CSs) can serve both EVs and HVs. In [23], electricity–hydrogen charging services are provided by a fully renewable multienergy microgrid, taking into account the charging time constraints of EVs and HVs in the optimal operation model of the microgrid. An off-grid electricity-hydrogen HCS powered by local solar photovoltaics (PVs) is considered in [24], and it discusses the major factors affecting the energy provision behavior of the HCS. Similarly, in [1], an off-grid electricity–hydrogen HCS operation under the uncertainty of solar energy, EV, and HV demands is studied. Some other related works concentrate on the interaction among multiple HCSs and the interaction between HCSs and other energy systems. For example, in [25], a two-stage optimization framework is developed for optimal energy management of multiple electricity–hydrogen HCSs, and electricity sharing among the HCSs is also considered. In [26], the multilateral multienergy trading among HCSs is explored, and the hydrogen–electricity transaction framework is proposed, incorporating the traffic flow of vehicles. In [27], a bilevel framework is proposed to describe the strategic interaction between an integrated energy system and an HCS, considering the uncertainty model of vehicles in the HCS. Similarly, a bilevel interactive framework for a distribution system operator and multiple HCSs is proposed in [28] along with the cooperative game among the HCSs in the lower level.
- •
We develop a multienergy trading mechanism that allows EVs and HVs to individually make price decisions. The aggregator serves as an auctioneer maximizing the sum of the utilities of all players in the system, achieving the value maximization of the sold electricity and hydrogen.
- •
We adopt the payment rule based on the Vickrey–Clarke–Groves (VCG) mechanism, which incentivizes EVs and HVs to truthfully report their prices. This guarantees the truthfulness of the vehicle information in the system, enabling the maximization of the true value of energy.
- •
We theoretically prove the properties of the proposed mechanism, namely, truthfulness, individual rationality, and social welfare maximization (SWM). Simulation results are presented to verify the properties. In addition, we define the information rents to eliminate the budget imbalance of the aggregator. The information rents are paid by the PV and hydrogen storage (HS) systems in the HCSs.
The rest of this paper is organized as follows. The system model is presented in Section 2. The electricity–hydrogen trading mechanism is designed in Section 3. The simulation results are demonstrated and discussed in Section 4. Finally, we conclude this paper in Section 5.
2. System Model
2.1. System Description
- •
Energy seller: The aggregator sells power and hydrogen to EVs and HVs, respectively. The goal of the aggregator is to maximize the social welfare, i.e., the sum of utilities of all players, by optimizing the operation of the electricity–hydrogen HCSs and making optimal decisions on energy allocation and payments for the vehicles. According to the theory of mechanism design [30, 31], we consider that the aggregator maximizes the social welfare rather than its own utility.
- •
Energy buyers: In the HCSs, EVs and HVs buy power and hydrogen, respectively. This paper considers that all vehicles take part in the same energy trading mechanism, although they are parked at different HCSs. The EVs and HVs submit their offer prices to the aggregator, who then determines the energy trading results of the vehicles. Thus, some vehicles may fail to obtain energy due to their unreasonable submitted prices.
- •
Information renters: When the total income of the aggregator cannot fully cover the operating cost of the aggregator, the PV and HS system operators should pay the information rents to address the budget imbalance. The budget imbalance is caused by the proposed payment rule that incurs extra costs from incentivizing EVs and HVs to report true prices.
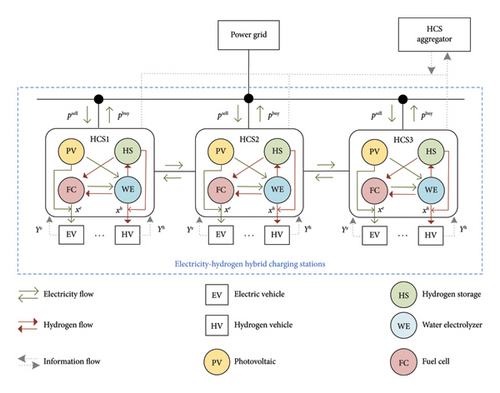
2.2. Electricity–Hydrogen HCS Model
In the following, we present the mathematical models of the system. Each HCS in the system is indexed by i ∈ I, where I is the set of all HCSs. Each vehicle is indexed by j ∈ J, where J is the set of all EVs and HVs. We consider the HCS decision-making problem and the energy trading model in discrete time intervals t ∈ T.
2.3. H2P and P2H Constraints
2.4. HS Balance Constraints
2.5. Power Constraints
Constraint (19) ensures that the aggregator cannot both buy and sell energy at the same time interval.
2.6. HCS Operating Costs
3. Electricity–Hydrogen Trading Mechanism
In this section, we present an electricity–hydrogen trading mechanism to implement the interaction between the aggregator and vehicles. Their interaction is formulated by auction-based rules. We consider that an auction is conducted at the beginning of each time interval. To simplify the notations, we focus on the auction model for a single time interval and omit the subscript t in this section since the model can be applied to every time interval.
3.1. Auction-Based Rules
- •
Step 1: Vehicle j first evaluates its own electricity/hydrogen requirement and determines an electricity price and a hydrogen price . The prices are only known by vehicle j itself. Yj represents the value of energy from the view of vehicle j. If the vehicle is an EV, it has no demand for hydrogen, and it can set . If the vehicle is an HV, then it has . Vehicle j would strategically report to maximize its individual utility, so the reported prices may not be equal to the true prices Yj.
- •
Step 2: Each vehicle j determines the reported prices and submits to the aggregator. The aggregator receives the set of prices .
- •
Step 3: Based on Ylie, the aggregator calculates the energy allocation result and the payment πj for each vehicle j by solving optimization problems. According to the results, vehicle j obtains units of charging power and units of hydrogen and pays πj units of money. Finally, the utility of vehicle j is defined as the value of purchased energy minus the payment made, that is
() - •
Step 4: Based on the energy allocation result and the payment of vehicles , the aggregator computes the information rents for each HCS to eliminate the budget imbalance. The information rents for electricity are paid by the PV system, and the information rents for hydrogen are paid by the HS system in an HCS, which will be discussed in subsequent sections.
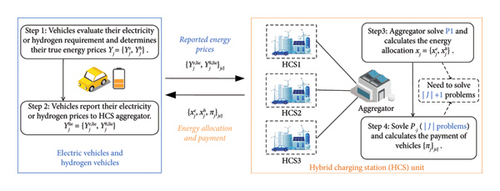
To maximize their own utilities, the EVs and HVs can strategically submit their offer prices. Vehicles are allowed to upload their true prices Yj or untrue prices . The proposed mechanism can be implemented regardless of whether the reported prices are true.
An important property of the proposed energy trading mechanism is truthfulness, which means that each vehicle can get its maximum utility if and only if it truthfully submits its prices. We will theoretically prove this property later. To get the maximum utility, all vehicles would choose to truthfully submit their prices Yj in Step 2, i.e., . Considering this individual rationality, we temporarily assume that all vehicles will truthfully submit their prices in the mechanism, simplifying the notations in the following problem formulation.
3.2. SWM Problem
3.3. Payment for Vehicles
3.4. Theoretic Analysis
The proposed energy trading mechanism is defined by the energy allocation described by P1 and the payment calculation given by (28). The proposed mechanism can ensure that all vehicles submit their true prices, which is formally expressed by the following proposition.
Proposition 1. (Truthfulness): In the proposed energy trading mechanism, each vehicle j can get its maximum utility if and only if it truthfully submits its prices Yj.
Proof. Consider that the true hydrogen and electricity prices of vehicle j are denoted by and its untrue prices are . Let {x∗, y∗} denote the optimal solution to P1 when vehicle j reports true prices Yj. Let {x0, y0} denote the optimal solution to P1 when vehicle j reports untrue prices . We assume that all other vehicles truthfully report . According to the objective function of SWM, we have
This shows that the utility of vehicle j reporting true prices Yj is no less than the utility of vehicle j reporting untrue prices . Thus, a rational vehicle always chooses to truthfully report its prices. Following the same way, we can easily derive , which means that truth-telling is the optimal decision of each vehicle j no matter what the other vehicles report.
Proposition 2. The proposed energy trading mechanism also can achieve SWM and individual rationality.
Proof. First, the proposed mechanism allocates energy to EVs and HVs according to the optimal solution to P1. Hence, SWM is ensured. Second, individual rationality indicates that each of the EVs and HVs has a nonnegative utility in the mechanism. Based on the truthfulness property, we have . According to the objective function of SWM, we get
It is proven by the Myerson–Satterthwaite impossibility theorem [30, 33] that it is impossible to create a mechanism that is truthful, social welfare maximizing, individually rational, and budget-balanced with private information. Budget imbalance means that the total payment received by the auctioneer may be insufficient to cover its cost, which is caused by the payment rule that incentivizes users to report true prices. Based on this fact, we introduce the information rents to deal with the budget imbalance of the aggregator.
3.5. Information Rents
From the perspective of the aggregator in our model, budget imbalance occurs when the total income paid by the vehicles in the mechanism cannot completely cover the operating cost in electricity–hydrogen generation and transmission, i.e., Fin(x∗) ≤ C(y∗), where Fin(x∗) is the actual income received by the aggregator. To eliminate the budget imbalance of the aggregator, additional payments can be imposed on the HCSs. These payments can be taken as the information rents, which guarantee the desired economic properties of the proposed mechanism. We consider that the market efficiency loss caused by strategic bidding of vehicles outweighs the information rents required to be paid under the VCG mechanism. Therefore, market participants are inclined to pay the information rents to mitigate greater losses. Here, we consider basic and additional information rents.
4. Numerical Result
4.1. Simulation Setting
| Parameter | Value |
|---|---|
| HSmax | 100 kg |
| EP2H | 0.0254 kg/kWh |
| CP2H | 2.5 $/h |
| [0.1, 0.4] MW | |
| [0.5, 1] MW | |
| HSmin | 30 kg |
| EH2P | 39.4 kg/kWh |
| CH2P | 5 $/h |
| [0.5, 1] MW | |
| [0.1, 0.4] MW | |
| [50, 70] kg | |
| ηP2H | 0.8 |
| ηH2P | 0.6 |
| Lbus | 1.5 MW |
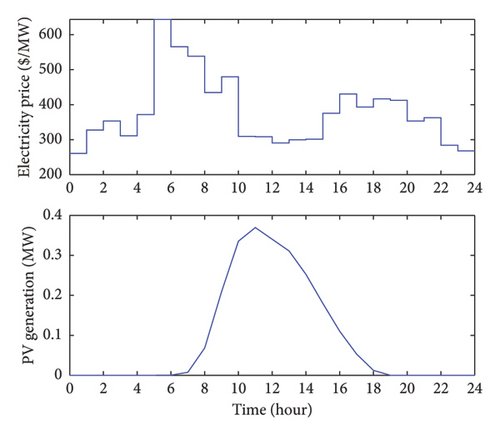
4.2. Power Management Results
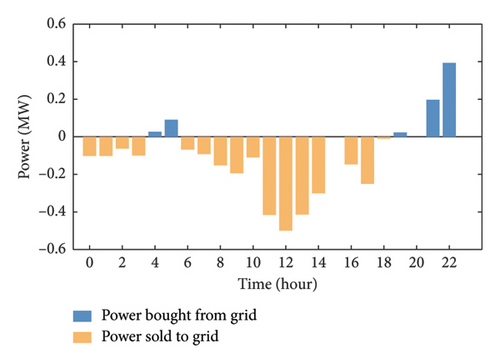
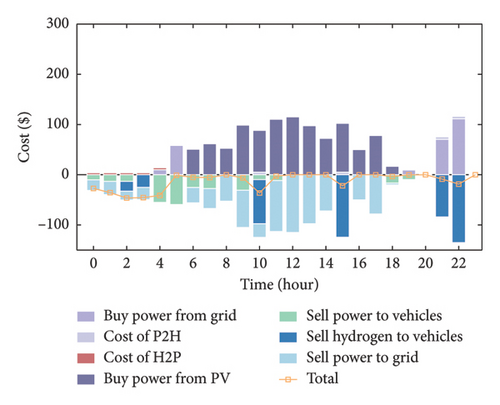
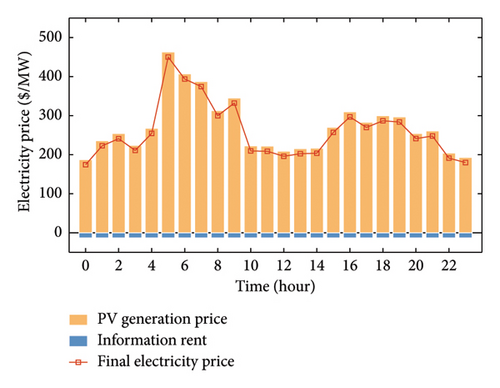
Figure 4 presents the trading power result between an HCS and the grid over 24 h. At time intervals 0–3, the HCS chooses to sell power to the grid due to the lower number of parked EVs in these intervals, resulting in lower energy demands. The PV system generates solar power at time intervals 6–18, which can be utilized by HCSs to fulfill their power requirements. Figure 5 shows the total cost of HCS1, which includes the operating costs of P2H and H2P conversions as well as energy trading costs with vehicles, the PV system, and the grid. On one hand, HCSs purchase power from the PV system and subsequently sell it to the grid at a higher price to get more revenue. On the other hand, HCSs sell electricity and hydrogen to parked vehicles through energy auctions to reduce their operating cost and maximize social welfare. Figure 6 shows the unit price of solar power considering information rents for the PV system. The information rents are distributed in each unit of generated solar power, which leads to a decrease in the final settlement of PV power price. It can be considered as the operating cost of the PV system to ensure the reliability of the information in the truthful system. The result shows that the information rents would not significantly increase the cost of the PV systems.
4.3. Energy Trading Results
Table 2 presents the energy trading results of 3 HCSs and the grid. Each HCS is connected to the grid and other HCSs, facilitating the exchange of electricity through energy transactions. Since the buying price of the grid electricity is lower than the price at which it is sold to vehicles, the HCSs opt to buy electricity from the grid to fulfill the electricity demands for EV charging and enhance their revenue. Note that we impose constraint (19) ensuring that the HCSs cannot both buy energy from and sell energy to the grid at the same time interval. When an HCS has surplus energy at this time interval, as observed in the case of HCS2 in Table 2, it chooses to sell the excess energy to other HCSs.
| Buy from grid | Buy from other HCSs | Sell to other HCSs | Sell to HVs (kg) | Sell to EVs | |
|---|---|---|---|---|---|
| HCS1 | 0.091 MW | 0.5 MW | 0 | 0 | 0.09 MW |
| HCS2 | 0 | 0 | 0.5 MW | 0 | 0 |
| HCS3 | 0.04 MW | 0 | 0 | 2 | 0.04 MW |
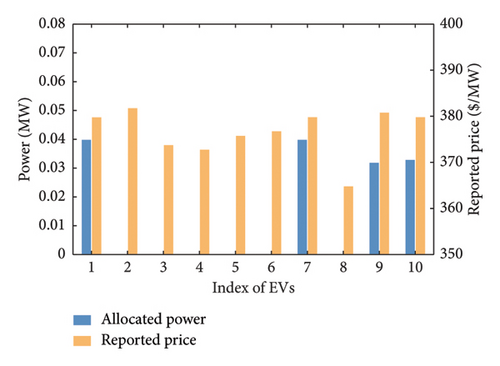
Figure 7 illustrates the allocated power and reported electricity price of each EV in a time interval. The result shows that the auctioneer prioritizes power to the EVs that report high electricity prices to maximize the value of resources and EV utilities. This auction-based energy allocation rule aims to maximize social welfare, but it may let vehicles reporting lower electricity prices have no allocated charging power. These vehicles can participate in the next round of auctions and increase their prices to meet their energy demands. Similarly, the allocation rule can be extended to hydrogen allocation.
4.4. Scalability Analysis
To show the scalability of the proposed mechanism, we carry out the simulations with the number of HCSs varying from 3 to 300 and the number of vehicles varying from 100 to 1500. A higher number of HCSs and vehicles means more decision variables and a larger scale of the problem, leading to a longer solver time, as shown in Figure 8. In scenarios with up to 300 HCSs and 1500 vehicles, we can obtain the solution and calculate the payments of all the vehicles within 1500 s. In general, in an auction with n vehicles, we need to solve n + 1 problems. In real-world scenarios, we solve P1 centrally, and then the remaining n problems (P−j) can be solved in parallel. This means that the computation time of the proposed mechanism is manageable. In addition, as the number of vehicles and HCSs increases, the scalability of the proposed mechanism can be improved by decomposing the large network into several subnetworks and applying the proposed mechanism to each subnetwork to enhance the computational efficiency in practical implementation. In the future, we would employ distributed optimization methods such as analysis target cascading and alternating direction methods of multipliers to coordinate between these subsystems to improve the scalability of the proposed mechanism. Therefore, the proposed mechanism is still practical for larger networks with a high number of HCSs and vehicles.
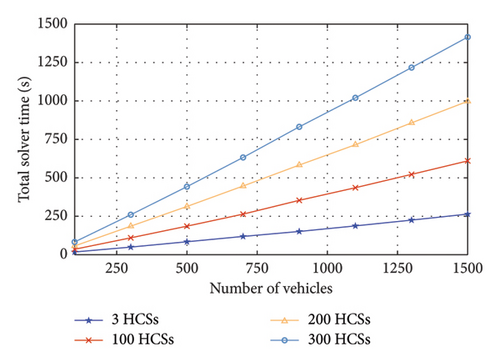
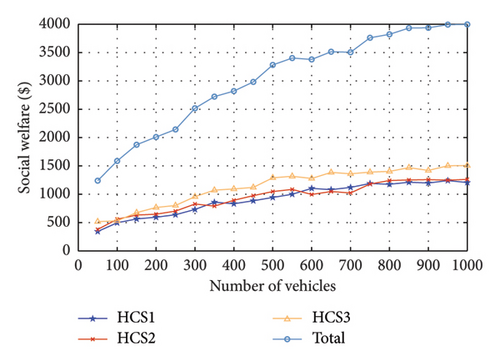
Figure 9 depicts the social welfare of the three HCSs under varying numbers of vehicles, where the social welfare denotes the objective function of P1. With the growing number of vehicles, the total social welfare of the HCSs rises due to the increase in revenue generated from selling energy to vehicles. When the number of vehicles reaches 950, the social welfare of the HCSs remains stable since the HS of HCSs is insufficient to serve all the vehicles, necessitating the purchase of more electricity from the grid. In this case, we can add more HCSs and increase the HS to serve more vehicles, enhancing the scalability of the proposed mechanism.
4.5. Parameter Analysis
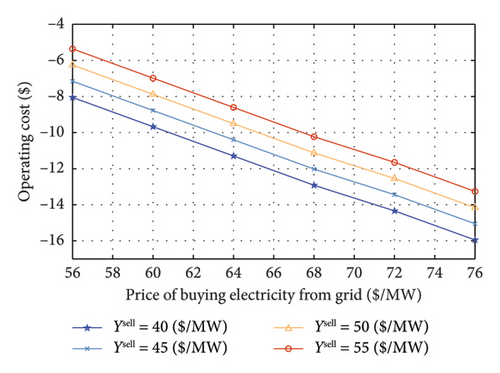
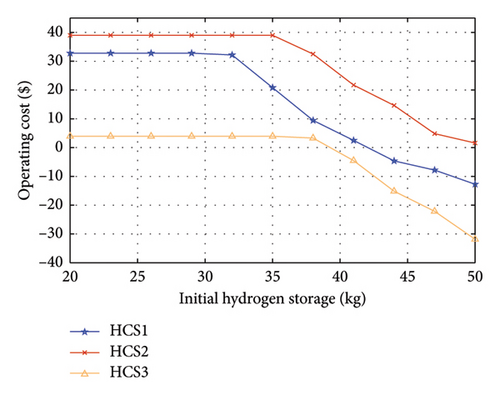
Simulations are carried out with the price of buying electricity varying from 56 to 76 $/MW and the price of selling electricity varying from 40 to 55 $/MW, as shown in Figure 10. The total social welfare of HCSs steadily rises with the rise in selling electricity prices. As the price of buying electricity increases, the total social welfare of HCSs decreases due to the escalated operating cost of buying electricity. Figure 11 shows the operating cost of three HCSs with the initial HS ranging from 20 to 50 kg. When the initial HSs of HCSs increase, the operating cost remains relatively constant initially and then decreases when initial HSs surpass the equilibrium point of hydrogen supply and demand. Each HCS has hydrogen demands for supplying the parked HVs and maintaining the storage balance of hydrogen tanks. Therefore, when the HSs meet the HCS’s demand, it can utilize the surplus hydrogen to generate electricity through H2P to fulfill its power demand and reduce its cost of buying electricity, leading to a decrease in operating costs.
4.6. Comparative Analysis
- •
Independent HCS: This model considers that each HCS is independent and removes the electricity trading between HCSs.
- •
Only CS: This model considers the HCSs acting as CSs and removes hydrogen trading of the parking HVs from the proposed model.
- •
Only HS: This model considers the HCSs acting as hydrogen stations (HSs) and removes the electricity trading of the parking EVs from the proposed model.
Table 3 shows the social welfare of different models in a scenario with 3 HCSs and 100 vehicles. In the independent HCS model, HCSs do not consider buying energy from other HCSs to meet their energy demand, leading to a higher cost of buying electricity from solar systems and the grid. In the only CS model, the CSs have no HS and demand, resulting in lower revenue from selling energy to vehicles and no H2P and P2H costs. In the only HS model, the HSs have less electricity demand and can activate H2P conversion to produce electricity and then sell to the grid, leading to the lowest cost of electricity trading with the solar system and the grid. Compared to models only HS and only CS, the proposed model has the highest revenue of energy trading with vehicles, which shows that incorporating both electricity and hydrogen trading can significantly increase the revenue of energy trading. Overall, the proposed model has the lowest total cost of −1587.37, which shows that the proposed model has a good performance in cost saving.
| Cost ($) | Independence HCS | Only CS | Only HS | Proposed |
|---|---|---|---|---|
| Electricity trading with the solar system and gird | 1295.22 | 382.95 | 87.81 | 846.05 |
| Operating cost of H2P | 80 | 0 | 75 | 75 |
| Operating cost of P2H | 0 | 0 | 48 | 48 |
| Energy trading with vehicles | −2274.82 | −922.57 | −1654.33 | −2556.42 |
| Total | −899.60 | −539.62 | −1443.52 | −1587.37 |
- Note: The bold value highlights the effectiveness of the proposed model in reducing the total system cost compared with other models.
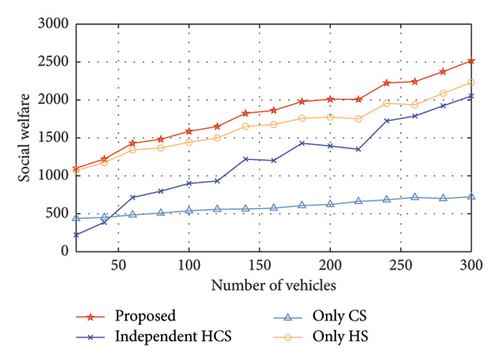
Simulations are carried out to show the social welfare of different models with the number of vehicles changing from 20 to 300, as shown in Figure 12. The ratio of EVs to HVs is 1:1. As the number of vehicles increases, the social welfare of HCSs in all models rises since HCSs can get more revenue from vehicle-level energy trading. The model independent HCS considers both energy trading with EVs and hydrogen trading with HVs, leading to a rapid increase in social welfare as the number of EVs rises. Models only HS and only CS, respectively, do not consider energy trading with EVs and hydrogen trading with HVs. When the number of vehicles is small, the social welfare gap between the only HS model and the proposed model is not significant. However, as the number of vehicles increases, the gap between them widens. In the only HS model, the HCSs can gain revenue from both selling electricity to the grid and selling hydrogen to HVs. In the only CS model, the CS does not benefit from hydrogen trading with HVs. The revenue from selling electricity to EVs increases because the CS generally earns slightly more by selling electricity to EVs compared to selling it to the grid. Therefore, the only HS model exhibits a faster growth rate of social welfare compared to the only CS model as the number of vehicles increases. Overall, the proposed model achieves the highest social welfare, demonstrating that incorporating both system-level and vehicle-level energy trading can significantly enhance social welfare.
4.7. Economic Properties
Three EVs are chosen from the three HCSs in a time interval, respectively, and their true charging prices are set to 75 $/MW to examine the truthfulness and individual rationality of the proposed mechanism. To demonstrate the impact of false charging price, we vary the reported charging prices of the three EVs from 50 to 100 $/MW. Figures 13(a) and 13(b) show the probabilities of getting a maximum and non-negative utility for an EV, respectively. Each probability point of a reported price in the Figures 13 and 14 is obtained from 100 trials. As illustrated in Figure 13, each EV has a 100% probability of getting maximum and non-negative utility when it reports its true charging price.
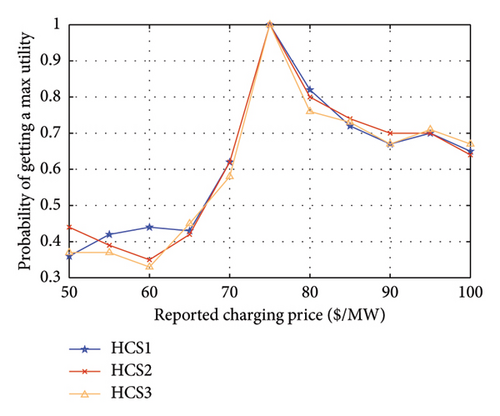
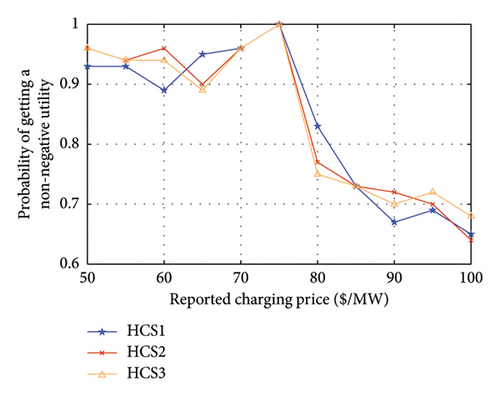
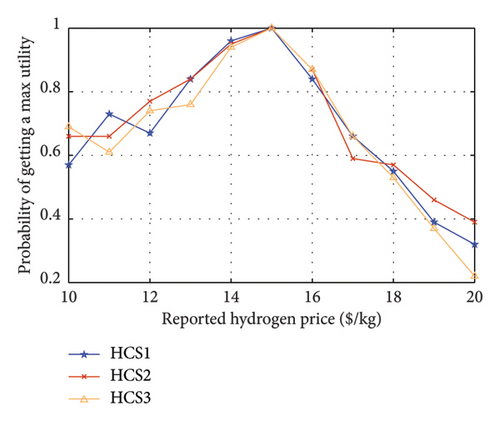
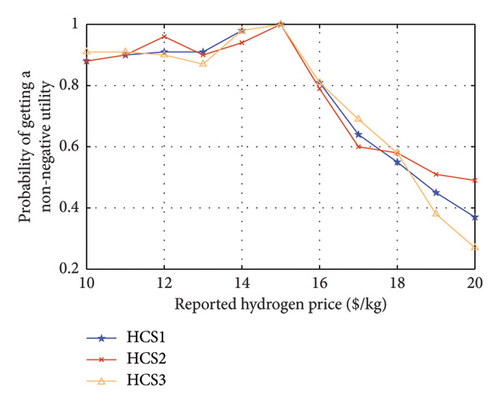
Similarly, three HVs are selected from the three HCSs in a time interval, and their actual hydrogen prices are set at 15 $/kg. The reported hydrogen prices of the three HVs range from 10 to 20 $/kg. As depicted in Figure 14, only when an HV reports its true hydrogen price, it achieves a 100% chance of getting a maximum and non-negative utility, which validates the truthfulness and individual rationality of the proposed mechanism. Therefore, all vehicles would opt to submit their true prices to get their maximum utilities. In this case, the energy trading system can efficiently achieve energy value maximization based on the true information.
5. Conclusions
In this paper, we explore multienergy trading among HCSs, the grid, and vehicles, with a focus on the vehicle-level perspective. First, we propose an electricity trading model for HCSs with H2P and P2H capabilities. Second, we employ the VCG mechanism to design the electricity and hydrogen trading system, allowing the parked EVs and HVs to strategically submit their energy offer prices to maximize their own utilities. Third, we prove the properties of truthfulness, individual rationality, and SWM of the proposed mechanism in theory. Subsequently, we define the information rents to eliminate the budget imbalance of the aggregator. The information rents can be considered as the operating costs of PV and HS in a truthful system. Finally, extensive experiments are carried out to evaluate the effectiveness of the proposed multienergy trading mechanism.
In comparative analysis, the proposed model achieves the highest social welfare compared to other models, demonstrating that incorporating both system-level and vehicle-level energy trading can significantly enhance social welfare. We also verify the economic properties. Numerical results show that each vehicle has a 100% probability of getting maximum and non-negative utility when it reports its true price, which validates the truthfulness and individual rationality of the proposed mechanism. The results of scalability analysis show that the proposed mechanism can be extended in larger networks with a high number of HCSs and vehicles.
In addition to social welfare, we plan to consider additional performance metrics, such as scalability and environmental impact of the mechanism in future work. We can also employ blockchain technology to ensure that every bid, energy allocation, and payment is transparent and cannot be altered after the fact, which would significantly enhance trust among participants.
Nomenclature
Sets
-
- I
-
- The set of all HCSs
-
- J
-
- The set of all EVs and HVs
-
- T
-
- The set of time interval
Parameters
-
- PP2H, min
-
- The minimum power of the P2H conversion
-
- PP2H, max
-
- The maximum power of the H2P conversion
-
-
- The energy conversion efficiencies of the P2H conversion
-
-
- The energy conversion efficiencies of the H2P conversion
-
-
- The minimum hydrogen storage at HCS i
-
-
- The maximum hydrogen storage at HCS i
-
-
- The maximum value of the PV power generation at time interval t
-
- Lbus
-
- The maximum power load of the bus between HCSs and the grid
-
-
- The price of HCS i buying electricity from the grid at time interval t
-
-
- The price of HCS i selling electricity to the grid at time interval t
-
-
- The cost parameter of power transmission among HCSs
-
-
- The price of buying solar power from the PV system at time interval t
Variables
-
-
- Binary variable indicates whether the H2P mode is activated by HCS i at time interval t
-
-
- Binary variable indicates whether the P2H mode is activated by HCS i at time interval t
-
-
- Binary variable indicates whether the HCS unit buys energy from the grid at time interval t
-
-
- Binary variable indicates whether the HCS unit sells energy from the grid at time interval t
-
-
- The power of P2H conversion at HCS i at time interval t
-
-
- The power of H2P conversion at HCS i at time interval t
-
-
- The hydrogen production of the P2H conversion at HCS i
-
-
- The hydrogen consumption of the P2H conversion at HCS i
-
- hsi,t
-
- The hydrogen storage at HCS i at time interval t
-
-
- The actual PV power generation in HCS i at time interval t
-
-
- The power sold to the grid of HCS i at time interval t
-
-
- The power sold to other HCSs in HCS i at time interval t
-
-
- The total power bought by EVs parked in HCS i at time interval t
-
-
- The total hydrogen consumption of the HVs parked at HCS i
Abbreviations
-
- HCS
-
- Hybrid charging station
-
- EV
-
- Electric vehicle
-
- HV
-
- Hydrogen vehicle
-
- H2P
-
- Hydrogen to power
-
- P2H
-
- Power to hydrogen
-
- VCG
-
- Vickrey–Clarke–Groves
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This research was supported by the Science and Technology Project of the China Southern Power Grid Co., Ltd. (Grant no 031200KK52222010).
Open Research
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.




