Electric vehicles (EVs) have caught significant attention in recent years due to their potential to reduce greenhouse gas emissions and dependency on fossil fuels. The reliability analysis of power electronic (PE) converters in EVs is crucial to improve their performance, cost-effectiveness, and long-term viability. In this paper, the lifetime estimation of IGBT in a hybrid EV unidirectional converter is evaluated based on control system impacts and statistical model uncertainties. For this purpose, a closed-loop model of a hybrid EV is developed in MATLAB using the Artemis mission profile to simulate the unidirectional converter output power. In the next step, the average model of the nonideal boost converter with Kharitonov’s controller is employed to calculate the IGBT losses. The robust controller is able to maintain converter model stability during long-term output power mission profile simulation. By applying the thermal impedance, the junction temperature profile of the switch is obtained, enabling lifetime analysis via rain flow (RF) and Miner’s rule methods. The results show that the controller selection considerably affects total consumed lifetime (TCL). Each controller can have a different TCL compared to other choices. Since the model coefficient for solder joint and bond wire failure mechanisms have been obtained based on the accelerated test results in the empirical method, considering the parameter statistical distribution and utilizing the Monte Carlo (MC) method can create a better view in the selection of IGBT and the converter design. Furthermore, based on the statistical results and the probability density function, it is feasible to determine how many percent of the IGBTs in the statistical community are damaged after a certain time. The B₁₀ parameter for the failure mechanisms of bond wire and solder is 11.2 and 450 years, respectively. This approach provides insights into risk assessment and design optimization.

1. Introduction

Nowadays, the thermal model is an integral part of the planning and evolution of power electronic (PE) converters. Since the thermal performance of power semiconductor component is one of the most important factors influencing the efficiency, reliability, and dimensions of a converter, it is essential to conduct accurate estimations and evaluations of device lifetime based on temperature to optimize the cost and design of power converters [1–3]. Additionally, semiconductor devices are among the most vulnerable components in PE converters and electrical systems. According to a research report based on field experiences of PE device manufacturers, about 31% of 56 respondents considered PE semiconductor devices the most fragile components [4]. Moreover, the assessment of PE semiconductor reliability has been conducted in many studies, such as solar cells [5–10], motor drives [11–13], wind turbines [14–16], and electric vehicles (EVs) [17–19]. These studies have demonstrated that semiconductor devices are usually one of the most prone devices to damage in such systems. EVs have received significant attention as a hopeful solution for reducing greenhouse gas emissions and dependency on fossil fuels [20–22]. With the surging demand for EVs, there is a crucial need to investigate the reliability and lifetime estimation of their electrical systems, including PE converters that control EV power [23, 24]. Reliability and lifetime estimation straightforwardly influence the performance and safety of the EVs, making them vital considerations for design. Moreover, the lifetime assessment of PE converters is imperative to ensure that the electrical devices of EVs can withstand continuous operational stress and deliver stable performance over a long time. Consequently, understanding the reliability and lifetime estimation of EVs, along with evaluating the reliability issues in PEs, is notable for advancing EV development and adoption [25, 26]. This includes evaluation of the device durability, predicting failure rates and implementing effective maintenance strategies to ensure long-term reliability. One of the aspects of studies in the field of reliability is based on the prediction of its level in a system. It can be categorized into three approaches for the IGBT in PE converters. The first relies on constant failure rate models presented in Military-Handbook-217F [27]. While simple, this method lacks accuracy due to not considering some factors such as wear-out and temperature effects. Notably, Military-Handbook-217F was abolished in 1995 and the updated version, MHB-217H, was presented based on the fundamental physics method [28]. The second approach stems from the empirical lifetime models derived from the experimental test data [13, 18, 29]. This method is widely used to estimate the lifetime of IGBTs, but the main drawback is that it relies on statistical data analysis. Therefore, they do not accurately describe the damage mechanisms [30]. Several empirical methods are utilized to estimate the lifetime of IGBTs in PE converters. In accelerated power cycling tests, IGBT modules are subjected to rapid and extreme temperature cycles (heating and cooling) to accelerate aging processes [29]. Data collected during these cycles (junction temperature swings, switching frequency, and current load) are then used to develop statistical models and predict lifetime under normal conditions. In field data analysis, operational data from IGBTs in real-world applications, such as operating temperatures, switching frequencies, and load currents, are collected. Statistical analysis of data is considered to identify trends and correlations between operating conditions and failure rates [31]. However, combined data from accelerated tests with field data to create more robust and accurate lifetime predictions are used [32]. The third approach involves physics of failure (PoF) modeling which accounts for strain and stress variations induced by thermal–mechanical cycles [33]. Although PoF provides deeper insight into failure mechanisms, its application is limited by the incompetence of precise material and structural data for IGBTs [32]. One aspect of this study is reliability from the control attitude. The reliability and lifetime of the PE converter in EVs are directly related to the control system of the PE converter. The control system of PE converters is one of the fundamental assignments of the power management systems of EVs. It plays a vital role in optimizing performance, reducing the risks of malfunction and failure, and increasing their reliability and lifetime. Consequently, the research and development in dynamic control methods and performance optimization of PE converters to improve reliability and lifetime remain a substantial concern in EV technology. The effect of island control and maximum power point tracking on efficiency and reliability in photovoltaic systems has been studied [34]. Reference [35] shows that the control algorithm can reduce motor losses of up to 70%. In EVs, where power cycles vary significantly, it is inevitable to use a controller for maintaining converter stability. Kharitonov’s theorem offers a framework for designing robust controllers to handle uncertainty [36], and its application for different converters has been investigated [37–39]. When it comes to using Kharitonov’s theorem, there is a range of controllers for the converter. Consequently, choosing an optimal controller for maximum lifetime can be challenging. Moreover, variations in empirical lifetime model coefficients and statistical analysis can also affect the device lifetime. The IGBT lifetime in PE converters is relevant to two well-known failure mechanisms: solder joint and bond wire failure [40]. When the amount of failure cycles attains a specific number, the solder joint and bond wire in the device will fail. The rain flow (RF) counting analysis is commonly used to extract cycles’ characteristics from junction temperature mission profiles [41].

It is assumed that each temperature cycle causes a certain amount of damage to IGBT [14]. Therefore, Palmgren–Miner’s rule model is used to estimate lifetime [42]. The Monte Carlo (MC) method can be employed to study variations of coefficients in lifetime models. It is employed to explore the statistical characteristics of heat and humidity in the PoF lifetime estimation model [43]. Reference [44] utilized MC simulation to analyze uncertainties in IGBT on-state saturation voltage degradation for online prognostic purposes. The geometrical effects of IGBT were investigated by the MC method [45]. The investigation into circuit and environmental effects on PE devices and converters was conducted in many papers [13, 18, 37].

In this paper, the impacts of the controller design and the empirical lifetime model coefficients are investigated using Kharitonov’s theorem and the MC method, respectively. The analysis is based on the Artemis motorway mission profile standard for hybrid EVs [46]. A nonideal average converter model enables rapid mission profile simulation while accounting for all parasitic elements. Moreover, this approach facilitates designing the optimal controller from the lifetime vantage point for a specific mission profile and calculating the IGBT loss profile simultaneously. Additionally, statistical analysis of semiconductor devices community based on lifetime model parameters provides more comprehensive information about converter reliability during the design phase. A robust controller provides the possibility to consider all uncertainties arising from mission profiles and converter working conditions. On the other hand, the robust controller designed via Kharitonov’s theorem ensures converter output voltage stability despite converter variable changes. This paper is classified into the following sections.

The mission profile in hybrid EV, the converter, and power analysis are introduced in Section 2. In Section 3, the recommended models are considered for studying the effect of the controller and specifications of the lifetime estimation model. In Section 4, the lifetime estimation method and failure mechanisms in IGBT are discussed. The simulation outcomes are proposed in Section 5. In Section 6, the conclusion is submitted.

2. Analysis of the Mission Profile, Power Relationships, and Controller in the Converter

For estimating the lifetime of the converter, it is indispensable to investigate the EV, the converter in question, and its power losses.

2.1. Vehicle Model, Mission Profile, and Required Power Analysis

The energy supply source in an EV can include a fuel cell [47–50], a battery, or a combination of a fuel cell with other energy storage systems such as batteries, ultra-capacitors, solar panels, and superconducting magnetic energy storage, collectively known as a hybrid EV [51–53]. The general scheme of a hybrid EV with two sources is illustrated in Figure 1 [47]. Stable power is catered by the two sources. The primary source supplies steady power while the second source is used for instantaneous power fluctuation during sudden acceleration or deceleration.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Hybrid EV configuration [17, 47].

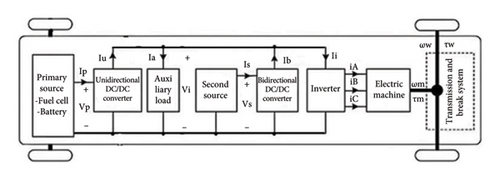
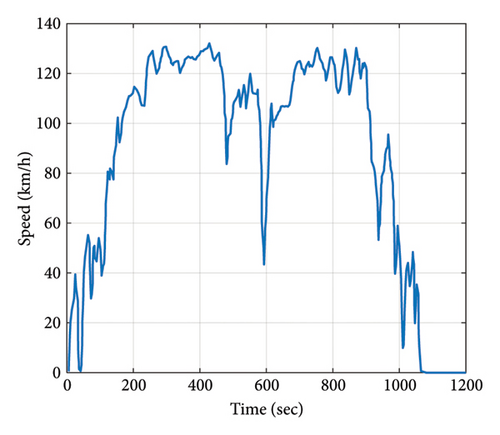
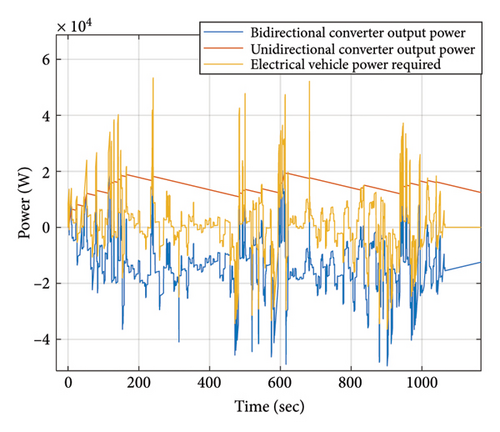
The Artemis motorway standard, depicted in Figure 2, serves as the input for the closed-loop model in Figure 3. This mission profile determines the contribution of unidirectional and bidirectional converters in supplying the vehicle energy demand. The specifications of the desired EV are presented in Table 1. It is achieved based on the weight and power requirements to follow the input speed mission profile in the closed-loop system. As can be seen from Figure 4, the vehicle maximum instantaneous power demand reaches approximately 50 kW. The unidirectional converter acts as a main power supplier. This converter cannot absorb power in deceleration modes. Therefore, its output power is always positive. A rate limiter with rising and falling rates of 600 and −30, respectively, separates the unidirectional converter from the bidirectional converter output power. The value of the falling rate is smaller than the rising rate to provide forward power flow for the unidirectional converter, while higher rates increase output power variation. Consequently, it broadens the range of uncertainty which results in the designing of a slower Kharitonov controller and a reduction in converter response. Figure 4 highlights both positive and negative power flows corresponding to acceleration and deceleration in the mission profile. The power flow in the unidirectional converter is from source to load called forward direction. This converter contributes to the base and positive power. The bidirectional one can flow the power in forward and backward directions to give/attract the power.

Table 1. Characteristics of modeled hybrid EV.

Specifications	Value
Maximum DC converters output power (kW)	50
DC link output voltage (V)	400
Primary battery voltage (V)	200
Primary battery internal resistance (Ω)	0.05
Vehicle wheel radius (m)	0.3
Vehicle mass (kg)	1000
Vehicle torque (N.m)	400

2.2. Parasitic Boost Converter

Parasitic realization in the boost converter is illustrated in Figure 5 [54]. Defining switch on time as T_on and the off time as T_off, the duty cycle is expressed as follows:

()

where F_s is the switching frequency. Using charge balance and volt-second laws, averaging model [54], and the state-space equations of the converter under steady-state conditions, the output voltage v_o is derived in terms of the input voltage v_g and D (equation (2)):

()

where

()

It should be mentioned that D^′ is defined in equation (4) in the nonideal state:

()

In addition, the dynamic equation of the state space is obtained using the averaging technique for the converter as equation (5):

()

Also, by utilizing Laplace transform and algebraic analysis, the small signal transfer function (TF) by considering the perturbations in v_o to D is obtained as equation (6) [54–57]:

()

where

()

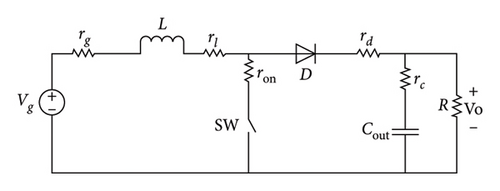
It should be mentioned that the average state-space equations are used as the converter model during output power mission profile simulation, and small signal TF is employed for controller design by Kharitonov’s theorem.

2.3. Kharitonov’s Theorem

Uncertainties in the converter arise from variations in each element, as presented in Figure 5. Since lifetime estimation is based on a mission profile that exhibits significant fluctuation in speed over time, the required power of the vehicle and the output power of the converters also vary considerably. To obtain the IGBT loss profile, it is necessary to simulate the average model of the converter based on its output power. However, classic controllers are not sufficient to maintain stable output voltage under uncertainties induced by the output power mission profile.

For systems with considerable parameter uncertainties, Kharitonov’s theorem provides a robust approach to controller design [36]. In a hybrid EV, the primary power source which might be a fuel cell or a battery results in input voltage variation due to internal resistance. Moreover, as shown in Figure 4, the output power varies during the mission profile simulation, leading to load fluctuations at each moment. By incorporating the mentioned uncertainties in equation (6), the TF with its uncertainty interval is achieved as

()

Any polynomial like K(s) with variable degree is stable if polynomials in equation (9) are stable.

()

The signs “+” and “−” indicate the upper and lower limits related to the converter uncertainties. Stability is verified using the Routh–Hurwitz criterion. Given a controller structure,

()

and considering the TF,

()

By applying Kharitonov equations, the closed-loop TF is defined as equation (12):

()

where K_I is the integral coefficient, K_p is the proportional coefficient, N_x is the numerator, and D_y is the denominator. According to the degree of controller and equation (17), for 16 systems (16-edge theorem), the Ruth–Hurwitz stability criterion should be investigated to find an acceptable region for controller selection.

2.4. Power Loss Analysis

In general, switching and conduction losses in power semiconductor switches are categorized into static and dynamic losses [42]. Static losses include conduction state (on-state) and shutdown state (cut-off) which can be ignored due to the negligible leakage current in switch. Dynamic losses occur during turn-on and turn-off events. Therefore, the most important losses in a switch are the switching and conduction ones, which are calculated using equation (13) [58]:

()

where P_sw and P_cond are switching and conduction losses, respectively.

2.4.1. Switching Loss Calculation in IGBT

Switching losses take place when the switch turns on and off. These losses are influenced by switching frequency, voltage across the switch, and the current passing through the switch. The physical size of the switch also plays a role in the switching losses, so increasing the size increases the intrinsic capacitance. Consequently, it leads to higher switching losses [42]. The switching loss of the switch is calculated as follows:

()

where E_on is the turn-on energy, E_off is the turn-off energy, and f_sw is the switching frequency of the converter.

2.4.2. Computation of Conduction Losses in IGBT

Conduction losses in an IGBT can be calculated by considering collector–emitter voltage in the zero current state (u_ce0) and the dynamic resistance of the collector–emitter. In this case, the voltage of the switch is given by [59]

()

where rc is the emitter–collector resistance and i_ce is the switch current. The instantaneous conduction power in the switch is expressed as equation (16):

()

And for average power, we have

()

where i_cav is the average current, i_crms is the effective current, and T_sw is the switching cycle time.

2.5. Thermal Model and Junction Temperature Estimation

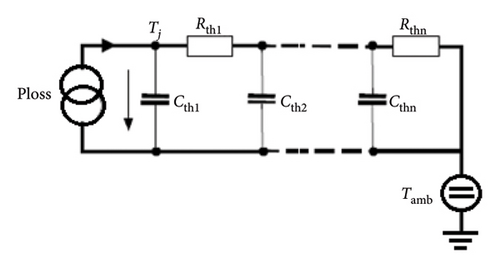
The junction temperature in the converter switch is determined based on the computed losses from the previous section. The electrothermal dynamic model is presented in Figure 6. T_j is the junction and T_amb represents the ambient temperatures. The values of capacitors and resistors are based on Cauer’s model [32].

The thermal impedance also stems from equation (18) [42]:

()

where R_thn is the thermal resistance of the n-th pole, c_thn is the thermal capacitance of the n-th pole, and N_p is the number of poles. The values of Z(t) and R_thn can be obtained from the datasheet of the IGBT manufacturer, while c_thn is derived from the relationship τ_thn = R_thn∗c_thn. Furthermore, the junction temperature of the switch is obtained using equation (19), as shown in Figure 6:

()

3. Lifetime Estimation Model for Two Perspectives

3.1. The Presented Model for Evaluating Controller Changes

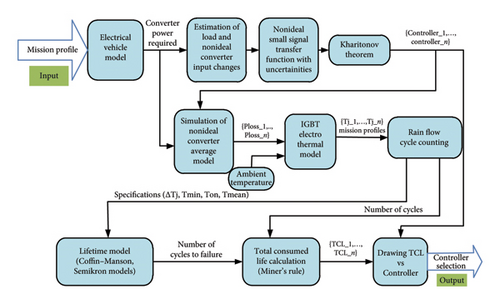
The process of analyzing the controller effect on the total consumed lifetime (TCL) is presented in Figure 7. This approach allows for choosing the optimal controller coefficients for the system. First, a mission profile is applied to the hybrid EV to determine its required power. Then, the output power of the unidirectional converter is determined using a rate limiter. Based on the unidirectional output power, variations in the load and input voltage resulting from the internal resistance of the primary source are acquired. In the following, the nonideal small signal model and parasitic elements are taken into account, and the range of coefficient variations based on Section 2 is obtained. According to the controller model, the interval closed-loop TF is created and Kharitonov’s theorem is applied to identify the acceptable area for controller selection. By selecting different points from the acceptable controller area and applying the required power to the average nonideal model of the converter, IGBT losses are obtained. Exerting the losses to the electrothermal model, the junction temperature is determined. Subsequently, the number of temperature cycles for each mission profile and their characteristics are obtained using the RF manner. For two common failure mechanisms in IGBTs, the number of cycles before device failure is attained. The calculation of TCL is performed using Miner’s rule method for different controllers. Finally, the TCL curve is obtained according to the coefficients of the controller so that the best controller is selected based on the minimum TCL.

3.2. The Model Presented to Investigate the Changes in the Coefficients of the Lifetime Estimation Model

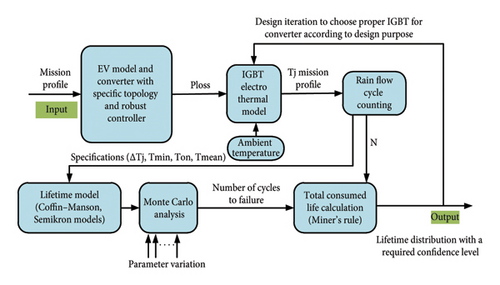
Figure 8 exhibits the MC analysis process. Similar to Figure 7, the mission profile is exerted on the EV model for acquiring unidirectional converter output power. In the next step, it is applied to the converter to determine the power loss in the IGBT. The junction temperature mission profile in IGBT is then derived by applying losses to the electrothermal model. This profile is analyzed using the RF method based on the number of cycles and their characteristics. It is crucial to note that the impact of speed variation in the EV mission profile is appeared in junction temperature cycles. Moreover, because the coefficients of the lifetime estimation models used in this paper are obtained based on a confidence level [32, 60], they follow a normal distribution with a specific standard deviation. In the following, the lifetime analysis is performed for a particular population of IGBTs using the MC method with details presented in the simulation section. The feedback from the output part to the electrothermal model of the IGBT enables the iterative design to select the best choice.

4. Estimation of Lifetime and Failure Mechanisms Based on the MC Method

Solder joint and bond wire failure mechanisms are two important factors that can lead to device failure and malfunction. Damages may occur due to changes in temperature, pressure, vibrations, or mechanical modifications [40]. The best lifetime model is one where the test conditions closely match the operational conditions. However, due to the time required, this is not practical. For this reason, accelerated testing concepts have been widely used in reliability engineering over the past decades to reduce testing time. The key challenge is choosing a suitable and justifiable model for lifetime estimation.

4.1. The Lifetime Model

A practical model for bond wire failure, as expressed in equation (20), has been used [42, 60, 61]:

()

where T_jm is the average temperature, ΔT_j is temperature fluctuation, and t_on is the duration of the cycle. The constant parameters A, β₁, β₂, and β₃ are specific to the construction of the device based on test data provided in [60].

Another model that focuses on bond wire failure in IGBTs is known as the Semikron model [42, 60]. Equation (21) determines the number of cycles before breakdown.

()

where ΔT_j is the temperature variations, T_j min is the minimum temperature, t_on represents the duration of the temperature period, bond wire current is I, tolerable IGBT voltage divided by 100 is V, and D is the bond wire diameter in µm. Likewise, A, β₁, and β₂ to β₆ are values related to the construction of the device and are based on test data from references [42, 60]. The results could be more reliable if the parameter values were obtained from real samples under actual working conditions. Nevertheless, to diminish the time and simultaneously obtain the conceptual lifetime model, the values from references [42, 60] have been widely accepted in reliability engineering.

4.2. The MC Analysis

Using equations (20) and (21) along with RF analysis finally results in a constant TCL for each failure mechanism. In contrast, this does not reflect reality, as it does not account for the statistical variations in the model parameters. In practice, the age of an IGBT varies due to variations in physical parameters, lifetime model coefficients, and different operating stresses. To address these uncertainties, a statistical approach based on MC simulation is considered in this paper to analyze parameter variations in the lifetime model. Parameters β₁ and β₂ which are associated with temperature variations and minimum temperature in equations (20) and (21) are modeled using a normal distribution. The sensitivity of TCL to each parameter is evaluated separately and cumulatively within a specific confidence interval. Further details are provided in Section 5.

4.3. Miner’s Rule Model

Lifetime expectancy is approximated using Miner’s rule model or the damage accumulation theorem. In practice, damage is quantified as the ratio of thermal cycles n to the number of cycles before failure N_f under a specific condition i, as given in equation (22). By considering all the conditions and summing the individual damages using Palmgreen–Miner’s theorem, the total accumulated damage is obtained using equation (23):

()

where CL(i) is the damage contribution from the i-th cycle and TCL is the total damage accumulated under all conditions. If TCL reaches a value of one, failure occurs in the device.

5. Simulation Results

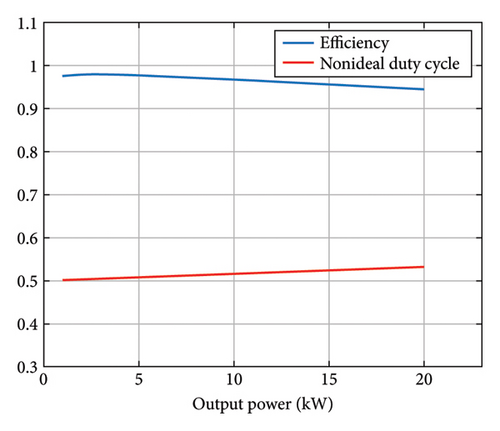
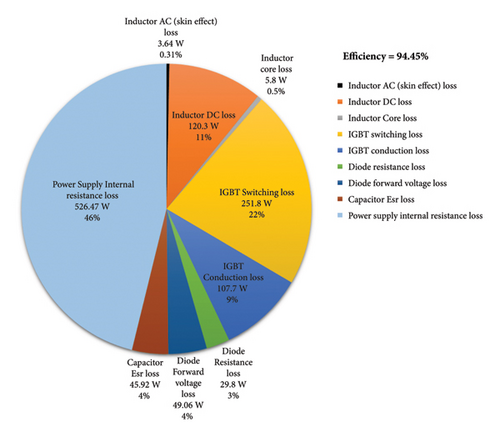
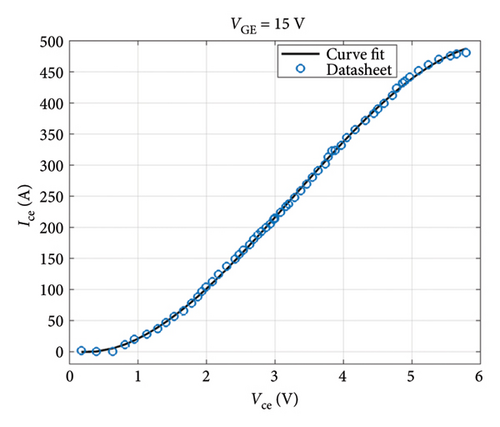
In order to design a unidirectional converter in a hybrid EV, it is first necessary to determine the mission profile and model of the EV. Therefore, the required power of the EV can be obtained as depicted in Figure 4. The nominal characteristics of the desired converter are designed and presented in Table 2, considering the output and input voltages as well as the output power of the unidirectional converter. Figure 9(a) illustrates the converter’s efficiency and duty cycle for different output power levels. As output power increases, converter efficiency decreases. Furthermore, the duty cycle escalates which plays a considerable role in enhancing power losses and reducing efficiency. Given that the converter power changes from 10.91 kW to 19.5 kW, converter efficiency varies from 96.6% to 94.45%. A pie chart in Figure 9(b) shows the distribution of different losses at 19.5 kW output power. The necessary information for IGBT and diode is extracted from the datasheet. The tolerable voltage and current, minimum thermal impedance, and losses are the criteria for selecting an IGBT to achieve a lower TCL. The diode is also chosen based on the tolerable voltage and current for the converter. To limit the size of the inductor, the peak-to-peak ripple inductor current ΔI_Lp−p is set to 20% of the average inductor current. Moreover, to minimize voltage fluctuations in the output voltage, the peak-to-peak ripple voltage ΔV_out is limited to 1% of the average output voltage. As evident from the analysis, the switch losses form an integral part of the converter total losses. The unidirectional converter efficiency at maximum output power is obtained as 94.45%.

Table 2. Characteristics of the hybrid EV unidirectional converter.

Specification		Value
Input voltage (V)	V_in	200
Output voltage (V)	V_out	400
Nominal duty cycle	D	0.5
Maximum output power (kW)	P_out	19.5
Switching frequency (kHz)	F_sw	20
Source inner resistance (Ω)	r_g	0.05
Inductor (µH)	L	258
Ripple inductor current (A)	ΔI_L	19.9
No. of turns	N	92
DC resistance (Ω)	R_dc	0.0114
AC resistance (Ω)	R_ac	0.112
Capacitor (µF)	C	700
Core type		High flux 58,337
ESR (Ω)	r_c	0.0182
Switch	IGBT	AUIRGPS4067D1
Diode	D	IDW100E60

5.1. Effect of Controller Changes on Lifetime

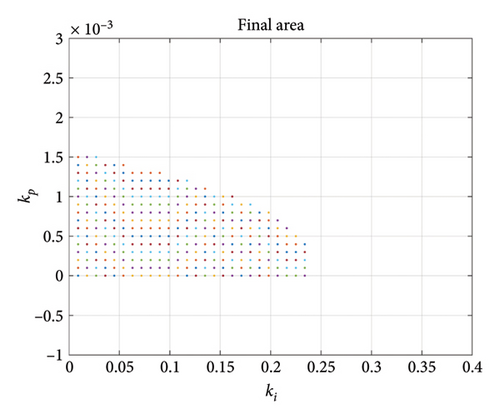
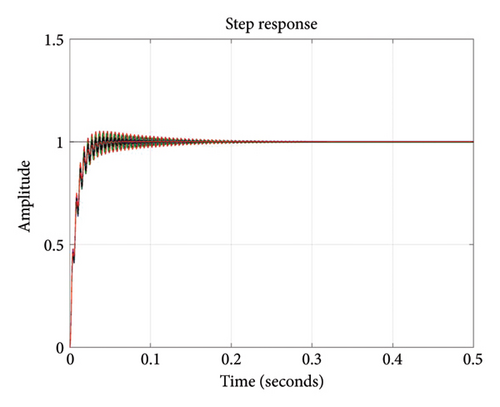
As presented in Figure 4, the power fluctuations at the output of the unidirectional converter range from 10.91 kW to 19.5 kW. Considering the inner resistance of the primary source, input voltage variations in the unidirectional converter range from 194.8 to 200 V. Considering the mentioned parameters variations, Table 3 illustrates the interval quantity of the coefficients of the converter TF for quantized changes and equation (23) expresses the TF interval. Using equations (8)–(11) and Ruth–Hurwitz stability criterion, the acceptable area for selecting a controller that ensures the stability of the converter output voltage due to variations in output power and input voltage is shown in Figure 10. For instance, selecting k_I = 0.2 and k_p = 0.0004, the step responses for 16 Kharitonov systems are obtained as shown in Figure 11, demonstrating that the system remains stable under all changes.

Table 3. Quantized values for the boost converter.

V_i (v)	P_o (KW)	D
194.8	19.5	0.5174
194.8	10.91	0.5152
200	19.5	0.5048
200	10.91	0.5026

()

Next, the required power in Figure 4 is applied to the average model of the nonideal converter, and a large number of controllers are selected from the acceptable area of Figure 10 for simulation. To determine IGBT losses, E_on and E_off relationships in terms of I_ce, as well as v_ce in terms of I_ce are used as shown in Figure 12. These relationships are extracted from the IGBT datasheet in Table 4. Equations (24) and (25) represent the curve fitted expressions for E_on and E_off obtained using MATLAB.

()

Table 4. Thermal characteristics of third-order Cauer’s model.

Parameter	Value
R_thi (°C/W)	0.0564	0.0888	0.0547
C_thi (°C/W)	0.0044858	0.0355292	0.2722669

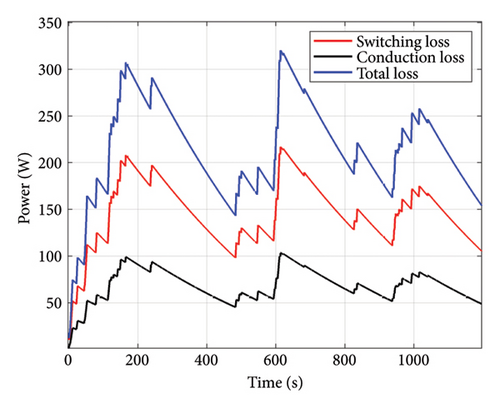
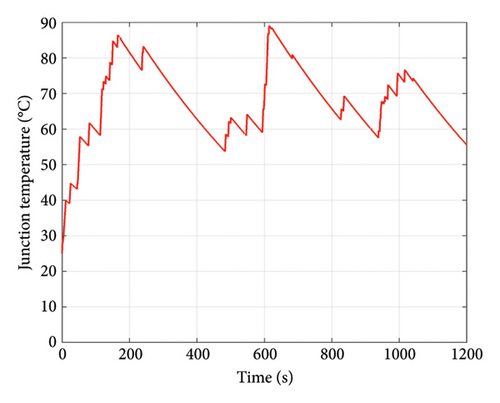
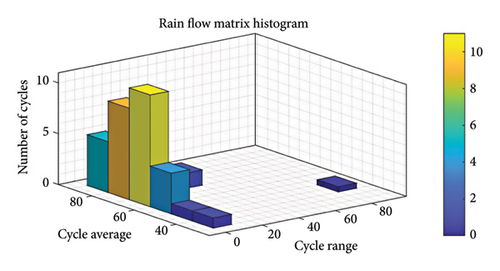
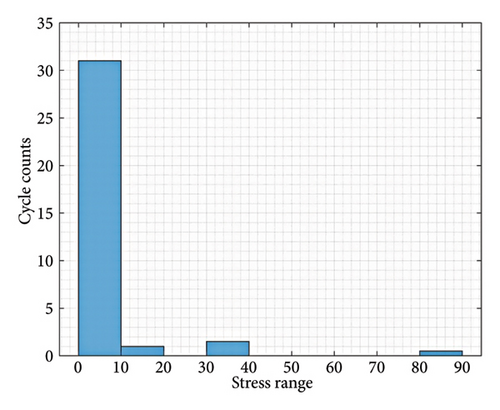
Figure 13 presents the conduction, switching, and total IGBT losses during the mission profile for k_I = 0.005 and k_p = 0.001. As observed, switching losses constitute a significant portion of the total losses. By applying the thermal model from the IGBT datasheet in Table 4, the junction temperature of the IGBT is achieved as shown in Figure 14. Moreover, the analysis of temperature cycles using the RF method is illustrated in Figure 15. This process is repeated for multiple controller selections from the acceptable area. Finally, Figure 16 presents TCL for two common failure mechanisms in the IGBT based on controller values. As it is known, there is no unique TCL applicable to all controllers. For some parameter selections, a lower TCL is achieved, indicating a better choice of controller from the reliability perspective in the converter.

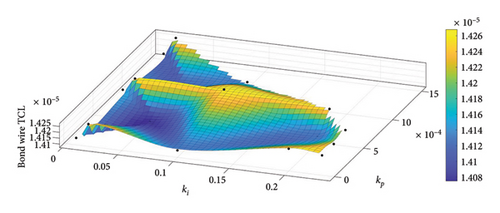
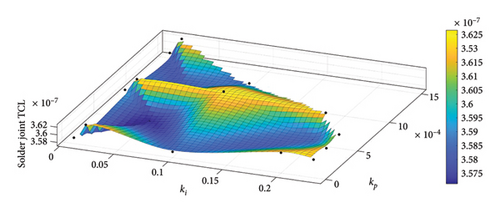
5.2. Changing the Converter Parameters and the MC Approach

In this part, the reliability investigation of the IGBT is conducted by considering the long-term performance and changes in the model parameters. Each lifetime model should be regarded as particular test conditions and limitations, such as device technology and failure mechanism. Moreover, there is variability in manufacturing quality, so the coefficients might vary among IGBTs. The statistical distributions of coefficients in the Coffin–Manson and Semikron lifetime models for IGBTs are determined through a combination of experimental data analysis and statistical inference. The applied lifetime models in this study are derived from the testing data. The variations of the constants in equations (20) and (21), as well as the boundaries of the testing conditions, are available based on the data shown in [60]. To investigate the sensitivity of TCL to the input parameters, sensitivity analysis has been conducted for lifetime models’ coefficients. The results indicate that β₁ and β₂ have the most significant influence on TCL. The two temperature-related constants β₁ and β₂ are considered sources of uncertainty in the lifetime model, respectively. They are specifications of the junction temperature mission profile and have a considerable impact on TCL and IGBT lifetime. The sensitivity of TCL and lifetime to β₁ and β₂ can be evaluated individually or collectively, and the distribution of the TCL and lifetime of the IGBT can be obtained, allowing for a lifetime analysis with a specified confidence level. The lifetime can ultimately provide a more accurate and interval-based estimation to the lifetime and TCL of solder and bond wire failure mechanisms in a population of 10,000 IGBTs. Therefore, a certain standard deviation and average for the parameters are considered, and the MC method is used to randomly select β₁ and β₂. Each selected parameter is assigned to a specific IGBT. Since the inputs (β₁ and β₂) are nondeterministic, the lifetime prediction is also nondeterministic. This means that the result of the lifetime analysis, based on β₁ and β₂ (inputs represented by probability distributions), is itself a probability distribution. It is assumed that β₁ and β₂ have variations of 5% and 20%, respectively [32, 60]. In Figure 17, the confidence interval is set to 95%.

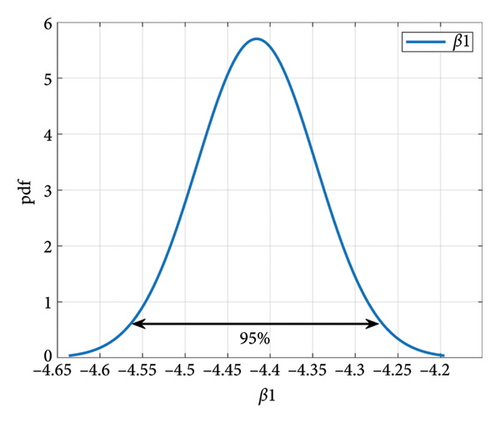
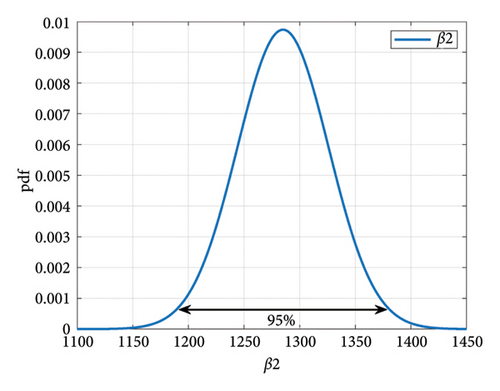
Considering k_I = 0.2 and k_p = 0.0007, the TCL of two failure mechanisms, using the MC method for a population of 10,000 IGBTs, is shown in Figures 18 and 19. Although β₂ has a large value and percentage change compared to β₁, the standard deviation of TCL distribution for both failure mechanisms is larger for β₁ changes than for β₂.

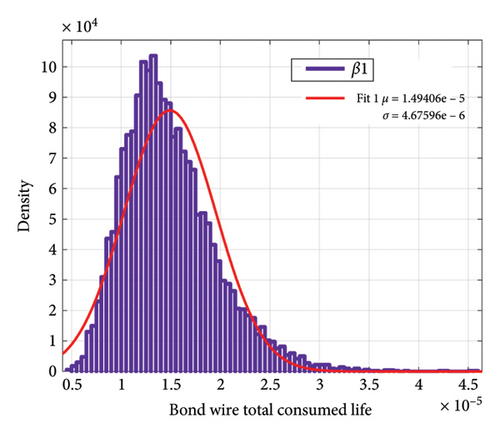
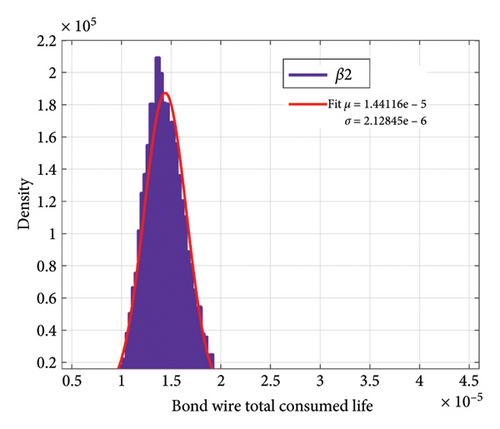
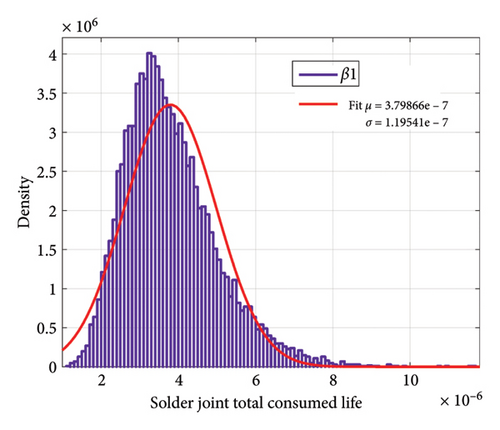
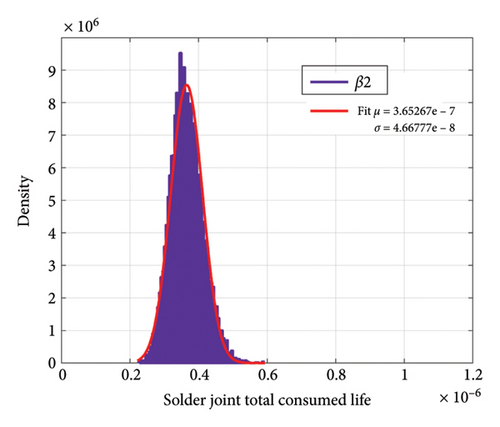
Figure 20 shows the changes in TCL according to the simultaneous changes of β₁ and β₂. As can be seen, in this case, the standard deviation in both failure mechanisms is larger than the effect of changes in either β₁ or β₂.

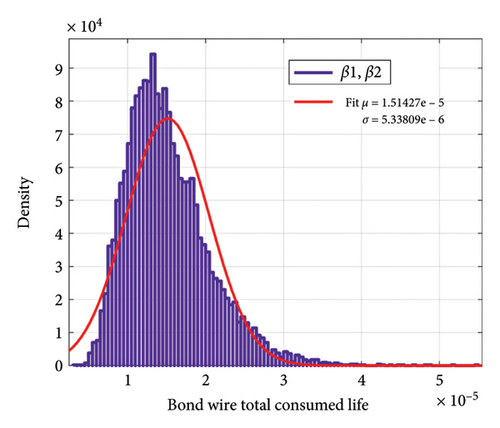
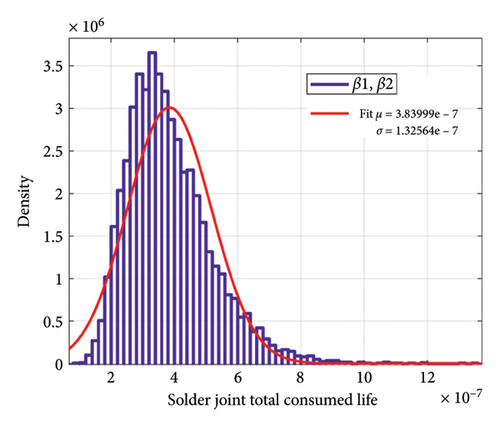
Now, if we consider the number of mission profile iterations in Figure 2 as 10 times a day, we can achieve the aging distribution of the IGBT converter according to the changes in the model parameters. Figure 21 indicates the distribution of sample ages for bond wire failure according to the changes in each of the parameters β₁ and β₂. In Figure 22, the distribution of the lifetime of the samples for solder joint failure is shown according to the changes in each of the parameters β₁ and β₂. Despite the large percentage of changes in β₂ compared to β₁, the standard deviation of the lifetime due to changes in β₂ for bond wire and solder joint failure mechanisms is 2.88 and 97.89 years, respectively, while these numbers are 6.37 and 252.6 years due to changes in β₁, respectively. Figure 23 indicates the distribution of lifetime for two failure mechanisms with the simultaneous shift in β₁ and β₂. With a confidence level of 95%, for the selected samples, for the bond wire failure mechanism, the age is between 6.1 and 34.6 years, while for the solder joint fatigue failure mechanism the age ranges from 245.2 to 1351.5 years.

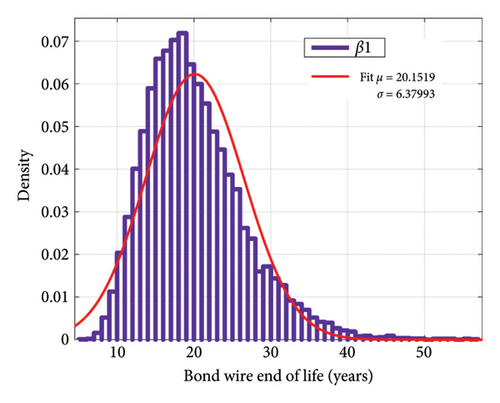
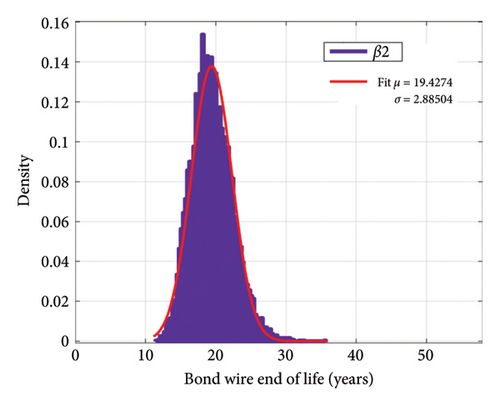
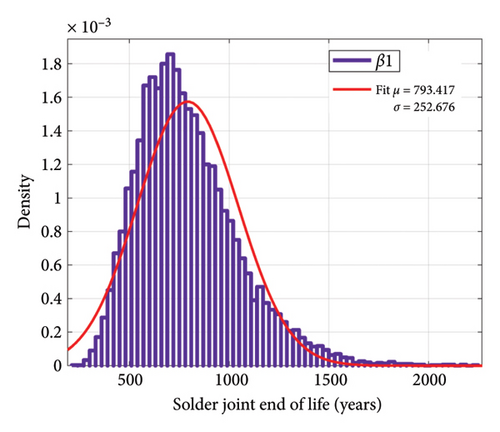
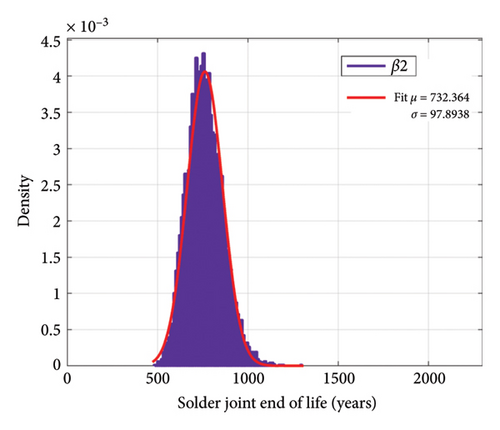
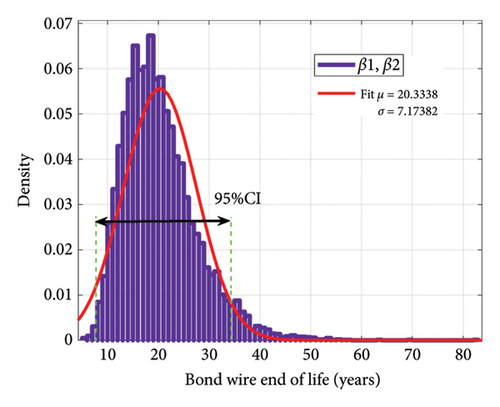
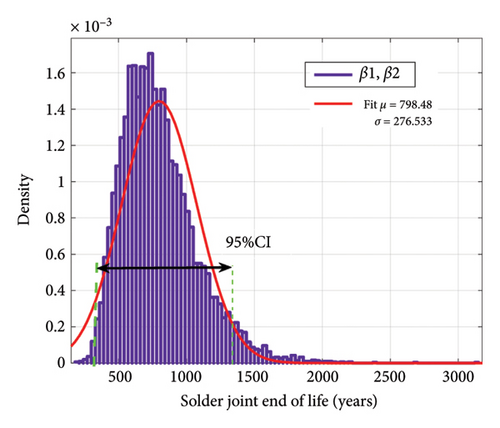
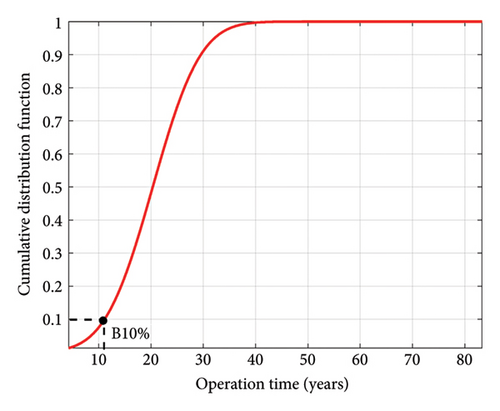
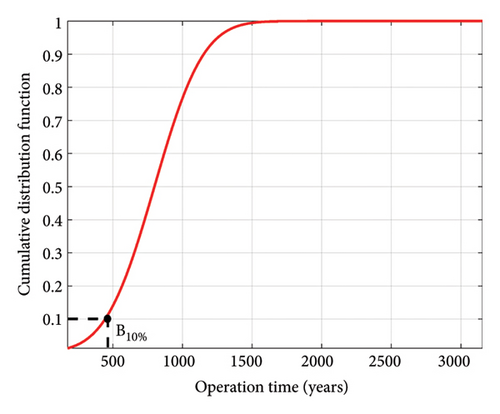
Figure 24 shows the cumulative distribution function for two IGBT failure mechanisms under simultaneous changes of β₁ and β₂. As it is known, 10% of IGBTs are expected to fail due to bond wire fatigue after 11.2 years and approximately 450 years for the solder fatigue failure mechanism. Considering the 50% and 90% failure rate of IGBTs, these numbers are 19.2 and 29.8 years for the bond wire failure mechanism and 750 and 1160 years for the solder joint fatigue mechanism, respectively.

6. Conclusion

In this paper, IGBT reliability analysis was conducted from two perspectives. Choosing a robust controller from the reliability vantage point and lifetime estimation might be controversial issues in the devising of PE converters. It is shown that the selection of the controller can affect the IGBT lifetime by several percent. The presented method can be used to design the converters and other electrical systems. From the statistical analysis point of view and MC, due to the use of the empirical method, normal distributions were considered for the coefficients of the lifetime model. Considering a statistical population of 10,000 IGBTs and a confidence level of 95%, the age range for bond wire and solder joint failures was between 6.1 and 34.6 and between 242.5 and 1351.5 years, respectively, for all parameter variations. The provided MC and control analysis can be applied to all the specifications in lifetime models and circuit variables to investigate their effects on the performance and reliability of the EV converter.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

The corresponding author contributed to the conception. All authors contributed to the study and model design. All authors commented on the manuscript. All authors read and approved the final manuscript.

Funding

No funding was received for this manuscript.

Open Research

Data Availability Statement

The data presented in this article are available on request from the corresponding author. The data of this study are displayed.

References

1 Wolfgang E., Examples for Failures in PEs Systems, ECPE on Reliability Power Electronic System. (2007) 1842–1847.
Google Scholar
2 Wang H., Liserre M., Blaabjerg F. et al., Transitioning to Physics-Of-Failure as a Reliability Driver in Power Electronics, IEEE Journal of Emerging and Selected Topics in Power Electronics. (2014) 2, no. 1, 97–114, https://doi.org/10.1109/jestpe.2013.2290282, 2-s2.0-84930246599.
10.1109/JESTPE.2013.2290282
Web of Science® Google Scholar
3 Ma K., Choi U., and Blaabjerg F., Reliability Metrics Extraction for Power Electronics Converter Stressed by Thermal Cycles, 2017 IEEE Energy Conversion Congress and Exposition (ECCE), October 2017, 3838–3843, https://doi.org/10.1109/ecce.2017.8096676, 2-s2.0-85041506902.
10.1109/ecce.2017.8096676
Google Scholar
4 Yang S., Bryant A., Mawby P., Xiang D., Ran L., and Tavner P., An Industry-Based Survey of Reliability in PE Converters, ECCE. (2009) 3151–3157.
Google Scholar
5 Chan F. and Calleja H., Reliability Estimation of Three Single-phase Topologies in Grid-Connected PV Systems, IEEE Transactions on Industrial Electronics. (2011) 58, no. 7, 2683–2689, https://doi.org/10.1109/tie.2010.2060459, 2-s2.0-79959308717.
10.1109/TIE.2010.2060459
Web of Science® Google Scholar
6 Ceccarelli L., Kotecha R. M., Bahman A. S., Iannuzzo F., and Mantooth H. A., Mission-Profile-Based Lifetime Prediction for a SiC MOSFET Power Module Using a Multi-Step Condition-Mapping Simulation Strategy, IEEE Transactions on Power Electronics. (2019) 34, no. 10, 9698–9708, https://doi.org/10.1109/tpel.2019.2893636, 2-s2.0-85068643938.
10.1109/TPEL.2019.2893636
Web of Science® Google Scholar
7 De León-Aldaco S. E., Calleja H., Chan F., and Jiménez-Grajales H. R., Effect of the Mission Profile on the Reliability of a Power Converter Aimed at Photovoltaic Applications-A Case Study, IEEE Transactions on Power Electronics. (2013) 28, no. 6, 2998–3007, https://doi.org/10.1109/tpel.2012.2222673, 2-s2.0-84879941514.
10.1109/TPEL.2012.2222673
Web of Science® Google Scholar
8 Ristow A., Begovic M., Pregelj A., and Rohatgi A., Development of a Methodology for Improving Photovoltaic Inverter Reliability, IEEE Transactions on Industrial Electronics. (2008) 55, no. 7, 2581–2592, https://doi.org/10.1109/tie.2008.924017, 2-s2.0-47049095543.
10.1109/TIE.2008.924017
Web of Science® Google Scholar
9 Zhang P., Wang Y., Xiao W., and Li W., Reliability Evaluation of Grid-Connected Photovoltaic Power Systems, IEEE Transactions on Sustainable Energy. (2012) 3, no. 3, 379–389, https://doi.org/10.1109/tste.2012.2186644, 2-s2.0-84883221230.
10.1109/TSTE.2012.2186644
Web of Science® Google Scholar
10 Moore L. M. and Post H. N., Five Years of Operating Experience at a Large, Utility-Scale Photovoltaic Generating Plant, Progress in Photovoltaics: Research and Applications. (2008) 16, no. 3, 249–259, https://doi.org/10.1002/pip.800, 2-s2.0-42249106532.
10.1002/pip.800
Web of Science® Google Scholar
11 Choi U., Vernica I., and Blaabjerg F., Effect of Asymmetric Layout of IGBT Modules on Reliability of Motor Drive Inverters, IEEE Transactions on Power Electronics. (2019) 34, no. 2, 1765–1772, https://doi.org/10.1109/tpel.2018.2828145, 2-s2.0-85045758507.
10.1109/TPEL.2018.2828145
Web of Science® Google Scholar
12 Garg P., Essakiappan S., Krishnamoorthy H. S., and Enjeti P. N., A Fault-Tolerant Threephase Adjustable Speed Drive Topology With Active Common-Mode Voltage Suppression, IEEE Transactions on Power Electronics. (2015) 30, no. 5, 2828–2839, https://doi.org/10.1109/tpel.2014.2361905, 2-s2.0-84920114557.
10.1109/TPEL.2014.2361905
Web of Science® Google Scholar
13 Vernica I., Choi U. M., Wang H., and Blaabjerg F., Wear-Out Failure of an IGBT Module in Motor Drives Due to Uneven Thermal Impedance of Power Semiconductor Devices, Microelectronics Reliability. (2020) 114, https://doi.org/10.1016/j.microrel.2020.113800.
10.1016/j.microrel.2020.113800
Web of Science® Google Scholar
14 Ma K., Liserre M., and Blaabjerg F., Lifetime Estimation for the Power Semiconductors Considering Mission Profiles in Wind Power Converter, 2013 IEEE Energy Conversion Congress and Exposition. (2013) 2962–2971, https://doi.org/10.1109/ecce.2013.6647087, 2-s2.0-84891076085.
10.1109/ECCE.2013.6647087
Google Scholar
15 Busca C. et al., An Overview of the Reliability Prediction Related Aspects of High Power Igbts in Wind Power Applications, Proceeding of the 22th European Symposium on the Reliability of Electron Devices, Failure Physics and Analysis, 2011.
Google Scholar
16 Liu H., Qin K., Loh P., and Blaabjerg F., Lifetime Estimation of MMC for Offshore Wind Power HVDC Application, IEEE Journal of Emerging and Selected Topics in Power Electronics. (2015) 2168–6777.
Google Scholar
17 Gadalla B., Schaltz E., Zhou D., and Blaabjerg F., Lifetime Prediction of Boost, Z-Source and Y-Source Converters in a Fuel Cell Hybrid Electric Vehicle Application, Electric Power Components and Systems. (2019) 46, no. 18, 1979–1991, https://doi.org/10.1080/15325008.2018.1528316, 2-s2.0-85060683675.
10.1080/15325008.2018.1528316
Google Scholar
18 Hirschmann D., Tissen D., Schroder S., and De Doncker R. W., Reliability Prediction for Inverters in Hybrid Electrical Vehicles, IEEE Transactions on Power Electronics. (2007) 22, no. 6, 2511–2517, https://doi.org/10.1109/tpel.2007.909236, 2-s2.0-36349001632.
10.1109/TPEL.2007.909236
Web of Science® Google Scholar
19 Van Mierlo J., Berecibar M., El Baghdadi M. et al., Beyond the State of the Art of Electric Vehicles: A Fact-Based Paper of the Current and Prospective Electric Vehicle Technologies, World Electric Vehicle Journal. (2021) 12, no. 1, https://doi.org/10.3390/wevj12010020.
10.3390/wevj12010020
Web of Science® Google Scholar
20 Liu T., Tang X., Wang H., Yu H., and Hu X., Adaptive Hierarchical Energy Management Design for a Plug-In Hybrid Electric Vehicle, IEEE Transactions on Vehicular Technology. (2019) 68, no. 12, 11513–11522, https://doi.org/10.1109/tvt.2019.2926733.
10.1109/TVT.2019.2926733
Web of Science® Google Scholar
21 Zhang H., Li X., Liu X., and Yan J., Enhancing Fuel Cell Durability for Fuel Cell Plug-In Hybrid Electric Vehicles through Strategic Power Management, Applied Energy. (2019) 241, 483–490, https://doi.org/10.1016/j.apenergy.2019.02.040, 2-s2.0-85062688030.
10.1016/j.apenergy.2019.02.040
Web of Science® Google Scholar
22 Ramesh M., Yadav A. K., and Pathak P. K., An Extensive Review on Load Frequency Control of Solar-Wind Based Hybrid Renewable Energy Systems, Energy Sources, Part A: Recovery, Utilization, and Environmental Effects. (2021) 47, 8378–8402, https://doi.org/10.1080/15567036.2021.1931564.
10.1080/15567036.2021.1931564
Web of Science® Google Scholar
23 Chakraborty S., Hasan M., Paul M. et al., Real-Life Mission Profile Oriented Lifetime Estimation of a SiC Interleaved Bidirectional HV DC/DC Converter for Electric Vehicle Drivetrains, IEEE Journal of Emerging and Selected Topics in Power Electronics. (2022) 10, no. 5, 5142–5167, https://doi.org/10.1109/jestpe.2021.3083198.
10.1109/JESTPE.2021.3083198
Web of Science® Google Scholar
24 Song Y. and Wang B., Evaluation Methodology and Control Strategies for Improving Reliability of HEV Power Electronic System, IEEE Transactions on Vehicular Technology. (2014) 63, no. 8, 3661–3676, https://doi.org/10.1109/tvt.2014.2306093, 2-s2.0-84908110389.
10.1109/TVT.2014.2306093
Web of Science® Google Scholar
25 Blaabjerg F., Wang H., Vernica I., Liu B., and Davari P., Reliability of Power Electronic Systems for EV/HEV Applications, Proceedings of the IEEE. (2021) 109, no. 6, 1060–1076, https://doi.org/10.1109/jproc.2020.3031041.
10.1109/JPROC.2020.3031041
CAS Web of Science® Google Scholar
26 Brüll M., Ayad A., Greif A., Rogge S., and Töns M., Lifetime Analysis of Electronics and Power Electronic Components in Electric Vehicles, 32nd Electric Vehicle Symposium (EVS32), 2019, 1–12.
Google Scholar
27 Department of Defense, Military Handbook: Reliability Prediction of Electronic Equipment, MIL-HDBK-217F.
Google Scholar
28 Harms J., Revision of MIL-HDBK-217, Reliability Prediction of Electronic Equipment, Reliability and Maintainability Symposium (RAMS), 2010, 1–3.
10.1109/RAMS.2010.5448046
Google Scholar
29 Morozumi A., Yamada K., Miyasaka T., Sumi S., and Seki Y., Reliability of Power Cycling for IGBT Power Semiconductor Modules, IEEE Transactions on Industry Applications. (2003) 39, no. 3, 665–671, https://doi.org/10.1109/tia.2003.810661, 2-s2.0-0038825362.
10.1109/TIA.2003.810661
CAS Web of Science® Google Scholar
30 Reigosa P., Wang H., Yang Y., and Blaabjerg F., Prediction of Bond Wire Fatigue of IGBTs in a PV Inverter under a Long-Term Operation, IEEE Transactions on Power Electronics. (2016) 31, no. 10.
Web of Science® Google Scholar
31 Pelka K. and Fischer K., Field-Data-Based Reliability Analysis of Power Converters in Wind Turbines: Assessing the Effect of Explanatory Variables, Wind Energy. (2023) 26, no. 3, 310–324, https://doi.org/10.1002/we.2800.
10.1002/we.2800
Web of Science® Google Scholar
32 Choi U., Jørgensen S., and Blaabjerg F., Advanced Accelerated Power Cycling Test for Reliability Investigation of Power Device Modules, IEEE Transactions on Power Electronics. (2016) 31, no. 12, 8371–8386.
Web of Science® Google Scholar
33 Yang L., Agyakwa P., and Johnson C., Physics-of-Failure Lifetime Prediction Models for Wire Bond Interconnects in Power Electronic Modules, IEEE Transactions on Device and Materials Reliability. (2013) 13, no. 1, 9–17, https://doi.org/10.1109/tdmr.2012.2235836, 2-s2.0-84874982305.
10.1109/TDMR.2012.2235836
CAS Web of Science® Google Scholar
34 Petrone G., Spagnuolo G., Teodorescu R., Veerachary M., and Vitelli M., Reliability Issues in Photovoltaic Power Processing Systems, IEEE Transactions on Industrial Electronics. (2008) 55, no. 7, 2569–2580, https://doi.org/10.1109/tie.2008.924016, 2-s2.0-47049125539.
10.1109/TIE.2008.924016
Web of Science® Google Scholar
35 Bruendlinger R., Bletterie B., Milde M., and Oldenkamp H., Maximum Power Point Tracking Performance Under Partially Shaded PV Array Conditions, Proceedings of the 21st European Photovoltaic Solar Energy Conference, Berlin, Germany, 2157–2160, September 2006.
Google Scholar
36 Barmish B. R., New Tools for Robustness of Linear Systems, 1994, Macmillian.
10.1016/S0889-5406(05)81148-5
Web of Science® Google Scholar
37 Saenz-Aguirre A., Zulueta E., Fernandez-Gamiz U., Teso-Fz-Betoño D., and Olarte J., Kharitonov Theorem Based Robust Stability Analysis of a Wind Turbine Pitch Control System, Mathematics. (2020) 8, no. 6, https://doi.org/10.3390/math8060964.
10.3390/math8060964
Web of Science® Google Scholar
38 Bevrani H., Ise T., Mitani Y., and Tsuji K., A Robust Approach to Controller Design for DC-DC Quasi-Resonant Converters, IEEJ Transactions on Industry Applications. (2004) 124, no. 1, 91–100, https://doi.org/10.1541/ieejias.124.91, 2-s2.0-77956536928.
10.1541/ieejias.124.91
Google Scholar
39 Bevrani H., Babahajyani P., Habibi F., and Hiyama T., Robust Control Design and Implementation for a Quadratic Buck Converter, International Power Electronics Conference, 2010.
Google Scholar
40 Chung H., Wang H., Blaabjerg F., and Pecht M., Reliability of PEs Converter Systems, 2015, The Institution of Engineering and Technology (IET).
10.1049/PBPO080E
Google Scholar
41 ASTM, ASTM American Society for Testing and Materials, Standard Practices for Cycle Counting in Fatigue Analysis, Designation: 1049-85 (Reapproved 1997), Annual Book of ASTM Standards, 2014, ASTM, West Conshohocken, PA, 1–10.
Google Scholar
42 Wintrich A., Nicolai U., Tursky W., and Reimann T., Application Manual Power Semiconductors, 2015, SEMIKRON International GmbH.
Google Scholar
43 Wilde J. and Zukowski E., Probabilistic Analysis of the Influences of Design Parameter on the Reliability of Chip Scale Packages, 7th International conference on thermal, Mechanical and Multiphysics in Micro-systems, April 2006, EuroSimE, 1–8.
Google Scholar
44 Bailey C., Tilford T., and Lu H., Reliability Analysis for PEs Modules, 30th International Spring Seminar on Electronics Technology (ISSE). (2007) 12–17.
Google Scholar
45 Alghassi A., Perinpanayagam S., Samie M., and Sreenuch T., Computationally Efficient, Real-Time, and Embeddable Prognostic Techniques for Power Electronics, IEEE Transactions on Power Electronics. (May 2015) 30, no. 5, 2623–2634, https://doi.org/10.1109/tpel.2014.2360662, 2-s2.0-84920186448.
10.1109/TPEL.2014.2360662
Web of Science® Google Scholar
46 Barlow T. J., Latham S., McCrae I. S., and Boulter P. G., A Reference Book of Driving Cycles for Use in the Measurement of Road Vehicle Emissions, Department for Transport Cleaner Fuels & Vehicle 4 Chris Parkin. (June 2009) 3.
Google Scholar
47 Pathak P., Yadav A., Padmanaban S., Alvi P. A., and Kamwa I., Fuel Cell-based Topologies and Multi-input DC–DC Power Converters for Hybrid Electric Vehicles: A Comprehensive Review, IET Generation, Transmission & Distribution. (2022) 16, no. 11, 2111–2139, https://doi.org/10.1049/gtd2.12439.
10.1049/gtd2.12439
Web of Science® Google Scholar
48 Shen D., Lim C., and Shi P., Robust Fuzzy Model Predictive Control for Energy Management Systems in Fuel Cell Vehicles, Control Engineering Practice. (2020) 98, https://doi.org/10.1016/j.conengprac.2020.104364.
10.1016/j.conengprac.2020.104364
Web of Science® Google Scholar
49 Hu X., Zou C., Tang X., Liu T., and Hu L., Cost-Optimal Energy Management of Hybrid Electric Vehicles Using Fuel Cell/Battery Health-Aware Predictive Control, IEEE Transactions on Power Electronics. (2020) 35, no. 1, 382–392, https://doi.org/10.1109/tpel.2019.2915675.
10.1109/TPEL.2019.2915675
Web of Science® Google Scholar
50 Purnima P. and Jayanti S., Fuel Processor-Battery-Fuel Cell Hybrid Drivetrain for Extended Range Operation of Passenger Vehicles, International Journal of Hydrogen Energy. (2019) 44, no. 29, 15494–15510, https://doi.org/10.1016/j.ijhydene.2019.04.081, 2-s2.0-85065097573.
10.1016/j.ijhydene.2019.04.081
CAS Web of Science® Google Scholar
51 García-Triviño P., Torreglosa J. P., Jurado F., and Fernández Ramírez L. M., Optimised Operation of Power Sources of a PV/Battery/Hydrogen-Powered Hybrid Charging Station for Electric and Fuel Cell Vehicles, IET Renewable Power Generation. (2019) 13, no. 16, 3022–3032, https://doi.org/10.1049/iet-rpg.2019.0766.
10.1049/iet-rpg.2019.0766
Web of Science® Google Scholar
52 De Souza L. L. P., Lora E. E. S., Palacio J. C. E., Rocha M. H., Renó M. L. G., and Venturini O. J., Comparative Environmental Life Cycle Assessment of Conventional Vehicles With Different Fuel Options, Plug-In Hybrid and Electric Vehicles for a Sustainable Transportation System in Brazil, Journal of Cleaner Production. (December 2018) 203, 444–468, https://doi.org/10.1016/j.jclepro.2018.08.236, 2-s2.0-85053214915.
10.1016/j.jclepro.2018.08.236
Web of Science® Google Scholar
53 Ahmadi S., Bathaee S. M. T., and Hosseinpour A. H., Improving Fuel Economy and Performance of a Fuel-Cell Hybrid Electric Vehicle (Fuel-Cell, Battery, and Ultra-capacitor) Using Optimized Energy Management Strategy, Energy Conversion and Management. (2018) 160, 74–84, https://doi.org/10.1016/j.enconman.2018.01.020, 2-s2.0-85044343103.
10.1016/j.enconman.2018.01.020
Web of Science® Google Scholar
54 Erickson R. W. and Maksimovic D., Fundamentals of Power Electronics, 2004, Kluwer Academic Publications.
Google Scholar
55 Siddhartha V. and Hote Y., Systematic Circuit Design and Analysis of a Non-Ideal DC–DC Pulse Width Modulation Boost Converter, IET Circuits, Devices and Systems. (2018) 12, no. 2, 144–156, https://doi.org/10.1049/iet-cds.2017.0168, 2-s2.0-85044091408.
10.1049/iet-cds.2017.0168
Web of Science® Google Scholar
56 Dave M. R. and Dave K. C., Analysis of Boost Converter Using Pi Control Algorithms, International Journal of Engineering Trends and Technology. (2012) 3, no. 2, 71–73.
Google Scholar
57 Su J. H., Chen J. J., and Wu D. S., Learning Feedback Controller Design of Switching Converters via MATLAB/SIMULINK, IEEE Transactions on Education. (2002) 45, 307–315.
10.1109/TE.2002.803403
Web of Science® Google Scholar
58 Infineon, Power Losses and Thermal Considerations, http://www.irf.com/electronics/power-losses.
Google Scholar
59 Graovac D. and Pürschel M., IGBT Power Losses Calculation Using the Data-Sheet Parameters, Application Note, Ver. (2009) 1, no. 1.
Google Scholar
60 Bayerer R., Hermann T., Licht T., Lutz J., and Feller M., Model for Power Cycling Lifetime of IGBT Modules-Various Factors Influencing Lifetime, Proceedings of the International Conference on Integrated Power Systems (CIPS), 2008, 1–6.
Google Scholar
61 Cui H., Accelerated Temperature Cycle Test and Coffin-Manson Model for Electronic Packaging, Annual Reliability and Maintainability Symposium. (2005) 556–560.
Google Scholar

All articles

Investigation of Robust Controllers and Model Uncertainty on Nonideal Boost Converter Lifetime in Hybrid Electric Vehicle

Abstract

1. Introduction

2. Analysis of the Mission Profile, Power Relationships, and Controller in the Converter