International Transactions on Electrical Energy Systems

Volume 2025, Issue 1 4779710

Research Article

Open Access

Numerical Analysis, Experimental Validation, and Application of DC Interruption With Parallel Vacuum Interrupters

Siyuan Liu,

Corresponding Author

Siyuan Liu

[email protected]

orcid.org/0000-0002-0395-1747

State Key Laboratory of Electrical Insulation and Power Equipment , Xi’an Jiaotong University , Xi’an , Shaanxi, China , xjtu.edu.cn

Search for more papers by this author

Yifan Chen,

Yifan Chen

State Key Laboratory of Electrical Insulation and Power Equipment , Xi’an Jiaotong University , Xi’an , Shaanxi, China , xjtu.edu.cn

Search for more papers by this author

Jinchao Chen,

Jinchao Chen

State Key Laboratory of Electrical Insulation and Power Equipment , Xi’an Jiaotong University , Xi’an , Shaanxi, China , xjtu.edu.cn

Search for more papers by this author

Mengze Yu,

Mengze Yu

Grid Planning & Research Center of Guangdong Power Grid Corporation , CSG , Guangzhou , Guangdong, China

Search for more papers by this author

Zhiyuan Liu,

Zhiyuan Liu

State Key Laboratory of Electrical Insulation and Power Equipment , Xi’an Jiaotong University , Xi’an , Shaanxi, China , xjtu.edu.cn

Search for more papers by this author

Yingsan Geng,

Yingsan Geng

State Key Laboratory of Electrical Insulation and Power Equipment , Xi’an Jiaotong University , Xi’an , Shaanxi, China , xjtu.edu.cn

Search for more papers by this author

Siyuan Liu,

Corresponding Author

Siyuan Liu

[email protected]

orcid.org/0000-0002-0395-1747

State Key Laboratory of Electrical Insulation and Power Equipment , Xi’an Jiaotong University , Xi’an , Shaanxi, China , xjtu.edu.cn

Search for more papers by this author

Yifan Chen,

Yifan Chen

State Key Laboratory of Electrical Insulation and Power Equipment , Xi’an Jiaotong University , Xi’an , Shaanxi, China , xjtu.edu.cn

Search for more papers by this author

Jinchao Chen,

Jinchao Chen

State Key Laboratory of Electrical Insulation and Power Equipment , Xi’an Jiaotong University , Xi’an , Shaanxi, China , xjtu.edu.cn

Search for more papers by this author

Mengze Yu,

Mengze Yu

Grid Planning & Research Center of Guangdong Power Grid Corporation , CSG , Guangzhou , Guangdong, China

Search for more papers by this author

Zhiyuan Liu,

Zhiyuan Liu

State Key Laboratory of Electrical Insulation and Power Equipment , Xi’an Jiaotong University , Xi’an , Shaanxi, China , xjtu.edu.cn

Search for more papers by this author

Yingsan Geng,

Yingsan Geng

State Key Laboratory of Electrical Insulation and Power Equipment , Xi’an Jiaotong University , Xi’an , Shaanxi, China , xjtu.edu.cn

Search for more papers by this author

First published: 10 February 2025

https://doi.org/10.1155/etep/4779710

Academic Editor: Narendra Babu P.

Share a link

Email
Wechat
Bluesky

Abstract

Large-capacity high voltage direct current circuit breakers (HVDC CBs) are critical equipment for achieving reliable operation of future multiterminal HVDC systems. The objective of this paper is to investigate the interruption characteristics of DCCB with parallel vacuum interrupters. In this paper, the proposed vacuum interrupter is modeled in detail and simulated in the PSCAD environment by taking into account the positive volt-ampere characteristics of the vacuum arc, the current transfer characteristics, and the current sharing characteristics between parallel vacuum interrupters. Then, the vacuum interrupter model is validated by experimental results. The performance of two types of large-capacity multimodule DCCBs is compared regarding operating reliability and actuator decentralization. Meanwhile, the current stress on the VSC branch and the DC interruption characteristics are analyzed. The comparison results show that the 6-module DCCB with series followed by parallel structure is more suitable for high voltage and large-capacity systems. In ±160 kV 4-terminal flexible DC grid, two typical DC fault interruption characteristics of the 6-module DCCB with series followed by parallel structure are simulated and analyzed. The results validate that the multimodule DCCB with series followed by parallel structure has better DC fault interruption performance in multiterminal HVDC systems.

1. Introduction

In recent years, the demand for renewable energy connections such as offshore wind farm and photovoltaic power plant has been gradually growing due to limited energy reserves, high cost, and environmental pollution problems [1]. The rapidly developing multiterminal flexible direct current (MTDC) transmission technology based on voltage source converter (VSC) provides a powerful solution for multiple renewable energy power stations to transmit power to multiple terminals [2, 3]. MTDC systems have a low impedance, resulting in higher fault current rise rates and larger peak values when short-circuit faults occur [4]. The vacuum interrupter (VI)-based direct current circuit breaker (DCCB) is critical equipment to protect the safe and stable operation of the MTDC system. To realize the timely interruption of DC fault, higher voltage and larger-capacity requirements for HVDC CBs are put forward [5, 6].

There are two main methods to promote DCCBs to higher voltage levels. One is to develop single-break DCCBs for higher voltage levels, and the other is to develop multibreak DCCBs [7, 8]. Since SF₆ is a strong greenhouse gas and is a crucial factor contributing to global warming [9, 10], vacuum circuit breakers (VCBs) have become an ideal choice to replace SF₆ CBs in higher voltage levels [11]. However, due to the saturation effect between the breakdown voltage of a VI and its vacuum gap, increasing the dynamic and static contact gaps cannot achieve a linear increase in the rated voltage level of single-break VCBs [12, 13]. The voltage level of the existing single-break VCB is limited to 145 kV [14], and further research is underway for a higher-grade 252 kV single-break VCB. In contrast, the multibreak VCB can fully utilize the insulation and arc extinguishing performance of the series vacuum short gap. As a result, the limitation of saturation effect is eliminated, and higher voltage levels can be achieved [15]. Ai et al. proposed a novel 6-break VCB by connecting VIs in series to increase the voltage level to 363 kV [16, 17], and uniform voltage distribution is effectively improved by connecting grading capacitors in parallel at each break [18].

The high-temperature rise due to high heat generation and limited heat transfer performance is a crucial constraint to the current-carrying ability of individual VI [19, 20]. Therefore, the scheme of connecting VIs in parallel to share the rated and fault current has been proposed. Due to the significant negative resistance characteristics of SF₆, the parallel connection of two gas interrupters (GIs) will increase the nonuniformity of the branch current [21]. In contrast, the vacuum arc has positive volt-ampere characteristics, which have a positive effect on balancing the parallel branch current [22] and contribute to the upgrading of DCCB current-carrying and interrupting performance [23, 24]. Zheng et al. modeled the current transfer process of a hybrid generator circuit breaker (HGCB) consisting of GI and VI in parallel [25]. The effects of different fault current types, arc voltages, and other factors on the current transfer time were investigated [26]. Smirnov et al. developed a vacuum arc and gas arc model for HGCB, and the effect of the contact separation moment of the GI on the current transfer time was investigated [27]. Liu et al. proposed a parallel VI scheme to cooperate in achieving generator circuit breaker (GCB) rated current-carrying and short-circuit current interruption. The reason for the arc initiation of the first operated VI was analyzed to be the change of current in the VI equivalent inductance [28]. Su et al. investigated the current uniformity characteristics of the parallel GCB based on highly coupled split reactors. They pointed out that the operating time difference between the operation of parallel VI and the differences in branch parameters have little influence on the current uniformity [5]. Han et al. proposed a large-capacity GCB scheme consisting of 6 VIs connected in parallel, and the current sharing of the static current-flow process, the current sharing of the dynamic arcing process, and the influence of external electromagnetic field on current sharing were analyzed [29].

Currently, the study mainly focuses on the parallel GCB for AC interruption, and the influence of the relevant parameters of each branch on the current uniformity and transfer time is investigated. For multimodule DCCB composed of multiple VIs connected in series and parallel, the study of DC interruption transient characteristics has not yet been reported.

The objective of this paper is to investigate the DC interruption transient characteristics of the multimodule DCCB. The rest of the paper is organized as follows: Section 2 presents a detailed mechanism of parallel current transfer, focusing on the current transfer and sharing stages. The VI in the 0–20 kA range is modeled, and the current simulation of parallel VI in comparison with experimental results is shown in Section 3. In Section 4, two types of multimodule DCCB are modeled, analyzed, and compared in terms of operating reliability and current uniformity characteristics. Then, the multimodule DCCB with series followed by parallel structure is simulated and verified in a 4-terminal MTDC system. Finally, conclusions based on the results of the study are presented in Section 5.

2. Mechanisms of Current Transfer in Parallel VIs

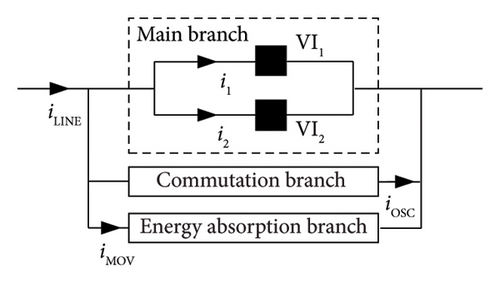
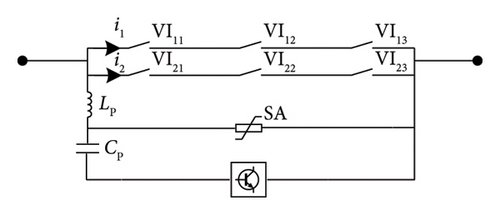
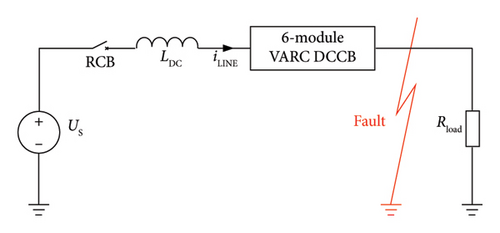
The parallel DCCB is mainly composed of the main branch, commutation branch, and energy absorption branch in parallel. The main branch comprises two or more parallel vacuum interrupters, VI₁ and VI₂, for normal conduction of line current i_LINE. The commutation branch generates oscillation current i_OSC, which is superimposed inversely with i_LINE, creating an artificial over-zero point to extinguish the arc. The energy absorption branch consists of surge arresters (SAs) with good nonlinear volt-ampere characteristics, absorbing the residual energy in the system after interruption.

Figure 1 illustrates the principal diagram of the parallel DCCB, where i_LINE is the line current through the DCCB, i₁ is the current through the VI₁, i₂ is the current through the VI₂, i_OSC is the oscillation current in the commutation branch, and i_MOV is the current through the energy absorption branch.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Principle diagram of the parallel DCCB.

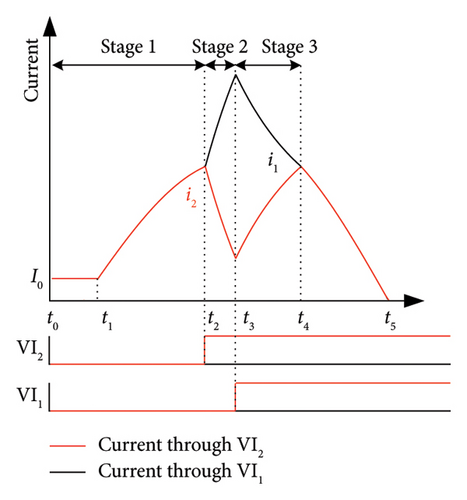
The current interruption process of the parallel DCCB can be divided into 3 stages according to whether VIs are operated or not. This section mainly analyzes the abovementioned three stages. Stage 1 is both parallel VIs are not operated. Stage 2 is when either VI is operated, and current transfer occurs in the two parallel branches. Stage 3 is when both VIs are operated, and current sharing occurs naturally. This section analyzes the abovementioned three stages specifically.

The timing indications of each VI and the variation of the current through the two parallel branches are shown in Figure 2. It needs to point out that the VIs are assumed to have the same contact resistance. The detailed operation sequence is explained as follows.

t₀ − t₁: at this stage, both VI₁ and VI₂ are closed. The two parallel branches share the line current equally, and i₁ = i₂ = I₀ exists.
t₁ − t₂: the fault occurs at the instant of t₁; therefore, i_LINE starts to increase gradually, and i₁ and i₂ also rise gradually and always share i_LINE equally. Due to the decentralization of the actuators, the two VIs are opened at different moments.
t₂ − t₃: this stage is the current transfer stage. At t₂, VI₂ is opened and VI₁ remains in the closed state. An arc is generated between the movable and static contacts of VI₂. The arc voltage leads the current to be transferred to the branch where VI₁ is located, as shown in the gradual decrease of i₂ and the gradual increase of i₁.
t₃ − t₄: this stage is the current sharing stage. Both VI₁ and VI₂ are opened at t₃. Since the vacuum arc has a positive volt-ampere characteristic, the arc voltage between the VI₁ contacts is higher than the arc voltage between the VI₂ contacts. Therefore, the arc voltage difference leads to a gradual increase in i₂ and a gradual decrease in i₁. It reaches i₁ = i₂ at t₄.
t₄ − t₅: the two parallel branches achieve the current uniformity again, shown as i₁ = i₂. Then, the current crosses the zero point at t₅.

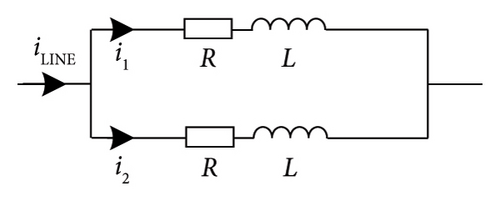
2.1. Stage 1

During regular operation of the DC power system, the main branch of the DCCB conducts, and the two parallel VIs share the i_LINE. R₁ and L₁ are the equivalent impedance of the branch where VI₁ is located, and R₂ and L₂ are the equivalent impedance of the branch where VI₂ is located. Helmer and Lindmayer pointed out that the parasitic capacitance across the gap of VI is 0.2 nF [30]. Thus, the current through the capacitors can be neglected due to the small capacitance value and small change in vacuum arc voltage.

Generally, the parameters of the VI of the same type are essentially identical. Ideally, it can be assumed that each branch has the same parameters, namely, R₁ = R₂ = R, L₁ = L₂ = L. Therefore, i₁ and i₂ will share i_LINE equally, as shown in equation (1). The corresponding equivalent circuit model is shown in Figure 3.

()

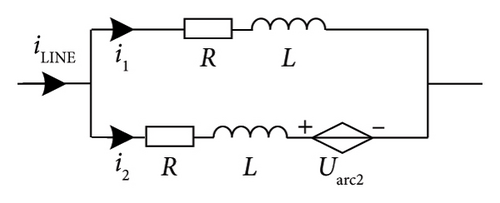
2.2. Stage 2

Due to the decentralization of the actuator, it is not easy to open the contacts of the two parallel VIs simultaneously. VI₂ is opened at t₂, an arc will be generated between the contacts of VI₂, and the arc voltage is U_arc2. At the instant, VI₁ remains closed. Therefore, branch impedances R and L only exist. The corresponding equivalent circuit model is shown in Figure 4.

From Figure 4, the circuit equations can be written as shown in equations (2) and (3), and the circuit model satisfies the initial conditions of equation (4). Based on equations (2), (3), and (4), the currents through VI₁ and VI₂, namely, i₁ and i₂, can be calculated by equation (5).

()

Based on equation (5), it can be seen that compared with Stage 1, i₂ tends to decrease and i₁ increases correspondingly. An unbalanced component exists between i₁ and i₂, defined as the transfer current i_trans, with the expression of equation (6).

()

From equation (6), the magnitude of i_trans is related to the operating moment t₁ of VI₁, the arc voltage U_arc2, and the branch impedance R and L. Therefore, equation (5) can be simplified to equation (7).

()

2.3. Stage 3

VI₁ is opened at t₃, and the arc begins to generate between the contacts of VI_1. The arc voltage is U_arc1. Currently, the two parallel branches are in the arcing state. The corresponding equivalent circuit model is shown in Figure 5.

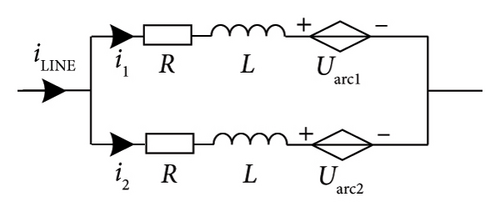
The current sharing phenomenon between VIs is due to the vacuum arc having a positive volt-ampere characteristic, which means the arc voltage increases with the increase of arc current. As the VI₁-operating moment lags behind VI₂, there has been i₁ > i₂. At the instant, the arc voltage difference exists between the two parallel branches. After VI₁ is operated, the voltage difference leads i₁ to transfer to the branch where VI₂ is located.

The model satisfies the current relationship of equation (3), the voltage relationship of equation (8), and the initial conditions of equation (9). To avoid the branch where VI₁ is located carrying the i_LINE alone, it should be noted that VI₁ should be operated before VI₂ extinguishes the arc.

()

Based on equations (3), (8), and (9), i₁ and i₂ can be calculated from equation (10). The i_ave in equation (10) is the current that is transferred again between branches after VI₁ is operated, which is defined as the uniform current and expressed as equation (11).

()

Comparing equations (5) and (11), the current difference of i₁ is i_ave. It can be seen that the current sharing phenomenon between the two parallel VIs is due to the new generation of U_arc2 based on Stage 2, which is supported by the form of i_ave.

3. Modeling and Experimental Validation of Current Transfer

3.1. Numerical Modeling of Vacuum Arc

The VI model is first established according to the state of VI, and the current interruption process is simulated and investigated. The state of the VI can be divided into three categories, namely, the closed state, the arcing state, and the open state. The equivalent parameters of the VI model in the different states above are shown in Table 1.

Table 1. Parameters of the VI model.

Parameters	Label	Value			Unit
Parameters	Label	Close	Arcing	Open	Unit
Branch resistance	R	8 × 10⁻⁵	8 × 10⁻⁵	10⁶	Ω
Branch inductance	L	2	2	2	μH
Arc voltage	U_arc	/	(12)	/	V

When the VI is in the close state, its contacts are closed and VI can be equivalent to a low impedance with R_close = 0.0008 Ω and L = 2 µH [31]. When the VI receives a trip signal, its contacts are gradually separated, generating a vacuum arc between the two contacts. The vacuum arc plasma formed between contacts is a kind of complex charged fluid, and its behavior is highly dynamic [32]. In the arcing process, the arc mode, plasma density, and contact surface temperature of VI are always changing [33]. In addition, there are some physical fields, such as the thermal field, electromagnetic field, and fluid field coupling with each other, affecting the behaviors of the vacuum arc [34]. Therefore, the complicated variation process of arc combustion and extinction cannot be simulated in the PSCAD environment. The arcing state of VI is equivalent to a low impedance and a DC voltage source in series by considering the vacuum arc characteristics [35]. The voltage source direction is the same as the current direction. It has been shown that the vacuum arc voltage increases with the increase of arc current, showing a positive volt-ampere characteristic. The voltage-current relationship of diffusion-type vacuum arc can be obtained by linear equation [36]. In [36, 37], the primary coefficient in the slope-intercept fitting equation of the vacuum arc is in the order of 0.38 and 2.6, which is influenced by the effects of contact type, contact material, and vacuum gap. In addition, the vacuum arc voltage is in the range of 20–100 V according to [38]. Therefore, the corresponding coefficients of the slope-intercept form are selected as 0.0015 and 20, and equation (12) is obtained finally. After the contacts of VI are entirely open and the arc has been extinguished, the VI is in an open state and can be equated to a high impedance with R_open = 10⁶ Ω and L = 2 µH [31].

()

3.2. Experiment Setup

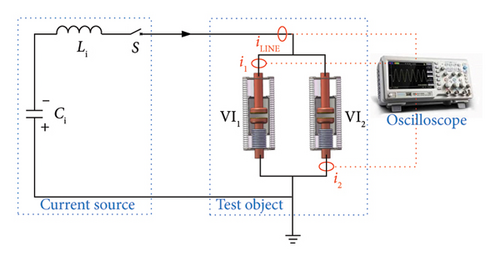
As shown in Figure 6, the synthetic experimental current source circuit comprises current source capacitance C_i, current source inductance L_i, and 12 kV closing switch CB₀ in series. The specific values of each parameter are shown in Table 2.

Table 2. Synthetic experimental current source circuit parameters.

Parameters	Label	Value	Unit
Current source capacitance	C_i	55.76	mF
Current source inductance	L_i	0.1867	mH
Charging voltage of Ci		1.6	kV
Frequency of fault current	f	50	Hz

The test object consists of two parallel vacuum interrupters VI₁ and VI₂. One terminal of the test object is connected to the current source, and the other terminal is directly grounded. CB₀ is disconnected, and C_i is precharged before the test starts. When the test begins, CB₀ is closed. At which instant, the current source circuit is conducted, and the test current is generated by discharging the precharged C_i.

3.3. Test Results and Analysis

The test results for the current interruption of the two parallel VIs are shown in Figure 7. In this test, the short-circuit current starts to be generated by the current source at t = 0 ms, and VI₁ and VI₂ carry i_LINE on average.

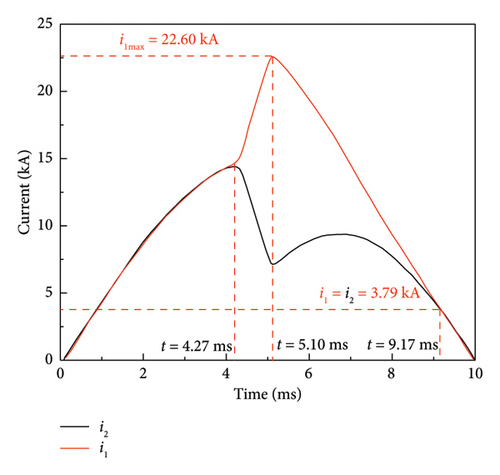
At t = 4.27 ms, VI₂ receives a trip signal. VI₂ opens and an arc is generated between the movable and static contacts of VI₂, VI₁ remains in the closed state. At this instant, the arc voltage at the break leads to a current transfer, corresponding to a gradual decrease in i₂ and a gradual increase in i₁. At the instant of t = 5.1 ms, the peak value of i₁ increases to 22.6 kA, and VI₁ receives the trip signal to operate. Both VI₁ and VI₂ are in the arcing state. Since the vacuum arc has a positive volt-ampere characteristic, the arc voltage generated between the contacts of VI₁ after the operation is relatively higher than that of VI₂. Therefore, the arc voltage difference between the two parallel branches leads i₂ to increase gradually and i₁ to decrease progressively. As seen in Figure 7, i₁ = i₂ = 3.79kA, and the two parallel branches achieve current uniformity again at the instant of t = 9.17 ms. At t = 10 ms, the current through VI₁ and VI₂ crosses zero, and the arc is extinguished.

VI is replaced in the PSCAD with the model consisting of a resistor, an inductor, and a voltage source in series. The test circuit shown in Figure 6 is also constructed, and the operating timing of the two parallel VI is set in the same as the experiments by delaying the operation of VI₁ compared with VI₂. Figure 8 shows the comparison of simulated and experimental results for i₁and i₂ in the current transfer and sharing process.

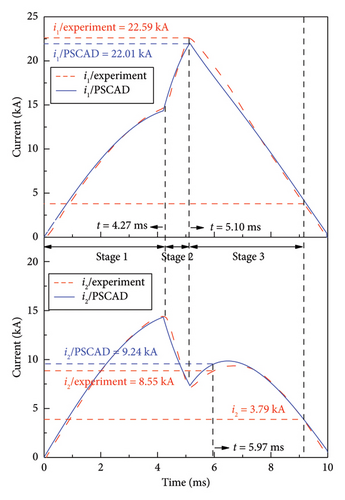
It can be seen that the simulated peak value of i₁ is 22.01 kA at t = 5.10 ms, which is decreased by 2.57% compared with the tested peak value of i₁ = 22.59 kA. In addition, the maximum difference between the simulation and experiment results of i₂ is in the current sharing process, which is 9.24 kA at t = 5.97 ms, and the error calculated is around 7.47%. There are slight differences between the measured and simulated current of i₁ and i₂, which stems primarily from the complicated variation process of arc combustion and extinction cannot be simulated accurately in the PSCAD environment. The actual influence of the arc mode, plasma density, contact surface temperature of VI, multiple physical fields, etc. is neglected when using equation (12) to represent the arcing state of VI.

In practice, VI is driven by an actuator to achieve opening and closing, the actuator consists of a moving conductive rod, an insulating rod, an opening and closing coil, a repulsion metal plate, and the charging capacitors for the two coils. Due to the deviations in the assembly process of the abovementioned key components composing the VI, decentralization also exists in the multiple operations for a single actuator. In the test, the decentralization of the ultrafast VI is no more than 50 μs when a single actuator is operated several times. In addition, the difference in the operating moments of the two parallel VI is described as the actuator decentralization, which is affected by factors such as the capacitance value of the storage capacitor, the charging voltage deviation, and the machining size deviation of the components, and is usually does not exceed 1 ms. It can be seen that the operating decentralization of the two VIs in Figure 8 is 0.91 ms.

It can be seen that the simulated current results and the experimental measurements are in good agreement during the whole test process. Therefore, the constructed model can continue to be applied to represent VI in the large current interruption simulation of multimodule DCCB. Then, DC interruption transient characteristics of the multimodule DCCB can be simulated and analyzed.

4. Performance Comparison of Two Types of Multimodule VARC DCCB

To adapt to the higher voltage level requirements of the system, several VIs are connected in series to satisfy the N-1 criterion and avoid overall failure due to a VI failure. In addition, VIs are connected in parallel to meet the higher requirements of rated current-carrying performance and short-circuit current interruption performance. Therefore, there are two types of structure for multimodule DCCBs, as shown in Figure 9, namely, series followed by parallel, and parallel followed by series.

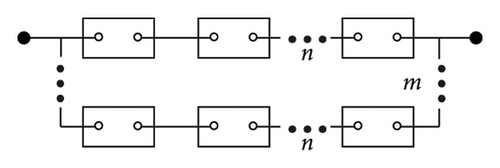
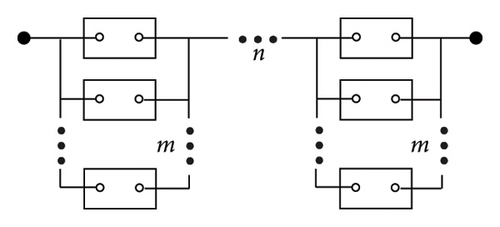
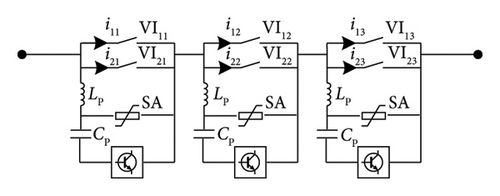
Figure 9(a) shows the type of series followed by parallel structure. n VIs are connected in series to constitute a branch, and the same m branches are connected in parallel to constitute the main branch of DCCB. Figure 9(b) shows the type of parallel followed by series structure. m VIs are connected in parallel to constitute a unit, and the same n units are connected in series to constitute the main branch of DCCB.

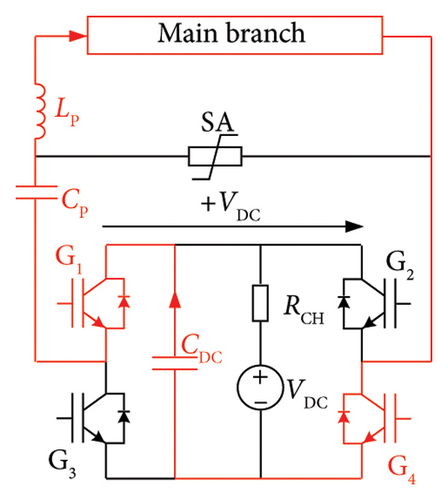
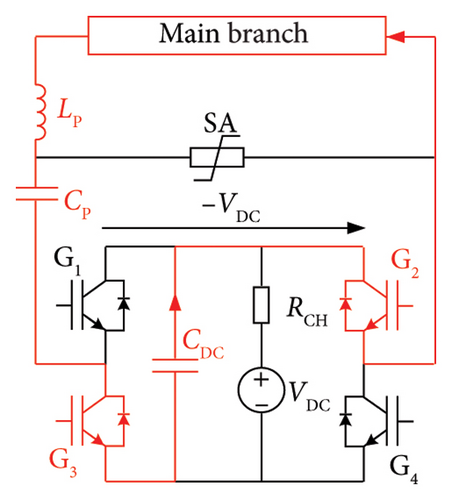
Ängquist et al. proposed the concept of VSC-assisted resonant current (VARC) DCCB and elaborated on the constitute and working principle of VARC DCCB [35, 39]. VARC DCCB consists of three branches in parallel, namely, the main branch, the commutation branch, and the energy absorption branch. The main branch comprises VIs in series and parallel, and the line current flows through the main branch during the normal operation of VARC DCCB. The commutation branch consists of two parts, as shown in Figure 10. The first part is an oscillation circuit composed of an oscillation capacitor (C_P) and an oscillation inductor (L_P). The second part is a VSC, an energy storage capacitor (C_DC), and a charging circuit (V_DC, R_CH) for C_DC. C_DC is precharged before the operation of VARC DCCB. The energy absorption branch consists of SAs, absorbing the residual electromagnetic energy stored in the system.

No matter the number and the structure type of VIs in the main branch, the commutation is achieved by converting the two states of VSC to generate the oscillation current i_OSC of gradually increasing amplitude. In the first state, G₁ and G₄ are triggered, forming an oscillation circuit of C_DC − G₁ − C_P − L_P − VI − G₄, as shown in Figure 10(a). C_DC discharges through the forming oscillation circuit until i_OSC crosses zero, and the first half-wave I_P of i_OSC is obtained by equation (13). Then, the commutation branch turns to the second state, in which G₂ and G₃ are triggered. Another oscillation circuit of C_DC − G₂ − VI − L_P − C_P − G₃ is formed, and C_DC continues to discharge through the newly formed oscillation circuit until i_OSC crosses zero again, as shown in Figure 10(b). Then, the two bridge arms in the VSC are conducted alternately at the oscillation frequency of the i_OSC, increasing the amplitude of i_OSC by 2 I_P every half cycle. Therefore, i_OSC increases continuously with the number of half-waves, which is superimposed inversely on the main branch to produce an artificial current-zero crossing (CZC). Then the arc between the mechanical contacts is extinguished.

()

Currently, the rated voltages of several typical MTDC systems are 160, 320, and 550 kV. Using 80 kV VI to constitute a branch of the DCCB main branch, it is necessary to connect 2 VIs in series to extend the rated voltage of the DCCB to 160 kV. After considering redundancy to satisfy the N-1 criterion in a 160 kV MTDC system, 3 VI modules of 80 kV are required for a branch of the DCCB main branch. Similarly, a branch of the DCCB main branch applied in the MTDC system at 320 kV and 550 kV consists of 5 VI modules of 80 kV and 8 VI modules of 80 kV in series, respectively. The number of branches in parallel to constitute the main branch is determined by the MTDC system and the rated short-circuit interruption current of the VI. The optimal number of VI modules required for the DCCB altogether is the product of the number of parallel branches of the main branch and the number of VIs in one branch.

To satisfy the 160 kV/20 kA system voltage and current interruption requirements, the main branch of the 160 kV VARC DCCB requires a total of 6 VIs of 80 kV/10 kA connected in series and parallel. Figure 11(a) shows the 160 kV 6-module VARC DCCB with series followed by parallel structure, the main branch of which constitutes 2 branches in parallel, and each branch consists of 3 VIs in series. The 160 kV 6-module VARC DCCB with parallel followed by series structure is shown in Figure 11(b), the main branch of which constitutes 3 units in series, and each unit consists of 2 VIs in parallel. The rated voltage of the SA in Figure 11(a) is 160 kV, and the rated voltage of each SA in Figure 11(b) is 80 kV. The operating voltage of the SA is selected as 1.5 times the rated voltage of the DC power system.

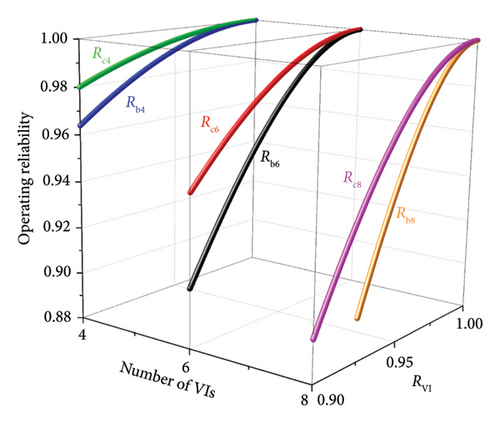
4.1. Comparison of Operating Reliability

It should be pointed out that the mechanical failure of VI on the main branch is considered. The effects of aging factors, such as environmental temperature and mechanical wear, on the operation of the actuators are difficult to obtain through theoretical analysis and are not considered. In engineering applications, the failure rate function of a product usually exhibits a bathtub curve [40], with the failure rate λ approximated as a constant. The life of VI obeys the most common form of exponential distribution [40, 41], and the operating reliability R_VI of VI is calculated by the following equation.

()

For the multimodule DCCB with series followed by parallel structure in Figure 9, it can work normally when any up to 2 VIs fail. R_c is the operating reliability of this type of DCCB, which can be calculated by equation (15). For the multimodule DCCB with parallel followed by series structure in Figure 9, it can work normally for any up to a VI fails. Therefore, the operating reliability R_b of this type of DCCB can be calculated by equation (16).

()

Figure 12 illustrates an example comparing the operational reliability of two types of 4-module, 6-module and 8-module DCCBs. R_c4, R_c6, and R_c8 are the operating reliability of the 4-module, 6-module, and 8-module DCCBs with series followed by parallel structure. R_b4, R_b6, and R_b8 are the operating reliability of the 4-module, 6-module, and 8-module DCCBs with parallel followed by series structure. Due to the low probability of VI failure, R_VI is greater than 0.9. In Figure 12, it can be seen that R_c4 > R_b4, R_c6 > R_b6, and R_c8 > R_b8. Therefore, the operational reliability of multimodule DCCBs with series followed by parallel structure is always higher than that of multimodule DCCBs with parallel followed by series structure regardless of the number of VIs.

According to [42], the failure rate of VI in an AC distribution system of 10 kV voltage level is λ = 0.006 times/a. Therefore, R_Vi = 0.994 can be calculated from (14). Based on the abovementioned analysis, the operating reliability R_c6 and R_b6 of the two types of 160 kV 6-module VARC DCCB can be calculated by equations (17) and (18), respectively. The specific details of R_c6 and R_b6 zoomed in Figure 12 are shown in Figure 13. It can be seen that R_{c6_VARC} = 99.978% and R_{b6_VARC} = 99.957% for R_vi = 99.4%.

()

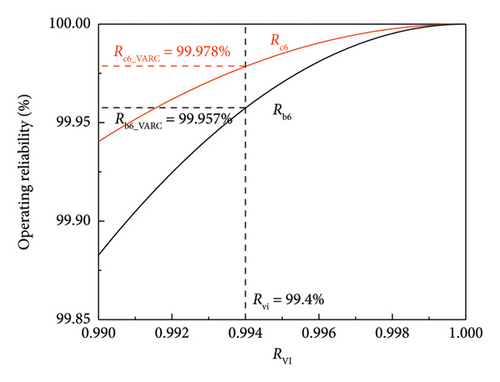
From Figure 13, the reliability of the 160 kV 6-module VARC DCCB with series followed by parallel structure is R_{c6_VARC} = 99.978%, higher than that of the 160 kV 6-module VARC DCCB with parallel followed by series structure. Therefore, the 160 kV 6-module VARC DCCB with series followed by parallel structure is more reliable. Similarly, the operating reliability of two types of DCCB can be calculated and compared at other voltage levels.

4.2. Comparison of Interruption Performance

The above two types of 160 kV 6-module VARC DCCB are modeled in the PSCAD environment, and the simulation model is shown in Figure 14. The rated voltage and rated current of the DC system are 160 kV and 1 kA, and the parameters are shown in Table 3.

Table 3. Synthetic experimental current source circuit parameters.

DC system parameters	Label	Value	Unit
Source voltage	U_s	160	kV
Inductance of fault current limiting reactor	L_DC	100	mH
Load resistance	R_load	160	Ω
Fault resistance	R_fault	0.1	Ω

The fault occurs at t = 20 ms, and the trip signal is sent to the 160 kV 6-module VARC DCCB at t = 22 ms. Then, actuators start to drive the separation of the VIs at the instant. The operating time of the 6 VIs is set to obey a general normal distribution with a mean µ = t_mean = 3 ms and standard deviation σ = 20 µs so that the difference between the VI operating moments is within 50 µs. Figure 15 shows the current interruption simulation results corresponding to the two types of 160 kV 6-module VARC DCCB of Figure 11.

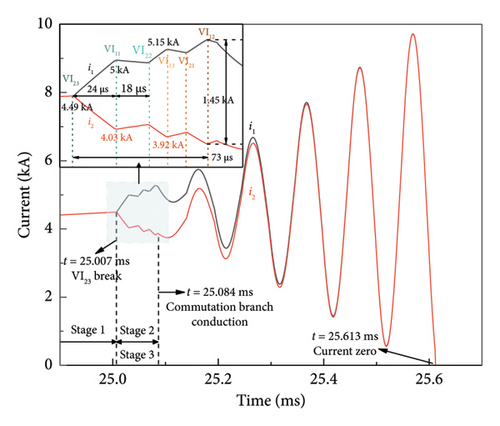
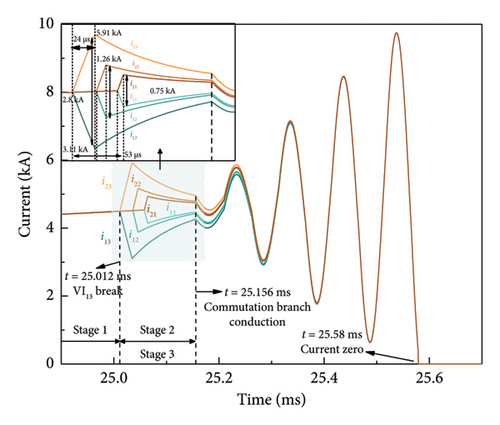
Figure 15(a) shows a typical current interruption simulation result for the 160 kV 6-module VARC DCCB with series followed by parallel structure. In the simulation, 6 VIs are operated sequentially in the order of VI₂₃, VI₁₁, VI₂₂, VI₁₃, VI₂₁, and VI₁₂. At t = 25.007 ms, i₁ = i₂ = 4.49 kA. At the instant, VI₂₃ is opened first and a vacuum arc is generated between the contacts of VI₂₃ and the remaining VIs are in the closed state. The arc voltage leads the current to transfer to the parallel branch, corresponding to a gradual decrease of i₂ from 4.49 kA to 4.03 kA and a gradual increase of i₁ from 4.49 kA to 5 kA. At t = 25.031 ms, VI₁₁ is operated, and the vacuum arc is generated between its contacts. The arc voltage difference between the two parallel branches leads i₁ and i₂ tend to be gradually uniform. At the instant of t = 25.049 ms, VI₂₂ is operated, and VI₂₃ and VI₂₂ on the same branch are arcing now. Since the arc voltage value of the short gap series is higher than that of the parallel branch, the current transfer occurs again. This is shown by a gradual decrease of i₂ to 3.92 kA and a gradual increase of i₁ to 5.15 kA based on the previous current sharing stage. Similarly, current sharing occurs again in the two parallel branches after VI₁₃ is operated. At the instant, VI₁₁ and VI₁₃ on the same branch are arcing now. The variation trend of i₂ and i₁ is similar to the abovementioned situation after VI₂₁ and VI₁₂ are operated sequentially, corresponding to the third occurrence of the current transfer and sharing process. It can be seen that there is a time difference of 73 µs between the last operated VI₁₂ and the first operated VI₂₃. In the period, the maximum current difference between i₁ and i₂ is 1.45 kA, which occurs at the operating moment of the VI₁₂. At t = 25.084 ms, VSC in the commutation branch is conducted, and the resulting gradual oscillation current is superimposed on the main branch in the reverse direction. In this process, i₁ and i₂ are gradually uniform. At t = 25.613 ms, an artificial over-zero point is generated, and i₁ and i₂ cross zero simultaneously.

Figure 15(b) shows a typical current interruption simulation result for the 160 kV 6-module VARC DCCB with parallel followed by series structure. In this simulation, 6 VIs are operated sequentially in the order of VI₁₃, VI₂₃, VI₁₂, VI₂₂, VI₁₁, and VI₂₁. At t = 25.012 ms, the current in each branch rises to 2.5 kA. At the instant, VI₁₃ is opened first and a vacuum arc is generated between the contacts of VI₁₃, the remaining VIs are in the closed state. Since VI₁₃ and VI₂₃ are connected in parallel, the arc voltage leads the current to transfer in the two branches, corresponding to i₁₃ and i₂ decreasing to 3.1 kA and i₂₃ and i₂ increasing to 5.91 kA. At t = 25.036 ms, VI₂₃ is operated, generating a vacuum arc between its contacts. At the instant, both VI₁₃ and VI₂₃ in the third unit are arcing now. The arc voltage difference leads i₁₃ and i₂₃ to be gradually uniform. The maximum difference between i₁₃ and i₂₃ is 2.8 kA during the above period. Since none of the remaining VIs are operated, the parallel branches within each unit continue to share the current uniformly. When VI₁₂ is operated, i₁₂ gradually decreases and i₂₂ gradually increases. The maximum difference between i₁₂ and i₂₂ is 1.26 kA. After VI₂₂ is operated, both VI₁₂ and VI₂₂ in the second unit are arcing. Similarly, the arc voltage difference leads i₁₂ and i₂₂ to be gradually uniform. The current variation is similar when VI₁₁ and VI₂₁ are operated, corresponding to a maximum difference of 0.75 kA between i₁₁ and i₂₁. It can be seen that the time difference between the last operated VI₂₁ and the first operated VI₁₃ is 53 µs, and the current difference between i₁₃ and i₂₃ is the largest within the 3 VI units. The reason is that the operating time difference between VI₁₃ and VI₂₃ is relatively more prolonged, and the current transfer value is also more significant. At t = 25.156 ms, VSC in the commutation branch of each VI unit is conducted, and the resulting gradual oscillation current is superimposed inversely on the main branch. In this process, the current in the parallel branch is gradually uniform and finally crosses zero at t = 25.58 ms.

It can be seen that in Figure 15(a), i₁ and i₂ change accordingly when 6 VIs are operated. In Figure 15(b), the current variation within each VI unit is affected by the two parallel VIs of that unit. Multiple repetitive simulations are performed since the differences in the operating time of the 6 VIs are always variable.

To quantify and analyze the effect of the actuator decentralization, the absolute value of the maximum difference between the parallel current in the current transfer and sharing process is defined as Δi by equation (19). Equation (20) defines the difference between the occurrence moment of Δi and the average operating time t_mean of the VI as Δt. t_mean refers to the average time from the receipt of the trip signal to the operation of the VI.

()

To compare the interruption performance of the two types of 160 kV 6-module VARC DCCB, the values of Δi and Δt in 50 simulations are statistically obtained in Figure 16.

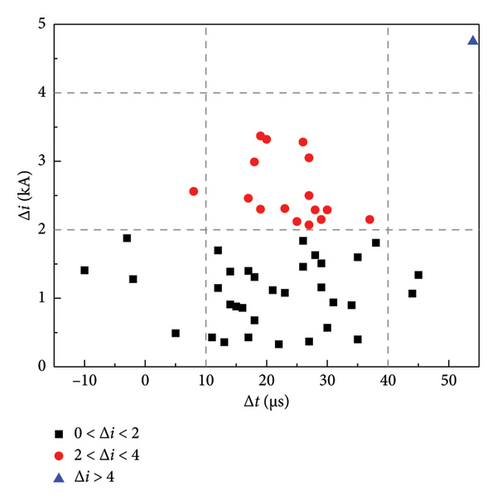
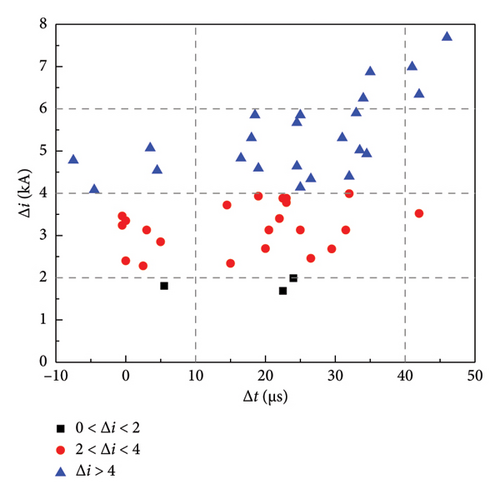
Figure 16(a) shows the variation of Δi when 160 kV 6-module VARC DCCB with series followed by parallel structure interrupts the current. The results indicate that the absolute value of the maximum difference between the parallel current Δi is basically in the range of 0–4 kA, where it is more in the range of 0–2 kA, accounting for 66% of the total number of simulations. Then, it is followed by 2–4 kA, which occurs 32% of the total number of simulations. While the case of Δi > 4 kA occurs only once. Figure 16(b) shows the variation of Δi when 160 kV 6-module VARC DCCB with parallel followed by series structure interrupts the current. The results indicate that the absolute value of the maximum difference between the parallel current Δi is more often between 2 and 6 kA, with occurrences between 2–4 kA and 4–6 kA accounting for 44% and 38% of the total number of simulations. Since the magnitude of the transferred current in the parallel branches is affected by the actuator decentralization, the occurrence time of Δi is always variable but within 10–40 µs after t_mean, regardless of which VARC DCCB is used.

Compared with the 160 kV 6-module VARC DCCB with parallel followed by series structure, the absolute value of the maximum difference between the parallel current Δi of the 160 kV 6-module VARC DCCB with series followed by parallel structure is relatively more minor. Therefore, the 160 kV 6-module VARC DCCB with series followed by parallel structure exhibits better interruption performance during the high current interruption process. In addition, it has a mitigating effect on the current imbalance caused by the actuator decentralization, and it is also more suitable for high voltage and large-capacity DC power systems.

4.3. Comparison of the Energy Absorption

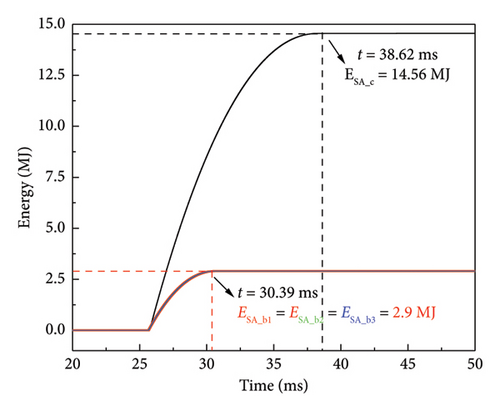
During the current interruption process, the system keeps charging C_P until its voltage reaches the clamping voltage of SA when an artificial CZC is created in the arc current. Then SA starts to conduct and the line current is commutated into the energy absorption branch. Figure 17 illustrates the comparison of SA energy absorption for the two types of 160 kV 6-module VARC DCCB. E_{SA_c} is the energy absorbed by SA in the VARC DCCB with series followed by parallel structure, and the absorbed energy of the SA is E_{SA_c} = 14.56 MJ. E_{SA_b} represents the absorbed energy of 3 SAs in the VARC DCCB with parallel followed by series structure, and the corresponding absorbed energy of each SA is 2.9 MJ. In this way, the total absorbed energy for 3 SAs is E_{SA_b} = 2.9 × 3 = 8.7 MJ. It can be seen that E_{SA_c} increases by 5.86 MJ over E_{SA_b}, and it is increased by 40.25% compared with E_{SA_b}. The cost and volume of the SA increase correspondingly. Moreover, the time taken for energy absorption is slightly affected by different operating voltages of SA. When an artificial CZC is created in the arc current, the system keeps charging C_P, and its voltage increases gradually. Therefore, the voltage across VI also increases, accelerating the speed of the fault current drop to zero. In Figure 17, the time taken for the same energy absorption by SA in the VARC DCCB with series followed by parallel structure is shorter than that in the VARC DCCB with series followed by parallel structure.

4.4. Comparison of Costs

The economy of DCCB is particularly important in promoting its application in engineering. The cost of components for the two types of 160 kV 6-module VARC DCCB is estimated according to the marketing investigation of component prices, and the comparison results are presented in Table 4. The cost of each component is represented separately by the nominal value, and 10,000 USD corresponds to 1 p.u. The costs of VIs in the main branch are largely determined by the system voltage and current levels. Since the main branch in the two types of 160 kV 6-module VARC DCCB consists of 6 VIs of 80 kV, the part of the cost is the same and not considered. In addition, the cost of inductors can be neglected because the prices are much lower than that of capacitors. Therefore, only the cost of C_P, C_DC, and IGBTs are considered in the commutation branch. The cost of the capacitors is proportional to their capacity, and the price coefficient is generally taken as 0.22 USD/J [43]. The same type of IGBT (5SNA3000K452300, 4.5 kV, 3 kA, 6195.31 USD) [44] is selected to enable a fair comparison. The cost of SA is proportional to the magnitude of the absorbed energy, and the coefficient is 13.76 USD/kJ [45]. From Figure 17, the absorbed energy E_{SA_c} and E_{SA_b} are obtained, and the cost of SAs required can be calculated, respectively.

Table 4. Cost comparison of the two types of 160 kV 6-module VARC DCCB.

Index		Series followed by parallel	Parallel followed by series
Capacity of VI		80 kV/10 kA
Oscillation component (C_P / C_DC)		5 μF/3 mF	6.25 μF/3 mF
Cost	C_P	3.17 p.u	2.97 p.u
	C_DC	1.07 p.u	1.07 p.u
	IGBT	2.48 p.u	7.44 p.u
	SA	20.03 p.u	11.97 p.u
	Total	26.75 p.u	23.45 p.u

Compared with the 160 kV 6-module VARC DCCB with parallel followed by series structure, the number of IGBT used in the 160 kV 6-module VARC DCCB with series followed by parallel structure is much lower, and the cost of the power electronic devices is saved. However, the energy absorbed by 160 kV 6-module VARC DCCB with series followed by parallel structure E_{SA_c} is increased by 40.25%, which increases the cost and volume of the SA correspondingly [46]. From Table 4, the overall cost of the 160 kV 6-module VARC DCCB with series followed by parallel structure is 12.34% higher than that of the 160 kV 6-module VARC DCCB with parallel followed by series structure.

In this section, the reliability, interruption performance, energy absorption, and costs of the two types of 160 kV 6-module VARC DCCB are compared. The comparison results suggest that the VARC DCCB with series followed by parallel structure has a higher operating reliability and better current interruption performance. It is less likely to fail and more suitable for high-voltage and large-capacity DC power systems. In addition, it features fewer IGBTs in the commutation branch, contributing to the simplification of the structure and control. Correspondingly, the requirements of energy absorption and the total cost for VARC DCCB with series followed by parallel structure are relatively higher, but the cost difference is not much. Therefore, it is chosen for the large-current interruption analysis in the later section due to the superior current interruption performance at a comparable cost for the two types of 160 kV 6-module VARC DCCB.

5. Interruption Performance in MTDC Systems

The comparative analysis of the two types of 160 kV 6-module VARC DCCB in the previous section indicates that the former 160 kV 6-module VARC DCCB with series followed by parallel structure has higher operating reliability and is less affected by the actuator decentralization when interrupting the current. Therefore, the 160 kV 6-module VARC DCCB with series followed by the parallel structure shown is selected to be applied in the MTDC system.

Figure 18 shows the configuration of ±160 kV 4-terminal MTDC system, and the specific parameters are shown in Table 5. All converters adopt the half-bridge submodule (HBSM) based modular multilevel converter (MMC), where MMC1 and MMC3 are connected to the onshore AC grid, MMC2 and MMC4 are connected to the offshore wind power plant. The 4 converters are connected by 100 km transmission cables. B is the 160 kV 6-module VARC DCCB with series followed by parallel structure, and the parameters are shown in Table 6. L is the line inductance of 75 mH.

Table 5. Parameters of the MTDC system.

Parameters	Converters
Parameters	MMC1	MMC2	MMC3	MMC4
Active power	1000 MW	600 MW	800 MW	800 MW
Control mode	PVdc	PQ	PQ	PQ
DC voltage	±160 kV
Number of bridge arm submodules	350
Bridge arm resistance	0.08 Ω
Bridge arm inductance	42 mH
Bridge arm capacitance	31 µF
Line inductance	75 µH

Table 6. Parameters of 160 kV 6-module VARC DCCB.

VARC DCCB parameters	Label	Value	Unit
Oscillation inductance	L_P	50	μH
Oscillation capacitance	C_P	5	μF
Energy storage capacitance	C_DC	3	mF
Charging voltage of CDC	V_DC	1.8	kV
Rated voltage of SA	V_R	160	kV

It should be pointed out that the HBSM topology is equivalent to a diode on-state during DC fault blocking, which does not have DC fault ride-through capability. Only the current interruption performance of the VARC DCCB in this case is considered in the paper.

The conventional full-bridge submodule (FBSM) during DC fault blocking can provide fault ride-through capability. In this case, when a DC fault occurs, the fault current is quickly cleared by the MMC, and the system tries to restore power transmission after a fault deemergence time of 100–150 ms. If the fault current does not continue to rise within 5 ms during this process, the short-circuit fault is transient and has been cleared, and transient DC fault ride-through can be achieved without DCCB operation. In contrast, if the system power is not successfully restored to transmission for three consecutive times, the short-circuit fault is permanent [47, 48]. After the MMC quickly clears the faulted line current, the VARC DCCB is also required to isolate the faulted line. After that, the MMC is put back into operation, and permanent DC fault ride-through is achieved. Therefore, when VARC DCCB is applied to an MTDC system composed of MMC with a fault ride-through capability, it should be operated when a permanent fault occurs to achieve residual current interruption and fault line isolation.

The short-circuit fault occurs on cable 24, which connects MMC2 to MMC4 at 50 km from MMC2. The fault type is the most severe bipolar short-circuit fault. Two representative fault current interruptions are mainly presented in the 4-terminal MTDC system: short-circuit current interruption and reverse short-circuit current interruption.

5.1. Short-Circuit Current Interruption

As shown in Figure 19, the interruption characteristic of the 160 kV 6-module VARC DCCB with series followed by parallel structure at the positive pole of cable 24 is illustrated.

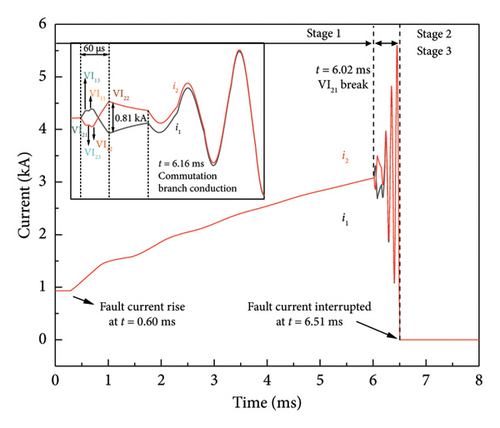
The fault occurs at t = 0 ms, and the line current rises consequently. The fault current at B42 starts to rise at the instant of t = 0.6 ms, and the two parallel branches are still sharing the current. When VI is triggered to operate, the contacts start to be separated by actuators. Considering the action decentralization, the operation sequence of VIs in this simulation is VI₂₁, VI₁₃, VI₂₃, VI₁₁, VI₁₂, and VI₂₂. First, VI₂₁ is operated at t = 6.02 ms, and the vacuum arc is generated between its contacts, which leads the current transfer to the parallel branch. Therefore, i₂ gradually decreases, and i₁ gradually increases. After VI₁₃ is operated, a vacuum arc is generated between its contacts, and the arc voltage difference between the two parallel branches leads i₁ and i₂ to be uniform gradually. Then, VI₂₃ is operated. Due to the arc voltage of the short gaps in series being higher than that of the parallel branch, the current transfer process occurs again, as shown in the fact that i₂ continues to decrease and i₁ continues to increase. Then, VI₁₁ is operated, and the current sharing between i₁ and i₂ occurs again based on the previous stage at the instant. After VI₁₂ is operated, all 3 breaks of the branch where VI₁₂ is located are in the arc state. Therefore, the transfer speed of i₁ to the parallel branch is accelerated, as shown by the increase of i₂ and the decrease of i₁. When VI₂₂ is operated, the current sharing occurs for the third time in the two parallel branches. It can be seen that there is a time difference of 80 µs between the latest operated VI₂₃ and the earliest operated VI₂₂. In this process, the absolute value of the maximum difference between the parallel current Δi = 0.81 kA. At t = 6.16 ms, the VSC in the commutation branch of the 160 kV 6-module VARC DCCB with series followed by parallel structure is conducted, and the resulting gradual oscillation current is superimposed inversely on the main branch. Finally, an artificial over-zero point is generated at t = 6.51 ms, and the short current is interrupted.

5.2. Reverse Short-Circuit Current Interruption

As shown in Figure 20, the interruption characteristic of the 160 kV 6-module VARC DCCB with series followed by parallel structure at the negative pole of cable 24 is illustrated.

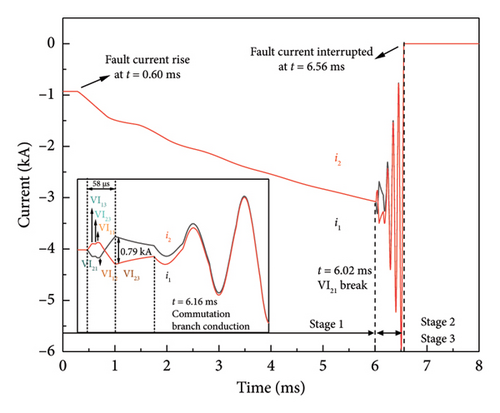
The current through the 160 kV 6-module VARC DCCB before the fault occurs is −1 kA. Similarly, the operating sequence of the 6 VIs when interrupting the reverse short-circuit current is the same as the previous one, except that there is a time difference of 58 µs between the latest operated VI₂₁ and the earliest VI₂₂. In this interruption process, the absolute value of the maximum difference between the parallel current Δi = 0.79 kA. Therefore, the 160 kV 6-module VARC DCCB with series followed by parallel structure is capable of bidirectional DC interruption in this configuration.

6. Conclusions

This paper proposes a VI model suitable for 0–20 kA, which can be used for series-parallel connected multimodule DCCBs for DC interruption, allowing for higher voltage levels and larger-capacity applications. The DC interruption transient characteristics of two types of 160 kV 6-module VARC DCCB with this model are compared and analyzed regarding operating reliability, interruption performance, energy absorption, and costs. The 160 kV 6-module VARC DCCB with series followed by parallel structure shows better performance. The following conclusions can be drawn from the abovementioned results.

The parallel current simulation results of the developed VI model are compared with the experimental data, and the current waveforms obtained from the simulation are in good agreement with the experimental results.

By connecting VIs in series and parallel, DCCB with higher voltage levels and larger interruption capacity can be realized. The 160 kV 6-module VARC DCCB with series followed by parallel structure has a higher reliability of 99.978%. It is less affected by the actuator decentralization, as shown by the absolute value of the maximum difference between the parallel current Δi lying in the smaller range of 0–2 kA, accounting for 66% of the 50 repetitive simulations.

The short-circuit and reverse short-circuit current interruption characteristics of the 160 kV 6-module VARC DCCB with series followed by parallel structure are verified in the ±160 kV 4-terminal MTDC system. The results show that the 160 kV 6-module VARC DCCB with this structure is capable of bidirectional current interruption and applies to MTDC systems.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the National Natural Science Foundation Project of China (grant numbers 52107166 and U22B20121), the National Key Research and Development Program of China (grant number 2022YFB2403702), the China Southern Power Grid Technology Project (grant number 030000KC22120008), and the China Postdoctoral Science Foundation (grant number BX20200263).

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Ito H., Current and Voltage Behaviours of HVDC Circuit Breakers, 2023 30th International Symposium on Discharges and Electrical Insulation in Vacuum (ISDEIV), 2023, Okinawa, Japan, 119–122, https://doi.org/10.23919/isdeiv55268.2023.10200913.
10.23919/isdeiv55268.2023.10200913
Google Scholar
2 Shi Z., Zhang Y., Jia S., Song X., Wang L., and Chen M., Design and Numerical Investigation of A HVDC Vacuum Switch Based on Artificial Current Zero, IEEE Transactions on Dielectrics and Electrical Insulation. (2015) 22, no. 1, 135–141, https://doi.org/10.1109/tdei.2014.004533, 2-s2.0-84923306112.
10.1109/TDEI.2014.004533
CAS Web of Science® Google Scholar
3 Slade P. G., The Application of Vacuum Interrupters in HVDC Circuit Breakers, IEEE Transactions on Plasma Science. (2022) 50, no. 11, 4675–4682, https://doi.org/10.1109/tps.2022.3210383.
10.1109/TPS.2022.3210383
Google Scholar
4 Xiao Y., Wu Y., Wu Y. et al., Study on the Dielectric Recovery Strength of Vacuum Interrupter in MVDC Circuit Breaker, IEEE Transactions on Instrumentation and Measurement. (2020) 69, no. 9, 7158–7166, https://doi.org/10.1109/tim.2020.2978599.
10.1109/TIM.2020.2978599
Web of Science® Google Scholar
5 Su X., Luo J., Xu B., and Li L., Research on Parallel Mean Flow Technology of High-Voltage Vacuum Circuit Breaker, 2022 IEEE International Conference on Electrical Engineering, Big Data and Algorithms (EEBDA), 2022, Changchun, China, 146–149, https://doi.org/10.1109/eebda53927.2022.9744928.
10.1109/eebda53927.2022.9744928
Google Scholar
6 Ma K., Research and Application of 220kV Short-Circuit Current Limiting Measures Based on Fast Switch, 2022 IEEE Asia-Pacific Conference on Image Processing, Electronics and Computers (IPEC), 2022, Dalian, China, 948–951, https://doi.org/10.1109/ipec54454.2022.9777440.
10.1109/ipec54454.2022.9777440
Google Scholar
7 Huang D., Qiu Z., Ruan J. G., Shu S., and Liao C., Static Voltage Distribution of 126 kV Modular Multi-Break Vacuum Circuit Breaker Prototype, 2011 1st International Conference on Electric Power Equipment-Switching Technology, 2011, Xi′an, China, 73–77.
Google Scholar
8 Zhang H., Liao M., Fu Y., Chen Z., Dong H., and Zou J., Effect of Arcing Time on Voltage Distribution of Double-Break Vacuum Circuit Breaker During the Transient Recovery Voltage Rising Phase, IEEE Transactions on Plasma Science. (2021) 49, no. 4, 1357–1362, https://doi.org/10.1109/tps.2021.3065739.
10.1109/TPS.2021.3065739
Google Scholar
9 Wang J., Geng Y., Liu Z., and Yan J., High Voltage Level Vacuum Switching Technology, High Voltage Apparatus. (2017) 53, no. 3, 1–11.
Google Scholar
10 Godbole M. and Jain A. M., Double Break Vacuum Circuit Breaker-A Brief Overview, 2016 10th International Conference on Intelligent Systems and Control (ISCO), 2016, Coimbatore, India, 1–4, https://doi.org/10.1109/isco.2016.7727112, 2-s2.0-85007401414.
10.1109/isco.2016.7727112
Google Scholar
11 Lavrinovich V. A., Rylskaya L. A., Schneider A. V., and Popov S. A., Development of a Vacuum Arc Extinguishing Chamber for a Single-Break Vacuum Circuit Breaker for 110 kV, 2020 29th International Symposium on Discharges and Electrical Insulation in Vacuum (ISDEIV), 2021, Padova, Italy, 396–400, https://doi.org/10.1109/isdeiv46977.2021.9587011.
10.1109/isdeiv46977.2021.9587011
Google Scholar
12 Min-fu L., Xiong-ying D., Ji-yan Z., Xing-ming F., and Hui S., Dielectric Strength and Statistical Property of Single and Triple-Break Vacuum Interrupters in Series, IEEE Transactions on Dielectrics and Electrical Insulation. (2007) 14, no. 3, 600–605, https://doi.org/10.1109/tdei.2007.369519, 2-s2.0-34250213677.
10.1109/TDEI.2007.369519
Google Scholar
13 Sugita M., Igarashi T., Kasuya H. et al., Relationship Between the Voltage Distribution Ratio and the Post Arc Current in Double-Break Vacuum Circuit Breakers, IEEE Transactions on Plasma Science. (2009) 37, no. 8, 1438–1445, https://doi.org/10.1109/tps.2009.2015883, 2-s2.0-69249223471.
10.1109/TPS.2009.2015883
Web of Science® Google Scholar
14 Saitoh H., Ichikawa H., Nishijima A. et al., Research and Development on 145 kV/40 kA One Break Vacuum Circuit Breaker, IEEE/PES Transmission and Distribution Conference and Exhibition. (2002) 2, 1465–1468, https://doi.org/10.1109/tdc.2002.1177697.
10.1109/TDC.2002.1177697
Google Scholar
15 Liao M., Duan X., Zou J., and Cong J., Analysis of Dynamic Dielectric Recovery and Statistical Properties for Vacuum Circuit-Breakers With Multi-Breaks, Proceedings of the CSEE. (2003) 23, no. 2, 82–87.
Google Scholar
16 Ai S., Xiao Y., Huang Y., Yang F., Fan Y., and Li X., Voltage Distribution Design of a Novel 363 kV Vacuum Circuit Breaker, 2018 IEEE International Conference on High Voltage Engineering and Application (ICHVE), 2018, Athens, Greece, 1–4.
Google Scholar
17 Yu X., Yang F., Li X. et al., Static Voltage Sharing Design of a Sextuple-Break 363 kV Vacuum Circuit Breaker, Energies. (2019) 12, no. 13, https://doi.org/10.3390/en12132512, 2-s2.0-85068466191.
10.3390/en12132512
Google Scholar
18 Shaogui A., Xiao Y., Yongning H., Fan Y., Yiping F., and Xing L., Study on Voltage Distribution Characteristic of a 363 kV Fast Multi-Break Vacuum Circuit Breaker, Journal of Engineering. (2019) 2019, no. 16, 2693–2697, https://doi.org/10.1049/joe.2018.8648.
10.1049/joe.2018.8648
Google Scholar
19 Li H., Geng Y., Liu Z., and Wang J., Development of 126 kV Single-Break Vacuum Circuit Breaker, 2018 IEEE Holm Conference on Electrical Contacts, 2018, Albuquerque, NM, USA, 154–158, https://doi.org/10.1109/holm.2018.8611686, 2-s2.0-85061788732.
10.1109/holm.2018.8611686
Google Scholar
20 Wu Z., Su H., Liu J., Mo Y., Fan S., and Jia S., Study on the Contact Resistance and Temperature-Rise Performance of High-Voltage Vacuum Interrupter, 2023 30th International Symposium on Discharges and Electrical Insulation in Vacuum (ISDEIV), 2023, Okinawa, Japan, 410–413, https://doi.org/10.23919/isdeiv55268.2023.10200582.
10.23919/isdeiv55268.2023.10200582
Google Scholar
21 Guo Z., Li X., Su H. et al., Interrupting Characteristics of Paralleled SF6 Circuit Breakers With a Highly Coupled Split Reactor, IEEE Transactions on Components, Packaging, and Manufacturing Technology. (2017) 7, no. 5, 768–776, https://doi.org/10.1109/tcpmt.2017.2677524, 2-s2.0-85016420750.
10.1109/TCPMT.2017.2677524
Web of Science® Google Scholar
22 Sato Y., Arazoe S., Okumo H., Takao N., and Yanabu S., Increase of Current Carrying Ability of Vacuum Interrupter, 24th ISDEIV 2010, 2010, Braunschweig, Germany, 198–201, https://doi.org/10.1109/deiv.2010.5625834, 2-s2.0-78650437167.
10.1109/deiv.2010.5625834
Google Scholar
23 Matsukawa M., Miura Y. M., Terakado T., Kimura T., Ohshima I., and Kawashima S., Development of a Vacuum Switch Carrying a Continuous Current of 36 kA DC, Proceedings ISDEIV. 19th International Symposium on Discharges and Electrical Insulation in Vacuum (Cat. No.00CH37041), 2000, Xi’an, China, 415–418, https://doi.org/10.1109/deiv.2000.879015.
10.1109/deiv.2000.879015
Google Scholar
24 Pertsev A. A., Chistjakov S. P., Rylskaya L. A., and Chistjakov R. S., Parallel Connection of Several Vacuum Interrupters in a Circuit-Breaker Pole, Proceedings ISDEIV. 19th International Symposium on Discharges and Electrical Insulation in Vacuum (Cat. No.00CH37041), 2000, Xi′an, China, 407–410, https://doi.org/10.1109/deiv.2000.879013.
10.1109/deiv.2000.879013
Google Scholar
25 Zheng X., Huang Z., Dong E. et al., Research on Key Influence Factors of Current-Transfer Process Based on Paralleled Breaking, 2013 2nd International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST 2013), 2013, Matsue, Japan, 1–4.
Google Scholar
26 Zheng X., Zou J., and Cheng Z., Current Transfer Process of Paralleled Vacuum Generator Circuit Breaker, High Voltage Engineering. (Nov. 2009) 35, no. 11, 2709–2715.
Google Scholar
27 Smirnov S. V., Evdokunin G. A., Petrova A. D., and Brilinskii A. S., Computer Simulation of Transient Processes in Hybrid Generator Circuit Breaker During Interruption of Short Circuit Current, 2020 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), 2020, St. Petersburg Moscow, Russia, 1320–1325, https://doi.org/10.1109/eiconrus49466.2020.9039412.
10.1109/eiconrus49466.2020.9039412
Google Scholar
28 Liu Z., Wang J., Wang Z., and Yuan S., Current Transfer Process in Open Operation Between Parallel Breaks of Vacuum Generator Circuit Breaker, 19th International Symposium on Discharges and Electrical Insulation in Vacuum, 2000, Xi′an, China, 403–406.
Google Scholar
29 Han X., Yang F., Chen H. et al., Parallel Current-Sharing Characteristics of Vacuum Multi-Breakers for Large-Capacity Generator Circuit Breakers, IEEE Transactions on Power Delivery. (2024) 39, no. 2, 1162–1173, https://doi.org/10.1109/tpwrd.2024.3350665.
10.1109/TPWRD.2024.3350665
Google Scholar
30 Helmer J. and Lindmayer M., Mathematical Modeling of the High Frequency Behavior of Vacuum Interrupters and Comparison With Measured Transients in Power Systems, Proceedings of 17th International Symposium on Discharges and Electrical Insulation in Vacuum. (1996) 323–331, https://doi.org/10.1109/deiv.1996.545375.
10.1109/DEIV.1996.545375
Google Scholar
31 Landry M., Turcotte O., and Brikci F., A Complete Strategy for Conducting Dynamic Contact Resistance Measurements on HV Circuit Breakers, IEEE Transactions on Power Delivery. (Apr. 2008) 23, no. 2, 710–716, https://doi.org/10.1109/tpwrd.2008.917694, 2-s2.0-42249103061.
10.1109/TPWRD.2008.917694
Web of Science® Google Scholar
32 Katare P., Chennu R., Ramachandra B., Reddy S. S., and Awasthi A., Estimation of Arc Voltage Characteristic for High Current Fault Arcs, 2017 International Conference on Smart Grids, Power and Advanced Control Engineering (ICSPACE), 2017, Bangalore, India, 283–287, https://doi.org/10.1109/icspace.2017.8343444, 2-s2.0-85047777222.
10.1109/icspace.2017.8343444
Google Scholar
33 Guan C., Yao X., Zheng J. et al., A Relationship Between Vacuum Arc Characteristics and Short-Circuit Current Interrupting Capability at Minimum Arcing Times, IEEE Transactions on Plasma Science. (2022) 50, no. 9, 2670–2680, https://doi.org/10.1109/tps.2022.3193945.
10.1109/TPS.2022.3193945
Google Scholar
34 Guan R. and Jia Z., DC Arc Numerical Calculations and Experimental Researches Based on the Arcing Horn Used in Over-head Line, 2020 IEEE International Conference on High Voltage Engineering and Application (ICHVE), 2020, Beijing, China, 1–4, https://doi.org/10.1109/ichve49031.2020.9280011.
10.1109/ichve49031.2020.9280011
Google Scholar
35 Liu S., Popov M., Mirhosseini S. S. et al., Modeling, Experimental Validation, and Application of VARC HVDC Circuit Breakers, IEEE Transactions on Power Delivery. (2020) 35, no. 3, 1515–1526, https://doi.org/10.1109/tpwrd.2019.2947544.
10.1109/TPWRD.2019.2947544
CAS Web of Science® Google Scholar
36 Shu S., Ruan J., Huang D., and Wu G., Influence of System Fault Parameters on Breaking Performance of Vacuum Circuit Breaker: Modeling and Simulation, Electric Power Automation Equipment. (2013) 33, no. 11, 81–87.
Google Scholar
37 Han X., Niu C., He H., Wu J., and Chen Z., Review of Condition Monitoring and Intelligent Assessment of Electromagnetic Circuit Breaker, Transactions of China Electrotechnical Society. (2023) 38, no. 8, 2191–2210.
Google Scholar
38 Shi W., Wang L., Lin R., Wang Y., Ma J., and Jia S., Experimental Investigation of Drawing Vacuum Arc Under Different TMF Contacts in Vacuum Interrupter, IEEE Transactions on Plasma Science. (2019) 47, no. 4, 1827–1834, https://doi.org/10.1109/tps.2019.2903557, 2-s2.0-85063939125.
10.1109/TPS.2019.2903557
Web of Science® Google Scholar
39 Ängquist L., Baudoin A., Norrga S., Nee S., and Modeer T., Low-Cost Ultra-Fast DC Circuit-Breaker: Power Electronics Integrated With Mechanical Switchgear, 2018 IEEE International Conference on Industrial Technology (ICIT), 2018, Lyon, France, 1708–1713, https://doi.org/10.1109/icit.2018.8352439, 2-s2.0-85046933164.
10.1109/icit.2018.8352439
Google Scholar
40 Yang L., Liu Z., Gao K., and Fu C., HV Circuit Breaker Lifetime Assessment Based on the Failure Model and Probability Statistics, East China Electric Power. (2009) 37, no. 2, 0210–0212.
CAS Google Scholar
41 Li W., Zhou J., Yan W., and Xie K., Reliability Based Method for Spare Planning of Power System Equipment, Proceedings of the CSEE. (2006) 26, no. 15, 7–11, 45.
CAS Google Scholar
42 Han L., Feng T., Gu S., Jiang Y., Wan Y., and Cheng L., Research on Reliability Optimization Method of Disconnecting Circuit Breakers, 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), 2019, Changsha, China, 997–1002, https://doi.org/10.1109/ei247390.2019.9062115.
10.1109/ei247390.2019.9062115
Google Scholar
43 Yi Q., Yang F., Wu Y. et al., Snubber and Metal Oxide Varistor Optimization Design of Modular IGCT Switch for Overvoltage Suppression in Hybrid DC Circuit Breaker, IEEE Journal of Emerging and Selected Topics in Power Electronics. (2021) 9, no. 4, 4126–4136, https://doi.org/10.1109/jestpe.2020.2985627.
10.1109/JESTPE.2020.2985627
Google Scholar
44 Wan C., Pei X., Zhou W., Li Z., Li P., and Zhang S., Novel Hybrid DC Circuit Breaker Based on Current Injection, Proceedings of the CSEE. (2023) 43, no. 12, 4726–4736.
Google Scholar
45 Zhang X., Chen X., Qi L., and Li W., High-Performance and Economical Forced Resonant DC Circuit Breaker: Topology, Design, and Development, IEEE Industrial Electronics Magazine. (2023) 17, no. 1, 46–54, https://doi.org/10.1109/mie.2022.3191816.
10.1109/MIE.2022.3191816
Google Scholar
46 Liu S., Yuan Z., Chen J. et al., A Cost-Effective Current-Limiting Hybrid DC Circuit Breaker Based on Hybrid Semiconductors, Electronics. (2024) 13, no. 10, https://doi.org/10.3390/electronics13101948.
10.3390/electronics13101948
Google Scholar
47 Xu Y., Tan Z., Li J., Feng Q., and Wu Z., A Light Weight MMC Topology With Recombined Half-Bridge Submodules for DC Fault Ride-Through, IET Generation, Transmission & Distribution. (2024) 18, no. 22, 3555–3566, https://doi.org/10.1049/gtd2.13282.
10.1049/gtd2.13282
Google Scholar
48 Dong P., Lyu J., and Cai X., Optimized Design and Control for Hybrid MMC With Reduced Capacitance Requirements, IEEE Access. (2018) 6, 51069–51083, https://doi.org/10.1109/access.2018.2869400, 2-s2.0-85053162208.
10.1109/ACCESS.2018.2869400
Web of Science® Google Scholar

All articles

Numerical Analysis, Experimental Validation, and Application of DC Interruption With Parallel Vacuum Interrupters

Abstract

1. Introduction