Bilateral energy transactions between electric vehicles (EVs) and the power grid are managed by entities called aggregators (AGGs) who work as private or network operator’s agents. The remarkable effects of the AGG’s behavior on network parameters entail the provision of coordinated schedules and consideration of network conditions and constraints. In this paper, a novel approach is presented for independent coordinated scheduling of EV charge/discharge via private AGGs, distributed generators (DGs), and the distribution network operator (DSO). The goal is the maximization of AGG profit from energy transactions along with the least network operation costs and improvement of network indices. The objective function of the proposed approach also includes AGG capability to provide the network with spinning reserve which brings incentive payments. For realistic addressing of the problem, the uncertainties related to EV arrival/departure times and their initial State of Charge (SOC) are simulated via different scenarios. The problem is solved using the fast alternating direction method of multipliers (FADMMs) which is well suited for independent-objective optimizations with a fast convergence rate. The proposed distributed algorithm is tested and evaluated on a standard distribution network consisting of AGG and DGs. The results indicate that ignoring network conditions and constraints leads to impractical decisions whereas consideration of DSO requirements by the distributed algorithm will deliver a profitable schedule for AGGs while protecting their privacy and fulfilling DSO’s economical and technical objectives.

1. Introduction

Volatility of fossil fuel prices driven by political and economic issues as well as the environmental concerns regarding the pollution by these nonrenewable sources has led to an increasing tendency toward electric vehicles (EVs) worldwide [1]. The replacement of conventional transportation fleet with EVs that consume cleaner forms of energy can significantly alleviate problems with fossil fuels and their associated hazard to the environment [2]. As reported by the international energy agency [3], EV sales in 2021 increased by 100% to reach 6.6 million vehicles out of around 16.5 million vehicle sales. However, as power system loads during their charging mode, EVs can cause significant challenges, if left uncoordinated, to the network through increased peak load, higher losses, and bus voltage limit violations [4]. However, the additional capability of these vehicles to inject power into the network, the so-called V2G scheme, turns them into virtual generators helping to increase network operation security and stability [5]. Due to their incomparable size relative to the large scale of the network, individual EVs cannot be expected to make positive impacts on the network’s economic and technical aspects. However, when EVs are collectively scheduled for coordinated charge and discharge operation through aggregators (AGGs), they turn into tremendous virtual power plants bringing significant benefits to the power system. AGGs can also plan, in coordination with other network entities, to provide ancillary services such as spinning reserves, frequency regulation, etc. to the grid [6]. In [7], an optimization approach is presented for EV AGGs based on V2G capability. A hierarchical scheme is developed to utilize EVs for frequency and voltage improvement in a smart grid. The results of implementation on a test network show that the V2G capability brings benefits for both EV owners and the grid operator through enhanced grid stability. In [8], a bilevel optimization algorithm for EV charge and discharge planning is proposed from the AGG’s viewpoint aimed at stabilizing frequency and EV charging cost reduction. The simulation on a real network indicates the economic benefits for all involved parties in the market. In [9], a multiobjective EV charge and discharge planning model is presented for smart grids attempting to reduce operation costs and pollutant emissions. The uncertainties associated with both the network load and EV charge and discharge actions are addressed in [10], where a stochastic model is proposed to maximize the AGG’s profit through ancillary service provision in the day-ahead market. In [11], a bilevel algorithm considering market constraints and incentives paid by grid operators is developed aimed at maximizing the AGG’s profit. The results once again verify that through a proper charge and discharge schedule it is feasible to simultaneously achieve high profits for AGG and EV while achieving improvement in the network’s voltage profile and reduced power losses. Also, Ren et al. [12] proposed an approach based on demand response to realize the objectives of the AGG, EV owners, and the grid operator. The algorithm yields charge and discharge schemes in a way that the AGG achieves maximum profit considering the EVs’ minimum state of charge with minimal network load shift. In [13], a powerful optimization approach is proposed for EV planning considering energy price uncertainties in the upstream network. The approach proves capable of providing proper strategies to AGGs to maximize their profit by taking uncertainties into account.

A more complete consideration of uncertainties is carried out in the EV planning approach in [14]. These include uncertainties in EV arrival/departure times, the initial state of charge, and energy price in the market. The results indicate that the risk-taking factor in EV planning directly affects the gained profits in a way that risk-oriented strategies lead to higher profits earned by AGGs. In [15], optimal AGG behavior in the energy and ancillary service market is modeled without consideration of network requirements. As the results of different research works indicate, EV charging and discharging schemes in coordination with other network participants including distributed generators (DGs) can financially and technically benefit EV owners, the AGGs, and the network operator at the same time. For this purpose, appropriate techniques and algorithms are essential and each of the works has attempted to prove the ability of their proposed approach commensurate with the scheduling model they have adopted. A detailed review of the literature reveals that most of the methods used including mixed integer programming [16], sequential quadratic programming [17], particle swarm optimization (PSO) [18], neural networks [19], etc. are centralized techniques.

Current methods for EV scheduling face challenges in privacy, scalability, and computational efficiency, particularly with large-scale, real-time coordination. Many centralized approaches require extensive data sharing, raising privacy concerns and struggling with scalability. Also, with the increasing size of the EV population, distribution network expansion and incorporation of new elements like DGs and energy storage systems (ESSs), the growth of the search space may yield the centralized problem intractable. In addition, the increasing significance of data security in preventing cyber-attacks and protecting the privacy of market participants as well as the not-yet-fully developed communication infrastructure which hinders efficient data exchange are obstacles facing the centralized methods. On this basis, decentralized and distributed methods have gradually replaced centralized schemes in a way that the distribution network operator (DSO), the AGGs, DGs, and other participants all contribute to the overall optimization plan. Unlike the centralized methods, distributed algorithms are developed in a way that the overall problem is broken into several subproblems each optimized locally by the relevant party and communicated to other participants [20]. Based on the Lagrange method as one of the commonly used decentralized techniques, the joint constraints are relaxed, and the optimization subproblems can be solved individually.

In [21], a decentralized strategy is proposed for EV charging control within the grid attempting to flatten the load curve. Also in another work, using predictor corrector proximal multiplier (PCPM) as a distributed algorithm, optimal microgrid management with minimized costs is achieved [22]. The microgrid management scheme is defined as an optimal power flow problem and the central and local controllers optimize a joint objective function. In [23], a bilevel energy planning within a smart grid is carried out to reduce operation costs in the presence of charging stations and DGs. A decentralized method of optimized EV charging is presented in [24] where each EV solves its local optimization problem and sends the results to the AGG. In [25], a load-flattening strategy for the distribution network along with EV charge cost reduction is presented which also takes care of the network technical constraints.

Another distributed algorithm which best suits convex optimization problems is ADMM. This method is a powerful tool to break down complex problems with large data sets while preserving their privacy [26].

Given the importance of preserving data privacy pertaining to EV charging and discharging times, AGG costs and revenues, privately owned distributed generation, and even the data belonging to the distribution grid owner, ADMM can be regarded as an attractive EV planning approach which meets the above requirements.

In [27], the ADMM algorithm is employed for AGG’s charge and discharge planning in a way to fulfill the network goal of minimizing losses. As shown, regardless of the EV’s V2G capability, the coordination of the charging schedule with the variations of network base load has a direct effect on the reduction of losses. The consideration of controllable loads, renewable and nonrenewable resources, and ESS equipment within microgrids further increases the complexity of the problem and the corresponding search space. However, using the ADMM algorithm for optimal energy management in [28], the operational costs are minimized while considering all the mentioned elements.

One of the main advantages of distributed algorithms over centralized ones is the considerable reduction in solution time. In [29], using the ADMM algorithm for the AGG’s optimal charging problem, it is demonstrated that the decentralized approach consumes much lower time than the centralized method with almost the same results. Also, in [30], the ADMM algorithm is used to lower operation costs of the distribution grid while fulfilling its technical requirements in the presence of DGs. The provided algorithm has managed to independently solve for the objective functions of AGG, DGs, and the network operator.

The ADMM algorithm has also been used in [31] to solve a different optimization problem focused on maintaining bus voltages within permissible limits while charging EVs. Given the fluctuations in network load and photovoltaic power generation, the algorithm manages to yield planning solutions that maintain the voltage level of the consumers within allowable limits. Data privacy of the AGG is guaranteed by ADMM as the main objective of the mentioned research. In [32], a combinational decentralized approach is proposed for coordination between the AGG and network hub. The objective function of each party has its parameters and complexities. However, the proposed approach proves capable to provide a joint plan for these two individual entities in coordination with the wholesale market while protecting their privacy and fulfilling their economic goals. For all the planning details considered, the proposed approach does not consider the network technical requirements, which somehow offsets the practical credibility of the results.

The mentioned references all assume the AGGs to be DSO agents. In this way, their main goal will focus on the improvement of network operating conditions. However, the modern grid practice proves that the increasing trend of privately owned AGGs can be more beneficial to overall network efficiency. On the other hand, those references considering private AGGs usually ignore the distribution network and its operating constraints to simplify complex multiobjective multiconstraint problems. An EV charge and discharge scheduling by the AGG overlooking the requirements of the network operator is not necessarily implementable.

In [33], EV charge and discharge planning is performed in a distributed manner to meet the technical and economic objectives. Also, the distributed resources are owned by private entities and EV charging is carried out domestically during night hours. The charging stations, on the other hand, provide services during day hours. Considering the network load profile, night charging is demonstrated to be more suitable to distribution grid and its owner.

To address the challenges of privacy concerns, scalability limitations, and inefficiencies in real-time coordination in existing decentralized methods, a distributed model is developed in this paper for coordinated scheduling by EV AGGs in the distribution network consisting of DGs. Compared with current decentralized methods, which often suffer from slower convergence and higher computational demands, the proposed approach ensures faster convergence and improved scalability while preserving privacy, making it well suited for real-time, multiactor coordination. The optimization objectives include the maximization of AGG profits from energy transactions with the market, supply of adequate spinning reserve quantity, reduced losses, and decreased DG operation costs. The stakeholders of these objectives are the EV AGGs and the network operator. In order to handle the problem complexity and also preserve private AGG data, a distributed algorithm based on ADMM, the so-called fast ADMM, is employed for EV charge and discharge planning in the distribution grid. Thus, each entity including the AGG, DGs, and the network operator solve their individual optimization problems independent of other parties and only exchange a single control signal between each other.

Overall, the novelties of this paper can be summarized as follows:

•
Decentralized stochastic programming for different independent parties within the distribution network taking into account the privacy aspects
•
Fulfilling the network technoeconomical requirements besides maximizing AGG profits from energy transactions with the grid and spinning reserve service
•
Using fast alternating direction method of multiplier (FADMM) as a decentralized approach with a very high convergence rate in combination with PSO to solve complex optimization problems.

The rest of this paper is organized as follows. Section 2 conveys the system model while Section 3 presents the problem formulation. Simulation results along with discussions are provided in Section 4. Finally, Section 5 draws the conclusions.

2. System Model

In EV charge and discharge planning, the distribution network is usually considered to encompass AGGs and DGs. In this section, the model for such a network is presented and then each of the mentioned players is modeled along with their respective constraints.

2.1. Distribution Network Model

A radial distribution network with N buses and E lines can be modeled as a graph represented by G = (N, E) such that the bus connected to the upstream network is assigned i = 0 and other buses are numbered i = 1, …, n. Thus, p_i(t) and q_i(t) are the active and reactive powers injected by bus i to the grid at any given time t, respectively. Also, the current in line (i, j) ∈ E is denoted by i_ij, the line impedance as Z_ij = r_ij + jx_ij, and the apparent power as S_ij(t) = P_ij(t) + jQ_ij(t). A constant voltage value (V₀) is assumed for the bus connected to the upstream network as the infinite bus. Other quantities are calculated based on the physical law for any branch (i, j) ∈ E at any given time t.

The main constraint to be considered for each bus is obtained by the balance of active and reactive powers at each bus as expressed by equations (1) and (2).

()

where

is the power delivered by AGG connected to bus j at time t,

is the power of DG connected to bus j at time t, and P_jk(t) and Q_jk(t) are the active and reactive powers of lines connected to bus j, respectively. Voltage and current values for all buses and lines are obtained through equations (3) and (4).

()

In these equations, v_j(t) and l_ij(t) are, respectively, the square of voltage at bus j and the square of current in line (i, j), as defined by equations (5) and (6).

()

Also, the voltage constraint for each bus j ∈ N\{0} is expressed as follows:

()

2.2. AGG Model

The economic activity of EV AGGs through EV charge and discharge planning consists of energy transactions with the grid plus the provision of ancillary services. The energy transactions are realized through off-peak charging and peak discharging operations leading to energy arbitrage with significant economic benefits to the AGG. As an ancillary service, the AGG allocates part of the stored EV battery energy under his management as a spinning reserve source for the sake of grid reliability. In fact, the AGG can offer up/downregulation reserve to the grid and gain further economic advantage thereof. The mathematical expressions for these activities follow next.

The total power

procured by the AGG as a moderator between EVs and the grid operator is given by the following equation:

()

where

is the exchanged power between AGG at bus j and the DSO. The positive/negative values indicate power sale (discharge)/purchase (charge). Also, N_ev is the number of vehicles managed by AGG, and

and

are the discharge and charge powers by EV d at time t. Since only one of the charging and discharging actions can be carried out at any given time, a binary indicating signal is defined as

()

where

and

are the binary variables indicating charge and discharge of EV d at time t, respectively.

The state of charge (SOC) of the batteries is determined based on their energy interactions with the grid as

()

where SOC_d(t) is the SOC of EV d at time t and

is the associated battery capacity. η^ch and η^disch are, respectively, the charge and discharge efficiencies. For battery protection purposes, the SOC of the EV battery is assumed to be within a permissible range as outlined by the following equation:

()

The other constraint is the minimum EV battery charge upon departure as given by the following equations:

()

where

and

are, respectively, the initial battery SOC of EV d by connection to the grid and the SOC upon departure as expected by the EV owner.

For ancillary services, it is assumed that the AGG can only offer regulation-down quantities upon charging and regulation-up service during discharge periods. These constraints are expressed in conjunction with the maximum charge and discharge power of EVs

through equations (13) and (14).

()

where

and

are the regulation-up and regulation-down quantities offered by AGG during charge and discharge of EV d at time t, respectively.

2.3. Distributed Generation Model

In this paper, DGs are assumed to be diesel generators independently controlled within the distribution network. The DG power factor is assumed unity and, therefore, DG output generation is within the range of the following equation:

()

where

is the maximum DG output power.

3. Problem Formulation

The purpose of the proposed approach is to optimize the performance of DSO, DG, and AGG at the same time in a way that leads to enhancement in network conditions. In this section, first, the multiobjective function is formulated and then using the FADMM algorithm, the required mathematical models are developed.

3.1. Objective Function

As mentioned in the previous section, different parties within the network including DSO, DG, and AGG each attempt at maximizing their own benefits. Since we assume the DSO’s ownership of DGs, the DSO’s objective will include minimized operation cost of DGs as well as minimized network losses. The private AGG’s objective will include maximized profit from both energy transactions with the grid and provision of spinning reserve.

To achieve the goals of this study, the objective function incorporates key terms that balance the AGG’s profitability with the DSO’s cost-efficiency. These include the following:

•
Network loss minimization: reducing line losses to improve energy efficiency and lower DSO costs.
•
AGG revenue: maximizing AGG profit through energy arbitrage and leveraging market price fluctuations.
•
Spinning reserve services: enhancing grid stability while generating additional revenue for the AGG.
•
DG costs: coordinating EV schedules with DG operations to minimize fuel and maintenance expenses.

Together, these components provide a framework that optimizes scheduling while benefiting both the AGG and DSO.

These are modeled in in the following equation:

()

where P_loss(t) are the network losses at time t. The second term, that is,

, is the AGG profit and the third term,

, is the DG operation cost. The relation for the revenue of AGG i is expressed as follows:

()

where P(S) is the occurrence probability of the given EV traffic scenario while Ω is the set of scenarios,

is the revenue of AGG i out of power transaction with the grid operator and

is his revenue from energy transactions with EV owners which can be either positive or negative. Also,

is his revenue from procuring spinning reserve to the grid. These terms are modeled by equations (18)–(20).

()

where

and

are the charge and discharge power of EV d at time t, respectively. Also, π^En(t) is the energy price at hour t and π^ave is the average energy price during EV charging period. According to (19), the AGG attempts to incentivize EV owners for V2G participation by paying them a discharge price which is 10% higher than the charging price so as to compensate for the EV battery degradation.

Also, the revenue from procuring spinning reserve to the grid is obtained by the following equation:

()

where π^Reg(t) is the spinning reserve tariff at time t. As for the DG operation costs, only fuel prices are considered. Although DGs are assumed to be owned by the DSO, the cost of power produced by these sources is significant in optimization problems. In the proposed approach, this objective is independently minimized.

Thus,

()

where α, β, and γ are constant coefficients of the DG cost [24].

3.2. FADMM

In designing a robust, privacy-preserving scheduling algorithm for EV AGGs, we evaluated ADMM and PSO for their strengths and limitations. ADMM is well suited for distributed optimization, breaking down complex problems into smaller, independent subproblems, which supports privacy and minimal data exchange. However, ADMM’s slower convergence in multiactor, data-intensive environments limits its effectiveness for real-time applications. PSO, a nature-inspired algorithm, excels at handling complex, nonconvex objectives but is computationally intensive and lacks structured privacy, making it less practical for real-time, multiactor coordination. FADMM was selected as combines ADMM’s privacy-preserving structure with enhanced convergence speed using an adaptive penalty factor to optimize independently for each entity with minimal data exchange. This balance of privacy, scalability, and fast convergence makes FADMM ideal for dynamic, real-time EV scheduling.

The general form of equations solved by ADMM is as follows [26]:

()

where A and B are matrices and C is a vector and the problem is solved for x and z. In each iteration, x and z are separately determined. Assuming a constant z, the equation is solved for x and then assuming constant x, the problem is solved for z. This process is repeated until it convergences to the final values. Using the Lagrange function, equation (22) can be rewritten as follows:

()

where λ is the Lagrange coefficient, ρ > 0 is the algorithm’s penalty factor, and ‖ ‖₂ is the Euclidian vector norm. During the iterations, x and z are obtained separately using equations (24) and (25). Also, the Lagrange coefficient is updated by equation (26) at each iteration.

()

The stopping criterion is expressed as (27) with the use of proper value for parameter e.

()

The convergence rate of ADMM can be further increased by developing it to FADMM. Compared with ADMM, the FADMM algorithm uses an increasing penalty factor which in turn increases the convergence leading to optimal results for a wide range of initial value settings.

This feature will be highlighted for bigger and more complex networks where the numbers of EVs and DGs as well as AGGs are higher.

The penalty factor at each iteration k is calculated as follows:

()

By dynamically updating ρ during each iteration, the algorithm ensures a balanced trade-off between convergence speed and solution stability. By setting initial values for ρ (ρ(1)) and ρ^max and assuming δ ∈ (1, 2), proper updating of ρ values through iterations is guaranteed.

3.3. Reformulation

Based on equations of Section 3.1, the objective function (16) can be rewritten in a form complying with the FADMM method. According to equations (29)–(31), DSO, AGG, and DG separately optimize their objective functions at each iteration and communicate the control signal λ to other parties.

()

Based on equation (29),

and

are the optimal exchanged power between DSO and AGG i and DG j at iteration (k + 1) as obtained by DSO’s optimization. λ(i, t) is the control signal for exchanged power between DSO and AGG_i at time t. λ(j, t) is the control signal for the exchanged power between DSO and DG_j as expressed by equation (26). ρ(k) is the penalty factor at iteration k whose initial value should be inputted at the start of the optimization process. Definitely, the obtained results are acceptable only when the network constraints are met. Also given the nonlinear relations such as the power flow equations, the PSO algorithm is employed to solve the optimization problem at each iteration of the algorithm. Thus, the optimal charge and discharge powers for AGGs and DGs are obtained using equations (30) and (31), respectively. Then, the control signals related to the AGG and diesel generator are updated using equations (32) and (33), respectively.

()

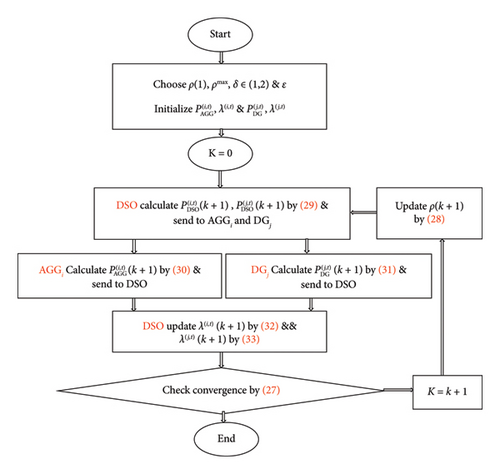
For a better outline of the proposed approach, the pseudocode of FADMM, as implemented in MATLAB, is given in Algorithm 1.

Algorithm 1: The FADMM.

1.
Choose ρ(1), ρ^max, δ ∈ (1, 2) & ε, k = 1
2.
Initialize to zeros and send to DSO
3.
Initialize to zeros and send to DSO
4.
While criteria for stopping not satisfied do
5.
DSO calculate by (29) & send to AGG_i and DG_j
6.
AGG_i calculate by (30) & send to DSO
7.
DG_j calculate by (31) & send to DSO
8.
DSO update λ^{(i, t)}(k + 1) by (32)
9.
DSO update λ^{(j, t)}(k + 1) by (33)
10.
Calculate ρ(k + 1) by (28)
11.
k = k + 1
12.
End while

Also, Figure 1 shows the flowchart of the proposed algorithm.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Flowchart of the proposed decentralized framework.

4. Numerical Results

To evaluate the proposed approach, the FADMM multiobjective optimization algorithm is implemented on a 33-bus network. The assumptions and results are as follows.

4.1. 33 Bus Test System

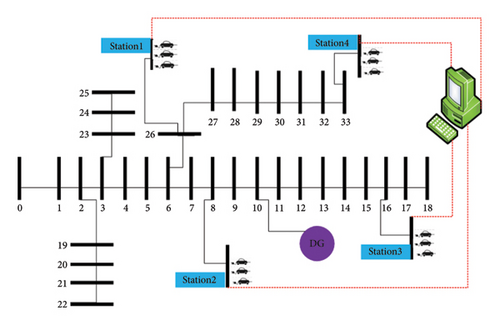
The test network is a 12.66 kV power system with 33 buses, 32 lines, and an overall power loss of 203 kW, as shown in Figure 2 [34]. Four public EV charging stations are assumed at buses 8, 16, 26, and 32 which are operated by a single AGG. Also, one DG unit is assumed to be located at bus 10.

Arrival/departure times and initial SOC, especially for public stations, are key yet uncertain factors in the AGG’s scheduling strategy, as they depend on daily travel habits and user preferences. As noted in [32], we address these uncertainties through a scenario-based approach using the Gaussian function to generate realistic variations. Multiple scenarios representing different combinations of arrival times, departure times, and SOC levels ensure robustness and accuracy by capturing realistic EV behavior at public stations. Table 1 summarizes these scenarios and their likelihoods, enhancing the model’s adaptability to real-world usage patterns.

Table 1. Scenarios for arrival time, departure time, and the initial state of charge of the EVs [32].

Scenario	Soc_in	t_in	t_out
1	0.58	5	20
2	0.57	7	17
3	0.22	5	22
4	0.50	6	19
5	0.20	9	20
6	0.12	5	22
7	0.34	6	17
8	0.42	8	22
9	0.69	11	18
10	0.24	7	18
11	0.76	10	21
12	0.80	7	20
13	0.60	9	17
14	0.31	8	19
15	0.66	6	18
16	0.46	7	21
17	0.57	12	19
18	0.20	7	20
19	0.36	7	19
20	0.37	5	21

As shown, 20 scenarios are considered for EV arrival/departure times during one daily cycle. The earliest arrival is at 5:00 while the latest departure happens at 22:00. It is also assumed that EVs stay at the station for the whole duration between their arrival and departure. EVs are 8 different best-selling types with the characteristics and market share mentioned in Table 2 [11].

Table 2. Electric vehicle characteristics [11].

EV type	Charger rate (kW)	Battery capacity (kWh)	Market share (%)
1	7.2	72	20.5
2	6.6	24.6	20.5
3	6.6	33	18
4	3.3	8.2	16
5	3.6	18	9
6	3.3	12.4	6
7	3.3	20.6	4.5
8	7.2	27	5.5

As given in Table 2, the minimum and maximum battery capacities are 8.2 kWh and 72 kWh with 16 and 20% of the market share, respectively. The whole EV fleet consists of 300 EVs equally allocated to the 4 charging stations. The number of EVs at each station for any given time varies according to the arrival/departure times. Also, DG’s maximum capacity is taken as 1 MW. Since planning is performed for an entire day, the hourly based per unit load variations for this period are assumed to follow the pattern of Figure 3 [24].

According to Figure 3, two peak periods are considered between hours 12–14 and 19–21 with the global peak occurring at hour 13 with a consumption of 0.98 p. u. Furthermore, the energy and spinning reserve ancillary service prices for the entire daily cycle are based on Figure 4 [30].

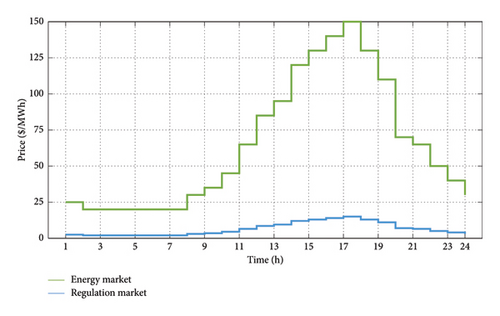
As seen, the highest energy price in the market is 150 $/MWh at hour 17. Also, the price for the spinning reserve is about 10% of the relevant energy price with the lowest prices between hours 2–7.

The proposed approach is tested under two different cases including the following:

•
Case 1: energy planning aimed at maximizing AGG profit without considering the network operational constraints.
•
Case 2: energy and spinning reserve planning aimed at maximizing AGG profit, reducing network losses and DG generation costs and taking into account the network voltage constraints.

4.1.1. Case 1

This case is dedicated to energy planning only from the AGG’s viewpoint. Therefore, the objective function only includes the AGG’s profit while DSO’s objectives including network losses, DG operation costs and bus voltage constraints are ignored. For this scenario, the results of EV charge and discharge planning, as well as DG generation schedule for a 24-h period using the proposed approach, are depicted in Figure 5.

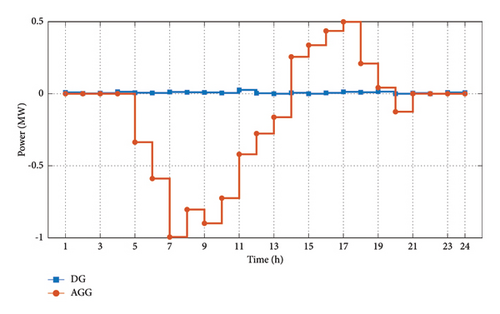
As shown, the DG output in this scenario is negligible during the whole 24-h period. This is because no relevant objective function for DG or DSO is considered. In fact, by omitting the operational constraints, no technical obligation is created for DG generation. According to Figure 5, the AGG purchases grid energy between hours 4–13, when prices are low, to charge EVs at the stations. Then, given the EV’s V2G capability and based on energy prices of Figure 3, energy sales by the AGG increase with the energy price such that the highest sales are realized at hour 17. Since this scenario overlooks the network constraints, the AGG continues to draw power from the grid and charge EVs during hours 12–14 when network power consumption is high so as to sell the stored energy during periods of the highest price. From the DSO’s viewpoint, however, this planning method may have harmful operational effects such as increased losses and voltage limit violations. Figure 6 shows the network losses before and after implementing the results of this scenario.

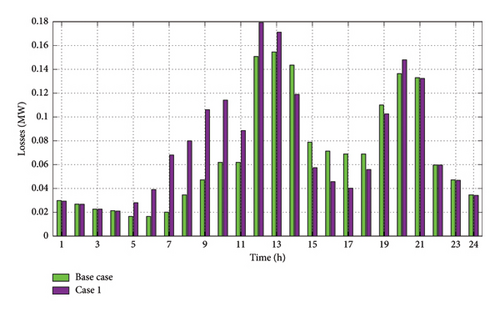
As demonstrated, this method of AGG’s planning will lead to a remarkable increase in power loss in the network lines especially during EV charging times, thus increasing the overall network losses in comparison to the base case in which no DG or EVs are present. Although the power losses decrease during EV discharging periods, i.e., hours 14–19, the overall daily power losses increase from 1.61 MW of the base case to 1.81 MW.

As expected, EV charge and discharge actions have a significant impact on the network losses such that during EV charging periods power losses are sensibly higher than the base case while during discharge periods, the charging stations act as generating sources bringing down the power losses during peak periods. Also, the increased network power loss at hour 20 is due to EV charging by the AGG who attempts to meet the minimum SOC demanded by EV owners before leaving the charging stations. After EV departure, no significant changes in network losses occur relative to the base case.

From the network voltage standpoint, scenario 1 leads to a profile shown in Figure 7.

As shown in Figure 7, the voltage limit of 0.95 p. u. has been violated in this scenario during peak periods because no voltage criteria have been considered in the optimization process. The voltage violation is exacerbated with increased EV charging during peak hours.

Also, with EV charging and no support from DGs, the voltage constraint is violated even during off-peak periods in a way that for buses further downstream of the network the voltage is reduced to 0.92 p. u.

4.1.2. Case 2

In this case, DG’s ownership belongs to DSO. Therefore, although DG operation cost is optimized independently, the generation amount is aimed to meet the requirements of the DSO. Hence, no direct participation in the market is considered for the DG. Figure 8 illustrates the planning outcome using the proposed approach for EV charge and discharge and DG generation for a 24-h period taking into account the objectives of AGG, DSO and network operational constraints.

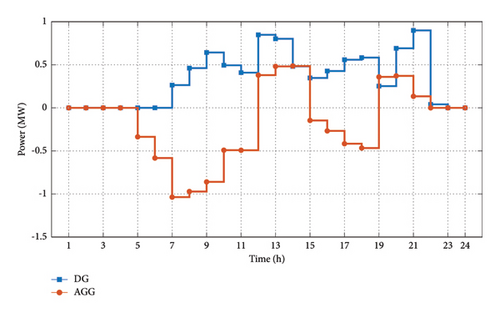
As Figure 8 shows, from hours 5 to 12, the low energy prices prompt the AGG to charge EV batteries, similar to Case 1. However, from hours 12 to 14, DSO’s objectives, namely, power loss and voltage constraints become dominant forcing the AGG to sell energy to the grid despite the low energy prices. From hour 15 to 18, despite the high energy price, the AGG attempts to charge EVs so as to both meet their final SOC requirements and help supply network demand at the peak period of 19–21. In fact, this action is required to protect bus voltages and reduce power loss during peak periods and the AGG thus agrees to lower his profit and sell cheap energy to the grid. Unlike the results of Case 1, by considering the DSO’s objectives besides those of the AGG, the DG output will increase. Hence, the DG generates power during hours 7–11 and 15–18 to help meet the network demand and fulfill EV charging requirements. This will guarantee voltage stability and low power losses. During peak periods, the DG generates near its maximum capacity and, together with the AGG, assists DSO meet its technical objectives.

Also in this scenario, significant amounts of regulation services have been realized by the AGG during EV charge and discharge operations, as demonstrated in Figure 9.

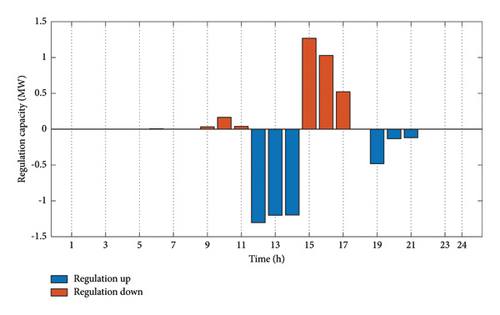
The available regulation up/down capacity is shown in Figure 9. Considered together with Figure 8, it is witnessed that the AGG is capable of regulation down service upon EV charging and regulation up service during EV discharging operation. This will bring further economic gain to the AGG in the form of spinning reserve revenues. It is noteworthy that the AGG is committed to adequate charging of all EVs within stations and the main profit is acquired from the provision of higher spinning reserve quantities. Therefore, during off-peak periods when prices are low and a lower number of EVs are available at the station, the AGG focuses on EV charging and no spare capacity is available to be allocated to spinning reserve operations. Conversely, during hours 15–17, the high energy prices, as well as higher number of EVs available at the stations, make the AGG able to fully participate in the spinning reserve service to the grid. As shown in Figure 9, during discharge periods of 12–14 and 19–21, the AGG provides regulation-up services. The maximum ancillary service offered by the AGG occurs at hours 12-14 due to the higher number of available EVs. This is reduced to an extent during the second period, i.e., hours 19–21.

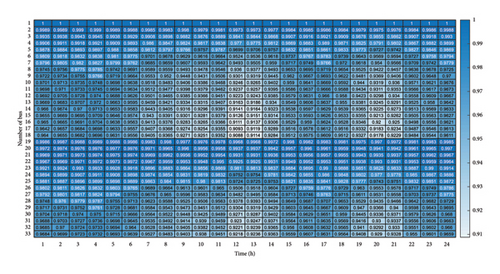
The voltage variation as a main planning constraint across the network is shown in Figure 10. Note that based on (7), the permissible voltage range is between 0.95 and 1.05 p. u.

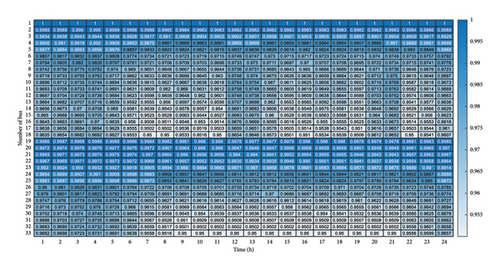
By comparing Figures 7 and 10, it is observed that the inclusion of the voltage constraint leads to improved voltage profile across all buses in a way that no voltage violation occurs during the whole planning period. The coordinated planning and interaction of AGG, DG, and DSO have successfully managed to maintain the voltage level even at the farthest buses, namely, buses 18 and 33 at the minimum allowable level of 0.95 despite simultaneous EV charging actions. The results obtained for buses 13–18 indicate that despite higher network load during hours 12–14 and 20–21 as the network peak periods, the voltage profiles have improved thanks to EV discharge operation. Having a significant impact on the voltage, the charge and discharge operations are in turn influenced, among other factors, by the final required SOC levels. Figure 11 shows the resulting trend of EV SOC during the planning period.

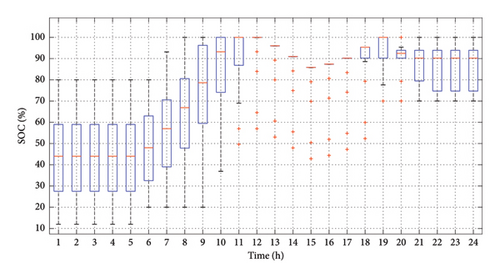
The obtained trend of EV SOCs as a result of charging and discharging operations is the outcome of considering different network conditions along with the defined objectives for different parties during the planning period. However, as shown in Figure 11, the initial SOC of around 30%–60% has been successfully increased to 70%–100% upon EV departures taking into account constraint (12).

Obviously, by the inclusion of EV planning and DG operation, the main feeder power undergoes significant changes compared to the base case. The load curves of the main feeder for different cases are shown in Figure 12.

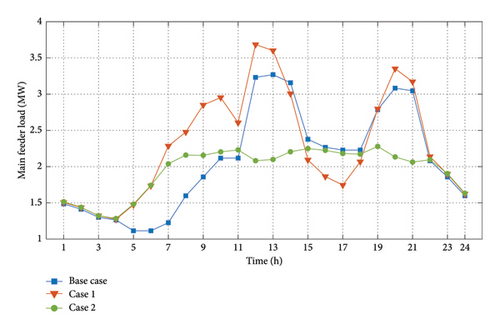
Considering the trend corresponding to Scenario 1, it is witnessed that an EV charge and discharge scheme only aimed at maximizing the AGG’s profit and overlooking the network indices will result in increased peak load and hence higher voltage drops and power losses. With a coordinated planning of AGG, DG, and DSO, however, the overall network load has reached a more flattened curve. These results are the output of the FADMM algorithm whose convergence for different objective functions is shown in Figure 13.

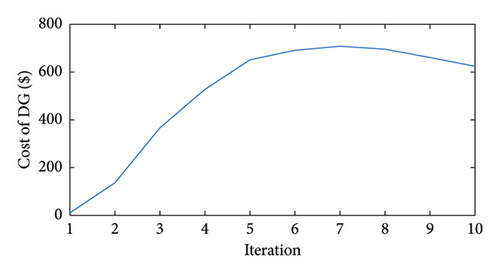
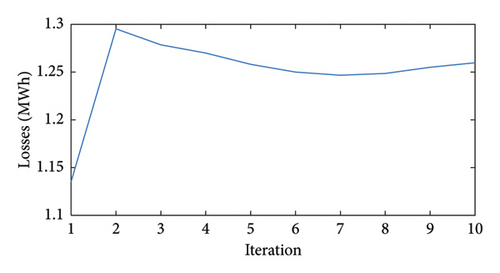
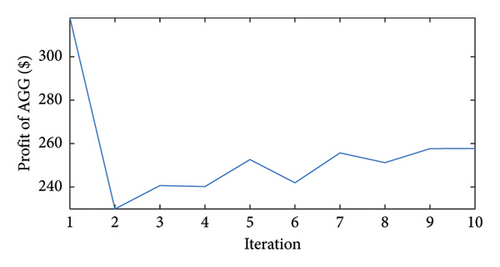
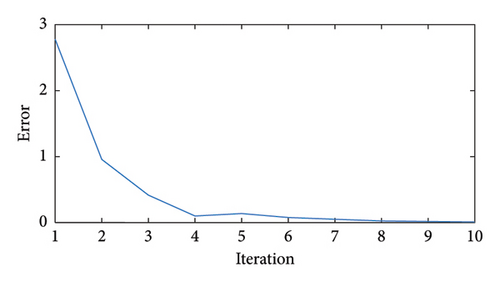
As shown in this figure, the required number of iterations to yield the optimal FADMM solution is 10. This is indicative of the fast-solving capabilities of the proposed planning algorithm. Beyond 10 iterations, the error is practically zero implying that a final solution fulfilling the objectives of all parties has been reached. The metrics of the planning task for the different study cases are compared in Table 3.

Table 3. Compare the output of cases.

	Base case	Case 1	Case 2
Losses(MWh)	1.61	1.81	1.25
C_DG ($)	—	12.42	624.21
Rev_Agg ($)	—	406.11	257.72

As explained, when only the AGG’s objectives are considered, i.e., Case 1, the corresponding profit for the AGG will reach a maximum of 406.11 $. However, the obtained charging/discharging schedule is infeasible to implement because of the violation of network technical constraints. With the implementation of the proposed approach, however, the network losses are reduced to below those of the base case and the network voltage is improved though the AGG’s profit is reduced to 257.72 $. Nevertheless, this planning scheme can be easily implemented as it meets the technoeconomic objectives of all involved parties.

4.2. Sensitivity Analysis

To evaluate the stability and adaptability of the proposed model, we performed a sensitivity analysis focusing on the weights assigned to different components in the objective function and their effect on the optimization results. The objective function combines multiple goals, such as AGG profit, network loss minimization, and DG operational costs. By adjusting the weights assigned to each component, we assess how changes in prioritization influence the optimization results. Table 4 presents the effect of varying these weights on each objective’s value, illustrating how different configurations impact the distribution of benefits among stakeholders.

Table 4. Sensitivity analysis of objective function weights and outcomes.

Weight configuration	w₁	w₂	w₃	Losses(MWh)	C_DG ($)	Rev_Agg ($)
High AGG revenue weight	0.2	0.2	0.6	1.41	324.21	292.11
High loss minimization	0.6	0.3	0.1	1.15	810.00	158.32
Balanced weights (baseline)	0.4	0.3	0.3	1.19	648.10	242.00

The sensitivity analysis results demonstrate how varying the weights of the objective function components affects the optimization outcomes. Prioritizing AGG revenue (w₃ = 0.6) results in the highest AGG profit (292.11$), but at the cost of increased network losses (1.41 MWh) and reduced DG operational costs (324.21$). Conversely, emphasizing loss minimization (w₁ = 0.6) significantly reduces network losses (1.15 MWh) but leads to lower AGG profit (158.32$) and higher DG costs (810.00$). A balanced configuration (w₁ = 0.4, w₂ = 0.3, w₃ = 0.3) achieves moderate results, balancing losses, DG costs, and AGG profits effectively. These findings underscore the adaptability of the proposed model to various prioritization scenarios, ensuring robust performance across different stakeholder objectives.

5. Conclusion

This paper introduced a planning framework using the FADMM algorithm for coordinated EV charge and discharge by AGGs as well as electricity generation by DSO-owned DGs in a way that meets the technical and economic objectives of each party. The results verify that EV charge and discharge planning aimed only at AGG’s objectives without thorough consideration of network constraints will result in impractical schemes. However, by simultaneous consideration of both AGG and DSO objectives, the resulting scheme delivers profit to AGG while flattening the network load curve leading to improve voltage profile and reduce losses. The results also indicate the feasibility of using energy stored in EV batteries as the spinning reserve, which can bring further profits to AGG. An advantage of the proposed approach is the use of the FADMM algorithm which is well-known for its high convergence while optimizing all objectives. The high convergence speed along with the insensitivity to initial values makes this algorithm highly suitable for EV charge and discharge coordination in large and complex networks. Future works can also incorporate more sophisticated features such as the economic interests of EV owners, private ownership of both renewable and conventional DGs, and direct power transactions by DSO.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funding was received for this research.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon request.

References

1 Hu J., Cao J., Rutkowski L., Xue C., and Yu J., Hierarchical Interactive Demand Response Power Profile Tracking Optimization and Control of Multiple EV Aggregators, Electric Power Systems Research. (2022) 208, https://doi.org/10.1016/j.epsr.2022.107894.
10.1016/j.epsr.2022.107894
Web of Science® Google Scholar
2 Zheng Y., Shao Z., Lei X., Shi Y., and Jian L., The Economic Analysis of Electric Vehicle Aggregators Participating in Energy and Regulation Markets Considering Battery Degradation, Journal of Energy Storage. (2022) 45, https://doi.org/10.1016/j.est.2021.103770.
10.1016/j.est.2021.103770
Web of Science® Google Scholar
3 International Energy Agency, Global EV Outlook 2022: Entering the Decade of Electric Drive, 2022, https://www.iea.org/reports/global-ev-outlook-2022.
Google Scholar
4 Das S., Thakur P., Singh A. K., and Singh S. N., Optimal Management of Vehicle-To-Grid and Grid-To-Vehicle Strategies for Load Profile Improvement in Distribution System, Journal of Energy Storage. (2022) 49, https://doi.org/10.1016/j.est.2022.104068.
10.1016/j.est.2022.104068
Web of Science® Google Scholar
5 Zheng Y., Niu S., Shang Y., Shao Z., and Jian L., Integrating Plug-In Electric Vehicles into Power Grids: A Comprehensive Review on Power Interaction Mode, Scheduling Methodology, and Mathematical Foundation, Renewable and Sustainable Energy Reviews. (2019) 112, 424–439, https://doi.org/10.1016/j.rser.2019.05.059, 2-s2.0-85066619273.
10.1016/j.rser.2019.05.059
Web of Science® Google Scholar
6 Lotfi S., Sedighizadeh M., Abbasi R., and Hosseinian S. H., Vehicle-to-grid Bidding for Regulation and Spinning Reserve Markets: A Robust Optimal Coordinated Charging Approach, Energy Reports. (2024) 11, 925–936, https://doi.org/10.1016/j.egyr.2023.12.044.
10.1016/j.egyr.2023.12.044
Web of Science® Google Scholar
7 Rehman U., A Robust Vehicle-To-Grid Aggregation Framework for Electric Vehicles Charging Cost Minimization and for Smart Grid Regulation, International Journal of Electrical Power & Energy Systems. (2022) 140, https://doi.org/10.1016/j.ijepes.2022.107911.
10.1016/j.ijepes.2022.108090
Web of Science® Google Scholar
8 Gao S., Li H., Jurasz J., and Dai R., Optimal Charging of Electric Vehicle Aggregations Participating in Energy and Ancillary Service Markets, IEEE Journal of Emerging and Selected Topics in Industrial Electronics. (2022) 3, no. 2, 270–278, https://doi.org/10.1109/jestie.2021.3102417.
10.1109/JESTIE.2021.3102417
Web of Science® Google Scholar
9 Zakariazadeh A., Jadid S., and Siano P., Multi-objective Scheduling of Electric Vehicles in Smart Distribution System, Energy Conversion and Management. (2014) 79, 43–53, https://doi.org/10.1016/j.enconman.2013.11.042, 2-s2.0-84891610155.
10.1016/j.enconman.2013.11.042
Web of Science® Google Scholar
10 Wu Z., Hu J., Ai X., and Yang G., Data-driven Approaches for Optimizing EV Aggregator Power Profile in Energy and Reserve Market, International Journal of Electrical Power & Energy Systems. (2021) 129, https://doi.org/10.1016/j.ijepes.2021.106808.
10.1016/j.ijepes.2021.106808
Web of Science® Google Scholar
11 Hashemi B., Shahabi M., and Teimourzadeh-Baboli P., Stochastic-based Optimal Charging Strategy for Plug-In Electric Vehicles Aggregator under Incentive and Regulatory Policies of DSO, IEEE Transactions on Vehicular Technology. (2019) 68, no. 4, 3234–3245, https://doi.org/10.1109/tvt.2019.2900931, 2-s2.0-85064661300.
10.1109/TVT.2019.2900931
Web of Science® Google Scholar
12 Ren H., Zhang A., Wang F. et al., Optimal Scheduling of an EV Aggregator for Demand Response Considering Triple Level Benefits of Three Parties, International Journal of Electrical Power & Energy Systems. (2021) 125, https://doi.org/10.1016/j.ijepes.2020.106447.
10.1016/j.ijepes.2020.106447
Web of Science® Google Scholar
13 Cao Y., Huang L., Li Y., Jermsittiparsert K., Ahmadi-Nezamabad H., and Nojavan S., Optimal Scheduling of Electric Vehicles Aggregator under Market Price Uncertainty Using Robust Optimization Technique, International Journal of Electrical Power & Energy Systems. (2020) 117, https://doi.org/10.1016/j.ijepes.2019.105628.
10.1016/j.ijepes.2019.105628
Web of Science® Google Scholar
14 Aliasghari P., Mohammadi-Ivatloo B., and Abapour M., Risk-based Scheduling Strategy for Electric Vehicle Aggregator Using Hybrid Stochastic/IGDT Approach, Journal of Cleaner Production. (2020) 248, https://doi.org/10.1016/j.jclepro.2019.119270.
10.1016/j.jclepro.2019.119270
Web of Science® Google Scholar
15 Yao E., Wong V. W. S., and Schober R., Optimization of Aggregate Capacity of PEVs for Frequency Regulation Service in Day-Ahead Market, IEEE Transactions on Smart Grid. (2018) 9, no. 4, 3519–3529, https://doi.org/10.1109/tsg.2016.2633873, 2-s2.0-85049041282.
10.1109/TSG.2016.2633873
Web of Science® Google Scholar
16 Choi S., Park S., Kang D.-J., Han S.-J., and Kim H.-M., A Micro-grid Energy Management System for Inducing Optimal Demand Response, Proceedings of the IEEE International Conference on Smart Grid Communications (SmartGridComm), October 2011, IEEE, 19–24, https://doi.org/10.1109/SmartGridComm.2011.6102291.
10.1109/SmartGridComm.2011.6102291
Google Scholar
17 Cecati C., Citro C., and Siano P., Combined Operations of Renewable Energy Systems and Responsive Demand in a Smart Grid, IEEE Transactions on Sustainable Energy. (2011) 2, no. 4, 468–476, https://doi.org/10.1109/tste.2011.2161624, 2-s2.0-80053192955.
10.1109/TSTE.2011.2161624
Web of Science® Google Scholar
18 Ghadi-Sahebi M., Ebrahimi R., and Parvin-darabad V., Optimal Probabilistic Operation Management of Smart Parking Lot and Renewable Sources in Microgrid to Reduce Cost and Improve System Reliability Considering Demand Response Program, International Transactions on Electrical Energy Systems. (2021) 31, no. 12, https://doi.org/10.1002/2050-7038.13108.
10.1002/2050-7038.13108
Web of Science® Google Scholar
19 Siano P., Cecati C., Yu H., and Kolbusz J., Real Time Operation of Smart Grids via FCN Networks and Optimal Power Flow, IEEE Transactions on Industrial Informatics. (2012) 8, no. 4, 944–952, https://doi.org/10.1109/tii.2012.2205391, 2-s2.0-84867953404.
10.1109/TII.2012.2205391
Web of Science® Google Scholar
20 Nimalsiri N. I., Mediwaththe C. P., Ratnam E. L., Shaw M., Smith D. B., and Halgamuge S. K., A Survey of Algorithms for Distributed Charging Control of Electric Vehicles in Smart Grid, IEEE Transactions on Intelligent Transportation Systems. (2020) 21, no. 11, 4497–4515, https://doi.org/10.1109/tits.2019.2943620.
10.1109/TITS.2019.2943620
Web of Science® Google Scholar
21 Rivera J., Goebel C., and Jacobsen H.-A., Distributed Convex Optimization for Electric Vehicle Aggregators, IEEE Transactions on Smart Grid. (2017) 8, no. 4, 1852–1863, https://doi.org/10.1109/tsg.2015.2509030, 2-s2.0-84953330249.
10.1109/TSG.2015.2509030
Web of Science® Google Scholar
22 Amini M. H., McNamara P., Weng P., Karabasoglu O., and Xu Y., Hierarchical Electric Vehicle Charging Aggregator Strategy Using Dantzig-Wolfe Decomposition, IEEE Design & Test. (2018) 35, no. 6, 25–36, https://doi.org/10.1109/mdat.2017.2759505, 2-s2.0-85030760080.
10.1109/MDAT.2017.2759505
Web of Science® Google Scholar
23 Bagher Sadati S. M., Moshtagh J., Shafie-khah M., Rastgou A., and Catalão J. P. S., Operational Scheduling of a Smart Distribution System Considering Electric Vehicles Parking Lot: A Bi-level Approach, International Journal of Electrical Power & Energy Systems. (2019) 105, 159–178, https://doi.org/10.1016/j.ijepes.2018.08.021, 2-s2.0-85052248372.
10.1016/j.ijepes.2018.08.021
Web of Science® Google Scholar
24 Shi W., Xie X., Chu C., and Gadh R., Distributed Optimal Energy Management in Microgrids, IEEE Transactions on Smart Grid. (2015) 6, no. 3, 1137–1146, https://doi.org/10.1109/tsg.2014.2373150, 2-s2.0-85027926062.
10.1109/TSG.2014.2373150
Web of Science® Google Scholar
25 Liu M., Phanivong P. K., Shi Y., and Callaway D. S., Decentralized Charging Control of Electric Vehicles in Residential Distribution Networks, IEEE Transactions on Control Systems Technology. (2019) 27, no. 1, 266–281, https://doi.org/10.1109/tcst.2017.2771307, 2-s2.0-85035761029.
10.1109/TCST.2017.2771307
Web of Science® Google Scholar
26 Boyd S., Parikh N., Chu E., Peleato B., and Eckstein J., Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers, Foundations and Trends in Machine Learning. (2010) 3, no. 1, 1–122, https://doi.org/10.1561/2200000016, 2-s2.0-80051762104.
10.1561/2200000016
PubMed Web of Science® Google Scholar
27 Fan H., Duan C., Zhang C., Jiang L., Mao C., and Wang D., ADMM-Based Multiperiod Optimal Power Flow Considering Plug-In Electric Vehicles Charging, IEEE Transactions on Power Systems. (2018) 33, no. 4, 3886–3897, https://doi.org/10.1109/tpwrs.2017.2784564, 2-s2.0-85039796745.
10.1109/TPWRS.2017.2784564
Web of Science® Google Scholar
28 Rokni S. G. M., Radmehr M., and Zakariazadeh A., Optimum Energy Resource Scheduling in a Microgrid Using a Distributed Algorithm Framework, Sustainable Cities and Society. (2018) 37, 222–231, https://doi.org/10.1016/j.scs.2017.11.016, 2-s2.0-85035042983.
10.1016/j.scs.2017.11.016
Web of Science® Google Scholar
29 Xu S., Yan Z., Feng D., and Zhao X., Decentralized Charging Control Strategy of the Electric Vehicle Aggregator Based on Augmented Lagrangian Method, International Journal of Electrical Power & Energy Systems. (2019) 104, 673–679, https://doi.org/10.1016/j.ijepes.2018.07.024, 2-s2.0-85050628556.
10.1016/j.ijepes.2018.07.024
Web of Science® Google Scholar
30 Mohiti M., Monsef H., and Lesani H., A Decentralized Robust Model for Coordinated Operation of Smart Distribution Network and Electric Vehicle Aggregators, International Journal of Electrical Power & Energy Systems. (2019) 104, 853–867, https://doi.org/10.1016/j.ijepes.2018.07.054, 2-s2.0-85051126386.
10.1016/j.ijepes.2018.07.054
Web of Science® Google Scholar
31 Rahman T., Xu Y., and Qu Z., Continuous-Domain Real-Time Distributed ADMM Algorithm for Aggregator Scheduling and Voltage Stability in Distribution Network, IEEE Transactions on Automation Science and Engineering. (2022) 19, no. 1, 60–69, https://doi.org/10.1109/tase.2021.3072932.
10.1109/TASE.2021.3072932
Web of Science® Google Scholar
32 Najafi A., Pourakbari-Kasmaei M., Jasinski M., Lehtonen M., and Leonowicz Z., A Hybrid Decentralized Stochastic-Robust Model for Optimal Coordination of Electric Vehicle Aggregator and Energy Hub Entities, Applied Energy. (2021) 304, https://doi.org/10.1016/j.apenergy.2021.117708.
10.1016/j.apenergy.2021.117708
Web of Science® Google Scholar
33 Lemeski A. T., Ebrahimi R., and Zakariazadeh A., Optimal Decentralized Coordinated Operation of Electric Vehicle Aggregators Enabling Vehicle-To-Grid Option Using Distributed Algorithm, Journal of Energy Storage. (2022) 54, https://doi.org/10.1016/j.est.2022.105213.
10.1016/j.est.2022.105213
Web of Science® Google Scholar
34 Baran M. E. and Wu F. F., Network Reconfiguration in Distribution Systems for Loss Reduction and Load Balancing, IEEE Transactions on Power Delivery. (1989) 4, no. 2, 1401–1407, https://doi.org/10.1109/61.25627, 2-s2.0-84863333614.
10.1109/61.25627
Web of Science® Google Scholar

All articles

Energy and Reserve Scheduling of Distribution Network in Presence of Electric Vehicle Aggregators: A Decentralized Approach

Abstract

1. Introduction