Optimized Selection of Renewable Energy Sources Based on Regional Potentials in Colombia: A Comparative Analysis of AHP and FAHP for Sustainable Development
Abstract
This study evaluates alternatives using the analytic hierarchy process (AHP) and Fuzzy AHP (FAHP) methodologies across five scenarios (SC1 to SC5), aiming to compare the effectiveness of both approaches in integrating environmental and technical criteria. The results indicate that, in SC1, AHP assigns weights of 14.35% to A1 and 16.22% to A2, while FAHP demonstrates greater dispersion, highlighting A6 with 35.22%. In SC2, AHP prioritizes A1 with 14.16%, whereas FAHP increases the weight of the environmental criterion to 21.18%. In SC3, A1 remains the preferred option in both methodologies, with close weights of 34.00% for AHP and 32.98% for FAHP. In SC4, both methods show similar trends, with A1 standing out at 11.12% and A4 at 34.87%. Finally, in SC5, AHP allocates 8.52% to A1, while FAHP evaluates it at 10.73%. The findings suggest that FAHP allows greater sensitivity to variations in sub-criteria, enabling a more precise evaluation aligned with sustainability objectives. The significance of environmental and social criteria across the scenarios underscores the necessity of incorporating more sustainable approaches into decision-making processes. It is concluded that, while AHP delivers consistent results, FAHP may be better suited for contexts characterized by complexity and uncertainty. Furthermore, sensitivity analysis is recommended to examine how variations in criterion weights impact final decisions.
1. Introduction
In recent decades, the international community has recognized the urgency of mitigating climate change effects and transitioning toward more sustainable economies. One of the fundamental pillars of this transition is the adoption of renewable energy sources, which offer a cleaner alternative to fossil fuels and promise to significantly reduce greenhouse gas emissions [1]. However, the implementation of renewable energies faces considerable challenges due to the variability of natural resources and the specific geographic and climatic conditions of each region. These factors directly influence the technical and economic feasibility of renewable technologies, complicating the efficient planning of energy matrices across diverse geographical areas [2].
Globally, countries like Germany, the United States, and China have made strides in diversifying their energy matrices by integrating a higher percentage of renewable energies such as solar, wind, and hydroelectric power. However, even in these nations, energy planning remains a complex task, requiring the analysis of multiple criteria to select the optimal energy sources based on regional characteristics and local energy needs [3]. Scientific literature has documented numerous approaches to support this decision-making process, with one of the most notable being the use of multicriteria decision-making methodologies, such as the analytic hierarchy process (AHP). These methodologies allow the decomposition of complex problems into hierarchical structures, facilitating the evaluation of alternatives based on technical, economic, social, and environmental criteria [4].
Colombia, a country characterized by its remarkable geographical and climatic diversity, faces a unique challenge in its transition toward a more sustainable energy system. Despite having abundant renewable resources, such as solar energy in the Caribbean and Orinoquía regions or wind potential in La Guajira, the diversification of its energy matrix has been limited [5]. The country’s historical reliance on hydropower, which accounts for ~70% of its installed capacity, has exposed Colombia to vulnerabilities from extreme weather events like El Niño, which directly impact the stability of its power supply. This underscores the urgent need to diversify energy sources, not only to reduce dependency on a single source but also to enhance the resilience of the national energy system [6].
Despite these challenges, energy planning in Colombia faces an additional obstacle: the variability of regional conditions. The country is divided into several geographical zones that differ significantly in terms of available energy resources, infrastructure, and energy demand needs [7]. Regions such as the Altiplano Cundiboyacense, the Eastern Plains, or the Pacific region present unique climatic and geographical conditions that make the application of a uniform national energy strategy unfeasible. In this context, it is imperative to develop an energy planning approach that adapts to the particularities of each region and allows the selection of the most appropriate energy sources based on a multicriteria analysis [8].
Previous literature has explored various approaches to address this problem. The AHP, developed by Thomas L. Saaty in the 1970s, has become a powerful tool for multicriteria decision-making in energy planning. This method allows complex problems to be broken down into a hierarchical structure that includes criteria and sub-criteria, facilitating the comparison of alternatives through both qualitative and quantitative evaluation [9]. AHP has been widely used in studies that address the selection of energy technologies in various contexts. However, one of the method’s main limitations lies in its inability to adequately handle the uncertainty and subjectivity inherent in human judgments, especially in situations where information is incomplete or imprecise. To address this issue, an extension of AHP that incorporates fuzzy logic has been proposed, known as the fuzzy AHP (FAHP). Fuzzy logic, introduced by Lotfi A. Zadeh in 1965, allows for the management of uncertainty and ambiguity by providing a mathematical framework to handle subjective judgments that cannot be expressed with numerical precision [10]. FAHP has proven particularly useful in applications where data is imprecise or incomplete, such as evaluating energy technologies in diverse geographical contexts with limited information. However, in Colombia, the application of FAHP in energy planning is still in its early stages, and research integrating this approach with the analysis of the country’s specific geographical and climatic conditions is scarce [11].
This study aims to close this gap in the literature by comparing the application of AHP and FAHP methodologies for selecting renewable energy sources across different regions of Colombia. The central hypothesis of this work is that the use of FAHP, in combination with traditional AHP, will provide a more robust decision-making tool, allowing for better management of uncertainty and subjectivity in judgments [12]. To this end, energy alternatives such as photovoltaic solar power, wind energy (onshore and offshore), biomass, geothermal energy, and hydroelectric power (large and small scale) will be evaluated. Each of these alternatives will be assessed based on a set of multidimensional criteria, including technical, economic, social, and environmental aspects. The implementation of these methodologies will not only allow for a more precise and adaptable evaluation of energy alternatives but also lead to more efficient and sustainable energy planning, tailored to the specific characteristics of each region. By integrating AHP and FAHP, this study will provide a practical guide for decision-making in Colombia’s energy planning, offering a methodological tool that can be replicated in other contexts with similar characteristics [13].
As a final comment, it is important to note that Colombia’s geographic and climatic diversity, spanning mountainous regions, extensive coastal areas, and arid zones, presents a unique challenge for energy planning. This study focuses on optimizing the integration of renewable energy within this diverse context, drawing lessons from countries such as Germany, the United States, and China. For instance, Germany has demonstrated the potential of wind energy in regions with limited resources, while the United States has implemented strategies for integrating renewable sources into extensive power grids. China, on the other hand, has excelled in decentralized production, an approach particularly relevant for Colombia’s Non-Interconnected Zones. These international experiences are adapted in this study to address Colombia’s specific needs, exploring solutions that tackle energy inequalities and optimize the use of local resources, such as solar energy in La Guajira and wind energy along the Caribbean coast.
1.1. Featured Research
The featured research is an essential part of any research, and in particular, when addressing methodologies such as the AHP and the FAHP, their importance becomes even more apparent. In this part, some outstanding research from the literature related to AHP and FAHP will be mentioned in order to highlight why this review is crucial, for this see Tables 1 and 2.
| Title | Summary | Reference |
|---|---|---|
| The process of analytic hierarchy |
|
[14] |
| Analytic hierarchy process: an overview of applications | This article, published in the “European Journal of Operations Research”, provides an overview of the applications of the Hierarchical Analytical Process (AHP) in multi-criteria decision-making. The authors, O. S. Vaidya and S. Kumar, explore how AHP has been used in various areas and contexts to solve decision problems involving multiple criteria and sub-criteria. | [15] |
| Selecting optimal fire station locations using fuzzy decision making and the analytic hierarchy process: a case study in Taiwan |
|
[16] |
| A comprehensive review of multi-criteria decision-making applications in renewable energy management using a new fuzzy and hesitant AHP method | This research presents a comprehensive review of the applications of Multi-Criteria Decision Making (MCDA) in renewable energy management. Of particular interest is the implementation of a new method that combines the hierarchical analytical process (AHP) with faltering fuzzy logic. This review addresses how these methodologies are applied in decision-making related to clean and sustainable energy sources, and highlights the use of a novel approach that can address uncertainty in decision-making. | [17] |
| An assessment of renewable energy selection for sustainability in Saudi Arabia: a multi-criteria decision analysis approach | This research focuses on evaluating the selection of renewable energy sources in Saudi Arabia from a sustainability perspective. They use a multi-criteria decision analysis (MCDA) approach to consider multiple criteria and sub-criteria in decision-making. The aim is to identify and evaluate renewable energy options that best contribute to sustainability in the context of Saudi Arabia. | [18] |
| A multi-criteria decision analysis framework for evaluating renewable energy projects for Egypt | The research presents a multi-criteria decision analysis (MCDA) framework for the evaluation of renewable energy projects in Egypt. The research focuses on providing a structured approach to making informed decisions in the selection and evaluation of renewable energy projects in the Egyptian context. The framework addresses the complexity of considering multiple criteria and sub-criteria when making strategic decisions related to sustainable energy in the country. | [19] |
| Multi-criteria decision analysis in renewable energy management: a critical review | This research provides a critical review on the use of multi-criteria decision analysis (MCDA) in renewable energy management. It focuses on analyzing and evaluating how MCDA methods, such as the hierarchical analytical process (AHP), are applied in decision-making related to clean and sustainable energy sources. The review addresses the relevance, benefits and limitations of these methodologies in the context of renewable energy management. | [20] |
| Renewable energy assessment: multi-criteria decision analysis (MCDA) approach | This research focuses on the evaluation of renewable energy sources using a multi-criteria decision analysis (MCDA) approach. Although I don’t have access to specific details of the research, the study is likely to explore how MCDA methods, such as the hierarchical analytical process (AHP), can be applied to make informed decisions in the selection and evaluation of renewable energy sources. This involves considering multiple criteria and sub-criteria to identify the most suitable options in the context of clean and sustainable energy. | [21] |
| Title | Summary | Appointment |
|---|---|---|
| A comprehensive review of multi-criteria decision-making applications in renewable energy management using a new fuzzy AHP method. | This study provides a comprehensive review of the applications of multi-criteria decision making in renewable energy management. It introduces a new method that combines diffuse and fuzzy AHPs and focuses on decision-making in the context of clean and sustainable energy | [22] |
| A hybrid FAHP-PROMETHEE approach to classifying renewable energy sources | This study proposes a hybrid approach that combines FAHP and the PROMETHEE method to classify renewable energy sources. The research focuses on the classification of different sources of clean energy | [23] |
| Wind turbine selection using the fuzzy analytical hierarchy (FAHP) process: a case study in Turkey | This research focuses on the selection of wind turbines using FAHP as a tool to evaluate wind energy alternatives in Turkey | [24] |
| A new FAHP-based approach to renewable energy source selection: a case study from Turkey | The study presents a new FAHP-based approach to the selection of renewable energy sources. It uses a case study in Turkey to demonstrate the applicability of the method | [25] |
| Comprehensive assessment of renewable energy sources in Pakistan using an Enhanced fuzzy AHP approach | This study offers a comprehensive assessment of renewable energy sources in Pakistan using an improved version of FAHP to address decision-making in the country’s energy context | [26] |
| Selecting renewable energy sources using fuzzy AHPs: a case study in India | The research focuses on the selection of renewable energy sources in India through the use of FAHPs and provides insights into preferences in the country’s energy context | [27] |
| Multi-criteria decision analysis for the selection of renewable energy sources for a sustainable environment: a case study from India | This study uses a multi-criteria decision analysis approach for the selection of renewable energy sources in India, with a focus on environmental sustainability | [28] |
- AHP, analytic hierarchy process; FAHP, fuzzy analytic hierarchy process.
This research provides examples of how the AHP has been applied in the evaluation and selection of renewable energy sources in various contexts.
Based on the information presented in Tables 1 and 2, this research opens significant opportunities for the Colombian and Latin American context by applying the AHP and FAHP methods in the selection of renewable energy sources. Although these approaches have been scarcely used in the region, their implementation offers a robust and systematic framework for decision-making in complex scenarios, such as identifying the most suitable energy source for each geographic region of Colombia. Given that Brazil has shown the greatest development in the application of these methodologies, Colombia still has a field to explore in this area, making this research pioneering in the country. Furthermore, Colombia’s geographic and climatic diversity provides an ideal setting for applying AHP and FAHP, adapting selection criteria to the energy needs of specific areas such as the Caribbean coast, the Andean region, and the Amazon [18]. This study will not only contribute to academic and scientific advancement but will also provide a key tool for the formulation of public policies that promote the efficient use of renewable energies in the country, aligning with the goals of sustainability and energy diversification. The literature review highlights the limitations of the AHP, particularly its reliance on crisp judgments, which can restrict its applicability in scenarios where decisions must account for inherent uncertainty. In contrast, the FAHP offers a solution by incorporating fuzzy logic, enabling a more accurate representation of subjective and ambiguous evaluations [29]. This approach is particularly relevant to energy planning in Colombia, given the uncertain nature of geographic, climatic, and socioeconomic variables that influence the selection of renewable energy sources. Thus, FAHP not only addresses the identified limitations of AHP but also aligns with the need for more robust and adaptable tools in complex contexts like Colombia.
The choice between the AHP and the FAHP in research depends on the nature and objectives of each study and each of these methodologies has advantages and disadvantages that from personal experience and the contribution of research such as those of [14] evidence these nature.
2. Material and Methodology
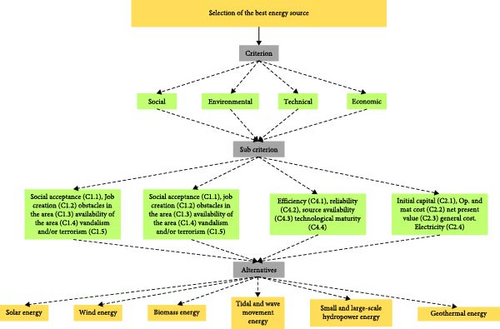
Today, the selection of suitable energy sources is a critical challenge faced by researchers, engineers, and decision-makers in the context of the transition to a more sustainable and efficient energy system. Growing awareness of environmental impacts, the depletion of fossil resources, and the demand for clean, renewable energy sources has driven the need to make informed decisions in the selection of energy sources. However, this decision-making process has become increasingly complex due to the multitude of variables and criteria that must be considered. In this context, metaheuristic methods have emerged as powerful and versatile tools to address the complexity of energy source selection. These advanced computational techniques allow researchers and practitioners to seek optimal solutions to highly complex and multidimensional decision problems [30]. Metaheuristic methods are based on heuristic search concepts, exploring and exploiting the solution space efficiently and effectively, Figure 1 masters the schematic diagram of the methodological process that is implemented in the AHP and FAHP methodologies in the present research [31].
The importance of metaheuristic methods lies in their ability to find approximate solutions to optimization problems in a reasonable time. In the context of energy source selection, this involves considering a wide range of factors, such as costs, environmental impact, resource availability, and energy demand, among others [31]. The complexity of these problems and the need to make decisions that balance multiple objectives make metaheuristic methods a natural choice. The implementation of metaheuristic methods in the selection of energy sources offers significant advantages. These techniques make it possible to evaluate the different alternatives in a comprehensive and efficient way, taking into account the constraints and preferences of the energy system in question. In addition, they provide an adaptable and scalable approach that can be applied in a variety of scenarios, from the selection of renewable energy technologies to large-scale energy system planning [32, 33].
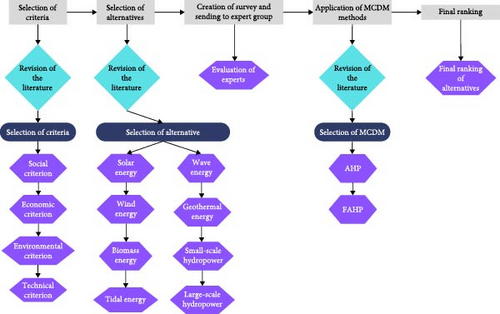
Figure 2 shows the five main steps that are required to be carried out for the implementation of a metaheuristic method, the first step consists of the selection of criteria and sub-criteria that will serve for the evaluation of the group of experts, these criteria and sub-criteria must be selected very carefully, for this it is required to consult the specialized literature, consultation with personnel of mastery of the research topic, as a second step is the choice of the group of energy alternatives that these energy alternatives must be in accordance with the existing potential in the area of implementation of the research, as a third step is the elaboration of a survey where they are allowed to compare according to the Thomas L. Saaty scale [34], alternatives, criteria, and sub-criteria, the survey is sent to the group of experts where they from their experience and knowledge will give their opinion, when the survey of the experts is available, each matrix of responses is evaluated and determined from the radius and the consistency index in order to determine the validity of the answers given by each expert consulted, if these values are among those allowed according to the size of each matrix, the implementation step of the selected metaheuristic method will be carried out, which in this research were the AHP and the FAHP, finally, the results of the implemented methods will be obtained and the weighting and hierarchization of criteria, subcriteria, and evaluated alternatives will be carried out [35].
The AHP is a methodology developed by mathematician and economist Thomas L. Saaty in the 1970s. This technique has become a fundamental tool in multi-criteria decision-making and has found applications in a wide variety of fields, from investment selection to natural resource management and strategic planning. Thomas L. Saaty, a leading scholar in the field of game theory and operations research, began developing the ideas that would lead to AHP in the early 1970s. The motivation behind their work was to provide a framework that would allow people to make more informed and logical decisions in complex situations involving multiple criteria and alternatives [36]. Saaty formulated the mathematical foundations of the AHP, which are based on matrix theory and mathematical logic.
The central idea of the AHP is to break down a decision-making problem into a hierarchical structure of criteria and sub-criteria, and then use a comparison matrix to capture the preferences and relationships between these elements [34]. In 1980, Thomas L. Saaty published the book entitled “The Process of Analytic Hierarchy” (AHP), in which he exhaustively presented the AHP methodology and its applications in decision-making. This book became a fundamental reference in the field of multicriteria decision-making [37].
As the benefits of the AHP methodology spread, its adoption in various disciplines increased. It has been used in investment project selection, natural resource management, decision-making in strategic planning, choice of technologies, and more recently in artificial intelligence and machine learning applications [38]. Over the decades, Saaty and other researchers have continued to develop and refine the AHP, introducing variants and extensions of the methodology to address specific problems and improve its applicability in real-world situations [34].
The methodology section of this article deploys a meticulous and rigorous approach to addressing the particular challenges associated with the evaluation of renewable energy sources in Colombia. The implementation of metaheuristic methods, specifically TOPSIS and TOPSIS with fuzzy logic, constitutes the backbone of our methodological strategy. These approaches were carefully selected due to their demonstrated ability to deal with the complexity inherent in decision-making in a changing and diverse environment such as Colombia’s [39]. The choice of TOPSIS and TOPSIS with fuzzy logic as metaheuristic methods is the result of careful evaluation of their suitability to address the variables and uncertainty associated with the selection of renewable energy sources. TOPSIS, with its ability to handle multiple criteria and provide trade-offs, offers a robust basis for the weighting and prioritization of energy options [40]. On the other hand, the integration of fuzzy logic in TOPSIS is justified by its ability to model the imprecision inherent in the variability of renewable energy sources, ensuring a more realistic and adaptive approach [41].
The methodology developed takes into account the geographical diversity of Colombia, characterized by variations in altitude, climates, and topographies. The application of these methods is tailored to the particularities of each region, recognizing that there is no single approach that can encompass the complexity of the country’s geographical conditions. The adaptability of TOPSIS and TOPSIS with fuzzy logic is presented as an essential element in ensuring that renewable energy decisions are contextually relevant and strategically informed [30]. The methodology section details the key steps of implementation, from data collection to final evaluation [42]. Specific criteria, such as the availability of natural resources, environmental impact, and economic viability, are included to ensure a holistic assessment of each renewable energy source. In addition, sensitivity analyses are integrated to evaluate the robustness of the results in the face of possible changes in environmental or technological conditions [43].
The validation of the results obtained by applying AHP and AHP with fuzzy logic is done through comparisons with conventional approaches and the review of experts in the field [44]. This validation process guarantees the reliability and practical applicability of the results, strengthening the contribution of this research to the emerging field of efficient renewable energy management in Colombia [45], for this research, seven energy alternatives were used as evidenced in Table 1 and were implemented in five possible scenarios, according to the five geographical regions that comprise the study area, as evidenced in Tables 3 and 4.
| A1 | Hydroelectric |
| A2 | Wave |
| A3 | Tidal |
| A4 | Biomass |
| A5 | General wind power |
| A6 | PV |
| A7 | Geothermal |
| SC1 | CARIBBEAN 1 |
| SC2 | PACIFICA 1 |
| SC3 | ANDEAN |
| SC4 | AMAZONIAN |
| SC5 | ORINOQUIA |
-
Caribbean Region (SC1): Colombia’s Caribbean Region, known for its cultural richness and Caribbean coastline, offers great potential for renewable energy generation. With a tropical climate, this region has abundant solar resources that make it ideal for the installation of photovoltaic solar energy systems. In addition, its extensive coastline provides opportunities for offshore wind energy, taking advantage of the winds that blow over the Caribbean Sea. Biomass is also a promising source in this region, given the availability of agricultural and forestry residues for energy production [47].
-
Pacific Region (SC2): The Pacific Region of Colombia, known for its biodiversity and its coastline on the Pacific Ocean, has great potential for renewable energy generation. Its dense jungles and humid climate offer optimal conditions for energy production using biomass and biogas, using organic waste and agricultural waste. In addition, its coastline exposed to Pacific winds makes it ideal for offshore wind energy, taking advantage of the strong winds that blow over the ocean [48].
-
Andean Region (SC3): Colombia’s Andean Region, characterized by its mountainous topography and fertile valleys, presents great potential for a variety of renewable energy sources. Its high mountains offer opportunities for large-scale hydroelectric power, taking advantage of the mighty rivers that descend from the Andes Mountains. In addition, its temperate climate and high altitude make it conducive to solar photovoltaic and wind energy in mountainous areas [49].
-
Amazon Region (SC4): Colombia’s Amazon Region, known for its lush rainforest and unique biodiversity, offers great potential for renewable energy generation. Its dense vegetation and humid climate make it ideal for energy production using biomass and biogas, using organic waste and forest waste. In addition, its extensive network of rivers, such as the Amazon River and the Caquetá River, offers opportunities for large-scale hydropower, harnessing the flow and energy of these waterways [50].
-
Orinoquia Region (SC5): Colombia’s Orinoquia Region, characterized by its vast plains and rushing rivers, offers great potential for renewable energy generation. Its wide lowland areas and tropical climate make it ideal for the installation of large-scale solar PV systems. In addition, its many rivers, such as the Meta River and the Orinoco River, offer opportunities for hydropower and biomass energy from agricultural and forestry residues [49].
As a synthesis of the methodology implemented in this research, it is expressed in Figure 1; however, in the following subsections a general explanation of each of the steps is made.
2.1. AHP Methodology
In summary, a series of explanatory steps for the implementation of the hierarchical analytical process methodology are presented, it is expected that this summary will be easy to understand:
2.1.1. Implementation of the AHP Methodology
2.1.1.1. Step 1: Modeling
In this phase, the hierarchical sequence of problems is implemented and the objectives, criteria, and alternatives to be implemented are defined according to the criteria of the experts. Next, the alternatives through which the criteria to be evaluated are established. These criteria should take into account the problem and identify attributes that help make good decisions [51]. These criteria should be measured at the level, which is the fundamental goal we must achieve to solve the problem, and at the second level, the criteria will be positioned according to a descending hierarchy of one or more variables for each criterion. The third and final layer will be the alternatives in decision-making [52].
2.1.1.2. Step 2: Reviews
Once the alternatives are understood and the criteria defined, each criterion is classified and weighted when selecting the alternatives. The intent of this process is to measure the importance that decision-makers assign to each criterion or alternative i, compared to each criterion or alternative j. A baseline scale of 1–9 was used to assess the relative preference of the items, Table 2 [53].
In this way, we proceed to construct the matrix of paired comparisons, where we obtain a square matrix Anxn = [aij], with 1 ≤ i, j≤ n.
-
Axiom of reciprocity: If A is a matrix of paired comparisons, then it is true that if aij = x then aji = 1/x with 1/9 ≤ x ≤ 9
-
Axiom of homogeneity: The elements that are compared with each other will be of the same order of magnitude and hierarchy.
-
Axiom of independence: When the decision-maker makes the comparisons, it is assumed that the criteria do not depend on the different alternatives.
By complying with the above axioms, it is possible to determine the desired comparison matrix, Table 5 and in Table 6, example of a comparison matrix.
| Value | Definition |
|---|---|
| 1 | Equal importance |
| 3 | Moderate importance |
| 5 | Great importance |
| 7 | Very important |
| 9 | Extreme importance |
| 2, 4, 6 and 8 | Intermediate values |
| Scale according to the degree of importance | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | A12 | A13 |
| A2 | A21 | 1 | A23 |
| A3 | A31 | A32 | 1 |
2.1.1.3. Step 3. Prioritization and Synthesis
After comparing the paired matrices, we proceed to calculate since this is a priority part to be made. This underscores the importance that decision-makers attach to each element.
The priority is represented as a vector or vectors, assuming that it is a matrix A (nxn), as obtained by making comparisons in pairs, we call the solution of the equation eigenvalues or eigenvectors of A (λ1, λ2,…,λn): det (A − λI) = 0. The principal eigenvalue (λmax) of the matrix is the maximum value of the eigenvalue obtained by performing the above formula [54].
The principal eigenvalue of {A} and {a} is the associated eigenvector. The eigenvectors associated with the value of probabilities are the weighting vectors that must be achieved [55].
Thus, the eigenvector achieved is that of the criteria matrix, which we call Vc, which represents the relative importance of each criterion selected in the joint evaluation of the alternatives on which we work [56]. When the eigenvector obtained is the eigenvector of the surrogate matrix for a given criterion, we call it Vai (column vector), which represents the relative importance of each surrogate matrix for criterion i where we obtain as many eigenvectors as standard. Something to keep in mind is that the final decision is the consistency of the decision-maker’s decision when completing the matching matrix [57].
In this way, the decision made by the insured is a personal judgment, which leads to an inconsistency that is evaluated to determine if the limits are below what corresponds.
2.1.1.4. Step 4. Consistency Analysis
This analysis takes into account the subjectivity of manufacturing decisions. When performing a process of comparing matrices in pairs, subjectivity is as real and objective as possible because the different elements of one matrix are in turn compared with another matrix [58].
On the other hand, there is a procedure to calculate it. If acceptable, the decision-making process can continue, but if not, more in-depth analysis is required, as it can review judgments about peer comparisons. Calculate the consistency ratio using Equation (1), see Figure 3 [60].

CI: Consistency Index
Subsequently, the CI obtained is compared with the random CI in Table 3:
The random consistency (CI) value as a function of the matrix size represents the CI value that would have been obtained if the numerical judgments of the scale had been entered into the comparison matrix in a completely random manner [34].
The calculation of the consistency coefficient should not be seen simply as a procedural step, but as a critical element to ensure that judges’ evaluations are fair and not arbitrary. A low consistency index (greater than or equal to 0.10) indicates a high level of agreement among the judges, which reinforces the validity and reliability of the results obtained from the analysis. Conversely, a higher proportion may suggest inconsistencies that need to be addressed to maintain the reliability of the findings. For those interested in understanding the precise methodology for calculating the consistency index, more details can be found in the articles mentioned above. These resources will guide you through the specific steps and formulas needed to accurately perform this important calculation, ensuring that the evaluation process remains robust and credible [34, 61]. Finally, a consistent matrix is considered when the stipulated values for the size of each matrix are not exceeded, Table 7. If a matrix exceeds the consistency coefficient, the assessments made are checked and modified. Figure 4 presents the methodological procedure addressed for each response of each expert in the calculation of the consistency index and radius of the present investigation.
| Die size (n) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Random consistency | 0.0 | 0.0 | 0.52 | 0.89 | 1.11 | 1.25 | 1.35 | 1.40 | 1.45 | 1.49 |
2.2. FAHP Methodology
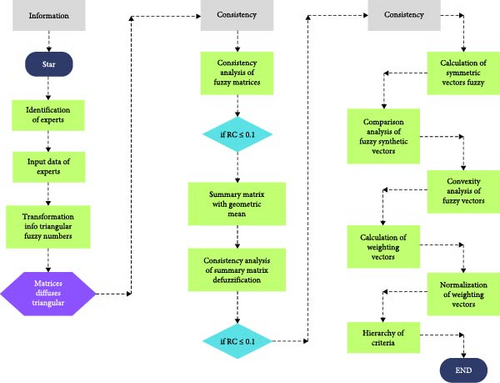
The AHP with FAHP methodology is an extension of the AHP that incorporates fuzzy logic to address uncertainty and ambiguity in multi-criteria decision-making. Although the exact history of its development is not as widely documented as that of the AHP. Fuzzy logic, developed by He, Lu, and Li [62] in the 1960s, provides a framework for representing and managing uncertainty in data and judgments [62]. In an effort to combine the advantages of AHP with fuzzy logic’s ability to deal with uncertainty, researchers began exploring the extension of AHP with fuzzy logic [61]. Throughout the 1990s and 2000s, there was significant growth in research and literature related to FAHP. Researchers from various disciplines, such as engineering, management, and artificial intelligence, contributed to the development and adaptation of FAHP methods for specific applications. As the FAHP methodology gained popularity, specific variants and extensions were developed to address problems [62]. These variants are tailored to the needs of a variety of applications and industries, including project management, engineering decision-making, and strategic planning. Although there is no specific event or prominent figure behind the development of the FAHP as in the case of the AHP, its evolution is a testament to the adaptability and versatility of multicriteria decision-making methods in response to decision-making needs in uncertain environments. The FAHP methodology has proven to be a valuable approach to addressing complex problems in which uncertainty and ambiguity are key elements [63].
In the same way that the steps for the AHP methodology were explained, the steps to achieve the implementation of the fuzzy hierarchical analytical process FAHP are now summarized, see Figure 5 [55]:

This section presents the fundamental concepts that guided this study. The intention is not to cover all topics, but to provide essential support information to understand in a very good way the objective of the research, the context and the results, in this research initially a characterization of a specific population, I seek to evidence the social, economic, environmental, and energy reality of this. To carry out this characterization, the different existing government and research databases were consulted.
It happens that the characterizations of the population nature manage to obtain as results information on the structure and large number of identity attributes of various groups of people with evolutionary continuity over time, which according to their differences configure particular ways of being and being in a territory, in this research it was taken to the department of La Guajira in the country of Colombia, because this area is a territory very rich in natural resources, which makes it a potential in the implementation of renewable energy sources; however, despite this natural disposition, this area of that country is one where its inhabitants suffer from a poor quality of life [65].
These studies that characterize a population in relation to its energy potential also allow us to focus attention on guaranteeing or restoring the effective enjoyment of the rights of population groups, the recognition of their diversity and multiculturalism as social wealth, the particularities and inequalities that hinder or enable their access to the dynamics and benefits of social and territorial development [66]. The importance of correctly directing the appropriate forms of population characterization exercises lies in the fact that they allow the design, adjustment, and implementation of public policies to be based with a view to transforming situations considered problematic and offering goods and services that satisfactorily respond to the needs and interests of population groups [67].
On the other hand, the hierarchical analytical method with fuzzy logic was implemented with the aim of prioritizing the barriers that may arise in the implementation of energies with renewable sources, in the aforementioned study area [68] for the explanation of this methodology was separated into sections for a better understanding.
2.2.1. Fuzzy Assembly Operations [69]
- •
The complementary set of a fuzzy set One is one whose characteristic function is defined by [70]:
- •
The union of two fuzzy sets A and B is a fuzzy set A ∪ B in U whose membership function is:
- •
The intersection of two fuzzy sets A and B is a fuzzy set A° B in U
2.2.2. Fuzzy Relationships [71]
Suppose R(x, y) and S(x, y)
- •
The max-min composition of the fuzzy relations R (U, V) and S (V, W) is a fuzzy relationship R ° S in U x W defined by the membership function
- •
The composition of the maximum product of the fuzzy relations R (U, V) and S (V, W) is a fuzzy relation to R ° S
2.2.3. Fuzzy Implication
In fuzzy logic, the Modus Ponens extends to what is called Generalized Modus Ponens and can be summarized as follows:
Premise 1: “u is A∗”
Premise 2: “if you are A THEN v is B”
Consequence: “v is B∗”
Where the fuzzy set does not necessarily have to be the same as the fuzzy set A of the rule’s antecedent and the fuzzy set does not necessarily have to be the same as the fuzzy set B that appears in the rule’s consequence.
2.2.4. Methods of Organizing
- •
Maximum Method: The output variable for which the characteristic function of the fuzzy output set is maximum is chosen. In general, it is not an optimal method, as this maximum value can be reached by several outputs.
- •
Centroid method: Uses the center of gravity of the output characteristic function as the output of the system. Mathematically [73]:
- •
Height method: The center of gravity of the diffuse output set Bm is calculated for each ruler and then the system output is calculated as the weighted average:
2.2.5. Fuzzy Logic Analysis
Key steps of the model proposed by Chang (1996) [32]
Step 3: The degree of chance that a fuzzy convex number is greater than k
The weight of the vector is given by
Where are n elements? Ai(i = 1, 2, 3, …, n)
In this case, it must be taken into account that W are no longer fuzzy numbers, but vectors with the final weights. Table 8 shows the values used in the conversion of the linguistic syntax used by the experts and their respective assessment into fuzzy triangular and triangular numbers. Finally, Figure 6 presents a diagram that explains how the hierarchical analytical process can be implemented or developed with fuzzy logic, with this scheme it is intended to provide an explanatory tool of this process for future research [14, 76].
| Linguistic scale | Triangular diffuse triangular |
|---|---|
| Just the same | (0,0,0) |
| Degradably important | (0,1,3) |
| Important | (1,3,5) |
| Much more important | (3,5,7) |
| Very strongly more important | (5,7,9) |
| Absolutely more important | (7,9,9) |
2.3. Advantages and Disadvantages of AHP and FAHP
2.3.1. Advantages of AHP [77]
- •
Clear hierarchical structure: AHP provides a hierarchical structure that facilitates the decomposition of complex problems into more manageable subproblems.
- •
Ease of implementation: AHP is widely used, and its implementation is relatively straightforward compared to FAHP.
- •
Wide acceptance: AHP has been used in a variety of fields and is well accepted in the scientific community.
- •
Clarity in the comparison of criteria: AHP allows criteria to be compared effectively, facilitating decision-making based on the relative importance of the criteria.
- •
Expert sensitivity: AHP allows the incorporation of expert experience and judgment into decision-making.
- •
Wide Software Availability: There are numerous software tools available to apply AHPs, making them easy to use.
- •
Facilitates prioritization: AHP helps prioritize alternatives based on weighted criteria.
- •
Deterministic approach: AHP is based on precise values and does not take uncertainty into account.
- •
Transparent approach: AHP allows for transparent and easy-to-understand assessment.
- •
Flexibility in hierarchical structure: It can be easily adapted to address different types of problems.
2.3.2. Advantages of FAHP [78]
- •
Uncertainty management: FAHP is suitable for dealing with uncertain and fuzzy data, which is common in practical research [36].
- •
Greater flexibility: You can model uncertainty and ambiguity in data, providing a more realistic representation of decision-making [37].
- •
Suitable for decision-making based on expert judgment: FAHP is effective when input comes from experts and is based on qualitative judgments.
- •
Incorporation of imprecise knowledge: Can handle knowledge that cannot be expressed accurately [38].
- •
Representation of uncertainty in weights: FAHP allows fuzzy weights to reflect uncertainty in the importance of the criteria.
- •
Greater robustness against inconsistencies: FAHP is less sensitive to inconsistencies in comparisons between criteria [39].
2.3.3. Disadvantages of AHP [79, 80]
- •
Value scale sensitivity: AHP is sensitive to the choice of value scales, which can affect the results.
- •
Does not take uncertainty into account: Does not effectively address uncertainty and imprecision of data [40].
- •
Not suitable for fuzzy data: AHP is not ideal for representing uncertain or fuzzy information.
- •
It can be subjective: The subjective interpretation of the values and weights of the criteria can influence the results [41].
- •
Requires an expert in the methodology: The correct application of AHP requires experience in the methodology.
- •
Time and resource demand: It can be expensive and time-consuming to implement AHP correctly.
- •
You need a well-defined hierarchy: The hierarchical structure needs to be carefully defined, which can be tricky in some cases.
- •
Complexity with multiple criteria: AHP can become complex and difficult to manage with a large number of criteria and alternatives [42].
- •
Inability to handle inconsistencies: Inconsistencies in comparisons can arise in real-world situations and affect the integrity of results.
- •
Requires considerable data entry: Data collection and comparisons between criteria and alternatives can be resource-intensive.
2.3.4. Disadvantages of FAHP
- •
Computational complexity: The implementation of FAHP is more computationally complex and may require more resources [43].
- •
Less general acceptance: FAHP is not as widely used and accepted as AHP in some fields [44].
- •
Less clarity in hierarchical structure: The hierarchical structure in FAHP may be less clear than in AHP.
- •
More learning time: Understanding and implementing FAHPs can take longer for researchers [45].
2.4. Identification of Problems and Alternatives
Colombia, a nation characterized by its geographical and climatic diversity, faces a diverse energy problem in its different regions. Historical dependence on non-renewable sources and variability in the availability of energy resources have led to significant challenges in the supply of sustainable and reliable energy. In response to this problem, a meticulous evaluation of energy alternatives is required, considering the economic, social, political and technical contexts of each region [15, 65].
2.5. Regional Energy Problems
-
Caribbean (SC1): Coastal regions face high potential for solar and wind energy, but lack of investment and political instability have limited the development of renewable projects. Vandalism and terrorism are also a concern in some areas.
-
Pacific (SC2): Despite their abundant hydropower and biomass potential, the Pacific regions face challenges in terms of infrastructure and limited grid access. In addition, the social acceptance of projects can be a problem.
-
Central and Western Andes (SC3): These mountainous regions present great potential for large-scale hydroelectric power generation. However, existing infrastructure needs to be updated and adapted to topographical challenges. In addition, the lack of grid access in some areas requires decentralized solutions, such as solar and small hydropower.
-
Amazon and Orinoco (SC4 and SC5): These vast regions have enormous potential in biomass and hydropower. However, the ecological impact and concerns about technological maturity require careful assessment.
2.6. Identification of Problems, Criteria, and Sub-Criteria
2.6.1. Workarounds [45]
-
Solar Energy (A6): Take advantage of solar radiation in regions with this potential.
-
Wind energy (A5): Use of wind speed in coastal and mountainous areas.
-
Biomass (A4): Use of agricultural and forestry residues.
-
Tidal and wave movement (A2 and A3): Exploiting the potential of the Caribbean and Pacific coasts.
-
Small and large-scale hydropower (A1 and A9): Development of projects suitable for mountainous regions and vast river basins.
-
Geothermal (A8): Exploitation of geothermal sources in specific regions.
2.6.2. Evaluation Criteria and Sub-Criteria [15]
-
Social Criterion (C1): Focuses on evaluating how a decision or project impacts communities. It includes aspects such as job creation, social equity, public acceptance, and effects on quality of life. In energy projects, this criterion is crucial to ensuring that solutions are inclusive and beneficial for the population. Considering sub-criteria such as social acceptance (C1.1), job creation (C1.2), obstacles in the area (C1.3), availability of the area (C1.4), vandalism, and/or terrorism (C1.5).
-
Economic Criterion (2): Evaluates the financial feasibility and costs associated with a project. It considers aspects such as initial costs, operational expenses, profitability, return on investment, and revenue generation. In energy projects, this criterion determines whether solutions are economically sustainable and competitive. Including sub-criteria such as initial capital (C2.1), op. and mat cost (C2.2), net present value (C2.3), general cost, electricity (C2.4).
-
Environmental Criteria (C3): Analyzes the impact of a decision or project on the natural environment. It considers factors such as reducing greenhouse gas emissions, sustainable resource use, biodiversity protection, and mitigating negative effects on ecosystems. This criterion aims to ensure long-term environmental sustainability. Addressing sub-criteria related to the renewable fraction (C3.1), the carbon footprint (C3.2), and the Impact on the ecosystem (C3.3).
-
Technical Criterion (C4): Examines the technical feasibility and performance of the proposed technologies or systems. It includes variables such as efficiency, reliability, infrastructure availability, and technological suitability for the specific context. This criterion ensures that solutions are technically viable and effective. Includes sub-criteria such as efficiency (C4.1), reliability (C4.2), source availability (C4.3), and technological maturity (C4.4).
It is important to note that the energy alternatives proposed in this research, as well as the criteria as well as the proposed sub-criteria, have been selected from previously carried out research and published in high-impact journals at an international level.
2.7. Expert Information
For this research, a survey was carried out in a specialized program, and 15 experts were consulted about their opinion regarding the evaluation of criteria, sub-criteria, and the best source of selection of renewable energy for each of the geographical regions of Colombia, some general characteristics of the experts consulted can be seen in Table 9, In this research, it was considered prudent to use 15 experts, this taking as a reference the number of experts who have been used in articles consulted in different specialized databases [65, 76].
| Number | Occupations | Years of experience |
|---|---|---|
| 1 | Field engineer (mechanical engineer) | 5 |
| 2 | Field engineer (mechanical engineer) | 8 |
| 3 | Field engineer (mechanical engineer) | 6 |
| 4 | Field engineer (mechanical engineer) | 4 |
| 5 | Field engineer (electrical engineer) | 5 |
| 6 | Field engineer (electrical engineer) | 8 |
| 7 | Field engineer (electrical engineer) | 7 |
| 8 | Field engineer (electrical engineer) | 4 |
| 9 | Field engineer (electrical engineer) | 4 |
| 10 | Field engineer (electrical engineer) | 5 |
| 11 | Senior project team leader | 5 |
| 12 | Senior project team leader | 6 |
| 13 | Senior project team leader | 6 |
| 14 | MCDM expert (industrial engineer) | 7 |
| 15 | MCDM expert (industrial engineer) | 8 |
3. Results and Discussions
The results of this research were grouped by each of the geographical regions, as well as according to the methodology implemented.
3.1. Results in the Caribbean Region
In the Colombian Caribbean region, a hierarchy of renewable energy sources was established using AHP methodologies, see Table 10. The results demonstrate that while the evaluated alternatives exhibit different weightings, they maintain a similar hierarchy, with photovoltaic solar energy, wind energy, and biomass emerging as the most relevant options. Photovoltaic solar energy enables the development of standalone systems for residential, community, and solar park applications. Wind energy offers opportunities in both offshore and onshore projects. Regarding biomass, its flexibility in selecting specific types expands its implementation potential, underscoring its importance in the transition to a more sustainable energy system.
| SC1 | ||||||
|---|---|---|---|---|---|---|
| Alternative vs methodology | A1 (%) | A2 (%) | A3 (%) | A4 (%) | A5 (%) | A6 (%) |
| AHP | 14.35 | 16.22 | 12.20 | 17.62 | 17.95 | 21.66 |
| FAHP | 14.34 | 4.89 | 5.46 | 18.72 | 21.37 | 35.22 |
- AHP, analytic hierarchy process; FAHP, fuzzy analytic hierarchy process.
The analysis of evaluation criteria for these energy sources, detailed in Table 11, reveals a lack of uniformity in the weightings assigned by experts, with social criteria being the most significant. This outcome highlights the necessity of proactively integrating social aspects into energy project planning, given their direct impact on the feasibility and acceptance of these initiatives. The social dimension stands out as a fundamental pillar in decision-making, particularly in a context where sustainability and community benefits are paramount.
| SC1 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alternative—methodology vs criterion | A1 | A2 | A3 | A4 | A5 | A6 | ||||||
| AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | |
| Technical | 18.25 | 18.35 | 22.56 | 20.58 | 21.22 | 22.78 | 19.57 | 21.33 | 9.35 | 8.21 | 9.05 | 8.75 |
| Environmental | 8.73 | 15.39 | 10.65 | 15.14 | 14.67 | 13.58 | 25.54 | 14.17 | 22.18 | 20.18 | 18.23 | 21.54 |
| Economic | 20.03 | 22.68 | 22.69 | 21.56 | 16.57 | 14.87 | 18.32 | 14.12 | 12.24 | 15.62 | 10.15 | 11.15 |
| Social | 6.75 | 7.79 | 5.63 | 9.78 | 13.28 | 12.25 | 18.25 | 17.56 | 33.51 | 26.89 | 22.58 | 25.73 |
- AHP, analytic hierarchy process; FAHP, fuzzy analytic hierarchy process.
Regarding the evaluated sub-criteria, the renewable fraction (C3.1) and the carbon footprint (C3.2) are identified as the most critical factors, as shown in Table 12. The renewable fraction underscores the importance of incorporating renewable energy sources in significant proportions to ensure sustainability and reduce dependence on non-renewable sources. Meanwhile, the carbon footprint emphasizes the need to mitigate environmental impacts and greenhouse gas emissions, essential aspects of the transition to a cleaner and more responsible energy matrix. These priorities reinforce the commitment to environmental sustainability and the development of projects aligned with global climate change mitigation goals.
| SC1 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sub-criteria vs methodology | C1.1 (%) | C1.2 (%) | C1.3 (%) | C1.4 (%) | C1.5 (%) | C2.1 (%) | C2.2 (%) | C2.3 (%) | C2.4 (%) | C3.1 (%) | C3.2 (%) | C3.3 (%) | C4.1 (%) | C4.2 (%) | C4.3 (%) | C4.4 (%) |
| AHP | 20.72 | 42.01 | 7.25 | 17.25 | 12.78 | 28.36 | 38.18 | 11.42 | 22.03 | 48.56 | 21.87 | 29.58 | 42.66 | 32.61 | 9.46 | 15.28 |
| FAHP | 35.62 | 25.62 | 8.64 | 14.08 | 16.03 | 2.98 | 28.26 | 34.66 | 34.09 | 6.06 | 85.01 | 8.93 | 8.76 | 43.54 | 22.18 | 25.52 |
3.2. Results in the Pacific Region
The Colombian Pacific region, rich in natural resources and diverse geography, exhibits significant potential for renewable energy implementation. As presented in Table 13, photovoltaic solar energy, wind energy, and biomass consistently rank as the most viable energy alternatives, regardless of the methodology applied. Abundant solar radiation, persistent coastal winds, and plentiful organic biomass resources provide favorable conditions for adopting clean and sustainable technologies. Photovoltaic solar energy leverages the region’s intense solar radiation, while wind energy capitalizes on its steady coastal winds. Biomass, derived from the area’s forestry and agricultural outputs, offers strategic benefits by mitigating environmental impacts and bolstering the local economy. These renewable energy sources represent critical pathways for diversifying the energy matrix, reducing reliance on fossil fuels, and fostering sustainable development in this region.
| SC2 | ||||||
|---|---|---|---|---|---|---|
| Alternative vs methodology | A1 (%) | A2 (%) | A3 (%) | A4 (%) | A5 (%) | A6 (%) |
| AHP | 6.23 | 7.58 | 8.96 | 24.57 | 25.10 | 27.56 |
| FAHP | 7.25 | 5.12 | 6.25 | 24.16 | 24.12 | 33.10 |
- AHP, analytic hierarchy process; FAHP, fuzzy analytic hierarchy process.
Table 14 underscores the centrality of social criteria in energy project planning for the Colombian Pacific region. Social considerations, such as job creation, social acceptance, and enhanced quality of life, are pivotal in ensuring that energy initiatives are not only economically viable but also socially equitable. The emphasis on environmental criteria further highlights the region’s ecological sensitivity, characterized by unique biodiversity and ecosystems. Energy projects must minimize ecological footprints to safeguard these natural assets while aligning with sustainability goals. This dual focus on social responsibility and environmental stewardship underscores the necessity of community-inclusive and ecologically mindful energy development in the Pacific region.
| SC2 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alternative—methodology vs criterion | A1 | A2 | A3 | A4 | A5 | A6 | ||||||
| AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | |
| Technical | 14.16 | 21.58 | 20.22 | 24.23 | 25.35 | 28.81 | 18.51 | 10.23 | 14.23 | 8.52 | 7.53 | 6.63 |
| Environmental | 15.12 | 21.58 | 16.52 | 11.26 | 16.52 | 12.57 | 18.54 | 15.69 | 14.58 | 18.75 | 18.72 | 20.15 |
| Economic | 21.18 | 22.53 | 18.56 | 21.68 | 16.57 | 19.51 | 14.78 | 13.26 | 12.58 | 13.11 | 16.33 | 9.91 |
| Social | 13.18 | 9.60 | 10.35 | 12.75 | 14.17 | 14.58 | 18.75 | 18.46 | 21.41 | 21.86 | 22.14 | 22.75 |
- AHP, analytic hierarchy process; FAHP, fuzzy analytic hierarchy process.
Table 15 reveals that the efficiency criterion (C4.1) and the renewable fraction sub-criterion (C3.1) are of paramount importance when assessing energy projects in the Colombian Pacific. Efficiency (C4.1) emphasizes optimizing energy use, which is critical in resource-limited settings and essential for sustainability. Meanwhile, the renewable fraction (C3.1) highlights the importance of transitioning toward renewable sources to reduce dependency on nonrenewable energy and achieve a cleaner energy matrix. These priorities underscore the imperative to integrate renewable energy on a significant scale, ensuring long-term resilience and sustainability for the region.
| SC2 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sub-criteria vs methodology | C1.1 | C1.2 (%) | C1.3 (%) | C1.4 (%) | C1.5 (%) | C2.1 (%) | C2.2 (%) | C2.3 (%) | C2.4 (%) | C3.1 (%) | C3.2 (%) | C3.3 (%) | C4.1 (%) | C4.2 (%) | C4.3 (%) | C4.4 (%) | |
| AHP | 20.19 | 42.32 | 6.75 | 16.96 | 13.78 | 26.89 | 40.53 | 10.96 | 21.63 | 40.45 | 29.75 | 29.81 | 44.00 | 29.10 | 11.13 | 15.76 | |
| FAHP | 18.31 | 9.36 | 26.08 | 18.30 | 27.95 | 20.40 | 49.54 | 22.68 | 7.37 | 84.17 | 4.86 | 10.96 | 24.02 | 33.61 | 28.45 | 13.92 | |
- AHP, analytic hierarchy process; FAHP, fuzzy analytic hierarchy process.
3.3. Andean Region Results
The Colombian Andean region presents a diverse energy potential, as evidenced by the application of AHP and FAHP methodologies, see Table 16. According to expert evaluations, large-scale hydroelectric energy, solar photovoltaic energy, and wind power emerge as the most prominent renewable energy sources, with minor differences in weighting compared to small-scale hydropower and geothermal generation. Large-scale hydroelectric energy and solar photovoltaic systems, in particular, display the highest weightings, while a technical correlation is observed between biomass and wind generation. These findings underscore the critical role of renewable energy implementation in this geographically and climatically varied region. The diversification of the energy matrix, incorporating solar and wind sources, alongside the contribution of large-scale hydropower, is essential for fostering sustainability and reducing reliance on non-renewable energy sources.
| SC3 | |||||
|---|---|---|---|---|---|
| Alternative vs methodology | A1 (%) | A4 (%) | A5 (%) | A6 (%) | A7 (%) |
| AHP | 34.00 | 8.96 | 24.36 | 25.10 | 7.58 |
| FAHP | 32.98 | 7.25 | 24.16 | 28.65 | 6.96 |
- AHP, analytic hierarchy process; FAHP, fuzzy analytic hierarchy process.
Economic considerations are pivotal in the decision-making process for energy projects in the Andean region, as reflected in the evaluation results (Table 17). The economic criterion consistently ranks as the most relevant across methodologies, highlighting the importance of financial feasibility. Ensuring cost-effective investment and long-term sustainability is essential for the successful implementation of energy initiatives. The prominence of economic factors stresses the necessity of balancing financial, social, environmental, and technical considerations to achieve sustainable and equitable energy development.
| SC3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Alternative—methodology vs criterion | A1 | A4 | A5 | A6 | A7 | |||||
| AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | |
| Technical | 15.23 | 22.76 | 21.78 | 25.95 | 24.58 | 30.91 | 20.36 | 11.23 | 18.05 | 9.15 |
| Environmental | 22.73 | 27.13 | 16.10 | 21.23 | 14.58 | 16.10 | 21.57 | 16.79 | 25.02 | 18.75 |
| Economic | 22.18 | 22.53 | 19.96 | 21.68 | 16.57 | 19.51 | 16.89 | 13.26 | 24.40 | 23.02 |
| Social | 25.68 | 19.90 | 10.45 | 18.59 | 19.03 | 16.58 | 22.69 | 21.46 | 22.15 | 23.47 |
- AHP, analytic hierarchy process; FAHP, fuzzy analytic hierarchy process.
The evaluation of sub-criteria (Table 18) further reinforces the importance of sustainability in energy project planning. The Renewable Fraction (C3.1) stands out as the most critical sub-criterion, emphasizing the need to increase the share of renewable energy in the regional energy mix. This approach is vital for reducing dependence on non-renewable sources and advancing toward a sustainable energy matrix. Additionally, the Carbon Footprint sub-criterion (C3.2) underscores the imperative of minimizing environmental impacts, particularly in a region with fragile ecosystems and high biodiversity. Addressing carbon emissions aligns with global climate commitments and supports the preservation of natural habitats. These sub-criteria reflect the region’s commitment to environmentally responsible and sustainable energy development.
| SC3 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sub-criteria vs methodology | C1.1 | C1.2 (%) | C1.3 (%) | C1.4 (%) | C1.5 (%) | C2.1 (%) | C2.2 (%) | C2.3 (%) | C2.4 (%) | C3.1 (%) | C3.2 (%) | C3.3 (%) | C4.1 (%) | C4.2 (%) | C4.3 (%) | C4.4 (%) | |
| AHP | 19.25 | 36.26 | 9.23 | 15.80 | 19.46 | 25.55 | 36.43 | 12.49 | 25.53 | 50.18 | 19.53 | 30.29 | 41.01 | 28.21 | 12.18 | 18.59 | |
| FAHP | 32.20 | 4.60 | 36.06 | 6.38 | 20.75 | 4.96 | 31.10 | 26.66 | 37.27 | 16.69 | 65.48 | 17.83 | 40.95 | 17.06 | 22.70 | 19.29 | |
- AHP, analytic hierarchy process; FAHP, fuzzy analytic hierarchy process.
3.4. Amazon Region Results
The weighting and prioritization of energy alternatives in the Colombian Amazon region, as detailed in Table 19, show a consistent hierarchy according to both AHP and FAHP methodologies. Photovoltaic solar energy ranks as the top priority, followed by biomass and hydroelectric power. These findings underline the importance of renewable energy sources tailored to the unique characteristics of the Amazon, which includes extensive rainforests and abundant river systems. Solar photovoltaic energy leverages the region’s high solar radiation, biomass benefits from abundant organic resources, and hydroelectric power capitalizes on the dense river network. Together, these options foster environmental sustainability while respecting the ecological and social fabric of the region.
| SC4 | ||||
|---|---|---|---|---|
| Alternative vs methodology | A1 (%) | A4 (%) | A5 (%) | A6 (%) |
| AHP | 11.12 | 34.87 | 25.96 | 28.05 |
| FAHP | 9.21 | 35.58 | 26.03 | 29.18 |
- AHP, analytic hierarchy process; FAHP, fuzzy analytic hierarchy process.
Table 20 outlines the weighting of decision-making criteria across energy alternatives. The AHP methodology prioritizes social and economic criteria, while FAHP emphasizes environmental and technical aspects. This divergence highlights the multifaceted considerations required for energy projects in the Amazon. The social criterion is particularly critical given the region’s indigenous and rural populations, necessitating projects that promote community participation and equitable benefits. Economic considerations focus on the financial viability and scalability of energy infrastructure in a resource-constrained setting. Environmental concerns hold immense weight, reflecting the imperative to preserve the Amazon’s unparalleled biodiversity. Technical efficiency is also essential, ensuring the adaptability and reliability of energy systems within the challenging geographical and climatic conditions of the region.
| SC4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Alternative—methodology vs criterion | A1 | A4 | A5 | A6 | ||||
| AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | |
| Technical | 23.15 | 22.76 | 27.25 | 25.95 | 25.85 | 30.91 | 23.75 | 20.38 |
| Environmental | 22.73 | 25.13 | 31.16 | 33.28 | 19.54 | 19.56 | 26.57 | 22.03 |
| Economic | 22.18 | 22.53 | 25.64 | 28.24 | 25.46 | 24.51 | 26.72 | 24.72 |
| Social | 25.68 | 25.54 | 25.96 | 24.76 | 22.57 | 25.14 | 25.79 | 24.56 |
- AHP, analytic hierarchy process; FAHP, fuzzy analytic hierarchy process.
Table 21 evaluates sub-criteria, underscoring the renewable fraction as a decisive factor linked to the environmental criterion. In a region where ecological preservation is paramount, the renewable fraction represents the regenerative capacity of energy sources, ensuring a sustainable and minimally invasive energy supply. This sub-criterion aligns with the broader goal of conserving natural resources and mitigating ecological disruption. Renewable energy sources like solar, wind, and biomass are particularly suited to the Amazon due to their capacity for regeneration and their alignment with conservation goals.
| SC4 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sub-criteria vs methodology | C1.1 (%) | C1.2 (%) | C1.3 (%) | C1.4 (%) | C1.5 (%) | C2.1 (%) | C2.2 (%) | C2.3 (%) | C2.4 (%) | C3.1 (%) | C3.2 (%) | C3.3 (%) | C4.1 (%) | C4.2 (%) | C4.3 (%) | C4.4 (%) |
| AHP | 18.93 | 37.33 | 9.37 | 14.75 | 19.62 | 31.39 | 31.64 | 12.54 | 24.44 | 49.74 | 18.48 | 31.78 | 42.38 | 28.67 | 11.52 | 17.43 |
| FAHP | 25.16 | 34.19 | 30.38 | 0.90 | 9.36 | 20.94 | 22.95 | 27.94 | 28.17 | 41.00 | 27.84 | 31.16 | 33.70 | 22.82 | 15.10 | 28.39 |
- AHP, analytic hierarchy process; FAHP, fuzzy analytic hierarchy process.
In conclusion, the renewable fraction and environmental considerations are indispensable in energy project planning for the Amazon region. Balancing energy generation with ecological preservation ensures that the region’s natural heritage and biodiversity remain intact while addressing its energy needs through sustainable, renewable solutions
3.5. Results of the Orinoquia Region
In the Colombian Orinoquia region, the importance of the implementation of renewable energy sources, such as biomass, photovoltaic solar energy, and wind energy, is highlighted. These energy resources are promising options for this area, given its unique characteristics and specific energy needs. Biomass, as a source of energy, stands out as an outstanding option in the Orinoquia, as evidenced in Table 22. This region has vast agricultural and forestry resources, making biomass a viable and sustainable option. Converting organic waste and local raw materials into energy can contribute significantly to energy self-sufficiency and waste management, while also boosting the local economy.
| SC5 | |||||
|---|---|---|---|---|---|
| Alternative vs methodology | A1 (%) | A4 (%) | A5 (%) | A6 (%) | A7 (%) |
| AHP | 8.52 | 33.22 | 22.14 | 25.89 | 10.23 |
| FAHP | 10.73 | 30.17 | 21.96 | 23.28 | 13.86 |
- AHP, analytic hierarchy process; FAHP, fuzzy analytic hierarchy process.
Photovoltaic solar energy is another essential alternative for the Orinoquia, considering its abundant exposure to the sun throughout the year. The capture of solar energy through photovoltaic panels is presented as an efficient and environmentally friendly option. Solar energy can be especially beneficial for remote areas of the region, where electricity infrastructure is limited. Wind energy, on the other hand, offers the advantage of using the constant winds that characterize the Orinoquia.
The region has vast tracts of land suitable for the installation of wind turbines, making wind energy a potentially valuable source for the region’s energy supply. Together, biomass, solar photovoltaic energy, and wind power are emerging as strategic options for the Colombian Orinoquia. These renewable energy sources can make a significant contribution to meeting the region’s energy needs while reducing its dependence on non-renewable and more polluting sources. The implementation of these energy sources also aligns perfectly with the area’s wealth of natural resources, contributing to sustainability and local economic development. The choice between these options will depend on specific factors, such as the availability of resources and infrastructure, but their relevance in the context of the Orinoquia is undeniable.
Regarding the results of the evaluation of criteria vs. alternatives, for this particular region, the data obtained for each of the methodologies differ greatly. In Table 23, it is observed that there are two criteria that have a greater weight in the alternatives evaluated, they are the economic and social criteria, while the data obtained by FAHP evidenced in this same table, they do not show a predominant criterion in the group of alternatives evaluated, on the contrary, it is evident that according to the energy alternative there was a criterion of greater predominance over the others. For example, in the “other alternatives” option, the criterion with the highest weighting is the technical criterion, showing the importance that must be taken into account when planning or implementing non-conventional energy sources or new emerging technologies, such as green hydrogen or any other.
| SC5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Alternative—methodology vs criterion | A1 | A4 | A5 | A6 | A7 | |||||
| AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | AHP (%) | FAHP (%) | |
| Technical | 8.69 | 14.96 | 37.45 | 38.46 | 13.18 | 9.21 | 18.15 | 16.11 | 22.53 | 21.26 |
| Environmental | 14.68 | 15.51 | 19.68 | 25.46 | 16.13 | 15.23 | 23.75 | 21.22 | 25.76 | 22.58 |
| Economic | 16.37 | 20.60 | 33.56 | 31.87 | 22.25 | 17.89 | 12.13 | 13.10 | 15.69 | 16.54 |
| Social | 5.41 | 10.54 | 22.89 | 21.78 | 17.89 | 15.68 | 21.62 | 23.46 | 32.19 | 28.54 |
- AHP, analytic hierarchy process; FAHP, fuzzy analytic hierarchy process.
In the context of the Colombian Orinoquia region, the results of the weighting and prioritization of renewable energy sources, through the AHP and FAHP methodologies, reveal an encouraging outlook. Both methodologies coincide in prioritizing biomass, solar PV, and wind as the most prominent options, supporting their potential to address the energy needs of this geographically unique region. It is important to note that, in addition to the choice of energy sources, the sub-criteria of efficiency and carbon footprint play a critical role in the implementation of energy projects in the Orinoquia. Efficiency is a key factor, as the region seeks to optimize the use of its resources and minimize energy waste. Implementing energy-efficient technologies can make a significant difference in reducing costs and responsibly managing available resources.
Carbon footprint also stands as a crucial sub-criterion, given the growing emphasis on sustainability and reducing greenhouse gas emissions. The Orinoquia is a region rich in biodiversity and sensitive ecosystems, so mitigating environmental impacts is essential.
The selection of energy sources with a reduced carbon footprint aligns with the region’s conservation and sustainability goals, while contributing to the global commitment to tackle climate change. The results obtained in Table 24 underscore the importance of considering specific criteria and sub-criteria when evaluating and selecting renewable energy sources in the Colombian Orinoquia. Biomass, solar PV, and wind power stand out as strategic options, and efficiency and carbon footprint emerge as critical factors to consider in planning energy projects in this region. These findings provide valuable guidance for informed and sustainable decision-making in the search for a cleaner and more efficient energy supply in the Orinoquia.
| SC5 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subcriteria vs methodology | C1.1 (%) | C1.2 (%) | C1.3 (%) | C1.4 (%) | C1.5 (%) | C2.1 (%) | C2.2 (%) | C2.3 (%) | C2.4 (%) | C3.1 (%) | C3.2 (%) | C3.3 (%) | C4.1 (%) | C4.2 (%) | C4.3 (%) | C4.4 (%) |
| AHP | 19.15 | 36.10 | 9.04 | 15.63 | 20.08 | 28.55 | 31.08 | 12.98 | 27.39 | 36.98 | 23.13 | 39.89 | 42.38 | 28.67 | 11.52 | 17.43 |
| FAHP | 19.35 | 21.20 | 24.76 | 14.20 | 20.49 | 14.34 | 5.61 | 39.77 | 40.28 | 32.02 | 48.35 | 19.62 | 1.65 | 34.81 | 22.18 | 41.37 |
- AHP, analytic hierarchy process; FAHP, fuzzy analytic hierarchy process.
4. Conclusion and Recommendations
This research has produced significant insights into the evaluation and selection of renewable energy sources across different regions of Colombia, using the AHP and FAHP methodologies. In examining various energy alternatives, solar PV consistently emerged as a promising option in most regions due to its feasibility and potential for deployment. However, it is crucial to recognize that each region has unique characteristics and resources that influence the weighting and ranking of energy sources. The differences in results between AHP and FAHP highlight the importance of incorporating uncertainty and subjectivity into energy projects. Both methodologies provide valuable, complementary perspectives and should be evaluated based on the specific circumstances and objectives of each region.
The application of AHP and FAHP revealed key differences in their mathematical foundations. AHP is based on linear algebra, while FAHP utilizes fuzzy logic, which addresses uncertainty. A major distinction lies in how these methodologies represent uncertainty—AHP overlooks it, while FAHP incorporates fuzzy logic to handle it. Additionally, AHP relies on subjective judgments, whereas FAHP minimizes subjectivity by applying de-fuzzification techniques.
In the first scenario (SC1), AHP assigns considerably higher weights to alternatives A1 and A2, with 14.35% and 16.22%, respectively. In contrast, FAHP displays more variability, with A6 reaching 35.22%, suggesting that FAHP may better capture fluctuations in preferences. The technical criterion holds significant weight in both methodologies, although FAHP assigns more relevance to environmental aspects, indicating a shift toward more sustainable decisions. FAHP’s greater range of variation in the sub-criteria suggests heightened sensitivity to changes in the evaluated criteria.
The second scenario (SC2) reflects a similar trend, with AHP assigning higher weights to A1 and A2. However, FAHP shows a more balanced weight distribution. The environmental criterion remains important, with AHP allocating 14.16% to A1, while FAHP assigns 21.18% to the same criterion. This highlights the growing importance of sustainability in decision-making, particularly in the context of environmental considerations. In the sub-criteria, FAHP demonstrates more variability, suggesting it is better suited to capturing decision complexities.
In the third scenario (SC3), AHP assigns substantial weight to A1 (34.00%), while FAHP presents a similar value of 32.98%. The environmental criterion remains dominant, with AHP awarding 22.73% to A1. The variability in sub-criteria is notable, with FAHP showing a broader range of weight assignment, indicating its sensitivity to differences in the assessed sub-criteria.
In the fourth scenario (SC4), both AHP and FAHP follow similar patterns, though FAHP places greater emphasis on environmental criteria. A1 and A4 are the leading alternatives, with AHP assigning 11.12% and 34.87%, respectively. The environmental criterion remains crucial, with AHP allocating 23.15% to A1. Variability in sub-criteria is evident, with FAHP exhibiting more dispersion, suggesting that it may more effectively capture decision-making complexity.
Finally, in the fifth scenario (SC5), AHP assigns a weight of 8.52% to A1, while FAHP assigns 10.73%. The environmental criterion retains its significance, with AHP giving 14.68% to A1. The variability in sub-criteria is marked, with FAHP displaying a broader range in weight assignments, suggesting its greater sensitivity to changes in the sub-criteria.
The use of metaheuristic methods in decision-making for renewable energy selection is crucial, especially in a geographically diverse country like Colombia. In such a context, conventional approaches may fall short. Metaheuristic methods like AHP and FAHP can manage the complexity of evaluating various energy alternatives and multidimensional criteria. Their ability to handle uncertainty and subjectivity, particularly in dynamic environments, provides valuable perspectives in decision-making. By overcoming the limitations of traditional methods, these techniques highlight the importance of accounting for the variability of energy potential and resource availability in each region. In Colombia, where geographic diversity means different regions may be more suited to specific renewable energy sources, metaheuristics offer more accurate, informed assessments and contribute to strategic planning for a sustainable, cleaner energy system.
The findings of this study are highly relevant not only for Colombia but also for the broader Latin American region and beyond. In Colombia, the results provide policymakers, energy planners, and industry stakeholders with a systematic, adaptable framework for selecting optimal renewable energy sources. This approach helps diversify the country’s energy matrix and enhance its resilience. The methodology accounts for uncertainty in regional energy planning, contributing to more sustainable and robust energy solutions, particularly in areas with limited data and high variability in natural resources. This approach can also be extended to other Latin American countries, many of which share similar geographical, economic, and environmental challenges. Nations in LATAM, with their own diverse energy potentials, can benefit from a replicable model that enables region-specific planning. On a global scale, this research contributes to the field of energy planning by demonstrating how combining AHP and FAHP can navigate the complexities of renewable energy transitions in countries with diverse geographic landscapes and uncertain resource availability. It serves as a model for other developing economies, supporting global efforts to combat climate change and promote energy sustainability.
Key recommendations include tailoring decisions to the specific characteristics of each region, considering the divergent results of methodologies, and promoting the use of FAHP or other metaheuristic techniques to better address uncertainty in future projects.
Disclosure
It is declared that this document has a forecast which has as cite: Christian Manuel Moreno Rocha, Daina Arenas Buelvas. Comparison between AHP and FAHP for the best Selection of Renewable Energies in Colombia, a country with diversity in its geographical regions: Optimization and Sustainability, February 01, 2024, PREPRINT (Version 1) available at Research Square [https://doi.org/10.21203/rs.3.rs-3910690/v1].
Conflicts of Interest
The authors declare no conflicts of interest.
Author Contributions
I, Christian Manuel Moreno Rocha, am writing to you with the purpose of presenting our article entitled “A Comprehensive Evaluation of Renewable Energy Sources in Colombian Regions Using AHP and FAHP Methodologies” for your consideration and possible publication. Our study focuses on an exhaustive analysis of renewable energy sources in several regions of Colombia, using the AHP and Fuzzy AHP methodologies. Adapting the selection of alternatives, including solar photovoltaic, onshore/offshore wind, biomass, geothermal and hydropower on a large and small scale, aims to provide sustainable solutions for the country’s growing energy demand. In our approach, we have considered multidimensional criteria covering social, economic, technical and environmental aspects, broken down into sub-criteria for meticulous evaluation. The results reveal different weightings and hierarchies for each region, influenced by the variability in energy potential and resource availability. We emphasize the importance of introducing innovative metaheuristic methods, especially AHP and FAHP, in the Colombian energy sector. In a geographically diverse country like Colombia, where regional variability demands flexible approaches, these methodologies emerge as crucial tools for decision-making. Our study not only offers a valuable guide for the effective implementation of renewable energies in Colombia, but also underlines the importance of accommodating regional variability in the transition toward a cleaner and more sustainable energy system. The application of metaheuristic methods contributes to a more effective strategic planning, promoting environmental sustainability within the Colombian context. We believe that this work contributes significantly to the existing knowledge in the field of renewable energies and decision-making in the energy sector. We hope you will consider our article for review and possible inclusion in the next issues. Finally, it is important to highlight the participation of each of the co-authors of this research, to thank Dr. Daina Arena, Mr. Itzjak Vega Machado and Mr. Juan Pacheco Peña, for accepting the invitation to conduct this research and their significant contributions. Thank you in advance for your time and consideration.
Funding
This research was funded with the authors’ resources, however the APC positions will be assumed by the University of Santiago de Compostela, Spain.
Open Research
Data Availability Statement
Data will be available upon request to the lead author.




