Twisted tapes are widely recognized as an effective passive method to enhance heat transfer in parabolic trough solar collectors. However, a major drawback is the substantial pressure drop caused by the high friction between the fluid flow and the tape surface. This study introduces hydrophobic twisted tapes as a solution to reduce pressure drop while sustaining enhanced heat transfer. A variety of twisted tapes with differing widths and twist ratios were fabricated and tested experimentally under laminar and turbulent flow regimes, focusing on pressure drop, efficiency, and performance index. The results demonstrate that hydrophobic twisted tapes can elevate the performance index from below one to above one. At the flow rate of 50 Lph, the performance index of the twisted tape with a hydrophobic surface increased by 125%. It was observed that increasing the tape width and reducing the twist ratio led to higher pressure drop, improved efficiency, and a better performance index. Additionally, the study compared the performance of twisted tapes with fixed versus variable widths. Experimental findings revealed that twisted tapes with variable widths exhibit superior performance compared to those with fixed widths. At a flow rate of 50 Lph, the performance index of the variable width twisted tape with a hydrophobic surface increased by 143%.

1. Introduction

Solar energy is considered the most important source of free, clean, and renewable energy that has no limits and has no impact on the environment [1, 2]. It can be defined as the energy originating from the sun that can be converted into heat and electricity. It produced energy for billions of years, yet its utilization has garnered significant technological attention, especially in the last decade [3, 4]. The increasing energy demand, limited fossil fuels, and environmental concerns related to fossil fuel usage, such as carbon dioxide emissions, drive the heightened focus on solar energy applications [5, 6]. The solar collector is a system that converts the energy from incident solar radiation into thermal energy in solar thermal applications. There are various solar collectors, but the most popular kind of high-temperature solar collector is the parabolic solar collector [7]. The solar collector absorbs solar radiation, converts it to heat, and subsequently transfers it to the working fluid. Therefore, achieving better heat transfer to the fluid results in a higher outlet temperature and increases the collector efficiency in the power cycle [8, 9].

There are three methods to improve heat transfer in thermal systems, including solar collectors [10]. The active method, often more complex in design, involves applying external forces to enhance heat transfer within a system [11]. Surface and fluid vibration and mechanical aids, as well as suction or injection, exemplify active techniques. The passive method typically involves surface or geometric modifications to the flow channel by incorporating inserts or additional devices. In this method, no external power is used. Examples include inserts as extra components, displaced enhancement devices, coiled tubes, extended surfaces, treated and rough surfaces, and additives for fluids [12, 13]. A combined approach integrates both active and passive techniques. However, due to its complex design, the combined approach is applicable only to specific applications [14].

Twisted tape inserts are recognized as one of the applications of the passive method employed to enhance the efficiency of solar collectors. These techniques primarily involve disturbing the boundary layer and inducing a swirling flow. This condition generates increased turbulence next to the surface tube of the solar collector, consequently enhancing heat absorption from the surface of the collector tube by the fluid. The impact of turbulators on heat transfer in heat exchangers is known to vary based on their shape and geometry.

Bellos and Tzivanidis [15] examined two enhancement techniques to improve the parabolic trough solar collector performance. They applied internal fins as well as a reflecting shield and found that the former could always increase thermal efficiency, while the latter was only useful for temperatures above 550 K. Eiamsa-ard et al. [16] applied multiple twisted tape bundle inserts to intensify the heat transfer experimentally. They tested coswirl and counter-swirl strip configurations for six, four, and two pieces of tape with twist ratios of 4.0, 5.0, and 6.0. Their experimental outcomes showed that all bundles of multiple twisted tapes increased heat transfer and the best performance was six twisted tapes with a twisted ratio of 4 with a Reynolds number of 6000.

Deshmukh et al. [17] conducted an experimental study using TiN nanoparticles and twisted tapes. Their experimental data indicated that solar thermal collector efficiency was 98.66% and 71.53% with and without twisted tape, respectively. The results demonstrated that using twisted tape notably decreased the average surface temperature.

According to previous studies, the use of twisted tapes increases the pressure drop which the friction of the surface of them with the passing fluid has a significant contribution in the increased pressure drop. A superhydrophobic surface, typically composed of micro- and/or nanoscale roughness that is chemically treated to be hydrophobic, is a promising and effective way to reduce skin friction [18, 19]. Hydrophobicity is a surface physical property of materials, characterizing the tendency of a material to repel water. This phenomenon minimizes the contact surface between water and nonpolar molecules [20]. After observing the pristine cleanliness of lotus leaves in marshes, extensive research was conducted in this field. Through an examination of 300 types of leaves using an electron microscope, it was observed that surfaces appearing macroscopically smooth exhibit microscopic roughness [21]. The air trapped within the rough surface of these leaves results in water forming droplets with high contact angles, enabling them to roll off and remove dust from the leaf surface. Over the years, numerous researchers have explored the application of surface hydrophobicity modification in various power systems to investigate the impact of hydrophobic phenomena on pressure losses and heat transfer [19, 20]. For instance, experimental results by Forrest et al. [22] revealed that the critical heat transmission amount on a surface with a thin layer of nanoparticles, under similar conditions, was 100%–200% higher than that on a plain surface. The findings from those studies indicated that the phenomenon of dynamic instability was not the sole influential factor, emphasizing the crucial role of surface properties. Shi et al. [23] employed surface oxidation and a chemical method to achieve a hydrophobic surface on metal foam where the mineral foam was partially inserted into the tube, with water serving as the working fluid. Experimental findings indicated that the tube containing hydrophobic metal foam exhibited better performance in pressure losses and heat transfer compared to the metal foam without hydrophobic treatment. In an experimental study conducted by Motamedi et al. [24], it was discovered that slip at the walls decreased the influence of the increased nanofluid viscosity, resulting in an average reduction of 17% in pressure drop relative to a smooth channel. Mandev and Manay [25] conducted experiments with many microchannel heat sinks featuring a variety of surface roughness values of 3.0, 1.8, and 1.1 µm; three varying microchannel widths of 700, 500, and 300 µm; and two different heights of 300 and 450 µm. Their study concluded that increasing the surface roughness increased the Nusselt number.

By reviewing the former studies, it is evident that using the twisted tape inserts has a negative effect on the solar collector performance, as it causes more pressure drop inside the solar collector absorber tube. This article presents the idea of making the surface of the twisted tape hydrophobic. In this way, it is possible to reduce the increment of the pressure losses caused by these tapes while keeping their benefits such as promoting better working fluid mixing and the ability to generate vortices that disrupt the thermal boundary layer. Various twisted tapes with different widths and twist ratios are made and examined experimentally based on pressure drop, efficiency, and performance index in laminar and turbulent flow regimes. Also, the performance of twisted tapes with fixed and variable widths is investigated.

2. Experimental Setup

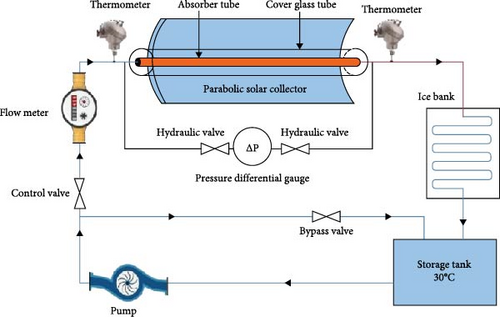
The present study evaluates the efficiency of the parabolic solar collector with twisted tapes experimentally. To reduce the pressure drop caused by the twisted tapes and improve the solar collector performance, the use of twisted tapes with a hydrophobic surface was researched. The solar collector performance with various twisted tapes was tested at six different values of flow rates of 50, 75, and 100 Lph (laminar flow) and 150, 200, and 250 Lph (turbulent flow). The inlet working fluid temperature in the solar collector was set at 30°C in all experiments. All the experiments were done during the summer and in the city of Tehran with a longitude of 51.39°E and a latitude of 35.69°N.

The main components of a parabolic solar collector include a reflector and an absorber tube. The reflector is made of a steel plate. The light-absorbing tube is made of copper where twisted tapes are placed in it. The solar energy is absorbed by the working fluid from the inner walls of the tube. The absorber copper tube is enclosed by a glass tube, and the air is discharged from the space between the two tubes to minimize the loss of energy to the surrounding environment and thus increase the performance of the heating system. The collector also has a medium-density fiberboard (MDF) body to increase its structural strength. Figure 1 shows the parts of a solar collector. Table 1 lists the characteristics of the collector reflector.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The parts of the solar collector.

Table 1. Characteristics of linear parabolic solar collector.

Parameter	Value	Unit
Reflector width	0.7	m
Reflector length	1.5	m
Reflector area	0.98	m²
Focal length	0.175	m
Edge angle	90	—
Reflection coefficient of the reflector	0.93	—
Outer diameter of the copper tube	28	mm
Thickness of the copper tube	1	mm
Outer diameter of the glass tube	60	mm
Thickness of the glass tube	5	mm

Figure 2 shows the operating cycle of a solar collector. A tank containing water with a low temperature was used to keep the inlet fluid temperature entering the solar collector system constant (30°C). The fluid in the cycle is circulated using a centrifugal pump made by Grundfos UPS2. System performance metrics are measured and recorded using a variety of measurement instruments. The solar power meter (TES model 1333R) measures the solar radiation intensity per unit area. To measure the temperature of the inlet fluid and the outlet fluid, two PT100 thermometers were positioned at the beginning and end of the absorber tube, respectively. To determine the flow rate of the working fluid in the solar collector system, a fan-type flow meter made by ZENNER with a precision of 0.001 Lph is used. The pressure difference between the outlet and the inlet fluid is also monitored with a Yokogawa differential pressure gauge. The device takes 12 V electricity and displays the pressure differential digitally.

3. Preparing Twisted Tape Inserts

Twisted tapes with different widths and twist ratios were examined. A copper plate with a thickness of 1 mm was divided into 12 tapes, each tape 1.5 m in length; nine tapes had a fixed width of 20, 16, and 12 mm; and three tapes had a variable width from 20 mm to zero. Additionally, three twisting ratios (TRs = 9, 7, and 5) were employed. Table 2 lists the variety of twisted tape models.

Table 2. Variety of twisted tape models.

Case No.	W	TR	Case No.	W	TR
Base case ^∗	—	—	Case#7	12	5
Case#1	20	5	Case#8	12	7
Case#2	20	7	Case#9	12	9
Case#3	20	9	Case#10	Variable (20 mm to 0)	5
Case#4	16	5	Case#11	Variable (20 mm to 0)	7
Case#5	16	7	Case#12	Variable (20 mm to 0)	9
Case#6	16	9	—	—	—

^∗Bare tube.

Figures 3 and 4 show a twisted tape with fixed width and variable width, respectively.

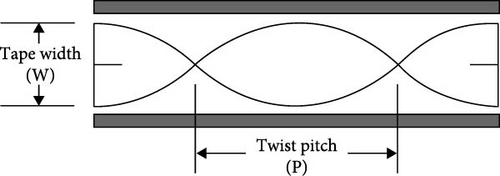
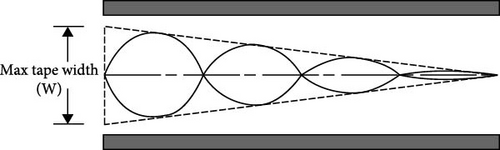
Based on the obtained results, the cases with the highest friction coefficient were identified among the fixed-width and variable-width (20 mm to zero) twisted tapes, and similar to these twisted tapes with the same parameters but with hydrophobic surfaces were prepared. The tests were repeated by these samples to determine the difference between the performance of the twisted tapes with a simple surface and the twisted tapes with a hydrophobic surface. Figure 5 shows the twisted tapes with hydrophobic surfaces.

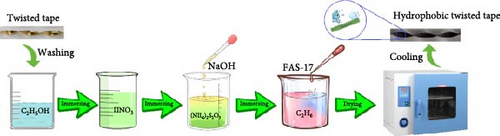
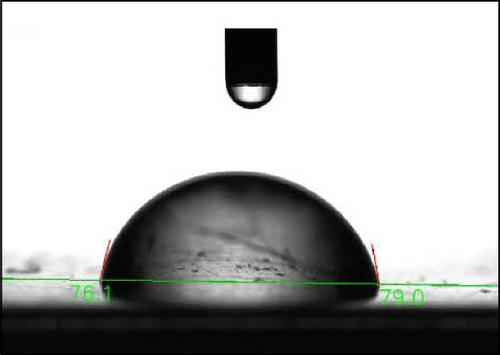
To produce hydrophobic twisted tapes, the twisted tapes were immersed in ethanol for 5 min. The twisted tapes are initially roughened by immersing them in 12 mol/L nitric acid (HNO₃) for 5 s, after which they are removed without any delay. They are submerged in a solution of 0.5 mol/L ammonium persulfate (NH₄)2S₂O₈ and 2.5 mol/L sodium hydroxide (NaOH) for 30 min after being cleaned with deionized water and allowed to dry in the air. The twisted tapes were washed with deionized water and then dried in air. After that, the twisted tape samples were stored for 2 days in hexane with a 0.5% (v/v) FAS-17 solution. The twisted tapes are finally dried in an oven set at 240°C for 3 h. A hydrophobic surface is obtained by cooling it in air. Figure 6 shows the production steps of twisted tapes with a hydrophobic surface. The device for measuring the contact angle and the contact angle between the water drop and solid surface in simple and hydrophobic treated surface of the twisted tape is shown in Figure 7. The droplet contact angle was measured with CAG-20 Jikan device. The test was carried out in the environmental conditions of 25°C, 88 kPa pressure, and 33% relative humidity. Distilled water with a density of 997 kg/m³ and a minimum droplet volume of 5 µL was used in the experiment [26].

4. Data Reduction

This section presents the equations used in the performance evaluation of the parabolic solar collector. The energy balance in the fluid volume gives the following definition of the heat absorbed by the working fluid [27]:

()

T_i and T_o represent the inlet and outlet bulk temperatures of fluid in the absorber tube, respectively, while denotes the mass flow rate of the fluid.

Radiant energy from the sun is calculated as follows [27]:

()

The ratio of the energy absorbed by the fluid to the total direct normal radiation energy incident on the collector aperture represents the thermal efficiency of solar collectors [27]:

()

The equation for determining the friction coefficient is as follows [28]:

()

The performance index is employed to evaluate the thermal performance of twisted tapes which is evaluated as follows [29]:

()

The working fluid is pure water. Based on the above equations, the thermal efficiency and friction coefficient can be calculated using the geometric characteristics of the collector. This involves measuring the inlet and outlet water temperatures in the absorber tube and applying the thermophysical properties of water at the average bulk temperature. Additionally, the incident normal irradiation on the collector and the flow rate must be measured experimentally

5. Uncertainty Analysis

Uncertainty analysis is a necessary and important aspect of experimental research. An experiment’s overall uncertainty is the sum of all the independent parameter uncertainties when dealing with several data points. The following equations can be used to determine the uncertainty in the parameters of thermal efficiency and friction coefficient [29]:

()

Table 3 shows the uncertainty in the measurement parameters in these experiments.

Table 3. Uncertainty analysis of variables during data reduction.

Parameter	Uncertainty
Temperature	±0.1 (°C)
Solar irradiance	±5 (W/m²)
Pressure drop	±0.065 (Pa)
Length of tube	±0.001 (m)
Flow rate	±0.01 (Lph)

According to the uncertainty of the measuring devices in Table 3, the uncertainty of collector thermal efficiency and friction coefficient is 2.9% and 2%, respectively.

6. Time Constant

The time constant of the solar collector is defined as the time when the temperature of the fluid outlet from the absorber tube reaches 0.632 from the final temperature of the fluid outlet in the steady state after the change in incident radiation. Determining this time constant is necessary for assessing the collector’s transient behavior. Equation (8) can be used to find the time constant [30, 31]:

()

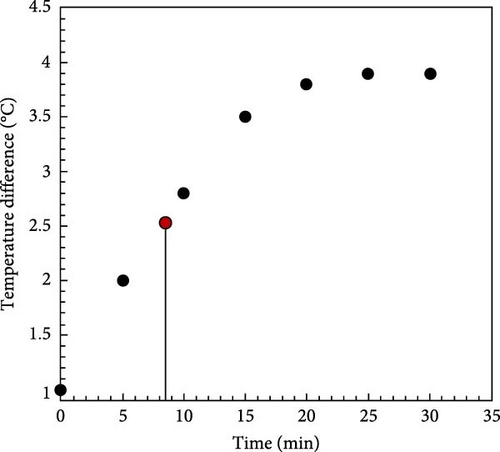
The temperature difference with time is shown in Figure 8, and the collector time constant is calculated to be around 8.5 min based on Equation (8).

7. Results and Discussion

In this section, the effect of using twisted tapes on solar collector performance is investigated. Twisted tapes are made with different widths and different twist ratios. Also, the impact of using twisted tapes with a hydrophobic surface in reducing the pressure losses and improving the solar collector performance was investigated. Equation (9) was applied to verify the experimental findings with the theoretical values for water [30]:

()

Here, L and d represent the length and diameter of the tube, respectively, Re is the Reynolds number, ρ denotes the fluid density, and u is the average velocity of the fluid within the tube.

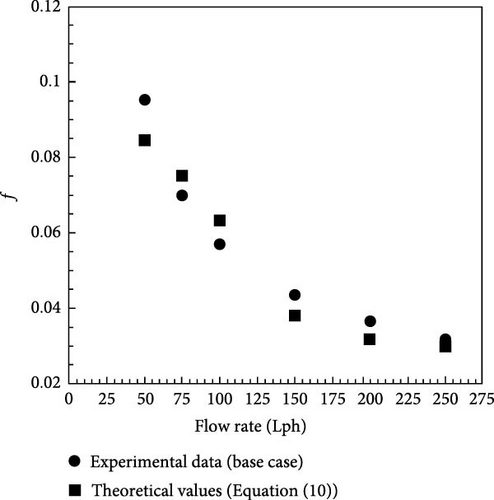
Figure 9 presents a comparison of the theoretical outcomes derived from Equation (9), with the experimental findings. The theoretical and experimental findings are fairly consistent. Also, the repeatability of the tests was checked.

7.1. Pressure Drop

Although the twisted tapes cause fluid mixing and reduce the thermal boundary layer thickness by creating vortices in the flow, they cause an increase in the pressure drop. This section examines how much different geometric shapes affect the pressure change inside the tube.

7.1.1. The Impact of the Width on the Pressure Drop

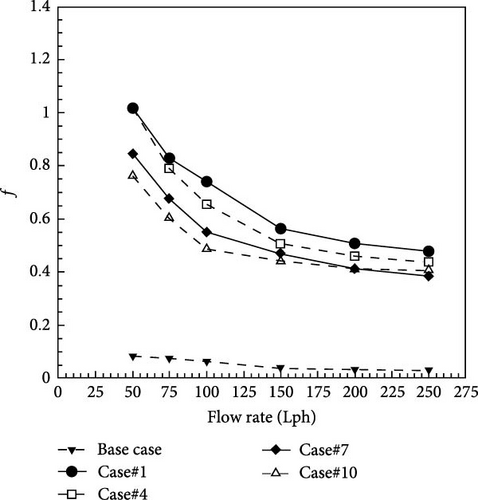
Figure 10 shows the effect of twisted tape width on the friction coefficient. According to the results, the friction coefficient significantly increases when twisted tapes are used because of the rise in pressure drop. At a flow rate of 50 Lph, Case#1 has a friction coefficient of 41.67% higher than the base case. On the other side, the friction coefficient decreases as the flow rate rises. For Case#1, increasing the flow rate from 50 to 250 Lph reduces the friction coefficient by 50%. At a flow rate of 100 Lph, for Cases#1, 4, 7, and 10, the friction coefficient was measured at 0.74, 0.65, 0.55, and 0.49, respectively, and the friction coefficient for the base case was 0.085. Moreover, at a flow rate of 250 Lph for Cases#1, 4, 7, and 10, the friction coefficient was 0.48, 0.44, 0.39, and 0.41, respectively, and the friction coefficient of the base case was 0.03. These findings confirm an increase in the friction coefficient with the widening of the twisted tape. In Cases#1, 4, 7, and 10, which have a fixed twist ratio, the pressure drop decreases as the width of the twisted tape decreases. But in Case#10, due to the variable width of the twisted tape in the flow direction, the lowest pressure drop is seen. At flow rates of 50, 75, and 100 Lph (i.e., laminar flow), by reducing the twisted tape width, the friction between the fluid and the twisted tape decreases, which results in a reduction in the friction coefficient. By increasing the flow rate to 150, 200, and 250 Lph (i.e., turbulent flow), the role of friction between the surface of the twisted tape and the fluid decreases against the pressure drop caused by the turbulent aspects of flow. Therefore, according to the results, the role of tape width in pressure drop is more vital in laminar flow than in turbulent flow.

7.1.2. The Impact of the Twist Ratios on the Pressure Drop

Figure 11 shows the friction coefficient for twisted tapes with varying twist ratios. The findings indicate that a lower twist ratio increases the friction coefficient. At flow rate of 50 Lph, for Cases#1, 2, and 3 with a constant width of 20 mm and twist ratio of 5, 7, and 9, the friction coefficients are 1.015, 0.93, and 0.85, respectively. Figure 11 displays that in laminar flow, the fluctuation of the friction coefficient is greater than in turbulent flow.

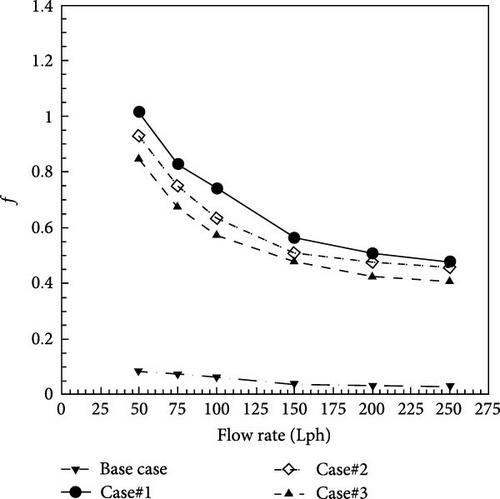
7.1.3. Effect of Hydrophobicity on Pressure Drop

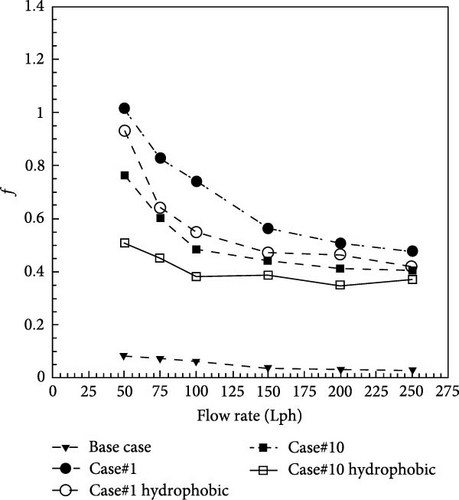
Figure 12 shows the difference in the friction coefficient between twisted tapes with a normal surface and twisted tapes with a hydrophobic surface at varying flow rates. The previous findings showed that the twist tapes with the largest width (i.e., 20 mm) and the lowest twist ratio (i.e., 5) have the maximum pressure drop (Case#1). Also, in the twisted tapes with variable width, Case#10 with a width of 20 mm and a twist ratio of 5 have the highest pressure drop. Therefore, these samples were made with the same sizes, and their surface was made hydrophobic by the previous described method. Twisted tapes with a hydrophobic surface were tested to compare the results. The results show that in Case#1, at a flow rate of 50 and 250 Lph, by using hydrophobic surfaces, the friction coefficient was reduced by 8.3% and 12%, respectively. Also, in Case#10, at a flow rate of 50 and 250 Lph, by using hydrophobic surfaces, the friction coefficient was reduced by 34.2% and 7.5%, respectively. It can be seen that the pressure drop reduction in laminar flow is more than in turbulent flow. This is because in laminar flow, the frictional pressure drop between the fluid and surfaces is dominant, and with the hydrophobicity of the twist tapes, a further decrease in pressure drop in laminar flow is observed. These results show that the use of the hydrophobic surface of the twist tapes can reduce the frictional losses between fluid and tape insert.

7.2. Collector Thermal Efficiency

This study examines the thermal efficiency of solar collectors while utilizing bare tubes and tubes with twisted tape. Thermal efficiency is defined as the ratio of the energy absorbed by the fluid to the total normal direct radiation energy incident to the collector aperture.

7.2.1. The Effect of Width on the Collector Efficiency

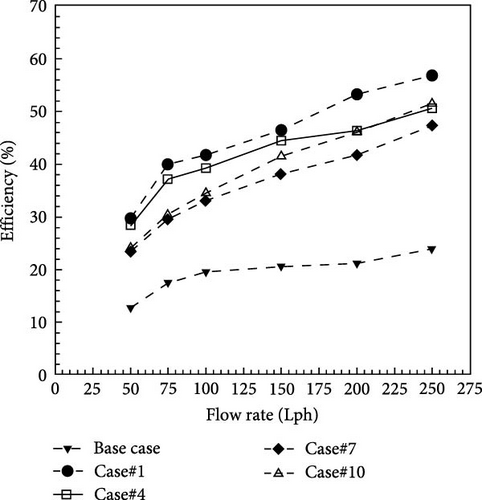
The effect of using twisted tape with different widths on solar collector efficiency is shown in Figure 13. The findings show that increasing the width of the twisted tape leads to an enhancement in the collector’s efficiency. According to Figure 13, Case#1 with the largest width has the highest efficiency in the constant twist ratio. In Figure 13, the efficiency reduces as the width of the twisted tape decreases. Also, Case#10 with variable width performs better than Case#7. Since the thickness of the thermal boundary layer is low in the entrance area of the pipe and the fluid flow is under thermal developing conditions, proper heat transfer is carried out. But along the length of the pipe, with the increase in the thickness of the thermal boundary layer, the heat transfer is reduced; therefore, by increasing the width of twisted tape (Case#10) and creating more powerful vortices, it is possible to create better performance than the twisted tape with a fixed width (Case#7). The results show that in Case#1, at a flow rate of 50 and 250 Lph, the collector efficiency was increased by 233.4% and 237.5%, respectively.

7.2.2. The Effect of the Twist Ratio on the Collector Thermal Efficiency

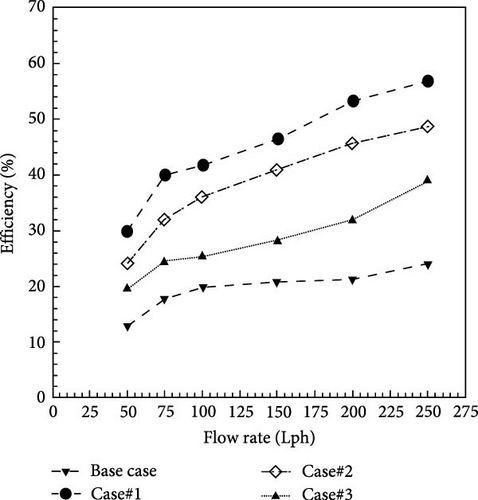
The effect of the twist ratio on solar collector efficiency is seen in Figure 14. The experimental results show that a lower twisted ratio generally improves the twisted tape performance and thus increases the efficiency of the solar collector. In twisted tapes with a fixed width, reducing the twist ratio further increases the solar collector efficiency. Experimental results show that Case#1 is more effective than Cases#2 and Cases#3, where the efficiency of each of them was equal to 29.79, 24.04, and 19.38, respectively. Also, Case#2 is more effective than Case#3. In Case#1, at a flow rate of 50, 75, 100, 150, 200, and 250 Lph, the collector efficiency was increased by 233.4%, 227.2%, 211.6%, 225.2%, 252.4%, and 237.5% compared to the base case, respectively.

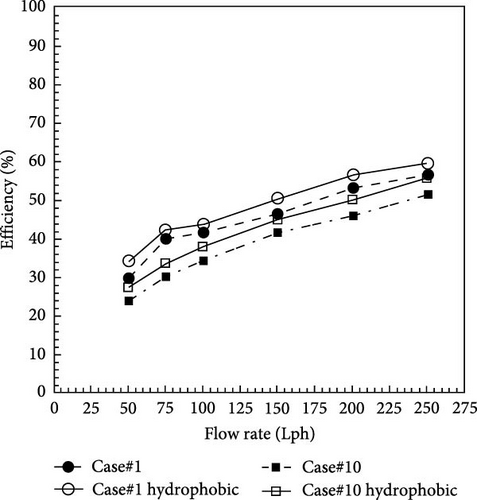
7.2.3. The Effect of Hydrophobicity on the Collector Efficiency

The experimental results showed that Case#1 among the twisted tapes with fixed width and Case#10 among the twisted tapes with variable width have the highest pressure drop. Therefore, these tapes were made with the same sizes, and their surface was made hydrophobic by the previously described method. After retesting the models with hydrophobic surfaces, the solar collector efficiency increases slightly. Figure 15 shows that the surface hydrophobicity of the twisted tapes could increase the efficiency of the solar collector by up to 4% in both laminar and turbulent flow regimes.

7.3. Performance Index

The performance index defined in Equation (5) can simultaneously evaluate the pressure drop and thermal energy absorbed by the fluid to choose a twisted tape with proper performance. Therefore, the proper design of the twisted tape leads to a higher performance index. Generally, the findings show that the performance index is highly affected by the width, twist ratio, flow rate, shape of the tape (fixed or variable width), and surface properties of the twisted strips. In the following, the twisted tapes are analyzed and compared according to tape width, twist ratios, and surface properties.

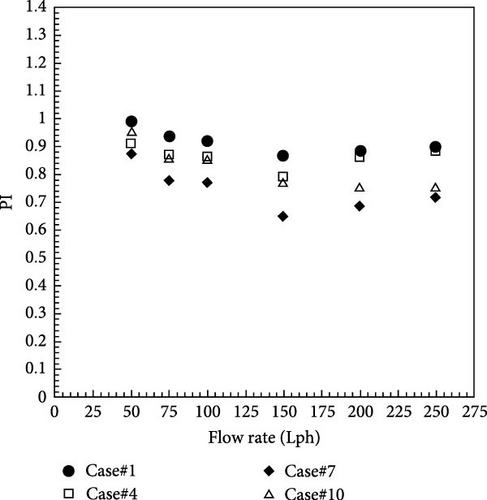
7.3.1. The Effect of Width on the Performance Index

The impact of the width of the twisted tapes on the performance index was investigated by keeping the twist ratio of the twisted tapes constant. Figure 16 shows the impact of the width of the twisted tapes on the performance index. By increasing the twisted tape width, the performance index is improved. Furthermore, constant or variable tape width can have a significant effect on the performance index. The performance index of Case#10 with variable width is higher than Case#7 with fixed width. According to Figure 16, twisted tapes perform better in laminar flow than in turbulent flow. Because in the turbulent flow, the interaction between the fluid and the pipe is naturally high, and the role of using the twisted tape is less.

7.3.2. The Effect of the Twist Ratio on the Performance Index

By keeping the width of the twisted tapes constant, the effect of the twist ratio of the twisted tapes on the performance index was inspected. The twisted tapes with twist ratios of 5, 7, and 9 were employed for the experiments. According to Figure 17, it was found that the twist ratios are an important and influential factor in the solar collector performance. Thus, as the twist ratio is decreased, the performance index of the solar collector is increased. At a flow rate of 50 Lph, Case#1 has a better performance index than Case#2 and Case#3 by 1.25% and 1.4%, respectively. Also, twisted tapes have a higher performance index in laminar flow than in turbulent flow.

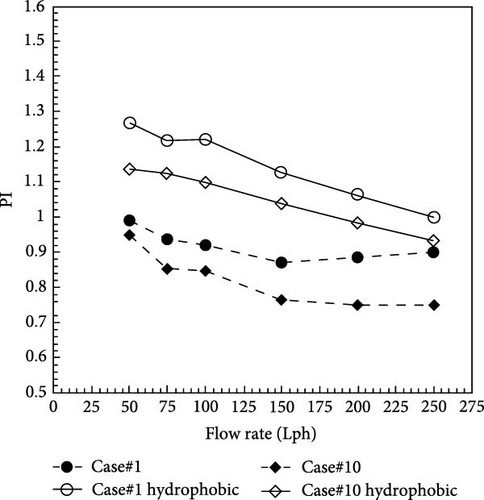
7.3.3. The Effect of Hydrophobicity on the Performance Index

One of the challenges in the performance of solar collectors equipped with twisted tapes is the increased friction between the fluid and the surface of the twisted tapes, which leads to an increase in the pressure drop. This paper proposes hydrophobic twisted tapes to solve this challenge. To investigate the hydrophobic effect of the surface of twisted tapes on the performance index, the twisted tape with a fixed width of 20 mm and a twist ratio of 5 with the highest friction coefficient among the fixed width twisted tapes was selected. A similar twisted tape was made with the same dimensions but with a hydrophobic surface. At the flow rate of 50 Lph, the performance index of the twisted tape with a hydrophobic surface increases by 125%. Similarly, the variable width twisted tape with a twist ratio of 5 with the highest friction coefficient among the variable width twisted tapes was selected. Then a similar twisted tape was made with the same dimensions but with a hydrophobic surface. At a flow rate of 50 Lph, the performance index of the variable width twisted tape with a hydrophobic surface increases by 143%. According to Figure 18, the hydrophobicity of the surface of the twisted tape increases the performance index to more than one.

The findings of this research are in good agreement with the findings of the experimental study on the effect of the twist ratio on heat transfer [32], the impact of the width of the twisted tape on heat transfer [33], and the effect of the width of fixed and variable width twisted tapes on heat transfer [34]. However, in the current research, it was found that the use of twisted tapes with a hydrophobic surface can increase the performance index to more than one.

8. Conclusion

This research introduces hydrophobic twisted tapes as a promising technique to improve the thermal efficiency of parabolic solar collectors. The obtained results indicate that hydrophobic twisted tapes can enhance the performance index from below one to over one. Moreover, the effect of using twisted tapes with various geometries—such as twist ratio and constant versus variable width—on the friction coefficient, efficiency, and performance index of the solar collector was investigated. The main conclusions of the research are as follows:

•
The use of twisted tapes with a lower twist ratio leads to increased pressure drop, efficiency, and performance index in the solar collector. To mitigate the pressure drop, twisted tapes with variable width can be employed.
•
The use of twisted tapes with a larger width results in a higher pressure drop, improved efficiency, and performance index in the solar collector. In this case, twisted tapes with a hydrophobic surface can be used to reduce the pressure drop.
•
Twisted tapes with variable width can lead to a lower pressure drop and higher efficiency and performance index than twisted tapes with fixed width in the solar collector.

In conclusion, the use of twisted tapes with a hydrophobic surface is demonstrated to reduce pressure drop while improving the performance index of the solar collector. Based on these findings, hydrophobic twisted tapes are proposed as a promising strategy for enhancing solar collector performance. Further research is recommended to explore the second law of thermodynamics, including exergy and entropy generation analyses, in solar collectors equipped with hydrophobic twisted tapes, alongside an assessment of their environmental impact. Finally, the authors propose the potential application of surface hydrophobicity to reduce pressure drop and enhance the performance of thermal systems as a broader aspect for future research.

Nomenclature

A_c:: Collector area (m²)
c_p:: Thermal capacity (J/(kg·K))
D_i:: Inner diameter of the absorber tube (m)
f:: Friction factor (−)
f₀:: Friction coefficient of the fluid without insert (−)
I:: Radiation intensity (W/m²)
L:: Length of the absorber tube (m)
:: Flow rate (kg/s)
P:: Twist pitch (m)
PI:: Performance index (−)
Δp:: Pressure drop (Pa)
Q₀:: Heat absorbed by the working fluid without insert (W)
Q_u:: Heat absorbed by the working fluid (W)
Q_s:: Heat flux of the sun (W)
T_i:: Inlet temperature (K)
T_o:: Outlet temperature (K)
T_oi:: Outlet temperatures at each time step (K)
T_os:: Steady-state outlet temperature (K)
TR:: Twist ratio (−)
U:: Uncertainty
u:: Fluid velocity (m/s)
W:: Tape width (m)
ρ:: Density (kg/m³)
η_th:: Thermal efficiency of solar collector (−).

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Ali Ismail Al-Shiblawi: data curation, formal analysis, resources, validation, writing–original draft. Mohammad Mahdi Heyhat: conceptualization, methodology, resources, supervision, writing–review and editing. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Open Research

Data Availability Statement

The data presented in this study are available in this article.

References

1 Jayapradha P. and Barik D., A Review of Solar Photovoltaic Power Utilizations in India and Impacts of Segregation and Safe Disposal of Toxic Components from Retired Solar Panels, International Journal of Energy Research. (2023) 2023, 11, https://doi.org/10.1155/2023/3196734, 3196734.
10.1155/2023/3196734
Web of Science® Google Scholar
2 Wang B., Liu Y., Wang D., Song C., Fu Z., and Zhang C., A Review of the Photothermal-Photovoltaic Energy Supply System for Building in Solar Energy Enrichment Zones, Renewable and Sustainable Energy Reviews. (2024) 191, https://doi.org/10.1016/j.rser.2023.114100, 114100.
10.1016/j.rser.2023.114100
Web of Science® Google Scholar
3 Maka A. O. M. and Alabid J. M., Solar Energy Technology and Its Roles in Sustainable Development, Clean Energy. (2022) 6, no. 3, 476–483, https://doi.org/10.1093/ce/zkac023.
10.1093/ce/zkac023
Web of Science® Google Scholar
4 Zafar I., Stojceska V., and Tassou S., Social Sustainability Assessments of Industrial Level Solar Energy: A Systematic Review, Renewable and Sustainable Energy Reviews. (2024) 189, https://doi.org/10.1016/j.rser.2023.113962, 113962.
10.1016/j.rser.2023.113962
Web of Science® Google Scholar
5 Kumar L., Hasanuzzaman M., Rahim N. A., and Sleiti A. K., Thermoeconomic Analysis of a Solar-Assisted Industrial Process Heating System, International Journal of Energy Research. (2024) 2024, 20, https://doi.org/10.1155/2024/4614066, 4614066.
10.1155/2024/4614066
Web of Science® Google Scholar
6 Ray S., Tripathy A. K., Sahoo S. S., and Bindra H., Performance Analysis of Receiver of Parabolic Trough Solar Collector: Effect of Selective Coating, Vacuum, and Semitransparent Glass Cover, International Journal of Energy Research. (2018) 42, no. 13, 4235–4249, https://doi.org/10.1002/er.4137, 2-s2.0-85050889248.
10.1002/er.4137
Web of Science® Google Scholar
7 Sarangi A., Sarangi A., Sahoo S. S., Mallik R. K., Ray S., and Varghese S. M., A Review of Different Working Fluids Used in the Receiver Tube of Parabolic Trough Solar Collector, Journal of Thermal Analysis and Calorimetry. (2023) 148, 3929–3954.
10.1007/s10973-023-11991-y
CAS Web of Science® Google Scholar
8 Xia Y., Lin X., Cheng Z., Xie F., and Huang J., Numerical Study on the Enhanced Thermal Performance of the Porous Media-Assisted Flat-Plate Solar Collector, International Journal of Energy Research. (2023) 2023, 19, https://doi.org/10.1155/2023/2244771, 2244771.
10.1155/2023/2244771
Web of Science® Google Scholar
9 Khattar M. and Heyhat M. M., Exergy Economic and Environmental Analysis of a Direct Absorption Parabolic Trough Collector Filled With Porous Metal Foam, Energies. (2022) 15, no. 21, https://doi.org/10.3390/en15218150, 8150.
10.3390/en15218150
CAS Web of Science® Google Scholar
10 Mousavi Ajarostaghi S. S., Zaboli M., Javadi H., Badenes B., and Urchueguia J. F., A Review of Recent Passive Heat Transfer Enhancement Methods, Energies. (2022) 15, no. 3, https://doi.org/10.3390/en15030986, 986.
10.3390/en15030986
CAS Web of Science® Google Scholar
11 Léal L., Miscevic M., and Lavieille P., et al.An Overview of Heat Transfer Enhancement Methods and New Perspectives: Focus on Active Methods Using Electroactive Materials, International Journal of Heat and Mass Transfer. (2013) 61, 505–524, https://doi.org/10.1016/j.ijheatmasstransfer.2013.01.083, 2-s2.0-84874852952.
10.1016/j.ijheatmasstransfer.2013.01.083
Web of Science® Google Scholar
12 Kanti P. K., Sharma K. V., Minea A. A., and Kesti V., Experimental and Computational Determination of Heat Transfer, Entropy Generation and Pressure Drop Under Turbulent Flow in a Tube With Fly Ash-Cu Hybrid Nanofluid, International Journal of Thermal Sciences. (2021) 167, 107016.
10.1016/j.ijthermalsci.2021.107016
CAS Web of Science® Google Scholar
13 Kanti P., Sharma K. V., Ramachandra C. G., and Gupta M., Thermal Performance of Fly Ash Nanofluids at Various Inlet Fluid Temperatures: An Experimental Study, International Communications in Heat and Mass Transfer. (2020) 119, 104926.
10.1016/j.icheatmasstransfer.2020.104926
CAS Web of Science® Google Scholar
14 Bergles A. E., Recent Developments in Enhanced Heat Transfer, Heat and Mass Transfer. (2011) 47, no. 8, 1001–1008, https://doi.org/10.1007/s00231-011-0872-y, 2-s2.0-80051793658.
10.1007/s00231-011-0872-y
Web of Science® Google Scholar
15 Bellos E. and Tzivanidis C., Enhancing the Performance of a Parabolic Trough Collector With Combined Thermal and Optical Techniques, Applied Thermal Engineering. (2020) 164, 114496.
10.1016/j.applthermaleng.2019.114496
CAS Web of Science® Google Scholar
16 Eiamsa-ard S., Changcharoen W., Beigzadeh R., Eiamsa-ard P., Wongcharee K., and Chuwattanakul V., Influence of Co/Counter Arrangements of Multiple Twisted-Tape Bundles on Heat Transfer Intensification, Chemical Engineering and Processing - Process Intensification. (2021) 160, https://doi.org/10.1016/j.cep.2021.108304, 108304.
10.1016/j.cep.2021.108304
CAS Web of Science® Google Scholar
17 Deshmukh K., Karmare S., and Patil P., Investigation of Convective Heat Transfer Inside Evacuated U Pipe Solar Thermal Collector With TiN Nanofluid and Twisted Tape Combination, Applied Solar Energy. (2022) 58, no. 6, 784–799, https://doi.org/10.3103/S0003701X2206007X.
10.3103/S0003701X2206007X
Google Scholar
18 Sotoudeh F., Mousavi S. M., Karimi N., Lee B. J., Abolfazli-Esfahani J., and Manshadi M. K. D., Natural and Synthetic Superhydrophobic Surfaces: A Review of the Fundamentals, Structures, and Applications, Alexandria Engineering Journal. (2023) 68, 587–609, https://doi.org/10.1016/j.aej.2023.01.058.
10.1016/j.aej.2023.01.058
Web of Science® Google Scholar
19 Gong W., Shen J., Dai W., Li K., and Gong M., Research and Applications of Drag Reduction in Thermal Equipment: A Review, International Journal of Heat and Mass Transfer. (2021) 172, https://doi.org/10.1016/j.ijheatmasstransfer.2021.121152, 121152.
10.1016/j.ijheatmasstransfer.2021.121152
Web of Science® Google Scholar
20 Zhang Y., Zhang Z., Yang J., Yue Y., and Zhang H., A Review of Recent Advances in Superhydrophobic Surfaces and Their Applications in Drag Reduction and Heat Transfer, Nanomaterials. (2022) 12, no. 1, https://doi.org/10.3390/nano12010044, 44.
10.3390/nano12010044
CAS Web of Science® Google Scholar
21 Neinhuis C. and Barthlott W., Characterization and Distribution of Water-Repellent, Self-Cleaning Plant Surfaces, Annals of Botany. (1997) 79, no. 6, 667–677, https://doi.org/10.1006/anbo.1997.0400, 2-s2.0-0030740868.
10.1006/anbo.1997.0400
Web of Science® Google Scholar
22 Forrest E., Williamson E., Buongiorno J., Hu L.-W., Rubner M., and Cohen R., Augmentation of Nucleate Boiling Heat Transfer and Critical Heat Flux Using Nanoparticle Thin-Film Coatings, International Journal of Heat and Mass Transfer. (2010) 53, no. 1–3, 58–67, https://doi.org/10.1016/j.ijheatmasstransfer.2009.10.008, 2-s2.0-71749116907.
10.1016/j.ijheatmasstransfer.2009.10.008
CAS Web of Science® Google Scholar
23 Shi J., Zheng G., Chen Z., and Dang C., Experimental Study of Flow Condensation Heat Transfer in Tubes Partially Filled With Hydrophobic Annular Metal Foam, International Journal of Heat and Mass Transfer. (2019) 136, 1265–1272, https://doi.org/10.1016/j.ijheatmasstransfer.2019.03.039, 2-s2.0-85063106342.
10.1016/j.ijheatmasstransfer.2019.03.039
CAS Web of Science® Google Scholar
24 Motamedi M., Chung C. Y., and Rafeie M., et al.Experimental Testing of Hydrophobic Microchannels, With and Without Nanofluids, for Solar PVT Collectors, Energies. (2019) 14, 3036.
Google Scholar
25 Mandev E. and Manay E., Effects of Surface Roughness in Multiple Microchannels on Mixed Convective Heat Transfer, Applied Thermal Engineering. (2022) 217, https://doi.org/10.1016/j.applthermaleng.2022.119102, 119102.
10.1016/j.applthermaleng.2022.119102
Web of Science® Google Scholar
26 Ahmadi S., Akhavan-Behabadi M. A., Sajadi B., and Ahmadpour M. M., Effect of Hydrophilic and Hydrophobic Metal Foams on Condensation Characteristics of Refrigerant Flow inside Annular Tubes: Experimental Study, Thermal Science and Engineering Progress. (2023) 40, https://doi.org/10.1016/j.tsep.2023.101785, 101785.
10.1016/j.tsep.2023.101785
CAS Web of Science® Google Scholar
27 Bellos E., Tzivanidis C., and Tsimpoukis D., Multi-Criteria Evaluation of Parabolic Trough Collector With Internally Finned Absorbers, Applied Energy. (2017) 205, 540–561, https://doi.org/10.1016/j.apenergy.2017.07.141, 2-s2.0-85026905449.
10.1016/j.apenergy.2017.07.141
Web of Science® Google Scholar
28 H. B M., Kanti P. K., Prakash S. B., and Sridhara S. N., Investigation of Entropy Generation and Thermohydraulic Characteristics of Al₂O₃–CuO Hybrid Nanofluid Flow in a Pipe at Different Inlet Fluid Temperatures, International Journal of Thermal Sciences. (2023) 193, https://doi.org/10.1016/j.ijthermalsci.2023.108541, 108541.
10.1016/j.ijthermalsci.2023.108541
CAS Google Scholar
29 Heyhat M. M. and Zahi Khattar M., On the Effect of Different Placement Schemes of Metal Foam as Volumetric Absorber on the Thermal Performance of a Direct Absorption Parabolic Trough Solar Collector, Energy. (2023) 266, https://doi.org/10.1016/j.energy.2022.126428, 126428.
10.1016/j.energy.2022.126428
Web of Science® Google Scholar
30 Heyhat M. M., Valizade M., Abdolahzade S., and Maerefat M., Thermal Efficiency Enhancement of Direct Absorption Parabolic Trough Solar Collector (DAPTSC) by Using Nanofluid and Metal Foam, Energy. (2020) 192, https://doi.org/10.1016/j.energy.2019.116662, 116662.
10.1016/j.energy.2019.116662
CAS Web of Science® Google Scholar
31 Standard S. A., Method of Testing to Determine the Thermal Performance of Solar Collectors, 2010, American Society for Heating, Refrigerating and Air-conditioning Engineers, Atlanta, USA.
Google Scholar
32 Thianpong C., Eiamsa-ard P., Wongcharee K., and Eiamsa-ard S., Compound Heat Transfer Enhancement of a Dimpled Tube With a Twisted Tape Swirl Generator, International Communications in Heat and Mass Transfer. (2009) 36, no. 7, 698–704, https://doi.org/10.1016/j.icheatmasstransfer.2009.03.026, 2-s2.0-67649119968.
10.1016/j.icheatmasstransfer.2009.03.026
CAS Web of Science® Google Scholar
33 Seemawute P. and Eiamsa-ard S., Thermohydraulics of Turbulent Flow Through a Round Tube by a Peripherally-Cut Twisted Tape With an Alternate Axis, International Communications in Heat and Mass Transfer. (2010) 37, no. 6, 652–659, https://doi.org/10.1016/j.icheatmasstransfer.2010.03.005, 2-s2.0-77953542459.
10.1016/j.icheatmasstransfer.2010.03.005
Web of Science® Google Scholar
34 Fagr M. H., Rishak Q. A., and Mushatet K. S., Performance Evaluation of the Characteristics of Flow and Heat Transfer in a Tube Equipped With Twisted Tapes of New Configurations, International Journal of Thermal Sciences. (2020) 153, https://doi.org/10.1016/j.ijthermalsci.2020.106323, 106323.
10.1016/j.ijthermalsci.2020.106323
Web of Science® Google Scholar

Citing Literature

All articles