International Journal of Energy Research
Volume 2025, Issue 1 5413946
Research Article
Open Access

Techno-Economic Design of a Hybrid Photovoltaic–Wind System for a Residential Microgrid Considering Uncertainties Using Dynamic Parameters Bald Eagle Algorithm

Mehrdad Ahmadi Kamarposhti, 

Corresponding Author

Mehrdad Ahmadi Kamarposhti

Department of Electrical Engineering , Jo.C. , Islamic Azad University , Jouybar , Iran , iau.ac.ir

Search for more papers by this author
Hassan Shokouhandeh, 

Hassan Shokouhandeh

Department of Electrical Engineering , National University of Skills (NUS) , Tehran , Iran , nus.ac.ir

Search for more papers by this author
Rachid Outbib, 

Rachid Outbib

LIS , UMR CNRS , Aix-Marseille University , 7020 , Marseille , France , univ-amu.fr

Search for more papers by this author
Ilhami Colak, 

Ilhami Colak

Faculty of Engineering and Natural Science , Department of Electrical and Electronics Engineering , Istinye University , Istanbul , Türkiye , istinye.edu.tr

Search for more papers by this author
El Manaa Barhoumi, 

El Manaa Barhoumi

Department of Electrical and Computer Engineering , College of Engineering , Dhofar University , Salalah , Oman , du.edu.om

Search for more papers by this author
First published: 21 July 2025
https://doi.org/10.1155/er/5413946
Academic Editor: Mahmoud Ahmed

Abstract

This paper presents a probabilistic cost-based model for grid-connected photovoltaic (PV)–wind hybrid system design, employing probability density functions (PDFs) and Monte Carlo simulation (MCS) to address renewable generation and load demand uncertainties. The proposed scenario-based approach features an innovative objective function incorporating weighted scenario costs, allowing controlled load shedding through energy not supplied (ENS) penalties while enforcing system reliability via a loss of power supply probability (LPSP) constraint. For optimization, we develop a dynamic parameter bald eagle search (DP-BES) algorithm, demonstrating through MATLAB simulations its superior performance over Whale Optimization Algorithm (WOA), Particle Swarm Optimization (PSO), and Grey Wolf Optimization (GWO) methods, with the hybrid PV–wind configuration achieving maximum cost reduction (41%) compared to standalone PV (33%) or wind (25%) systems.

1. Introduction

Renewable energy sources, particularly solar and wind power, have emerged as viable solutions to overcome the limitations of conventional distribution systems in microgrid applications [1]. Building on this potential, their distributed generation architecture offers two key advantages: (1) minimized ohmic losses through localized power production near consumption points and (2) increased feeder line capacity for meeting growing power demands [2]. Beyond these technical benefits, renewable integration demonstrates significant environmental and operational merits, including emission reduction, enhanced reliability during outages, improved voltage regulation, and economic viability, as established in recent studies [3].

Achieving optimal efficiency in hybrid microgrid systems presents complex challenges. The intermittent nature and spatiotemporal variability of renewable sources necessitate careful optimization of both quantity and capacity of generation units [4]. This optimization problem becomes particularly complex when considering three critical factors: power fluctuation profiles, load demand variability, and system reliability constraints [5]. In [6], a multi-objective optimization framework for designing hybrid PV/wind/battery systems that simultaneously addresses reliability, cost, and emissions for both stand-alone and grid-connected operations. The study demonstrates through case studies how this approach enables optimal system configurations balancing technical, economic, and environmental objectives, providing decision-makers with a practical tool for sustainable energy planning. A primary obstacle in this optimization process stems from inherent uncertainties in renewable systems. Photovoltaic (PV)–wind hybrids face three principal uncertainty sources: solar radiation intensity variations, wind speed fluctuations, and unpredictable microgrid load patterns [7]. These uncertainties underscore the need for robust modeling approaches in hybrid microgrid design.

Recent research has employed various methodologies to address these design challenges.

The lightning search algorithm in [8] optimizes PV/wind capacity and placement in grid-connected microgrids, accounting for bus voltage limits and generation uncertainties. Complementing this work, [9] presents a techno-economic analysis of PV–wind-battery systems, evaluating both grid-connected and off-grid configurations against constraints like land availability and resource complementarity. Further advancing the field, [10] combines particle swarm optimization (PSO) with fuzzy logic to enhance voltage stability and reduce power losses in distributed renewable systems. Notable hybrid approaches include the Dragonfly algorithm application in [11] for wind-PV-fuel cell systems with hydrogen storage and the teaching-learning-based optimization in [12] for grid-connected PV-battery configurations. Collectively, these studies demonstrate the critical importance of optimal design in achieving cost-effective, reliable hybrid microgrid systems.

Recent algorithmic developments continue to refine hybrid system optimization. In [13], the optimal capacity of distributed generation resources in a hybrid system is investigated with the aim of reducing costs and meeting reliability constraints, considering the balance between active and reactive power supply and demand. A modified particle swarm optimization (PSO) algorithm is proposed to solve the optimization problem, which has higher accuracy in solving the problem compared to the standard PSO algorithm. In [14], the optimal size of PV and wind resources along with battery storage in a microgrid is determined using the whale algorithm. The objective of the optimal design of the hybrid system is to reduce the operating cost of the microgrid, increase reliability, and reduce pollutant emissions. The broader context is provided by Soudagar et al. [15], which reviews optimization algorithms for both grid-tied and off-grid systems, highlighting cost reduction as a predominant objective. This perspective is reinforced by [16], where hybrid intelligent algorithms evaluate various renewable configurations, confirming that operating cost reductions depend critically on local conditions, load profiles, and precise system design.

In [17] an optimal design for an off-grid hybrid renewable energy system (HRES) in Zanjan, Iran, addressing uncertainties in both energy generation and load demand is proposed. The authors employ a robust optimization framework combining solar PV, wind turbines, and battery storage to minimize costs while ensuring reliability. Results demonstrate the cost-effectiveness and technical feasibility of the proposed HRES configuration for remote areas, offering insights applicable to regions with similar energy challenges. The work highlights the importance of uncertainty-aware planning in renewable energy system. In [18], a bi-level optimization framework is proposed for integrated energy systems, effectively coordinating renewable generation, energy conversion, storage technologies, and demand-side management. The approach enables synergistic operation of diverse energy components while addressing system-wide optimization challenges, demonstrating improved efficiency and cost-effectiveness in complex energy system design. In [19], a stochastic optimization model is developed for rural microgrids, incorporating hybrid hydrogen-electric vehicle storage with V2G capability. The design comprehensively considers multiple uncertainty sources in both renewable generation and load demand, with results showing enhanced system reliability alongside maintained economic viability for off-grid applications. In [20], a multi-level optimization and intelligent control framework is presented for fuel cell-based CHP systems. The hierarchical structure simultaneously addresses design optimization and real-time operational control challenges, significantly improving both system efficiency and dynamic performance across varying operating conditions.

Despite extensive research on hybrid power system design, key challenges persist, particularly the uncertainties in renewable energy sources, which complicate accurate simulations. This study explores the optimal design of a PV–wind hybrid system for a residential area, aiming to minimize energy costs while accounting for load and generation uncertainties using probability density functions (PDFs) and Monte Carlo simulation (MCS). An innovative objective function incorporates scenario probabilities, including investment, maintenance, scrapping, grid energy purchase costs, and blackout penalties, allowing controlled blackouts to reduce costs while penalizing them. To limit excessive blackouts, the loss of power source probability (LPSP) is constrained to 5%. The proposed dynamic parameters bald eagle search (DP-BES) algorithm is employed to optimize the capacities of PV and wind resources efficiently. The key contributions of this paper are as follows:
  • •

    Novel stochastic framework: A scenario-based probabilistic model for hybrid solar-wind system design, integrating cost-weighted scenarios and controlled load shedding to optimize system cost.

  • •

    Enhanced optimization algorithm: Implementation of the DP-BES algorithm to solve the optimization problem, enhancing convergence and accuracy

  • •

    Reliability-cost balance: Introduction of the LPSP constraint to prevent excessive load shedding while accounting for ENS penalties, ensuring a trade-off between system reliability and cost-effectiveness.

In the following article, the problem formulation is presented in the second section. This section introduces the structure of the electrical system of the under study residential complex, followed by a description of its component models. Then the proposed objective function and design constraints are presented. The third section briefly introduces the DP-BES algorithm. In the fourth section, the results obtained from simulations conducted in MATLAB are analyzed and discussed in three parts. The article concludes with a summary and suggestions for future research in the fifth section.

2. Problem Formulation

In this article, a residential complex similar to Figure 1 is selected as a home microgrid for conducting studies and simulations. This microgrid is connected to the main power grid via a 20KV/0.4KV distribution transformer and has the capability of continuously exchanging electrical energy with it. Due to the high costs of purchasing and maintaining batteries, no energy storage is implemented in the studied microgrid. In the event of excess power production by the PV and wind sources, the electricity is directly sold to the upstream grid.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Model of the under-study residential complex.

2.1. Load Model

In the studied residential complex, there are 25 homes, each with a purchased demand of ~5 kVA. The maximum electrical power in the complex, disregarding the diversity factor, would be 125 kW. Due to the random behavior of the consumers, uncertainty becomes an inevitable aspect of microgrid studies. The normal PDF can be an appropriate model to represent the uncertainty of the electrical load consumption in the microgrid, which is modeled in the form of Equation (1) [21].
()
where PL represents load consumption, also µPL represents the mean and σPL represents standard deviation of the load consumption.

2.2. PV Power Model

The power output of PV systems depends on the intensity of solar radiation and the surface temperature. The output power of a PV panel is calculated by Equation (2) [21]:
()
where PPV-r represents the nominal power of the PV panel, fPV denotes the power degradation coefficient due to surface dirt and losses, SiSTC is standard solar radiation intensity and TSTC is standard surface temperature of the array, with values of 100 W per square meter and 25 °C. The Si represents the random variable of solar radiation intensity, T represents the panel surface temperature, and ζPV is the temperature coefficient of power for the PV array. The PV panels used in this article are of the polycrystalline type, each with a maximum capacity of one kilowatt. Each panel occupies an area of ~1.64 square meters. Solar radiation intensity has a probabilistic nature, and the power received from the PV system is associated with uncertainty. In most studies, the beta PDF has been used to describe the variations in solar radiation intensity. Equation (3) shows the mathematical formula of the beta PDF [21].
()
where Γ is the gamma function, and αs and βs are the parameters of the beta distribution function.

2.3. Wind Turbine Power Model

Wind turbine power output is inherently uncertain due to the variability of wind speeds in a region. The Weibull PDF is a well-suited mathematical model to capture this uncertainty. The Weibull function is formulated as Equation (4) [21].
()
where υ (m/s) represents the wind speed as a random variable, αw is shape factor, and βw are is scale factor of the Weibull PDF. These parameters are used along with measured wind speed data to calculate the wind turbine’s power output at various wind speeds, as shown in Figure 2.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Power capacity of the wind turbine at various wind speeds.
The wind turbine’s output power is zero when the wind speed falls outside its operational range. This occurs when the wind speed is either below the cut-in speed (υcut-in) or exceeds the cut-out speed (υcut-out). Within this operational range (υcut-in < υ < υcut-out), the turbine generates electrical energy according to the relationship depicted in Figure 2, which can be mathematically expressed by Equation (5).
()

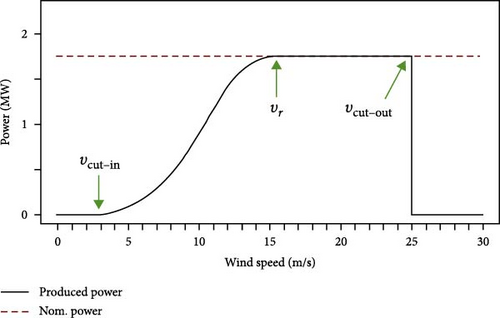
In the simulations conducted in this article, 1-kilowatt vertical-axis wind turbines were used. The area required for each turbine is ~3.14 square meters. The cut-in speed, cut-out speed, and rated speed for the turbine are 3, 25, and 11 m/s.

2.4. Uncertainties Modeling

In the framework of probabilistic analysis of the objective function, the problem is presented in the mathematical form y = f (Z), where Z is the vector of the random variables of the problem under study, each having a specific PDF. Under these conditions, for the probabilistic analysis of the problem using MCS, multiple scenarios are generated, and the objective function is calculated as shown in Equation (6) [22].
()
where πs is the probability of each scenario, which can be calculated by Equation (7).
()

The MCS technique can be applied to model and assess uncertainties in the optimal design of hybrid systems. As a probabilistic approach, MCS predicts the behavior of microgrid components. Steps for uncertainty calculation using the MCS method are:

Step 1: Establish the Mathematical Model of the Measurement System

Define the mathematical relationship between the output measurement quantity (Y) and the influencing input quantities (X1, X2, …, Xₙ).

Step 2: Assign PDFs to Input Quantities

Determine the appropriate PDFs for each input quantity (Xi), considering any dependencies or correlations between them.

Step 3: Generate PDFs for the Output Quantity
  • •

    For each input quantity (Xi), generate a large number (M) of random values based on their respective PDFs.

  • •

    Input these random values into the mathematical model to compute corresponding output values (Y).

  • •

    Using the resulting Y values, derive the PDF of the output quantity.

Step 4: Determine the Measurement System Uncertainty

Based on the PDF of the output quantity (Y), calculate:
  • •

    The mathematical expectation (mean) of Y (estimated value).

  • •

    The standard deviation of Y (standard uncertainty).

  • •

    The confidence interval for Y at a specified probability level.

2.5. Objective Function and Constraints

The main objective of this article is to design a hybrid PV and wind turbine system for a residential complex that minimizes cost and ensures reliable power supply under uncertain conditions. This system will connect to the main power grid. An optimization algorithm will be used to determine the optimal size of the PV and WT components. The objective function, detailed in Equation (8), considers all economic factors, including initial investment, operation and maintenance (O&M) costs, salvage value at the end of life, and the cost/revenue from electricity exchange with the grid.
()
where Ns is the number of scenarios selected by the MCS, Probs is the probability of occurrence of each scenario, CENS is the penalty cost for energy not supplied (ENS), Ii is the initial investment cost, RNPV-i is the replacement cost of hybrid system components, OMNPV_i is the operation and maintenance cost, SNPV_i is the revenue from the sale of salvaged components, Pb is the amount of electrical energy purchased from the grid, Ca is the cost per kilowatt of electrical energy purchased from the main grid, Pa is the amount of excess electrical energy sold to the grid, and Ia is the revenue from selling each kilowatt of electrical energy to the main grid. The initial investment cost for purchasing PV panels is calculated using Equation (9).
()
In the above equation, γPV is the initial cost per square meter of the PV panels, and Apv is the total area of the installed PV panels. It is important to note that the project lifespan is equal to the useful life of the PV panels, and the replacement cost for this resource will be zero (RNPV_PV = 0) [23]. If the annual maintenance and repair cost per square meter of the PV panels is considered to be OMNPV-PV, the total maintenance and repair cost of the PV panels over the project’s lifespan (N) is given in Equation (10) [23]:
()
where εpv is the annual increase rate of maintenance and repair costs and r is the interest rate. The revenue from the salvage of the panels will be calculated using Equation (11):
()
where SPV is the resale price per square meter of the PV panels. The following equations govern the calculation of the costs associated with wind turbines. The total initial investment cost and all replacement costs for the wind turbines in the hybrid system are calculated using Equation (12) [23].
()
where εw is the annual increase rate of the installation cost for the wind turbine, Aw is the area swept by the turbine blades, and LW is the useful life of the wind turbine. During the project lifespan (N), the wind turbine will need to be replaced. αW is the initial purchase cost, which is considered in dollars per square meter. The annual maintenance and repair cost for the wind turbine is calculated using Equation (13).
()
Revenue from the salvage and resale of wind turbines is calculated using Equation (14) [23]:
()
where Sd is the resale price of the wind turbine, which linearly decreases from Sd to SW.
()
where yd represents the number of years remaining from the last installation of the wind turbines until the end of the project lifespan.
The amount of electrical energy exchanged with the main grid depends on the dimensions of the hybrid system, solar radiation intensity, and wind speed in the area. The cost of purchasing electrical energy from the main grid is formulated by Equation (16) [23]:
()
Revenue from selling electricity to the main grid is calculated using Equation (17):
()
The penalty cost for ENS is calculated using Equation (18):
()
where ENS is the amount of ENS and CENS is the penalty cost of the ENS. The optimal design of a grid-connected hybrid PV and wind system is subject to technical constraints. The first constraint is that the generated power and the consumed power in the system must be equal after the installation of distributed generation sources.
()
To prevent widespread blackouts in the microgrid, the loss of power supply probability (LPSP) index is considered as a design constraint, which should not exceed 5% [24].
()
The number of PV panels and wind turbines that can be installed in the microgrid is limited.
()
()
where NPV and NWT are the maximum number of PV panels and wind turbines that can be installed in the area.

3. DP-BES

Inspired by the hunting strategies of bald eagles, the BES algorithm is a type of optimization technique that relies on populations. Bald eagles, known for their remarkable vision, can spot fish from afar while soaring at high altitudes. Despite the challenges of hunting from such a distance, they can strategically choose areas teeming with prey and plan their attack accordingly. Figure 3 showcases bald eagles in action during their hunt [25].

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Bald eagle search hunting procedure.
Limited by their energy consumption, bald eagles typically hunt within a 700-m radius of their nest. Mimicking this behavior, the BES algorithm employs a three-stage process: selection, search, and swoop. During the selection stage, eagles (represented by virtual agents in the algorithm) strategically choose the most promising area within the search space to find prey. Equation (23) mathematically models this selection process.
()
where α is a controlling parameter ranging from 1.5 to 2, and rand is a random number between 0 and 1. Pbest indicates the region with the highest nutritional value, while Pmean contains information from the previous stage. The search areas are selected in close proximity to each other based on the characteristics of the available food sources. Following the selection of promising areas, the virtual eagles transition to a search phase where they mimic the efficient hunting strategy of bald eagles: soaring in spiral patterns. This behavior is represented by the following equations:
()
where ψ and R are two key parameters control this behavior. ψ, ranging from 5 to 10, determines the tightness of the spiral, influencing how focused the search becomes. R, set between 0.5 and 2, controls the number of spiral loops, dictating the search duration. This spiraling allows the algorithm to both identify the best location (prey) and explore new areas. The polar plot (−1 to 1) suggests a good balance between focusing on promising areas and exploring new possibilities. By adjusting ψ and R, the algorithm can escape getting stuck on suboptimal solutions (local optima) and continuously find better solutions. The final stage, the swoop, mimics the eagle’s final attack and is described mathematically by Equation (25).
()
The swoop phase, inspired by the eagle’s final attack, mathematically determines the optimal location for the prey. The eagles’ diverse movements are represented using a polar equation. This equation considers the current position, the center point, and a random number to pinpoint the optimal spot. Parameters c1 and c2 further influence the intensity of the virtual eagle’s movement towards the optimal location and the center. To enhance the search process, the proposed BES algorithm employs dynamic parameters. Instead of using fixed values, α, ψ, and R are adjusted for each iteration. The following section details how these parameters are determined in each step of the algorithm.
()
()
()

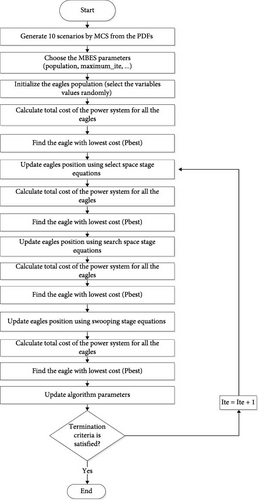
The algorithm determines the best values for α, ψ, and R in each iteration by considering several factors. αbest, ψbest, and Rbest represent the best values found for these parameters so far (up to iteration ite), αmin, ψmin, and Rmin define the minimum allowed values, ensuring they don’t fall below a certain threshold. Similarly, αmax, ψmax, and Rmax set the upper limit for each parameter. By considering these factors, the algorithm maintains a balance between exploring new areas and focusing on promising areas throughout the optimization process. Figure 4 illustrates the flowchart of this proposed DP-BES algorithm.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The proposed DP-BES flowchart for optimal hybrid system designing.

4. Simulation Results Analysis and Discussion

The simulation results are presented in three phases. In the first phase, the performance of the proposed DP-BES algorithm was evaluated through benchmark problem solutions and comparative analysis with other optimization algorithms. The second phase of simulations focused on optimal hybrid system design implementation using the DP-BES algorithm. This section aims to assess the performance of the proposed algorithm for hybrid system design through a comparison with the findings of the reference study. Finally, in the third section, the optimal design of the hybrid system using the proposed model in this paper has been carried out by the DP-BES algorithm and other algorithms. The simulations were conducted using MATLAB 2023 on an Acer laptop with an Intel Core i5-6200U CPU (2.3 GHz) and 8 GB of DDR3 RAM.

4.1. The DP-BES Performance Evaluation

The current analysis examines the computational efficacy of the DP-BES optimization technique through systematic evaluation using 10 benchmark functions, as specified in Table 1. These test functions have been carefully selected to represent varying levels of computational complexity: Functions f1 through f4 represent unimodal problems, f5 to f7 constitute multimodal challenges, while f8–f10 present fixed-dimension multimodal cases [26]. This comprehensive testing approach enables rigorous evaluation of the algorithm’s problem-solving capabilities, particularly in terms of solution precision and optimization performance across different function types.

Table 1. Optimization benchmark function.
Function Size Constraints Minimum value
30 [−100 100] 0
30 [−10 10] 0
30 [−100 100] 0
f4(x) = maxi{|xi|, 1 ≤ i ≤ n} 30 [−100 100] 0
30 [−5.12 5.12] 0
30 [−32 32] 0
30 [−600 600] 0
4 [0 10] −10.1532
4 [0 10] −10.4028
4 [0 10] −10.5363

The computational performance metrics of the proposed DP-BES algorithm are quantitatively compared with three established metaheuristics in Table 2. The presented data includes statistical measures (mean and standard deviation) derived from 20 independent executions across benchmark functions. The comparative algorithms comprise: (i) PSO, (ii) Whale Optimization Algorithm (WOA), and (iii) the Adaptive Dynamic Self-Learning Grey Wolf Optimization variant (ASGWO) [26].

Table 2. The benchmark function solving results.
PSO WOA ASGWO DP-BES
Mean Std Mean Std Mean Std Mean Std
f1 5.86 5.32 — 5.50e–07 1.72e–06 — 0 0 — 0 0
f2 9.31 8.56 — 2.57e–10 7.13e–10 — 9.489e–243 6.68e–243 — 4.609e–132 5.55e–133
f3 22.94 8.56 — 0.02275 0.0386 — 0 0 — 0 0
f4 1.28 0.40 — 0.01333 0.0266 — 1.185e–201 6.19e–201 — 1.176e–143 5.85e–144
f5 186.5 22.68 — 9.399e–12 2.839e–11 — 0 0 — 0 0
f6 3.05 0.47 — 1.154e–08 3.020e–08 — 1.141e–14 3.103e–15 — 1.1003e–14 1.731e–15
f7 0.70 0.17 — 2.285e–16 4.056e–13 — 0 0 — 0 0
f8 −8.33 1.75 — −2.4141 2.0658 — −9.22813 2.01878 — −10.3942 1.32954
f9 −6.19 1.91 — −1.9880 1.4711 — −9.0779 3.07231 — −10.7079 2.2599
f10 −7.15 1.37 — −1.81628 1.6834 — −10.2873 1.666e–05 — −10.6494 1.609e–05

The experimental results conclusively establish the enhanced optimization capability of the proposed DP-BES algorithm relative to conventional approaches including PSO, WOA, and ASGWO. Statistical analysis reveals DP-BES’s superior convergence characteristics, as evidenced by consistently minimized objective function values (mean) and reduced solution variability (standard deviation) across all benchmark evaluations. These findings substantiate DP-BES’s improved solution quality and algorithmic stability, suggesting its potential as a robust optimization tool for diverse engineering applications. The algorithm’s demonstrated performance advantages stem from its unique dynamic parameter adaptation mechanism, which enables more efficient exploration–exploitation balance throughout the search process.

4.2. Optimal Hybrid System Design

This section evaluates the performance of the proposed algorithm in designing a grid-connected solar-wind hybrid system through comparative analysis with the Modified Dragonfly Algorithm (MDA) [27, 28]. The optimization results of the hybrid system configuration are presented in Table 3.

Table 3. Optimal designing of hybrid system.
Algorithm PV panel WT Energy purchased (kWh) Energy cost ($) Total cost ($)
MDA 107 47 39,168 17,538 26,465
DP-BES 118 42 36,467 14,708 25,907

The comparative performance analysis between the MDA and the proposed DP-BES algorithm for hybrid PV-WT system design reveals significant cost and efficiency improvements. DP-BES favors a balanced configuration (42 WT units and 118 PV panels) compared to MDA’s 47 WT units and 107 PV panels, suggesting superior resource allocation. The DP-BES-optimized system achieves a lower total cost of 25,907 and substantially reduces energy costs to 14,708. This cost efficiency is achieved despite requiring less grid-purchased energy (36,467 vs. 39,168 kWh), demonstrating better renewable utilization. These results validate DP-BES as a more effective optimizer for hybrid renewable systems.

4.3. Optimal Design of the Proposed Hybrid System Model

The hybrid system simulation required collection of essential data, including network load variations, wind speed patterns, and solar radiation intensity in the study area. This data served as the basis for technical and economic design optimization through various algorithms. Alongside the proposed DP-BES algorithm, three additional well-established optimization techniques were implemented: PSO, WOA, and GWO, complemented by the standard BES algorithm. Table 4 summarizes the parameters used for each algorithm. Due to the stochastic nature of metaheuristic optimization algorithms, performance evaluation through multiple optimization cycles is essential. In this study, each algorithm was executed over multiple independent runs to assess its accuracy and robustness. The statistical results, including mean and standard deviation values, are reported to provide a comprehensive evaluation of algorithmic stability and convergence behavior. The statistical results, including mean and standard deviation values, are reported to provide a comprehensive evaluation of algorithmic stability and convergence behavior. Notably, all algorithms utilized a population size of 100 and a maximum of 50 iterations. Also, the optimization algorithms were executed 20 times, with the best-performing solution being reported in the results.

Table 4. The algorithms parameters.
WOA Population Iteration Σ ω µ
100 50 0.65 0.8 0.03
PSO Population Iteration C1 = C2 ωmin ωmax
100 50 2 0.7 0.95
GWO Population Iteration A β —
100 50 0.7 0.06 —
BES Population Iteration A ψ R
100 50 1.5 6 1.2
DP-BES Population Iteration A ψ R
100 50 1.8 8 1.5

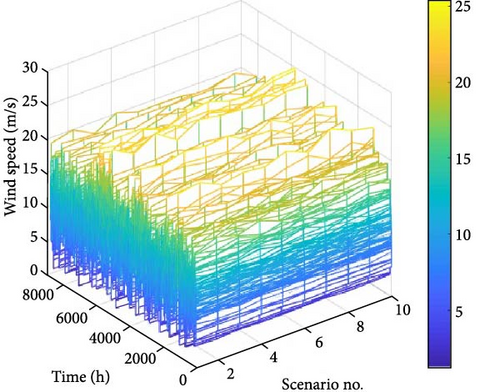
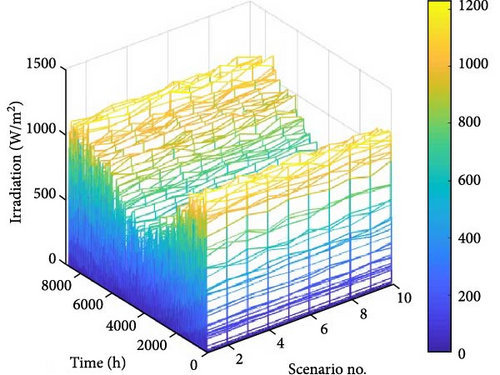
Figure 5 depicts the hourly variations in solar radiation intensity and wind speed throughout a year (8760 h) for 10 scenarios generated using MCS. These scenarios represent the uncertainties associated with renewable energy sources. The average wind speed in the study area is ~14.4 m/s, while the average solar radiation intensity is around 470 w/m2.

Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
(a) Average wind speed. (b) Average solar radiation intensity in the selected scenarios.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
(a) Average wind speed. (b) Average solar radiation intensity in the selected scenarios.

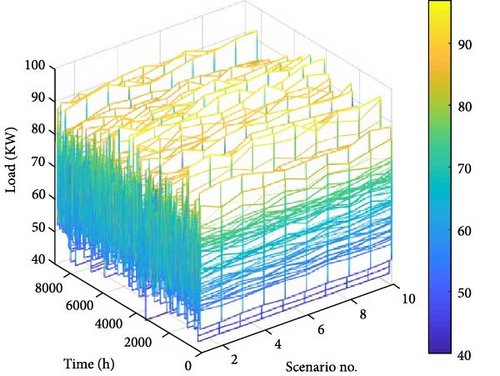
The energy consumption in the considered residential area over a 1-year period for 10 scenarios selected by MCS is shown in Figure 6. The normal PDF is used to generate these scenarios. The average electricity consumption in this area is considered to be 75 kW and its standard deviation is 20.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Average energy consumption.

Initial simulations, assuming no hybrid system, estimated an annual electricity consumption of 42,714 kilowatt-hours from the national grid, resulting in an energy cost of $18,673. To assess the impact of renewable energy integration, three sections were investigated: optimizing a PV (solar) system (Section I), optimizing a wind energy system (Section II), and implementing a hybrid optimal design of solar and wind systems (Section III) for the residential microgrid.

4.4. Section I (PV System)

In the first part of the simulations, only the installation of PV panels in the residential microgrid under study is considered. Figure 7 presents the convergence behavior of the optimization algorithms.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Convergence curve of optimization algorithms for PV system designing.

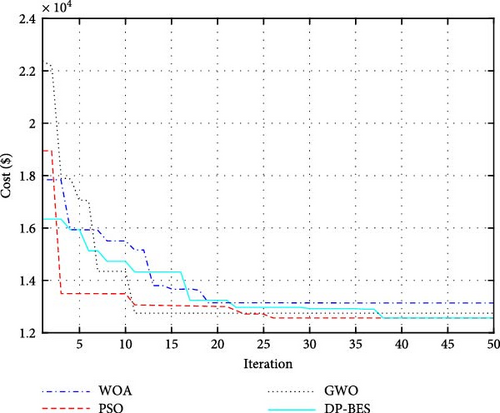
As observed, the DP-BES algorithm achieved the lowest cost ($12,563) after only 38 iterations, demonstrating superior efficiency compared to other algorithms. While PSO algorithm also reached $12,563, it required 26 iterations. The WOA algorithm converged to $13,135 after 19 iterations, and the GWO algorithm achieved $12,748 after 11 iterations. Both PSO and GWO exhibited slower convergence compared to DP-BES. The optimization results are accumulated in Table 5.

Table 5. Optimal design results of the PV system for the residential microgrid.
Algorithm Number of PV panels PV system cost ($) Energy purchased from grid (kWh) Energy purchase cost ($) ENS penalty ($) Total cost ($)
WOA 83 1707 33,541 10,589 839 13,135
PSO 86 1857 31,827 9843 863 12,563
GWO 91 2295 31,088 9670 783 12,748
BES 88 1900 32,500 10,100 850 12,650
DP-BES 86 1857 31,827 9843 863 12,563

The optimization algorithms identified distinct configurations for the PV system. Both PSO and DP-BES recommended installing 87 panels, incurring a cost of $1857. In contrast, WOA and GWO suggested 83 and 91 panels, with costs of $1707 and $2295. Following PV system installation, the annual energy purchased from the main grid varies depending on the chosen configuration. The PSO and DP-BES solution, with 86 panels, is estimated to require 31,827 kWh per year, resulting in an energy cost of $9843. The WOA solution necessitates slightly higher grid purchases (33,541 kWh) and a corresponding annual cost of $10,589. While the GWO solution achieves the lowest annual grid purchase (31,088 kWh), it translates to a slightly higher cost ($9670) due to the increased panel requirement.

4.5. Section II (Wind System)

Building upon the solar simulations, the next phase examined wind-based systems for the microgrid. Identical to the previous scenario, four optimization algorithms (WOA, PSO, GWO, and DP-BES) were employed to identify the optimal design. Figure 8 depicts the convergence behavior of these algorithms. The results showcase the effectiveness of DP-BES, achieving the lowest final objective function value of $14,127. PSO also performed well at $14,938. While WOA and GWO obtained results of $17,318 and $1493, DP-BES demonstrated superior optimization capability in this wind-based scenario.

Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Convergence curve of optimization algorithms for WT system designing.

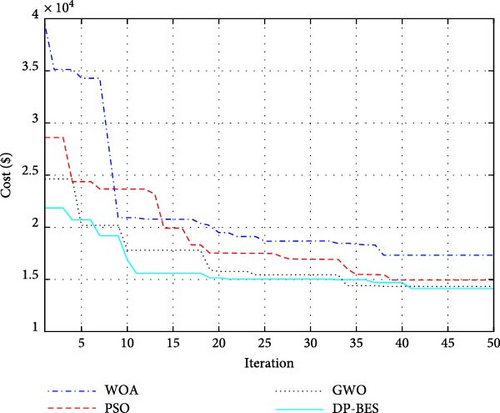
Table 6 summarizes the results obtained from the optimization by metaheuristic algorithms for the optimal design of the wind system for the residential microgrid under study. It is noteworthy that the LPSP in this scenario was also considered to be 5%.

Table 6. Optimal design results of the WT system for the residential microgrid.
Algorithm Number of WT WT system cost ($) Energy purchased from grid (kWh) Energy purchase cost ($) ENS penalty ($) Total cost ($)
WOA 63 1756 35,950 12,601 961 15,318
PSO 70 1938 35,498 12,074 926 14,938
GWO 75 1997 34,190 11,424 909 14,330
BES 76 2000 34,800 11,500 870 14,250
DP-BES 78 2078 34,355 11,201 848 14,127

The optimization algorithms identified varying configurations for the wind system. WOA, PSO, and GWO suggested installing 63, 70, and 75 wind turbines, with corresponding costs of $1756, $1938, and $1997 (including purchase, implementation, and maintenance). The proposed DP-BES algorithm achieved a lower system cost despite recommending a higher number of turbines (78 units at $2078). This is likely due to the optimization process prioritizing factors beyond just initial purchase cost. In terms of energy consumption, the 78-turbine solution from DP-BES requires slightly more energy from the main grid (34,355 kWh) compared to other configurations. The overall cost, including grid purchases, wind system costs, and a potential penalty for unmet energy, is minimized by DP-BES, reaching $14,312. This highlights the importance of considering all cost factors during optimization.

4.6. Section III (Hybrid System)

The final simulations explored the design of a hybrid PV–wind system under uncertainty conditions (LPSP < 5%). Similar to previous scenarios, all four optimization algorithms were employed. Figure 9 depicts their convergence behavior. DP-BES achieved the lowest final objective function value ($11,140), demonstrating its effectiveness in this complex scenario. PSO followed closely at $11,959. While WOA and GWO obtained results of $11,974 and $11,645, DP-BES again outperformed them.

Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
Convergence curve of optimization algorithms for hybrid system designing.

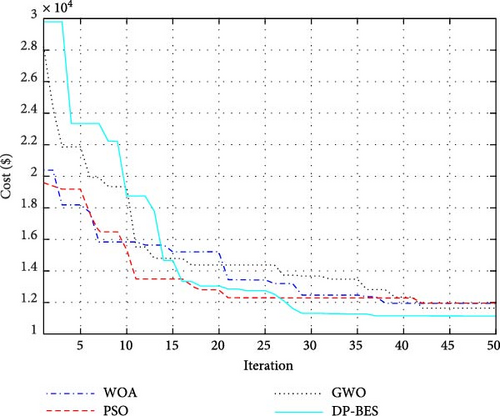
The results obtained from optimization in the third scenario indicate a considerable reduction in the energy supply cost in the residential microgrid compared to the previous two scenarios. Notably, Table 7 shows significant cost savings achieved through the hybrid PV-WT system design.

Table 7. Optimal design results of the hybrid system for the residential microgrid.
Algorithm Number of PV panel Number of WT Hybrid system cost ($) Energy purchased from grid (kWh) Energy purchase cost ($) ENS penalty ($) Total cost ($)
WOA 37 36 1606 27,870 9667 701 11,974
PSO 40 37 1563 28,626 9701 695 11,959
GWO 46 33 1559 27,371 9410 676 11,645
BES 50 30 1500 27,000 9200 670 11,200
DP-BES 53 28 1433 26,601 9056 651 11,140

The hybrid PV–wind system design (section III) achieved significant cost reductions compared to individual solar and wind-only systems (sections I and II). As shown in Table 4, the DP-BES-designed system minimizes grid dependance, requiring only 26,601 kWh annually, at a cost of $9056. This is lower than the grid energy needs and costs identified for the WOA, PSO, and GWO algorithms (27,870, 28,626, and 27,371 kWh with $9667, $9701, and $9410). Overall, the hybrid renewable energy approach substantially reduces energy purchase costs and penalties in the microgrid.

4.7. Results Analysis

To evaluate the accuracy of the proposed DP-BES algorithm compared to other algorithms, the cost values were calculated for three simulation scenarios, and the percentage reductions in costs are presented in Table 8.

Table 8. Percent of cost reductions.
Algorithm

Case 1

(only PV)

Case 2

(only WT)

Case 3

(PV and WT)
WOA 32.10 20.47 38.10
PSO 35.05 22.78 38.18
GWO 34.10 25.92 39.80
BES 34.60 26.33 42.10
DP-BES 35.05 26.97 42.41

The analysis of optimization algorithms’ performance in reducing hybrid system costs demonstrates that the DP-BES algorithm has achieved superior performance across all scenarios. In the hybrid configuration (PV and WT), DP-BES showed significant advantage with 42.41% cost reduction compared to WOA (38.10%), PSO (38.18%), GWO (39.80%), and BES (42.10%) algorithms. This superiority persists in standalone systems as well, where DP-BES achieved better performance with 26.97% cost reduction in wind-only systems (only WT) and 35.05% in PV-only systems (only PV). Notably, in all cases, DP-BES shows ~0.3% to 0.6% improvement in cost reduction over its base version (BES), confirming the effectiveness of the implemented modifications in this algorithm. Furthermore, result comparisons reveal that hybrid systems (Case 3) demonstrate on average about 15% better cost reduction performance compared to standalone systems. Finally, the results obtained from the optimal designs performed by the proposed DP-BES algorithm in the three scenarios are depicted in Figure 10 as a bar chart.

Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
Simulation results analysis.

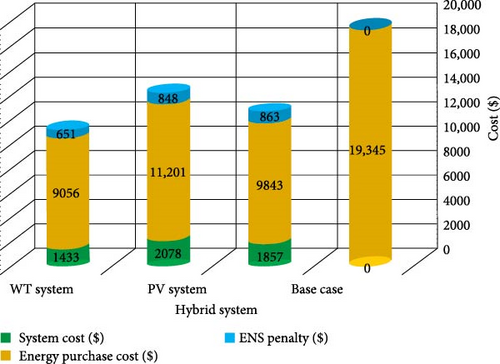
The results obtained from studies and simulations indicate that in the absence of utilizing distributed generation sources in the targeted residential microgrid, the cost of supplying electrical energy will exceed the overall cost in all scenarios. For reducing the costs of supplying electrical energy in this microgrid, it is essential to utilize PV and wind sources. Analysis of the results has shown that the total system cost when using only wind turbines exceeds that of the other two systems. The reason for this may include the high investment and maintenance costs of wind turbines as well as insufficient electricity production due to local wind conditions. The total energy supply cost in the residential microgrid when employing wind turbines has decreased by ~24.78% compared to the conditions where these sources are not utilized. When PV sources are used in the residential microgrid, the energy supply cost has decreased by ~33.41%. The lowest energy supply cost occurs when PV and wind sources simultaneously contribute to supplying part of the required electrical energy. In this case, the energy supply cost has decreased by ~41.35%.

5. Conclusion and Future Work

This paper presents a comprehensive optimization methodology for hybrid PV–wind residential microgrid systems using the novel DP-BES algorithm, demonstrating significant technical and economic improvements over conventional approaches. The research makes several key contributions to the field, beginning with a novel stochastic framework that integrates cost-weighted scenarios with controlled load shedding through a probabilistic model, enabling optimal system design under uncertainty. The developed enhanced optimization algorithm, DP-BES, shows superior convergence and accuracy compared to PSO, WOA, and GWO, achieving remarkable system cost reductions of 41% in hybrid configurations, 33% in PV-only, and 25% in wind-only systems. Furthermore, the study introduces an innovative reliability-cost balance mechanism incorporating LPSP constraints to prevent excessive load shedding while considering ENS penalties, ensuring optimal trade-offs between system reliability and cost-effectiveness. Through comparative analysis across three design scenarios—standalone PV, standalone wind, and hybrid PV-wind—the results consistently demonstrate DP-BES’s superior performance, with the hybrid configuration emerging as the most economically viable solution. These findings not only validate the effectiveness of the proposed methodology but also highlight the substantial economic advantages of renewable integration, particularly through optimized hybrid systems. Looking ahead, future research directions include extending this work to multi-objective optimization considering both economic and environmental factors, along with investigating real-world implementation challenges through case studies. The developed framework establishes a robust foundation for designing cost-effective and reliable HRESs, making a significant contribution to the global transition toward sustainable energy solutions.

Disclosure

All persons who have made substantial contributions to the work reported in the manuscript, but who are not contributors, that is, persons who do not fulfill all the ICMJE authorship criteria, are named in the Acknowledgment and have given me/us their written permission to be named. I/We hereby declare that I/We followed the guidelines provided by ICMJE (https://www.icmje.org/recommendations/browse/roles-and-responsibilities/defining-the-role-of-authors-and-contributors.html) while defining the authors and contributors in the manuscript.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Mehrdad Ahmadi Kamarposhti contributed to conceptualization, methodology/study design, software, validation, formal analysis, investigation, resources, data curation, writing – original draft, writing – review and editing, visualization, supervision, project administration. Hassan Shokouhandeh contributed to conceptualization, methodology/study design, validation, formal analysis, resources, data curation, writing – original draft, writing – review and editing, visualization, project administration. Rachid Outbib contributed to conceptualization, methodology/study design, software, validation, formal analysis, resources, data curation, writing – original draft, writing – review and editing, visualization, supervision, project administration. Ilhami Colak contributed to conceptualization, methodology/study design, software, validation, investigation, resources, data curation, writing – original draft, writing – review and editing, supervision, project administration. El Manaa Barhoumi contributed to conceptualization, methodology/study design, software, validation, investigation, resources, data curation, writing – original draft, writing – review and editing, supervision, project administration.

Funding

No funding was received for this manuscript.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.