International Journal of Energy Research

Volume 2025, Issue 1 3604772

Research Article

Open Access

Metaheuristic Optimization-Based Sliding Mode Control With Modified Perturb and Observe for Controlling MPPT of a PV Interfaced Grid Connected System

Anupama Ganguly,

Anupama Ganguly

orcid.org/0000-0001-6055-5364

Department of Electrical Engineering , National Institute of Technology Mizoram , Aizawl , India

Search for more papers by this author

Pabitra Kumar Biswas,

Pabitra Kumar Biswas

orcid.org/0000-0002-6733-780X

Department of Electrical Engineering , National Institute of Technology Mizoram , Aizawl , India

Search for more papers by this author

Suraj Gupta,

Suraj Gupta

orcid.org/0000-0003-0738-8629

Department of Electrical Engineering , National Institute of Technology Meghalaya , Shillong , 793003 , Meghalaya , India , nitmeghalaya.in

Search for more papers by this author

Furkan Ahmad,

Corresponding Author

Furkan Ahmad

orcid.org/0000-0003-1329-4274

Qatar Environment and Energy Research Institute , Hamad Bin Khalifa University , Qatar Foundation, Doha , Qatar , hbku.edu.qa

Search for more papers by this author

Anupama Ganguly,

Anupama Ganguly

orcid.org/0000-0001-6055-5364

Department of Electrical Engineering , National Institute of Technology Mizoram , Aizawl , India

Search for more papers by this author

Pabitra Kumar Biswas,

Pabitra Kumar Biswas

orcid.org/0000-0002-6733-780X

Department of Electrical Engineering , National Institute of Technology Mizoram , Aizawl , India

Search for more papers by this author

Suraj Gupta,

Suraj Gupta

orcid.org/0000-0003-0738-8629

Department of Electrical Engineering , National Institute of Technology Meghalaya , Shillong , 793003 , Meghalaya , India , nitmeghalaya.in

Search for more papers by this author

Furkan Ahmad,

Corresponding Author

Furkan Ahmad

orcid.org/0000-0003-1329-4274

Qatar Environment and Energy Research Institute , Hamad Bin Khalifa University , Qatar Foundation, Doha , Qatar , hbku.edu.qa

Search for more papers by this author

First published: 18 May 2025

https://doi.org/10.1155/er/3604772

Academic Editor: Muhammad Athar

Share a link

Email
Wechat
Bluesky

Abstract

Energy is always needed more and more as civilization advances. Since the supply of traditional fuels is gradually depleting, renewable energy sources are essential for meeting energy needs. The goal of the research is to maximize the electricity that can be produced from renewable resources. Solar energy performed better than any resource regarding efficiency, cleanliness, and pollution-free nature. However, the primary drawback of the resource is its erratic nature. The system must integrate the maximum power point (MPP) tracking (MPPT) method to overcome intermittency and produce continuous optimal power. The novelty of this article is the development of a sliding mode MPPT controller for photovoltaic (PV) systems working in sunny and shaded. Also, this article introduces the meta-heuristic algorithm mountain gazelle optimization (MGO), which is incorporated to optimize the parameters of the sliding mode controller (SMC) to ensure the solar PV (SPV) MPP extraction. The stability of the mentioned control topology is assessed in terms of error parameters. The modified perturb and observe (MPb&O) method is incorporated with MGO, called (MGO-MPb&O) for performing a better tracking ability and to overcome the inability of conventional Pb&O tracking during the shaded conditions. The suggested approach looks for every maximum point across a lengthy number of cycles to find the global maximum point after introducing (MGO-MPb&O), and the results of the MATLAB/Simulink show that the algorithm performs well under the arbitrary changes of the physical parameters of the proposed system and ambient scenario. Also, the proposed hybrid (MGO-MPb&O) is compared with two other hybrid control topologies that are (PSO-MPb&O) and (cuckoo search algorithm [CSA]-MPb&O) in terms of maximum power extracted, efficiency, and convergence time of the objective function. Results depict that the proposed algorithm outperforms in every aspect and also justify the robustness of SMC. The proposed algorithm was also tested in various shading fashion (SF) in partial shading conditions for analyzing the transient response. These two performance figures for various transition instances demonstrate that the suggested MPPT algorithm can determine the global MPP for the new shading pattern (SP) when it shifts from a uniform state to a partially shaded condition at 4s (middle of the x-axis).

1. Introduction

Today’s world is becoming more aware of the rapidly diminishing availability of conventional resources like coal and petroleum products, which makes renewable energy resources more critical. Because they are so readily available, photovoltaic (PV) systems have become increasingly popular in recent years. A PV system can be either freestanding or grid-linked, depending on the needs and amount of power it generates. The PV system connected to the grid is one of the primary methods for converting solar energy into electricity. Many articles have addressed PV’s maximum power point (MPP) projection. PV array characteristic functions, P–V and I–V, are usually nonlinear when the generated power is unknown. On the weather, sun radiation, and temperature. As a result, the PV system’s controller system adapts the maximum point to various conditions. Moreover, the DC/DC converters used in PV arrays must match the impedance to obtain the optimum quantity of power. Based on the understanding that the DC and AC impedance of the PV module occur in the MPP, several studies propose an incremental conductance approach [1]. Therefore, the MPP is attainable by infusing the ampere rating and calculating the impedance using the two techniques of dV/dI and V/I. The sources of errors in this technique could be ambient noise and circuit noise. The perturb and observe (Pb&O) method is among this area’s most widely used techniques [2, 3]. The fundamental concept is that dP/dV in the PV system’s P–V characteristic function equals zero at the maximum possible power point. It is stated that scanning the PV modules’ characteristic curve and using the data to apply the traditional Pb&O method [4]. In [5], the authors wish to instigate an elaborative review-based study on different schemes of MPP tracking (MPPT), classified as conventional hybridized and newly launched, considering input and output parametric alterations. In [6], it is reported that after modifying the boost chopper’s elemental values, the MPPT algorithms are employed in the PV generation system. Meta-heuristic approaches of MPPT strategies achieved acceptance among the researchers because of their precision and being independent of system dynamics [7–9]. Many research works suggested several MPPT algorithms that incorporated particle swarm optimization [10, 11], in addition to cuckoo search algorithm (CSA) [12], gray wolf optimization (GWO) [13], ant colony optimization (ACO) [14], artificial bee colony (ABC) [15], slap swarm optimization (SSO) [16], grasshopper optimization [17], teaching–learning-based algorithm (TLBA) [18], and flying squirrel search optimization (FSSO) [19]. To reach the MPP, attain steady-state error, and regulate MPPT, sliding mode control, or SMC is proposed [20–22]. Moreover, SMC is designed to provide improved functionality and seamless communication [23]. Sliding mode Extremum-seeking control is one of the sliding mode control methods introduced to deliver more effective performance [24]. Beltran,Benbouzid, and Ahmed-Ali [25] focused on the DFIG-based generator equipped with SMC with an amalgamation of conventional Pb&O algorithms to monitor the MPP. Weng and Hsu [26] furnished that the purpose of the sliding mode torque controller is to track the ideal torque for the DFIG-based generator to achieve MPPT. For MPPT, the digital adaptive hysteresis-current control approach is employed in [27]. Gosumbonggot and Fujita [28] used shade detection and the trend of slopes from each segment of the P–V curve; a global MPPT approach is adopted, it is suggested to use evolutionary algorithms to acquire the MPP proposed in [29, 30]. Haq and Khan [31] used an adaptive neural network-based adaptive global sliding mode MPPT controller for a standalone PV system. The requirements, technical difficulties, interconnections, topologies of inverter control, and potential uses of PV energy systems are described in [32]. In grid-connected PV systems, single-stage and multistage power conversion processes are frequently employed [33]. Saleem and Ali [34] proposed a new compensator called adaptive fractional order PID (A-FOPID), which uses self-adjusting fractional orders to maximize electricity from a standalone PV system in response to changing environmental circumstances. A feed-forward neural network is utilized to generate the reference voltage. Maintaining the unity power factor in the grid and harmonizing voltage and current with it are essential when connecting solar to the grid system [35]. Anjum and Khan [36] suggested an MPPT control in which feed-forward neural networks (FFNNs) generate the desired reference, which is tracked using a resilient nonlinear arbitrary order sliding mode-based control. The suggested control rule uses a few system states, which are approximated using a well-known nonlinear system flatness property and a high gain differentiator. Neuro-adaptive arbitrary order sliding mode control (NAAOSMC) is the name given to this artificial control technique. In this recent article, a newly introduced meta-heuristic algorithm, mountain gazelle optimization (MGO), is used to acquire and follow the true MPP for the PV system. In addition, modified Pb&O (MPb&O) are combined to maintain an updated tracking of the P–V curve of the solar PV (SPV) system and attain superiority in terms of accuracy as relatable with the earlier mentioned methodologies. The prominent contributions of the manuscript are briefed as pursues.

•
Formulation of sliding mode controller (SMC) to extract optimum power from the PV generation for the proposed structure of the PV system.
•
Incorporating the proposed hybrid (MGO-MPb&O) for achieving true MPP with minimal settling time, less % of overshoot, and superior accuracy.
•
The meta-heuristic optimization algorithm is evaluated based on error values, and transient responses are analyzed under various shading fashion (SF) in partial shading conditions.
•
The suggested hybridized optimization algorithm is compared with two other hybrid algorithms based on maximum power extracted, efficiency, and objective function convergence time.
•
Analytical assessment of the optimum power point (OPP) stability is based on parametric deviation of the PV system and thermal instability.

The entire manuscript is organized in the following manner: Section 2 depicts system modeling, Section 3 focuses on the formulation of an SMC, Section 4 discusses revolutionary hybrid algorithms to deal with unpredictability, and detailed simulation outcomes and explanations are furnished in Section 5. Lastly, some conclusions are drawn in Section 6.

2. System Modeling

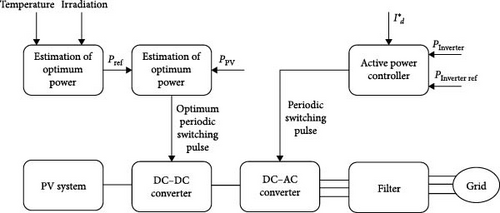
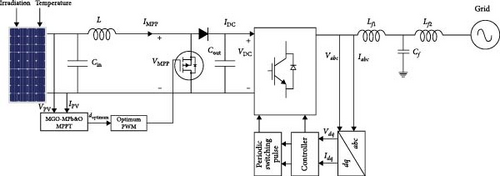
Figure 1a depicts the suggested workflow of the PV system, which consists of a PV cell coupled to a DC–DC converter, and Figure 1b shows the single-line diagram of the suggested layout. The output is connected to the inverter via a DC link. The PV cell supports the local load. The main grid is also utilized when PV low-power generation is used. The proposed structure consists of the following two essential parts:

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

(a) Suggested workflow diagram and (b) single line schematic circuit diagram of the proposed workflow diagram.

a.
Controller of the PV power that endeavors to extract maximum power reference from PV system concerning changing solar irradiation and ambient temperature. In this work, the DC–DC converter is controlled by PWM signals, and as a result, the PV power is adjusted to the specified value. The DC–DC converter is formulated according to the conventional formulae. Table 1 shows the parametric representation of the elements of the DC–DC converter.
b.
The controller for exchanging power between the main grid and distributed generation (DG). Inverter control pulses and PWM are used in this study, with the shared power determined by the DC/AC converter reference value.

Table 1. Parametric representation of DC–DC converter.

Sl. no.	Parameters	Values
1.	Switching frequency	25 kHz
2.	Capacitance (input) (C_in)	158 μF
3.	Capacitance (output) (C_out)	20 μF
4.	Inductance	31.8 mH

Since the PV system is made up of a diode and a parallel-connected current source, where R_s stands for metal junction loss, it is a nonlinear source. Figure 2 shows the system model of the PV generation. Electron flow causes the formation of PV current, which has a magnitude that is precisely proportional to the amount of irradiance (G), accompanied by minimal changes because of the temperature variation in surroundings and the incorporation of the Shockley Equation (1) [37].

()

The current of the PV system can be handled by Equation (2), while the PV panel’s output power is calculated using Equation (3).

()

The rated capacity of the PV panels determines the solar energy output accompanied by the derating factor of PV, a scaling factor that allows the influence of some losses, which in turn shows in degradation of the output of the PV generation as compared to the original value. SPVs can produce power that can be seen as Equation (4) [37].

()

P_s = computed capacity of the SPV array (kW), D_s = derating factor of SPV array (%), I_a = current SPV array incident, involving SPV irradiation (kW/m²), I_aSPV = incident SPV radiation under the parameters of the usual test (1kW/m²), β_a = power thermal coefficient (%), T_a = SPV array’s temperature (°C), T_SPV = temperature of the SPV cell under typical test conditions (25°C), and Ignoring β_a the power delivered by the grid interfaced PV system is conveyed by Equation (5).

()

For analyzing the convergence of the true MPP of a PV system, the corresponding sets of equations are formulated in Equation (6).

()

3. Formulation of SMC

One type of control with nonlinearity that is especially useful for system regulation is the sliding mode control using flexible structures. The core principles of the sliding mode control design are the feedback path at the output and the capability of switching control in the presence of a high-frequency component that, in perfect conditions, is limitless. This superior law of control directs the system orbits to a region of the state space that is often correlated with a sliding area or manifold. The prime benefits of a system in association with SMC attributes are as pursued [38]:

•
Intolerance for exogenous disturbances and unpatterned dynamics.
•
Straightforward and adaptable controller architecture.
•
The capacity to add an action error to the sliding manifolds and eliminate steady-state defects from the design of the SMC.
•
Using standard power converters, order elimination, disruption exclusion, distinguishing design strategies, sensitivity to parameter alterations, and ease of implementation are all advantages of SMC.

3.1. Architecture and Formulation of SMC

The sliding mode control topology consists of two different parts. The first part is responsible for designing the sliding surface that complies with guidelines for design. The later entails look after for selecting a law of control due to which the switching area/manifold will be imploring to the state of the system.

Considering a time-variant nonlinear switching system, which can be definable by the mentioned pair of Equations (7) and (8) [39].

()

where x is the variable of state vector lies within an n-dimensional region Rⁿ.f and g, the smooth vector field belongs to the same region and u is the interrupted control law. High-frequency oscillations known as “chattering” in system outputs caused by dynamics from actuators and sensors that are not taken into account in system modeling frequently aggravate the application of sliding mode control. Chattering was the primary barrier to the application of sliding mode control theory in its early stages of development. Fast dynamics, which were overlooked in the ideal model, may be the source of the chattering. Servomechanism, sensor, and data processor models typically ignore these “unmodeled” dynamics with tiny time constants. The usage of digital controllers with restricted sample rates, which results in “discretization chatter,” is the second cause of chattering [40].

Using asymptotic observers is an effective way to suppress chattering is to create the optimal sliding mode in the observer-included auxiliary loop.

Restriction of errors is the primary motto of the defined control law within a definable time duration; refer to Equation (9).

()

3.1.1. Designing the Sliding Surface

The initial step includes the definition of a certain system structure with a scalar function. Considering the trailing error and a number of the derivatives of it (e(1), e(2) … ……e(i)), defined as σ(i) in Equation (10).

()

A linear combination of the types listed in Equation (11) is the most popular option for the sliding manifold. Where, const_i is constant.

()

3.1.2. Formulation of the Law of Control

The second stage aims to find an accurate control law that will project system orbits onto the sliding manifolds. Numerous strategies are built upon the topology of sliding mode control.

•
Controlling the first-order conventional sliding mode control topology.
•
Application of high-order and low-order sliding mode control.

The authors of the manuscript keep their focus on the traditional first order as represented by Equation (12).

()

where U is a positive scalar constant, which is large enough, and the control input variable u will vary within the range of ±(U × u) in a stable range of operation.

3.2. Strategy of PQ Controlling

Three forms of DGs exist: consisting of high frequency like microturbines, direct energy conversion sources like PVs, and varying frequency sources like wind energy conversion systems. DG units must be used with power electronic components to enable safe and reliable power system operation to link them to the main grid with sustainable consummation [41]. The controlling mode of an inverter has a significant impact on the inverter-based DGs’ performance. The DG can operate efficiently if the power converter controller is appropriately designed. As depicted in Figure 1a,b, the control mode of the inverter has a prominent impact on the performance of inverter-oriented DGs. It is evident that, for inverter-oriented DG to function in grid-associated mode, PQ state controlling is necessary for the control of the inverter. Since these parameters are predominant in the main power system, the PQ mode uses the main grid to manage the voltage and frequency.

On the other hand, DG must regulate the frequency and voltage in an islanded mode of operation. Systems can benefit from the PQ control strategy since it can distribute networks with constant power [42]. The PV system’s PQ controller regulates the amplitude and phase angle of the inverter current to supply a predetermined amount of kW and kVAR to the main grid. The measured values of KW and KVAR are Equations (13)–(18) [43].

()

4. Consideration of Unpredictability and Proper Algorithms

On the solar system’s I–V curves, the MPP is the point at which a PV cell operates as efficiently as possible and produces its optimum output power. Since, due to the presence of intermittent in solar power generation, the proposed sliding mode control will not be enough for drawing and sustaining optimum power. For the PV system and its power electronics to locate and maintain the operational point at the MPP, the evolutionary meta-heuristic algorithms must be incorporated by contemplating the unpredictability. The MPPT controller, which independently controls the PV array’s voltage and current, accomplishes this. This manuscript introduces the algorithm, which is the amalgamation of the MPb&O and a newly introduced meta-heuristic optimization algorithm MGO for a precise trailing of the original MPP.

4.1. MPb&O

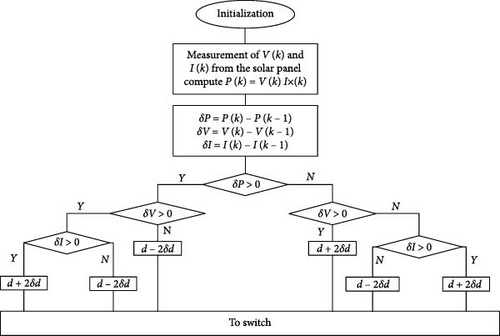
Among the different MPPT approaches, the Pb&O is a common technique. The voltage of the PV module can be measured using an implementation that relies on a voltage sensor [44]. However, this algorithm works well under uniform input conditions. When there is a variation in solar irradiation and ambient temperature, the conventional Pb&O algorithm cannot track the original MPP and creates multiple peaks around the same point. This limitation can be addressed and resolved using the MPb&O algorithm [45]. The voltage and current are sensed at the beginning, and power is computed, according to Figure 3. The MPb&O shows the advancement in the system response by introducing a third parameter, the deviation in current, in the algorithm’s flowchart. During constant irradiation conditions, the MPb&O works precisely like the conventional Pb&O. However, when the irradiation level changes rapidly, the modified version conflicts with the traditional one. When poor tracking is observed, the step size must double to intensify the tracking speed. By incorporating the procedure, the MPPT control may extricate whether the power deviation is due to the irradiation changes or disturbance in the reference potential. As a result of which, disparity from the true MPP can be abominated.

4.2. The MGO Technique

The MGO meta-heuristic optimization technique is grounded in the social interactions of untamed mountain gazelles. The gazelles are classified into four main categories such as male horde bachelor (MHB), maternity horde (MH), companionless territorial male horde (CTMH), and migration for searching food (MSF). During the tuning of the optimization process, any gazelle (Gaz_i) may be included as a part of these three hordes, and the improved solution may be obtained from any one of these three hordes. The MHB is the poorest solution among the entire optimizations. The best solution obtained is imitated to the upcoming repetitive iteration, and those solutions containing the least cost will be omitted from the population.

The MGO includes the input variables like the size of the population (NG), the optimum no of repetitive iterations (OptRIs), and the position of the gazelle. At the initial stage, an arbitrary population is developed (Gaz_i) (i = 1, 2 …. N). For each sample in CTMH, the region is calculated by Equation (19). The mature male gazelle (MMG) offers the best solution.

()

where MMG_pos is the position of MMG that is the globally sound best possible solution, random₁ and random₂ are arbitrarily induced integers. MHB is the coefficient of the herd vector of adolescent male gazelle and may get calculated by applying Equation (20) [45]. F and Coefficient_r are elucidated by Equation (21) and Equation (22), respectively [45].

()

where G_random be regarded as the arbitrarily chosen solutions related to adolescent males for the interval “random.” M_prandom shows randomly choose searching agents. The cumulative number of gazelles to be considered by NG.

()

where Num₁ depicts random numbers from the standard distribution, OptRI represents the maximum no of iterations, and iter shows the present recursive iteration.

()

The range of random₄and random₅ lie between 0 and 1. Num₂, Num₃ and Num₄ are the arbitrarily selected numbers. Y is computed with the help of Equation (23) [45].

()

MH is computed by Equation (24)

()

where MHB is a graphic illustrating the influence of young males, MMG_p is the most superior global solution in the present iteration, and X_random is the vector location of the gazelle chosen at random. MHB is estimated by Equation (25) [45].

()

where X (t) represents the gazelle’s position vector for the present iteration. ri_i for (i = 1–4) are the integers chosen arbitrarily, and Coefficient_r is the arbitrarily chosen vector of coefficient.

()

where random₅ is the randomly chosen number ranging between 0 and 1. MSF is computed by Equation (27) [45]. Where random₇ is the arbitrarily selected number.

()

To create fresh generations of gazelles CTMH. MHB, MH, and MSF processes are applied to all gazelles. After computing the fitness of the mechanisms, the habitat is expanded to include gazelles and the entire population is organized in ascending order. The greatest gazelles are updated and saved, with the NG number of the best gazelles across all populations [45]. This algorithm performs well in the situation where there is a slow change or no deviation in the solar irradiation. But when there exist various peaks of optimum power, the algorithm may not be able to track the original MPP. Also, the initial population is selected in such a way that it may be capable of following the local optima in place of the global optima. Thus, the amalgamation of MGO with MPb&O is suggested in continuation to accomplish the benefits of both methods to achieve the original MPP. The advantages of MGO are narrated below:

The MGO algorithm optimizes each search factor and iteration using four distinct processes. Every mechanism in use has unique qualities, and every tool available today enhances MGO’s performance in every intensification and diversity component.

In order to prevent slipping into the ideal local trap, the exploration and exploitation phases run concurrently throughout all optimization stages.

Lastly, the MGO algorithm’s population update procedure guarantees that search agents with better-quality solutions are taken into account and, in the end, that all search agents are collected in a single optimal.

4.3. Formulation of MGO-MPb&O Algorithm

The shortcomings of the previously mentioned two methods can be overcome by the amalgamation of these algorithms (MGO-MPb&O). In this algorithm, different DC/DC converter duty cycles make up the initial population members (M), which might impact the voltage and power of the best MPP accessible. MGO searches these different duty cycle values to obtain the algorithm’s convergence to the optimal MPP and duty cycle. More accurate MPP is produced when the MPb&O method is incorporated with the chosen duty cycle from this section. It is anticipated that the suggested algorithm will be able to reach the ideal MPP efficiently. When changes in power and voltage exceed the permitted range, the initial population gets updated by calculating the cost function for each gazelle from the random population to identify the best solution. Since MPP is frequently altered due to variations in the effective parameters of PV power, the suggested approach needs to respond quickly to either a rapid or gradual change in the parameters. The elaborative flow chart of the proposed (MGO-MPb&O) is furnished in Figure 4. The detailing of the algorithm is described as follows: as mentioned earlier, duty cycles of the DC–DC converter build the initial populations accompanied by assigning the parameters of the algorithm such as OptRI, size of the storage space (K), and the no. of gazelles. After that, the PV system’s voltage and current are sensed to compute the PV power. Then, applying a signed variable (Flag gazelle), the interrelated gazelle is assigned, and the new solution is created using the features described by Equations (19)–(27). Now, X fresh solutions are generated by repeating the entire process from the beginning. After that, the fresh solutions and the initial populations are kept together as (X + M) solutions in the variable and arranged in ascending order. As an outcome, the best K solutions are stored in space. The variable to keep the number of iterations (Flag RI) also gets updated in the unit step. The entire process will be repeated until the OptRI arrives, or there will be no or very negligible fluctuation in PV power within the mentioned number of repetitive iterations. If this condition is satisfied, the algorithm can offer the optimal duty cycle and follow the accurate MPP. The working ambiance of the PV system continuously varies due to the ever-changing weather scenario or load scenario, which, in turn, causes the global MPP to deviate. To overcome the issue, the MPb&O algorithm must be amalgamated to keep track of true MPP. The initialization starts with the condition derived from MGO. Here, authors of the manuscript employ Equation (28) to detect the abrupt change in the weather conditions due to shading. If Equation (28) satisfies, the algorithm will initialize MPb&O. Thus, it assures optimal duty cycle and follows accurate global MPP under erratic weather conditions. The authors of this research employ the proposed algorithm to accelerate the MPb&O by the accurate parameters of the SMC optimized by MGO, by incorporating a fitness function to define the control rule and the sliding surface.

()

Considering the functions of altered potential and current, authors outline a sliding surface,

()

The first-order sliding mode control is interpreted by Equation (30).

()

To provide an accurate duty ratio (D; refer to Equation (31)), the determined law of control is adapted by the SMC,

()

Using MGO all the five gains of the SMC (k_a, k_b, k_c, k_d and k_e) are tuned in this manuscript. There are so many matrices as objective or fitness functions like integral absolute error (IAE), integral time-weighted absolute error (ITAE), and integral square error (ISE) to analyze the stability of any optimized control topology. The authors of the study consider the performance metrics ITAE, IAE, and ISE as the objective functions for error minimization. Among them, ITAE is more prominent due to some benefits.

•
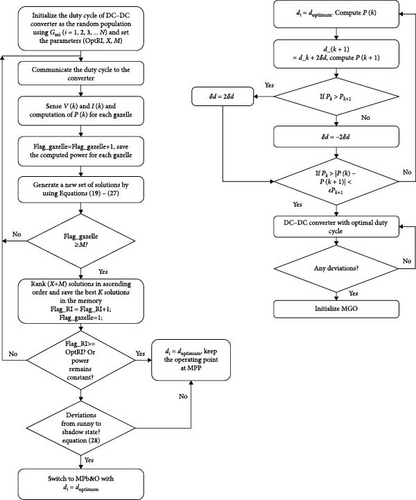
ITAE is capable of getting the setting of the controller during load and set point alteration.
•
When searching for controller parameters, particular alterations of load and/or set point can be obtained.
•
The ITAE technique penalizes larger deviations over a longer period of time and emphasizes minimizing the error during the initial transitory reaction.
•
Applications that require the fastest response time and settling period ought to apply this metric.

The numerical computation of ITAE, IAE, and ISE can be done by Equations (32)–(34), respectively.

()

5. Simulation and Discussion

To evaluate and simulate the MPPT performance, an example PV system that includes control architecture, PWM, and different components is created in MATLAB. Table 2 shows the parametric values of the PV array.

Table 2. Parametric values of the PV array.

Sl. no.	Parameters	Specification
1.	Optimum power output	214.92 watt
2.	Thevenin’s equivalent voltage (V_oc/V_TH)	48.3 volts
3.	Norton’s equivalent current (I_N/I_SC)	8.2 amp
4.	Potential at maximum point (V_MPP)	39.8 volts
5.	Maximum point current (I_MPP)	7.8 A
6.	Cell/module N_cell/mod)	72

The framework of the simulation can be described as follows:

Framework 1: Simulation of the system under traditional Pb&O MPPT algorithm under sunny and shaded conditions.

Framework 2: Simulation of the system under the proposed MGO-MPb&O MPPT algorithm under the same scenario.

Framework 3: Analysis of the transient response of the proposed MGO-MPb&O MPPT algorithm under various SF.

5.1. Framework 1: Simulation of the System Under Traditional Pb&O Algorithm Under Sunny and Shaded Conditions

In the framework, the PV generation system configuration, which includes a PV array, step-up chopper, and controller for managing the active power, PWM signals, and load, is built in the MATLAB/Simulink environment. The implementation of the internal circuitry of the DC–DC boost chopper is depicted in Figure 5, where MOSFET, whose pulse is provided by the MPPT, is responsible for controlling the potential level. The driving signal for Pb&O is induced by the measurement of the current and voltage of the PV panel. In fact, voltage and current are the MPPT controller’s inputs, and a DC signal that produces a PWM pulse is its output. Switching of MOSFET is dependent on this pulse for the controlling of the current and voltage. In Figure 6, a block representation of the traditional Pb&O method is furnished.

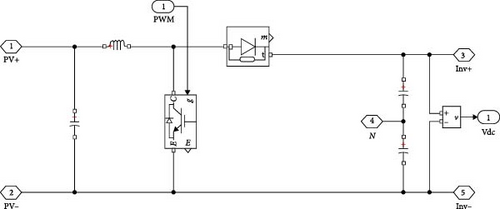
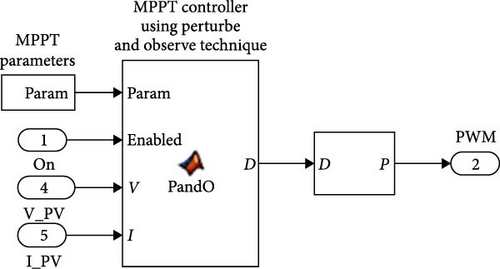
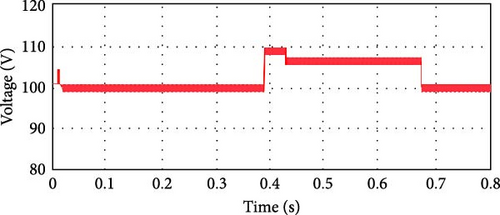
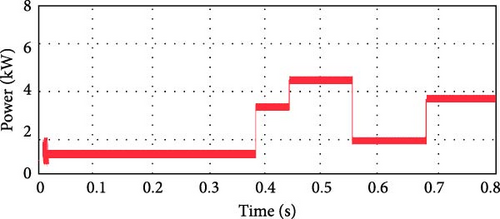
According to Figure 6, the controller receives the inputs of voltage, current, and MPPT parameters, and the PV power is calculated by the product of voltage and current. The incorporation of the delay block is responsible for measuring the deviation in power by (p(k) − p(k − 1)) where it is supposed to be maintained p(k − 1). The same logic is applicable for (v(k) − v(k − 1)). The PV array, where the point of regulating the PV cell’s diodes is constant, is structured using the MATLAB Sim-scape library. When the Pb&O control system is used to apply the attribute of deviations of power and voltage, the characteristics of the power and voltage obtained from the PV cell using the conventional Pb&O technique are shown in Figure 7. The deliberate system is designed to deliver 100 volts and 4 kW. Initially, power and voltage are adjusted in a raising approach and subsequently in a reducing approach to offer shade and sunny situations. According to Figure 7, in 0.39 s, the deviations in the power and the voltage are in the boost mode (from shaded to sunny state). During this tenure, the control arrangement of traditional Pb&O perceives the MPP that is accessed till the time. As a result, in this duration, the duty ratio of the DC–DC chopper gets reduced to enhance the voltage. In fact, when the Pb&O fails to identify the original MPP by boosting the voltage and degrading the power, it results in distance from the accurate MPP. In time 0.55 s, power is declining, and voltage fluctuation is growing, which in turn results in the position of the Pb&O controller remaining at the right half plane (RHP) of the MPP and attempting to degrade the voltage to retain to the MPP.

5.2. Framework 2: Simulation of the System Under the Proposed MGO-MPb&O Algorithm Under the Same Scenario

As stated earlier, the conventional Pb&O method is debased in the state switching from the shaded to sunny and results in loss of MPP. This also leads to abatement of power and long recovery time of MPP. To indemnify this problem, the proposed MGO-MPb&O algorithm is incorporated. In the methodology, the disturbance in voltage is responsible for achieving the deserved duty cycle, and then incorporating MGO, the MPP is reached by searching through all duty cycles. The parameters of MGO are showcased in Table 3.

Table 3. Parametric representation of mount gazelle optimization (MGO).

MGO parameters	Highest number of iterations	Cumulative no. of gazelles
MGO parameters	100	30

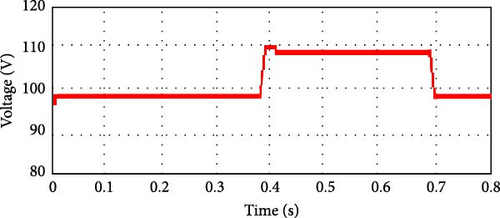
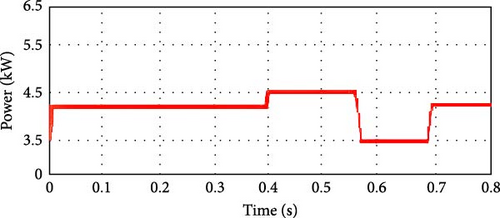
Table 4 shows theP–V data during the shaded state. Table 5 represents the variation of power and voltage of the SPV system during the mentioned state. Obviously, when switching from a shaded to a sunny state, the power is boosted up at various levels of potential, and thus the MPP is achieved at 99.98 V. The response of varying power and voltage by MGO-MPb&O is described in Figure 8. Comparing this one with Figure 7, the suggested algorithm’s fascination with less fluctuating convergence to the MPP, where the Pb&O method’s sharper responsiveness to voltage and power variation is more. It is also evident from the output that, incorporating MGO-MPb&O, the power inconstancy is mitigated as compared to conventional Pb&O which in turn results in superior tracking of accurate MPP. In Table 6 proposed hybrid MGO-MPb&O is compared to other two hybrid MPPT methods like PSO-MPb&O and CSA-MPb&O, in terms of acquired MPP, power/voltage, and duration of achieving the MPP.

Table 4. Detailing of the P–V data during the shading condition.

kW	Volts	kW	Volts	kW	Volts	kW	Volts
1.321	102.5	6.410	102.7	5.567	103.6	6.351	103.3
1.448	105.7	5.097	99.0	4.862	101.3	5.214	101.1
4.342	105.7	4.876	101.7	6.345	104.3	6.513	102.4
2.324	100.3	6.543	101.2	3.765	101.1	5.427	99.8
4.897	105.9	4.167	99.6	4.891	103.3	7.011	101.3
2.345	101.7	6.695	101.9	6.015	102.8	6.324	100.01
3.345	104.6	5.824	99.4	3.132	99.9	7.214	102.3
5.364	105.4	6.125	101.9	5.456	103.5	7.531	102.8
2.545	101.2	7.315	101.4	4.178	99.98	6.375	99.7
5.865	105.1	5.945	99.5	6.088	102.5	6.696	99.6
2.739	101.9	6.129	101.1	4.761	100.1	7.100	99.9
3.142	104.1	6.010	100.09	3.961	99.2	7.343	92.0

Table 5. P–V data during shaded to sunny state.

kW	Volts	kW	Volts	kW	Volts	kW	Volts
5.521	102.4	7.465	101.4	6.765	101.8	4.895	103.1
1.142	108.5	6.765	101.8	6.352	101.6	5.796	101.1
6.898	103.5	6.856	99.5	7.320	103.9	5.796	100.0
6.675	101.8	6.564	100.0	6.876	101.6	6.034	100.0
6.354	107.9	4.076	106.4	6.087	102.3	7.135	100.0
6.675	101.7	6.233	101.2	6.934	102.1	6.013	101.3
3.243	101.8	5.768	101.1	7.232	102.4	6.244	101.3
6.898	102.6	5.768	100.0	6.896	103.9	5.465	101.0
6.675	101.3	6.434	104.5	6.976	101.3	6.689	101.7
7.122	101.0	7.343	101.4	7.027	101.5	7.345	101.6
3.654	106.8	6.768	101.9	7.656	102.2	6.675	101.9

Table 6. Comparative performance analysis of proposed hybrid MGO-MPb&O algorithm with PSO-MPb&O and CSA-MPb&O.

Sl. no.	MPPT methods	Power (kW)	Voltage (V)	Time for acquiring MPP (s)
1.	PSO-MPb&O	6.35	98.0	0.8
2.	CSA-MPb&O	6.97	99.8	0.7
3.	MGO-MPb&O	7.53	99.98	0.65

In Figure 9, the comparative analysis of the proposed algorithm with the aforementioned two algorithms is done on the basis of achieving the MPP (power/voltage) w.r.t time.

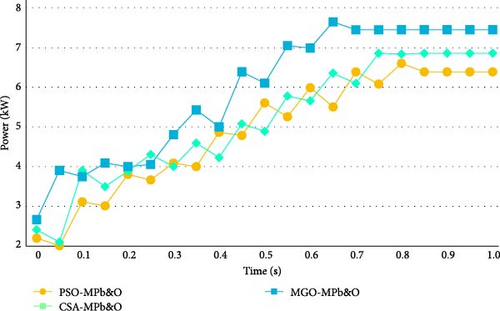
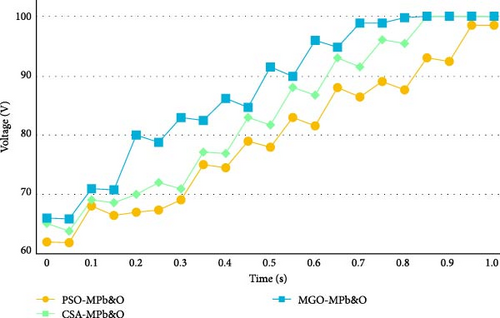
It is evident from the graphical representation that the proposed MGO-MPb&O acquires the global MPP is accomplished by the algorithm. Table 7 shows a comparative study between MGO-MPb&O, PSO-MPb&O, and CSA-MPb&O in terms of minimal settling time, less % overshoot, and a high degree of accuracy.

Table 7. Comparative study between MGO-MPb&O, PSO-MPb&O, and CSA-MPb&O.

Sl. no.	MPPT methods	Settling time (ms)	% Overshoot	Accuracy (%)	Rise time (ms)
1.	PSO-MPb&O	19.65	1.38	98	5
2.	CSA-MPb&O	19.43	1.02	99.8	4.98
3.	MGO-MPb&O	18.65	0.045	99.98	4.97

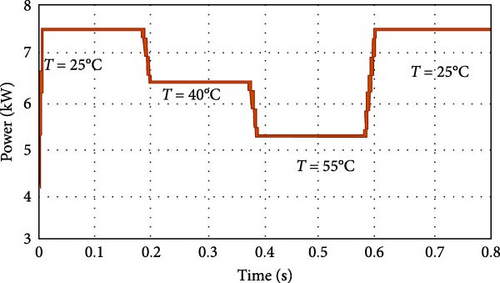
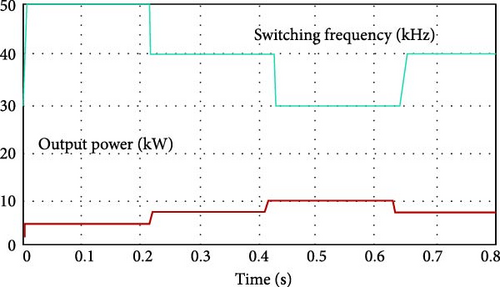
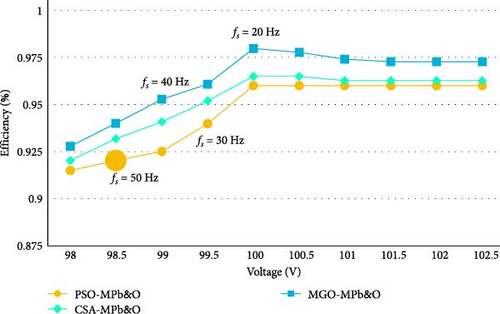
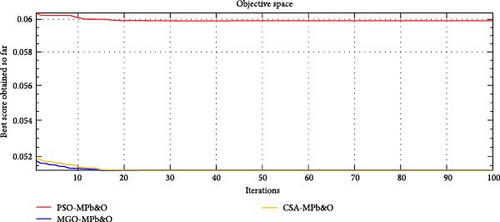
From Table 7, it is evidenced that the suggested hybrid algorithm (MGO-MPb&O) possesses the smallest settling time accompanied by the least % overshot and best accuracy compared to PSO-MPb&O and CSA-MPb&O. In Figure 10, the impact of thermal variation to achieve the accurate MPP is shown. Initially, the experiment starts with temperature 25⁰C; then, it increases up to 55⁰C and again comes back to the initial position. During every variation of temperature, the proposed MGO-MPb&O successfully and accurately tracks the true MPP, as furnished in the graph. The inverse proportional relation between the impact of switching frequency and the achievement of MPP of the PV system is studied in Figure 11. The suggested method’s possible output power decreases with increasing switching frequency because of increased switch loss. A comparative analysis of the efficacy of different hybrid MPPT methodologies (PSO-MPb&O) and (CSA-MPb&O) with the proposed one (MGO-MPb&O) is studied in Figure 12 due to the ever-changing switching frequency. It is evident that the efficacy of the suggested approach is superior to the other mentioned approaches w.r.t greater switching frequency. The convergence curve of the fitness function of MGO-MPb&O is showcased in Figure 13. It is observable that the proposed methodology converges in a lesser number of iterations as compared to other convetional methodologies mentioned in Table 7. Table 8 describes the optimal values of the controller gains followed by the minimum ITAE, IAE, and ISE.

Table 8. Comparative study of ITAE and gains of the controller of proposed MPPT with other methodologies.

Sl. no.	MPPT methods	ITAE	k_a	k_b	k_c	k_d	k_e	IAE	ISE
1.	PSO-MPb&O	0.059915	0.99976	−0.006076	0.15268	−0.10022	0.78675	2.4367e–3	1.0641e–6
2.	CSA-MPb&O	0.055802	0.77596	−0.78913	0.22918	−0.33107	0.26571	2.4358e–3	7.5469e–7
3.	MGO-MPb&O	0.051256.	0.99998	−0.6144	0.28939	−0.08538	0.71229	2.4349e–3	7.5459e–7

5.3. Framework 3: Analysis of the Transient Response of the Proposed MGO-MPb&O MPPT Algorithm Under Various SF

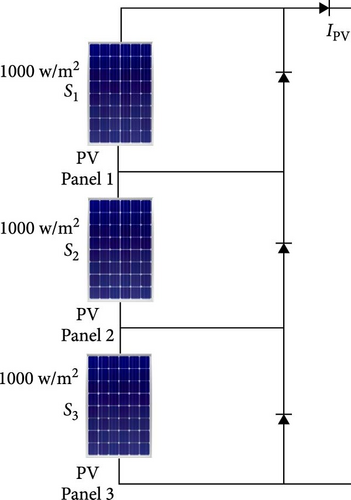
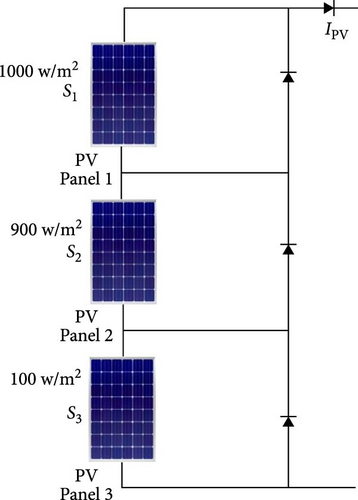
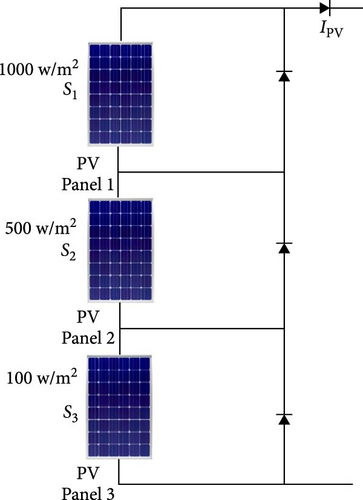
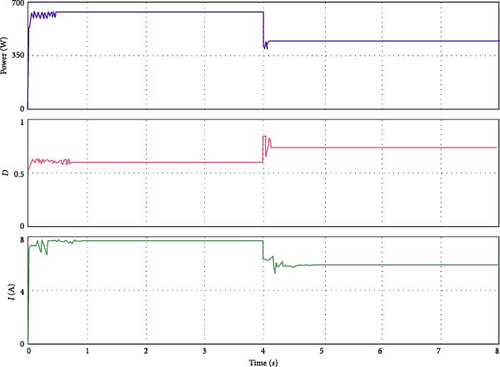
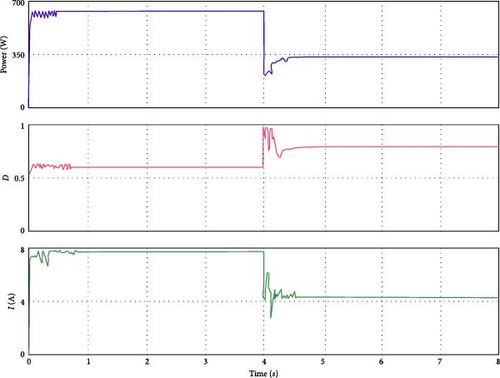
As this experiment shows, the suggested MGO-MPb&O-based MPPT can track the global MPP under both steady and transient shading patterns (SPs). We chose a few scenarios to demonstrate the tracking capability of the proposed MPPT approach because testing all nonuniform irradiance conditions is highly challenging. Table 9 and Figure 14 show the three SPs we examined. There is only one peak in the PV array’s P–I characteristic curve for SF1 since the irradiance on each PV panel is constant. There are several peaks for the remaining three SFs. Applying the MGO-MPb&O MPPT algorithm, the current in the PV string, average power, and actual power from the various shading configurations are measured and tabulated in Table 9. It demonstrates that the suggested MGO-MPb&O-based MPPT can follow the global MPP, ensuring that the power output is nearly identical to the optimal power in the three shading scenarios. This power output is based on the premise that there is no power leakage in the PV system due to wire connectivity power losses, DC–DC converter conversion efficiency, or other causes. Power cultivation will be lower than in this ideal scenario when this MPPT is used in a practical system. We looked at three scenarios to demonstrate the tracking capability of the suggested MGO-MPb&O-based MPPT algorithm in the presence of transient irradiance—Case 1: SF1–SF2, Case 2: SF switches from SF1 to SF3. For Cases 1 and 2, each PV string’s power transient characteristics, matching duty cycle, and current variable are displayed in Figures 15 and 16, respectively. These two performance figures for various transition instances demonstrate that the suggested MPPT algorithm can determine the global MPP for the new SP when it shifts from a uniform state to a partially shaded condition at 4 s (middle of the x-axis). For instance, when the case switches from SF1 to SF2 and SF1 to SF3, the power changes from 645 W to 480 W and 645 W and 344 W, respectively.

Table 9. Different shading arrangements.

Shading fashion	Solar irradiation (W/m²)	Theoretical value of power (W)	Measured value of power (W)	PV current at MPP (A)
SF1	S₁ = 1000 W/m² S₂ = 1000 W/m² S₃ = 1000 W/m²	645	645	7.8

SF2	S₁ = 1000 W/m² S₂ = 900 W/m² S₃ = 100 W/m²	480	480	6.3

SF3	S₁ = 1000 W/m² S₂ = 500 W/m² S₃ = 100 W/m²	344	344	4.2

6. Conclusion

In this manuscript, a novel combinatory hybrid algorithm is studied and validated by amalgamating a newly introduced meta-heuristic algorithm MGO with an MPb&O algorithm for sliding mode control topology for the superior tracking of the MPP in the PV generation system. Conventional Pb&O cannot keep track of a rapid ambiance change from sunny to shaded conditions. In the case of MGO, it alone obtains the local maximum point instead of keeping track of the global maximum. The shortcomings of the previously mentioned algorithms can be overcome by implementing the proposed MGO-MPb&O. This control topology is time-varying or nonlinear as they can respond to a sudden unpredicted perturbation in input parameters or dynamics of the system. From the point of view of efficacy, duration for convergence, and maximum obtainable power, the suggested algorithm proves to be the best compared to PSO-MPb&O and CSA-MPb&O. Also, the proposed methodology is the best among the other two mentioned regarding minimal settling time, less % overshoot, and accuracy. The proposed algorithm proves its superiority in partial shading conditions by analyzing the transient responses and considering three SFs. For future work, the performance of the proposed methodology can be tested and validated on some nonlinear systems considering unanticipated parameters. Many newly introduced meta-heuristic algorithms, like the meerkat optimization algorithm, osprey optimization algorithm, and transit search algorithm, can be employed with the suggested system.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

Open access funding is provided by Qatar National Library under the QNL–Wiley open access agreement. Further, this work is supported by the Qatar National Research Fund under Grant No. AICC05-0508-230001 for the project Solar Trade (ST): An Equitable and Efficient Blockchain-Enabled Renewable Energy Ecosystem – Opportunities for Fintech to Scale Up Green Finance for Clean Energy. Additional support from the Qatar Environment and Energy Research Institute (QEERI) is also gratefully acknowledged.

Open Research

Data Availability Statement

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

References

1 Mahmoud Y. A., Xiao W., and Zeineldin H. H., A Parameterization Approach for Enhancing PV Model Accuracy, IEEE Transactions on Industrial Electronics. (2013) 60, no. 12, 5708–5716, https://doi.org/10.1109/TIE.2012.2230606, 2-s2.0-84880295602.
10.1109/TIE.2012.2230606
Web of Science® Google Scholar
2 Elgendy M. A., Zahawi B., and Atkinson D. J., Assessment of Perturb and Observe MPPT Algorithm Implementation Techniques for PV Pumping Applications, IEEE Transactions on Sustainable Energy. (2012) 3, no. 1, 21–33, https://doi.org/10.1109/TSTE.2011.2168245, 2-s2.0-84859061094.
10.1109/TSTE.2011.2168245
Web of Science® Google Scholar
3 Salman S., AI X., and Wu Z., Design of a P &O Algorithm Based MPPT Charge Controller for a Stand-Alone 200 W PV System, Protection and Control of Modern Power Systems. (2018) 3, no. 1, https://doi.org/10.1186/s41601-018-0099-8, 2-s2.0-85061736438.
10.1186/s41601-018-0099-8
Google Scholar
4 Sellami A., Kandoussi K., El Otmani R., Eljouad M., Mesbahi O., and Hajjaji A., A Novel Auto-Scaling MPPT Algorithm Based on Perturb and Observe Method for Photovoltaic Modules Under Partial Shading Conditions, Applied Solar Energy. (2018) 54, no. 3, 149–158, https://doi.org/10.3103/S0003701X18030143, 2-s2.0-85053502127.
10.3103/S0003701X18030143
Google Scholar
5 Hanzaei S. H., Gorji S. A., and Ektesabi M., A Scheme-Based Review of MPPT Techniques With Respect to Input Variables including Solar Irradiance and PV Array’s Temperature, IEEE Access. (2020) 8, 182229–182239, https://doi.org/10.1109/ACCESS.2020.3028580.
10.1109/ACCESS.2020.3028580
Google Scholar
6 Mahafzah K. A., Obeidat M. A., AI-Shetwi A. Q., and Ustun T. S., A Novel Synchronized Multiple Output DC-DC Converter Based on Hybrid Flyback Cuk Topologies, Batteries. (2022) 8, no. 8.
10.3390/batteries8080093
PubMed Google Scholar
7 Zhang X., Yang B., Yu T., and Jiang L., Dynamic Surrogate Model Based Optimization for MPPT of Centralized Thermoelectric Generation Systems under Heterogeneous Temperature Difference, IEEE Transactions on Energy Conversion. (2020) 35, no. 2, 966–976, https://doi.org/10.1109/TEC.2020.2967511.
10.1109/TEC.2020.2967511
Google Scholar
8 Khanam N., Khan B. H., and Imtiaz T., Maximum Power Extraction of Solar PV System Using Meta-Heuristic MPPT Techniques: A Comparative Study, Proc Int Conf. Electr. Electron.Comput. Eng. (UPCON), 2018, Aligarh India, 1–6.
Google Scholar
9 Omine L. T., de Brito M. A. G., Pinto J. O. P., and Garcia R. C., Hybrid MPPT Algorithms for Photovoltaic Systems, Proc IEEE 4th Southern Power Electron. Conf.(SPEC), Singapore 2018;1-8.
Google Scholar
10 Ibrahim A.-W., Shafik M. B., Ding M., Sarhan M. A., Fang Z., Alareqi A. G., Almoqri T., and Al-Rassas A. M., PV Maximum Power Point Tracking Using Modified Particle Swarm Optimization Under Partial Shading Conditions, Chinese Journal of Electrical Engineering. (2020) 6, no. 4, 106–121, https://doi.org/10.23919/CJEE.2020.000035.
10.23919/CJEE.2020.000035
Google Scholar
11 Koh J. S., Tan R. H. G., Lim W. H., and Tan N. M. L., A Modified Particle Swarm Optimization for Efficient Maximum Power Point Tracking under Partial Shading Condition, IEEE Transactions on Sustainable Energy. (2023) 14, no. 3, 1822–1834, https://doi.org/10.1109/TSTE.2023.3250710.
10.1109/TSTE.2023.3250710
Google Scholar
12 Nugraha D. A., Lian K. L., and Suwarno, A Novel MPPT Method Based on Cuckoo Search Algorithm and Golden Section Search Algorithm for Partially Shaded PV System, Canadian Journal of Electrical and Computer Engineering. (2019) 42, no. 3, 173–182, https://doi.org/10.1109/CJECE.2019.2914723, 2-s2.0-85069984146.
10.1109/CJECE.2019.2914723
Web of Science® Google Scholar
13 Guo K., Cui L., Mao M., Zhou L., and Zhang Q., An Improved Gray Wolf Optimizer MPPT Algorithm for PV System with BFBIC Converter under Partial Shading Condition, IEEE Access. (2020) 8, 103476–103490, https://doi.org/10.1109/ACCESS.2020.2999311.
10.1109/ACCESS.2020.2999311
Google Scholar
14 Dhieb Y., Yaich M., Bouzguenda M., and Ghariani M., MPPT Optimization Using Ant Colony Algorithm: Solar PV Applications, Proc IEEE 21st Int Conf, 2022, Sci.Techn.Autom.ControlComput.Eng.(STA), Sousee, Tunisia, 503–507.
10.1109/STA56120.2022.10019072
Google Scholar
15 Padmanaban S., Priyadarshi N., Sagar Bhaskar M., Holm-Nielsen J. B., Ramachandaramurthy V. K., and Hossain E., A Hybrid ANFIS-ABC Based MPPT Controller for PV System With Anti-Islanding Grid-Protection: Experimental Realization, IEEE Access. (2019) 7, 103377–103389, https://doi.org/10.1109/ACCESS.2019.2931547.
10.1109/ACCESS.2019.2931547
Google Scholar
16 Mirza A. F., Mansoor M., Ling Q., Yin B., and Javed M. Y., A Salp-Swarm Optimization Based MPPT Technique for Harvesting Maximum Energy from PV System under Partial Shading Conditions, Energy Conversion and Management. (2020) 209, https://doi.org/10.1016/j.enconman.2020.112625.
10.1016/j.enconman.2020.112625
Google Scholar
17 Mansoor M., Mirza A. F., Ling Q., and Javed M. Y., Novel Grass Hopper Optimization Based MPPT of PV Systems for Complex Partial Shading Conditions, Solar Energy. (2020) 198, 499–518, https://doi.org/10.1016/j.solener.2020.01.070.
10.1016/j.solener.2020.01.070
Web of Science® Google Scholar
18 Rao R. V., Savsani V. J., and Vakharia D. P., Teaching-Learning Based Optimization: A Novel Method for Constrained Mechanical Design Optimization Problems, Computer-Aided Design. (2011) 43, no. 3, 303–315, https://doi.org/10.1016/j.cad.2010.12.015, 2-s2.0-78951475022.
10.1016/j.cad.2010.12.015
Google Scholar
19 Singh N., Gupta K. K., Jain S. K., Dewangan N. K., and Bhatnagar P., A Flying Squirrel Search Optimization for MPPT under Partial Shaded Photovoltaic System, IEEE Journal of Emerging and Selected Topics in Power Electronics. (2021) 9, no. 4, 4963–4978, https://doi.org/10.1109/JESTPE.2020.3024719.
10.1109/JESTPE.2020.3024719
Web of Science® Google Scholar
20 Siew-Chong Tan, Lai Y. M., and Tse C. K., Indirect Sliding Mode Control of Power Converters via Double Integral Sliding Surface, IEEE Transactions on Power Electronics. (2008) 23, no. 2, 600–611, https://doi.org/10.1109/TPEL.2007.915624, 2-s2.0-41549115098.
10.1109/TPEL.2007.915624
Google Scholar
21 Saravanakumar R. and Jena D., Validation of an Integral Sliding Mode Control for Optimal Control of a Three Blade Variable Speed Variable Pitch Wind Turbine, International Journal of Electrical Power & Energy Systems. (2015) 69, 421–429, https://doi.org/10.1016/j.ijepes.2015.01.031, 2-s2.0-84923226485.
10.1016/j.ijepes.2015.01.031
Web of Science® Google Scholar
22 Liu X., Han Y., and Wang C., Second-Order Sliding Mode Control for Power Optimization of DFIG-Based Variable Speed Wind Turbine, IET Renewable Power Generation. (2017) 11, no. 2, 408–418, https://doi.org/10.1049/iet-rpg.2015.0403, 2-s2.0-85017098865.
10.1049/iet-rpg.2015.0403
Web of Science® Google Scholar
23 Hu L., Xue F., Qin Z., Shi J., Qiao W., Yang W., and Yang T., Sliding Mode Extremum Seeking Control Based on Improved Invasive Weed Optimization for MPPT in Wind Energy Conversion System, Applied Energy. (2019) 248, 567–575, https://doi.org/10.1016/j.apenergy.2019.04.073, 2-s2.0-85064615127.
10.1016/j.apenergy.2019.04.073
Google Scholar
24 Yang B., Yu T., Shu H., Dong J., and Jiang L., Robust Sliding-Mode Control of Wind Energy Conversion Systems for Optimal Power Extraction via Nonlinear Perturbation Observers, Applied Energy. (2018) 210, 711–723, https://doi.org/10.1016/j.apenergy.2017.08.027, 2-s2.0-85027675026.
10.1016/j.apenergy.2017.08.027
Web of Science® Google Scholar
25 Beltran B., Benbouzid M. E. H., and Ahmed-Ali T., Second-Order Sliding Mode Control of a Doubly Fed Induction Generator Driven Wind Turbine, IEEE Trans Energy Convers. (2012) 27, no. 2, 261–269, https://doi.org/10.1109/TEC.2011.2181515, 2-s2.0-84861457658.
10.1109/TEC.2011.2181515
Google Scholar
26 Weng Y-T and Hsu Y-Y, Sliding Mode Regulator for Maximum Power Tracking and Copper Loss Minimization of a Doubly Fed Induction Generator, IET Renewable Power Generation. (2015) 9, no. 4, 297–305, https://doi.org/10.1049/iet-rpg.2014.0125, 2-s2.0-84928475978.
10.1049/iet-rpg.2014.0125
Web of Science® Google Scholar
27 Nguyen T. V., Abe R., and Tanaka K., MPPT and SPPT Control for PVconnected Inverters, Using Digital Adaptive Hysteresis Current Control, Energies. (2018) 11, no. 8, 2075.
Google Scholar
28 Gosumbonggot J. and Fujita G., Partial Shading Detection and Global Maximum Power Point Tracking Algorithm for Photovoltaic With the Variation of Irradiation and Temperature, Energies. (2019) 12, no. 2, https://doi.org/10.3390/en12020202, 2-s2.0-85060549202, 202.
10.3390/en12020202
Google Scholar
29 Teo K. T. K., Lim P. Y., and Chua B. L., Maximum Power Point Tracking of Partially Shaded Photovoltaic Arrays Using Particle Swarm Optimization, 4th International Conference on Artificial Intelligence With Applications in Engineering and Technology, 2014, Kota Kinabalu, 247–252.
Google Scholar
30 Koad R. B. A. and Zobaa A. F., Comparison Between the Conventional Methods and PSO Based MPPT Algorithm for Photovoltaic Systems, International Journal of Energy and Power Engineering. (2014) 8, no. 4, 697–702.
Google Scholar
31 Haq I. U. and Khan Q., Neural Network-Based Adaptive Global Sliding Mode MPPT Controller Design for Stand-Alone Photovoltaic Systems, PlosOne. (2022) 17, no. 1, 0260480.
10.1371/journal.pone.0260480
Google Scholar
32 Kjaer S. B., Pedersen J. K., and Blaabjerg F., A Review of Single-Phase Grid-Connected Inverters for Photovoltaic Modules, IEEE Transactions on Industry Applications. (2005) 41, no. 5, 1292–1306, https://doi.org/10.1109/TIA.2005.853371, 2-s2.0-26844560797.
10.1109/TIA.2005.853371
Web of Science® Google Scholar
33 Xie F., Zhenxiong L., and Dongyuan Q., Study on a Simplified Structure of a Two-Stage Grid-Connected Photovoltaic System for Parameter Design Optimization, Energies. (2019) 12, no. 11, https://doi.org/10.3390/en12112193, 2-s2.0-85067208596, 2193.
10.3390/en12112193
Google Scholar
34 Saleem O. and Ali S., Robust MPPT Control of Stand-Alone Photovoltaic Systems via Adaptive Self-Adjusting Fractional Order PID Controller, Energies. (2023) 16, no. 13, https://doi.org/10.3390/en16135039, 5039.
10.3390/en16135039
Google Scholar
35 Karbalaye Zadeh M., Gavagsaz-Ghoachani R., Pierfederici S., Nahid-Mobarakeh B., and Molinas M., Stability Analysis and Dynamic Performance Evaluation of a Power Electronics-Based DC Distribution System With Active Stabilizer, IEEE Journal of Emerging and Selected Topics in Power Electronics. (2016) 4, no. 1, 93–102, https://doi.org/10.1109/JESTPE.2015.2484218, 2-s2.0-84962332029.
10.1109/JESTPE.2015.2484218
Google Scholar
36 Anjum M. B. and Khan Q., Maximum Power Extraction from a Standalone Photo Voltaic System via Neuro-Adaptive Arbitrary Order Sliding Mode Control Strategy With High Gain Differentiation., Applied Sciences. (2022) 12, no. 6, 2773.
10.3390/app12062773
CAS Google Scholar
37 Ganguly A., Biswas P. K., Sain C., Azar A. T., Mahlous A. R., and Ahmed Saim, Horse Herd Optimized Intelligent Controller for Sustainable PV Interface Grid-Connected System: A Qualitative Approach, Sustainability. (2023) 15, no. 14, https://doi.org/10.3390/su151411160, 11160.
10.3390/su151411160
Google Scholar
38 Harrag A. and Messalti S., PSO- Based SMC Variable Step Size P&O MPPT Controller for PV Systems Under Fast Charging Atmospheric Conditions, Int J Numer Model Electron New Devices Fields. (2019) 32, no. 5, https://doi.org/10.1002/jnm.2603, 2-s2.0-85065393686, 2603.
10.1002/jnm.2603
Google Scholar
39 Islam M. R. and Iqbal J., Design and Comparison of Two Control Strategies for Multi-DOF Articulated Robotic Arm Manipulator, Control Engineering and Applied Informatics. (2014) 16, no. 2, 28–39.
Google Scholar
40 Iqbal J., Modern Control Laws for an Articulated Robotic Arm: Modeling and Simulation, Engineering, Technology & Applied Science Research. (2019) 9, no. 2, 4057–4061, https://doi.org/10.48084/etasr.2598.
10.48084/etasr.2598
Google Scholar
41 Chen M. R., Wang H., and Zeng G., Optimal PQ Control of Grid - Connected Inverters in a Microgrid Based on Adaptive Population Extremal Optimization, Energies. (2017) 11, no. 8.
Google Scholar
42 Al-Saedi W., Lachowicz S. W., Habibi D., and Bass O., Power Quality Enhancement in Autonomous Microgrid Operation Using Particle Swarm Optimization, International Journal of Electrical Power & Energy Systems. (2012) 42, no. 1, 139–149, https://doi.org/10.1016/j.ijepes.2012.04.007, 2-s2.0-84861000097.
10.1016/j.ijepes.2012.04.007
Web of Science® Google Scholar
43 Zhang Y., Jiang Z., and Yu X., Small-Signal Modeling and Analysis of Parallel Connected Voltage Source Inverters, IEEE 6th International Power Electronics and Motion Control Conference, 2009, IEEE, 377–383.
Google Scholar
44 Kamala Devi V., Premkumar K., Bisharathu Beevi A., and Ramaiyer S., A Modified Perturb & Observe MPPT Technique to Tackle Steady State and Rapidly Varying Atmospheric Conditions, Solar Energy. (2017) 157, 419–426, https://doi.org/10.1016/j.solener.2017.08.059, 2-s2.0-85028302378.
10.1016/j.solener.2017.08.059
Google Scholar
45 Jabbar R. I., Mekhilef S., Mubin M., and Mohammed K. K., A Modified Perturb and Observe MPPT for a Fast and Accurate Tracking of MPP Under Varying Weather Conditions, IEEE Access. (2023) 11, 76166–76176, https://doi.org/10.1109/ACCESS.2023.3297445.
10.1109/ACCESS.2023.3297445
Google Scholar

All articles

Metaheuristic Optimization-Based Sliding Mode Control With Modified Perturb and Observe for Controlling MPPT of a PV Interfaced Grid Connected System

Abstract

1. Introduction

2. System Modeling