A Review of Research on the Thermo-Force Characteristics of Scramjet Engine Wall Based on Neural Networks
Abstract
With the development of high-performance computing and advanced experimental methods, data-driven machine learning, especially neural network technology, has shown great potential in fluid mechanics research and has become a fourth paradigm research tool. In particular, remarkable achievements have been made in turbulence modeling, near-wall flow prediction, and combustion dynamic evolution. Researchers use neural network model to assist turbulence control, improve Reynolds average turbulence model, and harnesses the deep learning method to solve the problem of complex flow phenomenon prediction driven by large-scale data, which effectively improves the accuracy and efficiency of internal flow and wall effect simulation of supersonic combustion ramjet (scramjet) engine. These studies not only promote the development of fluid mechanics but also provide strong support for the design optimization of scramjet engines.
1. Introduction
A hypersonic vehicle refers to an aircraft that has a maximum flight speed greater than or equal to Ma5 and has a long-term maneuvering flight in the atmosphere or across the atmosphere. One of the key technologies of hypersonic vehicles is supersonic combustion (referred to as supersonic combustion, which refers to the physical and chemical process of mixing and combustion of a fuel in supersonic airflow) and supersonic combustion ramjet (scramjet) technology. SCRAMJET is a type of scramjet power plant that achieves hypersonic flight with air-breathing power after the traditional sub-fuel scramjet. Since the 1950s, the scramjet engine technology has made great progress. The flamelet model and probability density function (PDF) model [1] were developed, and the research methods of regenerative cooling and multiphysical field coupling were proposed. Ren et al. [2] reviewed the research on supersonic spray combustion of a scramjet engine. He et al. [3] summarized the coupling heat transfer mechanism of the regenerative cooling system of the scramjet engine. Choubye et al. [4] discussed the latest progress of the scramjet engine with cavity. Zhao et al. [5] summarized the research progress of the solid fuel scramjet engine. In addition, the scramjet engine is combined with the traditional turbine engine to form a turbine-based combined cycle engine, which is suitable for horizontal take-off and landing, reusable atmosphere-space aircraft; rocket based combind cycle (RBCC) is formed by the combination of scramjet and rocket engine, which is suitable for hypersonic flight from ground stationary state to atmosphere and outer space flight. The dual-mode SCRAMJET formed by the combination of scramjet and subsonic scramjet is suitable for flight from supersonic to hypersonic in the atmosphere. The dual combustor ramjet (DCR), which was first proposed by the United States, has been improved on the combustion chamber. The combustion chamber is composed of a precombustion chamber and a main combustion chamber, which is suitable for high-speed flight with a wide Mach number. The combination of the scramjet engine and a new concept detonation engine forms a combined cycle engine of scramjet and detonation, which is suitable for flight detection at high speed, high altitude, and high latitude [6].
With the development of technology, the research on scramjet engine is more and more in-depth. For a long time, experimental observation, theoretical research, and numerical simulation are the basic research paradigms of many disciplines, including fluid mechanics [7]. In the past few decades, due to the advancement of high-performance computing architecture and experimental measurement capabilities, data-driven machine learning has become a new paradigm for fluid mechanics research [8], that is, the fourth paradigm. Due to the complexity of turbulence, combustion, transition, and other problems, there are still many basic and engineering application problems to be solved urgently in scramjet engines, among which the study of wall thermo-mechanical characteristics is one of them. The traditional research paradigm has made great contributions to the establishment and development of fluid mechanics. The liquid equilibrium theory and the basic equations of incompressible fluid motion proposed by early scholars have prepared the conditions for the development of fluid mechanics. The N − S equation, which was jointly developed by Navey and Stokes, has become the basic theoretical guiding equation in the field of fluid mechanics [9]. On this basis, the Reynolds’ average equation has been developed. Using computer technology, finite difference [10], finite volume [11, 12], finite element [13], and spectral method [14] have been developed, and stability theory, numerical error dissipation, mesh adaptation technology, iteration, and accelerated convergence methods have been established [15]. Since the 21st century, the data-intensive scientific research paradigm will bring new development to fluid mechanics [16–19]. This paper provides a brief overview of the research on artificial neural networks (ANNs) applied to detached scramjet engines.
2. The Development of Neural Network and Its Application in Fluid Mechanics
2.1. Development of Neural Networks
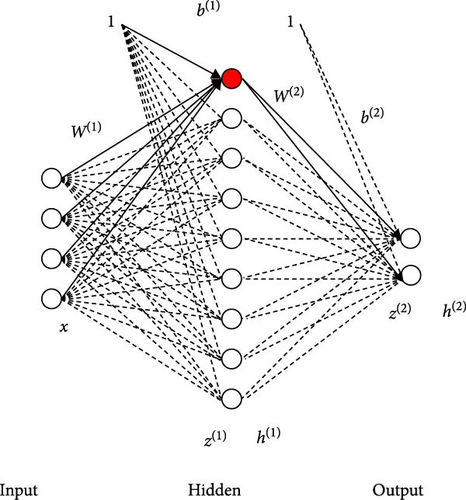
Machine learning involves enabling computers to mimic human learning behaviors, acquire new knowledge, reorganize existing information, and continuously enhance performance. Machine Learning, as defined in alignment with ACM/IEEE standards, is a subfield of artificial intelligence (AI) that focuses on the design, analysis, and implementation of computational algorithms and statistical models. These systems autonomously improve their performance on specific tasks through exposure to data (experience), without relying on explicit, task-specific programing. Machine learning is mainly used to design and analyze some algorithms that allow machines to learn automatically [20]. Connectionism [21] is one of the three major schools of machine learning, and neural network is one of the main research methods of connectionism. As early as 1943, the concept of “neural network” and M–P model proposed by McCulloch and Pitts [22] based on the principle of biological neurons marked the germination of ANN. In 1949, Hebb proposed Hebb synapse and Hebb learning rules [23], which laid a theoretical foundation for the development of ANNs. In the late 1960s, Rosenblatt [24] proposed the concept of the perceptron based on the M–P model, which is the first ANN with learning ability. In 1969, Minsky proposed the famous XOR problem, pointing out that perceptrons cannot process linearly inseparable data [25]. In 1974, Werbos proposed Backpropagation, which was developed into the backpropagation neural network (BPNN) in the 1980s, and proposed a multilayer perceptron (MLP) model [26] to solve the problems reflected by multilayer neural networks. In 1979, Fukushima [27] proposed an unsupervised learning neural network model, namely the Neocognitron model, which is the prototype of a convolutional neural network (CNN). In 1982, Hopfield [28] invented a recurrent neural network (RNN), the Hopfield neural network, which provides a model to simulate human memory. In 1985, Geoffrey Hinton and Terry Sejnowski invented the Boltzmann machine, which can learn internal expression and solve complex combinatorial optimization problems [29], but it does not show obvious advantages in solving practical problems. In 1986, Rumelhart, Hinton, Williams, Hetch, Nielsen et al. proposed the concept of MLP trained by the BP algorithm, which laid the foundation for deep learning [30]. Figure 1 provides a schematic diagram of the structure of the MLP.
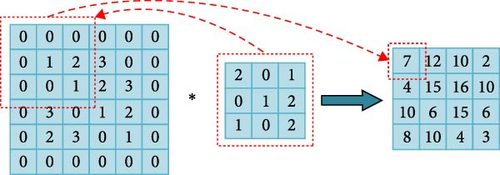
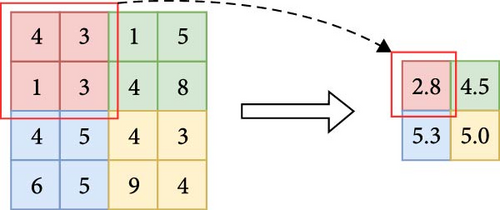
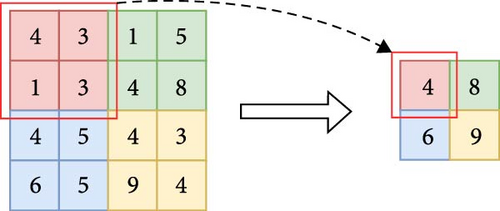
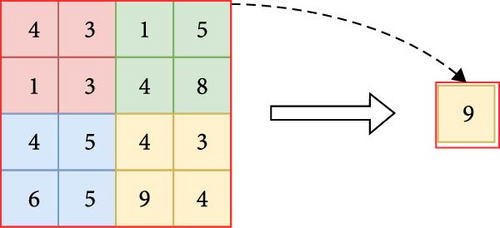
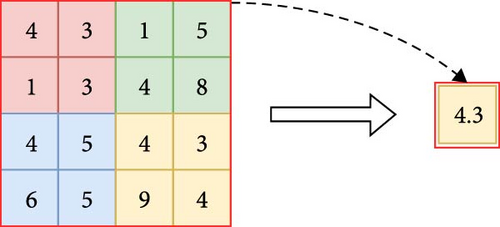
In the same year, M.I. Jordan and Jeffrey Elman proposed a turing-complete RNN with parameter sharing [32], which helps to minimize the total number of parameters in the neural network. Figures 2 and 3 respectively, provide schematic diagrams of the convolution and pooling operations. In 1998, Lecun [33] proposed the LeNet network for handwritten digit recognition, one of the earliest CNNs. It includes the fundamental CNN modules: convolutional, pooling, and fully connected layers, which serve as the foundation for other CNN models.
In 2006, Hinton et al. [34] proposed the neural network deep learning algorithm, which consists of multiple stacked restricted Boltzmann machines to form a deep belief network (DBN). On this basis, AlexNet [35], residual neural network (ResNet) [36], and deep Q-leaning network (DQN) [37] using a GPU for training have been developed successively. Recently, ANNs have seen active development across various research areas, achieving significant progress in fields such as image processing, medicine, and fluid mechanics.
2.2. Application of Neural Network in Fluid Mechanics
In the field of fluid mechanics, the traditional research methods are still mainly based on theoretical analysis, numerical calculation, and field experiments. Most of these basic research results are still directly dependent on human wisdom. As more and more data are generated in the process of computer simulation and experiment, it is a worthwhile research direction to use AI methods to process big data, and to alleviate/replace the dependance on the human brain at the theoretical/methodological level through machine learning.
In 1996, Kawthar-Ali and Acharya [38] proposed a neural network controller based on the unsteady pressure field to determine the leading edge suction control quantity, so as to suppress the periodic development of the dynamic stall vortex at the leading edge of the pitching airfoil. In the direct numerical simulation of low Reynolds number turbulent pipes, Lee et al. [39] by optimizing the structure and parameters of the neural network, they successfully reduced surface friction by 20% and pioneered the use of neural networks in turbulent closed-loop control. Milano and Koumoutsakos [40] first used neural networks to construct a self-mapping autoencoder that can realize flow snapshots, and realized data-driven nonlinear feature extraction for modeling near-wall turbulence. Tracey et al. [41] used a neural network to construct a gray box model to replace the source term of the control equation of the SA model, which improved the classical differential equation turbulence model. Sekar et al. [19] introduced a deep neural network approach for the rapid prediction of airfoil flow fields. The airfoil parameters are optimized by CNN. The input and output are airfoil parameters, Reynolds number, attack angle, and flow field distribution. The model trained by this method does not need to solve the complex flow field. The spatial distribution of the flow field can be output through the neural network, which not only has high computational efficiency but also has certain generalization ability. Ling et al. [42] developed a tensor basis neural network (TBNN) model incorporating Reynolds stress anisotropy, enabling a more accurate description of vortex structures in secondary flow and separation phenomena on the waveform wall. Zhang and Duraisamy et al. [43–45] improved the computational accuracy of the RANS model by establishing a data-driven model with modified coefficient distribution and additional source terms. Maulik et al. [46] established an artificial network model to predict the turbulent source term of temporal and spatial variation. Xie et al. [47] combined the neural network with the sub-grid model framework for turbulence modeling and compressible turbulence simulation. Raissi et al. [48–50] introduced the physical informed neural network (PINN) to solve partial differential equations, and used the control equation as the physical constraint. The neural network was trained using multiple observations of a specific flow field, allowing predictions of the flow in a given region without the need for boundary conditions. On this basis, Jagtap et al. [51] developed the Conservative PINN method, which divides the flow field into sub-regions and applies the PINN approach to solve each region separately, enhancing the original method’s applicability to complex boundary flow problems. In addition, Karpatne et al. [52] proposed the concept of physics-guided neural network (PGNN), and constructed a neural network that conforms to the physical law. In the construction of the loss function, physical prior information is added to guide the learning process of the neural network, which improves the accuracy of the neural network, and the output results also conform to the principle of physical consistency. Ye et al. [53] constructed a CNN and successfully predicted the pressure distribution with the velocity field, while Jin et al. [54] constructed a CNN and predicted the global velocity field with the cylinder surface pressure. Huang et al. [55] constructed a data-driven flame evolution process prediction model by using a deep neural network, and successfully obtained a three-dimensional structure through the two-dimensional flow field. Cai et al. [56, 57] studied the particle motion prediction method in PIV data by combining a neural network method. Fukami et al. [58] used low-resolution (LR) flow field images as input to train CNNs, which output high-resolution (HR) turbulent flow field images. The effectiveness of the method was verified in laminar flow around a circular cylinder and isotropic turbulence. This method does not need to solve the control equation, and the HR reconstruction of the flow field is achieved by the trained neural network model. Zhu et al. [59] and Geneva and Zabaras[60] proposed a physics-constrained surrogate (PCS) model, which uses the convolutional encoding-decoding neural network model to numerically solve the partial differential equation. The flow field image data is used as input, and the data is reduced by a small number of convolution kernels to represent the high-dimensional flow field data. Then the control equation and boundary conditions are included in the loss function. This method does not require any training data samples and can directly use the neural network to map out the numerical solution of the equation. Based on the sample-free data method, Karumuri et al. [61] used the deep fully connected residual network to solve the two-dimensional elliptic stochastic partial differential equation. Wei et al. [62] proposed a deep reinforcement learning (DRL) solver based on DRL, integrating control equations and boundary conditions into the loss function, and achieving convergence from the initial random distribution to the stable final solution. This method effectively captures shock wave discontinuities without generating numerical oscillations near the shock. Kou and Zhang [63] used multikernel neural networks for the first time and realized the approximation of the numerical results of the N–S equation by using the low-precision Euler results by extending the variable-precision model to the unsteady aerodynamic model. Ren et al. [64] proposed a data-driven adaptive control method for transonic airfoil buffeting based on a radial basis function neural network, which can completely suppress the transonic buffeting load in a certain flow range. Du [65] studied the aerodynamic calculation method of compressor internal flow by combining numerical simulation with deep learning, and accurately predicted the aerodynamic parameters of the internal flow field of turbomachinery. Xu et al. [66] introduced the spatiotemporal parallel physics-informed neural networks framework, addressing the flow field reconstruction problem in fluid dynamics inverse problems. They achieved an efficient and accurate solution under high Reynolds number turbulence. Luo et al. [67] developed a machine learning model based on upsampling CNNs, successfully predicting the cooling efficiency of a single-hole adiabatic gas film. Di Leoni et al. [68] improved the DeepONet neural operator model to efficiently predict the linear evolution of hypersonic boundary layers, effectively handling inverse problems and data assimilation. Yuan et al. [69] established a machine learning model to predict the wall temperature distribution of spiral tube water-cooled walls under orthogonal operating conditions, covering a wide parameter range. Pawar et al. [70] proposed a reduced-order modeling framework combining physical modeling and data-driven methods, successfully recovering hidden physical processes in fluid dynamics problems. Sun et al. [71] integrated proper orthogonal decomposition (POD), neural networks, and domain decomposition techniques, proposing an efficient nonintrusive reduced-order model that achieved precise predictions of flow fields with varying geometries in transonic flows. Jagtap et al. [72] utilized the extended PINNs (XPINNs) method to effectively address shock and expansion wave issues in supersonic flows, demonstrating the superior performance of XPINNs over traditional methods in solving complex flow fields. Dong et al. [73] established a heat flux density distribution prediction model for water-cooled walls based on an optimized support vector machine algorithm, successfully predicting the heat flux distribution in boiler water-cooled walls with certain generalization capabilities. Jiang et al. [74] proposed a physics-informed neural network method based on graph neural networks (PhyGNNets), which introduced spatial and temporal separation discretization to enhance the fitting and extrapolation capabilities in solving spatiotemporal partial differential equations, outperforming traditional PINN methods in terms of scalability in larger spatial regions. Li et al. [75] proposed a data-driven model integrating CNNs and long short-term memory (LSTM) networks, effectively predicting the remaining useful life of aviation engines with good stability. Liu et al. [76] established BP neural network and RBF neural network models based on artificial feature selection, mini-batching, and data normalization preprocessing techniques, achieving high-precision field reconstruction and prediction of combustion chamber wall cooling efficiency. Han et al. [77] introduced a selective deep neural network ensemble method, enhancing the accuracy and diversity of the ensemble model synchronously, improving the prediction accuracy of remaining useful life by nearly 20%. Kramer et al. [78] utilized the operator inference method for reduced-order modeling, learning physical structures from data while significantly reducing the computational burden of high-dimensional simulations, showing wide application prospects in engineering optimization, design, and control.
3. Application of Neural Network in Scramjet Engine
3.1. Reconstruction and In-Domain Generalization Based on Neural Networks
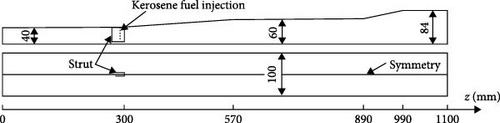
Kong et al. [79] introduced a deep learning method that combines data from ground experiments and numerical simulations, developing a velocity field prediction model based on experimental schlieren images to estimate the velocity field inside the isolator. Figure 4 provides the CNN structure of the model.
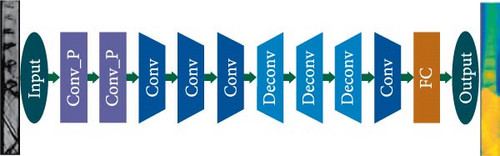
The input of the neural network is the schlieren image S and a corresponding reference velocity field Vref. The schlieren image is obtained through ground experiments, while the velocity field is derived from numerical simulations. Figure 5 shows the two-dimensional isolator and mesh model, while Figure 6 presents the images obtained from both experiments and simulations. The output is the predicted velocity field Vpre; the data set is derived from the ground supersonic direct-connected wind tunnel and numerical simulation. The wind tunnel can realize the continuous change of Mach number in the range of 1.8–2.4. At the same time, a transparent observation window composed of fuzed silica with a length of 260 mm and a height of 30 mm is installed. A high-speed camera records the schlieren image of the flow field, while 20 high-frequency pressure sensors are installed on the upper and lower walls of the isolator to measure the flow field pressure.

Numerical simulations were performed using FLUENT and compared with experimental results. The results show that the numerical simulations accurately generated the incident and reflected shock waves as well as larger separation zones. After 1000 training cycles, the model’s predicted results matched the pressure distribution obtained from CFD quite well. Figure 7 presents the results from the CFD and the model predictions. Within the interpolation range of incoming Mach numbers, the peak signal-to-noise ratio (SNR) of the predicted velocity field exceeded 25 dB, and the root mean square error was lower than 4 × 10−4 m/s. The relative prediction error of the velocity field at most spatial points was less than 5%. The correlation coefficient R > 0.999 between the predicted velocity field and the real data indicates a high level of consistency between the neural network’s predictions and the numerical simulation results obtained from CFD calculations. The deviations between the predicted results and the real data are primarily concentrated in regions with shock waves, boundary layer separation, and areas with large velocity gradients in high-speed flows. The complex flow characteristics in these regions impose higher demands on the neural network’s learning capability. This provides a new approach for ground experiments and theoretical design.
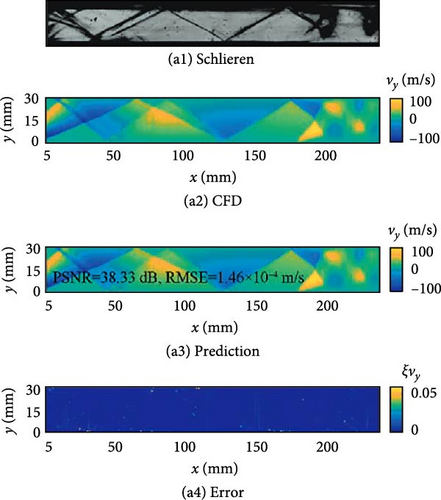
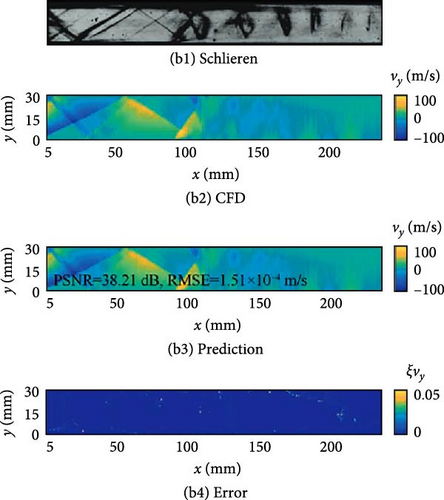
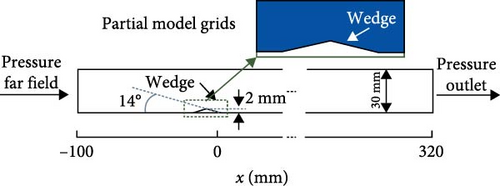
Chen et al. [80] proposed a deep learning-based method to reconstruct the flow field in the isolator and detect the leading edge of the shock train. They obtained flow field images from CFD data under various back pressure conditions, along with corresponding upper and lower wall pressure data, and constructed a dataset linking pressure and flow field information. The experimental setup is shown in Figure 8. By constructing and training a CNN, a mapping model is developed with pressure information as input and flow field images as output. The position of the shock train’s leading edge is then detected in the output flow field image. The calculation is based on the cross-sectional model of the ground direct-connected wind tunnel isolator from Harbin Institute of Technology [81]. In the case of Ma 2, five back pressure conditions were selected, and 500 sets of data were obtained, of which 70% were training sets and 30% were test sets.

The designed multilayer CNN is shown in Figure 9:

The flow field image is reconstructed using a CNN, and the distances between the shock separation points on the upper and lower walls and the inlet are compared to determine the location of the shock train’s leading edge. The point with the smaller distance is identified as the leading edge of the shock train. By changing the output of the last fully connected layer of the initial CNN model to 1, the improved CNN model can be obtained. The improved CNN model is shown in Figure 10. At this stage, it is no longer necessary to reconstruct the flow field in the isolator. Instead, the model, after training, can directly output the predicted position coordinates of the shock train’s leading edge, thus avoiding errors introduced by the reconstructed flow field.

The accuracy of flow field reconstruction is high and the effect is good, and the trained CNN model has certain robustness. By fine-tuning the CNN model, a new direct detection method for identifying the shock train’s leading edge is developed, reducing the root mean square error to 1.87 mm. This improves the convenience and accuracy of shock train leading edge detection.
Kong et al. [79] introduced a deep learning method combining experimental and numerical data for velocity field prediction. Their CNN-based architecture achieved a PSNR of 34.82 dB and SSIM of 0.95, outperforming traditional interpolation methods by 15% in accuracy. Chen et al. [80] proposed a shock train detection model using wall pressure data. Chen’s method reduced the root mean square error from 2.5 to 1.87 mm, demonstrating higher robustness under varying backpressure conditions. Additionally, Kong et al. [82] proposed a multichannel runoff field prediction model that predicts the flow field based on the wall pressure sequence. The model is primarily constructed using a CNN. Experimental datasets are created using supersonic experimental data under different evolution laws in the isolator. The independent experimental data are used to train and verify the flow field prediction model, and the prediction performance of the proposed model under different prediction spans is discussed in depth. The results show that even in the case of discontinuous change of the leading edge of the shock train, the predicted flow field is in good agreement with the real situation of the surface.
Deng et al. [83] proposed a dual-branch fusion model based on a multihead attention mechanism to reconstruct schlieren images of the flow field in a supersonic combustion chamber. The model employs a dual-path fusion approach. One branch consists of transposed and conventional convolutions, forming a symmetrical structure for dimensional enhancement and feature extraction. The other branch is composed of a multihead attention mechanism followed by a fully connected layer, using the attention mechanism to capture different sensitive features and enhance the model’s global perception. The model was trained and tested using experimental data from a hydrogen-fueled scramjet in a direct-connected supersonic pulse combustion wind tunnel with a Mach 2.5. The experiments show that the model effectively reconstructs the basic wave structure of the complex flow field, with results closely matching the original flow field. Their model achieved an average PSNR of 19.95 dB and SSIM of 0.605, significantly improving the resolution of shock wave boundaries compared to super-resolution CNN (SRCNN). The dual-path architecture effectively captured complex flow structures, such as the interaction between oblique shocks and boundary layers. Deng et al. [84] proposed a residual network model based on channel attention mechanisms (CAMs) and spatial attention mechanisms (SAMs) for reconstructing the self-luminous image of the flame from schlieren images of the flow field in a scramjet engine.
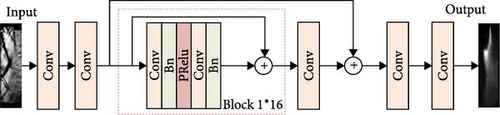
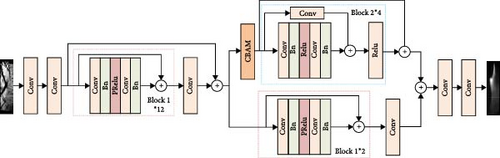
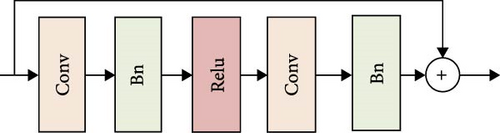
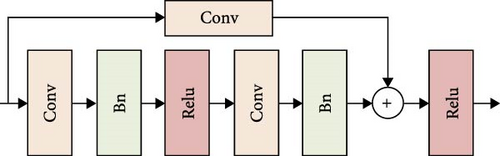
The title uses two types of residual network models to reconstruct the spontaneous light images of flames in a supersonic combustion chamber, namely ResNet16 and a residual reconstruction model based on channel and SAM (RRCBAM), where RRCBAM is further divided into single-path (RRCBAM_s) and dual-path (RRCBAM_d) structures. Figure 11 shows the three models. ResNet16 is a network composed of 16 residual modules designed to address the gradient vanishing problem in deep neural networks through residual connections. The input is a schlieren image of the supersonic combustion chamber, and the residual connections improve the gradient propagation in deep networks, allowing the model to train deeper layers. The RRCBAM model is an enhancement of ResNet16, aiming to improve the model’s expressive power and feature extraction capability without introducing additional computational overhead. The core improvement lies in the incorporation of CAM and SAM, which enhance the model’s ability to focus on key information while retaining the advantages of residual connections. Compared to ResNet16, the main additions in RRCBAM are the attention modules and the design of different network paths. CAM, through global average pooling (GAP) and global maximum pooling (GMP), allows the model to focus on the channels that contribute significantly to the flame features. SAM, using 7 × 7 convolutions, extracts important spatial information, making it easier for the model to capture critical flame regions. Block 1 (12 layers) is primarily used for low-level feature extraction and contains 3 × 3 convolutions, batch normalization, and PReLU activation functions. Block 2 (layers 4–8) is designed for higher-level feature extraction and introduces 1 × 1 convolutions in the residual connections to adjust the number of channels. To facilitate a more convenient comparison of the characteristics of the three models, Table 1 shows the differences between ResNet16 and RRCBAM. Figure 12 provides the skip connect module.

| Feature | ResNet16 | RRCBAM_s | RRCBAM_d |
|---|---|---|---|
| Uses attention mechanism | × | √ | √ |
| CAM | × | √ | √ |
| SAM | × | √ | √ |
| Residual connection | √ | √ | √ |
| Network depth | 16 layers | 12 layers + Block 2 | 12 layers + 2-path Block 2 |
| Computational complexity | Low | Medium | High |
| Feature extraction capability | General | Strong | Strongest |
| Applicable scenarios | Basic flame reconstruction | Complex flame structures | More extensive flame structures |
In the flame reconstruction task, both RRCBAM_s and RRCBAM_d outperform ResNet16. As a traditional residual network, ResNet16 effectively prevents the vanishing gradient problem but lacks the ability to focus on critical regions. RRCBAM_s enhances attention to the flame region through the attention mechanism, improving detail recovery. RRCBAM_d further strengthens global feature extraction, enabling the model to more accurately reconstruct the flame shape.
They compared the reconstruction performance of single-path and dual-path models under different conditions, demonstrating that residual connections can prevent gradient vanishing and enhance the model’s generalization ability. The proposed method was tested using supersonic combustion experiments at different equivalence ratios in a ground-based wind tunnel, where data on the combustion chamber flow field and flame evolution were recorded as a dataset. Extensive experiments and analyses were subsequently conducted on this dataset. The single-path model, with a deeper network, enabled the extraction of a sufficient number of semantic features, enhancing its generalization ability. The width model, compared to the single-path model, produced a wider but shorter structure, capable of extracting global texture features of the image, but with relatively poorer generalization ability. Therefore, models with appropriate depth and width can achieve better reconstruction results. The results show that the reconstructed images were consistent with the original flame images, accurately reconstructing the geometric features of the flame.
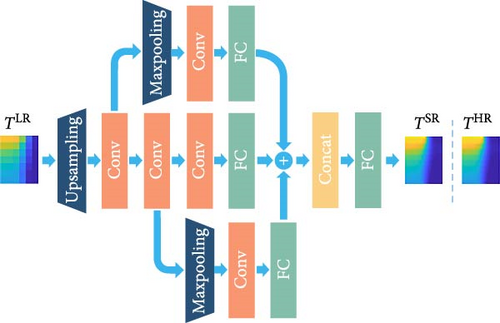
Xu et al. [85] proposed a data-driven three-dimensional super-resolution imaging method (3D-SR-GAN) to improve the spatial resolution of turbulent jet flames. This study employed a 3D super-resolution method based on generative adversarial networks (GANs). The training data came from the turbulent jet flame structure simulated by LES. The generator and discriminator networks in the GAN were used to learn flame features and infer HR flame structures from LR data. The 3D-SR-GAN method effectively improved the resolution of turbulent flames, successfully enhancing the resolution by a factor of two, with an overall error of approximately 4% and a PSNR = 37 dB. Additionally, the trained network could predict flame super-resolution structures at different Reynolds numbers without retraining, indicating strong generalization ability. However, the resolution improvement for high-frequency turbulent flame features showed some degradation. Brahmachary et al. [86] combined reduced-order modeling and machine learning techniques to rapidly predict the internal flow field of a scramjet engine’s intake. They used POD as a reduced-order modeling technique to reduce the dimensionality of flow field data, applying a moving least squares (MLSs)-based regression model and a MLP neural network for machine learning. Latin hypercube sampling and multiobjective optimization methods were used to generate flow field data. The results indicated that using POD combined with MLS and MLP methods allowed for rapid and accurate flow field predictions in two intake configurations of varying complexity. The MLP-based neural network outperformed the MLS regression model when processing configurations with six input variables. While this method demonstrated excellent performance in rapidly predicting flow fields, it still depended on high-quality training data, especially since sparse sampling issues could arise during flow field data sampling. Guo et al. [87] proposed a multipath asymmetric residual network (MARN) model for super-resolution reconstruction of the flow field during hydrogen-fueled scramjet auto-ignition. This model converted LR flow field data into HR flow field data. The method combined single-path SRCNNs and residual networks. To train the model, the study used combustion chamber flow field images from ground-based pulsed combustion wind tunnel tests with hydrogen fuel at different equivalence ratios. The neural network input consisted of LR schlieren images, and the output was HR flow field images. The model learned the mapping relationship between the LR images and the actual HR images to reconstruct the details. The results showed that the MARN model outperformed SRCNN and ResNet_16 in terms of PSNR, SSIM, and CORR metrics. In particular, the MARN model achieved a PSNR of 33.37 dB, significantly higher than other methods, and was able to capture turbulent fluctuations in the flow field more accurately. Despite the MARN model’s excellent performance in super-resolution reconstruction, its computational complexity was relatively high. Compared to ResNet_16, the MARN model reduced the number of layers and computational demands but still required more computational resources. Future research could further simplify the model structure and optimize training algorithms to reduce computational costs.
3.2. Spatiotemporal Evolution Based on Neural Networks
Guo et al. [88] proposed a CNN model based on multitimestamp pressure (MTPCNN) information fusion. This model uses the wall pressure sequence of a supersonic combustion chamber as input and predicts the flow field images at future timestamps through training. The experimental data came from a supersonic pulsed wind tunnel, consisting of 3425 sets of wall pressure and flow field image data under different injection pressures. The trained network was able to accurately predict the flow field of the combustion chamber at different time intervals (5, 6, and 10 ms), especially showing high accuracy in flow field prediction without chemical reactions. However, the prediction accuracy was lower for the chemical reaction flow field after hydrogen fuel ignition, mainly due to the interference of shock wave boundary layers and turbulent fluctuations. Increasing the input pressure data sequence helped improve the model’s prediction accuracy, particularly in long-term predictions. However, the model still showed insufficient prediction accuracy in regions with strong reverse pressure gradients, such as shock wave boundary layer interference and turbulent fluctuations. Huang et al. [55] used a deep learning model to directly predict the three-dimensional evolution of flames from experimental data. CNNs were employed to extract features from two-dimensional flame projections, and LSTM networks were used to build the time series of these features, thereby predicting the three-dimensional flame evolution. The experimental data were divided into training and testing sets, and 5-fold cross-validation was conducted. The results showed that this model could accurately predict the three-dimensional evolution of laminar diffusion flames and nonpremixed turbulent swirl-stabilized flames, with a prediction time scale in milliseconds. The computational time could be further reduced by increasing the GPU capacity. Compared to traditional CFD methods, this approach offered significant computational efficiency advantages, enabling real-time predictions. However, the model’s predictive capability depended on the quality and quantity of the training dataset. For complex flame structures, more training samples were needed to provide features to ensure prediction accuracy. Chen et al. [89] developed a memory-fusion cascaded network (MFCN) to successfully predict the flame image of a scramjet combustion chamber after a certain time span, using five flame evolution process image sequences constructed at different time intervals. They compared the prediction accuracy of this method with the Kongs model and the ResNet16 model. The results showed that the cascaded model design, which limited the model’s function to a smaller range, could solve the problem of complex networks being difficult to fit. MFCN outperformed other methods in terms of prediction accuracy and maintained stable prediction results in multitask and long-span tasks, laying the foundation for active control of scramjet combustion in real flight conditions.
Li et al. [90] proposed a real-time prediction method based on GANs to predict the performance of hypersonic vehicles in a fluid-thermal-structural coupling environment. By combining deep convolutional conditional GAN (DCCGAN) and GAN, they constructed a three-dimensional coupled field prediction model called fsGAN. The model was trained using coupled field data simulated from 400 different flight conditions of a virtual X-43A prototype. The fsGAN method demonstrated significant advantages in prediction accuracy and response speed compared to traditional KD-Tree interpolation algorithms and CNN models. This research proposed a method that effectively balances prediction accuracy and computational efficiency, making it suitable for real-time physical field prediction of hypersonic vehicles, especially in virtual flight tests. The accuracy and real-time capabilities of fsGAN were verified against NASA’s X-43A flight data under various flight states. However, due to the lack of real experimental data, the accuracy of training data was not discussed, and the scalability of the model and its prediction accuracy under higher-dimensional flight conditions still require further validation. Mohan and Gaitonde [91] utilized two sets of DNS data for forced isotropic turbulence and magnetohydrodynamic turbulence from the Johns Hopkins turbulence database, extracting dominant modes via POD and using LSTM to predict the time coefficients of these modes. LSTM was used as a replacement for traditional Galerkin projection methods to model the temporal evolution of turbulence. The study also compared the performance of traditional LSTM and bidirectional LSTM (BiLSTM). The results demonstrated that LSTM neural networks performed well in modeling the time evolution of turbulence, especially for short-term predictions, where LSTM could accurately predict the dynamic evolution of turbulent flow fields. However, as the prediction time range increased, the model’s accuracy decreased. Compared to BiLSTM, LSTM provided better prediction accuracy, possibly due to BiLSTM’s tendency to overfit the data. An et al. [92] proposed a novel deep learning framework called CFDNN that replaced traditional numerical solving methods with a deep CNN optimized with a U-Net architecture and inception modules. U-net is adept at multiscale feature extraction, which is suitable for the complex spatial distribution of combustion fields, while the inception module captures features at different scales through parallel convolution paths, enhancing the model’s expressive power. The output layer used a linear activation function, transforming the task from image segmentation to a regression problem, directly predicting the physical parameters of flow and combustion fields. The training data, obtained from CFD simulations, covered various inlet velocity conditions. The model utilized a time-series prediction strategy, where the current flow field data was inputted, and the physical quantity distribution at the next time step was outputted. The model simulated complete time series through recursive predictions. The results showed that CFDNN performed consistently with traditional CFD results both within and outside the training set, with prediction errors of less than 1% for temperature, velocity, and species distributions. This is the first deep learning-based method for reconstructing turbulent combustion fields, providing new approaches for real-time control, digital twins, and rapid optimization of complex systems such as gas turbines and scramjet engines. However, this study focused on concave-stabilized hydrogen flames and did not address more complex geometries or multiphysics couplings in actual combustion systems. Fujio et al. [93] proposed a predictive framework combining Gaussian process latent variable model (GPLVM) and deep learning to quickly, accurately, and reliably predict the flow field of scramjets. The design variables of the hypersonic vehicle, including the geometric parameters of the intake, fuel injection pressure, and angle, were input to the GPLVM, which compressed the flow field data into latent variables for training. A deep learning model then modeled the relationship between the design variables and these latent variables. The output included various physical variables of the flow field, such as static temperature, static pressure, velocity components, and mass fractions. GPLVM’s ability to perform nonlinear dimensionality reduction retained more information and enabled uncertainty quantification (UQ) to assess the reliability of predictions. The GPLVM + deep learning framework demonstrated excellent prediction accuracy, outperforming traditional POD models in predicting static temperature, static pressure, and velocity components. In the prediction of axisymmetric intake flow fields, the mean absolute error (MAE) for static temperature using the GPLVM model with an exponential kernel was 6.88, compared to 10.77 for the POD model, and the MAE for static pressure was 1155, compared to 1471, showing a significant accuracy improvement. In predicting a 2D fuel injection flow field, the GPLVM also outperformed POD, with a MAE of 0.604 for static temperature, compared to 2.0 for POD. Despite high overall prediction accuracy, there were larger errors in shock wave regions. Kong et al. [94] utilized deep learning techniques to directly use pressure and temperature sensor measurements on the intake wall, replacing traditional air data estimation methods to achieve more accurate real-time estimates of Mach number and intake air mass flow rate. Data required for training was obtained from numerical simulations, with inputs including pressure, static pressure, and static temperature at the intake. The network was trained using a CNN consisting of multiple convolutional and fully connected layers, with skip connections introduced to enhance the model’s expressive power and prevent gradient vanishing. The loss function used was MSE, and the network was optimized using the training set. The results showed that the deep learning-based model effectively reduced estimation biases caused by static temperature and static pressure errors. The model performed well on the test set, with a maximum relative error of 4.68% in Mach number estimation. Particularly at low Mach numbers, the model’s accuracy was significantly improved, reducing errors by 2%–4% compared to inertial navigation system estimates. The maximum relative error in mass flow rate estimation was 5.64%, much lower than the 20% error associated with inertial navigation system estimates. Although this method performed well on the test set, it relies on high-precision sensor data, and sensor errors in practical applications may affect the results. Furthermore, the model’s generalization ability under different flight conditions needs further exploration.
3.3. Target Optimization and Data Assimilation Based on Neural Networks
Brahmachary et al. [95] investigated the design optimization and nondesign state performance analysis of axisymmetric scramjet intakes. This study explored the performance of different intake structures during flight through multiobjective optimization, focusing on minimizing drag force and maximizing compression efficiency. The optimization method combined surrogate-assisted evolutionary algorithms with CFD, using the RANS equations to solve steady flow fields. The study shows that the general-purpose intake, by using smooth Bézier curves, provides the most flexible local shape control, achieving the highest compression efficiency of 94.8%, along with optimal flow uniformity and the highest total pressure recovery. The Busemann-type intake, although offering lower drag force and higher static pressure ratio, showed a loss in compression efficiency. The three-converging ramp intake exhibited larger compression efficiency losses and poorer flow uniformity compared to the Busemann-type and general-purpose intakes. The optimized intake still maintained good performance under various nondesign conditions, meeting constraints such as compression efficiency and exit temperature. However, due to the lack of real experimental data, the actual applicability of these optimization results could not be fully confirmed. Fujio and Ogawa [96] utilized deep learning techniques to optimize scramjet intake design to improve fuel mixing effectiveness. A MLP was used to predict the flow field, with inputs including six design variables and two coordinate variables, and outputs corresponding to four flow field attributes: static pressure, static temperature, axial velocity, and radial velocity. The network was trained using standardized training data to minimize the RMSE between predicted and actual values. The results from the MLP predictions showed that the RMSE for static pressure was 0.2556, while for static temperature, axial velocity, and radial velocity, the RMSE values were 0.1149, 0.1209, and 0.1508, respectively, with high R2 values, indicating good prediction accuracy. Houba et al. [97] employed an ensemble Kalman filter (EnKF) method combined with zero-dimensional flame models, one-dimensional shock models, Burgers’ equation, shock tubes, and other typical test cases to study the impact of different data assimilation strategies on combustion process prediction accuracy. The study demonstrated that the EnKF could effectively improve the predictive capabilities of simplified combustion models. Data assimilation made the model’s predictions of temperature changes and component concentrations during chemical reactions closer to experimental results. However, in high-complexity models, the data assimilation method proved highly sensitive to initial conditions, where even small initial deviations could lead to significant deviations in simulation results. Debnath and Roy [98] used an ANN model to predict the maximum combustion efficiency and thrust of the DLR scramjet engine. By combining ANN with CFD, they analyzed the performance of the scramjet engine under different structural angle variations. The study first used CFD simulations on 25 different DLR scramjet engine models, analyzing how different design parameters influenced combustion efficiency and thrust. The MLP-ANN model was trained using the Levenberg–Marquardt algorithm in MATLAB. The CFD simulation results showed that Model 21 had the highest combustion efficiency and thrust, while Model 5 had the lowest. The temperature distribution of different models showed that Model 21 had higher temperatures in the combustion chamber, which contributed to its superior combustion efficiency and thrust. The ANN model predictions were highly consistent with CFD results, with R2 = 0.997, RMSE = 0.038, and MAPE = 3.38 for combustion efficiency, and R2 = 0.999, RMSE = 0.016, and MAPE = 1.26 for thrust. These results demonstrated the high precision of the ANN model in predicting combustion efficiency and thrust. However, the study was limited to two parameters, support angle and expansion angle, and future work could extend the model to include more design parameters and expand the dataset to create more efficient ANN models. Gipe [99] employed surrogate modeling to optimize the combustion system design of a scramjet. Using the Kriging interpolation method, they combined sparse experimental data and high-cost CFD data to quickly generate the design space, thereby reducing computational time and costs during the design process. Multidimensional optimization techniques were used to search for the optimal parameter combinations in the design space. Local and global optimization methods were applied to evaluate the impact of various design variables on system performance. By introducing uncertainties in key parameters such as the reaction rate constant, they analyzed how these uncertainties affected the final design results. In the multidimensional design space, a Kriging surrogate model trained with 14 discrete data points controlled prediction errors within 7%, demonstrating the efficiency of the method. The optimization of different variables indicated that surrogate models could effectively fit complex combustion processes with fewer sample points. This method made the design of hypersonic vehicles more efficient. However, the study did not provide a robust evaluation system to guide the selection of data points.
3.4. Pattern Recognition and Classification Based on Neural Networks
An et al. [100] proposed a combustion mode analysis method that combines an autoencoder with the K-means algorithm. As shown in Figure 13, the method was evaluated using flame chemiluminescence and schlieren images of three combustion modes observed in the RBCC combustor. The model input consists of flame luminosity images captured by a high-speed camera, with an input size of 160 × 256 × 3, and schlieren images, with an input size of 160 × 256 × 1. Each input image is processed through an autoencoder, which outputs a dimensionally reduced latent space representation. This representation is a two-dimensional vector (2 × 1 × 1) that encodes the features of the image. A K-means algorithm is then applied to cluster the data in the latent space, ultimately classifying the combustion mode into one of three distinct combustion regimes.
Two autoencoders, each following the same encoder-decoder architecture, are developed to generate potential spatial representations of flame chemiluminescence and schlieren images. Figure 14 shows the autoencoder architecture. The K-means algorithm is used to determine the centroid and boundary of different combustion modes. Each autoencoder is trained on 750 images and tested on an additional 3,000 images.
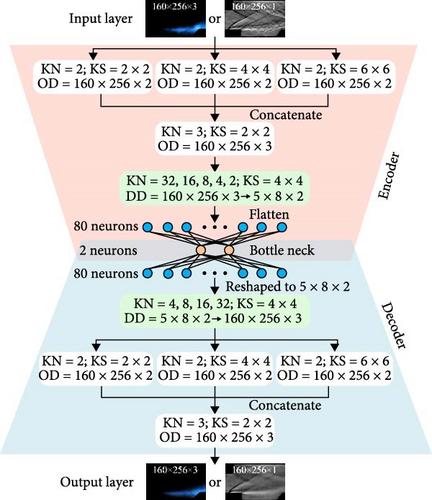
This method achieves 99% accuracy on both flame chemiluminescence and schlieren images. The images generated by the decoder demonstrate that the autoencoder captures key features of the reaction flow field. The autoencoder developed for flame chemiluminescence images also successfully detected combustion mode transitions during the ignition process, suggesting its potential for real-time combustion mode monitoring.
Kong et al. [101] proposed a general strategy for super-resolution reconstruction of the temperature field. Two deep learning models are employed to enhance the spatial resolution of the temperature field: the classical SRCNN and the novel multipath SRCNN (MPSRC) shown in Figure 15. In MPSRC, three paths, with and without pooling layers, are designed to fully capture the spatial distribution characteristics of the temperature field.
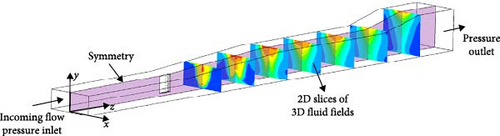
The combustion of the scramjet combustor at different Mach numbers was numerically simulated, and a data set for network training and testing was established. The corresponding HR temperature field was successfully reconstructed with significant accuracy. Kong et al. comprehensively investigated the reconstruction performance of these models and compared them with the bicubic interpolation method. Figure 16 is a schematic diagram of the computational domain and the two-dimensional temperature field slice.
The experimental results show that both DL methods can significantly improve the accuracy of super-resolution reconstruction, while MPSRC can provide better reconstruction results with lower mean square error and higher peak SNR.
Zhu et al. [102] proposed a combustion mode classification method based on a CNN, which directly learns features from the original pressure data collected during supersonic combustion experiments. The proposed method is compared with traditional machine learning techniques, such as MLP, k-means, feedforward neural networks, and support vector machines. Additionally, feature data are manually extracted from both the time and frequency domains, and the impact of different feature extraction methods on the performance of various models is studied by considering both the original and feature data. Figure 17 shows the models used.
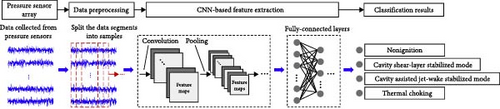
The results show that the proposed method based on CNN can reveal the intrinsic characteristics from the original data and effectively complete the classification of the four main combustion modes in the combustion chamber. Compared with other comparison methods, the new method achieves higher classification accuracy and better generalization performance.
Li et al. [103] employed an improved deep learning method for precise segmentation of schlieren images, extracting wave structures from the flow field of a supersonic combustion chamber. This method addresses the issue of low segmentation accuracy caused by background interference in traditional image segmentation techniques. A ResNet34-based fully convolutional network (FCN8S) was used as the main network, incorporating residual modules to solve problems related to gradient vanishing and explosion due to excessive network layers. Dilated convolution was introduced to expand the convolutional layers, enhancing the network’s ability to perceive global features and improving the aggregation of contextual information. Additionally, a CAM and SAM were incorporated, enabling the network to adaptively focus on shockwave regions in the image, further improving segmentation accuracy. The neural network’s input consisted of schlieren images from the flow field of the supersonic combustion chamber, with each image having a resolution of 1056 × 526, and a total of 1600 images were used. The output was the segmented image, primarily focusing on recognizing and extracting shockwave structures from the schlieren images. The deep learning model separated the shockwave regions from the background areas in the images, providing effective flow field information. The evaluation metrics used included pixel accuracy (PA), recall, intersection over union (IoU), and F1 score. The results showed PA = 78.47%, recall = 83.81%, IoU = 67.51%, and F1 score = 80.32%. Compared to the original FCN8S method, PA improved by 19.27%, recall increased by 10.79%, IoU increased by 7.82%, and the F1 score improved by 14.89%. The study demonstrated that the deep learning-based schlieren image segmentation method could effectively extract shockwave structures from the supersonic combustion chamber flow field, with significantly better segmentation accuracy and robustness than traditional image processing methods. By introducing an improved fully CNN and attention mechanisms, this method accurately distinguishes shockwaves from background noise in complex flow fields. This approach provides strong support for real-time monitoring and flow field control of future hypersonic vehicles. However, the schlieren image dataset used was obtained through wind tunnel experiments, and there is no publicly available standard dataset, which may affect the generalizability and scalability of this method.
3.5. Behavior Diagnosis and Performance Evaluation Based on Neural Networks
Labahn et al. [104] employed the EnKF as a data assimilation method, assimilating TPIV and OH–PLIF experimental data into LES to assess the FPV model’s ability to diagnose local flame extinction and reignition events in the short term. The experimental data were used as observations and compared with LES simulation results during the data assimilation process. EnKF improved the simulation results by updating the temperature and velocity fields, enhancing the accuracy of LES predictions for OH–LIF signals and axial velocity. In local flame extinction and reignition processes, the EnKF method successfully reproduced the main features observed in the experiments. Zhang et al. [105] introduced a framework based on field inversion and machine learning to improve the existing γ-Reθ transition model. The study utilized an iterative REnKF method to derive correction terms for transition initiation points, which were then solved numerically to improve the transition model. The RF algorithm was used to construct the mapping between flow field features and the β distribution, improving the model’s generalization and prediction accuracy. After introducing the correction term, the improved γ-Re θ transition model significantly enhanced the prediction accuracy for hypersonic boundary layer transition behavior. However, the improved model failed to accurately predict the heat flux peak at the end of the transition region for the blunt cone model at high Reynolds numbers. Chin and Gamba [106] used machine learning methods to predict shock train dynamics and potential engine instability in scramjet engines. They developed a method to predict shock train motion from limited observable quantities, particularly focusing on whether wall static pressure and schlieren visualization measurements could predict engine surge phenomena. The study employed a Recurrence Plot combined with a CNN. The time-series data were first converted into recurrence plots, allowing the problem to be treated as an image recognition task. The CNN then automatically identified features in the input data and classified the direction of shock train motion, achieving a classification accuracy of over 90%. One-dimensional pressure measurement data were used to predict the position of shocks at different future time points. Additionally, cross-spectral analysis was used to identify the high correlation frequencies between pressure fluctuations and shock oscillations, and filters were developed to improve prediction accuracy. For quasi-steady data, the filtered model reduced the maximum error from 68% to 52%, with an average prediction error of about 10 mm. For forced datasets, the model performed better, reducing the error from 7.3% to 3.3%, with a prediction error for individual shock positions reaching as low as 6 mm. The study found that the model performed best when both input and prediction included smaller time information, and that short-term predictions were more accurate than long-term predictions. Preliminary studies using schlieren images as input revealed overfitting issues. Fujio and Ogawa [107] explored the application of deep learning for predicting supersonic viscous flow fields, particularly focusing on changes in the flow state within scramjet intakes. The study further employed UQ to identify which flow fields and phenomena were difficult to predict accurately and explored how increasing training data could improve model performance. A MLP neural network was used for flow field prediction. The model inputs included design variables and coordinate variables, with outputs corresponding to flow properties such as static pressure, static temperature, axial velocity, and radial velocity. Five hundred geometries were generated using Latin Hypercube Sampling to train the neural network. UQ was performed using both ensemble-based and distance-based methods. The ensemble-based approach evaluated uncertainty by measuring variations in the outputs of multiple models, while the distance-based approach quantified uncertainty by assessing the similarity between inputs. The deep learning model provided accurate flow field predictions in most cases, but prediction errors were larger in flow fields involving strong boundary layer separations or shock-boundary layer interactions. Ispir et al. [108] combined numerical simulations with machine learning techniques to evaluate engine performance. Using CFD databases and one-dimensional expansion equations, they analyzed and estimated the performance of a dual-mode ramjet (DMR) engine, focusing on the impact of fuel parameters on supersonic combustion. The study integrated numerical simulations, regression models, and machine learning techniques, employing kernel regression, Gaussian process regression (GPR), and ANN for data regression. A database covering three design variables was created using CFD methods. Kernel regression, GPR, and ANN were used to regress combustion efficiency, total pressure recovery coefficient, and flow variables, assessing the accuracy of these models in diagnosing engine performance. All three models predicted combustion efficiency with over 90% accuracy in the first 80 cm of the combustion chamber, but in the latter half of the combustion zone, ANN outperformed the other methods, achieving superior prediction accuracy. The wedge angle of the fuel pillar had the greatest impact on combustion efficiency and engine performance, particularly regarding combustion efficiency and total pressure recovery. Different fuel pillar configurations had varying effects on combustion efficiency and thrust. However, the study was limited by a small dataset, containing only 100 design configurations, which may restrict the predictive accuracy of the regression models. Soize et al. [109] introduced probabilistic learning methods to enhance the prediction of complex flows in scramjets. They employed a manifold-based probabilistic learning method, which enhances the predictive capability of fluid dynamics models by discovering the geometric structure of the dataset and generating additional random vectors based on the expanded dataset. The input data included 11 uncertain model parameters and 10 output quantities of interest, such as combustion efficiency, stagnation pressure loss ratio, and turbulent kinetic energy at different flow positions. Additional samples were generated using the Markov chain Monte Carlo (MCMC) method to further improve the estimation of the probability distribution, providing more statistical information about reactive flows. The study demonstrated that, as the number of samples increased, the PDF of combustion efficiency gradually converged. For N = 256, the distribution of combustion efficiency was well-estimated across multiple datasets. The stagnation pressure loss ratio also showed convergence as the number of samples increased, exhibiting consistency between different datasets (d08 and d16). The PDF of turbulent kinetic energy showed convergence at various flow positions, and the statistical results of TKE gradually stabilized as the dataset grew. The research showed that the manifold-based probabilistic learning method significantly improved model prediction capabilities, especially in cases with limited computational samples, effectively expanding the dataset and improving the accuracy of uncertainty analysis. This method allowed valuable statistical information about the combustion process to be obtained, even with limited LES simulation samples, helping to understand the physical behavior of complex turbulent flows. However, while MCMC generated a large number of additional samples, this process still had a high computational cost, and its efficiency could decrease when handling high-dimensional data.
3.6. More Applications Based on Neural Networks
Bellemans et al. [110] proposed a machine learning framework to simplify the simulation of plasma-assisted combustion (PAC), using principal component analysis (PCA) and GPR to reduce the dimensionality of combustion mechanisms and improve computational efficiency. PCA was used to map multiple variables in complex chemical reaction mechanisms to a smaller space consisting of principal components, thus reducing dimensionality. PCA transformed the original 55 substances into 44 principal components. GPR was then employed to perform nonlinear regression on the reduced variables, further decreasing the computational resources required for the model. Through GPR, only two principal components were needed to effectively reconstruct the physical changes in the combustion process. However, for some substances not directly related to temperature, more principal components were required, leading to some reconstruction errors. Additionally, there was a significant bias in the predicted results for nitrogen mass fraction. Cui and Ou [111] proposed a novel modeling method based on a model transfer strategy and process similarity, which uses existing combustion chamber data combined with a small amount of new combustion chamber data to quickly build a high-precision combustion chamber model. This approach reduces modeling time and cost while maintaining prediction accuracy. The combustion chamber’s operating parameters were categorized into three types: configuration parameters, inlet parameters, and outlet parameters. The relationship between input variables X and output variables Y was described as P = R(X, Y), using a black-box approach to represent the combustion chamber characteristics, with a BP neural network simulating the input–output mapping. A base model F was trained using the bagging algorithm and BP neural network with existing combustion chamber data. The study found that approximately 20 sets of data were sufficient for base model transfer. A clustering estimation method was used to extract key data points from existing data, and a small number of experiments were conducted on the new combustion chamber to capture its unique features. The base model’s input and output spaces were adjusted by scaling and shifting to adapt to the new chamber’s data. The input space was then divided into several local regions, and bias compensation was applied for each region to create a global bias compensation model, improving prediction accuracy for nonlinear processes. The model was then validated with unused new combustion chamber data. The simulation used mechanism model-generated data to replace experimental data, comparing the base model, corrected model, and further corrected model with the actual values from the mechanism model. The results showed that the further corrected model had the least deviation from the mechanism model, achieving the highest prediction accuracy. The model demonstrated consistency with the mechanism model in predicting the total pressure recovery coefficient, confirming the method’s reliability. Compared to traditional CFD methods, this method eliminates the need for constructing complex physical equations and significantly reduces the computational burden by training with data points, but it may fail if there is insufficient new combustion chamber data for clustering or transfer. Ispir et al. [112] utilized machine learning methods for reduced-order modeling of multistrut fuel-air mixing processes, proposing a low-cost, efficient surrogate model capable of calculating hypersonic engine thrust with an error of less than 10%, and predicting mixing efficiency with an error of less than 4%. The study identified the wedge angle of the strut as the most crucial factor affecting fuel mixing efficiency, with smaller wedge angles enhancing turbulent mixing but increasing total pressure loss. Additionally, increasing the V-arrangement angle accelerated mixing but potentially created localized overpressure zones. This study provides important insights for the optimization design of scramjet engines, though future work should integrate combustion chemical reactions and reinforcement learning optimization to further enhance the model’s applicability. Xu et al. [113] proposed a machine learning-based noncontact temperature measurement technique for supersonic combustion chamber temperature measurement in high-noise environments. Temperature calculations were performed using the emission spectra of OH radicals, with spectral data generated through theoretical calculations and noise added to simulate the SNR in the experimental environment. The neural network’s input was preprocessed spectral data. For CNN and MLP, the input consisted of emission spectra of OH radicals in the 300–320 nm wavelength range, with noise and spectral resolution included. The input data was normalized before training, and Gaussian noise was added at various levels to simulate real measurement conditions. The output was the temperature predicted from the input spectral data. The study compared the performance of CNN and MLP in temperature inversion, especially under noisy conditions, finding that CNN outperformed MLP in suppressing the noise impact. The study highlighted that convolutional neural networks effectively resist noise interference, with prediction errors of less than 50 K in the 500–4000 K temperature range. Compared to traditional two-line spectroscopic methods, CNN demonstrated greater stability in noisy environments, with a RMSE of 55.8 K, while the two-line method showed an error of 1511.9 K. Experimental results also indicated that the CNN method was close to the temperature measurements obtained by tunable diode laser absorption spectroscopy, with a measurement error of about 400 K. While the method showed good noise suppression and high precision in the experiment, it had limitations. The assumption of local thermal equilibrium in OH radical emission spectra may not fully hold in actual high-temperature environments, leading to some error. Additionally, temperature measurement accuracy is limited by spectral resolution and instrument precision, which may require further optimization in both instruments and algorithms. Furthermore, the neural network’s training performance varies at different noise levels, particularly in low-SNR environments, where more data may be required to enhance reliability and robustness in practical applications.
As the application of various neural networks in the field of scramjet engines expands, more and more scholars are showing great interest in the network architectures, training datasets, and validation strategies of different methods. Table 2 below introduces the basic principles, network architectures, training datasets, validation strategies, evaluation metrics, computational efficiency, applications in scramjet engines, and existing issues of several different neural networks.
| Neural network model | Principle | Network structure | Training set | Validation strategy | Evaluation metrics | Computational efficiency | Application in hypersonic scramjet | Existing issues |
|---|---|---|---|---|---|---|---|---|
| Perceptron | Basic neural network model for linearly separable problems | Single-layer structure with direct input–output connections | Small-scale, linearly separable datasets | Typically evaluated on the training set without an independent validation set | Accuracy | High computational load, fast training speed | Simple classification tasks, e.g., flow field partitioning in iterative optimization | Unable to handle linearly inseparable problems |
| Multilayer perceptron | Handles nonlinear problems via hidden layers | At least one hidden layer with fully connected layers | Medium-scale datasets for classification/regression | Cross-validation or hold-out method | Accuracy, MSE | Moderate computational load, increases with layers/nodes | Performance prediction, e.g., mapping design parameters to predict flow field performance in scramjet | Overfitting risks requiring regularization |
| Convolutional neural network | Extracts local features via convolutional layers for image processing | Convolutional layers, pooling layers, and fully connected layers | Large-scale image datasets | Independent validation set or cross-validation | Accuracy, Recall, F1-score | High computational load, requires high-performance hardware | Image reconstruction/prediction, e.g., predicting velocity, pressure, and temperature fields in combustion chambers | Long training time and resource-intensive |
| Recurrent neural network | Processes sequential data via recurrent connections with memory capability | Layers with recurrent connections for time-series data | Time-series data | Time-split training/validation sets or sliding window | Accuracy, Graph Density | High computational load, slow training | Temporal prediction, e.g., pressure and temperature evolution in combustion chambers | Gradient vanishing/explosion, training instability |
| Long short-term memory | Improved RNN addressing gradient vanishing for long sequences | Gated recurrent units with memory cells | Long sequences (e.g., extended time-series) | Similar to RNN with time-split datasets | Accuracy, Graph Density | Higher computational load, slower training | Long-term temporal prediction, e.g., flame evolution, vortex simulation, and thrust prediction | Potential gradient explosion risks |
| Generative adversarial network | Generates data via adversarial training between generator and discriminator | Two networks: generator and discriminator | Unlabeled datasets for unsupervised learning | Training set evaluation; lacks independent validation | Data quality metrics | Unstable and complex training | Synthetic data generation, e.g., flow field/flame images for data augmentation to enhance simulation accuracy | Mode collapse and limited diversity |
| Physics-informed neural network | Integrates physical constraints into neural networks | Incorporates physical governing equations | Hybrid simulation/experimental data with physical laws | Cross-validation, physics-consistency evaluation | MSE, PSNR, SSIM, Physical-Consistency-Error | Long training time and requires extensive iterations | Physics-constrained optimization, e.g., embedding Navier–Stokes equations for combustion simulation, vortex modeling, and flow field prediction | Sensitive to boundary/initial conditions, slow convergence in complex scenarios |
The introduction of neural network in the research process of scramjet engine is an important direction for future development. At present, the research work needs to be deepened, mainly focusing on the following aspects:
3.6.1. Flow Field Prediction and Reconstruction
Based on neural networks, particularly CNNs, flow field prediction and reconstruction have been widely applied in the study of scramjet engines. Researchers have developed various flow field prediction models by integrating experimental data and numerical simulation results. CNNs can predict flow fields using wall pressure sequences, image data, or CFD data, offering high computational efficiency and accuracy. However, current flow field prediction models still face errors under high Mach numbers and complex flow conditions, especially in predicting shock wave locations and modeling complex turbulent regions. Additionally, predictions in sparse data regions may be unstable. Future research will focus on improving the generalization ability of neural network models, exploring more robust deep learning techniques to enhance flow field prediction accuracy and speed, and further improving model performance in high Mach number and complex flow scenarios. Furthermore, training with more high-quality experimental data will be explored to reduce prediction errors, and real-time flow field monitoring and control technologies will be developed.
3.6.2. Combustion Process Simulation and Prediction
Neural networks have been successfully applied to the prediction of combustion processes in scramjet engines. By extracting features of flame evolution from flow field data, neural networks can effectively predict the spatiotemporal evolution of flames within the combustion chamber. However, in complex combustion processes and hypersonic combustion conditions, issues such as the nonlinear behavior of flames, turbulence, and the coupling of reactive flows lead to significant prediction errors in neural network models. The interaction of multiple physical fields, such as the combustion chamber’s geometric structure and equivalence ratio, also makes predictions more challenging. Future research will focus on improving the adaptability of neural networks in hypersonic combustion environments, particularly in predicting complex flame structures. By incorporating models with multiphysics coupling and strategies that integrate deep learning with physics-driven models, prediction accuracy can be enhanced. Additionally, by combining real-time measurement data, intelligent systems capable of real-time flame monitoring and prediction will be developed.
3.6.3. Wall Thermodynamic Property Analysis
Neural networks have been widely applied in the prediction of wall thermodynamic properties, particularly in the simulation of parameters such as wall pressure, temperature, and heat flux density. By employing techniques like deconvolution networks, neural networks can directly predict complex thermodynamic properties from wall sensor data. However, current wall prediction models still lack sufficient accuracy under hypersonic and high thermal load conditions. Additionally, predictions of wall temperature and pressure are susceptible to the quality of input data and insufficient training data, particularly in engines with complex geometric configurations. Future research will focus more on improving the accuracy of wall property predictions under high-temperature and high-pressure environments. By integrating more HR sensor data and multisource information fusion, more precise thermodynamic models will be developed. At the same time, advanced deep learning algorithms will be employed to predict and optimize wall properties, enabling more accurate design and control.
3.6.4. Objective and Design Optimization
Neural networks have been widely applied in the optimization of design variables such as the intake duct, injection parameters, and combustion chamber structure in scramjet engines. Neural networks enable rapid prediction of design parameters, optimizing engine performance. However, existing optimization models often rely on limited training data, posing a risk of overfitting. The computational efficiency and generalization capability of these models still have room for improvement when exploring complex design spaces, requiring higher computational resources and data support. Future research will integrate more experimental data and efficient training algorithms to further improve the accuracy and computational efficiency of optimization models. Additionally, exploring intelligent optimization methods, such as DRL will help better handle complex design spaces and achieve a more intelligent design optimization process. The integration of multiphysics and multiobjective optimization methods will also be a key direction for future design optimization.
3.6.5. Turbulence Modeling and Control
Turbulence modeling and control is a critical area of research in scramjet engines. PINNs have been applied to improve turbulence models, effectively simulating complex flow phenomena such as near-wall turbulence. While neural networks have made some progress in turbulence modeling, their predictive capability remains limited in high Reynolds number flows and strong turbulence regions. Current models still lack accuracy when handling complex phenomena like multiscale turbulence, transition, and flow separation. Future research will focus on improving neural network architectures, particularly by integrating physical knowledge with data-driven approaches, to enhance the accuracy and stability of turbulence modeling. Additionally, by combining more experimental data with efficient simulation methods, intelligent algorithms capable of turbulence control under complex flow conditions will be developed to address the challenges faced by hypersonic vehicles in practical applications.
4. Closing Remarks
The rise and development of AI provide a new research paradigm for the study of fluid mechanics, and the problem of fluid mechanics brings new challenges to the development of AI. The development of AI methods represented by neural networks has brought new technical approaches to solve the experimental, theoretical, and computational problems of scramjet research. In the future, deep learning and neural networks can be used to construct complex nonlinear models to predict and optimize the design parameters of scramjet engines, such as aerodynamic shape, combustion chamber geometry, intake and exhaust duct design, etc., to improve combustion efficiency and overall performance; the fault diagnosis system based on neural network can be used to quickly identify potential failure modes, predict the remaining useful life, and improve the safety and reliability of the engine. Neural networks can also be used to simulate complex chemical reactions and turbulence phenomena in supersonic combustion processes to assist scholars in understanding and improving combustion strategies.
But it also faces several challenges. The internal environment of the scramjet engine varies under different flight conditions. Neural network needs to be able to deal with such uncertainties and variability to ensure that its prediction and control decisions under various operating conditions are robust enough. At the same time, it lacks certain interpretability and generalization ability in engineering applications. The model should not only be able to explain the existing experimental data, but also be able to make accurate predictions and control decisions under new conditions. If the neural network is used for real-time control of scramjet engines, the real-time response problem of neural network computing must be solved, including the implementation of embedded hardware and the low-latency optimization of the algorithm.
In summary, there are many challenges in the application of neural networks in the direction of scramjet engines. It requires interdisciplinary cooperation, combined with traditional physical models and advanced AI technologies, to overcome problems. At the same time, with the continuous improvement of computing power and the deepening of theoretical research, it is expected to make greater breakthroughs in this area in the future.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This study was supported by the National Natural Science Foundation of China (Grant 92252206) and the Science and Technology Program of Hunan Province (Grant 2023RC3018).
Open Research
Data Availability Statement
The research data are not shared.




