Volume 2025, Issue 1 9990362

Research Article

Open Access

Research on Joint Optimization of Reserve and Dispatching for Multivariety Emergency Materials Based on NSGA-II

Xi Zhu

orcid.org/0009-0009-8730-8131

National Demonstration Center of Experimental Teaching for Ammunition Support and Safety Evaluation Education , Army Engineering University of PLA , Shijiazhuang , 050003 , China , ust.com.cn

Search for more papers by this author

Kai Yao,

Kai Yao

National Demonstration Center of Experimental Teaching for Ammunition Support and Safety Evaluation Education , Army Engineering University of PLA , Shijiazhuang , 050003 , China , ust.com.cn

Search for more papers by this author

Aiqiang Guo,

Aiqiang Guo

National Demonstration Center of Experimental Teaching for Ammunition Support and Safety Evaluation Education , Army Engineering University of PLA , Shijiazhuang , 050003 , China , ust.com.cn

Search for more papers by this author

Tianpeng Li,

Tianpeng Li

National Demonstration Center of Experimental Teaching for Ammunition Support and Safety Evaluation Education , Army Engineering University of PLA , Shijiazhuang , 050003 , China , ust.com.cn

Search for more papers by this author

Weiyi Wu,

Weiyi Wu

Shijiazhuang Campus , Army Engineering University of PLA , Shijiazhuang , 050003 , China , ust.com.cn

Search for more papers by this author

Xinbao Gao,

Corresponding Author

Xinbao Gao

[email protected]

orcid.org/0000-0001-7935-4183

National Demonstration Center of Experimental Teaching for Ammunition Support and Safety Evaluation Education , Army Engineering University of PLA , Shijiazhuang , 050003 , China , ust.com.cn

Search for more papers by this author

Xi Zhu,

Xi Zhu

orcid.org/0009-0009-8730-8131

National Demonstration Center of Experimental Teaching for Ammunition Support and Safety Evaluation Education , Army Engineering University of PLA , Shijiazhuang , 050003 , China , ust.com.cn

Search for more papers by this author

Kai Yao,

Kai Yao

National Demonstration Center of Experimental Teaching for Ammunition Support and Safety Evaluation Education , Army Engineering University of PLA , Shijiazhuang , 050003 , China , ust.com.cn

Search for more papers by this author

Aiqiang Guo,

Aiqiang Guo

National Demonstration Center of Experimental Teaching for Ammunition Support and Safety Evaluation Education , Army Engineering University of PLA , Shijiazhuang , 050003 , China , ust.com.cn

Search for more papers by this author

Tianpeng Li,

Tianpeng Li

National Demonstration Center of Experimental Teaching for Ammunition Support and Safety Evaluation Education , Army Engineering University of PLA , Shijiazhuang , 050003 , China , ust.com.cn

Search for more papers by this author

Weiyi Wu,

Weiyi Wu

Shijiazhuang Campus , Army Engineering University of PLA , Shijiazhuang , 050003 , China , ust.com.cn

Search for more papers by this author

Xinbao Gao,

Corresponding Author

Xinbao Gao

[email protected]

orcid.org/0000-0001-7935-4183

National Demonstration Center of Experimental Teaching for Ammunition Support and Safety Evaluation Education , Army Engineering University of PLA , Shijiazhuang , 050003 , China , ust.com.cn

Search for more papers by this author

First published: 17 March 2025

https://doi.org/10.1155/ddns/9990362

Academic Editor: Giulio E. Cantarella

Share a link

Email
Wechat
Bluesky

Abstract

Emergency material reserve and dispatching are important measures to reduce casualties and property losses after natural disasters occur. However, there has not yet been research that optimizes both the reserve and distribution of emergency materials together. This paper investigates the joint optimization of reserve and dispatching for multivariety emergency materials. Considering the timeliness, economy, and safety of emergency rescue, a multiobjective joint optimization model for emergency material reserve and dispatching has been established, with the targets of minimizing the total delay time, minimizing the total cost, and maximizing the number of safely delivered. Given the uncertainty in the emergency rescue, this paper uses interval numbers to represent transportation speed and triangular fuzzy numbers to represent transportation costs. Then, we study the model solution method, which mainly includes the conversion of uncertain constraints and the NSGA-II algorithm used for calculating the proposed multiobjective model. In the end, a numerical example is provided to demonstrate the validity and effectiveness of the proposed model and solution method. The results of the comparative analysis indicate that the comprehensive weighting strategy proposed in this paper is more balanced than the strategy that uses a single objective value as the optimization objective.

1. Introduction

In recent years, natural disasters, mainly including floods, typhoons, earthquakes, and geological hazards, have frequently occurred in China. Taking the year 2023 as an example, these natural disasters collectively resulted in 95.44 million people being affected, 209,000 houses collapsing, and direct economic losses amounting to 345.45 billion yuan. Compared with the average of the past 5 years, the number of collapsed houses and direct economic losses increased by 96.9% and 12.6%, respectively [1]. It is crucial to scientifically reserve and promptly dispatch emergency materials to disaster-affected areas to reduce casualties and property losses [2]. Therefore, the reserve and dispatching of emergency materials have gradually become a focal point for researchers [3, 4].

Emergency materials reserve is a preparatory work for natural disasters before they occur. This usually involves predicting based on the local geographical location, terrain, climate, social environment, and the probability of natural disasters occurring [5]. On this basis, analyzing the situation of emergency materials reserve during disaster occurrences. Reasonable emergency materials reserve can reduce the time required for dispatching, as well as lower costs, and reduce casualties and economic losses. Currently, research in the field of emergency materials reserve mainly focuses on the site location of reserve depots. However, the location of the reserve depots is usually fixed, and the staff of the relevant institutions can generally make optimized decisions about the types and quantities of emergency materials reserved in each depot. At present, research in this area is still extremely rare. Otherwise, the dispatching of emergency materials occurs after natural disaster events [6]. The main work is to transport emergency materials from various reserve depots to disaster-stricken areas. It is necessary to comprehensively consider multiple factors such as road conditions and the environment. Swift, economical, and reasonable emergency materials dispatching can reduce economic losses and save lives. In addition, some papers have started to research the joint optimization of location and dispatching. According to our observation, no paper has yet studied the joint optimization of emergency material reserve and dispatching.

To address the identified gap, this paper examines the joint optimization of emergency material reserves and dispatching processes. By considering factors such as timeliness, cost-effectiveness, and safety, a multiobjective joint optimization model has been developed for the reserve and dispatch of diverse emergency materials. This model aims to minimize total delay time, reduce total costs, and maximize the safe delivery of emergency materials. To enhance the model’s applicability to real-world scenarios, uncertainties were incorporated during the modeling process, employing interval numbers and triangular fuzzy numbers to represent transportation speeds and costs, respectively. Furthermore, a solution method was proposed, which involves transforming uncertain constraints and utilizing the NSGA-II optimization algorithm. In the end, a comprehensive weighting strategy is adopted to select the optimal solution from the Pareto front.

The remainder of this article is organized as follows. Section 2 conducts a literature review based on the optimization research related to emergency materials. Section 3 describes the research questions and proposes the model assumptions. A joint optimization model for the reserve and dispatching of emergency materials is established in Section 4. Section 5 studies how the proposed model was solved, including uncertain constraints processing and optimization algorithm. A numerical example is presented in Section 6, demonstrating the effectiveness of the proposed model. The final section presents the conclusion of this paper.

2. Literature Review

Over the past few years, there has been a significant amount of research on the optimization of emergency materials. Before proceeding with further research, we have conducted a literature review of optimization research related to emergency materials. In Table 1, we reviewed 21 pieces of literature [7–27], which were mainly summarized in optimization problems, material variety, objective function, solution algorithm, and uncertainty.

Table 1. Overview of the optimization research related to emergency materials.

References	Optimization phase	Material variety	Objective function	Optimization solution	Uncertainty
Wang et al. [7]	Dispatching	Multiple	Minimize the time; minimize the cost	Ideal point method	No
Li et al. [8]	Dispatching	Single	Minimize the time; minimize the cost	Augmented ε-constraint method	Yes
Paul and Zhang [9]	Location; dispatching	Single	Minimize the cost	IBM ILOG CPLEX optimizer solver	Yes
Chen et al. [10]	Dispatching	Single	Minimize the time; minimize the cost	ABC	No
Sun, Ren, and Cai [11]	Dispatching	Single	Minimize the time; minimize the cost	NSGA-II	Yes
Lu and Sun [12]	Dispatching	Multiple	Minimize the penalty cost; minimize the sum of allocation cost	PSO	No
Du et al. [13]	Location; dispatching	Single	Maximize the efficiency	Heuristic algorithm	No
Tang et al. [14]	Dispatching	Multiple	Maximize the satisfaction	Ideal point method	No
Ding et al. [15]	Dispatching	Multiple	Minimize the time; minimize the cost; minimize the unsatisfaction	NSGA-II, PSO, CS, BA	No
Yan, Di, and Zhang [16]	Dispatching	Single	Minimize the response time; minimize the cost	Linear weighted sum method	Yes
Jiang and Ouyang [17]	Location	Single	Minimize the station setup costs; minimize the expected economic loss	Lagrangian relaxation-based algorithms	Yes
Yu [18]	Location; reserve	Single	Minimize the cost	Modified column-and-constraint generation method	Yes
Zhang et al. [19]	Dispatching	Single	Minimize the time; minimize the cost; maximize the satisfaction	GA, PSO	No
Li, Che, and Chu [20]	Location; dispatching	Single	Minimize the rescue costs	Gurobi	Yes
Yan et al. [21]	Dispatching	Multiple	Minimize the operating costs; maximize the satisfaction; maximize the effectiveness.	NSGA-II	No
Shu et al. [22]	Dispatching	Single	Minimize the time; minimize the cost	VNS-NSGA-II	No
Tang et al. [23]	Dispatching	Single	Minimize the cost	Interval interaction algorithm	Yes
Xu et al. [24]	Location; dispatching	Single	Minimize the time; minimize the cost	Robust optimization	Yes
Wang et al. [25]	Location; dispatching	Single	Minimize the time; minimize the cost	Benders decomposition	Yes
Yang et al. [26]	Location; dispatching	Single	Minimize the cost	Benders decomposition	Yes
Li et al. [27]	Location; dispatching	Single	Minimize the costs	Scenario-based decomposition heuristic algorithm	Yes
This paper	Reserve; dispatching	Multiple	Minimize the total delay time; minimize the total cost; maximize the emergency materials safely delivered	NSGA-II	Yes

Regarding the optimization problem, the reviewed papers mainly cover three aspects, namely, dispatching, location, and reserve. As can be seen from Table 1, a total of 19 articles have studied the problem of optimization for the dispatching of emergency materials. The study of the dispatching of emergency materials plays a crucial role in the emergency rescue process. Scholars have conducted extensive research on the dispatching of emergency materials, and the models for dispatching have been continuously optimized. There are a total of 9 articles that study the issue of site location for emergency material depots. The site location for emergency material depots is a complex process. To plan and layout systematically and rationally, it is necessary to fully consider the factors affecting the site location of emergency material depots. The model considers the reliability problem of facilities by linking the damage strength of a disaster to the partial capacity loss of an emergency facility within the robust optimization framework. Among the 21 articles, there are 7 that research the joint optimization of site location and dispatching, which promotes the research in this direction to be completer and more rigorous. A reasonable location for emergency material depots is the key to ensuring that emergency materials are supported to disaster areas on time, and whether emergency materials can be quickly delivered to disaster areas is also a verification of whether the location of the emergency material depot is reasonable. In our review of the literature, only 1 article studies [18] the reserve optimization of emergency materials, namely, how to reasonably determine the reserve type and quantity at different reserve depots.

Concerning the material variety, most of the papers studied the optimization of single-variety emergency materials. However, only 5 papers in Table 1 are targeted at multivariety emergency materials. In actual emergency rescue processes, the emergency materials that need to be reserved and dispatched often include multiple varieties, such as food, medical materials, and rescue tools.

With respect to the optimization objectives, recent studies on the optimization of emergency materials have generally included multiple optimization objectives, including minimizing the time, minimizing the cost, maximizing the efficiency, maximizing the satisfaction, minimizing the penalty cost, minimizing the unsatisfaction, and minimizing the expected economic loss. The objectives are primarily established from the four aspects of time, cost, efficiency, and satisfaction.

In regard to the optimization solution, models are primarily solved using three types of solution methods, namely, mathematic algorithm, heuristic algorithm, and optimization solver software. As can be observed from Table 1, 9 papers used heuristic algorithms to solve the model, including artificial bee colony algorithm (ABC) [10], NSGA-II [11, 15, 21], particle swarm optimization algorithm (PSO) [12, 15, 19], cuckoo search algorithm (CS) [15], bat algorithm (BA) [15], and genetic algorithm (GA) [19]. Heuristic algorithms generally find approximate or satisfactory solutions to problems within an acceptable time frame, especially when dealing with high complexity and large computational demands. However, they may sometimes get stuck in local optima. Eleven of the reviewed papers adopted the mathematic algorithm, such as the ideal point method [7, 14], augmented ε-constraint method [8], linear weighted sum method [16], Lagrangian relaxation-based algorithms [17], column-and-constraint generation method [18], interval interaction algorithm [23], robust optimization [24], and Benders decomposition [25, 26]. Mathematic algorithms have a higher level of precision, but they are more complex and often require a significant amount of computational resources and time. In addition, two papers used optimization solver software, namely, IBM ILOG CPLEX optimizer solver [9] and Gurobi [20].

Regarding uncertainty, half of the papers reviewed in Table 1 considered uncertainty. During emergency rescue operations, there are often many uncertain pieces of information. If these uncertainties can be taken into account during the modeling process, the optimization results can be closer to the actual situation.

Based on the above summarizes, the following can be concluded:

1.
Research on the optimization of emergency materials is mainly focused on the dispatching of emergency materials and the site location of reserve depots, with rare studies on the reserve of emergency materials. Based on our research findings, there is still no research on the joint optimization of emergency material reserve and dispatching.
2.
Studies on multivariety emergency materials are more in line with the actual situation of emergency rescue, but there are relatively few such studies at present.
3.
The multiobjective optimization of emergency materials has become mainstream, but there are rare studies that incorporate safety factors as part of the optimization objectives.
4.
The use of heuristic algorithms is the main approach for solving the optimization models of emergency materials, and it is faster and more efficient in solving complex models.
5.
Uncertainty is increasingly being incorporated into the field of emergency material optimization, making the emergency material optimization models more in line with the actual situation of emergency rescue.

Consequently, this paper studies the joint optimization of multivariety, multiobjective emergency material reserve and dispatching, incorporating safety as an optimization objective. In addition, we not only consider uncertainty but also use the NSGA-II algorithm to solve the proposed model.

3. Problem Description and Assumptions

3.1. Problem Description

In this paper, the support point is used to represent the reserve depot, and the demand point is used to represent the disaster area. Support points are the main reserve institutions for emergency materials, capable of reserving different types of emergency materials, and the total amount of reserved materials cannot exceed their maximum reserve capacity. Due to differences in reserve conditions, the costs of reserving different types of emergency materials in different depots are different. Demand points are the final destinations for the supply of emergency materials. The demand is usually estimated based on information such as the population of the area, the risk of disasters, and historical records. Support points and demand points are connected by supply lines, and the distance, unit transportation cost, and safety delivery probability of different lines are different.

We investigate the problem of joint optimization of emergency material reserve and dispatching between multiple support points and demand points. Emergency materials are transported from support points along supply lines to demand points. Emergency materials from one support point can be sent to different demand points, and one demand point can also receive emergency materials from different supply points, as shown in Figure 1. The main objective of this paper is to determine the reserve quantities of different support points and the supply relationships between support points and demand points through modeling and optimization.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Emergency material reserve and dispatching relationship.

3.2. Modeling Assumptions

The modeling assumptions used in this paper are as follows:

1.
This paper studies the joint optimization of reserve and dispatching for multivariety emergency materials and is conducted under a two-level emergency material reserve and support system composed of support points and demand points.
2.
The demand quantities of the demand points are known, and the reserve quantities of the support points are equal to the demand quantities, without considering redundant reserves or situations of support shortage.
3.
The transportation costs, distances, and safety delivery probability are known. The transportation speed is an interval number, and the transportation costs are triangular fuzzy numbers.
4.
The unit reserve costs of the emergency material support points are known, and these costs differ between different support points. In addition, the unit reserve costs for different types of emergency materials are also different.
5.
The time consumed for inventory in-take, out-take, and loading/unloading is not considered.
6.
Only land transportation is considered as the mode of transportation, and there is no capacity constraint on the transportation resources.

The notations used in this paper are listed in Table 2.

Table 2. Notations used in this paper.

Notations	Descriptions
I	The set of support points, traversed by i (i = 1, 2,…, m)
J	The set of demand points, traversed by j (j = 1, 2,…, n)
A	The collection of emergency material types, traversed by a (a = 1, 2,…, k)
s_i,a	The reserved quantity of emergency material a in the support point i
s_i	The maximum reserve of support point i
d_j,a	The demand for emergency material a at demand point j
x_i,j,a	The quantity of emergency material a supplied by support point i to demand point j
l_i,j	The distance between support point i and demand point j
v	The speed of transporting emergency materials
t_i,j	Time for emergency materials from support point i to demand point j
t_j	The expected delivery time of demand point j
c_i,a	Cost of reserve unit quantities of emergency material a at support point i
c_i,j	Unit transportation cost of emergency materials from support point i to demand point j
p_i,j	Probability of emergency materials safely delivered at demand point j from support point i
p_e	The expected probability of emergency materials safely delivered at the demand point from a support point

4. Reserve and Dispatch Joint Optimization Modeling

In this section, we construct an emergency material reserve and dispatching joint optimization model. An optimization objective function with the objectives of minimizing total delay time, minimizing total cost, and maximizing the number of safely delivered is established. Then, the constraint conditions functions are constructed.

4.1. Optimization Objective Function

Timeliness, economy, and safety are important factors affecting the emergency material reserve and dispatching [4]. Following a natural disaster, the demand for emergency materials in the affected area increases rapidly. It is essential to transport emergency materials promptly to the demand points to ensure the safety of lives and property. Consequently, this paper prioritizes timeliness as a primary consideration and constructs a function aimed at minimizing total delay time. In addition, although emergency rescue operations typically have weak economic efficiency, the reserve and dispatch of emergency materials require substantial resources, including funds, manpower, and material assets. Therefore, this paper designates total cost minimization as the second optimization objective to mitigate unnecessary waste. Due to the emergence of various safety hazards following a disaster, there may be certain losses in the dispatching of emergency materials. Therefore, this paper incorporates safety considerations by establishing the maximization of the quantity safely delivered as the third optimization objective. The specific expressions are as follows:

()

The specific meaning of each objective function can be expressed as follows.

Equation (1) represents the objective function of minimizing the total delay time of emergency material dispatch, where x_i,j,a denotes the quantity of emergency material supplied by support point i to demand point j, t_i,j denotes the time for emergency materials from support point i to demand point j, and t_j denotes the expected delivery time of demand point j.

Equation (2) represents the objective function of minimizing the total cost of emergency material reserve and dispatching, where s_i,a denotes the reserve quantity of emergency material a in the support point i, c_i,a denotes the cost of reserve unit quantities of emergency material a at support point i, c_i,j denotes the unit transportation cost of emergency materials from support point i to demand point j.

Equation (3) represents the objective function of maximizing the number of emergency materials safely delivered to demand points, where p_i,j denotes the probability of emergency materials safely delivering at demand point j from support point i. When the dispatching work starts, the supply line from the support point to the demand point has certain risks. Therefore, the line with fewer risks should be selected as far as possible. In this paper, the expected safe delivery quantity is used to represent the safety metrics, that is, the product of the safe delivery probability of the supply line and the supply quantity of emergency materials.

4.2. Model Constraints

Based on the problem description and modeling assumptions, here we proceed to construct the model constraints.

()

The specific meaning of each constraint expression is as follows.

Equation (4) indicates that the total reserve of material a at each support point is equal to the total demand of material a at each demand point.

Equation (5) indicates that the total quantity of emergency material a transported from each support point to a demand point is equal to the demand quantity of emergency material a at the demand point.

Equation (6) indicates that the total quantity of emergency material a transported out of a support point is equal to the reserve quantity of emergency material a of the support point.

Equation (7) indicates that the time required for emergency materials to be transported from support point i to demand point j is equal to the distance between support point i and demand point j divided by the transportation speed, where l_i,j denotes the distance between support point i and demand point j, v denotes the speed of transporting emergency materials, and t_i,j denotes the time for emergency materials from support point i to demand point j.

Equation (8) indicates that the transportation speed is an interval number, where v⁻ is the lower limit of the interval and v⁺ is the upper limit of the interval.

Equation (9) indicates that the unit transportation cost of emergency materials from support point i to demand point j is a triangular fuzzy number, where c_i,j,1 is the pessimistic value of the fuzzy number, c_i,j,2 is the normal value of the fuzzy number, and c_i,j,3 is the optimistic value of the fuzzy number.

Equation (10) indicates that the reserve of support point i is not greater than its maximum reserve, where s_i denotes the maximum reserve of support point i.

Equation (11) indicates that the reserve of emergency material a in support point i is a non-negative number.

Equation (12) indicates that emergency materials can only be passed when the probability of safe transportation from support point i to demand point j is not less than the expected probability, where p_e denotes the expected probability of emergency materials safely delivering at the demand point from a support point.

Equation (13) indicates that the quantity of emergency materials transported from support point i to demand point j is a non-negative number.

5. Model Solution

In this section, we investigate approaches to solve the developed model, including the conversion of uncertain constraints and the application of the NSGA-II algorithm to address the multiobjective optimization problem.

5.1. Uncertainty Constraint Processing

After major disasters, the external environment often differs significantly from normal conditions. Factors such as weather, road infrastructure, and economic conditions can introduce substantial uncertainty into the distribution of emergency supplies. For instance, transportation speeds may fluctuate due to road damage and congestion, while unit transportation costs may deviate from typical levels due to shortages of labor and materials.

To better align the model with the realities of disaster response, this paper introduces fuzzy numbers to express these uncertainties. Specifically, the interval numbers are used to represent the variability in transportation speeds and the triangular fuzzy numbers are used to model the uncertainty in transportation costs. This approach aims to enhance the fidelity of the optimization model to the actual rescue scenario. To enable computational tractability, this paper converts the fuzzy numbers into more readily calculable forms, which is a necessary step to facilitate the solution of the optimization problem.

5.1.1. Conversion of Interval Numbers

The transportation speed of emergency materials from the support point to the demand point is the interval number, as shown in equation (8), where v⁻ indicates the lower limit of the interval, v⁺ denotes the upper limit of the interval, and w(v) is the width of the interval number [28]. The relationship between them is shown in the following.

()

m(v) represents the midpoint of the interval.

()

If C is the interval number field and R is the real number field, an operator can be defined as follows:

()

where λ indicates the preference parameter.

()

For decision-makers with varying risk preferences, the parameter λ can be assigned different values to reflect their attitudes toward uncertainty. For the adventurous decision maker, λ is assigned a value within the range [−0.5, 0], which indicates a willingness to embrace a higher degree of risk and uncertainty. For the neutral decision maker, λ = 0, which indicates a balanced approach that does not explicitly favor either risk-seeking or risk-averse behaviors. For the conservative decision maker, λ is assigned a value within the range [0, 0.5], which reflects a preference for minimizing potential losses and maintaining a lower risk profile.

Through the abovementioned conversion relationship, the interval number relationship can be transformed into the corresponding real number relationship, and the decision preferences of different decision-makers can be incorporated into the joint optimization of reserves and transportation.

5.1.2. Conversion of Triangular Fuzzy Numbers

The unit transportation cost of emergency materials from support point i to demand point j is a triangular fuzzy number, as shown in equation (9), where c_i,j,1 indicates the minimum value of the triangular fuzzy number, c_i,j,2 is the middle value of the triangular fuzzy number, and c_i,j,3 denotes the maximum value of the triangular fuzzy number [29]. The calculation of the expected value of c_i,j is as follows:

()

Equation (18) is based on the central tendency of the triangular fuzzy number, which believes that the middle value c_i,j,2 contributes the most to the expected value, while the end values c_i,j,1 and c_i,j,3 contribute relatively less. This method of calculating the expected value is simple and intuitive and can well reflect the central tendency of the triangular fuzzy number. By the abovementioned method, the triangular fuzzy number is mapped to a corresponding real number, which becomes comparable and calculable.

5.2. Optimization Algorithms

The developed optimization model in this study integrates emergency material reserve and dispatching, presenting a complex multiobjective optimization challenge. The diverse objectives, including minimizing total delay time, total cost, and maximizing the safe delivery of emergency materials, inherently conflict and cannot be simultaneously optimized. Consequently, the NSGA-II optimization algorithm is employed to address this model. NSGA-II efficiently ranks individuals within the population based on Pareto priority order, offering rapid execution and strong convergence of solution sets [30, 31]. The procedural steps of NSGA-II are outlined in the following:

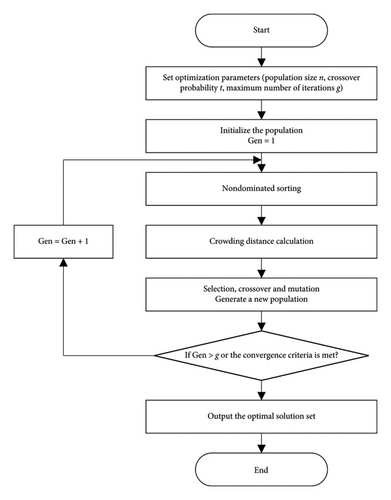
Step 1: set optimization parameters of NSGA-II. Determining optimization parameters such as population size n, crossover probability t, and maximum number of iterations g.
Step 2: initialize the population. Utilizing the objective function as the fitness criterion and initializing the individuals with decision variables.
Step 3: nondominated sorting. Employ an efficient nondominated sorting algorithm to categorize all individuals within the population. Conduct nondominated sorting to distinguish various Pareto-optimal fronts. The initial front comprises nondominated solutions, while subsequent fronts consist of solutions dominated solely by the prior fronts and so forth.
Step 4: crowding distance calculation. Calculate the crowding distance for each individual in the population.
Step 5: selection. Conduct selection utilizing the nondomination rank and crowding distance as criteria, preferring individuals with lower ranks and greater crowding distances.
Step 6: crossover and mutation. Implement crossover and mutation operations on the chosen individuals to produce new offspring.
Step 7: replacement. Merge the parent population with the offspring population. Conduct nondominated sorting and crowding distance calculation on the merged population.
Step 8: termination. Verify the fulfillment of termination criteria, such as the maximum number of generations. If the criteria are satisfied, present the Pareto-optimal front; otherwise, return to Step 2 to resume the optimization process.

The optimization process for the proposed model is given in Figure 2.

6. Numerical Example

In this section, we present a numerical example to validate the efficiency of the proposed model and solution methodology.

The example entails an earthquake-prone zone comprising five densely populated regions, which are denoted by J_n. In the event of seismic activity, there arises a necessity for emergency materials within these areas. By considering the population, disaster risk, and historical records of these regions, an approximate estimation of their material requirements can be derived. It is assumed that there is a demand for three types of emergency materials in these five regions, and the specific quantities required in each region are detailed in Table 3. There are three emergency materials support points in the area, which are denoted by I_m, and their maximum reserves and unit reserve costs are shown in Table 4. The original attribute values of the road from support points to demand points are shown in Table 5, including l_i,j, , and p_i,j. The expected delivery times of demand points are as follows: t₁ = 5.8, t₂ = 5.8, t₃ = 5.6, t₄ = 5.3, t₅ = 6.2, the expected probability of emergency materials safely arriving at the demand point from a support point p_e = 0.6, and the speed of transporting emergency materials .

Table 3. Emergency material demand at the demand points.

	A₁	A₂	A₃
J₁	35	40	60
J₂	40	70	120
J₃	60	100	180
J₄	30	30	40
J₅	35	60	100
Sum	200	300	500

Table 4. Maximum reserve quantity and unit reserve cost of support points.

Support point	Maximum reserve	Unit reserve cost
Support point	Maximum reserve	A₁	A₂	A₃
I₁	400	3	2	4
I₂	500	4	3	5
I₃	400	3	3	5

Table 5. Original attribute values of the road from support points to demand points.

	J₁			J₂			J₃			J₄			J₅
	l_i,j		p_i,j	l_i,j		p_i,j	l_i,j		p_i,j	l_i,j		p_i,j	l_i,j		p_i,j
I₁	300	[4, 6, 9]	0.7	380	[3, 5, 8]	0.5	490	[5, 7, 10]	0.9	360	[3, 5, 8]	0.7	320	[3, 5, 9]	0.7
I₂	390	[5, 6, 10]	0.6	330	[4, 5, 9]	0.6	280	[4, 7, 10]	0.7	400	[5, 6, 10]	0.9	480	[4, 6, 9]	0.7
I₃	450	[5, 7, 9]	0.8	430	[5, 8, 11]	0.9	340	[4, 6, 10]	0.8	290	[5, 7, 11]	0.7	410	[3, 5, 8]	0.8

It is assumed that the decision-makers are conservative; consequently, the value of λ is set at 0.25. According to Section 5.1, uncertainty constraints can be converted into deterministic constraints. Specifically, the interval number can be transformed as described in equation (16), and the triangular fuzzy number can be transformed as outlined in equation (18). By integrating the data presented in Table 5, the optimization attributes of the route from support points to demand points can be derived, as shown in Table 6.

Table 6. Optimization attributes of the road from support points to demand points.

	J₁			J₂			J₃			J₄			J₅
	t_i,j	c_i,j	p_i,j	t_i,j	c_i,j	p_i,j	t_i,j	c_i,j	p_i,j	t_i,j	c_i,j	p_i,j	t_i,j	c_i,j	p_i,j
I₁	5	6.25	0.7	6.3	5.25	0.5	8.1	7.25	0.9	6	5.25	0.7	5.3	5.5	0.7
I₂	6.5	6.75	0.6	5.5	5.75	0.6	4.7	7	0.7	6.7	6.75	0.9	8	6.25	0.7
I₃	7.5	7	0.8	7.2	8	0.9	5.7	6.5	0.8	4.8	7.5	0.7	6.8	5.25	0.8

Utilizing the aforementioned parameters, the NSGA-II algorithm is employed to solve the proposed model. In accordance with the algorithm’s design, programming in MATLAB M language was executed on a computer equipped with an Intel Core i7 @ 2.70 GHz CPU and 32.00 GB of RAM. The algorithm parameters are detailed in Table 7, with a population size of 500, a crossover probability of 0.8, and a total of 500 iterations.

Table 7. Parameter setting of the NSGA-II algorithm.

Parameter	Value
Population size	500
Crossover probability	0.8
Number of iterations	500

The Pareto front of the model optimization results is illustrated in Figure 3, where the coordinates of the three dimensions represent total delay time, total cost, and the number of emergency materials safely delivered, respectively. The objective values of each Pareto frontier point are summarized in Table A1 of the Appendix.

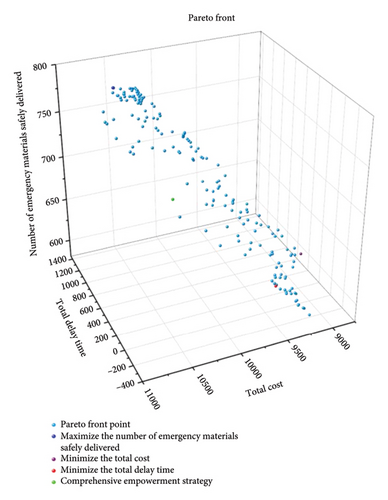
Figure 3 illustrates the optimal solutions that aim to minimize total delay time, minimize total cost, and maximize the safe delivery of emergency materials. A notable conflict exists among these optimization objectives, resulting in a significant separation between the corresponding points. These three strategies reflect distinct decision-making preferences, whereby improvement in one objective function typically necessitates a compromise in the others.

In practice, the preferences of decision-makers significantly influence the selection of the final solution. Consequently, a comprehensive weighting strategy is employed to identify the optimal solution while accounting for these preferences. The comprehensive weighting strategy first requires the determination of the weight coefficients for each objective function, which directly reflect the importance of the respective objective functions. The more significant the objective function, the greater the corresponding weight coefficient. Common methods for determining weight coefficients include expert evaluation [32], analytic hierarchy process [33], entropy method [34], and CRITIC weighting method [35].

Since the method for determining weight coefficients is not the focus of this paper, we plan to use a direct assignment approach to establish the weight coefficients. Future research can utilize relevant methods or software to solve the weight coefficients in conjunction with practical issues. Given the substantial disparity in the availability of emergency materials during the initial stages and the weak economy of emergency response [32, 36], the weights assigned to the three objectives are 0.5, 0.2, and 0.3, respectively.

In addition, due to the differing dimensional units of the various objective functions, it is essential to normalize these values to ensure comparability. This paper employs the 0-1 interval transformation method to convert the objective values. The transformation expression for the efficiency indicator (wherein a higher value signifies greater efficiency) is as follows:

()

The transformation expression for the cost indicator (wherein a lower value denotes greater efficiency) is as follows:

()

where x_min represents the minimum value of the sample data, x_max indicates the maximum value of the sample data, and x^′ denotes the normalized value.

Subsequently, the optimal point based on the comprehensive weighting strategy can be determined. The objective function values for the four strategies described above are presented in Table 8, while the comparative charts of objective values under different strategies are illustrated in Figures 4, 5, and 6, respectively.

Table 8. Optimization objective function values of the four strategies.

Strategy	Total delay time	Total cost	Number of emergency materials safety delivered
Minimizing the total delay time	−247.9	9556.5	632.4
Minimizing the total cost	217.7	8975.3	619.7
Maximizing the number of emergency materials safely delivered	851.3	10,656	798.8
Comprehensive weighting strategy	78.2	10,442	724.9

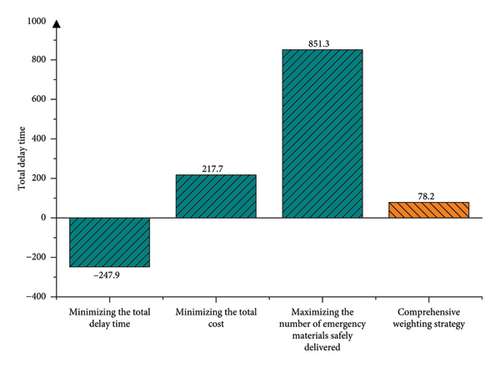
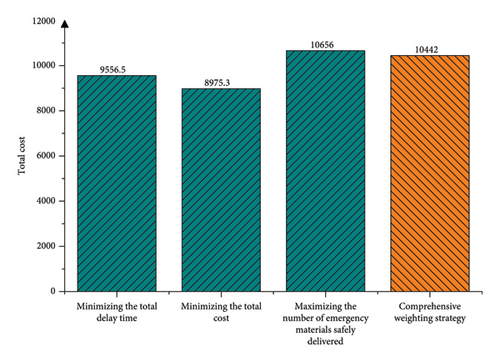
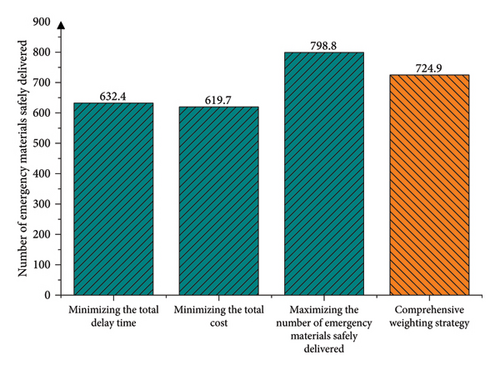
Comparatively, the multiobjective comprehensive empowerment strategy exhibits a more balanced approach compared with the strategy focused on a single objective value as the optimization target. This strategy allows for flexibility in adjustment according to the decision-maker’s preferences. For example, while the comprehensive weighting strategy resulted in a 9.25% reduction in the number of emergency materials safely delivered, it significantly decreased the total delay time by 90.81%, concurrently saving 2.01% of the total cost compared to maximizing the number of emergency materials safely delivered. Under the multiobjective comprehensive empowerment strategy, the emergency material reserves at the support points are depicted in Table 9, and the dispatch plan for emergency materials is detailed in Table 10.

Table 9. Emergency material reserves at support points.

	A₁	A₂	A₃
I₁	23	58	19
I₂	39	173	288
I₃	138	69	193

Table 10. Emergency material dispatching plan.

	J₁			J₂			J₃			J₄			J₅
	A₁	A₂	A₃	A₁	A₂	A₃	A₁	A₂	A₃	A₁	A₂	A₃	A₁	A₂	A₃
I₁	23	0	0	0	0	0	0	0	0	0	0	0	0	58	19
I₂	10	40	60	0	33	120	0	100	54	29	0	16	0	0	38
I₃	2	0	0	40	37	0	60	0	126	1	30	24	35	2	43

7. Conclusions

This paper investigated the joint optimization of reserve and dispatching for multivariety emergency materials. An optimization objective function with the targets of minimizing the total delay time, minimizing the total cost, and maximizing the number of safely delivered has been constructed. The calculation methods for uncertainty constraints and the optimization algorithms for the model have been proposed. The main conclusions are as follows:

1.
The multiobjective optimization model proposed in this paper can simultaneously optimize the reserve and dispatching of emergency materials, providing both reserve and dispatching plans, thus addressing the issue of not achieving a globally optimal solution when optimizing separately.
2.
By expressing the uncertainty in the emergency rescue process with fuzzy numbers, the model can better align with real rescue situations, thereby enhancing its credibility. Meanwhile, this paper presents the method for handling uncertainty constraints that converts fuzzy numbers into a more computable form.
3.
The NSGA-II optimization algorithm adopted in this paper can effectively solve the joint optimization model of emergency materials reserve and dispatching that involves multiple objectives and multiple variables.

In the end, the research findings in this paper can provide valuable references for decision-making in emergency materials reserve and dispatching, offering new insights for research in this field. This paper studies the optimization problem when supply and demand are equal in a two-level supply system, and future research could delve deeper into issues related to multilevel systems and supply–demand imbalance.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funding was received for this research.

Acknowledgments

The authors have nothing to report.

Appendix A: Supplementary data

Table A1. Objective values of each Pareto frontier point.

Number	VAL 1	VAL 2	VAL3
1	1238.8	10,274.8	773.2
2	1219.4	10,257.0	770.6
3	851.3	10,656.0	798.8
4	217.7	8975.3	619.7
5	−243.6	9162.5	587.4
6	1169.4	10,277.0	769.8
7	1227.5	10,271.3	772.5
8	1028.8	10,381.0	776.5
9	−171.9	9275.8	601.2
10	255.7	9027.3	625.1
11	−150.6	9469.5	648.7
12	−217.9	9207.5	594.4
13	−247.9	9556.5	632.4
14	262.0	9252.8	644.1
15	958.1	10,540.3	790.5
16	−222.3	9222.5	595.7
17	603.7	10,843.5	780.6
18	−12.4	9248.0	641.4
19	1123.6	10,377.3	780.0
20	−200.4	9265.5	598.3
21	743.0	10,803.8	782.8
22	811.4	10,625.8	792.5
23	1213.5	10,264.5	771.9
24	649.6	10,743.8	779.0
25	623.3	10,050.5	753.9
26	818.3	10,673.5	795.8
27	−22.9	9703.0	660.8
28	35.4	9171.0	636.7
29	505.8	10,160.0	741.5
30	661.6	9839.3	720.3
31	687.5	9785.5	717.4
32	755.6	10,389.5	765.1
33	892.2	10,242.3	758.2
34	827.5	9881.0	724.1
35	1019.4	10,313.8	768.1
36	941.4	9908.0	729.0
37	−91.5	9455.3	639.0
38	65.8	9540.8	654.7
39	374.1	10,708.5	761.1
40	−167.4	9385.3	614.6
41	−213.8	9526.8	630.3
42	290.9	9786.0	700.8
43	72.9	9301.3	658.7
44	311.2	10,026.3	719.9
45	611.7	10,068.3	752.0
46	571.4	10,015.0	745.9
47	681.6	10,487.3	773.1
48	128.3	9114.8	620.6
49	1070.3	10,378.8	774.2
50	233.5	9126.5	627.6
51	1085.1	10,299.5	772.3
52	594.5	10,830.3	779.3
53	196.7	9075.5	607.9
54	−63.0	9390.5	623.4
55	−228.7	9557.8	633.9
56	242.1	9451.0	674.0
57	63.6	9726.8	683.2
58	668.8	9665.3	708.7
59	278.4	9272.3	646.6
60	393.1	10,364.8	754.2
61	793.6	10,603.3	788.4
62	1041.4	9843.8	726.1
63	227.1	9831.0	694.7
64	181.5	9700.5	681.4
65	1055.1	10,357.5	772.6
66	847.1	9956.5	735.2
67	252.0	9941.5	701.8
68	−6.7	9685.5	666.4
69	1030.4	10,192.8	765.5
70	1114.9	10,360.3	777.9
71	1103.8	10,294.3	767.9
72	114.8	9570.3	668.1
73	1155.9	10,346.0	777.8
74	1206.1	10,253.8	769.5
75	−38.1	9365.8	634.3
76	−192.9	9278.0	603.9
77	−193.0	9255.0	598.1
78	−20.5	9220.0	602.9
79	17.4	9145.0	591.4
80	−238.5	9500.3	626.8
81	−207.1	9571.3	635.4
82	655.7	10,326.3	762.2
83	516.0	10,164.5	742.3
84	273.7	9717.5	695.5
85	86.0	10,041.5	709.0
86	541.9	10,208.0	746.5
87	693.4	10,543.0	777.2
88	452.0	9769.0	700.3
89	615.1	9616.5	699.1
90	629.7	10,173.0	756.8
91	837.3	10,531.8	784.6
92	351.2	9526.0	675.3
93	220.9	9080.3	621.9
94	949.5	10,508.8	787.0
95	904.0	10,318.3	766.6
96	205.1	9770.3	689.5
97	915.1	10,166.5	760.2
98	26.1	9919.3	687.3
99	1003.7	10,432.8	778.6
100	1166.1	10,216.3	765.8
101	1176.9	10,242.5	768.5
102	534.5	10,553.8	759.7
103	1146.4	10,249.5	766.8
104	463.3	10,799.5	771.3
105	366.2	10,680.8	758.9
106	−30.0	9308.3	619.7
107	−183.5	9392.5	614.2
108	−48.5	9440.0	626.6
109	−56.1	9328.8	620.4
110	−115.5	9308.5	609.9
111	−144.2	9385.0	615.3
112	588.5	10,300.8	759.3
113	440.7	10,463.5	756.4
114	339.4	9855.8	713.7
115	159.6	9624.8	678.6
116	359.6	9675.8	686.8
117	78.2	10,442.3	724.9
118	8.0	10,151.5	689.9
119	604.0	10,069.8	753.3
120	581.1	10,029.8	747.4
121	641.7	10,312.5	760.2
122	418.0	10,664.3	762.7
123	861.0	10,646.5	798.0
124	800.0	10,607.0	790.4
125	270.9	9935.0	709.6
126	285.0	9996.5	711.6
127	762.7	10,368.5	768.2
128	142.1	9492.5	671.2
129	453.1	9774.3	706.4
130	552.1	9995.0	727.6
131	356.2	9271.5	649.2
132	669.1	9851.8	721.3
133	169.1	9524.3	672.2
134	712.7	9886.8	725.8
135	94.5	10,100.8	710.8
136	329.2	9530.8	674.1
137	−75.4	9493.8	654.0
138	928.6	10,517.3	786.1
139	19.3	10,404.8	709.8
140	408.5	9806.3	701.5
141	302.9	9705.5	689.4
142	901.2	10,525.0	785.0
143	969.9	10,388.3	775.8
144	337.7	9599.3	674.9
145	774.0	10,255.3	763.9
146	251.5	9941.3	700.9
147	922.0	10,158.5	757.5
148	1047.5	10,320.5	768.9
149	987.6	10,189.0	764.6
150	883.2	10,603.8	788.5
151	1076.3	10,358.5	774.0
152	996.4	10,494.5	782.3
153	−80.5	9519.3	653.9
154	1096.2	10,273.3	766.1
155	−65.5	10,040.0	676.3
156	983.2	10,357.5	771.2
157	1197.4	10,274.8	770.9
158	1193.3	10,319.8	775.1
159	56.5	9413.0	644.9
160	1136.1	10,246.5	765.9
161	726.3	10,011.8	743.3
162	718.9	9974.8	740.4
163	41.4	9796.5	673.5
164	−154.9	9441.8	635.3
165	−130.8	9302.3	607.5
166	868.2	9782.8	718.0
167	15.8	9159.0	592.9
168	1.3	9811.3	670.8
169	−52.3	9772.3	658.6
170	−181.4	9520.8	636.2
171	704.4	10,437.5	763.2
172	387.5	9503.0	678.6
173	103.4	9327.0	664.1
174	500.6	10,030.0	732.8
175	174.0	10,252.3	730.7

Note: VAL 1 indicates the total delay time, VAL 2 denotes the total cost, and VAL 3 represents the number of emergency materials safely delivered.

Open Research

Data Availability Statement

All the data used to support the findings of this study are included within the article.

References

1 Ministry of Emergency Management of the People’s Republic of China, 2024, https://www.mem.gov.cn/gk/tjsj/.
Google Scholar
2 Hu H., He J., He X., Yang W., Nie J., and Ran B., Emergency Material Scheduling Optimization Model and Algorithms:A Review, Journal of Traffic and Transportation Engineering. (2019) 6, no. 5, 441–454, https://doi.org/10.1016/j.jtte.2019.07.001, 2-s2.0-85072644327.
10.1016/j.jtte.2019.07.001
Web of Science® Google Scholar
3 Luo J., Shi L., Xue R., and El-baz D., Optimization Models and Solving Approaches in Relief Distribution Concerning Victims’ Satisfaction: A Review, Applied Soft Computing. (2023) 143, https://doi.org/10.1016/j.asoc.2023.110398.
10.1016/j.asoc.2023.110398
Web of Science® Google Scholar
4 Kamyabniya A., Sauré A., Salman F. S., Bénichou N., and Patrick J., Optimization Models for Disaster Response Operations: a Literature Review, Spectrum. (2024) 46, no. 3, 737–783, https://doi.org/10.1007/s00291-024-00750-6.
10.1007/s00291-024-00750-6
Google Scholar
5 Yu W., A Robust Model for Emergency Supplies Prepositioning and Transportation Considering Road Disruptions, Operations Research Perspectives. (2023) 10, https://doi.org/10.1016/j.orp.2023.100266.
10.1016/j.orp.2023.100266
Web of Science® Google Scholar
6 Zhang L., Wang J., Wang X., Wang W., and Qu L., Intelligent Dispatching Optimization of Emergency Supplies to Multidisaster Areas in Major Natural Disasters, Journal of Tsinghua University. (2022) 63, no. 05, 765–774, https://doi.org/10.16511/j.cnki.qhdxxb.2022.21.038.
10.16511/j.cnki.qhdxxb.2022.21.038
Google Scholar
7 Wang H., Xu R., Zijie X. et al., Research on the Optimized Dispatch and Transportation Scheme for Emergency Logistics, Procedia Computer Science. (2018) 129, 208–214, https://doi.org/10.1016/j.procs.2018.03.043, 2-s2.0-85047061657.
10.1016/j.procs.2018.03.043
Google Scholar
8 Li Z., Liao Q., Zhang H. et al., Robust Optimization for Emergency Scheduling of Oil Products after Disaster, IEEE Access. (2019) 7, 110794–110811, https://doi.org/10.1109/ACCESS.2019.2934046.
10.1109/ACCESS.2019.2934046
Web of Science® Google Scholar
9 Paul J. A. and Zhang M., Supply Location and Transportation Planning for Hurricanes: A Two-Stage Stochastic Programming Framework, European Journal of Operational Research. (2019) 274, no. 1, 108–125, https://doi.org/10.1016/j.ejor.2018.09.042, 2-s2.0-85054804952.
10.1016/j.ejor.2018.09.042
Web of Science® Google Scholar
10 Chen T., Wu S., Yang J., Cong G., and Li G., Modeling of Emergency Supply Scheduling Problem Based on Reliability and its Solution Algorithm under Variable Road Network after Sudden-Onset Disasters, Complexity. (2020) 2020, 1–15, https://doi.org/10.1155/2020/7501891.
10.1155/2020/6632956
CAS Web of Science® Google Scholar
11 Sun Y., Ren Y., and Cai X., Biobjective Emergency Logistics Scheduling Model Based on Uncertain Traffic Conditions, Mathematical Problems in Engineering. (2020) 2020, 1–15, https://doi.org/10.1155/2020/3045472.
10.1155/2020/3045472
Web of Science® Google Scholar
12 Lu Y. and Sun S., Scenario-Based Allocation of Emergency Resources in Metro Emergencies: A Model Development and a Case Study of Nanjing Metro, Sustainability. (2020) 12, no. 16, https://doi.org/10.3390/su12166380.
10.3390/su12166380
Web of Science® Google Scholar
13 Du Y., Sun J., Duan Q., Qi K., Xiao H., and Liew K. M., Optimal Assignments of Allocating and Scheduling Emergency Resources to Accidents in Chemical Industrial Parks, Journal of Loss Prevention in the Process Industries. (2020) 65, https://doi.org/10.1016/j.jlp.2020.104148.
10.1016/j.jlp.2020.104148
Web of Science® Google Scholar
14 Tang Z., Li W., Yu S., and Sun J., A Fuzzy Multi-Objective Programming Optimization Model for Emergency Resource Dispatching under Equitable Distribution Principle, Journal of Intelligent and Fuzzy Systems. (2021) 41, no. 4, 5107–5116, https://doi.org/10.3233/JIFS-189996.
10.3233/JIFS-189996
Web of Science® Google Scholar
15 Ding Z., Zhao Z., Liu D., and Cao Y., Multi-objective Scheduling of Relief Logistics Based on Swarm Intelligence Algorithms and Spatio-Temporal Traffic Flow, Journal of Safety Science and Resilience. (2021) 2, no. 4, 222–229, https://doi.org/10.1016/j.jnlssr.2021.07.003.
10.1016/j.jnlssr.2021.07.003
Web of Science® Google Scholar
16 Yan Y., Di X., and Zhang Y., Optimization-driven Distribution of Relief Materials in Emergency Disasters, Complex & Intelligent Systems. (2021) 9, no. 3, 2249–2256, https://doi.org/10.1007/s40747-021-00290-4.
10.1007/s40747-021-00290-4
PubMed Web of Science® Google Scholar
17 Jiang Z. and Ouyang Y., Reliable Location of First Responder Stations for Cooperative Response to Disasters, Transportation Research Part B: Methodological. (2021) 149, 20–32, https://doi.org/10.1016/j.trb.2021.04.004.
10.1016/j.trb.2021.04.004
Web of Science® Google Scholar
18 Yu W., Pre-disaster Location and Storage Model for Emergency Commodities Considering Both Randomness and Uncertainty, Safety Science. (2021) 141, https://doi.org/10.1016/j.ssci.2021.105330.
10.1016/j.ssci.2021.105330
Web of Science® Google Scholar
19 Zhang Y., Zhu C., Ma B., Wang Q., and Xu E., Research on Bi-level Optimal Allocation of Emergency Materials Considering Material Competition and Game, 1–12.
Google Scholar
20 Li J., Che A., and Chu F., Prepositioning of Emergency Supplies for Predictable Disasters Using Distributionally Robust Optimization, IFAC-PapersOnLine. (2022) 55, no. 10, 3100–3105, https://doi.org/10.1016/j.ifacol.2022.10.205.
10.1016/j.ifacol.2022.10.205
Google Scholar
21 Yan F., Shan H., Fei J., and Li Y., Optimization Decision of Multi-Agent Collaborative Combination Scheme of Emergency Logistics Based on NSGA-II and TOPSIS Algorithms, 2023 11th International Conference on Traffic and Logistic Engineering (ICTLE), August 2023, IEEE, https://doi.org/10.1109/ICTLE59670.2023.10508814.
10.1109/ICTLE59670.2023.10508814
Google Scholar
22 Shu Z., Song A., Wu G., and Pedrycz W., Variable Reduction Strategy Integrated Variable Neighborhood Search and NSGA-II Hybrid Algorithm for Emergency Material Scheduling, Complex System Modeling and Simulation. (2023) 3, no. 2, 83–101, https://doi.org/10.23919/CSMS.2023.0006.
10.23919/CSMS.2023.0006
Google Scholar
23 Tang Z., Li W., Zhou S., and Sun J., Research on Railway Emergency Resources Scheduling Model under Multiple Uncertainties, 1–16.
Google Scholar
24 Xu F., Ma Y., Liu C., and Ji Y., Emergency Logistics Facilities Location Dual-Objective Modeling in Uncertain Environments, 1–34.
Google Scholar
25 Wang D., Peng J., Yang H., Cheng T. C. E., and Yang Y., Distributionally Robust Location-Allocation with Demand and Facility Disruption Uncertainties in Emergency Logistics, Computers & Industrial Engineering. (2023) 184, https://doi.org/10.1016/j.cie.2023.109617.
10.1016/j.cie.2023.109617
Web of Science® Google Scholar
26 Yang R., Li Y., Zhang B., and Yang R., Location–allocation Problem in the Emergency Logistics System Considering Lateral Transshipment Strategy, Computers & Industrial Engineering. (2024) 187, https://doi.org/10.1016/j.cie.2023.109771.
10.1016/j.cie.2023.109771
Web of Science® Google Scholar
27 Li J., Chu F., Che A., and Yin Y., A Three-Stage Relief Network Design Approach for Predictable Disasters Considering Time-dependent Uncertainty, IEEE Transactions on Intelligent Transportation Systems. (2024) 25, no. 6, 5418–5434, https://doi.org/10.1109/TITS.2023.3342319.
10.1109/TITS.2023.3342319
Web of Science® Google Scholar
28 Wu Y., Xu H., Xu C., and Chen K., Uncertain Multi-Attributes Decision Making Method Based on Interval Number with Probability Distribution Weighted Operators and Stochastic Dominance Degree, Knowledge-Based Systems. (2016) 113, 199–209, https://doi.org/10.1016/j.knosys.2016.09.023, 2-s2.0-84994851400.
10.1016/j.knosys.2016.09.023
Web of Science® Google Scholar
29 Ghaffari R. S. and Mesiar R., Fuzzy Number-Valued Triangular Norm-Based Decomposable Time-Stamped Fuzzy Measure and Integration, Fuzzy Sets and Systems, 430, 144–173, https://doi.org/10.1016/j.fss.2021.03.018.
10.1016/j.fss.2021.03.018
Google Scholar
30 Verma S., Pant M., and Snasel V., A Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems, IEEE Access. (2021) 9, 57757–57791, https://doi.org/10.1109/ACCESS.2021.3070634.
10.1109/ACCESS.2021.3070634
Web of Science® Google Scholar
31 Emmerich M. T. M. and Deutz A. H., A Tutorial on Multiobjective Optimization: Fundamentals and Evolutionary Methods, Natural Computing. (2018) 17, no. 3, 585–609, https://doi.org/10.1007/s11047-018-9685-y, 2-s2.0-85047918006.
10.1007/s11047-018-9685-y
CAS PubMed Web of Science® Google Scholar
32 Fan Y., Research on the Model of Materials Dispatching Based on Emergency of Multi-Demand Points, 2014, Chang’an University, Xi’an, China.
Google Scholar
33 Ishizaka A. and Labib A., Review of the Main Developments in the Analytic Hierarchy Process, Expert Systems with Applications. (2011) https://doi.org/10.1016/j.eswa.2011.04.143, 2-s2.0-79960028738.
10.1016/j.eswa.2011.04.143
Web of Science® Google Scholar
34 He D., Zhou H., Chen K. et al., Comprehensive Evaluation of the Influence of PEM Water Electrolyzers Structure on Mass Transfer Performance Based on Entropy Weight Method, International Journal of Heat and Mass Transfer. (2024) 231, https://doi.org/10.1016/j.ijheatmasstransfer.2024.125839.
10.1016/j.ijheatmasstransfer.2024.125839
Web of Science® Google Scholar
35 Wang Z., Zhong Y., Chai S., Niu S., Yang M., and Wu G., Product Design Evaluation Based on Improved CRITIC and Comprehensive Cloud-TOPSIS – Applied to Automotive Styling Design Evaluation, Advanced Engineering Informatics. (2024) 60, https://doi.org/10.1016/j.aei.2024.102361.
10.1016/j.aei.2024.102361
Web of Science® Google Scholar
36 Zhong S. and Ni J., Research on the Optimization of Emergency Material Hub-And-Spoke Supply Network Based on Urgency, Intelligent Computer and Applications, 13, no. 6.
Google Scholar

All articles

Research on Joint Optimization of Reserve and Dispatching for Multivariety Emergency Materials Based on NSGA-II

Abstract

1. Introduction

2. Literature Review