Predicting Course Grades Through Comprehensive Modeling of Students’ Learning Behavioral Patterns
This article is a republication of an article previously retracted due to concerns with the peer review process, https://doi.org/10.1155/2024/9896106. These concerns were not linked to the activity of the authors, and a subsequent peer review process has concluded that the article is suitable for publication. A tracked changes version is included in the supporting information for transparency.
Abstract
While modeling students’ learning behavior or preferences has been found to be a crucial indicator for their course achievement, very few studies have considered it in predicting the achievement of students in online courses. This study aims to model students’ online learning behavior and accordingly predict their course achievement. First, feature vectors are developed using their aggregated action logs during a course. Second, some of these feature vectors are quantified into three numeric values that are used to model students’ learning behavior, namely, accessing learning resources (content access), engaging with peers (engagement), and taking assessment tests (assessment). Both students’ feature vectors and behavior models constitute a comprehensive student’s learning behavioral pattern which is later used for the prediction of their course achievement. Lastly, using a multiple-criteria decision-making method (i.e., TOPSIS), the best classification methods were identified for courses with different sizes. Our findings revealed that the proposed generalizable approach could successfully predict students’ achievement in courses with different numbers of students and features, showing the stability of the approach. Decision tree and AdaBoost classification methods appeared to outperform other existing methods on different datasets. Moreover, our results provide evidence that it is feasible to predict students’ course achievement with high accuracy through modeling their learning behavior during online courses.
1. Introduction
Higher education establishments play a key role in today’s world and contribute immensely to people’s lives by training highly skilled students. While these institutes successfully graduate thousands of students across the world, they also face the issue of students’ failure in courses, leading to delays in their graduation or their dropout. Such problems can damage both students and our society, e.g., resulting in students’ loss of confidence and depression, which in some cases may lead to deferring their studies or their dropout from universities [1]. Needless to mention, such issues can increase university staff’s workload and thereby raise universities’ expenditures [2]. Taking Estonia as an example, while the average dropout rate of higher education students was about 19% in 2016, almost one-third of students majoring in IT dropped out in the first year [3, 4].
Multiple studies have reported that the detection of students who are likely to perform poorly in courses and informing their teachers and themselves to take necessary actions are among the most crucial steps toward boosting their academic success (e.g., [5–7]). Students’ grades, which usually indicate their ability to comprehend conveyed knowledge, are considered one of the main indicators of their success in the course [8]. Therefore, predicting students’ grades or achievement in courses could be one way to identify students at risk of failure (e.g., [9, 10]). Such predictions would enable teachers to provide students with timely feedback or additional support. Consequently, it can be argued that equipping online educational systems (such as learning management systems, LMSs) with automated approaches to predict students’ performance or achievement in a course is crucial.
Educational data mining (EDM) seeks ways to understand students’ behavior in such learning environments and accordingly enables students and teachers to take initiatives where and when necessary [11, 12]. For instance, it can offer individualized learning paths, recommendations, and feedback by predicting students’ performance or risk of failure in courses, contributing to their academic achievement [5, 7].
Basically, such prediction systems or approaches require different amounts of data, depending on the complexity of the parameter being predicted, to make good, highly accurate predictions. Many systems (or EDM approaches) require a large amount of data to develop highly performing and accurate prediction systems. However, the accessibility of big loads of data does not guarantee highly accurate predictions. One crucial task in achieving a decent prediction system is identifying and properly modeling the variables and their effect size on the parameter that is to be predicted. In other words, the key challenge is to find the relevant dynamic characteristics of an individual student for a specific prediction task, which would later help in properly adapting the learning object for them [13]. Among the most important dynamic characteristics of students in a course are their learning behavior or preferences regarding accessing learning resources, engaging with peers, and taking assessment tests [14]. Multiple pieces of research have concluded that students’ activity data logged in different LMSs (such as Moodle) could be used to represent their learning behavior in online courses (e.g., [14, 15]). Furthermore, they also found that students’ academic performance in terms of grades is highly correlated with their level of activity in online environments [16]. To simply put, it was found that different types of students’ online activities could indicate their performance in online courses. However, many studies surprisingly take into account nonacademic-related data or data related to students’ past performance while developing predictive models for online learning environments. Unfortunately, some of these studies ignore the fact that neither students nor teachers have control over the majority of these factors (e.g., [15, 17, 18]). More importantly, if students find that such factors are used in predicting their performance in courses, they may feel despair as they think their performance or circumstances in the past predispose them to failure in the present or future. Thus, similar to some recent studies, this study argues that more studies should consider employing students’ activity data during courses to develop predictive models.
Although modeling students’ learning behavior and preferences act as a key indicator in their course outcome or grade, one that is based on current behaviors, not prior history, very few research studies have modeled students’ learning behavior using their activity level to predict their course grades. Furthermore, the related research often ignores building students’ models considering different aspects of students’ learning behavior during a course (e.g., students’ behavior with respect to content access, engagement, and assessment during courses), the development of simple yet generalizable EDM approaches for predicting course grades, and predicting course grades using students’ models derived from their activity data. In addition, some models are too complex and difficult to use or interpret for practitioners. In this study, we aim to improve existing works by developing an EDM-based approach that consumes students’ activity data during online courses to model their learning behavior and accordingly predict their course achievement or grade.
The contributions of this work include the following: (1) providing educators with opportunities to identify students who are not performing well, (2) taking into account comprehensive students’ learning behavioral patterns (in terms of their content access, engagement, and assessment during courses) in predicting their course grades by developing a learning behavior model for each student in a course, (3) developing an easy-to-implement and interpret student modeling approach that is generalizable to different online courses, and (4) employing a multiple criteria decision-making method for automatically evaluating various classification methods to find the most suitable one for various datasets at hand (different courses with different numbers of features).
2. Related Research
2.1. Prediction of Students’ Performance
One of the most important areas of EDM is the prediction of learning behavior and the outcome of students (e.g., [19, 20]). This can further be categorized into three forms of predictive problems ([21]), including the prediction of students’ performance (e.g., [19, 20]), the prediction of students’ dropout (e.g., [22, 23]), and the prediction of students’ grades or achievement in a course (e.g., [24]).
Several research studies revolve around the prediction of students’ achievement, performance, or grades in online courses. For example, Parack, Zahid, and Merchant [25] used previous semester marks of students; Christian and Ayub [26] and Minaei-Bidgoli et al. [27] used prior GPA of students; Li, Rusk, and Song [28] used students’ performance in entrance exams; Kumar, Vijayalakshmi, and Kumar [29] used students’ class attendance; and Natek and Zwilling [30] employed data related to the demography of students (e.g., gender and family background) in their predictive models. Furthermore, Gray, McGuinness, and Owende [31] focused on psychometric factors of students to predict their performance.
Obviously, the majority of these studies either ignore that students have no control over such factors and informing them about such predictors may have destructive effects on them, or do not consider that such indicators might be unavailable due to multiple reasons (e.g., data privacy) [17, 18, 32]. More research should alternatively concentrate on using data related to students’ online learning behavior, which logically are the best predictors of their performance in courses.
2.2. Predicting Student Grade
Several EDM approaches have been applied to educational data for predicting students’ achievement or grades in courses. For instance, Elbadrawy et al. [33] employed matrix factorization and regression-based approaches to predict the grades of students in future courses. More specifically, they used course-specific regression models, personalized linear multiregression, and standard matrix factorization to predict students’ future grades in a specific course. According to their findings, the matrix factorization approach has shown better performance and generated lower error rates compared to other methods.
In another study, Meier et al. [9] proposed an algorithm to predict students’ grades in a class. The proposed algorithm learns the optimal prediction for each student individually in a timely manner by using different types of data, such as assessment data from quizzes. The authors evaluated their proposed approach using datasets obtained from 700 students, and their findings revealed that for around 85% of students, their approach can predict with 75% accuracy whether or not they will pass the course. In a different attempt, Xu, Moon, and Van Der Schaar [34] took into account the background and performance of the students, existing grades, and predictions of future grades to predict their cumulative grade point average (GPA). To do so, a two-layer model was proposed, wherein the first layer considers graduate students’ performance in related courses. A clustering method was used to identify related courses to the targeted courses. In the second layer, the authors used an ensemble prediction method that, by accumulating new students’ data, improves its prediction power. The proposed two-layer approach appeared to have outperformed other machine learning methods, including logistic and linear regression, random forest, and k-nearest neighbors. Strecht et al. [35] also proposed a predictive model to predict students’ grades using different classification methods such as support vector machines, k-nearest neighbors, and random forest. Their findings show that support vector machines and random forest are among the best and most stable methods in their predictive model. The problem of predicting students’ performance was also formulated as a regression task by Sweeney et al. [36]. The authors in their work employed regression-based methods, as well as matrix factorization–based approaches. Findings from this study showed that a combination of random forest and matrix factorization–based methods could outperform other approaches. Different from other related studies, a semisupervised learning approach was used by Kostopoulos et al. [37] to predict students’ final grades. The proposed approach applied the random forest method with the k-nearest neighbor to different types of students’ data. The findings from this study showed that the hybrid approach outperforms conventional regression methods.
Despite the positive results reported in these studies, some have weaknesses. For instance, some suffer from being too complex for practitioners to interpret or use (e.g., [9]), while others might be unsuitable for use in courses with small amounts of data. Moreover, most of the existing works ignore properly modeling student learning behavior or preferences during a course to predict their final grade [38]. To build on the existing works in the prediction of grades, this work proposes a simple, generalizable (yet practical) approach to develop student models, including students’ behavior regarding accessing learning resources, engaging with peers, and taking assessment tests. In other words, the proposed approach aims to predict students’ course grades or achievement by considering both students’ actions logged into the system and modeling their behavior or preferences in a course using various machine learning algorithms.
3. Methods
3.1. Description of the Problem
We assume that there exists a set of students’ actions logged to the system referred to as X = {x1, x2, …, x|X|} wherein each feature includes activity data of a set of students, referred to as S = {s1, s2, …, s|S|} that are aggregated into the system during a course. A set of student features is further used to model their learning behavior in each course, represented by M = (m1, m2, m3). More specifically, m1 denotes students’ behavior with regard to accessing the content of online learning materials-CA (such as course view, resource view, and URL view), m2 revolves around modeling students’ engagement behavior with other class members-EN (e.g., forum view discussion, add discussion, add comments, and so on), while m3 represents students’ assessment behavior during a course-AS (such as quiz view, quiz attempt, and assignment view). Each student s is associated with a pair of features Xs and Ms, respectively. Given the aforementioned information, we aim to predict students’ course achievement categories (or grades), that is, A, B, C, D, E, and F. To this end, this study considers whether students required learning activities regarding the course materials’ content access, engaging with other class members, and assessment during a course (see Table 1 for notations).
| Notation | Explanation |
|---|---|
| S, s | A set of students and a specific student, S = {s1, s2, …, s|S|} |
| X, x | A set of features and a specific feature, X = {x1, x2, …x|X|} |
| M, m | A set of models of learning behavior and a specific model of learning behavior, M = (m1, m2, m3) |
| U | A pair of student models and features, U = (X, M) |
| Grade | The student’s final grade |
| CA, EN, AS | The predefined list of features associated with each model of learning behavior (content access, engagement, and assessment), CA ⊂ X, EN ⊂ X, AS ⊂ X and CA∩EN∩AS = ∅ |
| TOPSIS | The ranking method takes performance measures of classification methods to produce the ranking of the best method for a given problem |
| P | The set of performance metrics |
| C | The classification methods |
4. Our Approach
Figure 1 illustrates the summary of our proposed EDM approach. The subsequent subsections explain our approach in more detail.
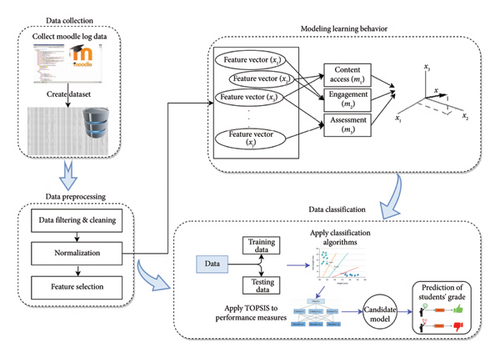
To develop feature vectors and feature vector spaces signifying student levels of activity and their learning behavior (student model) during online courses, various groups of students’ activity data are used. These include aggregating the action logs of students to establish the student’s feature vector, shown in equation (1), of which later were quantified into three numeric values that can be used to model students’ learning behavior through their activity levels (or to identify patterns of their online behavior), namely, accessing learning resources, engaging with peers, and taking assessment tests, see equation (2). Each student is presented using continuous feature vectors that include multiple continuous values. Moreover, for each course, each student’s learning behavior is modeled using a tuple of feature vector spaces, namely, m1, m2, and m3, for their learning behavior with respect to content access, engagement, and assessment.
Both students’ feature vectors and models later constitute a comprehensive students’ learning behavioral pattern for a course. The main assumption here is that the actions of students provide clues to their learning preferences as they imply intentionality. Therefore, the students’ learning behaviors could be considered as a way to infer their study preferences, which are correlated with their course achievement (see Analysis of the Correlation Between Student Models and Course Grades’ Section). In other words, students’ actions or activity data help to infer whether the student’s preference is to study by accessing learning materials (e.g., course view, resource view, and URL view), simply by taking assessment tests (e.g., quiz view, assignment view, quiz attempt, and assignment submission), by engaging with peers and/or the instructor (e.g., forum add discussion and forum view discussion), or maybe all. This would further help the learning system and educators to take necessary remedial actions, according to the students’ model, during the semester to ensure that students’ activities are kept within planned learning outcomes.
-
Algorithm 1: Modeling students’ learning behavior.
-
Input: feature vector X, CA, EN, and AS
-
Output: user model M
- 1
Initialize n = |X|, suml1 = 0, suml2 = 0, suml3 = 0
- 2
while i < n do
- 3
l1 = {x|xi ∈ CA}
- 4
l2 = {x|xi ∈ EN}
- 5
l3 = {x|xi ∈ AS}
- 6
For j in l1:
- 7
suml1 = suml1 + j
- 8
m1 = (suml1/|l1|)
- 9
For j in l2:
- 10
suml2 = suml2 + j
- 11
m2 = (suml2/|l2|)
- 12
For j in l3:
- 13
suml3 = suml3 + j
- 14
m3 = (suml3/|l3|)
- 15
M = (m1, m2, m3)
- 16
Return M
After modeling each student using their online learning behavior, derived from their activity data, a predictor is used to classify students into six different classes (i.e., grades A to F). To do so, each student’s vector, which consists of a pair of their feature vectors and models, is used as an input to several classification methods. Multiple performance measures were employed to find the best-performing classifier for the prediction of students’ course grades (see Algorithm 2). Once the performance measures are implemented, a multiple-criteria decision-making method (i.e., TOPSIS) is used to rank the most suitable method for the prediction of students’ grades. The reason why we have modeled the classification evaluation task as a multiple-criteria decision-making problem is that while some of these measures are closely related and belong to the same family, they possess some differences. For instance, they can act partially when it comes to the classification of different class sizes in a partition (e.g., toward the number of classes and features).
We employed the TOPSIS method for such ranking, underlining the most suitable approach for each dataset (course) [39].
In our experiment, which aims to evaluate classification methods, all metrics are considered as benefits requiring maximization (with no cost criteria requiring minimizing).
Finally, using the maximization of the ratio of , it ranks alternatives.
5. Experimental Results
5.1. Dataset
To evaluate our approach, we created 12 datasets of different sizes from three courses in the Moodle system. The courses are “carrying out and writing a research,” “digital writing skills,” and “teaching and reflection.” Datasets with different sizes would help find the most optimum number of features for each course to better predict the course achievement. To create the datasets, for each course, we extracted different types of action (activity) data, such as the number of times course resources were viewed, course modules viewed, course materials downloaded, feedback viewed, feedback received, forum discussion viewed, quizzes answered, discussion created in the forum, book chapters viewed, book list viewed, assignment submitted, assignment viewed, discussion viewed in the forum, post created in the forum, comments viewed, posts updated in the forum, as well as the number of posts, assignment grade, quiz grades, and final grade. More details on the number of features for each dataset are given in Table 2.
| No | Course name (short name) | Number of features (attributes) | Number of students (instances) |
|---|---|---|---|
| 1 | Carrying out and writing a research (CWR) | 12 | 75 |
| 15 | 75 | ||
| 18 | 75 | ||
| 21 | 75 | ||
| 2 | Digital writing skills (DWS) | 12 | 182 |
| 15 | 182 | ||
| 18 | 182 | ||
| 21 | 182 | ||
| 3 | Teaching and reflection (TR) | 12 | 98 |
| 15 | 98 | ||
| 18 | 98 | ||
| 21 | 98 | ||
5.2. Analysis of Correlation Between Student Models and Course Grades
Before proceeding with the analysis, it is essential to investigate whether there exists a relationship between students’ learning behavior model (derived from their activity level) and course grades. The main aim of this investigation is to attain a clear perception of how different types of students’ activity data (actions) in the online environment correlate with their course grades. To this end, students’ final grade is considered as an indicator of course achievement that is capable of reflecting both students’ level of engagement and knowledge. Table 3 illustrates descriptive statistics of students’ models for accessing learning materials, engaging with peers, and assessing their knowledge and the final grade of the courses called “digital writing skills” and “carrying out and writing a research” (see Table A1 in Appendix A for statistical analysis of the teaching and reflection course). As the Table 3 shows, there exists a positive correlation between content access, engagement, and assessment and the course grade in both courses. This shows that there are correlations between students’ models of learning behavior and the final grade of the course.
| Digital writing skills | ||||
|---|---|---|---|---|
| Content access (m1) | Engagement (m2) | Assessment (m3) | Final grade | |
| Content access (m1) | 1 | 0.5585 | 0.6237 | 0.5010 |
| Engagement (m2) | 0.5585 | 1 | 0.7771 | 0.7429 |
| Assessment (m3) | 0.6237 | 0.7771 | 1 | 0.9322 |
| Final grade | 0.5010 | 0.7429 | 0.9321 | 1 |
| Count | 182 | 182 | 182 | 182 |
| Mean | 0.0936 | 0.1721 | 0.3018 | 2.1154 |
| Std | 0.1139 | 0.1715 | 0.2279 | 2.3746 |
| Min | 0 | 0 | 0 | 0 |
| Max | 0.6108 | 0.6382 | 0.8049 | 5 |
| Carrying out and writing a research | ||||
| Content access (m1) | Engagement (m2) | Assessment (m3) | Final grade | |
| Content access (m1) | 1 | 0.5719 | 0.2434 | 0.2881 |
| Engagement (m2) | 0.5719 | 1 | 0.2930 | 0.3369 |
| Assessment (m3) | 0.2434 | 0.2930 | 1 | 0.4855 |
| Final grade | 0.2881 | 0.3369 | 0.4855 | 1 |
| Count | 75 | 75 | 75 | 75 |
| Mean | 0.2027 | 0.2460 | 0.4710 | 1.24 |
| Std | 0.1257 | 0.0935 | 0.1102 | 0.7505 |
| Min | 0 | 0 | 0 | 0 |
| Max | 0.7833 | 0.7 | 0.7054 | 5 |
-
Algorithm 2: Prediction of students’ course grades according to their model.
-
Input: U
-
Output: prediction of students’ grades (A to F)
- 1
classification algorithms C = { nearest neighbors, linear SVM, RBF SVM, Gaussian process, decision tree, random forest, neural network, AdaBoost, Naive Bayes }
- 2
Evaluation measure P = {accuracy, precision, F1, recall, Jaccard, and fbeta}
- 3
for i in C
- 4
Learning classification algorithm i with U
- 5
for j in P
- 6
Evaluating the results of i with j
- 7
end
- 8
end
- 9
Choose the best classification algorithm by using TOPSIS
- 10
Select the classification algorithm with the highest performance
- 11
Use the algorithm to predict course grade
- 12
return prediction of students’ course grade
5.3. Classification and Performance Measures
After modeling each student’s learning behavior, a pair of students’ features and the model are used to train a predictor for classifying students into six different classes (see Algorithm 2). Nine different classification methods were implemented on different courses (datasets) using six performance metrics. Table 4 shows the performance measures of classification methods, in 10-fold cross-validation, for a course called “digital writing skills” with different feature numbers.
| Features | Methods | Accuracy | Precision | F1 | Recall | Jaccard | fbeta |
|---|---|---|---|---|---|---|---|
| 12 | NN | 0.8956 | 0.5685 | 0.5856 | 0.6067 | 0.5685 | 0.5750 |
| L-SVM | 0.8956 | 0.5775 | 0.5977 | 0.6233 | 0.5775 | 0.5851 | |
| R-SVM | 0.8901 | 0.5766 | 0.5947 | 0.6193 | 0.5726 | 0.5832 | |
| GP | 0.8787 | 0.5712 | 0.5856 | 0.6050 | 0.5712 | 0.5766 | |
| DT | 0.9889 | 0.9333 | 0.9360 | 0.9400 | 0.9333 | 0.9343 | |
| RF | 0.8956 | 0.5775 | 0.5977 | 0.6233 | 0.5775 | 0.5851 | |
| NeuralN | 0.8956 | 0.5807 | 0.5996 | 0.6233 | 0.5807 | 0.5878 | |
| AB | 0.9564 | 0.7783 | 0.7938 | 0.8350 | 0.7783 | 0.7833 | |
| NB | 0.7681 | 0.5408 | 0.5278 | 0.5404 | 0.4903 | 0.5332 | |
| 15 | NN | 0.8956 | 0.5692 | 0.5859 | 0.6067 | 0.5692 | 0.5755 |
| L-SVM | 0.8956 | 0.5775 | 0.5977 | 0.6233 | 0.5775 | 0.5851 | |
| R-SVM | 0.8956 | 0.5775 | 0.5977 | 0.6233 | 0.5775 | 0.5851 | |
| GP | 0.8678 | 0.5051 | 0.5237 | 0.5467 | 0.5051 | 0.5121 | |
| DT | 0.9889 | 0.9267 | 0.9267 | 0.9267 | 0.9267 | 0.9267 | |
| RF | 0.8956 | 0.5787 | 0.5985 | 0.6233 | 0.5787 | 0.5861 | |
| NeuralN | 0.8956 | 0.5807 | 0.5996 | 0.6233 | 0.5807 | 0.5878 | |
| AB | 0.9564 | 0.7783 | 0.7938 | 0.8350 | 0.7783 | 0.7833 | |
| NB | 0.6026 | 0.5144 | 0.4197 | 0.4291 | 0.3668 | 0.4528 | |
| 18 | NN | 0.8956 | 0.5712 | 0.5899 | 0.6133 | 0.5712 | 0.5782 |
| L-SVM | 0.8956 | 0.5775 | 0.5977 | 0.6233 | 0.5775 | 0.5851 | |
| R-SVM | 0.8845 | 0.5745 | 0.5920 | 0.6168 | 0.5680 | 0.5808 | |
| GP | 0.8678 | 0.5273 | 0.5547 | 0.5900 | 0.5273 | 0.5375 | |
| DT | 0.9889 | 0.9333 | 0.9360 | 0.9400 | 0.9333 | 0.9343 | |
| RF | 0.8956 | 0.5787 | 0.5985 | 0.6233 | 0.5787 | 0.5861 | |
| NeuralN | 0.8956 | 0.5821 | 0.6005 | 0.6233 | 0.5821 | 0.5890 | |
| AB | 0.9564 | 0.7783 | 0.7938 | 0.8350 | 0.7783 | 0.7833 | |
| NB | 0.5971 | 0.5189 | 0.4269 | 0.4294 | 0.3735 | 0.4597 | |
| 21 | NN | 0.8956 | 0.5787 | 0.5985 | 0.6233 | 0.5787 | 0.5861 |
| L-SVM | 0.8956 | 0.5775 | 0.5977 | 0.6233 | 0.5775 | 0.5851 | |
| R-SVM | 0.8845 | 0.5745 | 0.5920 | 0.6168 | 0.5680 | 0.5808 | |
| GP | 0.8678 | 0.5264 | 0.5545 | 0.5900 | 0.5264 | 0.5369 | |
| DT | 0.9889 | 0.9333 | 0.9360 | 0.9400 | 0.9333 | 0.9343 | |
| RF | 0.8956 | 0.5775 | 0.5977 | 0.6233 | 0.5775 | 0.5851 | |
| NeuralN | 0.8956 | 0.5821 | 0.6005 | 0.6233 | 0.5821 | 0.5890 | |
| AB | 0.9564 | 0.7783 | 0.7938 | 0.8350 | 0.7783 | 0.7833 | |
| NB | 0.5974 | 0.5185 | 0.4238 | 0.4279 | 0.3698 | 0.4576 | |
- Abbreviations: AB, AdaBoost; DT, decision tree; GP, Gaussian process; L-SVM, linear SVM; NB, Naive Bayes; NeuralN, neural network; NN, nearest neighbor; RF, random forest; R-SVM, RBF SVM.
According to this result, for the course, in 12 (i.e., 12 + m1, m2, m3), 15 (i.e., 15 + m1, m2, m3), 18 (i.e., 18 + m1, m2, m3), and 21 (i.e., 21 + m1, m2, m3) features, the decision tree method outperforms other algorithms with accuracy and precision of 98% and 93% in 12, 15, 18, and 21 features, respectively. Regarding other performance measures, similarly, the decision tree seems to have a superior performance than other methods in all four different features (similar findings are presented in Table A2 in Appendix A for the teaching and reflection course). Interestingly, the performance of decision tree, L-SVM, and AdaBoost is similar regardless of feature numbers, while the performance of other methods appears to be affected by increments or decrements in the number of features.
Table 5 similarly illustrates the performance measures of classification methods for a course called “carrying out and writing a research” with different feature numbers. According to this result, for the course, in 12, 15, and 18 features, the AdaBoost method outperforms other algorithms with an accuracy and precision of 95% and 88% in 12, 15, and 18 features, respectively. This method also appears to have the best performance in 21 features when it comes to accuracy; however, with a precision of about 89%, it tends to perform better than other methods (including AdaBoost).
| Features | Methods | Accuracy | Precision | F1 | Recall | Jaccard | fbeta |
|---|---|---|---|---|---|---|---|
| 12 | NN | 0.6250 | 0.3813 | 0.3888 | 0.4326 | 0.3297 | 0.3793 |
| L-SVM | 0.6643 | 0.3382 | 0.3825 | 0.4583 | 0.3382 | 0.3537 | |
| R-SVM | 0.6786 | 0.3771 | 0.4089 | 0.4750 | 0.3605 | 0.3867 | |
| GP | 0.6786 | 0.4339 | 0.4445 | 0.4844 | 0.3993 | 0.4340 | |
| DT | 0.9071 | 0.8142 | 0.7943 | 0.7906 | 0.7656 | 0.8039 | |
| RF | 0.7304 | 0.4934 | 0.4947 | 0.5367 | 0.4434 | 0.4876 | |
| NeuralN | 0.7161 | 0.3917 | 0.4167 | 0.4667 | 0.3750 | 0.3990 | |
| AB | 0.9464 | 0.8829 | 0.8835 | 0.8933 | 0.8663 | 0.8822 | |
| NB | 0.4375 | 0.3733 | 0.3154 | 0.3780 | 0.2222 | 0.3340 | |
| 15 | NN | 0.6946 | 0.4601 | 0.4572 | 0.4888 | 0.3996 | 0.4545 |
| L-SVM | 0.6643 | 0.3382 | 0.3825 | 0.4583 | 0.3382 | 0.3537 | |
| R-SVM | 0.6911 | 0.4011 | 0.4210 | 0.4833 | 0.3678 | 0.4037 | |
| GP | 0.6929 | 0.4597 | 0.4732 | 0.5233 | 0.4228 | 0.4601 | |
| DT | 0.9339 | 0.8496 | 0.8435 | 0.8489 | 0.8218 | 0.8458 | |
| RF | 0.6768 | 0.3481 | 0.3850 | 0.4450 | 0.3418 | 0.3610 | |
| NeuralN | 0.7036 | 0.3996 | 0.4229 | 0.4750 | 0.3746 | 0.4059 | |
| AB | 0.9464 | 0.8829 | 0.8835 | 0.8933 | 0.8663 | 0.8822 | |
| NB | 0.7089 | 0.4706 | 0.4637 | 0.4866 | 0.4008 | 0.4634 | |
| 18 | NN | 0.6768 | 0.3833 | 0.4080 | 0.4667 | 0.3607 | 0.3892 |
| L-SVM | 0.6643 | 0.3382 | 0.3825 | 0.4583 | 0.3382 | 0.3537 | |
| R-SVM | 0.6643 | 0.3382 | 0.3825 | 0.4583 | 0.3382 | 0.3537 | |
| GP | 0.6786 | 0.3789 | 0.4106 | 0.4750 | 0.3623 | 0.3885 | |
| DT | 0.9196 | 0.8188 | 0.8058 | 0.8139 | 0.7743 | 0.8108 | |
| RF | 0.6500 | 0.3947 | 0.4052 | 0.4619 | 0.3463 | 0.3924 | |
| NeuralN | 0.7161 | 0.4021 | 0.4300 | 0.4833 | 0.3854 | 0.4105 | |
| AB | 0.9464 | 0.8829 | 0.8835 | 0.8933 | 0.8663 | 0.8822 | |
| NB | 0.4268 | 0.3708 | 0.3085 | 0.3637 | 0.2171 | 0.3286 | |
| 21 | NN | 0.6375 | 0.3107 | 0.3334 | 0.3921 | 0.2783 | 0.3156 |
| L-SVM | 0.6643 | 0.3382 | 0.3825 | 0.4583 | 0.3382 | 0.3537 | |
| R-SVM | 0.6643 | 0.3382 | 0.3825 | 0.4583 | 0.3382 | 0.3537 | |
| GP | 0.6643 | 0.3400 | 0.3841 | 0.4583 | 0.3400 | 0.3555 | |
| DT | 0.9339 | 0.8854 | 0.8852 | 0.9000 | 0.8604 | 0.8838 | |
| RF | 0.6643 | 0.3736 | 0.4026 | 0.4667 | 0.3509 | 0.3820 | |
| NeuralN | 0.6786 | 0.3374 | 0.3547 | 0.3938 | 0.3078 | 0.3419 | |
| AB | 0.9464 | 0.8829 | 0.8836 | 0.8933 | 0.8663 | 0.8822 | |
| NB | 0.4429 | 0.3704 | 0.3275 | 0.3730 | 0.2451 | 0.3408 | |
- Abbreviations: AB, AdaBoost; DT, decision tree; GP, Gaussian process; L-SVM, linear SVM; NB, Naive Bayes; NeuralN, neural network; NN, nearest neighbor; RF, random forest; R-SVM, RBF SVM.
Regarding other performance measures, similarly, AdaBoost seems to have superior performance than other methods in 12, 15, and 18 features. Nonetheless, in the 21 feature, the decision tree shows the highest performance in F1, recall, and fbeta, whereas AdaBoost slightly outperforms the decision tree in Jaccard. Such differences in the results of various performance measures usually make decision-making on the selection of the best method for the current datasets challenging, and an impartial method such as multiple criteria decision-making method (e.g., TOPSIS) would help to pick the best methods (see the following subsection).
Regarding different feature numbers, besides AdaBoost and L-SVM methods that show similar performance regardless of feature numbers, our findings reveal that all other methods seem to be affected by increments and decrements in the number of features. In other words, these methods appear to have a more stable performance than other methods when it comes to feature number changes. Overall, the smaller the number of features (15 in particular; it can be said that 15 is the optimum number of features for the current dataset), the better the performance of classification methods. Also, an increment in the number of features results in a decrement in the performance of classification methods (21 in particular). Table 5 shows the performance measure of classification methods for the course “carrying out and writing a research” with different feature numbers.
As mentioned earlier, the TOPSIS method is employed in this study to rank and highlight the most suitable classification method for each dataset. Even though some methods usually outperform others using some specific performance measures (e.g., see Table 4), in many real-world datasets, there exist cases where more than one method achieves the highest performance in different performance measures (e.g., see 21 features in Table 5). This makes the decision-making on which classification method to use a challenging task. For such reasons and to minimize partiality, if not fully avoided, this study employs the TOPSIS method to rank and select the best method for each dataset (course). According to Table 6, for the digital writing skills course, the decision tree followed by AdaBoost is ranked the best and second-best methods for all different datasets, respectively (different feature numbers). Similar findings are presented in Table A3 in Appendix A for the teaching and reflection course.
| Features | Nearest neighbors | Linear SVM | RBF SVM | Gaussian process | Decision tree | Random forest | Neural network | AdaBoost | Naive Bayes |
|---|---|---|---|---|---|---|---|---|---|
| 12 | 0.1654 | 0.1878 | 0.1794 | 0.1612 | 1.0000 | 0.1878 | 0.1922 | 0.6561 | 0.0000 |
| 15 | 0.3429 | 0.3612 | 0.3612 | 0.2400 | 1.0000 | 0.3626 | 0.3649 | 0.7369 | 0.0081 |
| 18 | 0.3390 | 0.3512 | 0.3384 | 0.2752 | 1.0000 | 0.3525 | 0.3563 | 0.7225 | 0.0000 |
| 21 | 0.3549 | 0.3536 | 0.3409 | 0.2770 | 1.0000 | 0.3536 | 0.3587 | 0.7236 | 0.0000 |
Table 7 shows the TOPSIS ranking of classification methods for carrying out and writing a research course. As it is apparent, AdaBoost followed by the decision tree are ranked the best and second-best methods for all different datasets, respectively (different feature numbers). It is interesting that while AdaBoost showed higher performance in only two metrics, namely, accuracy and Jaccard, decision tree has performed better in the other four performance measures, namely, precision, F1, recall, and fbeta, AdaBoost is still ranked the best method in 21 features. More explicitly, AdaBoost with 0.9947 earns the first-best rank and the decision tree with 0.9918 is ranked the second best for the classification of the data with 21 features.
| Features | Nearest neighbors | Linear SVM | RBF SVM | Gaussian process | Decision tree | Random forest | Neural network | AdaBoost | Naive Bayes |
|---|---|---|---|---|---|---|---|---|---|
| 12 | 0.1547 | 0.1663 | 0.1990 | 0.2490 | 0.8492 | 0.3358 | 0.2211 | 1.0000 | 0.0259 |
| 15 | 0.1640 | 0.0106 | 0.0881 | 0.1879 | 0.9231 | 0.0137 | 0.0908 | 1.0000 | 0.1767 |
| 18 | 0.2058 | 0.1742 | 0.1742 | 0.2087 | 0.8698 | 0.1932 | 0.2439 | 1.0000 | 0.0241 |
| 21 | 0.1039 | 0.1572 | 0.1572 | 0.1587 | 0.9918 | 0.1799 | 0.1356 | 0.9947 | 0.0481 |
5.4. Statistical Significance
To find out whether the differences between the results of different classification methods were due to differences in the models or statistical chance, we performed statistical significance tests. This also helps to check the validity of results produced by TOPSIS. Signed-rank and the t-test are among the most frequently used tests for this purpose [40, 41]. We chose to perform a t-test, and the results revealed a p-value smaller than 0.01 for all methods. This implies that the differences between the methods were likely due to differences in the models, confirming the findings of the TOPSIS method.
6. Discussion
In the previous section, the results presented reveal that our proposed EDM approach is capable of automatically modeling students according to their learning behavior and preferences, and can predict their achievements in different courses with high accuracy. This provides educators with opportunities to identify students who are not performing well and adjust their pedagogical strategies accordingly. The proposed EDM approach, see Algorithm 2, is generalizable and could be used in various online and blended courses. More specifically, any online learning environment that logs various students’ actions (or activity data) during a course could benefit from our approach. In brief, students’ aggregated action logs during a course will be used to build feature vectors for students (in other words, their logical representation), which would later be used to develop a three-layer student model for each student. In other words, some of the students’ feature vectors that fall within the category of accessing learning resources during a course will be used to develop the first layer of the student model called “content access,” some other features that are associated with students’ engagement with their peers will be used to build the second layer of the model called “engagement,” and finally, those features related to taking assessment tests will be employed to develop the last layer of the model called “assessment.” The rest of the features that are not used in developing the student model, along with the three-layer student model, constitute a comprehensive students’ learning behavioral pattern which is later used for the prediction of their course achievement. Finally, the TOPSIS method is used for the evaluation of various classification methods.
The proposed approach and results reported in this study differ, to some extent, from several existing EDM approaches for predicting students’ final grades in a course. For instance, there exist several EDM-based studies developing student modeling for students to later use for the prediction of their performance or achievement (e.g., [13, 42–44]). Most of these studies consider some specific type of collected data in the system that is related to students’ learning style such as the Felder–Silverman learning style model or try to involve data related to students’ personality traits, e.g., Big Five model, in their student model [44]. Even though these attempts might result in successful modeling of students, there is no guarantee that such student modeling, occasionally built upon static characteristics of students (not their dynamic characteristics that project their actual learning behavior during a course), could always be useful to educators and instructors for identifying weak students, improving retention, and reducing the academic failure rate. Moreover, although some of these student models consider both static and dynamic characteristics of students, they require specific types of data or their development is complex. For instance, Wu and Lai [43] distributed questionnaires of openness to experience and extraversion among students to collect data about their personality traits (based on the Big Five model) so as to model students and accordingly predict their achievement based on personality traits.
Similarly, modeling students based on their learning style, developed using specific models such as the Felder–Silverman learning style model [42], may require considering specific types of students’ data collected in the system (which may not exist in all online learning environments) and may ignore useful, informative students’ activity data readily available in all online learning environments. A generalizable approach should take into account the requirements and data types of different online learning environments and should be applicable to various learning systems on different platforms [45]. Our proposed approach benefits from a simple yet accurate algorithm that considers various types of students’ activity data during a course to build a multilayer student model, creating a comprehensive students’ learning behavioral pattern for later use in predicting their course achievement. Unlike many existing works that require specific types of data to build their predictive models, our generalizable approach constructs students’ models based on three different categories of their actions during a course: learning resource content access, engagement with peers, and taking assessment tests. In addition to these three categories, the proposed approach incorporates other important students’ features that do not fall within these categories. This way, comprehensive students’ learning behavioral patterns are taken into account in predicting their course grades. As our findings show, our proposed approach can predict students’ course grades in multiple courses with different sizes (ranging from courses with around 70 to 180 students), demonstrating the usefulness and accuracy of our approach even with less data. Besides the student model, our experiment considers different numbers of features in each course (ranging from 12 to 21), and regardless of the feature numbers, our approach appears to be highly successful, showing its stability. Furthermore, our generalizable approach benefits from a multiple-criteria decision-making method to compare and identify the most suitable classification methods for predicting students’ course achievement. This ensures that our proposed approach is impartial in selecting the most suitable classification method for each course with different numbers of features and students (as some performance measures can behave partially when it comes to the classification of different class sizes in a partition or be biased toward the number of classes and features, etc.).
In light of recent advancements in machine learning, particularly within educational and psychological research, it is imperative to consider the epistemological implications of adopting such methodologies. While our proposed EDM approach demonstrates significant predictive power and utility in educational settings, it is essential to recognize the potential limitations posed by the black-box nature of some machine learning algorithms. By prioritizing predictive accuracy, these models may unintentionally obscure some of the intricate dynamics underlying student learning behaviors and outcomes, potentially posing challenges to the development of comprehensive theoretical frameworks. Therefore, while our approach offers practical solutions for identifying at-risk students and optimizing pedagogical strategies, it is essential for researchers to remain vigilant in addressing the epistemological challenges posed by the adoption of machine learning methods in education and psychology. Future endeavors should strive to strike a balance between predictive accuracy and theoretical transparency, thereby fostering a more nuanced understanding of the complex phenomena under investigation.
7. Conclusions
This study investigated the effectiveness of a student modeling–based predictive model for estimating students’ achievement in a course. The proposed generalizable prediction approach includes both feature vectors, which are a logical representation of students (derived from their activity data), and models of their learning behavior, namely, content access, engagement, and assessment, to constitute a comprehensive student behavioral pattern used for predicting their course achievement. Furthermore, it employs the TOPSIS method to compare and evaluate various classification methods. It is important to note that some performance measures can behave partially when classifying different class sizes in a partition or show bias toward the number of classes and features.
To evaluate our proposed approach, data from three different courses with varying sizes at the University of Tartu’s Moodle system were used. Our findings revealed that our proposed approach can predict students’ course grades in multiple courses with different sizes, demonstrating the generalizability and accuracy of our approach even with less data. Decision tree and AdaBoost classification methods appeared to outperform other existing methods on 12 different datasets. Besides the student model, different numbers of features in each course were taken into account in our experiment, and regardless of the feature numbers, our approach appeared to be highly successful, indicating its stability. One main reason for such success could be the proper identification and modeling of the variables and their effect size on the predicted parameter. Moreover, our findings show that it is feasible to develop an easy-to-implement and interpret student modeling approach that is generalizable to different online courses.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea Government (MSIT) (No. 2021R1C1C2004868), and the University of Tartu ASTRA Project PER ASPERA, financed by the European Regional Development Fund.
Supporting Information
Table A1: Analysis of correlation between student models and course grades (teaching and reflection course).
Table A2: Performance measure of classification methods for course “teaching and reflection” with different feature numbers.
Table A3: TOPSIS ranking of classification methods for course “teaching and reflection” with different feature numbers.
Open Research
Data Availability Statement
The data used in this research cannot be made available as authors have signed a confidentiality agreement with the University of Tartu in Estonia.




