The Fractional Variable-Order Grassi–Miller Map: Chaos, Complexity, and Control
Abstract
In the topic of discrete variable-order systems governed by fractional difference equations, this study makes a significant contribution by introducing two innovative variable-order versions of the fractional Grassi–Miller system. These new formulations are aimed at deepening our understanding of the complex dynamics that such systems exhibit. The research specifically delves into the chaotic dynamical behaviors manifested by these systems: one version being the fractional Grassi–Miller map with commensurate variable order and the other being the fractional Grassi–Miller map with incommensurate variable order. To provide a comprehensive analysis, this study incorporates a variety of variable orders, encompassing both exponential and sinusoidal functions. These variable orders are crucial in exploring how different functional forms influence the behavior of the system. By varying these orders, the research seeks to uncover the patterns and chaotic dynamics that emerge under different conditions. A suite of advanced numerical methods is employed to rigorously analyze and validate the presence of chaotic attractors in these newly proposed variable fractional versions of the Grassi–Miller system. The methods used include bifurcation diagrams, phase portraits, Lyapunov exponents, approximate entropy, C0 complexity, and 0–1 test for chaos. Through the application of these numerical methods, the study thoroughly validates the existence of chaotic attractors in the proposed variable fractional versions of the Grassi–Miller system. The findings underscore the rich and complex behaviors that arise from different variable orders, offering new insights into the dynamics of fractional-order systems.
1. Introduction
Chaos has emerged as one of the most captivating subjects in nonlinear dynamics in recent decades due to its distinct characteristics and extensive potential applications [1–5]. These applications span various domains, including memristors [6], random number generators [7], and artificial neural networks [8]. Compared with continuous systems, discrete systems have simpler algebraic equations and higher computational efficiency in chaos-based industrial applications [9]. Currently, numerous researchers are engrossed in the study of chaotic dynamics, driven by unresolved issues in these fields. For instance, Lai et al. [10] developed a hyperchaotic discrete system that lacks fixed points and exhibits infinitely many coexisting attractors. This was achieved by coupling a sinusoidal discrete memristor with the Gaussian map, demonstrating the system’s complex and rich dynamical behavior. Similarly, in Reference [11], a 3D memristive hyperchaotic map was constructed by integrating a discrete memristor with a trigonometric map, showcasing another method of generating hyperchaotic dynamics through the interaction of different nonlinear components. In another example, Reference [12] presents a macroeconomic state space model for national economies, described by difference equations, which illustrates how chaotic dynamics can be applied to economic modeling to capture the complex, unpredictable behaviors observed in real-world economies. Ongoing research continues to underscore the substantial potential of chaotic maps in various applications, ranging from secure communications and cryptography to biological systems and financial markets [13]. These studies highlight the versatility and wide-reaching implications of chaotic maps in both theoretical research and practical applications.
The field of fractional calculus, which dates back more than three centuries [14], has seen significant development in recent decades. This surge in interest is primarily due to its widespread applications in fields such as signal processing, mechanical controls, and various other domains [15, 16]. Unlike integer-order derivatives, fractional-order derivatives provide enhanced accuracy and are valuable for characterizing memory effects in diverse materials and processes.
In recent years, there has been a burgeoning interest in the field of discrete fractional calculus. This area of study focuses on systems governed by fractional difference equations, which are equations of noninteger order that describe the evolution of system states in discrete time steps. These systems are particularly intriguing due to their ability to model complex, real-world phenomena that cannot be captured by traditional integer-order models.
A significant portion of this research has centered on the exploration of chaotic behaviors in fractional discrete systems [6, 10, 17, 18]. These systems are represented by nonlinear maps that exhibit high sensitivity to initial conditions, a hallmark of chaotic dynamics. The fractional nature of these difference equations introduces additional complexity and richness to the system’s behavior, making them a fertile ground for theoretical and applied research.
One notable study, referenced in [19], investigates the emergence of chaos in a fractional logistic map. The logistic map is a classic example of a simple nonlinear system that can exhibit chaotic behavior, and its fractional version extends this behavior into a new domain. The study examines how varying the order of the fractional difference equation influences the onset and nature of chaos, providing deep insights into the sensitivity of the system to changes in its parameters and initial conditions.
Another important contribution to the field is the examination of delayed fractional maps, as discussed in [20]. This research builds on previous studies by incorporating time delays into the fractional difference equations, adding another layer of complexity to the system. Delays are known to affect the stability and dynamics of systems significantly, and this study explores how they interact with fractional orders to produce or suppress chaotic behavior. The findings highlight the intricate interplay between delay and fractional order, offering a more comprehensive understanding of the factors that drive chaos in discrete systems.
Further research, such as that presented in [21], delves into the chaotic behaviors of non–integer-order maps that are characterized by special symmetries at their fixed points. These symmetries play a crucial role in determining the stability and bifurcation properties of the system. By focusing on maps with specific symmetrical properties, researchers have been able to identify novel types of chaotic attractors and bifurcation phenomena. This line of inquiry not only expands the theoretical framework of fractional discrete systems but also provides valuable insights into the potential applications of these models in various scientific and engineering disciplines.
In addition to these studies, there has been a growing interest in understanding the broader implications of chaotic dynamics in fractional discrete systems. Researchers have employed various numerical and analytical techniques to analyze the behavior of these systems, including bifurcation diagrams, Lyapunov exponents, and entropy measures. These tools have proven essential in characterizing the complexity and unpredictability inherent in fractional discrete systems [22–25]. Khennaoui et al. [22] integrate discrete maps, memristors, and fractional calculus to explore the hardware implementation of a fractional memristive Lozi map, illustrating the interdisciplinary nature of current research. Similarly, Reference [26] reports on a new chaotic fractional memristor map with hidden attractors. Additionally, numerical simulations have explored phenomena such as multistability and extreme multistability in certain fractional maps.
Recently, Wu et al. [27] introduced a method for constructing fractional difference equations with variable orders, specifically designed to exhibit short memory behavior. Their study highlighted the effectiveness of fractional variable-order equations in capturing the memory properties of discrete systems. Despite this progress, there has been limited exploration into variable-order fractional maps where the fractional order varies discretely over time [28, 29]. For instance, Reference [28] focuses on bifurcation analysis and phase portraits to understand the chaotic behavior in a variable-order fractional Tinkerbell map. Furthermore, Reference [29] utilizes the 0–1 test and C0 complexity method to verify the existence of chaos in a discrete fractional Hopfield neural network with noncommensurate variable order.
To date, there has been no investigation into incommensurate fractional-order maps concerning their dynamic behavior. Incommensurate orders refer to scenarios where each equation in a system possesses a distinct fractional order, thereby enhancing model flexibility. Therefore, there is a compelling rationale to focus on unraveling the intricate dynamic patterns of incommensurate fractional-order maps with varying orders. Such fractional variable-order formulations are anticipated to exhibit even more complex dynamics than their commensurate counterparts.
Drawing from previous considerations regarding systems with variable fractional orders, this paper is aimed at contributing to the field of fractional discrete systems. The primary contribution lies in the introduction of a novel fractional discrete system characterized by a variable order and a memory effect. This achievement is realized by integrating the Caputo-like difference operator with the Grassi–Miller map, thereby introducing greater flexibility to the utilized models. This idea of memory provides more space and chaos in the fractional discrete systems and make the numerical computation more practical. Employing numerical methodologies such as phase diagrams and bifurcation analyses, the study delves into the dynamic behaviors of these proposed variable order maps. Building upon previous research on systems with variable fractional orders, this study is aimed at making a distinctive contribution to the existing literature. It does so by introducing two novel variations of the discrete Grassi–Miller map featuring fractional orders that vary over time. Specifically, the research investigates the chaotic behaviors exhibited by these two versions: one with commensurate variable fractional orders and another with incommensurate variable fractional orders. Drawing from previous considerations regarding systems with variable fractional orders, this paper is aimed at contributing to the field of fractional discrete systems. The primary contribution lies in the introduction of novel fractional discrete systems characterized by a variable order and a memory effect. It achieves this by introducing two variations of the discrete Grassi–Miller map with fractional orders that can change over time. Specifically, the research delves into the complex chaotic behaviors of two versions: one with commensurate variable fractional orders and another with incommensurate variable fractional orders. This idea of memory provides more space and chaos in the fractional discrete systems and makes the numerical computation more practical.
To validate the presence of chaos in these innovative fractional versions of the Grassi–Miller map, a range of numerical tools has been employed. These include phase diagrams, bifurcation and Lyapunov exponent diagrams, approximate entropy (ApEn), C0 complexity, and the 0–1 test. The structure of the manuscript unfolds as follows: Section 2 not only offers foundational insights into discrete fractional calculus but also introduces the fractional Grassi–Miller map featuring commensurate variable orders. In Section 3, the chaotic dynamics of this map are meticulously analyzed under various commensurate variable orders, encompassing both exponential and sinusoidal laws. Moving to Section 4, the focus shifts to investigating the dynamic behaviors of the map with incommensurate variable orders. This investigation incorporates an exponential function for the order in the first difference equation, while the second and third difference equations employ distinct sinusoidal functions for their orders. The presence of chaotic attractors in the map with incommensurate variable orders is rigorously confirmed through the application of ApEn, C0 complexity, and the 0–1 test. Ultimately, numerical results substantiate the efficacy and robustness of the approach presented in this study.
2. The Fractional Grassi–Miller Map With Commensurate Variable Orders and Its Dynamics Analysis
In our simulations, we employed Matlab to implement the numerical Formula (9). Our primary focus was on examining the dynamic properties of the discrete Grassi–Miller map (7) under the influence of fractional variable order and system parameters. For instance, assuming τ = 0.1 and initial states (x1(0), x2(0), x3(0)) = (1,0.1,0), we explored three distinct fractional-order profiles: ν(s) = 0.97 + 0.03cos(s/2), ν(s) = 1/(1 + exp(−s)), and ν(s) = s/(s + 1).
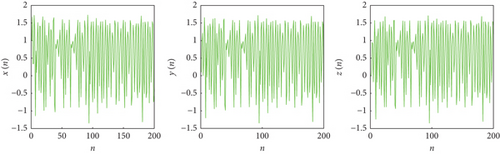
Our analysis reveals that the Grassi–Miller map (7) with commensurate variable fractional order exhibits chaotic attractors, as illustrated in Figures 1 and 2 for α = 1.6 and α = 1.68, respectively. Notably, these figures highlight that even a slight variation in the system parameter α leads to changes in the nature of strange attractors. Specifically, for the fractional-order profile ν(s) = (1/12)exp(sin((1/15)s)) + 0.76, we observe chaotic behavior when α = 1.6, as evidenced by the time evolution of the states depicted in Figure 3. Conversely, when α = 1.68, the system exhibits periodic behavior, indicating the significant influence of variable fractional order on the system’s dynamics.
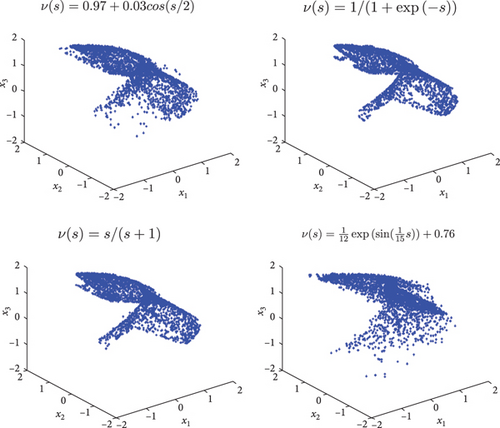
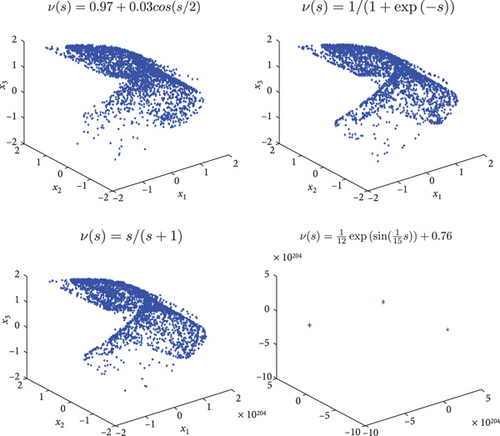
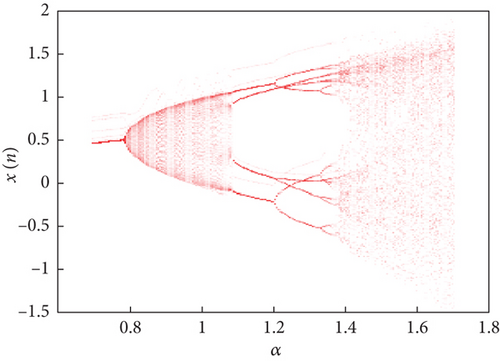
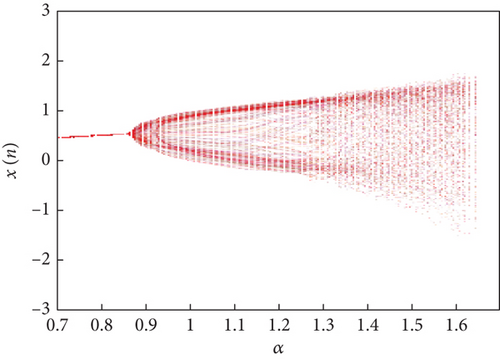
To explore the dynamics of the fractional map (7), we investigate the parameter α as the bifurcation parameter, generating bifurcation diagrams to understand system behavior. We specifically set α ∈ [0.7,1.8] as the bifurcation parameter, with τ = 0.1, initial conditions (x1(0), x2(0), x3(0)) = (1,0.1,0), and iterating over m = 1000 steps.
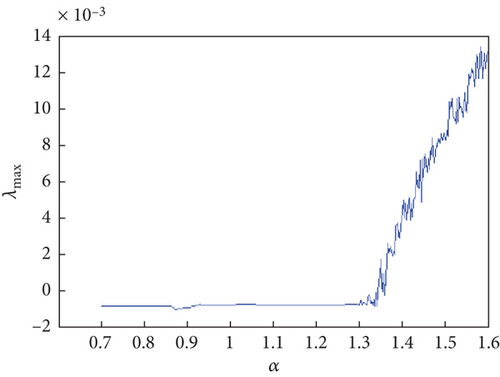
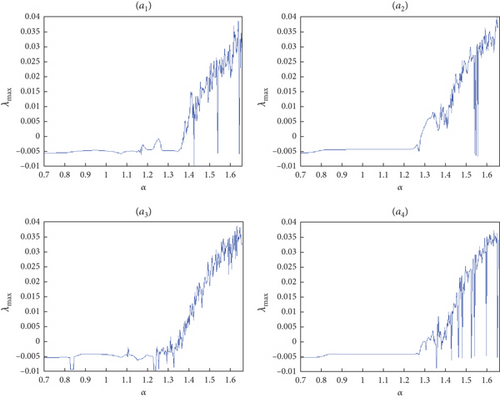
Bifurcation diagrams and maximal Lyapunov exponents versus α are computed for two distinct fractional-order profiles: ν(s) = 1/(1 + exp(−s)) and ν(s) = (1/12)exp(sin((1/15)s)) + 0.76, as illustrated in Figures 4 and 5, respectively. The maximal Lyapunov exponents of the proposed map (7) are determined using the Jacobian matrix method, a technique recently detailed by Wu et al. [25].
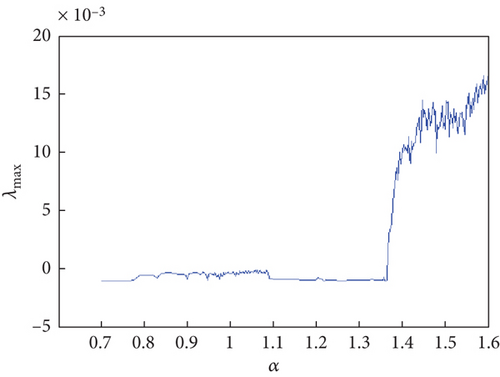
As commonly understood, a system exhibits chaotic behavior when its maximum Lyapunov exponent (λmax) is positive, indicating sensitivity to initial conditions and complex dynamics. Conversely, if λmax is negative, the system is in a periodic state.
Referring to the maximum Lyapunov exponents in Figure 4(b), for the fractional map (7) with ν(s) = 1/(1 + exp(−s)), we observe that the system initially displays a periodic state with negative maximum LE. Eventually, it transitions into chaos through period doubling around α = 1.1. A similar bifurcation pattern is observed when ν(s) = (1/12)exp(sin((1/15)s)) + 0.76, though the parameter α exerts a more constrained influence.
Furthermore, by analyzing Figure 4(b), it becomes evident that for α values within the ranges α ∈ [0.9220,0.9730] ∪ [1.3150,1.3210] ∪ [1.3270,1.3450] ∪ [1.3480,1.3570] ∪ [1.3600,1.4110] ∪ [1.4180,1.6540], the maximum Lyapunov exponents are positive. This signifies that the Grassi–Miller map with commensurate fractional variable order enters a chaotic state within these parameter ranges.
It is important to note that the dynamics of the variable fractional-order Grassi–Miller map (7) differ significantly from those discussed in [32], which primarily focuses on the fractional Caputo delta difference. Specifically, the discrete Grassi–Miller map (7) exhibits chaotic attractors under the conditions α = 1.68 and τ = 0.1. In contrast, the Grassi–Miller map with a fixed fractional order discussed in [32] does not display chaotic behavior under these parameter values.
To underscore this distinction in dynamic behavior, bifurcation diagrams and maximal Lyapunov exponent plots are constructed with respect to the parameter α, while keeping the initial states and parameter τ constant. In Figure 5(b), α ranges from 0.9220 to 0.9730, whereas in Figure 4(b), α ranges from 1.69 to 1.7830. The positive values of the Lyapunov exponent in these figures indicate that the proposed map (7) exhibits chaotic behavior. Conversely, the system described in [32] (with ν = 0.88) demonstrates periodic behavior within these parameter intervals.
The introduction of variable fractional-order dynamics into the discrete Grassi–Miller map enriches its behavior significantly. This comparison between the proposed map and the one discussed in Reference [32] underscores that employing different operators (fractional Caputo delta difference with constant order versus fractional Caputo delta difference with variable order) results in distinct dynamic behaviors between the two maps. This highlights the novel contribution of the conceived Grassi–Miller map with variable fractional order to the literature on hyperchaotic discrete time fractional systems with variable-order dynamics.
3. The Incommensurate Discrete Variable Fractional-Order Grassi–Miller Map
By investigating these equations, we aim to uncover the patterns and behaviors that characterize the system’s chaotic nature. The application of ApEn provides insights into the complexity and predictability of the system. The C0 complexity measure helps to quantify the irregularity of the system’s behavior, while the 0–1 test serves as a robust tool for distinguishing between regular and chaotic dynamics. Through these comprehensive analyses, we can better understand the conditions under which the incommensurate variable fractional-order Grassi–Miller map exhibits chaos.
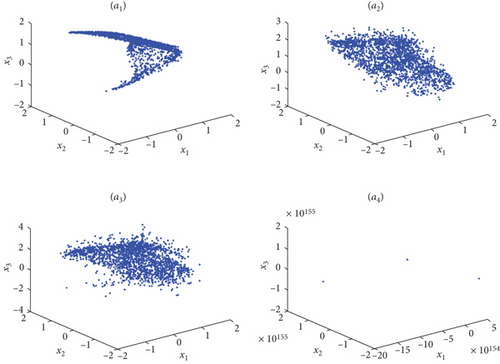
Here, Figures 6 and 7 illustrate the phase portraits of the chaotic attractors for various values of incommensurate fractional order. These chaotic attractors are calculated using the initial conditions (1,0.1,0), the system parameter τ = 0.1, and the following incommensurate fractional variable orders: (ν1(s), ν2(s), ν3(s)) = (1/(1 + exp(−s)), s/(s + 1), 0.7 + 0.2(exp(−s)/(1 + exp(−s)))), (ν1(s), ν2(s), ν3(s)) = (1/(1 + exp(−s)), 0.94 + (1/20)sin((1/5)s), 0.5 + 0.3cos(0.1s)), (ν1(s), ν2(s), ν3(s)) = ((1/12)expsin((1/15)s) + 0.76,0.94 + (1/20)sin((1/5)s), 0.5 + 0.3cos(0.1s)), and (ν1(s), ν2(s), ν3(s)) = (0.99 − (0.01/100)s, 0.94 + (1/20)sin((1/5)s), 0.5 + 0.3cos(0.1s)), The system parameter α is set to 1.6 and 1.68, respectively. These chaotic attractors exhibit a distinct structure compared to those observed in the commensurate order case. For the specific incommensurate variable fractional order (q1(r), q2(r), q3(r)) = (0.99 − (0.01/100)r, 0.94 + (1/20)sin((1/5)r), 0.5 + 0.3cos(0.1r)) and the system parameter α = 1.6, the fractional Grassi–Miller map diverges to an unbounded attractor. However, when the system parameter α is increased to 1.68, Figure 7(c) demonstrates that the system (13) becomes periodic. In greater detail, the attractors calculated with the initial conditions (1,0.1,0) and the incommensurate fractional variable orders exhibit rich dynamical behavior. The varied fractional orders influence the system’s trajectory in the phase space, leading to different attractor structures.
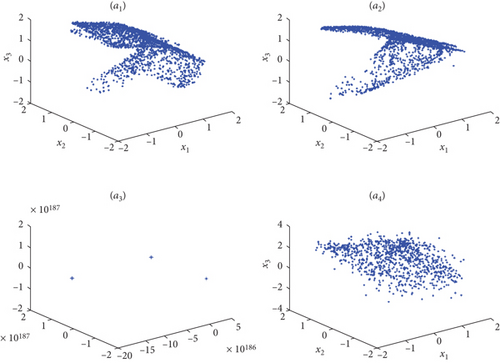
- •
(ν1(s), ν2(s), ν3(s)) = (1/(1 + exp(−s)), s/(s + 1), 0.7 + 0.2(exp(−s)/(1 + exp(−s))))
- •
(ν1(s), ν2(s), ν3(s)) = (1/(1 + exp(−s)), 0.94 + (1/20)sin((1/5)s), 0.5 + 0.3cos(0.1s))
- •
(ν1(s), ν2(s), ν3(s)) = ((1/12)exp(sin((1/15)s)) + 0.76,0.94 + (1/20)sin((1/5)s), 0.5 + 0.3cos(0.1s))
- •
(ν1(s), ν2(s), ν3(s)) = (0.99 − (0.01/100)s, 0.94 + (1/20)sin((1/5)s), 0.5 + 0.3cos(0.1s))
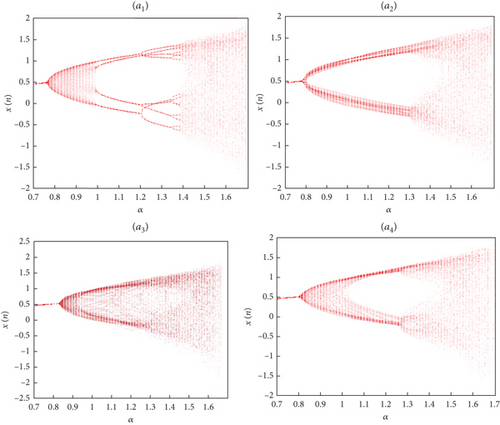
Evidently, Figure 9 demonstrates that adjusting the system parameter α results in significant modifications in the state of the bifurcation diagram while keeping the other parameters constant. Essentially, when the fractional order is assigned to (ν1(r), ν2(r), ν3(r)) = (1/(1 + exp(−s)), 0.94 + (1/20)sin((1/5)s), 0.5 + 0.3cos(0.1s)), the fractional map (13) transitions from a periodic state to a chaotic one through a period-doubling bifurcation path.
Additionally, it is evident that the chaotic intervals corresponding to the fractional order values exhibit distinct variations. The bifurcation diagrams reflect these variations and show how the system evolves from periodic to chaotic behavior as α changes.
4. Complexity Tests
4.1. ApEn
In information theory, entropy serves as a logarithmic measure that quantifies the rate at which information is transferred or generated within a system. Pincus introduced ApEn as a tool to evaluate the complexity or irregularity of a data series from a multidimensional perspective [35]. Higher ApEn values indicate greater complexity and irregularity in the data. This measurement is particularly useful for identifying and analyzing various chaotic systems.
The ApEn method serves as a fundamental tool for assessing the complexity and irregularities present in the output time series generated by the Grassi–Miller map with incommensurate variable fractional order. This method assigns a nonnegative numerical value to quantify these characteristics, with higher values indicating greater complexity within the sequence.
Figure 10 illustrates the ApEn values calculated for the suggested map (13) across various incommensurate variable fractional orders. The plot reveals distinct ranges where the ApEn values are notably elevated. This observation suggests that the dynamics described by the Grassi–Miller map, governed by Equation (13), exhibit heightened complexity within these specific parameter ranges.
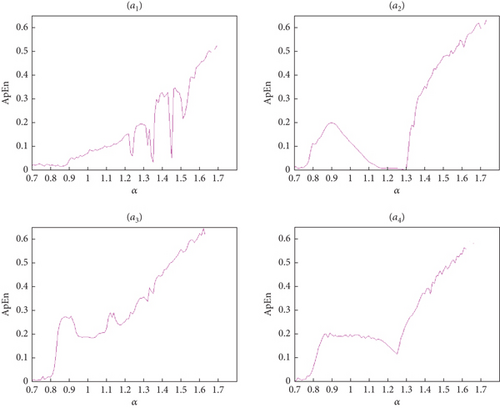
The ApEn metric provides valuable insights into how changes in the fractional orders (ν1, ν2, ν3) and the parameter α influence the system’s behavior. In particular, higher ApEn values indicate increased unpredictability and irregularity in the system’s output, highlighting the sensitivity of the Grassi–Miller map to variations in these parameters.
This analysis underscores the utility of ApEn in characterizing the intricate dynamics of fractional-order systems, offering a quantitative measure to discern and compare the complexities exhibited under different parameter settings.
4.2. The C0 Complexity
A complexity measure plays a significant role in analyzing the dynamic properties of chaotic systems. It is comparable to the Lyapunov exponent and bifurcation diagram in its ability to characterize system behavior. Higher complexity values indicate that a sequence is closer to a random sequence. C0 complexity, a randomness-based complexity measure, was first introduced by Shen et al. [36] to address the challenges of overly coarse graining during preprocessing. The C0 algorithm decomposes an original data series into two components: a regular part and an irregular part, with the irregular part being the primary focus. To investigate the impact of the system parameter α on the dynamic characteristics of the incommensurate fractional variable-order discrete system (13), we employ the C0 complexity technique.
Figure 11 displays the complexity of the Grassi–Miller map (13) evaluated using C0 complexity. The results indicate that the system exhibits varying levels of complexity across different values of the parameter α. Specifically, the plot highlights ranges where the C0 complexity is notably elevated, suggesting increased irregularity and complexity in the system’s behavior within these parameter regimes.
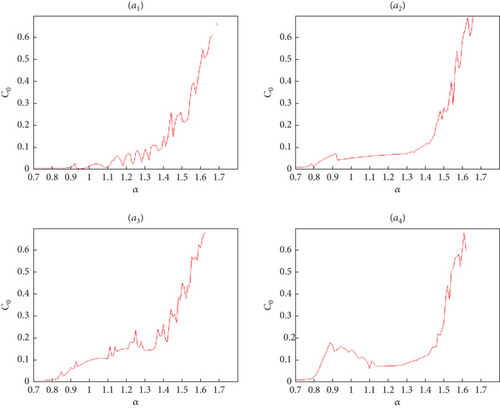
These findings are consistent with previous analyses and underscore that the discrete Grassi–Miller map (13) with incommensurate fractional variable order displays heightened complexity under specific conditions of α. Moreover, the complexity levels are influenced by the specific incommensurate fractional variable orders employed, as depicted in Figure 11. This characterization provides valuable insights into how changes in α and the fractional orders impact the system’s dynamics and predictability.
4.3. 0–1 Test for Chaos
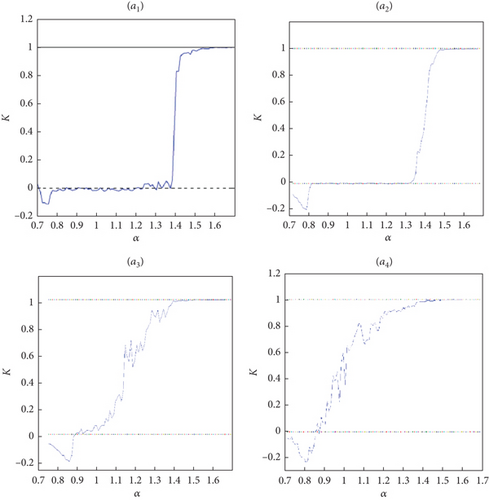
The 0–1 test for chaos is a relatively new test that can be applied to both continuous and discrete nonlinear systems or their time series responses. This test, introduced by Gottwald and Melbourne in [37], is designed to differentiate between regular and chaotic dynamics in deterministic systems. Unlike the Lyapunov exponents method, the 0–1 test can be applied to both known and unknown systems without relying on phase plane analysis. This makes it particularly effective in identifying chaos in data series without requiring phase space reconstruction.
In this paper, we further analyze the use of the 0–1 test for chaos in the case of incommensurate variable fractional order. Based on the set of states {g(r): r = 1, 2, ⋯, R}, we define the translation variables and where r ∈ {1, 2. ⋯ R} and c is chosen randomly in (0, π). Also note that bounded trajectories in the p − q plane correspond to regular dynamics, whereas Brownianlike (unbounded) trajectories correspond to chaotic dynamics.
Furthermore, the system demonstrates chaotic behavior as characterized by the parameter K, where K represents the median of . This metric indicates the asymptotic growth rate of deviations in the system’s state variables p and q.
When K approaches 1, the system exhibits chaotic dynamics, marked by sensitive dependence on initial conditions and complex, irregular behavior. Conversely, as K approaches 0, the system tends toward periodic behavior, characterized by regular and predictable patterns.
The analysis highlights that the suggested map (13) displays chaotic dynamics specifically when K approaches 1, occurring within a narrow range of the parameter α. These findings are corroborated by results from 0–1 test plots, which visually depict the transition between chaotic and periodic behavior. Additionally, measurements of the LLEs, bifurcation diagrams, C0 complexity assessments, and ApEn calculations consistently support this characterization.
Figure 12 presents the results of the 0–1 test for chaos applied to the system under study. The left panel illustrates the asymptotic growth of the mean square displacement (MSD) over time, where a linear growth pattern signifies nonchaotic behavior, while an erratic or quadratic growth pattern indicates chaos. The right panel displays the corresponding Poincaré plot, which visually represents the system’s dynamics in the transformed phase space. The presence of a scattered and irregular trajectory in this plot suggests chaotic behavior, reinforcing the findings obtained through the MSD analysis. Together, these graphical representations provide strong evidence supporting the existence of chaotic dynamics in the system.
Remark 1. Based on the numerical analysis and findings, it is evident that the variable fractional-order formulation of the Grassi–Miller model exhibits chaotic behavior across different scenarios of fractional orders, encompassing both commensurate and incommensurate cases. This observation underscores the dynamic sensitivity of systems described by Equations (7) and (13) to variations in the fractional orders of their variables, as well as changes in system parameters.
In both commensurate and incommensurate variable fractional-order configurations, the models (7) and (13) demonstrate distinct ranges of chaotic behavior. This variability in chaotic ranges emphasizes the intricate relationship between fractional-order dynamics and system behavior. Adjustments to the fractional orders of the variables lead to discernible shifts in the system’s dynamical characteristics, influencing the onset and persistence of chaotic regimes.
Furthermore, these findings suggest that the nature and extent of chaos observed in the Grassi–Miller model are not only influenced by changes in system parameters but are critically dependent on the precise values of the fractional orders assigned to the variables. This insight underscores the importance of considering fractional-order effects when studying and predicting the behavior of complex dynamical systems like those described by Equations (7) and (13).
5. Chaos Control
When dealing with chaotic dynamical systems, particular attention is given to the ability to control or stabilize these systems. By control, we mean the addition of adaptively updated terms to the chaotic system to drive its states asymptotically toward zero. One application of this approach is in robotics, where controlling the chaotic motion of a rigid body is of significant importance. In this section, we introduce the control strategy for the proposed discrete Grassi–Miller chaotic map (13), which operates under incommensurate fractional variable-order dynamics. The primary goal of this control scheme is to achieve stability by ensuring the asymptotic convergence of the system’s states toward zero. By implementing this stabilization technique, we aim to establish a robust control law that drives all states of the discrete Grassi–Miller map with incommensurate fractional variable order toward asymptotic stability at the origin.
The proposed control scheme focuses on mitigating the chaotic behavior in the system by dynamically adjusting the system parameters based on the current state. This involves developing a feedback mechanism that continuously monitors the system’s output and applies corrective actions to guide the states toward the desired equilibrium point. By leveraging the properties of the incommensurate fractional variable-order dynamics, the control law is designed to be both adaptive and responsive to changes in the system’s behavior.
To validate the stability of system (13) under the proposed control law (20), it is essential to generate phase diagrams and examine the temporal evolution of the system’s states (21).
Figures 13, 14, 15, and 16 illustrate that system (13) achieves stability under the proposed control law. It is observed that the system’s states converge to zero, indicating successful stabilization where the chaotic behavior of map (13) is suppressed.
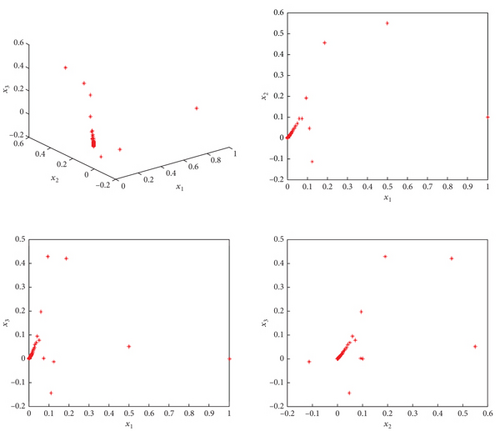
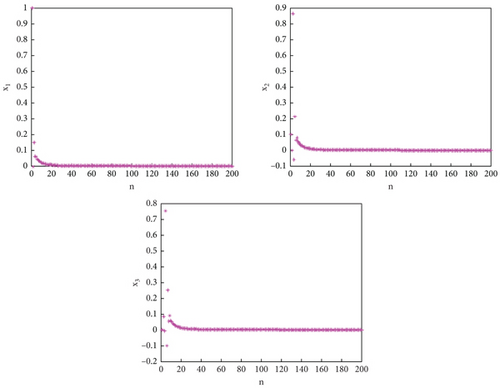
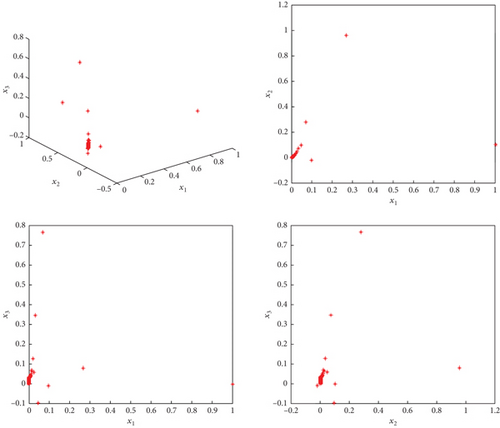
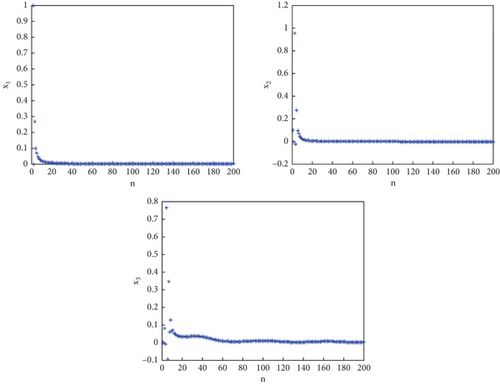
6. Discussion
6.1. Importance of Variable-Order Fractional Systems
Herein, the importance of variable-order fractional systems in science and engineering is discussed. According to a review that was published recently [38], variable-order fractional differential/difference equations with time (t), space (x), or other variable-dependent orders have become extremely significant in the field of research that investigates how systems evolve over time and/or space-dependent system dynamics. For example, the anomalous diffusion that characterizes heat conduction, solute transport, groundwater pollution, gas flow in heterogeneous porous media, relaxation in biopolymers, and propagation of seismic waves motivates the development of new mathematical tools based on variable-order fractional systems [38]. Namely, since the diffusion patterns change with time evolution, spatial variation, or system parameters, it is necessary to exploit variable-order derivative/difference operators for describing memory effects, hereditary properties, and delay behaviors in physical applications [38]. Referring to viscoelastic properties, it has been shown in literature that polymers, plastic, rubber, soil, oil, and concrete (all materials widely used in chemical/petroleum engineering, biology, and medicine) require variable-order fractional systems to model the memory behavior of these shape-memory materials [39]. Finally, referring to applications in the field of control engineering, in [40], it has been proposed a control technique that exploits a variable-order fractional controller to perform the control action, with the aim to stabilize the nonlinear behavior of a dynamic oscillator.
6.2. Comparisons with Chaos-Based Methods
In the previous subsection, we have analyzed the importance of variable-order fractional systems in science and engineering. It is worth noting that all the applications describe above regard the use of variable-order derivative/difference operators to study the behavior of complex systems, but none of the previous manuscript is related to chaotic behaviors generated by variable-order fractional systems. The only two papers in literature that deal with chaos in variable-order systems and, consequently, can be compared with this manuscript are References [28, 29]. For example, Reference [28] discusses the chaotic dynamics of the variable-order fractional Tinkerbell map. However, the dynamics of the Tinkerbell map are completely different from those of the Grassi–Miller map considered herein. Therefore, carrying out a numerical comparison between the two variable-order maps is meaningless. Similarly, in [29], the chaotic dynamics of a variable-order fractional discrete Hopfield neural network is studied in detail. However, its dynamics are completely different from those of the Grassi–Miller map considered herein, making the comparison meaningless. These considerations, besides indicating the novelty of the chaotic dynamics studied herein, explain why the only numerical comparison carried out throughout the paper regards the Grassi–Miller map considered in Reference [32]. Namely, the numerical comparison between the variable-order Grassi–Miller map conceived herein and the same map with constant order proposed in [32] has revealed that the former exhibits chaotic attractors when the system parameters are α = 1.68 and τ = 0.1, while the latter does not exhibit any chaotic behaviour for the same parameter values. This is a clear indication, from the system dynamics point of view, that using distinct operators (fractional Caputo delta difference with constant order in [32] and fractional Caputo delta difference with variable order) results in distinct dynamic behaviors in the two maps. Finally, we would point out that the Grassi–Miller map is one of the most well-known hyperchaotic discrete systems in literature. Thus, we feel that this is a good reason for exploring its rich dynamic behavior in a field that is unexplored, as is the case of its variable-order (commensurate and incommensurate) fractional dynamics.
7. Conclusion and Future Works
This study introduces two variants of the discrete Grassi–Miller map with fractional order, both incorporating variable-order dynamics. Specifically, the research investigates the chaotic behavior exhibited by the discrete Grassi–Miller system under both commensurate and incommensurate variable fractional orders. These variable orders are characterized by functions such as exponentials and sinusoids, expanding the exploration of system dynamics beyond traditional integer-order systems.
To validate the chaotic nature of the proposed fractional versions of the Grassi–Miller map, various numerical techniques have been employed. These include phase diagrams, bifurcation diagrams, Lyapunov exponents, ApEn estimation, C0 complexity, and 0–1 test plots. Through comprehensive analysis using these tools, the study confirms the presence of chaotic attractors in the system across different fractional-order scenarios.
In future research, we intend to further investigate this topic by implementing the previous model in the context of electrical circuit modeling and exploring its potential applications in cryptography. A primary focus will be the development of a novel fractional pseudorandom number generator based on fractional maps with variable orders. We aim to examine these aspects in greater detail to evaluate their feasibility and reliability in practical applications.
Conflicts of Interest
The authors declare no conflicts of interest.
Author Contributions
Conceptualization, A.A.K. and A.O.; methodology, A.H.; validation, A.O. and S.B.A.; formal analysis, A.O., G.G., and M.A.H.; investigation. All authors have read and agreed to the published version of the manuscript.
Funding
No funding was received for this research.
Acknowledgments
The authors have nothing to report.
Open Research
Data Availability Statement
Obtained numerical data were used to support the study.




