1. Introduction

Many countries have introduced carbon reduction policies in response to global warming, identifying transportation as primary source of carbon emissions. For example, “The Long-Term Strategy of The United States Pathways to Net-Zero Greenhouse Gas Emissions by 2050”, “The Action Plan for Peak Carbon Dioxide Emissions by 2030” issued by China, and “Clean Growth Strategy” issued by the United Kingdom. Encouraging travelers to choose environmentally friendly travel modes is crucial for reducing carbon emissions. Electric vehicles (EVs) are expected to reduce carbon emissions and air pollution, leading to extensive development of associated transportation infrastructure. As the transition unfolds, a mixed traffic flow comprising both oil-fueled vehicles (OFVs) and EVs will persist until EVs eventually replace OFVs entirely.

EVs also have some problems that need to be solved: First, charging stations is limited, and how to optimize the charging facilities are crucial; Secondly, the distance an EV can travel is short, causing anxiety among users on the route; Finally, the driving behavior of EV user is inconsistent with that of OFV, which could have new impacts on the road network. Therefore, scholars in academia are actively investigating topics such as EV path selection, charging behavior, and energy consumption.

In those studies on EVs charging behavior, Cai et al. [1] proposed two charging strategies: user optimization and system optimization. They pointed out that the user optimization strategy aims to guide individual charging behavior, while the system optimization strategy focuses on coordinating and controlling charging behavior at a broader level. Liu [2] developed a charging process function and vehicle energy consumption model to examine charging strategies for connected EVs. Wang et al. [3] proposed a model to predict EV charging demand, employing the Monte Carlo method to simulate EV travel characteristics. Yang et al. [4] analyzed factors that affect high-power charging for private EVs, considering travel time and driving distance. Wang et al. [5] designed a geometry-based charging guidance algorithm, suitable for intelligent charging services. Pan et al. [6] developed a charging choice behavior model for EV drivers based on a logit model to simulate charging decisions at the destination. Yang et al. [7] proposed a polynomial logit model and a nested logit model using survey data to compare travel behavior among EV and OFV drivers. Wang et al. [8] analyzed the charging behavior of EV drivers considering heterogeneity and satisfaction factors. Wang et al. [9] proposed a multistage optimization model to provide inter-city travel charging strategies for EV drivers. Xiong et al. [10] formulated an optimization model for charging station to minimize social costs, introducing a K-level nested quantum response equilibrium model to analyze the EV driver decision-making during the charging. He et al. [11] investigated the influence of EVs’ limited driving range and charging requirements on route choice, although a linear charging function was used for charging time calculation, without considering for charging piles location planning in the hybrid traffic network. Agrawal et al. [12] developed a multiclass dynamic user equilibrium model to investigate EV driver routes and their impact on traffic network performance.

Aiming at EV path selection, Chen et al. [13] proposed a bi-level programming model to optimize the location and capacity of charging facilities, striking a balance between EV route selection and charging waiting time. Jensen et al. [14] found that drivers’ preferences shift from travel time and travel distance before using EVs to route accessibility afterward. It implies that it may be necessary to modify the traffic planning model of EVs and the assumptions of path problems. Pourazarm and Cassandras [15] studied EV path problem in networks with charging nodes to minimize the total travel time. Shao et al. [16] proposed a path selection method for EVs, integrating charging time and variable travel time consideration based on distance limit and EV charging demand.

In the realm of energy consumption literature, Cai [17] developed a path planning model incorporating the energy consumption model for EVs and a nonlinear charging function. Song [18] proposed an energy consumption model under various driving conditions considering the correlation between battery energy consumption and the vehicle driving index. He et al. [19] proposed an emission model for EVs and OFVs based on energy consumption data. Zhang and Yao [20] developed an energy consumption factor model using actual driving condition data, considering the correlation between speed and link. Yao et al. [21] investigated an electricity consumption model and a gasoline consumption model to explore the influence of EV penetration on road traffic conditions and energy consumption. Zhong et al. [22] integrated environmental capacity constraints into mixed EV and OFV network traffic to mitigate emissions in protected areas, addressing suboptimal charging pricing scheme within fixed and elastic demand user equilibrium frameworks. Yao et al. [23] used vehicle-specific electricity as an intermediate variable to analyze energy consumption models disparities across distinct road structures, highlighting the pivotal role of the energy consumption coefficient in road energy consumption.

In summary, existing literature has explored the classification of charging piles in relation to travel, has not delved into traffic equilibrium assignment considering the hierarchical layout of charging piles within mixed traffic flows. As for the research on traffic equilibrium assignment, existing works modeled the EV route selection by limiting the range of EV, failing to consider the impact of user perception deviation and the state of charge (SOC). In addition, the effect of EV on the road network is unclear, the measurement method for network carbon emission requires further explored.

To address these research gaps, this paper develops a mixed user equilibrium (M-UE) traffic assignment model to analyze path selection, charging behavior, charging station utilization and traffic flow distribution. Factors such as traveler risk perception, perceived time deviation, and initial SOC are taken into account. A novel method is proposed to describe charging behavior by introducing minimum remaining charge and desired charge parameters. Additionally, a carbon-emission method is developed based on the mixed equilibrium assignment model.

The remainder of this paper is organized as follows: Section 2 presents a mixed traffic equilibrium assignment model and a carbon-emissions method. Section 3 presents a case study, and Section 4 outline important conclusions.

2. Methodology

This paper mainly investigates the impact of EVs on traffic flow assignment and carbon emissions in road network. EV users have range anxiety, and EV need to consider charging, leading to inconsistent path selection with fuel vehicles. Therefore, it is necessary to propose a new traffic assignment model to describe the impact of EVs on flow distribution. Then, a carbon emission calculation model is set up based on traffic volume obtained from traffic assignment model to analyze the impact of EVs in road network.

2.3. Solution Algorithm

The M-UE model is a convex programming problem with linear constraints, which can be solved using an iterative approach proposed by He et al. [11]. Given the consideration of both risk perception and perceived time deviation in our model, the problem can be reformulated as finding the shortest available path while accounting for the user’s perception of charging time, as shown in equation (21).

$$ ()

$$ ()

$$ ()

$$ ()

$$ ()

$$ ()

$$ ()

$$ ()

$$ ()

where $$ is theoretically the electric quantity in the charging station for users m; t_i1 represent fixed charging time; t_i2 is the variable of charging time, depending on the type of charger; $$ is the SOC after charging; L_max is the capacity of battery; $$ is the initial electric quantity. Δ is a node-path correlation matrix; $$ is a vector of length |N|; $$ and $$ are binary variables; k is the coefficient of comfort; H and K are constants that are arbitrarily and sufficiently large.

In the above model, the objective function formula (21) aims to minimize the total travel time; constraint formula (22) ensures traffic flow balance; constraint formulas (23) and (25) specify the electric quantity relationship for a selected path between the origin and destination. Travelers will not deplete the electric quantity completely in the constraint condition (24), and they prefer to keep some remaining electric quantity not less than the comfortable electric quantity.

Let $$ be the optimal solution of the objective function (21) for each type m ∈ M in the OD pair w ∈ W. The shortest available path can be obtained by solving $$; the minimum charging time can be obtained by solving $$ and $$, that is, $$. The following iterative calculation process can then be used to solve the M-UE. The flowchart of the algorithm is shown in Figure 1.

•  

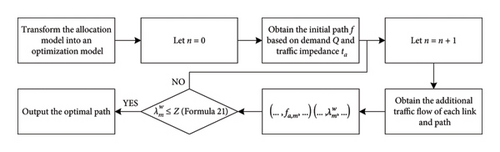
  Step 1: Convert the proposed traffic assignment model into an optimization model. The transformation model $$ is solved for each type of user (m ∈ M) between the OD pair (w ∈ W). The initial available path set $$ is obtained based on link flow x_a, and the minimum actual charging time is calculated by $$.

•  

  Step 2: Let iterations n = 0, and $$ is obtained based on traffic flow x_a. The M-UE model is solved to obtain the optimal road network traffic flow assignment ($$ and $$) based on the initial available path ($$).

•  

  Step 2.1: Let n = n + 1, calculate $$ based on the current traffic flow of each section $$.

•  

  Step 2.2: According to the travel time and OD traffic obtained in step 2.1, perform all or nothing traffic assignment to obtain the additional traffic flow of each link $$.

•  

  Step 2.3: Calculate the current link flow $$. Based on the traffic flow of each road, the traffic flow that can reach the path.

•  

  Step 3: If $$, $$ joins in $$. If $$, iteration stop, and the optimal path traffic $$ are output; otherwise, go to Step 1.

3. Analysis

This section uses two classic networks to analyze the proposed traffic assignment model and carbon emission calculation model. This paper analyzes the impact of four parameters on travel time and charging, including risk perception, safe remained electricity, initial electricity, and proportion. The carbon emission calculation model is tested by considering safe remained electricity, desired charging electricity, and road type.

3.1. Traffic Assignment

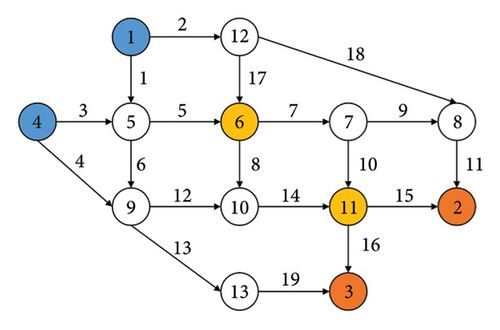
The Nguyen-Dupius network is a classical network commonly used to assess the traffic assignment models. It consists of 4 OD pairs, 19 links, and 13 nodes [24], as shown in Figure 2. Nodes 1 and 4 serve as origins, nodes 6 and 11 are designated charging nodes, and nodes 2 and 3 represent destinations. The parameters are shown in Table 1. The battery capacity (L_max) is set at 40 kWh, and ϖ = 0.167 kWh/km.

Table 1. Information of the network.

Link	Distance (km)	Free flow travel time (min)	Capacity (veh/h)
1	14	7	900
2	16	8	700
3	18	9	700
4	28	14	900
5	10	5	800
6	18	9	600
7	10	5	900
8	26	13	500
9	10	5	300
10	18	9	400
11	20	10	700
12	20	10	700
13	18	9	600
14	16	8	700
15	18	9	700
16	16	8	700
17	14	7	300
18	30	15	700
19	22	11	700
—	—	—	—

Given that the charging station exclusively offers fast charging facilities, a linear charging time function is further improved based on the work of He et al. [11].

$$ ()

where t_i1 represents the fixed time for charging, set at 5 min; t_i2 is a variable charging time dependent on a charging level of a charging pile, including $$ and $$. If the current electricity is lower than the charging electricity threshold, $$, otherwise, $$.

The EV penetration rate is assumed to be 30%. EV users are divided into three different types, with each type having a penetration rate is set to 10%. Other parameters such as demand, risk perception (θ_m), and perceived time errors (γ_m) are shown in Table 2. The safe electricity and initial electricity are provided in Table 3.

Table 2. Value of parameters.

OD	Demand	Users type	Risk perception θm	Perception time deviation γm and proportion	Proportion (%)
(1, 2)	400	BEV	1.1	(1.2, 50%; 1.5, 40%; 2, 10%)	10
			1.3		10
			1.5		10
(1, 3)	800	BEV	1.1	(1.2, 50%; 1.5, 40%; 2, 10%)	10
			1.3		10
			1.5		10
(4, 2)	600	BEV	1.1	(1.2, 50%; 1.5, 40%; 2, 10%)	10
			1.3		10
			1.5		10
(4, 3)	200	BEV	1.1	(1.2, 50%; 1.5, 40%; 2, 10%)	10
			1.3		10
			1.5		10

Table 3. Safe remained electricity and initial electricity.

θm	Safe remained electricity	Initial electricity and proportion
1.1	0.1Lmax	(0.15Lmax, 60%; 0.2Lmax, 30%; 0.25Lmax, 10%)
1.3	0.15Lmax	(0.15Lmax, 60%; 0.2Lmax, 30%; 0.25Lmax, 10%)
1.5	0.2Lmax	(0.15Lmax, 60%; 0.2Lmax, 30%; 0.25Lmax, 10%)

The results of the traffic assignment are shown in Table 4, indicating the utilization of 13 paths by travelers along with path flow and path travel time. In addition, paths 1, 6, and 13 have no EVs flows, due to there are no charging station in the path. Paths 3, 5, 9, 10, and 12 are unsuitable for EVs with low initial electricity due to limitations arising from distance and position of charging station node.

Table 4. Road flow and travel time under equilibrium conditions.

OD	Path ID	Path	Number of vehicles on the path (veh)				Travel time (min)
			EV	Energy consumption (kWh)	OFV	Total
(1, 2)	1	1-12-8-2	0	11.02	264	264	49.63
	2	1-5-6-7-8-2	120	10.69	0	120	51.09
	3	1-5-9-10-11-2	0	14.36	16	16	49.63
(1, 3)	4	1-5-6-7-11-3	240	11.36	0	240	50.53
	5	1-5-9-10-11-3	0	14.03	345	345	49.07
	6	1-5-9-13-3	0	12.02	215	215	49.07
(4, 2)	7	4-5-6-7-8-2	103	11.36	154	257	63.90
	8	4-5-6-7-11-2	77	12.36	0	77	63.90
	9	4-5-6-10-11-2	0	14.7	50	50	63.80
	10	4-9-10-11-2	0	13.69	216	216	63.90
(4, 3)	11	4-5-6-7-11-3	64	12.02	4	64	63.33
	12	4-9-10-11-3	0	13.36	10	10	63.33
	13	4-9-13-3	0	11.36	122	122	63.33

Figure 3 illustrate the number of charging vehicles at charging station node 6 and 11 under a mixed equilibrium. Node 6 has a higher number of charging vehicles compared to node 11, attributed to varying risk perceptions. However, the number of EV users choosing node 6 gradually decreases with the increase in risk perception and initial electricity. Correspondingly, the safe electricity and initial electricity increase with the improvement of risk perception. Additionally, node 11 is closer to the destination, leading to more EVs choose node 11 for charging.

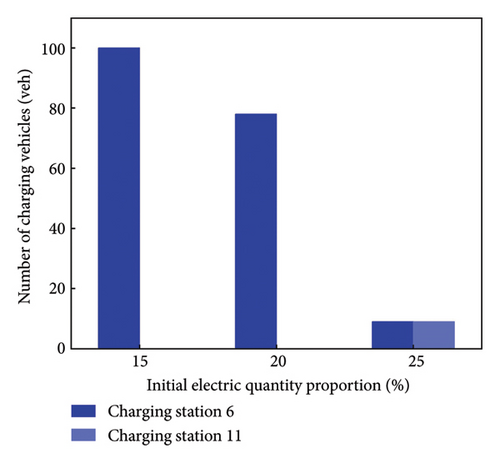
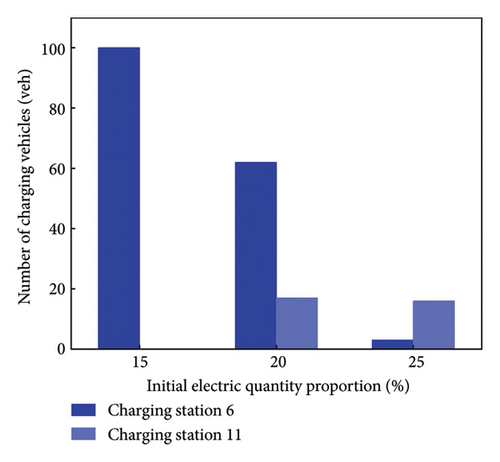
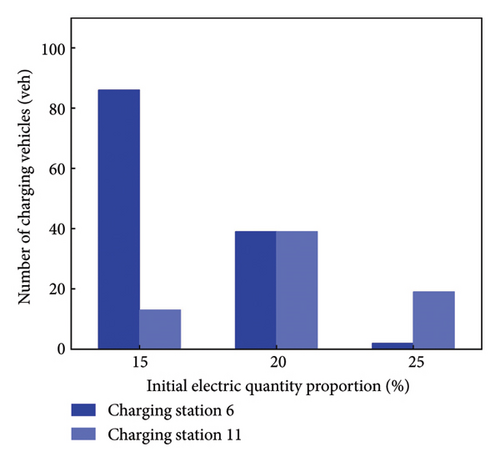
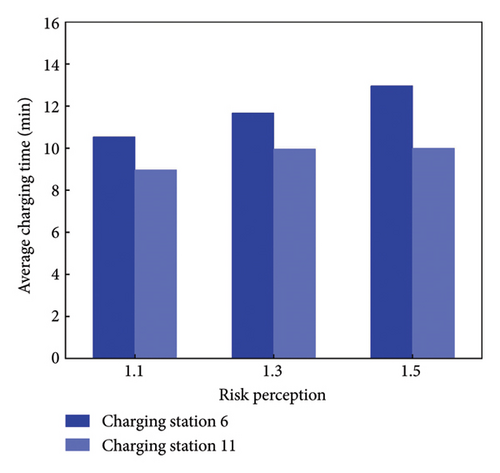
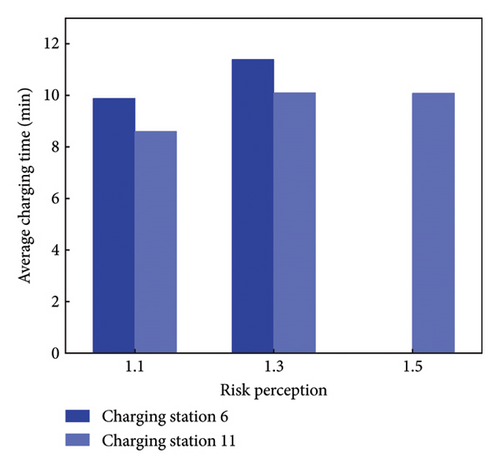
Figure 3 depicts the charging time of nodes 6 and 11. The average charging time at node six exceeds that of node 11, due to the latter’s proximity to the destination. More EVs opt for node 6 to ensure their remaining electricity surpassed the safe electricity threshold. EV users tend to increase their charging time to avoid the anxiety associated with heightened of risk perception. Comparison between Figures 4(a) and 4(b), reveals that perceived charging time is higher than the actual charging time.

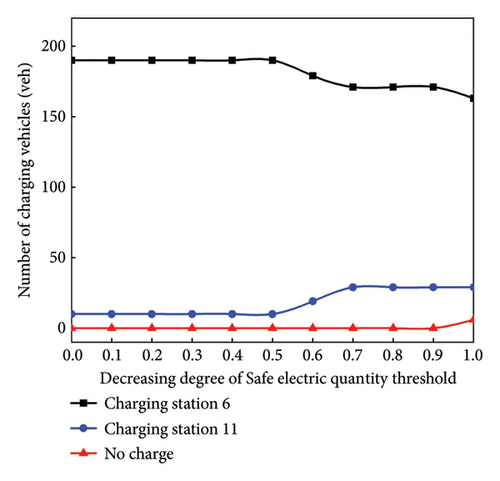
The impact of risk perception on the M-UE model is further analyzed by a reduction the initial electricity, as shown in Figure 5. The number at charging vehicles at charging station node 6 and node 11 is shown in Figure 5 under different risk perceptions. If θ_m = 1.1, a small number of EV users transition from node 6 to node 11for charging as the safe electricity diminishes. If the safe electricity reaches 0, most users choose to charge their EVs. If θ_m = 1.3, the number of EV users who charge at node 11 gradually increases as the safe electricity decreases. If θ_m = 1.5, the number of EVs users choosing not to charge their EV increases the most as the safe electricity decreases.

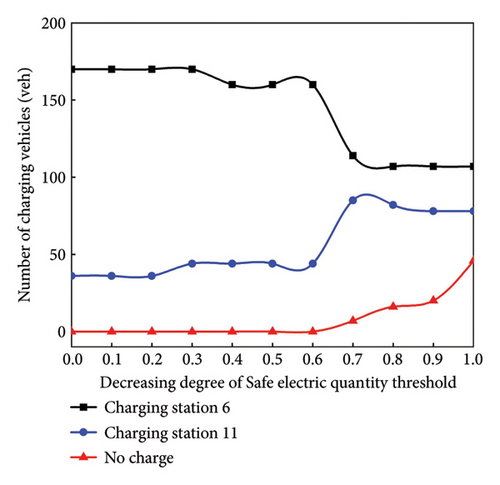
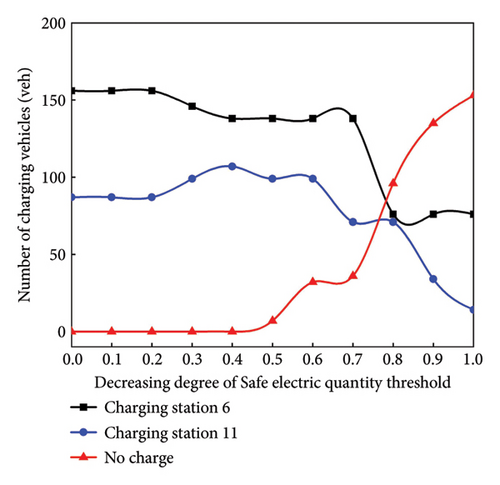
Based on the information provided in Table 4, it appears that some users do not charge their EVs on route, thereby making path 2 and path 4 suboptimal. Consequently, Table 5 presents detailed path information without considering the safe electricity. Comparing the travel time between Tables 4 and 5 reveals differences. Notably, the total travel time increases by 37.02% when considering the safe electricity.

Table 5. Traffic flow and travel time without safe remained electricity.

OD	Path ID	Node order	Total	Travel time (min)
(1, 2)	1	1-12-8-2	271	50.26
	2	1-5-6-7-8-2	92	50.25
	3	1-5-9-10-11-2	43	50.25
(1, 3)	4	1-5-6-7-11-3	193	49.35
	5	1-5-9-10-11-3	381	49.35
	6	1-5-9-13-3	226	49.35
(4, 2)	7	4-5-6-7-8-2	275	63.92
	8	4-5-6-7-11-2	65	63.92
	9	4-5-6-10-11-2	50	63.92
	10	4-9-10-11-2	210	63.92
(4, 3)	11	4-5-6-7-11-3	62	63.02
	12	4-9-10-11-3	12	63.02
	13	4-9-13-3	121	63.02

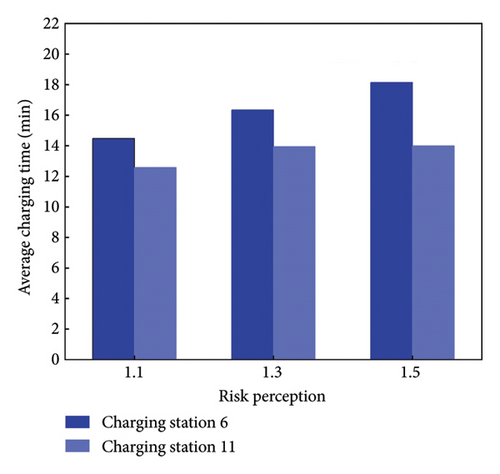
Figure 6 shows the average charging time for node 6 and node 11, without setting the safe electricity. Comparing with Figure 4, if θ_m = 1.1, the average charging time is smaller; if θ_m = 1.3 or θ_m = 1.5, the charging time at node 11 increases, because more EV users choose to charge at station 11 to supplement electricity without considering the safe electricity.

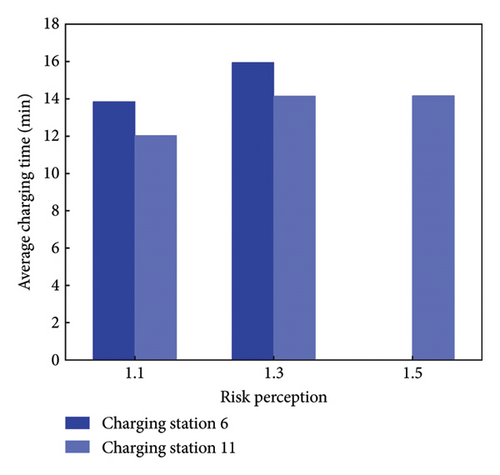
In summary, considering the safe electricity parameter leads to higher travel times for some paths compared to others. With the increase in risk perception, more EV users choose node 11 for charging, despite the potential increase in charging time. In addition, the influence of the safe electricity on the M-UE model is further analyzed in the N-D network.

3.2. Carbon Emissions and Energy Consumption

Figure 7 shows the test network, that consists of 2 OD pairs, 11 nodes and 14 links. The information of this network is shown in Table 6. The EV battery capacity is set at L_max = 24 kWh in this study. The charging stations are located at nodes 1, 9, and 10 respectively. The safe electricity values are shown in Table 7.

Table 6. Information of network.

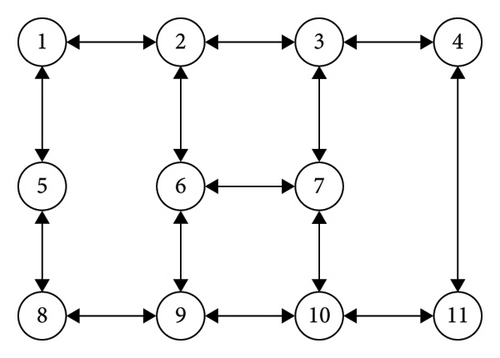
Link		Road degree	Road capacity (veh/h)	Road distance (km)	Road speed (km/h)
1	1–2	Main road	1400	14.5	12.27
2	2–3	Main road	1400	26.2	25.02
3	3–4	Main road	1400	37.5	16.26
4	4–11	Main road	1400	46.8	26.84
5	8–5	Main road	1400	14.2	37.72
6	9–8	Main road	1400	33.4	26.16
7	10–9	Main road	1400	24.2	26.22
8	11–10	Main road	1400	36.9	14.50
9	1–5	Secondary road	1000	44.5	17.78
10	2–6	Branch road	700	19.2	24.15
11	3–7	Branch road	700	7.4	25.43
12	6–9	Branch road	700	27.8	21.63
13	6–7	Branch road	700	26.4	25.39
14	7–10	Branch road	700	28.9	27.49

Table 7. Values of safe remained electricity.

Parameters	Value
α∗	$$, $$, $$
β∗	$$, $$

The results of traffic assignment, obtained using the network equilibrium, are shown in Table 8, serving as the basis for analyzing emissions and energy consumption.

Table 8. Results of traffic assignment.

OD	Demand	Path ID	Node order	Path distance (km)	Number of vehicles on path (veh)	Selection probability	Path travel time (min)
1–11	1400	1	1-2-3-4-11	125	263.29	0.19	127.00
		2	1-2-3-7-10-11	123.9	297.72	0.21	125.76
		3	1-2-6-7-10-11	125.9	197.66	0.14	129.86
		4	1-2-6-9-10-11	122.6	624.22	0.45	118.40
		5	1-5-8-9-10-11	153.2	17.11	0.01	154.28
4–8	1200	6	4-3-2-1-5-8	136.9	246.33	0.21	138.49
		7	4-3-2-6-9-8	144.1	109.77	0.09	146.54
		8	4-3-7-6-9-8	142.5	318.37	0.26	135.96
		9	4-3-7-10-9-8	141.4	362.19	0.30	134.69
		10	4-11-10-9-8	141.3	163.35	0.14	142.59

3.2.1. Road Type

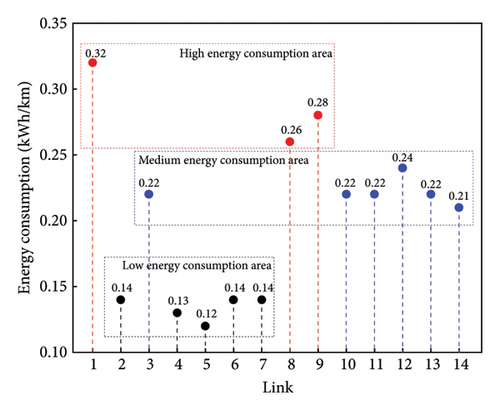
Figure 8 is a scatter diagram illustrating the energy consumption rate on roads, divided into three categories based on energy consumption. Road with an energy consumption rate below 0.15 kWh/km, are classified as low energy consumption areas; those with the energy consumption rate ranging from 0.15 to 0.25 kWh/km, are classified as medium energy consumption areas; while roads with rates exceeding 0.25 kWh/km are considered high energy consumption areas. Specifically, links 2 and 4 to 7 fall under the category of low energy consumption areas; links 1, 8 and 9 belong to the high energy consumption areas; links 3 and 10 to 14 are categorized in the medium energy consumption areas. According to Table 5, the energy consumption is found to be significantly related to speed and traffic volume.

The initial electricity is assumed to be full, and the safe electricity is 1%. Figure 9 illustrates the charging time, total travel time, and carbon emissions for four different road network categories. Category 1 is defined as main roads, category 2 is defined as secondary roads, category 3 is defined as branches, and category 4 is a mixed road network composed of the mentioned three types of roads.

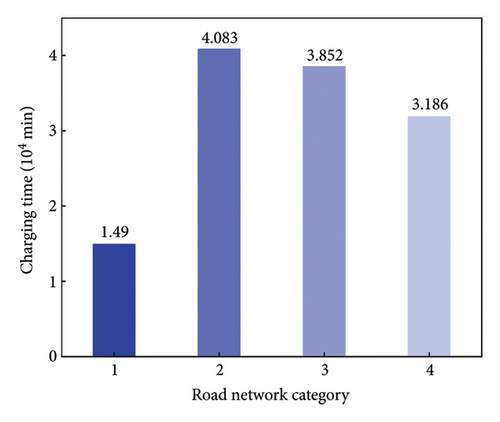
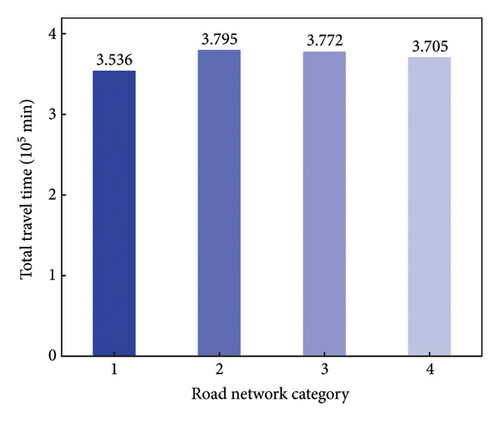
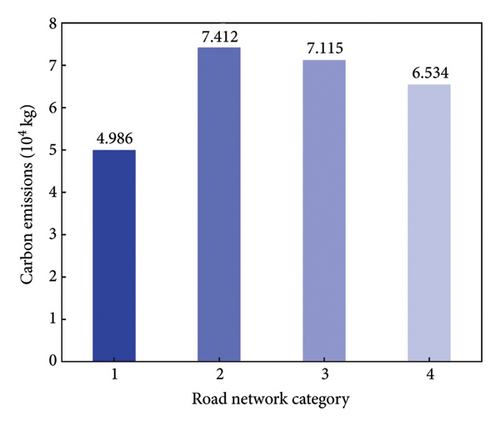
It is found from Figure 9 that the charging time, total travel time, and carbon emissions for category 1 are significantly lower than those for other categories. The charging time of category 4 is 113.83% higher than category 1, but 21.96% and 17.29% lower than category 2 and category 3, respectively. The total travel time of category 4 is 4.78% higher than category 1, but 2.37% and 1.77% lower than category 2 and category 3, respectively. The carbon emission of category 4 is 31.04% higher than category 1, but 11.84% and 8.16% lower than category 2 and category 3, respectively.

3.2.2. α^∗ − β^∗

The impact of safe remained electricity α^∗ and desired charging electricity β^∗ on travel time and energy consumption is analyzed, assuming a market penetration rate of 50% for EV in the test network.

The charging time is lower with low safe remained electricity and reaches its highest with medium safe remained electricity, as shown in Figure 10. If β^∗ = 80%, the charging time is significantly higher than that of β^∗ = 70%. As shown in Figure 11, if β^∗ = 70%, the total travel time with low safe remained electricity decreases by 0.57% and 0.43% (α^∗ = 1%) compared to medium (α^∗ = 3%) and high (α^∗ = 5%) safe remained electricity values. If β^∗ = 80%, the total travel time with low safe remained electricity decreases by 0.64% and 0.51% (α^∗ = 1%) compared to medium (α^∗ = 3%) and high (α^∗ = 5%) safe remained electricity values. In addition, the total travel time with β^∗ = 80% is significantly higher than β^∗ = 70%.

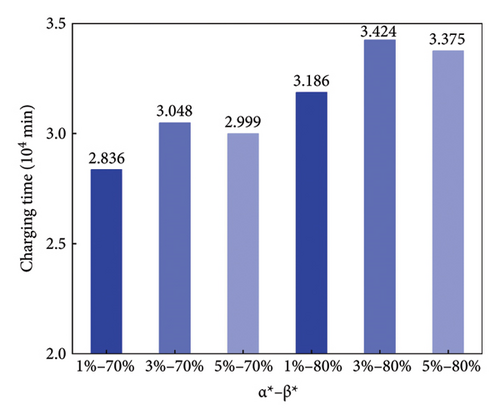
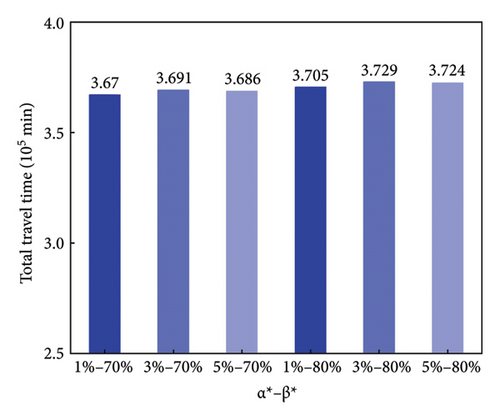
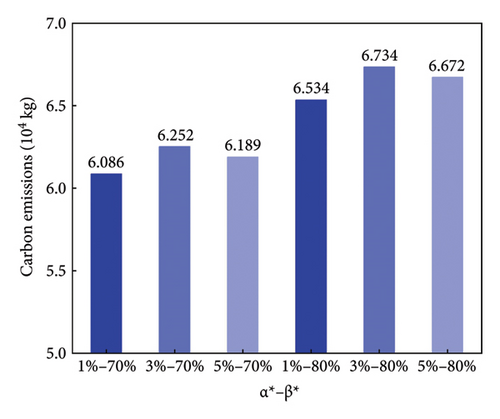
Figure 12 compares carbon emissions considering α^∗ and β^∗. It is observed that carbon emissions are lower with low safe remained electricity compared to medium and high remained safe electricity values. If β^∗ = 70%, the carbon emissions with low safe remained electricity decreases by 2.66% and 1.66% compared to those of medium and high safe remained electricity values respectively. If β^∗ = 80%, the carbon emissions with the low safe remained electricity are 2.97% and 2.07% lower than those of medium and high safe remained electricity values respectively. Furthermore, the total carbon emissions with β^∗ = 80% is significantly higher than that of β^∗ = 70%.

4. Conclusion

The paper develops a mixed equilibrium model to assess the impact of EVs on traffic assignment, considering the risk perception, perceived time deviation, and initial battery state for travelers. Additionally, a carbon emission model is built up based on traffic assignment to estimate CO₂ emission in the network. Two test cases are used to analyze the impact of EVs characteristics on the network with sensitivity analyses conducted for road type, safe remained electricity, desired charging electricity, and risk perception. The findings indicate that EVs will increase the total travel time in the road network, as they tend to choose paths with charging piles. The travel time of the road network has increased by 27%. The location of charging state and the user’s risk perception affect vehicle routing decisions. After we changed the location of a charging station, the total travel time has decreased by 0.2%, the total carbon emissions have decreased by 1.85%, and the balance of charging station utilization has decreased by 0.95%. Moreover, road type and average speed are important factors affecting carbon emissions. The charging time of mixed network is 113.83% higher than main road, but 21.96% and 17.29% lower than secondary and branch roads, respectively.

Existing research primarily focusses on a static road network, often virtual rather than real-life networks. Future research could explore charging strategies and traffic assignment in dynamic traffic flow networks using actual real-life data. In addition, considering users’ uncertainty in travel time, a hybrid stochastic user equilibrium model could be adopted for further investigation. In parallel, the analysis of charging station optimization could improve the road traffic efficiency and mitigate the EV users’ psychological “charging anxiety” in the future.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Z.Z.: formal analysis; investigation; writing–original draft; writing–review and editing. W.H.: conceptualization; funding acquisition; methodology; project administration; resources; supervision; methodology. Y.G.: software; validation; visualization. W.W.: methodology. Y.C.: writing–review and editing; S.L.: software, validation.

Funding

This work was supported by the Science and Technology Innovation Program of Hunan Province (2023SK2052, 2023RC1059) and The Changsha Science and Technology Plan Project Funding (kq2107009, kh2301004).