1. Introduction

Transportation management is a multifaceted discipline that encompasses the planning, execution, and oversight of the movement of goods and people. One of its primary goals is to ensure the safety and efficiency of transportation systems [1, 2]. This involves a range of activities, from route planning and vehicle maintenance to traffic management and the implementation of safety protocols [3, 4]. Sustainability in urban planning plays a crucial role in creating transportation systems that minimize environmental impact and promote long-term ecological balance [5–7]. A critical aspect of transportation management is road safety, particularly in areas prone to accidents, such as horizontal and vertical curves. These curves are especially hazardous due to the centrifugal force exerted on vehicles, which can lead to a loss of control if not properly managed. The design and maintenance of these road sections are crucial in mitigating risks and preventing accidents [8–10]. The safety of curves, especially on foreslopes, is dependent on some factors, the most important of which is the geometrical features of the road [11]. Enhancing the safety of horizontal and vertical curves, especially on mountain roads, is crucial due to the potential combination of horizontal curves with vertical alignments and steep foreslopes [12].

The condition of the pavement surface plays a vital role in ensuring road safety by providing necessary friction for vehicle control [13–15]. Pavement surface friction is a critical factor in road traffic safety. A low friction factor caused by surface polishing or improper implementation is considered a potential risk for the occurrence of an accident [16, 17]. In addition, low friction decreases the available friction and increases the required friction, which will raise the risk of an accident, especially in curves [18]. The coefficient f is referred to by various terms, including the side ratio, rotation ratio, friction factor, and side friction factor, of which, the last one is used here because of its increased application. Friction is defined under two longitudinal and radial (side) directions of movement [19, 20]. Based on this, the design guidelines define the allowed friction factors in two directions of movement. The wheels of the vehicle start to slide when the side friction factor reaches its upper limit, which is called the impending skidding point. The amount of friction is dependent on different parameters: the conditions and type of tires and pavement surfaces, weather conditions, vehicle type, driver performance, the ability to control the vehicle when leaving the road, changing driver behavior, and applying the braking force. Vehicle dynamics simulation can be used to predict and analyze the behavior of vehicles under various friction conditions, helping to design safer roads and improve vehicle control strategies [21–23]. As speed increases, the required friction also increases if the existing friction decreases at the same time [24–26]. Based on this, if the margin of safety has a value greater than zero (i.e., available side friction > necessary side friction), the road conditions are considered safe and suitable, but when it is less than zero (available side friction < necessary side friction), there is not enough friction for braking force and for returning to the moving path. In this case, it is necessary to provide safe conditions on vertical and horizontal curves with the following methods: modifying the geometry of horizontal and vertical curves, adjusting the geometry and slope of foreslopes, reducing the 85th percentile speed, and improving the friction conditions of the pavement surface [27, 28].

Zhu and Li analyzed the use and impact of roadside guardrails on Indiana’s highways, focusing on types, lengths, and positions. It examined 4657 run-off-the-road (ROR) crashes from 2004 and 2006, assessing crash frequencies, locations, and consequences, as well as factors such as road geometry, seasons, and traffic volume. The study also evaluated vehicle–guardrail crash features and predicted crash rates and severities, finding lower encroachment rates than the AASHTO guidelines. In addition, it reviewed guardrail repair costs, noting significant increases in steel prices and varying costs for different guardrail types. The average repair cost was $722 per crash, with annual maintenance at $0.305 per foot. ArcMap was used for managing and analyzing the data [29]. Montella and Pernetti analyzed 1092 ROR crashes on Italy’s A16 motorway (2001–2005) to identify the risk factors for improving safety measures. Findings revealed that motorcycle crashes were more severe than other vehicle types, while adverse conditions (nighttime and wet pavement) reduced crash severity. Crashes into ditches and slopes were more severe than those against steel barriers. Blunt-end terminals of safety barriers significantly increased crash severity compared to their longitudinal counterparts. Thrie-beam barriers outperformed older W-beam types, and New Jersey concrete barriers led to more severe crashes and rollovers compared to steel barriers, despite better performance in preventing penetration and override [30].

Delgado aimed to create regression models to estimate annual ROR crash costs for rural road segments, considering roadway and traffic characteristics, as well as the nature and dimensions of roadside hazards. These estimates would enable quick network-level evaluations. The models, which were based on Road Safety Analysis Program (RSAP) analysis and collected data, achieved a coefficient of determination (R²) of 0.80. They were used to replicate a 2005 Hillsborough County study, confirming the ranking of 19 sites for further engineering evaluation with minor variations in the risk index [31]. Bamzai et al. provided a detailed analysis of the safety impacts of shoulder attributes on Illinois state highways from 2000 to 2006. It began with a preliminary data analysis to identify correlations between shoulder-related ROR crashes and shoulder characteristics such as material type and paved width. An analytical procedure, incorporating empirical Bayesian (EB) analysis, cross-sectional analysis, and an optimization model, was then applied to assess the safety impacts of shoulder paving and prioritize highway segments for improvement. While human judgment remains essential, this method aids experts in making more informed decisions. The findings aimed to assist the Illinois Department of Transportation (DOT) in updating their design manuals [32]. Siddiqui delved into the issues related to single-vehicle ROR crashes, highlighting their significance and examining both traditional and modern countermeasures. It was indicated that these crashes accounted for 40.6% of fatal, 20% of injury, and 11.2% of property damage-only incidents in the United States. Key findings included a high prevalence of fatal crashes on rural roads and the dominant role of driver error. Effective countermeasures, such as shoulder rumble strips and electronic stability control, were crucial in reducing these incidents and improving safety. The analysis underscored the importance of addressing driver behavior, environmental conditions, and vehicle performance to mitigate ROR crashes [33].

Bham et al. analyzed winter crashes on depressed medians of four Southcentral Alaska freeways. Cross-median crashes (CMCs) were randomly distributed and were 2.5 times more likely to cause severe injuries than in-median crashes. Rollovers accounted for 72.9% of median crashes. Both flatter (6H: 1V) and steeper (4: 1/5: 1) slopes had similar CMC and rollover frequencies, but flatter slopes saw more nonrollover crashes. Median crashes were most frequent with a 32 ft width and decreased as width increased. Regression models linked median rollover crashes to severe injuries, driver inexperience, curves, specific median widths, ice, and certain times of day, while CMCs were linked to multiple vehicles, light trucks, nighttime, and rutting. The spatial analysis identified nine crash hotspots and six interchanges for further study [34]. Carrigan et al. performed a study that is one of the pioneering efforts to analyze ROR crash data for both urban and rural settings simultaneously. The research highlights notable differences between these areas. It was found that, with all other roadway characteristics being equal, urban roadways tend to have a higher incidence of ROR crashes compared to rural ones. Conversely, factors such as road curvature and grade significantly increase the likelihood of ROR crashes in rural areas but have minimal impact in urban settings. In addition, the presence of shielding affects crash severity more in rural areas than in urban ones. These findings suggest that the AASHTO Roadside Design Guide should incorporate these distinctions in future updates to better address the varying crash frequencies between urban and rural areas [35].

Chawla evaluated the impact and cost-effectiveness of various culvert safety treatments to reduce ROR crash risks. Analyzing crash data from January 2007 to August 2017, the study linked crash, culvert, and roadway data, resulting in a dataset of 500 crashes on 481 culverts. Crash rates were calculated for different road types and modeled using the RSAP. RSAP’s estimated crash rates were generally 2–13 times higher than actual rates. The findings suggest that safety grates on culvert openings are the most cost-effective solution, while guardrail installation was the least effective, often increasing crash numbers and costs. Extending culverts outside the clear zone was somewhat cost-effective but less so than installing safety grates [36]. The Kansas DOT (KDOT) funded a study to evaluate the cost-effectiveness of installing guardrails on low-volume rural roads to reduce ROR fatalities and costs. Using RSAPv3 simulations and local data, Wang analyzed traffic and road features to assess the benefits of guardrails. The findings indicated that new guardrails for bare culverts or embankments were not cost-effective. However, W-beam guardrails were beneficial for bridges with medium-hazard edges, while bridge-approach guardrails were not justified for TL-2 bridge rails. The study also identified key factors contributing to rural roadside crashes [37]. Yarmohammadisatri et al. introduced an enhanced multibody dynamics model that evaluates steering and suspension systems together. It examined how suspension geometry and the kingpin axis affect steering. The approach involved three steps: assessing suspension geometry’s impact on steering returnability and ride quality, using geometry model’s outputs to evaluate steering effects, and applying a probabilistic method with NSGA II for robust design. The model’s accuracy was validated through tests on a Renault Logan, including constant cornering and double-lane change tests, and compared with Adams Car simulations [38]. Lee et al. theoretically analyzed the overturning stability of small ROR vehicles, focusing on backward roll-over and lateral overturning. It identified critical angular velocity and traveling speed, which cause these instabilities. Findings showed that moving the vehicle’s center of gravity forward and increasing its width enhance stability. The results guided the design of stable small ROR vehicles for navigating narrow ridges and orchards and provided a foundation for further research on agricultural machinery stability [39].

2. Methodology

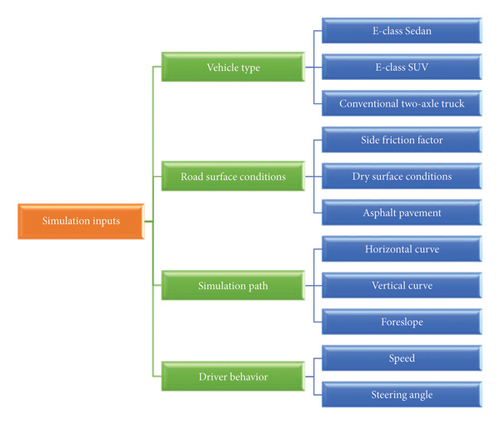
This section begins with introducing the simulation software utilized in this study. Following this, the process of inputting various data types, such as vehicle classifications, roadway information, and the specifics of the analysis procedure, is detailed. Figure 1 illustrates the variables incorporated in the simulations.

2.2. Vehicle Types

Taking into account the diverse range of vehicles on the road and their fundamental differences in mechanical and geometrical characteristics, this research investigates various vehicle parameters by selecting a representative sample of vehicles for the simulation. The simulation trials included three types of vehicles: two passenger cars (E-class Sedan and E-class SUV) and a conventional two-axle truck.

Due to the distinct geometrical and mechanical characteristics of the E-class Sedan and E-class SUV, these vehicles were chosen as representatives of typical passenger cars in the simulations. In addition, a conventional two-axle truck was included as a representative of cargo vehicles. It is important to note that the E-class SUV, given its geometrical features, has a higher risk of rollover or skidding compared to the E-class Sedan. Figure 2 provides images of the vehicles, while Table 1 details their geometrical characteristics.

Table 1. Specifications of the vehicles used in the simulation.

Parameters	Values
	E-class sedan	E-class SUV	Two-axle truck
			Cargo	Driver room
Weight	1653 kg	1592 kg	6789 kg	4457 kg
Mass center height	590 mm	719 mm	1800 mm	1173 mm
Wheel center height from the ground	375 mm	385 mm	—	—
Axel span	3048 mm	2950 mm	—	—
Height	1480 mm	1800 mm	1000 mm	3200 mm
Width	1880 mm	1875 mm	2000 mm	2438 mm
Length	4250 mm	4220 mm	3000 mm	—

2.3. Surface Conditions and Road Geometry

The maximum friction coefficient of a pavement surface is a numerical value that represents the interaction between the pavement and vehicle tires. This coefficient is influenced by the type of pavement, such as concrete, asphalt, or soil, and the condition of the pavement surface, whether it is dry, wet, or frozen. In this study, we focused on asphalt pavement under dry conditions, and the maximum friction coefficient has been assumed to be 0.9 [43]. This value is crucial for understanding vehicle dynamics and ensuring safety in road design and traffic management. By accurately determining this coefficient, engineers can better predict vehicle behavior, optimize pavement materials, and enhance overall road safety.

To design various route conditions and simulate different placements of the slopes of the foreslopes at the curves, this study has applied different states of horizontal and vertical curves with foreslopes. Moreover, to better compare the slopes of the foreslopes with each other, three slope modes of 1: 3, 1: 4, and 1: 10 have been considered for the embankment foreslope, which is the most common mode on curves.

The route plan design includes three simple horizontal curves, as well as four sag vertical curves and one crest vertical curve with grades of (−2, +2), (−2, +6), (−6, +2), (−6, +6), and (+6, −6), in accordance with the AASHTO guidelines. Figure 3 illustrates an example of a route plan for roads with horizontal and vertical curves to examine the safe slope of the foreslopes.

2.4. Driver Behavior

In this research, the driver behavior is simulated by defining variables, such as speed and steering wheel angle. In the performed simulations, the speed of the vehicle is three constant speeds of 80, 100, and 120 km/h for the horizontal curve and two constant speeds of 80 and 100 km/h for the vertical curve. These speeds were chosen based on standard speed limits on rural highways and expressways and reflect typical driving conditions, ensuring the study’s relevance to real-world scenarios.

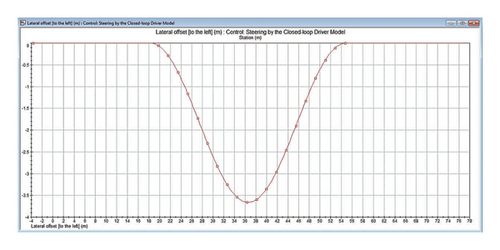
When the vehicle is traveling on curves with various foreslope slopes at different speeds, the steering scenarios are considered so that the changes in the behavior of drivers are simulated and investigated in 4 modes of angle changes to exit the roadway on horizontal curves and 3 modes of angle changes to exit the roadway on vertical curves. In this regard, the vehicles depart from the roadway at an angle of 7.5, 15, 20, and 25° for horizontal curves and 7.5, 15, and 25° for vertical ones. These angles were chosen to represent common scenarios where vehicles might unintentionally depart from the roadway due to driver error, road conditions, or other factors. Figure 4 illustrates the simulation of one scenario where a vehicle departs from the road and then returns to the simulated path.

3. Results

3.1. Analysis of the Forces on the Wheels

In the current study, to calculate the side friction factors of the moving vehicle, graphs of lateral and vertical forces on vehicle wheels have been used, as shown in Figure 5 for one of the simulation tests. The results show that the maximum lateral force on wheels after the vehicle leaves the road and when the steering angle change reaches its maximum occurs on the curve path on the foreslopes. Figure 6 indicates the graph of lateral force on vehicle wheels on the foreslope.

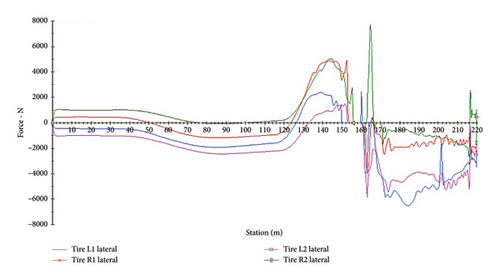
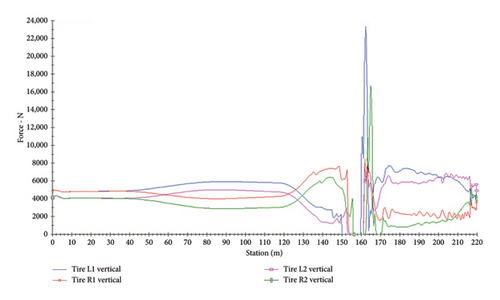
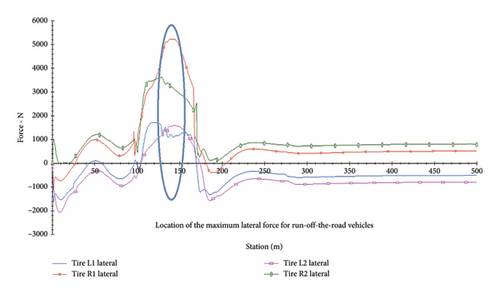
As illustrated in Figure 6, at the maximum departure angle of the vehicle’s steering wheel from the roadway, the vehicle wheels are subjected to the maximum lateral force, which is 5%–10% more than that exerted when traveling the roadway outside on the foreslope in various tests. As a result, this point is most likely to cause the vehicle to skid. It should be noted that the accidents related to ROR are mostly because of the vehicles’ skidding and the lack of control of steering wheel angles when leaving roads on foreslopes.

According to the simulations performed regarding the influencing variables in these simulations, the results of the considered path for vertical curves with the foreslope according to Tables A1, A2, A3, A4, A5, and A6 have been presented for applied forces on the wheels of vehicles in various conditions, including lateral (F_y), vertical (F_z), and longitudinal (F_x) forces. Also, the results of the path considered for horizontal curves with the foreslope according to Tables A7, A8, A9, A10, A11, A12, A13, A14, and A15 have been provided.

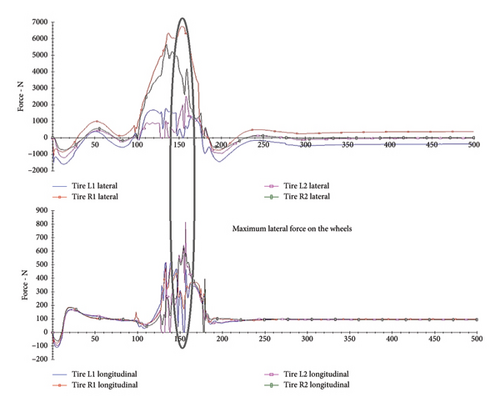
According to the results shown in Tables A1, A2, A3, A4, A5, A6, A7, A8, A9, A10, A11, A12, A13, A14, and A15, the longitudinal, lateral and vertical forces on vehicle wheels undergo many changes when passing over the foreslope. According to the graphs of lateral and vertical forces, it is revealed that when the lateral force in all wheels reaches its maximum value, the vertical force for the inner wheels is at its minimum value when the vehicle leaves the road on the foreslope, and for the outer wheels on the foreslope, it reaches its maximum value. The reason for this is that the centrifugal force causes the vertical load on the wheels to be uneven, which is a proof of a defect with the point mass model. Furthermore, if one of the wheels has a lower vertical force than the others, it is more likely that the wheel will skid than the others. This issue is shown in Figure 7.

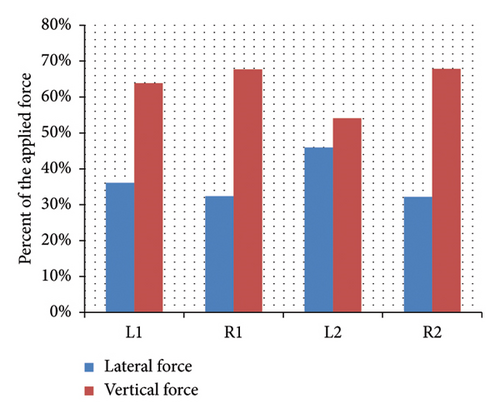
According to the distribution of the forces on the wheels of Sedans, SUVs, and trucks, as shown in Figure 8, it can be observed that the maximum lateral and vertical force is exerted on the wheels on the left side of the vehicle. According to the obtained results, 61% of the lateral forces and 52% of the vertical forces enter the left wheels of the Sedan. The maximum lateral and vertical forces are also exerted on the left wheels of the SUV. In addition, 54% of the lateral forces and 50% of the vertical forces enter the SUV vehicle’s left wheels. On the other hand, maximum lateral forces enter the left wheels and maximum vertical ones the right wheels of the truck vehicle. In addition, 59% of lateral forces are applied to the left wheels and 60% of them are exerted on the left wheels of the truck vehicles. Hence, unlike AASHTO’s assumption in which forces are distributed evenly between the wheels, they are actually distributed based on vehicle weight, rotation angle, and speed.

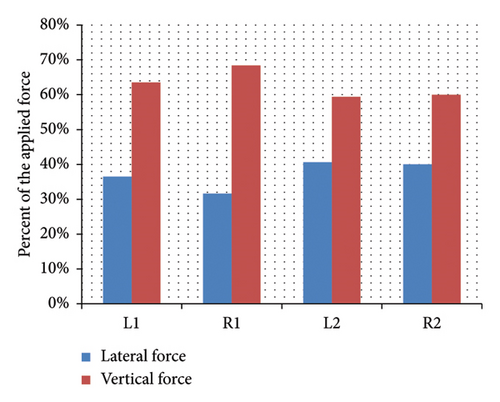
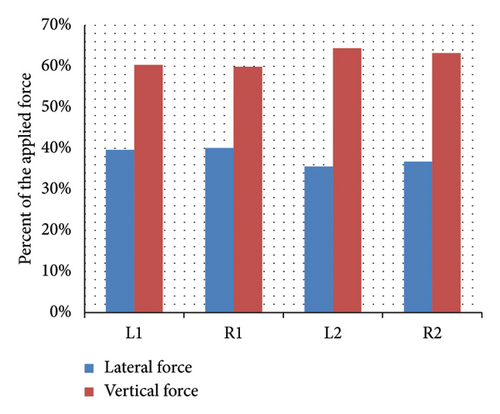
3.2. Side Friction Factor Results

According to the results of the simulations, the forces exerted on each of the wheels of the vehicle have been obtained for all vehicles in different defined conditions. By the use of these results and equation (1), side friction factors can be achieved for each of the defined tests. Tables A16 and A17 show the lateral and longitudinal friction factors calculated from the simulation, respectively, for the vertical and horizontal curves placed on the foreslopes in each of the simulation tests.

Using the outputs of Tables A16 and A17, results such as the comparison of side friction factors in different vehicles can be obtained at different speeds, and these data have been examined and analyzed in the following.

3.2.1. Comparison of the Side Friction Factor for Different Vehicles in Horizontal Curves With the Foreslopes

Figure 9 indicates the side friction factor changes at different speeds for Sedans, SUVs, and trucks, and Figure 10 illustrates the side friction factor changes in different driving behaviors for these vehicles in the off-road mode in horizontal curves with the foreslope.

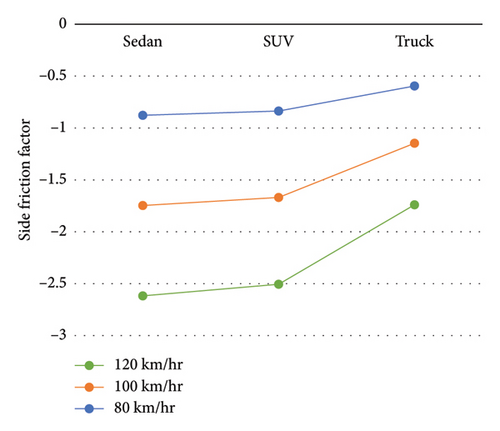
According to Figure 9, at lower speeds, the difference in side friction factor applied to vehicles is greater; however, at all speeds, the side friction factor of the truck vehicles is less than that of Sedan and SUV vehicles. The observed differences in side friction factors at lower speeds are based on the vehicle dynamics and the inherent characteristics of each vehicle type. The truck vehicles, being heavier, exert more vertical force on their wheels, resulting in lower side friction compared to Sedans and SUVs. This difference is more pronounced at lower speeds due to the reduced influence of aerodynamic forces and higher reliance on the tire–pavement interaction.

Also, in Figure 10, based on the various driving behaviors, the friction factor for vehicle departure angle of 7.50° from the road for different vehicles is reduced in the negative direction, which decreases up to the angle of 20° for the truck vehicle. It is also observed that at all speeds, Sedans and SUVs have very similar friction factors at higher departure angles. Therefore, according to Figures 9 and 10, the side friction factor as an effective parameter in ensuring vehicle safety can be improved in the truck compared to SUVs and Sedans. Also, among these three vehicles, the truck has the largest range of friction changes and is therefore more critical.

By examining the output of side friction factors in different vehicles, it is concluded that compared to Sedans and SUVs, trucks have lower side frictions since they exert more vertical force on wheels due to being heavier than the other two vehicles, and the results will be a decrease in side frictions developed between the pavement and the wheels of this vehicle. Therefore, they are less prone to skidding in all defined conditions. It should also be noted that the observed differences in side friction factors at lower speeds are based on the vehicle dynamics and the inherent characteristics of each vehicle type. This difference is more pronounced at lower speeds due to the reduced influence of aerodynamic forces and higher reliance on the tire–pavement interaction.

3.2.2. Comparison of the Side Friction Factor for Different Vehicles in Vertical Curves With the Foreslopes

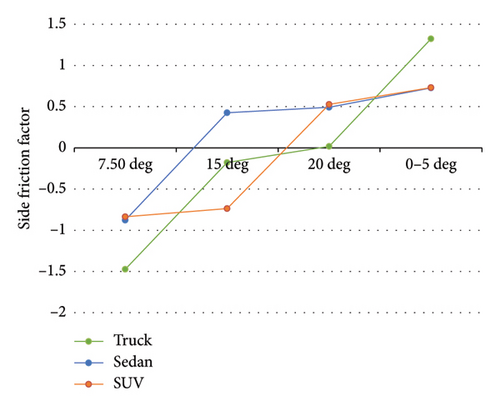
Figure 11 displays the side friction factor changes at different speeds, and Figure 12 demonstrates the side friction factor changes in different driving behaviors for Sedan, SUV, and truck vehicles in off-road mode with a vertical curve over a foreslope.

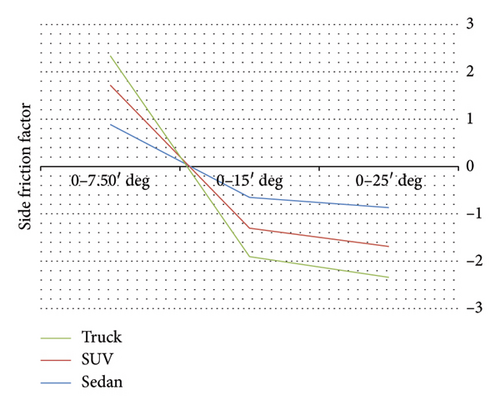
According to Figure 11, at all speeds, the side friction factor of the truck vehicles is less than that of Sedan as well as SUV vehicles. Also, in Figure 12, according to the different behaviors during driving, it is obvious that the friction factors for all vehicle types change direction between the departure angle of 7.50°–15° of the vehicle from the road and decrease in a certain way. It is also clear that at all speeds, side frictions of Sedans as well as SUVs are similar at higher departure angles. Therefore, according to Figures 11 and 12, in comparison with SUV and Sedan, trucks have improved friction factors as an important parameter in vehicle safety, and also among these three vehicles, Sedan has the largest range of friction changes and, therefore, is more critical.

3.2.3. Variations of the Side Friction Factor Based on Speed Changes and Different Driving Behaviors in Horizontal Curves

Examining the results from Figures 13, 14, and 15 and the results of the simulations on the horizontal curves with a foreslope, especially in the turns and mountainous areas with 4 modes of leaving the vehicle from the road for different vehicles, show that the greatest effect of this behavior changes for vehicles occurs in the first third of the curves. In the case of changing the driver’s behavior by 7.5°, in the event that a vehicle leaves the road, it can return to the surface of the road, but in the case of 15° and at a speed of 120, the vehicle returns to the road surface and the travel lane with a jump and lack of proper control. This problem can be solved by softening the slope of the foreslope. At an angle of 20° and 25°, light vehicles jump and then roll immediately after the most critical point of the applied forces, but for trucks, before reaching a third of the radius of the curve, the vehicle rolls without slipping or jumping.

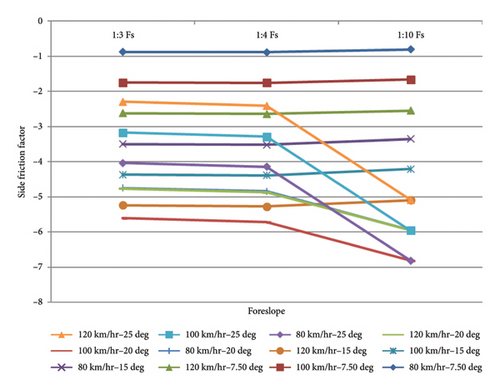
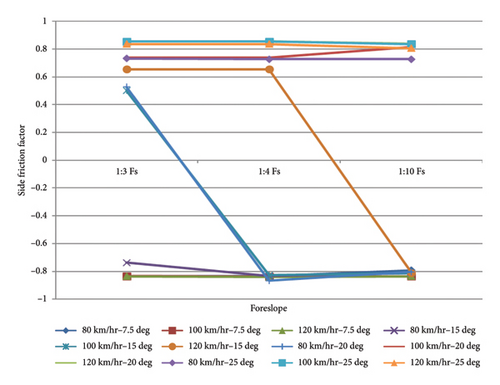
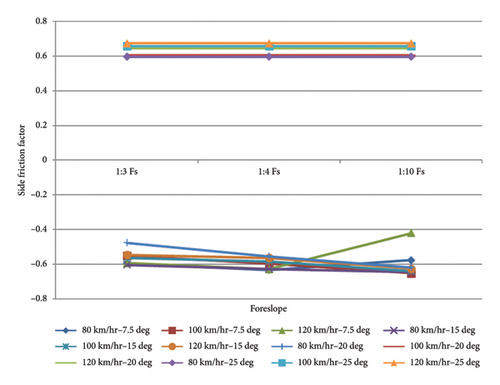
According to the amount of force exerted on the vehicles, the 20- and 25-degree off-road conditions are the most critical and worrying possible conditions for a vehicle when leaving the road, especially at high speeds.

3.2.4. Variations of the Side Friction Factor Based on Speed Changes and Different Driving Behaviors in Vertical Curves

According to the investigations carried out according to the results of Figures 16, 17, and 18, at the angle of 7.5 when leaving the road, the vehicle faces constant forces applied to it, and skidding is not observed in these cases. In the case of 15 degrees of change in the drivers’ behavior, Sedan and SUV jump and turn over at 100 km/h speed, and at all three speeds, the truck rolls. In the condition of exiting the roadway at a 25-degree angle, the Sedan and SUV vehicles turn over and the truck rolls. In the case of 25°, it can be said that the Sedan and SUV vehicles, after slipping and sliding on the foreslope, turn over at the studied speeds, and this is in the form of rolling in the truck vehicle without slipping and sliding.

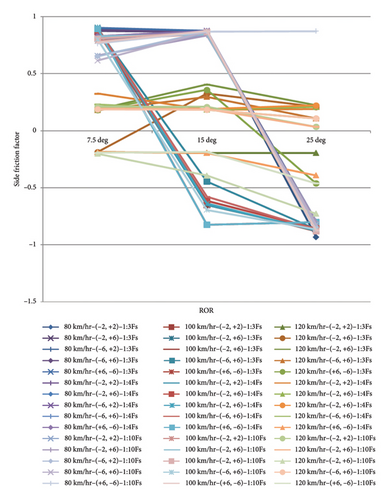
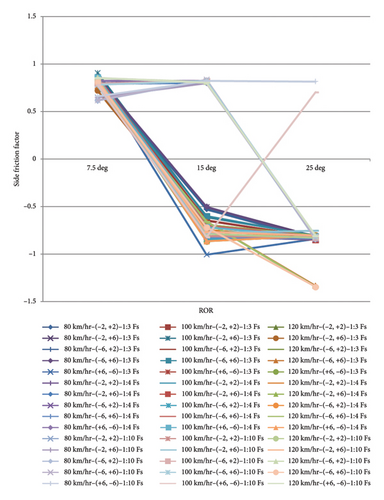
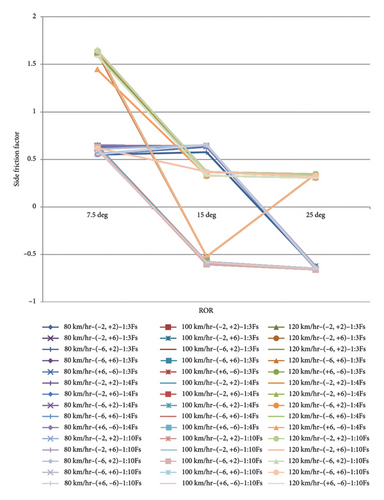
The results also show that a 15-degree departure angle from the road for driving behavior indicates a change in the direction of forces exerted on the vehicles when exiting vertical curves on the foreslopes, in which negative friction factors are observed. During the most critical and worst states of movement, the force applied to vehicle wheels changes direction, resulting in negative friction factors. This critical finding suggests that at certain angles, the forces acting on the vehicle can lead to a loss of control, emphasizing the need for careful design and management of foreslopes to enhance safety.

For a Sedan vehicle, the rolling point for a 7.5-degree departure angle from the road occurs one-third after the point of concavity or convexity of the curve. This is for an angle of 15° after the point of concavity or convexity of the curve but before one-third of the point, and for a 25° departure angle from the road before the convexity or concavity of curves, it is the place where skidding and rolling occurs for this vehicle. This pattern highlights the importance of considering vehicle departure angles in road design to prevent rollovers and skidding.

The difference between the rolling points for the SUV and Sedan vehicles is that at a 15-degree departure angle from the road, it acts like a 25-degree departure angle, that is, before the point of convexity or concavity of curves, it slips and then turns over, and due to the greater height and weight of this type of vehicle in comparison with Sedan, the intensity of this is greater and the change in the direction of forces on the vehicle is shown as a yaw moment with skidding at the rolling points. The rolling points of the truck vehicle are at the same points as for the Sedan vehicle, but the intensity of yaw moments, especially at the departure angle of 15° and 25° from the road, causes the vehicle to roll with negative friction, which is the worst case for a heavy vehicle, which has been observed many times in mountainous areas and passes.

By examining Figures 16, 17, and 18 and analyzing the results of the simulations performed on vertical curves, it can be concluded that in the case of (−6, +6) for the sag vertical curve and (+6, −6) for the crest vertical curve, the driver’s behavior is the worst and most critical condition for a vehicle that has ROR. Also, the changes in the side friction factor are very noticeable in both speed modes for different foreslopes and different modes of driving behavior. As the slope of the foreslopes becomes gentler, side friction factors change less and obtained shapes become more reasonable.

3.3. Side Friction Factor Modeling

In this section, by using the simulation outputs and SPSS software for each of the vehicles, a multiple regression model has been presented to calculate the side friction factor to enhance the safety of road geometric designs through new relationships. These relations show the change of the side friction factor (dependent variable) in terms of the speed of the vehicle, and its departure angle from the roadway and the slope of the foreslope as independent variables.

3.3.1. Side Friction Factor Modeling for Horizontal Curves

3.3.1.1. Sedan Vehicle

For calculating the side friction factor for sedan vehicles, equation (2) is found to be the best model according to the modeling performed. Based on Table 2, it can be seen that the achieved model exhibits a good correlation coefficient (R). In addition, according to the Sig. value of each variable, it is observed that all the variables used, except the speed variable, have a significant effect on the side friction factor in this model. Also, the model indicates that as the departure angle increases, the side friction factor also increases, highlighting the increased risk of skidding at higher departure angles. The negative coefficient for the foreslope slope suggests that steeper foreslopes reduce the side friction factor, making Sedan vehicles more prone to skidding in horizontal curves.

$$ ()

where f_y is the side friction factor, Fs is the slope of the foreslope, and ROR is the vehicle departure angle from the roadway (degree).

Table 2. Summary of the side friction factor model vehicle in the horizontal curve for Sedan.

Model	R	R2	Adjusted R2	Std. error of the estimate	Durbin–Watson
1	0.659a	0.435	0.418	0.62498
2	0.716b	0.513	0.483	0.58893	1.787

• Note: Dependent variable is f_y.
• ^aPredictor: constant and ROR.
• ^bPredictor: constant, ROR, and foreslope.

A regression equation’s fit to the data is determined by the R coefficient, which is 0.659 in the case of ROR and 0.716 in the case of ROR and foreslope.

Table 3 indicates the ANOVA test results, in which, the F value is equal to 26.148 and 17.369 for modeling ROR and modeling ROR and foreslope, respectively.

Table 3. ANOVA test results for Sedan vehicles in horizontal curves.

Model		Sum of squares	df	Mean square	F	Sig.
1	Regression	10.214	1	10.214	26.148	0.000a
	Residual	13.280	34	0.391
	Total	23.494	35
2	Regression	12.048	2	6.024	17.369	0.000b
	Residual	11.446	33	0.347
	Total	23.494	35

• ^aPredictor: constant and ROR.
• ^bPredictor: constant, ROR, and foreslope.

Also, the results related to the coefficients of the model are presented in Table 4, where B is the coefficient of regression models, std. error indicates the amount of change in the response variable per one standard deviation change in the independent variable, t indicates the amount of influence (number) and the way of influence (positive or negative sign) of each variable in the regression model, and Sig. shows the importance of each variable in the regression models, and a value less than 0.05 indicates the high importance of the desired variable.

Table 4. Coefficients of the side friction factor model vehicle in the horizontal curve for Sedan.

Model		Unstandardized coefficient		Standardized coefficient	t	Sig.
		B	Std. error	Beta
1	Constant	−1.500	0.291		−5.150	0.000
	ROR	0.082	0.016	0.659	5.114	0.000
2	Constant	−1.273	0.292		−4.366	0.000
	ROR	0.082	0.015	0.659	5.427	0.000
	Foreslope	−0.005	0.002	−0.279	−2.300	0.028

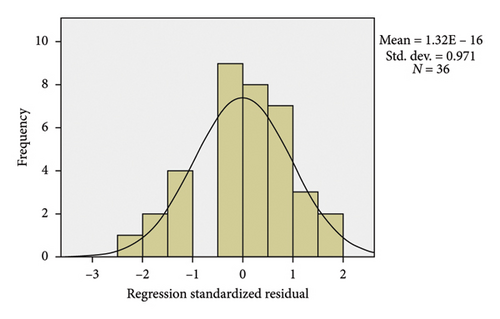
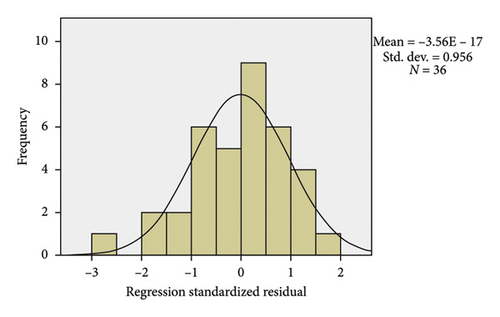
Figure 19 shows the results of the histogram diagram of the side friction factor model for Sedan vehicles in horizontal curves, which is obtained from the data achieved from the analysis of the forces applied to Sedan. Also, Figure 20 shows the correlation diagram of the side friction factor model of these vehicles, in such a way that the illustrated line shows the trend of changes in the model and the circle points represent each of the input data. According to Figure 20, the model generally has a good correlation, so the R value of this model is equal to 0.716.

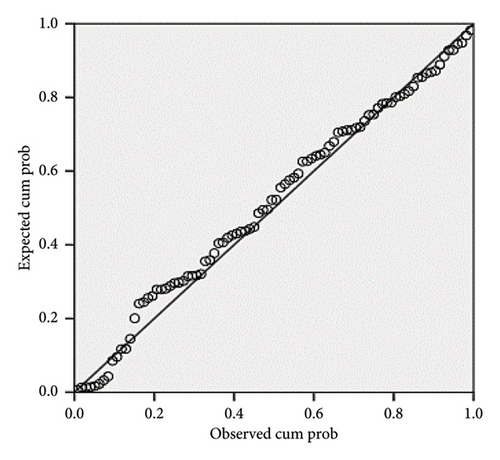
3.3.1.2. SUV Vehicle

Equation (3) represents the best model for calculating the side friction factor of a SUV according to the modeling. R coefficient indicates that the model has a good correlation and all variables have significant effects, as can be seen in the results. It can be seen that as the departure angle becomes steeper, the side friction factor also rises, indicating a greater chance of skidding at higher departure angles. The positive coefficient for speed indicates that higher speeds increase the side friction factor, emphasizing the need for speed management on horizontal curves. The negative coefficient for the foreslope slope again suggests that steeper foreslopes reduce the side friction factor, increasing the risk of skidding.

$$ ()

where V is the speed of the vehicle over vertical curves (kph), f_y is the side friction factor, Fs is the slope of the foreslope, and ROR is the vehicle departure angle from the roadway (degree). For modeling ROR alone, the R coefficient has a value of 0.718. Also, in ROR and speed modeling, as well as ROR, speed, and foreslope modeling, the R coefficient has values of 0.775 and 0.806, respectively.

In Table 5, the R coefficient has a value of 0.718 for modeling ROR, 0.775 for modeling ROR and speed, and 0.806 for modeling ROR, speed, and foreslope.

Table 5. Summary of the side friction factor model for the SUV vehicle in horizontal curves.

Model	R	R2	Adjusted R2	Std. error of the estimate	Durbin–Watson
1	0.718a	0.516	0.502	0.56702
2	0.775b	0.601	0.577	0.52229
3	0.806c	0.650	0.617	0.49728	2.398

• Note: Dependent variable is f_y.
• ^aPredictor: constant and ROR.
• ^bPredictor: constant, ROR, and speed.
• ^cPredictor: constant, ROR, speed, and foreslope.

In Table 6, the results of the ANOVA test for the SUV side friction factor model are shown, in which, the F value is obtained equal to 36.223, 24.883, and 19.766, respectively, for ROR modeling, ROR and speed modeling, and ROR, speed, and foreslope modeling. Also, the results related to the coefficients of the presented model are indicated in Table 7.

Table 6. ANOVA test results for the SUV vehicle in horizontal curves.

Model		Sum of squares	df	Mean square	F	Sig.
1	Regression	11.646	1	11.646	36.223	0.000a
	Residual	10.931	34	0.322
	Total	22.578	35
2	Regression	13.576	2	6.788	24.883	0.000b
	Residual	9.002	33	0.273
	Total	22.578	35
3	Regression	14.664	3	4.888	19.766	0.000c
	Residual	7.913	32	0.247
	Total	22.578	35

• ^aPredictor: constant and ROR.
• ^bPredictor: constant, ROR, and speed.
• ^cPredictor: constant, ROR, speed, and foreslope.

Table 7. Coefficients of the side friction factor model for the SUV vehicle in horizontal curves.

Model		Unstandardized coefficient		Standardized coefficient	t	Sig.
		B	Std. error	Beta
1	Constant	−1.520	0.264		−5.755	0.000
	ROR	0.088	0.015	0.718	6.019	0.000
2	Constant	−2.938	0.586		−5.014	0.000
	ROR	0.088	0.013	0.718	6.534	0.000
	Speed	0.014	0.005	0.292	2.660	0.012
3	Constant	−2.763	0.564		−4.899	0.000
	ROR	0.088	0.013	0.718	6.863	0.000
	Speed	0.014	0.005	0.292	2.793	0.009
	Foreslope	−0.004	0.002	−0.220	−2.098	0.044

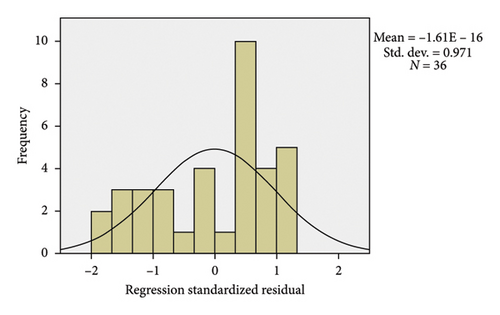
Figure 21 shows the result of the histogram diagram for the side friction factor model of the SUV in the horizontal curve. Also, Figure 22 shows the correlation diagram for this model, according to which, all the data are located around the model fit line, which indicates the validity of the model, so that the R value for this model is equal to 0.806.

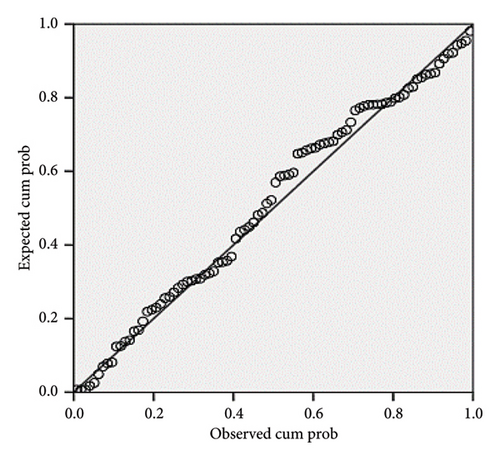
3.3.1.3. Truck Vehicle

In this section, the best model for calculating the side friction factor according to equation (4) is presented for the truck vehicle. As can be seen, a good correlation is evident in the model based on the R value. In addition, all variables except foreslope significantly affect the model. The positive correlation between the departure angle and the side friction factor suggests that as the departure angle increases, the side friction factor also rises, indicating an elevated risk of skidding at higher departure angles in horizontal curves. In addition, higher speeds can further increase the risk of skidding, underscoring the importance of managing speed when navigating curves.

$$ ()

Table 8 also shows the R coefficient for the side friction factor model of truck vehicles, which has a value of 0.802 for modeling ROR and 0.833 for modeling ROR and speed.

Table 8. Summary of the side friction factor model of the SUV vehicle in horizontal curves.

Model	R	R2	Adjusted R2	Std. error of the estimate	Durbin–Watson
1	0.802a	0.642	0.632	0.37260
2	0.833b	0.694	0.675	0.35011	2.564

• Note: Dependent variable is f_y.
• ^aPredictor: constant and ROR.
• ^bPredictor: constant, ROR, and speed.

The results of the ANOVA test for the truck side friction factor model are represented in Table 9, where the F value is equal to 61.085 and 37.344 for modeling ROR and modeling ROR and speed, respectively. Also, the results related to the coefficients of the current model are presented in Table 10.

Table 9. ANOVA test results for the truck vehicle in horizontal curves.

Model		Sum of squares	df	Mean square	F	Sig.
1	Regression	8.480	1	8.480	61.085	0.000a
	Residual	4.720	34	0.139
	Total	13.200	35
2	Regression	9.155	2	4.578	37.344	0.000b
	Residual	4.045	33	0.123
	Total	13.200	35

• ^aPredictor: constant and ROR.
• ^bPredictor: constant, ROR, and speed.

Table 10. Coefficients of the side friction factor model in the horizontal curves for the truck vehicle.

Model		Unstandardized coefficient		Standardized coefficient	t	Sig.
		B	Std. error	Beta
1	Constant	−1.346	0.174		−7.756	0.000
	ROR	0.075	0.010	0.802	7.816	0.000
2	Constant	−2.185	0.393		−5.562	0.000
	ROR	0.075	0.009	0.802	8.318	0.000
	Speed	0.008	0.004	0.226	2.347	0.025

The results related to the histogram diagram of the side friction factor model of the truck vehicle over the horizontal curve are presented in Figure 23. Figure 24 also shows the correlation diagram for this model for the truck vehicle, where the model and the input data have an appropriate correlation, so that the R value of this model is equal to 0.833.

3.3.2. Side Friction Factor Modeling for Vertical Curves

3.3.2.1. Sedan Vehicle

According to the modeling results for the vertical curves, the best model for calculating the side friction factors of Sedan vehicles on curves is according to equation (5). In Table 11, the R coefficient for the side friction factor model of the Sedan vehicle in vertical curves is presented, where, respectively, for ROR modeling, ROR and speed modeling, and ROR, speed, and foreslope modeling, the R coefficient is equal to the value of 0.826, 0.844, and 0.856. Also, the achieved model represents a suitable correlation and according to the Sig. value for each variable, it is evident that all the variables used indicate a significant influence on this model. The negative coefficients for departure angle and speed indicate that higher departure angles and speeds increase the risk of skidding in vertical curves. The positive coefficient for the foreslope slope suggests that gentler foreslopes improve vehicle stability in these curves.

$$ ()

Table 11. Summary of the side friction factor model for the Sedan vehicle in vertical curves.

Model	R	R2	Adjusted R2	Std. error of the estimate	Durbin–Watson
1	0.826a	0.683	0.679	0.46165
2	0.844b	0.713	0.706	0.44185
3	0.856c	0.733	0.723	0.42877	2.319

• Note: Dependent variable is f_y.
• ^aPredictor: constant and ROR.
• ^bPredictor: constant, ROR, and speed.
• ^cPredictor: constant, ROR, speed, and foreslope.

In Table 12, the results of the ANOVA test for the side friction factor model of the Sedan vehicle for the vertical curve are illustrated; in this Table 12, the value of F equals 189.563, 107.999, and 78.590, respectively, for ROR modeling, ROR and speed modeling, and ROR, speed, and foreslope modeling. Also, the results related to the coefficients of the Sedan vehicle side friction factor model for vertical curves are presented in Table 13.

Table 12. ANOVA test results for the Sedan vehicle in vertical curves.

Model		Sum of squares	df	Mean square	F	Sig.
1	Regression	40.401	1	40.401	189.563	0.000a
	Residual	18.755	88	0.213
	Total	59.155	89
2	Regression	42.170	2	21.085	107.999	0.000b
	Residual	16.985	87	0.195
	Total	59.155	89
3	Regression	43.345	3	14.448	78.590	0.000c
	Residual	15.811	86	0.184
	Total	59.155	89

• ^aPredictor: constant and ROR.
• ^bPredictor: constant, ROR, and speed.
• ^cPredictor: constant, ROR, speed, and foreslope.

Table 13. Coefficients of the side friction factor model of the Sedan vehicle in vertical curves.

Model		Unstandardized coefficient		Standardized coefficient	t	Sig.
		B	Std. Error	Beta
1	Constant	1.610	0.118		13.643	0.000
	ROR	−0.093	0.007	−0.826	−13.768	0.000
2	Constant	2.872	0.434		6.615	0.000
	ROR	−0.093	0.006	−0.826	−14.385	0.000
	Speed	−0.014	0.005	−0.173	−3.011	0.003
3	Constant	2.757	0.424		6.507	0.000
	ROR	−0.093	0.006	−0.826	−14.824	0.000
	Speed	−0.014	0.005	−0.173	−3.103	0.003
	Foreslope	0.003	0.001	0.141	2.528	0.013

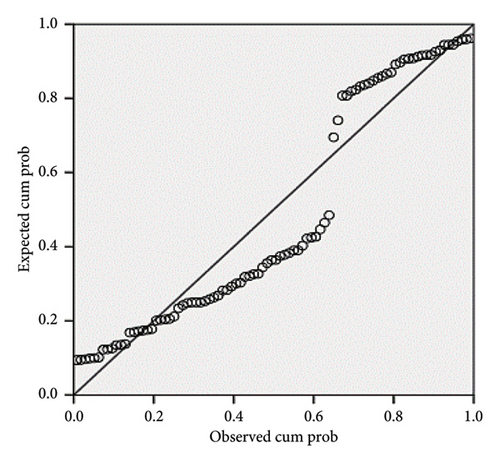
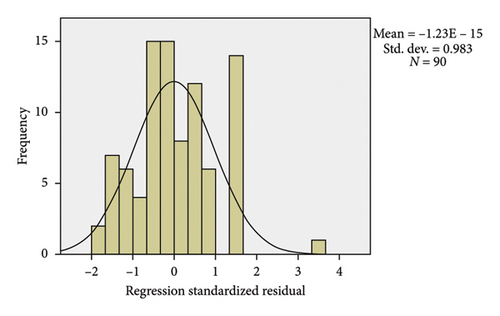
In Figure 25, the results of the histogram diagram of the side friction factor model of a Sedan vehicle are shown for vertical curves. Also, Figure 26 shows the correlation diagram of the side friction factor model of a Sedan vehicle. According to Figure 26, all the input data are located around the model line, which indicates the validity of the model, so that the R value for this model is equal to 0.856.

3.3.2.2. SUV Vehicle

The best model for calculating the side friction factors of SUV for the vertical curves is presented according to the modeling performed in equation (6). Table 14 shows that the R coefficient has a value of 0.718 for modeling ROR as well as 0.775 for ROR and foreslope modeling. As the results have shown, the model represents good correlations with respect to the R parameter, and all variables except the speed significantly affect the model. Similarly, the negative coefficient for the departure angle indicates that higher departure angles increase the risk of skidding in vertical curves, while the positive coefficient for the foreslope slope suggests that gentler foreslopes improve vehicle stability.

$$ ()

Table 14. Summary of the side friction factor model for the SUV vehicle in vertical curves.

Model	R	R2	Adjusted R2	Std. error of the estimate	Durbin–Watson
1	0.715a	0.512	0.506	0.56167
2	0.750b	0.563	0.553	0.53456	2.437

• Note: Dependent variable is f_y.
• ^aPredictor: constant and ROR.
• ^bPredictor: constant, ROR, and foreslope.

Table 15 illustrates the results of the ANOVA test for modeling of the side friction factor of SUV vehicles in vertical curves, and the F value of 92.230 and 55.988 was obtained for modeling ROR and modeling ROR and foreslope, respectively. Also, the results related to the coefficients of the SUV side friction factor model for vertical curves are represented in Table 16.

Table 15. ANOVA test results for the SUV vehicle in vertical curves.

Model		Sum of squares	df	Mean square	F	Sig.
1	Regression	29.096	1	29.096	92.230	0.000a
	Residual	27.761	88	0.315
	Total	56.857	89
2	Regression	31.997	2	15.998	55.988	0.000b
	Residual	24.860	87	0.286
	Total	56.857	89

• ^aPredictor: constant and ROR.
• ^bPredictor: constant, ROR, and foreslope.

Table 16. Coefficients of the side friction factor model of the SUV vehicle in vertical curves.

Model		Unstandardized coefficients		Standardized coefficients	t	Sig.
		B	Std. error	Beta
1	Constant	1.284	0.144		8.947	0.000
	ROR	−0.079	0.008	−0.715	−9.604	0.000
2	Constant	1.104	0.148		7.467	0.000
	ROR	−0.079	0.008	−0.715	−10.091	0.000
	Foreslope	0.004	0.001	0.226	3.186	0.002

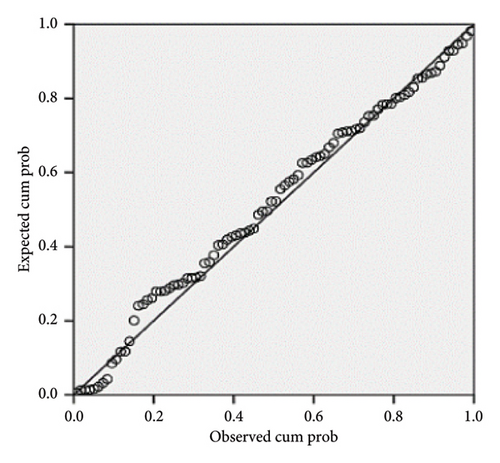
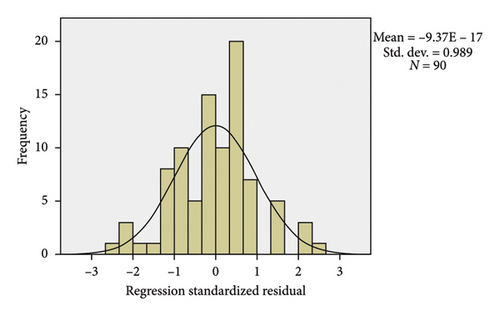
Figure 27 shows the result of the histogram diagram of the side friction factor model of the SUV vehicle for vertical curves. Figure 28 also shows the correlation diagram for this model for the SUV vehicle, in which all the data are located around the fit line, which shows the validity of the model, so that the R value for this model is equal to 0.750.

3.3.2.3. Truck Vehicle

In this section, for vertical curves, the best model for calculating the side friction factor of the truck vehicle according to equation (7) is presented. As is obvious, in Table 17, the R value for the side friction factor model has a value of 0.810 for modeling ROR as well as 0.862 for ROR and speed modeling, which shows that the model has an appropriate correlation and also all variables applied except foreslope significantly have an effect on the performed modeling. It can be seen that the negative coefficients for both variables indicate that higher departure angles and speeds increase the risk of skidding in vertical curves, emphasizing the need for careful management of these factors in road design.

$$ ()

Table 17. Summary of the side friction factor model for the truck vehicle in vertical curves.

Model	R	R2	Adjusted R2	Std. error of the estimate	Durbin–Watson
1	0.810a	0.656	0.652	0.36990
2	0.862b	0.744	0.738	0.32094	2.821

• Note: Dependent variable is f_y.
• ^aPredictor: constant and ROR.
• ^bPredictor: constant, ROR, and speed.

For the truck side friction factor model on vertical curves, ANOVA test results are represented in Table 18, according to which the F value is equal to 165.766 and 124.884 for modeling ROR and modeling ROR and speed, respectively. Also, the results related to the coefficients of this model are indicated in Table 19. Figure 29 shows the result of the histogram diagram of the side friction factor model for truck vehicles in vertical curves. Also, Figure 30 shows the correlation diagram for this model, which indicates the proper correlation of the data in the model according to R equal to 0.862.

Table 18. ANOVA test results of the truck vehicle in vertical curves.

Model		Sum of squares	df	Mean square	F	Sig.
1	Regression	22.681	1	22.681	165.766	0.000a
	Residual	11.904	87	0.137
	Total	34.585	88
2	Regression	25.727	2	12.863	124.884	0.000b
	Residual	8.858	86	0.103
	Total	34.585	88

• ^aPredictor: constant and ROR.
• ^bPredictor: constant, ROR, and speed.

Table 19. Coefficients of the side friction factor model of the truck vehicle in vertical curves.

Model		Unstandardized coefficient		Standardized coefficient	t	Sig.
		B	Std. error	Beta
1	Constant	1.136	0.096		11.871	0.000
	ROR	−0.071	0.005	−0.810	−12.875	0.000
2	Constant	2.809	0.319		8.815	0.000
	ROR	−0.071	0.005	−0.814	−14.910	0.000
	Speed	−0.019	0.003	−0.297	−5.438	0.000

4. Conclusion

5. Contributions, Limitations, and Future Research Directions

This research makes several significant contributions to the field of road safety and vehicle dynamics. First, it enhances the understanding of how different departure angles, speeds, and foreslope slopes affect vehicle stability on curves. This detailed analysis provides crucial insights for engineers and designers aiming to improve road safety and vehicle performance. Second, the study develops multiple regression models for predicting side friction factors for different vehicle types. These models serve as valuable tools for road designers and safety engineers, offering a method to estimate side friction factors based on key variables. Lastly, the research identifies specific conditions, such as departure angles and foreslope slopes that significantly impact vehicle stability. These actionable insights can inform road design and safety measures, potentially reducing the risk of accidents.

This study primarily relies on simulations using CarSim and TruckSim, which, while advanced, may not fully capture the complexity of real-world driving conditions. The accuracy of the results is contingent upon the precision of the simulation models and the assumptions made during the simulation process. In addition, the study focuses on three types of vehicles: Sedans, SUVs, and trucks, excluding other vehicle types such as motorcycles and buses, which may limit the generalizability of the findings. Environmental factors such as weather conditions, road surface conditions, and lighting were not considered in the simulations, which could significantly influence vehicle dynamics and side friction factors. These limitations suggest that while the findings provide valuable insights, they should be interpreted with caution and validated with real-world data.

Future research should aim to broaden the scope of this study by including a wider variety of vehicle types, such as motorcycles, buses, and electric vehicles, to ensure that the findings are applicable across different vehicle categories. In addition, investigating other types of curves, such as spiral curves, and different foreslope designs, such as ditch and barrier foreslopes, would provide a more comprehensive understanding of vehicle dynamics. Incorporating environmental variables such as weather conditions, road surface conditions, and lighting in future simulations would enhance the robustness of the findings. Real-world validation of the simulation results through field experiments and data collection would also strengthen the reliability of the predictive models. Furthermore, investigating the effects of other variables, such as road surface condition, weather, driver behavior, and vehicle load, on the safety of curves and foreslopes would provide valuable insights for improving road safety.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Ali Abdi Kordani: conceptualization, project administration, and supervision. Ali Attari: methodology, data curation, and writing–original draft. Seyed Mohsen Hosseinian: methodology, investigation, writing, review, and editing.

Funding

The authors received no financial support for the research, authorship, and/or publication of this article.