The two-dimensional (2D) nonlinear coupled sine-Gordon equations play a significant role in nonlinear physics, describing phenomena in areas such as solid-state physics, fluid dynamics, and nonlinear optics. Fundamentally, the sine-Gordon equation is a nonlinear partial differential equation (PDE) commonly used to model wave propagation, soliton dynamics, and particle interactions across various physical systems. This article focuses on the analytical solution of the 2D nonlinear coupled sine-Gordon equations in nonlinear wave contexts, considering specific boundary and initial conditions. The solution approach combines the triple Sumudu transform (TST) with an iterative method, detailing the analytical techniques and discussing their convergence properties. The exact solution, presented as a convergent series, is visually depicted through graphs. To address the nonlinear part of the equations, a successive iterative method was applied. The efficiency of the proposed method is illustrated through two test problems, with examples from engineering applications demonstrating its applicability. In conclusion, this method proves to be highly effective, efficient, and promising for finding exact solutions. Overall, the 2D nonlinear coupled sine-Gordon equations capture the intricate dynamics of nonlinear wave propagation, soliton interactions, and energy conservation in systems with multiple interacting components, making them a powerful tool for modeling a broad range of physical systems.

1. Introduction

Many physical systems are mathematically modeled using linear or nonlinear partial differential equations (PDEs) as noted by Evans [1]. One such PDE is the sine-Gordon equation, which is widely used to describe physical systems in engineering sciences. It is a key evolution equation with significant applications in both engineering and physical sciences. The sine-Gordon equation is employed to model various phenomena such as nonlinear waves, fluxon propagation, and other complex problems, as noted by Deresse, Mussa, and Gizaw [2]. These researchers obtained the analytical solution of 2D sine-Gordon equations using the triple Laplace transform (TLT) method in combination with an iterative approach. The sine-Gordon equation is often applied to describe the behavior of nonlinear waves, particularly solitons waves that preserve their shape over long distances. In 2D, these waves can interact and propagate in intricate ways, with nonlinear interactions between wave components leading to effects such as wave diffraction and soliton collisions as noted by Nikan, Avazzadeh, and Rasoulizadeh [3].

Additionally, Deresse, Mussa, and Gizaw [4] derived the analytical solution for the nonlinear 2D sine-Gordon equation with given initial conditions by employing the reduced differential transform method:

()

The examination of the coupled sine-Gordon equations began over two decades ago. Khusnutdinova and Pelinovsky [5] were the first to introduce and find a solution for a system of coupled sine-Gordon equations in one dimension, as given below:

()

Building upon earlier research, other scholars refined the equation and ultimately arrived at a solution. Deresse [6] successfully solved a slightly modified version of Equation (2) using the discrete sine transform (DST) in combination with an iterative method. Their findings highlighted the effectiveness and efficiency of this approach. Moreover, the researchers noted that the coupled sine-Gordon equation has garnered significant attention in the study of soliton solutions.

Watugala [7] introduced the Sumudu transform as a valuable tool for solving diverse differential equations in various engineering fields, providing accurate approximate solutions to applied problems. Subsequently, Watugala [8] extended the application of the Sumudu transform to two-dimensional (2D) problems, focusing on solutions to PDEs. Additionally, Mechee and Naeemah [9] employed the double Sumudu transform method to address various differential equations in specific application areas.

Various researchers have investigated different variants of the sine-Gordon equation, employing diverse methods to obtain solutions. Ji [10] utilized a mesh-free approach to solve the nonlinear sine-Gordon equation. Additionally, Liu, Sun, and Wu [11] and Duan et al. [12] have addressed generalized sine-Gordon equations using space–time spectral methods and lattice Boltzmann methods, respectively. Furthermore, Polyanin and Sorokin [13] have obtained reductions and exact solutions for nonlinear wave-type equations with delays.

The triple Sumudu transform (TST) with iterative method (TSIM) is a valuable tool for solving nonlinear coupled sine-Gordon equations in various scientific studies. Ahmad et al. [14] applied the Laplace–Sumudu transform method to obtain solutions for certain sine-Gordon type PDEs. They analyzed the convergence properties of the double Sumudu transform method. Furthermore, the iterative method coupled with the double Laplace transform was used to solve the nonlinear telegraph equation by Dhunde and Waghamare [15]. Yassein [16] employed the adapted iterative method to solve sine-Gordon equations. Additionally, exact solutions for various types of nonlinear PDEs were obtained using the double integral transform combined with the iterative method by Ahmed, Qazza, and Saadeh [17], Eshag [18], and Addam [19].

Several significant studies in nonlinear physics have been published, exploring various aspects of this complex field. Among these, Gao [20–22] has computed a solution for the 2D generalized nonlinear evolution system, which has implications for fluid dynamics and other areas of nonlinear physics.

The TST combined with the iterative method (TSIM) is a valuable technique for solving some complex PDEs, particularly for addressing nonlinear coupled-wave equations. This article applies the TST along with the iterative method to solve a nonlinear coupled 2D sine-Gordon equation. The problem under consideration in this study really new in its definition with initial and boundary conditions. To the best of the authors’ knowledge, no previous studies have explored the solution of the 2D nonlinear coupled sine-Gordon equation using the Sumudu transform method.

2. Problem Formulation

This study considered 2D nonlinear coupled sine-Gordon equation in the form of:

()

where Ω = [a₁, b₁] × [a₂, b₂] and t > 0.

with initial conditions:

()

and boundary constraints (Cauchy type BCs);

()

domain of the problem is Ω = (x, y) : a ≤ x ≤ b, c ≤ y ≤ d, t > 0.

Function ϕ(x, y) represents Josephsone current density and the functions ϕ₁(x, y) and ϕ₂(x, y) are specified wave modes and velocity.

First the source function η (x, y, t) breakdown into η₁ (x, y, t) and η₂ (x, y, t) to solve the system of sine-Gordon Equation (3). η₁ (x, y, t) and terms in (3) resulted into the simple algebraic equation when the inverse double Sumudu transform is applied. The part η₂(x, y, t) is joined with the nonlinear term of Equation (3) to eliminate the noise terms during the iteration. A similar decomposition is applied to the function τ(x, y, t) and can be decomposed as τ (x, y, t) = τ₁ (x, y, t) + τ₂ (x, y, t).

Definition 1. Let η(t) be a function defined for all real number t > 0, then its Simudu transform β(p) is

()

In similar manner for both functions η(x) and η(y) as the functions β (k) and β (m) are given, respectively.

Definition 2. Let β⁻¹[Φ(p)] = η(t) be the inverse Sumudu transform of a function Φ(p) and Bromwich contour integral given as:

()

Similarly for both functions Φ(k) and Φ(m).

Definition 3. Let η (x, y, t) be defined in the first octant of xyt-space and can be represented with convergent infinite series. Let , then the TST of the function η in the first octant of xyt-space is given by:

()

where k, m, p are the transform variables for x, y, and t, respectively, provided that the improper integral is convergent.

Definition 4. The inverse TST is defined by:

()

Definition 5. If η (x, y, t) is a continuous with a second partial derivative, then TST of partial derivative of the first and the second are given below by Diriba [19].

TST for the first partial derivative with respect to t, y, and x, respectively, are given by:

()

TST for the second partial derivatives with respect to t, y, x, respectively, are given by:

()

3. Convergence Theorem of TST

3.1. Existence and Uniqueness of the TST

Let η (x, y, t) has an exponential order in the equation |η(x, y, t)| = Ke^bx+cy+dt, then b, c, and d as x → ∞, y → ∞ and t → ∞, and if there exists a positive constant K such that ∀x > X, y > Y and t > T, then; |η(x, y, t)| = Ke^bx+cy+dt, and we write η (x, y, t) = Oe^bx+cy+dt, as x → ∞, y → ∞, and t → ∞. ⇒, .

Hence, η (x, y, t) is called an exponential order as x → ∞, y → ∞ and t → ∞ and it does not grow faster than Ke^{(bx + cy + dt)} as x → ∞, y → ∞ and t → ∞.

Theorem 6. Existence of the TST

If η (x, y, t) is continuous in all intervals (0, X), (0, Y), and (0, T) and for exponential order e^bx+cy+dt, then the TST of η (x, y, t) exists for all , and provided that , and

Theorem 7. Uniqueness of the TST

Let η, ρ, τ are continuous functions defined for x, y, and t have TSTs Φ (k, m, p), Ψ (k, m, p), and λ (k, m, p), respectively. If Φ (k, m, p) = Ψ (k, m, p) = λ (k, m, p), then η (x, y, t) = ρ (x, y, t) = τ (x, y, t).

4. Iterative Method

Let L is a nonlinear operator in a Banach space such that L: B → B and b is a given element of the Banach space B, Daftardar-Gejji and Jafari [23] have defined the functional equation as:

()

Now, z is supposed to be the solution of Equation (17) its series expansion is given by;

()

The operator L can be breakdown as

()

Employing Equations (18) and (19), Equation (17) is equivalent to

()

From Equation (20), the recurrence relation can be defined as:

()

Thus,

()

Hence,

()

Therefore, nth term approximate solution of Equation (18) is given by;

()

5. Convergence Theorem of the New Iterative Method

Theorem 8. If L is differentiable and its derivative is continuous in a neighborhood of u_o and w_o, then ‖L⁽ⁿ⁾(u_o)‖, ‖L⁽ⁿ⁾(w_o)‖≤M ≤ e⁻¹∀n, then the series and are absolutely convergent.

If function plugged in say u (x, y) from the above operators, then resulted in;

and

The operator β in third-order differential equation is a triple differentiable function. And the domain of β is the triple differentiable function on an open interval I. The terminology β of the function u (x, y) is used to describe β u (x, y) and the range of the function on I. Hence, β u (x, y) is also a function. These are some simple examples of operators due to derivative and integral.

6. TST Properties

1.
Linearity property: If η (x, y, t), ρ (x, y, t), and τ (x, y, t) are three functions of x, y, t such that β_xβ_yβ_t{η(x, y, t)} = Φ(k, m, p), β_xβ_yβ_t{ρ(x, y, t)} = Ψ(k, m, p), and β_xβ_yβ_t{τ(x, y, t)} = λ(k, m, p), then:
()
Where μ and α are real constants.
2.
Change of scale property: If η (x, y, t), ρ (x, y, t), and τ (x, y, t) are three functions of x, y, t such that β_xβ_yβ_t{η(x, y, t)} = Φ(k, m, p), β_xβ_yβ_t{ρ(x, y, t)} = Ψ(k, m, p), and β_xβ_yβ_t{τ(x, y, t)} = λ(k, m, p), then:
- i.
- ii.
where the constants d, c, and b are different from zero.
3.
First shifting property: If β_xβ_yβ_t{η(x, y, t)} = Φ(u, w), then:
()
4.
Second shifting property: If β_xβ_yβ_t{η(x, y, t)} = Φ(k, m, p), then;
()
the heaviside unit step function λ (x, y, t) given as:
()

7. TST Coupled With Iterative Method

A TST with an iterative method offers a potent approach to solving nonlinear coupled sine-Gordon equations. This technique involves applying the TST to the first and second partial derivatives with respect to the independent variables x and y, as well as the dependent variable time (t). The convergence properties of the TST provide a theoretical foundation for solving these equations. As a generalization of Laplace and Fourier transforms, the Sumudu transform has found applications in various fields, including signal processing, image analysis, and mathematical biology. Recently, it has been employed to solve fractional differential equations in diverse systems.

The TST of the function η (x, y, t) in the positive octant of xyt-space is;

where x, y, t are variables of the functions and k, m, p are the transform variables for x, y, and t, respectively, by ensuring the convergence of the improper integral.

8. Method of Solution

TST with iterative method is employed to find the solution of coupled Sine-Gordon equations. The solution is expressed in the series form.

9. Outcomes and Discussion

Given 2D nonlinear coupled sine-Gordon equation in the form of:

()

where Ω = [a₁, b₁]x[a₂, b₂] and t > 0.

subject to the initial conditions:

()

and boundary conditions (Cauchy type BCs);

()

within the problem domain of Ω = (x, y) : a ≤ x ≤ b, c ≤ y ≤ d, t > 0.

The function ϕ(x, y) represents Josephsone current density and the function ϕ₁(x, y) and ϕ₂(x, y) are specified wave modes and velocity.

Solution:

Step-1: Applying the TST.

Applying the TST to both sides of the system of Equation (29), we have:

()

Step-2: Applying the inverse TST.

()

where

, and

are Sumudu transforms of functions of three variables.

Therefore, the solution of the system of SGEs Equations (29) –(31) in series form is given by

()

Step-3: Test the convergence of obtained series solution

Finally, to show the convergence of the series solution by iterative method Theorem 8 will be applied.

Thus implies;

By the first derivative of the functions u and w respect to x, y, and t are zero.

Similarly,

The second derivative of the functions u and w respect to x, y, and t are zero.

Therefore,

where L is an operator of nonlinear continuously differentiable functional in a neighborhood of functions u and w.

10. Illustrative Examples

Two examples are given below to show the validity and effectiveness of the method.

Example 9. Consider the following initial boundary value problem (IBVP) for 2D coupled sine-Gordon equation on Ω = [0, Π]², t > 0:

()

with initial conditions,

()

and boundary conditions

()

Solution

Step-1: Applying the TST

Applying the TST to both sides of the system of Equation (36), we get

()

Applying the TST to both sides of the system of Equation (29), we have:

()

Step-2: Applying the inverse TST.

()

Applying the new iterative method to a system of Equation (42), we obtained

()

This implies;

()

For i = 1

()

Similarly, we obtained

()

and so on.

Hence, the solution of Example 9 in the sense of Equation (35) is

()

which is sketched in Figure 1

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The solution graphs of Example 9, when t = 0.2: (a) u(x, y, t) = e^{(x + y−2t)}, and (b) w(*x, y, t*) = sin(x + y + t).

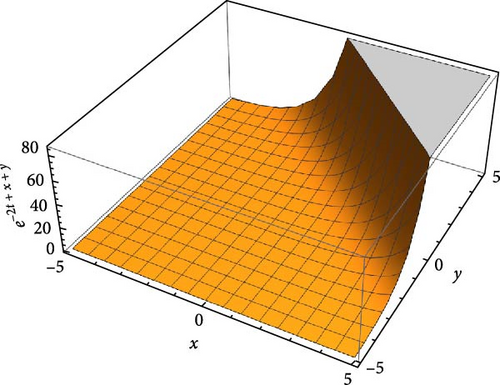
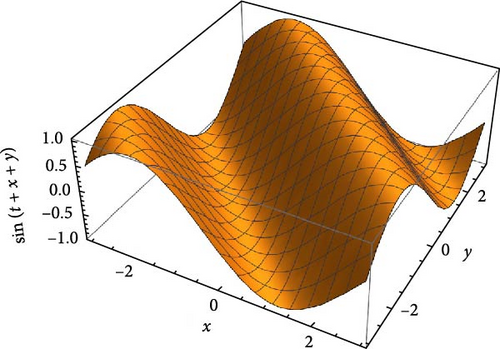
Step-3: Solution graph.

Step-4: Test the convergence of the obtained series solution.

Now, let us test the convergence of the obtained series solution. From the system of Equation (42), we have that;

()

for all x, y, t ≥ 0

()

And similarly, we have that:

()

for all k ≥ 0 by the principle of mathematical induction.

As the conditions of Theorem 8 are satisfied, the series solution obtained by the new iterative method is convergent on the domain of interest.

Example 10. Consider the following IBVP for 2D coupled sine-Gordon equation on Ω = [0, Π]², t > 0

()

with initial conditions,

()

and boundary conditions,

()

Solution.

Step-1: Applying the TST

Applying the TST to both sides of the system of Equation (52), we obtained

()

Multiplying both sides each equations in the system Equation (56) by k²m²p², we obtained

()

Step-2 Applying the inverse TST.

()

and so forth. Hence, the solution of Example 10 in the sense of Equation (35) is

()

Step-3: The solution graph is sketched in Figure 2.

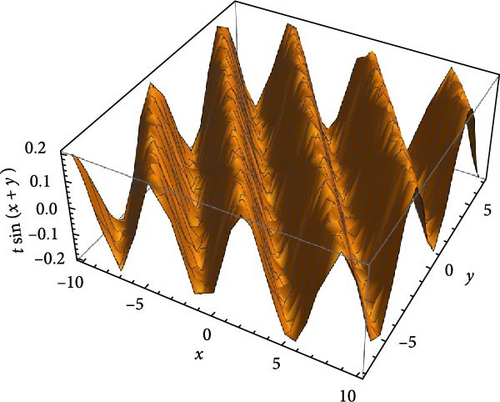
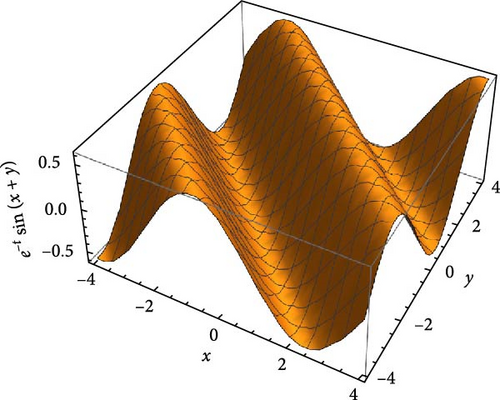
Step-4: Test the convergence of the obtained series solution.

Now, let us test the convergence of the obtained series solution. From the system of Equation (58) we have that;

()

Here for all x, y, t ≥ 0, we obtained

()

Therefore,

()

Therefore,

()

And similarly, we have that:

()

for all k ≥ 0 by the principle of mathematical induction.

As the conditions of Theorem 8 are satisfied, the series solution obtained by the new iterative method is convergent on the domain of interest.

11. Computational Efficiency of the TST With Iterative Method

Despite certain challenges, the TST combined with iterative methods offers significant computational advantages under specific conditions.

11.1. Reduction in Complexity Through Transform

The Sumudu transform is particularly useful for reducing the complexity of nonlinear differential equations by transforming them into algebraic or simpler differential equations. This transformation:

•
Simplifies the solution process in the transformed domain.
•
Avoids directly handling nonlinearity, making the iterative process more efficient.

This reduction in complexity allows iterative methods to solve a simplified problem, enhancing overall computational efficiency.

11.2. Faster Convergence for Mild Nonlinearities

For problems with mild or moderate nonlinearity, the combination of TST and iterative methods converges faster than many direct numerical approaches. The gradual refinement of the solution avoids the high computational overheads associated with traditional solvers, such as finite-difference or finite-element methods. Furthermore, since the Sumudu transform simplifies the original equation, fewer iterations are generally required to achieve a satisfactory approximation.

11.3. Efficient Handling of Large Systems

In multidimensional problems or coupled systems, such as the sine-Gordon equation, direct numerical methods can be computationally expensive. Using TST reduces the original system’s complexity, allowing iterative methods to be applied more efficiently. This approach decreases the computational burden and memory requirements compared to methods that require full domain discretization.

11.4. Adaptability to Parallel Computing

Iterative methods are highly adaptable to parallel computing architectures, which is crucial for solving large-scale multidimensional problems. The step-by-step nature of the iterative process supports concurrent computation, significantly reducing computation time when applied to extensive systems.

11.5. Efficient Memory Usage

Unlike finite-element or finite-difference methods, which require large matrices to store discretized data, the TST combined with iterative approaches reduces memory usage. This is especially advantageous in large-scale or high-dimensional problems where memory resources are limited.

11.6. Computational Trade-Offs in High-Iteration Scenarios

Although iterative methods generally require less memory and computational power per iteration, the required number of iterations can become prohibitively large in certain cases. When the nonlinearity is strong or boundary conditions are complex, the method might require many iterations, offsetting some of the computational benefits.

12. Challenges in Computational Efficiency

Despite these advantages, the TST with iterative methods faces several challenges:

•
High iteration counts: In cases with strong nonlinearity or poor initial guesses, the number of iterations may increase significantly, leading to higher computational costs.
•
Complex boundary conditions: Nontrivial boundary conditions may require additional modifications to the method, increasing both computation time and complexity.
•
Multidimensional problems: As the problem dimensionality increases, so does the complexity of applying both the Sumudu transform and iterative methods, which may reduce the computational advantages.

The TST with an iterative approach provides a computationally efficient technique for nonlinear PDEs under many conditions. It is especially effective for problems with mild nonlinearities and straightforward boundary conditions. However, its efficiency can be diminished by complex boundary conditions, strong nonlinearities, or high iteration requirements for convergence. Despite these challenges, the TST combined with iterative methods remains a competitive option against traditional numerical techniques, particularly when used alongside modern computational tools like parallel processing.

13. Validation With Existing Solutions

To validate the effectiveness of the TST combined with iterative methods, we compare our results with existing analytical solutions from the literature. This comparison serves to assess both the accuracy and computational efficiency of the proposed method.

13.1. Comparison With Analytical Solutions

For certain types of nonlinear PDEs, analytical solutions exist that allow direct comparison. This step helps verify the accuracy of the TST approach.

14. Analytical Solution

By analyzing the structure of the equations and using the initial and boundary conditions, we propose the following analytical solutions:

()

These solutions satisfy both the PDEs, the initial conditions, and the boundary conditions.

15. Verification of the Solution

15.1. Substitution Into the PDEs

For u(x, y, t) = e^x+y−2t, we calculate the second derivatives:

Substituting into the first equation in (36):

which is satisfied.

For w(x, y, t) = sin(x + y + t), we compute:

Substituting into the second equation in (36):

which is also satisfied.

Hence, the TST with iterative method give the same result with analytical solution of Equation (36).

16. Conclusions

This study presents an analytical solution for a 2D nonlinear system of sine-Gordon equations using a TST-augmented iterative method. The efficacy of the method is demonstrated through two illustrative examples, with their solutions visualized graphically. The convergence properties of the series solutions are also analyzed in detail. The results suggest that this approach is a promising tool for solving similar problems in mathematical physics.

Nomenclature

PDE:: partial differential equation
2D:: two-dimensional
DST:: double Sumudu transform
ODEs:: ordinary differential equations
MATLAB:: matrix laboratory
IM:: iterative method
IVP:: initial value problem
BCs:: boundary conditions
BVPs:: boundary value problems
TST:: triple Sumudu transform
TSIM:: triple Sumudu transform with iterative method
TDNSGE:: two-dimensional nonlinear sine-gordon equation
SGE:: sine-Gordon equation
CSGE:: coupled sine-Gordon equation
TLT:: triple Laplace transform
L^′:: nonlinear first order
L^″:: nonlinear second order
L³:: nonlinear third order
L^k:: k^th continuously differentiable function

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

The authors equally contributed and approved the final article for submission.

Funding

The authors received no fund to conduct this study.

Open Research

Data Availability Statement

The data used to support the findings of this study are included within the article.

References

1 Evans L. C., Partial Differential Equations, 2022, 19, American Mathematical Society.
Google Scholar
2 Deresse A. T., Mussa Y. O., and Gizaw A. K., Solutions of Two-Dimensional Nonlinear Sine-Gordon Equation via Triple Laplace Transform Coupled With Iterative Method, Journal of Applied Mathematics. (2021) 2021, 15, https://doi.org/10.1155/2021/9279022, 9279022.
10.1155/2021/9279022
Google Scholar
3 Nikan O., Avazzadeh Z., and Rasoulizadeh M. N., Soliton Solutions of the Nonlinear Sine-Gordon Model With Neumann Boundary Conditions Arising in Crystal Dislocation Theory, Nonlinear Dynamics. (2021) 106, no. 1, 783–813, https://doi.org/10.1007/s11071-021-06822-4.
10.1007/s11071-021-06822-4
Web of Science® Google Scholar
4 Deresse A. T., Mussa Y. O., and Gizaw A. K., Analytical Solution of Two-Dimensional Sine-Gordon Equation, Advances in Mathematical Physics. (2021) 2021, 15, https://doi.org/10.1155/2021/6610021, 6610021.
10.1155/2021/6610021
Web of Science® Google Scholar
5 Khusnutdinova K. R. and Pelinovsky D. E., On the Exchange of Energy in Coupled Klein–Gordon Equations, Wave Motion. (2003) 38, no. 1, 1–10, https://doi.org/10.1016/S0165-2125(03)00022-2, 2-s2.0-0038543060.
10.1016/S0165-2125(03)00022-2
Google Scholar
6 Deresse A. T., Double Sumudu Transform Iterative Method for One-Dimensional Nonlinear Coupled Sine-Gordon Equation, Advances in Mathematical Physics. (2022) 2022, 15, https://doi.org/10.1155/2022/6977692, 6977692.
10.1155/2022/6977692
Web of Science® Google Scholar
7 Watugala G. K., Sumudu Transform: A New Integral Transform to Solve Differential Equations and Control Engineering Problems, International Journal of Mathematical Education in Science and Technology. (1993) 24, no. 1, 35–43, https://doi.org/10.1080/0020739930240105, 2-s2.0-0006219608.
10.1080/0020739930240105
Google Scholar
8 Watugala G., The Sumudu Transform for Functions of Two Variables, Mathematical Engineering in Industry. (2002) 8, no. 4, 293–302.
Google Scholar
9 Mechee M. S. and Naeemah A., A Study of Double Sumudu Transform for Solving Differential Equations With Some Applications, International Journal of Engineering and Information Systems (IJEAIS). (2020) 4, no. 1, 20–27.
Google Scholar
10 Ji Y., Meshless Singular Boundary Method for Nonlinear Sine-Gordon Equation, Mathematical Problems in Engineering. (2018) 2018, 11, https://doi.org/10.1155/2018/6460480, 2-s2.0-85050184439, 6460480.
10.1155/2018/6460480
Google Scholar
11 Liu W., Sun J., and Wu B., Space–Time Spectral Method for the Two-Dimensional Generalized Sine-Gordon Equation, Journal of Mathematical Analysis and Applications. (2015) 427, no. 2, 787–804, https://doi.org/10.1016/j.jmaa.2015.02.057, 2-s2.0-84955634951.
10.1016/j.jmaa.2015.02.057
Web of Science® Google Scholar
12 Duan Y., Kong L., Chen X., and Guo M., Lattice Boltzmann Model for Two-Dimensional Generalized Sine-Gordon Equation, Journal of Applied Analysis & Computation. (2018) 8, no. 6, 1645–1663, https://doi.org/10.11948/2018.1645, 2-s2.0-85059485671.
10.11948/2018.1645
Google Scholar
13 Polyanin A. D. and Sorokin V. G., Reductions and Exact Solutions of Nonlinear Wave-Type PDEs With Proportional and More Complex Delays, Mathematics. (2023) 11, no. 3, https://doi.org/10.3390/math11030516, 516.
10.3390/math11030516
Google Scholar
14 Ahmed S. A., Elzaki T. M., Elbadri M., and Mohamed M. Z., Solution of Partial Differential Equations by New Double Integral Transform (Laplace-Sumudu Transform), Ain Shams Engineering Journal. (2021) 12, no. 4, 4045–4049, https://doi.org/10.1016/j.asej.2021.02.032.
10.1016/j.asej.2021.02.032
Web of Science® Google Scholar
15 Dhunde R. R. and Waghamare G., Double Laplace Transform Combined With Iterative Method for Solving Non-Linear Telegraph Equation, Journal of the Indian Mathematical Society. (2016) 83, no. 3-4, 221–230.
Google Scholar
16 Yassein S. M., Modified Iterative Method for Solving Sine-Gordon Equations, Iraqi Journal of Science. (2023) 64, no. 3, 1361–1368, https://doi.org/10.24996/ijs.2023.64.3.29.
10.24996/ijs.2023.64.3.29
Google Scholar
17 Ahmed S. A., Qazza A., and Saadeh R., Exact Solutions of Nonlinear Partial Differential Equations via the New Double Integral Transform Combined With Iterative Method, Axioms. (2022) 11, no. 6, https://doi.org/10.3390/axioms11060247, 247.
10.3390/axioms11060247
Google Scholar
18 Eshag M. O., On Double Laplace Transform and Double Sumudu Transform, American Journal of Engineering Research. (2017) 6, no. 5, 312–317.
Google Scholar
19 Addam Y., Analytical Solution of Two Dimensional Fourth Orders Parabolic Partial Differential Equation Using Triple Laplace Transform Coupled With Iterative Method, 2022.
Google Scholar
20 Gao X. Y., Symbolic Computation on a (2+1)-Dimensional Generalized Nonlinear Evolution System in Fluid Dynamics, Plasma Physics, Nonlinear Optics and Quantum Mechanics, Qualitative Theory of Dynamical Systems. (2024) 23, no. 5, https://doi.org/10.1007/s12346-024-01045-5, 202.
10.1007/s12346-024-01045-5
Google Scholar
21 Gao X. Y., In the Shallow Water: Auto-Bäcklund, Hetero-Bäcklund and Scaling Transformations via a (2+1)-Dimensional Generalized Broer-Kaup System, Qualitative Theory of Dynamical Systems. (2024) 23, no. 4, 1–11, https://doi.org/10.1007/s12346-024-01025-9.
10.1007/s12346-024-01025-9
Google Scholar
22 Gao X.-Y., Auto-Bäcklund Transformation With the Solitons and Similarity Reductions for a Generalized Nonlinear Shallow Water Wave Equation, Qualitative Theory of Dynamical Systems. (2024) 23, no. 4, https://doi.org/10.1007/s12346-024-01034-8, 181.
10.1007/s12346-024-01034-8
Google Scholar
23 Daftardar-Gejji V. and Jafari H., An Iterative Method for Solving Nonlinear Functional Equations, Journal of Mathematical Analysis and Applications. (2006) 316, no. 2, 753–763, https://doi.org/10.1016/j.jmaa.2005.05.009, 2-s2.0-29844442304.
10.1016/j.jmaa.2005.05.009
Web of Science® Google Scholar

All articles

Analytical Treatments for a Coupled (2+1)-Dimensional Partial Differential Equations in Nonlinear Physics

Abstract

1. Introduction

2. Problem Formulation

3. Convergence Theorem of TST

3.1. Existence and Uniqueness of the TST

4. Iterative Method

5. Convergence Theorem of the New Iterative Method

6. TST Properties

7. TST Coupled With Iterative Method

8. Method of Solution

9. Outcomes and Discussion

10. Illustrative Examples

11. Computational Efficiency of the TST With Iterative Method

11.1. Reduction in Complexity Through Transform

11.2. Faster Convergence for Mild Nonlinearities

11.3. Efficient Handling of Large Systems

11.4. Adaptability to Parallel Computing

11.5. Efficient Memory Usage

11.6. Computational Trade-Offs in High-Iteration Scenarios

12. Challenges in Computational Efficiency

13. Validation With Existing Solutions

13.1. Comparison With Analytical Solutions

14. Analytical Solution

15. Verification of the Solution

15.1. Substitution Into the PDEs

16. Conclusions

Nomenclature

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information