Volume 2025, Issue 1 3089008

Research Article

Open Access

A Newmark Integral Method in Nonhomogeneous Materials With Parallel Cracks Based on Hyperbolic Heat Conduction

Yanyan Zhang,

Corresponding Author

Yanyan Zhang

[email protected]

orcid.org/0000-0002-0933-3253

College of Aviation Engineering , Civil Aviation Flight University of China , Guanghan , 618307 , China , cafuc.edu.cn

Department of Mechanical Engineering , University of Alberta , Edmonton , AB T6G1H9 , Canada , ualberta.ca

Search for more papers by this author

Tao Zheng,

Tao Zheng

School of Astronautics , Harbin Institute of Technology , Harbin , 150001 , China , hit.edu.cn

Search for more papers by this author

Liangzhong Ao,

Liangzhong Ao

College of Aviation Engineering , Civil Aviation Flight University of China , Guanghan , 618307 , China , cafuc.edu.cn

Search for more papers by this author

Shanqiao Huang,

Shanqiao Huang

School of Astronautics , Harbin Institute of Technology , Harbin , 150001 , China , hit.edu.cn

Search for more papers by this author

Zengtao Chen,

Corresponding Author

Zengtao Chen

[email protected]

orcid.org/0000-0002-0106-9638

Department of Mechanical Engineering , University of Alberta , Edmonton , AB T6G1H9 , Canada , ualberta.ca

Search for more papers by this author

Yanyan Zhang,

Corresponding Author

Yanyan Zhang

[email protected]

orcid.org/0000-0002-0933-3253

College of Aviation Engineering , Civil Aviation Flight University of China , Guanghan , 618307 , China , cafuc.edu.cn

Department of Mechanical Engineering , University of Alberta , Edmonton , AB T6G1H9 , Canada , ualberta.ca

Search for more papers by this author

Tao Zheng,

Tao Zheng

School of Astronautics , Harbin Institute of Technology , Harbin , 150001 , China , hit.edu.cn

Search for more papers by this author

Liangzhong Ao,

Liangzhong Ao

College of Aviation Engineering , Civil Aviation Flight University of China , Guanghan , 618307 , China , cafuc.edu.cn

Search for more papers by this author

Shanqiao Huang,

Shanqiao Huang

School of Astronautics , Harbin Institute of Technology , Harbin , 150001 , China , hit.edu.cn

Search for more papers by this author

Zengtao Chen,

Corresponding Author

Zengtao Chen

[email protected]

orcid.org/0000-0002-0106-9638

Department of Mechanical Engineering , University of Alberta , Edmonton , AB T6G1H9 , Canada , ualberta.ca

Search for more papers by this author

First published: 09 June 2025

https://doi.org/10.1155/admp/3089008

Academic Editor: S. A. Edalatpanah

Share a link

Email
Wechat
Bluesky

Abstract

The strong, transient working conditions where heat transfer involves extremely large temperature gradients, extremely large heat fluxes, and extremely short time durations of thermal disturbances may occur in engineering materials and structures. Fourier heat conduction assumes heat propagation at an infinite speed, which is not suitable for strong, transient thermal working conditions. In this paper, a Newmark integral method is presented to deal with the strong, transient heat conduction in nonhomogeneous materials based on the hyperbolic heat conduction theory. The second-order differential equation of the strong transient temperature field is discretized in the spatial and temporal domains through the finite element method (FEM) and the Newmark integral method, respectively. This allows them to be solved directly without the necessity to convert them into a pair of first-order differential equations using the Newmark integral method. Several test examples are presented to demonstrate the application of the current method. Firstly, the stability of the Newmark integral method is analyzed to ensure that the numerical oscillation is suppressed in the calculation. Then the time-related temperature field of functionally graded material (FGM) plate under strong transient thermal shock is analyzed. Finally, the thermal stress intensity factors (TSIFs) in an FGM plate with parallel cracks are extracted after combining with interaction energy integral methods (IEIMs). The results confirm that the Newmark integral method can efficiently address the transient thermal problem and ensure stability. The temperature overshooting phenomenon and thermal wave singularity are visualized at the finite speed of heat propagation. Moreover, the numerical results agree well with analytical solutions. The current method can be well applied to the design and evaluation of thermal protective materials in extreme thermal environments.

1. Introduction

Nonhomogeneous materials such as piezoelectric materials, thermal coating materials, functionally graded materials (FGMs), and biomimetic materials have some unique, excellent properties compared to homogeneous materials. The materials are widely used in aerospace, integrated circuits, and biomedical fields. In the engineering uses of nonhomogeneous materials, working conditions often involve extreme temperatures or heat transfer at the micro-/nanotemporal or spatial scales. Under high-temperature gradients, fast heat flow [1], very low temperatures [2], and microscopic temporal and spatial scales [3], heat transfer exhibits different features than what Fourier heat conduction predicts [4]. In the case of transient, high-temperature gradients, where materials undergo sudden temperature changes in a very short temporal and spatial scale, a time delay is expected in the response to these ultra-fast heat fluxes or time-dependent temperature changes. This delay occurs because of the time required for heat propagation [5]. Thus, the Fourier heat conduction model assuming an infinite speed of heat propagation is not appropriate for dealing with the transient heat conduction process. To account for the delayed thermal response, time-dependent non-Fourier heat conduction models have been developed. Many non-Fourier heat conduction models, such as nonlocal phase-lag heat conduction, three-phase-lag heat conduction, and nonlocal C–V heat conductioncan, can be applied to the design and evaluation of the materials in thermal protection systems of internal combustion engines and key components of high-speed aircraft.

In recent years, laser, microwave, and other heat sources with extremely high frequencies and short durations have become more widely used in modern technology. Thermal fracture analysis in nonhomogeneous materials has become a popular topic based on the non-Fourier heat conduction theories [6–12]. Cattaneo [6] and Vernottee [7] proposed a hyperbolic heat conduction equation coupled to the local energy balance. Ozisik and Tzou [8] analyzed the characteristics of heat wave propagation and proved that the energy equation can be reduced to that governing the heat transport through the metal lattice in the microscopic, two-step model. Wang and Han [9] obtained the heat flux intensity factor in a two-layer composite structure with an interface crack under a transient, thermal flux. Guo et al. [10] investigated the non-Fourier effect on the thermoelastic fields in a semi-infinite ceramic medium under a heating shock. Yang et al. [11] analyzed the thermal fracture of a Griffith interface crack in an orthotropic, functionally graded coating/substrate structure based on the non-Fourier heat conduction theory. Jin and Paulino [12] obtained a first-order, analytical temperature solution for FGMs using a multilayer material model. For directly handling thermal problems of nonhomogeneous materials, methods like integral transforms and singular integral equations were typically employed for analytical solutions. Babaei and Chen [13] investigated one-dimensional, transient hyperbolic heat conduction in a functionally graded hollow cylinder, assuming power-law variations in material properties. Akbarzadeh and Chen [14] developed a heat conduction model in the FGM based on the dual-phase-lag heat conduction theory. Xue et al. [15] investigated an insulated crack in a thermoelastic half-space made of FGMs using the memory-dependent heat conduction model. Fu et al. [16] studied the non-Fourier heat conduction model in a sandwich panel containing a cracked foam core. Huang et al. [17] developed a piecewise exponential model in a nonhomogeneous coating substrate structure with the interface crack under steady thermal loading. Other researchers employed perturbation methods to obtain the transient temperature distribution of FGMs [18–20]. In most existing research, analytical results for the transient temperature have been obtained for relatively simple structures or homogeneous materials [21, 22]. However, in the case of nonhomogeneous materials, the material properties distribute arbitrarily and can be a complex function of spatial locations, and consequently, the heat conduction equation becomes nontrivial for analytical methods. Researchers have, respectively, promoted the optimization of mechanical properties of materials and numerical simulations in terms of fatigue performance [23], impact toughness [24], and computational efficiency [25]. Balci and Yalcin [26] and Yildirim et al. [27] both used finite element method (FEM) to solve the surface crack problem under thermal shock load and generated numerical results of the fracture response using transient thermomechanical analysis and displacement-related techniques, respectively. Santra and Behera [28], Santra [29], and Santra and Mohapatra [30] proposed a high-precision numerical solution system for multiclass complex, fractional order, integral partial differential equations based on the simultaneous space–time Hermite wavelet method, a hybrid numerical method that combines a higher order finite difference method (FDM) and the multidimensional Hermite wavelets, and an efficient recursive algorithm. Compared with the analytical technique, the numerical technique has been widely applied to solve problems with complex material properties and/or complex geometries in engineering applications. Rathish Kumar et al. [31] numerically investigated the thermo-hydrodynamic performance of a high-speed slider bearing conducting to a stationary pad. Su et al. [32] obtained a new, second-order, two-dimensional FEM for the parabolic-type equation with rapidly oscillating coefficients. Zhang et al. [33] developed a multiple, spatially, and temporally scaled method for simulation in periodic, nonhomogeneous materials considering the effect of non-Fourier heat conduction. Yasbolaghi and Khoei [34] developed a novel coupling technique for the analysis of temperature field problems in the continuum–atomistic multiscale framework.

Till now, numerical research on the non-Fourier heat conduction model in nonhomogeneous materials/structures under thermal shock loading is still very limited. Wang and Tian [35] obtained the time-dependent temperature distribution in a nonhomogeneous material. Wang et al. [36] developed a finite element code to dealing with the one-dimensional, transient temperature, and thermal stress based on a nonclassical heat conduction model. Zhang et al. [37] developed a numerical method for obtaining the transient temperature fields in nonhomogeneous materials with inclusions. Later, Zhang et al. [38] investigated the thermal shock resistance in FGMs. In these studies, the first-order differential equation of the temperature in the temporal domain was discretized by the backward FDM based on the Fourier heat conduction theory. However, at extremely short time scales or very small length scales where non-Fourier heat conduction applies, the FDM will heavily rely on the size of the iterative time step and mesh dimensions.

The Newmark integral method [39] allows the direct solution of second-order differential equations without the necessity to convert them into a pair of first-order differential equations [40–43]. The time integration of structural dynamics using the Newmark algorithm is used in most finite element packages, such as the head–disk interface dynamics in magnetic recording technology [44], initialization for the implicit and explicit dynamics phase-field fracture model [45], and so on. Gedney and Navsariwala [46] presented a method that couples different integral methods stemming from both the Newmark families and Euler+θ integration methods for analysis of structural dynamics. The Newmark integral method is unconditionally stable and minimizes the truncation error for a particular choice of certain controlling parameters [47]. The generalized alpha method is an extension of the Newmark time integral method and is widely used in the field of structural dynamics [48]. However, the numerical calculations for transient temperature fields in nonhomogeneous materials using the Newmark integral method have not yet been reported. For nonhomogeneous materials under transient, thermal shock loading, a numerical method to solve the time-related, transient temperature responses is of great importance. In this paper, a numerical technique is developed for solving the time-related temperature field within the framework of hyperbolic heat conduction theory. Section 2 discusses the thermal conduction equation under transient thermal loading, Section 3 gives a numerical scheme for strong transient temperature, and Section 4 presents numerical examples and discussions of the results. The Newmark integral method is used to resolve the time-related temperature response, which shows its stability under a strong transient temperature environment. The computational efficiency is greatly improved by the adaptive adjustments in the time and space increments. The numerical results confirm that the fictitious numerical oscillations can be suppressed by a proper choice of the related parameters β and γ in the Newmark integral method. The time-related temperature responses are analyzed for nonhomogeneous materials under strong, transient thermal loading. The following major contributions can be drawn from the current work:

1.
The Newmark integral method is developed to deal with the transient, thermal response in nonhomogeneous materials.
2.
The temperature overshooting phenomenon and thermal wave singularity are visualized at the finite speed of heat propagation.
3.
The Newmark integral method can be used to solve transient, thermal fracture problems with the IEIM.

2. Thermal Conduction Equation Under Transient Thermal Loading

To describe the finite speed of heat propagation, the thermal relaxation time is introduced in heat conduction theories. This concept leads to the development of a non-Fourier heat transfer model characterized by equations describing heat transfer in a wave-like manner so that thermal waves are used to spread the heat [5]. The following heat flux model is suggested in Tzou and Cattaneo [4, 6]:

()

where q, τ_q, t, ∇, λ, and T are the heat flux vector, the relaxation time of heat flux, time, gradient operator, thermal conductivity, and absolute temperature, respectively. The relaxation time of heat flux is the delay between the update of the temperature field and the attainment of thermal equilibrium. The local energy balance equation can be written as follows [46]:

()

where c and ρ are the respective specific heat capacity and mass density.

By combining the local energy equilibrium Equation (2) and heat conduction Equation (1), we derive the governing equation for the hyperbolic heat conduction as follows [5]:

()

where ∇² is the Laplacian operator. The temperature boundary conditions for heat conduction are presented as follows [49, 50]:

1.
This is the first-type (or Dirichlet) temperature boundary condition, where the temperature on the boundary is defined as

()

2.
This is the second-type (or Neumann) temperature boundary condition, where heat flux density on the boundary is determined by

()

3.
The third-type (or the combination of Dirichlet and Neumann) temperature boundary condition can be expressed as follows:

()

where h_t is the convective heat transfer coefficient.

3. Numerical Scheme for Strong Transient Temperature

For nonhomogeneous materials, the thermomechanical parameters λ(x), α(x), c(x), E(x), τ_q(x), and ρ(x) can be defined as a function with respect to the spatial position x. The space of the material can be discretized into n elements, which are interconnected at nodal points. The temperature and the nodal coordinates of elements can be expressed as follows:

()

where [N] represents the matrix of the interpolation function. The function related to the temperature field can be written as follows:

()

For simplicity, the first-type (or Dirichlet) temperature boundary condition is used in examples. Let the first-order functional in Equation (8) be zero; the approximation by FEM for the second-order differential equation of hyperbolic heat conduction can be described as follows:

()

in which

()

where the heat conduction matrix [K₁], the heat convection matrix [K₂], the conduction coefficient matrix [D], the partitioned matrix [B], and the heat capacity matrix [K₃] are the same as those shown in Rathish et al. [31], and [M] is the thermal relaxation matrix. T(x, y, t),

, and

are the temperature scalar and its first-order and second-order time derivatives, respectively.

The temperature and its first-order time derivative can be expressed by Taylor series expansions as follows:

()

where Δt is the time step. Using the mean value theorem, the third-order time derivative of the temperature can be written as follows:

()

Substituting Equation (13) into Equations (11) and (12), the original equations can be rewritten as follows:

()

where β and γ are parameters in the Newmark integral method, which will be discussed later. By rearranging Equation (15), the explicit expression

can be obtained:

()

Then, the explicit expression of

can be obtained by substituting Equation (16) into Equation (14):

()

Substituting the expressions of

(Equation (16)) and

(Equation (17)) into the second-order differential Equations (9) and (10), we obtain the following:

()

where

denotes the equivalent stiffness matrix and

represents the equivalent thermal load vector; δ₁–δ₆ are expressed as follows:

()

Equation (18) represents an explicit expression of temperature in terms of the corresponding values of temperature and its first- and second-order time derivatives at the previous step. After getting the values of , and , the approximation of T_n+1(x, y) can be calculated.

Newmark’s method is considered to be conditionally convergent; that is, convergence is guaranteed only for a specific, finite range of step sizes. If 2β − γ ≥ 0 is satisfied, the Newmark integral method is unconditionally stable. Several typical applications include the following: the explicit central difference scheme (γ = 1/2, β = 0), stable when ω_minΔt ≤ 2 (ω_min is the minimum natural vibration period of the structure); the average acceleration method (γ = 1/2, β = 1/4), which offers unconditional stability; and the linear acceleration method (γ = 1/2, β = 1/6), known for its conditional stability.

4. Numerical Examples and Discussions

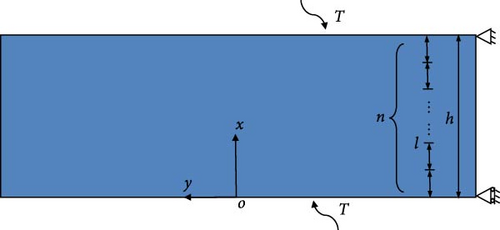
Several test examples with nonhomogeneous material plates are presented in this section to illustrate the feasibility of this numerical technique. A plane strain state is assumed. In other word, all variables and material properties are functions of x-coordinate and independent of z-coordinate.

4.1. Verification

4.1.1. Verification of the Accuracy

The two-dimensional plate problem studied by Guo et al. [51] was investigated to verify the proposed method in this study, as shown in Figure 1. The two-dimensional plate is similar to an infinite-long plate when the ratio of the long side to the short side is greater than five in Figure 1. In this problem, it is one-dimensional heat transfer along the x direction. In detail, initially, a uniform temperature T₀ is set for the entire plate. The temperature of the upper and lower surfaces is suddenly reduced to a value of zero. The boundary conditions are defined as follows:

()

for the thermal condition, and

()

for the mechanical conditions.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic of a plate of nonhomogenous material subjected to thermal shocks.

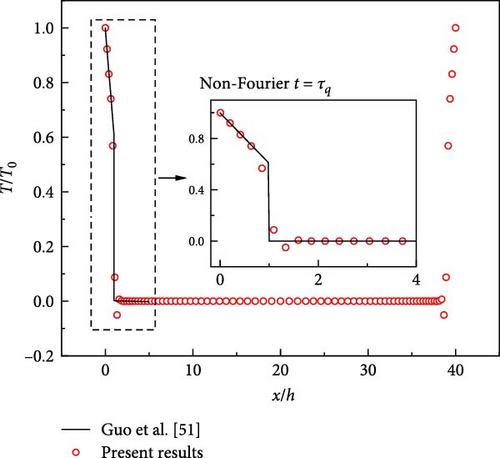
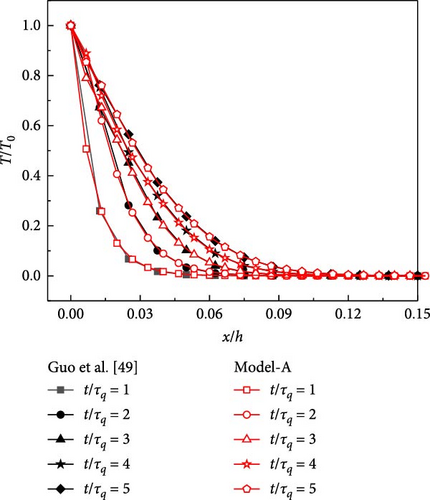
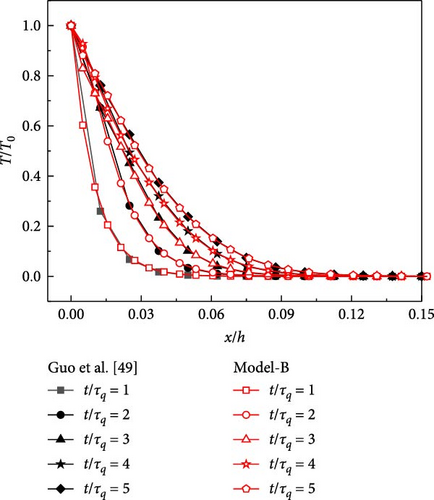
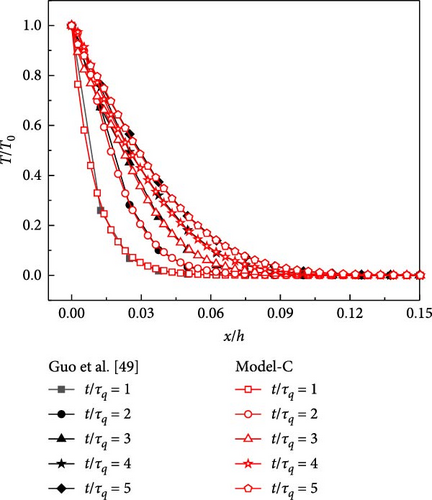
The thermomechanical properties of the material are given as τ_q(x) = 0.625, c(x) = ρ(x) = λ(x) = 1, h = 40l, where and κ = λ/cρ, and κ is thermal diffusivity. Figure 2a shows the results of the proposed method compared to the analytical solution given by Guo et al. [51]. Our results agree well with the analytical solutions, demonstrating that the current method is valid for the transient thermal response based on hyperbolic heat conduction.

Notably, the solution to the Fourier heat conduction equation can be obtained from Equation (18) by setting τ_q = 0. In Figure 1, the thermal boundary conditions of the FGM plate are redefined as follows:

()

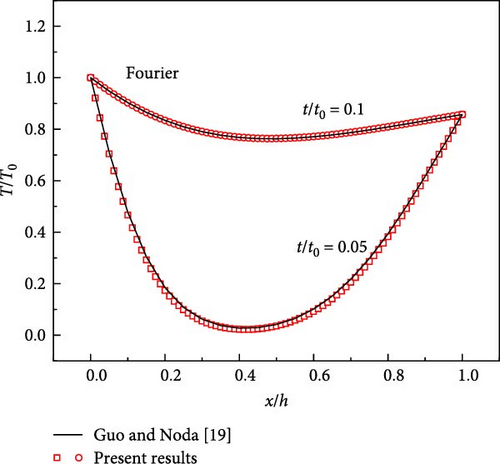
The mechanical condition is the same as those in Equations (23)–(25).

The results are depicted in Figure 2b, which also shows great agreement with the analytical solutions of Zhang et al. [20]. With those results, we are confident that the proposed method works well for the temperature response to heat transfer of both Fourier heat conduction and hyperbolic heat conduction.

4.1.2. The Stability of the Newmark Integral Method

The oscillation of calculated results is an inherent problem when using the Newmark integral method to solve transient temperature fields. Wang et al. [36] employed the backward FDM scheme to resolve the time-dependent temperature response, and the oscillations can be suppressed by properly choosing the length of time step and meshes, but this method provides a very slight improvement for the current Newmark integral method. Similar to the undamped system in the Newmark integral method, the unconditional stability of the numerical results can be obtained when the following conditions are satisfied [41, 42]:

()

Figure 3 displays the numerical results of temperature distribution in the specimen from the current method with different values of γ. It can be observed that the numerical results present fictitious oscillations of temperature near the upper and lower surfaces. The variation of transient temperature exhibits severe oscillations when using the average acceleration method (γ = 0.50). However, the oscillations can be greatly reduced when γ = 0.65.

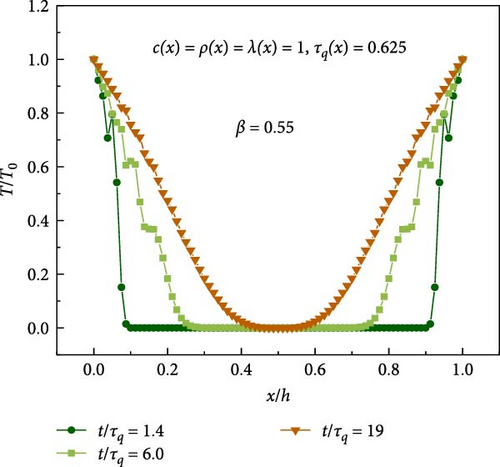
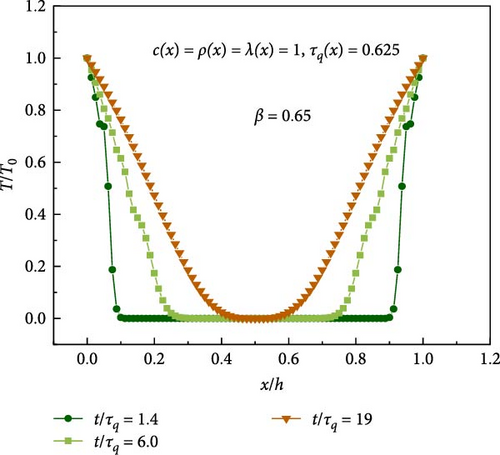
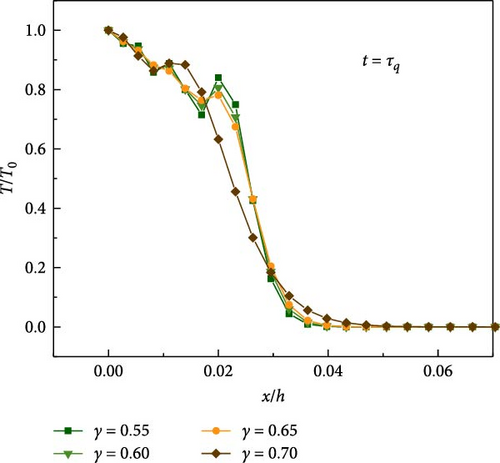
The convergence of numerical results with respect to γ are studied. As shown in Figure 4, the oscillations of transient temperature are compared among four different values of γ (γ = 0.55, 0.60, 0.65, 0.70). It can be found that the oscillations of numerical results decrease with the increase of γ. However, inaccurate numerical results are obtained when γ is equal to 0.70, which may be caused by the artificial damping of the Newmark method [52]. Therefore, to balance the convergence and stability, the following parameters are adopted in the following numerical examples:

()

4.1.3. Dependence of Element Meshing

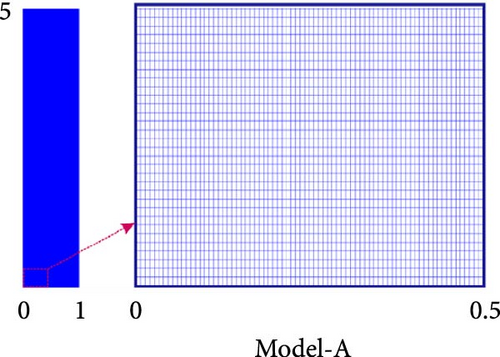
To verify the mesh dependence of numerical results by using the Newmark method, three different FEM models are chosen (Model-A, Model-B, and Model-C). As shown in Figure 5, there are 60,702 nodes and 60,150 elements in Model-A, 22,952 nodes and 22,650 elements in Model-B, and 12,312 nodes and 12,080 elements in Model-C. Figure 6 shows the transient temperature computed for different finite element meshing schemes (space increment). The results of transient temperature from the FEM models are perfectly coincident with each other, illustrating insignificant mesh dependence. Therefore, the integrations are computed using the meshing scheme Model-C in all the following examples. Time step and corresponding number of iterations as shown in Table 1.

Table 1. Time step and corresponding number of iterations.

Number of iterations	5	5	3	6	2
Time step	0.001	0.002	0.01	0.025	0.07
Time	0.005	0.01	0.03	0.15	0.14

4.1.4. Dependence of Iterative Time Step

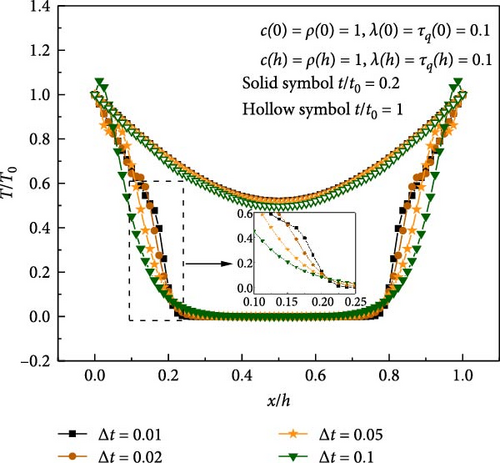
The iteration time step is an important factor affecting the calculation accuracy of the numerical method. Figure 7 shows the transient temperature response with varying time steps. It can be seen that the influence of the time step on transient temperature is larger, and the thermal wavefront of the small time step is obvious, which is the disadvantage of the present method. However, the computational efficiency can be improved by setting the adaptive time step to reduce the number of iterations. The time step is initially encrypted at extremely short time scales and then amplified with increasing time.

4.2. Transient Temperature Field in a Nonhomogeneous Plate With an Edge Crack

Compared with homogeneous materials, nonhomogeneous materials have a wider range of applications in engineering. Next, we take FGMs as an example to consider the transient temperature field of the FGM plate. It is noted that the boundary temperature conditions are the same as those in Equations (23)–(25) and (30) of Section 4.1. The conductivity of the FGM across the thickness is described by a power-law function (g = 1, 2) or an exponential function dependent on its x coordinates:

()

where λ(0) and λ(h) are the heat conductivity of materials at the lower and upper surfaces of the FGM plate.

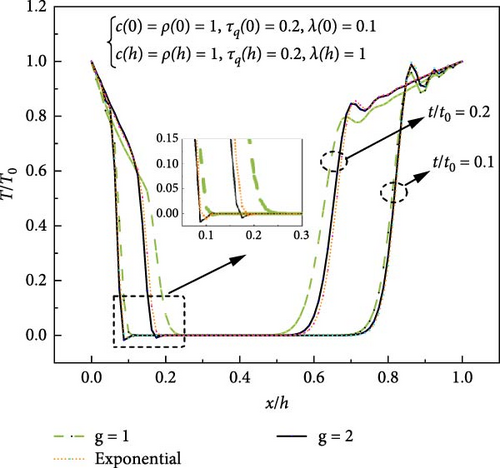
The transient temperature distributions for different materials distribution patterns of the FGM are compared in Figure 8. It is obvious that the difference in the temperature distribution changes with time.

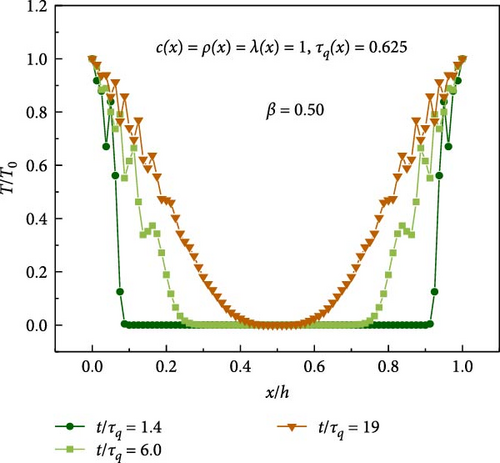
The transient temperature distributions along the FGM plate thickness for different thermal relaxation times are shown in Figure 9. The thermal relaxation time affects the variation patterns of the transient temperature. The overshooting phenomenon [53] of transient temperature occurs at some positions and for different values of relaxation time. As the thermal relaxation time increases from 0.3 to 3, the overshooting phenomenon becomes milder. In particular, when the thermal relaxation time approaches 3, there is no temperature overshooting as shown in Figure 9. Therefore, there may be an optimal thermal relaxation time that minimizes the overshooting phenomenon. In addition, longer thermal relaxation time leads to a delay in the temperature response, because more time is required to reach a steady state.

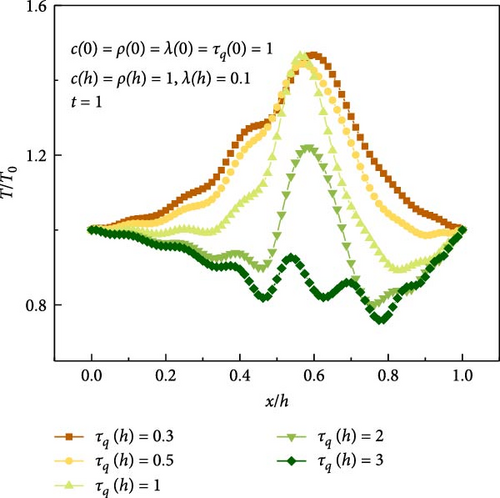
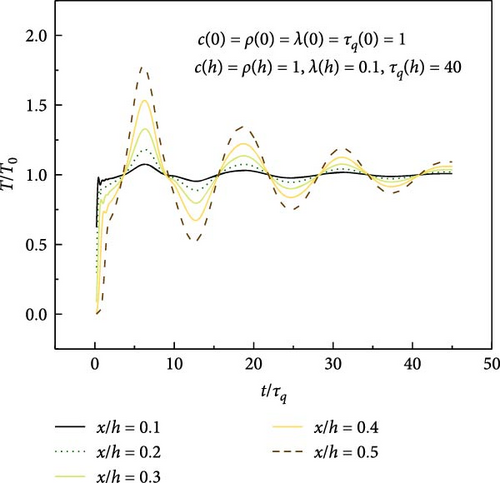
Figure 10 displays the variation of temperature along with the dimensionless time at different positions across the plate, denoted by various ratios of x to h. The value of the ratio varies from 0.1 to 0.5. The overshooting phenomenon of transient temperature becomes significant as the position x/h moves from the lower surface to the center of the plate.

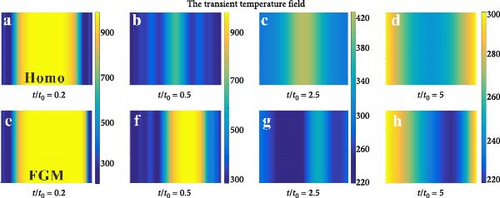
Next, the transient temperature fields are presented in Figure 11 at different times t/t₀ = 0.2, 0.5, 2.5, and 5, respectively. It can be seen that the temperature distributes symmetrically in homogeneous material under symmetrical loading, and significant temperature fluctuations can be observed; temperature in FGMs propagates faster on the side with higher thermal conductivity. It should be noted that the present method can solve the transient temperature fields based on either hyperbolic heat conduction theory or Fourier heat conduction theory.

4.3. Thermal Stress Intensity Factor (TSIF) in an FGM Plate With Parallel Cracks

The TSIF is one of the key fracture parameters to characterize the singular stress field around the crack tip for thermal fracture problems. A crack IEIM [38, 54] is employed to extract the TSIF of FGM. An FGM plate of infinite length featuring parallel edge cracks is shown in Figure 12. Here, S and N are the crack spacing and crack number in the FGM plate, respectively. It is noted that the boundary temperature conditions are the same as those in Equation (30) of Section 4.1, and

()

for the mechanical conditions.

The strong transient, TSIFs can be obtained through the transient IEIM. In this method, the actual fields (u^aux(t), σ^aux(t), ε^aux(t)) and the auxiliary fields (u(t), σ(t), and ε(t)) substituted into the J integral to yield a interaction part. The interaction part I(t) can be expressed as that in Zhang et al., Yu et al., and Yu et al. [55–57] are adopted. Then we have

()

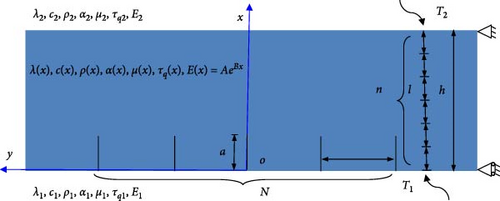
Here, K_I and K_II are Mode-I TSIF and Mode-II TSIFs, respectively, for the plane stress case, and for the plane strain case.

Then, taking

and

to be {1, 0} and {0, 1}, respectively, the TSIFs can be solved from Equation (35). The mixed-mode, transient TSIFs can be determined as follows:

()

It should be pointed out that the crack at y = 0 is not affected by the boundary conditions when N takes an odd number. Therefore, the present work selects the crack at y = 0 to represent the parallel cracks in the FGM plate in the following calculations. The TSIFs can be normalized by . The normalized time is defined as t/t₀ = λ₁t/(c₁ρ₁h²). The thermomechanical parameters are shown in Table 2.

Table 2. Thermomechanical properties of the model materials given in [58].

Materials	Specific heat (J/kgK)	Thermal conductivity (W/(Mk))	Coefficient of thermal expansion (×10⁻⁶/K)	Density (kg/m³)	Young’ modulus (GPa)	Poisson’s ratio
x = 0	c₀ = 456.7	λ₀ = 2.09	α₀ = 10.0	ρ₀ = 5331	E₀ = 151.0	v₀ = 0.33
x = h	c₁ = 537.0	λ₁ = 7.5	α₁ = 9.5	ρ₁ = 4420	E₁ = 116.7	v₁ = 0.33

To verify the IEIM, the current results are compared to the analytical results given by Noda and Guo [58], as shown in Figure 13. Perfect agreement between the results of the current method and analytical results verifies the correctness of the IEIM.

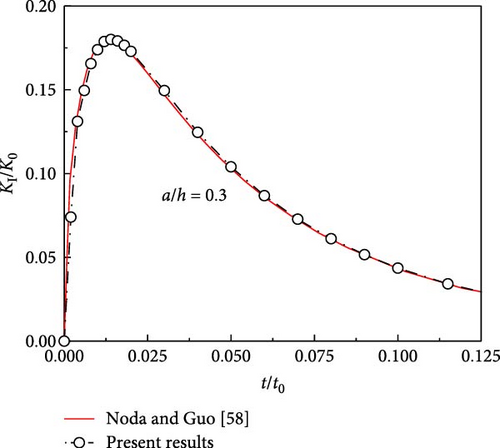
Figure 14 displays the relationship between the TSIF and plate thickness. It can be observed that the TSIF increases with the decreasing thickness, and there are some disturbances in the TSIF after the peak for small-thickness plates, which is caused by the thermal relaxation time. The parallel cracks still alternate between opening and closing after peak value when h = 5 l, so that the TSIFs fluctuate between positive and negative values.

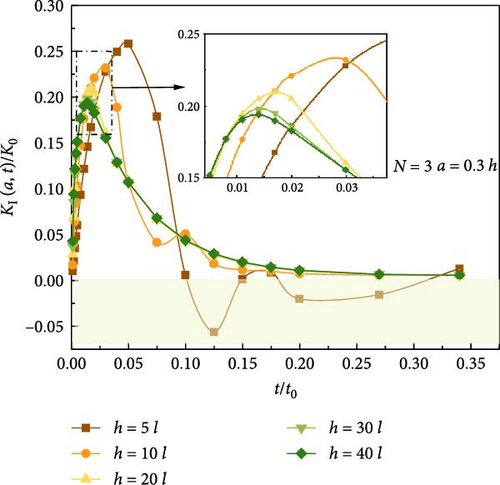
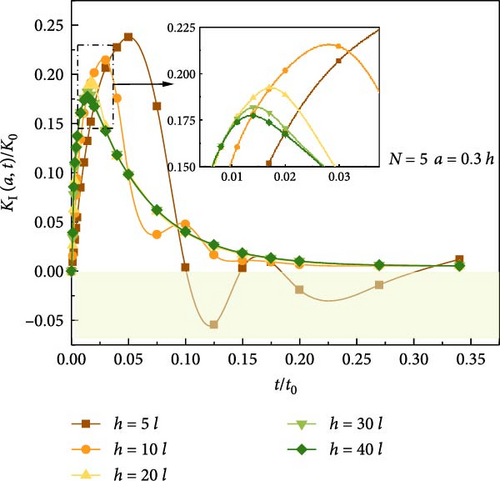
Next, the influence of parallel crack spacing on the TSIF is shown in Figure 15. It can be observed that as the crack spacing decreases, the value of the TSIF decreases. Therefore, the occurrence of multiple parallel cracks may improve the fracture performance of the material.

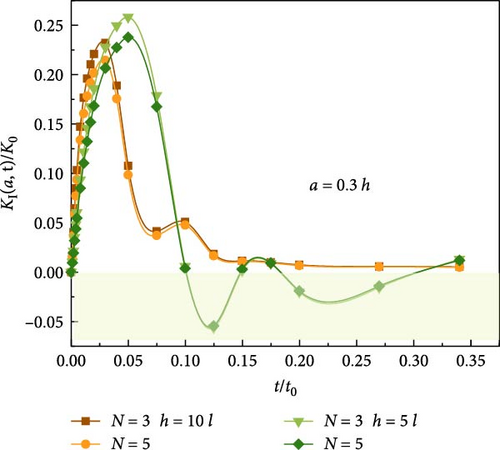
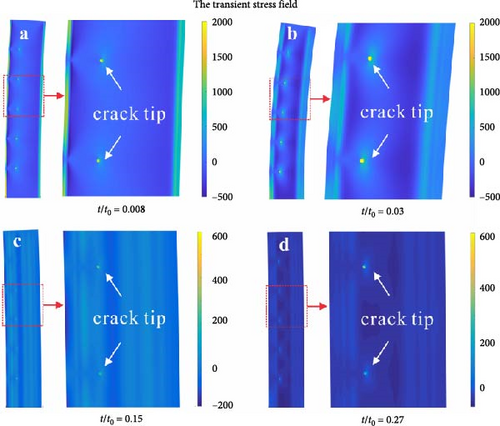
Figure 16 displays the transient stress field in the crack tip region of an FGM plate with parallel cracks (N = 5, a = 0.3 h) under transient thermal shock based on hyperbolic heat conduction. It is observed that the stress field exhibits obvious fluctuations because of the influence of thermal waves, and the fluctuations are more significant at the edges of the plate in the early stage of thermal shock, which is because the hyperbolic heat conduction is more suitable for small-sized spaces and short time.

The transient temperature field in nonhomogeneous materials is solved by the present scheme which can directly solve the second-order differential equation, without the need to convert it into a pair of first-order differential equations. As an example, the numerical results of FGM indicate that the transient temperature can be efficiently obtained, and obvious temperature overshooting occurs when considering the finite speed of heat propagation. Therefore, the present method can be applied to calculate the transient temperature in nonhomogeneous materials and can be combined with other methods to effectively deal with transient thermal fracture problems.

5. Conclusions

In this paper, a new finite element scheme using the Newmark integral method is provided for the computation of strong transient temperature based on hyperbolic heat conduction theories. The Newmark integral method enables the direct solution of a second-order differential equation of heat conduction. This study highlights significant scientific and industrial contributions, particularly in thermal analysis and fracture mechanics of nonhomogeneous materials under extreme thermal conditions. The novel finite element scheme using the Newmark integral method enhances transient temperature computation with improved efficiency, stability, and accuracy.

Industrially, phenomena like thermal wavefronts and dynamic overshooting emphasize the need for hyperbolic heat conduction theory over Fourier heat conduction in high-stress environments, crucial for aerospace, nuclear, and energy applications. The compatibility of the method with interaction energy integration extends its use in thermal fracture analysis and structural integrity assessment. This work provides a solid foundation for design and optimization of materials for extreme thermal environments. The following conclusions can be drawn from the current work:

1.
The new finite element scheme is much more convenient for application than other available numerical methods. The numerical results of the transient thermal response agree very well with the theoretical results under thermal shock loading. The Newmark integral method for strong transient temperature shows excellent stability and accuracy, which is the major contribution of the present work.
2.
The overshooting phenomenon and the thermal wavefronts of transient temperature could be observed in nonhomogeneous materials based on the hyperbolic heat conduction theory, which is different from those in Fourier heat conduction. It is necessary to consider these effects in engineering applications under extreme thermal environments.
3.
By combining this present method with the interaction energy integration method, the fracture parameters can be effectively extracted. Therefore, this method can be readily combined with other methods to deal with transient thermal fracture problems.

Nomenclature

q:: Heat flux vector
λ:: Heat conductivity
α:: Thermal expansion coefficient
c:: Specific heat
E:: Young’s modulus
ρ:: Density
T:: Temperature
τ_q:: Relaxation time of heat flux
Δt:: Time step
β, γ:: Precision and stability parameter
l:: Characteristic length parameter
κ:: Thermal diffusivity
N:: Crack number
K:: TSIFs
μ:: Shear modulus
s:: Crack spacing
t₀:: Normalized time
a:: Crack length
h:: Thickness of the FGM plate.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Yanyan Zhang: conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing–original draft, writing–review and editing, visualization. Tao Zheng: conceptualization, methodology, writing–original draft. Liangzhong Ao: writing–review and editing, funding acquisition. Shanqiao Huang: software. Zengtao Chen: formal analysis, investigation, resources, writing–review and editing, supervision, project administration, funding acquisition.

Funding

This work is supported by the Foreign Expert Program of the Ministry of Science and Technology (No. G2023203001L), the National Natural Science Foundation of China (No. 62406207), the Science and Technology Research Projects of Sichuan Province (No. 2023ZYD0135), and the Fundamental Research Funds for the Central Universities (No. ZJ2023-005, 25CAFUC01011, 25CAFUC04028, 25CAFUC09001).

Acknowledgments

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Sundar R. and Ganesh P., Laser Shock Peening and its Applications: A Review, Lasers in Manufacturing and Materials Processing. (2019) 6, no. 4, 424–463, https://doi.org/10.1007/s40516-019-00098-8.
10.1007/s40516-019-00098-8
Google Scholar
2 Atkin R. J. and Fox N., The Dependence of Thermal Shock Wave Velocity on Heat Flux in Helium II, Journal of Physics C: Solid State Physics. (1984) 17, no. 7, 1191–1198, https://doi.org/10.1088/0022-3719/17/7/013, 2-s2.0-2242487835.
10.1088/0022-3719/17/7/013
CAS Google Scholar
3 Tzou D. Y., The Generalized Lagging Response in Small-Scale and High-Rate Heating, International Journal of Heat and Mass Transfer. (1995) 38, no. 17, 3231–3240, https://doi.org/10.1016/0017-9310(95)00052-B, 2-s2.0-0029410955.
10.1016/0017-9310(95)00052-B
CAS Web of Science® Google Scholar
4 Tzou D. Y., Macro-to Micro-Scale Heat Transfer: the Lagging Behavior, 1996, CRC Press, Boca Raton.
Google Scholar
5 Chen Z. T. and Akbarzadeh A., Advanced Thermal Stress Analysis of Smart Materials and Structures, 2020, Springer International Publishing, Structural Integrity.
10.1007/978-3-030-25201-4
Google Scholar
6 Cattaneo C., Sur une Forme de l’equation de la Chaleur Eliminant la Paradoxe d’une Propagation Instantantee, Comptes Rendus de l’Académie des Sciences. (1958) 247, 431–433.
Google Scholar
7 Vernotte P., Les Paradoxes de la Theorie Continue de l’equation de la Chaleur, Comptes Rendus de l’Académie des Sciences. (1958) 246, 3154–3155.
Google Scholar
8 Ozisik M. N. and Tzou D. Y., On the Wave Theory in Heat Conduction, Journal of Heat Transfer. (1994) 116, no. 3, 526–535, https://doi.org/10.1115/1.2910903, 2-s2.0-0028039735.
10.1115/1.2910903
CAS Web of Science® Google Scholar
9 Wang B. L. and Han J. C., Non-Fourier Heat Conduction in Layered Composite Materials With an Interface Crack, International Journal of Engineering Science. (2012) 55, 66–75, https://doi.org/10.1016/j.ijengsci.2012.02.006, 2-s2.0-84859363502.
10.1016/j.ijengsci.2012.02.006
Web of Science® Google Scholar
10 Guo S. L., Zhang Y. X., Wang K. F., Wang B. L., and Zhang C. W., Effects of Non-Fourier Heat Conduction and Surface Heating Rate on Thermoelastic Waves in Semi-Infinite Ceramics Subject to Thermal Shock, Ceramics International. (2021) 47, no. 12, 17494–17501, https://doi.org/10.1016/j.ceramint.2021.03.067.
10.1016/j.ceramint.2021.03.067
CAS Web of Science® Google Scholar
11 Yang W. Z., Pourasghar A., and Chen Z. T., Non-Fourier Thermal Fracture Analysis of a Griffith Interface Crack in Orthotropic Functionally Graded Coating/Substrate Structure, Applied Mathematical Modelling. (2022) 104, 548–566, https://doi.org/10.1016/j.apm.2021.12.006.
10.1016/j.apm.2021.12.006
Web of Science® Google Scholar
12 Jin Z. H. and Paulino G. H., Transient Thermal Stress Analysis of an Edge Crack in a Functionally Graded Material, International Journal of Fracture. (2001) 107, no. 1, 73–98, https://doi.org/10.1023/A:1026583903046, 2-s2.0-0035136151.
10.1023/A:1026583903046
CAS Web of Science® Google Scholar
13 Babaei M. H. and Chen Z., Transient Hyperbolic Heat Conduction in a Functionally Graded Hollow Cylinder, Journal of Thermophysics and Heat Transfer. (2010) 24, no. 2, 325–330, https://doi.org/10.2514/1.41368, 2-s2.0-77951550030.
10.2514/1.41368
CAS Web of Science® Google Scholar
14 Akbarzadeh A. H. and Chen Z. T., Heat Conduction in One-Dimensional Functionally Graded Media Based on the Dual-Phase-Lag Theory, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. (2013) 227, no. 4, 744–759, https://doi.org/10.1177/0954406212456651, 2-s2.0-84880838902.
10.1177/0954406212456651
Web of Science® Google Scholar
15 Xue Z. N., Tian X. G., and Liu J. L., Thermal Shock Fracture of a Crack in a Functionally Gradient Half-Space Based on the Memory-Dependent Heat Conduction Model, Applied Mathematical Modelling. (2020) 80, 840–858, https://doi.org/10.1016/j.apm.2019.11.021.
10.1016/j.apm.2019.11.021
Web of Science® Google Scholar
16 Fu J. W., Akbarzadeh A. H., Chen Z. T., Qian L. F., and Pasini D., Non-Fourier Heat Conduction in a Sandwich Panel With a Cracked Foam Core, International Journal of Thermal Sciences. (2016) 102, 263–273, https://doi.org/10.1016/j.ijthermalsci.2015.11.011, 2-s2.0-84953258318.
10.1016/j.ijthermalsci.2015.11.011
Web of Science® Google Scholar
17 Huang S. Q., Guo L. C., Zhang L., and Zhang Y. Y., The Interface Crack Problem Under Steady Heat Flux for a Functionally Graded Coating-Substrate Structure With General Coating Properties, Theoretical and Applied Fracture Mechanics. (2020) 109, 102675.
10.1016/j.tafmec.2020.102675
Web of Science® Google Scholar
18 Noda N., Thermal Stresses in Functionally Graded Materials, Journal of Thermal Stresses. (1999) 22, no. 4-5, 477–512, https://doi.org/10.1080/014957399280841, 2-s2.0-0032631352.
10.1080/014957399280841
Web of Science® Google Scholar
19 Guo L. C. and Noda N., Investigation Methods for Thermal Shock Crack Problems of Functionally Graded Materials-Part I: Analytical Method, Journal of Thermal Stresses. (2014) 37, 292–324.
10.1080/01495739.2013.839853
Web of Science® Google Scholar
20 Zhang Y. Y., Guo L. C., and Noda N., Investigation Methods for Thermal Shock Crack Problems of Functionally Graded Materials-Part II: Combined Analytical-Numerical Method, Journal of Thermal Stresses. (2014) 37, no. 3, 325–339, https://doi.org/10.1080/01495739.2013.839854, 2-s2.0-84897746432.
10.1080/01495739.2013.839854
CAS Web of Science® Google Scholar
21 Wu B., Zhu B.-Y., Song H.-M., and Huang Q.-A., Theoretical Analysis of Two Collinear Cracks in an Orthotropic Solid Under Linear Thermal Flux and Linear Mechanical Load, Advances in Mathematical Physics. (2022) 2022, 9, https://doi.org/10.1155/2022/8371954, 8371954.
10.1155/2022/8371954
Web of Science® Google Scholar
22 Nourazar M., Yang W., and Chen Z., Dynamic Thermal Response of Multiple Parallel Cracks in a Half Plane Under General Transient Thermal Loading, Advances in Mathematical Physics. (2024) 2024, 12, https://doi.org/10.1155/2024/1250343, 1250343.
10.1155/2024/1250343
Web of Science® Google Scholar
23 Hu Q., Liu W., Song Y., Li H., Zhao C., and Xiao M., Influence of Solid Solution Treatment on Fatigue Crack Propagation Behavior in the Thickness Direction of, 2519A, Aluminum Alloy Thick Plates, Engineering Fracture Mechanics. (2024) 302, https://doi.org/10.1016/j.engfracmech.2024.110069, 110069.
10.1016/j.engfracmech.2024.110069
Web of Science® Google Scholar
24 Huang M., Wang L., and Wang C., et al.Optimizing Crack Initiation Energy in Austenitic Steel via Controlled Martensitic Transformation, Journal of Materials Science & Technology. (2024) 198, 231–242, https://doi.org/10.1016/j.jmst.2024.02.019.
10.1016/j.jmst.2024.02.019
CAS Web of Science® Google Scholar
25 Wang X., Zhang Y., Wen M., and Mang H. A., A Simple Hybrid Linear and Nonlinear Interpolation Finite Element for the Adaptive Cracking Elements Method, Finite Elements in Analysis and Design. (2025) 244, https://doi.org/10.1016/j.finel.2024.104295, 104295.
10.1016/j.finel.2024.104295
Web of Science® Google Scholar
26 Balci M. N. and Yalcin M. A., Delamination Behavior of Elastic Surface Coatings Subjected to Thermal Shock, Procedia Structural Integrity. (2024) 61, 331–339, https://doi.org/10.1016/j.prostr.2024.06.042.
10.1016/j.prostr.2024.06.042
Google Scholar
27 Yildirim B., Dag S., and Erdogan F., Three Dimensional Fracture Analysis of FGM Coatings Under Thermomechanical Loading, International Journal of Fracture. (2005) 132, no. 4, 371–397, https://doi.org/10.1007/s10704-005-2527-9, 2-s2.0-23644446135.
10.1007/s10704-005-2527-9
Web of Science® Google Scholar
28 Santra S. and Behera R., Simultaneous Space-Time Hermite Wavelet Method for Time-Fractional Nonlinear Weakly Singular Integro-Partial Differential Equations, Communications in Nonlinear Science and Numerical Simulation. (2025) 140, https://doi.org/10.1016/j.cnsns.2024.108324, 108324.
10.1016/j.cnsns.2024.108324
Web of Science® Google Scholar
29 Santra S., Analysis of a Higher-Order Scheme for Multi-Term Time-Fractional Integro-Partial Differential Equations With Multi-Term Weakly Singular Kernels, Numerical Algorithms. (2024) 1–47, https://doi.org/10.1007/s11075-024-01927-4.
10.1007/s11075-024-01927-4
Web of Science® Google Scholar
30 Santra S. and Mohapatra J., An Efficient Computational Approach for the Solution of Time-Space Fractional Diffusion Equation, International Journal of Modelling and Simulation. (2023) 43, no. 4, 393–405, https://doi.org/10.1080/02286203.2022.2085976.
10.1080/02286203.2022.2085976
Web of Science® Google Scholar
31 Rathish Kumar B. V., Srinivasa Rao P., and Sinha P., A Numerical Study of Performance of a Slider Bearing With Heat Conduction to the Pad, Finite Elements in Analysis and Design. (2001) 37, no. 6-7, 533–547.
10.1016/S0168-874X(00)00062-7
Google Scholar
32 Su F., Xu Z., Dong Q.-L., and Li H.-S., A Second-Order and Two-Scale Computation Method for Heat Conduction Equation With Rapidly Oscillatory Coefficients, Finite Elements in Analysis and Design. (2011) 47, no. 3, 276–280, https://doi.org/10.1016/j.finel.2010.10.010, 2-s2.0-78449250639.
10.1016/j.finel.2010.10.010
Web of Science® Google Scholar
33 Zhang H. W., Yang D. S., Guo X., and Bi J. Y., Multiple Spatial and Temporal Scales Method for Numerical Simulation of Non-Classical Heat Conduction Problems: One Dimensional Case, International Journal of Solids and Structures. (2005) 42, no. 3-4, 877–899, https://doi.org/10.1016/j.ijsolstr.2004.06.054, 2-s2.0-11244264471.
10.1016/j.ijsolstr.2004.06.054
Web of Science® Google Scholar
34 Yasbolaghi R. and Khoei A. R., A Continuum-Atomistic Multi-Scale Analysis of Temperature Field Problems and Its Application in Phononic Nano-Structures, Finite Elements in Analysis and Design. (2022) 198, https://doi.org/10.1016/j.finel.2021.103643, 103643.
10.1016/j.finel.2021.103643
Web of Science® Google Scholar
35 Wang B.-L. and Tian Z.-H., Application of Finite Element-Finite Difference Method to the Determination of Transient Temperature Field in Functionally Graded Materials, Finite Elements in Analysis and Design. (2005) 41, no. 4, 335–349, https://doi.org/10.1016/j.finel.2004.07.001, 2-s2.0-9544243698.
10.1016/j.finel.2004.07.001
CAS Web of Science® Google Scholar
36 Wang B. L., Han J. C., and Sun Y. G., A Finite Element/Finite Difference Scheme for the Non-Classical Heat Conduction and Associated Thermal Stresses, Finite Elements in Analysis and Design. (2012) 50, 201–206, https://doi.org/10.1016/j.finel.2011.09.010, 2-s2.0-84155171083.
10.1016/j.finel.2011.09.010
Web of Science® Google Scholar
37 Zhang Y. Y., Guo L. C., Huang K., Bai X. M., Pang J. C., and Zhang Z. F., A Numerical Method for the Thermal-Shock Crack Problems of Nonhomogeneous Materials With Inclusions Based on an Interaction Energy Integral Method, Engineering Fracture Mechanics. (2018) 190, 159–174, https://doi.org/10.1016/j.engfracmech.2017.11.021, 2-s2.0-85039422157.
10.1016/j.engfracmech.2017.11.021
Web of Science® Google Scholar
38 Zhang Y. Y., Guo L. C., Wang X. L., Shen R. L., and Huang K., Thermal Shock Resistance of Functionally Graded Materials With Mixed-Mode Cracks, International Journal of Solids and Structures. (2019) 164, 202–211, https://doi.org/10.1016/j.ijsolstr.2019.01.012, 2-s2.0-85060339968.
10.1016/j.ijsolstr.2019.01.012
Web of Science® Google Scholar
39 Newmark N. M., A Method of Computation for Structural Dynamics, Journal of the Engineering Mechanics Division. (1959) 85, no. 3, 67–94, https://doi.org/10.1061/JMCEA3.0000098.
10.1061/JMCEA3.0000098
Google Scholar
40 Lindfield G. and Penny J., Numerical Methods, 2019, fourth edition, Academic Press is an imprint of Elsevier, 265–270.
Google Scholar
41 Uchino K. and Debus J. C., Applications of ATILA FEM Software to Smart Materials, 2012, Elsevier.
Google Scholar
42 Barkeshli S., Sabbagh H. A., Radecki D. J., and Melton M., A Novel Implicit Time-Domain Boundary-Integral/Finite-Element Algorithm for Computing Transient Electromagnetic Field Coupling to a Metallic Enclosure, IEEE Transactions on Antennas and Propagation. (1992) 40, no. 10, 1155–1164, https://doi.org/10.1109/8.182447, 2-s2.0-34249280434.
10.1109/8.182447
Web of Science® Google Scholar
43 Gang S. and Bo L., Generalized High-Order Accurate Newmark Method for Head-Disk Interface Dynamics in Magnetic Recording Technology, Finite Elements in Analysis and Design. (1998) 29, no. 2, 87–103, https://doi.org/10.1016/S0168-874X(98)00016-X, 2-s2.0-0032093376.
10.1016/S0168-874X(98)00016-X
Web of Science® Google Scholar
44 Wu J.-Y., Nguyen V. P., Nguyen C. T., Sutula D., Sinaie S., and Bordas S. P. A., Phase-Field Modeling of Fracture, Advances in Applied Mechanics. (2020) 53, 1–183, https://doi.org/10.1016/bs.aams.2019.08.001.
10.1016/bs.aams.2019.08.001
Web of Science® Google Scholar
45 Grange S. and Bertrand D., Implicit Coupling of Heterogeneous and Asynchronous Time-Schemes Using a Primal Approach Based on Velocity Continuity at the Subdomain Interface, Finite Elements in Analysis and Design. (2021) 196, https://doi.org/10.1016/j.finel.2021.103604, 103604.
10.1016/j.finel.2021.103604
Web of Science® Google Scholar
46 Gedney S. D. and Navsariwala U., An Unconditionally Stable Finite Element Time-Domain Solution of the Vector Wave Equation, IEEE Microwave and Guided Wave Letters. (1995) 5, no. 10, 332–334, https://doi.org/10.1109/75.465046, 2-s2.0-0029394166.
10.1109/75.465046
Web of Science® Google Scholar
47 Chung J. and Hulbert G. M., A Time Integration Algorithm for Structural Dynamics With Improved Numerical Dissipation: the Generalized-α Method, Journal of Applied Mechanics. (1993) 60, no. 2, 371–375.
10.1115/1.2900803
Google Scholar
48 Tzou D. Y., Macro-to Microscale Heat Transfer: the Lagging Behavior, 1997, Taylor & Francis.
Google Scholar
49 Jiang R. Q., The Non-Classical Effects Investigation of the Rapid Transient Heat and Mass Diffusions, 2002, Harbin Engineering University, 19–24.
Google Scholar
50 Zhen Z. C., Mechanical Vibration, 1986, China Machine Press, Beijing.
Google Scholar
51 Guo S. L., Wang B. L., and Li J. E., Surface Thermal Shock Fracture and Thermal Crack Growth Behavior of Thin Plates Based on Dual-Phase-Lag Heat Conduction, Theoretical and Applied Fracture Mechanics. (2018) 96, 105–113, https://doi.org/10.1016/j.tafmec.2018.04.007, 2-s2.0-85045769406.
10.1016/j.tafmec.2018.04.007
Web of Science® Google Scholar
52 Chester M., Second Sound in Solids, Physical Review. (1963) 131, no. 5, 2013–2015, https://doi.org/10.1103/PhysRev.131.2013, 2-s2.0-0000172887.
10.1103/PhysRev.131.2013
Google Scholar
53 Yang W. Z. and Chen Z. T., Investigation of the Thermal-Elastic Problem in Cracked Semi-Infinite FGM Under Thermal Shock Using Hyperbolic Heat Conduction Theory, Journal of Thermal Stresses. (2019) 42, no. 8, 993–1010, https://doi.org/10.1080/01495739.2019.1590170, 2-s2.0-85063672383.
10.1080/01495739.2019.1590170
Web of Science® Google Scholar
54 Zhang Y. Y., Chen Z. T., Guo F. N., Zhou T. Y., and Zeng Z. W., Investigation of the Fracture Problem of Functionally Graded Materials With an Inclined Crack Under Strong Transient Thermal Loading, Theoretical and Applied Fracture Mechanics. (2022) 119, https://doi.org/10.1016/j.tafmec.2022.103324, 103324.
10.1016/j.tafmec.2022.103324
Web of Science® Google Scholar
55 Zhang Y. Y., Zhou H. X., Chen Z. T., Wang X. Y., and Guo F. N., Fracture Analysis of a Non-Homogeneous Coating Structure With Dual Interfaces Under Thermal Shock, Engineering Fracture Mechanics. (2022) 269, 108499.
10.1016/j.engfracmech.2022.108499
Web of Science® Google Scholar
56 Yu H. J., Wang J., and Shimada T., et al.An I-Integral Method for Crack-Tip Intensity Factor Variation due to Domain Switching in Ferroelectric Single-Crystals, Journal of the Mechanics and Physics of Solids. (2016) 94, 207–229, https://doi.org/10.1016/j.jmps.2016.04.031, 2-s2.0-84977576298.
10.1016/j.jmps.2016.04.031
CAS Web of Science® Google Scholar
57 Yu H., Wu L., Guo L., He Q., and Du S., Interaction Integral Method for the Interfacial Fracture Problems of Two Nonhomogeneous Materials, Mechanics of Materials. (2010) 42, no. 4, 435–450, https://doi.org/10.1016/j.mechmat.2010.01.001, 2-s2.0-77949264327.
10.1016/j.mechmat.2010.01.001
Web of Science® Google Scholar
58 Noda N. and Guo L.-C., Thermal Shock Analysis for a Functionally Graded Plate With a Surface Crack, Acta Mechanica. (2008) 195, no. 1–4, 157–166, https://doi.org/10.1007/s00707-007-0562-5, 2-s2.0-38749145889.
10.1007/s00707-007-0562-5
Web of Science® Google Scholar

All articles

A Newmark Integral Method in Nonhomogeneous Materials With Parallel Cracks Based on Hyperbolic Heat Conduction

Abstract

1. Introduction

2. Thermal Conduction Equation Under Transient Thermal Loading

3. Numerical Scheme for Strong Transient Temperature