This study explores the impact of Soret and Dufour effects on an magnetohydrodynamics (MHD) variable-viscosity Casson nanofluid over a stretching sheet with heat generation and absorption. The Buongiorno model is employed to incorporate nanoparticle properties such as Brownian motion and thermophoresis. The governing equations are transformed into first-order ordinary differential equations, and an analytical solution is obtained using the homotopy analysis method with the BVPh2.0 package in Mathematica. Numerical results reveal that velocity profiles increase with the Soret and Dufour effects, variable viscosity, Casson characteristics, and heat generation and absorption but decrease with the Lewis number and Forchheimer coefficient. Temperature profiles rise with the Dufour number, heat generation and absorption, and variable viscosity, while they decline with the Se number, Casson factor, and stretching parameter. Similarly, concentration profiles exhibit opposing trends, increasing with the Forchheimer coefficient, Soret number, and Casson factor while decreasing with the Dufour number, variable viscosity, and heat generation and absorption. The results highlight significant parameter-driven variations in transport properties. An increase in the Casson parameter reduces the skin friction coefficient by 40.95%, enhances heat transfer by 15.63%, and decreases mass transfer by 6.72%, indicating a shift toward Newtonian-like behavior. The Darcy number lowers skin friction by 18.44% and boosts heat transfer by 23.03%, confirming improved permeability-driven fluid motion. The magnetic parameter slightly increases skin friction by 0.40%, while the Prandtl number enhances heat transfer by 18.36%. The variable viscosity parameter plays a critical role, reducing skin friction by 28.92%, decreasing heat transfer by 34.32%, and increasing mass transfer by 24.86%. Additionally, the Eckert number significantly reduces heat transfer due to viscous dissipation, whereas the radiation parameter enhances both heat and mass transfer. These findings provide valuable insights into fluid transport mechanisms, with applications in industrial and biomedical systems requiring optimized thermal and mass transport. A comparative analysis with existing literature validates the robustness of the results.

1. Introduction

The study of nanofluids has gained considerable traction in recent years due to their superior thermal conductivity and distinctive properties compared to traditional fluids. Comprising a base fluid and suspended nanoparticles, nanofluids exhibit enhanced thermal characteristics, particularly in thermal conductivity and heat transfer efficiency. Research shows that these fluids can significantly boost the performance of cooling systems and heat exchangers, making them ideal for energy applications [1]. The addition of nanoparticles not only improves the thermophysical properties of the base fluids but also enables innovative solutions in thermal management, such as in energy storage devices [2]. Furthermore, hybrid nanofluids, which incorporate multiple types of nanoparticles, have demonstrated superior thermal and rheological properties compared to single-component nanofluids, thereby expanding their applicability across various engineering fields [1]. Studies on nanoparticle deposition during boiling processes further highlight its influence on surface characteristics and long-term thermal performance, underscoring the potential of nanofluids in enhancing heat transfer [3]. Overall, the versatility and efficiency of nanofluids position them as a pivotal technology for advancing sustainable energy solutions [4].

Casson fluids, recognized for their yield stress behavior, are crucial in numerous industrial applications due to their unique flow properties. Research indicates that the flow dynamics of Casson fluids can be affected by factors such as thermal radiation, chemical reactions, and porous media, which in turn influence their velocity and temperature profiles. For example, increased thermal radiation and porosity have been shown to enhance the velocity profile of Casson fluids, whereas the Casson parameter and magnetohydrodynamics (MHD) effects may reduce velocity [5]. Additionally, incorporating heat generation and viscous dissipation into Casson fluid models reveals a decrease in the skin-friction coefficient and Nusselt number with rising radiation and suction parameters [6]. The inclusion of couple stress in microchannels also improves thermal performance compared to scenarios involving only the Casson parameter [7]. These findings emphasize the complexity and adaptability of Casson fluids in engineering applications [8–10].

MHD is essential for understanding the behavior of electrically conductive fluids in magnetic fields, particularly in complex settings such as astrophysical phenomena, nuclear fusion, and advanced manufacturing. The interaction of plasma flows with magnetic fields can lead to the formation of MHD shock waves and electromagnetic waves, which are critical in various astrophysical contexts, including neutron star collisions and accretion onto black holes [11, 12]. Recent advancements in MHD simulations, such as high-order numerical methods and physics-informed neural networks, have enhanced the accuracy and efficiency of modeling these interactions, leading to better predictions of fluid behavior in turbulent magnetized plasmas [13–15]. Moreover, MHD turbulence significantly impacts processes like star formation and cosmic ray propagation, underscoring its importance in both theoretical and practical applications [16]. Understanding these dynamics is vital for leveraging MHD in technologies such as nuclear fusion and advanced manufacturing processes.

The flow of nanofluids over a stretching sheet is a critical area in fluid mechanics, particularly relevant for applications such as polymer processing and material manufacturing. The stretching of the sheet affects the flow profile, subsequently influencing heat and mass transfer rates [17, 18]. Studies indicate that incorporating nanoparticles, such as copper and aluminum oxide, enhances heat and mass transfer due to the improved thermal conductivity and viscosity of nanofluids [19]. Additionally, factors like heat generation and thermal radiation can significantly alter the thermal boundary layer, with higher heat source parameters resulting in elevated temperature profiles [20]. The influence of magnetic fields and slip conditions is also crucial, as they can dampen fluid velocity while enhancing temperature distribution [21, 22]. Understanding these dynamics is essential for optimizing various engineering processes and ensuring efficient thermal management and material performance.

The effects of heat generation or absorption on the thermal behavior of fluid systems add complexity to heat transfer analyses. For instance, internal heat absorption or generation in a horizontal cavity markedly influences fluid dynamics and heat transfer processes, as numerical simulations reveal alterations in the Nusselt number and flow characteristics [23]. Similarly, the heat generation parameter enhances thermal characteristics in mixed convection scenarios, leading to improved heat transfer rates [24]. In non-Newtonian fluids, the interplay between heat generation and magnetic fields can cause significant variations in thermal performance, with studies indicating that heat generation can substantially increase the thermal performance index [25]. Furthermore, the effects of heat generation and radiation on unsteady laminar flows around geometries like truncated cones illustrate the critical role of these parameters in modifying skin friction and heat transfer rates [26]. Thus, comprehending these interactions is vital for optimizing thermal systems.

The Soret and Dufour effects notably influence fluid dynamics, particularly in heat and mass transfer processes. The Soret effect, related to thermal diffusion, enhances the concentration profile of a fluid as the temperature gradient increases, while the Dufour effect, or diffusion-thermo, leads to a decrease in the temperature profile with rising concentration differences [27]. Various studies have shown that increasing the Soret number elevates fluid velocity and concentration profiles, whereas the Dufour number tends to raise fluid temperature [28]. The impacts of Soret and Dufour in nanofluids increase skin friction and Nusselt numbers, leading to higher heat transfer rates [29]. The interplay of these effects is crucial in applications such as cooling processes and chemical engineering, where precise control over heat and mass transfer is essential [30, 31]. Overall, understanding these effects is vital for optimizing fluid flow in industrial applications.

Recent research on Casson nanofluids has investigated various conditions and geometries, showcasing their versatility in thermal applications. For instance, Alnahdi and Gul [32] investigated the flow of Casson hybrid nanofluids over a Riga plate, pointing out their enhanced heat transfer features due to the inclusion of single- and multi-walled carbon nanotubes, which are critical for drug delivery systems. Mohamad et al. [33] examined the stability of Casson nanofluid flow in a permeable layer, revealing how through flow can regulate convective motions, vital for heat transfer efficiency in thermal systems. Additionally, Poply et al. [34] analyzed melting heat transfer in a Casson nanofluid across a stretching sheet, adding to the understanding of cooling systems. El Harfouf et al. [35] studied squeezing flow between parallel plates with thermophoretic effects, while Soomro et al. [36] studied MHD flow past a stretching cylinder, demonstrating Casson nanofluids’ diverse applications in industrial processes. Nagari et al. [37] researched how thermal radiation and Joule heating impact the flow of variable viscosity Casson nanofluid over a stretching sheet in Darcy-Forchheimer porous media.

Based on the literature reviewed above, this study presents novel contributions to MHD Casson nanofluid flow by investigating the combined effects of the Soret and Dufour effects, thermal radiation, and Joule heating on heat and mass transfer in MHD variable viscosity Casson nanofluid flow over a stretching sheet with heat generation/absorption. The novelty of this work lies in the systematic incorporation of these effects, which have been largely unexplored in previous research, thereby offering a more comprehensive understanding of the complex heat and mass transfer phenomena in nanofluid flows. Furthermore, the study extends the work of Nagari et al. [37] by including the Soret and Dufour effects, along with heat source/sink conditions, significantly enhancing the model’s accuracy and relevance in practical applications. The primary objectives of this research are as follows:

1.
Investigate the impact of Soret and Dufour effects on MHD variable viscosity Casson nanofluid flow.
2.
Extend existing models by incorporating thermal radiation and Joule heating.
3.
Employ the homotopy analysis method (HAM) with Mathematica and BVPh2.0 to solve the governing equations.
4.
Provide insights that can aid in the optimization of industrial processes and technologies involving heat and mass transfer.

By using HAM, the governing equations are solved efficiently, and the results are validated against existing literature, demonstrating strong agreement. The findings offer valuable insights that contribute to enhancing the efficiency and performance of systems and processes where heat and mass transfer are critical, such as in cooling systems, energy systems, and material processing. This research provides a unique, in-depth analysis of the combined effects of multiple physical phenomena, making it an important step forward in the study of nanofluids.

2. Mathematical Modeling of the Problem

2.1. The Governing Equations

Within the realm of an incompressible and isotropic Casson fluid, the rheological equation governs the behavior of a steady, incompressible two-dimensional laminar boundary layer encountering Soret–Dufour effects in an MHD variable viscosity Casson nanofluid passing over a stretching surface in the presence of heat generation/absorption. The flow model illustrated in Figure 1 incorporates a comprehensive range of mass and heat transfer mechanisms, including thermophoresis, Brownian motion, viscous dissipation, chemical reaction, Soret and Dufour effects, thermal radiation, variable viscosity, heat generation/absorption, and magnetic dissipation. The velocity components u and v are aligned along the x- and y-axes, respectively, while the parameters T_∞, U_∞, and C_∞ represent the ambient temperature, velocity, and concentration, respectively.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Physical geometry and flow model.

Incorporating the Buongiorno model, which accounts for the effects of Brownian motion and thermophoresis, this study investigates the enhanced transport properties of the nanofluid. The model considers the diffusion of nanoparticles due to Brownian motion, as well as the migration of nanoparticles in the direction of the temperature gradient due to thermophoresis. This addition allows for a more accurate description of the nanofluid’s behavior in the context of heat and mass transfer processes. The boundary conditions for the MHD variable-viscosity Casson nanofluid over a stretching sheet are defined to capture the behavior of fluid dynamics, heat, and mass transfer. At the surface of the sheet, the velocity component u(x, 0) is set as bx, indicating the stretching velocity, and the normal velocity component v(x, 0) is zero, ensuring no fluid penetration. The temperature at the sheet surface is prescribed as T_w, and the concentration at the surface is C_w, both of which reflect the thermal and concentration conditions imposed on the fluid. As the fluid moves far from the sheet, the velocity approaches the free-stream value U_∞(x) = ax, while the temperature and concentration approach their ambient values T_∞ and C_∞, respectively, ensuring that the fluid returns to a stable state at infinity. These boundary conditions provide a realistic representation of the system, incorporating the effects of Soret–Dufour phenomena, thermal radiation, Joule heating, Brownian motion, and thermophoresis on the nanofluid flow. They also ensure that the boundary layer equations remain well-posed, making it possible to study the heat and mass transfer characteristics of the nanofluid in various engineering and industrial applications, such as cooling systems, material processing, and biomedical applications.

The temperature-dependent viscosity of the nanofluid is expressed as follows [38]:

()

where

and

are constants. Here, r is the viscosity variation coefficient, with a < 0 for gases and a > 0 for liquids.

For incompressible and isotropic Casson fluid flow, the rheological equation is given by the following equation [39–41].

()

Here, P_y = e_ij · e_ji, where e_ij signifies the deformation rate at the (i, j)th component, and P_y represents the fluid stress yield. Additionally, π is the square of the deformation rate component, while π_c is the critical value of this product. Similarly, μ_B stands for the plastic viscosity of the non-Newtonian fluid. Assuming π < π_c, Equation (2) transforms to:

()

where

denotes the Casson nanofluid parameter and

Therefore, by integrating the mentioned assumptions and incorporating the impacts of Soret–Dufour on boundary layer equations in the context of heat generation/absorption past a stretching surface, the governing partial differential equations (PDEs) for continuity, energy, and concentration are structured as follows [37]:

()

With the following boundary conditions, following [38, 42–44]:

()

Here, a and b are positive constants with dimensions of inverse time. The parameters defined as follows represent various characteristics: ρ for nanofluid density, for the ratio of nanoparticle to base fluid heat capacity, D_b for Brownian diffusion, D_T for thermophoretic diffusion, C_P for the specific heat capacity of the nanofluid at constant pressure, γ for chemical reaction, k for thermal conductivity, β for Casson nanofluid behavior, σ for electrical conductivity, K for Darcy porous medium effects, Q_g denotes the heat generation/absorption coefficient, C_s for concentration susceptibility, K_T for thermal diffusion ratio, D_m for mass diffusivity, k^∗ for mean absorption coefficient, σ ^∗ for Stefan–Boltzman constant, and F_c for Forchheimer porous media behaviors.

Taking dimensionless variables, Equations (4)–(7) can be transferred to nondimensional form to obtain similar solutions [37, 43, 45]:

()

Stream function can be given as follows:

()

Dimensionless form of variable viscosity: where, θ_r is the fluid viscosity parameter, μ_∞ is the fluid dynamic viscosity.

The transformed equations can be presented as follows:

()

With the dimensionless boundary conditions:

()

where the Darcy number (

), the chemical reaction parameter (

), the Eckert number (

), the Forchheimer (second-order porous resistance) parameter (

), the Brownian motion factor (

), the thermophoretic parameter (

), the Prandtl number (

), the radiation parameter (

), Lewis number (

), the magnetic parameter (

), the stretching (velocity ratio) parameter (

), the Dufournumber (

), the Soretnumber (

), and heat generation/absorption parameter (

2.2. Physical Quantities of Engineering

The quantities under scrutiny in this study encompass the drag coefficient, local Nusselt number (wall heat transfer rate), and local Sherwood number (wall mass transfer). Consequently, the nondimensional representations of these parameters are outlined as follows [37, 38]:

()

Equation (15) simplify as follows:

()

where

and

represent the local Reynolds numbers for wall friction and the rate of mass and heat transfer, respectively. Furthermore, the percentage change in them is calculated using the formula:

where P₁ is the value of the physical quantity at the low parameter and P₂ is the value of the physical quantity at the high parameter.

3. Numerical Solutions

The HAM, known as the Homotopy Analysis Method, is utilized in various research to address boundary layer flow problems, showcasing its effectiveness as a semianalytical method. For instance, it has been effectively applied to obtain semianalytical solutions for thermal convection boundary layer flow of incompressible micropolar fluids, incorporating factors like viscous dissipation and heat sink effects, which are crucial in polymer coating applications [46]. Furthermore, HAM has been used to obtain mathematical expressions for velocity and heat transfer in boundary layer flows with thermal radiation, demonstrating its ability to handle nonlinear boundary value problems [47]. The method has also been employed in MHD studies, revealing the influence of parameters such as magnetic and Prandtl numbers on flow characteristics [48]. Furthermore, the BVPh2.0 package can facilitate the implementation of HAM, allowing for efficient computation of solutions in complex boundary layer scenarios involving nanofluids and viscoelastic fluids [49].

Employing the HAM allowed us to derive the analytic solutions for Equations (11)–(13) with the prescribed boundary conditions (14), using selected initial guesses and linear operators for the functions f, θ, and ϕ:

()

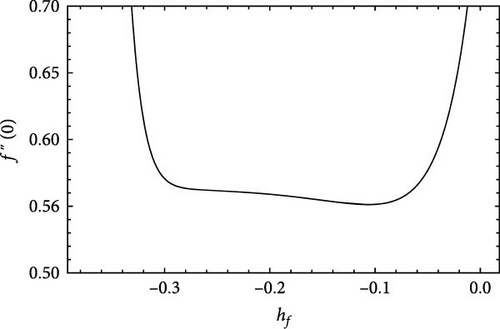
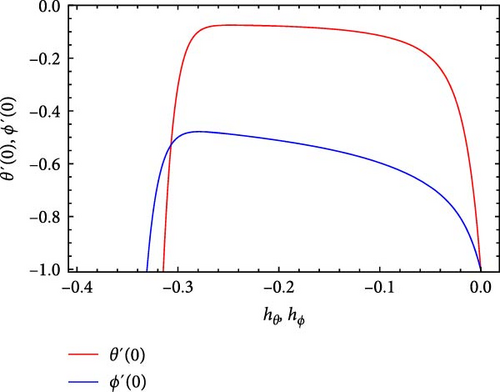
We denote the nonzero auxiliary parameters for the functions f, θ and ϕ by h_f, h_θ and h_ϕ respectively. Given the Equations (17) and (18), the higher order deformation equations are formulated which are solved by symbolic computational software Mathematica. The admissible values of the auxiliary parameters can be determined from the line segment parallel to h-axis in Figure 2. It can be seen that the permissible range of values of h_f, h_θ, and h_ϕ are −0.28 ≤ h_f ≤ −0.08, −0.27 ≤ h_θ ≤ −0.06, and −0.28 ≤ h_ϕ ≤ −0.07, respectively. In addition, the governing differential system has also been solved numerically through the Mathematica software.

4. Results and Discussions

The interactive influences of nanofluid parameters (thermophoresis and Brownian motion parameters) along with the Casson parameter, porous medium, viscous dissipation, heat generation/absorption parameter, Soret number, Dufour number, magnetic field, thermal radiation, and variable viscosity parameters on the velocity, temperature, solutal, wall friction, and Sherwood number past a stretching sheet were investigated through numerical computations. The range of parameters used in this article is as follows: 0 ≤ F ≤ 20, 0.1 ≤ β < ∞, 0 ≤ De ≤ 40, 1 ≤ Da ≤ ∞, 0 ≤ M ≤ 10, 1 ≤ θ_r < ∞, 0 ≤ R ≤ 10, 0.1 ≤ Nb ≤ 12, 0 ≤ Nt ≤ 30, 0 ≤ γ₁ ≤ 10, 0.62 ≤ Pr ≤ 10, 0 ≤ Ec ≤ 12, 0.1 ≤ λ ≤ 1, −10 ≤ q ≤ 10, 0 ≤ Se ≤ 12, and 0 ≤ Le ≤ 12. The numerical solution obtained matches the findings presented in an earlier publication, as it is validated by comparing the local wall friction in a specific manner, as shown in Table 1.

Table 1. The comparison of numerical values of drag force for different values of λ with β = Da = θr = ∞, F = M = R = q = De = Se = 0.

λ	Duguma et al. [43]	Nagari et al. [37]	Present result
0.0	1.232587650	1.232587650354941	1.232587650354534
0.2	1.051132999	1.051132999807877	1.051139998064241
0.5	0.713294956	0.713294495427695	0.713294495427514
1.0	0.000000000	0.000000000000000	0.000000000000000

Table 2 presents numerical results illustrating the effects of key physical parameters on skin friction, heat transfer, and mass transfer rates in Casson nanofluid flow over a stretching sheet in the presence of heat generation/absorption. The results indicate that increasing the Casson parameter (β) leads to a significant reduction in the skin friction coefficient by 40.95%, suggesting that as the fluid transitions to a more Newtonian-like behavior, flow resistance decreases. Simultaneously, heat transfer is enhanced by 15.63%, highlighting improved thermal convection, whereas mass transfer is reduced by 6.72%, indicating weakened species diffusion. Similarly, a rise in the Darcy number (Da) lowers skin friction by 18.44% and enhances heat transfer by 23.03%, confirming that higher permeability facilitates fluid movement and improves thermal transport. The magnetic parameter (M) marginally increases skin friction by 0.40%, aligning with the influence of Lorentz forces, while the Prandtl number (Pr) leads to an 18.36% rise in heat transfer. Moreover, the variable viscosity parameter (θ_r) significantly affects all transport properties, reducing skin friction by 28.92% and heat transfer by 34.32% while increasing mass transfer by 24.86%, demonstrating the critical role of temperature-dependent viscosity in fluid flow behavior. Other parameters, such as the Eckert number (Ec), show a drastic reduction in heat transfer due to the dominance of viscous dissipation, while the radiation parameter (R) enhances both heat and mass transfer. These findings provide insights into optimizing fluid transport properties for industrial and biomedical applications, ensuring improved thermal and mass transport efficiency under different physical conditions.

Table 2. The impacts of different parameters on dimensionless shear stress, heat transfer rate, and mass transfer rate when Pr = 0.72, Da = 3, θ_r = R = 3, λ = 0.2, β = M = F = Nt = Se = q = De = Ec = Le = Nb = 0.1.

Parameters	Diverse values		−(1 + R)θ^′(0)	−ϕ^′(0)
β	0.10	9.86057	0.848531	0.399242
β	0.20	5.82277	1.005730	0.372395
Da	1.00	13.2039	0.602002	1.759040
Da	2.00	10.7690	0.782083	1.638720
F	0.10	9.86057	0.848531	0.399242
F	0.20	9.84383	0.849998	0.399003
M	0.40	9.78120	0.854049	0.398395
M	0.50	9.82095	0.851286	0.398819
λ	0.10	11.0626	0.729911	0.416297
λ	0.20	9.86057	0.848531	0.399242
Pr	0.72	9.86057	0.848531	0.399242
Pr	1.00	9.78861	1.039340	0.382961
Ec	0.10	9.86057	0.848531	0.399242
Ec	0.20	9.90012	0.474840	0.462573
N_t	0.10	9.86057	0.848531	1.596970
N_t	0.20	9.86138	0.828790	1.248130
N_b	0.10	9.86057	0.848531	0.399242
N_b	0.20	9.86373	0.833612	0.441843
Le	0.10	9.86057	0.848531	0.399242
Le	0.20	9.86062	0.847817	0.413823
θ_r	2.00	13.8716	1.292000	0.299985
θ_r	3.00	9.86057	0.848531	0.399242
R	1.00	9.71125	0.610282	0.320892
R	2.00	9.79772	0.767323	0.382259
De	0.10	9.86057	0.848531	1.596970
De	0.20	9.86512	0.820694	1.602800
Se	0.10	9.86057	0.848531	0.399242
Se	0.20	9.86043	0.848328	0.390699
γ₁	0.10	9.86057	0.848531	0.399242
γ₁	0.20	9.86058	0.848272	0.403963
q	0.10	9.86057	0.848531	0.399242
q	0.20	9.87027	0.776448	0.407708

4.1. Velocity Profile With Change of Parameters

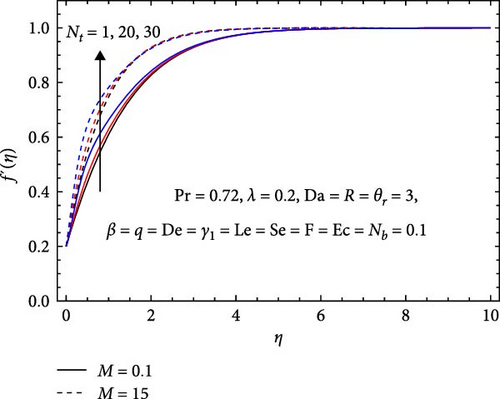
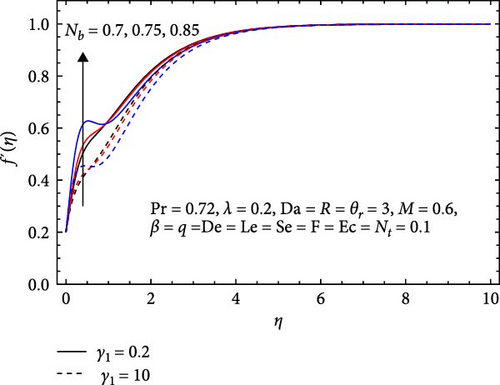
Figures 3–6 depict the influences of different parameters, including the Forchheimer number (F), Casson parameter (β), heat generation/absorption parameter (q), porous media parameter (Da), the stretching parameter (λ), variable viscosity parameter (θ_r), magnetic parameter (M), Eckert number (Ec), Prandtl number (Pr), thermophoresis parameter (N_t), Brownian motion parameter (N_b), Lewis number (Le), chemical reaction parameter (γ₁), Soret number (Se), Dufour number (De), and radiation parameter (R), on the velocity field f^′(η) of the Casson nanofluid flow.

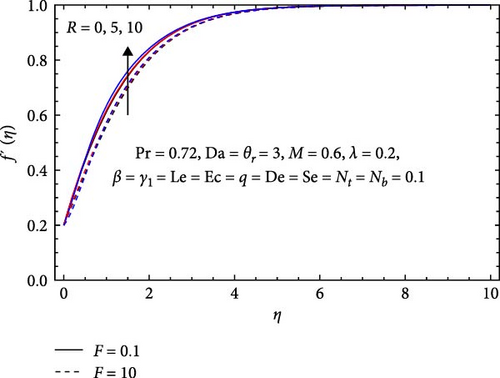
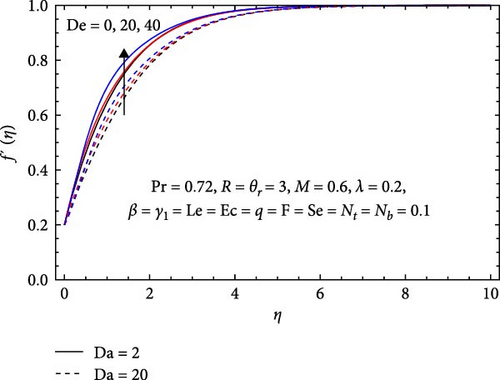
As thermal radiation causes an increase in temperature, the velocity profile in Figure 3a increases with the radiation parameter (R). Consequently, the system experiences reduced viscosity at higher temperatures, lower flow resistance, and higher velocities. On the other hand, as the Forchheimer number (F) increases, indicating that the opposition from the porous medium outweighs the inertial forces, the velocity profile decreases due to a greater obstruction to the fluid’s flow through the porous medium. From Figure 3b, the increase in the velocity profile with increasing Dufour number (De) is primarily due to enhanced mass transfer, reduced viscosity, and the effects of thermal and concentration gradients. These factors collectively contribute to a more dynamic flow regime, leading to higher velocities in the fluid. In contrast, the velocity profile in porous media flow (Darcy flow) drops as the Darcy number (Da) grows because of increasing flow resistance, a greater pressure drop, less permeability, and the predominance of viscous forces over inertial forces.

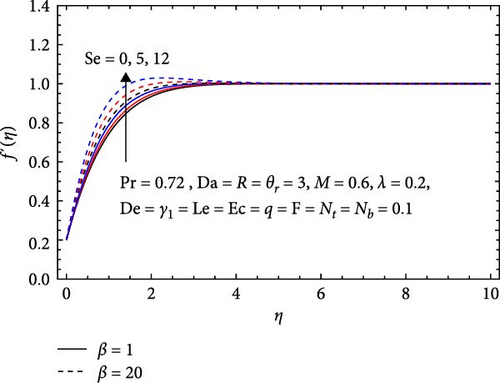
Figure 4a illustrates how the Soret number (Se) and Casson factor (β) affect the velocity profile. Higher velocities in non-Newtonian fluid flow are the result of enhanced yield stress effects, boundary layer dynamics, and shear thinning behavior when the Casson parameter is increased. Moreover, stronger temperature gradients cause the velocity profile to rise with the Soret number, which alters the viscosity and distribution of nanoparticles in the MHD Casson nanofluid flow.

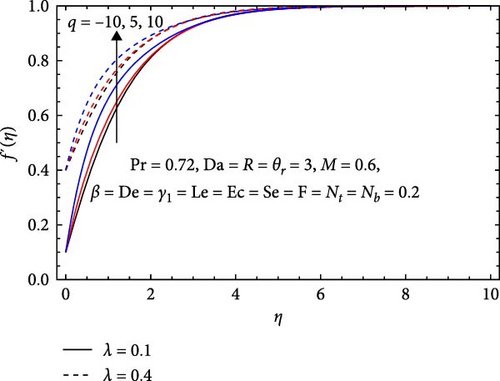
In Figure 4b, the interaction between the stretching parameter (λ) and the heat generation/absorption parameter (q) in the velocity profile is depicted. The velocity profile increases with an increasing stretching parameter due to the stretching effect, which causes the flow field to expand and accelerate. This expansion leads to higher velocities as the flow field is stretched, increasing the fluid’s speed and momentum. Moreover, increasing heat generation/absorption boosts the velocity profile due to thermal expansion, changes in thermophysical properties, enhanced thermal convection, and modifications in boundary layers, leading to higher velocities in the fluid flow.

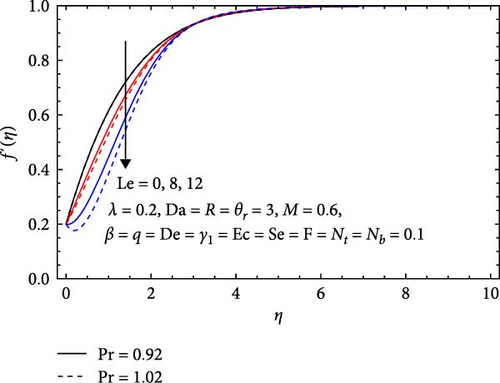
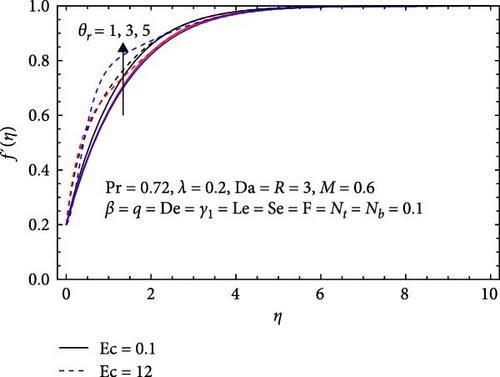
Figure 5a,b showcases the impact of various parameters on the velocity field: Prandtl number (Pr), Lewis number (Le), Eckert number (Ec), and the variable viscosity parameter (θ_r). The velocity profile demonstrates nuanced behaviors with respect to these parameters. As the Prandtl number increases, thermal diffusivity effects overpower momentum diffusivity, leading to a decrease in the velocity profile. Also, the velocity profile diminishes with rising Lewis number as mass diffusivity takes precedence over momentum diffusivity, hindering the fluid’s momentum transport. Whereas, an elevation in the Ec results in an augmented velocity profile due to the heightened influence of kinetic energy compared to thermal energy, driving fluid flow more vigorously. Moreover, an increasing variable viscosity parameter amplifies the velocity profile by reducing the fluid’s resistance to deformation, facilitating smoother flow and higher velocities in the system.

Figure 6a,b visually articulate how the magnetic parameter (M), thermophoresis parameter (N_t), chemical reaction parameter (γ₁), and Brownian motion parameter (N_b) influence the velocity profile. A higher magnetic parameter enhances momentum transfer, reduces viscosity, modifies boundary layer dynamics, and stabilizes flow, leading to increased velocities nearby the stagnation point as the magnetic field strength rises. In an MHD variable viscosity Casson nanofluid, elevated thermophoresis parameter boosts velocity due to temperature gradient changes and viscosity reduction. Conversely, an increasing chemical reaction parameter can lower velocity by affecting energy absorption, viscosity, by-products generation, pressure gradients, and species transport dynamics. Additionally, a higher Brownian motion parameter increases velocity near a surface through enhanced particle dispersion, turbulence, boundary layer disruption, improved heat transfer, and higher collision frequency, collectively accelerating fluid flow.

4.2. Temperature Profile With Change of Parameters

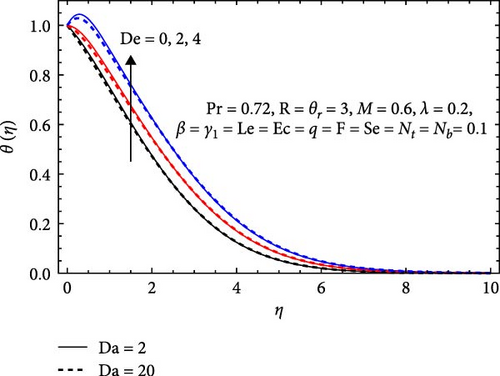
The effects of different embedded parametric factors including Casson, Forchheimer, heat generation/absorption, stretching, magnetic, thermal radiation, and thermophoresis parameters, along with Eckert, Lewis, Darcy, Soret, Dufour, and Prandtl numbers on the dimensionless temperature and its associated boundary layer thickness are demonstrated in Figures 7–10.

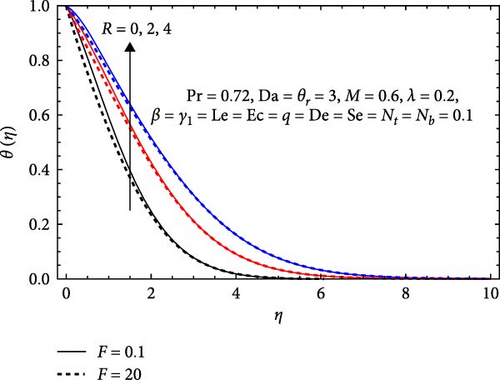
In Figure 7a, the temperature profile rises as the radiation parameter (R) increases, driven by the heightened influence of radiation heat transfer. With a boost in the radiation parameter, more energy is transferred through radiation mechanisms, lifting the system’s temperature. This effect is a result of the improved absorption and emission of thermal radiation linked to higher radiation parameters, enhancing overall heat exchange processes and causing an upward shift in the temperature profile. Conversely, approaching the surface, the temperature profile declines as the Forchheimer number (F) surges due to increased porous media resistance. A higher Forchheimer number intensifies resistance within the porous medium, hindering heat flow toward the surface and diminishing heat transfer efficiency, leading to a temperature decrease near the surface.

In Figure 7b, the temperature profile increases with a higher Dufour number (De) because of enhanced thermal diffusion efficiency, improving heat transfer processes and raising temperatures in the system. On the other hand, the temperature profile decreases with an increasing Darcy number (Da) due to heightened fluid flow resistance. As the Darcy number increases, resistance within the porous medium intensifies, reducing heat transfer efficiency by impeding heat flow, resulting in a temperature profile decrease within the system.

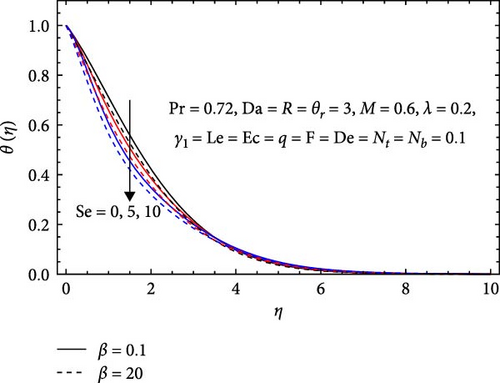
In Figure 8a, the temperature profile diminishes with rising Casson parameter (β) and Soret number (Se). The decrease in the temperature profile with an increasing Casson parameter stems from the intensified resistance to flow imparted by the Casson fluid model. As the Casson factor rises, the fluid’s resistance to deformation and flow increases, leading to reduced heat transfer efficiency. This heightened resistance impedes the flow of heat within the system, leading to a decrease in the dimension temperature as the Casson factor increases. The temperature profile decreases with an increasing Soret number due to the augmented impact of thermal diffusion. As the Soret number rises, the influence of thermal diffusion becomes more pronounced, resulting in a more efficient transfer of heat within the system. This enhanced thermal diffusion causes a reduction in the dimensionless temperature as the Soret number increases.

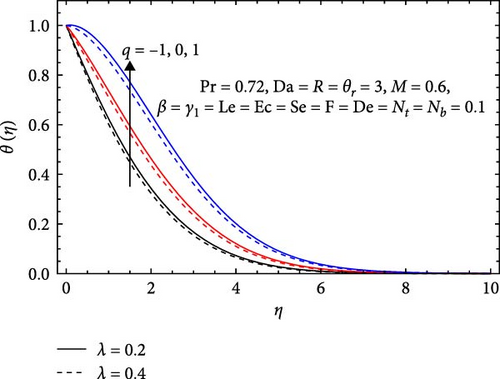
In Figure 8b, the dimensionless temperature decreases as the stretching parameter (λ) increases, attributed to the elongation effect on the flow field. With a higher stretching parameter, the flow field experiences greater elongation, resulting in reduced heat transfer efficiency. This elongation restricts heat flow within the system, leading to a decline in the dimensionless temperature as the stretching parameter rises. On the contrary, it rises with an increasing heat generation parameter (q) due to the additional heat injected into the system. As the heat generation/absorption parameter increases, more heat is either generated or absorbed within the system, boosting the overall temperature. This supplementary heat input enhances the temperature profile by supplying extra energy to the system, causing temperatures to increase as the heat generation-absorption parameter escalates.

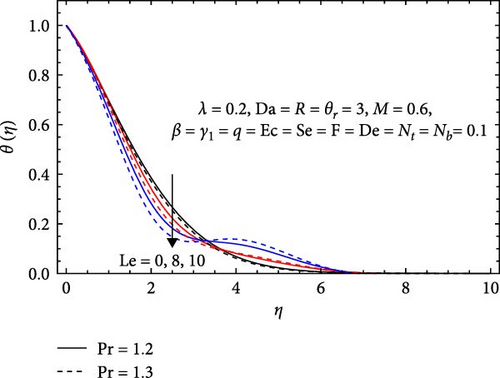
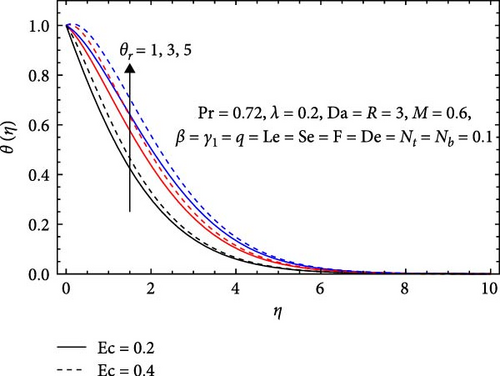
In Figure 9a, the temperature profile near the surface decreases as the Prandtl number (Pr) increases, signifying the prominence of thermal diffusion over momentum diffusion, resulting in more efficient heat conduction as far from the surface. The temperature profile near the surface diminishes with a rising Lewis number (Le) due to the increasing impact of species mass diffusion, enhancing the effective transfer of species as far from the surface. In Figure 9b, the temperature profile ascends with an increasing Eckert number (Ec) because of the heightened influence of kinetic energy, resulting in a greater conversion of kinetic energy into thermal energy and a consequent temperature elevation. Furthermore, the temperature profile also increases with a growing variable viscosity parameter (θ_r), the viscosity’s responsiveness to temperature changes. With the variable viscosity parameter on the rise, the fluid’s viscosity becomes more sensitive to temperature fluctuations, prompting alterations in flow dynamics and an upsurge in the temperature profile.

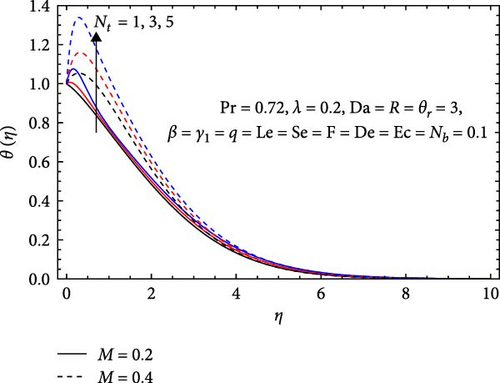
In Figure 10a, the temperature profile escalates with a rising magnetic parameter (M) as it exerts a stronger influence on fluid behavior. Enhanced fluid motion and altered heat transfer characteristics result from the increasing magnetic parameter, contributing to an upward trend in the dimensionless temperature. Similarly, it increases with a growing thermophoresis parameter (N_t), accentuating the impact of thermophoresis on heat transfer dynamics. The pronounced effect of temperature gradient-induced particle motion, as Nt increases, drives changes in heat transfer behaviors, culminating in an overall temperature profile increase.

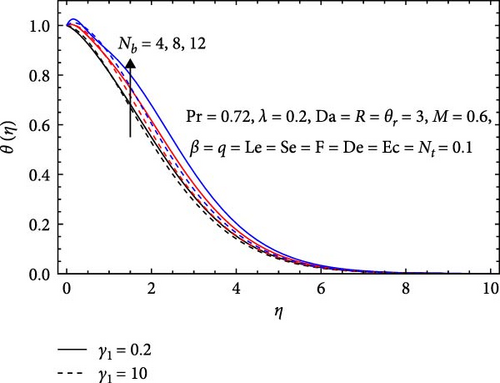
In Figure 10b, the temperature declines with an ascending chemical reaction parameter (γ₁) owing to the exothermic nature of the reaction process. With an increase in γ₁, heightened heat generation within the system occurs due to the reaction’s exothermic characteristics, resulting in a decrease in it. Conversely, it rises with an increasing Brownian motion parameter (N_b), intensifying the impact of Nt on heat transfer mechanisms. The augmented random particle motion, as the Brownian motion parameter increases, enhances heat conduction efficiency, leading to an overall elevation in the temperature profile.

4.3. Concentration Profile With Change of Parameters

In Figures 11–14, the effects of embedded parametric factors, including the Casson, stretching, Brownian motion, heat generation/absorption parameter, magnetic, thermal radiation, thermophoresis parameters, alongside the Eckert, Lewis, Darcy, Forchheimer, Soret, Dufour, and Prandtl numbers on the dimensionless concentration (ϕ(η)) and the corresponding solutal/species boundary layer thickness are demonstrated.

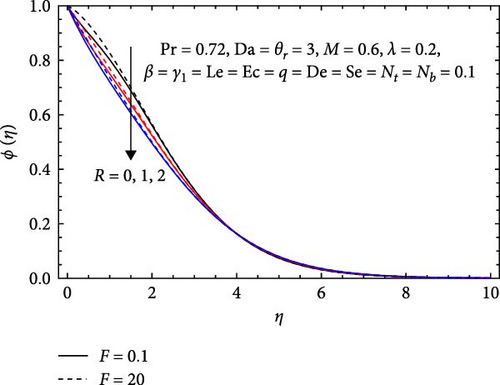
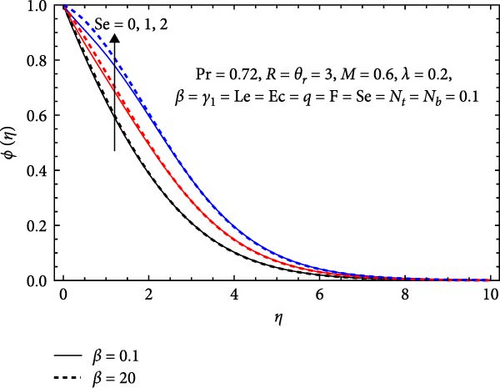
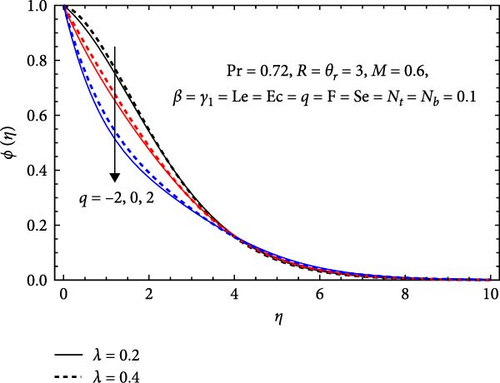
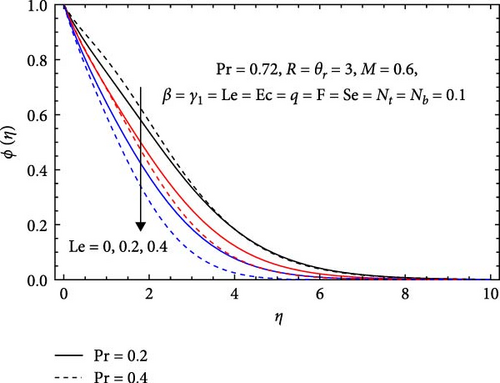
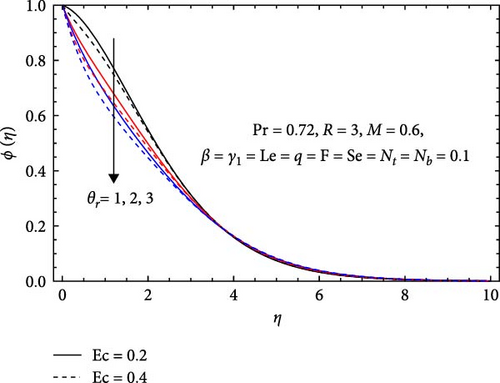
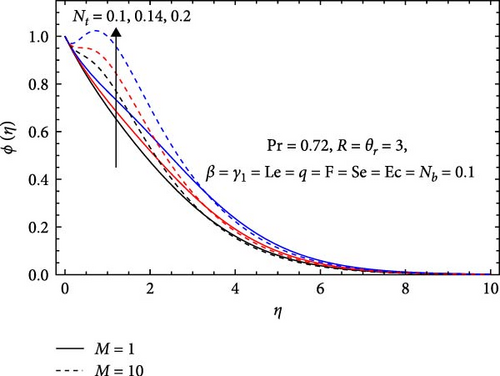
In Figure 11a, the Forchheimer number (F) and radiation parameter (R) influence the concentration profile. The concentration profile increases with a rising Forchheimer number due to enhanced resistance to fluid past in the porous media, leading to greater flow resistance and a buildup of concentration. Conversely, it decreases with increasing radiation parameter due to enhanced absorption, altered solubility from higher temperatures, and accelerated reactions consuming reactants. Radiation also affects particle mobility and diffusion, resulting in greater dispersion and lower concentrations in high-radiation areas.

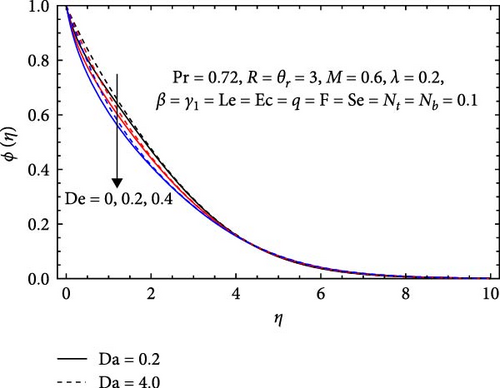
In Figure 11b, the concentration profile is affected by the Darcy number (Da) and Dufour number (De). The profile increases with an increase in Darcy number due to enhanced permeability, which facilitates fluid and solute flow. In contrast, the profile decreases with an increasing Dufour number due to stronger thermal diffusion effects that redistribute species, leading to lower local concentrations.

In Figure 12a, the effects of the Casson parameter (β) and Soret number (Se) on the solutal profile are illustrated. The concentration profile increases with a higher Casson parameter due to greater yield stress, enhancing flow resistance and allowing for solute accumulation. Slower flow rates and increased viscosity further limit solute dispersion, contributing to a higher concentration profile. Similarly, the concentration profile rises with an increasing Soret number, driven by stronger thermal diffusion that enhances solute migration toward temperature gradients, leading to better segregation and improved transport.

In Figure 12b, the effect of the stretching parameter (λ) and heat generation/absorption parameter (q) on the solutal profile is shown. The concentration profile increases with a higher stretching parameter due to enhanced fluid flow, which improves solute transport and leads to accumulation in lower pressure regions, reduced dispersion, and better mixing, resulting in higher local concentrations. In contrast, it decreases with an increasing heat generation/absorption parameter, as elevated temperatures can reduce solubility and accelerate reactions that consume solutes. Additionally, increased diffusion may cause greater dispersion, preventing solute accumulation and leading to lower local concentrations.

In Figure 13a, the effects of Prandtl (Pr) and Lewis (Le) numbers on the solutal profile are illustrated. It decreases with an increasing Prandtl number due to several factors. A higher Prandtl number signifies greater viscosity relative to thermal diffusivity, leading to reduced mixing and lower solute transport. This increased flow resistance hinders solute motion, resulting in lower concentrations. Additionally, stronger thermal gradients can inhibit solute migration, contributing to a more uniform but diminished concentration profile. The concentration profile also decreases with an increasing Lewis number because a higher Le indicates slower heat transfer relative to mass diffusion. This reduces the thermal gradients essential for solute migration, leading to lower solute concentrations and greater transport resistance, as well as more uniform distributions that further diminish localized concentrations.

In Figure 13b, the concentration profile decreases with an increasing Eckert number (Ec) because a higher Ec points out that kinetic energy dominates over thermal energy, disrupting effective solute transport. While increased turbulence enhances mixing, it also causes a wider dispersion of the solutes, preventing accumulation. This results in lower localized concentrations and reduced solute retention times in specific areas. Similarly, increasing variable viscosity parameter (θ_r) decreases because a higher viscosity increases flow resistance, reducing fluid flow and solute transport. This leads to lower flow rates, impaired diffusion, and greater dispersion of the solutes, resulting in a more uniform but reduced concentration profile.

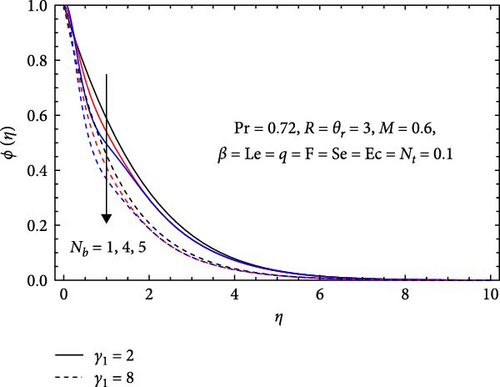
In Figure 14a, the concentration profile increases with a higher magnetic parameter (M) because a stronger magnetic field enhances the Lorentz force, directing solute motion and promoting accumulation. It also reduces turbulent diffusion, leading to more orderly flow and higher local concentrations. Similarly, it increases with an increment in the thermophoresis parameter (N_t) due to stronger thermophoretic forces driving solute particles toward cooler regions, resulting in localized accumulation. Greater temperature gradients improve solute migration and reduce random dispersion, contributing to higher concentrations. In Figure 14b, the concentration profile decreases with increasing chemical reaction parameter (γ₁) as faster reaction rates consume solutes, leading to lower concentrations. Higher γ₁ enhances solute depletion and reduces accumulation, resulting in a more uniform but diminished concentration profile. Additionally, it decreases with an increasing Brownian motion parameter (N_b) because of the enhanced dispersion of solute particles, which prevents accumulation and leads to lower localized concentrations, creating a more uniform concentration profile.

5. Influence of Parameters on the Physical Quantities of Engineering

5.1. Influence of Parameters on the Skin Friction Coefficient

The effect of parameters on skin friction (a resistant force exerted on an object moving in a fluid) is discussed in Figures 15–17.

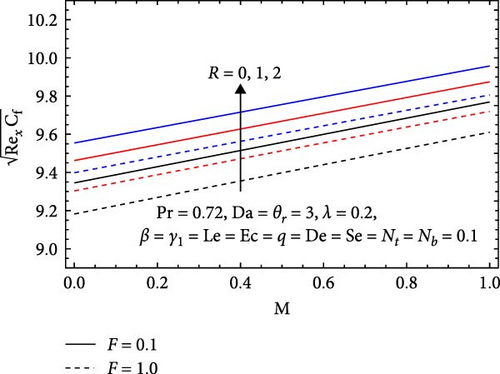
In Figure 15a, the Forchheimer number (F), radiation parameter (R), and magnetic parameter (M) all influence the skin friction coefficient. The coefficient decreases with an increasing Forchheimer number because, as inertial forces dominate over viscous forces, the flow becomes more streamlined, reducing wall shear stress. Additionally, in porous materials, higher flow rates create more efficient pathways, further decreasing friction. Conversely, the skin friction coefficient increases with the radiation parameter as enhanced heat transfer leads to greater temperature gradients near the surface, which boosts momentum transfer and raises friction. Similarly, a higher magnetic parameter results in an increase due to the Lorentz force exerted by a stronger magnetic field on the conducting fluid, creating additional resistance to flow and enhancing shear stress.

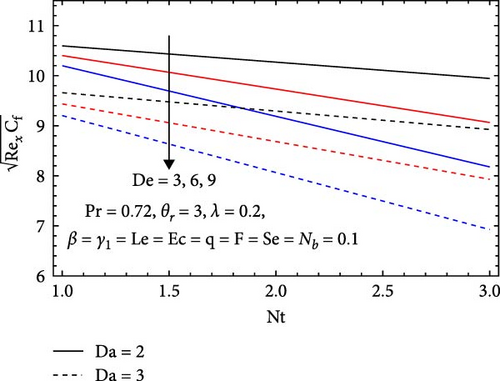
In Figure 15b, the Darcy number (Da), Dufour number (De), and thermophoresis parameter (Nt) all influence skin friction. It decreases with an increasing Da, as higher values indicate greater permeability, which facilitates a more streamlined flow. This streamlining reduces shear stress at the surface and lowers effective resistance to flow, leading to decreased skin friction. Similarly, an increase in De results in higher thermal diffusion, promoting more uniform temperature distributions that reduce fluid viscosity and flow resistance, thereby enhancing flow efficiency and lowering shear stress. Likewise, as thermophoresis increases, enhanced particle motion due to temperature gradients contributes to a more uniform temperature distribution, further decreasing fluid viscosity and resistance to flow, ultimately improving flow efficiency and reducing skin friction.

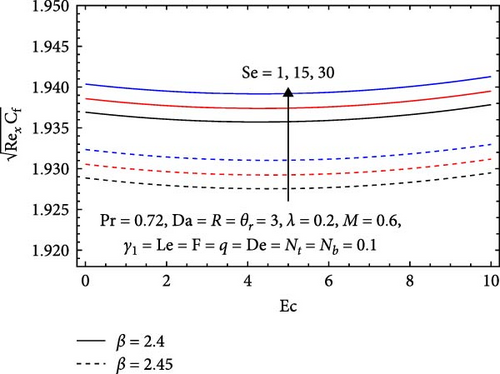
In Figure 16a, the influences of the Casson parameter (β), Soret number (Se), and Eckert number (Ec) on the skin friction coefficient are illustrated. It decreases with an increasing Casson parameter, as a higher value signifies greater shear-thinning behavior in non-Newtonian fluids. This results in reduced effective viscosity, facilitating easier flow and streamlined motion, thereby lowering shear stress at the surface. Conversely, the skin friction coefficient increases with the Soret number, as elevated Soret numbers enhance thermal and concentration gradients, which can increase the fluid’s viscosity. This rise in viscosity leads to greater flow resistance and higher shear stress at the surface, resulting in an increased skin friction coefficient. In contrast, It remains relatively constant with rising Eckert numbers because the effects of kinetic and thermal energies tend to balance each other. Consequently, changes in temperature and viscosity do not significantly affect flow characteristics, leading to minimal variation in it.

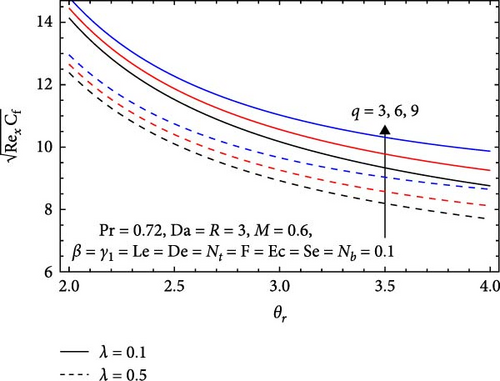
In Figure 16b, the influences of the stretching parameter (λ), heat generation/absorption parameter (q), and variable viscosity parameter (θ_r) are depicted. The skin friction coefficient decreases with an increasing stretching parameter, as the stretching surface facilitates more streamlined flow, which reduces shear stress at the surface. This enhanced flow decreases resistance to flow and lowers effective viscosity, leading to reduced skin friction. Conversely, the skin friction coefficient rises with higher heat generation/absorption parameters, as increased thermal gradients elevate the fluid’s viscosity, resulting in greater flow resistance. This, in turn, raises shear stress at the surface, increasing the skin friction coefficient. Additionally, the skin friction coefficient decreases with an increasing variable viscosity parameter, as higher values signify shear-thinning behavior, which reduces effective viscosity. This allows for easier flow and lower shear stress at the surface, ultimately decreasing skin friction.

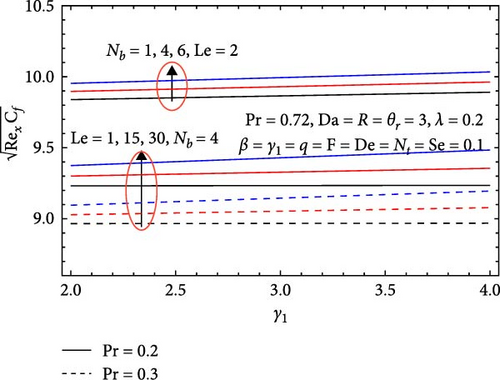
Figure 17 illustrates the effects of the Prandtl number (Pr), Brownian motion parameter (N_b), Lewis number (Le), and chemical reaction parameter (γ₁) on the skin friction coefficient. The skin friction coefficient decreases with an increasing Prandtl number, as a higher Prandtl number indicates that momentum diffuses more rapidly than heat. This results in a thicker thermal boundary layer, which reduces surface temperature gradients and lowers effective viscosity, ultimately decreasing shear stress and the skin friction coefficient. Conversely, the skin friction coefficient increases with the Brownian motion parameter; greater particle motion enhances interactions within the fluid, leading to increased effective viscosity. This rise in viscosity results in higher flow resistance and elevated shear stress at the surface, thereby increasing the skin friction coefficient. Similarly, it rises with the Lewis number, as a higher Lewis number signifies greater thermal diffusion relative to mass diffusion, often resulting in increased effective viscosity and higher shear stress. Lastly, it also increases with the chemical reaction parameter due to higher reaction rates, which enhance fluid interactions and typically raise viscosity. This increase in viscosity leads to greater flow resistance and elevated wall shear stress, further contributing to an increased skin friction coefficient.

5.2. Influence of Parameters on Local Nusselt Number

The local Nusselt number (heat transfer rate) is influenced by the Forchheimer parameter (F), Casson parameter (β), Lewis number(Le), Darcy number (Da), Prandtl number (Pr), Eckert number (Ec), Soret number (Se), Dufour number (De), stretching parameter (λ), heat generation/absorption parameter (q), magnetic parameter (M), thermal radiation parameter (R), and thermophoresis parameter (N_t), as depicted in Figures 18–20.

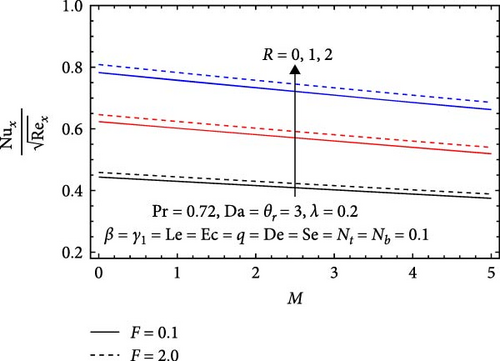
In Figure 18a, the impacts of the Forchheimer number (F), radiation parameter (R), and magnetic parameter (M) on the Nusselt number are depicted. It increases with the Forchheimer number, as higher values enhance inertial effects, leading to improved flow dynamics and mixing. This results in better thermal convection, a thinner thermal boundary layer, and overall more effective heat transfer. Similarly, the Nusselt number rises with the radiation parameter; increased radiation enhances heat transfer by creating steeper temperature gradients, which facilitate more efficient heat transfer between the fluid and the surface. Conversely, the Nusselt number decreases with an increasing magnetic parameter, as stronger magnetic fields dampen fluid flow and reduce flow velocities. This results in less effective mixing and convection, leading to a thicker thermal boundary layer and diminished heat transfer efficiency.

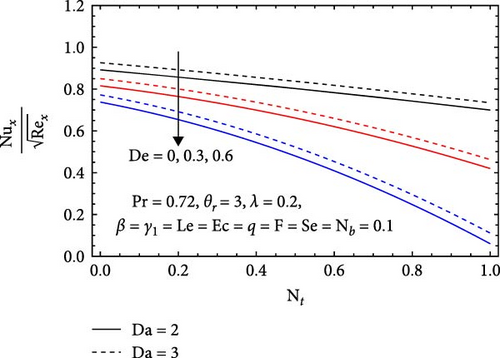
In Figure 18b, the influences of the Darcy number (Da), Dufour number (De), and thermophoresis parameter (N_t) on the Nusselt number are presented. It increases with the Darcy number, as higher values signify greater permeability, which enhances fluid flow and mixing. This improvement in flow dynamics boosts thermal convection and results in a thinner thermal boundary layer, facilitating more effective heat transfer between the fluid and the surface. Conversely, the Nusselt number decreases with increasing Dufour number, as higher values indicate a stronger dominance of mass diffusion over thermal diffusion, disrupting effective heat transfer. This leads to reduced convection efficiency and a thicker thermal boundary layer, ultimately lowering the Nusselt number. Similarly, it decreases with an increasing thermophoresis parameter, as stronger particle motion in response to temperature gradients disrupts fluid flow dynamics. This disruption results in reduced mixing, diminished convection efficiency, and a thicker thermal boundary layer, impairing heat transfer.

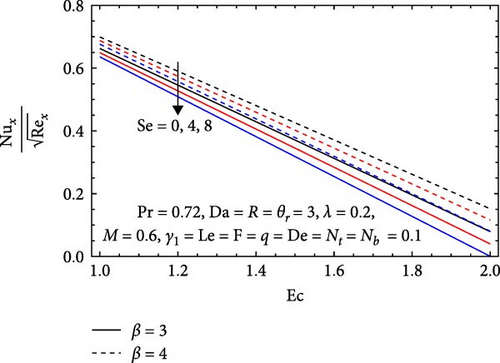
In Figure 19a, the influences of the Casson parameter (β), Soret number (Se), and Eckert number (Ec) on the Nusselt number are illustrated. It increases with the Casson parameter, as higher values signify more pronounced shear-thinning behavior in non-Newtonian fluids. This enhanced flow promotes better thermal convection and results in a thinner thermal boundary layer, ultimately increasing the Nusselt number. Conversely, It decreases with rising Soret numbers, which indicates stronger thermal diffusion that leads to less effective mixing of thermal energy. This results in poorer heat transfer and a thicker thermal boundary layer, thereby reducing the Nusselt number. Additionally, the Nusselt number declines with increasing Ec numbers, as higher values suggest that kinetic energy dominates over thermal energy. This shift reduces heat transfer efficiency and contributes to a thicker thermal boundary layer, impairing overall heat transfer.

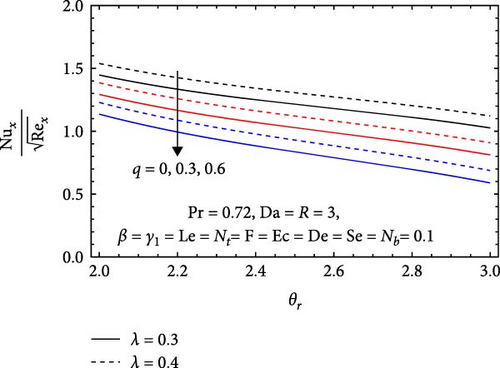
In Figure 19b, the impacts of the stretching ratio (λ), heat generation/absorption parameter (q), and variable viscosity parameter (θ_r) on the Nusselt number are depicted. It increases with the stretching parameter, as greater stretching enhances flow dynamics and promotes more streamlined flow near the surface. This improvement in flow facilitates better convection and heat transfer, leading to a thinner thermal boundary layer and greater overall heat transfer efficiency. Conversely, it decreases with an increasing heat generation/absorption parameter, as higher values create steeper temperature gradients that reduce convection efficiency, resulting in a thicker thermal boundary layer that impairs effective heat transfer. Additionally, the Nusselt number decreases with rising variable viscosity parameter, as significant changes in viscosity hinder effective flow dynamics, leading to reduced convection and heat transfer efficiency, along with a thicker thermal boundary layer.

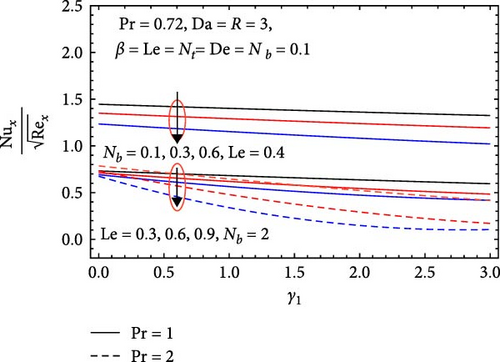
In Figure 20, the influences of the Prandtl number (Pr), Brownian motion parameter (N_b), Lewis number (Le), and chemical reaction parameter (γ₁) on the Nusselt number are depicted. It decreases with increasing Prandtl number, as higher values signify that momentum diffuses more rapidly than thermal energy. This imbalance results in thicker thermal boundary layers and less effective thermal convection, ultimately reducing heat transfer efficiency. Similarly, the Nusselt number decreases with an increasing Brownian motion parameter; stronger particle motion enhances mass diffusion, which impairs effective mixing and convection, leading to reduced heat transfer and thicker thermal boundary layers. It also declines with a rising Lewis number, as higher values indicate that thermal diffusion is less effective than mass diffusion, resulting in decreased heat transfer efficiency, ineffective mixing, and a thicker thermal boundary layer. Finally, the Nusselt number decreases with increasing chemical reaction parameter because faster reaction rates disrupt fluid dynamics and reduce heat transfer efficiency, often resulting in thicker thermal boundary layers that further impair heat transfer between the fluid and the surface.

5.3. Influence of Parameters on Local Sherwood Number

The local Sherwood number (mass transfer rate) is influenced by the Casson factor (β), Lewis number (Le), Darcy number (Da), Forchheimer parameter (F), Prandtl number (Pr), Eckert number (Ec), Soret number (Se), Dufour number (De), stretching parameter (λ), heat generation/absorption parameter (q), magnetic parameter (M), thermal radiation parameter (R), Brownian motion parameter (N_b), and thermophoresis parameter (N_t), as depicted in Figures 21–23.

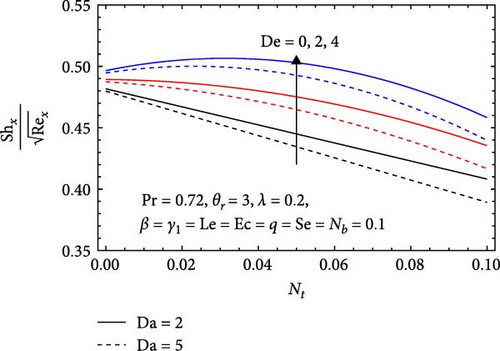
In Figure 21a, the impacts of the Forchheimer number (F), radiation parameter (R), and magnetic parameter (M) on the Sherwood number are illustrated. The Sherwood number decreases with an increasing Forchheimer number, as higher values signify stronger inertial effects that diminish the role of diffusion in mass transfer. This results in thicker concentration boundary layers, which further impede mass transfer efficiency. Similarly, the Sherwood number decreases with an increasing radiation parameter, since higher values indicate that radiative heat transfer dominates over convective mass transfer, leading to reduced convection efficiency and thicker concentration boundary layers. Conversely, the Sherwood number increases with the magnetic parameter, as higher values enhance flow stability, improving mixing and mass transfer. This results in a thinner concentration boundary layer, thereby boosting mass transfer efficiency between the fluid and the surface.

In Figure 21b, the effects of the Darcy number (Da), Dufour number (De), and thermophoresis parameter (N_t) on the Sherwood number are presented. The Sherwood number decreases with increasing Darcy number, as higher values indicate reduced flow velocities in porous media. This decline in velocity diminishes convective mass transfer efficiency and leads to thicker concentration boundary layers, which further hinder mass transfer between the fluid and the surface. Conversely, the Sherwood number increases with the Dufour number, as higher values enhance thermal diffusion, thereby improving mass transfer efficiency. This results in steeper temperature gradients and a thinner concentration boundary layer, facilitating more effective mass transfer. However, the Sherwood number decreases with an increasing thermophoresis parameter, where stronger particle motion disrupts fluid flow dynamics and reduces mixing efficiency, leading to a thicker concentration boundary layer that further impedes mass transfer between the fluid and the surface.

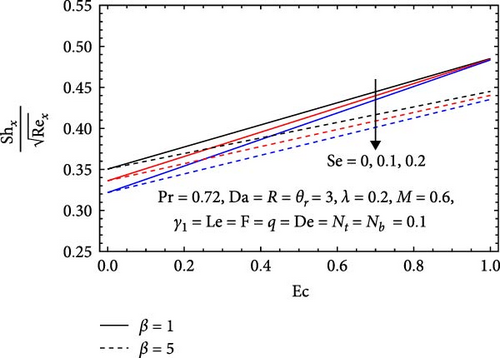
In Figure 22a, the impacts of the Casson parameter (β), Soret number (Se), and Eckert number (Ec) on the Sherwood number are illustrated. The Sherwood number decreases with an increasing Casson parameter, as higher values indicate greater fluid viscosity, which hinders effective mixing and reduces mass transfer efficiency. This results in thicker concentration boundary layers that further obstruct mass transfer between the fluid and the surface. Similarly, the Sherwood number declines with an increasing Soret number, as higher values signify a greater dominance of thermal diffusion over mass diffusion, leading to reduced mixing efficiency and thicker concentration boundary layers that impede mass transfer. In contrast, the Sherwood number increases with the Eckert number; higher values signify greater kinetic energy, enhancing fluid flow and mixing. This improvement results in a thinner concentration boundary layer, ultimately facilitating more effective mass transfer between the fluid and the surface.

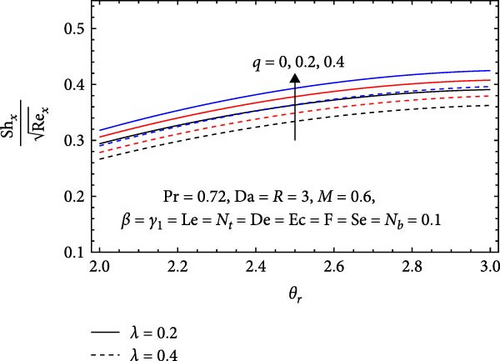
In Figure 22b, the impacts of the stretching parameter (λ), heat generation/absorption parameter (q), and variable viscosity parameter (θ_r) on the Sherwood number are illustrated. The Sherwood number decreases with an increasing stretching parameter, as higher values can induce greater flow instability, which diminishes effective mixing and convective mass transfer. This leads to thicker concentration boundary layers that further hinder mass transfer between the fluid and the surface. Conversely, the Sherwood number increases with the heat generation/absorption parameter; higher values enhance thermal convection and create steeper temperature gradients, resulting in a thinner concentration boundary layer that promotes more effective mass transfer. Additionally, the Sherwood number rises with the variable viscosity parameter, as increased values improve flow dynamics, leading to better mixing and enhanced convective mass transfer, which also results in a thinner concentration boundary layer, facilitating more effective mass transfer between the fluid and the surface.

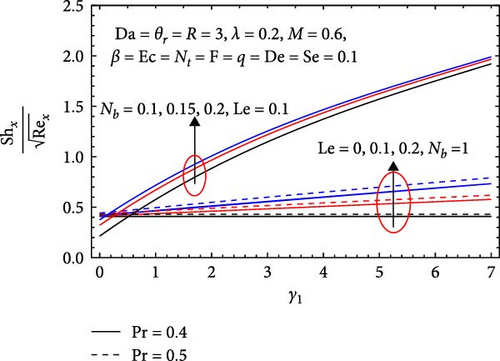
In Figure 23, the effects of the Prandtl number (Pr), Brownian motion parameter (N_b), Lewis number (Le), and chemical reaction parameter (γ₁) on the Sherwood number are analyzed. It increases with the Prandtl number, as higher values enhance thermal convection, leading to improved mixing and increased mass transfer efficiency. This results in a thinner concentration boundary layer, facilitating more effective mass transfer between the fluid and the surface. Similarly, it rises with the Brownian motion parameter, as greater particle motion enhances mass diffusion and mixing, resulting in a thinner concentration boundary layer that boosts mass transfer efficiency. The increase in the Lewis number also correlates with a higher Sherwood number, as it indicates more effective mass diffusion relative to thermal diffusion, leading to steeper concentration gradients and a thinner concentration boundary layer that further enhances mass transfer. Lastly, the Sherwood number increases with the chemical reaction parameter due to more vigorous reactions that enhance reactant consumption and promote mass transfer, resulting in improved mixing and a thinner concentration boundary layer that further boosts mass transfer efficiency.

6. Conclusion and Future Directions

The study of the effects of Soret and Dufour on MHD variable viscosity Casson nanofluid past a stretching sheet in the presence of heat generation/absorption has been performed. This exploration assesses how various governing parameters collectively influence dimensionless concentration, temperature, velocity, skin friction, and rates of mass and heat transfer. The model’s PDEs are initially transformed into nonlinear ordinary differential equations (ODEs) via the similarity transformation technique. Subsequently, utilizing the HAM through the BVPh2.0 package of Mathematica, numerical solutions are computed based on the prescribed boundary conditions. We have obtained the following results:

•
Higher values of R, De, Se, β, q, λ, θ_r, Ec, N_t, N_b, and M result in an increase in the dimensionless velocity.
•
An increase in Le, Pr, Da, γ₁, and F leads to a decrease in the dimensionless velocity.
•
The dimensionless temperature rises with higher values of R, De, q, θ_r, Ec, N_t, M, and N_b.
•
Increasing values of F, Pr, β, Da, Se, Le, γ₁, and λ lead to a decrease in the dimensionless temperature.
•
Higher values of F, Da, Se, β, λ, Nt, and M lead to an increase in the solutal profile.
•
Increasing values of R, De, q, Le, Pr, Ec, θ_r, γ₁, and N_b result in a decrease in the solutal profile.
•
The drag coefficient rises with higher values of R, M, Se, q, N_b, Le, and γ₁.
•
Increasing values of Da, F, De, N_t, β, λ, θ_r, and Pr result in a decrease in the drag coefficient.
•
The wall heat transfer rate increases with higher values of R, F, Da, β, and λ.
•
Increasing values of M, N_t, N_b, γ₁, θ_r, Se, De, q, Pr, Ec, and Le lead to a decrease in the wall heat transfer rate.
•
The wall mass transfer rate increases with higher values of M, De, Ec, q, θ_r, Nb, Le, γ₁, and Pr.
•
Increasing values of F, R, N_t, Da, Se, β, and λ result in a decrease in the wall mass transfer rate.

This study introduces novel insights into MHD variable viscosity Casson nanofluid flow by incorporating Soret and Dufour effects, Joule heating, thermal radiation, and heat generation/absorption, which have been less explored in the previous research. The results reveal how these factors significantly influence temperature, concentration, and velocity profiles, offering new perspectives on heat and mass transfer in nanofluid based systems. Future research could expand the study to different geometrical configurations, one-phase flow models, non-Newtonian fluids, and the effects of variable thermal conductivity and magnetic fields. These findings have practical applications in industries like cooling systems, material processing, and biomedical applications, enhancing the performance of thermal management systems and energy efficient devices.

Nomenclature

a, b:: Positive constants
C_f:: Local skin friction coefficient
B₀:: Uniform magnetic field
C_p:: Specific heat transfer
C:: Concentration
T_∞:: Ambient temperature
U_∞:: Free stream velocity
C_∞:: Ambient concentration
Da:: Darcy number
D_B:: Brownian motion
D_T:: Thermophoresis diffusion
e_ij:: The strain tensor rate
Ec:: Eckert number
f:: Stream function
F_C:: Forchheimer drag coefficient
F:: Forchheimer number
q:: Dimensionless heat source/sink
MHD:: Magnetohydrodynamics
HAM:: Homotopy analysis method
K:: Porous medium permeability
R:: Radiation parameter
M:: Magnetic parameter
Q_g:: Heat generation/absorption
k:: Thermal conductivity
k^∗:: The mean absorption coefficient
Le:: Lewis number
N_b:: Brownian motion parameter
N_t:: Thermophoresis parameter
Nu_x:: The local Nusselt number
Pr:: Prandtl number
P_y:: Fluid yield stress
Sh_x:: Sherwood number
q_s:: Mass flux
q_w:: Heat flux
u, v:: Velocity along x and y
T:: Temperature
C_s:: Concentration susceptibility
D_m:: Mass diffusivity
T_k:: Thermal diffusion ratio
De:: Dufour number
Se:: Soret number

Greek Symbols

α:: Thermal diffusivity
β:: The Casson parameter
λ:: Stretching parameter
μ_∞:: Free stream viscosity
ν_∞:: Free stream kinematic viscosity
π:: Rate of deformation
π_c:: π’s critical value
ρ_∞:: Free stream density
σ^∗:: The Stefan–Boltzman constant
σ:: Electrical conductivity
η:: Similarity variable
θ:: Fluid dimensionless temperature
μ_B:: Viscosity of Casson fluid
θr:: Variable viscosity parameter
τ_ij:: Stress tensor components
τ_w:: Wall friction
:: Nanoparticles’ heat capacity ratios
ϕ:: Dimensionless concentration
γ₁:: Chemical reaction parameter.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Ebba Hindebu Rikitu and Mitiku Daba Firdi contributed to conceptualization, supervision, and formal analysis. Hundasa Chala Nagari contributed to writing–review and editing. All authors have read and agreed to the published version of the manuscript.

Funding

No funding was received for this research.

Open Research

Data Availability Statement

The tabular data used to support the findings of this study are included within the article.

References

1 Scott T. O., Ewim D. R. E., and Eloka-Eboka A. C., Hybrid Nanofluids Flow and Heat Transfer in Cavities: A Technological Review, International Journal of Low-Carbon Technologies. (2022) 17, 1104–1123.
10.1093/ijlct/ctac093
CAS Web of Science® Google Scholar
2 Lishchuk P., Vashchuk A., and Rogalsky S., et al.Thermal Transport Properties of Porous Silicon Filled by Ionic Liquid Nanocomposite System, Scientific Reports. (2023) 13, no. 1, https://doi.org/10.1038/s41598-023-32834-8, 5889.
10.1038/s41598-023-32834-8
CAS PubMed Web of Science® Google Scholar
3 Pereira J., Moita A., and Moreira A., The Pool-Boiling-Induced Deposition of Nanoparticles as the Transient Game Changer a Review, Nanomaterials. (2022) 12, no. 23, 4270.
10.3390/nano12234270
CAS PubMed Web of Science® Google Scholar
4 Sohel Murshed S. M., Nanofluids and Nanofluidics, Nanomaterials. (2022) 12, no. 17.
Google Scholar
5 Omar N. F. M., Osman H. I., Mohamad A. Q., Jusoh R., and Ismail Z., Analytical Solution of Unsteady Mhd Casson Fluid With Thermal Radiation and Chemical Reaction in Porous Medium, Journal of Advanced Research in Applied Sciences and Engineering Technology. (2023) 29, no. 2, 185–194.
10.37934/araset.29.2.185194
Google Scholar
6 Ekang I. F., Joshua E. E., and Senge I. O., Casson Fluid Flow With Heat Generation and Radiation Effect Through a Porous Medium of an Exponentially Shrinking Sheet, World. (2022) 14, no. 1b, 56–61.
Google Scholar
7 Roja A., Repercussions of Couple Stress Casson Fluid Flow Through a Vertical Microchannel With Darcy-Forchheimer Condition, 2023, Authorea, Inc..
10.22541/au.168363479.92084498/v1
Google Scholar
8 Sene N., Solution Procedure for Fractional Casson Fluid Model Considered With Heat Generation and Chemical Reaction, Sustainability. (2023) 15, no. 6, 5306.
10.3390/su15065306
Web of Science® Google Scholar
9 Israel-Cookey C., Davies O. A., and Ngeri A. P., Magnetohydrodynamic Forced Convection and Heat Transfer of a Casson Fluid Flow in an Anisotropic Porous Channel With Isoflux Boundaries, World Journal of Advanced Research and Reviews. (2023) 18, no. 3, 1332–1347.
10.30574/wjarr.2023.18.3.1214
CAS Google Scholar
10 Sekhar P. R., Sreedhar S., and Kumar P. V., et al.Investigating Radiative Heat Transfer, Varied Wall Thickness, and Slip Effects on Casson Nanofluid Flow over a Stretched Sheet with Heat Source, International Journal of Modelling and Simulation. (2024) 1–17.
10.1080/02286203.2024.2345256
Web of Science® Google Scholar
11 Mizuno Y. and Rezzolla L., General-Relativistic Magnetohydrodynamic Equations: The Bare Essential, 2024, arXiv preprint arXiv: 2404.13824https://doi.org/10.1007/978-981-97-8522-3.
10.1007/978-981-97-8522-3
Google Scholar
12 Bisnovatyi-Kogan G. S., Kondratyev I. A., and Moiseenko S. G., Electromagnetohydrodynamics, 2023, https://arxiv.org/abs/2306.17724.
Google Scholar
13 Guan X., Hu B., Mao S., and Wang X., MHDnet: Multi-Modes Multiscale Physics Informed Neural Networks for Solving Magnetohydrodynamics Problems, CoRR, 2023.
Google Scholar
14 Seo J. and Ryu D., HOW-MHD: A High-Order WENO-Based Magnetohydrodynamic Code With a High-Order Constrained Transport Algorithm for Astrophysical Applications, The Astrophysical Journal. (2023) 953, no. 1, https://doi.org/10.3847/1538-4357/acdf4b, 39.
10.3847/1538-4357/acdf4b
Web of Science® Google Scholar
15 Kumari P. S., Ibrahim S. M., and Lorenzini G., Chemical Reaction on Williamson Nanofluid’s Radiative MHD Dissipative Stagnation Point Flow Over an Exponentially Inclined Stretching Surface With Multi-Slip Effects, Frontiers in Heat and Mass Transfer. (2024) 22, no. 6, 1839–1863, https://doi.org/10.32604/fhmt.2024.057760.
10.32604/fhmt.2024.057760
Web of Science® Google Scholar
16 Popova E. and Lazarian A., Outlook on Magnetohydrodynamical Turbulence and Its Astrophysical Implications, Fluids. (2023) 8, no. 5, https://doi.org/10.3390/fluids8050142, 142.
10.3390/fluids8050142
Web of Science® Google Scholar
17 Badak K., Sharma R. P., and Ibrahim S. M., A Comprehensive Study on Maxwell Hybrid Nanostructure and Maxwell Nanostructure on 2d Flow Model Over a Stretching Sheet With Non-Uniform Heat Generation/Absorption and Binary Chemical Reaction, Journal of Thermal Analysis and Calorimetry. (2024) 150, 521–535.
10.1007/s10973-024-13754-9
Web of Science® Google Scholar
18 Sekhar P. R., Sreedhar S., Ibrahim S. M., Kumar P. V., and Omprakash B., Numerical Investigation of Heat Radiation on MHD Viscoelastic Nanofluid Flow over a Stretching Sheet With Heat Source and Slip Conditions, International Journal on Interactive Design and Manufacturing (IJIDeM). (2024) 18, no. 5, 2991–3000, https://doi.org/10.1007/s12008-023-01407-4.
10.1007/s12008-023-01407-4
Web of Science® Google Scholar
19 Chandrakala P. and Srinivasa Rao V., Effect of Heat and Mass Transfer Over Mixed Convective Hybrid Nanofluids Past an Exponentially Stretching Sheet, CFD Letters. (2024) 16, no. 3, 125–140, https://doi.org/10.37934/cfdl.16.3.125140.
10.37934/cfdl.16.3.125140
Google Scholar
20 Ayegbusi F. D., Doungmo Goufo E. F., and Tchepmo P., Motion of Micropolar and Walters-B Nanofluids Towards a Stretching Sheet With the Significance of Heat Generation, Thermal Radiation and Soret–Dufour Mechanisms, Arab Journal of Basic and Applied Sciences. (2023) 30, no. 1, 429–439, https://doi.org/10.1080/25765299.2023.2223023.
10.1080/25765299.2023.2223023
Google Scholar
21 Abbas W., Megahed A. M., Ibrahim M. A., and Said A. A. M., Non-Newtonian Slippery Nanofluid Flow due to a Stretching Sheet Through a Porous Medium With Heat Generation and Thermal Slip, Journal of Nonlinear Mathematical Physics. (2023) 30, no. 3, 1221–1238, https://doi.org/10.1007/s44198-023-00125-5.
10.1007/s44198-023-00125-5
Web of Science® Google Scholar
22 Sama N. A. A., Bachok N., and Arifin N. M., The Significant Effect of Hydromagnetic on Carbon Nanotubes Based Nanofluids Flow and Heat Transfer Past a Porous Stretching/Shrinking Sheet, Journal of Advanced Research in Fluid Mechanics and Thermal Sciences. (2023) 106, no. 1, 51–64, https://doi.org/10.37934/arfmts.106.1.5164.
10.37934/arfmts.106.1.5164
Google Scholar
23 Bakar N. A. and Roslan R., Mixed Convection in a Lid-Driven Horizontal Cavity in the Presence of Internal Heat Generation or Absorption, Journal of Advanced Research in Numerical Heat Transfer. (2020) 3, no. 1, 1–11.
Google Scholar
24 Yashodha S., Hakeem A. K. A., Ganga B., and Renuka P., Heat Transfer Analysis of Water-Ethylene Glycol (50:50) Based Nanofluid Over a Cone With the Influences of Magnetic Field and Uniform Heat Generation/Absorption, Mathematics and Computers in Simulation. (2024) 222, 24–37, https://doi.org/10.1016/j.matcom.2023.06.024.
10.1016/j.matcom.2023.06.024
Web of Science® Google Scholar
25 Nemati M., Reddy N. K., Sefid M., Karimipour A., and Chamkha A. J., Power-Law Nanofluid Magnetohydrodynamics Combined Convection in the Presence of Heat Absorption/Generation: A Lattice Boltzmann Analysis to Compute Thermal Performance Index, Journal of Nanofluids. (2023) 12, no. 8, 2381–2399, https://doi.org/10.1166/jon.2023.2107.
10.1166/jon.2023.2107
Web of Science® Google Scholar
26 Ajay C. K. and Srinivasa A. H., et al. The Effects of Thermal Radiation, Internal Heat Generation (Absorption) on Unsteady MHD Free Convection Flow About a Truncated Cone in Presence of Pressure Work, 2023, Proceedings, Materials Today.
Google Scholar
27 Isa S. S. P. M., Azmi H. M., Arifin N. M., and Haliza R., et al.Soret-Dufour Effects on Heat and Mass Transfer of Newtonian Fluid Flow Over the Inclined Sheet and Magnetic Field, Journal of Advanced Research in Numerical Heat Transfer. (2023) 14, no. 1, 39–48, https://doi.org/10.37934/arnht.14.1.3948.
10.37934/arnht.14.1.3948
Google Scholar
28 Durojaye M. O., Kazeem J. A., Ogunfiditimi F. O., and Ajie I. J., Method of Lines Analysis of Soret and Dufour Effects on an Unsteady Heat and Mass Transfer MHD Natural Convection Couette Flow, Physical Science International Journal. (2023) 27, no. 2, 10–18, https://doi.org/10.9734/psij/2023/v27i2780.
10.9734/psij/2023/v27i2780
Google Scholar
29 Aastha A. and Chand K., Soret and Dufour Effects on Chemically Reacting and Viscous Dissipating Nanofluid Flowing Past a Moving Porous Plate in the Presence of a Heat Source/Sink, Acta Mechanica et Automatica. (2023) 17, no. 2, 263–271, https://doi.org/10.2478/ama-2023-0030.
10.2478/ama-2023-0030
Web of Science® Google Scholar
30 Jayanthi S. and Niranjan H., A Vertical Surface Flow Analysis of MHD Nanofluids Influenced by Radiation, Viscous Dissipation, and Joule Heating With Soret and Dufour Effects, Contemporary Mathematics. (2024) 5, no. 2, 2296–2314, https://doi.org/10.37256/cm.5220244318.
10.37256/cm.5220244318
Google Scholar
31 Isa S. S. P. M., Balakrishnan N., Ismail N. S., Arifin N. M., and Ali F. M., The Velocity, Temperature, and Concentration Profiles for Triple Diffusive Casson Fluid Flow Subjected to the Soret-Dufour Parameters, CFD Letters. (2024) 16, no. 3, 15–27.
Google Scholar
32 Alnahdi A. S. and Gul T., Casson Hybrid Nanofluid Flow Over a Riga Plate for Drug Delivery Applications With Double Diffusion, Chinese Physics B. (2024) 33, no. 10, https://doi.org/10.1088/1674-1056/ad624e, 104701.
10.1088/1674-1056/ad624e
CAS Web of Science® Google Scholar
33 Mohamad A. M., Yadav D., Awasthi M. K., Ragoju R., Bhattacharyya K., and Mahajan A., Analytical and Numerical Examinations on the Stability Investigation of Casson Nanofluid Flow in a Permeable Layer Controlled by Vertical Throughflow, World Journal of Engineering. (2024) https://doi.org/10.1108/WJE-02-2024-0056.
10.1108/WJE-02-2024-0056
Web of Science® Google Scholar
34 Poply V., Mondal S., and Kumar P., Effect of Casson Nanofluid’s Outer Velocity With Melting Heat Transmission Beyond a Stretching Sheet, Computational Simulation and Experimental Techniques for Nanofluid Flow. (2024) 8, 86–93, https://doi.org/10.2174/9789815223705124010007.
10.2174/9789815223705124010007
Google Scholar
35 El Harfouf A., Herbazi R., and Abouloifa W., et al.Numerical Examination of a Squeezing Casson Hybrid Nanofluid Flow considering Thermophoretic and Internal Heating Mechanisms, WSEAS Transactions on Heat and Mass Transfer. (2024) 19, 41–51, https://doi.org/10.37394/232012.
10.37394/232012.2024.19.5
Google Scholar
36 Soomro A. M., Fadhel M. A., Lund L. A., Shah Z., Alshehri M. H., and Vrinceanu N., Dual Solutions of Magnetized Radiative Flow of Casson Nanofluid Over a Stretching/Shrinking Cylinder: Stability Analysis, Heliyon. (2024) 10, no. 8, https://doi.org/10.1016/j.heliyon.2024.e29696, e29696.
10.1016/j.heliyon.2024.e29696
CAS PubMed Web of Science® Google Scholar
37 Nagari H. C., Firdi M. D., and Rikitu E. H., Investigation of Thermal Radiation and Joule Heating Effects on Variable Viscosity Casson Nanofluid Flow Over a Stretching Sheet in Darcy–Forchheimer Porous Medium, Numerical Heat Transfer, Part A: Applications. (2024) 1–29, https://doi.org/10.1080/10407782.2024.2382929.
10.1080/10407782.2024.2382929
Web of Science® Google Scholar
38 Mabood F., Ibrahim S. M., Kumar P. V., and Lorenzini G., Effects of Slip and Radiation on Convective MHD Casson Nanofluid Flow Over a Stretching Sheet Influenced by Variable Viscosity, Journal of Engineering Thermophysics. (2020) 29, no. 2, 303–315, https://doi.org/10.1134/S1810232820020125.
10.1134/S1810232820020125
CAS Web of Science® Google Scholar
39 Animasaun I. L., Effects of Thermophoresis, Variable Viscosity and Thermal Conductivity on Free Convective Heat and Mass Transfer of Non-Darcian MHD Dissipative Casson Fluid Flow With Suction and Nth Order of Chemical Reaction, Journal of the Nigerian Mathematical Society. (2015) 34, no. 1, 11–31, https://doi.org/10.1016/j.jnnms.2014.10.008.
10.1016/j.jnnms.2014.10.008
Google Scholar
40 Subba Rao A., Ramachandra Prasad V., Bhaskar Reddy N., and Anwar Bég O., Heat Transfer in a Casson Rheological Fluid From a Semi-Infinite Vertical Plate With Partial Slip, Heat Transfer-Asian Research. (2015) 44, no. 3, 272–291, https://doi.org/10.1002/htj.21115, 2-s2.0-84927174165.
10.1002/htj.21115
Web of Science® Google Scholar
41 Nakamura M. and Sawada T., Numerical Study on the Flow of a Non-Newtonian Fluid Through an Axisymmetric Stenosis, 1988.
Google Scholar
42 Khan W. A., Makinde O. D., and Khan Z. H., Non-Aligned MHD Stagnation Point Flow of Variable Viscosity Nanofluids Past a Stretching Sheet With Radiative Heat, International Journal of Heat and Mass Transfer. (2016) 96, 525–534, https://doi.org/10.1016/j.ijheatmasstransfer.2016.01.052, 2-s2.0-84957557967.
10.1016/j.ijheatmasstransfer.2016.01.052
Web of Science® Google Scholar
43 Duguma K. A., Makinde O. D., and Enyadene L. G., Stability Analysis of Dual Solutions of Convective Flow of Casson Nanofluid Past a Shrinking/Stretching Slippery Sheet With Thermophoresis and Brownian Motion in Porous Media, Journal of Mathematics. (2023) 2023, 25, https://doi.org/10.1155/2023/5954860, 5954860.
10.1155/2023/5954860
Web of Science® Google Scholar
44 Tulu A. and Ibrahim W., Effects of Second-Order Slip Flow and Variable Viscosity on Natural Convection Flow of (CNTs-Fe₃O₄) Water Hybrid Nanofluids due to Stretching Surface, Mathematical Problems in Engineering. (2021) 2021, 18, 8407194.
10.1155/2021/8407194
Web of Science® Google Scholar
45 Tadesse F. B., Makinde O. D., and Enyadene L. G., Mixed Convection of a Radiating Magnetic Nanofluid Past a Heated Permeable Stretching/Shrinking Sheet in a Porous Medium, Mathematical Problems in Engineering. (2021) 2021, 21, https://doi.org/10.1155/2021/6696748, 6696748.
10.1155/2021/6696748
Web of Science® Google Scholar
46 Bég O. A., B V., and Ray A. K., et al.Homotopy Simulation of Dissipative Micropolar Flow and Heat Transfer From a Two-Dimensional Body With Heat Sink Effect: Applications in Polymer Coating, Chemical and Biochemical Engineering Quarterly. (2020) 34, no. 4, 257–275, https://doi.org/10.15255/CABEQ.2020.1849.
10.15255/CABEQ.2020.1849
CAS Web of Science® Google Scholar
47 Ghotbi A. R., Homotopy Analysis Method for Solving the MHD Flow Over a Non-Linear Stretching Sheet, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 6, 2653–2663, https://doi.org/10.1016/j.cnsns.2008.08.006, 2-s2.0-58349112941.
10.1016/j.cnsns.2008.08.006
Web of Science® Google Scholar
48 Nazari N. L., Abd Aziz A. S., David V. D., and Md Ali Z., Heat and Mass Transfer of Magnetohydrodynamics (MHD) Boundary Layer Flow Using Homotopy Analysis Method, MATEMATIKA. (2018) 34, no. 3, 189–201, https://doi.org/10.11113/matematika.v34.n3.1150.
10.11113/matematika.v34.n3.1150
Google Scholar
49 Rasheed H., Rehman A., Sheikh N., and Iqbal S., MHD Boundary Layer Flow of Nanofluid Over a Continuously Moving Stretching Surface, Applied and Computational Mathematics. (2017) 6, no. 6, 265–270, https://doi.org/10.11648/j.acm.20170606.15.
10.11648/j.acm.20170606.15
Google Scholar

All articles

Analyzing Soret and Dufour Effects on MHD Variable Viscosity Casson Nanofluid Flow Past a Stretching Sheet With Heat Source/Sink

Abstract

1. Introduction

2. Mathematical Modeling of the Problem

2.1. The Governing Equations

2.2. Physical Quantities of Engineering

3. Numerical Solutions

4. Results and Discussions

4.1. Velocity Profile With Change of Parameters

4.2. Temperature Profile With Change of Parameters

4.3. Concentration Profile With Change of Parameters

5. Influence of Parameters on the Physical Quantities of Engineering

5.1. Influence of Parameters on the Skin Friction Coefficient

5.2. Influence of Parameters on Local Nusselt Number

5.3. Influence of Parameters on Local Sherwood Number

6. Conclusion and Future Directions

Nomenclature

Greek Symbols

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Analyzing Soret and Dufour Effects on MHD Variable Viscosity Casson Nanofluid Flow Past a Stretching Sheet With Heat Source/Sink

Abstract

1. Introduction

2. Mathematical Modeling of the Problem

2.1. The Governing Equations

2.2. Physical Quantities of Engineering

3. Numerical Solutions

4. Results and Discussions

4.1. Velocity Profile With Change of Parameters

4.2. Temperature Profile With Change of Parameters

4.3. Concentration Profile With Change of Parameters

5. Influence of Parameters on the Physical Quantities of Engineering

5.1. Influence of Parameters on the Skin Friction Coefficient

5.2. Influence of Parameters on Local Nusselt Number

5.3. Influence of Parameters on Local Sherwood Number

6. Conclusion and Future Directions

Nomenclature

Greek Symbols

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information